Abstract
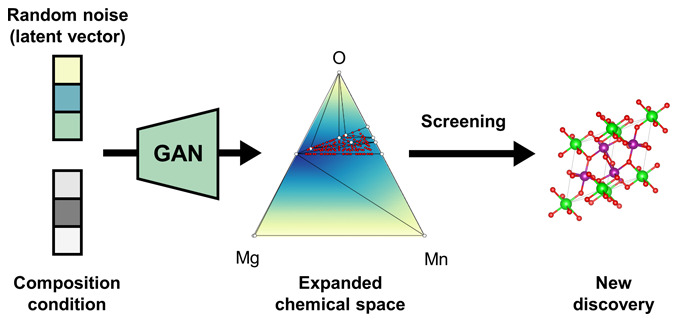
The constant demand for novel functional materials calls for efficient strategies to accelerate the materials discovery, and crystal structure prediction is one of the most fundamental tasks along that direction. In addressing this challenge, generative models can offer new opportunities since they allow for the continuous navigation of chemical space via latent spaces. In this work, we employ a crystal representation that is inversion-free based on unit cell and fractional atomic coordinates and build a generative adversarial network for crystal structures. The proposed model is applied to generate the Mg–Mn–O ternary materials with the theoretical evaluation of their photoanode properties for high-throughput virtual screening (HTVS). The proposed generative HTVS framework predicts 23 new crystal structures with reasonable calculated stability and band gap. These findings suggest that the generative model can be an effective way to explore hidden portions of the chemical space, an area that is usually unreachable when conventional substitution-based discovery is employed.
Short abstract
The generative high-throughput screening framework based on GAN in this research can expand chemical space by discovering novel promising photoanode materials in the hidden portion of chemical space.
Introduction
Addressing the worldwide increasing energy demand requires the discovery of novel functional materials by exploring the vast chemical space. An important subspace of chemical space is the space of crystalline materials. The essence of the successful discovery of crystal materials with desired properties depends on the exploration efficiency of chemical space. Two general strategies for this goal are either to use chemical intuition and empirical rules to improve the performance of existing materials or to search general-purpose databases of known materials, such as the experimental inorganic crystal structural database (ICSD).1 The latter method, known as high-throughput virtual screening (HTVS),2,3 has been demonstrated to be quite successful for various applications. Some of them include the discovery of promising photocatalyst materials,4,5 electrode materials for Li-ion batteries,6−8 2D materials,9−11 and porous materials for propylene/propane separation.12 In these examples cited, promising materials have been identified and experimentally verified using computational screening of the experimental database.
Since the currently available experimental crystal databases such as the ICSD1 (∼200 000 structural data) and the Landolt–Bornstein database13 (6836 structural and diverse properties data) are orders of magnitude smaller than the possible chemical space of inorganic crystals, as a way to further expand the search space, the elemental substitution strategy to these known crystals is employed in many HTVS studies. Here, one performs a combinatorial elemental substitution on the existing crystal structural motifs followed by DFT calculations to generate new large computational crystal databases. Some examples of these large-scale computational databases are Materials Project,14 Open Quantum Materials Database (OQMD),15 and AFLOW-lib.16 These large computational databases have been successful in generating many new discoveries in areas such as light-harvesting materials,17 cathode coatings of Li-ion batteries using OQMD,18 and novel antiferromagnetic Heusler compounds using AFLOW-lib.19 Despite these promising results, one fundamental limitation of the substitution-based HTVS approach is that it cannot go beyond the template of existing crystal structures in the database.
Some of the promising methods to explore beyond the known crystal structure motifs include crystal structure prediction (CSP) methods using global optimization,20 and generative models in machine learning. Among various global optimization methods (e.g., basin hopping,21 simulated annealing,22−24 metadynamics,25 minima hopping,26 quasirandom structure search,27,28 and evolutionary algorithm29,30), evolutionary algorithms are widely used in predicting crystal structures since these algorithms are population-based, can find various global and local optima with various initial guesses, and often show more robust searching without being trapped in local minima. Different evolutionary strategies29,30 exist but generally involve two key steps: first, the initialization of structural pool (i.e., population) for the given specific chemical composition and, second, update of the population after evaluating the target property (e.g., formation enthalpy) of each crystal structure using DFT calculations. Several promising results using evolutionary algorithms include the crystal structure predictions for thermodynamically stable tungsten borides,31 Lennard-Jones cluster,32 superhard materials,33 superconductors,34 and various 2D layered materials.35 The quasirandom structure sampling method such as ab initio random structure searching (AIRSS)27,28 is also noteworthy due to its simplicity in quasirandom structure generation with certain rules (e.g., symmetry, volume, and coordination) and their effectiveness to find a global minimum with highly parallel implementation.
Generative models, on the other hand, focus on building a continuous materials vector space (or latent space) to encode the information embedded in the materials data set and use the previously constructed latent space to generate a new data point (i.e., a material). In addition, by building a mapping between the latent space and the property space, an inverse mapping of new materials with a target property can be possible. This approach is a potential solution to the long-sought goal of the community of inverse design.36,37 Even without this the latent-space-property mapping, the new set of materials generated via generative models can be employed as feeder structures for a more unbiased or unstructured sampling of chemical space by means of HTVS. Since the generated materials can have completely different structures and compositions from the known materials, this generative-HTVS approach can also lead to novel discoveries that are not possible using conventional HTVS limited by the existing crystal databases. This latter approach, a crystal generative model followed by HTVS, is the subject of this work.
Two of the most popular generative models in chemistry are the variational autoencoder (VAE)38 and generative adversarial networks (GAN).39−43 VAE typically consists of two deep neural networks (i.e., encoder and decoder) and explicitly constructs the latent space using known prior distributions such as a Gaussian distribution. The encoder network encodes the chemical space into a low-dimensional latent space, and the decoder network performs the inverse mapping that generates material structures from it. On the other hand, a GAN uses a decoder (or generator) and discriminator to learn the materials data distribution implicitly. We will further describe the framework in the Composition-Conditioned Crystal GAN section. In both VAE and GAN approaches, a key component of crystal structural generative models is the invertibility from material representation (features) to real structure of material since the features generated from the latent vector should eventually be inverted back to the real structure of material in order to confirm the generated material.44
Although many representations, such as those based on fragment descriptors or graph-based encoding for crystal structures,45,46 were proposed with great promise for predicting key properties of materials (e.g., formation energy, energy above the convex hull, band gap, bulk moduli, etc.), most of these descriptors and representations are not invertible (or have not been demonstrated to be invertible) to the real 3D structure. Thus, constructing an invertible representation is still an important task for developing a crystal structure generative model. One of the first suggested representations to encode crystal structures was a 3D-image representation37 which led to the first generative model (iMatGen) for inorganic solids, which employed a VAE architecture. A similar approach was also proposed by Hoffmann et al.47 by using 3D atomic density representations and VAE, in which an additional U-net network was employed to classify element information from the generated 3D atomic density. Kim et al.48 proposed a WGAN-based generative model to discover new zeolite materials with desired energy and heat of adsorption. While these 3D voxel image representations opened the door to the generative modeling of the inorganic crystals, there is room for improvements for practical applications. Some of the challenges to overcome using this approach include the following: (1) Inverting representations to materials structures requires user-defined postprocessing. (2) the unit cell size of the crystal material is limited by the cubically scaling three-dimensional grids. (3) representations are memory-intensive, leading to long training time. Finally, (4) images are inherently not translational-, rotational-, and supercell-invariant.
In this work, we use a crystal representation that is inversion-free with a low memory requirement (by a factor of 400 compared to the 3D voxel representation used in iMatGen,37 for example). We represent the crystal structure as a set of atomic coordinates and cell parameters, inspired by “point cloud”49−53 used for image classification and segmentation in machine-learning fields, where objects are considered as a set of points and vectors with 3D-coordinates. As an application, we construct a GAN to generate new crystal structures with a desired chemical composition and apply it to the Mg–Mn–O ternary system. The Pourbaix stability and band gaps of these materials are then evaluated to find a promising photoanode material for water splitting in the HTVS manner.4 The employed generative-HTVS predicts 23 novel Mg–Mn–O structures as a potential photoanode which could not have been found using the conventional substitution-based database enumeration approach.
Representation
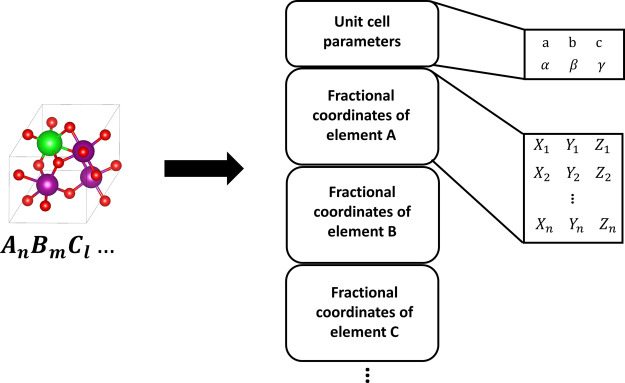
To encode the crystal structure, we employ a 2D matrix representation inspired by a “point cloud”50 which includes both unit cell and fractional coordinates of each atom in the unit cell where the permutational invariance is imposed by symmetry operation used in network encoding the proposed 2D representation (see the Composition-Conditioned Crystal GAN section for model detail). Since the representation is the material structure itself, there is no need for the inversion from the representation to the material. One limitation is the lack of translational, rotational, and supercell invariances (i.e., invariance under the repeating of the unit cells with respect to the lattice vectors) of the representation, and we address them by data augmentation as outlined later. The representation is summarized graphically in Figure 1. Since our representation only requires the atomic coordinates and cell information, it requires almost no preparation and memory cost to store the raw input data, in contrast to the 3D voxel representations which require substantial memory space to store the grid data.
Figure 1.
Point cloud representation of crystal structure. The representation is composed of unit cell parameters and the sets of rescaled fractional coordinates of atoms.
We note that a similar representation was recently used to generate new ternary hydride structures by learning their binary counterparts with a cross-domain learning strategy.54 Interestingly, the method generated the structures of a more complex domain with reasonable interatomic distances by imposing constraints in the training process. However, it differs from our work in that it is a cross domain model: generating structures of a more complex domain (ternary) from the structures of a less complex domain (binary). More representations for solid-state materials are surveyed elsewhere.55
Training Data Set and Data Preprocessing
As mentioned previously, for an application of the proposed GAN model for crystal structure generation, we considered the ternary Mg–Mn–O system to generate new crystal structures of various compositions. The training set for the Mg–Mn–O system was constructed using the elemental substitution of the ternary compounds in the Materials Project (MP) database.56 After removing duplicates, we retain a total of 1240 unique structures with 112 compositions in the initial training set. We note that this data set has the data imbalance in the composition and affine invariance issues such as supercell, translation, and rotation. To address them, we used data augmentation, which is a commonly used technique in the machine-learning field to alleviate such a data imbalance and invariance problem.57−61 Specifically, we added the supercell structures as well as the structures in which translational and rotational (i.e., swapping the axes of the unit cell) operations are applied until these augmentations yield 1000 structures for each composition. Since the original training data set includes 112 Mg–Mn–O compositions, a total of 112 000 Mg–Mn–O structures were used for the training of the current generative model. In addition, for the robust training of the classifier, when the training data was put in the models, atomic permutation operations were randomly applied to training data. Information for the V–O data set is described in Section S6 in the Supporting Information, SI. The learning curve of the composition-conditioned crystal GAN and the effects of data augmentation for addressing symmetry invariance are described in Sections S3 and S7 in the SI, respectively. Compared to a model without data augmentation, the analyses in Figure S11 show that data augmentation clearly improves the model’s ability to recognize the same materials represented in different input features (translated, rotated, or supercell repeated) as identical.
Composition-Conditioned Crystal GAN
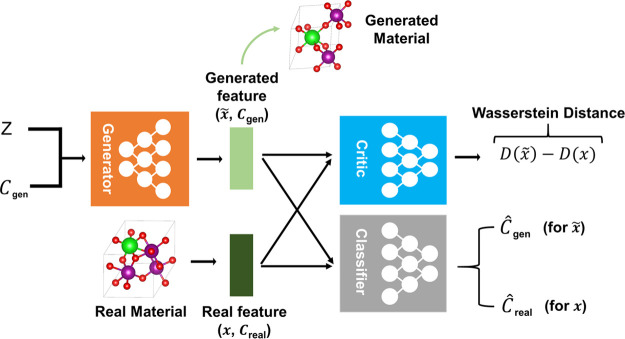
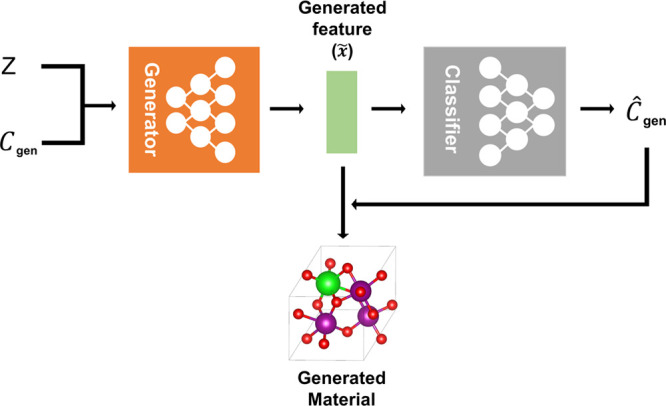
Our GAN model consists of three network components: a generator, a critic, and a classifier as shown in Figure 2. The generator takes the random Gaussian noise vector (Z) and one-hot encoded composition vector (Cgen) as the input to generate new 2D-representations. The one-hot encoded composition vector is used as a condition to generate materials with target composition. The critic computes the Wasserstein distance which represents dissimilarity between the true and trained data distributions, and by reducing this distance the generator would generate more realistic materials. The critic network is composed of three-shared multilayers perceptions (MLPs) followed by average pooling layers to ensure the permutation invariance under the reordering of points in the 2D-representation.50 We note that the permutation invariance under the reordering of input is satisfied by using shared weight parameters and average pooling since the averaged value is unchanged under the change of orders. The classifier network, which outputs the composition vector from the input 2D-representation, is used to ensure that the generated new materials meet the given composition condition. The loss of the classifier is back-propagated to the generator only if the generated 2D-representation (x̃) is taken as input. More details on the architecture of each neural network, hyperparameters for the model, and loss function are described in Section S2 of the SI.
Figure 2.
Composition-Conditioned Crystal GAN proposed in this work for inorganic crystal design. Z, Cgen, and Creal denote a random input noise, user-desired composition condition, and composition of real material, respectively. The variables x̃ and x denote the feature (representation) of generated and real materials, respectively. Ĉgen and Ĉreal denote the predicted composition of the generated and real features, respectively. D(x) is the critic function also known as the critic network.
Results and Discussion
Comparison with iMatGen
Before applying the current model to the Mg–Mn–O system, we first compared the results on the V–O system that was employed in the iMatGen37 work, which represents the first generative model for inorganic crystal structures, and therefore, it is a useful baseline to explore. After using a data-augmented version of the V–O training data, we generated samples of V3O4, V4O5, V5O6, V5O8, and V6O7 structures to compare the chemical space generated from the iMatGen based on VAE. About 40% of the metastable polymorphs of V–O (Ehull ≤ 200 meV/atom) discovered by iMatGen were rediscovered by the current GAN model, indicating some similarity in the latent space trained by each generative model. The remaining 60% difference in the two (VAE and GAN) generative models can thus be interpreted as a difference in the latent space structure or sampling method in each generative model. Particularly, in the V3O4 and V6O7 composition, the present model generated more stable polymorphs than the most stable ones generated via iMatGen. Thus, the performance of the current coordinate-based GAN model seems comparable to that of iMatGen. Given that the current model can sample the compounds with user-desired composition with various invariances also addressed for a larger crystal unit cell, it can be particularly useful for discovering materials with specific compositions. The other training details and the results for the V–O system are summarized in Section S6 in the SI.
Generative High-Throughput Screening of Ternary Mg–Mn–O Photoanode Materials
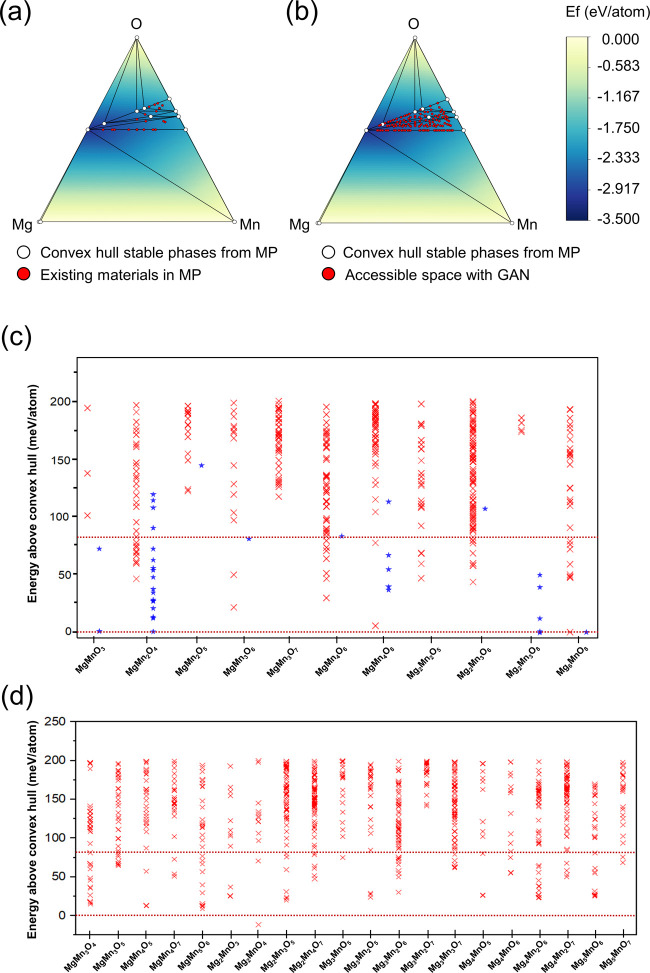
We generated ternary Mg–Mn–O materials and evaluated their photoanode properties to find structures with an improved performance. A previous study4 demonstrated that Mn oxides combined with Mg resulted in reasonable catalytic activity but with relatively weak aqueous stability in experimental conditions (pH and voltage). Thus, to further enhance the aqueous stability, a computational HTVS study based on an elemental substitution of the MP database (total 7356 candidates) was previously performed which resulted in a new discovery of Mg2MnO4 with reasonable stability and activity (also experimentally verified).56 In this work, we apply the proposed generative model to perform generative-HTVS to find new Mg–Mn–O structures beyond the existing structural motifs in the database. To achieve this, first we set total 133 candidate compositions (see Figure 4b) that meet the condition of the Mn oxidation state (2 ≤ OSMn ≤ 4), which are expanded from the chemical space consisting of existing materials (see Figure 4a). Among 133 compositions, we selected a total of 31 compositions (11 compositions included in MP, and 20 compositions not included in MP) by considering the number of atoms in the unit cell due to the computational cost of DFT. Then, we sampled a total of 9300 Mg–Mn–O structures using the proposed crystal GAN: 3300 structures (300 structures in 11 compositions included in MP, see Figure 4c) and 6000 structures (300 structures in 20 new compositions not in MP, see Figure 4d). The process of sampling materials is described in Figure 3. These generated crystal structures are then fed to the DFT calculations for property evaluation.
Figure 4.
Phase diagram and DFT calculated thermodynamic stability (i.e., the energy above the convex hull) for the generated Mg–Mn–O materials. Ternary phase diagram of the Mg–Mn–O system constructed using the convex hull stable phases taken from the materials project database (green circle), including (a) metastable Mg–Mn–O compositions (red circle) taken from materials project or (b) possible compositions that can be explored by our proposed generative model. The stability of the crystal structure in the form of the energy above the convex hulls is computed using DFT for (c) 11 compositions included in the MP database, and (d) 20 new compositions not in the MP database. Red crosses are the generated materials with composition-conditioned, and blue stars in part c correspond to the materials in the MP database. (There are no metastable (Ehull ≤ 200 meV/atom) structures having Mg2Mn2O5 composition in MP database.) The horizontal dotted red lines represent 80 and 0 meV/atom, respectively.
Figure 3.
Schematic of the generation process for crystals with the desired composition. The composition of generated material is determined by the output of the classifier network.
The energy above hull (formation stability) of the generated materials is first summarized in Figure 4c. Among the 3300 newly generated materials for the existing compositions in MP (Figure 4c), 368 Mg–Mn–O materials are predicted as theoretically metastable (i.e., Ehull ≤ 200 meV/atom, red crosses in Figure 4c) where 35 structures are considered as potentially synthesizable62 (i.e., Ehull ≤ 80 meV/atom). Among those 368 newly generated materials with Ehull ≤ 200 meV/atom, 60 of them are the same as those discovered by the previous HTVS on the 7500 substituted data set.56 In particular, for the MgMn4O8 composition, the current model-generated structure is very close to the convex hull (i.e., Ehull = 5 meV/atom), much more stable than all the related polymorphs found in MP. This shows that the present crystal generative model can discover new stable compounds missed out by conventional substitution-based methods.
The formation stability for the compositions that are not in the MP database is next summarized in Figure 4d. Among the 6000 generated structures, 753 Mg–Mn–O materials are predicted as theoretically metastable (i.e., Ehull ≤ 200 meV/atom, red crosses in Figure 4d) where 113 structures are considered as potentially synthesizable (i.e., Ehull ≤ 80 meV/atom). In particular, for Mg2MnO4, a composition not in MP, we discovered a structure corresponding to the convex hull minimum indicating that our model can discover an entirely new ground state material within the DFT accuracy.
Since Mg–Mn–O compounds are considered here as photoanode materials, their Pourbaix stability (ΔGpbx) and the band gaps (EgHSE) are further considered as the next screening criteria for those newly generated structures that satisfy Ehull ≤ 80 meV/atom (35 materials in Figure 4c and 113 materials in Figure 4d). The Pourbaix hull represents the stability of a material in an aqueous electrochemical environment at a given pH and electrochemical condition63 (i.e., difference of the free energy from the ground state). We evaluated such aqueous electrochemical stability described by the minimum of Pourbaix hull Gibbs free energy at 1.5 V vs RHE over the 0–14 pH range, ΔGpbx, which was calculated as implemented in the Pymatgen64 module (also refer to Noh et al.56 for computational details). Therefore, a material with low ΔGpbxmin represents a (meta-)stable phase in an aqueous electrochemical environment, and for those materials meeting ΔGpbx(Eform) ≤ 0.8 eV/atom, the HSE calculations are further performed to calculate the band gap.
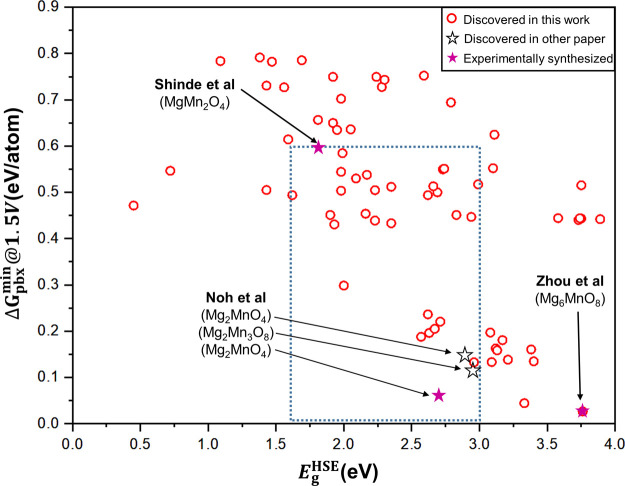
Following Shinde et al.,4 we finally identified 28 Mg–Mn–O materials (Figure 5) with ΔGpbxmin(Eform) ≤ 0.59 eV/atom and 1.6 eV≤ Eg ≤ 3.0 eV as a potential photoanode material. Out of these 28 Mg–Mn–O materials, 14 materials correspond to new compositions not included in database, meaning that those are entirely new structures. The remaining 14 materials are composed of 8 existing compositions in the database, among which 5 of them correspond to the previous findings by Noh et al.56 based on substitutional HTVS; we have used the Structure Matcher function in the Pymatgen python package to estimate the structural similarity, and more detailed discussion is described in Section S5.2 in the SI. Experimentally, in MgMn2O4,4 Mg6MnO8,65 and Mg2MnO456 compositions, promising photoanode materials were synthesized. We found several promising photoanode materials in many other compositions which could not be considered in conventional HTVS (see Figure S9). Some of the 23 newly found photoanode candidates (14 materials in new compositions, and 9 materials in existing compositions) are depicted in Section S5.3 in the SI.
Figure 5.
Pourbaix stabilities and HSE band gap energies of stable structures generated by the proposed crystal GAN model (red circles). The dashed blue box is the target region for the promising photoanode material. Stars represent the promising photoanode materials discovered by other previous works (i.e., conventional HTVS),4,56,65 and purple stars are materials synthesized experimentally.
Discussion
The proposed generative framework can be compared with crystal structure prediction methods using evolutionary algorithms29,30 and quasirandom searching (i.e., AIRSS27,28). As briefly described in the Introduction, evolutionary algorithms search an optimal state (material) by repeating the series of specific evolutionary processes rather than learning the distribution of the whole target chemical space as in GAN. The quality of the results (e.g., how close the final structure is to the global minimum and how diverse the local minimum structures are) and computational cost to obtain the optimal state might be sensitive to this initialization in the case of exploring entirely new chemical space as evolutionary algorithms start from a randomly initialized population. In the case of the quasirandom searching approach,27,28 it randomly samples the structures to maximize the exploration but usually steered by human-intuitive constraints, such as symmetry and coordination numbers, toward more realistic structures. In general, the large computational cost to find new materials would be a main challenge of most global optimization-based strategies, so there have been additional efforts to reduce the computational cost of evaluating property by assisting or replacing the ab initio approach via the property predictive machine learning models.66
Compared to the aforementioned global optimization strategies which explore new local minima by utilizing the previous trajectories on the configurational space (i.e., on-the-fly approach), the generative framework generates new data (material) from the continuous latent space that encodes the information on the entire chemical space used in the training stage. This means that the efficiency and accuracy of structure prediction are largely dependent on the structural diversity of the training data set. Of course, the computational cost to prepare the training data set and optimize the generated structures is also a burden for the present generative model-based prediction as in most other global optimization techniques. Thus, the methods based on global optimization and the generative-HTVS seem comparable and complementary in the sense that the former is efficiently searching for a global minimum by learning the geometric information on the potential energy surface (or functional manifold) with specific structure generation rules, while the latter is learning the whole distribution of crystal structures in the training data set and then sample the new data from this machine-learned distribution.
There are several limitations and promising directions for the proposed composition-based generative framework to be used as a general-purpose inverse design. The current model generates new crystal structures with only the target composition conditioned, and thus, subsequent HTVS of properties are required to make a final functional discovery. To be a truly inverse design in which the machine generates the functional material directly without HTVS, one thus should add to the composition other materials properties (e.g., band gap energy, dielectric constant, and etc.) as input conditions to guide the materials discovery. Another way of achieving the inverse design goals would be to combine the generative process with reinforcement learning.40 In addition, while the current model can produce ternary crystal compounds, extending it to quaternary and higher-order compounds would be straightforward by adding more rows or channels in the input format, or by separately adding a segmentation network to classify elemental information (although preparing the training data for higher-order compounds would be more challenging due to a combinatorial complexity when including more than 4 elements). Other important aspects in need of further developments are the quantitative metrics related to the novelty of generated samples compared to the existing data, as well as the uncertainty (or validity) of the generated data. The synthesizability prediction of the newly generated materials would also be an essential ingredient for the practical inverse design of crystals for experimental verification.
Conclusions
We proposed to employ the generative adversarial network (GAN) for crystal structure generation using a coordinate-based (and therefore inversion-free) crystal representation inspired by point clouds. By conditioning the network with the crystal composition, our model can generate materials with a desired chemical composition. As an application, we applied it to generate new Mg–Mn–O ternary compounds to find potential photoanode materials and discovered 23 new crystal compounds with reasonable stability in an aqueous environment and band gap. Two of the structures (in MgMn4O8 and Mg2MnO4) corresponded to the convex hull minimum, a stable new phase, or very close to it within the DFT accuracy. We expect that the proposed model can be extended to a general-purpose inverse design by incorporating materials properties into the model in future work.
Acknowledgments
We acknowledge generous financial support from NRF Korea (NRF-2017R1A2B3010176).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.0c00426.
Additional data and figures including schematics, a learning curve, structures, DFT calculated formation energies, and an output distribution (PDF)
Author Contributions
⊥ S.K. and J.N. contributed equally to this work.
The authors declare no competing financial interest.
Notes
Source codes and the datasets used to train the models are available at https://github.com/kaist-amsg/Composition-Conditioned-Crystal-GAN.
Supplementary Material
References
- Inorganic crystal structure database. http://icsd.fiz-karlsruhe.de.
- Gómez-Bombarelli R.; Aguilera-Iparraguirre J.; Hirzel T. D.; Duvenaud D.; Maclaurin D.; Blood-Forsythe M. A.; Chae H. S.; Einzinger M.; Ha D.-G.; Wu T. Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach. Nat. Mater. 2016, 15 (10), 1120. 10.1038/nmat4717. [DOI] [PubMed] [Google Scholar]
- Pyzer-Knapp E. O.; Suh C.; Gómez-Bombarelli R.; Aguilera-Iparraguirre J.; Aspuru-Guzik A. What is high-throughput virtual screening? A perspective from organic materials discovery. Annu. Rev. Mater. Res. 2015, 45, 195. 10.1146/annurev-matsci-070214-020823. [DOI] [Google Scholar]
- Shinde A.; Suram S. K.; Yan Q.; Zhou L.; Singh A. K.; Yu J.; Persson K. A.; Neaton J. B.; Gregoire J. M. Discovery of manganese-based solar fuel photoanodes via integration of electronic structure calculations, pourbaix stability modeling, and high-throughput experiments. ACS Energy Lett. 2017, 2 (10), 2307. 10.1021/acsenergylett.7b00607. [DOI] [Google Scholar]
- Wu Y.; Lazic P.; Hautier G.; Persson K.; Ceder G. First principles high throughput screening of oxynitrides for water-splitting photocatalysts. Energy Environ. Sci. 2013, 6 (1), 157. 10.1039/C2EE23482C. [DOI] [Google Scholar]
- Jain A.; Hautier G.; Ong S. P.; Moore C. J.; Fischer C. C.; Persson K. A.; Ceder G. Formation enthalpies by mixing GGA and GGA+ U calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84 (4), 045115. 10.1103/PhysRevB.84.045115. [DOI] [Google Scholar]
- Kirklin S.; Chan M. K. Y.; Trahey L.; Thackeray M. M.; Wolverton C. High-throughput screening of high-capacity electrodes for hybrid Li-ion–Li–O 2 cells. Phys. Chem. Chem. Phys. 2014, 16 (40), 22073. 10.1039/C4CP03597F. [DOI] [PubMed] [Google Scholar]
- Kirklin S.; Meredig B.; Wolverton C. High-throughput computational screening of new Li-ion battery anode materials. Adv. Energy Mater. 2013, 3 (2), 252. 10.1002/aenm.201200593. [DOI] [Google Scholar]
- Gorai P.; Toberer E. S.; Stevanović V. Computational identification of promising thermoelectric materials among known quasi-2D binary compounds. J. Mater. Chem. A 2016, 4 (28), 11110. 10.1039/C6TA04121C. [DOI] [Google Scholar]
- Li X.; Zhang Z.; Yao Y.; Zhang H. High throughput screening for two-dimensional topological insulators. 2D Mater. 2018, 5 (4), 045023. 10.1088/2053-1583/aadb1e. [DOI] [Google Scholar]
- Mounet N.; Gibertini M.; Schwaller P.; Campi D.; Merkys A.; Marrazzo A.; Sohier T.; Castelli I. E.; Cepellotti A.; Pizzi G. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotechnol. 2018, 13 (3), 246. 10.1038/s41565-017-0035-5. [DOI] [PubMed] [Google Scholar]
- Yeo B. C.; Kim D.; Kim H.; Han S. S. High-throughput screening to investigate the relationship between the selectivity and working capacity of porous materials for propylene/propane adsorptive separation. J. Phys. Chem. C 2016, 120 (42), 24224. 10.1021/acs.jpcc.6b08177. [DOI] [Google Scholar]
- Springer Materials–The Landolt-Börnstein-Database. https://materials.springer.com/.
- Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1 (1), 011002. 10.1063/1.4812323. [DOI] [Google Scholar]
- Kirklin S.; Saal J. E.; Meredig B.; Thompson A.; Doak J. W.; Aykol M.; Rühl S.; Wolverton C. The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies. NPJ. Comput. Mater. 2015, 1, 15010. 10.1038/npjcompumats.2015.10. [DOI] [Google Scholar]
- Curtarolo S.; Setyawan W.; Wang S.; Xue J.; Yang K.; Taylor R. H.; Nelson L. J.; Hart G. L. W.; Sanvito S.; Buongiorno-Nardelli M. AFLOWLIB. ORG: A distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 2012, 58, 227. 10.1016/j.commatsci.2012.02.002. [DOI] [Google Scholar]
- Castelli I. E.; Hüser F.; Pandey M.; Li H.; Thygesen K. S.; Seger B.; Jain A.; Persson K. A.; Ceder G.; Jacobsen K. W. New light-harvesting materials using accurate and efficient bandgap calculations. Adv. Energy Mater. 2015, 5 (2), 1400915. 10.1002/aenm.201400915. [DOI] [Google Scholar]
- Aykol M.; Kim S.; Hegde V. I.; Snydacker D.; Lu Z.; Hao S.; Kirklin S.; Morgan D.; Wolverton C. High-throughput computational design of cathode coatings for Li-ion batteries. Nat. Commun. 2016, 7 (1), 1. 10.1038/ncomms13779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balluff J.; Diekmann K.; Reiss G.; Meinert M. High-throughput screening for antiferromagnetic Heusler compounds using density functional theory. Phys. Rev. Mater. 2017, 1 (3), 034404. 10.1103/PhysRevMaterials.1.034404. [DOI] [Google Scholar]
- Oganov A. R.; Pickard C. J.; Zhu Q.; Needs R. J. Structure prediction drives materials discovery. Nat. Rev. Mater. 2019, 4 (5), 331. 10.1038/s41578-019-0101-8. [DOI] [Google Scholar]
- Wales D. J.; Doye J. P. K. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 1997, 101 (28), 5111. 10.1021/jp970984n. [DOI] [Google Scholar]
- Kirkpatrick S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984, 34 (5–6), 975. 10.1007/BF01009452. [DOI] [Google Scholar]
- Schön J. C.; Jansen M. First step towards planning of syntheses in solid-state chemistry: determination of promising structure candidates by global optimization. Angew. Chem., Int. Ed. Engl. 1996, 35 (12), 1286. 10.1002/anie.199612861. [DOI] [Google Scholar]
- Wille L. T. Searching potential energy surfaces by simulated annealing. Nature 1986, 324 (6092), 46. 10.1038/324046a0. [DOI] [Google Scholar]
- Martoňák R.; Laio A.; Bernasconi M.; Ceriani C.; Raiteri P.; Zipoli F.; Parrinello M. Simulation of structural phase transitions by metadynamics. Z. Kristallogr. Cryst. Mater. 2005, 220 (5/6), 489. 10.1524/zkri.220.5.489.65078. [DOI] [Google Scholar]
- Goedecker S. Minima hopping: An efficient search method for the global minimum of the potential energy surface of complex molecular systems. J. Chem. Phys. 2004, 120 (21), 9911. 10.1063/1.1724816. [DOI] [PubMed] [Google Scholar]
- Deringer V. L.; Pickard C. J.; Csányi G. Data-driven learning of total and local energies in elemental boron. Phys. Rev. Lett. 2018, 120 (15), 156001. 10.1103/PhysRevLett.120.156001. [DOI] [PubMed] [Google Scholar]
- Pickard C. J.; Needs R. J. Ab initio random structure searching. J. Phys.: Condens. Matter 2011, 23 (5), 053201. 10.1088/0953-8984/23/5/053201. [DOI] [PubMed] [Google Scholar]
- Wang Y.; Lv J.; Zhu L.; Ma Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183 (10), 2063. 10.1016/j.cpc.2012.05.008. [DOI] [Google Scholar]
- Glass C. W.; Oganov A. R.; Hansen N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Commun. 2006, 175 (11–12), 713. 10.1016/j.cpc.2006.07.020. [DOI] [Google Scholar]
- Li Q.; Zhou D.; Zheng W.; Ma Y.; Chen C. Global structural optimization of tungsten borides. Phys. Rev. Lett. 2013, 110 (13), 136403. 10.1103/PhysRevLett.110.136403. [DOI] [PubMed] [Google Scholar]
- Lv J.; Wang Y.; Zhu L.; Ma Y. Particle-swarm structure prediction on clusters. J. Chem. Phys. 2012, 137 (8), 084104. 10.1063/1.4746757. [DOI] [PubMed] [Google Scholar]
- Lyakhov A. O.; Oganov A. R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO 2. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84 (9), 092103. 10.1103/PhysRevB.84.092103. [DOI] [Google Scholar]
- Hu C.-H.; Oganov A. R.; Zhu Q.; Qian G.-R.; Frapper G.; Lyakhov A. O.; Zhou H.-Y. Pressure-induced stabilization and insulator-superconductor transition of BH. Phys. Rev. Lett. 2013, 110 (16), 165504. 10.1103/PhysRevLett.110.165504. [DOI] [PubMed] [Google Scholar]
- Wang Y.; Miao M.; Lv J.; Zhu L.; Yin K.; Liu H.; Ma Y. An effective structure prediction method for layered materials based on 2D particle swarm optimization algorithm. J. Chem. Phys. 2012, 137 (22), 224108. 10.1063/1.4769731. [DOI] [PubMed] [Google Scholar]
- Gómez-Bombarelli R.; Wei J. N.; Duvenaud D.; Hernández-Lobato J. M.; Sánchez-Lengeling B.; Sheberla D.; Aguilera-Iparraguirre J.; Hirzel T. D.; Adams R. P.; Aspuru-Guzik A. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 2018, 4 (2), 268. 10.1021/acscentsci.7b00572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noh J.; Kim J.; Stein H. S.; Sanchez-Lengeling B.; Gregoire J. M.; Aspuru-Guzik A.; Jung Y. Inverse Design of Solid-State Materials via a Continuous Representation. Matter 2019, 1 (5), 1370. 10.1016/j.matt.2019.08.017. [DOI] [Google Scholar]
- Kingma D. P.; Welling M.. Auto-encoding variational bayes. arXiv, 2013, arXiv:1312.6114. http://arXiv.org/abs/1312.6114.
- Putin E.; Asadulaev A.; Ivanenkov Y.; Aladinskiy V.; Sanchez-Lengeling B.; Aspuru-Guzik A.; Zhavoronkov A. Reinforced adversarial neural computer for de novo molecular design. J. Chem. Inf. Model. 2018, 58 (6), 1194. 10.1021/acs.jcim.7b00690. [DOI] [PubMed] [Google Scholar]
- Sanchez-Lengeling B.; Outeiral C.; Guimaraes G. L.; Aspuru-Guzik A.. Optimizing distributions over molecular space. An objective-reinforced generative adversarial network for inverse-design chemistry (ORGANIC). ChemRxiv, 2017. https://chemrxiv.org/articles/ORGANIC_1_pdf/5309668.
- Guimaraes G. L.; Sanchez-Lengeling B.; Outeiral C.; Farias P. L. C.; Aspuru-Guzik A.. Objective-reinforced generative adversarial networks (organ) for sequence generation models. arXiv, 2017, arXiv:1705.10843. http://arXiv.org/abs/1705.10843.
- Zhavoronkov A.; Ivanenkov Y. A.; Aliper A.; Veselov M. S.; Aladinskiy V. A.; Aladinskaya A. V.; Terentiev V. A.; Polykovskiy D. A.; Kuznetsov M. D.; Asadulaev A. Deep learning enables rapid identification of potent DDR1 kinase inhibitors. Nat. Biotechnol. 2019, 37 (9), 1038. 10.1038/s41587-019-0224-x. [DOI] [PubMed] [Google Scholar]
- Goodfellow I.; Pouget-Abadie J.; Mirza M.; Xu B.; Warde-Farley D.; Ozair S.; Courville A.; Bengio Y.. Generative adversarial nets. NIPS 2014, 2672; http://papers.nips.cc/paper/5423-generative-adversarial-nets.
- Noh J.; Gu G. H.; Kim S.; Jung Y.. Machine-Enabled Inverse Design of Inorganic Solid Materials: Promises and Challenges. Chemical Science 2020, in press. 10.1039/D0SC00594K [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isayev O.; Oses C.; Toher C.; Gossett E.; Curtarolo S.; Tropsha A. Universal fragment descriptors for predicting properties of inorganic crystals. Nat. Commun. 2017, 8 (1), 1. 10.1038/ncomms15679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie T.; Grossman J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 2018, 120 (14), 145301. 10.1103/PhysRevLett.120.145301. [DOI] [PubMed] [Google Scholar]
- Hoffmann J.; Maestrati L.; Sawada Y.; Tang J.; Sellier J. M.; Bengio Y.. Data-Driven Approach to Encoding and Decoding 3-D Crystal Structures. arXiv, 2019, arXiv:1909.00949. http://arXiv.org/abs/1909.00949.
- Kim B.; Lee S.; Kim J. Inverse design of porous materials using artificial neural networks. Sci. Adv. 2020, 6 (1), eaax9324. 10.1126/sciadv.aax9324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu W.; Qi Z.; Fuxin L.. Pointconv: Deep convolutional networks on 3d point clouds. arXiv, 2019, arXiv:1811.07246. https://arxiv.org/abs/1811.07246.
- Qi C. R.; Su H.; Mo K.; Guibas L. J.. Pointnet: Deep learning on point sets for 3d classification and segmentation. CVPR 2017, 652; http://openaccess.thecvf.com/content_cvpr_2017/html/Qi_PointNet_Deep_Learning_CVPR_2017_paper.html. [Google Scholar]
- Lang A. H.; Vora S.; Caesar H.; Zhou L.; Yang J.; Beijbom O.. Pointpillars: Fast encoders for object detection from point clouds. arXiv, 2019, arXiv:1812.05784. https://arxiv.org/abs/1812.05784.
- Li J.; Chen B. M.; Hee Lee G.. So-net: Self-organizing network for point cloud analysis. arXiv, 2018, arXiv:1803.04249. https://arxiv.org/abs/1803.04249.
- Zhou Y.; Tuzel O.. Voxelnet: End-to-end learning for point cloud based 3d object detection. arXiv, 2018, arXiv:1711.06396. https://arxiv.org/abs/1711.06396.
- Nouira A.; Sokolovska N.; Crivello J.-C.. Crystalgan: learning to discover crystallographic structures with generative adversarial networks. arXiv, 2018, arXiv:1810.11203. http://arXiv.org/abs/1810.11203.
- Schmidt J.; Marques M. R. G.; Botti S.; Marques M. A. L. Recent advances and applications of machine learning in solid-state materials science. NPJ. Comput. Mater. 2019, 5 (1), 1. 10.1038/s41524-019-0221-0. [DOI] [Google Scholar]
- Noh J.; Kim S.; ho Gu G.; Shinde A.; Zhou L.; Gregoire J. M.; Jung Y. Unveiling new stable manganese based photoanode materials via theoretical high-throughput screening and experiments. ChemComm. 2019, 55 (89), 13418. 10.1039/C9CC06736A. [DOI] [PubMed] [Google Scholar]
- Fawzi A.; Samulowitz H.; Turaga D.; Frossard P. Adaptive data augmentation for image classification. IEEE 2016, 3688. 10.1109/ICIP.2016.7533048. [DOI] [Google Scholar]
- Furukawa H.Deep learning for target classification from SAR imagery: Data augmentation and translation invariance. arXiv, 2017, arXiv:1708.07920. https://arxiv.org/abs/1708.07920.
- Thickstun J.; Harchaoui Z.; Foster D. P.; Kakade S. M.. Invariances and data augmentation for supervised music transcription. arXiv, 2018, arXiv:1711.04845. https://arxiv.org/abs/1711.04845.
- Ding J.; Chen B.; Liu H.; Huang M. Convolutional neural network with data augmentation for SAR target recognition. IEEE Geosci. Remote. Sens. Lett. 2016, 13 (3), 364. 10.1109/LGRS.2015.2513754. [DOI] [Google Scholar]
- Hernández-García A.; König P.; Kietzmann T. C.. Learning robust visual representations using data augmentation invariance. arXiv, 2019, arXiv:1906.04547. https://arxiv.org/abs/1906.04547.
- Singh A. K.; Montoya J. H.; Gregoire J. M.; Persson K. A. Robust and synthesizable photocatalysts for CO 2 reduction: a data-driven materials discovery. Nat. Commun. 2019, 10 (1), 443. 10.1038/s41467-019-08356-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A. K.; Zhou L.; Shinde A.; Suram S. K.; Montoya J. H.; Winston D.; Gregoire J. M.; Persson K. A. Electrochemical stability of metastable materials. Chem. Mater. 2017, 29 (23), 10159. 10.1021/acs.chemmater.7b03980. [DOI] [Google Scholar]
- Ong S. P.; Richards W. D.; Jain A.; Hautier G.; Kocher M.; Cholia S.; Gunter D.; Chevrier V. L.; Persson K. A.; Ceder G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314. 10.1016/j.commatsci.2012.10.028. [DOI] [Google Scholar]
- Zhou L.; Shinde A.; Guevarra D.; Richter M. H.; Stein H. S.; Wang Y.; Newhouse P. F.; Persson K. A.; Gregoire J. M. Combinatorial screening yields discovery of 29 metal oxide photoanodes for solar fuel generation. J. Mater. Chem. A 2020, 8 (8), 4239. 10.1039/C9TA13829C. [DOI] [Google Scholar]
- Jennings P. C.; Lysgaard S.; Hummelshøj J. S.; Vegge T.; Bligaard T. Genetic algorithms for computational materials discovery accelerated by machine learning. NPJ. Comput. Mater. 2019, 5 (1), 1. 10.1038/s41524-019-0181-4. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.