Hierarchical dynamics as a macroscopic organizing principle of the human brain

Significance

Accumulating evidence suggests that, during task performance, information is encoded at shorter timescales in primary sensory regions as compared to longer timescales in higher-order cortical regions. These encoding timescales correlate with the timescales of activity within these regions. Here, we test the hypothesis that a hierarchy of activity timescales represents a general organizing principle of brain function. Using functional imaging of the human brain in the eyes-open resting state, we find that the timescales of ongoing activity are hierarchically organized as gradients across the entire cerebral cortex. Further, whole-brain coverage permitted examination of subcortical structures, which exhibited hierarchical timescale gradients parallel to cerebral cortex. Altogether, our results support the existence of hierarchical gradients that globally organize human brain dynamics.

Abstract

Multimodal evidence suggests that brain regions accumulate information over timescales that vary according to anatomical hierarchy. Thus, these experimentally defined “temporal receptive windows” are longest in cortical regions that are distant from sensory input. Interestingly, spontaneous activity in these regions also plays out over relatively slow timescales (i.e., exhibits slower temporal autocorrelation decay). These findings raise the possibility that hierarchical timescales represent an intrinsic organizing principle of brain function. Here, using resting-state functional MRI, we show that the timescale of ongoing dynamics follows hierarchical spatial gradients throughout human cerebral cortex. These intrinsic timescale gradients give rise to systematic frequency differences among large-scale cortical networks and predict individual-specific features of functional connectivity. Whole-brain coverage permitted us to further investigate the large-scale organization of subcortical dynamics. We show that cortical timescale gradients are topographically mirrored in striatum, thalamus, and cerebellum. Finally, timescales in the hippocampus followed a posterior-to-anterior gradient, corresponding to the longitudinal axis of increasing representational scale. Thus, hierarchical dynamics emerge as a global organizing principle of mammalian brains.

Brain activity continuously evolves over a wide range of spatiotemporal scales extending from ∼10²-Hz microcircuit dynamics to infraslow (<0.1 Hz) fluctuations synchronizing large-scale brain networks (1). The identification of large-scale organizing principles provides context for relating this complexity to macroscopic brain functions. Most prior work has sought to examine large-scale variation of oscillatory activity at frequencies >1 Hz (2, 3). However, as viewed from a broadband perspective, neural activity is aperiodic and scale-free, that is, exhibits a 1/f-like spectral characteristic (1, 3–5). Are there general principles describing the functional organization of this activity?

Multimodal evidence suggests that neural dynamics support a hierarchy of cortical functions (6, 7). Thus, dynamics are shaped by increasing temporal windows of sensory information as one moves from early sensory to higher-order cortical regions (7, 8). Importantly, regions deemed to have longer “temporal receptive windows” were subsequently found to exhibit more slowly changing activity (7, 9). Similarly, at a cellular level, Murray et al. (10) found that the single-unit activity autocorrelation function (ACF) decays relatively rapidly in early sensory areas and more slowly in distant cortical regions (see also ref. 11). These results suggest that hierarchical timescales may emerge from properties intrinsic to brain functional anatomy (12, 13).

Indeed, it is now apparent that hierarchy is deeply embedded within the functional architecture of neocortex (14) and, hence, likely shapes dynamics accordingly (12, 15). Yet, while the above-mentioned evidence is derived from selected cortical regions, multimodal evidence supports a global hierarchy of cortical organization, placing at opposing ends early sensorimotor (unimodal) and association (transmodal) regions (16). Moreover, nonneocortical structures also exhibit hierarchically organized functional properties at the macroscale (parallel to neocortex or otherwise) (e.g., refs. 17–19). The possibility emerges that hierarchical dynamics represent a general, intrinsic organizing principle of mammalian brains. Testing this possibility requires brain-wide coverage, which is not feasible with invasive electrophysiology.

Functional MRI (fMRI) provides full-brain coverage, albeit at infraslow frequencies (<0.1 Hz), which fall well below frequencies studied in conventional electrophysiology (5, 20). Nonetheless, in a series of elegant experiments, Hasson, Honey and colleagues have used fMRI [as well as human electrophysiology (9)] to demonstrate both functional relevance and hierarchical structure of infraslow dynamics (7, 8). Indeed, the hierarchical structure of brain dynamics appears temporally scale-invariant (10, 21). Thus, across the broad range of temporal scales over which all regions operate, anatomical hierarchy biases relative regional timescales. Accordingly, temporal structure of large-scale dynamics may be examined via resting-state fMRI (rsfMRI), which measures ongoing brain activity manifesting in fluctuations of the blood oxygen level-dependent (BOLD) signal (22) (and hence is not restricted to task-responsive regions). Such an investigation is further motivated by work suggesting a fundamental relationship between intrinsic timescale and functional connectivity (FC) (12), the conventional measure of interest in rsfMRI research.

Several prior rsfMRI studies have examined regional variation in spectral content (e.g., refs. 23–26). However, these studies have incorporated variable metrics, regions of interest, and behavioral conditions, often with minimal attention to artifact (Discussion), leaving unresolved the question of how infraslow intrinsic timescales vary throughout the brain. Crucially, the possibility of organized timescales within subcortical structures also remains unexplored. Moreover, the relevance of spectral content to FC has typically been assessed by examining the frequency dependence of FC over a broad frequency range (e.g., refs. 27 and 28), or indirectly, by contrasting spectral content of functional systems (e.g., ref. 24). Less attention has been given to a potentially fundamental relationship between infraslow spectral content and FC topology (29), which may be essential to FC generative mechanisms (12). Accordingly, the present study investigates intrinsic timescales from a brain-wide perspective, relating timescale patterns to both large-scale cortico-subcortical functional networks as well as FC topology.

Results

Cortical Dynamics Follow Hierarchical Gradients.

We assessed temporal dynamics in two healthy adult human rsfMRI datasets collected in the awake, eyes-open state. The primary dataset comprises 6-min eyes-open runs collected from a large population (1,139 individuals) (30). A second dataset comprises 10, 30-min eyes-open rsfMRI runs from each of 10 individuals (31). Using the atypically long runs in the secondary dataset, we first confirmed that rsfMRI signals exhibit a scale-free, 1/f-like spectral characteristic across all regions of the brain (4) over nearly two decades (SI Appendix, Fig. S1). Next, regional deviations from this roughly consistent spectral characteristic were assessed in the primary dataset at the group level following denoising according to conventional rsfMRI FC practice (Methods). Intrinsic timescale (cf. correlation length) was characterized at each voxel by the decay of the temporal ACF (10), quantified here as the time taken for the ACF to decay to a value of 0.5 (i.e., half of the full width at half maximum) (Fig. 1A and Methods). We found that intrinsic timescales are organized along spatial gradients extending from (unimodal) sensorimotor regions to (transmodal) association cortex, peaking at regions including medial prefrontal cortex and the temporoparietal junction (7) (Fig. 1B).

Fig. 1.

Hierarchy of intrinsic timescales revealed from fMRI autocorrelation. (A) Intrinsic timescale was estimated for each cortical vertex as the temporal autocorrelation decay during the resting state, quantified as half of the full width at half maximum of the ACF (Methods). (B) Vertex-wise map of mean intrinsic timescale (n = 1,139 subjects).

Hierarchical Gradients Are Prominent outside of Neocortex.

Importantly, prior work on intrinsic timescales has either neglected subcortical structures (e.g., refs. 7, 10, and 12) or has treated each structure as a functional unit (24, 26). Yet, striatum, thalamus, cerebellum, and hippocampus are each heterogeneous in their functional anatomy, which is evident at the resolution of fMRI (e.g., refs. 32–34). Hence, we extended our timescale analysis to these structures. Consistent with prior literature (e.g., refs. 4, 23, and 26), we found that striatum, thalamus, and hippocampus exhibited much higher-frequency content than cerebral cortex, which may in large part reflect relatively lower signal-to-noise ratio (SNR) in these structures (26).

We proceeded to examine timescale variability within each of these structures as well as the cerebellum. We found that each structure exhibited large-scale intrinsic timescale gradients (Fig. 2). Moreover, as in the cerebral cortex, gradients reflected known hierarchical functional organization within each of these structures, with longer timescales in higher-order regions. Thus, timescale gradients in the striatum followed a posterolateral-to-rostromedial progression, broadly corresponding to motor-to-associative/limbic cortical input zones (35–37). Thalamic gradients generally progressed in a ventrolateral-to-dorsomedial pattern, corresponding to approximate locations of first-order versus higher-order nuclei [as well as a recently described within-pulvinar hierarchical functional gradient (38)]. Cerebellar timescales increased along a gradient extending from lobules I–IV toward posterior portions of Crus I/II (as well as lobule IX), matching the dominant functional gradient found within this structure (18, 39). Finally, the hippocampus exhibited a posterior-to-anterior timescale gradient along the longitudinal axis. This parallels the marked decrease in granularity of spatial and temporal representations (19, 34), as well as cellular-level intrinsic frequency within the theta range (40, 41) (see also ref. 42). The present result suggests a similar gradient of intrinsic frequencies at a much coarser spatiotemporal scale. Interpretation of this result should also consider the potential contribution of signal dropout, which is more prominent anteriorly (43, 44). Nonetheless, these large-scale patterns make specific predictions regarding neural dynamics in each of these structures that can be validated in the future via multisite electrophysiological recordings.

Fig. 2.

Hierarchical timescales in nonneocortical structures. Three-dimensional renderings rotated to highlight the major axes of variation in mean intrinsic timescale (n = 1,139 subjects) in the left and right (A) striatum, (B) thalamus, (C) hippocampus, and (D) cerebellum. Timescales are given in seconds. Direction labels indicate dorsal (D), posterior (P), and (anatomical) rightward (R). Three-dimensional maps generated from MNI152 voxel coordinates.

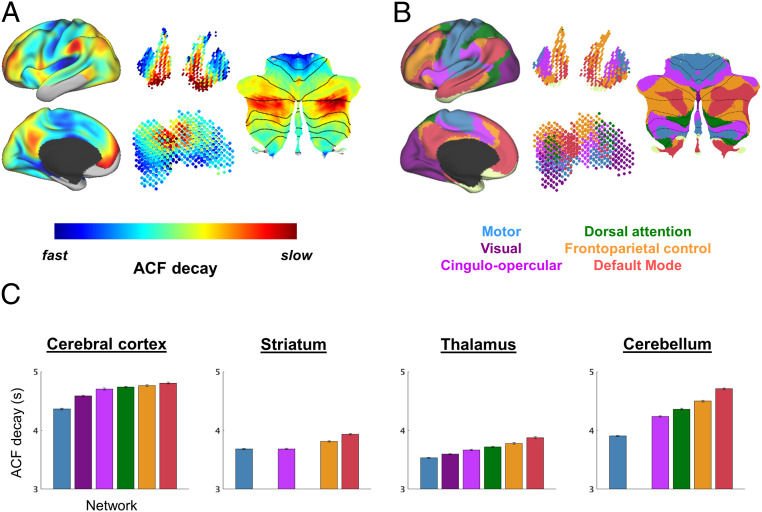
Large-Scale Cortico-Subcortical Networks Exhibit Systematic Spectral Differences.

The cortical topography of intrinsic timescale (Fig. 1) closely resembles recently described hierarchical gradients in FC, in which modular large-scale functional networks occupy stereotypical positions (45) (see also refs. 39 and 46). Accordingly, to determine spectral variability among discrete functional networks, we quantified mean autocorrelation decay within six canonical networks (30). We found systematic spectral differences among networks corresponding to their hierarchical relationships (45) (Fig. 3 and SI Appendix, Fig. S2). The observed ordering of timescales closely followed the single-unit results reported by Murray et al. (10), but in a much slower and compressed range. Thus, absolute timescales reported here are an order of magnitude slower and have a smaller relative spread in comparison with single-unit timescales.

Fig. 3.

Cortical and subcortical timescale gradients relate to functional organization. (A) Group-averaged intrinsic timescales computed for cortical (as in Fig. 1) and nonneocortical (as in Fig. 2) structures, including striatum and thalamus (Middle) and cerebellum [Right, shown as flatmap (119)] (separate scale used for each structure). (B) Canonical large-scale functional networks as defined by refs. 30, 32, and 33 (Methods). (C) Mean intrinsic timescale (ACF decay) computed within each network for each brain structure analyzed. Mean and SE (error bars) computed across subjects (n = 1,139).

The striatum, thalamus, and cerebellum each exhibit functional organization parallel to cortex, raising the question of whether this organization is reflected in their respective timescale gradients. In each of these structures, we observed hierarchical organization of intrinsic timescales according to functional system (Fig. 3C), as defined by FC (32, 33) (Methods). Importantly, subcortical topographic ordering was parallel to that of the cerebral cortex: Timescales were shortest in sensorimotor regions and longest in the default mode network. These findings were replicated in an independent dataset (SI Appendix, Fig. S2C).

Intersubject Variability in Spectral Content Predicts Intersubject Variability in FC.

The present results indicate that the default mode network, the functional system with the most extensive structural as well as FC (47), exhibits the slowest dynamics both cortically and subcortically. This finding is consistent with prior work suggesting that relatively slow dynamics are a correlate of extensive FC, that is, strong correlations with regions widely distributed throughout the brain (12, 29). To further investigate this correspondence, we asked whether this relation extends to individual differences in FC. Using the second dataset of highly sampled individuals (31), we found that an individual’s own map of intrinsic timescale tended to best predict their cortical topography of FC “strength” or mean FC magnitude of a given region (P < 0.001; Methods) (Fig. 4 and see SI Appendix, Fig. S3 for individual maps; see also SI Appendix, Quantifying Extensive Functional Connectivity and Fig. S4). This result remained after accounting for spectral variability prior to FC computation (SI Appendix, Fig. S5 and Methods). Hence, intersubject variability in FC (31) is related to intersubject variability in intrinsic timescales, further supporting a biological link between FC topology and intrinsic timescale (12). In one individual (MSC03), the subject’s own timescale map was not the best predictor of FC strength. This subject exhibited aliased respiratory artifact (48) and an anomalous timescale map (SI Appendix, Fig. S3); accordingly, future work should examine contribution of aliased physiological artifact to <0.1 Hz BOLD spectral content.

Fig. 4.

Individual variability in FC is linked to individual variability in intrinsic timescales. (A) Maps of cortical ACF decay (Left) and mean FC magnitude (i.e., FC strength; Methods) (Right) for two example individuals, MSC05 (Upper) and MSC06 (Lower). Compressed ACF decay range is due to high-pass filtering specific to this analysis (Methods). (B) For each individual, spatial correlation between the individual’s mean FC magnitude and all 10 individuals’ maps of intrinsic timescale (i.e., ACF decay) topography. The subject’s own map of intrinsic timescale is represented by solid colors.

Discussion

The present findings support the previously articulated hypothesis that broadband spectral content is hierarchically organized across the entire cerebral cortex (6, 7). In particular, our results provide empirical support for emergent hierarchical dynamics previously predicted from a large-scale dynamical model of macaque cortex incorporating hierarchical heterogeneity in synaptic excitation (12). We additionally extend the observation of hierarchical dynamics to the striatum, thalamus, cerebellum, and hippocampus. Thus, intrinsic timescale hierarchies may represent a fundamental organizing principle of the mammalian brain.

Relationship to Prior fMRI Spectral Analyses.

The topic of intrinsic timescales has attracted interest from researchers using diverse modalities. Following Murray et al. (10), autocorrelation decay has become a standard measure of intrinsic timescale and is likewise used in the present fMRI analyses. However, fMRI spectral content has itself been a topic of interest for many studies employing diverse analyses. In most cases, these analyses were not performed with the intent to obtain characteristic regional timescales. Below we summarize the unique aspects of the present investigation and address findings of the most relevant studies.

Most prior fMRI spectral analyses have been performed in the frequency domain. Temporal autocorrelation- versus frequency-based representations of spectral content are inherently linked via the Wiener–Khinchin theorem, but discrepancies arise from the different ways in which these representations are typically quantified. First, many analyses quantify low-frequency power over a broad range [e.g., the widely used “(fractional) amplitude of low-frequency fluctuation (ALFF)” (49, 50) measures]. However, these measures essentially report variance within the low-frequency range of interest (e.g., 0.01 to 0.1 Hz). Variance and slower spectral content tend to spatially covary in fMRI signals (24, 25) [e.g., see (f)ALFF topographies of refs. 49 and 50], but this need not be the case (as evident from SI Appendix, Fig. S1). The frequency-domain approach most similar to ACF decay in the infraslow range is to quantify, for a given region, the spectral distribution of <0.1-Hz power. Previous studies have modeled fMRI power spectral density [e.g., as log-log (24) or log-linear (29)] and assessed regional variability in a single parameter used for fitting this model (e.g., slope). From a signal variance perspective, log transformations of power are not ideal as they nonlinearly distort the relative importance of different frequencies. More generally, model-based measures [which can also include time-domain measures such as Hurst exponent (24, 51)] require assumptions of spectral behavior over a broad frequency range (e.g., monofractality); thus, regional differences in these measures can be driven by differences in goodness of fit. These assumptions are not necessary in the present study.

Methodological differences likely account for discrepant results between the present findings and prior work. For example, Baria et al. (29) modeled spectra using log-linear fitting over a frequency range extending to 0.2 Hz and obtained cortical results broadly consistent with ours, but with portions of visual cortex exhibiting relatively increased low-frequency content. We found similar results using the same analysis strategy, but to a much lesser extent when excluding frequencies above 0.1 Hz (SI Appendix, Fig. S6). We believe it is better to avoid modeling frequencies above 0.1 Hz because of diminishing SNR (52, 53). High-frequency noise would negatively impact all spectral measures extended to this frequency range, but would disproportionately affect log-linear spectral slope estimates as this measure weights higher frequencies in great excess of their proportional variance. Fitting power spectra via log-log slope appropriately weights the lowest frequencies, but this method is subject to error from undersampling of low frequencies because of finite duration acquisitions. Finally, zones of signal dropout [e.g., orbitofrontal and temporal poles and ventral striatum (44)] are prone to both high-frequency artifact and low-frequency head motion drifts. Hence, these regions—mostly restricted to the cortical and subcortical limbic network (30, 33)—were excluded from the present analyses.

In addition to technical factors, state dependence is another crucial variable in fMRI spectral analysis. For example, using an autocorrelation-based approach, Kaneoke et al. (25) showed thresholded maps that agree well with our results, as regions with slowest dynamics fell within the bounds of the canonical frontoparietal and default mode networks. However, medial visual cortex also showed, to a lesser extent, low-frequency activity; this is expected as subjects were scanned in the eyes-closed state, in which low-frequency content in this region is dramatically enhanced (e.g., refs. 54–56) [interestingly, this feature is likely intrinsic to the eyes-closed state and not explained by reduced visual input (56, 57)]. fMRI spectral content is also sensitive to arousal state (52, 58, 59) and, in high-motion subjects, low frequencies are preferentially enhanced within sensorimotor cortex relative to associative cortex (60, 61) (likely reflecting decreased arousal rather than motion artifact per se).

Here, we use a straightforward, model-free estimate of autocorrelation decay to study intrinsic timescales in the eyes-open, awake state. This approach minimizes the above-discussed technical issues and is readily combined with motion censoring as it does not require continuous time series (62). To our knowledge, one cortex-wide autocorrelation-based fMRI timescale analysis in the awake, eyes-open state has been published: In a recent rsfMRI investigation of autism, Watanabe et al. (63) derived intrinsic timescales that were relatively faster in sensorimotor cortex, showed excellent correspondence with electroencephalography-derived timescales, and, interestingly, had significant and reproducible behavioral and structural correlates (63). The present study also replicates findings—including relatively fast fluctuations in visual cortex and thalamus—across two large, independent datasets. Task-based fMRI studies of functional timescales similarly suggest faster timescales in visual cortex (8, 64), as does neurophysiological evidence (e.g., refs. 6 and 10).

Biological Basis for Hierarchical Dynamics.

Regional variability of intrinsic timescales likely emerges through a combination of hierarchically organized fine-scale features (14, 16, 65, 66) and long-range, macroscopic patterns of connectivity (12, 16, 29, 67). The interaction between these two features has been modeled (12). Relevant fine-scale features in neocortex include pyramidal cell dendritic spine density (68, 69) and the associated degree of recurrent excitation (12, 15, 70). Excitation gradients are complemented by inhibitory interneuron densities along the same hierarchical axis (14, 65, 66). Topographically parallel gene expression gradients may also be present in basal ganglia, thalamus, and cerebellum (71–75). These structures lack local recurrent excitation but contribute to recurrent activity within cortico-subcortical loops (70, 76, 77). Fine-scale gradients along the hippocampal longitudinal axis are also well-established (19). Intrinsic timescales are also linked to relative connection degree (29, 67, 78), which parallels anatomical hierarchy (79).

The present work examines infraslow intrinsic timescales. In theory, the above-mentioned interplay between recurrent excitation and connectivity architectures can account for the emergence of infraslow fluctuations on the basis of millisecond-scale neuronal dynamics (e.g., refs. 80 and 81). However, growing evidence supports a contribution from neuromodulatory processes that are intrinsically slow (82–84). The distinction between fast and slow processes has been articulated (20, 85, 86). Still, these timescales are intrinsically interdependent. For example, the phase of ongoing infraslow fluctuations substantially explains variability of higher-frequency activity (20). In this context, it is interesting that regions with slower infraslow dynamics preferentially couple with slower narrowband carrier frequencies (87).

The present study is based on fMRI, which measures hemodynamic correlates of infraslow electrical activity rather than electrophysiology directly. Nonetheless, similar hierarchical dynamics have been demonstrated in the infraslow envelopes of broadband high-frequency activity using electrocorticography (ECoG) (9), providing strong evidence that the long timescales we report are functionally relevant and not simply due to hemodynamic low-pass filtering. This evidence also argues against a purely vascular explanation for hierarchical heterogeneity of fMRI spectral content, although we cannot exclude this possibility. Finally, it should be mentioned that intrinsic timescales reflect just one way in which anatomical hierarchies can manifest in the temporal domain (e.g., ref. 88).

Functional and Theoretical Significance of Hierarchical Dynamics.

Intrinsic timescales are informative of brain structure and function. The correspondence of slower dynamics to increased structural and FC (and thus, increased integration) can be viewed as a result of a population acting as a low-pass filter of its aggregate inputs, to a degree that varies as a function of its connectivity (29) (see also refs. 79, 89, and 90). In turn, slower dynamics can provide longer windows of opportunity for temporal summation and integration of inputs (7, 10). Thus, a series of elegant neuroimaging and ECoG experiments in humans have defined a hierarchy of “temporal receptive windows” (analogous to spatial receptive fields) within multiple large-scale sensory pathways in relation to experimentally controlled, time-varying sensory stimuli (reviewed in ref. 7). Several of these studies explicitly link these sensory hierarchies to those inferred from intrinsic timescales (i.e., measured from ongoing brain activity) within the same infraslow frequency range (9, 91, 92). More generally, evidence obtained from multiple organisms over a wide range of spatiotemporal scales has explicitly linked intrinsic timescales to behavior (10, 93–96). This correspondence suggests that hierarchical dynamics are intrinsic to brain function, which has important implications for understanding the contribution of a given brain region to network-wide dynamics (12, 97, 98) [and hence, behavior (99)].

The present work extends the notion of hierarchical dynamics to ongoing activity within large-scale cortico-subcortical systems. From this perspective, the brain’s global functional architecture hypothetically reflects an evolved embedding of deep temporal structure within the (exteroceptive, proprioceptive, and interoceptive) sensorium (6, 67). Theories along these lines appeal to early cybernetic formulations of self-organization, for example the good regulator theorem (100). For a brain, this theorem implies that adaptively regulating homeostasis (allostasis) requires, at some level, an internal predictive model of the multiscale statistical contingencies and probable causes of sensory samples, including those generated from the organism’s own actions (101, 102). This fundamental feature is reflected in the architectures of deep temporal models from computational neuroscience and machine learning (103–106). The added predictive value of increasingly slow processes may support emergence of new functionalities in diverse biological systems (107). Accordingly, it is noteworthy that the spatiotemporal hierarchy described herein strongly resembles phylogenetic and ontogenetic maps of cortical expansion (108). Thus, the ability to integrate over long timescales may be essential to the functions enabled by late-emerging large-scale association networks (109).

Methods

Primary Dataset: Genomics Superstruct Project.

A large dataset (1,139) was obtained from the Harvard–Massachusetts General Hospital Brain Genomics Superstruct Project (GSP). Details regarding the GSP dataset are published elsewhere (30, 110). Briefly, imaging was performed with a 3T Siemens Tim Trio scanner. All participants were simply instructed to keep their eyes open, remain still, and not fall asleep. Two 6-min fMRI runs (repetition time [TR] = 3.0 s; 3.0-mm isotropic voxels) were acquired per subject included in the present analyses.

Secondary Dataset: Midnight Scan Club.

A second, independent dataset was used to validate findings from the primary dataset, examine spectral content over long scan durations, and investigate individual differences. The Midnight Scan Club (MSC) dataset comprises 10 healthy, right-handed individuals aged 24 to 34 y (five females). Details regarding the MSC dataset are published elsewhere (31). Briefly, subjects each underwent 10 scanning sessions performed at midnight. Images were collected on a Siemens Trio 3T MRI scanner and included 30 contiguous minutes of eyes-open rsfMRI per session (TR = 2.2 s; 4.0-mm isotropic voxels), totaling 300 min per subject. During rsfMRI acquisition, subjects fixated a white cross-hair against a black background.

fMRI Processing.

Functional data were preprocessed to reduce artifact, maximize cross-session registration, and resample to an atlas space. Details of further processing are included in SI Appendix. Briefly, atlas-transformed data underwent motion-censoring (54), low-pass filtering to retain frequencies <0.1 Hz and regression of nuisance signals as well as the whole-brain mean. Processed data were converted to CIFTI format, which projects data from cortical voxels to a surface while retaining volumetric time series from the subcortex and cerebellum (111). Surface-projected time courses were downsampled to a ∼4,000-vertex-per-hemisphere (∼6-mm spacing) “fs_LR” (112) atlas-registered surface to improve SNR and reduce computational demand. All computations were performed on these ∼6-mm-resolution cortical vertices and 3-mm-resolution subcortical voxels. See SI Appendix for further details.

Network Parcellation.

Cortical, striatal, and cerebellar parcellations were obtained from refs. 30, 32, and 33 and resampled to the 4k surface (cortex) or 3-mm resolution (subcortex). Low SNR [i.e., limbic (30)] and underrepresented [dorsal attention and visual in striatum (74); visual in cerebellum (32)] networks were excluded (see SI Appendix for further details). To generate a comparable parcellation for the thalamus, we applied a similar winner-take-all strategy as in Buckner et al. (32) to 1,139 individuals from the original parcellation dataset (i.e., GSP). This resulted in a parcellation broadly consistent with known functional organization of the thalamus as well as published functional parcellations at the level of fMRI (e.g., refs. 113–116 and Fig. 3). This parcellation is publicly available at https://github.com/RaichleLab.

Intrinsic Timescale Estimation.

To obtain a model-free estimate of intrinsic timescale while allowing for the exclusion of high-motion time points, we used a previously described method for computing lagged (auto-) covariance using blocks of contiguous time points (117). The precise abscissa corresponding to an autocorrelation value of 0.5 (i.e., half of the ACF full width at half maximum) was estimated by computing the zeros of a spline fit to the ACF. This method was applied to low-pass-filtered time series (<0.1 Hz) (24). Full details of this procedure are provided in SI Appendix. Custom MATLAB code for intrinsic timescale estimation as described in this paper is publicly available at https://github.com/RaichleLab.

Comparison with FC.

We quantified the extent of FC for each region by the graph metric of node strength, the weighted network equivalent of node degree. For this analysis, BOLD time series were high-pass-filtered (>0.01 Hz) to account for idiosyncratic drift artifacts that presented as outlier timescales in regions surviving the group-level SNR mask. Filtering primarily influenced signal dropout regions in cortex (by reducing outlier timescales likely arising from low-frequency head motion drift) and compressed overall timescale range, without substantively changing hierarchical topographies (SI Appendix, Fig. S3). For each individual, we computed FC strength of each cortical vertex as its mean (absolute value) Fisher z-transformed correlation across all other vertices. The intrinsic timescale (ACF decay) map for each of the 10 MSC individuals was subsequently correlated with the FC strength map of each individual, and these correlations were assembled into a 10 × 10 matrix. Statistical comparison between within-subject and between-subject ACF decay:FC strength correlations was performed via a two-tailed t test comparing the diagonal of this matrix (within-subject) against all other values (between-subjects).

Due to use of absolute value FC, a potential trivial explanation for the statistically significant relationship observed between intrinsic timescale and FC strength (P < 0.001) is that slower dynamics translate to fewer independent temporal samples, thereby biasing FC magnitudes toward higher values in regions with lower-frequency signals (117). To rule out this possibility, we computed the mean cortical power spectrum, $P\left(\omega \right)$, averaged over all 100 available MSC sessions (10 per subject) and applied the amplitudes (i.e., square root of the power spectrum at each frequency bin) to each fMRI time series, $x\left(t\right)$:

$$\begin{array}{c}\stackrel{\sim }{x}\left(t\right)=z\left(F^{-1}\left(P^{\frac{1}{2}}\cdot \text{exp}\left(i\cdot \text{arg}\left[F\left(x\right)\right]\right)\right)\right),\end{array}$$ [1]

where $F\left(x\right)$ and$F^{-1}\left(x\right)$ are the Fourier and inverse Fourier transforms of $x$, arg denotes the phase, $i$ is the imaginary unit, and z denotes standardization (i.e., enforcing a zero-mean, unit variance condition). Thus, the original Fourier phase spectra are preserved, while the amplitudes are made to be uniform across vertices. Following spectral amplitude normalization $\left(x\to \stackrel{\sim }{x}\right)$, we recomputed FC strength maps for each individual. In this way, we removed any trivial (i.e., purely mathematical) relationship between correlation magnitudes and spectral content. This maneuver did not materially change the results (SI Appendix, Fig. S5).

Use of absolute value FC is motivated from the perspective that strong anticorrelations reflect true antagonistic relationships, as evidenced, for example, by stimulation (118). See SI Appendix, Quantifying Extensive Functional Connectivity and Fig. S4 for further consideration of this topic.

Data Visualization.

Cortical surface displays and volume images were rendered using Connectome Workbench software (111). Cerebellar flatmap representations of volume-averaged results were generated using the SUIT toolbox (119) and used for display purposes only.

Data Availability.

The GSP dataset is publicly available at https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/25833. The MSC dataset is publicly available in the OpenfMRI data repository at https://openneuro.org/datasets/ds000224. Processing scripts for the latter dataset have been made available at https://github.com/MidnightScanClub/MSCcodebase. Code for spectral analyses as performed in this paper, as well as the thalamic network parcellation, have been made publicly available at https://github.com/RaichleLab.