Neuronal spike-rate adaptation supports working memory in language processing

Significance

To understand an utterance, words have to be remembered and rapidly combined into an interpretation. How neurobiology supports this feat is currently unknown. One proposal that we investigate here is that information is stored and manipulated within single neurons. Depending on input history, neurons show different spike responses, and this adaptation constitutes a form of processing memory on short timescales. We implemented this approach as spike-rate adaptation that decreases neuronal excitability. Through computer simulations we show that this mechanism is suitable to establish meaning relations in sequential language processing. This account of working memory complements the more traditional views that information is stored in persistent spiking activity or short-lived synaptic changes.

Abstract

Language processing involves the ability to store and integrate pieces of information in working memory over short periods of time. According to the dominant view, information is maintained through sustained, elevated neural activity. Other work has argued that short-term synaptic facilitation can serve as a substrate of memory. Here we propose an account where memory is supported by intrinsic plasticity that downregulates neuronal firing rates. Single neuron responses are dependent on experience, and we show through simulations that these adaptive changes in excitability provide memory on timescales ranging from milliseconds to seconds. On this account, spiking activity writes information into coupled dynamic variables that control adaptation and move at slower timescales than the membrane potential. From these variables, information is continuously read back into the active membrane state for processing. This neuronal memory mechanism does not rely on persistent activity, excitatory feedback, or synaptic plasticity for storage. Instead, information is maintained in adaptive conductances that reduce firing rates and can be accessed directly without cued retrieval. Memory span is systematically related to both the time constant of adaptation and baseline levels of neuronal excitability. Interference effects within memory arise when adaptation is long lasting. We demonstrate that this mechanism is sensitive to context and serial order which makes it suitable for temporal integration in sequence processing within the language domain. We also show that it enables the binding of linguistic features over time within dynamic memory registers. This work provides a step toward a computational neurobiology of language.

Working memory (WM) is the capacity to maintain and manipulate information over short time periods, and it plays a crucial role in many cognitive domains. Memory on short timescales has been characterized as elevated neural activity that persists beyond stimulus offset (1, 2). On this account, information is encoded in spike trains and maintained within memory through sustained firing that is supported by appropriately tuned synaptic feedback (3, 4) or cellular multistability (5–7). More recent evidence, however, suggests that neural activity can be highly variable during maintenance (8–10) and is significantly reduced by dual-task demands (11). In some cases, the identity of items held in WM has been decoded reliably from the blood-oxygen-level–dependent (BOLD) response without sustained activity (12). Other studies have found discrete bursts in $\gamma$-band frequency during encoding and retrieval (13) which is difficult to reconcile with the persistent activity view. For these reasons, the contribution of neural activity to WM remains a matter of ongoing debate (14). Another approach has argued that WM is supported by transient changes in synaptic efficacy (15, 16). In a network model, short-term synaptic facilitation (17) induced stimulus-specific patterns of functional connectivity during encoding. Following a period of low spiking activity, information could be reactivated by an unspecific retrieval cue and decoded successfully. Thus, sustained firing was not necessary for memory maintenance in these simulations.

Both persistent activity and synaptic theories of WM have been developed in simple delayed response tasks where a small number of items have to be remembered and recalled explicitly after delay. In other cognitive domains, the processing demands on WM differ substantially from this paradigm. For instance, in language processing the system is exposed to rapid serial input without pauses or delays. There are no recall cues in the input, and the explicit recollection of words is not an objective. Instead, the language system actively transforms auditory or visual input in order to construct an interpretation within WM in an online, incremental fashion. Cues to meaning can occur anywhere in a sentence and nonadjacent to the location of context-dependent use. Furthermore, processing memory needs to be sensitive to precedence relations in order to process languages where word order matters (e.g., “dog bites man” and “man bites dog” contain the same bag of words but differ in meaning). Whether persistent activity or synaptic models of WM could achieve fast, online temporal integration that is order-sensitive and context-dependent is an open question. We propose a neurocentric account of WM that meets these requirements. This account is based on the principle of intrinsic plasticity which describes changes in neuronal excitability as a function of input history. Intrinsic plasticity can be expressed, among others, as a decrease of the spike–release threshold, a reduction in spike after-hyperpolarization, or changes in resting membrane potential (18, 19). These effects lead to higher neuronal sensitivity and an increase in firing rate. Conversely, excitability can decrease in response to overstimulation, causing a down-regulation of output rates as in spike-rate adaptation (20, 21). Thus, various forms of intrinsic plasticity can temporarily modulate excitability and alter the functional state of neurons (22). Intrinsic plasticity has been implicated in the homeostatic regulation of network activity, counteracting dynamic instability due to Hebbian plasticity (23). Additional evidence indicates that there is a causal link between intrinsic plasticity and memory. Changes in neuronal excitability support engram formation and maintenance by modulating the threshold for the induction of long-term potentiation (24–26). Importantly, it has also been suggested that intrinsic plasticity can serve as a transient storage device on shorter timescales (19, 27, 28). Recent findings on the learning of interval durations, for instance, have shown that cells responded with temporally specific modulations of their firing rate (over several hundred milliseconds) while internal synaptic drive was pharmacologically blocked (29). This suggests that memory traces for temporal relations were maintained through intracellular changes in excitability. These changes are governed by the fast activation or deactivation of membrane conductances, and this makes neuronal responses dependent on input history and levels of activity. Thus, short-term memory could be based solely on intrinsic plasticity mechanisms, without synaptic changes or persistent activity (27, 30). To test this hypothesis, we implemented WM as short-lived neuronal adaptation in simulated circuits of spiking neurons which gradually reduces neuronal excitability as a function of experience. We first describe this basic mechanism and show that it provides short-term memory that is context-dependent and sensitive to serial order. Then we investigate the functional role of neuronal memory in the processing of linguistic sequences where semantic relations have to be established between words. Finally, we outline a neurobiological read–write memory that is based on coupled dynamic variables at different timescales.

Results

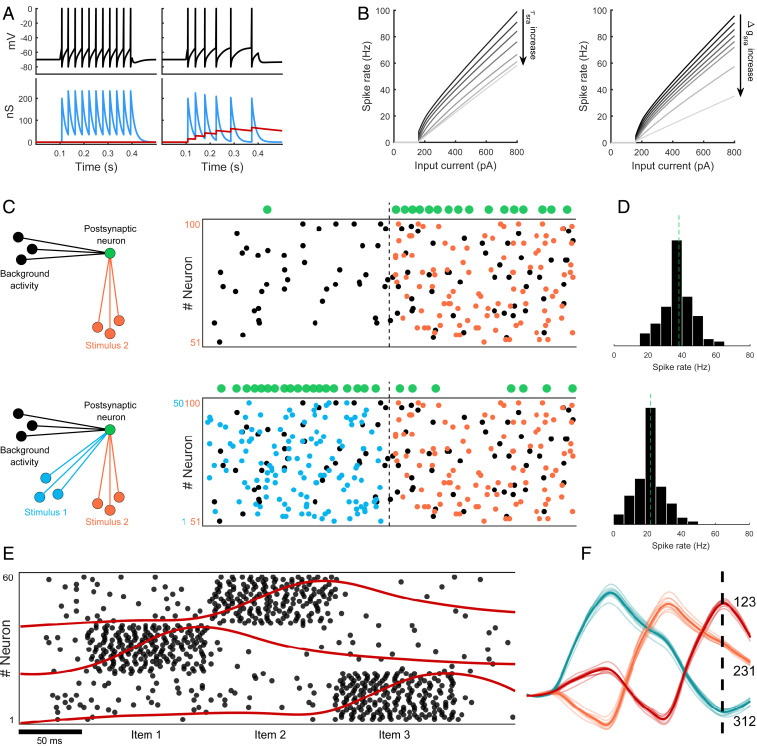
Within the range of observed intrinsic plasticity (18, 19), we focus on the decrease in excitability due to spike-rate adaptation (SRA) which has been found in many types of excitatory cortical neurons (20, 31). Leaky integrate-and-fire neurons with a fixed voltage threshold were used, and SRA was modeled as a spike-triggered, ${\mathrm{C}\mathrm{a}}^{2+}$-mediated ${\mathrm{K}}^{+}$-conductance $g_{\text{sra}}$ (32). Following a spike, $g_{\text{sra}}$ was increased by a small amount $g_{\text{sra}}\leftarrow g_{\text{sra}}+\mathrm{\Delta }{g}_{\text{sra}}$, and it decayed back to zero with time constant ${\tau }_{\text{sra}}$ otherwise. The conductance increase generated an ionic current that hyperpolarized the cell membrane which effectively reduced neuronal excitability. This adaptation effect is shown in Fig. 1A where the action of $g_{\text{sra}}$ on the membrane potential gradually increases interspike intervals in a neuron driven by a constant current. The magnitude of $\mathrm{\Delta }{g}_{\text{sra}}$ controls how fast the neuron adapts while ${\tau }_{\text{sra}}$ determines the lifetime of adaptation. Generally, an increase of either parameter leads to a decrease in firing rates (Fig. 1B). When the adaptive neuron is driven by low random background activity, it responds with an occasional spike (green dots, Fig. 1C, Top) whereas the evoked response to a sensory stimulus (orange) is much stronger. If, on the other hand, the same input (orange) is preceded by another sensory stimulus (blue), the neuron adapts rapidly and shows a different spike response pattern on the second stimulus (Fig. 1C, Bottom). SRA is clearly visible in the downshift of mean firing rates collected from 100 simulations in each condition (Fig. 1D). Thus, for identical stimuli, the neuron responds in a history-dependent manner which is a form of memory on timescales that are related to the ${\tau }_{\text{sra}}$. This memory mechanism can distinguish two different contexts—the presence or absence of the blue stimulus—in which the target item (orange) occurred. Furthermore, neuronal memory is sensitive to the serial order of inputs. To show this, a network of adaptive neurons was exposed to sequences of three stimuli. Each stimulus projected to a random subpopulation of neurons (sorted by stimulus for visual ease; Fig. 1E). Evoked spiking activity drove neuronal adaptation conductances up (red traces, population average) which then decayed back to baseline after the stimulus was removed. These averaged conductances can be viewed as a population memory trace. The stimuli were then reordered (as 123, 231, and 312, respectively), and memory traces were recorded for each sequence from 10 randomized network simulations. Fig. 1F shows a linear combination of these traces for the different sequences (bold lines, mean). Each sequence generated a characteristic profile of adaptive conductances over time. After stimulus offset (dashed line), the three sequences of items could still be distinguished from the corresponding mixture of traces (separability). Thus, neuronal adaptation maintains serial order in memory, and this information is accessible to simple linear readout processes (33).

Fig. 1.

Neuronal adaptation as a neurobiological correlate of WM. (A) Adaptive neuron is driven by a step current with amplitude 400 pA for a duration of 300 ms. Tonic spiking with uniformly spaced interspike intervals (Left) due to a refractory conductance $g_{\text{ref}}$ (blue). Spike rate conductance $g_{\text{sra}}$ (red) adaptively decreases excitability and stretches out spike times (Right). Both conductances are spike-triggered but differ in magnitude and their decay time constants. (B) f–I curves show neuronal spike rates as a function of input current strength. As the time constant ${\tau }_{\text{sra}}$ of $g_{\text{sra}}$ increases (from 10 ms to 1.5 s; Left), spike rates decrease (black to gray gradient) because neuronal adaptation lasts longer. Likewise, as the magnitude of the spike-triggered change $\mathrm{\Delta }{g}_{\text{sra}}$ increases (from 1 to 200 nS; Right), spike rates decrease (black to gray gradient) because adaptation becomes stronger. (C) Single neuron spike response (green dots) to a Poissonian input stimulus (orange; 0.5 kHz) from 50 presynaptic neurons, when preceded only by background noise (black; 0.25 kHz) or another sensory stimulus (blue; 0.5 kHz). (D) Histograms display SRA (dashed line indicates mean) which encodes context-dependent neuronal behavior in response to the orange stimulus. Memory of the blue stimulus is maintained in the hyperpolarized membrane state of the postsynaptic neuron (green). (E) Population-averaged memory traces $g_{\text{sra}}$ (red) over time, induced by a sequence of three items (y position of traces aligned with corresponding population). (F) Linear combination of these traces can distinguish the sequential order of inputs (123, 231, or 312) after stimulus offset (dashed line).

Unlike the persistent activity account of WM, neuronal memory does not rely on elevated activity or sustained firing. Rather, information is encoded in the hyperpolarized membrane state and maintained in the adaptation conductance $g_{\text{sra}}$. Memory traces do not need to be refreshed perpetually for retention, and memory span is linked to the time constant that controls $g_{\text{sra}}$ decay. Similar to synaptic WM (15), this account avoids the high metabolic cost of spike generation and feedback signaling incurred by persistent activity maintenance (34). Instead, the functional role of spiking activity in neuronal WM is to recode information into (hidden/silent) dynamic variables that move at slower timescales than action potentials or subthreshold membrane leakage. Thus, spiking activity can be viewed as a write-to-memory operation that stores information in neuronal memory registers. Since these dynamic variables are coupled to the cell membrane, previous information is continuously read back from memory into the active network state. In this way, memory traces constantly influence and shape future processing behavior (35). These cycles of encoding and retrieval could form the basis of a local, neurobiological read–write memory.

Context-Dependent Sequence Processing.

This proof of concept establishes that neuronal memory is sensitive to context of occurrence and can maintain serial order information. Next, we investigated whether transient adaptation due to intrinsic plasticity could also serve as WM in a more demanding task. This was a sequence processing task similar to language comprehension which required integration over longer temporal windows. Sentence comprehension was modeled as the online, incremental assignment of thematic roles to phrases (“who does what to whom?”). These roles specify semantic relations between event participants (e.g., agent, theme, and goal) and are part of most linguistic theories of adult meaning (36). Cues to sentence meaning include lexical semantics, morphology, and syntax, and these cues can occur anywhere in the input sequence and at variable distance from the location where they are being interpreted. For instance, in the sentence “The cheese is eaten by the mouse,” noun animacy (cheese, mouse), verb identity (eat), inflectional morphemes (-en), and function words (by) jointly support an interpretation of mouse as the agent of the action. However, depending on context, the word mouse can assume different semantic roles in the same sentence position (e.g., “the cat is chasing the mouse”). Early in sentences, there typically was temporary ambiguity, but semantic relations became more deterministic toward the sentence-final noun phrase (NP). Thus, in order to accomplish this task, contextual information needs to be maintained in WM and cues to meaning integrated within the processing memory.

To test neuronal memory for this ability, a network with 1,000 adaptive spiking neurons was used where ${\tau }_{\text{sra}}$ was set to 200 ms. The network was sparsely connected (1% synaptic density) and had a feed-forward graph to eliminate possible contributions to WM from recurrent connectivity. It was driven by a stream of sentence input, generated from construction grammar templates and their syntactic alternations (e.g., active/passive “cat chases toy” versus “toy is chased by cat”). The complete input language is described in SI Appendix, Table S1. Synaptic projections from input words into the network were excitatory and random, following an exponential distribution to create heterogenous evoked dynamics. Statistically, each word targeted 5% of all neurons in the circuit and word exposure times were proportional to orthographic length. During input processing at a target rate of 5 Hz, spatiotemporal patterns of spiking activity were recorded from the network, and a classifier was calibrated to decode these states onto desired categorical output (semantic relations). We emphasize that the decoder is not considered part of the network model. It is merely an external measurement device that is used to assess its memory characteristics under different neurobiological assumptions about the processing infrastructure.

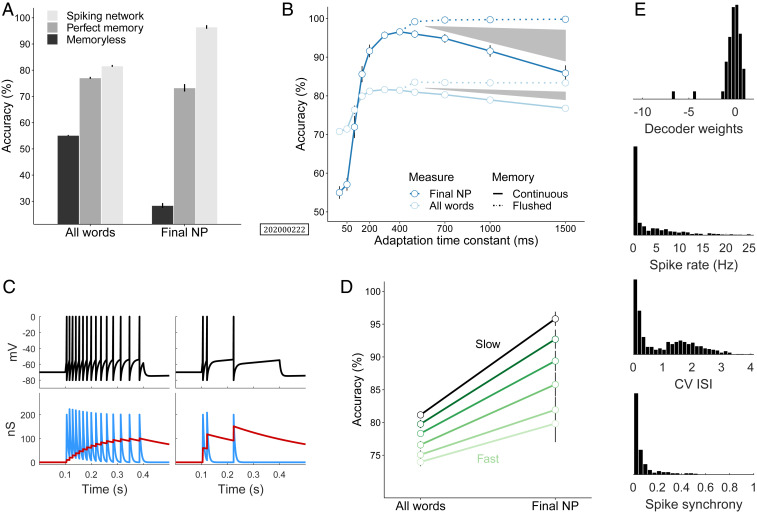
To put the task into perspective, we compared this network to a memoryless regression model and another back-off N-gram model with perfect memory of sentence context (see SI Appendix for details). The memoryless model achieved $\sim$50% accuracy on all words but failed on the sentence-final NP (Fig. 2A) where memory demands were the highest. The perfect memory model reached $\sim$75% accuracy on both measures, whereas the spiking network outperformed both, with a sentence-final accuracy of 94% and $\sim$80% on all words. This indicates that the spiking network had adequate processing memory for this task, and its internal dynamics made semantic generalizations available to the downstream readout. Decoder weights were normally distributed around mean 0 with a few large negative values (Fig. 2E). The firing rate distribution showed a heavy tail which is typical of cortical neurons, with some regular firing (coefficient of variation of interspike intervals [CV ISI close to 0]), and input-driven, irregular bursting (CV ISI above 1). Spike synchrony (measured as the pairwise correlation coefficient) across the neural population was low (Fig. 2E). These observations are consistent with previous findings that SRA supports the asynchronous irregular regime (37) which has been argued to play a critical role in cortical information processing (38). To test the effect of different adaptation time constants, we systematically varied ${\tau }_{\text{sra}}$ that controls SRA decay (Fig. 2B). There was a sharp increase in accuracy from ${\tau }_{\text{sra}}=$ 50 ms to peak performance at ${\tau }_{\text{sra}}\hspace{0.17em}=$ 400 ms [mean, 96.6%, sentence-final NP; ${\chi }^2$ (1) $=$ 48.5, $p\hspace{0.17em}<$ 0.001]. Hence, ${\tau }_{\text{sra}}$ was directly related to memory span. For ${\tau }_{\text{sra}}\hspace{0.17em}>\hspace{0.17em}$400 ms, however, accuracy decreased again toward a mean of 85.9% (sentence-final NP) for a conductance decay of 1.5 s [${\chi }^2$ (1) $=$ 48.9, $p\hspace{0.17em}<$ 0.001]. Slower relaxation entails longer retention of past information, and as memory span increased, word information was eventually carried across sentence boundaries and contaminated the processing of the next sequence. To isolate this interference effect, dynamic variables in the network were reset at the end of each sentence. Such rapid clearance of the hidden state has also been observed experimentally during memory-guided behavior (39). In this condition with memory reset, accuracy continued to increase to near ceiling with longer ${\tau }_{\text{sra}}$ [mean, 99.8%; ${\chi }^2$ (1) $=$ 15.5, $p\hspace{0.17em}<$ 0.001]. Thus, flushing WM between items prevented traces of previous input sentences from interfering with the interpretation of the upcoming sentence.

Fig. 2.

Network sequence processing. (A) Model comparison on semantic role assignment task in sentence comprehension. Accuracy is measured on all words in a sequence and on the sentence–final noun phrase. Spiking network outperforms memoryless logistic regression and perfect memory model which has access to the entire sentence context in WM. (B) Network accuracy improves with increasing time constant for neuronal adaptation. Peak performance occurs around ${\tau }_{\text{sra}}$ = 400 ms. Subsequent decline is due to interference in WM and can be prevented by flushing memory at the end of each sentence. Shaded regions indicate the size of interference effects on both measures. (C) Slow versus fast adapting neurons, controlled by the magnitude of the spike-triggered increase in adaptation conductance $\mathrm{\Delta }{g}_{\text{sra}}$. (D) Semantic role assignment accuracy parametrically varies with the degree of neuronal excitability for $\mathrm{\Delta }{g}_{\text{sra}}$ ranging from 4 nS (slow adapting) to 500 nS (fast adapting). (E) Spiking network statistics (see SI Appendix for details): distribution of readout weights (log-scale), histograms of neuronal spike rates, coefficient of variation of interspike intervals (CV ISI), and pairwise spike synchrony (from top to bottom). Error bars in A, B, and D show 95% confidence intervals for 10 model subjects.

Another feature of the adaptive neuron was the magnitude of spike-triggered ${\mathrm{K}}^{+}$-conductance change $\mathrm{\Delta }{g}_{\text{sra}}$. It controls how fast adaptation occurs in response to an input current. Note that $\mathrm{\Delta }{g}_{\text{sra}}$ does not affect the rheobase of neurons (Fig. 1B). Fig. 2C shows the evolution of the membrane potential of slow and fast adapting neurons. Both were driven by the same current and had identical adaptation time constants ${\tau }_{\text{sra}}$, but the conductance change $\mathrm{\Delta }{g}_{\text{sra}}$ was an order of magnitude larger in the fast adapting neuron. This leads to larger spike after-hyperpolarization and a rapid decrease in excitability. Evidence suggests that excitability is modulated by the transcription factor CREB (cAMP response element-binding) which changes the ${\mathrm{K}}^{+}$-conductance of neurons. CREB overexpression results in smaller spike after-hyperpolarization and enhanced excitability, and this has been linked to memory formation (see ref. 40 for a review). Here we tested whether levels of excitability also had an influence on WM function by systematically varying the magnitude of $\mathrm{\Delta }{g}_{\text{sra}}$ in the adaptive neuron. Since memory was dependent on network spike rates (SI Appendix, Fig. S1), activity was kept constant at a rate of 5 Hz for different $\mathrm{\Delta }{g}_{\text{sra}}$ by globally tuning synaptic connectivity strength up or down. The results show that sequence memory was strongly modulated by the degree of neuronal excitability when the adaptation time constant ${\tau }_{\text{sra}}$ was fixed at 400 ms for all simulations (Fig. 2D). A decrease in excitability led to a decrease in semantic role assignment accuracy across measures [${\chi }^2$ (1) $=$ 39.8, $p\hspace{0.17em}<$ 0.001], and accuracy on the sentence-final NP dropped by more than 15% when moving from slow to fast adaptation. This suggests that enhanced neuronal excitability was beneficial to WM in sequence processing. Although memory traces reside in the hyperpolarized membrane state, fast adaptation was not conducive since some spiking activity is needed to write information into memory registers in the first place.

Feature Binding.

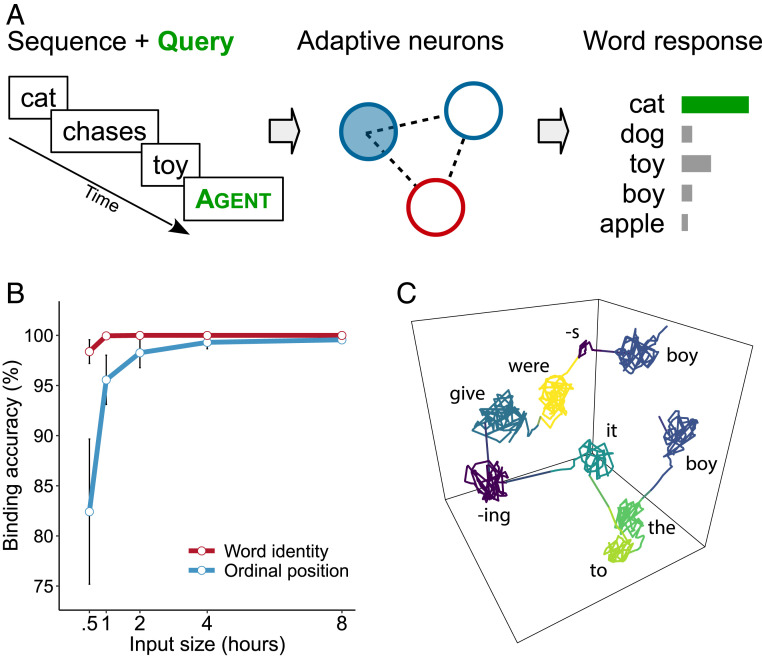
The temporary binding of features is crucial for the unity of perception and also plays an important role in language comprehension. In the previous online processing task, the readout was binding semantic roles to words in time. In order to construct a sentence-level interpretation, these binding relations have to be maintained in memory until the utterance is completed. An interpretation that was adopted early in a sentence may have to be revised later on. Similar to the design of a delayed response task, we tested whether neuronal memory was able to maintain information that allowed feature binding across words in a sequence. At the end of each test item, the network was queried with a randomly selected semantic role label that was appropriate for this sentence. For instance, after the item “the cat chases a toy” had been processed, the role query “agent” was injected into the network (SI Appendix), and the activity evoked by the query was being nonlinearly mixed with the network’s memory of the preceding sentence. Then, a readout was estimated to map the resulting state onto the target content word for this query (Fig. 3A). In the example sentence, the correct readout response to “agent” would be “cat.” The role query acts as a semantic variable which is temporarily bound to a feature value by the readout, i.e., the word that fills this role slot in the test sentence. Target words could occur anywhere in the sentence and at variable distance to the position of the query.

Fig. 3.

Binding of words to semantic roles. (A) After each input sentence, the network is queried with a semantic role label. The readout maps the network state onto a probability distribution of word responses for the queried role. A correct response occurs if the noun is identified that fills the query slot. (B) Feature binding accuracy for sentences with two occurrences of the target word as a function of the amount of language input. One readout identifies the lexical target, and the other readout returns the ordinal position of the target word. Error bars show 95% confidence intervals. (C) Example sentence and its trajectory through state space. Multiple occurrences of the same lexical noun (boy) in different semantic roles (agent, recipient) are separated by history-dependent neuronal processing.

To obtain a robust estimate of binding, networks were tested on 5,000 queries. Since the test sentences were unique and novel, binding required substantial generalization beyond previous experience. Across queries, the network achieved $\sim$90% role-to-word binding accuracy which is within adult human range (41). Binding relations are particularly challenging when items contain multiple occurrences of the same noun in different semantic roles (Problem of Two; ref. 36). We tested this in datives where animate nouns could occupy both agent and recipient roles (e.g., “a nice man gave the man a book”). Two parallel readouts were calibrated, one that mapped role queries onto lexical fillers (as before) and another one that mapped onto the ordinal number of the word’s occurrence. Combining both readouts uniquely identifies a noun response (e.g., in the above dative, the correct response to the query “recipient” would be “man”/2nd position). In this condition, target words and their relative position could be decoded with more than 95% accuracy after just 1 h of language input (2,200 sentences), and eventually, perfect identification was reached with longer exposure (Fig. 3B). Thus, neuronal WM can distinguish multiple occurrences of the same item, and this allows the resolution of feature binding ambiguity.

Dimensionality reduction of neural trajectories (SI Appendix) showed that repeated words were separated in state space due to the history dependence of neuronal responses (Fig. 3C). These results indicate that binding relations were implicit in the dynamic registers of neuronal memory as the network was forced by external input into a state from which these relations could be recovered by a readout. This account of feature binding differs from other neural approaches to binding in that it does not require specialized operators to form complex representations such as tensors or convolutions (42, 43) or the construction of explicit structural representations in neural tissue (44). It also does not require neural markers to signal binding, such as synchrony (45) or polychronous spiking (46). The high-dimensional end state of neural trajectories already represents the correct binding relations between words and semantic roles, and this suggests that neuronal WM can support fast, automatic sequence processing in language. In order to reason about feature bindings explicitly, downstream inference machinery can query representations held in neuronal WM registers and extract these relations when needed.

Discussion

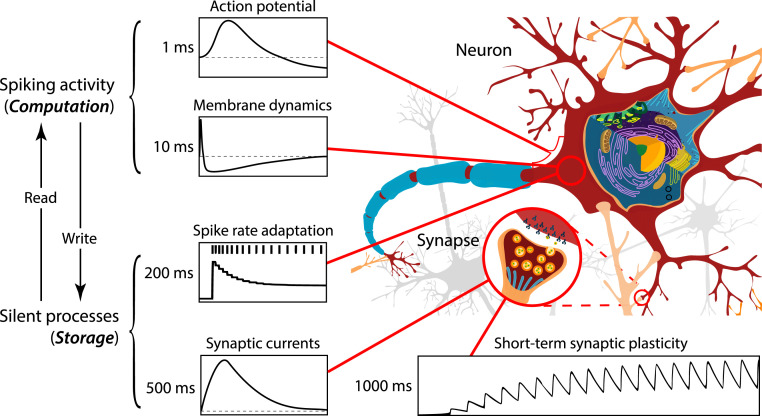
In the present work, we propose that intrinsic plasticity, expressed as neuronal SRA, can provide a cellular mechanism for WM on short timescales where information is stored and maintained in physiological processes that regulate neuronal excitability as a function of experience. On this account, action potentials in the fast membrane dynamics ($dV/dt$ with time constant ${\tau }_m$) trigger neuronal adaptation which is governed by dynamic variables with longer time constants (e.g., $d\alpha /dt$ with ${\tau }_m\ll {\tau }_{\alpha }$). Spiking activity in $V$ recodes information into these slower dynamic variables $\alpha$, and this can be interpreted as writing to memory. Hence, dynamic variables act as memory registers that store real numbers, and these variables are the physical address of the memorandum. In the case of neuronal memory, stored numbers correspond to the instantaneous value of a membrane conductance that is localized to a point in space. Memory traces in $\alpha$ can persist in the absence of sustained firing, excitatory feedback, or synaptic plasticity and are unaffected by membrane reset or the integration of new information into the membrane state. Conversely, since adaptation variables are coupled to the membrane potential, memory traces continuously exert an influence on the active membrane state which corresponds to reading from memory. These cycles of encoding and retrieval between coupled dynamic variables with different timescales could form the basis of a neurobiological read-write memory (Fig. 4). On this view, the fast-changing membrane dynamics transforms analog input to binary output, and slower adaptive processes provide for information storage. Hence, memory and computation are implemented within single neurons, and their functional distinction is based on timescales only. The distinction between information encoding, maintenance, and retrieval is similarly blurred. Encoding corresponds to a change in the neuron’s excitability in response to a stimulus, maintenance is the persistence of this adaptive change in the neuronal state, and retrieval amounts to the changed neuronal response itself (see also ref. 47). To control reading and writing, a functional dependence can be introduced to steer the information exchange between $V$ and $\alpha$, as in $dV/dt=f_V\left(V,{\tau }_m,\alpha ,\dots ,\mathcal{R}\right)$ and $d\alpha /dt=g_{\alpha }\left(V,\alpha ,{\tau }_{\alpha },\dots ,\mathcal{E}\right)$, where $f_V$ describes the membrane evolution, $g_{\alpha }$ the dynamics of $\alpha$, and $\mathcal{E}$ and $\mathcal{R}$ are additional dynamic variables that control encoding and retrieval, respectively. For instance, if $\mathcal{E}$ acts multiplicatively on $V$ in $g_{\alpha }$, $V$ cannot write information into $\alpha$ when $\mathcal{E}$ is near zero (e.g., via shunting inhibition), and $\mathcal{R}$ could assume a similar role in retrieval.

Fig. 4.

Neurobiological read–write memory on multiple timescales. Sustained neural spiking activity has been viewed as a correlate of memory on short timescales. However, physiological processes other than the evolving membrane state provide dynamic variables for information storage on successively longer timescales. These include intrinsic plasticity, temporally extended synaptic currents, and short-term synaptic plasticity. Coupling of these processes to the membrane state creates read–write cycles where past information, held in slower dynamic variables (storage), is continuously folded back into the fast-changing, active network state (computation). The functional distinction between memory and computation is based on the timescales of dynamic variables.

In single-neuron simulations, we have shown that neuronal WM is sensitive to context of occurrence. The same stimulus can evoke different responses depending on input history. Since adaptation decays over time, different inputs carry a temporal signature in memory, and this can be used by a downstream readout to establish serial order relations. When placed into a network architecture, neuronal WM proved suitable to process structured sequences and bind linguistic features over time. The time constant of adaptation was directly linked to WM span, and interference effects occurred when past information persisted in WM for too long. While in delayed response tasks the main focus is on retention and explicit recall, in other domains such as language, WM function also includes the active processing of memory content. Language input is not stored passively in a short-term memory buffer and loaded back into the comprehension system when needed. Instead, the integration of cues takes place in an online, incremental fashion, as soon as they become available to the processing machinery (48). The meaning of an utterance is constructed within WM as it unfolds in time, suggesting that memory for language is actively computing (49). Neuronal WM naturally implements such an active processing memory since memory registers themselves are dynamic and transform maintained information over continuous time.

We emphasize that this account of WM is compatible with other accounts that have implicated elevated firing (1, 2, 14) or synaptic changes (15–17), and it is likely that multiple interacting mechanisms contribute to memory function. For instance, persistent activity might serve to refresh traces in neuronal WM. On our account, these traces are physically located in adaptive cellular conductances rather than neural spiking activity per se. Thus, we interpret a sequence of action potentials not as the substrate of information encoding and maintenance but as an index of where and when information is being written into memory registers. Neuronal WM is also compatible with a role of transient changes in synaptic efficacy through short-term facilitation and depression which might supply timescales beyond intrinsic plasticity (Fig. 4). In contrast to synaptic memory, however, neuronal WM does not require explicit cues for recall and can function with sparse, random connectivity which obviates the need for fine-tuned excitatory feedback or strongly connected cell assemblies. Consequently, it can cope with novel inputs and with novel combinations of familiar inputs. In fact, all tested sequences in Figs. 2D and 3B were of this kind.

A neuronal account of WM is consistent with observed stimulus-induced bursts of activity during encoding (13) and a rapid firing rate transition into lower activity regimes even before stimulus offset (50). These findings might be explained by neuronal adaptation taking effect during the stimulation period. On this account, adaptation speed determined levels of neuronal excitability which in turn influenced WM characteristics (Fig. 2D). Thus, memory-guided performance should be inversely related to the slope of firing rate decrease during encoding which could be tested experimentally. Another prediction of our account is that WM span should systematically covary with the time constant of neuronal adaptation. Although some evidence suggests that encoding and maintenance are related to distinct intrinsic neuronal time constants (51), the link between the temporal properties of adaptation and mnemonic behavior is currently unknown. Since information was maintained in the hyperpolarized neuronal state, our model predicts that it should be possible to decode memories from population responses in the absence of sustained firing. Preliminary evidence from noninvasive recordings in humans supports this prediction (12, 39, 52) in that item-specific information was decodable even though there was no elevated delay activity. These findings suggest that memories were not stored in the active membrane state. Related to this issue, the process of encoding information into neuronal WM causes SRA that persists for some time. Therefore neural activity should be inversely related to memory load, and this prediction is supported by recent evidence that firing rates during maintenance were inversely proportional to the number of items held in WM (50).

Here we have investigated decreases in excitability as a neuronal correlate of WM, but transiently enhanced excitability might also play a role (7, 19, 27, 28). Indeed, while a large fraction of neurons showed memory-related spike frequency decreases, which is consistent with adaptation memory, other neurons showed a firing rate increase during maintenance (10). Spike-triggered increases in excitability could be modeled as a depolarizing conductance or an adaptive lowering of the spike release threshold. Future work needs to examine how the inclusion of diverse intrinsic plasticity principles, which enable both the up- and down-regulation of neural excitability, plays out in shaping network dynamics. A neuronal account of WM broadly supports a dynamic coding framework according to which information is maintained not as a stationary state but as a transient process which is characterized as a variable path of neural activity through a high-dimensional state space (10, 13, 51, 53).

Materials and Methods

Neuron Model.

Leaky integrate-and-fire neurons used in our simulations had a fixed voltage threshold with conductance-based mechanisms for refractoriness and SRA (32). The subthreshold membrane dynamics is described by the equation

$$\begin{array}{c}\hfill C_m\frac{dV\left(t\right)}{dt}=\hspace{0.17em}\frac{1}{R_m}\left(V_{\text{rest}}-V\left(t\right)\right)+I\left(t\right)-\left(g_{\text{sra}}\left(t\right)+g_{\text{ref}}\left(t\right)\right)\left(V\left(t\right)-E_K\right),\end{array}$$ [1]

where $V_{\text{rest}}$ is the resting potential, $R_{\text{m}}$ denotes the leakage resistance, $C_{\text{m}}$ is the membrane capacitance, and $I\left(t\right)$ is the total current flowing into the neuron at time $t$. When the membrane potential reached threshold $V_{\text{th}}$, a spike occurred, and $V$ was reset to $V_{\text{rest}}$. SRA was modeled as a ${\mathrm{K}}^{+}$-conductance $g_{\text{sra}}$ with reversal potential $E_K$. Following a spike, this conductance was increased by $g_{\text{sra}}\leftarrow g_{\text{sra}}+\mathrm{\Delta }{g}_{\text{sra}}$, and it decayed back to 0 exponentially with time constant ${\tau }_{\text{sra}}$ otherwise.

$${\tau }_{\text{sra}}\frac{d{g}_{\text{sra}}\left(t\right)}{dt}=-g_{\text{sra}}\left(t\right).$$ [2]

Another conductance $g_{\text{ref}}$ generated a relative refractory period during which neurons were prevented from spiking. Its dynamics was also modeled as an exponential decay with time constant ${\tau }_{\text{ref}}$. Both conductances modeled spike aftereffects and acted homeostatically to prevent runaway activity in the network. While $g_{\text{ref}}$ had a strong, short-term impact on the neuron, $g_{\text{sra}}$ was smaller but decayed more slowly (e.g., ${\tau }_{\text{sra}}=$ 200 ms, ${\tau }_{\text{ref}}=$ 2 ms).

Synaptic Coupling.

Neurons were interconnected through synapses to transmit signals. For simplicity, current-based synapses were used. The shape of synaptic currents $I_{ij}\left(t\right)$ was modeled as an instantaneous rise, triggered by a presynaptic spike, followed by an exponential decay with time constant ${\tau }_{\text{syn}}$,

$$\frac{d{I}_{ij}\left(t\right)}{dt}=-\frac{I_{ij}\left(t\right)}{{\tau }_{\text{syn}}}+w_{ij}\sum _{t_j}\delta \left(t-t_j\right),$$ [3]

where $w_{ij}$ is the synaptic weight from the presynaptic neuron $j$ to the postsynaptic neuron $i$, $\delta \left(.\right)$ is the Dirac delta, and $t_j$ are the spike times of the presynaptic neuron $j$. The total current into each neuron was the sum of the individual contributions of excitatory and inhibitory synaptic currents from within the network, currents generated by the adaptive conductances, and the external drive due to language input.

Network Graphs.

Spiking networks were composed of 1,000 neurons with 80% excitation (E) and 20% inhibition (I) and had directed feed-forward graphs. These were obtained by inserting a synapse $w_{ij}$ between randomly chosen pairs of neurons $j$ and $i$. If the synapse created a cycle, it was discarded, else it was retained. This procedure was iterated until the target connection density was reached. Synaptic weights were drawn uniformly from the interval [0,1] $\hspace{0.17em}\subset \mathbb{R}$. To globally balance E and I, inhibitory synapses were scaled to be five times stronger on average than excitatory ones. Weights were kept constant throughout the simulations. Networks were simulated with a temporal resolution of 0.2 ms, and Euler’s method was used for numerical integration. All neuron, synapse, network, and simulation parameter values are listed in Table S3.

Language Input.

Language sequences were generated from English construction grammar templates that were instantiated over a lexicon of 75 words from 9 word categories (SI Appendix, Table S1). As network input, $\sim$1,500 unique sentences were randomly generated from this grammar and concatenated into a sequence of 12,500 words. Sentences were between 2 and 17 words long with a mean utterance length of 8.6 words. Exposure time for each word was proportional to its orthographic length (e.g., “apple”, 5$\times 50$ ms = 250 ms). The language generated approximately $1.67\times 10^9$ distinct utterances, and network input consisted of less than 0.0001% of the total number of sentences licensed by the grammar.

State Decoding.

Network states were defined as vectors of membrane potentials $V$ with each component corresponding to the current voltage of one neuron (SI Appendix). States were sampled at a constant rate of 200 Hz and averaged within words for each neuron. The collection of states was split into input and test sets (fivefold cross-validation) and standardized before entering into a logistic regression classifier. The classifier mapped network states onto target semantic role labels and was estimated using conjugate gradient descent with regularization.

Model Evaluation.

Accuracies reported in Figs. 2 and 3 are based on a $\kappa$ statistic for multinomial classification with $\kappa =\left(acc-rand\right)/\left(1-rand\right)$, where acc is the raw labeling accuracy and rand is the expected accuracy of a random classifier obtained through permutation of the semantic roles (or words in case of binding queries) assigned by the decoder. The conservative $\kappa$ measure factors out what could be achieved by chance on the same distribution of labels.

Data Availability.

Simulation data and model code data have been deposited in the Max Planck Institute for Psycholinguistics Archive (https://hdl.handle.net/1839/8a42116e-77a7-46e1-b838-beee60e4e11a).