Properties of Aqueous Trehalose Mixtures: Glass Transition and Hydrogen Bonding

Abstract

Trehalose is a naturally occurring disaccharide known to remarkably stabilize biomacromolecules in the biologically active state. The stabilizing effect is typically observed over a large concentration range and affects many macromolecules including proteins, lipids, and DNA. Of special interest is the transition from aqueous solution to the dense and highly concentrated glassy state of trehalose that has been implicated in bioadaptation of different organisms toward desiccation stress. Although several mechanisms have been suggested to link the structure of the low water content glass with its action as an exceptional stabilizer, studies are ongoing to resolve which are most pertinent. Specifically, the role that hydrogen bonding plays in the formation of the glass is not well resolved. Here we model aqueous trehalose mixtures over a wide concentration range, using molecular dynamics simulations with two available force fields. Both force fields indicate glass transition temperatures and osmotic pressures that are close to experimental values, particularly at high trehalose contents. We develop and employ a methodology that allows us to analyze the thermodynamics of hydrogen bonds in simulations at different water contents and temperatures. Remarkably, this analysis is able to link the liquid to glass transition with changes in hydrogen bond characteristics. Most notably, the onset of the glassy state can be quantitatively related to the transition from weakly to strongly correlated hydrogen bonds. Our findings should help resolve the properties of the glass and the mechanisms of its formation in the presence of added macromolecules.

1. Introduction

An effective way for living cells to tackle stresses imposed by their environment involves the reversible accumulation of osmolytes, small molecules used to regulate cellular osmolality.¹ Unique among these osmolytes is the disaccharide trehalose (α-d-glucopyranosyl-α-d-glucopyranoside, see Figure 1A for chemical structure), known to serve an important role in the survivability of biological live forms, including plants, algae, yeasts, bacteria, and insects.² At the molecular level, trehalose is known for its exceptional ability to thermodynamically stabilize macromolecules such as proteins in their biologically active native state³⁻⁶ and to prevent their aggregation.^7,8 Moreover, it was observed to be an efficient stabilizer of lipid membranes,^6,9 and has even been reported to have a protective effect against β and γ radiation on DNA.¹⁰ Consequently, trehalose is continuously integrated into various biotechnological applications: as an additive in foods and cosmetics,^11,12 in antibody products,¹¹ and even in organ preservation for transplants.¹³⁻¹⁵

Figure 1.

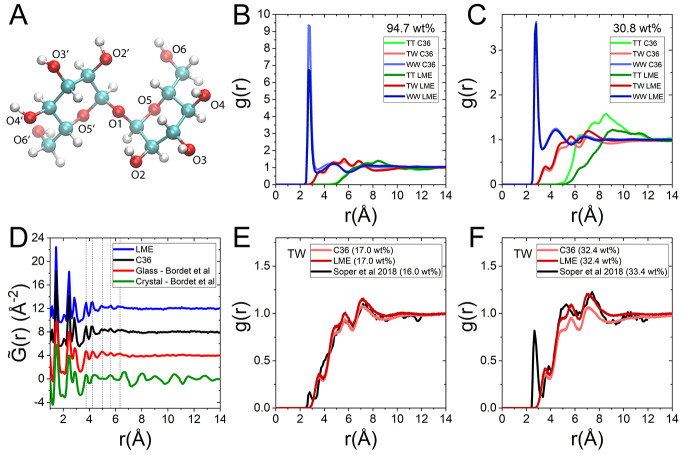
Structure of binary trehalose–water mixtures, in solution and in the glassy state. (A) Schematic structure of α,α-trehalose, denoting the eight hydroxyl groups and three etheric oxygens. (B) Comparison of radial distribution functions (RDF) g(r) derived from C36 and LME force fields, shown for trehalose–trehalose (TT), trehalose–water (TW), and water–water (WW) correlations, at high trehalose content (94.7 wt %) and at 298 K. (C) Same plots as part B shown for lower trehalose content (30.8 wt %, 1.3 molal). (D) Pair distribution function G̃(r) for pure trehalose in the crystalline and glassy states of 100 wt % trehalose, derived from simulations and from experimentally reported data.⁶⁰ Data sets are shifted for clarity. (E and F) Simulated radial distribution function g(r) compared to X-ray guided EPSR simulation-derived function, as reported in ref (62), shown for TW correlations at two concentrations.

Vitrification of trehalose to an amorphous glassy state is strongly implicated in trehalose’s protective capabilities.¹⁶ Indeed, at exceptionally high concentrations, trehalose allows some organisms including yeast, nematodes and possibly tardigrades to undergo anhydrobiosis in response to desiccation and heat stress, resulting in a protective state where cellular components are set in the sugar’s glassy matrix.¹⁷⁻¹⁹ Glassy states generally form when a liquid is cooled lower than its melting temperature, T_m. The viscosity of the supercooled liquid then quickly rises to the point that, at the glass transition temperature, T_g, relaxation and thus equilibrium are unattainable on experimental time scales.²⁰ This transition is also witnessed in thermodynamic parameters, including heat capacities and thermal expansion.²¹ Notably, the glass transition temperature for trehalose is significantly higher than other disaccharides such as sucrose,²²⁻²⁶ with a difference of ∼50° C in T_g between the two.²⁶

Several molecular mechanisms have been proposed to explain the extraordinary propensity of trehalose toward macromolecular stabilization and the link to its glass forming properties. The water entrapment hypothesis suggests that trehalose enables water encapsulation at the macromolecular interface as trehalose is strongly excluded from the macromolecular interface.²⁷ This is supported by the known preferential exclusion of trehalose from macromolecules evidenced in much more dilute solutions,^3,28,29 from simulations of lysozyme in trehalose glass,³⁰ and from calorimetry performed in the glassy state.³¹ Alternatively, the water replacement hypothesis relates stabilization to the exchange of macromolecular hydrogen bonding with water in favor of hydrogen bonding with trehalose,³² thus emphasizing the more direct interaction between trehalose and the stabilized macromolecule. Somewhat related, the anchorage hypothesis, states that trehalose’s stabilizing effect is a consequence of the coupling of protein to the sugar–water matrix through a strong hydrogen bonding network that makes it “harder” for proteins to unfold, as it involves restructuring the embedding medium.^33,34 Water is thought to act as the anchor between the macromolecule and the glass matrix.³⁰ It was further suggested that higher viscosity of the trehalose solution results in hindered fluctuations of macromolecules.^35,36 Because of the significant difference in T_g, the viscosity of trehalose mixtures remains higher than many other disaccharides and thus may enhance its protective effect. Although these and additional suggested mechanisms are not mutually exclusive, they highlight the challenges in studying the highly concentrated glassy state and the possible considerations that may play a vital role in macromolecular stabilization.

While several mechanisms underscore the slowed dynamic aspect of the trehalose glass, vitrification alone is insufficient in explaining trehalose stabilizing abilities, as the direct hydrogen bonding between trehalose and macromolecule have also been shown to be crucial.²⁶ For example, the shift in the amide II FTIR band in lysozyme, which is observed when water is removed, is greatly reduced in the presence of trehalose, indicating a replacement of water by trehalose hydrogen bonding.³² Yet, as was found for lysozyme in simulation, trehalose glass may be unable to fully replace all the hydrogen bonds that are available in diluted solution.³⁰ Beyond the direct macromolecule–sugar interactions, water–sugar hydrogen bonds may affect the glass matrix properties; for example, inelastic neutron scattering (INS) measurements show trehalose to be destructive to the water hydrogen bonding network.³⁷ In contrast, recent neutron diffraction experiments have shown little effect of trehalose on water structure.³⁸ Thus, despite increasing efforts, a comprehensive understanding of the role of hydrogen bonding in stabilizing the glassy state of trehalose glass is still lacking.

Here, we probe properties of binary water–trehalose mixtures by using molecular dynamics (MD) simulations. While MD simulations have been widely used to predict molecular mechanisms and solution structures of trehalose–water mixtures,^30,39 they often lack the accuracy required to faithfully represent important mixture properties. Indeed, over aggregation is usually observed in simulations of aqueous solutions for a wide array of related solute molecules.⁴⁰ We have previously shown that within CHARMM-type force fields, trehalose tends to over aggregate in simulated binary solutions compared to experiments.³⁹ Modified CHARMM36 force fields calibrated with thermodynamic solution data have recently been suggested to resolve this overaggregative nature.^41,42

Thus, the aims of this study are two-fold: to validate current available force fields and to use these to resolve the role of hydrogen bonding in glass formed by trehalose. Toward the first goal, we asses the fidelity of available contemporary models of trehalose across a wide temperature range and over the entire concentration range: from dilute solutions to highly concentrated solutions, reaching the glassy state. This validation is essential to fully resolve the impact of trehalose (and other osmolytes) in binary mixtures and is a necessary precursor to modeling realistic solutions that contain additional macromolecules such as proteins. We validate and compare trehalose properties in solutions using the CHARMM36 force field and a recent modified version proposed by Lay et al.⁴¹ (which we herein denote LME). We interrogate these two force fields by comparing structural (pair distribution functions) and thermodynamic (osmotic pressure and T_g) properties of water–trehalose mixtures in simulations and experiments. As we show in the following, while “dry” or glassy mixtures show similar structures and properties in both force fields, differences in structure are observed for dilute solutions, due to the added trehalose–trehalose mutual exclusion in the LME force field, leading to increased trehalose hydration. The difference in structure is followed by an improved agreement between calculated and experimental osmotic pressure in hydrated mixtures using LME. The T_g values we obtained from simulations are in close agreement with experimental data for both force fields.

Our second goal in this study is to resolve the role of hydrogen bonding in the stabilization of trehalose’s glassy state. We show that our recently suggested methodology for estimating the hydrogen bond strength in simulations is uniquely and intimately related to the transition from the liquid to the glassy states. Specifically, we find that upon transition to the glassy state, hydrogen bond free energies reflect a change from weakly correlated hydrogen bonds in the hydrogen bond network to a strongly correlated (cooperative) network of entropically stabilized hydrogen bonds.

2. Methods

All-atom molecular dynamics (MD) simulations were performed with the GROMACS⁴³ package. Two force fields were used and compared: unmodified CHARMM36⁴⁴ (denoted herein C36) and a reparametrized version of CHARMM36 calibrated by Lay et al.⁴¹ The calibration is designed to reproduce experimental osmotic pressure for sucrose and its interaction with diglycine, as osmotic pressure has become an established tool to adjust sugar^41,45 and salt⁴⁶ force-fields. While LME was calibrated for sucrose, the common atom types and the fact their methodology involved modifications of sucrose–sucrose interactions make their parameters transferable and appropriate for trehalose. In all simulations, the water model used is TIP4P-ew.⁴⁷ This water model is different than the original one used with the LME and C36 force fields and is motivated by its good performance in protein folding simulations.⁴⁸ In the following, we verify the validity of these force fields with this particular water model in our current implementation.

All simulations were conducted in the isobaric-isothermic ensemble (NPT), while all bonds to hydrogen atoms were constrained with the LINCS algorithm.⁴⁹ Pressure was maintained at 1.01 bar using the Parrinello–Rahman method,^50,51 and temperature coupling was achieved with a Nosé–Hoover extended ensemble.^52,53 Electrostatic calculations were performed using fast Smooth Particle-Mesh Ewald (SPME) electrostatics with 1.3 Å grid spacing.^54,55 Lastly, van der Waals interactions were cutoff at a distance of 12 Å, with a smooth switching distance of 10 Å. Mixtures of 24 different trehalose concentrations were generated (see Table S1 in the Supporting Information), in cubic simulation boxes with edge lengths ranging from 45 to 60 Å.

To derive the glass transition temperature, T_g, an annealing protocol was used as follows: each mixture was run for 50 ns at high temperatures (480 K or 600 K for concentrated mixtures over 90 wt % trehalose), followed by a cooling cycle to 100 K at a constant rate of 10 K/ns. The cooling cycle was performed by running short isothermal simulations lasting 0.5 ns while using the previous step’s final trajectory as a starting point for the next isothermal simulation at a lower temperature. At each iteration, the temperature is decreased by 5 K (see Figure S1 in the Supporting Information). In addition, a heating cycle was also performed to account for hysteresis of the glass under heating/cooling cycles, whereby a faster initial cooling rate of 500 K/ns was used to drop the temperature from 480 K or 600 K down to 100 K, followed by heating at a rate of 10 K/ns back to the initial annealing temperature. Only the second half of each trajectory in the heating/cooling cycle is used in the analysis of the glass transition temperature (0.25 out of 0.5 ns for each temperature between 100 K to 480 K/600 K), and each data point shown is an average of the results from the cooling and heating cycles. Enthalpy and volume for the T_g analysis were calculated by the g_energy script, while diffusion coefficients were calculated with the g_msd script; both scripts are part of the Gromacs package. Spatial distribution functions were calculated using the Travis package.⁵⁶

Certain structural and thermodynamical analyses, i.e., the radial distribution function, osmotic pressure, and hydrogen bonding free energies, required more extensive statistical sampling. To this aim, longer isothermic simulations of 20 ns were conducted for each mixture at different temperatures ranging from temperatures below T_g to above T_g of each specific concentration (Table S2 in the Supporting Information). The initial frames for the 20 ns runs were taken from the cooling cycle trajectories. All the mixtures below 41 wt % at 298 K were simulated for 50 ns, of which the last 30 were used for analysis. Lastly, to account for the metastable nature of glass, the cooling cycle and the longer isothermic simulation were repeated five times in total to probe and average the thermodynamic quantities over different realizations of the same thermodynamic state.

3. Results and Discussion

3.1. Radial and Spatial Distribution Functions

To probe the structure of the trehalose–water mixtures in the two different force fields, LME and C36, we first compare radial distribution functions, g(r), defined as

1

where ρ(r) is the local number density of water or trehalose with respect to a reference atom (the oxygen for water and O₁ for trehalose, see Figure 1A), and ρ₀ is its bulk density. Figure 1B,C shows the radial distribution function for each type of interacting particle pairs in the trehalose–water binary mixtures (water–water, trehalose–water, and trehalose–trehalose). These radial distribution functions are calculated from simulation at two representative concentrations at 298 K, one corresponding to the aqueous solution state (30.8 wt % trehalose, equivalent to 1.3 molal that is well below the solubility limit, Figure 1C) and the second for a much lower water content corresponding to the glassy state (94.7 wt % trehalose chosen to allow comparisons with experimental data available at 33% relative humidity,⁵⁷Figure 1B).

For water–water (WW) interactions, we find no significant difference between the C36 and LME force fields. The first solvation peak is located at 2.8 Å for both concentrations, while the second solvation peak moves from 4.4 Å to 4.8 Å as trehalose content is increased from 30.8 wt % to 94.7 wt %. The shift in the second WW peak from 4.5 Å in pure water⁴⁷ to 4.4 Å in 30.8 wt % is in good agreement with published EPSR simulations, where at 43 wt % the peak is shifted from 4.56 Å to 4.34 Å.^58,59 In contrast, interactions that involve trehalose (T) molecules (i.e., TW and TT interactions) are more sensitive to the force field. Specifically, at low trehalose content (Figure 1C), the location of the first TT correlation peak varies by ∼0.6 Å between the two force fields (compare 8.5 Å in C36 with 9.1 Å for LME) and the peak height is significantly lower for LME (Figure 1C light versus dark green). These differences result from the increased trehalose–trehalose repulsions introduced in LME, allowing for bulklike densities to be reached already at shorter TT separations. This increased repulsion also implicitly induces increased trehalose water attraction, resulting in an enhanced hydration of trehalose molecules.

Figure 1C shows the complementary TW radial distribution function, indicating stronger hydration for LME at 30.8 wt % (seen as higher hydration peak compared to C36) as water effectively interacts more strongly with trehalose in LME compared to the same interaction in C36. By contrast, at low water content (Figure 1B), no significant difference is observed between the two force fields for the corresponding TT (in green) and TW (in red) correlation functions (compare Figure 1B light versus dark colors). These findings underscore the subtle balance of interactions in the binary mixture. Specifically, at low enough water content, the reparameterization of sugar–sugar interactions has little effect on the structure of the sugar matrix. However, as water content increases, water–sugar interactions become important and impact the mixture structure.

To validate and compare the structure of trehalose in the glassy state in simulation and experiment, we further compared our results with the recently reported structure of pure trehalose in the glassy and crystalline states, as resolved using X-ray powder diffraction.⁶⁰ The structure was reported in terms of the pair distribution function,⁶¹ defined as G̃(r) = 4πr[ρ^e(r) – ρ₀^e], where ρ^e(r) and ρ₀ are the electron density at distance r and in the bulk, respectively. The calculation of the pair distribution function from simulations is performed using the relation,⁶¹

2

where b_i is the scattering power of the ith atom, taken here for comparison with the X-ray experiments as the number of electrons of the specified atom.

Figure 1D shows G̃(r) calculated from simulations using both C36 (shown in black) and LME (blue) for 100 wt % trehalose in the amorphous state at T = 298 K as well as the experimental distribution for the amorphous (red) and the crystalline (green) states. We find a very good correspondence between the two force fields as well as with the experimentally resolved function for the glass. As could be expected, all curves are similar below 4 Å, corresponding mostly to intramolecular distances. Above this distance, both intermolecular and intramolecular pairs contribute to G̃(r), and in accordance the distribution of the crystal phase (Figure 1D, green) deviates significantly from that of the glass (red). This difference reflects the long-range order in the crystalline phase with multiple correlation peaks, contrasted with the more weakly correlated glassy state, where above 6.3 Å, G̃(r) of the glass levels off in both simulation and experiment. Importantly, for both force fields the simulated glass is in good agreement with the experimental structure over the whole range of distances. Vertical dotted lines mark the position of each significant peak in the experiment for the glassy state, indicating the close proximity of peak position in all amorphous-state curves (experimental and simulated). This similarity between force fields in the structure of the glassy state is also reflected in Figure 1B,C, as discussed above.

For another comparison with experiments, Figure 1E,F juxtaposes our simulation results with experimentally based EPSR simulations by Soper et al.⁶² In very diluted mixtures, trehalose–water (TW) correlations in experiment and simulations are in close agreement, as seen in the radial distributions of mixtures with similar concentrations (17 wt % in simulations compared with 16 wt % in the experiments and see also additional comparison with experimentally derived structure factor, Figure S2 in the Supporting Information). For a more concentrated liquid mixture (32.4 wt % and 33.4 wt % for simulations and experiments, respectively, panel F), trehalose–water interactions for LME are close to those reported by Soper et al., while C36 shows consistently lower values for the correlation function all the way to bulk values, suggesting overall weaker trehalose hydration in this force field. We note in passing that the apparent peak at ∼2.6 Å in the TW curve from EPSR for 33.4 wt % may be artifactual since it is absent at all other concentrations reported (both higher and lower)⁶² and is also absent in all our simulation results.

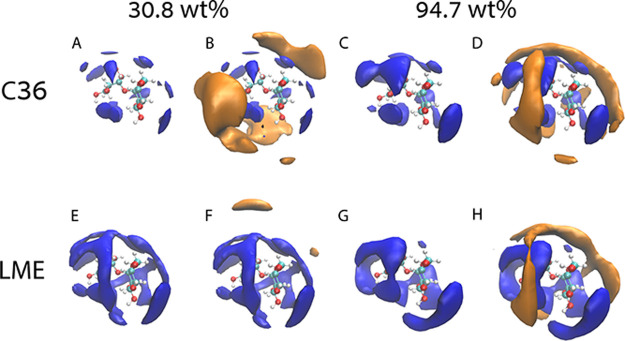
Additional insights to the mixtures’ structure are afforded by the spatial distribution functions (SDFs), Figure 2. All SDFs were calculated with the central etheric trehalose oxygen (O1 in Figure 1A) and the two adjacent carbons as the reference frame. Results are presented as iso-surfaces for particle densities for finding any atom of a water molecule (shown in blue) or a trehalose molecule (orange) in specific spatial relation with respect to trehalose molecules. The SDF for the 30.8 wt % mixture shows a significantly larger number of neighboring water molecules in LME compared with C36 (Figure 2A,E), while the reverse is seen for trehalose (Figure 2B,F), so that less sugar molecules surround the reference trehalose in LME compared to C36. Note that since trehalose−trehalose correlations are considerably stronger for the C36 force field, the iso-surface of trehalose was reduced in C36 for 30.8 wt % compared to LME for 30.8 wt %, (Figure 2B,F, from an iso-value of 0.7 nm⁻³ to 0.78 nm⁻³, see Figure S3 for a comparison that uses the same iso-value). A similar trend can be observed at the glassy state (94.7 wt % of trehalose), where the local density of water around trehalose increases (Figure 2C,G) and sugar decreases (Figure 2D,H); however, the difference between force fields is much smaller.

Figure 2.

Spatial distribution function (SDF) of the same mixtures as in Figure 1B,C. (A) C36, 30.8 wt % showing the water iso-surface (blue), i.e., particle number density iso-surface of water molecules around trehalose reference atom. (B) Same as in part A but in addition also showing the trehalose iso-surface (orange). (C) C36 for 94.7 wt % and water iso-surface. (D) Same as in part C but in addition also showing the trehalose surface. (E–H) The same as in parts A–D for LME. For 30.8 wt % water surfaces (A, B, E, F) the iso-value is 3.5 nm^–3, while trehalose surface iso-value is 0.78 nm^–3 for C36 (B) and 0.7 nm^–3 for LME (F). For 94.7 wt % water surfaces (C, D, G, H), the iso-value is 4.52 nm^–3 and for trehalose (D and H) 2.70 nm^–3. See Figure S3 for comparison of parts B and F with the same iso-value.

3.2. Osmotic Pressure from Kirkwood–Buff Solution Theory

After comparing the mixture’s structure from the two force fields with experiments, we turn to compare physical and thermodynamic properties of the mixtures. We start with the variation of osmotic pressure with concentration, a property known to be sensitive to the effective interactions in solution. The Kirkwood–Buff (KB) theory of solutions⁶³⁻⁶⁵ links the radial distribution function, g(r) with the (derivative of) osmotic pressure, Π, allowing us to compare simulation and experimentally derived osmotic pressures. The KB integral for the interaction of species i and j is defined as

3

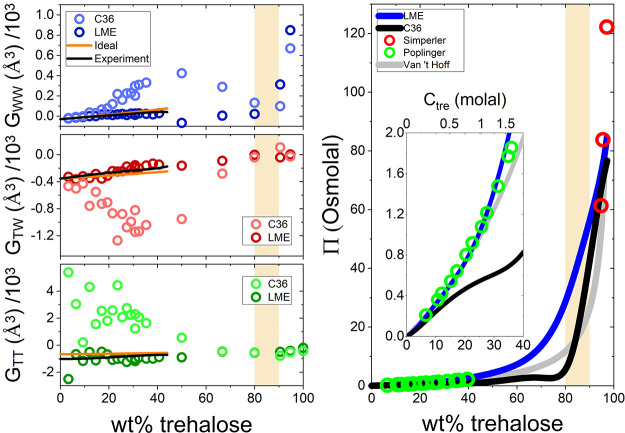
where g_ij(r) is the radial distribution function for the different pairs’ correlations (TT, TW, and WW) in the binary mixture, featured in Figure 1. In principle, r_bulk in eq 3 should extend to infinity but in practice it is truncated in finite sized simulation. This truncation of r_bulk may produce inaccuracies in the calculated KB integrals. Methods formulated over the past decade to obtain KB integrals from MD simulations can overcome this issue and help avoid other convergence difficulties in the integration.^66,67 However, it was also shown that with large enough simulated systems and longer simulated times that allow proper convergence, these methodologies give comparable results with the traditional method, allowing further insight into spatially resolving the origin of preferential interactions.⁶⁷ We validated the convergence of our results and show their agreement with experiments in the following. The values of G_ij converge at the bulk as g_ij(r) get closer to 1 (Figure S4). The left panels in Figure 3 show the KB integrals for all pairs over a wide range of concentrations. In all cases, the KB integrals for LME (dark color) are in considerably better agreement with both the ideal curve and experimental results (see section S3 in the Supporting Information for details) as compared to C36 (light color). In line with the overaggregative nature of this force field, C36 shows a strong net exclusion of water molecules from trehalose (red), with a corresponding strong inclusion of trehalose molecules around trehalose (green) as well as water around water (blue). Yet, at high trehalose content (above T_g, orange shaded bar), the KB integrals from both force fields converge to similar values. Taken together, this may suggest that the mixture’s intermolecular interactions are properly represented in both force fields at very concentrated states, as also concluded from the structural comparisons of g(r) and SDF.

Figure 3.

Osmotic pressure in simulations and experiments. (left) Kirkwood–Buff integrals for the pairwise interactions in aqueous trehalose solution as a function of concentration. Light circles represent C36, dark circles represent LME, the orange line is data calculated from van ’t Hoff’s law (ideal solution), the black line indicates the experimental result^12,39 derived by Kirkwood−Buff inversion⁶⁸ (see section S3 in the Supporting Information). (right) Osmotic pressure calculated for both LME (blue) and C36 (black) force fields from 0 wt % to the most concentrated mixture with experimental data available, 97.1 wt %. The experimental values are from Poplinger et al.¹² (green circles) and Simperler et al.⁵⁷ (red circles). The orange bar presents the range in which a glass transition occurs at room temperature, estimated from our heat capacity data (see text for details). The inset zooms in on the solution regime up to the saturation limit (∼1.6 molal).

The derivative of the reduced osmotic pressure Π̃ = Π/RT (typically reported in units of osmolal), with respect to water density is related to the KB integrals through,⁶³

4

where m_w is the molality of pure water. This relation allows calculation of Π̃ by integration over water density, ρ_w, from low to high trehalose concentrations.

The right panel in Figure 3 shows the resulting osmotic pressures as a function of concentration compared to experimentally derived Π̃ by Popilinger et al. for trehalose solutions¹² and Simperler et al. for the glass.⁵⁷ Osmotic pressure values derived using LME are close to the van ’t Hoff (ideal solution) values up to 25 wt % (∼1 molal). Importantly, LME faithfully reproduces the small positive deviation from ideality that is observed experimentally between ∼1 molal and ∼1.6 molal (seen in the right panel inset), which is close to the saturation limit²³ (∼36 wt %). By contrast, C36 deviates already around 10 wt % (0.3 molal), reaching osmotic pressures much lower than both the experimental and ideal values. Note that experimental osmotic pressure is lacking between ∼36 wt % and ∼94.7 wt %, probably because trehalose tends to phase separate in that range, i.e., the homogeneous water–trehalose mixture is metastable. In the simulations it is in principle possible to follow the metastable state from which it is possible to link values of osmotic pressure from the high and low concentration phases.

The shaded band in Figure 3 indicates the range in which the mixture goes through the glass transition in both experiments and simulations (as further discussed below). We find that above this transition concentration, at high trehalose concentrations (∼90 wt % and above), osmotic pressure values for LME and C36 become similar, with osmotic pressure slightly higher for LME compared to C36. This finding is supported by the similar structure found in both force fields as discussed for both g(r) and G̃(r) at these high trehalose contents, i.e., the mutual exclusion of water and trehalose in both force fields is comparable at low water content, with trehalose molecules being slightly more excluded in LME compared to C36.

3.3. Glass Transition Temperature

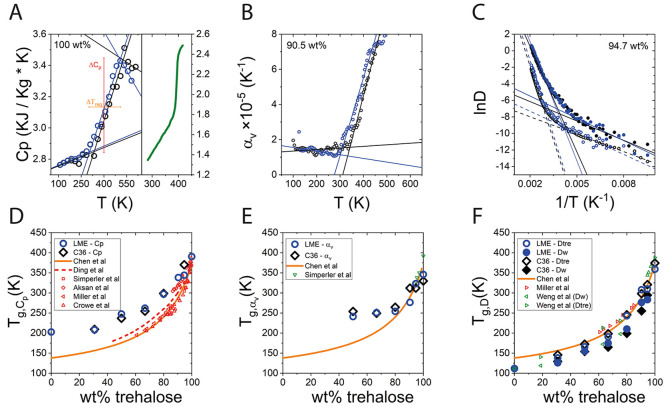
An important parameter that requires validation for mixtures undergoing a liquid to glassy state transition is the glass transition temperature (T_g), which is also sensitive to molecular interactions. There is a variety of methods to estimate T_g, and each may reflect a different feature in the glass transition.⁶⁹Figure 4 panels A–C show three commonly used methods for deriving T_g as applied to trehalose–water mixtures. Panels D–F show corresponding T_g values versus trehalose weight percent in simulations. For comparison, we show also relevant experimental results (red), previously reported simulations (green), and a Gordon–Taylor fit (orange line) to a large ensemble of reported T_g values by Chen et al.²³ Each value of T_g in simulation was averaged over the cooling and heating cycles to minimize the influence of hysteresis.

Figure 4.

Methods for determining of the glass transition temperature in simulations and experiments. Top row: (A) Heat capacity derived at different temperatures during the heating cycle (details in Figure S1), calculated for 100 wt % (left panel), and derived experimentally using DSC by Ding et al.⁷³ (right panel, in green). (B) Thermal expansion coefficient at different temperatures for 90.5 wt %, during the heating cycle. (C) The natural logarithm of the diffusion coefficient for 94.7 wt %, during the cooling cycle. Full circles are for water diffusion and empty circles are for trehalose diffusion. Bottom row: Temperature of glass transition, T_g, derived by (D) heat capacity, (E) thermal expansion coefficient, and (F) diffusion coefficient. In all panels, blue is for LME and black is for C36. Experimental data reproduced from refs (24, 25,57, 72, and 75).

The first method we used relies on changes in heat capacity,

5

Figure 4A demonstrates a typical curve of C_p versus temperature, showing three distinct regimes: the glassy state (below ∼300 K), the transition region (between 300 K and 500 K), and the rubbery state (above ∼500 K), as characterized by different slopes. For a glass transition, the heat capacity does not diverge (as in first order phase transitions) but rather varies smoothly between regimes. Heat capacities calculated from classical simulation are known to be significantly overestimated compared with experimentally derived heat capacities, since quantum atomic vibrations are not accounted for.⁷⁰ However, although harmonic quantum corrections may improve the accuracy of the calculated heat capacity values, the position of the phase transition as seen in the change of heat capacity with temperature does not change significantly.⁷¹ We therefore use the temperature dependence of the MD-derived heat capacity to evaluate T_g, using the methodology previously reported.⁷² Three linear fits to each regime are used to determine the temperature at the intersections; T_g is typically defined as the average of temperatures at the intersection points. For comparison, plotted in green to the right of the calculated heat capacity is the corresponding experimental heat capacity as reported by Ding et al.⁷³ The transition region is characterized by both the extent of change in heat capacity along the transition (ΔC_p, red) and the spread of the glass transition region (ΔT_reg, orange). Overall, ΔC_p is very similar in both force field and in experiments with values of ∼0.58 kJ kg^–1 K^–1 and 0.68 kJ kg^–1 K^–1 in LME and C36 compared to the experimental value of ∼0.55 kJ kg^–1 K^–1 for the fully dry glass,^69,73Figure 4A. However, ΔT_reg found in simulation is somewhat larger than experimental values. This is perhaps not surprising, as this has been reported previously in simulations⁷² and can be attributed to the fast cooling rate in simulation (10 K/ns) compared to the much slower experimental rates (∼10^–8–10^–12 K/ns). Since the mixture is not allowed enough time to vitrify as in typical DSC experiments, heat capacity changes are smeared over larger temperature ranges. Also, the finite size effect may cause the widening of ΔT_reg in simulation compared to experiments. Both ΔC_p and ΔT_reg are in good agreement with reported values from other reported simulations (see Table S4 and Figure S6 in the Supporting Information). The overshoot seen in the heat capacity toward the high temperature end of the glass transition is evident in both simulation and experiment and is typically attributed to enthalpic relaxation.^25,74

At high concentrations, T_g, Cp derived from the heat capacity (Figure 4D) is in good agreement with the experimental data for both force fields, while deviating to larger T_g values than experiments at lower trehalose concentrations, converging to a value of T_g, Cp = 211 K for pure TIP4P-ew water. At high concentrations (above 80 wt %) LME results in a slightly improved value for T_g compared to C36, which suggest a better representation for TT molecular interactions in LME. No improvement is noted for lower trehalose concentrations, where T_g, Cp is practically the same in both force fields. This may be the result of the water model that eventually dominates the heat capacity at higher water contents.

Another method to determine T_g involves the thermal expansion coefficient, defined as

6

The change in volume of a vitrified trehalose–water mixture with temperature has a different behavior from the rubbery liquid state, i.e., the glassy state shows weaker thermal expansion, compared with the liquid state.²⁰ This can be used to determine T_g, from the point where the thermal expansion coefficient changes its trend. Figure 4B shows that for the glass state, α_V is observed to be almost constant, while in the liquid state α_V increases with the temperature. Two lines are fitted to the different regimes, and T_g is taken as their intersection. For the concentrated mixtures (i.e., 80–100 wt %), the T_g values derived from the thermal expansion coefficient (panel E) shows improvement when using LME compared to C36, similarly to the heat capacity derived T_g. We note that T_g values at trehalose content below 50 wt % could not be estimated by thermal expansion coefficient, as a noticeable kink in α_v vs T impedes the identification of the glass transition point (see Figure S7).

The diffusion coefficient in simulations can be calculated based on the Einstein relation,

7

where |r_l(t) – r_l(0)|² is the mean square displacement at time t and the ⟨···⟩ represent ensemble averaging. The natural logarithm of the diffusion coefficient is typically assumed to follow the Arrhenius relation ln D ∝ −E_a/RT.⁷² The glass transition is then typically found to indicate the onset of a change in the activation energy for diffusion.^20,21,76 Thus, an estimate of T_g can be derived from the intersection of the linear extrapolation of the glass and liquid regimes, Figure 4C. The T_g values derived from diffusion (Figure 4F) show the smallest improvement in T_g prediction between C36 to LME. Typically, T_g values derived from trehalose diffusion are higher than T_g derived from water diffusion. This result is not surprising as the smaller water molecules can maintain higher diffusion rates over the entire range, compared to the bulky trehalose. This is also highly dependent on the water model we chose that reproduces diffusion quite well, while its melting temperature is considerably lower than experiment.^47,77 The higher values derived from trehalose diffusion conform better to the experimental fit of Chen et al.²³

Taken together, the results indicate that the weakening of the TT attractions resulting from the parametrization in LME compared to C36 has an impact on the derived values of T_g calculated in simulations. The improvement in T_g derived from LME simulations compared with C36, based on values of heat capacity and thermal expansion, can be related to the overall better representation of interactions in the mixed water–trehalose mixtures. This is particularly evident at high trehalose contents for T_g. Interestingly the osmotic pressure and RDFs are more sensitive to mixtures with high water content, in contrast to T_g analysis which is more sensitive to the force-field in higher trehalose concentrations. This can be expected since at low sugar concentration, i.e., the van ’t Hoff regime, interactions are dominated by the water model, as osmotic pressure is a colligative property. Being a colligative property, the osmotic pressure is determined mainly by solute concentration and not its identity (i.e., by water activity). At slightly higher concentrations, deviations from ideality are of course dependent on the solute parameters, which are also reflected in the osmotic pressure (Figure 3). For T_g, the models are still hampered to some extent by the water force field that seems to dominate the results in the dilute regime.

3.4. Hydrogen Bond Thermodynamics

Recently, we have developed a new methodology for determining the hydrogen bonding strength from atomistic simulations,⁷⁸ which is based on an information-theoretic approach.⁷⁹ The method allows one to calculate the free energy, ΔG_HB, associated with the formation of the configurational probability distribution of a hydrogen bond (Hbond) observed in simulation out of a randomly distributed reference state. The analysis is based on purely geometric properties of the neighboring hydrogen-bonded molecules in the mixture (specifically donor–acceptor distances and angles). Importantly, there is no need to define a specific or exact Hbond conformation or parameter range, which makes the method a practical tool for calculating the strength of a hydrogen bond. Herein, we present an enhanced version of our methodology, validate it against a simple analytically solvable two-level model system, and then apply the methodology for all types of Hbonds in the aqueous trehalose mixtures (details of the method and comparison with the model are outlined in section S5 in the Supporting Information).

The method we use is very general, and it has been shown that when the system is coupled to a thermal bath only through heat exchange, the methodology yields exact energetic and entropic contributions to the free energy.⁷⁹ The simple analytically solvable model system coupled to a heat bath allows us to demonstrate this property (see section S5 in the Supporting Information). Specifically, we show that the method results in exact values of free energy, entropy, and energy (Figure S8). In the following, we further exploit our methodology to gain new insight into the role of hydrogen bonding in the changes the water–trehalose system undergoes upon transitioning from liquid solution to the glassy state. Specifically, we demonstrate how changes in hydrogen bond free energies can be traced to the changes in the properties of the Hbond network and link these to the glass transition.

Adam and Gibbs have shown, using a molecular-kinetic theory, that the relaxation properties of many supercooled liquids are closely related to the size of cooperatively rearranging regions, defined as “the smallest region that can undergo a transition to a new configuration without a requisite simultaneous configurational change on and outside its boundary”.⁸⁰ These regions, therefore, contain molecules which are highly correlated between them but are weakly correlated to the environment. The size of these cooperative regions decreases with temperature^20,80,81 and is expected to be negligible in the liquid phase (at least compared to the glass). Forming a link between kinetic and thermodynamic properties, in this theory the size of the regions is also inversely proportional to the entropy of the entire system.⁸¹ Here we find an analogous thermodynamic behavior of the Hbond network. Specifically, we find that the glass transition temperature marks the onset of decoupling of hydrogen bonding pairs to their surrounding Hbond neighbors as temperature is increased. This correlated nature of the glass thus implies that a change in the system (i.e., the hydrogen bond) energy would not simply be absorbed from or expelled to the bath but would also impact the close surroundings in other ways that change the surrounding’s microscopic energy states. This type of thermodynamic process is known to be equivalent to work performed on the surroundings.⁸² Practically, this makes the surroundings behave differently than a simple heat reservoir, and instead, a certain part of the surroundings act together with the system in work.

An analogy may be helpful: a well-known and illuminating example, where both system and reservoir are coupled, is the hydrophobically driven folding of proteins.⁸³ As the protein (here, the system) folds, simply following the changes in protein chain entropy would indicate that the entropy will decrease, as fewer states are available to the system. However, in many cases of hydrophobic protein folding, the reverse is observed, and a gain in system entropy is measured. This change is not due to the states of the protein chain itself but rather stems from the combined protein–water states. The protein is thus coupled through changes in the number of available states to its immediate surrounding. In a similar way, we might expect hydrogen bonds in the glassy matrix to be strongly coupled to their neighboring water/trehalose molecules and “neighboring” Hbonds and not act as uncorrelated entities coupled to their surroundings through heat exchange alone. In the following, we show that this expectation is indeed born out in our trehalose–water simulations and demonstrate that the transition to the glassy state for the water–trehalose Hbonded system is characterized as a transition from a system of largely independent Hbonds in liquid solution to a strongly correlated system of bonds in the glassy, supercooled state.

Because we have already concluded that the intermolecular interactions are better represented over the entire concentration range in LME, in the following Hbond analysis we use this force field as described in section S5 in the Supporting Information. Figure 5 shows the free energy associated with formation of hydrogen bonds as a function of temperature for two representative concentrations, one of a mixture that is in the liquid state at room temperature (30.8 wt %, Figure 5A) and the other that is in the glass state at room temperature (90.5 wt %, Figure 5B). We consider five different types of Hbonds: water–water (WW), water–trehalose hydroxide (WH), water–trehalose etheric oxygen (WO), trehalose hydroxide–trehalose hydroxide (HH), and trehalose hydroxide–trehalose etheric oxygen (HO). The free energies derived at different temperatures were fitted, and heat capacities (Figure 7) were determined based on derivatives taken from those fits (for additional information, see section S5 in the Supporting Information).

Figure 5.

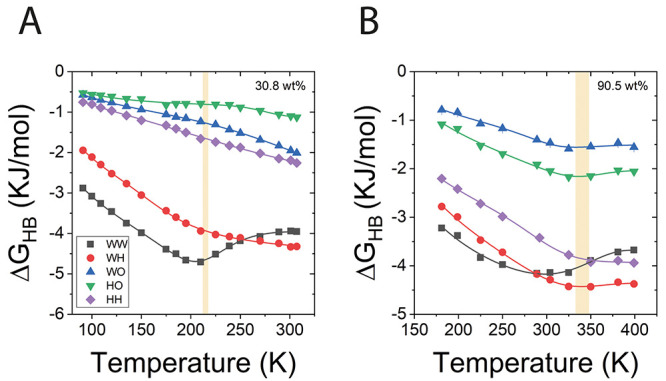
Free energy of hydrogen bonds versus temperature for all interaction pairs: water–water (WW), water–trehalose hydroxide (WH), water–trehalose etheric oxygen (WO), trehalose hydroxide–trehalose hydroxide (HH), and trehalose hydroxide–trehalose etheric oxygen (HO). For two representative concentrations: (A) trehalose content of 30.8 wt % and (B) trehalose content of 90.5 wt %. The lines are fitted as described in section S5 and eq S13 in the Supporting Information, and the shaded bar represents the range of T_g, Cp from Figure 4D.

Figure 7.

Heat capacity from hydrogen bonding free energies (top) and information entropies (bottom) for different concentrations, calculated from WW ΔG_HB: (A and D) 0 wt %, (B and E) 30.8 wt %, and (C and F) 90.5 wt %. The shaded bars are as described in the caption of Figure 5.

The free energies of trehalose–water and trehalose–trehalose Hbonds for 30.8 wt % trehalose decrease with temperature over the whole range (Figure 5A), while WW interactions reach a minimum at ∼210 K. This trend is observed also for the concentrated mixture of 90.5 wt % (panel B) with a minimum at ∼289 K for WW. Interestingly, the temperature at which the slope changes for WW and WH in the dilute mixture (30.8 wt %) and those at which the slope changes for trehalose Hbonds in the concentrated mixture (90.5 wt %) are closely related to the T_g values calculated from heat capacity (T_g values of 214 K and 340 K, respectively). The corresponding T_g based on heat capacity for the specific concentration was added to the figure as a shaded bar. The range of T_g, seen as the width of the bar, was estimated from the difference in T_g based on the cooling and heating cycles as calculated from C_p analysis (section 3.3). This change of trend at the glass transition temperature is not apparent in other extractable thermodynamic variables, such as the variation in the entropy derived directly from the Hbond probability distribution (the so-called Gibbs–Shannon information entropy, ΔS_info, see the Supporting Information for definitions) nor in the variation of the Hbond potential of mean force, PMF_HB (Figure S11, see section S5 in the Supporting Information for definitions). Indeed, both PMF_HB and ΔS_info are monotonic over the entire temperature range.

The change in slope observed in ΔG_HB at T_g is strongly related to the change in the correlation of trehalose Hbonds to its surroundings in liquid mixtures compared to the supercooled glass matrix. As long as the temperature is high enough, the Hbonded pair is fairly independent from its close surroundings. Correspondingly, for the independent WW Hbonded pair, we observe the typical expected signature, i.e., a positive slope of ΔG_HB vs T, associated (through the van ’t Hoff relation) with a negative change in entropy, ΔS_HB, upon formation of a directed Hbond from a randomly distributed one. At high enough temperature, the WW ΔG_HB reaches a plateau. Similarly, trehalose Hbonds show a similar plateau at temperatures above ∼325 K in 90.5 wt % trehalose.

Close to T_g, we find that the Hbond pair system becomes significantly correlated to its surrounding as temperature decreases, indicated by a positive ΔS_HB, in contrast to the uncorrelated Hbonds at higher temperatures, characterized by negative or close to zero values of ΔS_HB (see Figure S12 in the Supporting Information). Since the information-derived entropy due to a single Hbond is always negative (due to the restrictive nature of the Hbonded pair), Figure S11 in the Supporting Information, it follows that the positive ΔS_HB at low temperatures is dominated by contributions from the environment and is a direct result of the formation of correlated Hbond clusters. These clusters are related to the cooperative kinetic subsystems becoming larger as temperature decreases. At lower temperatures, several correlated Hbonds effectively form a cluster that is coupled with the heat reservoir, so that the entropy derived from ΔG_HB is no longer simply that of a single Hbond in contact with a heat reservoir but is rather the entropy of the entire correlated thermodynamic system. Specifically, the entropy change of this effective system can be significantly different than the entropy of a single Hbond, due to the increase of effective system size with decreasing temperature and correlation with neighboring Hbonds. Though the exact molecular mechanism leading to the positive entropy change is currently unknown, we suggest that it could be related to the number of possible correlated arrangements of Hbonds within the cluster that changes with the cluster size. We note that the increase in WW Hbond correlation with the environment starts at lower temperatures compared with trehalose related Hbonds. This “lag” may be related to a higher configurational freedom of water.

A close look at the two mixtures at lower and higher trehalose content, shown in Figure 5, reveals the effect of water content on the Hbond network. In addition to the significant weakening of WW interaction for 90.5 wt % compared to 30.8 wt % (see also Figure 6A), an enhancement of both HH and HO Hbonds is observed as trehalose content is increased. We find a concomitant weakening of water–trehalose Hbonds (WO and WH) as water content decreases. This result may underscore the importance of the sugar–water coupling to trehalose’s stabilization properties as described by the anchoring hypothesis.

Figure 6.

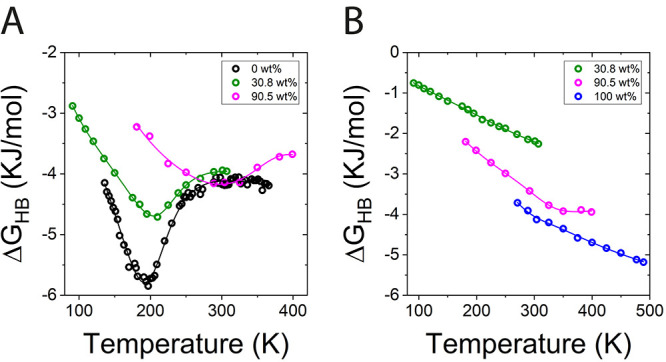
Trehalose concentration effect on hydrogen bonding interactions: (A) water–water (WW) Hbond free energy versus temperature and (B) sugar hydroxyl–sugar hydroxyl (HH) Hbond free energy versus temperature.

Figure 6 shows the same free energies for Hbonds shown in Figure 5 compared for specific Hbonds. Panel A shows ΔG_HB for WW, and panel B shows ΔG_HB for HH pairs for the different concentrations. As trehalose is added to water, we find an overall increase in the values of ΔG_HB along the entire concentration range, except around ∼300 K where WW interaction is stronger in the glass (90.5 wt % compared to 0 and 30.8 wt %, see Table S6 in the Supporting Information). This increase in ΔG_HB is most pronounced at the minimum. Moreover, as trehalose is added we also find a shift in the free energy minimum to higher temperatures (compare 30.8 and 90.5 wt % curves). Interestingly, Raman scattering experiments show a destructive effect of sugars on the water hydrogen bonding network, especially at trehalose contents above 30.8 wt %,⁸⁴ which may explain the shift we find in the free energy minimum.

Figure 6B indicates a strengthening of HH hydrogen bonding with trehalose concentration seen in the decrease of the free energy. This strengthening of trehalose–trehalose interactions at high trehalose content is also evident in the g(r) in Figure 1B, where the first peak of the TT curve in the concentrated 94.7 wt % is shifted to shorter distances compared to its value for 30.8 wt % (8.4 Å versus 9.1 Å, respectively). This finding is supported by the water plasticizing effect on the trehalose glass network that was reported based on positron annihilation lifetime spectroscopy experiments, which showed a linear increase in the average trehalose matrix free volume hole size with water concentration.⁸⁵

The relation between hydrogen bonding free energy and the glass transition temperature is most strikingly manifested in the changes in Hbond heat capacity with temperature, from which the glass transition temperature T_g, HB can be directly estimated. The procedure for calculating T_g, HB starts with calculation of the change in heat capacity between the randomly distributed state and the hydrogen bonded state,

8

From the change in heat capacity, the value of T_g was obtained in the same manner as the heat capacity reported in Figure 4, i.e., using three linear fits to different regimes of the heat capacity versus temperature plots and subsequent averaging of the two intersection temperature points. Figure 7 shows the calculated ΔC_p from both the hydrogen bond free energy (ΔG_HB, top panels) and based on information entropy (ΔS_info, bottom panels), both extracted from WW pairs. To appreciate the correlation of the glass transition temperature derived from Hbond free energy and the one based on the system heat capacity, we added a shaded bar corresponding to T_g, Cp based on heat capacity. The values we extract for ΔC_p, HB based on ΔG_HB for WW interactions and at low temperatures start as small negative values save for pure water where it is positive (panels A–C). We note that ΔC_p, HB typically changes sign at least once along the concentration range and interestingly, this change in sign is found at a temperature that is very close to T_g, Cp. By contrast, heat capacities defined by information entropy ΔC_p, info are consistently positive (panels D−F). We note that the large values of ΔC_p, info for 90.5 wt % at very low temperatures (∼185 K in panel F) are a result of the sharp kink in the ΔS_info (see Figure S11 in the Supporting Information) and may be artifactual.

We finally turn the examine the correlation between T_g, Cp determined by simulation-derived heat capacity (section 3.3), and the transition temperature estimated by the Hbond analysis (i.e., from ΔC_p, HB), T_g, HB, Figure 8. Additionally, for comparison, Figure 8 also contains T_g, info and T_g, PMF, which are derived from ΔC_p, info(Figure 7) and ΔC_p, PMF (not shown), respectively. We note that ΔC_p, PMF is too monotonic to calculate T_g, PMF for 100 wt %, and therefore T_g, PMF at this concentration is absent in Figure 8.

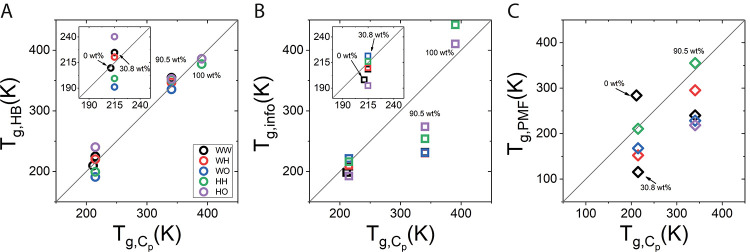
Figure 8.

Correlation plot of glass transition temperature, T_g, based on Hbonds, information entropy, and PMF_HB analysis to those calculated from the heat capacity method (see Figure 4D). (A) Glass transition temperature calculated from the Hbond free energy T_g, HB. (B) Glass transition temperature calculated from information entropy, T_g, info. (C) Same as parts A and B calculated from PMF_HB, T_g, PMF. All T_g values (HB, info, and PMF_HB) are extracted from the appropriate heat capacity. Data corresponds to 0, 30.8, 90.5, and 100 wt % trehalose. Concentrations are indicated in each panel and insets zoom in on 0 and 30.8 wt %.

From Figure 8 it is clear that the correlation between T_g, HB and T_g, Cp is very strong at both low concentrations of 0 and 30.8 wt % and at high concentrations of 90.5 and 100 wt %. Interestingly, at the low concentration regime, WW interactions give a better prediction of T_g compared to trehalose interactions, as the HO interactions (purple) overestimate while HH and WO (green) underestimate T_g. By contrast, in concentrated mixtures, the T_g prediction by trehalose-related interactions is comparable to the predication from WW pairs, which suggests a more integrated hydrogen bonding network of trehalose and water in the concentrated mixture compared to solution, where trehalose is less coupled to its surroundings. For T_g, info a good correlation is observed only for the diluted systems. At higher concentration, the values of the information theory-based T_g, info strongly diverge from the T_g, Cp derived from the thermodynamic system parameters. The deviation is negative for 90.5 wt % and positive for 100 wt % trehalose. Notably, T_g, PMF deviates from T_g, Cp further than T_g, info over the entire temperature range, except HH interaction, which gives a good estimate for both solution (30.8 wt %) and glass (90.5 wt %).

The strong correlation of T_g, Cp and T_g, HB derived from ΔG_HB is a direct consequence of the Hbond free energy sensitivity to the coupling of hydrogen bonded pairs to their surroundings. Compared to ΔG_HB, other conventional measures, including ΔS_info and ΔG_PMF, do not display this tight relation between the microscopic Hbond properties to macroscopic glass matrix and to the glass transition temperature, and we find they are insensitive to the changes in correlation between hydrogen bonded pairs upon glass formation.

Generally, the methodology we present here can be used to study the role of hydrogen bonds in molecular solvation and self-assembly. The increase in hydrogen bond correlation at low temperatures is expected to impact the structure of macromolecules that are embedded in the glassy matrix. Thus, this methodology may shed light on known and even more exotic macromolecular behavior observed for supercooled system, such as the refolding of Trp-cage protein in water at 54 K below freezing temperature.⁸⁶

4. Conclusions

The modeling of molecular liquid mixtures, even simple binary water–sugar mixtures, can be challenging, especially when attempted over the entire possible concentration range. Here, we performed a comparison of models for the disaccharide trehalose using two force fields: CHARMM36 and a recently reparametrized version, LME. The comparison comprised both structural and thermodynamic properties, i.e., RDFs, SDFs, osmotic pressures (Π), and glass transition temperatures (T_g) determined using different observables. Both force-field are in good agreement with available experimentally measured osmotic pressures and glass transition temperatures. The agreement is primarily good in the concentrated mixtures, although T_g values of LME derived from heat capacity C_p and compressibilities α_V are closer to the experiments. In both force fields at low concentration, T_g predicted by changes in diffusion constant is the same, whereas T_g derived from C_p and α_V is hampered by the water model. Interestingly, LME gives an improved prediction of the osmotic pressure. Further RDF and SDF analysis relate the improvement seen in LME to the reduction of the overaggregative nature of trehalose seen in C36. Indeed, water molecules are excluded to a lesser degree from trehalose in LME compared to C36, especially in the liquid-state solution, i.e., at low concentration mixtures. The delicate balance of trehalose–trehalose, trehalose–water, and water–water interactions are overall represented better in LME.

Using the reliable LME force field for water–sugar interactions, we then probed the thermodynamic signature of hydrogen bonding using a newly developed methodology to estimate hydrogen bonding strength in molecular simulations. The methodology enables the calculation of the reversible work, i.e., free energy for forming hydrogen bonds (ΔG_HB), while taking into account the entire configurational ensemble. The strength of hydrogen bonds was determined at different concentrations and temperatures. This allowed us to detect the plasticizing effect of water on the trehalose–trehalose hydrogen bonding, and vice versa, through modifications in bonding free energies. We find a strong correlation of the glass transition temperature with the corresponding change in hydrogen bonding heat capacity. This underscores a fingerprint of the change in the correlated behavior of hydrogen bonded pairs from liquid to glass that is not seen when following other more traditional thermodynamic parameters describing the hydrogen bond. Our methodology thus allows to link the change in hydrogen bond properties and the onset of the glassy state, which other conventional methods cannot. This methodology should become a useful tool in analyzing properties of molecular glasses that are formed through a strong contribution of hydrogen bonding. Specifically, the method directly highlights changes in the correlation between hydrogen bonds above and below the glass transition temperature.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.9b01071.

• Tables, figures, and details of the molecular dynamics simulations, structure factors, the SDF with equal iso-value, KBI convergence, densities, heat capacity change, spread of glass transition region, thermal expansion coefficient in diluted mixtures, HB methodology, two-level system example, HB extrapolation, information entropy, PMF, and further data analysis (PDF)

Author Contributions

^§ G.I.O. and L.S. contributed equally. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.