Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jan 30;142(7):3626–3635. doi: 10.1021/jacs.9b13942

Aromatic Nanosandwich Obtained by σ-Dimerization of a Nanographenoid π-Radical

Liliia Moshniaha †, Marika Żyła-Karwowska †, Piotr J Chmielewski †, Tadeusz Lis †, Joanna Cybińska †,‡, Elżbieta Gońka †, Johannes Oschwald #, Thomas Drewello #, Samara Medina Rivero §, Juan Casado §, Marcin Stępień †,*
PMCID: PMC7467677  PMID: 31997634

Abstract

graphic file with name ja9b13942_0011.jpg

A 139-π-electron nanographenoid radical was obtained by expanding the periphery of a naphthalimide–azacoronene hybrid with a methine bridge. The radical was isolated in the form of its σ-dimer, which was shown to possess a conformationally restricted two-layer structure both in the solid state and in solution. The dimer is cleaved into its parent radicals when exposed to ultraviolet or visible radiation in toluene solutions but is resistant to thermally induced dissociation. Under inert conditions, the radicals recombine quantitatively into the σ-dimer with observable kinetics, but they are oxidized into a ketone derivative in the presence of atmospheric oxygen. Combined structural, spectroscopic, and theoretical evidence shows that the σ-dimer contains a weak C(sp3)–C(sp3) bond, but is stabilized against thermal dissociation by a very strong dispersive interaction between the overlapping π surfaces.

Introduction

Dimerization of π-conjugated radicals is a fundamentally important process providing control over magnetism and reversible covalent bond formation in organic materials.1 Two π radicals can recombine by formation of a covalent bond to produce a so-called σ-dimer, in which one atom of each π system has been converted into a tetrahedral center. As these bonds often have relatively low dissociation energies, σ-dimerization provides an important mechanism for assembly of complex architectures by dynamic covalent bonding.2−11 σ-Dimerization of radical cation moieties is also involved in radical cation couplings in inter-12 and some intramolecular13 oxidative coupling reactions. Alternatively, two radicals may undergo π-dimerization, which occurs without the formation of a covalent bond. In the resulting dimer, the two radicals are stacked, to produce a strong interaction (“pancake bond”) between the π systems. π-Dimers can be observed in solution and in the solid state and may produce unusual temperature-dependent magnetic phenomena.14−23

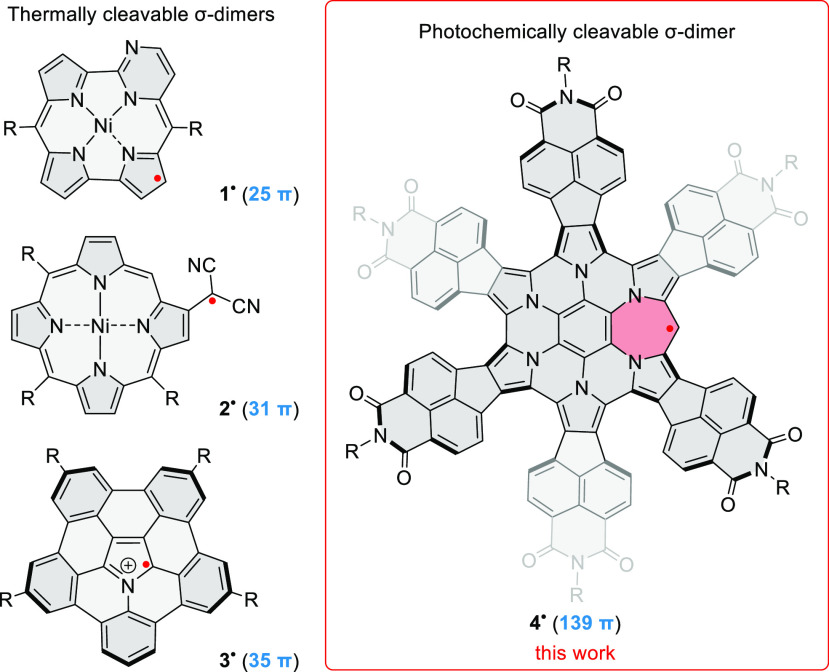
The ability of π radicals to form dimers can be inhibited by such structural features as large extent of spin delocalization, charge, or steric hindrance.24 Large π-radical systems often have a limited tendency to dimerize, and instances of σ-dimers with extended π surfaces are rarely reported.5,11,25−28 Among recent examples, nickel(II) pyrimidinenorcorrole radical 1• (Chart 1) regioselectively forms a σ-dimer that reversibly dissociates upon heating in solution.27 The (β-porphyrinyl)dicyanomethyl radical 2• showed temperature-dependent exocyclic σ-dimerization, while its meso-porphyrinyl isomer was found not to dimerize at all.5 Similarly, the azabuckybowl radical cation 3• was observed to σ-dimerize in the solid state and in solution at low temperatures, whereas only π-dimerization was observed for its near-planar analogue.28 In the related case of the C59N σ-dimer,26 dissociation into radicals could be observed by ESR at 500 K.29 Generally, the preference for σ-dimerization and its regioselectivity depends on fine structural details and is not readily predictable.

Chart 1. Examples of σ-Dimerizing π Radicalsa.

Chart 1

Open in a new tab

a The position of the radical dot indicates the observed σ-dimerization site. Formal π electron counts are provided in parentheses.

Here we describe the interconversion between a giant radical 4•, containing 139 electrons in its π system (Chart 1), and the corresponding σ-dimer 42 (Scheme 1). This radical is derived from hexapyrrolohexaazacoronene (HPHAC),30 a versatile platform for structural modification that has so far been transformed by subunit replacement,31,32 edge expansion,32−34 core replacement,35 peripheral fusion,36,37 and helical distortion.37 These alterations have produced π-conjugated systems exhibiting variable emission behavior,31 susceptibility to multiple oxidation33 or reduction,36,37 and tunable aromaticity.32,34 The present design combines radial fusion of electron-deficient subunits with edge expansion, to produce an odd-electron donor–acceptor π system, which undergoes spontaneous σ-dimerization. The resulting dimer is thermodynamically stabilized by balancing dispersion, distortion, and covalent forces, but can be cleaved into the π radicals using photochemical excitation.

Scheme 1. Synthesis of the Nanosandwich 42 by Electrophilic Bridging,

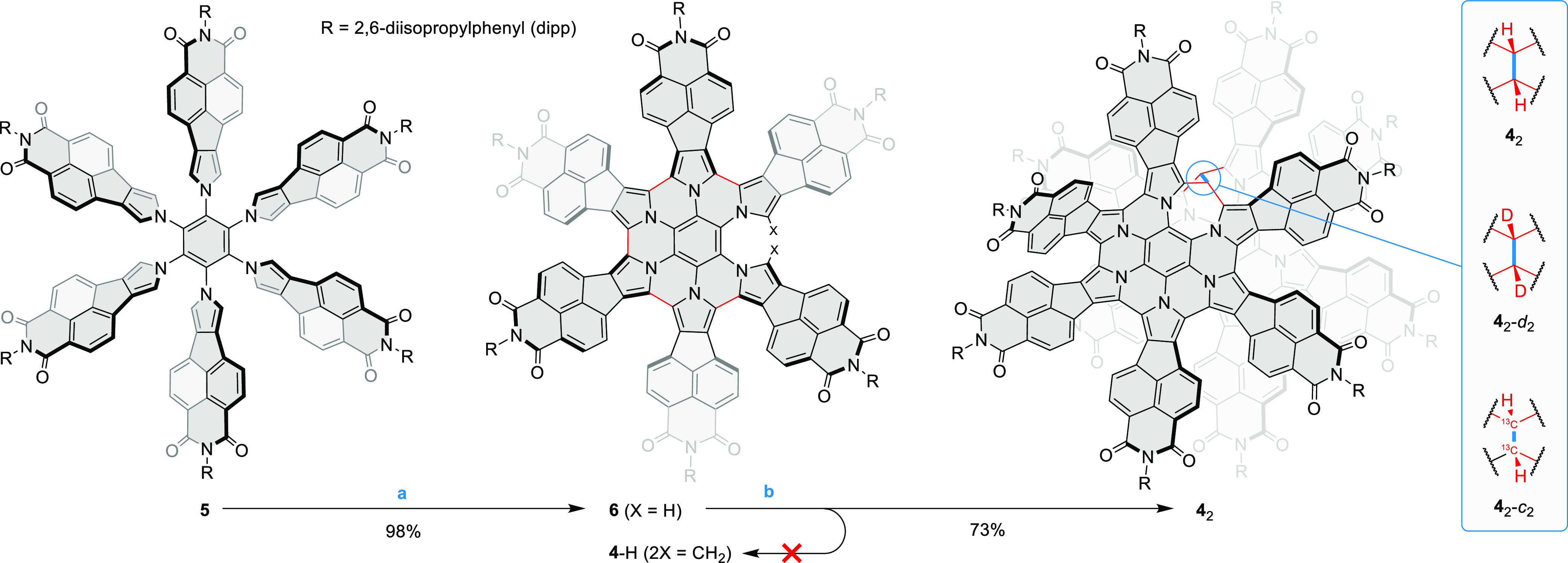
Scheme 1

Open in a new tab

Reagents and conditions: (a) 10 equiv FeCl3, 5% MeNO2 in DCM, 1 h, 18 °C; (b) 6 equiv 10-camphorsulfonic acid, 4 equiv paraformaldehyde, CHCl3, pressure tube, 90 °C, 17 h.

Paraformaldehyde-d2 and paraformaldehyde-13C were used to synthesize 42-d2 and 42-c2, respectively.

Results and Discussion

Formation of the Nanosandwich

The target radical 4• is an analogue of the previously reported HPHAC fused with six naphthalenemonoimide (NMI) units,36 which is further modified by insertion of an extra methine bridge on the periphery. Given its unique size, 4 is of inherent interest as a model of a paramagnetic defect in a two-dimensional π-conjugated system. In our efforts to synthesize 4•, we initially followed our earlier strategy,33 trying to obtain bridged hexapyrrolylbenzenes by acid-catalyzed condensation between various aldehydes and the naphthaleneimide-fused precursor 5(36,38,39) bearing bulky 2,6-diisopropylphenyl (dipp) substituents (Scheme 1). Compound 5 showed however insufficient selectivity in its reactions with aldehydes to be used for efficient bridging. We therefore turned our attention to the quintuply coupled system 6, which is easily obtained in high yields by mild oxidation of 5 with ferric chloride. We anticipated that the presence of only two reactive pyrrolic α positions in 6 should improve the selectivity of condensation reactions. However, 6 would not react with aromatic aldehydes, presumably because of the combined steric bulk of the NMI units in 6 and the aryl substituent of the aldehyde. Instead, it underwent intramolecular oxidative coupling to the fully fused HPHAC system under these conditions.

We reasoned that efficient condensation might be achievable by reducing the steric bulk of the aldehyde reactant. Indeed, when paraformaldehyde was reacted with 6 in the presence of 10-camphorsulfonic acid as the catalyst, it produced a single well-defined product in a 73% isolated yield. Unexpectedly, this product was identified as the σ-dimer 42, on the basis of detailed structural and spectroscopic data (vide infra). The expected primary product of condensation between 6 and a formaldehyde equivalent, 4-H, possesses a saturated methylene bridge, which might be subjected to final dehydrogenation to yield 4• (Scheme 1). However, we were not able to observe 4-H among the products, possibly because of its rapid subsequent oxidation to the dimer. Isotope-labeled derivatives 42-d2 and 42-c2, containing respectively 12C–2H and 13C–1H bridges, were conveniently obtained by condensing 6 with appropriately labeled paraformaldehydes.

Structure of the σ-Dimer

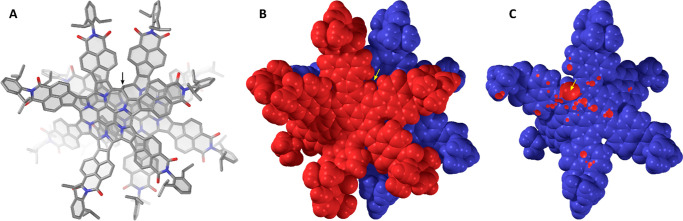
The dimeric structure of 42 was revealed in an X-ray diffraction (XRD) analysis (Figure 1). The molecule has the shape of an irregularly ruffled disk, decorated with bulky dipp groups, with an approximate van der Waals diameter of 3.5 nm. The two monomer subunits are linked via an elongated C–C bond (1.64(1) Å) and adopt a relative gauche arrangement with a torsion of ca. 65°. As a consequence, the central benzene rings of the two subunits are set apart by 5.14 Å. Nevertheless, a significant overlap of the aromatic surfaces is retained, leading to extensive interdigitation of the tilted NMI subunits. Because of the strong nonplanar distortion of the surfaces, the stacking distance cannot be uniquely defined; however, interatomic distances between subunits as short as 3.18 Å can be found in the solid-state geometry. The van der Waals envelopes of the two subunits intersect at multiple points (Figure 1C), indicating a strong dispersive interaction between the π surfaces, which may be enhanced by contributions from the bulky dipp substituents. In comparison, a recently reported bilayer nanographene showed a graphite-like interlayer separation of ca. 3.56 Å.40 Shorter interplanar distances were observed in phenalene π-dimers (3.2–3.3 Å)17 and antiaromatic norcorrole dimers (3.05–3.09 Å),41,42 a feature attributable to 3D π-conjugation effects. As discussed below, the local compression of interlayer distances in 42 is more likely caused by a combination of dispersive and steric forces rather than by additional bonding interactions between the π systems.

Figure 1.

Figure 1

Open in a new tab

Molecular structure of 42 determined in an X-ray diffraction analysis. The location of the C(sp3)–C(sp3) bond is indicated with an arrow. (A) Perspective view with H atoms and solvent molecules removed for clarity. (B) van der Waals representation with the two subunits shown respectively in red and blue. (C) Structure with the top subunit removed and sub van der Waals contacts indicated in red.

Each of the monomer subunits shows a very significant out-of-plane distortion, caused by steric congestion of the outer NMI fragments and interactions with the other subunit. This feature resembles the monkey-saddle distortion of the original NMI-HPHAC system,36 which displayed alternating helicities of the bay regions around the HPHAC core, with a (P,M,P,M,P,M) relative stereochemistry.37 In 42, each subunit has only five regions with defined helicity, because the sixth bay is expanded by the inserted sp3 bridge. Relative helicities for the front subunit of 42 (as oriented in Figure 1, clockwise) are (P,P,M,P,M), whereas the back subunit has a different stereochemistry, namely, (P,M,P,P,M). Thus, the two subunits of 42 are stereochemically nonequivalent in the solid state, and neither of them preserves the alternating helicity pattern found in the HPHAC parent.

NMR Spectroscopy

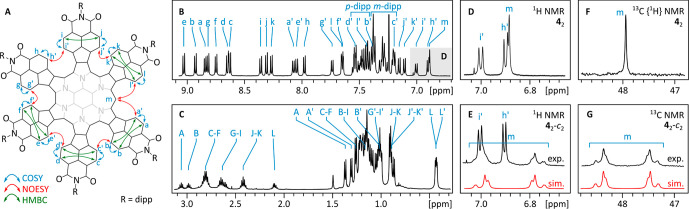
The 1H NMR spectrum of 42 (CDCl3, Figure 2) corresponds to an effective C2 molecular symmetry, which can be inferred from the number of NMI signals (12 AB spin systems) and the number of CH signals of the dipp substituents (12). The symmetry observed in solution is therefore higher than that found in the crystal (C1) and indicates complete equivalence of the two subunits. Thus, the helical stereochemistry of both subunits is identical in solution or, more likely, the helicities are dynamically averaged to produce a more symmetrical spectrum. However, the rotation around the C(sp3)–C(sp3) bond is slow on the NMR time scale, because a higher symmetry spectrum (C2v or C2h) would be observed for rapidly rotating subunits. A DOSY spectrum recorded for 42 showed a reduced diffusion coefficient relative to that of 6, consistent with the formation of a dimeric structure.

Figure 2.

Figure 2

Open in a new tab

NMR spectroscopic analysis for 42. (A) 1H NMR connectivities established in 42 on the basis of 2D spectra (see Figure S5 for assignment details). (B and C) 1H NMR spectrum of 42 (600 MHz, CDCl3, 300 K). (D through G) The appearance of the C(sp3)–H resonances (m) in the 1H and 13C NMR spectra of 42 and 42-c2. Simulated spectra correspond to an AA′XX′ spin system (A = 1H, X = 13C) with 1JCH = 132 Hz, 1JCC = 28 Hz, 2JCH = −5.8 Hz, 3JHH = 3.4 Hz.

Signal overlaps in the 1H NMR spectrum precluded complete assignment of resonances, but a partial analysis could nevertheless be performed with the aid of 2D correlation methods (Figures 2A,B, S5). The C(sp3)–H resonance of the sp3 bridge appears as a singlet at 6.88 ppm, and its identity was further verified by a correlation with a 13C signal at 47.9 ppm found in the HSQC spectrum. The bridge signal was also absent in the 1H NMR spectrum of the deuterated derivative 42-d2. The 13C-labeled dimer, 42-c2, showed a characteristic AA′XX′ spin system in its 1H and 13C NMR spectra, the latter recorded with gated 1H decoupling (Figure 2E,G). The splitting pattern was successfully simulated by assuming strong coupling between the two 13C centers (1JCC = 132 Hz), consistent with the formation of a direct C–C bond between the two bridges.

Mass Spectrometry

The positive-ion MALDI mass spectrum of 42, obtained using DCTB (trans-2-[3-(4-tert-butylphenyl)-2-methyl-2-propenylidene]malononitrile) as the matrix material, is shown in Figure 3. The most prominent signal, (M/2)+, corresponds to the cation of the azacoronene monomer fragment (4+, Figure 3B). A sizable M+ signal, corresponding to the radical cation [42]•+, was however also observed (Figure 3C). The MALDI spectrum of 42-c2 showed an analogous pair of (M/2)+ and M+ ions, with expected mass shifts of one and two mass units, respectively (Figure 3D and E). The formation of the radical cation [42]•+ is expected, as DCTB operates as an electron transfer matrix.43 The abundant formation of 4+ in the MALDI experiment is due to either (a) direct photodissociation of 42 followed by ionization of 4• to 4+ or (b) dissociation of the initially formed [42]•+ into 4• and 4+. Unexpectedly, 42 formed an abundant sodium adduct MNa+ (Figure 3C and E). Sodiation is here likely to occur by binding adventitious Na+ during sample preparation rather than in the gas phase during the MALDI process. The sodium cation is thought to be chelated by a pair of spatially adjacent imide CO groups located at the periphery of the stacked azacoronenes in 42. Sodiation of the azacoronene monomer 4• is much less abundant (2.6% relative intensity compared to 4+). This apparent lower propensity of 4• for the addition of Na+ is consistent with the absence of chelating sites in the azacoronene monomer.

Figure 3.

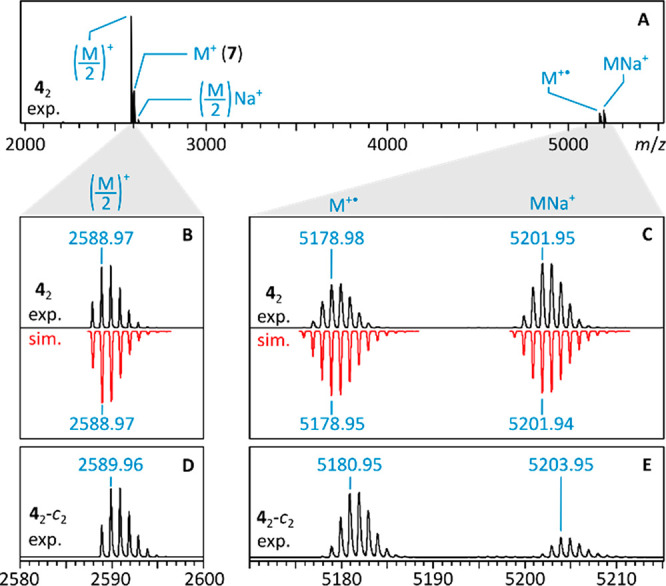
Figure 3

Open in a new tab

Positive-ion MALDI mass spectrum of 42 (A) and isotopic profiles for key ions (B and C). Isotopic profiles for 42-c2 are shown for comparison (D and E).

Computational Analysis

Because of the size of the 42 dimer (652 atoms, 1918 electrons), a complete high-level density functional theory (DFT) analysis was unfeasible. Grimme’s extended tight-binding model (GFN2-xTB),44,45 including dispersion and solvation corrections, was therefore used as a cost-effective alternative. Reoptimization of the solid-state geometry at this level of theory produced only minor structural changes (Figure S23), while retaining all key characteristics of the dimer. Specifically, the calculation reproduced the elongated C(sp3)–C(sp3) bond (1.601 Å). This value is in good agreement with the analogous bond lengths reported for the neutral σ-dimers of 2,6-di-tert-butyl-4-methoxyphenoxyl (DBMP2, 1.606 Å, XRD)46 and C59N (1.609 Å, DFT)47 and is larger than the corresponding distance in 7,7′-bi-1,3,5-cycloheptatriene (1.533 Å, XRD),48 which is formally a fragment of 42. The torsion between subunits in 42 is reduced to 62° in the xTB geometry, leading to a somewhat smaller distance between centroids of the inner benzene rings (4.954 Å). The area of sub van der Waals contacts between the two subunits is larger than in the XRD geometry. It extends in the vicinity of the C(sp3)–C(sp3) linkage, suggesting its largely steric origin.

Electronic Properties

The absorption spectrum of 42 is very similar to that of the bridge-free precursor 6, with a nearly identical λmax of the lowest-energy band (600 vs 601 nm in CH2Cl2, respectively, Figure S2). These features indicate that the ground-state electronic structure of the chromophore is insignificantly affected in the dimer. Similarly to 6, 42 showed deep-red fluorescence, with an apparently lower quantum yield of emission (ΦF = 0.22 vs 0.40 in toluene, λex = 360 nm). The ΦF value determined for 42 may however be underestimated because of partial photodissociation of the sample during measurements (see below). 42 could be separated into enantiomers using chiral HPLC, indicating that the C2 conformer observed by NMR is configurationally rigid. CD spectra of the enantiomers showed significantly lower intensities than those of the related propeller-shaped HPHACs.37 Voltammetric analyses of 42 showed two oxidations at 0.60 and 0.85 V and at least eight reduction events in the −1.37 to −1.99 V potential range (vs Fc/Fc+, cf. Figures S7–S10). Such an extended electron-accepting ability is a general characteristic of multi-NMI-fused nanocarbon systems.36,37,39,49−51 For 42, however, electroreduction was partly irreversible, producing a new species when held at potentials below −1.37 V. The latter unidentified species was identifiable by an emerging redox couple at −0.75 V. Electrooxidation of 42 above its first oxidation potential (0.60 V) produced small amounts of another new species yielding characteristic redox couples at −0.11 and −1.13 V.

Cleavage and Recombination of the Dimer

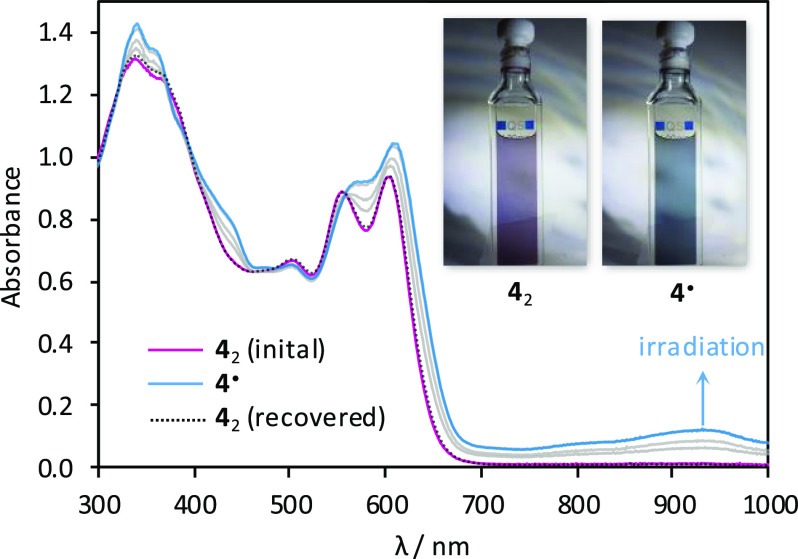
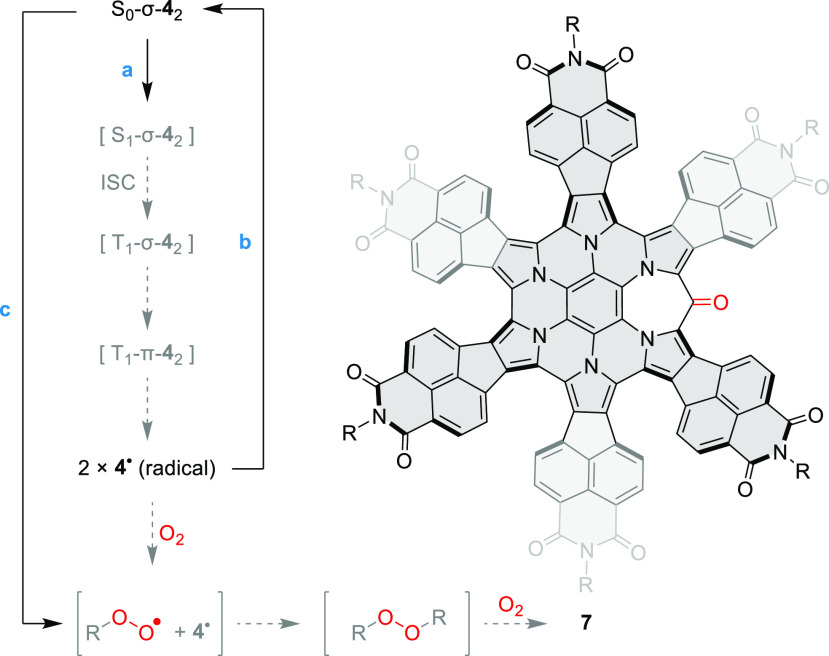
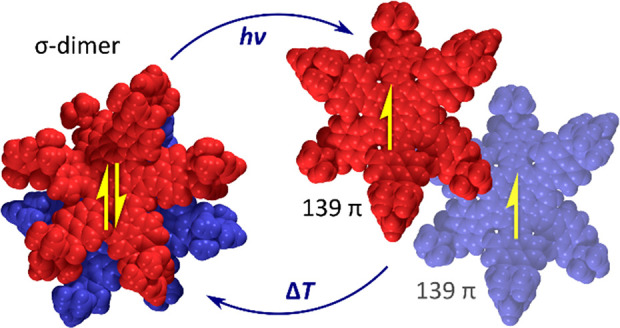
The spontaneous formation of 42 is reminiscent of formal σ-dimerizations previously reported for certain macrocyclic oligopyrroles,25,52−55 and we similarly suspected that it could originate from a radical recombination process. We were however intrigued whether, in contrast to the above reports, the parent radical 4• could actually be observed experimentally. The long C(sp3)–C(sp3) distance observed in 42 is generally characteristic of weak covalent bonding; however, such elongated bonds are not always easily dissociated.56 Samples of 42 were found to always yield a moderately intense ESR signal both in solution and in the solid state (see below). The intensity of the ESR signal showed however a negligible increase upon heating in toluene in the 300–420 K temperature range, indicating that thermal cleavage of 42 did not occur. Subsequently, we found that in toluene solutions 42 underwent dissociation when irradiated with either UV radiation or visible light. Interestingly, the process did not occur in other typical solvents, i.e., methanol, dichloromethane, benzene, and cyclohexane. Under optimized conditions (3.8 × 10–5 M in degassed toluene, 365 nm UV source), we observed a gradual conversion of 42 into a new species. The process was monitored using absorption spectroscopy (Figure 4), yielding well-defined isosbestic points, when irradiation was carried out in short intervals.

Figure 4.

Figure 4

Open in a new tab

Photodissociation of 42 into 4• and subsequent recombination (365 nm irradiation, toluene, rt).

The photoproduct has a smaller optical bandgap (ca. 1.01 eV), with near-infrared absorptions extending in a ca. 700–1200 nm wavelength range, and was identified as the radical 4• on the basis of the strong increase of ESR signal intensity observed after irradiation. The electronic spectrum of 4• was semiquantitatively reproduced in a time-dependent (TD)-DFT calculation (Figure S25). Interestingly, the optical bandgap of the radical matches the electrochemical gap determined for the oxidation product of 42 observed in voltammetric experiments, suggesting that the radical 4• might form by spontaneous dissociation of the radical cation dimer [42]•+. This process would be analogous to the route (b) proposed above for the formation of 4+ observed in the MALDI spectra.

1H NMR spectra of a 8 × 10–5 M solution of 42 in toluene-d8 showed a 64% decrease of signal intensities following irradiation with a 365 nm UV source. This value underestimates the actual conversion to 4•, because the sample partly recovered prior to the NMR measurement. Thus, even though the completeness of photodissociation could not be precisely determined, high conversions can nevertheless be expected for dilute solutions. In degassed toluene, irradiation with a variety of UV and visible-light sources produced an identical initial absorption spectrum, suggesting that either the dissociation is indeed driven to completion or the photostationary state is independent of the wavelength. The photogenerated 4• quantitatively recombined into 42 when the samples were stored for 10–12 h in the dark, provided that dioxygen was rigorously excluded. Accordingly, the ESR signal of the photogenerated radical was found to decay exponentially, indicating well-defined recombination kinetics. Irradiation of solutions exposed to air produced a markedly different result. At 5 × 10–7 M, the accumulation of 4• was not detectable, a behavior previously observed for other benzylic π radicals.57 Instead of 4•, a different species was formed, characterized by an absorption spectrum resembling that of 42 and a somewhat enhanced fluorescence (Figure S4C). This intermediate, which we presume to be the peroxide R–O–O–R (Scheme 2), subsequently decayed to produce ketone 7 as the final oxidation product. The above oxygenation sequence is analogous to that proposed for oxophlorin radicals.527 was also obtained on a preparative scale by exposing solutions of 42 to air and ambient light for extended periods of time and was completely characterized using spectroscopic methods (Supporting Information).

Scheme 2. Photodissociation and Photooxidation of 42–

Scheme 2

Open in a new tab

Reagents and conditions: (a) degassed toluene, 365 nm irradiation ca. 80 s; (b) room temperature, darkness, overnight; (c) toluene, 365 nm irradiation, air.

Hypothetical steps are shown in gray; reversibility is not indicated.

R is the azacoronene moiety bound to oxygen via the peripheral bridge carbon.

Properties of the Radical

In toluene solution, 4• yields an ESR spectrum with g = 2.00292 and hyperfine coupling with aH = 6.8 G, which was attributed to the proton of the methine bridge (Figure 5). Indeed, the deuterated radical 4•-d, obtained by splitting 42-d2, shows no resolvable splitting (aD < 1 G), consistent with the above assignment. The ESR spectrum of the 13C-labeled radical 4•-c contained an additional splitting (aC = 12.3 G), indicating that a significant amount of spin density resides on the methine carbon. The calculated spin density distribution (Figure 5) shows that the unpaired electron is distributed predominantly in one-half of the π system surrounding the methine bridge with significant amplitudes in the imide fragments. Mulliken spin densities at the methine C and H atoms are respectively 0.498 and −0.022. Interestingly, the spin is insignificantly delocalized into the central benzene ring of 4•.

Figure 5.

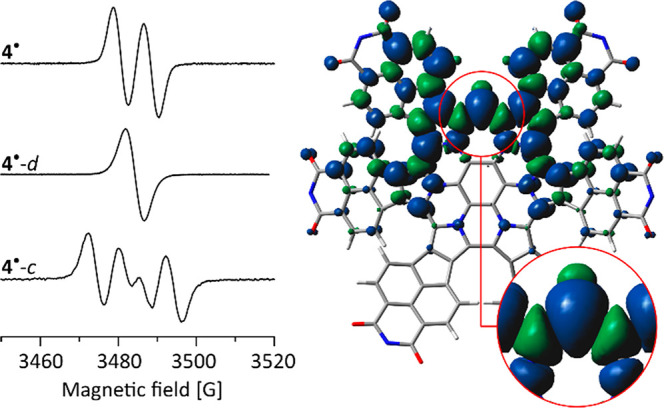
Figure 5

Open in a new tab

Left: ESR spectra of 4• and its isotope-labeled derivatives (toluene, 300 K). Right: Spin density distribution for 4• (ωB97XD/6-31G(d,p), dipp substituents omitted for clarity).

Computational data indicate that 4• preferentially adopts a monkey-saddle conformation with alternating helicities of the adjacent bay regions (Figure S20). This conformer is analogous to the structure reported for the parent HPHAC–NMI hybrid.36 However, since the subunits of 42 adopt different stereochemistry in the solid-state structure, the radical appears to be sufficiently flexible to adjust its geometry upon dimerization. 4• features a very large π system, formally containing 139 electrons. This system is however only partially involved in spin delocalization, with the methine bridge acting as a “spin defect” in the π-conjugated framework. As this methine bridge is not sterically protected, the radical remains susceptible to dimerization and addition of dioxygen. Both of these processes are consistent with relatively low stabilization of the radical.

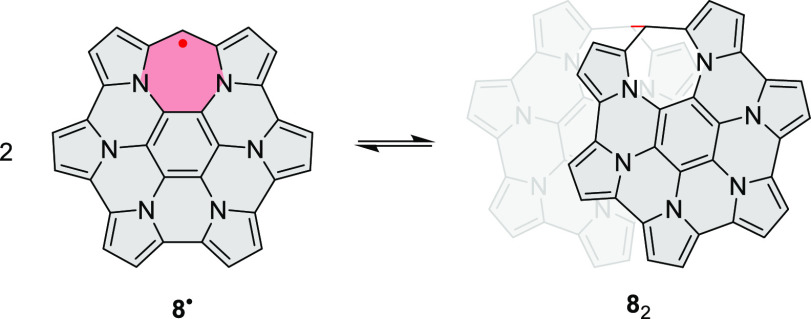
Energetics of Dimerization

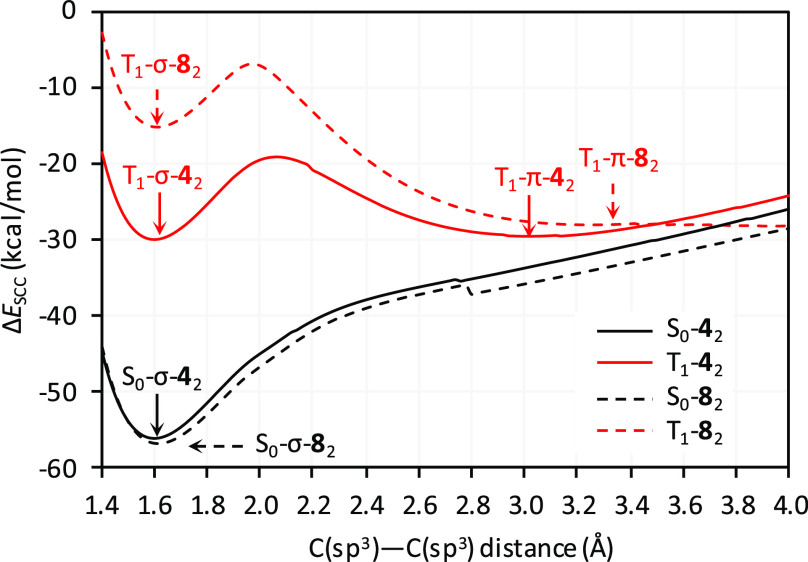
The energetics of dimerization were probed for 42 (Table 1) and the reference system 82 devoid of NMI-dipp units (Scheme 3, Table S1). Initially, the ground-state singlet (S0) and triplet (T1) energy hypersurfaces were scanned for each system at the GFN2-xTB level of theory (CH2Cl2 solvation), as a function of the C(sp3)–C(sp3) distance d (Figures 6 and S22). For S0-42 and S0-82, one minimum was located along this coordinate, corresponding to a σ-dimer with an elongated single bond (d ≈ 1.60 Å). The large d distance predicted for S0-82 indicates that the elongation may be relatively independent of the steric congestion around the C(sp3)–C(sp3) bond. For both 42 and 82, the S0 σ-dimer was stabilized by over 55 kcal/mol relative to the corresponding pair of radicals. On the triplet surface, 42 showed two minima at ca. 1.6 and 3.0 Å, corresponding respectively to the σ- and π-dimers, T1-σ-42 and T1-π-42, each with an energy of ca. – 30 kcal/mol. Two, less stabilized minima were similarly observed for T1-82; that is, for both 42 and 82, the S0-σ-dimer is significantly more stabilized than the corresponding triplets (T1-σ and T1-π). Scanning at larger d distances resulted in a sliding displacement of the subunits and rather uneven energy profiles (Figure S22). This behavior is likely caused by strong dispersive interactions and multiple clashes between the subunits. However, the ΔESCC energy remained negative at all distances, suggesting that the dissociation into radicals may be essentially barrierless19 for both 42 and 82.

Table 1. Energetics of Dimerization for 42.

energya S0-σ-42
 T1-σ-42 T1-π-42
(kcal/mol) total ΔEXdefb ΔEXintb total total
ΔESCC –55.6 57.2 –112.9 –29.8 –29.1
ΔEdisp –104.8 –0.5 –104.3 –105.5 –105.5
ΔEsolv 40.5 4.1 36.3 39.9 44.0
ΔEel 8.7 53.5 –44.9 35.7 32.4
ΔG298 –20.8     0.6 –0.2
C–C (Å) 1.602     1.601 3.029
Open in a new tab
a

GFN2-xTB energies (CH2Cl2 solvation) relative to 4•. ΔEel = ΔESCC – ΔEsolv – ΔEdisp, where ΔESCC, ΔEsolv, and ΔEdisp are respectively the self-consistent charge, solvation, and dispersion energy.

b

Deformation and interaction energy components; X corresponds respectively to SCC, disp, solv, and el.

Scheme 3. Reference Dissociation Process.

Scheme 3

Open in a new tab

Figure 6.

Figure 6

Open in a new tab

GFN2-xTB relaxed potential energy scans for 42 and 82 performed along the C(sp3)–C(sp3) bond length coordinate on singlet and triplet hypersurfaces. Energies are given relative to 4• and 8•, respectively.

The curvature of the ΔESCC energy profile around the S0-σ-42 minimum provides an estimated force constant for the C(sp3)–C(sp3) bond of ca. 2.3–2.7 mdyn/Å (see the Supporting Information for a full analysis). This value is lower that reported for the corresponding bond in the DBMP2 dimer (3.6 mdyn/Å)46 and ethane (4.5 mdyn/Å),58 but it is significantly larger than the values determined for the longest C(sp3)–C(sp3) bond reported to date (1.806 Å, 1.08 mdyn/Å)56 and for a multicenter bond in a dianionic tetracyanoethylene dimer (0.45 mdyn/Å).59 The force constant calculated for 42 would thus correspond to a bond of medium strength, which is however weaker than conventional C(sp3)–C(sp3) bonds. These theoretical predictions are in line with the tentative assignment of the C–C bond stretching mode at 887 cm–1 observed in the solid-state 532 nm Raman spectrum of 42 (Figures S15 and S16). This value is indeed smaller than typically observed for C–C stretching modes (ca. 1000 cm–1) but markedly exceeds the uniquely low value of 587 cm–1 recorded for the longest C–C bond.56

For 42, ΔESCC energies are dominated by a large stabilizing dispersion contribution ΔEdisp (ca. −105 kcal/mol), which is approximately constant for all three dimers. The solvation contribution ΔEsolv is in each case destabilizing (ca. +40 kcal/mol). While dispersion and solvation effects may be difficult to separate computationally,60 the large positive ΔEsolv is consistent with partial desolvation required to form a close contact between the π surfaces of the reacting 4• radicals. The remaining contribution, ΔEel = ΔESCC – ΔEsolv – ΔEdisp, combines other energetic effects, in particular those of covalent bonding, geometrical distortion, and Pauli repulsion between the monomers. Importantly, ΔEel values are positive for S0-σ-42 and its triplet counterparts, implying that the observed stabilization of the dimer is provided by dispersion forces (cf. refs (61)–65). For 82, dispersion remains the dominant stabilizing effect, but the ΔEel contribution takes significantly lower values and becomes negative for S-σ. These large dispersion contributions help explain why 42 is resistant to thermal dissociation, even though it apparently contains a weaker C–C bond than the thermally cleavable DBMP2 dimer.46

A deformation–interaction (ΔEdef/ΔEint) analysis66 performed for the S-σ dimers (Tables 1 and S1) showed that while the total dimerization energy ΔESCC for 42 and 82 is similar (−56 vs −57 kcal/mol, respectively), the deformation component ΔESCCdef in the former system is larger (+57 vs +41 kcal/mol). This increase is balanced by a more negative interaction component ΔESCCint (−113 vs −98 kcal/mol). As expected, ΔESCCdef of each system is dominated by the electronic contribution, whereas ΔESCCint results from balancing electronic, dispersion, and solvation effects. In 42, dispersion dominates the interaction energy component (ΔEdispint = −104.3 kcal/mol), whereas in 82, the interaction energy originates primarily from electronic effects.

Gibbs energies ΔG298 calculated for the stationary points located in the above relaxed scans indicated high thermodynamic stability of the 42 σ-dimer on the S0 surface (−20.8 kcal/mol) and lack of stabilization for the triplet dimers (+0.6 and −0.2 kcal/mol for T1-σ-42 and T1-π-42, respectively). A qualitatively similar picture was predicted for the reference system 82, both using GFN2 and a full DFT treatment (PCM(CH2Cl2)/ωB97XD/6-31G(d,p), Table S1). The energies calculated for 42 and the apparent lack of bond-breaking barrier may be responsible for the observed stability of the dimer toward thermal cleavage. A potential mechanism of photodissociation67 may therefore involve initial excitation of S0-σ-42 to the S1 state, followed by intersystem crossing (ISC) to the T1 surface (Scheme 2). On the triplet surface, the weakly bound dimers T1-σ-42 and T1-π-42 may either dissociate into free 4• radicals or recombine into 42 via another ISC process. The resulting photostationary state appears to strongly favor dissociation, according to our experimental data. Recombination of the 4• radicals is thought to involve a reverse mechanistic sequence, with intermediate formation of triplet dimers followed by a rate-limiting ISC to the S0 surface.

Conclusions

This work describes the synthesis and properties of a heteroaromatic radical obtained by peripheral expansion of a naphthalimide-fused hexapyrrolohexaazacoronene. It exhibits extensive spin delocalization in its 139-electron π system and spontaneously dimerizes into a stable σ-dimer, which is susceptible to photochemical rather than thermal cleavage. Such a selectivity is untypical: dissociation of σ-dimers in solution is usually induced thermally2−10,27,28 or, occasionally, by each of these stimuli.68 Herein, the switching between the radical and its σ-dimer relies on homolytic rupture of a weak C(sp3)–C(sp3) bond but is controlled by a balance between π-conjugative stabilization, internal strain,69 and nonbonding interactions. The latter contribution has a decisive influence on the overall energetics of dimer formation and cleavage, which can be viewed as a unique case of a dispersion-controlled photoprocess.70,71 Reversible dimerization of giant π-conjugated radicals such as the one described herein provides an opportunity to manipulate a single electron spin in a nanoscale molecular object and may be used to design magnetically active nanocarbon systems.

Acknowledgments

Financial support from the National Science Center of Poland (UMO-2014/15/N/ST5/00714, E.G. and L.M.) and the Foundation for Polish Science (TEAM POIR.04.04.00-00-5BF1/17-00, M.S.) is gratefully acknowledged. Quantum-chemical calculations were performed in the Wrocław Center for Networking and Supercomputing. We thank Stefan Grimme (Universität Bonn) for providing the xTB code and helpful discussions. J.C. (Málaga) acknowledges financial support from Ministerio de Ciencia, Innovación y Universidades of Spain (PGC2018-098533-B-I00) and the Junta de Andalucía (UMA18-FEDERJA-057). J.O. and T.D. acknowledge Wolfgang Donaubauer for help with the MALDI experiments and financial support by the DFG (SFB 953 “Synthetic Carbon Allotropes”, project Z1).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.9b13942.

  • Synthetic and spectroscopic details, computational data (PDF)

  • X-ray data (CIF)

  • Additional information (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ja9b13942_si_001.pdf (4.6MB, pdf)
ja9b13942_si_002.cif (5.5MB, cif)
ja9b13942_si_003.zip (84.9KB, zip)

References

  1. Kubo T. Synthesis, Physical Properties, and Reactivity of Stable, π-Conjugated, Carbon-Centered Radicals. Molecules 2019, 24 (4), 665. 10.3390/molecules24040665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Chen X.; Wang X.; Zhou Z.; Li Y.; Sui Y.; Ma J.; Wang X.; Power P. P. Reversible σ-Dimerizations of Persistent Organic Radical Cations. Angew. Chem., Int. Ed. 2013, 52 (2), 589–592. 10.1002/anie.201207412. [DOI] [PubMed] [Google Scholar]
  3. Beaudoin D.; Levasseur-Grenon O.; Maris T.; Wuest J. D. Building Giant Carbocycles by Reversible C–C Bond Formation. Angew. Chem., Int. Ed. 2016, 55 (3), 894–898. 10.1002/anie.201509608. [DOI] [PubMed] [Google Scholar]
  4. Yuan L.; Han Y.; Tao T.; Phan H.; Chi C. Formation of a Macrocycles-in-a-Macrocycle Superstructure with All- Gauche Conformation by Reversible Radical Association. Angew. Chem., Int. Ed. 2018, 57 (29), 9023–9027. 10.1002/anie.201804720. [DOI] [PubMed] [Google Scholar]
  5. Adinarayana B.; Shimizu D.; Furukawa K.; Osuka A. Stable Radical versus Reversible σ-Bond Formation of (Porphyrinyl)Dicyanomethyl Radicals. Chem. Sci. 2019, 10 (23), 6007–6012. 10.1039/C9SC01631G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Okino K.; Hira S.; Inoue Y.; Sakamaki D.; Seki S. The Divergent Dimerization Behavior of N-Substituted Dicyanomethyl Radicals: Dynamically Stabilized versus Stable Radicals. Angew. Chem., Int. Ed. 2017, 56 (52), 16597–16601. 10.1002/anie.201710354. [DOI] [PubMed] [Google Scholar]
  7. Zhang R.; Peterson J. P.; Fischer L. J.; Ellern A.; Winter A. H. Effect of Structure on the Spin-Spin Interactions of Tethered Dicyanomethyl Diradicals. J. Am. Chem. Soc. 2018, 140 (43), 14308–14313. 10.1021/jacs.8b08628. [DOI] [PubMed] [Google Scholar]
  8. Okino K.; Sakamaki D.; Seki S. Dicyanomethyl Radical-Based Near-Infrared Thermochromic Dyes with High Transparency in the Visible Region. ACS Mater. Lett. 2019, 1 (1), 25–29. 10.1021/acsmaterialslett.9b00049. [DOI] [Google Scholar]
  9. Kobashi T.; Sakamaki D.; Seki S. N-Substituted Dicyanomethylphenyl Radicals: Dynamic Covalent Properties and Formation of Stimuli-Responsive Cyclophanes by Self-Assembly. Angew. Chem., Int. Ed. 2016, 55 (30), 8634–8638. 10.1002/anie.201603409. [DOI] [PubMed] [Google Scholar]
  10. Wang D.; Capel Ferrón C.; Li J.; Gámez-Valenzuela S.; Ponce Ortiz R.; López Navarrete J. T.; Hernández Jolín V.; Yang X.; Peña Álvarez M.; García Baonza V.; Hartl F.; Ruiz Delgado M. C.; Li H. New Multiresponsive Chromic Soft Materials: Dynamic Interconversion of Short 2,7-Dicyanomethylenecarbazole-Based Biradicaloid and the Corresponding Cyclophane Tetramer. Chem. - Eur. J. 2017, 23 (55), 13776–13783. 10.1002/chem.201702659. [DOI] [PubMed] [Google Scholar]
  11. Oda K.; Hiroto S.; Shinokubo H. NIR Mechanochromic Behaviours of a Tetracyanoethylene-Bridged Hexa-Peri-Hexabenzocoronene Dimer and Trimer through Dissociation of C-C Bonds. J. Mater. Chem. C 2017, 5 (22), 5310–5315. 10.1039/C7TC01270E. [DOI] [Google Scholar]
  12. Heinze J.; Frontana-Uribe B. A.; Ludwigs S. Electrochemistry of Conducting Polymers—Persistent Models and New Concepts †. Chem. Rev. 2010, 110 (8), 4724–4771. 10.1021/cr900226k. [DOI] [PubMed] [Google Scholar]
  13. Chaolumen; Murata M.; Wakamiya A.; Murata Y. Unsymmetric Twofold Scholl Cyclization of a 5,11-Dinaphthyltetracene: Selective Formation of Pentagonal and Hexagonal Rings via Dicationic Intermediates. Angew. Chem., Int. Ed. 2017, 56 (18), 5082–5086. 10.1002/anie.201701054. [DOI] [PubMed] [Google Scholar]
  14. Song H.; Reed C. A.; Scheidt W. R. Dimerization of Metalloporphyrin. Pi.-Cation Radicals. Zinc Complex [Zn(OEP. Bul.)(OH2)]2(ClO4)2, a Novel Dimer. J. Am. Chem. Soc. 1989, 111 (17), 6867–6868. 10.1021/ja00199a071. [DOI] [Google Scholar]
  15. Schulz C. E.; Song H.; Mislankar A.; Orosz R. D.; Reed C. A.; Debrunner P. G.; Scheidt W. R. [Fe(OEP •)(X)] + π-Cation Radicals: Characterization and Spin–Spin Interactions. Inorg. Chem. 1997, 36 (3), 406–412. 10.1021/ic961053d. [DOI] [Google Scholar]
  16. Fujita W.; Awaga K. Room-Temperature Magnetic Bistability in Organic Radical Crystals. Science 1999, 286 (5438), 261–262. 10.1126/science.286.5438.261. [DOI] [PubMed] [Google Scholar]
  17. Goto K.; Kubo T.; Yamamoto K.; Nakasuji K.; Sato K.; Shiomi D.; Takui T.; Kubota M.; Kobayashi T.; Yakusi K.; Ouyang J. A Stable Neutral Hydrocarbon Radical: Synthesis, Crystal Structure, and Physical Properties of 2,5,8-Tri- Tert -Butyl-Phenalenyl. J. Am. Chem. Soc. 1999, 121 (7), 1619–1620. 10.1021/ja9836242. [DOI] [Google Scholar]
  18. Suzuki S.; Morita Y.; Fukui K.; Sato K.; Shiomi D.; Takui T.; Nakasuji K. Aromaticity on the Pancake-Bonded Dimer of Neutral Phenalenyl Radical as Studied by MS and NMR Spectroscopies and NICS Analysis. J. Am. Chem. Soc. 2006, 128 (8), 2530–2531. 10.1021/ja058387z. [DOI] [PubMed] [Google Scholar]
  19. Lü J.-M.; Rosokha S. V.; Kochi J. K. Stable (Long-Bonded) Dimers via the Quantitative Self-Association of Different Cationic, Anionic, and Uncharged π-Radicals: Structures, Energetics, and Optical Transitions. J. Am. Chem. Soc. 2003, 125 (40), 12161–12171. 10.1021/ja0364928. [DOI] [PubMed] [Google Scholar]
  20. Small D.; Zaitsev V.; Jung Y.; Rosokha S. V.; Head-Gordon M.; Kochi J. K. Intermolecular π-to-π Bonding between Stacked Aromatic Dyads. Experimental and Theoretical Binding Energies and Near-IR Optical Transitions for Phenalenyl Radical/Radical versus Radical/Cation Dimerizations. J. Am. Chem. Soc. 2004, 126 (42), 13850–13858. 10.1021/ja046770i. [DOI] [PubMed] [Google Scholar]
  21. Itkis M. E.; Chi X.; Cordes A. W.; Haddon R. C. Magneto-Opto-Electronic Bistability in a Phenalenyl-Based Neutral Radical. Science 2002, 296 (5572), 1443–1445. 10.1126/science.1071372. [DOI] [PubMed] [Google Scholar]
  22. Pal S. K.; Itkis M. E.; Tham F. S.; Reed R. W.; Oakley R. T.; Haddon R. C. Resonating Valence-Bond Ground State in a Phenalenyl-Based Neutral Radical Conductor. Science 2005, 309 (5732), 281–284. 10.1126/science.1112446. [DOI] [PubMed] [Google Scholar]
  23. Morita Y.; Suzuki S.; Fukui K.; Nakazawa S.; Kitagawa H.; Kishida H.; Okamoto H.; Naito A.; Sekine A.; Ohashi Y.; Shiro M.; Sasaki K.; Shiomi D.; Sato K.; Takui T.; Nakasuji K. Thermochromism in an Organic Crystal Based on the Coexistence of σ- and π-Dimers. Nat. Mater. 2008, 7 (1), 48–51. 10.1038/nmat2067. [DOI] [PubMed] [Google Scholar]
  24. Kato K.; Osuka A. Platforms for Stable Carbon-Centered Radicals. Angew. Chem., Int. Ed. 2019, 58 (27), 8978–8986. 10.1002/anie.201900307. [DOI] [PubMed] [Google Scholar]
  25. Balch A. L.; Noll B. C.; Reid S. M.; Zovinka E. P. Carbon-Carbon Bond Formation in the Dimerization of (Octaethyloxophlorin Radical)Nickel(II). J. Am. Chem. Soc. 1993, 115 (6), 2531–2532. 10.1021/ja00059a071. [DOI] [Google Scholar]
  26. Hummelen J. C.; Knight B.; Pavlovich J.; González R.; Wudl F. Isolation of the Heterofullerene C59N as Its Dimer (C59N)2. Science 1995, 269 (5230), 1554–1556. 10.1126/science.269.5230.1554. [DOI] [PubMed] [Google Scholar]
  27. Liu B.; Yoshida T.; Li X.; Stępień M.; Shinokubo H.; Chmielewski P. J. Reversible Carbon-Carbon Bond Breaking and Spin Equilibria in Bis(Pyrimidinenorcorrole). Angew. Chem., Int. Ed. 2016, 55 (42), 13142–13146. 10.1002/anie.201607237. [DOI] [PubMed] [Google Scholar]
  28. Yokoi H.; Hiroto S.; Shinokubo H. Reversible σ-Bond Formation in Bowl-Shaped π-Radical Cations: The Effects of Curved and Planar Structures. J. Am. Chem. Soc. 2018, 140 (13), 4649–4655. 10.1021/jacs.8b00798. [DOI] [PubMed] [Google Scholar]
  29. Simon F.; Arčon D.; Tagmatarchis N.; Garaj S.; Forro L.; Prassides K. ESR Signal in Azafullerene (C59N)2 Induced by Thermal Homolysis. J. Phys. Chem. A 1999, 103 (35), 6969–6971. 10.1021/jp9912915. [DOI] [Google Scholar]
  30. Takase M.; Enkelmann V.; Sebastiani D.; Baumgarten M.; Müllen K. Annularly Fused Hexapyrrolohexaazacoronenes: An Extended π System with Multiple Interior Nitrogen Atoms Displays Stable Oxidation States. Angew. Chem., Int. Ed. 2007, 46 (29), 5524–5527. 10.1002/anie.200701452. [DOI] [PubMed] [Google Scholar]
  31. Takase M.; Narita T.; Fujita W.; Asano M. S.; Nishinaga T.; Benten H.; Yoza K.; Müllen K. Pyrrole-Fused Azacoronene Family: The Influence of Replacement with Dialkoxybenzenes on the Optical and Electronic Properties in Neutral and Oxidized States. J. Am. Chem. Soc. 2013, 135 (21), 8031–8040. 10.1021/ja402371f. [DOI] [PubMed] [Google Scholar]
  32. Żyła M.; Gońka E.; Chmielewski P. J.; Cybińska J.; Stępień M. Synthesis of a Peripherally Conjugated 5–6-7 Nanographene. Chem. Sci. 2016, 7 (1), 286–294. 10.1039/C5SC03280F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Gońka E.; Chmielewski P. J.; Lis T.; Stępień M. Expanded Hexapyrrolohexaazacoronenes. Near-Infrared Absorbing Chromophores with Interrupted Peripheral Conjugation. J. Am. Chem. Soc. 2014, 136 (46), 16399–16410. 10.1021/ja508963v. [DOI] [PubMed] [Google Scholar]
  34. Oki K.; Takase M.; Mori S.; Uno H. Synthesis and Isolation of Antiaromatic Expanded Azacoronene via Intramolecular Vilsmeier-Type Reaction. J. Am. Chem. Soc. 2019, 141 (41), 16255–16259. 10.1021/jacs.9b09260. [DOI] [PubMed] [Google Scholar]
  35. Oki K.; Takase M.; Mori S.; Shiotari A.; Sugimoto Y.; Ohara K.; Okujima T.; Uno H. Synthesis, Structures, and Properties of Core-Expanded Azacoronene Analogue: A Twisted π-System with Two N-Doped Heptagons. J. Am. Chem. Soc. 2018, 140 (33), 10430–10434. 10.1021/jacs.8b06079. [DOI] [PubMed] [Google Scholar]
  36. Żyła-Karwowska M.; Zhylitskaya H.; Cybińska J.; Lis T.; Chmielewski P. J.; Stępień M. An Electron-Deficient Azacoronene Obtained by Radial π Extension. Angew. Chem., Int. Ed. 2016, 55 (47), 14658–14662. 10.1002/anie.201608400. [DOI] [PubMed] [Google Scholar]
  37. Navakouski M.; Zhylitskaya H.; Chmielewski P. J.; Lis T.; Cybińska J.; Stępień M. Stereocontrolled Synthesis of Chiral Heteroaromatic Propellers with Small Optical Bandgaps. Angew. Chem., Int. Ed. 2019, 58 (15), 4929–4933. 10.1002/anie.201900175. [DOI] [PubMed] [Google Scholar]
  38. Biemans H. A. M.; Zhang C.; Smith P.; Kooijman H.; Smeets W. J. J.; Spek A. L.; Meijer E. W. Hexapyrrolylbenzene and Octapyrrolylnaphthalene. J. Org. Chem. 1996, 61 (25), 9012–9015. 10.1021/jo961192c. [DOI] [PubMed] [Google Scholar]
  39. Zhylitskaya H.; Cybińska J.; Chmielewski P.; Lis T.; Stępień M. Bandgap Engineering in π-Extended Pyrroles. A Modular Approach to Electron-Deficient Chromophores with Multi-Redox Activity. J. Am. Chem. Soc. 2016, 138 (35), 11390–11398. 10.1021/jacs.6b07826. [DOI] [PubMed] [Google Scholar]
  40. Evans P. J.; Ouyang J.; Favereau L.; Crassous J.; Fernández I.; Perles J.; Martín N. Synthesis of a Helical Bilayer Nanographene. Angew. Chem., Int. Ed. 2018, 57 (23), 6774–6779. 10.1002/anie.201800798. [DOI] [PubMed] [Google Scholar]
  41. Nozawa R.; Tanaka H.; Cha W.-Y.; Hong Y.; Hisaki I.; Shimizu S.; Shin J.-Y.; Kowalczyk T.; Irle S.; Kim D.; Shinokubo H. Stacked Antiaromatic Porphyrins. Nat. Commun. 2016, 7, 13620. 10.1038/ncomms13620. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Nozawa R.; Kim J.; Oh J.; Lamping A.; Wang Y.; Shimizu S.; Hisaki I.; Kowalczyk T.; Fliegl H.; Kim D.; Shinokubo H. Three-Dimensional Aromaticity in an Antiaromatic Cyclophane. Nat. Commun. 2019, 10 (1), 1–7. 10.1038/s41467-019-11467-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Vasil’ev Y. V.; Khvostenko O. G.; Streletskii A. V.; Boltalina O. V.; Kotsiris S. G.; Drewello T. Electron Transfer Reactivity in Matrix-Assisted Laser Desorption/Ionization (MALDI): Ionization Energy, Electron Affinity and Performance of the DCTB Matrix within the Thermochemical Framework. J. Phys. Chem. A 2006, 110 (18), 5967–5972. 10.1021/jp060568f. [DOI] [PubMed] [Google Scholar]
  44. Grimme S.; Bannwarth C.; Shushkov P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All Spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13 (5), 1989–2009. 10.1021/acs.jctc.7b00118. [DOI] [PubMed] [Google Scholar]
  45. Bannwarth C.; Ehlert S.; Grimme S. GFN2-XTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15 (3), 1652–1671. 10.1021/acs.jctc.8b01176. [DOI] [PubMed] [Google Scholar]
  46. Wittman J. M.; Hayoun R.; Kaminsky W.; Coggins M. K.; Mayer J. M. A C-C Bonded Phenoxyl Radical Dimer with a Zero Bond Dissociation Free Energy. J. Am. Chem. Soc. 2013, 135 (35), 12956–12959. 10.1021/ja406500h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Andreoni W.; Curioni A.; Holczer K.; Prassides K.; Keshavarz-K M.; Hummelen J.-C.; Wudl F. Unconventional Bonding of Azafullerenes: Theory and Experiment. J. Am. Chem. Soc. 1996, 118 (45), 11335–11336. 10.1021/ja962279i. [DOI] [Google Scholar]
  48. Friedrich U.; Korber N. Crystal Structure of 7,7’-Bi-1,3,5-Cycloheptatrien, C14H14. Z. Kristallogr. - New Cryst. Struct. 2014, 227 (4), 455–456. 10.1524/ncrs.2012.0206. [DOI] [Google Scholar]
  49. Seifert S.; Shoyama K.; Schmidt D.; Würthner F. An Electron-Poor C64 Nanographene by Palladium-Catalyzed Cascade C–C Bond Formation: One-Pot Synthesis and Single-Crystal Structure Analysis. Angew. Chem., Int. Ed. 2016, 55 (22), 6390–6395. 10.1002/anie.201601433. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Shoyama K.; Würthner F. Synthesis of a Carbon Nanocone by Cascade Annulation. J. Am. Chem. Soc. 2019, 141 (33), 13008–13012. 10.1021/jacs.9b06617. [DOI] [PubMed] [Google Scholar]
  51. Liu G.; Koch T.; Li Y.; Doltsinis N. L.; Wang Z. Nanographene Imides Featuring Dual-Core Sixfold [5]Helicenes. Angew. Chem., Int. Ed. 2019, 58 (1), 178–183. 10.1002/anie.201810734. [DOI] [PubMed] [Google Scholar]
  52. Fuhrhop J. H.; Besecke S.; Subramanian J.; Mengersen C.; Riesner D. Reactions of Oxophlorines and Their. Pi. Radicals. J. Am. Chem. Soc. 1975, 97 (24), 7141–7152. 10.1021/ja00857a029. [DOI] [Google Scholar]
  53. Krattinger B.; Nurco D. J. Novel Synthesis and New Chemistry of Naphthochlorins. Chem. Commun. 1998, (7), 757–758. 10.1039/a708765i. [DOI] [Google Scholar]
  54. Khoury R. G.; Jaquinod L.; Paolesse R.; Smith K. M. New Chemistry of Oxophlorins (Oxyporphyrins) and Their π-Radicals. Tetrahedron 1999, 55 (22), 6713–6732. 10.1016/S0040-4020(99)00319-1. [DOI] [Google Scholar]
  55. Maurya Y. K.; Noda K.; Yamasumi K.; Mori S.; Uchiyama T.; Kamitani K.; Hirai T.; Ninomiya K.; Nishibori M.; Hori Y.; Shiota Y.; Yoshizawa K.; Ishida M.; Furuta H. Ground-State Copper(III) Stabilized by N-Confused/N-Linked Corroles: Synthesis, Characterization, and Redox Reactivity. J. Am. Chem. Soc. 2018, 140 (22), 6883–6892. 10.1021/jacs.8b01876. [DOI] [PubMed] [Google Scholar]
  56. Ishigaki Y.; Shimajiri T.; Takeda T.; Katoono R.; Suzuki T. Longest C-C Single Bond among Neutral Hydrocarbons with a Bond Length beyond 1.8 Å. Chem. 2018, 4 (4), 795–806. 10.1016/j.chempr.2018.01.011. [DOI] [Google Scholar]
  57. Font-Sanchis E.; Aliaga C.; Bejan E. V.; Cornejo R.; Scaiano J. C. Generation and Reactivity toward Oxygen of Carbon-Centered Radicals Containing Indane, Indene, and Fluorenyl Moieties. J. Org. Chem. 2003, 68 (8), 3199–3204. 10.1021/jo026666o. [DOI] [PubMed] [Google Scholar]
  58. Robinson E. A.; Lister M. W. A Linear Relationship between Bond Orders and Stretching Force Constants. Can. J. Chem. 1963, 41 (12), 2988–2995. 10.1139/v63-439. [DOI] [Google Scholar]
  59. Casado J.; Burrezo P. M.; Ramírez F. J.; Navarrete J. T. L.; Lapidus S. H.; Stephens P. W.; Vo H.-L.; Miller J. S.; Mota F.; Novoa J. J. Evidence for Multicenter Bonding in Dianionic Tetracyanoethylene Dimers by Raman Spectroscopy. Angew. Chem., Int. Ed. 2013, 52 (25), 6421–6425. 10.1002/anie.201207813. [DOI] [PubMed] [Google Scholar]
  60. Pollice R.; Bot M.; Kobylianskii I. J.; Shenderovich I.; Chen P. Attenuation of London Dispersion in Dichloromethane Solutions. J. Am. Chem. Soc. 2017, 139 (37), 13126–13140. 10.1021/jacs.7b06997. [DOI] [PubMed] [Google Scholar]
  61. Grimme S.; Schreiner P. R. Steric Crowding Can Stabilize a Labile Molecule: Solving the Hexaphenylethane Riddle. Angew. Chem., Int. Ed. 2011, 50 (52), 12639–12642. 10.1002/anie.201103615. [DOI] [PubMed] [Google Scholar]
  62. Schreiner P. R.; Chernish L. V.; Gunchenko P. A.; Tikhonchuk E. Y.; Hausmann H.; Serafin M.; Schlecht S.; Dahl J. E. P.; Carlson R. M. K.; Fokin A. A. Overcoming Lability of Extremely Long Alkane Carbon-Carbon Bonds through Dispersion Forces. Nature 2011, 477 (7364), 308–311. 10.1038/nature10367. [DOI] [PubMed] [Google Scholar]
  63. Fokin A. A.; Chernish L. V.; Gunchenko P. A.; Tikhonchuk E. Yu.; Hausmann H.; Serafin M.; Dahl J. E. P.; Carlson R. M. K.; Schreiner P. R. Stable Alkanes Containing Very Long Carbon-Carbon Bonds. J. Am. Chem. Soc. 2012, 134 (33), 13641–13650. 10.1021/ja302258q. [DOI] [PubMed] [Google Scholar]
  64. Wagner J. P.; Schreiner P. R. London Dispersion in Molecular Chemistry-Reconsidering Steric Effects. Angew. Chem., Int. Ed. 2015, 54 (42), 12274–12296. 10.1002/anie.201503476. [DOI] [PubMed] [Google Scholar]
  65. Rösel S.; Becker J.; Allen W. D.; Schreiner P. R. Probing the Delicate Balance between Pauli Repulsion and London Dispersion with Triphenylmethyl Derivatives. J. Am. Chem. Soc. 2018, 140 (43), 14421–14432. 10.1021/jacs.8b09145. [DOI] [PubMed] [Google Scholar]
  66. Nagase S.; Morokuma K. An Ab Initio Molecular Orbital Study of Organic Reactions. The Energy, Charge, and Spin Decomposition Analyses at the Transition State and along the Reaction Pathway. J. Am. Chem. Soc. 1978, 100 (6), 1666–1672. 10.1021/ja00474a005. [DOI] [Google Scholar]
  67. Autrey T.; Devadoss C.; Sauerwein B.; Franz J. A.; Schuster G. B. Solvent Cage Recombination of 4-Benzoylphenylthiyl Radicals: Fast Intersystem Crossing of Triplet Sulfur-Centered Radical Pairs. J. Phys. Chem. 1995, 99 (3), 869–871. 10.1021/j100003a005. [DOI] [Google Scholar]
  68. Edkins R. M.; Probert M. R.; Robertson C. M.; Howard J. A. K.; Beeby A. Photocrystallisation of the 2C-2′C Dimer of a Triphenylimidazolyl Radical. RSC Adv. 2014, 4 (11), 5351–5356. 10.1039/C3RA43892A. [DOI] [Google Scholar]
  69. Abe M.; Furunaga H.; Ma D.; Gagliardi L.; Bodwell G. J. Stretch Effects Induced by Molecular Strain on Weakening σ-Bonds: Molecular Design of Long-Lived Diradicals (Biradicals). J. Org. Chem. 2012, 77 (17), 7612–7619. 10.1021/jo3016105. [DOI] [PubMed] [Google Scholar]
  70. Schweighauser L.; Strauss M. A.; Bellotto S.; Wegner H. A. Attraction or Repulsion? London Dispersion Forces Control Azobenzene Switches. Angew. Chem., Int. Ed. 2015, 54 (45), 13436–13439. 10.1002/anie.201506126. [DOI] [PubMed] [Google Scholar]
  71. Strauss M. A.; Wegner H. A. Exploring London Dispersion and Solvent Interactions at Alkyl-Alkyl Interfaces Using Azobenzene Switches. Angew. Chem., Int. Ed. 2019, 58 (51), 18552–18556. 10.1002/anie.201910734. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja9b13942_si_001.pdf (4.6MB, pdf)
ja9b13942_si_002.cif (5.5MB, cif)
ja9b13942_si_003.zip (84.9KB, zip)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES