Apparent scaling of virus surface roughness—An example from the pandemic SARS-nCoV

Abstract

This paper investigates the scaling of the surface roughness of coronavirus, including the SARS-nCoV based on fractal and spectral analyses of their published electron microscopy images. The box-counting fractal dimensions obtained are subjected to ANOVA tests for statistical significance. Results show that the SARS-nCoV particles could not statistically be resolved by their shape on the basis of the fractal dimension values, but they could be distinguished from the earlier SARS-CoV particles. MANOVA test results require interaction of factors used for classifying virions into different types. The topological entropies, a measure of randomness in a system, measured for the images of varying size show correlation with the fractal dimensions. Spectral analyses of our data show a departure from power-law self-similarity, suggesting an apparent scaling of surface roughness over a band of maximum an order of magnitude. The spectral crossover that corresponds to characteristic length scale may represent average viral size. Our results may be useful in inferring the nature of surface-contact between the viral and human cell, causing infection and also in providing clues for new drugs, although it is too early to say. In addition, limitations of this study, including possible ways to avoid the bias in scaling exponents due to the use of different techniques are discussed.

Highlights

• •Morphological diversity of nCoV particles is not statistically significant.
• •Classification requires the interaction of envelope-shape and spike distribution.
• •Slightly oval and elongated nCoV and CoV particles are statistically distinguished.
• •Viral surface roughness does not support power-law scaling.

1. Introduction

An accurate characterization of surface roughness has gained large interest in the study of nonlinear, complex natural phenomena in many applications of physical [1], [2] and biological sciences [3], [4], [5]. Protein surfaces show self-similar scaling in a certain range in radius, as measured from fractal analysis of their 3-D structures [5]. The variations in fractal dimension (FD), D explaining the surface irregularity could be related to molecular interactions of structural features [4], and thus can help in deciphering the underlying surface interaction patterns [3]. While there are many qualitative and subjective methods for analyzing the complexity of surface roughness, fractal geometry is the quantitative and robust measure of describing it [6]. The FD-based techniques provide useful information in analyzing natural structures by means of their space filling properties in many applications in biology [4].

The degree of roughness varies with scale. Surface roughness data can be analyzed in time and frequency domain for estimating the scaling exponents [7], [8], the parameters that describe the dynamics of the underlying process at multiple spatial and temporal scales. This work investigates the morphological complexity of virions from fractal scaling of the surface roughness of the novel corona virus SARS-nCoV (hereafter referred to as nCoV), within the scope of biophysics.

The 2019 nCoV outbreak causes human respiratory disease namely COVID-19, presenting a severe global health threat. The nCoV is more readily transmitted from human to human than the earlier reported CoV, spreading the infection to the whole world.

After this outbreak, there have been several studies on nonlinear epidemiological models of COVID-19 spreading based on analysis of epidemiological data in mainland China and other countries [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19]. A power-law scaling feature of COVID-19 spread is found in networks of cities in different parts of the world [9]. Optimal control theory-based epidemic model (Susceptible, Quarantined, Exposed, Infected, Asymptomatic, and Recovered individuals, SQEIAR) [10] is proposed for eradication of infection by following quarantine and treatment policies in China and Spain for different types of disease (COVID-19, Ebola, and Influenza). However, little is known about the roughness structure of the virus surface including its shape, structure, protein distribution, and nature of contact causing infection. Here, we claim to investigate these properties as they provide clues to understanding how virus enters human cells, providing ways to design drugs or vaccines to combat the virus [20].

Viruses have a variety of shapes and structures. They are classified into four groups based on shape: filamentous, isometric (or icosahedral), enveloped, and head and tail. A complete virus particle (virion) consists of a nucleic acid (RNA or DNA) surrounded by a coating, referred to as an envelope. The shape of a viral coat has implications on how a virus infects a host. The protein distribution on the envelope provides clues for drugs [17]. Thus both the viral elements (envelope and proteins) together describe a complex system with mesoscopic properties [3].

Fractal geometry, because of its scale invariance property over many orders of magnitude, can describe complex geometry of structures [4], [6]. Fractal scaling of proteins’ surfaces has been supported both theoretically and experimentally [3], [5], [21] after the landmark work of Lewis & Rees [4]. Determination and interpretation of fractal dimension associated with the complexity of viral surface could provide information on nature of contact causing the infection, and provide clues in developing new vaccines or at least antiviral strategies that are seemingly unknown for nCoV. Hence, from a utilitarian angle with the emergence of the pandemic, we made a first attempt to study the complex geometry associated with the surface roughness based on the systematic analysis of the electron microscope images of nCoV.

2. Data & fractal and spectral analyses

We analyzed electron microscopy images (both color and gray-scale) of 55 virions of the novel nCoV and earlier CoV of varying shapes and S-protein (spike) distributions from published studies [22], [23]. Our analysis is based on calculation of fractal (box-counting) dimension, radially averaged power spectra (radial spectra for short), and entropy of the images processed using the following approach.

The RGB color images are converted to gray-scale images to be segmented (binarized) by thresholding, allowing most of the detailed features of the virions to be preserved. The entropy-based thresholding algorithm of Kapur [24] obtains the optimal threshold values by maximizing the sum of entropies for object (gray-scale value higher than threshold, set as white) and background (gray-scale value lower than threshold, set as black) of the image. Finally a binary image, created by assigning each pixel to 1 or 0 in reference to the label of pixels, is subjected to fractal analyses.

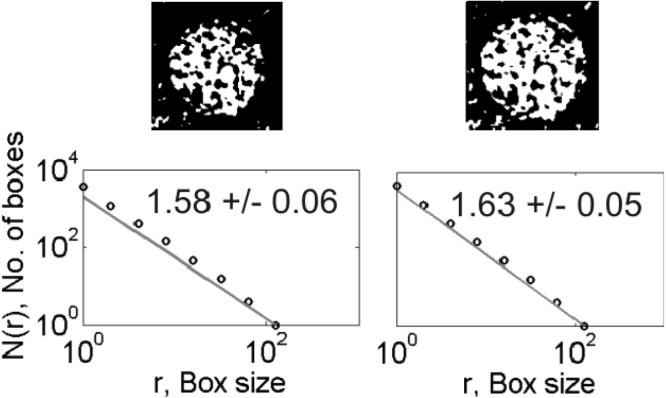
We estimated fractal dimension using the box-counting method. The method is based on overlaying an image $A\in R^2$ with a grid of squares of size r and counting the number of squares, N(r) necessary to cover the object in the thresholded image. The number of boxes of size r needed to cover a fractal object follows a power-law $N\left(r\right)\propto r^{-D}$, where D is the box-counting fractal dimension obtained from the linear portion of the log[N(r)] versus log[r] plot. The algorithm is applied to binary images obtained after segmentation of original color/gray scale images with a threshold.

Next, we calculated radial spectra of the thresholded images. Here the power spectrum is averaged over all possible directions. It provides a convenient means of representing the information of 2-D spectra in 1-D. The spectra present a multi-scale characteristic of the images, with the frequency as a proxy for scale variable. Finally, we computed the entropy of the images to characterize the texture and studied their relation with fractal dimensions obtained.

2.1. Topological entropy and fractal dimension

The generalized Shannon (Renyi) entropy quantifies the randomness in information distribution in a system, which is defined for order $q\ge 1$ as, $S_q\left(X\right)=\frac{1}{1-q}{log}_b{\sum }_i^m{p}_i^q$ where X is a discrete random variable, ${\mathit{p}}_i$ is the probability of the event $\{X=x_i\}$, and b is base of logarithm [25]. The cases $q=0$ and 1 correspond to topological and Shannon entropy, respectively. Topological entropy as a function of the size of the support of X can be defined as $S_0\left(r\right)=ln{\sum }_{i=1}^{m\left(r\right)}{p}_i^0=lnm$ which depends only on the number of events m with the probability ${\mathit{p}}_i$ > 0 [26]. ${\mathit{S}}_0\left(r\right)$ and D can be related as $S_0\left(r\right)=Dlnr$. The more generalized relation for different order q, and base of logarithm b is $S_q\left(r\right)=D_q{log}_{b}r$ [27].

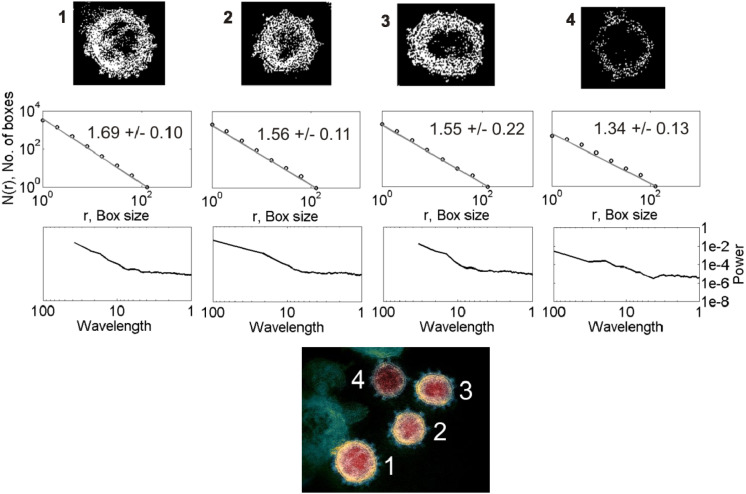
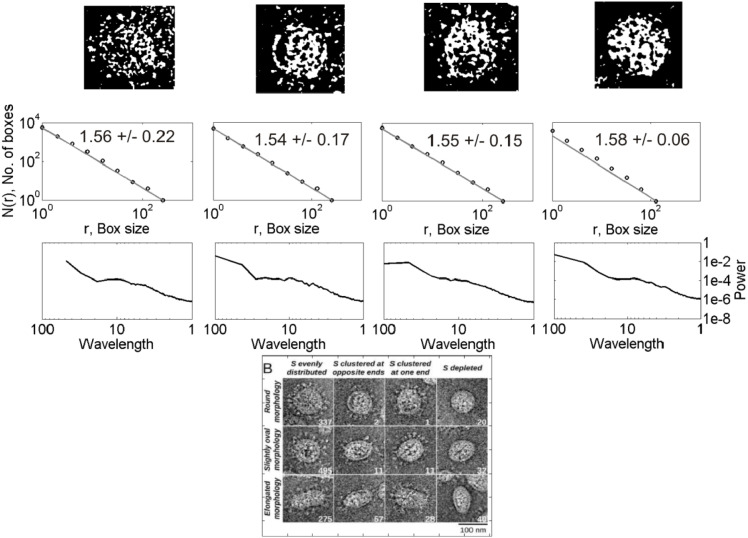
Figs. 1 and 2 show examples of data analysis applied to the representative images of nCoV and CoV, respectively. The nCoV shown here has four virions (marked as 1–4) of different shape and size visually. The CoV has twelve virions classified according to the envelope shape (rounded, slightly oval, and elongated) and nature of spike distributions (evenly distributed, clustered at opposite ends, clustered at one end, and depletion of spikes). All the nCoV particles analyzed here are characterized by spiked envelopes. As presented in the following section, we systematically compared the shapes of the nCoV images with those of the CoV images of Fig. 2 to find in which category of those mentioned in Fig. 2 all the nCoV images analyzed are framed and then compared them with that category. Once all the nCoV images are classified into the 12 categories of CoV presented in Fig. 2, the results are compared from a media analysis, ANOVA for their statistical significance. The 1st row of plots shows the 2-D gray-scale binary images obtained after pre-processing the original color images. The 2nd and 3rd rows show the fractal and spectral analyses results, respectively.

Fig. 1.

(Bottom) A representative electron microscopy image of nCoV [22] with four virions, marked as 1–4, is shown with the spikes protruding from their envelopes. (1st row) Binary maps (thresholded images) of the virions 1–4. (2nd row) Log–log plot of box size versus number of boxes. The slope of the fitted straight line gives the D value, expressed as mean $\pm$ standard deviation (SD). (3rd row) Radially averaged spectra for each image shown as a function of wavelength. Note the units of variables used are arbitrary.

Fig. 2a.

(Bottom) Classification of the CoV particles according to a classification scheme based on envelope-shape and spike distribution [29]. Remaining features shown are same as Fig. 1 but for the virions of the first row of classification shown at the bottom figure .

3. Results

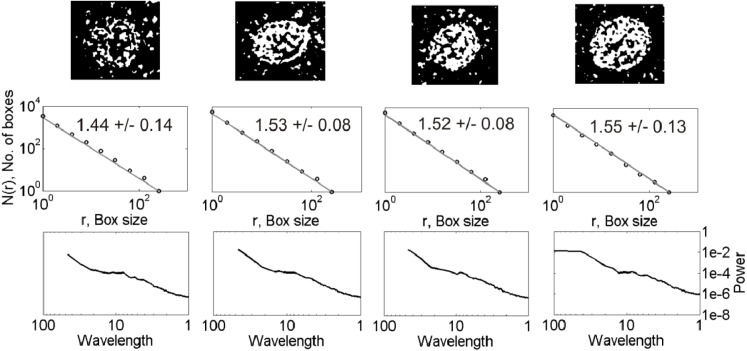
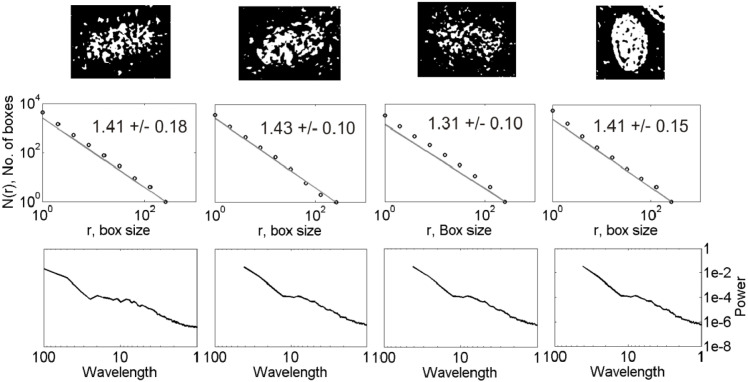
The D values for the 12 CoV particles of different shapes and spike distributions lie in the range 1.31–1.58 (2nd row, Fig. 2a, Fig. 2b, Fig. 2c). The corresponding power spectra show linear decay in log–log domain at low wavelengths over a maximum of one order of magnitude ($\sim$ 1–10 units of wavelength) (3rd row, Fig. 1). The D values for the 43 nCoV particles analyzed of different shapes lie in the range 1.34–1.85. The D estimates obtained are subjected to the ANOVA tests for statistical significance of the results, described as follows.

Fig. 2b.

Same as Fig. 2a but for the virions of the second row of classification shown at the bottom of Fig. 2a.

Fig. 2c.

Same as Fig. 2b but for the virions of the third row of classification shown at the bottom of Fig. 2b .

3.1. Analysis of variance (ANOVA) test results

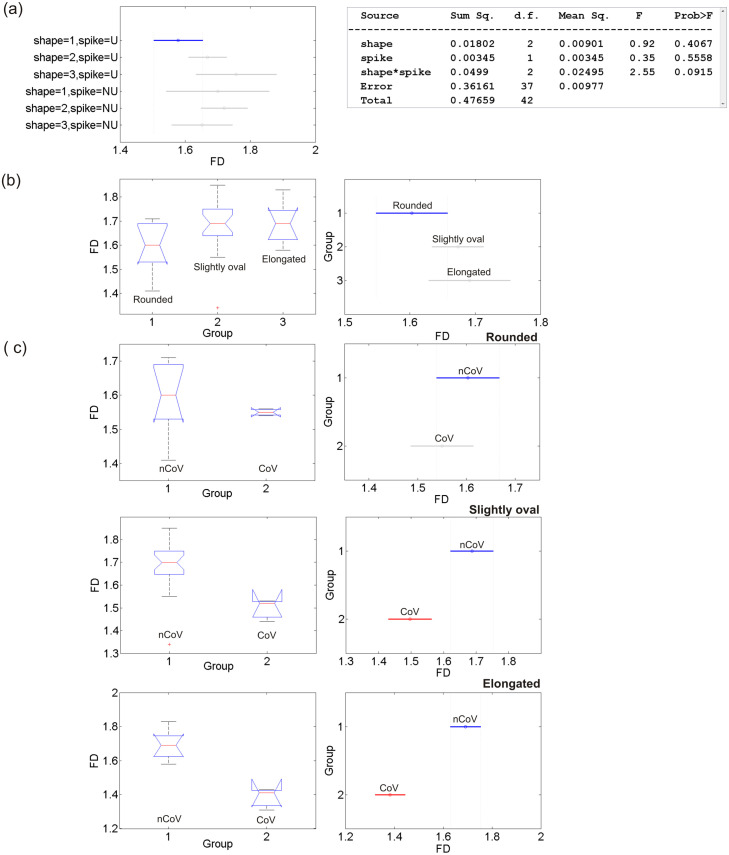
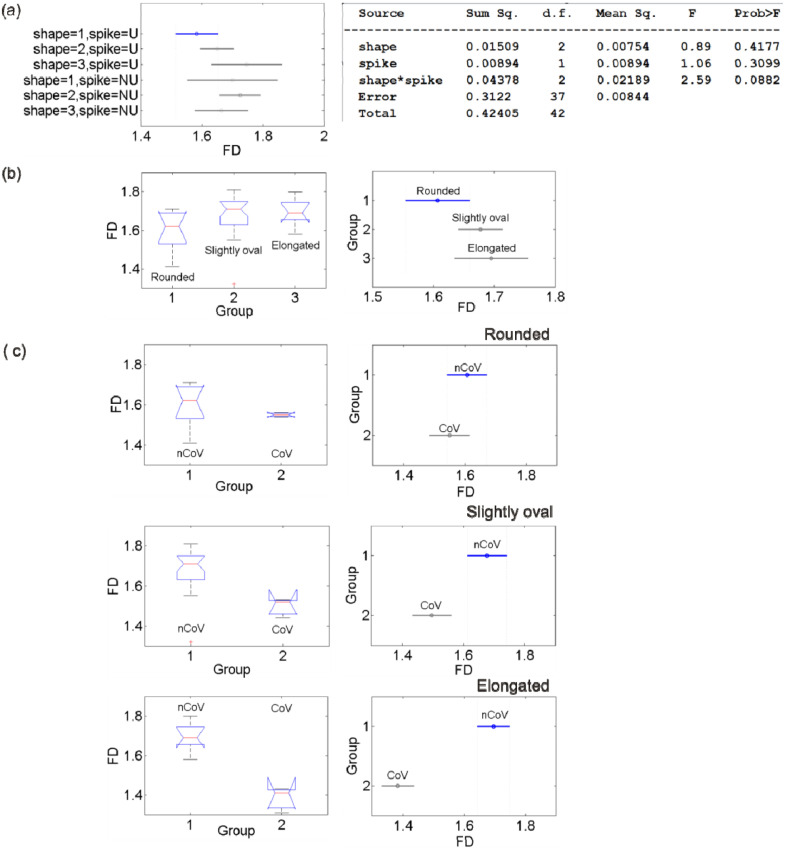
The D estimates, expressed as mean $\pm$ S.D., were subjected to ANOVA test, a statistical test exhibiting whether or not the means of several groups are equal and assessing the statistical significance of results obtained. The ANOVA box plot represents the size of the F-statistic and the p-value. The p-value is compared to significance level (say, 0.05 at 95% confidence level) to assess the null hypothesis that the means of different groups are equal. Thus, the lower the p-values than the significance level and the higher the F-statistic, statistically significant are the results. Large differences in the center lines of the boxes correspond to large F-statistic and small p-values. 1-way ANOVA is done to test if the mean in each group is same; 2-way ANOVA is to test (i) if the mean in each group is same, and (ii) if there is any interaction among different factors. We systematically conducted the ANOVA tests to the D estimates for the following cases (Fig. 3(a–c)): 1-way ANOVA tests (i) between the three groups of CoV by envelope shape (rounded, slightly oval, and elongated) to see whether their means are equal, (ii) between the four groups of CoV by spike distribution (evenly distributed, clustered at opposite ends, clustered at one end, and spike depleted) to see whether their means are equal, (iii) same as (i) but for nCoV, (iv) between similar groups by shape of CoV, and 2-way/multiple ANOVA (MANOVA) test for examining the relation between the D values and the interaction of two factors (shape and spike distribution) for nCoV. The results show the following major features. (1) For CoV, the elongated virions are statistically distinguished from other two (rounded and slightly oval), while the others are not distinguished from each other ($p=0.0011$); the virions are not statistically distinguished from each other based on their spike distribution ($p=0.8862$). Because we could not differentiate the virions by their spike distribution, hereafter ‘group’ in virus is referred to by their shape. (2) For nCoV, all three groups are not statistically distinguished based on their D values ($p=0.1297$), and their confidence intervals overlap (Fig. 3(b)). (3) CoV and nCoV are statistically distinguished by shape, except the rounded ones characterized by high and low p values with respect to (wrt) the significance level for rounded, and slightly oval and elongated shapes, respectively (${\mathit{p}}_{rounded}=0.3831$, ${\mathit{p}}_{slightlyoval}=0.0065$, and ${\mathit{p}}_{elongated}=0$.0003): nCoV particles are characterized by statistically higher D values than CoV ones (Fig. 3(c)). (4) The D-based classification rather depends on the shape*spike (shape can be any one of three groups: rounded, slightly oval and elongated, spike means whether the spike proteins are distributed evenly/uniformly, U or not, NU) interaction instead of on the individual factors (${\mathit{p}}_{shape\ast spike}$ = 0.0915, p${}_{shape}$ = 0.4067, and p${}_{spike}$ = 0.5558). This simple classification (U vs NU) in spike distribution, instead of the original classification into four types shown in Fig. 2, was considered in 2-way ANOVA test based on (i) our observations of nCoV particles, and (ii) the results obtained from the 1-way ANOVA test that the nature of spike distribution could not be resolved based on the D values, as mentioned above. MANOVA test for this interaction shows that no groups have means significantly different from Group-1 (Shape = 1, Spike = U), as found from the overlapped 95% confidence intervals for different groups (Fig. 3(a)). Overall, the two types of corona viruses presented here are statistically distinguished based on the D values for two groups (slightly oval and elongated), and the classification of nCoV particles into different types depends on the interaction of shape and their spike distribution (evenly distributed or not), as evidenced from small p-value for the shape*spike interaction (0.0915), and relatively large p-values for shape (0.4067) and spike (0.5558) obtained separately (see the MANOVA Table in Fig. 3(a)).

Fig. 3.

ANOVA results for testing the statistical significance of the fractal analysis results. (a) MANOVA 95% confidence interval (error) plot for the fractal dimensions obtained with the shape*spike interaction of the nCoV particles and the corresponding MANOVA table shown on right. (b) ANOVA box plot of the D values for three groups of nCoV. The red line indicates the median, the blue box extends between the first and third quartiles, and the black dashed lines (whiskers) extend between the minimum and maximum values excluding outliers (red points). (c) ANOVA box and error plots for testing the statistical significance between the means of the CoV and nCoV particles for rounded, slightly oval and elongated shapes.. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

4.1. Explaining viral features based on fractal analyses

Our D values obtained with the nCoV data analyses are in the range 1.34–1.85, differing from the Euclidean dimension of 2.0, suggesting a considerable degree of surface complexity. This complexity can be interpreted in terms of the nature of surface contact/binding/infected-site between the viral and host cells, and thus in terms of the patterns of surface interactions [3]. A rough (smooth) site may indicate a potentially stronger (weaker) interaction between protein and the binding molecule [4]. The borders of binary images show irregularity in the image shape; the D values suggest how their complex shapes deviate from classic geometric figures.

It is worth mentioning that in few cases the quality of fit is relatively poor in an intermediate scale (see 4th column, Fig. 2a as an example). This could be attributed to several factors such as experimental/measurement noise resulting from the use of different electron microscopy techniques, and the extracellular background (part of the region of interest, ROI, of the image outside the viral surface border), implying the D values in this range are likely overestimated. It was found that a small change in ROI of the image outside the viral surface slightly improves the quality of fit, but their overall effect is not statistically significant, at least true for the images we analyzed (see Figs. A.1–A.2, Appendix). The effect of the use of different techniques on D estimation cannot be excluded, with a caution in interpretation, however.

Fig. A.1.

(1st row) Binary maps of a CoV particle with varying ROIs: (left panel) 115 × 115 pixels, and (right panel) 125 × 125 pixels. The corresponding log–log plots of box size versus number of boxes (2nd row). The slope of the fitted straight line gives the D value, expressed as mean $\pm$ SD. Note a slight improvement in the fit with a change in ROI, as seen from the plot shown in right. The units of variables used are arbitrary.

Fig. A.2.

Same as Fig. 3 of the main text but after introducing the change in ROI into the original dataset used (image shown in 4th column, Fig. 2a of the main text) in Fig. 3. See text for details.

Here we discuss the implications of the ANOVA test results presented in the last section. Morphological diversity of nCoV particles is not statistically significant (D falling in a narrow overlapping range within error limits, Fig. 3(a)), in accordance with ANOVA test results (#2, Section 3.1). These observations strongly suggest the D value as one of the intrinsic properties of virion, although its measurement could be influenced by factors such as the methods used, finiteness in data, etc., to be discussed later. The slightly oval and elongated shapes of both the virus types (nCoV and CoV) could statistically be resolved (#3). The classification seems more complex with the shape*spike interaction than without interaction of the features (#4).

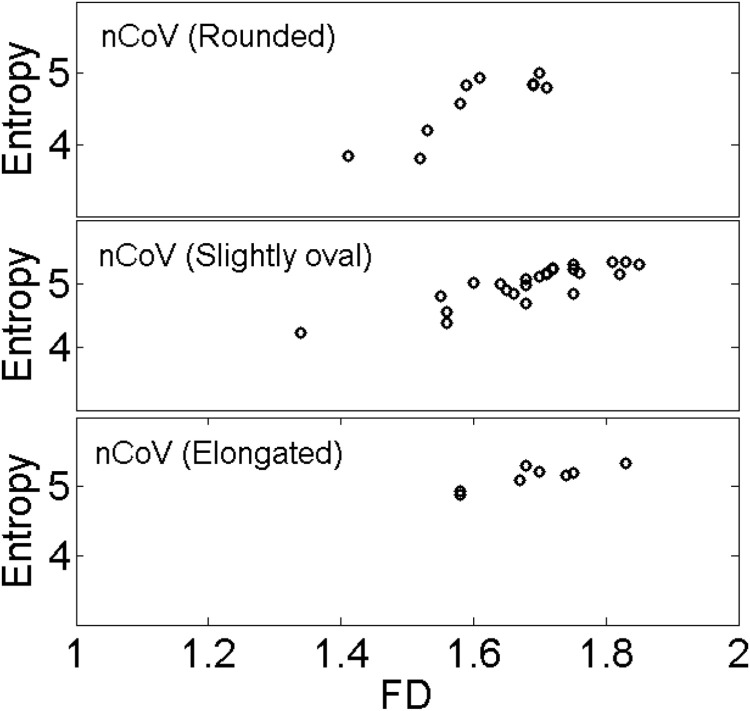
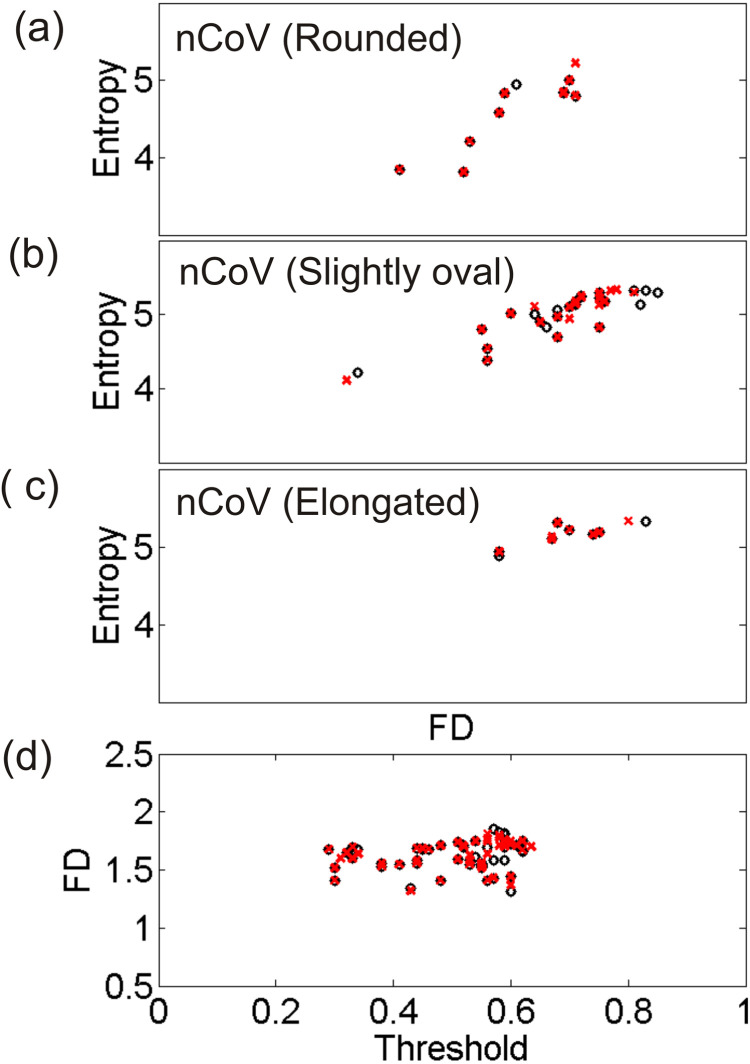
Topological entropy was measured from the images of varying size and then they were compared with the D values obtained. Entropy shows an increasing trend with fractal dimension for the nCoV particles of different type by shape (Fig. 4), in agreement with theory. It is worth mentioning that the bias in D could produce results similar to those shown in Fig. 4 for different virus shapes. We investigated the influence of small change in ROI of the images analyzed on the D values obtained and on the results shown in Fig. 4 (see Fig. A.2, Fig. A.3, Appendix). On comparing the changed results with the original ones, we hardly found any noticeable influence (Fig. A.3(a–c), Appendix). We also found from the MANOVA analysis that small changes in ROI produce fractal analysis results that are not significantly different from the original results (Fig. A.2, Appendix). However, the effect of the use of different techniques for taking the images on the measured D values cannot be excluded, so care must be taken when interpreting the D values and their relations to entropy for different virus shapes.

Fig. 4.

Dependence of entropy on fractal dimension for the nCoV particles of different shape.

Fig. A.3.

Influence of small changes in ROI of the images analyzed on the results obtained and their relationship. (a–c) Dependence of entropy on fractal dimension for the nCoV particles of different shape. (d) Dependence of the fractal dimension on threshold values. The estimates obtained using the original dataset (black circles) and the dataset with the changes in ROI included (red crosses) are plotted to the same scale for comparison.

Fractal analysis of binary images depends on the threshold values used for image segmentation. The D estimates used for discrimination of tissue structures at the multiscale level were found to be independent of the threshold selected [28]. Our threshold values, obtained with an automated version of the Kapur’s algorithm [24] for image segmentation, lie in the range 0.3–0.65 for the D estimates obtained. We expect their influence, at least with the current technique, on fractal scaling is minimal [29]. In addition, we investigated the dependence of the D values on threshold for small changes in ROI of the images. We found their dependency is again not influenced significantly with small changes in ROI (see Fig. A.3(d), Appendix), in agreement with the findings of an earlier study on the automatic selection of threshold for image segmentation [29].

4.2. Evaluating nature of scaling based on spectral analyses

The radial spectra are analyzed to describe the complexity of texture at different scales that contain information of fine (small scale) and coarse (large scale) structures as well as the morphology of the virions. We qualitatively analyzed them to evaluate the nature of scaling. For nCoV, a cross-over at $\sim$5-10 units of wavelength, depending on the virion classification, separates the low-wavelength (high-frequency) regime from the high-wavelength (low-frequency) one (3rd row, Fig. 1). The cross-over, a measure for characteristic length scale, may represent the average size of virion. A linear spectral decay at low wavelengths is observed over less than an order of wavelength with a slow decay, although it is difficult to visualize them from the figures shown (3rd row, Fig. 1).

CoV exhibits spectral properties almost similar to those of nCoV, with a few exceptions mentioned as follows. The former (3rd rows, Fig. 2a, Fig. 2b, Fig. 2c) shows a relatively faster spectral decay at low wavelengths than the latter (3rd row, Fig. 1). A spectral decay of opposite nature is observed between them at high wavelengths, however. Because scaling analyses generally look for linearity in high-frequency spectral decay in log–log domain, we are hardly interested in the nature of low-frequency spectra. For the spike-less virions, the transition between the two regimes is not clear, however. Their low-wavelength spectral decay is relatively faster than others, suggesting the significance of the spike-distribution on the observed spectral decay. Overall analyses suggest that a power-law self-similar scaling over few orders of magnitude is clearly missing, with an apparent scaling at low wavelengths over a maximum of one order of magnitude corresponding to the linearity in log–log domain.

Images taken with different electron microscopy techniques are characterized by different bandwidth limits, lateral resolution limits, and maximum analysis size, which may subsequently bias the results. Thus, the spectra defined over the whole frequency range cannot be reliably measured. The resulting low-frequency noise may explain why the linear trend in the observed spectra is distorted in the intermediate to large wavelength range (3rd rows, Figs. 1–2). Thus, the spectra in this range may not represent true morphological variations of the virions. There are ways one can standardize them to avoid the resulting bias [30]. The first one, mostly experiment-based, involves combining results from various techniques and multiple measurements of the images per technique. The other one (numerical-based) involves analysis of the synthetic spectra for the computer-generated surfaces created under the assumptions of the random process model of surface roughness [31]. The influence of noise on the measured power spectral density (PSD) can be tested by adding white noise into the synthetic viral surface characterized by a well-defined PSD. The fact that white noise gives constant power spectrum can be used to detect it [30]. Comparison of the synthetic with the measured spectra enables us to calculate the upper limits on wavelength that can reliably be measured.

In any case, the spectra presented here are still useful, which enable the calculation of upper and lower bounds on wavelength. The lower bound on wavelength is related to resolution of the instrument (pixel size) and the upper bound to the ROI of the image analyzed [30]. The spectra shown here can also be extrapolated to learn about a surface beyond the limits of the measurement technique.

The spectral scaling suggests that the viral surface roughness features are prevalent over a limited small-scale (short-wavelength) range. Surface properties such as the contact area thus increasingly depend on the accuracy of these short-wavelength measurements/information. So care must be taken when measuring and analyzing the spectra at a wider scale range.

The limitation of this study is that our data are limited and consequently subtleties like the exact nature of spike distribution could not be resolved. Another source of error could be the use of technique, such as the binary box-counting method for determining D, where the intensity information is lost and all the viral features are not contrasted from the background pixels. Also, image segmentation may cause some loss of information for estimating the D values [32]. The advantage here is the use of automated entropy-based thresholding for image segmentation thereby avoiding/having minimal influence of threshold on the D values. In any case, attending all these aspects, including the ways to standardize the images to avoid any bias of the results, as already presented, is beyond the scope of this short communication, but is the scope of future studies with the availability of a larger dataset to tightly constrain our current findings. By then the results can be considered as first order, but still useful for better understanding of nCoV in the framework of basic virology and clinical practice. Finally, the scope of this study can be extended to investigate some important dynamic features of nCoV, such as (i) changes in envelope-shape at different stages of infection where structural changes are expected to occur, and (ii) virion size that depends on the interactions between all its components. It is possible with the availability of high-quality data from both the low angle X-ray and light scattering experiments.

5. Conclusions

We assessed the complexity of surface roughness of nCoV particles. ANOVA results show that the nCoV particles of different shapes (rounded, slightly oval, and elongated) could not be statistically resolved with their D values falling on a narrow overlapping range. The latter two groups (slightly oval and elongated) of nCoV could, however, be distinguished from the earlier counterpart (CoV). The interaction of shape and spike distribution plays a major role for the classification to be statistically significant. Topological entropy describing the randomness of information in the images correlates with the D values. The effect of the use of different techniques for taking the images on the D estimation cannot be excluded, so care is required to accurately interpret the results for different virus shapes. Our data support apparent scaling (weakly self-affine) of viral surface roughness over a narrow band, with a maximum of one order of wavelength. Studies of this type have important implications on structure of virion, a key element in developing drugs, and on nature of contact causing infection with the organ. Detailed investigations of a large dataset at different scales, however, are essential to further constrain the nature of scaling, as a scope of future study. By then our results are treated as first order, providing clues to fight against COVID-19 with a hope for new vaccine.

CRediT authorship contribution statement

Simanchal Padhy: Conceptualization, Methodology, Formal analysis, Writing - original draft, Writing - review & editing, Investigation. Vijay P. Dimri: Investigation, Writing - review & editing, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Communicated by V.M. Perez-Garcia

Appendix.

In this Appendix, we describe in detail the effects of some of the image features during processing including the effect of threshold for image segmentation on the results obtained towards their accuracy and robustness.

A.1. Influence of ROI of the image on the results obtained

Influence of ROI on the estimates of fractal dimension and its statistical significance

We manually checked the fractal analysis results for each of the images analyzed for the best fit in the intermediate scale for accurate estimation of the D values with minimal bias. Of all the 55 images analyzed, we found for the 14 images the quality of fit over this range is relatively poor. In order to investigate how the ROI of the images influences the fit and hence the D estimates, we re-analyzed those 14 images by adjusting the ROI such that it includes the details of the viral features plus small contribution from the extracellular background. Results showed that a small change in the ROI in reference to the original one improves the quality of fit. Fig. A.1 shows an example of fractal analysis applied to one of the CoV particle images (shown in 4th column, Fig. 2a) with two different ROIs (115 x 115 pixels and 125 x 125 pixels): a small increase in ROI slightly improves the quality of fit. The D values of both the datasets (original dataset of the 55 D values, and the same data set except with the 14 D values revised after introducing the change in ROI) are then subjected to the ANOVA and MANOVA analyses for testing the statistical significance of the changes induced by the ROI. On comparing the MANOVA test results for both the data sets (Fig. 3 for the original data set and Fig. A.2 for the changed data set), we found the nature of dependence of viral features for classifying the nCoV particles is similar to that presented earlier, i.e., our primary results. This is evidenced from the similar estimates of the p-values: relatively large p-values for the shape and spike obtained separately, and small p-value for their interaction (${\mathrm{p}}_{\mathrm{shape}\ast \mathrm{spike}}=0.0915$, ${\mathrm{p}}_{\mathrm{shape}}\mathrm{M}=0.4067$, ${\mathrm{p}}_{\mathrm{spike}}=0.5558$, see MANOVA Table in Fig. 3 of the main text; ${\mathrm{p}}_{\mathrm{shape}\ast \mathrm{spike}}=0.0882$, ${\mathrm{p}}_{\mathrm{shape}}=0.4177$, ${\mathrm{p}}_{\mathrm{spike}}=0.3099$, MANOVA Table in Fig. A.2). This comparison suggests that the influence of the ROI on the primary results presented is not statistically significant. Similar conclusions emerge from both the data sets when they are interpreted in terms of the relative changes in D values obtained.

Influence of the ROI on the dependence of entropy on fractal dimension

In order to test the influence of the ROI on the entropy and its dependence on fractal dimension, we compared the estimates of fractal dimension and entropy for both the data sets (Fig. A.3(a–c)). We hardly find any noticeable influence of the ROI on the dependence of entropy on fractal dimension obtained for different virus shapes of the nCoV particles.

A.2. Dependence of fractal dimension on threshold for image segmentation

We examined the dependence of fractal dimension on threshold obtained for both the data sets using an automated version [29] of the Kapur’s algorithm [24] for image segmentation. The threshold values lie in the range 0.3–0.65. The dependence of fractal dimension on threshold is again not significantly influenced by a small change in ROI of the images analyzed (Fig. A.3 (d)), in agreement with the findings of a previous study using the automated procedure of selecting the threshold for image segmentation [29].