Emerging Consensus on the Collapse of Unfolded and Intrinsically Disordered Proteins in Water

Abstract

Establishing the degree of collapse of unfolded or disordered proteins is a fundamental problem in biophysics, because of its relation to protein folding and to the function of intrinsically disordered proteins. However, until recently, different experiments gave qualitatively different results on collapse and there were large discrepancies between experiments and all-atom simulations. New methodology introduced in the past three years has helped to resolve the differences between experiments, and improvements in simulations have closed the gap between experiment and simulation. These advances have led to an emerging consensus on the collapse of disordered proteins in water.

1. Introduction

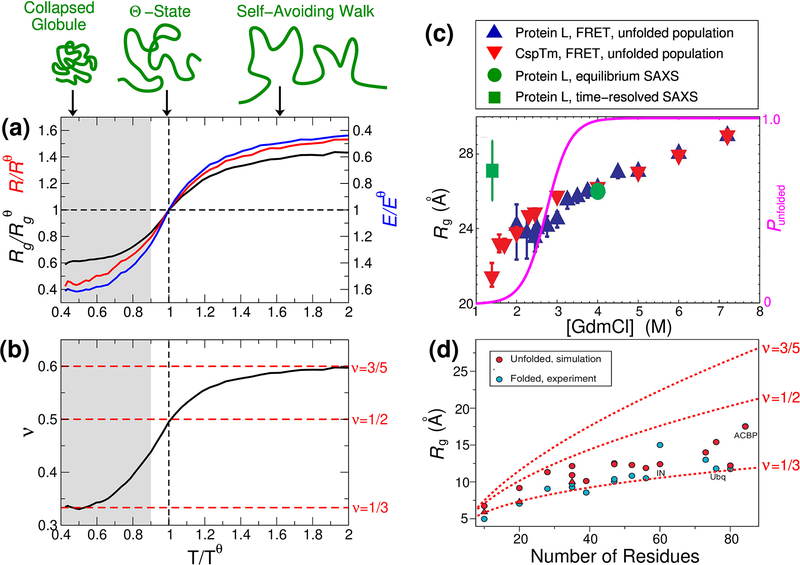
Since unfolded or intrinsically disordered proteins lack an ordered structure, they are often well approximated as disordered polymers. In general, polymers will undergo a collapse transition as the interactions with the solvent are varied, as is well known in the case of homopolymers [1]. That is, sufficiently weak interactions with the solvent (poor solvent) will lead to a maximally compact, collapsed chain. Collapse can be quantified in terms of the radius of gyration R_g, which is defined as $R_g^2=\frac{1}{2}{\langle {\left|r_i-r_j\right|}^2\rangle }_{i,j}$, where the average runs over all intramolecular atom pairs (i, j) with positions r_i, r_j. The degree of collapse is usually characterized in terms of a length scaling exponent ν, describing the relation between average R_g and the number of residues in the protein N, as R_g ∝ N^ν, or similarly between the average end-end distance R and N, R ∝ N^ν. For example, it is obvious that ν = 1/3 for chains which are maximally compact collapsed globules (such as folded proteins) (Fig. 1 (a),(d)). On the other hand, strong interactions with the solvent (good solvent), or high temperature, will lead to a very expanded chain where ν can be shown to be ~ 3/5 (more precisely, 0.588) for homopolymers, the behaviour expected for purely repulsive chains (self avoiding walks). At an intermediate solvent quality, where the interactions with the solvent perfectly balance the interactions of the chain with itself, ν = 1/2, the same scaling as for a ghost chain (i.e. without self-interactions), a condition known as the Θ-solvent, or Θ-state (Fig. 1(a)). Thus a fundamental property of any disordered protein is its degree of collapse, which varies with solution conditions and temperature. Proteins, of course, are heteropolymers, hence their collapse is more likely to involve interactions of some residues (e.g. hydrophobic ones) than others, [2–4] and collapse is expected to depend on both the average properties of the sequence (such as hydrophobicity or charge [5–8]) and on sequence order [9, 10]. Nonetheless, the theory of homopolymer collapse provides a useful starting point for analyzing the properties of unfolded proteins, especially when the sequence is well mixed [11]. The scaling exponent ν is often used to characterize the extent of collapse: for very long chains ν tends towards only three possible limits (1/3, 1/2, 0.588), but as proteins are usually relatively short, ν is more properly referred to as an apparent scaling exponent and can also take on intermediate values (Fig. 1(b)).[12]

Figure 1:

Background on unfolded protein collapse. (a) Polymer collapse illustrated from simulations of Val-100 with the ABSINTH model[67] (data from Zheng et al.[69]). Variation of radius of gyration R_g, end-end distance R and FRET efficiency E with temperature, all quantities being normalized by their respective values at the Θ temperature, T^θ. Here, increasing temperature is analogous to adding chemical denaturant, as both lessen the importance of intramolecular interactions. The transfer efficiency E was computed with a Förster radius of R₀ ≈ R^θ. (b) Corresponding variation of length scaling exponent ν with temperature. Here ν was approximated from the scaling of internal distances for residues separated by a number of peptide bonds N_p, i.e. ${\langle {\left|r_i-r_j\right|}^2\rangle }_{\left|i-j\right|=N_p}\propto N_p^v$. Shaded region respresents collapse not usually observed in unfolded or disordered proteins. Schematic figures illustrating degree of collapse are shown at top. (c) Discrepancy between FRET and SAXS experiments prior to recent methodological advances [33]: R_g for protein L and CspTm from FRET, and for protein L from SAXS as a function of denaturant concentration. Right axis shows equilibrium unfolded population of Protein L (magenta curve). (d) Comparison of R_g of unfolded proteins from simulations with the R_g of their respective folded states. [49] Length scaling laws with power law exponents of 1/3, 1/2 and 3/5 are shown.

Chain collapse is clearly significant for protein folding, since a protein folding into a globular structure implies collapse – but is there a non-specific collapse (i.e. involving primarily non-native interactions, and without formation of specific meta-stable intermediates) which occurs before folding, or is collapse concomitant with folding? [13] And how does the degree of collapse prior to folding depend on sequence, or native structure [14–16]? Answers to these questions depend on methods to quantify the dimensions of disordered proteins under different conditions. The degree of collapse is also highly relevant to the function of intrinsically disordered proteins (IDPs). Most obviously, a number of IDPs, or proteins which contain intrinsically disordered regions (IDRs), are associated with the formation of so-called “membraneless organelles” driven by liquid-liquid phase transitions [17]. In the case of homopolymers, the Θ conditions for a single chain are correlated with the critical conditions for phase separation [1], because the underlying interactions driving collapse and phase separation are the same. Indeed it has recently been demonstrated numerically that this holds approximately for proteins also [18]. Therefore the extent of collapse of a monomeric protein is a general indication of its propensity to phase separate [19]. To give a second example, there are a number of IDPs which have been shown to bind other biomolecules in a state which is still largely disordered [20–22]. Thus modulation of collapse could influence binding energetics, kinetics and mechanism [22]. Despite the evident importance of quantifying the degree of chain collapse in unfolded proteins, until the last few years, different experiments yielded results that conflicted with each other, as well as with most molecular simulations.

2. Discrepancies amongst experiments and simulations

2.1. Differences amongst experiments

Chemical denaturants such as urea or guanidinium chloride (GdmCl) have long been used in protein folding studies to destabilize proteins, which is generally believed to occur via weak association of denaturant molecules with the unfolded protein [23–25]. A landmark collaborative study of a large number of proteins in high concentrations of chemical denaturant established a scaling exponent of ν = 0.598(0.028) [26], within error of the self-avoiding walk scaling exponent of 0.588. This would suggest that all sequences are close to the “good solvent” limit at high denaturant concentrations, presumably because of sufficiently favourable molecular interactions with denaturants. Other studies reached a similar conclusion using other techniques, notably establishing the length scaling via several different labelling pairs in single molecule FRET spectroscopy [8].

However, until recently, there was some controversy over the properties of different protein sequences under more biologically relevant denaturant-free conditions. Many studies had shown a reduction of unfolded state R_g as denaturant was diluted, using single-molecule FRET [8, 11, 27–34]. FRET measures the distance between a pair of fluorophores (or dyes) attached to the protein at specific positions, with the efficiency of energy transfer between excited states of the fluorophores being dependent on the distance between them via the Förster relation [35]. From the average distance measured, an average radius of gyration can be inferred. A reduction in R_g with denaturant was also observed by contact quenching experiments[36], while nuclear magnetic resonance (NMR) [37], dynamic light scattering (DLS)[38] and two-focus fluorescence correlation spectroscopy [8] indicated a consistent reduction of the hydrodynamic radius R_h with lowered denaturant concentration. In Fig. 1(c) [33] is shown an example of the unfolded-state collapse inferred from a FRET study of protein L and the cold-shock protein CspTm as guanidinium chloride concentration is reduced. The length scaling exponent in water determined by FRET experiments using multiple labelling sites was approximately 1/2, suggesting that water is close to Θ-solvent conditions for many unfolded proteins (a notable exception being sequences with a high net charge)[8]. It is important to note that this implies a small compaction relative to high concentrations of denaturant, but the R_g is still much larger than for a fully collapsed globule.

The scattering function I(q) measured in small-angle X-ray scattering experiments is related to the distribution of intramolecular pair distances, and hence is a sensitive measure of the R_g. In contrast to the results from FRET and other methods, most studies using small-angle X-ray scattering had concluded that R_g was approximately independent of denaturant concentration, and hence that water was close to the “good solvent” limit [39–44], although there were exceptions [37]. For example, the SAXS data for protein L in Fig. 1(c) show a clear contrast with the FRET-derived R_g (the first example where the same protein was studied by both methods, eliminating protein-specific differences as the origin of the disagreement) [29, 33, 39]. This discrepancy regarding the properties of proteins in water firstly raised the technical question of which of the SAXS or FRET results was more accurate. Secondly, the differences regarding the compaction of proteins in water raised questions over the quality of water as a solvent for unfolded proteins, as well as over the mechanism of chemical denaturation: the accepted mechanism of denaturation is that it occurs via weak association of denaturant molecules with the unfolded chain, which should cause a swelling of the chain at higher denaturant concentrations[23].

In spite of the abovementioned issues, SAXS and FRET experiments and some simulations were in at least qualitative agreement in some cases, for example the chain collapse brought about by raising the temperature [45,46], due to a strengthening of the hydrophobic effect, but also the solvation properties of charged and hydrophilic residues [19,47]. This suggested that the apparent differences amongst experiments and simulations could eventually be reconciled.

2.2. Differences between experiments and all-atom simulations

A second and unrelated discrepancy was evident when comparing the properties of atomistic simulations in explicit solvent to experiment: the R_g obtained with most force fields was much below experimental estimates [46, 48] (much more than experimental estimates of R_g differed from each other). In many cases, unfolded states in simulations had R_g barely larger than the folded state (Fig. 1(d)), with a larger amount of secondary structure formation than is inferred from experiment [46, 49, 50]. Thus, it was essentially impossible to make quantitative comparisons between experiment and simulation.

3. Resolving the discrepancy between SAXS and FRET experiments

It has recently been possible to obtain quantitatively consistent results for R_g from both FRET and SAXS experiments [51–55], as well as when comparing experiments to unbiased molecular simulations [25,56,57]. What were the key issues in resolving the earlier discrepancies?

3.1. Choice of experimental systems

For a foldable protein sequence, the folded state becomes close to 100% populated at low denaturant concentration, which makes it challenging to study the unfolded state by ensemble methods, because the signal is averaged over both folded and unfolded populations. For example, the unfolded population of protein L is plotted in Fig. 1(c). This limits the range of equilibrium SAXS experiments to high denaturant concentrations. In the case of protein L, time-resolved SAXS was used to estimate R_g at low denaturant before folding occurs [39] (green square in Fig. 1(c)), but such experiments are inherently noisy and require large amounts of material. Single molecule FRET can resolve the unfolded population down to much lower denaturant concentrations and hence study collapse over a wider range of conditions, as seen in Fig. 1(c). Since, as seen in Fig. 1(c), most of the collapse observed by FRET occurs at the lowest denaturant concentrations, it will be missed if the unfolded state cannot be observed under these conditions [51, 53].

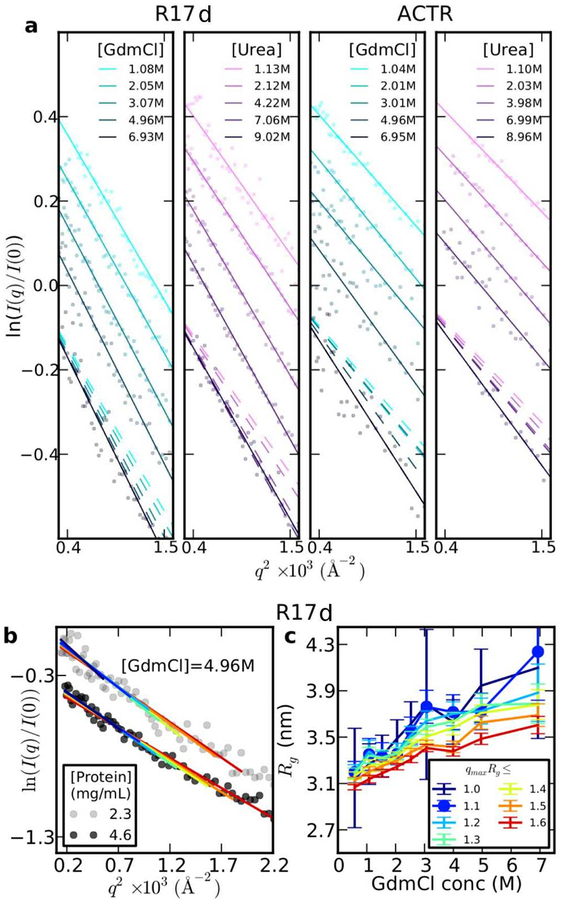
A key aspect of recent studies has therefore been the careful choice of proteins which do not fold, or fold only at very low denaturant concentrations, allowing equilibrium SAXS to be used. A second requirement is that the proteins should be highly soluble even in the absence of denaturant, in order that SAXS experiments can be performed without the complications of transient aggregation. The first such study was that by Borgia et al. [51], in which the intrinsically disordered protein ACTR and a destabilized variant of the spectrin R17 domain were studied over a range of urea and guanidinium chloride concentrations by four different techniques, including SAXS and FRET. Both of these proteins were shown by dynamic light scattering to remain highly soluble at low denaturant concentrations. As in earlier studies, the FRET data showed a collapse with denaturant dilution (Fig. 2(d)). An analysis of the SAXS data using Guinier analysis, the simplest method for determining R_g, also showed a contraction with decreasing denaturant concentration. Guinier analysis relates R_g to the slope of a plot of the log-SAXS intensity ln I(q) vs q², where q is the scattering vector (ln $I\left(q\right)\propto -\frac{1}{3}{R}_g^2{q}^2$) [58]. As evident in Fig. 2(a), there is a clear change of slope with decreasing denaturant concentration, indicating compaction. Thus, SAXS and FRET results were in at least qualitative agreement.

Figure 2:

Qualitative consistency of SAXS and FRET. (a) Guinier plots for R17 at different concentrations of GdmCl and urea. Note that the primary data and fits are offset on the y-axis for clariy; broken lines show the fitted curves without offset to compare slopes. (b) Guinier fits carried out for R17 in 4.96 M GdmCl with different fitting ranges [0, q_max], where q_maxR_g is the number shown in the legend in (c). (c) R_g inferred from Guinier fits in (b), for different q_maxR_g. (d) Primary FRET data for unfolded R17 in GdmCl and urea. (e) End-end distance R inferred from R17 FRET in GdmCl, assuming Gaussian chain or SAW polymer models as labelled. (f) R_g inferred from R using fixed conversion factor for Gaussian chain or SAW.

3.2. Identifying shortcomings of standard SAXS analysis methods

Choosing a protein which can be studied down to a low denaturant concentration, however, does not completely resolve all discrepancies. For example, past studies on reduced RNase A, which can be unfolded by reducing the disulfide bonds, showed no change of R_g with denaturant concentration [41], provided the disulfides were fully reduced to avoid artifacts [38, 59]. In this case, R_g could be studied down to zero denaturant concentration without folding. The lack of change in R_g in this case might be partially explained by the fact that the approximation used in Guinier analysis is valid only at small q. This was tested in a systematic Guinier analysis of SAXS data for R17 [51], varying the q range fitted to get R_g. Indeed, it was found that using too large a range of q suppressed variations in R_g (red curves in Fig. 2(b),(c)) with denaturant concentration. This would lead to an underestimate of the change of R_g with denaturant. While using a smaller q range may reduce this systematic error, it results in unacceptably large statistical error (blue curves in Fig. 2(b),(c)), because of the larger experimental error on data points close to q = 0. The smaller range of validity of the Guinier approximation relative to folded proteins is essentially due to the greater asphericity of expanded states relative to globular states [60]. Overall, these results confirm that Guinier analysis is a relatively insensitive method for inferring R_g from unfolded proteins, as has long been known for random coils [61]. We note that the alternative Debye expression for the scattering from a Gaussian chain [62] in principle allows more data to be used in the fit, but it tends to overestimate R_g [60].

3.3. Identifying shortcomings of standard FRET analysis methods

There were also shortcomings in the analysis of FRET, because the observed mean FRET efficiency is an average over a very broad distribution of inter-fluorophore distances P(r), that is $\langle E\rangle ={\int }_0^{\infty }E\left(r\right)P\left(r\right)dr$, where E(r) = (1 + (r/R₀)⁶)⁻¹ and R₀ is the Förster radius. In order to infer an average distance $R={\int }_0^{\infty }rP\left(r\right)dr$ from a single FRET measurement 〈E〉, a polymer model distribution for P(r) with a single adjustable parameter was usually used, for example a Gaussian chain or self-avoiding walk (SAW). However, the inferred R was quite sensitive to polymer model chosen [63, 64]. The dependence of the inferred R on polymer model is illustrated in Fig. 2(e) for R17 in GdmCl, and similarly for the derived R_g (Fig. 2(f)) [51]. A further problem with using a single polymer model to interpret all data is that the ratio $\lambda =R^2/R_g^2$ used to convert R to R_g is fixed in each case, which we will see below is not valid.

3.4. New analysis methods: Bayesian ensemble refinement

As indicated above, better methods of analysis were needed for both SAXS and FRET data. A central problem of interpreting both SAXS and FRET data for unfolded proteins is that they are averaged over a broad distribution of structures. Thus, any model for the data needs to account for this distribution, a challenging inference problem, given limited data. An alternative to using simplified analytical models such as a Gaussian chain for FRET or the corresponding Debye model for SAXS is to use an explicit molecular model, such as that which can be generated by molecular simulations. An atomistic simulation model can realistically represent the protein chain and the specific interactions within it, and allows any ensemble-averaged static property to be computed. However, it usually will not exactly reproduce the experimental data due to small inaccuracies in the energy functions used in the simulations. These inaccuracies can be overcome by reweighting the simulation data to match experiment – this must be done with care not to overfit, which can be achieved by including appropriate regularization [51, 52, 65, 66]; in addition it is important that the initial ensemble be sufficiently close to the true ensemble that reweighting is possible [66]. If performed carefully, this procedure should in principle provide the most realistic representation of the disordered ensemble. From the perspective of Bayesian statistics, such reweighting corresponds to using the simulation model as a prior, which is then augmented by the experimental data to give the final model. The procedure is thus referred to as Bayesian Ensemble Refinement [65].

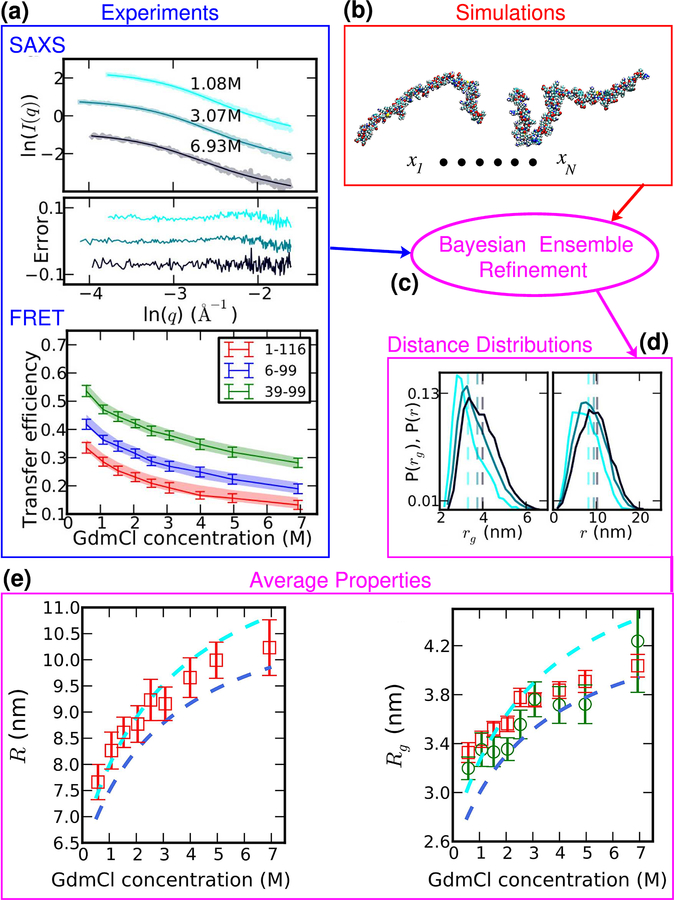
Fig. 3 shows an application of ensemble refinement to reconciling SAXS and FRET data from unfolded R17 [51]. SAXS and FRET measurements were made on R17 in a number of denaturant concentrations in exactly matched buffers; the only difference between the samples apart from protein concentration was that the protein was labelled with fluorophores for FRET, but not SAXS. The two sets of data were used jointly to reweight an ensemble of structures for R17 generated from simulations with the ABSINTH model [67] to obtain a good match with experiment. The good fit of the ensemble to both sets of data suggests that the SAXS and FRET data sets are self-consistent; moreover, ensembles derived from fitting to only SAXS or only FRET data had similar properties to those from a combined fit. The ensembles thus derived can then be used to compute molecular properties and distributions directly. Note the absence in the distributions of distance r and r_g (Fig. 3) of any sharp features that would indicate overfitting. The average properties R and R_g show that indeed the protein collapses as denaturant is diluted. Moreover, the R_g inferred from Guinier analysis with a very small q range (green symbols) agrees with that from the ensemble reweighting, but with much larger error bars.

Figure 3:

Ensemble refinement to interpret SAXS and FRET data. (a) SAXS and FRET data are recorded for the same unfolded protein (here: R17) under identical conditions as a function of denaturation concentration. (b) Unbiased simulations are performed using an implicit solvent model to generate an initial realistic molecular ensemble. (c) Bayesian ensemble refinement seeks to make the minimal perturbation to the simulation ensemble (by reweighting) in order to match the experimental data – ensemble averages after reweighting are overlaid on experimental data in (a) as thin curves. (d) Distance and radius of gyration distributions computed from the reweighted ensemble show an expansion with denaturant concentration. (e) Ensemble average R and R_g from ensemble refinement versus GdmCl concentration (red symbols) are compared with estimates from Gaussian chain (cyan) and SAW (navy) models from FRET and from Guinier analysis using the smallest practical range of q (green symbols).

The comparison between the average distance R and R_g inferred from the ensemble refinement and those inferred from FRET using either a Gaussian chain or SAW model is very revealing (Fig. 3). The ensemble estimates are close to those from the Gaussian chain at low denaturant concentration, but more similar to the SAW at high denaturant concentration. This is presumably because the improvement in solvent quality from water to high denaturant causes the chain to transition from being close to Θ-solvent conditions to closer to the self-avoiding walk limit. As can be seen, this means that using a single polymer model (either Gaussian chain or SAW) to analyze all the data would in general give an overestimate of the change in R with denaturant concentration. This problem is compounded when converting from R to R_g using a fixed conversion factor $\lambda =R^2/R_g^2$, because the relative change in R is larger than that in R_g, hence λ should get larger with increasing denaturant. This decoupling between R and R_g is true even for homopolymers (see Fig. 1(a)), although it may be further enhanced in heteropolymeric sequences [52]. All of these factors conspire to yield overestimates for the change in R_g with denaturant when a single polymer model is applied to FRET data.

3.5. Other new analysis methods

We have seen that modelling the unfolded state using Bayesian ensemble refinement helps to overcome the shortcomings of conventional analyses of SAXS data (by Guinier analysis) and of FRET data (by polymer models), which respectively tend to under- and overestimate changes of R_g with denaturant concentration, contributing to the earlier controversy. A similar algorithm formalized in terms of maximum entropy [68] was applied to SAXS and FRET data for a set of intrinsically disordered proteins [52], also finding that the molecular ensemble could provide a consistent explanation for both experiments.

Another new approach that is closely related to ensemble refinement is the recently introduced “molecular form factor” (MFF) method [53]. In this approach, ensembles of structures are pre-generated by simulations with different solvent quality or temperature, which are each characterized by their scaling exponent ν. The form factor I(q; ν) is calculated as an average over the ensemble at each value of ν, and converted to a dimensionless form M(qR_g; ν) = I(qR_g)/I₀. Then, any new experimental data set I(q) is fitted with I₀M(qR_g; ν) via I₀, R_g for each value of ν using the precalculated M(qR_g; ν), generating a set of coupled (ν, R_g) pairs. The optimal (ν, R_g) pair is that which minimizes the deviation from the experimental data as measured by the χ² function. The MFF method allows more of the experimental scattering data to be used for fitting, overcoming the limited range of validity of the Guinier approximation. When applied to a number of destabilized proteins, it revealed a collapse at lower denaturant concentrations – including for cases where it could not be detected before, such as RNase A[41, 53]. As mentioned above, the MFF approach has a lot in common with ensemble refinement, the main difference being that the ensembles are precomputed. This offers a great advantage in efficiency and easy of use over ensemble refinement. However, if the protein under consideration is not well described as a random coil (if it includes sufficient residual structure, or at the extreme, a folded domain), the MFF approach is not applicable. The ensemble refinement method is thus more general, if more demanding to use.

A couple of other methods have also recently been developed which, similar in spirit to the MFF approach, can easily be applied to extract accurate R_g and ν without the need to run simulations or perform ensemble refinement. The first is the “extended Guinier” model, which adds an additional term to the standard Guinier model and can therefore be fitted analytically to a broader range of q[60]. Like the MFF, it yields coupled estimates for both R_g and ν. The second is the SAW-ν model for interpreting FRET experiments in terms of a distance distribution P(r) [69]. It uses a ν-dependent P(r; ν) based on the P(r) expression for a self-avoiding walk, thus effectively interpolating between different solvent conditions. For example, this would avoid the overestimation of changes in R and R_g encountered when using a single polymer model to try and fit FRET data at all denaturant concentrations.

3.6. Potential influence of FRET fluorophores on collapse

An alternative explanation which has been advanced to explain some of the discrepancy between FRET and SAXS results is the hydrophobicity of the fluorophores [43, 53, 70], which might then cause additional collapse in FRET versus SAXS. It is worth noting that while the fluorophores are large and have extended conjugated aromatic surfaces, they also usually carry a net charge (e.g. −2 in the case of the commonly used AlexaFlour 488 and AlexaFlour 594). The potential influence of the fluorophores has been investigated in several studies. As mentioned above, consistent results could be obtained from ensemble refinement for R_g with a standard AlexaFlour 488/594 dye pair, whether the refinement was done using FRET, SAXS without dyes, or a combination of FRET and SAXS. However, for an alternative more hydrophobic dye pair, the R_g from an independent refinement using just the FRET data was significantly smaller than estimated from SAXS[51], indicating that the fluorophores did perturb the protein. Thus, selection of suitable fluorophores for FRET studies is critical in order to obtain reliable results, but the results with a well chosen set of fluorophores were completely consistent with SAXS [51].

In a second tour de force study of dye effects, SAXS experiments were done on samples labelled with FRET fluorophores as well as samples without labels, for a series of intrinsically disordered proteins. [52] This is challenging because of the large amount of labelled material that must be prepared, but allows the effect of the labels to be addressed directly. The comparison of labelled and unlabelled proteins showed that the addition of the fluorophores sometimes caused a small change in R_g outside the error bars, however the shift was as often an increase in R_g as a decrease, indicating that the effect is not systematic. [52, 54, 71, 72] More recently, an N-terminal disordered fragment of pertactin (the full length protein is folded in water) was studied by SAXS without labels, or with one or two AlexaFlour 488 dyes attached to it. [70] The results indicated a statistically insignificant change in R_g for addition of a single label, relative to unlabelled protein. When two labels were attached, there was a significant additional reduction in the radius of gyration in water relative to the unlabelled protein, but with large errors arising from the noisy SAXS data for the labelled samples.

In summary, the fluorophores used to probe distance changes in FRET experiments can of course slightly perturb the protein properties and should be chosen with care. Ideally, results from multiple dye pairs should be compared [21, 51]. However, from the accumulated evidence so far, they do not systematically favor collapse.

4. Resolving the discrepancy between experiments and all-atom simulations

Some simple changes to simulation force fields in recent years have helped to correct the excessive collapse of disordered proteins in water seen earlier. These modifications included a global scaling of protein water interactions [73, 74], and the introduction of a new water model with stronger dispersion interactions [48, 75], and have been recently reviewed.[50] Evidence of the progress which has been made is the impressive agreement with SAXS data obtained with unbiased simulations [56, 57]. From the perspective of simulating protein collapse in denaturant, an accurate model for the denaturant is also required. Older models were able to capture the relative effects of denaturant on the solubility of different amino acids, but the denaturants in most force fields bound the protein too strongly [76]. A careful reparameterization of the denaturant model to capture experimental solubility data for model peptides[77] allowed for predictive accuracy in all-atom simulations of an IDP [25]. These simulations were helpful in discounting several alternative explanations for earlier SAXS/FRET discrepancies, such as preferential partitioning of the denaturant molecules toward the center of the chain, or systematic differences between labelled and unlabelled molecules[25].

5. Emerging consensus on properties of unfolded proteins and IDPs in water

The results coming from carefully chosen experimental systems as well as novel analysis methods have shown that FRET and SAXS experiments yield a generally consistent picture of the dimensions of unfolded proteins at different denaturant concentrations. In order to make quantitative comparisons, however, it is essential that all data be analyzed with state of the art methods. This means, in the case of FRET, using either ensemble refinement [51, 52] or the simple SAW-ν model[69] to infer changes of R and R_g with denaturant. For SAXS, it means using ensemble refinement [51, 52], the molecular form factor method [53], or the extended Guinier method [60]. Comparing results using new analysis methods with those obtained with old methods [71] is misleading, considering all the drawbacks of older methods pointed out above.

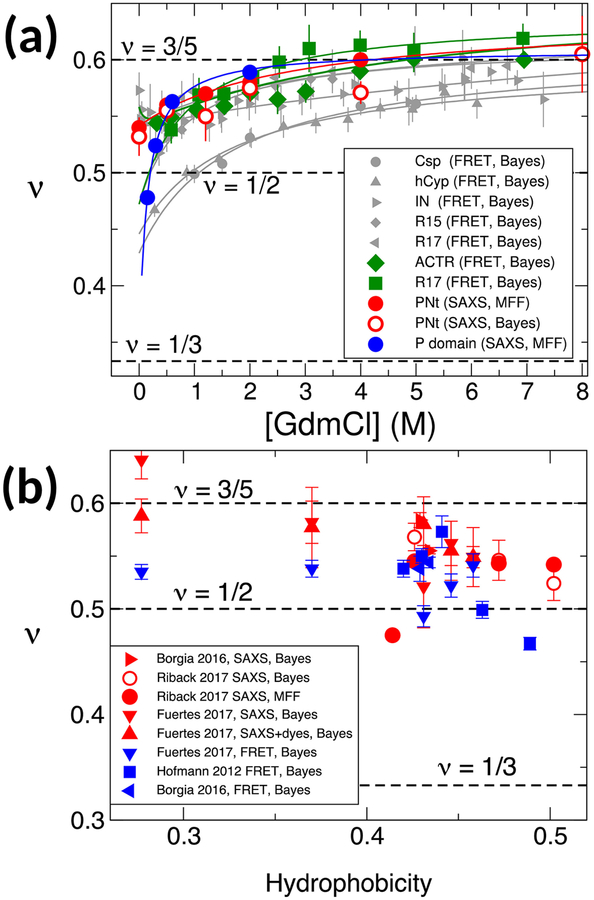
For this reason, a recent study reanalyzed FRET and SAXS data from earlier papers (as well as newer ones) using the same set of state of the art, consistent analysis procedures [54]. To be able to compare data for multiple proteins of different sequence length and composition, only the derived scaling exponents ν are plotted in Fig. 4. These show firstly that the most recent methods such as the MFF approach and Bayesian ensemble refinement give very consistent results when applied to the same data sets (e.g. compare results for PNt in Fig. 4(a)), thus analysis methods are no longer a source of discrepancies. Secondly, all proteins considered have a scaling exponent ~ 3/5 at high denaturant concentration. Thirdly, as denaturant concentration is reduced to zero, all proteins shown undergo a compaction and corresponding reduction in ν to a value in the range 0.45–0.55, close to Θ-solvent conditions (highly charged proteins still remain close to the SAW limit in water [8]); a majority of the proteins have ν slightly greater than 1/2, but still clearly below the value estimated at high denaturant. Like ν, the reduction in radius of gyration between high and low denaturant is sequence-specific, but generally in the range of 10–20 %. Notably, however, none of the proteins considered even come close to collapsing to a globular state (with ν ≈ 1/3) in water.

Figure 4:

Consistent analysis of multiple SAXS, FRET data sets. (a) Dependence of scaling exponent ν on denaturant concentration from SAXS data from Riback et al. [53] (red, blue symbols), and FRET data from Hofmann et al. [8] (grey symbols) and Borgia et al. [51] (green symbols). Analysis methods – Bayesian refinement or MFF – are given in legend in each case. (b) Dependence of scaling exponent on mean Kyte-Doolittle hydrophobicity for proteins studied by Borgia et al. [51], Fuertes et al. [52], Hofmann et al. [8] and Riback et al. [53]. Experimental methods and analysis methods are indicated in the legend.

Further evidence for the consistency between SAXS and FRET experiments comes from a recent study on the unfolded state of NTL9[55]. Instead of using single molecule experiments to separate folded and unfolded states (requiring large fluorophores), time resolved experiments were performed using a continuous-flow microfluidic mixing device to capture the unfolded state before folding occurs. This allowed the use of small fluorophores, p-cyanophenylalanine and tryptophan as FRET labels, which ought to be even less perturbing to the unfolded state than single molecule probes. The results confirmed the picture that FRET and SAXS reflect a compatible reduction of the R_g in water, with the statistical properties of the chain in water being close to Θ-solvent conditions. Interestingly, in this case the collapse in water was also accompanied by adoption of some specific residual structure.

6. Implications for Protein Folding and Intrinsically Disordered Proteins

What are the implications of these findings for protein folding? It appears that for the relatively small, mostly two-state folding proteins considered here, there is a modest reduction in R_g from high to low denaturant. However, nanosecond fluorescence correlation spectroscopy has shown reconfiguration times in the unfolded state are on the order of 100 ns [78, 79], and so the relaxation time after dilution from high to low denaturant is expected to be on a similar time scale, i.e. much faster than any mixing method for reducing denaturant concentration, and also much faster than even the fastest folding proteins, which fold in ~ 1μs [80] (typical proteins are much slower). This initial collapse is a rapid re-equilibration of the unfolded protein once it is transferred to folding conditions (low denaturant), but is unlikely related to folding mechanism. In addition, the absence of any fully collapsed population other than the folded state suggests that, for these proteins, collapse to globule-like dimensions only occurs during folding transitions. There are of course numerous examples from the literature of significant collapse occurring prior to folding, but these mostly involve larger proteins which populate folding intermediates, and collapse tends to be associated with formation of stable structure in these intermediates [81]. A second implication for protein folding is that the collapse as denaturant is diluted supports a denaturation model in which denaturant preferentially associates with unfolded states, as elegantly illustrated by Ziv and Haran[32].

Although the degree of collapse of intrinsically disordered proteins varies with their sequence, the fact that many IDP sequences are close to Θ-solvent conditions in water may be significant for their function. Being near the midpoint of the collapse transition, is exactly where the chain properties would be most susceptible to post-translational modifications such as phosphorylation, or to changes in environmental conditions [22]. Furthermore the correlation between the Θ-conditions for a single chain and the critical conditions for phase separation [18] suggests that estimates of the scaling exponent from FRET or SAXS measurements, now an integral part of new analysis methods, should help to predict which disordered proteins are prone to phase separation. Being close to Θ-solvent conditions may also have advantages for protein folding. On the one hand, being closer to the collapse transition will require a smaller energy to collapse in order to fold. On the other hand, not being too far below the collapse transition helps to avoid non-native collapse and trapping before folding, which may slow folding rates [82].

7. Conclusions

Through careful experimental work and analysis, it has been possible to resolve apparent contradictions between the results of different experimental measurements of R_g for unfolded and intrinsically disordered proteins. This resolution rested on a three advances: (i) Careful choice of proteins, using either intrinsically disordered proteins or destabilized variants of folded proteins that can be studied down to very low denaturant concentration without populating the folded state. (ii) Development of better methods than the Guinier approximation for analyzing SAXS data of unfolded proteins, such as Bayesian ensemble refinement, the MFF method or the extended Guinier approach. (iii) Development of improved methods for interpreting FRET measurements, such as Bayesian ensemble refinement, or the SAW-ν method. These allow the form of the distance distribution to vary with solvent conditions, and also explicitly account for the “decoupling” between R and R_a that occurs as solvent conditions are varied (such that R usually changes by more than R_g). These developments were all essential to the resolution of the earlier controversy.

Although studying protein collapse as a function of denaturant concentration may seem a fairly abstract problem, the efforts to resolve it have yielded a rich toolbox of new methods that will allow SAXS and FRET measurements (as well as related methods) to be more quantitatively applied to studying protein folding and the properties and function of intrinsically disordered proteins.