Abstract
Cell crawling on two-dimensional surfaces is a relatively well-understood phenomenon that is based on actin polymerization at a cell’s front edge and anchoring on a substrate, allowing the cell to pull itself forward. However, some cells, such as cancer cells invading a three-dimensional matrigel, can also swim in the bulk, where surface adhesion is impossible. Although there is strong evidence that the self-organized engine that drives cells forward in the bulk involves myosin, the specific propulsion mechanism remains largely unclear. Here, we propose a minimal model for in-bulk self-motility of a droplet containing an isotropic and compressible contractile gel, representing a cell extract containing a disordered actomyosin network. In our model, contraction mediates a feedback loop between myosin-induced flow and advection-induced myosin accumulation, which leads to clustering and locally enhanced flow. The symmetry of such flow is then spontaneously broken through actomyosin-membrane interactions, leading to self-organized droplet motility relative to the underlying solvent. Depending on the balance between contraction, diffusion, detachment rate of myosin, and effective surface tension, this motion can be either straight or circular. Our simulations and analytical results shed new light on in-bulk myosin-driven cell motility in living cells and provide a framework to design a novel type of synthetic active matter droplet potentially resembling the motility mechanism of biological cells.
Significance
The mechanism through which cells move in three dimensions in the absence of a substrate is important because it underlies cell motility inside tissues and in cancer but is not well understood yet. Here, we provide a minimal model for such in-bulk self-motility. We study with theory and simulations the dynamics of a droplet containing an isotropic, compressible contractile gel, representing a cell extract containing a disordered actomyosin network. Our key result is that contraction alone is sufficient to drive motion, even without any underlying substrate. We identify the physical mechanism of contractility-driven motion. First, a feedback loop between contraction and advection leads to myosin clustering and locally enhanced flow. The flow then becomes asymmetrical through membrane-actomyosin interactions, leading to motion.
Introduction
Understanding the rules governing cell motion is a fascinating problem in biophysics because the engine governing motility is purely self-organized (1,2). The mechanism of cell motility is also of major biomedical relevance because this process is central to the self-assembly of tissues in a growing embryo, is required for wound healing, and is important to understand the pathway through which cancer cells metastasize.
Crawling on a solid substrate (1, 2, 3, 4, 5, 6) is the motility mode currently best characterized, both experimentally and theoretically. It requires polymerization of the actin cytoskeletal network, which pushes the cell forward by ratcheting the motion of its plasma membrane or actin cortex (7,8). For this mechanism to work, the actin cytoskeleton needs to be anchored to the substrate at least transiently to avoid backslip of the whole network after polymerization. Indeed, anchoring points are well documented for crawling cells: these are “focal adhesions,” formed by clusters of transmembrane proteins binding to the substrate (2,5). This mechanistic understanding of cell crawling has been described in various successful models, quantitatively explaining, in particular, the locomotion of keratocyte cells on a substrate (9,10).
Crucially, however, some cells can also move through tissue or the extracellular matrix (11), where there is no underlying substrate. Cancer cells invading a three-dimensional (3D) matrigel have a spherical morphology, possess no lamellipodia, and show an accumulation of actin at their back (12,13) rather than front, making it unlikely that actin polymerization is directly responsible for locomotion. (Indeed, myosin II motors are known to be important for cancer cell spreading (14).) This example suggests that the mechanism for in-bulk cell motion, which is not understood in detail (11), must be fundamentally different from that of crawling in two dimensions. The challenge of moving without a substrate can be appreciated by comparing the mechanism allowing birds to fly through 3D space with that exploited by animals to walk on the ground.
Our goal in this work is to provide a model and mechanism for in-bulk cell motility that is both minimal and generic. Because myosin is currently the best candidate to provide the engine for 3D cell motility through some form of ATP-dependent contractility (15,16), we model isotropic contraction of a compressible actomyosin gel confined in a droplet, mimicking a cell extract (i.e., a bag of actomyosin enclosed by a membrane). Previous work proposed related models of contractility-induced motility (15, 16, 17, 18, 19, 20). The closest studies we are aware of are those in (16,20), which, however, model motion close to a substrate, which enters the model effectively via a frictional term. Instead, here our goal is to show that contraction-induced motion is also possible when this frictional term is zero, a situation that corresponds to in-bulk motility or cell swimming rather than crawling. Additionally, the model developed in (20) considers actin polymerization at the front of the cell, whereas this is not needed for motion in our study. Other existing contributions on contractility-induced motion in bulk rely on completely different mechanisms for motility, for instance, the rectification of splay fluctuations in anisotropic and incompressible active nematic droplets (15,17,18), or contain additional ingredients such as a thin cortex to which motors can bind dynamically (18,19). In contrast, here we consider a minimal model, and consequently, the physics of our self-motile droplets is simpler. Specifically, the mechanism for in-bulk motility hinges on a combination of a few generic ingredients naturally present in most motile cells: 1) a positive feedback loop between myosin contractility and compressible actomyosin flow generates myosin aggregation and 2) effective myosin-membrane interactions based on steric effects enhance any initial asymmetry of the myosin aggregate within the droplet, which then, because of advection, deforms and starts to move with the myosin in its rear. The first ingredient was previously identified in theories of steady pattern formation in compressible active gels (21), but here, we show that it can also be exploited to trigger a transition between quiescence and motility. The identification of this minimal mechanism for contraction-induced motion in bulk is the key result of this work. Although our finding may therefore shed new light on cell motility and cell swimming, it may also be used as a design principle to create synthetic self-motile droplets.
After our work was completed, we learned that related but distinct results were obtained recently in a 3D model for a spherical droplet with an actomyosin cortex (22).
Model and Methods
Equations of motion
We describe a subcellular actomyosin gel as an isotropic compressible active gel with stress tensor
| (1) |
where is the velocity field of the active gel, μ is its dynamic viscosity, λ is the bulk viscosity, and measures myosin-induced contraction. The strength of contractility depends on the concentration of myosin motors, m, through the functional form f(m) = , which ensures saturation at m ≫ m0, with m0 a constant (23). Because actomyosin is contractile, > 0. (Note that Eq. 1 disregards passive isotropic contributions to the pressure, which we assume are negligible with respect to active ones as in (16).)
To model myosin transport, we use an advection-diffusion equation. Here, the local advection velocity of myosin may be different from that of the active gel because motors can dynamically attach or detach from actin filaments with a rate depending on the environment (24). We therefore introduce the dimensionless parameter αm ∈ [0, 1] to quantify the affinity of myosin with actin, where αm = 1 means all motors are permanently attached to the actomyosin gel. Additionally, force balance (where inertial terms can be neglected at cellular scales) yields the following set of continuum equations of motion for the myosin density field m(x, t) and the actomyosin velocity field v(x, t):
| (2) |
where Dm is the myosin diffusion coefficient and γ the friction coefficient, which 0 only with an underlying substrate. The equations vx, y have been obtained by taking the divergence of the stress tensor and then balancing it with a frictional force. As shown in the following, friction is not necessary to initiate the motility. We formulated our model in two dimensions to allow for systematic parameter sweeps; extension to three dimensions is straightforward and should lead to analogous results.
To reduce the parameter space to its essential dimensions, we now use tu = μ/ and xu = as time and space units, whereas is a reference value for contractility. We introduce dimensionless parameters η λ/μ (ratio of bulk/dynamic viscosity), χ (contraction strength), and Γ (reduced substrate friction, Γ = 0 without a substrate) and use dimensionless fields = m/m0 and .
Inspired by previous works (25,26), we use a phase-field approach to model enclosure of actomyosin within a membrane to mimic a cell extract. Thus, we define a phase field ϕ(x, t) and a corresponding equation of motion featuring two fixed points representing locally uniform phases: ϕ ≈ 1, representing the interior of the cell, and ϕ ≈ 0, representing the space outside it. In dimensionless units and with the phase field, our minimal model reads (omitting tildes):
| (3) |
Here, is an effective energy to constrain myosin within the cell boundaries, which can be viewed as an effective way to impose no-flux boundary conditions; the constant term β is introduced to avoid singularities. The “deformation resistance” Dϕ quantifies the ability of the cell to oppose deformation: its effect is similar to surface tension, which would, however, enter the equations of motion in a formally different way (27,28). The term U′(ϕ) = ϕ(ϕ − 1) is the derivative of the double-well potential U, whose fixed points ϕ = 0 and ϕ = 1 describe the outside and inside of the cell extract. The droplet interface (cell boundary) has a characteristic width of (8Dϕ/Γϕ)1/2. The term restores the instantaneous cell volume toward a characteristic target volume Vtar. (Note: this way to compute V is more accurate than in phase-field theory (29).) Finally, represents advection of the actomyosin network.
To get an intuition for the order of magnitude of our model parameters, we set experimentally relevant length, time, and viscosity scales for cell extracts and actomyosin droplets as xu ∼1 μm, tu ∼1 s, and μ ∼10 Pa s (30,31). These give Dm ∼1 μm2 s−1 and ∼10 Pa; the former value is close to the in vivo myosin diffusion coefficient, and to gauge the latter, we note that a myosin concentration of ∼1 μM (30,32) and a force per motor of 10 (30,33,34) create a contractility of (calculated assuming a myosin size ∼50 nm (1)). Finally, concentration of myosin II (the myosin type mainly involved in contraction processes) has been measured to be a few micromolars for yeast and Dictyostelium (35,36), with an actin-myosin dissociation constant Kd of a few micromolars (37,38). Additionally the cytoplasm concentration of F-actin in these organisms is reported to be ∼102 μM (39), which gives a value of αm (which can be seen as the percentage of bound myosin) close to 1. The value of αm may be computed using act-myosin dissociation constant Kd = [F − actin] × [myosin]f/[myosin]b, where [myosin]b is the concentration of myosin bound to actin and [myosin]f the concentration of myosin that is not bound. Because αm is the percentage of bound myosin, then αm = [myosin]b/[myosin]tot, where the suffix “tot” means the total concentration. Finally, this leads to Kd = ([F − actin]tot − αm[myosin]tot)(1 − αm)/ αm.
Nevertheless, actin cytoskeleton is highly dynamic, and smaller values of αm can be expected where F-actin concentration is locally smaller.
Simulation details
To solve our equations, we discretize them by using a standard finite difference method. Note that the equations for the flow field v (second and third equations in Eq. 3) assume fast relaxation to steady state. In practice, we have solved them via a relaxation method, in which we have introduced a fictitious time-dependent partial differential equation, which, for vx, reads
| (4) |
Instead of periodic boundary conditions, we have set v = 0 far from the cell interior. This allows us to perform larger simulations and leads to very similar results as selected simulations with periodic boundary conditions and flow everywhere. This observation is also corroborated by independent lattice Boltzmann simulations of our equations for in-bulk motion of a self-assembled actin droplet with periodic boundary conditions and flow everywhere (51). Our chosen boundary conditions correspond to having in-bulk motion in the presence of a no-slip boundary far from the membrane.
Initial conditions for our set of partial differential equations are m = m0 with small noise (uniform between −0.1 and 0.1) if ϕ > 0.5, m = 0 otherwise. The velocity is initialized randomly in the first relaxation loop and with the value at the previous time in subsequent relaxation loops. Lattice spacing and time steps are Δx = 0.1 and Δt = 10−6; the velocity is set to 0 whenever ϕ < 10−4.
Results
Contractility-induced cell motility
To explore the dynamics of actomyosin droplets, we simulate Eq. 3. As parameters, we use η = −2/3 (40) (which simplifies the momentum balance equation), εm = 20, β = 10−4, and α0 = 50. We choose Γϕ/Dϕ = 160, fixing the shape and width of the cell boundary throughout our simulations. We also begin by setting Γ = 0 to study in-bulk motility, m0 = 1, and choose initial conditions as m = m0 + δm and v = δv, where δm and δv represent small fluctuations.
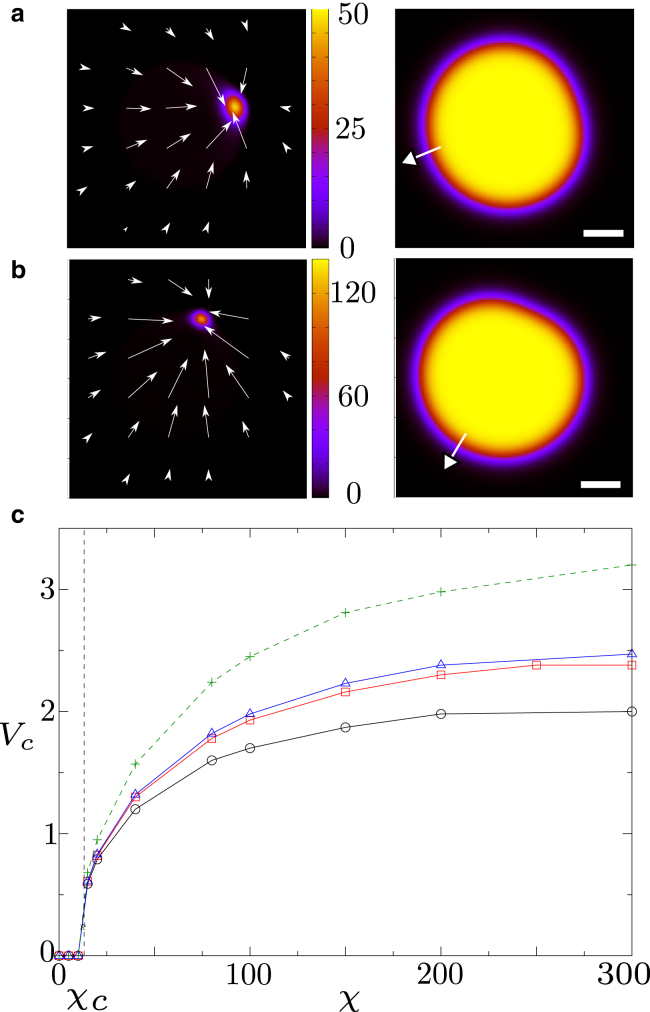
We first consider the limit at which myosin has a strong affinity with actin (αm = 1.). For small contractility χ, myosin remains uniform within the cell, which is stationary. However, when χ surpasses a threshold, a myosin spot forms at one edge of the cell (Fig. 1, a and b; Videos S1 and S2). While this spot grows, the cell deforms. Strikingly, it then starts to move away from the myosin spot, now sitting at its rear. Soon, the cell reaches a constant velocity and moves along a straight line (Video S1).
Figure 1.
(a and b) Left: concentration of myosin and v-field for Vtar = 12.5, Dϕ = 20, αm = 1, and γ = 0. Right: the corresponding phase field. The white arrow gives the direction of cell motion, and the scale bar represents 1. The contractility is χ = 80 in (a) (see Videos S1 and S2 for the corresponding dynamics for ϕ and m, respectively) and χ = 200 in (b) (see Videos S3 and S4 for the corresponding dynamics for ϕ and m, respectively). (c) Overall cell velocity as a function of χ. The solid lines and the dashed line correspond to simulations with Γ = 0 and Γ = 0.2, respectively. Black line and circles: Dϕ = 10; red line and squares: Dϕ = 20; blue line triangles: Dϕ = 25; green dashed line and crosses: Dϕ = 25. To see this figure in color, go online.
Video of a Self-Motile Droplet, Rectilinear Motion, Phase-Field (Contractility=80), Related to Fig. 1a
Video of a Self-Motile Droplet, Rectilinear Motion, Myosin (Contractility=80), Related to Fig. 1a
Video of a Self-Motile Droplet, Rectilinear Motion, Phase-Field (Contractility=200), Related to Fig. 1b
Video of a Self-Motile Droplet, Rectilinear Motion, Myosin (Contractility=200), Related to Fig. 1b
Although we do not directly model the flow of the underlying aqueous solvent, a viable pattern is one that opposes actomyosin flow by going through the membrane, which is permeable on the relevant timescales (41, 42, 43). This flow would ensure that the whole system (actomyosin plus aqueous solvent) is incompressible, whereas the actomyosin itself is instead a compressible polymeric fluid.
To better understand the parameter dependence of the droplet velocity, we now perform a systematic parameter scan; as a result, we find that the droplet speed increases not only with contractility but also with Dϕ (Fig. 1 c), so that stiff circular cells move faster than easily deformable ones. Intriguingly, we also find a moderate friction with a substrate, Γ > 0, increases the droplet speed, whereas strong friction (Γ ≫ 1) entirely suppresses motion (see Fig. S1). We find that the cell velocity vanishes for Γ 50 in the case Dϕ = 25, χ = 150, αm 1, and Vtar = 12.5, which corresponds to γ 5 × 10−10 N ⋅ s ⋅ μm−4. This result is consistent with a previous study, which finds that a friction coefficient of about 10−9 N ⋅ s ⋅ μm−4 stops cell motion (44).
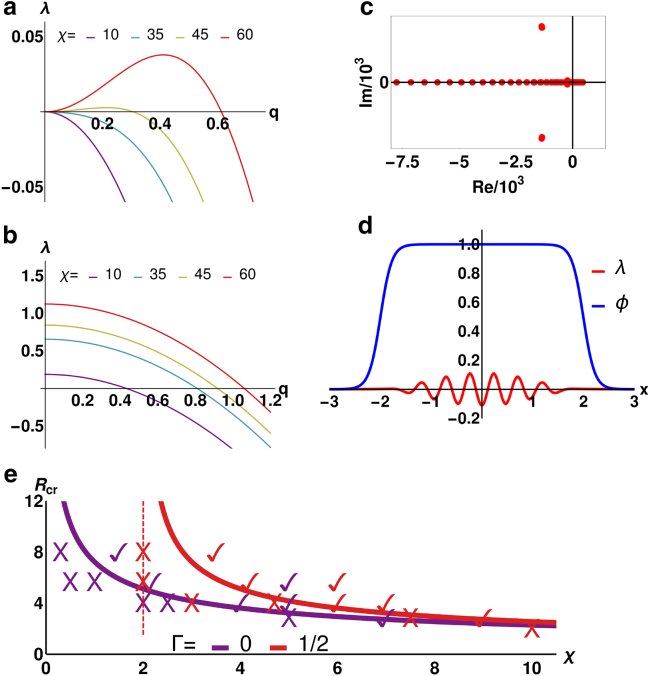
To understand the instability mechanism leading to contractility-induced motility, as well as the threshold value for χ, we perform a linear stability analysis. Considering an infinite system first, i.e., ϕ 1, we find the following dispersion relation (Fig. 2, a and b), describing the growth rate of small fluctuations around the uniform phase as a function of the wavenumber q (see Supporting Materials and Methods):
| (5) |
Figure 2.
Linear stability analysis: (a and b) ϕ = 1 (no droplet confinement); growth rate λ(q) of small fluctuations around the uniform phase with friction (Γ = 1, a) and without (Γ = 0, b). (c and d) ϕ 1: red dots show eigenvalues λ1 … λN, whose real parts determine the growth rate of actomyosin-fluctuations within a droplet. Dots right of the Re = 0-line represent unstable modes; the fastest growing one shown in (d) represents instability within the droplet and its suppression at the droplet boundaries, meaning contractility-induced cell motility can only occur in large enough cells (see Supporting Materials and Methods). Parameters: χ = 4.5; R = = 2 and L = 3; dx = 0.01; N = 601 (for discretization); others as in simulations. (e) shows χ-dependent critical cell radii for different Γ. Symbols ✓ (cell motion) and X (no motion) correspond to parameters of simulation runs and are in agreement with our linear stability analysis. Dashed lines show critical χ-values, below which contractility-induced motility is impossible, even for very large cells. To see this figure in color, go online.
Linear instability of the uniform phase occurs when (the real part of) λ(q) is positive for some wavevector q (in Fig. 2 a, this corresponds to the red and the dark yellow curves), which leads to the instability criterion
| (6) |
This result shows that the uniform phase is unstable to patterning if χ is strong enough (or simply >0 in absence of friction; Fig. 2 b).
Extending our stability analysis to the case in which a nonuniform phase field is present, we find the above criterion still holds, but only if the cell is sufficiently large (see Supporting Materials and Methods). In fact, as visualized in Fig. 2 d, the fastest growing mode (Fig. 2 c) is localized in the center of the cell and gets suppressed at the boundaries. If the droplet is too small, the boundary suppression destroys myosin patterns, and the droplet is stationary. We quantify this argument by requiring that the shortest possible unstable wavelength (e.g., for the red line in Fig. 2 a, this is about l ≈ 2π/0.62) be smaller than the diameter of the cell (2R) to allow for myosin accumulation within the droplet (and hence droplet motion). Through Eq. 5, this leads to the critical contractility
| (7) |
For the parameters used in simulations presented in Fig. 1 (Vtar = 12.5 and αm = 1), χc 13.2 with Γ = 0 and χc 14 with Γ = 0.2. The critical radius Rcr is plotted as a function of χ with and without friction and is in good agreement with numerics (see Fig. 2 e). Equation 7, in dimensional units, suggests that key control parameters are for and for γ = 0; when these are large enough, the droplet moves.
Circular droplet motion
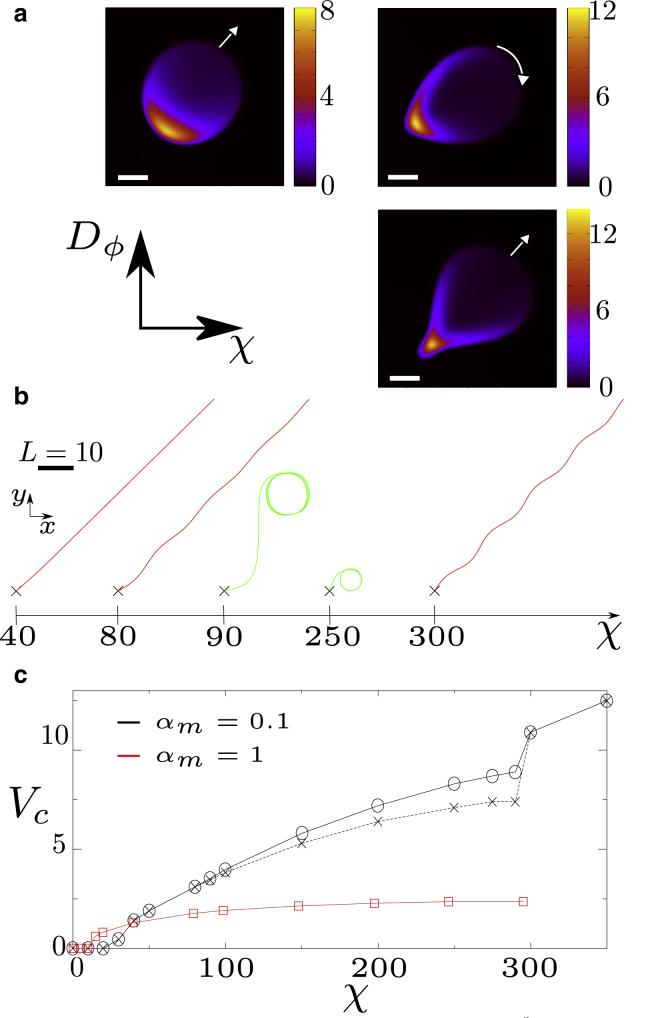
We now explore the case of low affinity between myosin and actin, αm < 1, again for Γ = 0. In this case, our droplets do not always swim straight but may follow oscillatory trajectories or lock into a regular circular motion, depending on the value of χ and Dϕ (see Fig. 3 a). These circular trajectories have been observed experimentally for keratocyte cells (45).
Figure 3.
Simulation results for Vtar = 12.5, Γ = 0, and αm = 0.1. (a) Top left panel: myosin profile for χ = 80 and Dϕ = 20. Top right panel: myosin profile for χ = 200 and Dϕ = 20. Bottom right panel: myosin profile for χ = 200 and Dϕ = 5. Scale bar, 1. (b) Different trajectories of the droplet center depending on χ for Dϕ = 20. Trajectories have been aligned artificially to ease visualization. (The direction of motion is chosen randomly, although there is some tendency for cell velocity to lock to the lattice directions or diagonals at long time, which is expected for a finite difference simulation on a square lattice.) (c) The velocity of the droplet is shown as a function of contractility χ for Dϕ = 20. The black solid line with circles corresponds to the droplet center of mass, and the black dashed line with crosses to the myosin center of mass. The red curves with squares correspond to αm = 1. To see this figure in color, go online.
What is the mechanism underlying deviations from linear motility? For αm < 1, myosin is advected slower than the actin network, whose speed is approximately equal to the overall cell velocity. As a consequence of its slower speed, the myosin spot, which is elliptical for large αm (Fig. 1, a and b), reshapes into a crescent-like form (see Fig. 3 a) as myosin accumulates at the lateral cell boundaries. As we increase χ, the crescent becomes longer and thinner. Crucially, for our noisy initial conditions, the crescent “grows” asymmetrically at both sides of the cell. This asymmetric growth results in a torque because contraction takes place along the myosin concentration gradient, which pulls the cell perpendicular to its direction of motion, leading to curved motion. Remarkably, because the cell moves faster than myosin, the curved motion further enhances the asymmetry of the crescent; thus, a sufficiently strong initial asymmetry of the crescent triggers a positive feedback loop between crescent asymmetry and cell-turning rate, ultimately yielding circular motion. This mechanism is only valid for a relatively undeformed cell. If Dϕ is small, the cell can respond to the emerging torque simply by deforming, disrupting the feedback loop described above. This picture is in line with our simulations showing that for αm < 1 and small Dϕ, the droplet forms a tail at the rear, confining the myosin spot and hampering the formation of a large and asymmetric crescent (Fig. 3 a).
However, for αm = 0.1, for which the droplet membrane strongly deforms, the phase field does not simply act as a “rigid confinement,” but rather participates in the emergence of an instability. This shifts the critical χ to somewhat lower values than predicted by Eq. 7 for αm ≪ 1; i.e., when reducing αm to values αm ≪ 1, Eq. 7 predicts the right trend for the critical χ but does not apply quantitatively (see Figs. 3 c and 4 b).
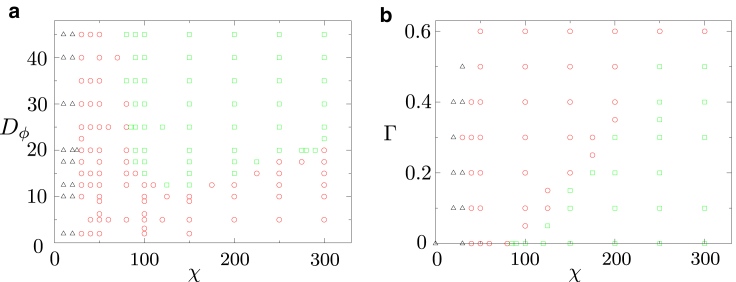
Figure 4.
(a) χ − Dϕ phase diagram for αm = 0.1 and Γ = 0. Black triangles, red circles, and green squares denote stationary cells, straight motion, and curved motion, respectively. (b) χ − Γ phase diagram for αm = 0.1 and Dϕ = 25. To see this figure in color, go online.
It is instructive to explore how the droplet velocity Vc varies as a function of χ for αm < 1 (Fig. 3 c). For αm = 0.1, the contractility threshold before cell motion sets in is larger than for αm = 1, as predicted by Eq. 7. Interestingly, beyond this threshold, the reduced actin-myosin affinity leads to faster droplet motion. Finally, for strong contraction, when we reach the regime of circular motion, the velocity of the center of mass of the myosin cluster is smaller than Vc. This means that the myosin center of mass is closer to the middle of the trajectory than the cell center, consistent with our physical argument for circular motion.
To get a more comprehensive overview of the parameter regimes leading to straight, oscillatory, or circular cell motion, we performed a large number of simulations for different parameter regimes, and summarize our results in two phase diagrams, depending on χ, Dϕ for in-bulk motility (Γ = 0, Fig. 4 a) and on χ, Γ for motion with friction (, Fig. 4 b). These diagrams show three different phases: 1) quiescent, 2) rectilinear motion, and 3) circular motion. We find that friction favors a rectilinear motion over a circular one.
Conclusions
In conclusion, we have proposed a generic mechanism exploiting motor-induced contractility to yield in-bulk motility of an isotropic actomyosin droplet. In-bulk motility arises when contractile stresses exceed a threshold scaling inversely with the cell size; hence, even a very weak contractility may be enough to propel large droplets. Although our mechanism is independent of the presence of a substrate, we have shown that friction (which would arise, e.g., from wall contact) may both enhance the droplet speed or entirely suppress motion, depending on its magnitude.
Our results in Figs. 1 and 3 suggest that typical values of contractile cellular stresses may well be enough to create in-bulk motility. Therefore, our model may provide a potential explanation for the observed motion of cells through 3D tissues in vivo or through matrigel in vitro, where friction with the substrate is likely negligible. It is important to compare and contrast our results with those obtained in (15), which pertained to self-motility of droplets of incompressible active nematic gels. In that case, the actomyosin network in the droplet was assumed to be in the ordered nematic phase, and motility relied on the spontaneous onset of splay fluctuations in the orientational order. Here, there is no orientational order because the actomyosin system is assumed to be in the disordered phase, and actomyosin compressibility is necessary to yield motility because the mechanism we have identified requires coupling between density fluctuations and flow. The two cases (isotropic and nematic droplets) are therefore fundamentally different, and which is more relevant to real cells is an open question. The work performed here applies to cases in which the orientational order within the intracellular actomyosin network is weak, which may apply to nonadhering cells (46,47).
Our focus on in-bulk motility renders our study complementary to that of (20), which addresses the case of myosin effects on motile keratocyte-like cells, which are normally crawling on a substrate and associated with a lamellipodium, a configuration that is solely encountered in cell crawling. One of the main findings of (20) is that contractility favors circular motion in a substrate. Our work shows that in-bulk circular motion is also observed, but under the condition that myosin motors stick to actin weakly. Other interesting examples of circular motility in cells and soft deformable particles were reported in (48,49). The mechanisms leading to circular motility were distinct from the one discussed here: in (48), circular motility arises from the coupling between reaction-diffusion mechanisms and cellular shape; in (49), particles are always self-motile, and circular motion requires sufficiently large self-propulsion.
Besides being potentially relevant to explain cell swimming in bulk, our model may also serve as a framework to design contractility-powered self-motile synthetic actomyosin droplets in the lab (50). Directly testable predictions of our work include the speedup of motion with increasing contractility and stiffness and the emergence of circular motion in bulk.
Author Contributions
T.L.G., B.L., and D.M. designed the research project. T.L.G., B.L., and D.M. developed the codes for this project. T.L.G. and B.L. performed simulations. T.L.G., B.L., and D.M. analyzed data. T.L.G., B.L., and D.M. wrote the manuscript.
Acknowledgments
We thank EPSRC (grant EP/J007404/1) for support. B.L. gratefully acknowledges receiving funding by a Marie Skłodowska Curie Intra-European Fellowship (G.A. no 654908) within Horizon 2020.
Editor: Andrew Spakowitz.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.06.029.
Supporting Material
References
- 1.Bray D. Second Edition. Garland Publishing; New York: 2001. Cell Movements: From Molecules to Motility. [Google Scholar]
- 2.Phillips R., Kondev J., Theriot J.A. Garland Science; New York: 2008. Physical Biology of the Cells. [Google Scholar]
- 3.Schaub S., Bohnet S., Verkhovsky A.B. Comparative maps of motion and assembly of filamentous actin and myosin II in migrating cells. Mol. Biol. Cell. 2007;18:3723–3732. doi: 10.1091/mbc.E06-09-0859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stricker J., Falzone T., Gardel M.L. Mechanics of the F-actin cytoskeleton. J. Biomech. 2010;43:9–14. doi: 10.1016/j.jbiomech.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Barnhart E.L., Lee K.C., Theriot J.A. An adhesion-dependent switch between mechanisms that determine motile cell shape. PLoS Biol. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Le Goff T., Liebchen B., Marenduzzo D. Pattern formation in polymerizing actin flocks: spirals, spots, and waves without nonlinear chemistry. Phys. Rev. Lett. 2016;117:238002. doi: 10.1103/PhysRevLett.117.238002. [DOI] [PubMed] [Google Scholar]
- 7.Peskin C.S., Odell G.M., Oster G.F. Cellular motions and thermal fluctuations: the Brownian ratchet. Biophys. J. 1993;65:316–324. doi: 10.1016/S0006-3495(93)81035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mogilner A., Oster G. Cell motility driven by actin polymerization. Biophys. J. 1996;71:3030–3045. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kruse K., Joanny J.F., Prost J. Contractility and retrograde flow in lamellipodium motion. Phys. Biol. 2006;3:130–137. doi: 10.1088/1478-3975/3/2/005. [DOI] [PubMed] [Google Scholar]
- 10.Wolgemuth C.W., Stajic J., Mogilner A. Redundant mechanisms for stable cell locomotion revealed by minimal models. Biophys. J. 2011;101:545–553. doi: 10.1016/j.bpj.2011.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Evan-Ram S., Yamada K.M. Cell migration in 3D matrix. Curr. Opin. Cell Biol. 2005;17:524–532. doi: 10.1016/j.ceb.2005.08.015. [DOI] [PubMed] [Google Scholar]
- 12.Keller H., Zadeh A.D., Eggli P. Localised depletion of polymerised actin at the front of Walker carcinosarcoma cells increases the speed of locomotion. Cell Motil. Cytoskeleton. 2002;53:189–202. doi: 10.1002/cm.10063. [DOI] [PubMed] [Google Scholar]
- 13.Poincloux R., Collin O., Chavrier P. Contractility of the cell rear drives invasion of breast tumor cells in 3D Matrigel. Proc. Natl. Acad. Sci. USA. 2011;108:1943–1948. doi: 10.1073/pnas.1010396108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Betapudi V., Licate L.S., Egelhoff T.T. Distinct roles of nonmuscle myosin II isoforms in the regulation of MDA-MB-231 breast cancer cell spreading and migration. Cancer Res. 2006;66:4725–4733. doi: 10.1158/0008-5472.CAN-05-4236. [DOI] [PubMed] [Google Scholar]
- 15.Tjhung E., Marenduzzo D., Cates M.E. Spontaneous symmetry breaking in active droplets provides a generic route to motility. Proc. Natl. Acad. Sci. USA. 2012;109:12381–12386. doi: 10.1073/pnas.1200843109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Recho P., Putelat T., Truskinovsky L. Contraction-driven cell motility. Phys. Rev. Lett. 2013;111:108102. doi: 10.1103/PhysRevLett.111.108102. [DOI] [PubMed] [Google Scholar]
- 17.Whitfield C.A., Marenduzzo D., Hawkins R.J. Active polar fluid flow in finite droplets. Eur Phys J E Soft Matter. 2014;37:8. doi: 10.1140/epje/i2014-14008-3. [DOI] [PubMed] [Google Scholar]
- 18.Whitfield C.A., Hawkins R.J. Instabilities, motion and deformation of active fluid droplets. New J. Phys. 2016;18:123016. [Google Scholar]
- 19.Hawkins R.J., Poincloux R., Voituriez R. Spontaneous contractility-mediated cortical flow generates cell migration in three-dimensional environments. Biophys. J. 2011;101:1041–1045. doi: 10.1016/j.bpj.2011.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nickaeen M., Novak I.L., Mogilner A. A free-boundary model of a motile cell explains turning behavior. PLoS Comput. Biol. 2017;13:e1005862. doi: 10.1371/journal.pcbi.1005862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bois J.S., Jülicher F., Grill S.W. Pattern formation in active fluids. Phys. Rev. Lett. 2011;106:028103. doi: 10.1103/PhysRevLett.106.028103. [DOI] [PubMed] [Google Scholar]
- 22.Farutin A., Étienne J., Recho P. Crawling in a fluid. Phys. Rev. Lett. 2019;123:118101. doi: 10.1103/PhysRevLett.123.118101. [DOI] [PubMed] [Google Scholar]
- 23.Moore T., Wu S.K., Neufeld Z. Self-organizing actomyosin patterns on the cell cortex at epithelial cell-cell junctions. Biophys. J. 2014;107:2652–2661. doi: 10.1016/j.bpj.2014.10.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Adelstein R.S., Eisenberg E. Regulation and kinetics of the actin-myosin-ATP interaction. Ann. Rev. Biomech. 1980;49:921–956. doi: 10.1146/annurev.bi.49.070180.004421. [DOI] [PubMed] [Google Scholar]
- 25.Shao D., Levine H., Rappel W.-J. Coupling actin flow, adhesion, and morphology in a computational cell motility model. Proc. Natl. Acad. Sci. USA. 2012;109:6851–6856. doi: 10.1073/pnas.1203252109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dreher A., Aranson I.S., Kruse K. Spiral actin-polymerization waves can generate amoeboidal cell crawling. New J. Phys. 2014;16:055007. [Google Scholar]
- 27.Folch R., Casademunt J., Ramírez-Piscina L. Phase-field model for Hele-Shaw flows with arbitrary viscosity contrast. I. Theoretical approach. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;60:1724–1733. doi: 10.1103/physreve.60.1724. [DOI] [PubMed] [Google Scholar]
- 28.Biben T., Misbah C. Tumbling of vesicles under shear flow within an advected-field approach. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;67:031908. doi: 10.1103/PhysRevE.67.031908. [DOI] [PubMed] [Google Scholar]
- 29.Nonomura M. Study on multicellular systems using a phase field model. PLoS One. 2012;7:e33501. doi: 10.1371/journal.pone.0033501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Norstrom M., Gardel M.L. Shear thickening of F-actin networks crosslinked with non-muscle myosin IIB. Soft Matter. 2011;2011:3228–3233. doi: 10.1039/C0SM01157F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wottawah F., Schinkinger S., Käs J. Optical rheology of biological cells. Phys. Rev. Lett. 2005;94:098103. doi: 10.1103/PhysRevLett.94.098103. [DOI] [PubMed] [Google Scholar]
- 32.Janson L.W., Kolega J., Taylor D.L. Modulation of contraction by gelation/solation in a reconstituted motile model. J. Cell Biol. 1991;114:1005–1015. doi: 10.1083/jcb.114.5.1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Finer J.T., Simmons R.M., Spudich J.A. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. 1994;368:113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- 34.Bendix P.M., Koenderink G.H., Weitz D.A. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys. J. 2008;94:3126–3136. doi: 10.1529/biophysj.107.117960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Robinson D.N., Cavet G., Spudich J.A. Quantitation of the distribution and flux of myosin-II during cytokinesis. BMC Cell Biol. 2002;3:4. doi: 10.1186/1471-2121-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wu J.-Q., Pollard T.D. Counting cytokinesis proteins globally and locally in fission yeast. Science. 2005;310:310–314. doi: 10.1126/science.1113230. [DOI] [PubMed] [Google Scholar]
- 37.Furch M., Geeves M.A., Manstein D.J. Modulation of actin affinity and actomyosin adenosine triphosphatase by charge changes in the myosin motor domain. Biochemistry. 1998;37:6317–6326. doi: 10.1021/bi972851y. [DOI] [PubMed] [Google Scholar]
- 38.Murphy C.T., Spudich J.A. The sequence of the myosin 50-20K loop affects Myosin’s affinity for actin throughout the actin-myosin ATPase cycle and its maximum ATPase activity. Biochemistry. 1999;38:3785–3792. doi: 10.1021/bi9826815. [DOI] [PubMed] [Google Scholar]
- 39.Yumura S., Fukui Y. Spatiotemporal dynamics of actin concentration during cytokinesis and locomotion in Dictyostelium. J. Cell Sci. 1998;111:2097–2108. doi: 10.1242/jcs.111.15.2097. [DOI] [PubMed] [Google Scholar]
- 40.Batchelor G.K. Cambridge University Press; Cambridge, UK: 2000. An Introduction to Fluid Dynamics; p. 144. [Google Scholar]
- 41.Fettiplace R., Haydon D.A. Water permeability of lipid membranes. Physiol. Rev. 1980;60:510–550. doi: 10.1152/physrev.1980.60.2.510. [DOI] [PubMed] [Google Scholar]
- 42.Mathai J.C., Tristram-Nagle S., Zeidel M.L. Structural determinants of water permeability through the lipid membrane. J. Gen. Physiol. 2008;131:69–76. doi: 10.1085/jgp.200709848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shinoda W. Permeability across lipid membranes. Biochim. Biophys. Acta. 2016;1858:2254–2265. doi: 10.1016/j.bbamem.2016.03.032. [DOI] [PubMed] [Google Scholar]
- 44.Barnhart E., Lee K.-C., Mogilner A. Balance between cell-substrate adhesion and myosin contraction determines the frequency of motility initiation in fish keratocytes. Proc. Natl. Acad. Sci. USA. 2015;112:5045–5050. doi: 10.1073/pnas.1417257112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ream R.A., Theriot J.A., Somero G.N. Influences of thermal acclimation and acute temperature change on the motility of epithelial wound-healing cells (keratocytes) of tropical, temperate and Antarctic fish. J. Exp. Biol. 2003;206:4539–4551. doi: 10.1242/jeb.00706. [DOI] [PubMed] [Google Scholar]
- 46.Linsmeier I., Banerjee S., Murrell M.P. Disordered actomyosin networks are sufficient to produce cooperative and telescopic contractility. Nat. Commun. 2016;7:12615. doi: 10.1038/ncomms12615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bray D., White J.G. Cortical flow in animal cells. Science. 1988;239:883–888. doi: 10.1126/science.3277283. [DOI] [PubMed] [Google Scholar]
- 48.Camley B.A., Zhao Y., Rappel W.J. Crawling and turning in a minimal reaction-diffusion cell motility model: coupling cell shape and biochemistry. Phys. Rev. E. 2017;95:012401. doi: 10.1103/PhysRevE.95.012401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ohta T., Ohkuma T. Deformable self-propelled particles. Phys. Rev. Lett. 2009;102:154101. doi: 10.1103/PhysRevLett.102.154101. [DOI] [PubMed] [Google Scholar]
- 50.Nishigami Y., Ito H., Ichikawa M. Non-periodic oscillatory deformation of an actomyosin microdroplet encapsulated within a lipid interface. Sci. Rep. 2016;6:18964. doi: 10.1038/srep18964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Negro G., Lamura A., Gonnella G., Marenduzzo D. Hydrodynamics of contraction-based motility in a compressible active fluid. E. P. L. 2019;127:58001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Video of a Self-Motile Droplet, Rectilinear Motion, Phase-Field (Contractility=80), Related to Fig. 1a
Video of a Self-Motile Droplet, Rectilinear Motion, Myosin (Contractility=80), Related to Fig. 1a
Video of a Self-Motile Droplet, Rectilinear Motion, Phase-Field (Contractility=200), Related to Fig. 1b
Video of a Self-Motile Droplet, Rectilinear Motion, Myosin (Contractility=200), Related to Fig. 1b