The αβTCR mechanosensor exploits dynamic ectodomain allostery to optimize its ligand recognition site

Significance

$\alpha \beta$T cell receptors (TCRs) recognize antigenic peptide bound to major histocompatibility complex (pMHC) molecules with exquisite sensitivity. An emerging concept is that $\alpha \beta$TCR functions as a mechanosensor whereby the complex between its ligand-binding TCR$\alpha \beta$ heterodimer and pMHC increases the bond lifetime under physiological-level force, the so-called catch bond. This study reveals the physical mechanism for catch bond behavior. Multiple layers of control are identified, including the dynamics of interfacial contacts, and the motion and geometry of the four subdomains of TCR$\alpha \beta$, all of which are influenced by the load applied to the TCR$\alpha \beta$-pMHC complex. These findings shall contribute to understanding the TCR mechanobiology and shall assist with design of future TCR-based immunotherapies.

Abstract

Each $\alpha \beta$T cell receptor (TCR) functions as a mechanosensor. The TCR is comprised of a clonotypic TCR$\alpha \beta$ ligand-binding heterodimer and the noncovalently associated CD3 signaling subunits. When bound by ligand, an antigenic peptide arrayed by a major histocompatibility complex molecule (pMHC), the TCR$\alpha \beta$ has a longer bond lifetime under piconewton-level loads. The atomistic mechanism of this “catch bond” behavior is unknown. Here, we perform molecular dynamics simulation of a TCR$\alpha \beta$-pMHC complex and its variants under physiologic loads to identify this mechanism and any attendant TCR$\alpha \beta$ domain allostery. The TCR$\alpha \beta$-pMHC interface is dynamically maintained by contacts with a spectrum of occupancies, introducing a level of control via relative motion between V$\alpha$ and V$\beta$ variable domains containing the pMHC-binding complementarity-determining region (CDR) loops. Without adequate load, the interfacial contacts are unstable, whereas applying sufficient load suppresses V$\alpha$-V$\beta$ motion, stabilizing the interface. A second level of control is exerted by C$\alpha$ and C$\beta$ constant domains, especially C$\beta$ and its protruding FG-loop, that create mismatching interfaces among the four TCR$\alpha \beta$ domains and with a pMHC ligand. Applied load enhances fit through deformation of the TCR$\alpha \beta$ molecule. Thus, the catch bond involves the entire TCR$\alpha \beta$ conformation, interdomain motion, and interfacial contact dynamics, collectively. This multilayered architecture of the machinery fosters fine-tuning of cellular response to load and pMHC recognition. Since the germline-derived TCR$\alpha \beta$ ectodomain is structurally conserved, the proposed mechanism can be universally adopted to operate under load during immune surveillance by diverse $\alpha \beta$TCRs constituting the T cell repertoire.

TCR$\alpha \beta$ is a disulfide-linked heterodimer containing one $\alpha$ and one $\beta$ chain. Each chain consists of a single immunoglobulin (Ig)-like variable (V) and a single constant (C) extracellular domain, a connecting peptide, a transmembrane segment, and a short cytoplasmic tail. Every TCR$\alpha \beta$ binds to its specific antigenic peptide sitting in the groove of a major histocompatibility complex molecule (pMHC) (1–3). (Here, we shall use the $\alpha \beta$TCR designation to indicate the entire complex including its cluster of differentiation 3 [CD3] signaling subunits and the TCR$\alpha \beta$ designation to refer to the pMHC ligand-binding heterodimer.)

Together with CD4 and CD8 coreceptors and arrayed adhesion molecules, the $\alpha \beta$TCR can recognize as few as a single copy of its target out of about ${\mathrm{10}}^5$ different pMHCs displayed on the surface of an antigen-presenting cell (4–6). Yet, conventional measures indicate a low binding affinity between TCR$\alpha \beta$ and pMHC, in the micromolar to hundreds of micromolar range. Elucidating the mechanism for such high sensitivity and specificity despite the low affinity in the absence of somatic hypermutation as observed with immunoglobulins (7) has been a major challenge in understanding TCR function (8, 9).

An emerging concept in this regard is that the $\alpha \beta$TCR is a mechanosensor (8, 10–12). The $\alpha \beta$TCR-pMHC bond lifetime increases in response to 10-pN to 20-pN force, which is a typical load experienced by the complex when a T cell moves over an antigen-presenting cell during immune surveillance. In vitro single-molecule experiments using an isolated TCR$\alpha \beta$-pMHC system showed that TCR$\alpha \beta$ alone without any other cellular components necessary for T cell activation exhibits load-induced enhancement of bond lifetime in a ligand-dependent manner (13). The so-called catch bond behavior reconciles the high selectivity of TCR$\alpha \beta$ with its low affinity for pMHC, where load enhances agonist pMHC recognition that has similar equilibrium binding affinity as other nonagonist pMHCs without load. During immune surveillance, since TCR$\alpha \beta$ operates under force, catch bond formation may be an inherent property across different TCR$\alpha \beta$ systems (11, 12). A multitude of additional studies support the notion that force is tied to T cell activation (14–21). Furthermore, it has been shown that preTCR, the $\alpha \beta$TCR precursor composed of a mature $\beta$-chain and a pT$\alpha$-chain that lacks the V$\alpha$ domain, is also a mechanosensor (22–27), underscoring the importance of mechanics for the development and function of TCR$\alpha \beta$.

The structural basis of catch bond formation in TCR$\alpha \beta$ remains unknown. Unlike other catch bond systems that exhibit load-dependent conformational changes (28–30), available structures of TCR$\alpha \beta$ or TCR$\alpha \beta$-pMHC complexes do not show any notable variation in conformations that might hint at catch bond formation. To elucidate dynamical properties of these static structures, molecular dynamics (MD) simulation has been used (31–34). Until now, computational approaches addressing the TCR$\alpha \beta$-pMHC catch bond have used the steered MD (SMD) method, where the complex is rapidly pulled apart with a constant speed so that bond dissociation can happen within the nanosecond-scale simulation time (32, 33). Authors of these studies argue that transiently formed hydrogen bonds (H-bonds) during the dissociation process are responsible for the catch bond. However, formation of transient contacts depends on the loading direction, e.g., transverse (32) or longitudinal (33). Also, to foster dissociation within the nanosecond-order simulation time that is much shorter than seconds-long bond lifetime observed biologically, the SMD simulation exerts forces 2 to 3 orders of magnitude higher than experimental values. Whether transient H-bonds observed under such a high load along a fixed direction are actually important is unclear. Even with confirmatory mutagenesis experiments showing that abolishing those H-bonds impairs catch bond while load-free equilibrium binding affinity remains unchanged, such analysis would only reveal which residues are important for a specific system. Since a catch bond is a macromolecular phenomenon that arises from the collective action of the molecule (28), focusing only on individual contacts without considering global conformational motion is unlikely to reveal a structural mechanism on physical grounds.

Given that catch bond formation is a general $\alpha \beta$TCR feature, we posit that the conserved part of the TCR$\alpha \beta$ ectodomain “chassis,” rather than solely the contacts with pMHC per se, is responsible. We tested this notion in the present simulation, studying an isolated TCR$\alpha \beta$ and its complex with pMHC under more biologically relevant loads than those used in previous simulations. To elucidate the allosteric mechanism of catch bonds, we also studied various subsets of the TCR$\alpha \beta$-pMHC system. We found that unloaded V$\alpha$ and V$\beta$ domains undergo destabilizing conformational motion where their relative orientation affects the geometry of the interface with pMHC. Physiological level force on the complex suppresses V$\alpha$-V$\beta$ motion and stabilizes the interface with pMHC. Thus, the catch bond is largely formed by preserving a group of contacts under load rather than by making additional transient contacts. We also found that the C-module (C$\alpha$ and C$\beta$) allosterically controls the V$\alpha$-V$\beta$ motion by imposing a slight mismatch in the interfaces among the four subdomains of TCR$\alpha \beta$ and with pMHC. This interfacial mismatch is reduced and interfaces are stabilized by the applied load. Thus, V-C interactions provide an additional fail safe mechanism in conjunction with the V$\alpha$-V$\beta$ motion in screening for the specific agonist pMHC under load. Unlike the hypervariable complementarity-determining region 3 (CDR3) loops that bind pMHC, interfaces among the domains within the TCR$\alpha \beta$ chassis are more conserved. Therefore, the mechanism observed in the present study likely applies to $\alpha \beta$TCR mechanosensing broadly.

Results

Model Systems.

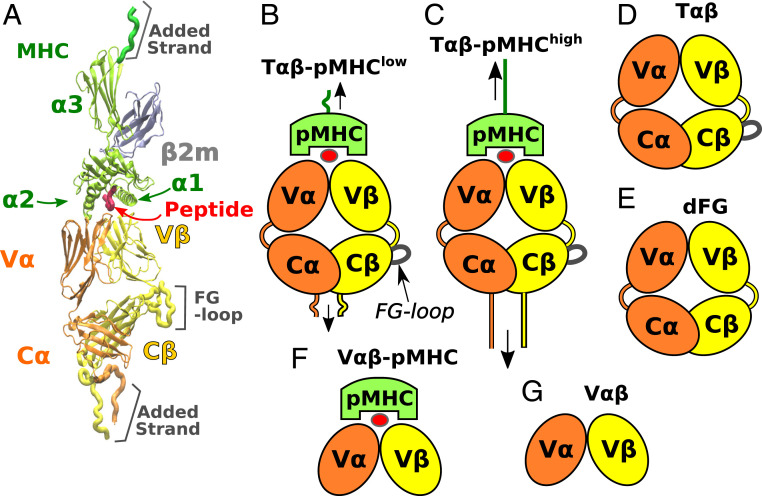
Simulations were based on Protein Data Bank (PDB) structure 1OGA, which is currently the highest resolution structure of any TCR$\alpha \beta$-pMHC complex (1.4 Å; Fig. 1A) (35). This human TCR is directed against an immunodominant influenza A matrix peptide MP58–66 bound to HLA-A$\star$0201. Systems with different loading conditions and truncations were used (Fig. 1). For the full TCR$\alpha \beta$-pMHC complex (Fig. 1 B and C), harmonic constraints were applied to residues at the ends of the complex with different extensions, where T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ was extended by 14.8 Å more than T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$. (Herein, we use T$\alpha \beta$ to refer to the simulation system and TCR$\alpha \beta$ as the molecule in general.) These extensions were selected based on a series of short laddered-extension simulations (Materials and Methods). The force fluctuates in time (Movie S1), with the average after the initial 200 ns being 10.4 pN for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and 16.4 pN for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$. The latter value is close to the force at which the longest bond lifetime and optimal activation was observed in single-molecule optical-tweezer experiments for an N15 TCR$\alpha \beta$ complexed with the agonist peptide VSV8 bound to H-2${\mathrm{K}}^b$ MHC (13, 21). Thus, the applied loads were realistic in magnitude with those and other measurements (12, 20). Although our simulation times are much shorter than the seconds-long bond lifetimes, our goal is not to observe dissociation of the complex but to study how load affects TCR$\alpha \beta$ conformations and its interaction with pMHC, for which 500 to 560 ns for each system was sufficient. Furthermore, we added 8 to 17 residues to the carboxy-terminal ends to provide room for conformational motion under load (Fig. 1A). With the added strands, the complex can fluctuate both transversely and longitudinally, where transverse motion was up to 3.3 and 2.1 nm for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$, respectively (Movie S1). Thus, the interface experiences realistic loads compared with the longitudinal or transverse displacements with higher force magnitudes used in previous simulations (32, 33).

Fig. 1.

Systems studied. (A) Overview of the TCR$\alpha \beta$-pMHC complex (PDB 1OGA) (35). The class-I MHC molecule consists of the $\alpha$ chain and ${\beta }_2$ microglobulin ($\beta 2m$). The $\alpha 1$ and $\alpha 2$ helices flank the antigenic peptide. (B and C) T$\alpha \beta$-pMHC complexes with low (B) and high (C) extensions. Loads are tensile on average (vertical arrows), although they fluctuate in time (Movie S1). (D) T$\alpha \beta$. (E) dFG, lacking the C$\beta$ FG-loop. (F and G) Systems without the C-module. (F) V$\alpha \beta$-pMHC. (G) V$\alpha \beta$. V-C connecting peptides are given in the relevant systems for $\alpha$ and $\beta$ in orange and yellow, respectively. The FG-loop adjacent to the V$\beta$-C$\beta$ connector is also shown.

We also studied T$\alpha \beta$ only and dFG lacking the C$\beta$ FG-loop (Fig. 1 D and E). dFG has been shown to impair catch bond behavior, which indicates the allosteric role of the FG-loop (13). Systems lacking the C-module, V$\alpha \beta$-pMHC and V$\alpha \beta$ (Fig. 1 F and G), were used to examine the influence of the C-module on the conformational motion of the V-module. Finally, we tested two versions of dFG-pMHC complexes, and a T$\alpha \beta$-pMHC complex without any load applied.

Outline of Analysis.

Our analysis is organized from local to global: we start by examining the interfacial contacts between the V-module and pMHC. We then broaden our scope, to analyze the conformational motion. We first study the relative motion between V$\alpha$ and V$\beta$ within the V-module, followed by the relative motion between the V-module and the C-module. To further elucidate the allosteric control of the catch bond behavior, we study two dFG-pMHC complexes with load and another T$\alpha \beta$-pMHC complex without load. The combined analysis of interfacial contact dynamics and conformational motion in different systems reveals how load influences the entire molecule, in turn stabilizing the contacts between TCR$\alpha \beta$ and pMHC.

Load-Induced Stabilization of Contacts between TCR$\mathit{\alpha }\mathit{\beta }$ and pMHC.

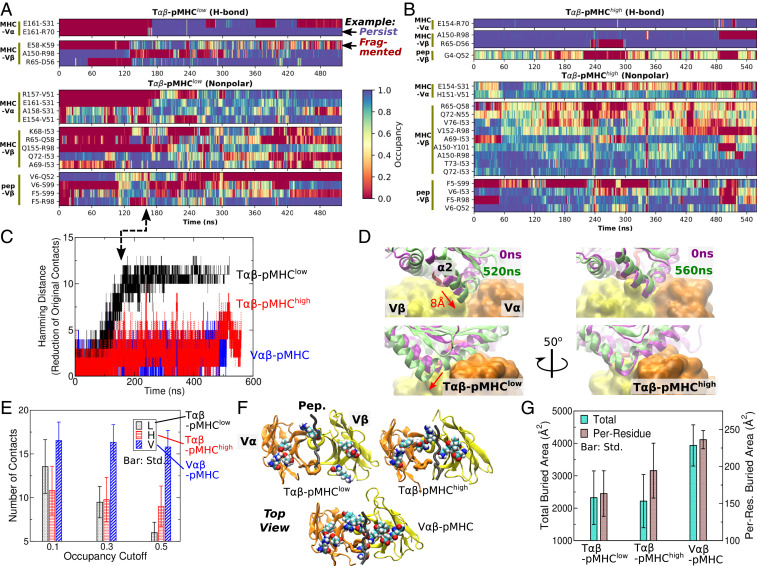
For T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$, T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$, and V$\alpha \beta$-pMHC, we identified residue pairs that form H-bonds (including salt bridges) or nonpolar contacts. Contacts formed and broke to varying extents throughout the simulation. The total number of unique interactions that formed during the simulation, regardless of their duration, is much larger for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ (226 contacts) than those of T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ (134 contacts) or V$\alpha \beta$-pMHC (119 contacts) because the T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ interface forms many transient contacts, indicative of disruption of the interface. Instead of simply counting the number of contacts, we devised two criteria to evaluate the quality of contacts. The first is the average occupancy during a given simulation period, i.e., the fraction of time over which the contact is present. The second is the instantaneous occupancy measured as a rolling average with a 0.8-ns time window. If the average occupancy is close to 100%, the instantaneous occupancy is also high. However, few contacts had near 100% occupancy. We regarded a contact to be “stable” if it has a reasonably high average occupancy (temporal abundance) and if it can reach a high instantaneous occupancy (intensity). We varied occupancy cutoffs for these criteria for a more objective evaluation of contacts.

Occupancy heat maps were generated for contacts with the average occupancy greater than 30% and the maximum instantaneous occupancy greater than 80%. This revealed that contacts formed and broke more frequently in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ than in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$, as the former has a more fragmented contact heat map, while the latter better preserves the initial high-occupancy contacts, suggesting that its interface is more stable (Fig. 2 A and B). The initial contacts are even better preserved in V$\alpha \beta$-pMHC (SI Appendix, Fig. S1A).

Fig. 2.

Dynamics of the interface. (A and B) Occupancy heat map of T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ (A) and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ (B) (SI Appendix, Fig. S1A for V$\alpha \beta$-pMHC). Only contacts with overall and maximum instantaneous occupancies greater than 30 and 80%, respectively, are shown. Examples of persistent and fragmented contacts are marked in A. High-occupancy contacts (blue) persist more in B. (C) Hamming distance from the initial set of contacts. Given there are 11 to 13 initial high-occupancy contacts, a comparable Hamming distance for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ indicates almost all initial contacts were lost. Arrow denotes the time point when the Hamming distance for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ plateaus in A. (D) Overlay of structures at 0 ns and at the end of the simulation (SI Appendix, Fig. S1B for V$\alpha \beta$-pMHC). Structures were aligned relative to the V-module (shown in surface representation for clarity) to reveal relative positioning of pMHC. Bottom row is a view rotated by ${\mathrm{50}}^{○}$ about the vertical axis compared with the top row. In T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$, pMHC displaces by about 8 Å (red arrows). (E) Number of contacts with the average occupancy cutoffs indicated on the abscissa and a 80% maximum instantaneous-occupancy cutoff. The number of contacts in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ steeply declines with the average occupancy cutoff since it has fewer contacts that persist through the simulation. (F) Locations of residues forming contacts with pMHC with the average occupancy greater than 50%, shown in van der Waals representation and viewed from pMHC (not shown) at the interface with TCR$\alpha \beta$. The residues are more scattered in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$. Structures at the end of the simulation were used for rendering. (G) Buried area of residues with higher than 80% instantaneous contact occupancy with pMHC at each frame. Per-residue buried area is the smallest for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$, which reflects a sparser distribution of residues.

Persistence of the initial contacts can be quantified by the Hamming distance (36), defined as the number of initial high-occupancy contacts (higher than 80% occupancy during the first 50 ns) lost. For T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$, it steadily increases until nearly all initial high-occupancy contacts are lost after about 180 ns (Fig. 2C). This is consistent with the extensive arrangement of contacts around the same time (arrow between Fig. 2 A and C). The increase in the Hamming distance in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ is caused by the dislocation of pMHC relative to the V-module. During 150 to 200 ns, the $\alpha 2$ domain of MHC slides into the crevice between V$\alpha$ and V$\beta$ and stays until the end of the simulation (Fig. 2D, arrows). In comparison, for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ and V$\alpha \beta$-pMHC, the position of pMHC relative to V$\alpha \beta$ stays stable throughout the simulation (Fig. 2D, Right and SI Appendix, Fig. S1B). In V$\alpha \beta$-pMHC, the absence of the C-module imparts more conformational flexibility so that V$\alpha \beta$ can dock more firmly to pMHC. For T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$, load prevents sliding of $\alpha 2$ between V$\alpha$ and V$\beta$ as it would further reduce the distance between the two molecules.

To compare the stability of the altered interface in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and those of the other two systems, we used the trajectory after the initial 200 ns for analysis. Unless noted otherwise, all calculations below were after the initial 200 ns. We counted the number of contacts with the average occupancy greater than 10, 30, or 50% and with the maximum instantaneous occupancy greater than 80% (Fig. 2E). At all three occupancy cutoffs, V$\alpha \beta$-pMHC maintained the largest number of contacts (Fig. 2E). On the other hand, T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ had more contacts than T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ at 10% cutoff, but the number decreased as the average occupancy cutoff increased. At 50% cutoff, T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ had a lower number of contacts compared with T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ (Fig. 2E). This suggests that most of the high instantaneous-occupancy contacts in the altered interface of T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ were transient and had low average occupancy, which is consistent with the fragmented appearance of its contact heat map (Fig. 2A). In the other two systems, the high instantaneous-occupancy contacts were more persistent and had high average occupancy, as also suggested by longer stretches of high occupancy regions in the contact heat map (blue in Fig. 2B and SI Appendix, Fig. S1A).

For a visual comparison of the spatial distribution of contacts, residues in the V-module that form contacts with pMHC with greater than 50% average occupancy were identified (Fig. 2F). If the cutoff is too low, all three systems will show similarly crowded residues. Conversely, a very high cutoff will reveal only a few residues that would make it difficult to discern spatial distribution of residues important for maintaining contacts. With the 50% cutoff, the selected residues are scattered over the interface in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$, whereas they are more clustered in the other two systems (Fig. 2F). At a given moment, not all of these residues simultaneously form contacts with pMHC. As a more quantitative measure of the clustering of contacts at each coordinate frame, we calculated the buried area of residues in the V-module whose instantaneous contact occupancy was greater than 80%. The total buried area of these residues was comparable between T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$. However, the latter had a greater per-residue buried area, indicative of its higher degree of clustering (Fig. 2G). By comparison, V$\alpha \beta$-pMHC had both the total and per-residue buried area greater than the other two systems, again supporting the robustness of the interface.

These results suggest that the T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ interface consists of short-lived and sparsely distributed contacts, which would be more vulnerable to breakage. By comparison, the higher load in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ prevents dislocation and stabilizes the interface close to the initial state where contacts are more clustered and protected from attacks of water molecules. The observation that contacts were the most persistent and clustered in V$\alpha \beta$-pMHC indicates that the C-module has an allosteric effect on the V-module that destabilizes the interface with pMHC under a low load.

Relative Motion between V$\alpha$ and V$\beta$.

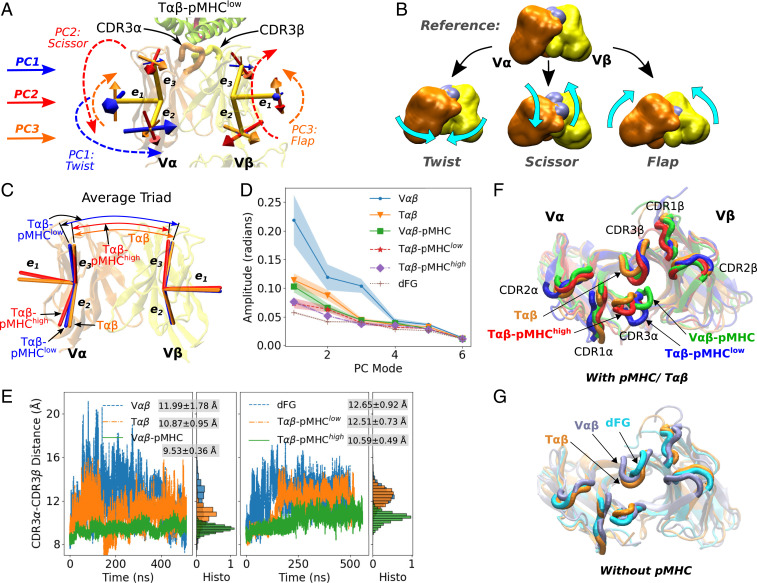
To elucidate how binding to pMHC and load affects the V-module, we constructed triads (orthonormal unit vectors) as positional and orientational markers for V$\alpha$ and V$\beta$ (37). In a triad, the unit vector ${\mathbf{e}}_{\mathbf{3}}$ is parallel to the strands of the $\beta$-sheet and points toward the interface with pMHC. ${\mathbf{e}}_{\mathbf{1}}$ and ${\mathbf{e}}_{\mathbf{2}}$ are perpendicular to ${\mathbf{e}}_{\mathbf{3}}$ (Fig. 3A). Triads were assigned to the $\beta$-sheet core of V$\alpha$ and V$\beta$ that possess low rms fluctuation during simulation, so that they capture the whole-body motion and are minimally affected by the fluctuation of peripheral loops (Materials and Methods).

Fig. 3.

Relative motion between V$\alpha$ and V$\beta$. (A) Directions of the first three PCs (Materials and Methods). For a given PC, straight arrows denote directions of motion of the triads, in the direction of increasing PC values. For a given PC, a larger arrow on an arm indicates a greater range of motion compared with other arms. Directions of PCs in other systems are in SI Appendix, Fig. S2 A–E. Also see Movies S3–S5. (B) Illustration of the three major PC motions (Movie S2). CDR3 loops are denoted by gray spheres, whose separation is affected the most by scissor. (C) Average triads (see SI Appendix, Fig. S2 F and G for other systems). (D) Amplitudes of PCs. Shaded bands: SD over the first, middle, and the last half of the coordinate frames after the first 200 ns. For T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ and dFG, SDs are too small to render visible bands. (E) CDR3 distance trajectories. Normalized histograms after the initial 200 ns, as well as averages and SDs are shown. The CDR3 distance is the smallest and fluctuates the least in V$\alpha \beta$-pMHC and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ that maintain a stable interface. T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ behaves similarly to systems without pMHC. The CDR3 distance as a function of each PC mode is in SI Appendix, Fig. S3. (F and G) Top view of coordinate frames where the CDR3 distances are close to respective averages, and triads are also close to the average structures. T$\alpha \beta$ (orange) is shown in both F and G as a reference.

Coordinate frames were aligned to the V-module to study the relative motion between V$\alpha$ and V$\beta$. (The motion between the V- and C-module is analyzed in the next section.) The average distance between the centroids of the two triads varied by less than 0.5 Å during the simulation, so the V$\alpha$-V$\beta$ motion is mainly rotational. Principal component analysis (PCA) (38) was performed on the six arms of the two triads. A principal component (PC) describes a mode of collective motion, the lowest (PC1) being the largest, and the amplitude of motion decreases with the mode number (PC2, PC3, etc.). Each PC is an 18-dimensional unit vector spanned by the 2 triads, whose individual arms move to different extents (proportional to the size of straight arrows in Fig. 3A). Directions of motion in PC1 to PC3 are similar among different systems, which we call qualitatively as “twist,” “scissor,” and “flap” (Fig. 3 A and B and Movies S2–S5). Twist refers to the rotation of one or both of the V-domains about the TCR$\alpha \beta$-pMHC longitudinal axis. Scissor is the rotation of V$\alpha$ and V$\beta$ about the horizontal axis in opposite directions. Flap denotes the rotation about an axis out of the page in Fig. 3 A and B, which is named since ${\mathbf{e}}_1$ appears to “flap” like a wing (Movies S2–S5). These terms are used as convenient descriptors, and they do not affect our analysis. For T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$, PC1 to PC3 correspond, respectively, to twist, scissor, and flap (Fig. 3A and SI Appendix, Fig. S2A). However, the correspondence varies in other systems, e.g., for V$\alpha \beta$, PC1 is scissor (SI Appendix, Fig. S2E).

We compared average triads among different systems. Compared with T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ or T$\alpha \beta$, T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ has a narrower angle between the two ${\mathbf{e}}_{\mathbf{3}}$ vectors and more twisted V$\alpha$ (Fig. 3C). Note that the orientation of the average triad is different from the PC mode that denotes the direction of motion about the average triad. Average triads of V$\alpha \beta$-pMHC are closer to those of T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ than T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ (SI Appendix, Fig. S2F), where the latter has average triads closer to other unliganded systems (Fig. 3C and SI Appendix, Fig. S2G). As explained below, the similarity in the conformations of average triads between T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ and V$\alpha \beta$-pMHC is related to their stable interface with pMHC.

As expected with increasing constraints, the amplitude of motion about each average triad was the largest for the unliganded V$\alpha \beta$ and T$\alpha \beta$, followed by V$\alpha \beta$-pMHC and subsequently T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ (Fig. 3D). This trend indicates that the V$\alpha$-V$\beta$ motion is suppressed by a bound pMHC and further by load. However, dFG, despite being unliganded, had the lowest amplitude (Fig. 3D). This is due to a stronger binding between V$\alpha$ and V$\beta$ (cf., Fig. 4A). Beyond PC3, all systems had similar amplitudes, and except for V$\alpha \beta$, amplitudes of PC3 were also similar. Our analysis was thus up to PC3.

Fig. 4.

Conformational behavior of TCR$\alpha \beta$. (A) Number of V$\alpha$-V$\beta$ contacts. Contacts were counted using the same criteria as for the third group in Fig. 2E. For other interfaces within TCR$\alpha \beta$, see SI Appendix, Fig. S4 A and B. (B–D) First three PCs of the BOC model for T$\alpha \beta$. Structure at the beginning of the simulation is shown transparent as a visual guide. The BOC model was averaged over time. With the C-module as the reference for motion, the V$\alpha$-V$\beta$ relative motion is small, and the triads for the V-module serve mainly as orientational markers for the V-module (Movies S6 and S7). (E) Amplitudes of PC1 to PC4. (Bar: SD.) (F) Comparison among time-averaged BOC and triads. View is about ${\mathrm{45}}^{○}$ between B and C. The upward shift of the $\beta$-hinge in dFG is marked by a vertical solid arrow. Insets show differences in triad positions. (G and H) Two coordinate frames of T$\alpha \beta$ and dFG that have the corresponding BOC close to the average states. (G) R15-D221 and K16-D221 hydrogen bonds between V$\beta$ and the FG-loop are present in all systems except for dFG (SI Appendix, Fig. S5). The alpha-carbon atoms of R15 and K16 are shown as orange (T$\alpha \beta$) and cyan (dFG) spheres. The rotation of the hinge between T$\alpha \beta$ and dFG is marked by an arrow. (H) Positional differences in the CDR loops in V$\beta$ between T$\alpha \beta$ and dFG. View is from behind of C. The $\alpha$-chain is not shown for clarity. The center of mass of the loops translates by 11.3 Å. (Inset) Lifting near the hinge in dFG in the absence of contacts with the FG-loop.

Since the two triads inform relative orientational motion between V$\alpha$ and V$\beta$, differences in the behaviors of PCs and average triads can affect the positioning and motion of the pMHC-binding CDR loops, among which CDR3 is the most important for antigen recognition (39) (marked in Fig. 3A). We measured the center of mass distance between the two CDR3 loops (herein called the CDR3 distance; Fig. 3E). The first three largest average distances were in V$\alpha \beta$, dFG, and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$, in the 12.0- to 12.7-Å range. V$\alpha \beta$-pMHC (9.5 Å) and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ (10.6 Å) had the smallest CDR3 distances as well as the smallest fluctuations. Thus, the CDR3 distance correlates with the stability of binding. Furthermore, the distance for T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ increased between 150 and 200 ns, during which the interface dislocated (Fig. 2A vs. 3E, Right). CDR1 and CDR2 loops also differ somewhat in their positions (Fig. 3 F and G), but the CDR3 distance is sufficient to demonstrate that the V$\alpha$-V$\beta$ motion impacts the arrangement of CDR loops.

To find the degree of the correlation between each PC and the CDR3 distance, we sorted coordinate frames according to the corresponding PC values (SI Appendix, Fig. S3). Overall, a PC possessing a larger amplitude had a larger variation of the CDR3 distance, where scissor exhibited a pronounced correlation, as for PC2 of T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and T$\alpha \beta$ and for PC1 of V$\alpha \beta$ (SI Appendix, Fig. S3 A, D, and F). With a larger scissoring, V$\alpha$ and V$\beta$ form a greater angle, which separates the CDR3 loops more (Fig. 3B and Movie S2).

These results, together with the contact analysis, suggest that load suppresses the V$\alpha$-V$\beta$ motion, which in turn stabilizes the positions of CDR loops and their contacts with pMHC. Absence of load allows greater motion, leading to positional mismatch and weakening of contacts at the interface with pMHC. The sparser distribution and smaller buried area of residues forming high-occupancy contacts with pMHC in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ (Fig. 2 F and G) are also consistent with the increase and larger fluctuation of the CDR3 distance, which is closer to the values for unliganded systems (Fig. 3E).

Dynamic Origin of the V-C Allostery.

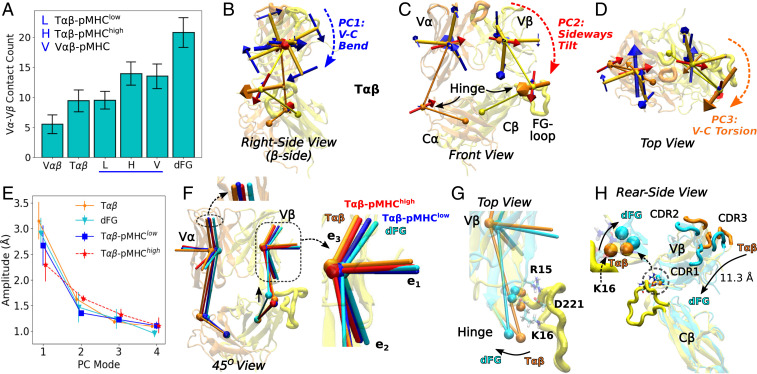
We next considered the role of the C-module for the conformational behavior of the V-module. The V$\alpha$-V$\beta$ relative motion was smaller for T$\alpha \beta$ compared with V$\alpha \beta$, suggesting that the presence of the C-module does have an effect (Fig. 3D). On the other hand, dFG exhibited the least V$\alpha$-V$\beta$ motion. Examining interdomain contacts further revealed the allosteric effect of the C-module. Among all systems, dFG had the largest number of high-occupancy contacts between V$\alpha$ and V$\beta$, followed by T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ and V$\alpha \beta$-pMHC that form a stable interface with pMHC (Fig. 4A). T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ had nearly the same number of V$\alpha$-V$\beta$ contacts as the unliganded T$\alpha \beta$, which suggests that binding of pMHC with low load does not strengthen the V$\alpha$-V$\beta$ interface. The fewest number of contacts were observed for V$\alpha \beta$, in agreement with its large amplitude of motion (Fig. 3D). The labile V-module interface is stabilized by the presence of the C-module and further by the applied load through pMHC. Lacking the C-module, V$\alpha \beta$-pMHC had a comparable number of V$\alpha$-V$\beta$ contacts as in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ (Fig. 4A). This indicates a requirement for coordinating the interfaces between the V-module and the other domains. When the V-module contacts both the C-module and pMHC, the interfaces are not snugly fit. The fit is improved by load, or in the absence of the competing interface with the C-module as in V$\alpha \beta$-pMHC, giving the V-module more freedom to adjust and strengthen contacts with pMHC and also within V$\alpha$-V$\beta$.

Among the other intra-TCR$\alpha \beta$ interfaces, V$\alpha$-C$\alpha$ and C$\alpha$-C$\beta$ contained the smallest (1.9 to 3.3) and the largest (27.3 to 33.1) average number of contacts, respectively (SI Appendix, Fig. S4A). V$\beta$-C$\beta$ (8.2 to 9.1) had more than twice the number of contacts compared with V$\alpha$-C$\alpha$, where there are additional 1.4 to 2.3 V$\beta$–FG-loop contacts (SI Appendix, Fig. S4B). These interfaces thereby play different roles: C$\alpha$-C$\beta$ provides a robust foundation. V$\alpha$-C$\alpha$, with its smallest number of contacts, responds passively, and V$\beta$-C$\beta$ more strongly influences the conformational behavior of the V-module, as demonstrated by the firm V$\alpha$-V$\beta$ binding in dFG.

We studied the V-C domain motion by building a Bead-On-Chain (BOC) model of TCR$\alpha \beta$ (Materials and Methods). “Beads” were assigned to the four domains and hinges (Fig. 4 B–D). After aligning coordinate trajectories relative to the C-module, we performed PCA on the BOC models. In all systems, directions of PCs were similar (Fig. 4 B–D, SI Appendix, Fig. S4 C–E, and Movies S6 and S7), which contrasts with variations in the directions for the V$\alpha$-V$\beta$ motion across different systems (Fig. 3A, SI Appendix, Fig. S2 A–E, and Movies S3–S5). PC1 is the bending of the V-module toward the C-module, where V$\alpha$ moves to a greater extent (blue dashed arrow in Fig. 4B). PC2 is sideways tilt of the V-module toward C$\beta$ (red dashed arrow in Fig. 4C). PC3 is a clockwise torsion of the V-module viewed from pMHC, where the V$\beta$ hinge moves the most (orange dashed arrow in Fig. 4D). The amplitude of PC1 (V-C bending) is larger for the unliganded T$\alpha \beta$ and dFG compared with the liganded complexes, with T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ having the smallest amplitude, as expected (Fig. 4E). However, compared with PCs of the V-module triads (Fig. 3D), amplitudes of PCs of the BOC models do not differ significantly. Instead, the average conformation shows more systematic differences (Fig. 4F). T$\alpha \beta$ and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ are the least bent as their ${\mathbf{e}}_3$ vectors of the V-module indicate (Fig. 4F, Inset, orange and red). For T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$, ${\mathbf{e}}_3$ of V$\alpha$ is aligned close to those of T$\alpha \beta$ and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$, but ${\mathbf{e}}_3$ of V$\beta$ is more bent (Fig. 4F, Inset, blue), as the two ${\mathbf{e}}_{\mathbf{3}}$ vectors have a wider angle in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ (Fig. 3C).

dFG is more distinct. The average triads of the V-module themselves are similar to those of T$\alpha \beta$ and V$\alpha \beta$ (SI Appendix, Fig. S2G), but relative to the C-module, the V-module changed the orientation the most, in the direction of PC1 (bending) and PC2 (tilt) (compare Fig. 4 B and C and Insets of Fig. 4F). The $\beta$-hinge of dFG also had a notable positional shift, which moved up (solid arrow in Fig. 4F) and turned in the direction as in PC3 (torsion; Fig. 4G). dFG lacks two major H-bonds between V$\beta$ and the FG-loop, R15-D221 and K16-D221, that are present in all other systems (Fig. 4G and SI Appendix, Fig. S5 A, C, and E). These contacts hold down V$\beta$ near the hinge, and their absence in dFG results in lifting and rotation of the hinge (Fig. 4 F and G), which shifts the average position of the V$\beta$ CDR loops relative to T$\alpha \beta$ by about 11.3 Å (Fig. 4H). Its impact on pMHC binding is explained in the next section.

Thus, the C-module affects the dynamics of the V-module by providing interfaces that need to be reconciled with the V$\alpha$-V$\beta$ interface and the interface with pMHC, and also by affecting the average orientation of the V-module. In both cases, C$\beta$ has a greater influence compared with C$\alpha$.

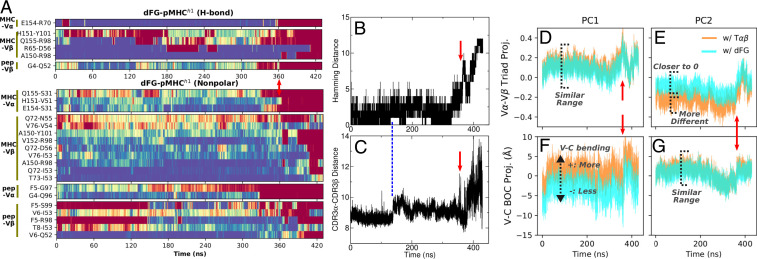
Dissociation Mechanism of the dFG-pMHC Complex.

Given that the directions and amplitudes of PCs of the BOC models were similar, an important question is the extent to which the average conformation affects the pMHC-binding interface. In particular, dFG, which substantially attenuates the catch bond behavior (13), has the most bent conformation (Fig. 4 F–H). To test its interaction with pMHC, we performed two different simulations of the dFG-pMHC complex (Materials and Methods). In the first, named dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h1}$, the FG-loop was removed from the initial structure of T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ so that the simulation started with dFG in the loaded conformation that had the FG-loop. In the second, named dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h2}$, we prepared a dFG-pMHC complex from the initial structure of T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and performed simulations to increase the extension similarly as we did to prepare T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$. In dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h2}$, dFG thus had more time to conformationally adjust in the absence of the FG-loop before the beginning of the simulation.

Remarkably, the complex dissociated in both cases. In dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h1}$, severe dislocation at the interface occurred by about 360 ns (vertical arrows in Fig. 5 and Movie S8). In dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h2}$, contacts started to break at about 240 ns, and a complete dissociation occurred by 330 ns (SI Appendix, Fig. S6 and Movie S9). The Hamming distance started to increase before the actual dissociation as disruption of the interfacial contacts preceded (Fig. 5B). Concomitantly, the CDR3 distance increased and fluctuated more, which is consistent with an increased V$\alpha$-V$\beta$ motion without pMHC (Fig. 5C). Disruption of the interface was also observed in dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h2}$, but it started earlier, before about 100 ns (SI Appendix, Fig. S6 A–C). Its faster response is consistent with the initial state where the effect of deleting the FG-loop was already present, whereas in dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h1}$, dFG started from a conformation that was nearly identical to T$\alpha \beta$ under load so that the interface was initially more stable.

Fig. 5.

Dissociation process of dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h1}$ (see SI Appendix, Fig. S6 for dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h2}$). Vertical red arrows are at the same time point (360 ns) across the figure, when a major disruption of the interface occurs. (A) Contact occupancy heat map, created the same way as in Fig. 2. Also see Movie S8. (B) Hamming distance (cf., Fig. 2C). (C) CDR3 distance (cf., Fig. 3E). Its increase at about 140 ns coincides with a modest increase in the Hamming distance (vertical dashed line). (D–G) Projection of V$\alpha$-V$\beta$ triads (D and E) and V-C BOC (F and G), onto the corresponding PCs of T$\alpha \beta$ and unliganded dFG as references.

Since the duration before dissociation started was short, it was difficult to apply PCA. Instead, using PCs of T$\alpha \beta$ and unliganded dFG as references, we projected the triads and BOCs of dFG in the complex along respective principal directions, to examine resemblance in conformational behaviors to these references. Regarding the triads of the V-module, projections of PC1 onto the two references were similar for both dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h1}$ and dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h2}$ (Fig. 5D and SI Appendix, Fig. S6D). This is because the two references have similar equilibrium V$\alpha$-V$\beta$ triads (SI Appendix, Fig. S2G) and similar PC1 directions (twist; SI Appendix, Fig. S2 C and D). Projections of PC2 differed more (Fig. 5E and SI Appendix, Fig. S6E). The smaller magnitude of the projection with unliganded dFG compared with T$\alpha \beta$ suggests that dFG in the complex behaves closer to the former. The trend is opposite for the V-C conformational motion, where the PC1 projection (V-C bending) differs more between the two references than for PC2 (V-C tilt) (Fig. 5 F and G and SI Appendix, Fig. S6 F and G). As a greater value of PC1 corresponds to more bending (Fig. 4B), negative values of the PC1 projection with the unliganded dFG as reference indicates that dFG in the complex is less bent, since the molecule is under load.

The tendency of dFG to bend will exert a peeling action on the interface with pMHC, but the observation that dissociation occurred within the simulation time was unexpected, since in the case of N15 TCR$\alpha \beta$, the bond lifetime of the dFG mutant is on the order of 0.2 to 2 s in in vitro experiments (13). A possible explanation for the rapid dissociation in our simulation is that bending of dFG results in shortening of the molecule and increases the tension on the complex. We tested this by calculating the force on the complex in 20-ns intervals. For comparison, we also calculated forces on T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ and T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$ (SI Appendix, Fig. S7A). Due to the short duration of the time window, the calculated forces fluctuate. In complexes of T$\alpha \beta$, the forces are overall smaller and fluctuate rapidly compared with complexes of dFG (SI Appendix, Fig. S7). In the latter, a sustained increase in force occurred prior to dissociation, reaching 81 pN for dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h1}$ and 31 pN for dFG-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^{h2}$ (SI Appendix, Fig. S7B). In addition to the larger magnitude, the sustained application of force in an oblique direction would have a greater destabilizing effect on the interface. Thus, dFG’s tendency to bend was responsible for the increased loading and resulted in rapid dissociation of the complex.

Instability of Unloaded TCR$\mathit{\alpha }\mathit{\beta }$-pMHC Complex.

We next considered the stability of the complex in the absence of load. Although T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ was less stable compared with T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$, it was still under a 10.4-pN load. We thus performed another simulation, T$\alpha \beta$-${\mathrm{p}\mathrm{M}\mathrm{H}\mathrm{C}}^0$, where no restraint was applied to T$\alpha \beta$. Only a weak positional restraint was applied to the stably folded $\beta$-strand region in $\alpha 3$ of MHC (cf., Fig. 1A), to prevent rotation of the molecule in the elongated simulation box (Materials and Methods). In this case, contacts with V$\alpha$ were lost early, by 180 ns, while contacts with V$\beta$ were mostly maintained until near the end of the simulation (SI Appendix, Fig. S8A). A large increase in the CDR3 distance was observed before dissociation of V$\alpha$, again indicative of the destabilizing V$\alpha$-V$\beta$ motion (SI Appendix, Fig. S8B). This further supports the critical importance of load in stabilizing the interface. Although the crystal for the TCR$\alpha \beta$-pMHC complex in PDB 1OGA was formed without load, we found that the complexes are longitudinally packed. The abundant crystal contacts likely suppressed conformational motion in lieu of force (SI Appendix, Fig. S8C).

Discussion

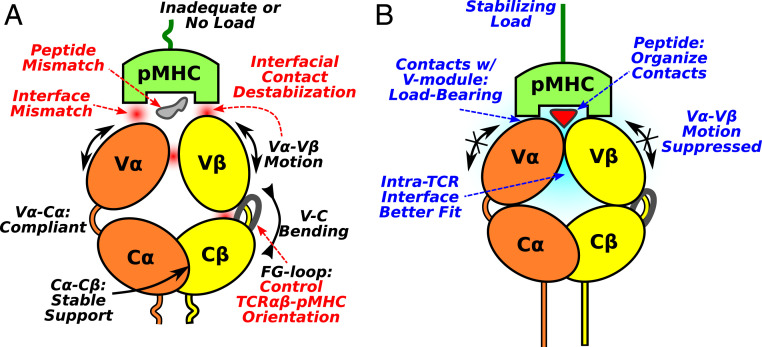
Based on present results, we propose a mechanistic model of the TCR$\alpha \beta$ catch bond machinery (Fig. 6). It contains several elements. The first is the dynamic nature of the interactions between TCR$\alpha \beta$ and pMHC. Contacts form and break throughout the simulation. It is thus necessary to collectively consider contacts in maintenance of the interface. In a given time frame, although residues that form contacts are necessary to hold the complex together, they are not the sole contributors to binding. Surrounding residues that do not form contacts with pMHC directly must provide an environment that stabilizes the transient contacts. This dynamic view of the interface offers a solution to the paradox of how the antigenic peptide can be recognized despite a greater number of contacts with MHC than with the peptide itself (1–3). Namely, our findings imply that contacts with MHC are load-bearing, thereby suppressing the V$\alpha$-V$\beta$ motion (Fig. 6B). In comparison, the small number of contacts with the antigenic peptide, but not an irrelevant peptide bound to the same MHC (13), arrange the dynamic environment to support the load-bearing contacts. By analogy to a key, the peptide plays the role of grooves and teeth, ensuring a correct fit while contacts with the MHC play the role of the main key stem that can exert torque for opening the lock.

Fig. 6.

Proposed mechanism of antigen screening and catch bond activation in TCR$\alpha \beta$-pMHC. (A) Mismatching interfaces, the V$\alpha$-V$\beta$ motion, and orientation of the V-module relative to the C-module destabilize contacts with pMHC. Due to the dynamic nature of the contacts with pMHC, without a proper load, the complex is not sufficiently stable even with the agonist pMHC. (B) With a matching pMHC under a loaded state, the V$\alpha$-V$\beta$ motion is suppressed through the load-bearing contacts with MHC. Deformation of TCR$\alpha \beta$ also enhances overall fit among the various interfaces. The antigenic peptide plays a more significant role in organizing the interfacial contacts rather than bearing the load.

The second element is the plasticity of the V$\alpha$-V$\beta$ interface. The V$\alpha$-V$\beta$ motion directly affects the geometry of the V domain’s ligand binding CDR loops (Fig. 6A). Such adaptability provides a highly sensitive means with which to screen for a matching pMHC; an applied load via the matching pMHC suppresses motion, stabilizing the interface with the V-module as well as the V$\alpha$-V$\beta$ interface (Fig. 6B). Plasticity of the V$\alpha$-V$\beta$ interface has previously been indicated in X-ray studies that reported “scissoring motion” of the two domains upon pMHC binding (40). In that study, reduction in the temperature factor deep into the V-module upon pMHC binding has also been noted, which is consistent with stabilization of the V$\alpha$-V$\beta$ interface.

The third element is the C-module. With extensive C$\alpha$-C$\beta$ contacts (SI Appendix, Fig. S4A), it serves as a stable handle to allosterically control the V$\alpha$-V$\beta$ motion and, consequently, the interface with pMHC. The C-module imposes slight mismatches among the four-domain interfaces of TCR$\alpha \beta$, which negatively impacts binding of the pMHC unless an adequate level of load is applied to deform the molecule. In a related operation, the C-module controls the average orientation of the V-module to ensure that the disposition of the CDR loops is suitable for binding to pMHC (Fig. 6A).

The allosteric role of the FG-loop is demonstrated by the dFG variant that has the most extensive V$\alpha$-V$\beta$ contacts leading to the least mobile V-module (Figs. 3D and 4A). Its over-bent conformation (Fig. 4F) also leads to the higher and sustained force generation under the same restraint on the complex with pMHC as well as makes the interface tilted. This tilt contributes to easier pMHC dissociation and is consistent with significant shortening of bond lifetime under force in single molecule optical-tweezer experiments (13).

Conversely, pMHC binding affects the behavior of the C-module. Previous solution NMR studies detected mobility changes in certain parts of the C-module upon pMHC binding, notably the FG-loop (9, 41). In our simulation, conformational fluctuation of the FG-loop depends not only on binding to pMHC but also on load, where it is more mobile in T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{low}}$ compared with T$\alpha \beta$ or T$\alpha \beta$-p${\mathrm{M}\mathrm{H}\mathrm{C}}^{\text{high}}$. While such mobility changes likely impact interaction between the C-module and the noncovalently associated CD3 subunits of the $\alpha \beta$TCR complex (42, 43), the functional significance of the flexibility changes detected in solution NMR in the absence of load remains unclear (9).

In a single-molecule optical-tweezer experiment, ligand-dependent, 5- to 9-nm conformational transitions have been observed both in vitro and on the cell (13). Introducing the H57 antibody that binds to the FG-loop (44) abolishes the major transition while extending the bond lifetime by more than 10-fold (13). Thus, the large conformational transition per se is not required for the catch bond machinery, although it is associated with bond lifetime extension (26). The major conformational transition is more likely to involve the C-module, since the V module must maintain the interface with pMHC during reversible transitioning (26). Partial or full unfolding of the C-module will reduce its influence on the V-module, which potentially reinforces contacts with pMHC, as seen in our simulation of V$\alpha \beta$-pMHC. This feature might be important for reversible transitioning seen in high-resolution TCR-pMHC and preTCR-pMHC optical-tweezer experiments (26).

A recent study used the SMD simulation to observe elongation of pMHC accompanied by the detachment of $\beta$2m from the $\alpha 1\alpha 2$ domain (cf., Fig. 1A) (33). Aside from the large force (several hundred piconewtons or higher) employed in their simulation, in bioforce probe experiments, extensions were observed only about 15% of the time, making the functional significance unclear. In ref. 33, a disulfide mutant that links $\beta$2m to $\alpha 1\alpha 2$ showed a reduced catch bond behavior. As shown in our simulations of dFG-pMHC, any changes in the loading geometry of the complex will impact the bond lifetime. The disulfide mutant of pMHC might mediate a similar effect by altering the loading direction of pMHC. The unbinding pathway in an SMD simulation can also differ from that without load if the line of action passes through a particular point within the interface (45). As explained above, the goal of our simulation was to study the conformational response of the system under load, rather than determine the unbinding pathway. In addition, the direction of force varies and the line of action across the interface is also not fixed due to the transverse fluctuation of the complex (Movie S1).

Knapp and coworkers performed extensive simulations of various TCR$\alpha \beta$ and TCR$\alpha \beta$-pMHC complexes, observing neither significant differences between immunogenic vs. nonimmunogenic peptides (46) nor any notable conformational changes within the TCR$\alpha \beta$ molecule upon complex formation with pMHC (34). These simulations were performed without any load and each simulation lasted 100 ns, whereas our simulations show that load matters and at least 200 ns is needed for the complex to conformationally relax from the initial crystallographic state and behave as a unit embedded in the solvated environment.

When a TCR$\alpha \beta$ forms, only the CDR3 loops undergo somatic V(D)J recombination, whereas the amino acid sequence for the rest of the molecule is predetermined by the gene segments used. This includes the germline CDR1 and CDR2 loops of the V-module and the entire C-module including the C$\beta$ FG-loop (2, 39). Thus, responses to load are likely very similar among TCR$\alpha \beta$ systems that share the same combination of gene segments. Systems formed from other gene segments may behave differently in details. However, main features of the proposed mechanism (Fig. 6), i.e., the stabilization and enhancement of the interfacial contacts under load, are likely general since the thymic selection process for the TCR$\alpha \beta$ clonotype as well as peripheral immune surveillance involve mechanically loaded conditions (10–12, 27).

We also found the $\beta$-chain plays a greater mechanical role through its extensive V$\beta$-C$\beta$ contacts including the FG-loop. The $\alpha$-chain, with its more limited V$\alpha$-C$\alpha$ contacts, imposes a topological constraint whereupon the applied load can stabilize the V$\alpha$-V$\beta$ interface as well as the interface with pMHC (Fig. 6). The greater mechanical role of the $\beta$-chain is consistent with its role in $\beta$ selection by self-pMHC beginning at the double-negative 3b thymocyte stage, where preTCRs are expressed and utilize the same CD3 signaling molecules as in $\alpha \beta$TCRs (25, 47). In preTCRs, the load is borne entirely by each $\beta$-chain in complex with the invariant pT$\alpha$ subunit, the TCR$\alpha$ chain surrogate lacking a V$\alpha$ domain. PreTCRs are arrayed on the thymocyte surface membrane prior to emergence of $\alpha \beta$TCRs at the more mature double-positive thymocyte stage (26). Of note, the pT$\alpha$-C$\beta$ interface is robust and comparable to that of C$\alpha$-C$\beta$ (44), and preTCR also exhibits ligand-dependent catch bond behavior based upon results from biomembrane force probe and optical-tweezer experiments (25–27).

More generally, the present study contributes to the emerging concept of dynamic allostery (48), where catch bonds work by modulating contact dynamics and domain motion without involving a clear conformational change. The physical mechanism by which the increased bond lifetime under load leads to activation of intracellular signaling via the surrounding CD3 molecules (42, 43, 49) is a subject of future studies.

Materials and Methods

Simulations were performed using CHARMM (50). We used CHARMM and custom-written C++, FORTRAN95, and Python codes to analyze simulation data. Molecular structures were rendered using VMD (51). See SI Appendix for details.

Data Availability.

All study data are included in the article and SI Appendix.