Detecting Allele-Specific Alternative Splicing from Population-Scale RNA-Seq Data

Summary

RNA sequencing (RNA-seq) is a powerful technology for studying human transcriptome variation. We introduce PAIRADISE (Paired Replicate Analysis of Allelic Differential Splicing Events), a method for detecting allele-specific alternative splicing (ASAS) from RNA-seq data. Unlike conventional approaches that detect ASAS events one sample at a time, PAIRADISE aggregates ASAS signals across multiple individuals in a population. By treating the two alleles of an individual as paired, and multiple individuals sharing a heterozygous SNP as replicates, we formulate ASAS detection using PAIRADISE as a statistical problem for identifying differential alternative splicing from RNA-seq data with paired replicates. PAIRADISE outperforms alternative statistical models in simulation studies. Applying PAIRADISE to replicate RNA-seq data of a single individual and to population-scale RNA-seq data across many individuals, we detect ASAS events associated with genome-wide association study (GWAS) signals of complex traits or diseases. Additionally, PAIRADISE ASAS analysis detects the effects of rare variants on alternative splicing. PAIRADISE provides a useful computational tool for elucidating the genetic variation and phenotypic association of alternative splicing in populations.

Introduction

Alternative splicing (AS) is a key molecular mechanism for diversifying the eukaryotic transcriptome and proteome.¹ Through varying combinations of exon inclusion and splice site usage, AS enables the production of multiple mRNA and protein isoforms from a single gene. AS plays an important role in gene regulation, and its perturbation underlies many pathological processes, as a large percentage of human disease mutations disrupt splicing and generate aberrant gene products.²

AS can be affected by cis-acting sequence polymorphisms, and such genetic variation of AS can modulate complex traits and diseases in human individuals.^3,4 The advent of RNA sequencing (RNA-seq) and the accumulation of population-scale RNA-seq data for diverse human tissues and cell types have provided rich resources for discovering AS variation in human populations.⁵ Splicing quantitative trait loci (sQTL) analysis is a widely used approach to uncover genetic variation of AS. In an sQTL analysis, the splicing level of a given exon or splice site is treated as a quantitative trait and tested for association with genotype across a population. A variety of computational tools have been developed for identifying sQTLs.^{6, 7, 8, 9, 10} For example, we previously developed GLiMMPS,⁶ a generalized linear mixed model for sQTL association testing that accounts for the measurement uncertainty of mRNA isoform ratios in RNA-seq data. Analyses of population-scale RNA-seq and genotype data have revealed thousands of sQTLs in human genes, including numerous sQTLs associated with genome-wide association study (GWAS) signals of human traits or diseases.⁵

An alternative strategy for uncovering associations between sequence polymorphisms and AS is allele-specific alternative splicing (ASAS) analysis. ASAS analysis identifies differential splicing events between mRNA transcripts originating from two different haplotypes within an individual. Specifically, heterozygous SNPs present in mRNAs are used to assign RNA-seq reads to two alleles, and differential splicing between the two alleles is tested using RNA-seq read counts.^{11, 12, 13} A unique feature of the ASAS approach, compared to the sQTL approach, is that the two alleles of a single individual should share an identical cellular environment, so splicing differences between the two alleles should arise from genetic effects. However, although a number of statistical models and computational tools have been developed for sQTL analysis,^{6, 7, 8, 9, 10} rigorous methods for ASAS analysis are lacking. Approaches used in previous works were ad hoc and had important methodological limitations. ASAS was often discovered as allele-specific expression of individual exons, but such exon expression is itself confounded by allele-specific gene expression.^12,14,15 Moreover, ASAS events were detected in one cell line or individual at a time, by comparing isoform-specific read counts (e.g., Fisher exact test of exon inclusion versus skipping counts) between the two alleles.^{11, 12, 13} However, by performing ASAS analysis for each individual separately, signals from multiple individuals were not combined, likely reducing the statistical power.

To address these limitations and to fill an important methodological gap, we have developed PAIRADISE (Paired Replicate Analysis of Allelic Differential Splicing Events), a statistical framework and software program for detecting ASAS from replicate or population-scale RNA-seq data. In the PAIRADISE methodology, we have framed the problem of ASAS detection as a specialized case of differential AS analysis with paired replicates; in this scenario, two alleles within each individual are paired, while replicate samples or multiple individuals in a population represent replicates. By aggregating ASAS signals across multiple replicates or individuals using a novel paired statistical model for differential AS, PAIRADISE substantially boosts the power of ASAS detection and reveals ASAS events regulated by rare variants. PAIRADISE is freely available, and links to the software and a stand-alone Bioconductor R package can be found in the Web Resources section.

Material and Methods

PAIRADISE Statistical Model

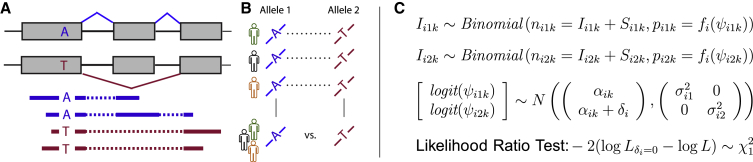
PAIRADISE utilizes a hierarchical framework to detect ASAS by modeling the paired differences between the two alleles across a population. The PAIRADISE model simultaneously accounts for both the estimation uncertainty of AS levels in each allele within each individual (or replicate) and the variability in AS levels between alleles and across individuals (or replicates). While the model is applicable to different AS patterns, here we use exon skipping to illustrate the model and computational procedure.

Briefly, for a given individual (or replicate), RNA-seq reads are aligned to the genome and the transcriptome in an allele-specific manner using the individual’s SNP and haplotype data, and allele-specific RNA-seq reads are identified. For each exon skipping event, we count the number of reads supporting the exon inclusion or skipping isoform for each allele separately, using RNA-seq reads that span both the exon inclusion or skipping splice junction and a SNP at a flanking constitutive exon that enables allele-specific read assignment (Figure 1A). These read counts are used to estimate the allele-specific exon inclusion level (denoted as $\psi$, or PSI, percent spliced in Katz et al.¹⁶). We then combine all replicates or all individuals in a population that are heterozygous for the SNP of interest (Figure 1B). Let ${\psi }_{i1k}$ and ${\psi }_{i2k}$ be the exon inclusion levels of exon i for the kth individual in allele group 1 and 2, respectively. To account for the RNA-seq estimation uncertainty of $\psi$ as influenced by the sequencing coverage for the AS event, for each allele PAIRADISE models the observed RNA-seq counts of the exon inclusion/skipping isoforms as arising from the following binomial distributions:

$$I_{i1k}|{\psi }_{i1k},n_{i1k}\sim Binomial\left(n_{i1k}=I_{i1k}+S_{i1k},p_{i1k}=f_i\left({\psi }_{i1k}\right)\right),$$

$$I_{i2k}|{\psi }_{i2k},n_{i2k}\sim Binomial\left(n_{i2k}=I_{i2k}+S_{i2k},p_{i2k}=f_i\left({\psi }_{i2k}\right)\right)$$ (Equation 1)

Here, I and S represent the number of allele-specific RNA-seq reads corresponding to the exon inclusion or skipping isoform, respectively. The function $f_i$ is a length normalization function, which accounts for the effective length of each isoform (i.e., number of unique isoform-specific read positions; note that the length normalization function has been defined in detail along with a graphic illustration in our rMATS paper, see Figure S1 in Shen et al.¹⁷ for the illustration). Although each exon has its own index i, the model is applied to each exon independently, and no information is shared across exons.

Figure 1.

The PAIRADISE Statistical Framework for Identifying Allele-Specific Alternative Splicing (ASAS)

(A) ASAS analysis aims to identify differential AS between two alleles within an individual. Heterozygous SNPs are used to assign RNA-seq reads to specific alleles.

(B) PAIRADISE aggregates ASAS signals across multiple replicates of a given individual or multiple individuals in a population.

(C) PAIRADISE uses a binomial distribution to model the read count from the exon inclusion isoform given the exon inclusion level for each allele in each individual, and uses a logit-normal distribution to model the variation of allele-specific (allele 1 or allele 2) exon inclusion levels among individuals. For exon i and the k^th individual, the total RNA-seq read counts for the exon inclusion plus skipping isoforms are denoted as $n_{i1k}$ and $n_{i2k}$ for allele groups 1 and 2, respectively. The read counts for the exon inclusion isoform are denoted as $I_{i1k}$ and $I_{i2k}$. The read counts for the exon skipping isoform are denoted as $S_{i1k}\text{and}{S}_{i2k}$. The exon inclusion levels are denoted as ${\psi }_{i1k}$ and ${\psi }_{i2k}$. The proportion of the read count from the exon inclusion isoform is adjusted by a normalization function $f_i$ that considers the lengths of the exon inclusion and skipping isoforms. The baseline exon inclusion level common to both alleles of the k^th individual is represented by the subject effect ${\alpha }_{ik}$, while ${\delta }_i$ captures the expected difference between the two alleles.

PAIRADISE uses an additive structure to model the variability in AS levels between the two alleles and across individuals (or replicates). Specifically, the logit transformed exon inclusion levels logit$\left({\psi }_{i1k}\right)$ and logit$\left({\psi }_{i2k}\right)$ are modeled using the following normal distributions:

$$logit\left({\psi }_{i1k}\right)\sim N\left(\mu ={\alpha }_{ik},{\sigma }_{i1}^2\right),$$

$$logit\left({\psi }_{i2k}\right)\sim N\left(\mu ={\alpha }_{ik}+{\delta }_i,{\sigma }_{i2}^2\right).$$ (Equation 2)

The baseline exon inclusion level common to the two alleles is represented by the subject effect ${\alpha }_{ik}$, which follows the normal distribution:

$${\alpha }_{ik}\sim N\left({\mu }_i,{\sigma }_i^2\right)$$ (Equation 3)

Thus, the first source of variability in exon inclusion levels, i.e., the variability of the baseline exon inclusion level among individuals that is common to both alleles of a given individual, is attributable to ${\sigma }_i^2$. The second source of variability, captured by the variance terms ${\sigma }_{i1}^2$ and ${\sigma }_{i2}^2$ of the two allele groups, is allele specific. The parameter ${\delta }_i$ represents the expected difference in the logit-transformed exon inclusion levels between the two alleles. Note that both sample groups share the random variable ${\alpha }_{ik}$, which leads to covariance between logit$\left({\psi }_{i1k}\right)$ and logit$\left({\psi }_{i2k}\right)$. After integrating out ${\alpha }_{ik}$, the pair follows a bivariate normal distribution with mean $\left[{\mu }_i,{\mu }_i+{\delta }_i\right]$ and covariance ${\sigma }_i^2+diag\left(\left[{\sigma }_{i1}^2,{\sigma }_{i2}^2\right]\right)$.

To determine the statistical significance of ASAS, a likelihood ratio test is performed to test the null hypothesis ${\delta }_i=0$ against the alternative hypothesis ${\delta }_i\ne 0$. As the variables logit$\left({\psi }_{i1k}\right)$, logit$\left({\psi }_{i2k}\right)$, and ${\alpha }_{ik}$ are regarded as latent (unobserved) variables, we utilize an optimization procedure that first calculates the maximum likelihood estimates (MLEs) of the observed data likelihood based on the current estimates of the latent variables, and then updates the estimates of the latent variables based on the current MLEs. This procedure is iterated until the model parameters converge (see Supplemental Material and Methods for details of the modeling and parameter estimation procedures). The test statistics of the likelihood ratio test are compared to a ${\chi }^2$ distribution with one degree of freedom to derive the p value. The Benjamini-Hochberg method is used to calculate the false discovery rates (FDRs) from p values.¹⁸ The PAIRADISE statistical model is summarized in Figure 1C.

Datasets

RNA-seq data from six RNA-seq replicates of the human GM12878 B-lymphocyte cell line from a European female were generated by the three labs listed in Table S1 along with their sample IDs from the ENCODE project (ENCODE: ENCSR000AED, ENCSR000AEF, and ENCSR000AEG). We also used the Geuvadis dataset containing RNA-seq and genotype data of B-lymphocyte cell lines of 445 individuals from five populations.¹¹ Sample IDs are available in Table S1. Genotype data for these individuals were from the Phase 3 of the 1000 Genomes Project (release 05-02-2013).¹⁹

Allele-Specific Alignment of RNA-Seq Data

The inputs of the PAIRADISE program are the FASTQ files of RNA-seq data and VCF files of phased genotype data. The pipeline also uses a human reference genome, a GTF file of gene/transcript annotations, and a list of RNA editing sites that are masked for allele-specific read assignment. The following annotation files and parameters were used in our PAIRADISE analysis of ASAS: -r hg19.fa -gtf Homo_sapiens.Ensembl.GRCh37.75.gtf -e Human_AG_all_hg19_v2.txt -anchorLength 8 –N 6 –M 20 -gz. Details of the PAIRADISE running parameters and download links for the program, along with annotation files, are provided at our website (see Web Resources). The program conducts allele-specific read mapping onto AS events following the procedures in rPGA.²⁰ Specifically, the first step of the allele-specific read mapping is to personalize the reference genome based on the phased genotype data of each individual. For each individual, we modify the human reference genome (hg19) according to its phased genotype, resulting in two versions of personal genome sequences per individual (one for each haplotype), which we refer to as haplotype 1 and haplotype 2. The second step is to align RNA-seq reads to both personal genomes with STAR²¹ v.2.6.0a, allowing six mismatches and restricting splice junctions to canonical splice sites only. The third step is the allele-specific read assignment. For each uniquely mapped read, we first identify all heterozygous SNPs that the read covers, and whether the read carries the haplotype 1 or haplotype 2 allele at each base. Reads carrying haplotype 1 (or 2) alleles at the majority of the heterozygous SNP positions are assigned to haplotype 1 (or 2). Reads that do not meet either of these requirements are removed.

PAIRADISE Analysis of Allele-Specific Alternative Splicing

The PAIRADISE program analyzes ASAS using allele-specific read alignment. The allele-specific bam files mapped onto the two haplotypes are merged together to detect AS events using rMATS (v.3.2.5).¹⁷ The merged allele-specific bam files of all samples are used together in the rMATS analysis to ensure a consistent set of AS events across all samples. For all haplotype-specific reads covering a given exon skipping event and a heterozygous SNP (or multiple heterozygous SNPs) at flanking constitutive exons, we measure the association of allele types at a given SNP with the AS pattern (exon inclusion or skipping). Then, we match such data for each AS event-SNP pair across samples to generate the input data for the PAIRADISE statistical model. To ensure proper length normalization in calculating allele-specific exon inclusion levels, for the two splice junctions of the exon inclusion isoform, only reads supporting the splice junction on the same side of the SNP with respect to the alternative exon are counted. In the case where an AS event is linked to multiple heterozygous SNPs at flanking constitutive exons via haplotype-specific reads, the AS event-SNP pair is matched across people for each SNP separately. All SNPs within the alternatively spliced exon are excluded in the subsequent PAIRADISE analysis because these SNPs can only be detected from the exon inclusion isoform. Although the haplotype information is used in RNA-seq read mapping to obtain haplotype-specific reads, in downstream analyses we associate AS events with individual SNPs and match AS event-SNP pairs across people based on each SNP separately. This is done to avoid the complication that there could be more than two haplotypes across a set of SNPs within a population so haplotypes cannot be matched across people.

Next, the PAIRADISE statistical model is used to detect ASAS events. To avoid using unreliable exon skipping events, we filtered the events according to the following criteria: (1) the average exon inclusion level across all individuals is between 5% and 95% for at least one allele, and (2) the average total read counts of all individuals are no less than 10 for both alleles.

sQTL Analysis

We analyzed sQTLs in the five Geuvadis populations. RNA-seq data from the five populations were processed together by rMATS to generate a consistent set of AS events for all populations. We filtered out the AS events in each population separately, according to the following criteria: (1) the median number of splice junction reads across individuals is no less than 5, where the number of splice junction reads is given by (UJ + DJ)/2 + SJ, with UJ, DJ, and SJ being the number of upstream, downstream, and skipping splice junction reads, respectively; (2) the range (maximum - minimum) of exon inclusion levels across all individuals is greater than 10%; and (3) at least 3 individuals in the population have exon inclusion levels different than the median exon inclusion level. We used the GLiMMPS⁶ statistical model to discover sQTLs by testing the association of exon inclusion level with SNPs within 200 kb upstream or downstream of alternative exons. For each AS event, the GLIMMPS sQTL p value was defined as the p value of the SNP with the most significant association within the 200 kb window. The linkage disequilibrium (LD) correlations between SNPs were calculated by the 1000 Genomes Project. GWAS traits and associated SNPs were collected from the NHGRI-EBI GWAS catalog (version 1.0.2).²²

Simulation Study Comparing PAIRADISE to Alternative Statistical Models for Identifying ASAS Events

We evaluated the performance of PAIRADISE in identifying ASAS events against the paired t test, paired Wilcoxon signed-rank test, rMATS paired test,¹⁷ and Fisher’s combined method, using a simulation study. Each simulation was performed by generating 5,000 exon skipping events and varying the number of replicates (M = 3, 5, 10, 20, 50) as well as the variability among replicates, i.e., ${\sigma }_{i1}$, ${\sigma }_{i2}$, and ${\sigma }_i$. These standard deviations were chosen from the 1^st, 2^nd, and 3^rd quartiles (corresponding to low, medium, and high variability) of their corresponding estimated distributions obtained from applying PAIRADISE to the Geuvadis CEU dataset. Because true values of the parameter ${\delta }_i$ were not known, to generate null (|${\delta }_i$| = 0) and alternative (|${\delta }_i$| ≠ 0) cases, we set the middle 50% of the empirical estimates of ${\delta }_i$ to 0, and then randomly sampled one ${\delta }_i$ value per event; as a result, roughly 50% of the events were generated from the null hypothesis of no splicing difference between groups. The remaining simulation parameters, i.e., the total read counts $n_{i1k}$ and $n_{i2k}$, effective lengths $l_{iI}$ and $l_{iS}$, and mean logit inclusion level ${\mu }_i$, were similarly obtained empirically from the Geuvadis CEU dataset. The logit exon inclusion logit$\left({\psi }_{i1k}\right)$ and logit$\left({\psi }_{i2k}\right)$ were sampled from the normal distributions given by Equation 2 using the empirically sampled parameter values. The read counts of the exon inclusion isoforms were then sampled from the binomial distributions given by Equation 1 using the generated values for the exon inclusion levels, as well as the sampled values for the total read counts and effective lengths. PAIRADISE and other paired tests were applied to the simulated data to compute the p value and FDR of differential splicing for each simulated event.

Results

Simulation Studies Comparing PAIRADISE to Alternative Statistical Models

To evaluate the performance of PAIRADISE, we compared it to four alternative statistical models through simulation studies. The four alternative models are the paired t test, paired Wilcoxon signed-rank test, rMATS paired test,¹⁷ and Fisher’s combined method. The paired t test and paired Wilcoxon signed-rank test are conducted on point estimates of $\psi$ values derived from RNA-seq read counts, while ignoring the estimation uncertainty of $\psi$ as influenced by sequencing coverage. The rMATS paired test is a model we proposed previously for differential AS analysis of RNA-seq data with paired replicates.¹⁷ It uses a covariance structure with a correlation parameter to model the correlation among matched pairs. Fisher’s combined method uses Fisher’s exact test on allele-specific read counts to obtain a p value of ASAS for each individual separately, and then uses the Fisher’s combined probability test to aggregate p values across all individuals. We designed a set of simulation studies with varying sample size (number of replicates) and variability among replicates. We measured the performance of each method by analyzing its receiver operating characteristic (ROC) curve for the task of classifying a simulated event as being differentially spliced versus non-differentially spliced.

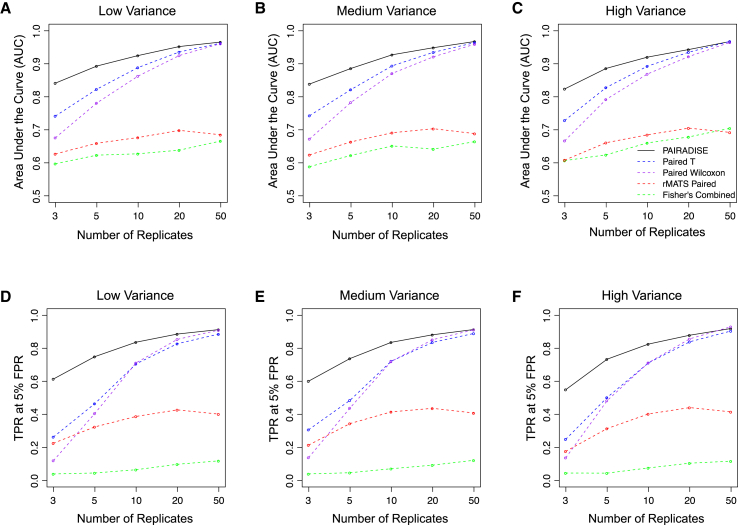
PAIRADISE outperformed all other statistical models in virtually every simulation setting, based on the area under the curve (AUC) of the ROC curve or the true positive rate (TPR) at 5% false positive rate (FPR) (Figure 2). The increased performance of PAIRADISE over other models was even more pronounced when the sample size was small. For example, in the simulations with three replicates and low variance, the AUC values for PAIRADISE, paired t test, paired Wilcoxon test, rMATS paired test, and Fisher’s combined method were 84%, 74%, 68%, 63%, and 60%, respectively (Figure 2A). PAIRADISE continued to outperform other methods in simulations with medium or high variance (Figures 2B and 2C). We observed the same trend for the TPR at 5% FPR (Figures 2D–2F). For example, in the simulations with three replicates and low variance and at 5% FPR, the TPR values for PAIRADISE, paired t test, paired Wilcoxon test, rMATS paired test, and Fisher’s combined method were 61%, 26%, 12%, 23%, and 4%, respectively (Figure 2D). Additionally, across almost all variance settings, other models required at least 2–3 times larger sample sizes to achieve the same AUC and TPR values as a sample size of 3 replicates for PAIRADISE (Figure 2). Among the five models tested, Fisher’s combined method had the worst performance. This is not surprising, as Fisher’s combined method is particularly sensitive to outliers in large datasets.^23,24 Taken together, these simulation studies indicate that PAIRADISE outperforms other statistical models and requires fewer replicates to achieve the same level of performance.

Figure 2.

Simulation Studies to Compare the Performance of PAIRADISE, rMATS Paired Model, Paired t Test, Paired Wilcoxon Signed-Rank Test, and Fisher’s Combined Method

(A–C) Area under the curve (AUC) values of all methods in simulation settings with the number of replicates equal to 3, 5, 10, 20, and 50, and three settings of variability (low in A, medium in B, and high in C) sampled from the first, second, and third quartiles of the empirical variance estimated from the Geuvadis CEU dataset.

(D–F) True positive rate (TPR) values at 5% false positive rate (FPR) of all methods in various simulation settings.

We also evaluated the power of PAIRADISE with different RNA-seq read counts on the event of interest and different numbers of replicates (Figure S1). As expected, both read count and number of replicates strongly affect the power and performance of our method, with increasing power and better performance at increasing read count and sample size. Assuming a fixed total number of individuals in an RNA-seq dataset, these results indicate (as expected) that the power of PAIRADISE is influenced by allele frequency and the number of individuals that are heterozygous for a given SNP.

When detecting ASAS from replicate RNA-seq data, some studies may simply pool reads from replicates, and then perform a statistical test on the pooled read counts to detect differential AS. To assess the importance of modeling replicates versus pooling, we conducted another simulation study to compare the performance of PAIRADISE to a simple pooling strategy that performs a Fisher’s exact test using reads pooled from all replicates of the two alleles (“Fisher’s pooled”). We followed the same simulation procedures and settings used for comparing other methods and generated two sets of simulated data in the absence or presence of an outlier sample. Specifically, for the simulated data with an outlier sample, we randomly selected one allele and set the PSI value for one of its replicates as randomly drawn from a [0, 1] uniform distribution. In the absence of an outlier, both models performed similarly in the low and medium variance settings, while PAIRADISE modestly outperformed Fisher’s pooled in the high variance setting (Figure S2; solid lines). When an outlier was introduced during the simulation, there was a reduction in the performance of both models, while PAIRADISE outperformed Fisher’s pooled by a substantial margin and recovered more rapidly with increasing sample size (Figure S2; dashed lines). These data demonstrate that by modeling replicates, PAIRADISE is more robust against outliers in the RNA-seq data, as compared to a simple pooling strategy.

PAIRADISE Analysis of Allele-Specific Alternative Splicing in GM12878

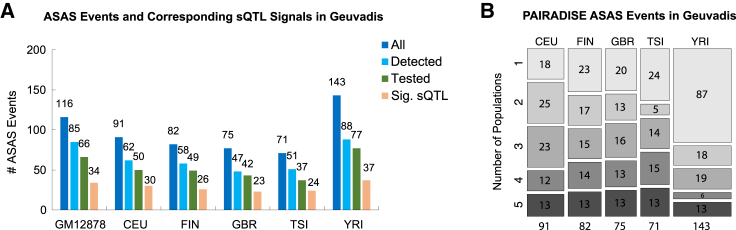
As a proof of concept analysis, we used PAIRADISE to discover ASAS events in six RNA-seq replicates of the human GM12878 B-lymphocyte cell line from a European female. The data were generated by three different labs with two biological replicates per lab (Table S1), allowing us to evaluate the ability of PAIRADISE to aggregate ASAS signals over multiple RNA-seq replicates of a given individual. Using the SNP and haplotype information of GM12878, PAIRADISE identified 116 significant ASAS events (i.e., AS event-SNP pairs) at FDR ≤ 10% (Table S2), of which 33 were in high (r² > 0.8) linkage disequilibrium (LD) with GWAS trait/disease-associated SNPs in the NHGRI-EBI GWAS catalog (v1.0.2)²² (Table S3).

To assess the PAIRADISE results using an orthogonal strategy applied to an independent dataset, we compared these events to sQTLs identified by GLiMMPS⁶ on 89 CEU (Utah Residents with European Ancestry) B-lymphocyte cell lines, whose RNA-seq and genotype data were available from the Geuvadis project (Table S1). We note that due to multiple reasons, not all ASAS events detected by PAIRADISE were analyzed by GLiMMPS for potential sQTL signals. The PAIRADISE pipeline identifies and analyzes AS events involving both known and novel splice sites,²⁰ while the GLiMMPS pipeline is restricted to known AS events identified using the rMATS pipeline.^6,17 Additionally, certain ASAS events were filtered due to the AS event or the SNP not passing method-specific filters required for GLiMMPS (see details in Material and Methods). Of the 116 PAIRADISE ASAS events, 85 were detected by GLiMMPS as AS events, and 66 passed all method-specific filters and were tested by GLiMMPS for potential sQTL signals (Figure 3A). 34 of the 66 tested AS events were significant sQTLs (GLiMMPS p < 1e−5). The 34 PAIRADISE ASAS events with significant sQTL signals had more significant PAIRADISE p values compared to the other 32 PAIRADISE ASAS events without significant sQTL signals (p = 0.0003, one-sided Wilcoxon rank-sum test).

Figure 3.

ASAS and sQTL Analysis of GM12878 and the Five Geuvadis Populations

(A) PAIRADISE ASAS events and corresponding GLiMMPS sQTL signals in GM12878 and the five Geuvadis populations. The barplots show the total number of ASAS events detected by PAIRADISE at FDR ≤ 10% (“All”), the number of these ASAS events where the AS events were also detected by GLiMMPS in Geuvadis (“Detected”), the number of detected AS events passing the GLiMMPS filtering criteria and subsequently tested for potential sQTL signals (“Tested”), and the number of tested events for which at least one SNP within a 400 kb window around the alternative exon had GLiMMPS p < 1e−5 (“Sig. sQTL”).

(B) Mosaic plot indicating the number of significant ASAS events that are shared among the five populations. Values in the top rectangles represent ASAS events detected only in a single population and values in the bottom rectangles represent ASAS events shared by all five populations.

PAIRADISE Analysis of Allele-Specific Alternative Splicing in 445 Individuals

To test PAIRADISE on a population-scale RNA-seq dataset across multiple individuals and populations, we applied the method to the Geuvadis RNA-seq data of 445 B-lymphocyte cell lines from 5 populations.¹¹ These include 89 CEU (Utah Residents with European Ancestry), 92 FIN (Finnish in Finland), 86 GBR (British in England and Scotland), 91 TSI (Toscani in Italia), and 87 YRI (Yoruba in Ibadan, Nigeria) individuals with both RNA-seq and genotype data (Table S1). At FDR ≤ 10%, PAIRADISE identified 91 ASAS events in CEU, 82 in FIN, 75 in GBR, 71 in TSI, and 143 in YRI (Figure 3B). Some events were detected across multiple populations, while some were detected only in a single population (Figure 3B). For example, 13 events were significant ASAS events in all 5 populations. As expected, the 4 European populations had a higher level of shared ASAS events, while the YRI African population had the highest number (87) of ASAS events detected only in a single population. We should caution that an ASAS event could be detected only in a single population due to limited statistical power in other populations, and a rigorous comparison of ASAS signals across populations would require a formal statistical test. In fact, there is evidence that a considerable fraction of ASAS events detected only in a single population are associated with population-specific SNPs. As shown in Figure S3, YRI ASAS events that were also detected in some of the European populations had high and comparable MAFs across all European and African populations. By contrast, YRI ASAS events that were detected only in YRI had significantly lower MAFs in European populations. In each of the European populations, approximately half of such YRI ASAS events had a MAF of 0. These data indicate that a considerable fraction of ASAS events were detected only in YRI because their associated SNPs are population specific. However, it is entirely plausible that if a particular European individual is heterozygous for such a SNP, the SNP would have the same association with AS, and an ASAS signal would be observed in that individual.

We also conducted an sQTL analysis on all five populations using GLiMMPS (Figure 3A). Of the PAIRADISE ASAS events detected in the five populations, 50, 49, 42, 37, and 77 were detected as AS events by GLiMMPS and passed all method-specific filters to be analyzed for potential sQTL signals in CEU, FIN, GBR, TSI, and YRI, respectively. Among these, 30, 26, 23, 24, and 37 had significant sQTL signals (GLiMMPS p < 1e−5). Consistent with the observation made on GM12878, the Geuvadis ASAS events that had significant sQTL signals had more significant PAIRADISE p values than Geuvadis ASAS events that did not have significant sQTL signals (p = 8.2e−08, one-sided Wilcoxon rank-sum test).

To compare ASAS detection by different statistical models on real datasets, we applied all six models (PAIRADISE, paired t test, paired Wilcoxon test, rMATS paired, Fisher’s combined, Fisher’s pooled) to the GM12878 dataset and the Geuvadis CEU dataset. In both datasets, PAIRADISE detected the intermediate number of significant events, and the majority of its significant events were detected by the majority of the models (≥4) (Table S4). Fisher’s combined and Fisher’s pooled detected the largest numbers of significant events. This result is not surprising, because both models are sensitive to outliers which likely lead to numerous false positive detections. At the other end of the spectrum, the paired Wilcoxon test and the paired t test detected the smallest numbers of significant events. This result was particularly true in the GM12878 dataset, where the sample size of 6 replicates was underpowered for these two models and neither detected any ASAS event reaching the 10% FDR threshold.

PAIRADISE Discovery of Functional Splicing Variation in Human Populations

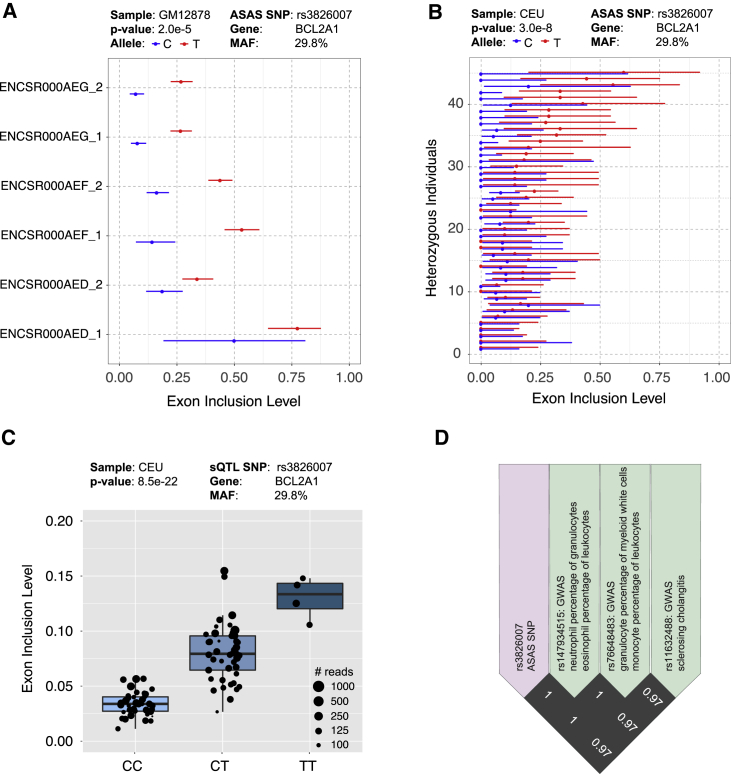
PAIRADISE identified ASAS events with potential biological functions. For example, exon 2 of BCL2A1 (BCL2 related protein A1) had significant ASAS signals in multiple datasets (Figures 4A and 4B). In GM12878, the T allele of SNP rs3826007 had a significantly higher exon inclusion level than the C allele across all six RNA-seq replicates (Figure 4A). The T allele also had a significantly higher exon inclusion level than the C allele across 45 individuals heterozygous for this SNP in the CEU population (Figure 4B). A consistent trend was observed in sQTL analysis of the CEU population, with the TT and CC genotypes having high and low exon inclusion levels and the CT genotype having intermediate exon inclusion levels (Figure 4C). The proteins encoded by the BCL2 family are involved in a range of cellular activities, including embryonic development, homeostasis, and tumorigenesis.²⁵ BCL2A1 regulates the release of pro-apoptotic cytochrome c from mitochondria and blocks caspase activation.²⁶ This ASAS/sQTL SNP (rs3826007) is in high LD with three GWAS SNPs (rs147934515, r² = 1; rs76648483, r² = 1; rs11632488, r² = 0.97). rs147934515 has previously been associated with neutrophil percentage of granulocytes and eosinophil percentage of leukocytes; rs76648483 has been associated with granulocyte percentage of myeloid white cells and monocyte percentage of leukocytes; rs11632488 has been associated with sclerosing cholangitis (Figure 4D).

Figure 4.

Genetic Variation and GWAS Association of an AS Event in BCL2A1

(A) An ASAS event in BCL2A1 with respect to SNP rs3826007 in the six replicates of GM12878. The 95% confidence intervals of exon inclusion levels are indicated as the error bars for each allele. Each line of the y axis represents one of the biological replicates of GM12878.

(B) The same event in 45 individuals heterozygous for rs3826007 in the CEU population.

(C) An sQTL event in BCL2A1 with respect to SNP rs3826007 in the CEU population. Each dot represents data from a particular individual, and the size of the dot indicates the number of reads covering the AS event in that individual. The middle line of the boxplot represents median value. The low and high ends of the box represent the 25% and 75% quantile, respectively.

(D) LD plot for the CEU population showing three GWAS SNPs (green boxes) linked with the ASAS/sQTL SNP rs3826007 (purple box) in BCL2A1.

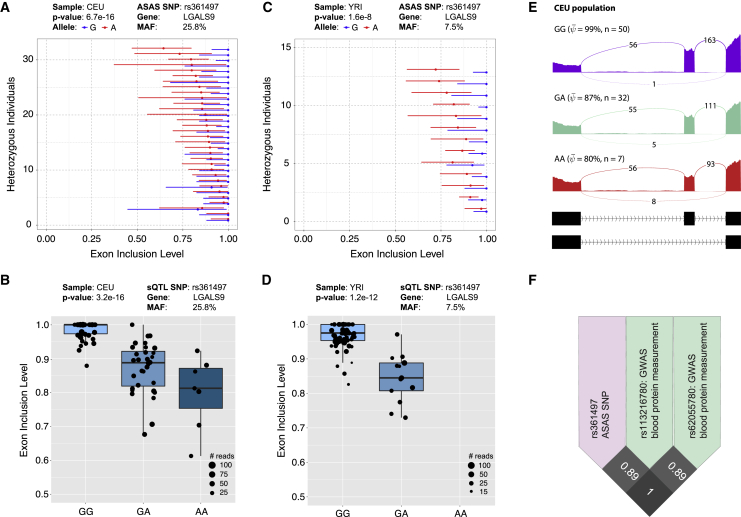
Another ASAS event identified by PAIRADISE is for exon 6 of LGALS9 (galectin 9), which shows consistent splicing differences between the G/A alleles in all five populations (Figure 5A, CEU, PAIRADISE ASAS p value = 6.7e−16; Figure 5C, YRI, PAIRADISE ASAS p value = 1.6e−8). The same SNP rs361497 was also significantly associated with exon 6 splicing in the sQTL analysis (Figure 5B for CEU and Figure 5D for YRI; also see Figure 5E for the RNA-seq sashimi plot of each genotype in the CEU population). Galectin 9 is an S-type lectin involved in modulating cell-cell and cell-matrix interactions^27,28 and has been implicated in the impairment of natural killer cells²⁹ and the maturation and migration of human dendritic cells.^30,31 This ASAS/sQTL SNP (rs361497) is in high LD with two GWAS SNPs (rs113216780, r² = 0.89; rs62055780, r² = 1), previously identified as being associated with blood protein measurement (Figure 5F).

Figure 5.

Genetic Variation and GWAS Association of an AS Event in LGALS9

(A) An ASAS event in LGALS9 with respect to SNP rs361497 in 32 individuals heterozygous for this SNP in the CEU population. The 95% confidence intervals of exon inclusion levels are indicated as the error bars for each allele. Each line of the y axis represents an individual with the heterozygous SNP.

(B) An sQTL event in LGALS9 with respect to SNP rs361497 in the CEU population. Each dot represents data from a particular individual, and the size of the dot indicates the number of reads covering the AS event in that individual. The middle line of the boxplot represents median value. The low and high ends of the box represent the 25% and 75% quantile, respectively.

(C) The same ASAS event in (A) across 13 individuals heterozygous for rs361497 in the YRI population.

(D) The same sQTL event in (B) in the YRI population.

(E) Sashimi plots corresponding to the ASAS event in LGALS9 shown in (A) with average exon read density and splice junction counts for the three genotypes of the CEU population.

(F) LD plot for the CEU population showing two GWAS SNPs (green boxes) linked with the ASAS/sQTL SNP rs361497 (purple box) in LGALS9.

We analyzed the LD associations of significant ASAS SNPs found in the five Geuvadis populations with GWAS trait/disease-associated SNPs (defined by the NHGRI-EBI GWAS catalog²²). We found 52, 35, 18, 22, and 42 ASAS events (AS event-SNP pairs) in CEU, FIN, GBR, TSI, and YRI, respectively, whose SNPs were in high LD with GWAS SNPs, suggesting that many ASAS events identified by PAIRADISE may contribute to population variation in complex traits and diseases. To investigate whether ASAS can enrich GWAS signals, for the ASAS events detected in each dataset (the five populations in Geuvadis, and GM12878), we counted the non-redundant number of ASAP SNPs in high LD with GWAS SNPs. To obtain a random expectation of this number based on a control set of non-ASAP SNPs, for each ASAS SNP we randomly selected one SNP from a region of ±1,000 bp of the ASAS exon, excluding the ASAS SNP itself and other SNPs within the LD block of the ASAS SNP. We then counted the number of these random non-ASAP SNPs in high LD with GWAS SNPs. We repeated this process 10,000 times to obtain a distribution. As illustrated in Figure S4, ASAS SNPs were significantly enriched for LD with GWAS SNPs as compared to the random expectation (p value < 1e−4 in each of the six datasets). The full list of ASAS events associated with GWAS traits is provided in Table S3.

PAIRADISE Analysis of Rare Variants

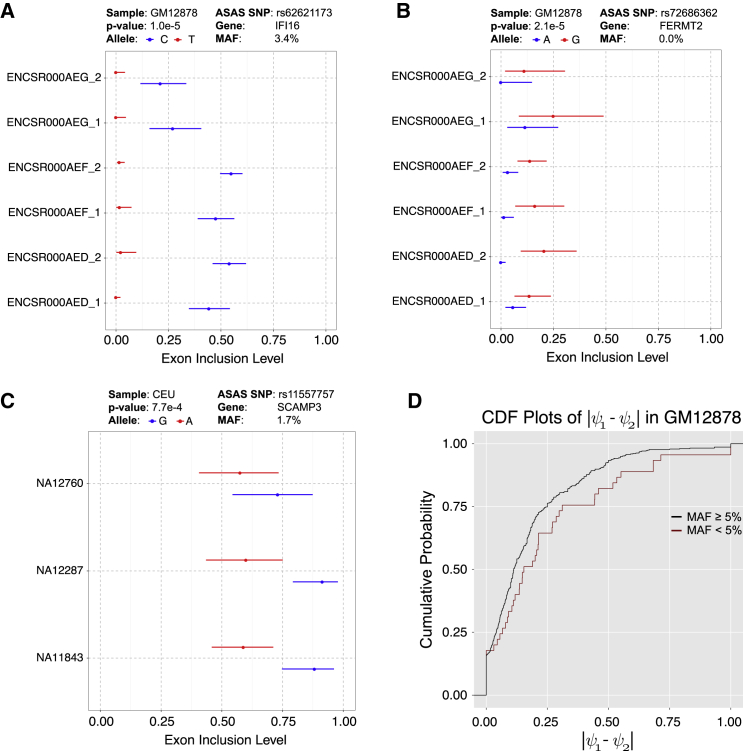
Compared to sQTL analysis across individuals in a population, which detects the effects of common variants on splicing, a unique advantage of ASAS analysis is the ability to examine allelic differences in AS levels of rare variants. In GM12878, by aggregating signals from six RNA-seq replicates, PAIRADISE identified ten genetically regulated exon skipping events as being significantly associated with rare variants (minor allele frequency or MAF < 5% in CEU). For example, an exon skipping event in IFI16 (interferon gamma inducible protein 16) was significantly associated with SNP rs62621173. The MAF of this SNP was only 3.4% in CEU, so this SNP would conventionally be filtered out in an sQTL analysis due to low MAF.³² However, the six RNA-seq replicates of GM12878 showed a reproducible difference in exon inclusion levels between the two alleles, generating a significant ASAS signal (Figure 6A, PAIRADISE ASAS p = 1.0e−5), with the minor allele associated with lower exon inclusion. IFI16 plays a role in innate immunity by acting as a sensor for intracellular DNA.³³ The IFI16 exon skipping isoform contains one less copy of the 56-amino acid serine-threonine-proline (S/T/P)-rich spacer region within the protein product.³⁴ This rare variant (rs62621173) was reported to be associated with the age of onset of Alzheimer disease.³⁵ Another example is FERMT2 (fermitin family member 2), in which an exon skipping event is significantly associated with a rare variant (rs72686362) (Figure 6B). The minor allele G was consistently associated with higher exon inclusion across the six GM12878 RNA-seq replicates. This SNP had a MAF of 0% in the Geuvadis CEU population and 1% in the CEU population of the 1000 Genomes project.¹⁹ Taken together, these examples demonstrate that PAIRADISE can identify and interpret rare variants’ effects on AS and disease.

Figure 6.

PAIRADISE Identifies Rare Variants’ Effects on AS

(A) An ASAS event in IFI16 with respect to SNP rs62621173 (CEU MAF: 3.4%; C: 96.6%, T: 3.4%) identified from the six RNA-seq replicates of GM12878. The 95% confidence intervals of exon inclusion levels are indicated as the error bars for each allele.

(B) An ASAS event in the FERMT2 gene with respect to SNP rs72686362 (1000 Genomes Project CEU MAF: 1%; A: 99%, G: 1%). None of the 89 individuals in the Geuvadis CEU population possess the minor allele G.

(C) An ASAS event in SCAMP3 with respect to SNP rs11557757 (CEU MAF: 1.7%; G: 98.3%, A: 1.7%) identified from three heterozygous individuals in the CEU population.

(D) The cumulative density function (CDF) comparing the absolute value of the allelic difference of exon inclusion levels for ASAS events associated with rare variants (MAF < 5%) or common variants (MAF ≥ 5%) in GM12878.

PAIRADISE also identified 11, 10, 6, 5, and 32 significant ASAS events associated with rare variants in the five populations of the Geuvadis data (CEU, FIN, GBR, TSI, and YRI, respectively). A significant ASAS event in the gene SCAMP3 (secretory carrier membrane protein 3) was associated with the rare variant rs11557757, identified from three individuals in the CEU population (Figure 6C). The major allele G had an average exon inclusion level of 84% compared to 59% for the minor allele A. As expected, rare variants associated with ASAS events had larger effect sizes than common variants. In GM12828, which had no ascertainment bias in detecting the ASAS signals of common versus rare variants, the average allelic difference in exon inclusion levels was 25% for ASAS-associated rare variants, as compared to 18% for common variants (Figure 6D; two-sided Wilcoxon p = 0.09).

Discussion

We introduce PAIRADISE, a statistical model for detecting allele-specific AS from population-scale RNA-seq data. PAIRADISE leverages the pairing structure of two alleles within any given individual to identify consistent allelic differences in AS across multiple replicates of a single individual or multiple individuals in a population. We demonstrate through simulation studies that PAIRADISE outperforms alternative statistical models for ASAS analysis. In particular, for datasets with small sample size, PAIRADISE requires approximately 2–3 times smaller number of replicates to achieve the same level of performance as compared to alternative models (Figure 2). Additionally, as we demonstrate in both single-individual (GM12878) and population-scale (Geuvadis) RNA-seq datasets (Figure 6), a particular advantage of PAIRADISE is that it can detect the effects of rare genetic variants on AS.

The PAIRADISE model shares similarities with the rMATS paired model, previously developed for differential AS analysis of RNA-seq data with paired replicates.¹⁷ Both models use a binomial distribution to account for the RNA-seq estimation uncertainty of PSI values in individual samples (alleles). However, these two models have a key difference in how they model the paired structure. The rMATS paired model uses a covariance structure with a correlation parameter to model the correlation among matched pairs.¹⁷ However, this extra correlation parameter lacks an intuitive statistical interpretation, and unreliable estimation of the correlation parameter can lead to inflated p values. PAIRADISE uses an additive structure to model the variability in PSI values between the two alleles and across individuals (or replicates). The difference between matched pairs (alleles) is modeled by an intuitive and interpretable parameter ${\delta }_i$ (Equation 2). This leads to a significant improvement in the model performance of PAIRADISE over rMATS paired, as evidenced by our simulation studies (Figure 2).

PAIRADISE adopts the widely used PSI metric^5,16 to define and quantify individual AS events. The statistical framework of PAIRADISE is designed to analyze basic types of AS patterns, such as exon skipping events. Such an event-based analytic approach allows allelic splicing differences to be attributed to splicing regulation at specific exons or splice sites while circumventing the challenging problem of inferring and quantifying full-length mRNA isoforms from short-read RNA-seq data.⁵ Unlike the sQTL analysis that tests the association between splicing levels and genotypes across all individuals, the ASAS analysis tests the allelic difference in AS in heterozygous individuals. Each approach has its distinct features and requirements, so not all AS events can be analyzed by both approaches. The ASAS approach has a unique advantage of detecting rare variants’ effects on AS. Additionally, the two alleles of any given individual are exposed to the same cellular environment, potentially reducing the influence by other non-genetic confounding factors or batch effects in population-scale RNA-seq datasets. The sQTL approach, on the other hand, is not limited by the distance between the SNP and the AS event, and can be used to test the association with any exonic or intronic SNP. We should note that the PAIRADISE ASAS test, as well as other methods for testing sQTLs, are designed to identify the associations between genetic variants and AS events. We envision many of the identified SNPs as tagging (i.e., in very strong LD with) the causal SNPs that affect splicing regulation, while the causal SNPs could be located within the alternative exons or nearby intronic regions and are not tested by PAIRADISE.

Several published methods, such as MMSEQ^36,37 and EAGLE,³⁸ model expression levels or ratios derived from RNA-seq read count data and can be used to test for differential allelic expression or isoform ratio. However, they do not account for paired structure of data. The key distinction—and contribution—of PAIRADISE is that the data are treated as matched pairs of replicates, and the detection of ASAS is framed as a statistical problem of identifying differential ratios from count data with paired replicates. The use of pairing information can help reduce the individual-specific variation and improve the statistical power. Of note, setting ${\sigma }_i$= 0 in PAIRADISE will remove the correlation between matched pairs and reduce PAIRADISE to an unpaired model similar to EAGLE and rMATS.

We emphasize that our approach and results were intentionally conservative with respect to the number of ASAS events detected because we did not restrict ${\sigma }_{i1}$ to be equal to ${\sigma }_{i2}$. By allowing ${\sigma }_{i1}\ne {\sigma }_{i2}$, a large portion of the differences in PSI values is absorbed into the variance parameters instead of ${\delta }_i$; hence, the constrained and unconstrained models perform more similarly than they otherwise would. We have left it as a user option to assume equal variances between the two alleles; this will produce more significant events. By running PAIRADISE with ${\sigma }_{i1}={\sigma }_{i2}$, the number of significant ASAS events increased from 116 to 133 in GM12878 and from 91 to 153, 82 to 116, 75 to 101, 71 to 104, and 143 to 199 in the Geuvadis CEU, FIN, GBR, TSI, and YRI populations, respectively. The choice to set ${\sigma }_{i1}={\sigma }_{i2}$ is left as a user option in the PAIRADISE software.

In PAIRADISE, RNA-seq reads are aligned to haplotype-modified personal genomes following the procedures in our rPGA pipeline.²⁰ Then, for any given exon, PAIRADISE tests one SNP at a time for evidence of ASAS. Aligning reads to haplotype-modified personal genomes can correct for reference genome bias in RNA-seq read mapping and enable optimal haplotype assignment of RNA-seq reads. If a read contains multiple SNPs, the read is assigned to a specific haplotype based on majority voting or discarded if there is a draw. Additional quality-control criteria are used to filter out spurious alignment or mapping bias. For example, we require that any read assigned to a specific haplotype has to be aligned to both versions of the haplotype-modified personal genomes uniquely at the same location. In addition to our approach of aligning reads to haplotype-modified personal genomes, other approaches for reducing the reference genome bias in RNA-seq read mapping exist. These approaches include mapping reads to the N-masked version of the genome at all heterozygous SNP sites,³⁹ as well as the allele swapping and RNA-seq remapping strategy employed by WASP.¹⁵ The PAIRADISE model can be applied to allele-specific count data generated by alternative RNA-seq alignment procedures.

The PAIRADISE model is designed to detect consistent ASAS signals across multiple individuals sharing a given heterozygous SNP. It is possible that the ASAS signals of certain alternative exons may vary across individuals, depending on other factors, such as other cis SNPs or the concentration or activity of trans-acting splicing regulators. In future work, we plan to address this issue by introducing an additional layer into the PAIRADISE hierarchical framework to model an individual-specific allelic difference as being dependent on a certain covariate, such as the status of an adjacent cis SNP or the expression level of a trans-acting splicing regulator in the individual. However, a much larger population sample size would be needed to identify potential covariates that affect the magnitude of ASAS signals across individuals. Another important limitation of the PAIRADISE ASAS approach, especially for short-read RNA-seq data, is that it requires a heterozygous SNP outside of the alternative exon to enable allele-specific read assignment, but this SNP also needs to be close enough to the AS event for them to be detected on the same RNA-seq read. SNPs located within or too distant from alternative exons cannot be analyzed by PAIRADISE using short-read RNA-seq data.

In summary, PAIRADISE provides a powerful tool for elucidating the genetic variation and phenotypic association of AS using RNA-seq and genotype data. The statistical model of PAIRADISE is a generic model for testing differential isoform proportions between alleles and is applicable to other forms of allele-specific isoform variation, such as allele-specific RNA editing.³⁹ Moreover, use of paired replicates is a popular study design in many basic and clinical RNA-seq research projects. The PAIRADISE model can be used in other RNA-seq studies with paired replicates, such as paired discovery of cancer-specific AS using RNA-seq data of patient-matched tumor-normal pairs.

Declaration of Interests

Y.X. is a scientific co-founder of Panorama Medicine Inc.

Published: August 10, 2020

Web Resources

• 1000 Genomes Project, https://www.internationalgenome.org/

• ENCODE, https://www.encodeproject.org/

• Geuvadis, https://www.internationalgenome.org/data-portal/data-collection/geuvadis

• GLiMMPS, https://github.com/Xinglab/GLiMMPS

• NHGRI-EBI GWAS Catalog v1.0.2, https://www.ebi.ac.uk/gwas/

• PAIRADISE, https://github.com/Xinglab/PAIRADISE

• PAIRADISE Bioconductor R package, https://bioconductor.org/packages/release/bioc/html/PAIRADISE.html

• rMATS, http://rnaseq-mats.sourceforge.net/

• rPGA, https://github.com/Xinglab/rPGA

• STAR, https://github.com/alexdobin/STAR