Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Aug 10;16(9):5685–5694. doi: 10.1021/acs.jctc.0c00580

Machine Learning Approaches toward Orbital-free Density Functional Theory: Simultaneous Training on the Kinetic Energy Density Functional and Its Functional Derivative

Ralf Meyer 1, Manuel Weichselbaum 1, Andreas W Hauser 1,*
PMCID: PMC7482319  PMID: 32786898

Abstract

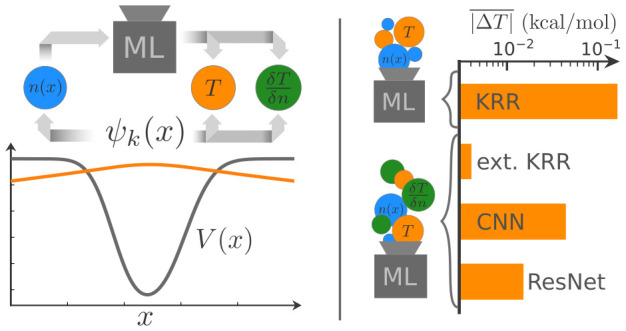
graphic file with name ct0c00580_0003.jpg

Orbital-free approaches might offer a way to boost the applicability of density functional theory by orders of magnitude in system size. An important ingredient for this endeavor is the kinetic energy density functional. Snyder et al. [Phys. Rev. Lett. 2012, 108, 253002] presented a machine learning approximation for this functional achieving chemical accuracy on a one-dimensional model system. However, a poor performance with respect to the functional derivative, a crucial element in iterative energy minimization procedures, enforced the application of a computationally expensive projection method. In this work we circumvent this issue by including the functional derivative into the training of various machine learning models. Besides kernel ridge regression, the original method of choice, we also test the performance of convolutional neural network techniques borrowed from the field of image recognition.

1. Introduction

Over past decades density functional theory (DFT) has evolved into a powerful standard tool of computational chemistry.1,2 Although originally intended as an orbital-free ansatz, where all contributions to the electronic energy of a system are represented by functionals of the electron density, the reintroduction of orbitals within the Kohn–Sham framework is a de facto standard of most modern programs.3,4 The crucial term which triggered this development is the expression of the kinetic energy for a system of interacting fermions, which is much better covered within the picture of occupied molecular orbitals, i.e., eigenfunctions of an effective one-electron operator in a mean-field approximation. In modern functionals, the small deviations from the true kinetic energy are compensated by approximative functional expressions for the exchange and correlation interactions of an N-electron system. Although the local density approximation (LDA) of Kohn and Sham4 is uniquely defined by the properties of the uniform gas, the strategy for further refinements is not clear at all.

Among the most successful current approaches for kinetic energy density functionals (KEDFs) is the class of nonlocal functionals, which are built from three parts:

1. 1

with TTF = CTF∫n5/3 dr as the Thomas–Fermi functional,5−7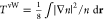Inline graphic as the semilocal von Weizsäcker functional,8 and TNL as an additional nonlocal term. A widely used ansatz for the nonlocal part is of the form

1. 2

with ω denoting a dimensionless kernel, typically assumed to be a function of |r – r′|, and the exponents α and β as parameters. This form encompasses state-of-the-art nonlocal functionals such as the Wang–Teter,9 Smargiassi–Madden,10 Perrot,11 Wang–Govind–Carter,12,13 Huang–Carter14 and Mi–Genova–Pavanello15 functionals. With varying degrees of success, these functionals have been applied to metallic and semiconducting bulk systems containing up to 1 million atoms,16−19 to metallic clusters,20−22 and to molecular systems.23,24

Following ref (25), the idea of using machine learning (ML) methods to approximate density functionals has been investigated by several groups recently. The original ML model for the KEDF has been shown to successfully describe bond breaking26 and was extended to include basis set independence27 as well as scale-invariance conditions.28 The same ML model has also been employed for direct fits of F[n], the universal part of the total energy density functional.29 A very interesting ML model was investigated by Yao and Parkhill, who used a 1D convolutional neural network to fit the kinetic energy as a function of the density projected onto bond directions.30 Machine learning approximations, in particular neural networks, have also been suggested for semilocal KEDFs.31−33 However, all of these ML-based KEDFs were deemed to be inadequate for an application in iterative calculations of the minimum energy density, mostly due to large errors on the predicted functional derivative. As a consequence, the focus has shifted toward a direct prediction of the minimum energy density from the nuclear potential, thereby bypassing the need for iterative calculations.34−39

One of the earliest machine learning models for density functionals was presented by Tozer et al. for the exchange–correlation (XC) functional.40 In addition to explorations of the XC functional,41−44 machine learning approximations have also been applied to other technicalities of DFT.45−48

In this article, we follow up on the first tests by Snyder et al.25 and investigate if the original idea of learning the kinetic energy functional for a usage in iterative calculations can be “salvaged” by a simultaneous training of the machine learning model on both the kinetic energy functional and its functional derivative. In addition to the application of kernel ridge regression, we evaluate the performance of convolutional neural networks, one of the most successful and widely used ML architectures to date. Our approach is motivated by the fact that the underlying mathematical expression is very similar to the nonlocal contribution given by eq 2 (if the kernel ω is assumed to be a function of |r – r′|) and shows translational invariance, which might enable a better generalization, especially for large systems.

2. Methods

2.1. Data Generation

A one-dimensional model system of noninteracting spinless Fermions is used to train and test the ML KEDFs. It consists of N particles in a hard wall box within the interval 0 ≤ x ≤ 1 and an external potential built from a linear combination of three Gaussians:25

2.1. 3

with parameters a, b, and c randomly sampled from uniform distributions in the intervals [1, 10], [0.4, 0.6], and [0.03, 0.1], respectively. The 1D Schrödinger equation for these potentials is solved on a grid of G = 500 points using Numerov’s method,49 yielding a set of eigenfunctions ψjk(x) and corresponding eigenvalues Ej for each potential Vj(x), ordered from lowest to highest energy with increasing index k. These solutions are then used to calculate all components of the training data for an N-particle system, namely the density

2.1. 4

the kinetic energy density, here defined as

2.1. 5

the kinetic energy

2.1. 6

and the kinetic energy functional derivative

2.1. 7

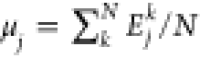with Inline graphic denoting the total energy per particle. The discretized version of these functions, written as vectors for clarity nj(x) → nj, τj(x) → τj, and δT[nj]/δnj(x) → ∇njTj/Δx, are used to train the ML models. The error in the eigenenergies due to discretization is estimated to be below 10–3 kcal/mol by comparing the solutions to calculations on a 10 times finer grid. However, in the context of the ML models all of the computed quantities are considered exact. The M = 100 parameter triplets for a, b, and c as listed in the Supporting Information of ref (25) are used as training data in order to recreate the original study as closely as possible. On the basis of eq 3, we generate 1000 additional random potentials as a test set.

2.2. Kernel Ridge Regression

We start with a brief review of the kernel ridge regression (KRR) approach as introduced in ref (25). This ansatz is then extended by the inclusion of the functional derivative into the training in order to improve its capabilities. Details on the derivation of the equations used in the following can be found in section 2 of the Supporting Information. An elaborate discussion of KRR model training can be found in ref (50).

In KRR the simple regularized linear fit of ridge regression is extended toward nonlinear data through the introduction of a kernel function:

2.2. 8

with αj as the fit coefficients, the kernel function k(ni, nj), which can be interpreted as a measure of similarity between two densities, and with {n1, ..., nM} as the M training examples. The coefficients αj are determined by minimizing the cost function

2.2. 9

where the second term is a regularization function scaled by the parameter λ and Tj are the kinetic energies corresponding to the training densities nj. Setting the derivative with respect to the αj equal to zero yields a matrix equation for the fit coefficients:

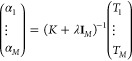2.2. 10

The matrix K contains the values of the kernel function for the M training examples, so Kij = k(ni, nj) and IM is a unit matrix of size M.

Snyder et al.25 have shown already that the discretized functional derivative can easily be calculated from eq 8, yielding

2.2. 11

In our study, we expand on this idea by including the functional derivatives of the training examples into the model using additional fit coefficients βj. The kinetic energy of the extended model is then given by

2.2. 12

Derivation with respect to the input density gives the new formula for the functional derivative:

2.2. 13

Note that each of the newly introduced coefficients βj is a vector of size G. Therefore, the number of parameters grows from M to M(1 + G). The cost function is extended by the squared error of the functional derivative and an additional regularization term for the new weights βj:

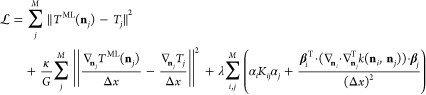2.2. 14

with ∇njTj/Δx denoting the reference value for the discretized functional derivative corresponding to the training density nj. Minimizing this extended cost function with respect to the coefficients yields

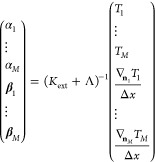2.2. 15

with an extended regularization matrix

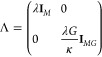2.2. 16

where IM and IMG are unit matrices of size M and MG, respectively, and an extended kernel matrix

2.2. 17

where K is a (M × M) matrix with elements Kij = k(ni, nj); J and J′ are matrices of size (MG × M) and (M × MG), respectively, and contain the gradient vectors of k(ni, nj) with respect to the input densities

2.2.

and

2.2.

Finally, H is a (MG × MG) blocked matrix consisting of the Hessian matrices of k(ni, nj) given by

2.2.

Following ref (25), we use the squared exponential kernel for all of the presented KRR models:

2.2. 18

where the hyperparameter σ denotes the length scale on which the training densities vary.

2.3. Convolutional Neural Networks

Convolutional neural networks51,52 (CNNs) are on the forefront of the ongoing deep learning revolution53,54 and achieve unprecedented accuracy in their main field of application: image recognition.55 CNNs represent a subclass of standard feed-forward neural networks, designed for the specific purpose of an efficient inclusion of spatial information in pixel-based image processing. Despite their origin in visual pattern recognition, CNNs have been applied successfully to numerous other tasks, including also the approximation of density functionals.30,43,45

A single convolutional layer typically consists of several filters or steps of input processing. A pass through a single convolutional filter in one dimension is given by

2.3. 19

where the index “(g)” refers to the gth element of a vector (parentheses are used to distinguish grid point indices from training example indices), f is an activation function, b is a bias parameter, w is a vector of weight parameters for the filter (commonly referred to as “kernel”), and σw is the filter width. Equation 19 is only valid for indices (g) where the input and the convolutional kernel w fully overlap (referred to as “valid padding”). The resulting output vector z is therefore smaller than the input. Alternatively, the input vector can be padded with zeros to ensure that the output is of the same size as the input, a technique referred to as “same padding”.

In the course of this article we investigate the performance of both a standard CNN and a residual neural network (ResNet),56 with the latter referring to a network featuring a more sophisticated architecture: In addition to conventional convolutional layers, ResNets use so-called skip connections through which the feed-forward signal can bypass several layers and is directly added to the output of a later layer. Connections of this type are known to improve the training process, in particular if training data is limited, as they are forming a less complicated, “coarse” network within the actual network structure.

Both investigated models use 32 filters per convolutional layer with a filter width of σw = 100 and employing the softplus activation function.57,58 The standard CNN consists of five convolutional layers using valid padding. This results in an flattened output vector containing 160 entries, which is then reduced to a single scalar, the kinetic energy prediction, using a weighted sum, referred to as “linear dense layer” in community parlance. The more complicated ResNet model consists of three blocks of two convolutional layers. Each of these blocks is bypassed by a skip connection. The three blocks are followed by a final convolutional layer with a single filter. In order to allow for skip connections, all convolutions employ same padding. This architecture results in an output vector of the same size as the input density, which is interpreted as kinetic energy density. Finally, the kinetic energy (see eq 6) is calculated by integrating over the output using the trapezoidal rule. The batch normalization layers59 typically employed in ResNets worsen the training performance in regression tasks and are therefore not used. Schematics of both models are presented in Figure 1. We use the keras60 and tensorflow61 python packages to implement and train both types of neural networks.

Figure 1.

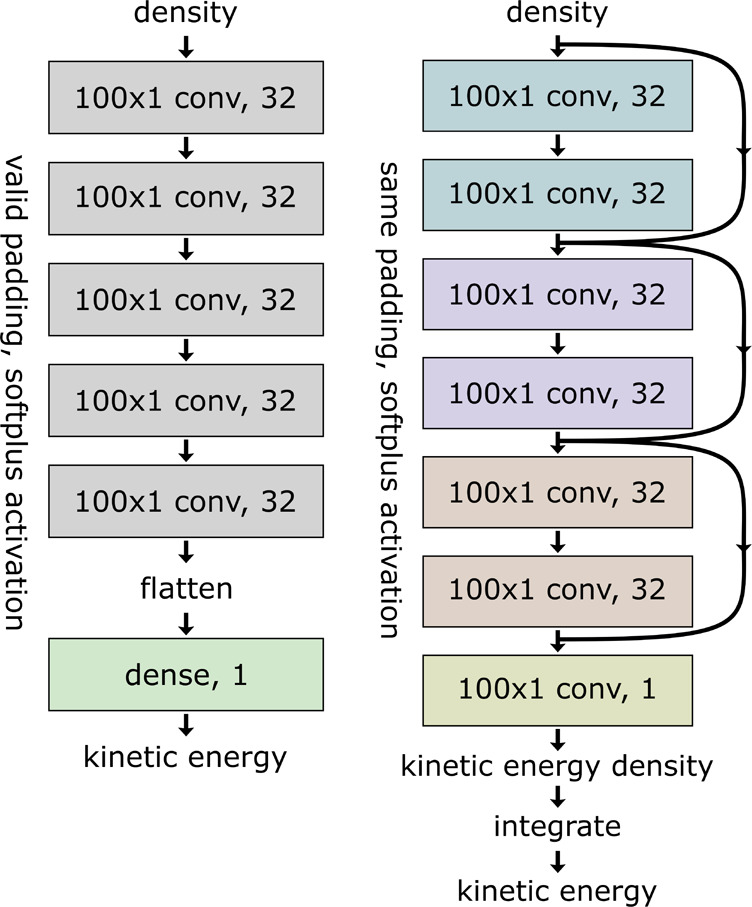
Figure 1

Open in a new tab

Schematic depiction of the NN architectures used for the standard CNN (left) and the ResNet model (right). Note the appearance of skip connections for the latter.

The bias and weight parameters are determined by minimizing a cost function similar to eq 14. Since the ResNet model offers predictions of the kinetic energy densities τj, an additional error term can be added to the cost function

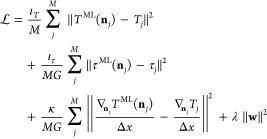2.3. 20

where the weighting coefficients are set to ιT = 0.2, ιτ = 0, κ = 1, and λ = 2.5 × 10–4 for the standard CNN (since it does not predict the kinetic energy density) and to ιT = 0, ιτ = 1, κ = 1, and λ = 2.5 × 10–4 for the ResNet. The L2-regularization term is applied to weight parameters exclusively and not to bias parameters.

The network parameters are initialized randomly according to the “Glorot uniform” tensorflow method62,63 and trained using the Adam optimizer64 for 100 000 epochs. We use a two-stage learning rate schedule, where the learning rate stays constant at 10–4 for the first 21 800 epochs and is lowered by 10% every 1000 epochs for the remaining training procedure, resulting in an exponential decay. This greatly improves the overall convergence, as the inclusion of derivative information leads to large variations of the cost function during the training. A more detailed discussion of the training procedure as well as its convergence behavior is given in section 4 of the Supporting Information.

3. Results and Discussion

Each of the following investigations can be split into two different parts with respect to their objectives. In the first part, the model performance is tested by using the exact densities of the test set as input to the ML models and evaluating the error of both the kinetic energy and the functional derivative. In the second part, the derivative prediction of the ML models is used to iteratively find the minimum energy density for the potentials of the test set. For these densities, the error of the kinetic energy is reported together with the deviation from the exact minimum energy density. This way, the impact and the magnitude of both types of error contributions, one stemming from the model itself and the other caused by wrong minimum energy density predictions, should become clear and traceable for the reader.

3.1. Training on the Functional Derivative

As a first test, we investigate if the inclusion of derivative information can improve the fit quality of the machine learning models on the data sets for N = 1. Table 1 summarizes the mean value, the standard deviation, and the maximum value of both the absolute error of the kinetic energy |ΔT| and the integral over the absolute error of the functional derivative 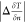Inline graphic for all of the investigated models.

Table 1. Absolute Error Values on the N = 1 Test Set for All of the Machine Learning Models (in kcal/mol).

  |ΔT|
graphic file with name ct0c00580_m041.jpg
model mean std max mean std max
KRR, ref  25 0.15 0.24 3.2 – – –
KRR, this work 0.163 0.29 4.6 29313.2 345.5 30610.9
ext KRR 0.004 0.02 0.6 3.4 4.3 50.7
CNN 0.044 0.10 2.3 31.5 25.0 370.1
ResNet 0.015 0.02 0.3 10.1 7.0 110.7
Open in a new tab

As a reference, we reproduce the KRR results from ref (25) by using the reported hyperparameters (σ = 43 and λ = 12 × 10–14). Slight deviations between our results and the previous work in Table 1 can be attributed to the fact that we use a different randomly generated test set. The hyperparameters for the extended KRR model including derivative information (referred to as “ext KRR” in Table 1) are determined using a rough grid search and 5-fold cross-validation. The minimum of the sum of the mean absolute validation errors for kinetic energy and functional derivative is obtained for σ = 30.58 and λ = 10–12. The influence of the weighting parameter κ, which is set to 1, as well as a more detailed description of the hyperparameter search is given in section 3 of the Supporting Information.

Comparison of the two KRR models shows that the inclusion of derivative information into the KRR approach not only drastically reduces the error on the functional derivative, as illustrated for a sample potential in Figure 2, but also improves the accuracy of the kinetic energy prediction. Section 3 of the Supporting Information shows that the cross-validation error of the kinetic energy is actually lowest for the hyperparameter values σ = 11.50 and λ = 10–14, whereas the lowest error on the functional derivative is obtained for σ = 30.58 and λ = 10–12.

Figure 2.

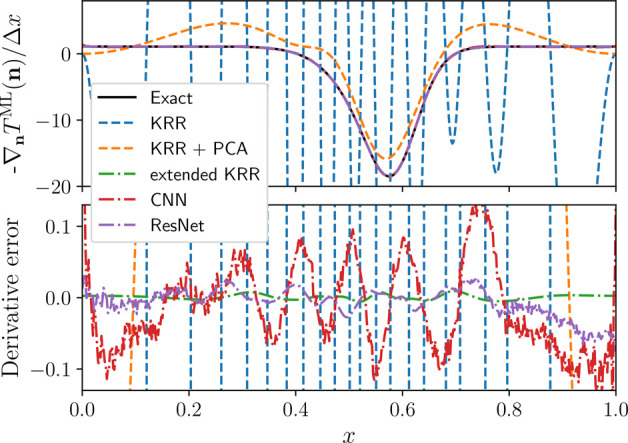
Figure 2

Open in a new tab

Comparison of exact functional derivative (solid lines) and predictions by standard KRR with and without the PCA projection detailed in section 3.2 (dashed lines) as well as prediction from the ML models trained on derivative information (dashed–dotted lines). The parameters for the shown potential are a = {4.43, 7.18, 9.03}, b = {0.0532, 0.587, 0.568}, and c = {0.0754, 0.0406, 0.0554}.

Both the simpler CNN and the more sophisticated ResNet achieve lower mean absolute errors for both the kinetic energy and its derivative than the standard KRR model. We attribute the better performance of the extended KRR method to a lack of smoothness exhibited by the neural network models as shown in the bottom panel of Figure 2.

3.2. Finding Minimum Energy Densities Using Principal Component Analysis

In the next step we address the question of applicability with respect to a direct minimization of kinetic energy density. As will be shown in the following, an unconstrained search still remains impossible despite the drastic improvements in the prediction accuracy of the functional derivative.

The reason for this failure lies in the notoriously noisy nature of machine learning approximations. Already emphasized in ref (25), this was discussed in greater detail in a follow-up investigation on nonlinear gradient denoising.65 For reasons of comparability, we use the same local principal component analysis (PCA) approach as was introduced in the original publication as an ad hoc remedy and investigate if the improved accuracy of the models trained on the functional derivative translates to lower errors on the iteratively found densities. Additionally, we test if the PCA search space can be increased for these models.

Starting from the average density of all training examples, 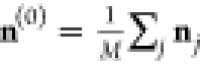Inline graphic, the minimum energy density is found by simple gradient descent

3.2. 21

where the projection matrix Pm,l(n) is acting on the functional derivative and constraining the search space, η is the step size, and V is the discretized potential. We note that more sophisticated optimization methods such as conjugate gradient are known to significantly accelerate the convergence,66 but this is not relevant for the intended comparison. For a given density n the local PCA algorithm starts by calculating the difference matrix XT = (nj1 – n, ..., njm – n) for the m closest training densities and diagonalizing the covariance matrix C = XTX/m. The projection matrix is then constructed from the eigenvectors wk corresponding to the l largest magnitude eigenvalues 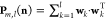Inline graphic. Figure 2 shows the effect of this projection on the functional derivative prediction made by the standard KRR model with parameters m = 30 and l = 5. For all calculations presented in this article we keep m = 30, but we vary the size of the search space via the parameter l. Section 7 of the Supporting Information shows the effect of the projection on the functional derivative prediction for different values of l. The iterative minimization algorithm is considered converged once the integral over the absolute projected functional derivative is smaller than 10–6 hartree/particle. We use a step size of η = 10–3 and restrict the maximum number of iterations to 4000 cycles.

The results for all of the 1000 random potentials in the test set are summarized in Table 2. Again, the inclusion of derivative information reduces both errors significantly when compared to those obtained with the simple KRR. The final error can be attributed to two different sources. The first contribution stems from the model error due to the ML approximation as has already been discussed in section 3.1. A second contribution arises due to the difference in the corresponding minimum energy densities Δn, which is in turn caused by the model error and the restriction of the search space in the PCA. This limited flexibility in the search for l = 5 is likely the cause of the similar error values achieved by all of the ML models using derivative information. We therefore also investigated larger l values while keeping m = 30. Runs using standard KRR fail for every value l > 5, not reaching convergence and predicting sharply peaked densities instead. Similarly, the performance of the simple CNN deteriorates quickly for l > 10. For the ResNet and extended KRR models the errors reduce up to an l value of about 15, at which point the iterative algorithm leaves the valid region of the ML models. Note, however, that for l values in the range between 10 and 15 the ML approximations including derivative information achieve errors an order of magnitude lower than standard KRR.

Table 2. Absolute Kinetic Energy Errors ΔT for the Iteratively Found Densities (in kcal/mol) as Well as the Integrated Absolute Error of the Densities Δn for the N = 1 Test Set.

    |ΔT|
 |Δn| × 104
model l mean std max mean std max
KRR, ref 25 5 3.0 5.3 46 – – –
KRR, this work 5 2.85 7.00 87.34 45.0 54.0 503.9
ext KRR 5 0.46 1.05 15.35 14.9 11.5 85.0
ext KRR 10 0.04 0.22 5.95 0.8 0.7 10.7
ext KRR 15 0.04 0.22 5.97 0.3 0.5 10.8
CNN 5 0.57 1.40 21.69 15.2 12.0 95.5
CNN 10 0.29 0.77 13.26 5.5 8.5 171.0
ResNet 5 0.51 1.25 19.59 14.9 11.5 85.5
ResNet 10 0.09 0.21 5.72 1.0 0.9 14.7
ResNet 15 0.09 0.22 5.86 2.0 2.4 19.6
Open in a new tab

Alternatively, KRR can also be used in iterative calculations without the PCA by introducing a constant offset

3.2. 22

and using a small length scale hyperparameter σ in the kernel function. This can be used to penalize densities far from the training data and effectively acts similarly to PCA, while using all of the training densities (m = M). This approach is inspired by the use of Gaussian process regression for molecular geometry optimization,67−69 where a similar idea ensures that the iterative search does not stray too far from the training data. A more detailed explanation as well as results for the densities provided by this method can be found in section 6 the Supporting Information. However, both the need for local PCA and the alternative approach of small length scales and a constant offset are indications that the ML density functionals do not properly generalize and are only valid in close vicinity of the training examples.

3.3. Toward a Real-World Use Case

While section 3.2 shows that models trained on the functional derivative allow for significantly larger search spaces, the iterations will, given enough flexibility, inevitably leave the region where the machine learning approximations are valid. This typically leads to sharply peaked or rapidly oscillating densities. A straightforward solution for this problem is to use physically motivated penalty terms for these unphysical densities such as the von Weizsäcker kinetic energy functional8 and to train the machine learning model on the difference between the exact kinetic energy and the von Weizsäcker model:

3.3. 23

The prediction of a previously unseen density is then given by the sum of the machine learning and the von Weizsäcker model functionals, TML + TvW, where the derivative term n′(x) = dn/dx in the latter contribution is introducing an energy penalty for rapid changes in the density, which effectively restricts the search space to physically reasonable densities. Since the von Weizsäcker model already yields the exact solution for the case of a single spatial orbital (discussed in section 2), we test this approach for two-particle densities instead. In our toy model, this already corresponds to the occupation of two spatial orbitals since there is no spin degree of freedom taken into consideration.

At first, we again investigate the model performance for fixed densities. The hyperparameters for both the standard and the extended KRR models are readjusted using the same grid search and 5-fold cross-validation as in section 3.1. This yields σ = 35.16 and λ = 10–12 for the standard KRR and σ = 26.59, λ = 10–12, and κ = 1.0 for the extended KRR. More details on the hyperparameter search are provided in section 3 of the Supporting Information.

As can be seen in Table 3, all of the three investigated models achieve significantly better performance on the two-particle densities than on the single-particle densities. The analysis of the training sets in section 1 of the Supporting Information suggests that even though kinetic energies in the N = 2 data set are showing a larger variance, most of it can be captured by a simple linear model. We attribute this to the fact that the second particle is less influenced by the relatively shallow potentials and the more difficult to learn semilocal contribution is already covered by the von Weizsäcker functional. Even though chemical accuracy is achieved by all models on this less challenging data set, extended KRR yields a mean absolute error for the kinetic energy that is 2 orders of magnitude lower than that obtained with either ResNet or standard KRR.

Table 3. Error Values of the Machine Learning Approximations on the N = 2 Test Set (in kcal/mol).

  |ΔT|
graphic file with name ct0c00580_m042.jpg
model mean std max mean std max
KRR 0.0355 0.0588 0.8752 2957.85 16.00 2990.36
ext KRR 0.0002 0.0008 0.0233 0.12 0.15 2.18
ResNet 0.0483 0.2837 6.8116 6.78 11.36 223.35
Open in a new tab

Regarding efficiency and feasibility, the local PCA introduces a significant computational overhead and would most likely prohibit a large scale application of ML density functionals to realistic problems. We therefore opt for a more traditional approach of using a basis of sine functions instead. This introduces the necessity of ensuring both the positivity and the proper normalization of the density throughout the iterative algorithm. While the correct norm can simply be enforced by a Lagrange multiplier, the positivity constraint is typically included by iterating on the variable 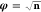Inline graphic instead of the density. The steepest descent update rule for this new variable is given by

3.3. 24

where PK is a projection matrix and μ is the Lagrange multiplier used to ensure the conservation of the number of particles N. A detailed derivation of this result, a possible way of determining μ as well as an explanation why this procedure is not necessary for the local PCA, is provided in section 5 of the Supporting Information. The matrix used to project the functional derivative onto the basis of sine functions is constructed via

3.3. 25

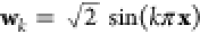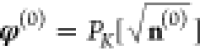with Inline graphic. Note that this matrix does not need to be reconstructed in every iteration as it is no longer dependent on the density at step j. The size of the search space is now determined by the maximum wavenumber K. 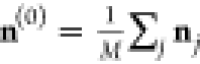The starting value for the variable φ is the square root of the initial density n(0) projected onto the basis of sine functions Inline graphic, where the starting density is again given by the average over the training data Inline graphic. 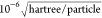The maximum number of iterations is restricted to 4000 and calculations are considered converged once the integral over the absolute projected functional derivative drops below a threshold of Inline graphic. Note that this differs from the convergence criterion in section 3.2 because convergence is monitored using the functional derivative with respect to the variable φ instead of the density. The step size is reduced to η = 10–4 in order to avoid oscillations in the convergence behavior.

Our results are summarized in Table 4. The large errors on the functional derivative of the standard KRR model lead to poor results for iteratively found densities. This is further emphasized by the steadily increasing error when the search space grows from K = 10 to K = 20 and K = 40. The iterative search is, however, stable even for the larger K values due to the von Weizsäcker penalty term. Extended KRR clearly yields the best predictions for the minimum energy densities, while the ResNet approach barely manages to achieve a mean absolute error for the kinetic energy within chemical accuracy.

Table 4. Absolute Kinetic Energy Error ΔT for the Iteratively Found Densities (in kcal/mol) as Well as the Integrated Absolute Error of the Densities Δn on the N = 2 Test Set, Compared between the KRR variants and ResNet for Increased Search Spaces.

    |ΔT|
 |Δn| × 104
model K mean std max mean std max
KRR 10 8.431 1.138 16.686 109.0 23.0 222.8
KRR 20 21.365 0.826 22.456 133.9 18.4 194.9
KRR 40 23.882 0.846 25.003 139.8 18.4 200.5
ext KRR 10 0.523 0.827 7.353 24.8 16.0 102.1
ext KRR 20 0.074 0.069 0.789 0.5 0.6 2.9
ext KRR 40 0.076 0.069 0.789 0.1 0.1 1.1
ResNet 10 1.239 6.537 142.649 25.8 18.6 248.9
ResNet 20 0.877 6.634 146.324 2.9 11.8 253.3
ResNet 40 0.877 6.635 146.327 2.7 11.8 253.3
Open in a new tab

3.4. Larger Training Set

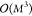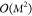The previous sections are somewhat biased due to the small number of training examples—a regime where KRR excels. In a final test we therefore investigate the performance of the neural network based density functional for an increasing number of training examples. A similar investigation for the extended KRR model is not feasible since the training effort for the KRR model scales with Inline graphic and the memory requirements grow with Inline graphic. We note, however, that an alternative approach to reduce the computational effort would be to use sparse kernel based machine learning algorithms such as support vector regression70−72 or sparsified Gaussian process regression.73−75 These methods could combine the high accuracy of kernel ridge regression even for small training sets with the potential of increasing the region where the model is valid by incorporating a significantly wider range of training examples.

The hyperparameters of the ResNet model and the training procedure have to be adjusted due to the increased number of examples. Instead of evaluating the cost function involving all of the training data (batch learning), a random subset or “batch” of 100 examples is used to calculate the gradient descent step and to update the NN parameters (i.e., minibatch learning). The models are trained for a total of 300 000 such iterations with a learning rate of 10–4 during the first 40 000 steps, after which the learning rate is reduced by 10% every 2000 steps. In addition, the regularization factor λ is lowered as well (see section 4 of the Supporting Information for details).

Table 5 shows that the larger amount of training examples leads to a steady reduction in every error score. The most significant improvement is observed for the standard deviation and the maximum error, the metrics most closely related to the generalization properties of the model.

Table 5. Absolute Error Values for the Kinetic Energy ΔT and Its Functional Derivative (in kcal/mol) on the N = 2 Test Set, Achieved by the ResNet Model Trained on Sets of Varying Size.

  |ΔT|
graphic file with name ct0c00580_m043.jpg
M mean std max mean std max
100 0.049 0.284 6.814 6.78 11.36 223.36
1 000 0.012 0.063 1.922 3.12 2.81 66.31
10 000 0.007 0.018 0.528 2.79 1.92 45.19
100 000 0.007 0.009 0.138 2.39 1.36 19.40
Open in a new tab

We use a basis of K = 40 sine functions for the iterative calculation of minimum energy densities. Instead of enforcing a convergence threshold, the calculations stop after a fixed number of 10 000 iterations for the sake of simplified parallelization on GPUs. Typically, the final error values are reached within the first 10% of the iterations. The large overhead in terms of iterations is used to investigate the numerical stability of the iterations on noisy ML predictions of the derivative.

The error scores on the iteratively found densities, summarized in Table 6, are clearly improving with an increasing number of training examples. The ResNet trained on 100 000 densities achieves a performance similar to the extended KRR model trained on just 100 examples. While this may suggest that KRR should be the obvious choice, one has to keep in mind that the evaluation times for the ResNet model are independent of the number of training examples, and that training examples are typically available in abundance: In fact, every single step in a self-consistent Kohn–Sham DFT calculation could serve as training input.

Table 6. Absolute Kinetic Energy Error ΔT (in kcal/mol) as Well as the Integrated Absolute Error Δn of the Iteratively Found Densities on the N = 2 Test Set, Employing the ResNet on Training Sets of Increasing Size.

  |ΔT|
 |Δn| × 104
M mean std max mean std max
100 0.856 6.591 145.58 2.7 11.8 253.0
1 000 0.151 1.196 32.65 0.7 1.9 50.5
10 000 0.062 0.228 6.48 0.6 0.6 13.7
100 000 0.047 0.070 0.89 0.6 0.5 5.5
Open in a new tab

4. Conclusion

The predictive capabilities of kernel ridge regression and convolutional neural networks, two well-established machine learning techniques, have been tested on a one-dimensional model system of noninteracting spinless fermions with respect to the kinetic energy and its functional derivative. Extending the work of Snyder et al.,25 we have investigated if the original idea of learning the kinetic energy functional for usage in iterative calculations of minimum energy densities can be “salvaged” by a simultaneous training of machine learning models on both the kinetic energy functional and its functional derivative. Besides kernel ridge regression, the method of choice in the original paper, we have evaluated the performance of convolutional neural networks, one of the most successful and widely used machine learning architectures to date.

In general, the inclusion of the functional derivative not only improves the prediction accuracy for the functional derivative, but also leads to better generalization toward out-of-training data. This is underlined by the fact that iterative calculations of the minimum energy density are significantly more stable and lead to lower deviations in both the final kinetic energy and the converged density. However, the usage of derivative information in the kernel ridge regression technique increases the computational effort significantly and prohibits its application to larger data sets. Neural networks, on the other hand, do not show these limitations. Of the two flavors tested in this study, conventional convolutional networks and the more advanced ResNets, the latter variant achieves competitive results already on small training sets and improves its performance steadily with increasing data at minimal additional computational cost.

Very recently, it has already been shown for the exchange–correlation functional that convolutional neural network based density functionals can easily be extended toward three-dimensional systems.43 Using similar techniques for the kinetic energy functional might bring us closer to the ambitious objective of a truly orbital-free density functional theory.

Acknowledgments

Financial support by the Austrian Science Fund (FWF) under Grant P29893 is gratefully acknowledged. We thank the Central Informatics Service (ZID) of the Graz University of Technology for providing high performance computing resources and technical support. Furthermore, we are grateful for resources and support offered by Colaboratory, a free service of Google Research.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00580.

  • Detailed analysis of data sets, derivation of both standard formalism and extended KRR formalism, details on choice of hyperparameters for KRR and neural network models, description of algorithm used to find minimum energy densities, investigation of an alternative to local PCA using KRR models with an offset term, analysis of PCA projected functional derivative predictions, learning curve showing accuracy as a function of number of training examples, computational timings for evaluation of machine learning models (PDF)

  • Tabulated values for the parameter triplets a, b, and c used to generate the potentials of the training and test sets (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ct0c00580_si_001.pdf (847.6KB, pdf)
ct0c00580_si_002.zip (9.3MB, zip)

References

  1. Perdew J. P.; Ruzsinszky A. Fourteen easy lessons in density functional theory. Int. J. Quantum Chem. 2010, 110, 2801–2807. 10.1002/qua.22829. [DOI] [Google Scholar]
  2. Becke A. D. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 2014, 140, 18A301. 10.1063/1.4869598. [DOI] [PubMed] [Google Scholar]
  3. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  4. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  5. Thomas L. H. The calculation of atomic fields. Math. Proc. Cambridge Philos. Soc. 1927, 23, 542–548. 10.1017/S0305004100011683. [DOI] [Google Scholar]
  6. Fermi E. Statistical method to determine some properties of atoms. Rend. Accad. Naz. Lincei 1927, 6, 602. [Google Scholar]
  7. Fermi E. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente. Eur. Phys. J. A 1928, 48, 73–79. 10.1007/BF01351576. [DOI] [Google Scholar]
  8. Weizsäcker C. F. v. Zur Theorie der Kernmassen. Eur. Phys. J. A 1935, 96, 431–458. 10.1007/BF01337700. [DOI] [Google Scholar]
  9. Wang L.-W.; Teter M. P. Kinetic-energy functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 45, 13196–13220. 10.1103/PhysRevB.45.13196. [DOI] [PubMed] [Google Scholar]
  10. Smargiassi E.; Madden P. A. Orbital-free kinetic-energy functionals for first-principles molecular dynamics. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 5220–5226. 10.1103/PhysRevB.49.5220. [DOI] [PubMed] [Google Scholar]
  11. Perrot F. Hydrogen-hydrogen interaction in an electron gas. J. Phys.: Condens. Matter 1994, 6, 431–446. 10.1088/0953-8984/6/2/014. [DOI] [Google Scholar]
  12. Wang Y. A.; Govind N.; Carter E. A. Orbital-free kinetic-energy functionals for the nearly free electron gas. Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 58, 13465–13471. 10.1103/PhysRevB.58.13465. [DOI] [Google Scholar]
  13. Wang Y. A.; Govind N.; Carter E. A. Orbital-free kinetic-energy density functionals with a density-dependent kernel. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, 16350–16358. 10.1103/PhysRevB.60.16350. [DOI] [Google Scholar]
  14. Huang C.; Carter E. A. Nonlocal orbital-free kinetic energy density functional for semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 045206. 10.1103/PhysRevB.81.045206. [DOI] [Google Scholar]
  15. Mi W.; Genova A.; Pavanello M. Nonlocal kinetic energy functionals by functional integration. J. Chem. Phys. 2018, 148, 184107. 10.1063/1.5023926. [DOI] [PubMed] [Google Scholar]
  16. Hung L.; Carter E. A. Accurate simulations of metals at the mesoscale: Explicit treatment of 1 million atoms with quantum mechanics. Chem. Phys. Lett. 2009, 475, 163–170. 10.1016/j.cplett.2009.04.059. [DOI] [Google Scholar]
  17. Chen M.; Jiang X.-W.; Zhuang H.; Wang L.-W.; Carter E. A. Petascale Orbital-Free Density Functional Theory Enabled by Small-Box Algorithms. J. Chem. Theory Comput. 2016, 12, 2950–2963. 10.1021/acs.jctc.6b00326. [DOI] [PubMed] [Google Scholar]
  18. Shao X.; Mi W.; Xu Q.; Wang Y.; Ma Y. O. N log N) scaling method to evaluate the ion-electron potential of crystalline solids. J. Chem. Phys. 2016, 145, 184110. 10.1063/1.4967319. [DOI] [PubMed] [Google Scholar]
  19. Shao X.; Xu Q.; Wang S.; Lv J.; Wang Y.; Ma Y. Large-scale ab initio simulations for periodic system. Comput. Phys. Commun. 2018, 233, 78–83. 10.1016/j.cpc.2018.07.009. [DOI] [Google Scholar]
  20. Aguado A.; López J. M.; Alonso J. A.; Stott M. J. Melting in Large Sodium Clusters: An Orbital-Free Molecular Dynamics Study. J. Phys. Chem. B 2001, 105, 2386–2392. 10.1021/jp0018504. [DOI] [Google Scholar]
  21. Aguado A.; López J. M. Molecular dynamics simulations of the meltinglike transition in Li13Na42 and Na13Cs42 clusters. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 075415. 10.1103/PhysRevB.71.075415. [DOI] [Google Scholar]
  22. Gavini V.; Knap J.; Bhattacharya K.; Ortiz M. Non-periodic finite-element formulation of orbital-free density functional theory. J. Mech. Phys. Solids 2007, 55, 669–696. 10.1016/j.jmps.2006.09.011. [DOI] [Google Scholar]
  23. Xia J.; Carter E. A. Density-decomposed orbital-free density functional theory for covalently bonded molecules and materials. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 86, 235109. 10.1103/PhysRevB.86.235109. [DOI] [Google Scholar]
  24. Xia J.; Huang C.; Shin I.; Carter E. A. Can orbital-free density functional theory simulate molecules?. J. Chem. Phys. 2012, 136, 084102. 10.1063/1.3685604. [DOI] [PubMed] [Google Scholar]
  25. Snyder J. C.; Rupp M.; Hansen K.; Müller K.-R.; Burke K. Finding Density Functionals with Machine Learning. Phys. Rev. Lett. 2012, 108, 253002. 10.1103/PhysRevLett.108.253002. [DOI] [PubMed] [Google Scholar]
  26. Snyder J. C.; Rupp M.; Hansen K.; Blooston L.; Müller K.-R.; Burke K. Orbital-free bond breaking via machine learning. J. Chem. Phys. 2013, 139, 224104. 10.1063/1.4834075. [DOI] [PubMed] [Google Scholar]
  27. Li L.; Snyder J. C.; Pelaschier I. M.; Huang J.; Niranjan U.-N.; Duncan P.; Rupp M.; Müller K.-R.; Burke K. Understanding machine-learned density functionals. Int. J. Quantum Chem. 2016, 116, 819–833. 10.1002/qua.25040. [DOI] [Google Scholar]
  28. Hollingsworth J.; Li L.; Baker T. E.; Burke K. Can exact conditions improve machine-learned density functionals?. J. Chem. Phys. 2018, 148, 241743. 10.1063/1.5025668. [DOI] [PubMed] [Google Scholar]
  29. Li L.; Baker T. E.; White S. R.; Burke K. Pure density functional for strong correlation and the thermodynamic limit from machine learning. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 245129. 10.1103/PhysRevB.94.245129. [DOI] [Google Scholar]
  30. Yao K.; Parkhill J. Kinetic Energy of Hydrocarbons as a Function of Electron Density and Convolutional Neural Networks. J. Chem. Theory Comput. 2016, 12, 1139–1147. 10.1021/acs.jctc.5b01011. [DOI] [PubMed] [Google Scholar]
  31. Seino J.; Kageyama R.; Fujinami M.; Ikabata Y.; Nakai H. Semi-local machine-learned kinetic energy density functional with third-order gradients of electron density. J. Chem. Phys. 2018, 148, 241705. 10.1063/1.5007230. [DOI] [PubMed] [Google Scholar]
  32. Seino J.; Kageyama R.; Fujinami M.; Ikabata Y.; Nakai H. Semi-local machine-learned kinetic energy density functional demonstrating smooth potential energy curves. Chem. Phys. Lett. 2019, 734, 136732. 10.1016/j.cplett.2019.136732. [DOI] [Google Scholar]
  33. Fujinami M.; Kageyama R.; Seino J.; Ikabata Y.; Nakai H. Orbital-free density functional theory calculation applying semi-local machine-learned kinetic energy density functional and kinetic potential. Chem. Phys. Lett. 2020, 748, 137358. 10.1016/j.cplett.2020.137358. [DOI] [Google Scholar]
  34. Brockherde F.; Vogt L.; Li L.; Tuckerman M. E.; Burke K.; Müller K.-R. Bypassing the Kohn-Sham equations with machine learning. Nat. Commun. 2017, 8, 872. 10.1038/s41467-017-00839-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Alred J. M.; Bets K. V.; Xie Y.; Yakobson B. I. Machine learning electron density in sulfur crosslinked carbon nanotubes. Compos. Sci. Technol. 2018, 166, 3–9. 10.1016/j.compscitech.2018.03.035. [DOI] [Google Scholar]
  36. Grisafi A.; Fabrizio A.; Meyer B.; Wilkins D. M.; Corminboeuf C.; Ceriotti M. Transferable Machine-Learning Model of the Electron Density. ACS Cent. Sci. 2019, 5, 57–64. 10.1021/acscentsci.8b00551. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Fabrizio A.; Grisafi A.; Meyer B.; Ceriotti M.; Corminboeuf C. Electron density learning of non-covalent systems. Chem. Sci. 2019, 10, 9424–9432. 10.1039/C9SC02696G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Chandrasekaran A.; Kamal D.; Batra R.; Kim C.; Chen L.; Ramprasad R. Solving the electronic structure problem with machine learning. npj Comput. Mater. 2019, 5, 22. 10.1038/s41524-019-0162-7. [DOI] [Google Scholar]
  39. Fowler A. T.; Pickard C. J.; Elliott J. A. Managing uncertainty in data-derived densities to accelerate density functional theory. JPhys. Materials 2019, 2, 034001. 10.1088/2515-7639/ab0b4a. [DOI] [Google Scholar]
  40. Tozer D. J.; Ingamells V. E.; Handy N. C. Exchange-correlation potentials. J. Chem. Phys. 1996, 105, 9200–9213. 10.1063/1.472753. [DOI] [Google Scholar]
  41. Nagai R.; Akashi R.; Sasaki S.; Tsuneyuki S. Neural-network Kohn-Sham exchange-correlation potential and its out-of-training transferability. J. Chem. Phys. 2018, 148, 241737. 10.1063/1.5029279. [DOI] [PubMed] [Google Scholar]
  42. Schmidt J.; Benavides-Riveros C. L.; Marques M. A. L. Machine Learning the Physical Nonlocal Exchange-Correlation Functional of Density-Functional Theory. J. Phys. Chem. Lett. 2019, 10, 6425–6431. 10.1021/acs.jpclett.9b02422. [DOI] [PubMed] [Google Scholar]
  43. Zhou Y.; Wu J.; Chen S.; Chen G. Toward the Exact Exchange-Correlation Potential: A Three-Dimensional Convolutional Neural Network Construct. J. Phys. Chem. Lett. 2019, 10, 7264–7269. 10.1021/acs.jpclett.9b02838. [DOI] [PubMed] [Google Scholar]
  44. Nagai R.; Akashi R.; Sugino O. Completing density functional theory by machine learning hidden messages from molecules. npj Comput. Mater. 2020, 6, 43. 10.1038/s41524-020-0310-0. [DOI] [Google Scholar]
  45. Lin S.-C.; Oettel M. A classical density functional from machine learning and a convolutional neural network. SciPost Phys. 2019, 6, 025. 10.21468/SciPostPhys.6.2.025. [DOI] [Google Scholar]
  46. Ryczko K.; Strubbe D. A.; Tamblyn I. Deep learning and density-functional theory. Phys. Rev. A: At., Mol., Opt. Phys. 2019, 100, 022512. 10.1103/PhysRevA.100.022512. [DOI] [Google Scholar]
  47. Bhavsar R.; Ramakrishnan R. Machine learning modeling of Wigner intracule functionals for two electrons in one-dimension. J. Chem. Phys. 2019, 150, 144114. 10.1063/1.5089597. [DOI] [PubMed] [Google Scholar]
  48. Lin S.-C.; Martius G.; Oettel M. Analytical classical density functionals from an equation learning network. J. Chem. Phys. 2020, 152, 021102. 10.1063/1.5135919. [DOI] [PubMed] [Google Scholar]
  49. Press W. H.; Teukolsky S. A.; Vetterling W. T.; Flannery B. P.. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
  50. Hansen K.; Montavon G.; Biegler F.; Fazli S.; Rupp M.; Scheffler M.; von Lilienfeld O. A.; Tkatchenko A.; Müller K.-R. Assessment and Validation of Machine Learning Methods for Predicting Molecular Atomization Energies. J. Chem. Theory Comput. 2013, 9, 3404–3419. 10.1021/ct400195d. [DOI] [PubMed] [Google Scholar]
  51. Fukushima K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. 10.1007/BF00344251. [DOI] [PubMed] [Google Scholar]
  52. LeCun Y.; Bottou L.; Bengio Y.; Haffner P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. 10.1109/5.726791. [DOI] [Google Scholar]
  53. Goodfellow I.; Bengio Y.; Courville A.. Deep Learning; MIT Press: 2016; http://www.deeplearningbook.org. [Google Scholar]
  54. LeCun Y.; Bengio Y.; Hinton G. Deep learning. Nature 2015, 521, 436–444. 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
  55. Krizhevsky A.; Sutskever I.; Hinton G. E.. Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems 25 (NIPS 2012); Neural Information Processing Systems Foundation, Inc.: 2012; pp 1097–1105. [Google Scholar]
  56. He K.; Zhang X.; Ren S.; Sun J.. Deep Residual Learning for Image Recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: 2016; pp 770–778. [Google Scholar]
  57. Dugas C.; Bengio Y.; Bélisle F.; Nadeau C.; Garcia R. In Advances in Neural Information Processing Systems 13; Leen T. K., Dietterich T. G., Tresp V., Eds.; MIT Press: 2001; pp 472–478. [Google Scholar]
  58. Glorot X.; Bordes A.; Bengio Y.. Deep Sparse Rectifier Neural Networks. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA; Proceedings of Machine Learning Research: 2011; pp 315–323. [Google Scholar]
  59. Ioffe S.; Szegedy C.. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 2015; Proceedings of Machine Learning Research: 2015; pp 448–456. [Google Scholar]
  60. Chollet F.; et al. Keras; 2015. https://keras.io. [Google Scholar]
  61. Abadi M.; Agarwal A.; Barham P.; Brevdo E.; Chen Z.; Citro C.; Corrado G. S.; Davis A.; Dean J.; Devin M.; Ghemawat S.; Goodfellow I.; Harp A.; Irving G.; Isard M.; Jia Y.; Jozefowicz R.; Kaiser L.; Kudlur M.; Levenberg J.; Mané D.; Monga R.; Moore S.; Murray D.; Olah C.; Schuster M.; Shlens J.; Steiner B.; Sutskever I.; Talwar K.; Tucker P.; Vanhoucke V.; Vasudevan V.; Viégas F.; Vinyals O.; Warden P.; Wattenberg M.; Wicke M.; Yu Y.; Zheng X.. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems; 2015. http://tensorflow.org/. [Google Scholar]
  62. Glorot X.; Bengio Y.. Understanding the difficulty of training deep feedforward neural networks. Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics; Proceedings of Machine Learning Research: 2010; pp 249–256. [Google Scholar]
  63. LeCun Y. A.; Bottou L.; Orr G. B.; Müller K.-R. In Neural Networks: Tricks of the Trade; Montavon G., Orr G. B., Müller K.-R., Eds.; Springer: 1998; pp 9–48. [Google Scholar]
  64. Kingma D. P.; Ba J.. Adam: A Method for Stochastic Optimization. ArXiv (Machine Learning), 2014, 1412.6980. http://arxiv.org/abs/1412.6980.
  65. Snyder J. C.; Rupp M.; Müller K.-R.; Burke K. Nonlinear gradient denoising: Finding accurate extrema from inaccurate functional derivatives. Int. J. Quantum Chem. 2015, 115, 1102–1114. 10.1002/qua.24937. [DOI] [Google Scholar]
  66. Jiang H.; Yang W. Conjugate-gradient optimization method for orbital-free density functional calculations. J. Chem. Phys. 2004, 121, 2030–2036. 10.1063/1.1768163. [DOI] [PubMed] [Google Scholar]
  67. Denzel A.; Kästner J. Gaussian process regression for geometry optimization. J. Chem. Phys. 2018, 148, 094114. 10.1063/1.5017103. [DOI] [Google Scholar]
  68. Garijo del Río E.; Mortensen J. J.; Jacobsen K. W. Local Bayesian optimizer for atomic structures. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 100, 104103. 10.1103/PhysRevB.100.104103. [DOI] [Google Scholar]
  69. Meyer R.; Hauser A. W. Geometry optimization using Gaussian process regression in internal coordinate systems. J. Chem. Phys. 2020, 152, 084112. 10.1063/1.5144603. [DOI] [PubMed] [Google Scholar]
  70. Vapnik V.; Golowich S. E.; Smola A. J. In Advances in Neural Information Processing Systems 9; Mozer M. C., Jordan M. I., Petsche T., Eds.; MIT Press: 1997; pp 281–287. [Google Scholar]
  71. Drucker H.; Burges C. J. C.; Kaufman L.; Smola A. J.; Vapnik V. In Advances in Neural Information Processing Systems 9; Mozer M. C., Jordan M. I., Petsche T., Eds.; MIT Press; 1997; pp 155–161. [Google Scholar]
  72. Smola A. J.; Schölkopf B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. 10.1023/B:STCO.0000035301.49549.88. [DOI] [Google Scholar]
  73. Smola A. J.; Bartlett P. L. In Advances in Neural Information Processing Systems 13; Leen T. K., Dietterich T. G., Tresp V., Eds.; MIT Press: 2001; pp 619–625. [Google Scholar]
  74. Snelson E.; Ghahramani Z. In Advances in Neural Information Processing Systems 18; Weiss Y., Schölkopf B., Platt J. C., Eds.; MIT Press: 2006; pp 1257–1264. [Google Scholar]
  75. Titsias M.Variational Learning of Inducing Variables in Sparse Gaussian Processes. Proceedings of the Twelfth International Conference on Artificial Intelligence and Statistics, Clearwater Beach, FL, USA; Proceedings of Machine Learning Research: 2009; pp 567–574. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct0c00580_si_001.pdf (847.6KB, pdf)
ct0c00580_si_002.zip (9.3MB, zip)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES