Abstract
The mainstream interventions used during the 2014–2016 Ebola epidemic were contact tracing and case isolation. The Ebola outbreak in Nigeria that formed part of the 2014–2016 epidemic demonstrated the effectiveness of control interventions with a 100% hospitalization rate. Here, we aim to explicitly estimate the protective effect of case isolation, reconstructing the time events of onset of illness and hospitalization as well as the transmission network. We show that case isolation reduced the reproduction number and shortened the serial interval. Employing Bayesian inference with the Markov chain Monte Carlo method for parameter estimation and assuming that the reproduction number exponentially declines over time, the protective effect of case isolation was estimated to be 39.7% (95% credible interval: 2.4%–82.1%). The individual protective effect of case isolation was also estimated, showing that the effectiveness was dependent on the speed, i.e. the time from onset of illness to hospitalization.
Keywords: statistical model, effectiveness, epidemiology, emerging infectious disease, symptoms
1. Introduction
Ebola virus disease (EVD) is an acute severe human infection caused by the Ebola virus, which was first identified in Zaire in 1976 [1–3]. Once infected, the incubation period (i.e. the time from exposure to the onset of illness) ranges from 2 to 21 days, with a mean of 9.1 days and standard deviation (SD) of 7.3 days [4]. Clinical signs and symptoms include fever, headache, fatigue, diarrhoea, vomiting, stomach pain, unexplained bleeding or bruising and muscle pain. Because of its zoonotic nature, EVD is transmitted to the human population primarily from wildlife, notably fruit bats or primates [5]. Subsequently, human-to-human transmission occurs via direct contact with bodily fluids, with the handling of deceased victims (e.g. during burials) being a particularly significant channel for transmission. The largest ever epidemic of EVD occurred in West Africa during 2014–2016 and generated more than 28 600 confirmed, probable and suspected cases, with 11 325 deaths [6]. During the 2014–2016 epidemic, this highly fatal disease initially appeared in Guinea and then spread to neighbouring countries in West Africa, most notably Liberia and Sierra Leone. Besides the three countries most affected, small local outbreaks were reported in Nigeria and elsewhere [4], with the Nigerian outbreak notable for being contained swiftly.
With regards to possible countermeasures against EVD, no effective vaccines were available during the early stage of the 2014–2016 outbreak, while various clinical studies were conducted during the later period of the epidemic [7–9]. Thus, the mainstream interventions employed during the 2014–2016 epidemic were non-pharmaceutical and, for instance, included interventions at healthcare settings relying on contact tracing and case isolation, i.e. restricting the movement of contacts of diagnosed and infectious individuals, respectively. Including analysis of early transmission dynamics, epidemiological modelling studies were performed to assess the effectiveness of public health interventions that encompass hospital admission, case isolation and contact tracing [9–23]. Nigeria successfully contained its EVD outbreak by using contact tracing and case isolation, and, by means of published datasets on the outbreak in Lagos and Port Harcourt, Nigeria documented the epidemiological dynamics in detail [24,25].
Supporting the effectiveness of hospital admission and case isolation, a seminal paper by Kucharski et al. [17] demonstrated that building a substantial number of EVD treatment centres helped to curb the epidemiological dynamics of EVD, which actually became the mainstream of strategic global support for the control of EVD from 2014 to 2016. However, such evaluation has been restricted to a population-level impact (i.e. the effectiveness of building provisional hospitals in reducing the incidence of EVD) [10,15,16,18,23] or to evaluations that measured the overall transmission risk at the population level (e.g. household secondary attack risk [14]). To fully understand the protective effect of case isolation, it is important to infer the effect of preventing secondary transmission at an individual level.
As part of the post-epidemic evaluation, here we devised a novel statistical model to assess the protective effect of case isolation against EVD transmission. Addressing the biased nature of observed data associated with interventions (e.g. shortened time interval between onset of illness for primary and secondary cases), the present study aims to quantify the protective effect of case isolation from the transmission network data for EVD. Specifically, we explore a well-traced dataset on EVD from Nigeria in 2014.
2. Material and methods
2.1. Description of the EVD outbreak data from Nigeria
Two published datasets from the Nigerian EVD outbreak were used [24,25]. The outbreak involved 20 cases in total, including one imported case, with all cases being confirmed and reported during 17 July 2014 to 20 October 2014. After rapid detection of the index case, the government established an Emergency Operations Centre with an Incident Management System to coordinate a quick response and decision making using previous experience dealing with a polio outbreak in 2012 [25]. The index case potentially exposed 72 people and resulted in 894 traced contacts, of whom 891 were followed up [25]. Because of the concerted control efforts, the proportion of cases hospitalized in Nigeria was 100%, and here we aim to estimate the protective effect of the hospitalization. Based on contact tracing, the dates of onset of illness and hospitalization were recorded, and links between infectors and infectees were established. Throughout this article, the source of infection (i.e. infectors) is denoted as v. Additionally, exposure date is written as te, date of onset of illness is ts, hospitalization date is th and date of death is td.
In the present study, we combined the datasets from two independent publications [24,25]. In principle, the data we used were taken from Folarin et al. [24], but we also referred to another study [25] because of missing information. Electronic supplementary material, S1 describes the details of our procedure for reconstruction of the original data. Even with the merger of the data, the dataset was incomplete, specifically the dates t and sources of infection v. There was only one case where the source of infection was unknown. For the only case with an unknown infector, we summarized a list of six possible infectors. On the other hand, there were several cases in the outbreak for whom dates were missing, in particular dates of onset of illness ts and hospitalization th, making it necessary to impute dates. Specifically, there were 10 cases for whom both dates were known and 10 cases for whom either date was missing and hence dates had to be imputed.
2.2. Definition of time events and time intervals
Here, we reconstruct the epidemic tree using the partially observed dataset, applying similar methods to those published elsewhere [26,27], and subsequently estimate the protective effect of case isolation. For this reason, we first define several time events and intervals that would be central for reconstruction. Let i serve as an index of individuals. We have four different time events; namely, dates of exposure , onset of illness , hospitalization and death . As is usually the case, these timelines are incomplete (figure 1), but knowing the dates of onset of illness and hospitalization is essential to evaluate the protective effect of case isolation. For each case, there was at least one observed time event. From these time events, there are two types of time lag distributions, i.e. the incubation period τes and the time from onset of illness to hospitalization τsh. We calculate τxy = ty − tx, where the superscripts x and y represent e, s or h. Then, missing events are estimated using time lag distributions fl(τ), where τ is time lag and l is a time lag that bridges the observed and missing dates for each individual. To impute missing dates, we prioritized the use of the incubation period, because parameter estimates of the distribution were derived from a published study with a large sample size [4] (see electronic supplementary material, S2 and figure S1A). For example, for a case i, while the date of exposure is observed and the onset of illness is missing, the date of onset of illness is quantified from the date of exposure and the estimated incubation period τes, rather than working backwards and estimating from hospitalization . The corresponding probabilities are summarized in the electronic supplementary material, tables. Moreover, theoretical boundaries for quantifying missing dates are described in electronic supplementary material, S3.
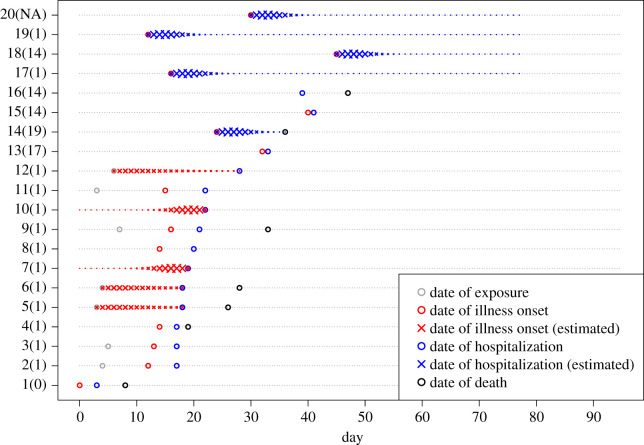
Figure 1.
The reconstructed timelines consisting of observed time events and the probability of reconstructed (missing) time events (n = 20 cases). The observed time events are denoted by open circles. The probabilities of reconstructed time events are measured by cross size. The grey, red, blue and black symbols denote the dates of exposure, onset of illness, hospitalization and death, respectively. The numbers shown on the y-axis represent case identity numbers (and associated infectors, where NA means that the infector is missing).
2.3. Model descriptions
Our modelling approach employs the so-called renewal equation,
| 2.1 |
where j(t) is the incidence (or the transient number of new infections) at calendar time t and A(t, τ) is the transmission rate per case at calendar time t and the infection age (i.e. the time since infection) τ, which may satisfy A(t, τ) = R(t)s(τ), where R(t) is the instantaneous reproduction number and s(τ) is the probability density function of the serial interval [28,29]. Note that the serial interval captures the transmissibility during illness progress, including time after death or recovery, but does not differ by individual severity, for example considering the high viral load in the later stage of illness or between survivors and non-survivors [19]. We supposed that cases who died were infectious and had infected others during burials while discharged cases would still be infectious via, for example, sexual intercourse (however, this was not observed in this outbreak).
Case isolation was performed during the course of the Nigerian epidemic. Throughout this study, we took the time of hospitalization as the time of case isolation, as the two occurred simultaneously in Nigeria. Let ε denote the relative reduction in the rate of secondary transmission in an isolated individual, quantified as a fixed parameter between 0 and 1, mirroring the protective effect of case isolation, where ε = 1 represents perfect isolation during the entire outbreak (i.e. no infection since the onset of isolation). Only during case isolation is the transmission rate assumed to be reduced to (1 − ε)A(τ, t) per isolated case, i.e.
| 2.2 |
The time lag from onset of illness to hospitalization varies by individual, and thus the reduction in the number of secondary transmissions at an individual level is described as
| 2.3 |
where S(τ) is the cumulative distribution function of the serial interval. We specifically consider εi for an individual i because secondary transmissions averted by case isolation vary with the time delay from onset of illness for the primary case. If a case was isolated immediately after the onset of illness, , then the individual effect is maximized, i.e. εi = ε (εi < ε otherwise).
Case isolation results in two different consequences for the transmission dynamics that are governed by the renewal equation. First, case isolation reduces secondary transmissions, i.e.
| 2.4 |
| 2.5 |
where represents the disease age (i.e. the time since onset of illness) at which the primary case i was isolated. Second, isolation shortens the serial interval distribution, i.e.
| 2.6 |
| 2.7 |
where is the reduction effect of the primary case vi. Hereafter, we refer to s(τ) in the absence of case isolation as the unbiased serial interval, while the observed time interval in the presence of case isolation is referred to as the biased serial interval. Using the reduced reproduction number and the distribution of shortened serial interval , we intend to estimate the protective effect of case isolation ε.
2.4. Source of infection
In terms of the transmission tree, the source of infection was unknown for one case, while for all other cases it was known. For the case with an unknown source of infection (case 20), six possible candidates for the primary case existed, and a probabilistic reconstruction was conducted [30,31] (see electronic supplementary material, S4).
2.5. Likelihood functions
We first suppose that all data D are observed. In this model, the likelihood function denoted as L(θ|D) consists of two parts: the number of observed secondary transmissions Lr(θ|D) and the length of observed serial intervals Ls(θ|D),
| 2.8 |
The former consists of all reported cases, while the latter consists of only non-imported cases. Only successful contacts are included as we focus on the impact of case isolation instead of quarantine. In practice, unsuccessful contacts are not available because of lacking contact tracing information over time.
The observed secondary case number ri produced by each case i is assumed to follow a distribution p with the same mean value as the reproduction number at onset of illness. Three alternative distributions exist: geometric, Poisson and negative binomial. The likelihood of observing secondary case numbers is written as
| 2.9 |
We assume an exponential decreasing dynamic in the calendar time as R(t) = R0 e−δt, where R0 is the reproduction number at time zero and δ is the exponential rate. The simple exponential decline in R(t) has been empirically shown to fit better than the constant reproduction number in other outbreak case studies [32,33]. In this study, we assume all cases in both locations (Lagos and Port Harcourt) share the same R(t) universally in the country.
The observed serial intervals are assumed to follow a distribution , in which the unbiased distribution s(τ) follows two alternative distributions, gamma and Weibull (see electronic supplementary material, S5). The likelihood is written as
| 2.10 |
where is the serial interval from the onset of illness in the primary case vi to that in the secondary case i. Owing to the assumption of a closed population, all cases except imported cases D1 are included in calculating the serial intervals.
None of the time events were fully observed, but instead were estimated using maximum-likelihood estimation. See the electronic supplementary material for further details on the reconstruction of time events.
2.6. Bayesian parameter estimation
Bayesian inference with Markov chain Monte Carlo (MCMC) was adopted to obtain parameter estimates. This approach resembles the data augmentation strategy used elsewhere to estimate the source of infection during MERS-CoV transmission [32]. The prior distribution was assumed to be non-informative and flat. Because of the difficulties in simultaneous direct sampling of the posterior distribution of parameters and the source of infection, the distribution was approximated using the Metropolis–Hastings Markov chain Monte Carlo (MH-MCMC) algorithm. In each MH-MCMC iteration step, parameters were updated and then the source of infection was sampled given the proposed parameters. To improve mixing, the proposed distribution of the infector was not flat, as assumed for the prior distribution of other parameters, but was weighted according to the transmission probability of each of the six listed possible infectors (see electronic supplementary material, S1 and S4).
The simulation using the MH-MCMC algorithm was performed by 1 000 000 iterations with thinning of every 500th sample to reduce autocorrelation. Despite visually converged chains suggesting that the samples are well mixed, the sampling was replicated in four independent chains with a burn-in length of half in each chain [34]. A total of 4000 samples represented the posterior distribution. The algorithm was implemented in R v. 3.4.3 (Kite-Eating Tree) on Mac OSX and R v. 3.4.4 (Someone to Lean On) on Linux (available from: https://github.com/imlouischan/ebola-ng).
2.7. Model selection and alternative time-dependent assumption
Regarding the combinations of alternative distributions used in observing the number of secondary cases (i.e. Poisson, geometric or negative binomial) and unbiased serial interval (i.e. gamma and Weibull), six possible combinations existed. The best combination was selected according to three criteria, namely the Akaike information criterion (AIC), the Bayesian information criterion (BIC) and model posterior distribution. We obtain a better model when AIC or BIC are lower. AIC and BIC are point estimators that take the best sample among 4000. By contrast, we obtain a better model with a higher model posterior. Determining the model posterior given a uniform prior is as simple as calculating the weight of marginal likelihoods. The marginal likelihoods are calculated using the posterior harmonic mean (PHM) estimator [35].
Besides comparing six possible combinations for Lr and Ls, we also evaluated the impact of time dependence in the reproduction number on our estimate of the protective effect of case isolation. That is, identifying the best-fitted combination, we have additionally compared the reproduction number with and without exponential decline as a function of time. In the time-independent model, we set δ = 0.
3. Results
The time from onset of illness to hospitalization was fitted better by Weibull than by gamma distribution (electronic supplementary material, figure S1B), yielding estimates of the mean (and s.d.) at 4.0 (2.3) days that we used to reconstruct the timeline. Figure 1 shows the reconstructed timelines consisting of both the observed time events and the probabilistically reconstructed (missing) time events.
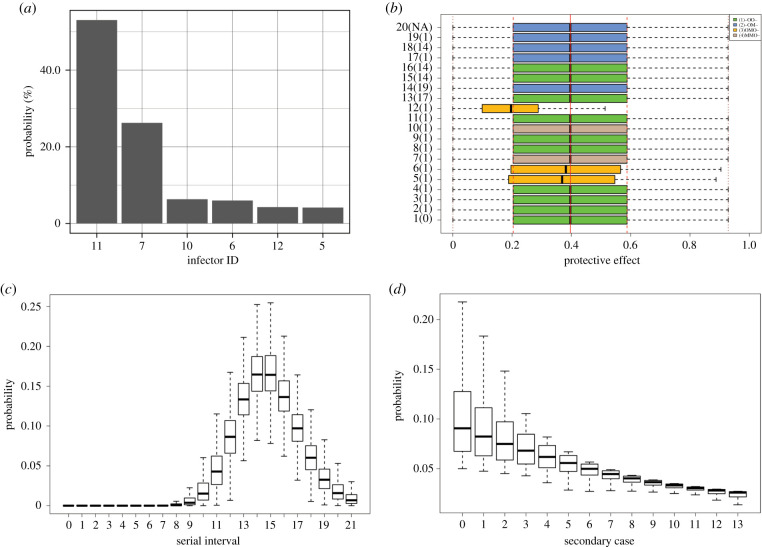
Employing Bayesian inference with MCMC, all three criteria (i.e. AIC, BIC and model posterior) indicated that the best model matches our assumptions, namely that in which the number of secondary cases per primary cases is geometrically distributed and the unbiased serial interval is gamma-distributed (table 1). The corresponding model posterior is 52.0%. The second-best model is the one with alternative assumptions employing negative binomial and gamma distribution. Although this runner-up was estimated with the lowest log-likelihood of −64.4, it is not favoured according to the selection criteria because of a higher number of estimated parameters. There was one unobserved branch of the transmission tree, and the possible primary case associated with this branch was probabilistically identified and statistically ranked by the posterior distribution (figure 2a). The most likely primary case of case 20 was case 11 with probability 53.1%, followed by case 7 with 26.3% and case 10 with 6.3%.
Table 1.
Model comparison employing different distributions. Six possible models are compared using three different criterion values. AIC and BIC were calculated using the maximum values of log-likelihood among MCMC samples. Model posteriors were calculated using marginal likelihoods.
| secondary cases | serial interval | AIC | BIC | posterior (%) | |
|---|---|---|---|---|---|
| geometric | gamma | −65.3 | 142.6 | 148.6 | 52.0 |
| geometric | Weibull | −67.3 | 146.6 | 152.6 | 19.7 |
| Poisson | gamma | −67.9 | 147.9 | 153.9 | 4.5 |
| Poisson | Weibull | −70.1 | 152.1 | 158.1 | 0.8 |
| negative binomial | gamma | −64.4 | 142.8 | 149.8 | 20.7 |
| negative binomial | Weibull | −66.4 | 146.8 | 153.7 | 2.5 |
Figure 2.
(a) The posterior distribution of the primary case of case 20. Case 11 was considered the most likely primary case with a probability of 53.1%, followed by case 7 with 26.3% and case 10 with 6.3%. (b) The posterior distribution of the individual protective effect of case isolation, εi, for each case. The green, yellow, blue and brown boxes show four observed patterns. O represents observed, M indicates missing and - indicates unused (i.e. observed or missing); the order of events follows the dates of exposure, onset of illness, hospitalization and death. The third pattern in yellow showed significantly lower individual protective effect than the other three patterns. The red solid, dashed and dotted lines show, respectively, the mean, interquartile range, and minimum and maximum of the protective effect of case isolation without delay, ε. (c) The posterior distribution of unbiased serial intervals s(τ) with mean at 15.3 (95% CI: 14.2–16.6) and s.d. at 2.3 (95% CI: 1.6–3.5) days. The unbiased distribution represents the situation in the absence of case isolation. The shape and scale parameters of the gamma distribution were estimated as 45.0 (95% CI: 19.6–92.0) and s.d. at 0.3 (95% CI: 0.2–0.8), respectively. (d) The posterior distribution of the secondary case number per primary case p(r), given the mean as the reproduction number at time zero, which was estimated to be 10.0 (95% CI: 3.0–18.5). The distributions shown in the figure were derived from the best-fit model that employs geometric and gamma distributions, respectively, to describe the distributions of the observed number of secondary cases per primary case and the unbiased serial interval. The posterior distributions are shown using black boxes, ranging from the lower to the upper quartiles along with the median.
The individual protective effect of case isolation εi and the protective effect without delay in case isolation ε are summarized in figure 2b. The mean of ε was estimated as 39.7% (95% credible interval (CI): 2.4%–82.1%). Smaller estimates of the individual protective effect were observed in cases 5, 6 and 12, for whom the date of onset of illness was reconstructed using the incubation period distribution (figure 2b), while the individual effect was similarly distributed to ε (i.e. without time delay). Given the posterior shape and scale parameters of the gamma distribution, figure 2c shows the unbiased serial interval distribution (i.e. in the absence of case isolation). The mean and s.d. were 15.3 (95% CI: 14.2–16.6) and 2.3 (95% CI: 1.6–3.5) days. The distribution of the secondary case number per primary case, the mean of which is the reproduction number at time zero, is shown in figure 2d. Assuming that the reproduction number declined over time, the mean at time zero and the rate of exponential decline were estimated to be 10.0 (95% CI: 3.0–18.5) and 0.14 (95% CI: 0.07–0.23), respectively.
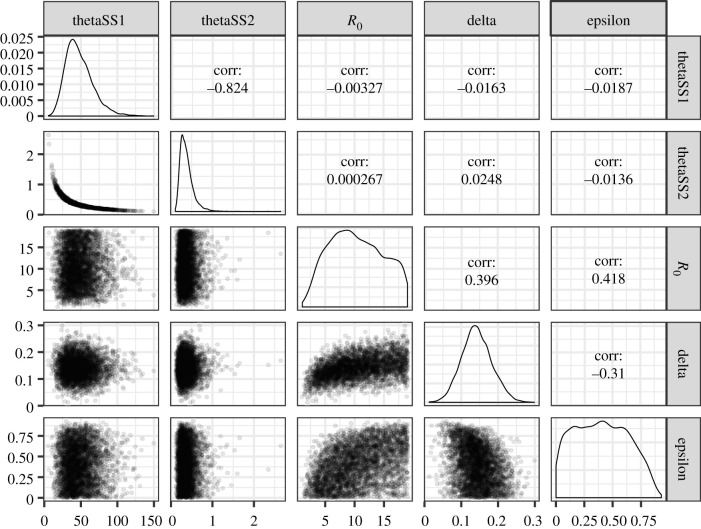
Figure 3 shows pairwise distributions of the parameter posterior and the marginals. There are two interesting pairs of parameters. First, the shape and scale parameters of the unbiased serial interval distribution are strongly negatively correlated and exhibit a banana-shaped distribution. Second, a positive correlation was observed between the reproduction number at time zero R0 and the protective effect without time delay ε, with the correlation coefficient being 0.418.
Figure 3.
The posterior distributions of parameters, derived from the best-fit model that employs geometric and gamma distributions, respectively, to describe the distributions of the observed number of secondary cases per primary case and the unbiased serial interval. The parameters include the shape (thetaSS1) and scale (thetaSS2) of the unbiased serial interval, the reproduction number at time zero (R0), the exponentially decreasing rate of secondary transmission (delta) and the protective effect of case isolation without time delay (epsilon). The diagonal plots show the marginal distributions. The lower diagonal reflects dependence between parameters by scatter plots. The upper diagonal indicates correlation between parameters.
Sensitivity analysis was performed to examine the dependence of the estimated protective effect of case isolation without time delay ε to variable assumption on the reproduction number. Specifically, we compared two scenarios, involving time-dependent and constant reproduction numbers, using , where we assumed δ > 0 for the time-dependent model and δ = 0 for the constant model. Table 2 and figure 4 show the comparison of the posterior parameter distribution between these two model scenarios. Using two models, the shape and scale parameters of the unbiased serial interval and the identified primary case of case 20 were similarly distributed, but exert a strong negative effect on the distributions of the reproduction number R0 and protective effect of case isolation without time delay ε. With δ = 0, the constant reproduction number was estimated as 3.2 (95% CI: 0.8–16.4), and the mean protective effect of case isolation was 67.2% (95% CI: 3.7%–94.2%). Nevertheless, all three model comparison criteria indicated that δ > 0 fits better than δ = 0. The lower panel of figure 4 illustrates the estimated reproduction number over time, of which the declining mean crosses the criticality of 1 on day 16.
Table 2.
The parameters estimated in two scenarios. Scenarios 1 and 2 represent that the reproduction number decreased exponentially and remained constant over time, respectively. The parameters include the protective effect of case isolation without time delay (epsilon), the reproduction number at time zero (R0), the exponentially decreasing rate of secondary transmission (delta) and the shape (thetaSS1) and scale (thetaSS2) of the unbiased serial interval. The corresponding mean and s.d of the unbiased serial interval s(τ) are included.
| scenario 1 | scenario 2 | |
|---|---|---|
| parameters | mean (95% CI) | mean (95% CI) |
| epsilon (%) | 39.7 (2.4–82.1) | 67.2 (3.7–94.2) |
| R0 | 10.0 (3.0–18.5) | 3.2 (0.8–16.4) |
| delta (day− 1) | 0.14 (0.07-0.23) | 0 |
| thetaSS1 | 45.0 (19.5–92.0) | 44.6 (18.2-88.2) |
| thetaSS2 | 0.3 (0.2–0.8) | 0.3 (0.2–0.9) |
| s(τ) mean (day) | 15.3 (14.2–16.6) | 15.3 (14.2, 16.6) |
| s(τ) s.d. (day) | 2.3 (1.6–3.5) | 2.3 (1.6, 3.6) |
Figure 4.
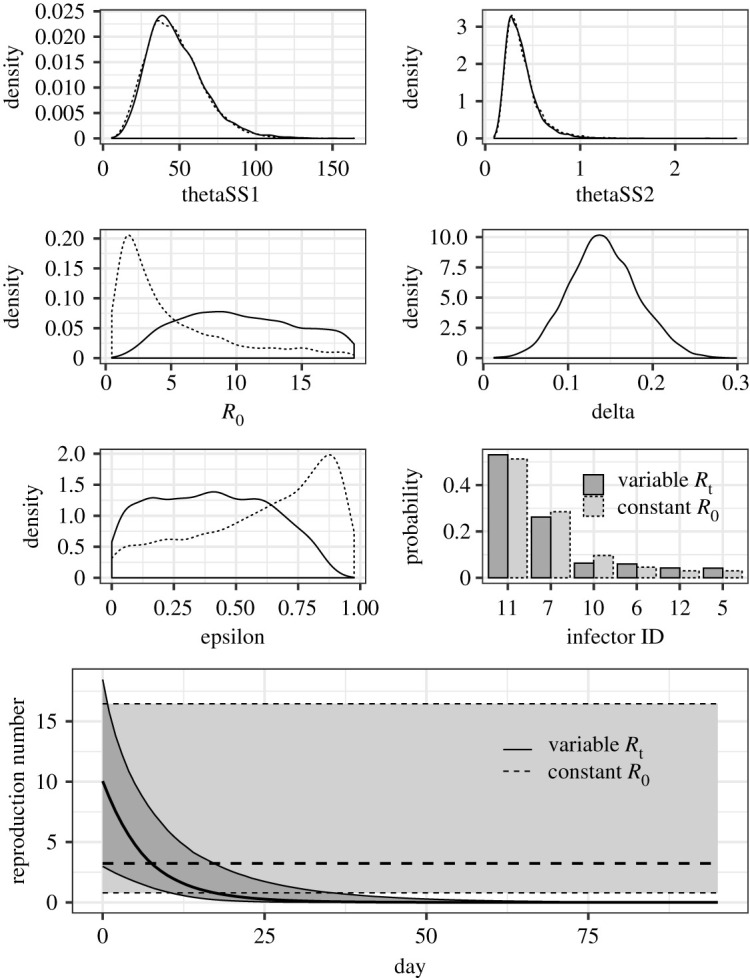
The marginal parameter posterior distributions of two different model scenarios. The solid and dashed lines show the model scenario in which the reproduction number decreased exponentially and remained constant over time, respectively. The parameters include the shape (thetaSS1) and scale (thetaSS2) parameters of the unbiased serial interval, the reproduction number at time zero (R0), the exponentially decreasing rate of the reproduction number (delta), the protective effect of case isolation without time delay (epsilon) and an identified primary case of case 20. The lower panel shows the estimated reproduction number during the outbreak. The thicker lines show the mean and the grey regions represent the 95% CI.
4. Discussion
The present study estimated the protective effect of case isolation during the 2014 EVD outbreak in Nigeria, using partially observed contact tracing data for a total of 20 cases. We developed a statistical model that features the time interval between onset of illness for the primary case and the secondary case and also the number of secondary transmissions per primary case, while addressing problems of missing data for time events (e.g. date of hospitalization) and partially reconstructing the transmission dynamics. We have shown that the observed serial intervals are likely to be shorter than the unbiased serial intervals, and also that case isolation probably resulted in the observed number of secondary cases per single primary case being smaller than it would otherwise have been. Assuming that the effective reproduction number exponentially declines over time, the protective effect of case isolation in reducing secondary transmission was estimated at 39.7% (95% CI: 2.4%–82.1%), successfully quantifying the contribution of case isolation to the transmission dynamics in Nigeria during 2014. While the theoretical aspects of study designs for determining vaccine effect have been broadly discussed [36], to our knowledge, the present study is the first to apply the proposed model to EVD data with reconstruction of both time events and transmission network.
The most important take-home message from the present study is that the effectiveness of case isolation could be explicitly estimated from observational data, provided that the transmission network is known (at least partially) as are the dates of onset of illness and/or hospitalization. The estimated protective effect ε is interpreted as a relative reduction of the secondary transmission rate, representing the transient reduction in the frequency of secondary transmission. Since the delay from onset of illness to case isolation varies by case, we have also estimated the protective effect of each individual εi, where its maximum value ε is considered as the protective effect without time delay. From the formulation used for this estimation, we have shown that the individual protective effect depends on the rapidity of case finding and public health response, as well as the individual observed patterns of data in our model. However, the estimated ε varied greatly according to model assumptions regarding the time dependence of the reproduction number. While the mean value of ε was 39.7%, with an exponentially declining reproduction number, the value with a stationary (i.e. time-independent) reproduction number reached 67.2%. This refers to the relatively lower ε due to naturally decreasing secondary cases in the first assumption, while the protect effect is required to be higher in order to eliminate the disease given the constant R0 higher than 1 in the second assumption. In both assumptions, the uncertainty bound was very broad. Although all three model selection criteria favoured the exponentially declining reproduction number (potentially due to a super-spreading event by the index case), the discrepancy here is caused by the existence of assumptions that are not fully supported, and, thus, the protective effect of case isolation still involves a degree of uncertainty. In Nigeria, contact tracing and case isolation were the mainstream interventions in 2014, and in hospitals standard precautions were practised by healthcare professionals [24,25]. The present study indicates that, although the uncertainty bound remains wide, the practice of case isolation has successfully reduced secondary transmissions by 40–67%.
Additionally, it should be noted that the proposed model also estimated the unbiased reproduction number, i.e. the reproduction number without case isolation. Assuming an exponential decline, the reproduction number at time zero was estimated at 10.0 (95% CI: 3.0–18.5), while under an assumption of stationary transmissibility the reproduction number at time zero was estimated to be about one-third of this level, i.e. 3.2 (95% CI: 0.8–16.4). The sample mean of observed (and biased) number of secondary transmissions was 0.9 (s.d. 3.0). These cannot be directly compared against the basic reproduction number estimates, i.e. ranging from about 1.3 to 2.6, from a larger scale epidemic [11,23,37,38], but at least our estimates demonstrate that the unbiased reproduction number that adjusts the protective effect of case isolation can exceed the series of estimates derived from models that did not explicitly take into account the impact of case isolation.
We have also estimated the unbiased length of the serial interval, with the estimated mean at 15.3 (95% CI: 14.2–16.6) days and s.d. at 2.3 (95% CI: 1.6–3.5) days. The sample mean and s.d. of the serial interval in the presence of case isolation were 14.8 and 2.5 days, respectively, indicating that although the mean was not greatly shortened it was at least shortened by half a day (electronic supplementary material, figure S2). The two-week interval resembled the published estimates [37,38]. Two technical points should be further discussed. First, as mentioned in the electronic supplementary material, we adopted published estimates of the incubation period distribution from a larger epidemic [4]. Their use has led to some differences among individuals in protective effects (i.e. figure 2b) that reflect their observation patterns. The reconstruction of dates of the onset of illness using the incubation period (type 3 in electronic supplementary material, table S1) and the reconstruction using the time from onset of illness to hospitalization (types 2 and 4 in electronic supplementary material, table S1) have different characteristics because of the distributions from different samples and outbreaks. However, we believe that the way we addressed those distributions might be the best practice, simultaneously addressing issues of limited sample size and effectively using the available dataset. Second, individual variations existed in the number of secondary transmissions. In fact, the index case was the main patient who infected 13 individuals and became a super-spreader. The above-mentioned large difference between time-dependent and time-independent reproduction numbers can be partially explained by the existence of this index case (figure 4, lower panel). It has also contributed to forming a heavy tail in the distribution of secondary transmissions. However, dealing with the trade-off between the goodness of fit and simplicity, geometric distribution is more favoured than negative binomial distribution.
The present study has various limitations that must be discussed. First, our model assumed that infectiousness starts from the date of onset of illness, which is not broadly applicable, e.g. HIV/AIDS. Second, strictly speaking, serial interval and generation time are used interchangeably in many studies, but the present study explicitly handled the time of onset of illness and strictly used the serial interval. Third, the serial interval distribution was assumed to be stationary, which means it is independent of calendar time throughout the outbreak. On the other hand, the reproduction number was allowed to vary with calendar time to capture the transmission dynamics. Strictly speaking, both would vary with time and infection age. Fourth, the application of the model to this dataset from Nigeria was limited by a few missing pieces of information, namely in some cases either the date of onset of illness or hospitalization of each individual was not observed. The time event reconstruction was relatively simple and the reconstruction was limited to one dimension. However, the surveillance data of individuals during unexpected outbreaks are often imperfectly collected and require complicated reconstruction. In the future, we plan to extend our modelling approach by applying it to datasets with higher dimensional imputations.
In conclusion, the present study has shown that the case isolation of the 2014 EVD outbreak in Nigeria was effective, and the public health interventions by the Nigerian government should be commended for successfully controlling the outbreak. Accounting for the protective effect of case isolation, we demonstrate that the observed number of secondary cases per primary case and serial interval were, respectively, reduced and shortened.
Supplementary Material
Acknowledgements
We thank the Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.
Data accessibility
Additional data are available in the electronic supplementary material.
Authors' contributions
H.N. conceived the principle of the estimation method, and Y.H.C. formulated the reconstruction method of the transmission network and revised the total likelihood. Y.H.C. arranged the data and carried out Bayesian estimation, and H.N. validated the statistical analyses. Y.H.C. drafted an early version of the manuscript and Y.H.C and H.N. jointly revised the manuscript. Both authors approved the final version of the manuscript.
Competing interests
We declare we have no competing interest.
Funding
Y.H.C. thanks the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, for his PhD scholarship programme. H.N. received funding from the Japan Agency for Medical Research and Development (AMED) (grant no. JP18fk0108050); the Japan Society for the Promotion of Science (JSPS) KAKENHI (grant nos. H.N.: 17H04701, 17H05808, 18H04895 and 19H01074), the Inamori Foundation, and the Japan Science and Technology Agency (JST) CREST program (grant no. JPMJCR1413).
References
- 1.Bowen ET, Platt GS, Lloyd G, Baskerville A, Harris WJ, Vella EE. 1977. Viral haemorrhagic fever in southern Sudan and northern Zaire. Preliminary studies on the aetiological agent. Lancet 309, 571–573. ( 10.1016/S0140-6736(77)92001-3) [DOI] [PubMed] [Google Scholar]
- 2.Pattyn S, Van Der Groen G, Jacob W, Piot P, Courteille G. 1977. Isolation and partial characterisation of a new virus causing acute haemorrhagic fever in Zaire. Lancet 1, 569–571.65661 [Google Scholar]
- 3.Pattyn SW, Jacob W, Van der Groen G, Piot P, Courteille G. 1977. Isolation of Marburg-like virus from a case of haemorrhagic fever in Zaire. Lancet 309, 573–574. ( 10.1016/S0140-6736(77)92002-5) [DOI] [PubMed] [Google Scholar]
- 4.WHO Ebola Response Team. 2014. Ebola virus disease in West Africa—the first 9 months of the epidemic and forward projections. N. Engl. J. Med. 2014, 1481–1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ponce L, Kinoshita R, Nishiura H. 2019. Exploring the human-animal interface of Ebola virus disease outbreaks. Math. Biosci. Eng. 16, 3130–3143. ( 10.3934/mbe.2019155) [DOI] [PubMed] [Google Scholar]
- 6.Centers for Disease Control and Prevention. 2019 2014–2016 Ebola outbreak in West Africa. See https://www.cdc.gov/vhf/ebola/history/2014-2016-outbreak/index.html.
- 7.Henao-Restrepo AM. et al. 2015. Efficacy interim results from the Guinea ring vaccination cluster-randomised trial. Lancet 386, 857–866. ( 10.1016/S0140-6736(15)61117-5) [DOI] [PubMed] [Google Scholar]
- 8.Henao-Restrepo AM. et al. 2017. Efficacy final results from the Guinea ring vaccination, open-label, cluster-randomised trial (Ebola Ça Suffit!). Lancet 389, 505–518. ( 10.1016/S0140-6736(16)32621-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kucharski AJ, Eggo RM, Watson CH, Camacho A, Funk S, Edmunds WJ. 2016. Effectiveness of ring vaccination as control strategy for Ebola virus disease. Emerg. Infect. Dis. 22, 105–108. ( 10.3201/eid2201.151410) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pandey A, Atkins KE, Medlock J, Wenzel N, Townsend JP, Childs JE, Nyenswah TG, Ndeffo-Mbah ML, Galvani AP. 2014. Strategies for containing Ebola in West Africa. Science 346, 991–995. ( 10.1126/science.1260612) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shen M, Xiao Y, Rong L. 2015. Modeling the effect of comprehensive interventions on Ebola virus transmission. Sci. Rep. 5, 15818 ( 10.1038/srep15818) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Drake JM, Kaul RB, Alexander LW, O’Regan SM, Kramer AM, Pulliam JT, Ferrari MJ, Park AW. 2015. Ebola cases and health system demand in Liberia. PLoS Biol. 13, e1002056 ( 10.1371/journal.pbio.1002056) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chowell D, Castillo-Chavez C, Krishna S, Qiu X, Anderson KS. 2015. Modelling the effect of early detection of Ebola. Lancet Infect. Dis. 15, 148–149. ( 10.1016/S1473-3099(14)71084-9) [DOI] [PubMed] [Google Scholar]
- 14.Fang LQ. et al. 2016. Transmission dynamics of Ebola virus disease and intervention effectiveness in Sierra Leone. Proc. Natl Acad. Sci. USA 113, 4488–4493. ( 10.1073/pnas.1518587113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kucharski AJ, Camacho A, Flasche S, Glover RE, Edmunds WJ, Funk S. 2015. Measuring the impact of Ebola control measures in Sierra Leone. Proc. Natl Acad. Sci. USA 112, 14366–14371. ( 10.1073/pnas.1508814112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lokuge K. et al. 2016. Successful control of Ebola virus disease: analysis of service based data from rural Sierra Leone. PLoS Negl. Trop. Dis. 10, e0004498 ( 10.1371/journal.pntd.0004498) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kucharski AJ. et al. 2015. Evaluation of the benefits and risks of introducing Ebola community care centers, Sierra Leone. Emerg. Infect. Dis. 21, 393–399. ( 10.3201/eid2103.141892) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Merler S. et al. 2015. Spatiotemporal spread of the 2014 outbreak of Ebola virus disease in Liberia and the effectiveness of non-pharmaceutical interventions: a computational modelling analysis. Lancet Infect. Dis. 15, 204–211. ( 10.1016/S1473-3099(14)71074-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yamin D, Gertler S, Ndeffo-Mbah ML, Skrip LA, Fallah M, Nyenswah TG, Altice FL, Galvani AP. 2015. Effect of Ebola progression on transmission and control in Liberia. Ann. Intern. Med. 162, 11–17. ( 10.7326/M14-2255) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rivers CM, Lofgren ET, Marathe M, Eubank S, Lewis BL. 2014. Modeling the impact of interventions on an epidemic of Ebola in Sierra Leone and Liberia. PLoS Curr. 6 ( 10.1371/currents.outbreaks.4d41fe5d6c05e9df30ddce33c66d084c) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Webb G, Browne C, Huo X, Seydi O, Seydi M, Magal P. 2015. A model of the 2014 Ebola epidemic in West Africa with contact tracing. PLoS Curr. 7 ( 10.1371/currents.outbreaks.846b2a31ef37018b7d1126a9c8adf22a) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Camacho A. et al. 2015. Temporal changes in Ebola transmission in Sierra Leone and implications for control requirements: a real-time modelling study. PLoS Curr. 7 ( 10.1371/currents.outbreaks.406ae55e83ec0b5193e30856b9235ed2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lewnard JA, Mbah ML, Alfaro-Murillo JA, Altice FL, Bawo L, Nyenswah TG, Galvani AP. 2014. Dynamics and control of Ebola virus transmission in Montserrado, Liberia: a mathematical modelling analysis. Lancet Infect. Dis. 14, 1189–1195. ( 10.1016/S1473-3099(14)70995-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Folarin OA. et al. 2016. Ebola virus epidemiology and evolution in Nigeria. J. Infect. Dis. 214(suppl_3), S102–S109. ( 10.1093/infdis/jiw190) jiw190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shuaib F. et al. 2014. Ebola virus disease outbreak—Nigeria, July–September 2014. MMWR Morb. Mortal. Wkly Rep. 63, 867–72. [PMC free article] [PubMed] [Google Scholar]
- 26.Eichner M, Dietz K. 2003. Transmission potential of smallpox: estimates based on detailed data from an outbreak. Am. J. Epidemiol. 158, 110–117. ( 10.1093/aje/kwg103) [DOI] [PubMed] [Google Scholar]
- 27.Stockdale JE, Kypraios T, O’Neill PD. 2017. Modelling and Bayesian analysis of the Abakaliki smallpox data. Epidemics 19, 13–23. ( 10.1016/j.epidem.2016.11.005) [DOI] [PubMed] [Google Scholar]
- 28.Fraser C. 2007. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE 2, e758 ( 10.1371/journal.pone.0000758) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chowell G, Nishiura H. 2008. Quantifying the transmission potential of pandemic influenza. Phys. Life Rev. 5, 50–77. ( 10.1016/j.plrev.2007.12.001) [DOI] [Google Scholar]
- 30.Wallinga J, Teunis P. 2004. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol. 160, 509–516. ( 10.1093/aje/kwh255) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hens N, Calatayud L, Kurkela S, Tamme T, Wallinga J. 2012. Robust reconstruction and analysis of outbreak data: influenza A(H1N1)v transmission in a school-based population. Am. J. Epidemiol. 176, 196–203. kws006 ( 10.1093/aje/kws006) [DOI] [PubMed] [Google Scholar]
- 32.Cauchemez S. 2016. et al. Unraveling the drivers of MERS-CoV transmission. Proc. Natl Acad. Sci. USA 113, 9081–9086. ( 10.1073/pnas.1519235113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nishiura H, Schwehm M, Kakehashi M, Eichner M. 2006. Transmission potential of primary pneumonic plague: time inhomogeneous evaluation based on historical documents of the transmission network. J. Epidemiol. Community Health 60, 640–645. ( 10.1136/jech.2005.042424) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. 2013. Bayesian data analysis. Boca Raton, FL: CRC Press. [Google Scholar]
- 35.Vyshemirsky V, Girolami MA. 2007. Bayesian ranking of biochemical system models. Bioinformatics 24, 833–839. ( 10.1093/bioinformatics/btm607) [DOI] [PubMed] [Google Scholar]
- 36.Halloran ME, Longini IM, Struchiner CJ, Longini IM. 2010. Design and analysis of vaccine studies, vol. 18 New York, NY: Springer. [Google Scholar]
- 37.Chowell G, Nishiura H. 2014. Transmission dynamics and control of Ebola virus disease (EVD): a review. BMC Med. 12, 196 ( 10.1186/s12916-014-0196-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nishiura H, Chowell G. 2015. Theoretical perspectives on the infectiousness of Ebola virus disease. Theor. Biol. Med. Modell. 12, 1 ( 10.1186/1742-4682-12-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Additional data are available in the electronic supplementary material.