Populations of in silico myocytes and tissues reveal synergy of multiatrial‐predominant K⁺‐current block in atrial fibrillation

Abstract

Background and Purpose

Pharmacotherapy of atrial fibrillation (AF), the most common cardiac arrhythmia, remains unsatisfactory due to low efficacy and safety concerns. New therapeutic strategies target atrial‐predominant ion‐channels and involve multichannel block (poly)therapy. As AF is characterized by rapid and irregular atrial activations, compounds displaying potent antiarrhythmic effects at fast and minimal effects at slow rates are desirable. We present a novel systems pharmacology framework to quantitatively evaluate synergistic anti‐AF effects of combined block of multiple atrial‐predominant K⁺ currents (ultra‐rapid delayed rectifier K⁺ current, I_Kur, small conductance Ca²⁺‐activated K⁺ current, I_KCa, K_2P3.1 2‐pore‐domain K⁺ current, I_K2P) in AF.

Experimental Approach

We constructed experimentally calibrated populations of virtual atrial myocyte models in normal sinus rhythm and AF‐remodelled conditions using two distinct, well‐established atrial models. Sensitivity analyses on our atrial populations was used to investigate the rate dependence of action potential duration (APD) changes due to blocking I_Kur, I_K2P or I_KCa and interactions caused by blocking of these currents in modulating APD. Block was simulated in both single myocytes and one‐dimensional tissue strands to confirm insights from the sensitivity analyses and examine anti‐arrhythmic effects of multi‐atrial‐predominant K⁺ current block in single cells and coupled tissue.

Key Results

In both virtual atrial myocytes and tissues, multiple atrial‐predominant K⁺‐current block promoted favourable positive rate‐dependent APD prolongation and displayed positive rate‐dependent synergy, that is, increasing synergistic antiarrhythmic effects at fast pacing versus slow rates.

Conclusion and Implications

Simultaneous block of multiple atrial‐predominant K⁺ currents may be a valuable antiarrhythmic pharmacotherapeutic strategy for AF.

Abbreviations

1D

one dimensional

AF

atrial fibrillation

AP

action potential

APD_xx

action potential duration at xx% of repolarization

B

coefficient

CV

conduction velocity

CZ

Colman–Zhang model

ERP

effective refractory period

GB

Grandi–Bers model

I_K,Ach

the ACh activated inward rectifier K⁺ current

I_K2P

the K_2P3.1 2‐pore‐domain K⁺ current

I_KCa

the small conductance Ca²⁺‐activated K⁺ current

I_Kr

the rapid delayed rectifier K⁺ current

I_Kur

the ultra‐rapid delayed rectifier K⁺ current

I_Na

fast Na⁺ current

nSR

normal sinus rhythm

RD

rate dependence

RMP

resting membrane potential

RR

repolarization reserve

WL

wavelength

What is already known

• Current pharmacological therapeutic strategies for atrial fibrillation (AF) remain unsatisfactory.

• Atrial‐predominant current block has been proposed as a promising anti‐AF strategy.

Wha this study adds

• Combined block of multiple atrial‐predominant K⁺ currents promotes synergistic prolongation of action potential and refractoriness.

• This synergy displays favourable positive rate dependence (fast‐rate selectivity) and dose dependence.

What is the clinical significance

• Combined multiple atrial‐predominant K⁺‐current blockade may be a valuable anti‐AF strategy.

1. INTRODUCTION

The development of effective and safe pharmacotherapy for treatment of atrial fibrillation (AF), the most common cardiac arrhythmia, remains an important unmet clinical need. This is partly due to limited efficacy and undesired side effects of available pharmacotherapies, including an increased risk for lethal ventricular arrhythmias (Yap & Camm, 2003). Atrial‐predominant K⁺ currents, including the ultra‐rapid delayed rectifier K⁺ current, I_Kur, the small conductance Ca²⁺‐activated K⁺ current, I_KCa, the K_2P3.1 2‐pore‐domain K⁺ current, I_K2P, and the acetylcholine‐activated inward rectifier K⁺ current, I_K,Ach, are attractive targets for AF pharmacotherapy, in that their modulation may enable antiarrhythmic effects without disturbing normal ventricular function. Selectively blocking any one of these currents has been proposed as a novel approach to anti‐AF pharmacotherapy (Hancox, James, Marrion, Zhang, & Thomas, 2016; Peyronnet & Ravens, 2019; Voigt & Dobrev, 2016). Additionally, combination therapy may reduce deleterious side effects (Calvo, Filgueiras‐Rama, & Jalife, 2018), by allowing synergistic antiarrhythmic drug responses and thus reducing therapeutic doses. Recently, there has been a growing interest in exploring and utilizing synergistic antiarrhythmic effects of multi‐channel or multi‐compound blockade schemes (Aguilar, Xiong, Qi, Comtois, & Nattel, 2015; Kirchhoff, Goldin Diness, Sheykhzade, Grunnet, & Jespersen, 2015; Ni et al., 2017; Reiffel et al., 2015) for terminating AF. Yet it is not known whether combined inhibition of multiple atrial‐predominant currents can render beneficial synergistic anti‐AF effects in the atria. Further, it is well known that K⁺ channel blockers/class III antiarrhythmic drugs exhibit reverse (negative) rate dependence (RD) (So, Hu, Backx, Puglisi, & Dorian, 2006; Virág et al., 2009; Wang, Pelletier, Talajic, & Nattel, 1990), that is, greater action potential (AP) duration (APD) lengthening at slow versus fast pacing rates. However, as AF is characterized by rapid and irregular atrial activations, antiarrhythmic drugs exhibiting positive rate dependence are preferable. Compounds should display potent antiarrhythmic effects at fast rates (efficacy) and minimize side effects at slow rates (safety). It remains unknown how combined blockade of atrial‐predominant K⁺ currents modulates rate dependence of action potential duration changes.

Quantitative Systems Pharmacology approaches have been successfully employed to dissect arrhythmia mechanisms (Bers & Grandi, 2011) and quantitatively predict complex responses of cardiac electrophysiology to various forms of drug modulation (Aguilar et al., 2015; Cummins, Dalal, Bugana, Severi, & Sobie, 2014; Ellinwood, Dobrev, Morotti, & Grandi, 2017b, 2017a; Grandi, Dobrev, & Heijman, 2019; Grandi & Maleckar, 2016; Morotti, McCulloch, Bers, Edwards, & Grandi, 2016; Ni et al., 2017; Ni, Zhang, Grandi, Narayan, & Giles, 2019). These methods provide integrative frameworks to complement preclinical studies seeking to optimize antiarrhythmic therapy. Furthermore, given variable drug efficacy and susceptibility to side effects, population‐based computational approaches have proven valuable for understanding inter‐subject variability in electrophysiological properties and cardiotoxicity (Cummins et al., 2014; Morotti & Grandi, 2017; Ni, Morotti, & Grandi, 2018; Passini et al., 2017; Sarkar & Sobie, 2011; Sobie, 2009). These methods are especially useful in AF, which is characterized by various degrees of AF‐associated remodelling and a multitude of mechanisms and aetiologies.

Here, we developed a novel Quantitative Systems Pharmacology framework to simulate and quantitatively assess synergistic anti‐AF effects on human atrial biomarkers obtained when blocking multiple atrial‐predominant K⁺ currents simultaneously. A general workflow is illustrated in the Supporting Information. We have simulated virtual populations of human atrial myocytes and one‐dimensional tissue strands to quantify effects of blocking three atrial‐predominant currents (I_Kur, I_KCa and I_K2P) on atrial action potential duration and excitation wavelength (WL). We apply sensitivity analyses of AP biomarkers and atrial repolarization reserve (RR) to understand the interactions and rate dependence of multicurrent block in affecting these outcomes. Finally, we perform population‐based simulations of current block to confirm synergistic effects of multicurrent block that exhibit positive rate dependence. Our results show that simultaneous inhibition of atrial‐predominant K⁺ currents leads to significant synergy (i.e. greater than additive effects) in action potential duration and wavelength prolongation, especially at fast atrial rates (as in AF), suggesting that this poly‐therapy may be a valuable strategy for anti‐AF pharmacotherapy.

2. METHODS

2.1. Models

To simulate human atrial myocyte electrophysiology, we employed our previously developed computational models: Colman–Zhang model (CZ, Colman et al., 2013) with recent updates (Ni et al., 2017; Ni et al., 2019) and Grandi–Bers model (GB, Grandi et al., 2011) with updates (Ellinwood et al., 2017a, 2017b; Morotti et al., 2016). These two models represent distinct morphological subtypes of human atrial AP (Wang, Fermini, & Nattel, 1993): Colman–Zhang model displays a type‐1 AP with notch‐and‐dome morphology and a pronounced plateau phase, whereas Grandi–Bers model simulates a type‐3 AP with typical triangular shape. We included formulations of I_KCa and I_K2P in both atrial models, adapted from Skibsbye et al. (2016) and Schmidt et al. (2015), respectively.

2.2. Generation and calibration of populations of models

We first created normal sinus rhythm populations by randomly perturbing transmembrane ionic current and transporter parameters of Colman–Zhang and Grandi–Bers baseline models (Table 1) using the approach proposed by Sobie (2009). Specifically, in both models, each maximum conductance and transport rate parameter was allowed to vary independently according to a log‐normal distribution. We chose σ = 0.2 based on previous studies (Ellinwood et al., 2017a; Morotti & Grandi, 2017; Sobie, 2009) to cover a range of variability similar to that seen in experiments, while limiting the number of non‐physiological model variants to be excluded upon calibration. A workflow and details on the generation and size of each normal sinus rhythm and AF population are given in Supporting Information.

TABLE 1.

Glossary for human atrial model parameters that were perturbed for constructing populations of atrial models

Parameter	Model		Note
	CZ	GB
GNa a	✓	✓	Fast sodium current, maximal conductance
GNaL b	✓	N/A	Late component of sodium current, maximal conductance
GCaL	✓	✓	L‐type calcium current, maximal conductance
Gto	✓	✓	Transient outward current, maximal conductance
GKur	✓	✓	Ultra‐rapid delayed rectifier potassium current, maximal conductance
GKr	✓	✓	Rapid delayed rectifier potassium current, maximal conductance
GKs	✓	✓	Slow delayed rectifier potassium current, maximal conductance
GK1	✓	✓	Inward rectifier potassium current, maximal conductance
GKCa	✓	✓	Small‐conductance calcium‐activated potassium current, maximal conductance
GK2P	✓	✓	K2P3.1 2‐pore‐domain potassium current, maximal conductance
GNaCa	✓	✓	Sodium/calcium exchange current, maximal exchange rate
GNaK	✓	✓	Sodium/potassium pump current, maximal pump rate
GbNa	✓	✓	Background sodium current, maximal conductance
GbCa	✓	✓	Background calcium current, maximal conductance
GCaP	✓	✓	Sarcoplasmic calcium pump current, maximal pump rate
GClCa c	N/A	✓	Calcium activated chloride current, maximal conductance
GClB c	N/A	✓	Background chloride current, maximal conductance

^aIn Grandi–Bers (GB) model, the fast Na⁺ current was described using a Markov formulation as in Morotti et al., 2016 and thus changing G_Na depicts scaling of both fast and slow components of Na⁺ current.

^bIn Colman–Zhang model (CZ) , G_NaL describes the late component of the Na⁺ current, which was modelled independently of the fast inactivating component.

^cTwo Cl⁻ currents are present in GB but not CZ model: background (I_ClB) and Ca²⁺ activated (I_ClCa) Cl⁻ current.

We used experimental AP biomarkers to calibrate the model populations (Britton et al., 2013; Muszkiewicz et al., 2016) by excluding the model variants in which simulated biomarkers were outside the experimentally observed range reported by Ravens et al. (2014). Specifically, we compared action potential duration measured at 90% and 50% repolarization, APD_{90 ,} APD₅₀ and resting membrane potential (RMP) of each virtual cell (steady‐state values at 1 Hz pacing) with those experimentally measured in Ravens et al. (2014). Model variants were excluded if any biomarker was found differing more than 3 SDs from the experimental mean (Figure 1a,c). Additionally, we removed virtual cells displaying abnormal resting membrane potentials (same constraints as 1 Hz in the absence of resting membrane potential measurements at 3 Hz from the same source) when paced at 3 Hz.

FIGURE 1.

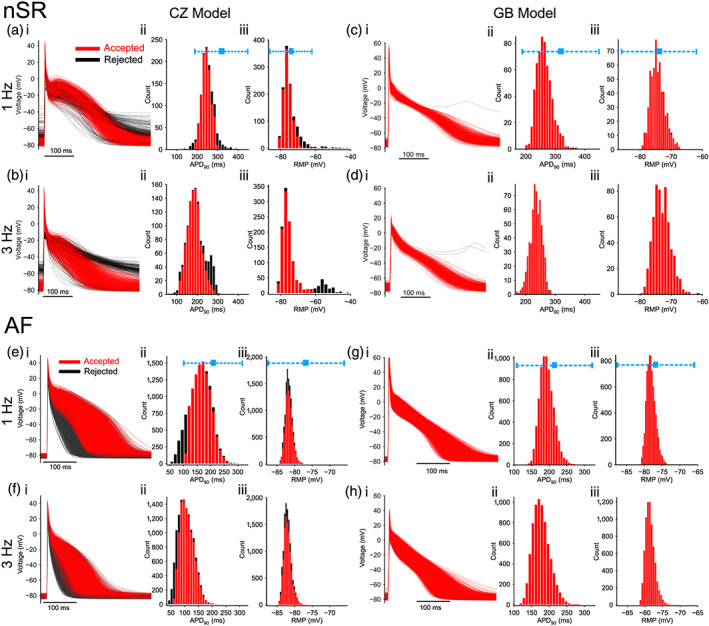
Simulated action potentials (APs) for human atrial myocytes populations. (a–d) normal sinus rhythm (nSR) populations. (e–h) AF populations. Myocytes were paced at 1 Hz (panels a, c and e, g) and 3 Hz (panels b, d and f, h). The left panels (a, b, e, f) show data for Colman–Zhang (CZ) model while results from Grandi–Bers (GB) model are plotted on the right (c, d, g, h). In each panel, column (i) superimposed APs of the atrial populations; column (ii) and (iii) distribution of action potential duration and resting membrane potential, respectively. Action potential duration was measured at 90% repolarization (APD₉₀). Rejected model variants following experimental data calibration are indicated in black. Ranges of experimental measurements (mean ± 3 × SD) are indicated in blue symbols and bars

Starting from the accepted normal sinus rhythm model variants, we further created populations of virtual atrial cells with AF‐induced cellular remodelling effects. We simulated AF‐induced remodelling of atrial electrophysiology as described in previous studies (Colman–Zhang model model as in Colman et al., 2013; Colman, Ni, Liang, Schmitt, & Zhang, 2017; Ni et al., 2017, and Grandi–Bers model as in Grandi et al., 2011). In addition to these well‐established models of AF‐remodelling, we considered various, sometimes contradictory, reported alterations of I_Kur, I_KCa and I_K2P in AF myocytes from published experimental studies. Indeed, while several studies showed no AF‐associated changes in I_Kur (Bosch et al., 1999; Grammer, Bosch, Kühlkamp, & Seipel, 2000; Workman, Kane, & Rankin, 2001), significant reductions in this current have also been well‐documented (Caballero et al., 2010; Gonzalez de la Fuente et al., 2012; Wagoner, Pond, McCarthy, Trimmer, & Nerbonne, 1997). Similarly, I_KCa was found increased following burst pacing (Ozgen et al., 2007) or atrial tachypacing (Qi et al., 2014) but decreased in myocytes from AF patients (Skibsbye et al., 2014). Further, AF substantially enhances the activity of I_K2P (Schmidt et al., 2015, 2017), but this increase is mitigated in the presence of left ventricular dysfunction (Schmidt et al., 2017). To address the complexity and variability in AF remodelling collectively revealed by these studies, which could affect the atrial response when targeting I_Kur, I_KCa and I_K2P, we considered various possible permutations of reported AF‐remodelling effects on each of the three currents (Table S1).

Lastly, to calibrate the AF‐model populations we compared the AP biomarkers (steady‐state APD₉₀, APD₅₀, and resting membrane potential values at 1 Hz pacing) to those measured in atrial myocytes from AF patients (Ravens et al., 2014). Again, models exhibiting biomarkers more than 3 SDs from the experimental mean were excluded.

2.3. Simulations of atrial‐predominant K⁺ current blockade in AF

We simulated blockade of the atrial‐predominant K⁺ currents with a simple pore block scheme (Yuan, Bai, Luo, Wang, & Zhang, 2015) (i.e. only changing maximum current conductance) and evaluated effects of 50% block of I_Kur, I_KCa, and/or I_K2P on the virtual atrial myocytes in AF. When quantifying the effects of current block, we chose APD₉₀ as a biomarker that closely relates to refractoriness and is frequently quantified in investigations of class III antiarrhythmic drugs. For simplicity, we denote APD₉₀ as action potential duration unless otherwise specified. We determined the interaction between effects of multicurrent block on action potential duration and defined synergy for combined effects being greater than additive sum of separate effects and antagonism for less‐than‐additive effects.

Two frequencies (1 and 3 Hz) are chosen as low and high to evaluate the effect of current block during normal sinus rhythm and fast atrial rate. We did not simulate faster atrial rates to avoid the frequent occurrence of action potential duration alternans seen in atria of AF patients (Narayan, Franz, Clopton, Pruvot, & Krummen, 2011), which would have prevented meaningful assessment of action potential duration prolongation. Accordingly, upon data analysis, we also excluded model variants exhibiting alternans of beat‐to‐beat APD₉₀ variation greater than 5 ms in either the baseline or blockade conditions.

To assess whether our results depend on the extent of current blockade, we modelled additional percentages of current blockade (25%, 75% and 100%). Considering the substantial computational cost, we selected two subpopulations (#1 and #5 in Table S1). In these two subpopulations, I_Kur was reduced by 50% and I_K2P increased by threefold accounting for AF‐remodelling, following the AF parameterizations in previous modelling studies (Colman et al., 2013; Ellinwood et al., 2017a; Grandi et al., 2011; Ni et al., 2017); we considered two different effects of AF‐remodelling on I_KCa, a 50% reduction in #1 and twofold increase in #5 to cover the different observations from Ozgen et al. (2007), Qi et al. (2014), and Skibsbye et al. (2014).

2.4. One‐dimensional strand models of human atrial tissue

We constructed one‐dimensional (1D) models of human atrial strands to evaluate the responses of the action potential duration (APD), effective refractory period (ERP), conduction velocity (CV) and wavelength (WL) to K⁺ current blockade in tissue. Considering the substantial computational cost of performing simulations of populations of tissues, we limited one dimensional simulations to Colman–Zhang model (less computationally expensive to solve than Grandi–Bers model) and selected AF subpopulations (#1 and #5 as above). We anticipate differences between Colman–Zhang and Grandi–Bers model in one dimensional simulations would be consistent with those seen at the single‐cell level. To understand whether AF‐induced changes in cell–cell coupling, for example, due to fibrosis (Burstein & Nattel, 2008), affect the tissue responses to current block, we considered both normal and 40% reduced tissue conductivity. The resulting conduction velocity of 0.62 versus 0.46 m·s⁻¹, respectively (Table S6) was comparable to that seen in normal and remodelled atrial tissue (Hansson et al., 1998; Krul et al., 2015).

2.5. Sensitivity analysis

To study the sensitivity of action potential duration and current block‐induced action potential duration change to model parameters, we performed multivariable linear regression, as detailed in previous studies by Dr Sobie's group (Cummins et al., 2014; Sarkar & Sobie, 2011; Sobie, 2009). Parameter sensitivity of action potential duration predicts effects of blocking ionic currents on action potential duration: If the sensitivity coefficient (B) is positive, current block would shorten action potential duration, and if negative, inhibiting this current would prolong action potential duration.

Sensitivity analysis of action potential duration can also shed light on rate dependence of action potential duration changes through comparing the sensitivity coefficients between fast and slow pacing rates (Cummins et al., 2014). Here, to quantitatively assess rate dependence of action potential duration modulation when blocking the atrial‐predominant K⁺ currents (I_K2P, I_KCa, and I_Kur), for each model parameter, we define rate dependence coefficients (B _RD) as the weighted difference between the sensitivity coefficients of 1 Hz (B ₁) and 3 Hz (B ₃) groups (B _RD = B ₁ − B ₃) (see details for scaling and comparing sensitivity coefficients in Supporting Information). As such, a positive B_RD (i.e. B₁ > B₃) indicates a decrease in the model parameter (e.g. by current block) will lengthen action potential duration more at fast than slow pacing rate (i.e. ΔAPD_fast > ΔAPD_slow) and thus is associated with positive rate dependence. Similarly, a negative B_RD suggests negative rate‐dependent action potential duration modulation when inhibiting the underlying ionic current.

Further, sensitivity analysis can be applied to understand modulations by ionic parameters of repolarization reserve (RR), a concept describing the prevention of excessive action potential duration lengthening subsequent to inhibiting one repolarizing current through compensation by other repolarizing currents (Varró & Baczkó, 2011). This procedure requires quantification of repolarization reserve, which can be derived from action potential duration change following block of a current (Sarkar & Sobie, 2011). Here, we extended sensitivity analysis of repolarization reserve to identify interactions among ion channel modulators. We derived three quantitative descriptions of the repolarization reserve using our simulated data of atrial populations before and after block of either of I_K2P, I_KCa, or I_Kur. Specifically, in a population of atrial cells, the repolarization reserve (RR) of each cell derived from simulated block of current X (RR _X) was calculated as

$$R{R}_X=\frac{\mathit{AP}{D}_{\mathit{\text{Block}}-\mathit{\text{free}}}}{\mathit{AP}{D}_{X\mathit{\text{block}}}},$$

where X represents either I_K2P, I_KCa, or I_Kur. APD _Block‐free is the action potential duration rate dependence of the cell in the absence of the block at current I_X, and APD_{X block} is the action potential duration after I_X block. Hence, a greater value of RR_X indicates stronger repolarization reserve of the cell and vice versa. If all RR_X values for the population were then used as the dependent variable (as for action potential duration previously) in a sensitivity analysis, the fitted coefficients indicate how each current in the model affects repolarization reserve (during simultaneous block of I_X): A negative sensitivity coefficient indicates that decreasing a given current would enhance the repolarization reserve, whereas a positive coefficient suggests that reducing the current would impair the repolarization reserve. Therefore, for a given current (I_Y), a negative sensitivity coefficient indicates that a reduction (e.g.,block) of I_Y in the cell can enhance its repolarization reserve (greater RR_X thus smaller $\frac{\mathit{AP}{D}_{X\mathit{\text{block}}}}{\mathit{AP}{D}_{\mathit{\text{Block}}-\mathit{\text{free}}}}$ or lower action potential duration prolongation). In other words, in the presence of I_Y block the action potential duration prolongation due to I_X block is reduced, suggesting competition/antagonism between blocking I_Y and I_X in lengthening the action potential duration. Conversely, a positive coefficient indicates that blocking I_Y would impair repolarization reserve and exaggerate the action potential duration prolongation caused by blocking I_X, thus indicating the presence of synergy between block of I_Y and I_X in lengthening the action potential duration.

2.6. Data and statistical analysis

We applied the non‐parametric bootstrap method to characterize the rate dependence of action potential duration (and other tissue‐level biomarkers) changes and interactions of multiple channel blockades, as detailed in the Supporting Information ‐ Supporting Methods. Specifically, the RD of APD change was deemed positive if the lower limit of the confidence interval (CI) for the median of ΔAPD_3Hz – ΔAPD_1Hz is > 0, and negative if the upper limit of CI is < 0. Potential interactions were assessed by comparing changes due to combined block and the sum of the effects of each individual current block. Using again APD as an example, the interaction between I_K2P and I_Kur block is calculated as

$${\text{Interaction}}_{\text{K2P+Kur}}{\text{=ΔAPD}}_{\text{K2P+Kur block}}‐{\text{(ΔAPD}}_{\text{K2P block}}+{\text{ΔAPD}}_{\text{Kur block}}\text{)}$$ (1)

where for each current block, ${\text{ΔAPD}}_{\text{X block}}\text{=}\frac{{\text{APD}}_{\text{X block}}‐{\text{APD}}_{\text{Block‐free}}}{{\text{APD}}_{\text{Block‐free}}}\times 100(\%)$ Hence, an interaction exists if the CI for the median Interaction _K2P+Kur does not contain 0, and is deemed synergistic if the lower limit of CI is > 0 and antagonistic if the upper limit of CI is < 0. CIs were obtained with confidence levels set to 95% with Bonferroni‐type correction for each group of analysis (i.e., considering 7 comparisons for RD characterizations and 4 comparisons/combinations for interactions for each subpopulation). The data and statistical analysis comply with the recommendations of the British Journal of Pharmacology on experimental design and analysis in pharmacology (Curtis et al., 2018).

2.7. Software availability

Details on software and numerical methods are in the Supporting Information. Source code and documentation are freely available at http://elegrandi.wixsite.com/grandilab/downloads and https://github.com/drgrandilab.

2.8. Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Harding et al., 2018) and are permanently archived in the Concise Guide to PHARMACOLOGY 2019/20 (Alexander et al., 2019).

3. RESULTS

3.1. Calibrated populations of simulated myocytes under normal sinus rhythm and AF conditions

We utilized our well‐established models of human atrial AP and Ca²⁺ handling, Colman–Zhang (CZ, Colman et al., 2013) and Grandi–Bers (GB, Grandi et al., 2011) to generate populations of atrial cell model variants in normal sinus rhythm (Figure 1a–d). Distributions of action potential duration and resting membrane potential for the simulated atrial populations at both 1 and 3 Hz following calibration with experimentally measured action potential duration (APD) and resting membrane potential data from (Ravens et al., 2014) are in Table S2. By incorporating AF‐remodelling effects into the normal sinus rhythm variants, we obtained 12 AF‐subpopulations including variable sign and degree of remodelling on I_K2P, I_KCa and I_Kur (Table S1), reflecting the variability in reported AF‐remodelling effects on these currents. APD₅₀, APD₉₀ and resting membrane potential distributions for the aggregate AF population and each of these 12 subpopulations were then calibrated to the experimental data from (Ravens et al., 2014) (Figure 1e–h) and are shown in Tables S2 and S3, respectively.

3.2. Sensitivity analysis revealed rate dependence of APD modulation

Rate‐dependent action potential duration modulation is an important property of class III antiarrhythmic drugs, which often present unfavourable reverse (negative) rate dependence (So et al., 2006; Virág et al., 2009; Wang et al., 1990). A previous study demonstrated that sensitivity analysis of action potential duration provides insights into rate dependence of ventricular action potential duration changes following alterations in ionic currents (Cummins et al., 2014). We applied sensitivity analysis to predict rate dependence of action potential duration changes when blocking these atrial‐predominant K⁺ currents (Figure 2 and Figure S1). First, we used multivariable linear regression analysis to calculate action potential duration sensitivity coefficients (Sobie, 2009), which, as might be anticipated, were generally negative for G_Kur, G_KCa and G_K2P (Figure 2a,c,e,g), suggesting that block of these currents would tend to prolong action potential duration, with the exception of I_Kur in the Grandi–Bers model population at 1 Hz. Then, comparing the sensitivity coefficients of slow versus fast pacing rate, we derived rate dependence coefficients (B _RD, as described in Section 2). Positive B_RD indicates that current blockade causes greater action potential duration prolongation at fast versus slow rates, that is positive rate dependence, and vice versa. Analysis of B_RD (Figure 2b,d) revealed that, in normal sinus rhythm myocyte simulations, inhibiting I_Kur produces positive rate dependence in action potential duration prolongation for both model populations, whereas I_K2P block favours positive rate dependence in Colman–Zhang model but not Grandi–Bers model population. In AF, B _RD (Figure 2h) for G_Kur, G_KCa, and G_K2P for the Grandi–Bers model populations were positive, suggesting that inhibiting these currents would produce positive rate dependence of action potential duration prolongation. In contrast, in Colman–Zhang model populations (Figure 2f), positive B _RD was seen for G_Kur only, indicating that I_Kur block is associated with positive, but I_KCa and I_K2P inhibition with negative rate dependence of action potential duration change.

FIGURE 2.

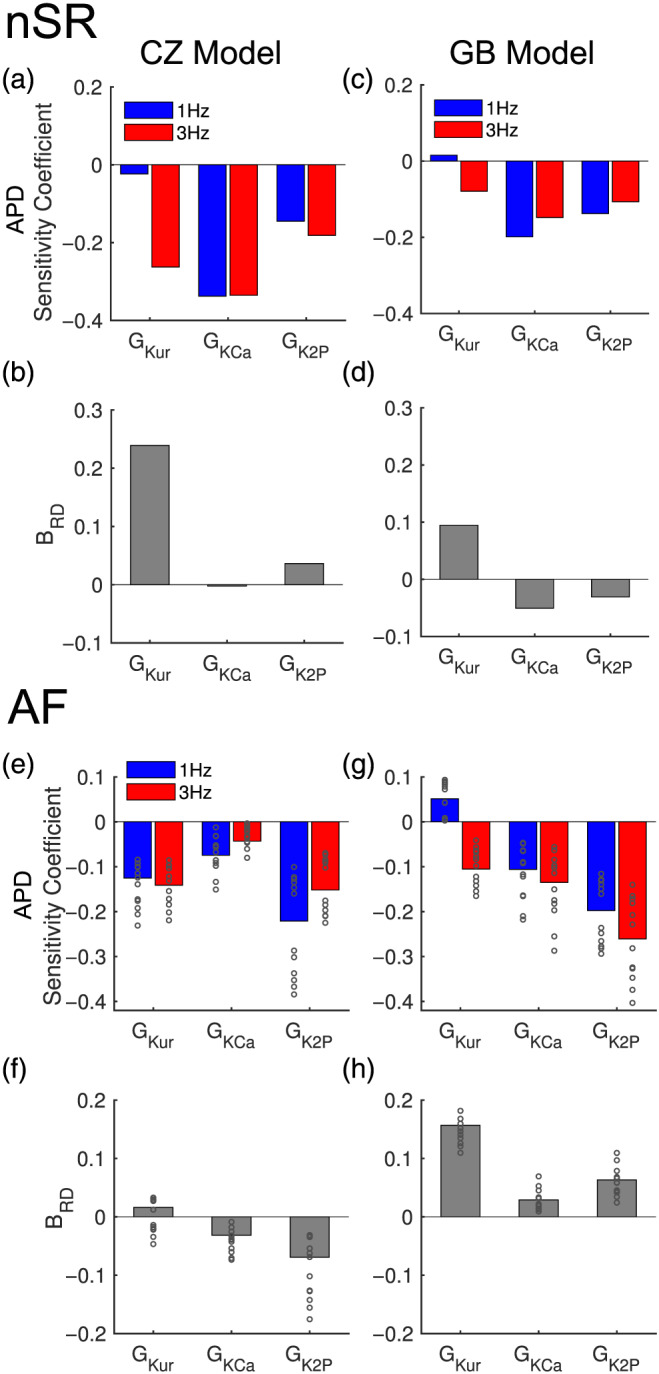
Sensitivities of action potential duration and rate‐dependent action potential duration modulation for atrial‐predominant K⁺ parameter (G_Kur, G_K2P,and G_KCa). We applied multivariable linear regression to virtual atrial (a–d) normal sinus rhythm (nSR) and (e–h) AF myocyte populations. (a, c, e, g) Sensitivity coefficients of action potential duration to perturbations of three parameters of interest (G_Kur, G_KCa and G_K2P) for myocytes paced at 1 and 3 Hz. (b, d, f, h) action potential duration (APD) rate‐dependence (RD) coefficients (B_RD) for these currents. Positive B_RD indicates inhibition of this current favours producing positive rate dependence of action potential duration prolongation and vice versa. In (e–h), results for each AF subpopulation are plotted as open circles and those for the aggregate dataset are represented by bar plots. For the 12 AF‐subpopulations, the variability in AF‐remodelling effects caused variations in sensitivity coefficients. Results of the sensitivity analysis for the full set of model parameters varied in simulations are shown in Figure S1

3.3. Simulations of K⁺‐current block validated predicted rate dependence

Focusing our subsequent analyses on the AF model populations, we simulated effects of blocking atrial‐predominant K⁺ currents (I_Kur, I_KCa,and I_K2P) to verify the rate dependence of action potential duration modulation predicted by the sensitivity analysis (B_RD) when each current is blocked and assessed rate dependence of action potential duration changes when multiple currents are inhibited in combination. Qualitative assessment of AP traces (Figure and Figure S2) reveals that I_K2P block modified both phase 2 and 3 of the AP (Figure 3a), whereas I_KCa block predominantly affected phase 3 (Figure 3b) and I_Kur mostly impacted phase 2 (Figure 3c). Both phase 2 and phase 3 changes were seen in multicurrent block simulations (Figure 3d–g). For quantitative assessment, we calculated both absolute and fractional action potential duration changes due to block of each individual K⁺ current (Figure 4a–d, first three columns), paired block (Figure 4a–d, fourth to sixth column) and combined block of all three currents (Figure 4a–d, last column) at 1 and 3 Hz (Figure 4a,c and Figure 4b,d, respectively, and Table S4). Notably, simulations generally predicted action potential duration prolongation, with the exception of a substantial fraction of Grandi–Bers model variants in which I_Kur block alone or combined with I_KCa block shortened action potential duration at 1‐Hz pacing (Figure 3c, ii and f, ii, Figure 4a,c and Table S4). Note that these results agree well with the predictions from the sensitivity analysis, with negative coefficients (associated with action potential duration prolongation) for all atrial‐predominant K⁺ conductances except for G_Kur at 1 Hz in Grandi–Bers model population (Figure 2e,g). Overall, individual current block produced minor to moderate effects on action potential duration; I_K2P block caused greater ΔAPD than either I_Kur or I_KCa block, consistent with previous experimental studies on effects of I_K2P (Schmidt et al., 2015), I_Kur (Ford et al., 2016), and I_KCa (Skibsbye et al., 2014) block.

FIGURE 3.

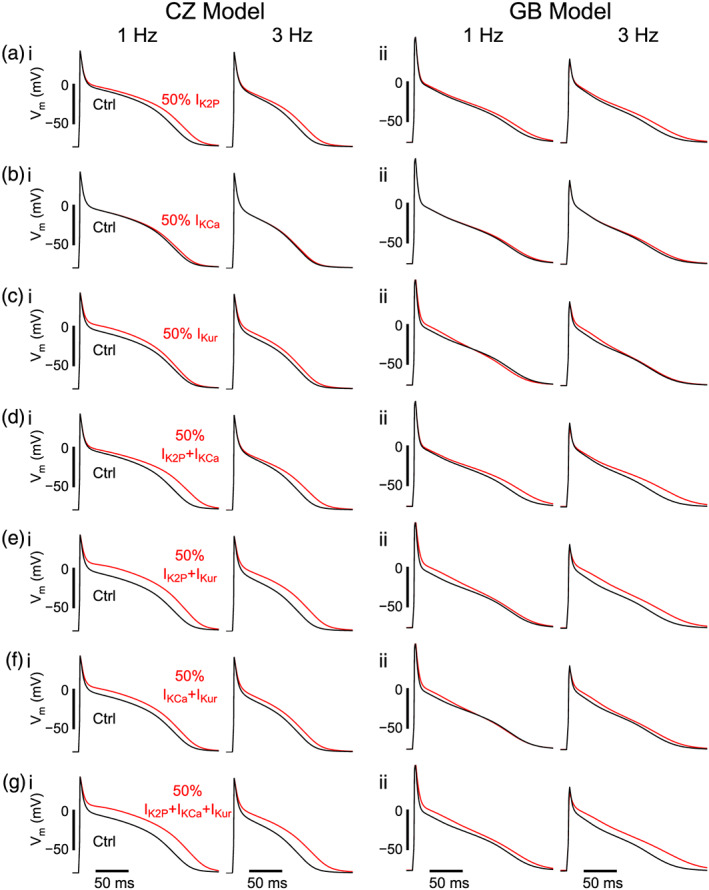
Action potential (AP) waveform changes due to block of atrial‐predominant K⁺ currents. Example of AP modulations at 1 and 3 Hz following various regimens concerning 50% block of I_K2P, I_KCa and I_Kur. Each row depicts APs with/without 50% block of (a) I_K2P, (b) I_KCa, (c) I_Kur, (d) I_K2P + I_KCa, (e) I_K2P + I_Kur, (f) I_KCa + I_Kur and (g) I_K2P + I_KCa + I_Kur from simulations with (left columns) Colman–Zhang model (CZ ; subpopulation #5, variant #310) and (right columns) Grandi–Bers (GB) models (subpopulation #5, variant #287)

FIGURE 4.

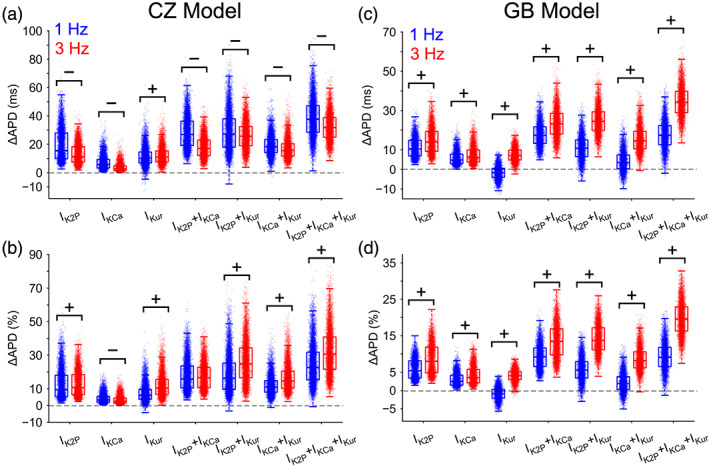
Effects of 50% block of I_K2P, I_KCa or I_Kur on action potential duration in AF‐remodelled atrial populations at slow and fast pacing rates. In these simulations, three atrial‐predominant‐K⁺ currents are partially (50%) inhibited individually or in combination during pacing at 1 Hz (blue) and 3 Hz (red). (a, b) Simulation results for Colman–Zhang model (CZ) population. (c, d) Results obtained from Grandi–Bers model (GB) population. The top (a, c) and bottom (b, d) panels illustrate absolute and fractional action potential duration changes, respectively. The sign of ΔAPD (action potential duration) rate dependence (RD) from confidence interval analysis (Figure S3) is indicated as follows: “+” for positive RD and “–“for negative RD

To describe the rate dependence of ΔAPD upon atrial‐predominant K⁺‐current block, we applied bootstrap analysis to estimate CIs of median difference ΔAPD for fast versus slow pacing rate as described in Section 2 (Figure S3). The analysis showed that action potential duration prolongation due to blocking I_Kur in both Colman–Zhang and Grandi–Bers model populations exhibited positive rate dependence (highlighted in black bars, Figure 4a,c), in agreement with positive sensitivity coefficients B_RD (Figure 2f,h). Interestingly, this favourable positive rate dependence of action potential duration modulation has been reported for XEN‐D0103 (Ford et al., 2016), a selective I_Kur blocker. In the Grandi–Bers model population, positive rate dependence was found upon blocking each current individually, and also seen in multicurrent block (Figure 4c,d, Table S4). In Colman–Zhang model simulations, negative rate dependence was predominantly found in absolute ΔAPD, but positive rate dependence was found in fractional ΔAPD (Figure 4a,b). This discrepancy could be explained by shorter baseline (drug‐free) action potential duration at 3 Hz versus 1 Hz (Figure 1e,ii and f,ii). Multicurrent block generally produced stronger positive rate dependence than individual current block, especially when I_Kur, I_K2P and I_KCa were all blocked simultaneously (Figure 4b,d and Figure S3). Collectively, these results verified predictions from our sensitivity analyses and show that multi‐atrial‐predominant K⁺‐current block promoted positive rate dependence of action potential duration modulation, a favourable property for class III antiarrhythmics.

3.4. Sensitivity analysis of atrial repolarization reserve revealed synergistic APD prolongation

Repolarization reserve refers to the concept that when one repolarizing current is inhibited other repolarizing currents may compensate and prevent excessive action potential duration lengthening (Varró & Baczkó, 2011). Here, we define atrial repolarization reserve as the ratio of block‐free action potential duration to action potential duration upon K⁺‐current block and apply sensitivity analysis of repolarization reserve to uncover interactions among multicurrent blockade in modulating action potential duration (see Section 2). In Figure 5a, we calculated repolarization reserve as $\frac{\mathit{AP}{D}_{\mathit{\text{Block}}-\mathit{\text{free}}}}{\mathit{AP}{D}_{\mathit{IK}2P\mathit{\text{block}}}}$. Blocking currents associated with negative sensitivity coefficients can enhance repolarization reserve through increasing $\frac{\mathit{AP}{D}_{\mathit{\text{Block}}-\mathit{\text{free}}}}{\mathit{AP}{D}_{\mathit{IK}2P\mathit{\text{block}}}}$, thus suggesting a competition/antagonistic effect between blocking this current and I_K2P in prolonging the action potential duration. Conversely, if a current is associated with a positive sensitivity coefficient, blocking this current is expected to synergistically interact with I_K2P block in lengthening the action potential duration. In the Colman–Zhang model population, the negative sensitivity coefficient for G_Kur at 1 Hz shifted towards positive at 3 Hz (Figure 5ai), suggesting that inhibition of I_Kur would compete against I_K2P block in lengthening action potential duration at 1 Hz and this was diminished at 3 Hz. Consistently, positive sensitivity coefficients were seen for G_KCa in the Colman–Zhang model population and both G_Kur and G_KCa in the Grandi–Bers model population (Figure 5a, i‐ii), suggesting synergistic effects in action potential duration prolongation for I_Kur + I_K2P or I_KCa + I_K2P block. Given our definition of repolarization reserve, large coefficients were associated with the current being blocked (I_K2P in Figure 5a, I_KCa in Figure 5b, and I_Kur in Figure 5c), as also shown in Sarkar and Sobie (2011)).

FIGURE 5.

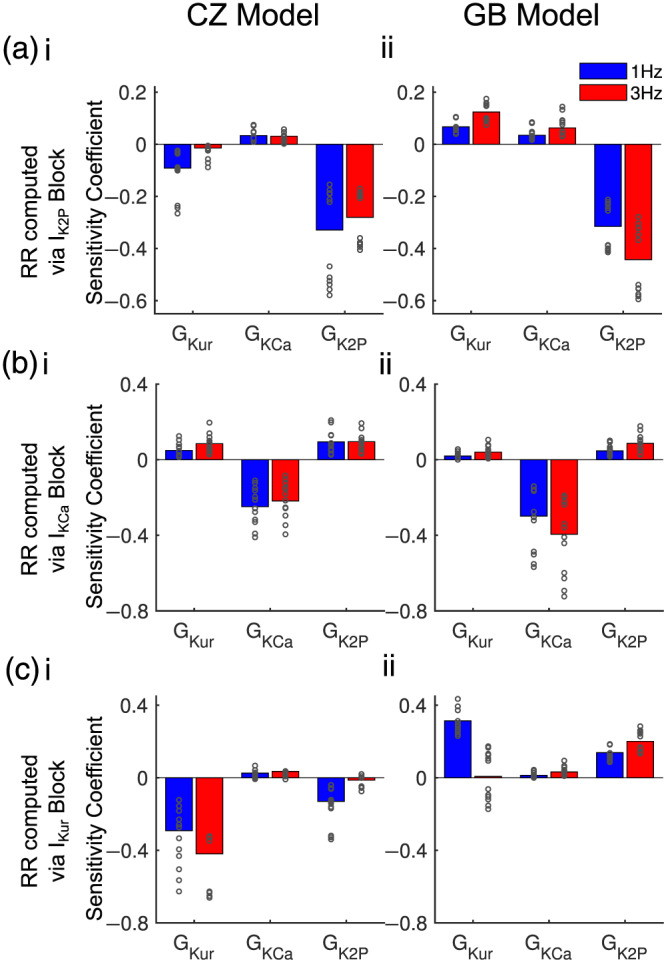
Parameter sensitivity of repolarization reserve (RR) for G_Kur, G_KCa,and G_K2P. (a–c) Sensitivity coefficients of repolarization reserve derived from the ratio between action potential durations before and after 50% block of (a) I_K2P, (b) I_KCa and (c) I_Kur. Columns are sensitivity coefficients for the (i) Colman–Zhang model (CZ) and (ii) Grandi–Bers model (GB) populations. Results for each AF subpopulation are plotted with open circles and those for the aggregate AF dataset are shown in bar plots. Complete set of sensitivity coefficients are illustrated in Figure S4. Given our definition of repolarization reserve, the parameter related to a given blocked current is associated with a large coefficient

Similarly, applying sensitivity analysis to repolarization reserve computed as $\frac{\mathit{AP}{D}_{\mathit{\text{Block}}-\mathit{\text{free}}}}{\mathit{AP}{D}_{\mathit{\text{IKCa block}}}}$, positive coefficients for G_Kur and G_K2P in both populations indicated potential synergy in lengthening action potential duration for I_Kur + I_KCa or I_K2P + I_KCa block (Figure 5b). Further, sensitivity analysis of repolarization reserve measured as $\frac{\mathit{AP}{D}_{\mathit{\text{Block}}-\mathit{\text{free}}}}{\mathit{AP}{D}_{\mathit{\text{IKur block}}}}$ (Figure 5c) revealed interactions in I_Kur + I_K2P and I_Kur + I_KCa block consistent with the analyses above (Figure 5a,b): the sensitivity coefficient for G_K2P was negative at 1 Hz and shifted towards positive at 3 Hz in the Colman–Zhang model populations; positive coefficients were seen for G_KCa in both Colman–Zhang and Grandi–Bers model populations and for G_K2P in Grandi–Bers model population. Further, the coefficient for G_Kur itself was positive at 1 Hz for the Grandi–Bers model population (Figure 5c, ii), which indicates that increasing G_Kur would result in greater $\frac{\mathit{AP}{D}_{\mathit{\text{Block}}-\mathit{\text{free}}}}{\mathit{AP}{D}_{\mathit{\text{IKur block}}}}$ and thus less action potential duration prolongation, in agreement with the observation that I_Kur block shortened action potential duration (Figure 4c). Interestingly, coefficients for G_Kr were positive across pacing rates and Colman–Zhang and Grandi–Bers model populations (Figure S4), suggesting synergy in action potential duration prolongation when blocking the rapid delayed rectifier K⁺ current (I_Kr) along with the atrial‐predominant K⁺ currents.

Values of coefficients for G_K2P, G_KCa and G_Kur are summarized in Table S5, allowing for quantitative comparison of interactions on ΔAPD. Note that the results of interactions in combined block were reciprocal, that is, similar results could be obtained by quantifying repolarization reserve via block of either current and computing the sensitivity of the other. Importantly, in both populations, these sensitivity coefficients were generally more positive at 3 Hz versus 1 Hz, indicating the synergistic action potential duration prolonging effects due to inhibition of multiple atrial‐predominant K⁺‐currents exhibit positive rate dependence.

3.5. Interactions between effects of current inhibition confirmed in simulated multicurrent block

We verified the findings from sensitivity analysis of repolarization reserve by comparing the fractional ΔAPD following multicurrent block with the additive effects of individual current block. Specifically, interactions were deemed synergistic if the effect of combined current block was greater than the additive effects of individual current block or antagonistic with less‐than‐additive effect (Figure 6 and Figure S5). Combined I_K2P + I_KCa block consistently exhibited synergistic action potential duration prolongation in both Grandi–Bers and Colman–Zhang model populations. This was also seen in simulated combined block of I_KCa + I_Kur with Colman–Zhang model populations and most subpopulations with the Grandi–Bers model, consistent with the coefficients of G_Kur and G_K2P in Figure 5b. Interestingly, the pair I_K2P + I_Kur exhibited competition in action potential duration prolongation at 1 Hz in the CZ model and this shifted towards synergy at 3 Hz, matching the predictions from the coefficients of G_Kur in Figure 5a, i. On the other hand, this pair (I_K2P + I_Kur) consistently displayed synergy at both pacing rates in Grandi–Bers model populations. Furthermore, combined block of all three atrial‐predominant K⁺ currents (I_K2P + I_KCa + I_Kur) exhibited stronger interactions, producing synergistic action potential duration prolongation for all Grandi–Bers model subpopulations and all Colman–Zhang model subpopulations at 3 Hz and many Colman–Zhang model subpopulations at 1 Hz. Importantly, in both model populations, synergy was stronger at 3 Hz versus 1 Hz. Note that these results match well with the sensitivity coefficients in Figure 5 and Table S5, in the sense that the extent and nature of the interactions agree well with the sign and magnitude of the sensitivity coefficients. The fact that the synergy was stronger at 3 Hz versus 1 Hz suggests that the synergistic action potential duration prolongation shows positive rate dependence, which is favourable for anti‐AF pharmacotherapy.

FIGURE 6.

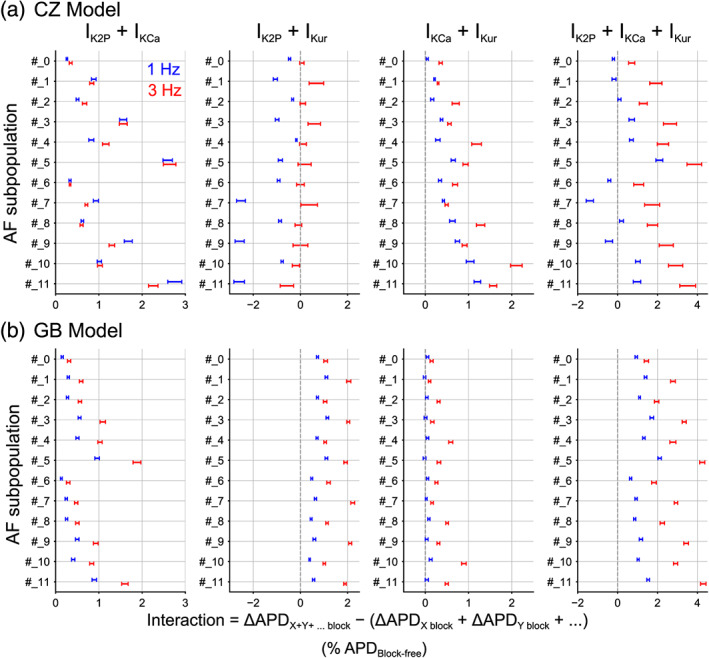
Interaction among I_K2P, I_KCa and I_Kur blockade in lengthening action potential duration. Confidence intervals were computed for the median interactions in multicurrent block defined as the difference in ΔAPD (action potential duration) for the combined effects versus the additive sum of separate effects. The interaction in ΔAPD is normalized to cell‐matched block‐free action potential duration. In these simulations, each current was subjected to 50% block. Positive interaction indicates synergism whereas negative difference suggests antagonism. Data of 1 Hz are shown in blue and 3 Hz in red

We performed additional simulations with selected AF subpopulations (#1 and #5) to determine if the interactions persist when the currents were subjected to a broader range of blockade (Figure 7). Changing the extent of block generally did not alter the nature of synergism or antagonism, and the strength of the interaction exhibited positive “dose dependence”: competition (Figure 7a, I_K2P + I_Kur and I_K2P + I_KCa + I_Kur for subpopulation #1 at 1 Hz) or synergy (Figure 7, rest plots) were substantially enhanced when simulated current block was increased from 25% to 100%. Figure S6 depicts exemplary APs for I_K2P + I_Kur block showing antagonism at 1 Hz but synergism at 3 Hz. Further, the interactions were generally stronger at 3 Hz versus 1 Hz, confirming positive rate dependence across all percentages of block.

FIGURE 7.

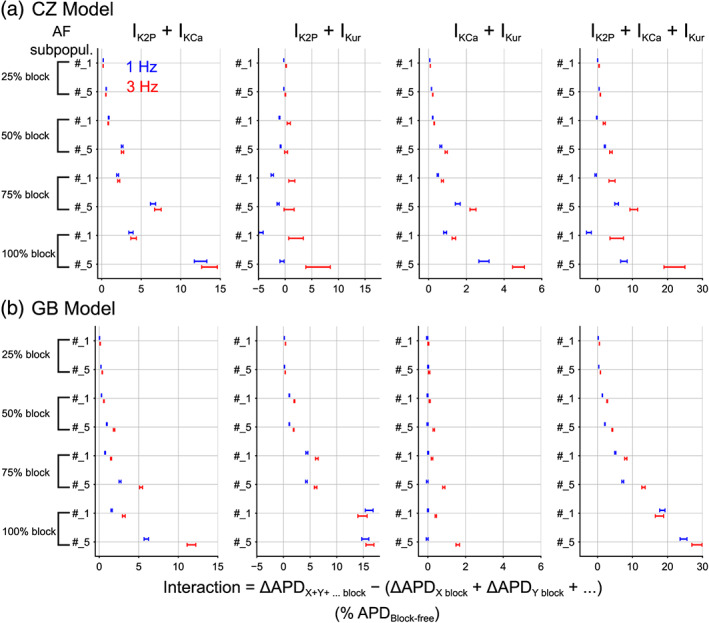
Dose dependence of interactions among multicurrent block on ΔAPD (action potential duration). Confidence intervals were computed for the median interactions in multicurrent block defined as the difference in ΔAPD for the combined effects versus the additive sum of separate effects for selected subpopulations when each current was subjected to 25% to 100% block. The interaction in ΔAPD is normalized to cell‐matched block‐free action potential duration. Positive difference indicates synergism whereas negative difference suggests antagonism. Data of 1 Hz are shown in blue and 3 Hz in red

3.6. Multicurrent block interaction effects were also present in tissue

We evaluated changes in action potential duration, effective refractory period (ERP), conduction velocity (CV) and wavelength (WL) in one dimensional tissues of two representative AF subpopulations (subpopulations #1 and #5) of the Colman–Zhang model population paced at both 1 and 3 Hz and considering both normal and reduced cell‐to‐cell electrical coupling in tissue (Figure 8, Figures S7–S10 and Table S6). Figure 8a illustrates an example of AP propagation in tissue and measurement of effective refractory period using the S1–S2 protocol. The modulating effects of atrial‐predominant K⁺ current block on action potential duration in tissue closely resembled those seen in the isolated cells (Figure 8b) and were also reflected in effective refractory period (Figure 8c). The effects of blocking these K⁺‐currents on conduction velocity were negligible, although generally greater at 3 Hz versus 1 Hz (Figure S8 and Table S6). Consequently, the ΔWL due to K⁺‐current block follows ΔAPD (Figure 8d). Indeed, positive rate dependence was generally observed for ΔAPD, ΔERP and ΔWL in groups involving I_Kur block (Figures S9 and S10).

FIGURE 8.

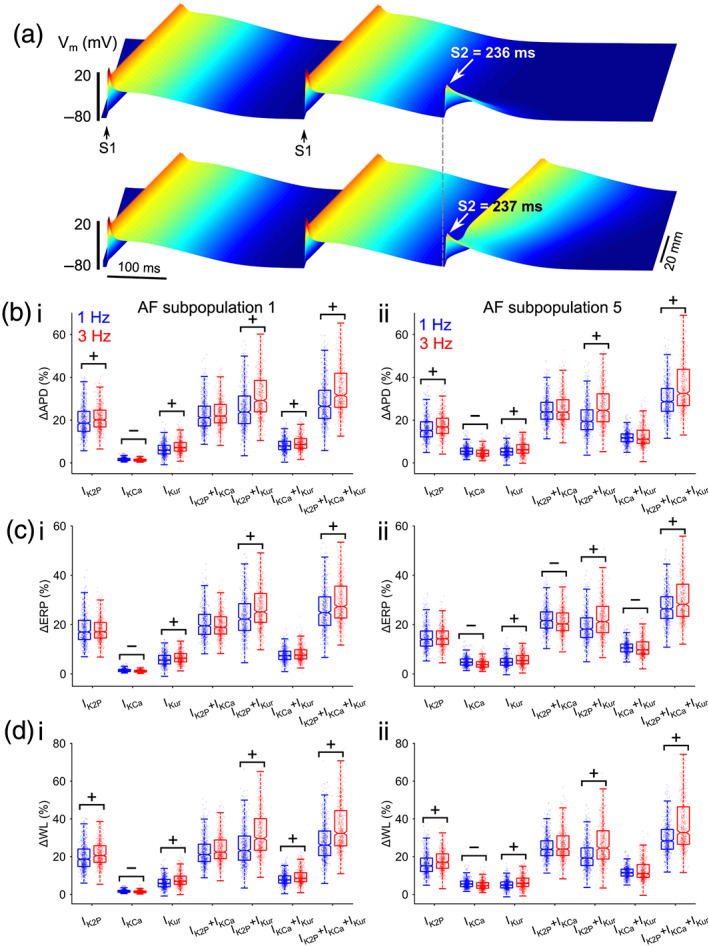
Effects of mono‐K⁺ or multi‐K⁺‐current block on virtual atrial tissue populations using the Colman‐Zhang model. (a) Example of AP propagation in one dimensional (1D) strand tissue paced at 3 Hz and measurement of effective refractory period (ERP) with an extra stimulus S2, which failed at 236 ms (top row) but succeeded capturing tissue at 237 ms (bottom row). (b–d) Each row depict change in (b) action potential duration (APD) (c) effective refractory period (ERP) and (d) wavelength (WL) due to current block obtained from virtual atrial strand populations paced at 1 Hz (blue) and 3 Hz (red). Each column describes results from (i) AF subpopulation 1 and (ii) AF subpopulation 5, respectively. WL was computed as the product of APD and conduction velocity (CV). Rate dependence (RD) deemed from analysis of CI in difference in 3 Hz versus 1 Hz in Figure S9, is shown as: “+” for positive RD and “–“for negative RD

Additionally, analysis of the confidence intervals for the median difference of ΔAPD, ΔERP and ΔWL between combined and individual current block (additive) effect in tissue confirmed the interactions emerged at the cellular level (Figure S11). We found antagonism between I_Kur and I_K2P in lengthening action potential duration (APD), effective refractory period (ERP) and wavelength (WL) at 1 Hz and this shifted to synergy at 3 Hz. Further, the synergistic effects in tissue also generally exhibited positive rate dependence.

The results above in response to multi K⁺‐channel block were maintained in the presence of reduced tissue coupling (Figures S7, S8B, S10, S11B and Table S6), to account for AF‐induced gap junction remodelling and fibrosis (Burstein & Nattel, 2008), despite expected conduction velocity and wavelength reductions in the less‐well coupled tissue (Table S6).

4. DISCUSSION

Atrial‐predominant and multichannel block are promising strategies for effective and safe antiarrhythmic pharmacotherapy in AF. We have evaluated effects of blocking multiple atrial‐predominant K⁺ currents (I_Kur, I_K2P, and I_KCa) on human atrial electrophysiologic parameters utilizing a population‐based Quantitative Systems Pharmacology framework. Through sensitivity and statistical analyses of our atrial cell and tissue populations, we found that synergistic (i.e. greater than additive) action potential duration prolongation could be achieved by multi‐atrial‐predominant K⁺‐current block and this synergy displayed favourable positive rate‐dependence (Figure 6) and dose‐dependence (Figure 7). Our study points to simultaneous block of two or more atrial‐predominant currents as a valuable strategy for antiarrhythmic therapy in AF.

4.1. Effects of atrial‐predominant K⁺‐current block

Inhibition of atrial‐predominant currents, such as I_Kur, I_K2P, I_KCa and I_K,ACh, is a promising strategy for anti‐AF pharmacological therapies to limit adverse proarrhythmic (ventricular) effects of antiarrhythmic drugs (Hancox et al., 2016; Ravens, 2017; Voigt & Dobrev, 2016). However, atrial‐predominant‐K⁺ current blockers have not yet been successful in producing significant antiarrhythmic effects in the clinic. For example, MK‐0448, the first clinically studied I_Kur inhibitor, did not significantly prolong atrial refractoriness in healthy individuals (Pavri et al., 2012). A recent clinical trial, DIAGRAF‐IKUR, was prematurely terminated as XEN‐D0103 did not exert clinically relevant reduction in AF burden (Camm et al., 2019; Shunmugam et al., 2018). The efficacy of I_K,ACh blockers has been questioned, as AZD2927 failed to prolong left atrial effective refractory period in atrial flutter patients (Walfridsson et al., 2015). Non‐cardiac side effects have also drawn attention for blockers of I_K,ACh and I_K2P, whereas I_KCa modulators have yet to be tested in humans (Peyronnet & Ravens, 2019). In agreement with these clinical results, our simulation results demonstrated that 50% blockade of individual atrial‐predominant K⁺ current produced minor to moderate effects on action potential duration (Figures 3 and 4, Table S4), indicating moderate to low efficacy in suppressing AF circuits in the atria.

4.2. Synergistic antiarrhythmic effect of multiple atrial‐predominant K⁺‐current block

Multicurrent block has been increasingly recognized as an attractive strategy for AF management, based on the observation that most clinically approved antiarrhythmic drugs target multiple ionic currents (Peyronnet & Ravens, 2019) and preclinical data demonstrating synergistic anti‐AF effects of multicurrent block schemes (Aguilar et al., 2015; Kirchhoff et al., 2015, 2016; Ni et al., 2017; Reiffel et al., 2015). Application of multicurrent block regimens may therefore have important implications, including increasing the efficacy of antiarrhythmic pharmacotherapy and reduction of unwanted adverse effects on the heart and non‐cardiac systems through decreasing effective compound doses.

Here we combined the atrial‐predominant and multicurrent block strategies as a novel anti‐AF paradigm, and evaluated antiarrhythmic effects of simultaneously inhibiting multiple atrial‐predominant K⁺ currents on human atrial myocytes and tissues. To account for biological variability in atrial electrophysiology (including cell–cell and patient–patient variation, regional heterogeneity, and diverse aetiology and manifestation of AF), we employed two distinct human atrial models and simulated various degrees and combinations of AF‐remodelling effects on I_Kur, I_K2P and I_KCa based on experimental data. The two models exhibited quantitative differences in action potential duration prolongation and rate‐dependent changes (Figure 4). Yet, in both populations, combined block of these atrial‐predominant currents substantially increased fractional action potential duration prolongation and enhanced its positive rate dependence as compared to block of each current individually. Our analyses revealed synergistic (greater than merely additive) action potential duration prolongation upon simulated multicurrent block (Figures 6), and this effect also increases with the degree of block (Figure 7). Importantly, this synergy in action potential duration prolongation consistently exhibited favourable positive rate dependence in the two distinct atrial model populations, despite some variability in the presence and strength of interaction within the AF subpopulations. Interestingly, in the Colman–Zhang model the pair I_K2P + I_Kur displayed competition in lengthening action potential duration at 1 Hz; this interaction may limit excessive action potential duration prolongation at slow pacing rates thus preventing proarrhythmic (ectopy) events including early afterdepolarizations. Antiarrhythmic synergistic interactions also emerged in tissues, where myocytes were electrically coupled; simulated multicurrent block regimens produced interaction and rate dependence patterns consistent with single cell results for prolongation of in‐tissue action potential duration, effective refractory period and, more importantly, wavelength, a biomarker frequently used to determine the required substrate size for re‐entry circuit maintenance. Collectively, our results demonstrate that combined block of two or more atrial‐predominant K⁺ currents can exert synergistic and positive rate‐dependent antiarrhythmic effects and therefore is a valuable therapeutic for AF.

Remarkably, additional atrial‐ventricular differences can be employed to achieve atrial‐selectivity for AF pharmacotherapy (Burashnikov, Diego, Zygmunt, Belardinelli, & Antzelevitch, 2007), including targeting of the atrial predominant I_K,ACh, which we have not incorporated as part of this initial investigation. Further, we (Ni et al., 2017) and others (Aguilar et al., 2015; Kirchhoff et al., 2015; Reiffel et al., 2015; Sicouri, Burashnikov, Belardinelli, & Antzelevitch, 2010) have previously shown that synergistic and atrial‐selective antiarrhythmic effects can be achieved by combined block of Na⁺ and K⁺ currents. It remains to be tested whether combined Na⁺ current and multiple atrial‐predominant K⁺‐current block displays favourable rate‐ and atrial‐selective anti‐AF effects.

4.3. Sensitivity analysis for investigating rate dependence and interactions of multicurrent block

We successfully applied sensitivity analysis and statistical analysis of population‐based model simulations to inform rate dependence and extended the approach to identify interactions between modulations of K⁺‐current block on atrial action potential duration. To understand the influence of transmembrane current strength on action potential duration at both fast and slow pacing frequencies, we derived rate dependence coefficients B_RD as the difference in action potential duration sensitivity coefficients at the slow versus fast pacing rates (Figure 2) and validated that B_RD was a good predictor of rate dependence of action potential duration prolongation due to current blockade in subsequent simulations of K⁺‐current block (Figure 4). Additionally, sensitivity analysis of repolarization reserve (quantified by ΔAPD following I_Kr block) has proven valuable to reveal the contribution of other ionic currents to ventricular repolarization reserve (Sarkar & Sobie, 2011). Here, we demonstrated that sensitivity analysis of repolarization reserve could also provide insight into the sign (synergy or competition) and extent of interactions of multicurrent blockade in lengthening action potential duration (Figure 5). The predicted interactions were confirmed through subsequent simulations of multicurrent block and comparisons to single‐current block (Figures 6). These results suggest that sensitivity analysis of repolarization reserve is a powerful approach for dissecting interactive effects among block of multiple currents on modulating action potential duration. This method has broader applicability to other “atrial‐selective” targets including I_K,ACh and the fast Na⁺ current, I_Na (Ravens, Poulet, Wettwer, & Knaut, 2013), and systems models, for example, ventricular myocyte models.

4.4. Model‐ and AP‐shape independence of positive rate‐dependent synergy of multicurrent block

It is well known that human atrial myocytes display at least three distinct characteristic AP morphologies; among them type‐1 AP shows significant plateau phase 2 repolarization and type‐3 AP exhibits triangular‐shaped repolarization phases (Ravens et al., 2014; Wang et al., 1993; Workman et al., 2001). Hence, we ran simulations with two mathematical models of human atrial AP displaying distinct type‐1 (Colman–Zhang model) and type‐3 (Grandi–Bers model) AP morphologies. In fact, it is well appreciated that effects of I_Kur block on APD₉₀ are dependent on baseline AP morphology (Wettwer et al., 2004; Workman et al., 2001), with both prolongation and shortening in APD₉₀ being reported experimentally, and also seen in our previous modelling (Colman et al., 2017; Ellinwood et al., 2017a, 2017b). While some of the differences in model responses might be related to distinct AP morphologies, we cannot exclude model‐dependencies due to distinct cellular model structure and models of ionic and Ca²⁺ handling processes. Interestingly, however, analyses using both models demonstrated that combined block of the three atrial‐predominant K⁺ currents enhanced positive rate dependence of action potential duration prolongation and produced positively rate‐dependent synergistic action potential duration prolongation. Collectively, these results demonstrate that combined blockade of the three currents consistently produced favourable anti‐AF effects independent of the baseline electrophysiological characteristics and/or ionic remodelling effects.

Our biophysically detailed models allow investigating the mechanistic underpinnings of the favourable anti‐AF consequences. For example, the mechanism underlying I_Kur (pore) block‐mediated positive rate dependence was explained by the Nattel group with the increased relative contribution of I_Kur to AP repolarization at fast pacing rates due to reduced activation of I_Kr (Aguilar, Feng, Vigmond, Comtois, & Nattel, 2017). Nevertheless, the mechanisms underlying rate dependence of action potential duration change upon ion channel block are complex, and our preliminary analyses suggest that, in addition to the previously described mechanisms, rate‐dependent changes in Na⁺ and Ca²⁺ homeostasis mainly mediate the positive rate dependence of action potential duration, by both influencing the rate‐dependent contribution of the atrial‐predominant K⁺ current (e.g. Ca²⁺‐dependent increase of I_KCa) and causing rate‐dependent shifts in electrogenic Na⁺ and Ca²⁺ transporters (Grandi et al., 2011). Future systematic investigations of these mechanisms are required.

4.5. Limitations and future work

In this study, we simulated block of K⁺ currents without describing any specific, existing compound or compound combinations, which are likely to exert off‐target effects not considered here. We emphasize that we are not advocating reconsideration of previously failed drugs, but rather suggesting that in preclinical developments there are quantitative grounds for pursuing investigation of polytherapy targeting those atrial‐predominant currents we have addressed here, which may also extend to other atrial‐specific synergies.

While our approach shows promise, factors we have disregarded warrant discussion and should be addressed in future investigations. For example, other atrial‐predominant targets could be included (e.g. I_K,ACh and I_Na), and the extent of blockade for each atrial‐predominant K⁺ current could be optimized to achieve desired antiarrhythmic effects while limiting drug doses. We have shown that synergy in prolonging action potential duration increases with the extent of current block, but our approach could be applied to simulating permutations of different degrees of channel block, to identify the optimal combination of targets and their relative block that maximize synergy. Additionally, while we simulated a simple pore block scheme, it might be important to incorporate state‐dependence and use‐dependence of channel blockers in evaluating realistic compounds (Ellinwood et al., 2017a, 2017b; Ni et al., 2017). State‐dependent block models would require additional data describing the affinity of the drug compound to various channel conformational/gating modalities (e.g. open, closed, and/or inactivation state block), binding kinetics, drug polarity and charge for the drug‐channel interaction (Yang et al., 2020). This type of information is relatively sparse for drugs targeting the atrial predominant K⁺ currents, particularly relative to the binding characteristics of Na⁺ channel blockers, which are much better characterized and known to play an important role for atrial selective I_Na block (Burashnikov et al., 2007; Morotti et al., 2016). Specific data are available that characterize binding mechanisms for I_Kur (Lagrutta, Wang, Fermini, & Salata, 2006) and differing modes of block (pore‐block versus modulatory) and their regulation by voltage and pH are known differentiating characteristics for I_KCa inhibitors (Brown, Shim, Christophersen, & Wulff, 2020). Less extensive characterization is available for I_K2P antagonists, although many AF‐relevant drugs are known to inhibit the TASK‐1 channels simulated here. The range of questions evoked by including model variations for these characteristics would be poorly constrained at this point and applying modelling approaches to explore the possible alterations due to those dynamic effects is far beyond the scope of the current study. However, questions of that type provide an excellent basis for extending understanding of the synergistic characteristics we have observed here. Further, while we can simply simulate certain degrees of current block, the cellular concentrations of a same systemic drug dose can vary across individuals. Thus, future studies should account for both (population) pharmacokinetic (PK) and pharmacodynamic (PD) drug interactions.

Although both the Colman–Zhang and Grandi–Bers models have been well established and widely used, it is worth noting that the APD₉₀ produced from the two models are lower than those from the experimental measurements (Figure 1). This limitation might be explained by the fact that the models were originally built to reflect different experimental sources and that published human atrial myocyte data are quite variable and is mitigated, at least in part, by the use of two model populations that account for some of the variability.

We calibrated our model populations to the observed experimental ranges. Calibration to experimental distribution (Lawson et al., 2018) could be implemented in future studies to attain model populations with higher fidelity of clinical variabilities. Although we started from well‐validated baseline models, since we only used action potential duration and resting membrane potential as biomarkers, parameter unidentifiability is a potential limitation, which could be attenuated if broader experimental datasets were available. Further, we simulated AF model populations with variable degrees of AF‐remodelling. As AF is a progressive disease, the proposed multiple atrial‐predominant‐current block might have different efficacy for various AF stages, e.g. in paroxysmal AF, which displays distinct AP and Ca²⁺ biomarkers compared to chronic AF (Nattel & Dobrev, 2016). The complexity of AF‐related fibrosis (Burstein & Nattel, 2008) may present complex tissue responses to the proposed multicurrent block strategy and require more realistic heterogenous descriptions in tissue simulations (Zahid et al., 2016).

We analysed the effects of current block by quantifying changes in APD₉₀ at the cellular level and effective refractory period and wavelength in tissue. This approach is consistent with the accepted mechanisms of action of class III antiarrhythmics, but is limited in that it required exclusion of model variants exhibiting action potential duration alternans, which prevented ΔAPD analysis. Nevertheless, mechanisms underlying both AF and antiarrhythmic drugs' action are highly complex and future investigations might account for composite metrics (Yang et al., 2016), including, for example APD₅₀, Ca²⁺‐related biomarkers (Ellinwood et al., 2017a, 2017b), presence of afterdepolarizations or alternans, and AP propagation dynamics in tissue.

Autonomic regulation of atrial function contributes importantly to the onset and maintenance of AF (Linz et al., 2019). The autonomic nervous system regulates atrial electrophysiology and modulates the function of multiple atrial‐predominant currents, for example I_K,Ach, which becomes constitutively active in AF (Dobrev et al., 2005). Therefore, it may be important to incorporate autonomic regulations in future pharmacology investigations.

4.6. Conclusions

Using state‐of‐the‐art Quantitative Systems Pharmacology approaches, we showed that multi‐atrial‐predominant K⁺‐current block produces favourable positive rate‐dependent synergistic antiarrhythmic effects, suggesting that this strategy may be effective against AF and limit cardiac side effects.

AUTHOR CONTRIBUTIONS

H.N. and E.G. designed the research. H.N. performed the research. H.N., A.F.I., W.R.G, S.M.N., H.Z., A.G.E., S.M., and E.G. analysed the data. H.N. and E.G. wrote the manuscript. A.F.I., W.R.G., S.M.N., H.Z., A.G.E., and S.M. revised the manuscript.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

DECLARATION OF TRANSPARENCY AND SCIENTIFIC RIGOUR

This Declaration acknowledges that this paper adheres to the principles for transparent reporting and scientific rigour of preclinical research as stated in the BJP guidelines for Design and Analysis and as recommended by funding agencies, publishers and other organisations engaged with supporting research.

Supporting information

Table S1. AF model subpopulations created with different combinations of AFremodeling induced modulations on I_Kur, I_KCa and I_K2P.

Table S2. Summary of action potential duration (APD) and resting membrane potential (RMP) of the simulated atrial populations in nSR and AF conditions.

Table S3. Summary of APD and RMP for each AF subpopulation with the CZ and GB models.

Table S4. APD₉₀ changes due to 50% of mono‐ or multi‐ K₊ currents in the CZ and GB AF‐populations.

Table S5. Summary of sensitivity coefficients describing influence of G_K2P, G_KCa and GKur on atrial repolarization reserve measured via blocking I_K2P, I_KCa or I_Kur, respectively.

Table S6. Summary of simulated APD₉₀, wavelength (WL) and effective refractory period (ERP) in the 1D strand tissue models in AF conditions in the absence or presence of AFremodeling on tissue electrical coupling.

Figure S1. Parameter sensitivity analysis of APD and rate‐dependent APD modulation for the virtual atrial populations. (A‐D) nSR populations. (E‐H) AF populations. (A,C,E,G) Sensitivity coefficients of APD to perturbations of transmembrane currents for myocytes paced at 1 Hz and 3 Hz. (B,D,F,H) APD rate‐dependence coefficients (B_RD) for these transmembrane currents. Positive B_RD indicates inhibition of this current favors producing positive rate‐dependence of APD prolongation, and vice versa. In (E‐H), results for each AF subpopulation are plotted as open circles and those for the aggregate dataset are represented by bar plots.

Figure S2. Example of AP modulations at 1 and 3 Hz by 100% block of (A) I_K2P, (B) I_KCa, (C) I_Kur, (D) I_K2P+I_KCa, (E) I_K2P+I_Kur, (F) I_KCa+I_Kur and (G) I_K2P+I_KCa+I_Kur from simulations with (left columns) CZ (subpopulation #5, variant #310) and (right columns) GB models (subpopulation #5, variant #287). Cells were chosen so that the block‐free APD and ΔAPD of single‐current block were close to the median values of the population shown in Fig. 4 of the main text.

Figure S3. Confidence interval of rate‐dependent changes in ΔAPD (3 Hz vs 1 Hz) shown in Figure 4 of the main text. RD of ΔAPD is defined as RD = ΔAPD_3Hz ‐ΔAPD_1Hz.

Figure S4. Parameter sensitivity of repolarization reserve. (A‐C) Sensitivity coefficients of repolarization reserve (RR) derived from the ratio between APD before and after 50% block of (A) I_K2P, (B) I_KCa and (C) I_Kur. Columns are sensitivity coefficients for the (i) CZ and (ii) GB populations. Results for each AF subpopulation are plotted with open circles and those for the aggregate AF dataset are shown in bar plots.

Figure S5. Boxplot of interactions among multi‐current block in APD modulation for cells in each subpopulation. The interactions were defined as the difference in ΔAPD for the combined effects vs the additive sum of the separate effects and normalized to the cell‐matched block‐free APD. In these simulations, each current was subjected to 50% block. Positive interaction indicates synergism whereas negative difference suggests antagonism. Data of 1 Hz are shown in blue and 3 Hz in red.

Figure S6. Example of AP traces showing antagonism in prolonging APD at 1 Hz but synergism at 3 Hz following 100% block of I_K2P and I_Kur with CZ model (subpopulation #5, variant #383).

Figure S7. Effects of mono‐K₊ or multi‐K₊‐current block on virtual atrial tissue populations considering 40% cell‐to‐cell decoupling. Each row depict change in (A) APD, (B) ERP and (C) WL due to current block obtained from virtual atrial strand populations paced at 1 Hz (blue) and 3 Hz (red). Columns describe results from (i) AF subpopulation #1 and (ii) AF subpopulation #5, respectively. WL was computed as the product of APD and CV. RD was deemed from analysis of CI in difference between 3 Hz vs 1 Hz group: “+” for positive RD and “−” for negative RD.

Figure S8. Effects of mono‐ or multi‐K₊ current block on conduction velocity from 1D strand models of AF‐remodeled atrial tissue paced at 1 Hz (blue) and 3 Hz (red) compared to baseline conditions. (A‐B) Simulations results from virtual atrial tissue with (A) control and (B) 40% reduction of cell‐to‐cell coupling. Left and right columns describe results from (i) AF subpopulation 1 and (ii) AF subpopulation 5, respectively.

Figure S9. Confidence interval analysis of rate‐dependent changes in ΔAPD, ΔERP and ΔWL (3 Hz vs 1 Hz) shown in Figure 8 of the main text.

Figure S10. Confidence interval analysis of rate‐dependent changes in ΔAPD, ΔERP and ΔWL (3 Hz vs 1 Hz) with 40% cell‐to‐cell decoupling shown in Figure S7.

Figure S11. Analysis of interactions among I_K2P, I_KCa and I_Kur blockade in modulating APD, ERP and WL in tissue simulations. Confidence intervals were computed for the median interactions in multi‐current block defined as the difference in ΔAPD, ΔERP or ΔWL for the combined effects vs the additive sum of the separate effects. Values were normalized to cell‐matched block‐free values. In these simulations, each current was subjected to 50% block. Positive interaction indicates synergism whereas negative difference suggests antagonism. Data of 1 Hz are shown in blue and 3 Hz in red.

Ni H, Fogli Iseppe A, Giles WR, et al. Populations of in silico myocytes and tissues reveal synergy of multiatrial‐predominant K⁺‐current block in atrial fibrillation. Br J Pharmacol. 2020;177:4497–4515. 10.1111/bph.15198