Modelling the effects of the contaminated environments on tuberculosis in Jiangsu, China

Highlights

• •A tuberculosis model incorporating contaminated environments is developed.
• •A threshold theorem of the model is established.
• •The annual average of the basic reproduction number is obtained.
• •TB in Jiangsu is an endemic disease and will persist for a long time.

Abstract

Tuberculosis (TB) is still an important public health issue in Jiangsu province, China. In this study, based on the TB transmission routes and the statistical data of TB cases, we formulate a novel TB epidemic model accounting for the effects of the contaminated environments on TB transmission dynamics. The value of this study lies in two aspects. Mathematically, we define the basic reproduction number, ${\mathcal{R}}_0$, and prove that ${\mathcal{R}}_0$ can be used to govern the threshold dynamics of the model. Epidemiologically, we find that the annual average ${\mathcal{R}}_0$ is $1.13,>1$ and TB in Jiangsu is an endemic disease. Therefore, in order to control the TB in Jiangsu efficiently, we must decrease the virus shedding rate or increase the recovery rates, and increase the environmental clearance rate.

1. Introduction

Tuberculosis (TB) is an ancient and chronic infectious disease, which is caused by infection with the Mycobacterium tuberculosis (MTB) (Blower et al., 1996). Normally, the TB bacteria are put into the air when a person with TB disease, and TB patients are mainly transmitted by droplets produced by coughing, sneezing, laughing, loud talking, etc. Droplet transmission is the most important way of transmission of TB. When a person breathes in TB bacteria, the bacteria can settle in the lungs and begin to grow (Global, 2018).

It is now widely believed that droplet transmission occurs when a person is in close contact (within 1 m) with someone who has respiratory symptoms (e.g., coughing or sneezing) and is therefore at risk of having his/her mucosae (mouth and nose) or conjunctiva (eyes) exposed to potentially infective respiratory droplets. Transmission may also occur through fomites in the immediate environment around the infected person (Ong et al., 2020). MTB is so small that normal air currents can keep the particles containing MTB airborne and transport them through rooms or some buildings (Dye and Williams, 2000). Thank the insightful work on HFMD (Wang et al., 2016a, Wang et al., 2016b) and COVID-19 (Ding et al., 2020, World Health, 2020), we can believe that MTB can attach to things (such as door handles, towels, handkerchiefs, toys, utensils, bed and toilet seat, bathroom washbasin tap lever, bathroom ceiling-exhaust louvre and stethoscope or thermometer, and so on) used by the TB patients.

TB is closely associated with overcroding and malnutrition, which makes it to be one of the major diseases in poor areas (Lawn and Zumla, 2011). Those at high risk thus include: people who inject illicit drugs, inhabitants and employees of locales where vulnerable people gather (e.g. prisons and homeless shelters), medically underprivileged and resource-poor communities, high-risk ethnic minorities, children in close contact with high-risk category patients, and health-care providers serving these patients (Griffith and Kerr, 1996), include alcoholism (Lawn and Zumla, 2011) and diabetes mellitus (threefold increase) (Restrepo, 2007).

Currently, there are approximately 95$\%$ of the estimated 8 milion new cases of TB occuring in developing countries each year, and two-thirds of which appears in India (27%), China (9%), Indonesia (8%), Philippines (6%), Pakistan (5%), Nigeria (4%), Bangladesh (4%) and South Africa (3%), where 80$\%$ occur among people between the ages of 15 to 59 years. And only 6% of global cases occur in Europe (3%) and the Americas (3%) (Global, 2018).

In recent years, the Chinese government has increased its investment in public health, and the laws and regulations for disease prevention and control has been constantly improved, which provides an important basic guarantee for coping with major public health emergencies, preventing infectious diseases and ensuring the health of the people, thus effectively controlling major infectious diseases. In particular, the incidence of tuberculosis has decreased significantly. According to the report from the World Health Organization, in 2011, China had an estimation of 1.4 million existing TB and 1 million incident TB; in 2017, China had an estimation of 778,390 existing TB and 773,150 incident TB (Global, 2018); in 2018, China had 823,342 new and relapse TB (Survey of the epidemic situation of notifiable infectious diseases in China, 2018). Obviously, TB is still an important public health issue in China (Hu and Sun, 2013).

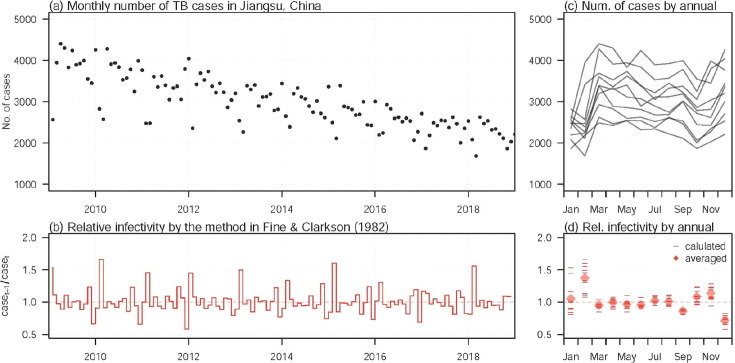
It was known that 80% of TB exists in rural areas, particularly in north and north-western regions with low socioeconomic status in China (Hu and Sun, 2013). But in the past 20 years in Jiangsu province, China (see Fig. 1 for the location of Jiangsu province in China), one of the most developed areas in China in economy, technology and culture and the total output is one of the largest in the nation, TB ranked first in the number of notifiable B infectious diseases (The reported tuberculosis cases in Jiangsu province, 2018). In 2011, Jiangsu had 39,589 existing TB, and in 2017, 28,402 existing TB and in 2018, there is 26,506 incident TB. In particular, the incidence of tuberculosis has decreased significantly (see Fig. 3(a) for more details). However, the situation of prevention and control of TB in Jiangsu province is still very serious.

Fig. 1.

The location of Jiangsu province in China.

Fig. 3.

The TB incidences times series and the relative infectivity in Jiangsu, China from 2009 to 2018. Panel (a) shows the monthly number of TB incidences. Panel (c) is an annualised version of panel (a). Panel (b) shows the relative TB infectivity from 2009 to 2018. Panel (d) is an annualised version of panel (b), where the short bars are the relative infectivity of each month of different years, and the diamonds are the average of each month.

It is worthy to notice that mathematical models have played a key role in the formulation of TB control strategies. Waaler et al. (1962) introduced the first mathematical model for TB in ordinary differential equations. The simplest TB transmission models include classes of susceptible, exposed, and infectious individuals, and hence, they are known as the SEI models. Of course, there are more factors that includes drug-resistant strains, fast and slow progression, confection with HIV, relapse, reinfection, migration, treatment, seasonality, and vaccination are incorporating into studying the transmission dynamics has been searched by many authors. Dye et al. (1998) present a model with explicit fast and slow progression from two latent classes. Ziv et al. (2004) used mathematical models to predict the potential public health impact of new TB vaccines in high-incidence countries. Porco and Blower (1998) included the aspect of disease relapse into their model. Then, there are mathematical models of TB including reinfection in some authors’ article and they assumed that the rate of reinfection is a multiple of the rate of first infection (Feng et al., 2000, Suzanne et al., 2005, Liu et al., 2010).

On the other hand, the TB can survive for a long period outside the host in suitable conditions, and hence contaminated environments may play important role in TB infection. There are some scholars investigated the disease dynamics in the contaminated environments. Wang et al., 2016a, Wang et al., 2016b, Chadsuthi and Wichapeng (2018) investigated the roles that asymptomatic individuals and contaminated environments played in Hand-foot-mouth disease dynamics. Machado et al. (2017) developed and implemented an integrative epidemiologic cross-sectional study that allows identifying and characterising exposure pathways of populations living and working on the shores of a contaminated estuarine environment.

There naturally comes a question that how do the contaminated environments affect the transmission dynamics of TB in Jiangsu, China?.

The main focus of this paper is to investigate how contaminated environments affect TB dynamics through studying the threshold dynamics of a general TB model. And the rest of the paper is organized as follows. In Section 2, we formulate the model in details. In Section 3, we give the dynamics analysis of the model, we introduce the basic reproduction number ${\mathcal{R}}_0$ and prove that ${\mathcal{R}}_0$ can be used to govern the threshold dynamics of the model. In Sections 4, we give the TB epidemics in Jiangsu, China via numerical simulations. In Section 5, we provide a brief discussion and the summary of the main results.

2. Model derivation

Suppose that the total population individuals $N\left(t\right)$ divide into susceptible $S\left(t\right)$, infectious but not yet symptomatic, i.e., pre-symptomatic $T_e\left(t\right)$, infectious with symptoms $T\left(t\right)$, and recovered $R\left(t\right)$. We further consider the TB virus concentration in environment as $W\left(t\right)$, which is the density of pathogen of the contaminated environments including door handles, towels, handkerchiefs, toys, utensils, bed and toilet seat, bathroom washbasin tap lever, bathroom ceiling-exhaust louvre etc. at time t. And our model involves two typical transmissions: one is the direct transmission between susceptible $S\left(t\right)$ and infected individuals (including pre-symptomatic $T_e\left(t\right)$ and symptomatic $T\left(t\right)$) with rate of ${\beta }_1\left(t\right)$; the other is the indirect transmission to susceptible individuals and infected individuals (i.e., $T_e\left(t\right)$ and $T\left(t\right)$) by contaminated environments $W\left(t\right)$ with rate of ${\beta }_2\left(t\right)$. A seasonality in the long-term patterns of TB incidences time series can be observed evidently (see Fig. 3), and there is a growing awareness that seasonality can cause population fluctuations ranging from annual cycles to multiyear oscillations (Liu et al., 2010), and hence we assume that the transmission rates ${\beta }_1$ and ${\beta }_2\left(t\right)$ to be continuous and non-negative periodic functions with period of $\omega$. A flow diagram describing the model is depicted in Fig. 2 .

Fig. 2.

Flow diagram representing TB transmission routes.

Thus we can establish the following TB epidemic model involving five ordinary differential equations:

$$\left\{\begin{array}{cc}\frac{\mathrm{d}S}{\mathrm{d}t}=\mathrm{\Lambda }-\mu S-{\beta }_1\left(t\right)S\frac{T}{N}-{\beta }_2\left(t\right)\mathit{SW}+\rho R,\hfill & t>0,\hfill \\ \frac{\mathrm{d}{T}_e}{\mathrm{d}t}=(1-p){\beta }_1\left(t\right)S\frac{T}{N}+(1-q){\beta }_2\left(t\right)\mathit{SW}-(\mu +\upsilon +{\gamma }_1)T_e,\hfill & t>0,\hfill \\ \frac{\mathrm{d}T}{\mathrm{d}t}=\upsilon T_e+p{\beta }_1\left(t\right)S\frac{T}{N}+q{\beta }_2\left(t\right)\mathit{SW}-(\mu +\delta +{\gamma }_2)T,\hfill & t>0,\hfill \\ \frac{\mathrm{d}R}{\mathrm{d}t}={\gamma }_1{T}_e+{\gamma }_{2}T-\mu R-\rho R,\hfill & t>0,\hfill \\ \frac{\mathrm{d}W}{\mathrm{d}t}=\alpha T-\mathit{cW},\hfill & t>0,\hfill \end{array}\right)$$ (2.1)

with the initial conditions

$$\begin{array}{c}S\left(0\right)=S_0,T_e\left(0\right)=T_{e0},T\left(0\right)=T_0,R\left(0\right)=R_0,W\left(0\right)=W_0,\hfill \end{array}$$ (2.2)

and $N=S+T_e+T+R$.The meanings of each variables and parameters in model (2.1) are as follows.

• • $\mathrm{\Lambda }$: the recruitment rate of susceptible;
• • $\mu$: the per capita natural mortality rate;
• • ${\beta }_1\left(t\right)$: the rate of the susceptible get infected by direct individual-to-individual transmission;
• • ${\beta }_2\left(t\right)$: the rate of the susceptible get infected by indirect contaminated environment transmission;
• • p: proportion of TB symptomatic infectious by direct transmission;
• • q: proportion of TB symptomatic infectious by indirect transmission;
• • $\upsilon$: reactivation rate the pre-symptomatic infectious;
• • ${\gamma }_1$: the recovery rate of the pre-symptomatic infectious;
• • ${\gamma }_2$: the recovery rate of the symptomatic infectious;
• • $\rho$: the rate from recovered to susceptible.
• • $\delta$: disease-related death;
• • $\alpha$: the virus shedding rate from symptomatic infected individuals;
• • c: the clearance rate of the virus in the environments.For the sake of conveniently analysis, set $u\left(t\right)=(u_1,u_2,u_3,u_4,u_5)=(T_e,T,W,R,S)$. Then model (2.1) with (2.2) is equivalent to the following system:

$$\left\{\begin{array}{cc}\frac{\mathrm{d}{u}_1}{\mathrm{d}t}=(1-p){\beta }_1\left(t\right)u_5\frac{u_2}{N}+(1-q){\beta }_2\left(t\right)u_5{u}_3-(\mu +\upsilon +{\gamma }_1)u_1,\hfill & t>0,\hfill \\ \frac{\mathrm{d}{u}_2}{\mathrm{d}t}=\upsilon u_1+p{\beta }_1\left(t\right)u_5\frac{u_2}{N}+q{\beta }_2\left(t\right)u_5{u}_3-(\mu +\delta +{\gamma }_2)u_2,\hfill & t>0,\hfill \\ \frac{\mathrm{d}{u}_3}{\mathrm{d}t}=\alpha u_2-{\mathit{cu}}_3,\hfill & t>0,\hfill \\ \frac{\mathrm{d}{u}_4}{\mathrm{d}t}={\gamma }_1{u}_1+{\gamma }_2{u}_2-\mu u_4-\rho u_4,\hfill & t>0,\hfill \\ \frac{\mathrm{d}{u}_5}{\mathrm{d}t}=\mathrm{\Lambda }-\mu u_5-{\beta }_1\left(t\right)u_5\frac{u_2}{N}-{\beta }_2\left(t\right)u_5{u}_3+\rho u_4,\hfill & t>0,\hfill \end{array}\right)$$ (2.3)

with initial conditions

$$u\left(0\right)=u_0,u_i\left(0\right)=u_i^0(i=1,2,\cdots 5)\text{.}$$

Theorem 2.1

Model (2.3) has a unique and bounded solution with the initial value $u_0\in {\mathbb{R}}_{+}^5$ , i.e,

$${\displaystyle \underset{t\to \infty }{\lim }}N\left(t\right)⩽\frac{\mathrm{\Lambda }}{\mu },{\displaystyle \underset{t\to \infty }{\lim }}{u}_3\left(t\right)⩽\frac{\alpha \mathrm{\Lambda }}{c\mu }\text{.}$$

Proof

Considering the non-negativity of I, i.e., $I⩾0$, the total population $N\left(t\right)$ can be determined by the following model:

$$\left\{\begin{array}{c}\frac{\mathrm{d}N}{\mathrm{d}t}=\mathrm{\Lambda }-\mu N-\delta I⩽\mathrm{\Lambda }-\mu N,\hfill \\ N\left(0\right)=u_1^0+u_2^0+u_4^0+u_5^0=N_0\text{.}\hfill \end{array}\right)$$ (2.4)

It is easy to see that the linear differential equation $\frac{\mathit{dN}}{\mathit{dt}}=\mathrm{\Lambda }-\mu N$ has a unique equilibrium $N^{\ast }=\frac{\mathrm{\Lambda }}{\mu }$, which is globally asymptotically stable. The comparison principle implies that ${\lim }_{t\to \infty }N\left(t\right)⩽\frac{\mathrm{\Lambda }}{\mu }$.Then $\forall \epsilon >0$, there exists a $t_0>0$ such that

$$N\left(t\right)⩽N^{\ast }+\epsilon ,t>t_0\text{.}$$ (2.5)

Then we have

$$\frac{\mathrm{d}{u}_3}{\mathrm{d}t}⩽\alpha (N^{\ast }+\epsilon )-{\mathit{cu}}_3,t>t_0\text{.}$$

It follows from the comparison principle that ${\lim }_{t\to \infty }{u}_3\left(t\right)⩽\frac{\alpha \mathrm{\Lambda }}{c\mu }$. This completes the proof.

Let ${\mathrm{\Phi }}_{A(·)}\left(t\right)$ be the fundamental solution matrix of equation $\frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}=A\left(t\right)\mathbf{x}$, where $A\left(t\right)$ is a continuous, cooperative, irreducible and $\omega$-periodic $n\times n$ functional matrix. Let $r\left({\mathrm{\Phi }}_{A(·)}\right(\omega \left)\right)$ be the spectral radius of ${\mathrm{\Phi }}_{A(·)}\left(\omega \right)$.

Lemma 2.2

[Zhang and Zhao, 2007, Lemma 2.1] Let $\xi =\frac{1}{\omega }\ln r\left({\mathrm{\Phi }}_{A(·)}\right(\omega \left)\right)$ . Then there exists a positive $\omega$ -periodic function $v\left(t\right)$ such that $e^{\xi t}v\left(t\right)$ is a solution of $\frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}=A\left(t\right)\mathbf{x}$ .

3. Dynamics analysis

3.1. Basic reproduction number

Following (Diekmann et al., 1990, Van den Driessche and Watmough, 2002, Diekmann and Heesterbeek, 2000), let $\mathcal{F}\left(u_i\right)$ be the input rate of newly infected individuals and $\mathcal{V}\left(u_i\right)$ be the rate of transfer of individuals, then

$$\mathcal{F}\left(u_i\right)=\left(\begin{array}{c}\hfill (1-p){\beta }_1\left(t\right)u_5\frac{u_2}{N}+(1-q){\beta }_2\left(t\right)u_5{u}_3\hfill \\ \hfill p{\beta }_1\left(t\right)u_5\frac{u_2}{N}+q{\beta }_2\left(t\right)u_5{u}_3\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right)$$

and

$$\mathcal{V}\left(u_i\right)=\left(\begin{array}{c}\hfill (\mu +\upsilon +{\gamma }_1)u_1\hfill \\ \hfill -\upsilon u_1+(\mu +\delta +{\gamma }_2)u_2\hfill \\ \hfill -\alpha u_2+u_3\hfill \\ \hfill -({\gamma }_1{u}_1+{\gamma }_2{u}_2-\mu u_4-\rho u_4)\hfill \\ \hfill -\left(\mathrm{\Lambda }-\mu u_5-{\beta }_1{u}_5\frac{u_2}{N}-{\beta }_2{u}_5{u}_3+\rho u_4\right)\hfill \end{array}\right)\text{.}$$

Obviously model (2.3) admits a disease free equilibrium (DFE) $E_0=\left(0,0,0,0,\frac{\mathrm{\Lambda }}{\mu }\right)$.

Then

$$\begin{array}{c}F\left(t\right)=\left(\frac{\partial {\mathcal{F}}_i\left(u_i\right)}{\partial u_i}\right){|}_{E_0}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \left(1-p\right){\beta }_1\left(t\right)\hfill & \hfill \frac{\left(1-q\right){\beta }_2\left(t\right)\mathrm{\Lambda }}{\mu }\hfill \\ \hfill 0\hfill & \hfill p{\beta }_1\left(t\right)\hfill & \hfill \frac{q{\beta }_2\mathrm{\Lambda }}{\mu }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),i=1,2,3,\hfill \\ V\left(t\right)=\left(\frac{\partial {\mathcal{V}}_i\left(u_i\right)}{\partial u_i}\right){|}_{E_0}=\left(\begin{array}{ccc}\hfill \mu +\upsilon +{\gamma }_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\upsilon \hfill & \hfill \mu +\delta +{\gamma }_2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\alpha \hfill & \hfill c\hfill \end{array}\right),i=1,2,3\text{.}\hfill \end{array}$$

Let $Y(t,s)(t⩾s)$ be the evolution operator of the linear $\omega$-periodic system

$$\frac{\mathrm{d}y}{\mathrm{d}t}=-V\left(t\right)y\text{.}$$ (3.1)

That is, for each $s\in \mathbb{R}$, the $3\times 3$ matrix $Y(t,s)$ satisfies

$$\frac{\mathrm{d}Y(t,s)}{\mathrm{d}t}=-V\left(t\right)Y(t,s),\forall t⩾s,Y(s,s)=\mathbb{I},$$

where $\mathbb{I}$ is the $3\times 3$ identity matrix. Thus, the monodromy matrix ${\mathrm{\Phi }}_{-V}\left(t\right)$ of (3.1) equals $Y(t,0),t⩾0$.

Following the method established by Wang and Zhao (2008), let $\varphi \left(s\right)$ be $\omega$-periodic in s and the initial distribution of infectious individuals. So $F\left(s\right)\varphi \left(s\right)$ is the rate of new infections produced by the infected individuals who are introduced at time s. When $t⩾s,Y(t,s)F\left(s\right)\varphi \left(s\right)$ gives the distribution of those infected individuals who are newly infected by $\varphi \left(s\right)$ and remain in the infected compartments at time t. Naturally,

$${\int }_{-\infty }^{t}Y(t,s)F\left(s\right)\varphi \left(s\right)\mathrm{d}s={\int }_0^{\infty }Y(t,t-a)F(t-a)\varphi (t-a)\mathrm{d}a$$

is the distribution of accumulative new infections at time t produced by all those infected individuals $\varphi \left(s\right)$ introduced at time previous to t.

Let $C_{\omega }$ be the ordered Banach space of all $\omega$-periodic functions from $\mathbb{R}$ to ${\mathbb{R}}^3$, which is equipped with the maximum norm $\Vert ·\Vert$ and the positive cone $C_{\omega }^{+}≔\{\varphi \in C_{\omega }:\varphi (t)⩾0,\forall t\in \mathbb{R}\}$. Then we can define a linear operator $\mathcal{L}$ implies that

$$\left(\mathcal{L}\varphi \right)\left(t\right)≔{\int }_0^{\infty }Y(t,t-a)F(t-a)\varphi (t-a)\mathrm{d}a,\forall t\in \mathbb{R},\varphi \in C_{\omega },$$

which is called the next infection operator, and the spectral radius of $\mathcal{L}$ is defined as the basic reproduction number:

$${\mathcal{R}}_0≔r\left(\mathcal{L}\right)\text{.}$$ (3.2)

In order to characterise ${\mathcal{R}}_0$, we introduce the linear $\omega$-periodic system

$$\frac{\mathrm{d}w}{\mathrm{d}t}=\left(-V\left(t\right)+\frac{F\left(t\right)}{\lambda }\right)w,t\in {\mathbb{R}}_{+}$$ (3.3)

with parameter $\lambda \in \mathbb{R}$. Let $W(t,s,\lambda ),t⩾s$ be the evolution operator of system (3.3) on ${\mathbb{R}}^3$. Clearly, ${\mathrm{\Phi }}_{F-V}\left(t\right)=W(t,0,1),t⩾0$. Hence, we derive

$${\mathrm{\Phi }}_{\frac{F}{\lambda }-V}\left(t\right)=W(t,0,\lambda )\text{.}$$

Following the general calculation procedure in Wang and Zhao (2008, Theorem 2.1), the basic reproduction number ${\mathcal{R}}_0$ is the unique solution of $r\left(W\right(\omega ,0,\lambda \left)\right)=1$.

Following Wang and Zhao (2008), we can obtain the relation between ${\mathcal{R}}_0$ and $r\left(W\right(\omega ,0,\lambda \left)\right)=1$ shown in the following lemma.

Lemma 3.1

[Wang and Zhao, 2008, Theorem 2.2] The following statements are valid:

• (i)  ${\mathcal{R}}_0=1$ iff $r\left({\mathrm{\Phi }}_{F-V}\right(\omega \left)\right)=1$;

• (ii)  ${\mathcal{R}}_0>1$ iff $r\left({\mathrm{\Phi }}_{F-V}\right(\omega \left)\right)>1$;

• (iii)  ${\mathcal{R}}_0<1$ iff $r\left({\mathrm{\Phi }}_{F-V}\right(\omega \left)\right)<1$.

Remark 3.2

In the special case of ${\beta }_1\left(t\right)={\beta }_1$ and ${\beta }_2\left(t\right)={\beta }_2$, the basic reproduction number ${\mathcal{R}}_0$ of model (2.3) is ${\bar{\mathcal{R}}}_0=r\left({\mathit{FV}}^{-1}\right)$, i.e.,

$${\mathcal{R}}_0≔{\mathcal{R}}_0^{\mathrm{dir}}+{\mathcal{R}}_0^{\mathrm{ind}}=\frac{c\mu {\beta }_1(\mu p+p{\gamma }_1+\upsilon )+\mathrm{\Lambda }\alpha {\beta }_2\left(\mu q+q{\gamma }_1+\upsilon \right)}{c\mu \left(\mu +\upsilon +{\gamma }_1\right)\left(\mu +\delta +{\gamma }_2\right)},$$ (3.4)

where

$$\begin{array}{c}{\mathcal{R}}_0^{\mathrm{dir}}≔\frac{{\beta }_1(\mu p+p{\gamma }_1+\upsilon )}{\left(\mu +\upsilon +{\gamma }_1\right)\left(\mu +\delta +{\gamma }_2\right)},{\mathcal{R}}_0^{\mathrm{ind}}≔\frac{{\beta }_2\mathrm{\Lambda }\alpha \left(c\mu q+q{\gamma }_1+\upsilon \right)}{c\mu \left(\mu +\upsilon +{\gamma }_1\right)\left(\mu +\delta +{\gamma }_2\right)}\text{.}\hfill \end{array}$$

Here, ${\mathcal{R}}_0^{\mathrm{dir}}$ indicates the average number of secondary infections generated by a single infected individual introduced into a completely susceptible population directly during their life cycle. ${\mathcal{R}}_0^{\mathrm{ind}}$ indicates the average number of secondary infections generated by the virus that is released into the environment during their life cycle.

Remark 3.3

From (3.4), we can know that the basic reproduction number ${\mathcal{R}}_0$ can be decomposed into two parts, i.e., the direct, ${\mathcal{R}}_0^{\mathrm{dir}}$, and indirect reproduction number, ${\mathcal{R}}_0^{\mathrm{ind}}$. Because of the complexity of ${\mathcal{R}}_0$, defined as the spectral radius of $\mathcal{L}$, and hence, in the numerical simulation in Section 4.2.2, ${\mathcal{R}}_0^{\mathrm{dir}}$ is modeled as a constant to be estimated, ${\mathcal{R}}_0^{\mathrm{ind}}$ denoted by ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$, to be a periodic time-varying function constructed by a step function. According to the strong seasonality in both TB incidences and relative infectivity, the periodicity of ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$ is considered to be one year, i.e., ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)={\mathcal{R}}_0^{\mathrm{ind}}(t+\mathrm{oneyear})$. We model ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$ changes across different months, in other words, we can obtain different values of ${\mathcal{R}}_0^{\mathrm{ind}}$s in each month. The value of ${\mathcal{R}}_0^{\mathrm{ind}}$ is restricted to be the same within each month.

3.2. Threshold dynamics

Theorem 3.4

If ${\mathcal{R}}_0<1$ , the DFE $E_0=(0,0,0,0,\mathrm{\Lambda }/\mu )$ of model (2.3) is global asymptotically stable.

Proof

Consider an auxiliary system

$$\left\{\begin{array}{c}\frac{\mathrm{d}{w}_1}{\mathrm{d}t}=(1-p){\beta }_1\left(t\right)w_2+(1-q){\beta }_2\left(t\right)(N^{\ast }+∊)w_3-(\mu +\upsilon +{\gamma }_1)w_1,\hfill \\ \frac{\mathrm{d}{w}_2}{\mathrm{d}t}=p{\beta }_1\left(t\right)w_2+q{\beta }_2\left(t\right)(N^{\ast }+∊)w_3+\upsilon w_1-(\mu +\delta +{\gamma }_2)w_2,\hfill \\ \frac{\mathrm{d}{w}_3}{\mathrm{d}t}=\alpha w_2-{\mathit{cw}}_3,\hfill \end{array}\right)$$ (3.5)

which is equivalent to

$$\frac{\mathrm{d}w}{\mathrm{d}t}=\left(F\right(t)-V(t)+∊M(t\left)\right)u,$$

where $w={(w_1,w_2,w_3)}^{\mathrm{T}}$ and

$$M\left(t\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill (1-q){\beta }_2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill q{\beta }_2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

It follows Lemma 2.2 that there exits a positive $\omega$-periodic function $v\left(t\right)=(v_1,v_2(t),v_3(t\left)\right)$ such that $e^{\mathit{pt}}v\left(t\right)$ is a solution of (3.5), where $p=\frac{1}{\omega }\ln r\left({\mathrm{\Phi }}_{F-V+\epsilon M}\right)$. Choose $t_1>t_0$ and a small number $\alpha >0$ such that $w\left(t_1\right)⩽\alpha v\left(0\right)$. Then we can get $w\left(t\right)⩽\alpha v(t-t_1)e^{p(t-t_1)}$ for $t>t_1$. By the comparison principle, we have

$${\left(u_1\right(t),u_2(t),u(t\left)\right)}^{\mathbf{T}}⩽w\left(t\right)⩽\alpha v(t-t_1)e^{p(t-t_1)},\forall t>t_1,$$

where $\mathbf{T}$ is the transposition of the vector. It follows from ${\mathcal{R}}_0<1$ that $r\left({\mathrm{\Phi }}_{F-V}\right(\omega \left)\right)<1$. Since $r\left({\mathrm{\Phi }}_{F-V+\epsilon M}\right(\omega \left)\right)$ is continuous for all small $\epsilon$, we can choose $\epsilon >0$ small enough such that $r\left({\mathrm{\Phi }}_{F-V+\epsilon M}\right(\omega \left)\right)<1$. Hence, we get $p<0$. It follows that $w\left(t\right)\to 0$ as $t\to \infty$. Hence ${\lim }_{t\to \infty }(u_1,u_2,u_3)=(0,0,0)$. By the fourth and fifth equation of model (2.3), we get ${\lim }_{t\to \infty }{u}_4\left(t\right)=0,{\lim }_{t\to \infty }{u}_5\left(t\right)=\frac{\mathrm{\Lambda }}{\mu }$. This indicates that DFE $E_0$ of model (2.3) is global asymptotically stable.

In the following, we attempt to explore the uniform persistence of model (2.1) when ${\mathcal{R}}_0>1$. Define

$$\begin{array}{c}X≔\left\{\right(u_1,u_2,u_3,u_4,u_5):u_i⩾0,i=1,2,\cdots 5\},\hfill \\ X_0≔\left\{\right(u_1,u_2,u_3,u_4,u_5)\in X:u_i>0,i=1,2,3,4\},\hfill \\ \partial X_0≔X⧹X_0\text{.}\hfill \end{array}$$

Lemma 3.5

X and $X_0$ are positively invariant.

Proof

From the fifth equation of model (2.3), we can derive that

$$\frac{\mathrm{d}{u}_5}{\mathrm{d}t}⩾\mathrm{\Lambda }-a\left(t\right)u_5,$$

where $a\left(t\right)=\mu +{\beta }_1\left(t\right)\frac{u_1}{N}+{\beta }_2\left(t\right)u_3$. Then

$$u_5\left(t\right)⩾e^{-{\int }_0^{t}a\left({\tau }_1\right)\mathrm{d}{\tau }_1}\left(u_5^0+\mathrm{\Lambda }{\int }_0^t{e}^{{\int }_0^{{\tau }_2}a\left({\tau }_1\right)\mathrm{d}{\tau }_1}\mathrm{d}{\tau }_2\right)>0,\forall t>0\text{.}$$ (3.6)

By (Smith, 1996, Theorem 4.1.1) as generalized to nonautonomous systems, the irreducibility of the cooperative matrix

$$\stackrel{\sim }{M}\left(t\right)=\left(\begin{array}{cccc}\hfill -(\mu +\upsilon +{\gamma }_1)\hfill & \hfill (1-p){\beta }_1\left(t\right)\frac{u_5}{N}\hfill & \hfill (1-q){\beta }_2\left(t\right)u_5\hfill & \hfill 0\hfill \\ \hfill \upsilon \hfill & \hfill p{\beta }_1\left(t\right)\frac{u_5}{N}-(\mu +\delta +{\gamma }_2)\hfill & \hfill q{\beta }_2\left(t\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \alpha \hfill & \hfill -c\hfill & \hfill 0\hfill \\ \hfill {\gamma }_1\hfill & \hfill {\gamma }_2\hfill & \hfill 0\hfill & \hfill -(\mu +\rho )\hfill \end{array}\right)$$

implies that ${\left(u_1\right(t),u_2(t),u_3(t),u_4(t\left)\right)}^{\mathrm{T}}\gg 0,\forall t>0$. Thus, X and $X_0$ are positively invariant. Clearly, $\partial X_0$ is relatively closed in X.

Let $P:X\to X$ be the Poincaré map associated with model (2.3), that is,

$$P\left(u_0\right)=u(\omega ,u_0),\forall u_0\in X,$$

where $u(t,u_0)$ is the unique solution of model (2.3) with $u\left(0\right)=u_0$. Then

$$P^m\left(u_0\right)=u(m\omega ,u_0),\forall m⩾0\text{.}$$

From Theorem 2.1, we know that P is a dissipative point on ${\mathbb{R}}_{+}^5$. Thus P admits a global attractor, which attracts every bounded set in ${\mathbb{R}}_{+}^5$. We then introduce the following lemma.

Lemma 3.6

If ${\mathcal{R}}_0>1$ , there exists a ${\sigma }^{\ast }>0$ such that, $\forall u_0\in X_0$ , when $\Vert u_0-E_0\Vert ⩽{\sigma }^{\ast }$ , there is

$${\displaystyle \underset{m\to \infty }{\lim \sup }}d\left(P^m\right(u_0),E_0)⩾{\sigma }^{\ast },$$

where $d\left(P^m\right(u_0),E_0)$ represents distance between $P^m\left(u_0\right)$ and $E_0$ .

Proof

Since ${\mathcal{R}}_0>1$, Lemma 3.1 implies that $r\left({\mathrm{\Phi }}_{F-V}\right(\omega \left)\right)>1$. Then we can choose $∊>0$ small enough that $r\left({\mathrm{\Phi }}_{F-V+M_{∊}}\right(\omega \left)\right)>1$, where

$$M_{∊}\left(t\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{2∊(1-q){\beta }_2\left(t\right)}{N^{\ast }+∊}\hfill & \hfill (1-q){\beta }_2\left(t\right)∊\hfill \\ \hfill 0\hfill & \hfill \frac{2∊q{\beta }_2\left(t\right)}{N^{\ast }+∊}\hfill & \hfill q{\beta }_2\left(t\right)∊\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$ (3.7)

By the continuity of the solutions with respect to the initial values, for $∊>0$, there exists a ${\sigma }^{\ast }>0$ such that $\forall u_0\in X_0$ with $\Vert u_0-E_0\Vert ⩽{\sigma }^{\ast }$, we can obtain

$$\Vert u(t,u_0)-u(t,E_0)\Vert ⩽∊,\forall t\in [0,\omega ]\text{.}$$

We proceed by contradiction to prove that

$${\displaystyle \underset{m\to \infty }{\lim \sup }}d\left(P^m\right(x_0),E_0)⩾{\sigma }^{\ast }\text{.}$$

If not, we can get

$${\displaystyle \underset{m\to \infty }{\lim \sup }}d\left(P^m\right(x_0),E_0)<{\sigma }^{\ast }\mathrm{for}\mathrm{some}{u}_0\in X_0\text{.}$$

Without loss of generality, we can assume that $d\left(P^m\right(u_0),E_0)<{\sigma }^{\ast }$ for all $m⩾0$. Then we can get

$$\Vert u(t,P^m(u_0\left)\right)-u(t,E_0)\Vert ⩽∊,\forall t\in [0,\omega ]\text{.}$$

For any $t⩾0$, let $t=m\omega +t\prime$, where $t\prime \in [0,\omega ]$ and $m=\left[\frac{t}{\omega }\right]$, which is the greatest integer less than or equal to $\frac{t}{\omega }$. Then,

$$\Vert u(t,P^m(u_0\left)\right)-u(t,E_0)\Vert =\Vert u(t\prime ,P^m(u_0\left)\right)-u(\prime ,E_0)\Vert ⩽∊,\forall t⩾0\text{.}$$

It follows from (2.5) that there exists $t_2>t_0$ that $N^{\ast }-∊⩽u_5\left(t\right)⩽N^{\ast }+∊,0⩽u_i⩽∊,i=1,2,3,4$ and $\frac{u_5}{N}⩾\frac{N^{\ast }-∊}{N^{\ast }+∊}=1-\frac{2∊}{N^{\ast }+∊}$ for $t>t_2$.

Consider the following auxiliary system

$$\left\{\begin{array}{cc}\frac{\mathrm{d}{\overline{w}}_1}{\mathrm{d}t}=(1-p){\beta }_1\left(t\right)\left(1-\frac{2∊}{N^{\ast }+∊}\right){\overline{w}}_2+(1-q){\beta }_2\left(t\right)(N^{\ast }-∊){\overline{w}}_3-(\mu +\upsilon +{\gamma }_1){\overline{w}}_1,\hfill & t>0,\hfill \\ \frac{\mathrm{d}{\overline{w}}_2}{\mathrm{d}t}=p{\beta }_1\left(t\right)\left(1-\frac{2∊}{N^{\ast }+∊}\right){\overline{w}}_2+q{\beta }_2(N^{\ast }-∊){\overline{w}}_3+\upsilon u_1-(\mu +\delta +{\gamma }_2){\overline{w}}_2,\hfill & t>0,\hfill \\ \frac{\mathrm{d}{\overline{w}}_3}{\mathrm{d}t}=\alpha {\overline{w}}_2-c{\overline{w}}_3,\hfill & t>0\text{.}\hfill \end{array}\right)$$ (3.8)

which is equivalent to

$$\frac{\mathrm{d}\overline{w}}{\mathrm{d}t}=\left(F\right(t)-V(t)-M_{∊}(t\left)\right)u,$$

where $\overline{w}={({\overline{w}}_1,{\overline{w}}_2,{\overline{w}}_3)}^{\mathrm{T}}$ and $M_{∊}\left(t\right)$ defined as in (3.7).

It follows from Lemma 2.2 that there exists a positive $\omega$-periodic function $\overline{v}\left(t\right)=({\overline{v}}_1,{\overline{v}}_2(t),{\overline{v}}_3(t\left)\right)$ such that $e^{\overline{p}t}\overline{v}\left(t\right)$ is a solution of (3.5), where $\overline{p}=\frac{1}{\omega }\ln r\left({\mathrm{\Phi }}_{F-V-M_{∊}}\right)>0$. Choose $t_3>t_2$ and a small number $\overline{\alpha }>0$ such that $\overline{w}\left(t_3\right)⩾\overline{\alpha }\overline{v}\left(0\right)$, Then we have get $\overline{w}\left(t\right)⩾\overline{\alpha }\overline{v}(t-t_3)e^{\overline{p}(t-t_3)}$ for $t>t_3$. By the comparison principle, we have

$${\left(u_1\right(t),u_2(t),u(t\left)\right)}^{\mathbf{T}}⩾\overline{w}\left(t\right)⩾\alpha \overline{v}(t-t_3)e^{\overline{p}(t-t_3)},\forall t>t_3\text{.}$$

Then ${\left(u_1\right(t),u_2(t),u(t\left)\right)}^{\mathbf{T}}\to \infty$ as $t\to \infty$, a contradiction. This completes the proof.

Define

$$M_{\partial }≔\{u_0\in \partial X_0:P^m(u_0)\in \partial X_0,m⩾0\}\text{.}$$

Lemma 3.7

P is uniformly persistent with respect to $(X_0,\partial X_0)$.

Proof

Now we first prove

$$M_{\partial }=\left\{\right(0,0,0,0,u_5)\in X,u_5⩾0\}\text{.}$$ (3.9)

Noting that

$$\left\{\right(0,0,0,0,u_5)\in X,u_5⩾0\}\subseteq M_{\partial },$$

we only need to prove that

$$M_{\partial }\subseteq \left\{\right(0,0,0,0,u_5)\in X,u_5⩾0\}\text{.}$$

It suffices to prove that for any $u_0\in M_{\partial }$, we have $u_i\left(m\omega \right)=0,\forall m⩾0,i=1,2,3,4$. If it is not true, there exists an $m_1⩾0$, such that ${\left(u_1\right(m_1\omega ),u_2(m_1\omega ),u_3(m_1\omega ),u_4(m_1\omega \left)\right)}^{\mathrm{T}}>0$. Thus (3.6) implies that

$$u_5\left(t\right)>0,\forall t>m_1\omega$$

by replacing the initial time 0 with $m_1\omega$. Similarly, By (Smith, 1996, Theorem 4.1.1) as generalized to nonautonomous systems, it follows that ${\left(u_1\right(t),u_2(t),u_3(t),u_4(t\left)\right)}^{\mathrm{T}}\gg 0,\forall t>m_1\omega$. where the initial value ${\left(u_1\right(m_1\omega ),u_2(m_1\omega ),u_3(m_1\omega ),u_4(m_1\omega \left)\right)}^{\mathrm{T}}>0$. Then we have $u\left(t\right)\in X_0,\forall t>m_1\omega$, i.e,

$$u\left(t\right)\notin \partial X_0,\forall t>m_1\omega \text{.}$$

Thus, if $u_0\notin \left\{\right(0,0,0,0,u_5)\in X,u_5⩾0\}$, then $u_0\notin M_{\partial }$, which contradicts with $u_0\in M_{\partial }$. Hence, $M_{\partial }\subseteq \left\{\right(0,0,0,0,u_5)\in X,u_5⩾0\}$,which implies that (3.9) holds. Clearly, $E_0$ is the only fixed point of P and acyclic in $\partial M$. Moreover, Lemma 3.6 implies that $E_0$ is an isolated invariant set in X and $W^s\left(E_0\right)\cap X_0=\varnothing$, where $W^s\left(E_0\right)$ is the stable set of $E_0$. By the acyclicity theorem on uniform persistence for maps  citep[Thorem 3.1.1]zhao2003dynamical, it follows that P is uniformly persistent with respect to $(X_0,\partial X_0)$.

Definition 3.8

(Zhao et al., 2003, p.18) (Uniformly persistent) Model (2.3) is said to be uniformly persistent if there exists a constant $\varsigma >0$ such that any solution $u\left(t\right)=(u_1,u_2,u_3,u_4,u_5)$ with $u_0\in X_0$ satisfies

$$\min \left\{{\displaystyle \underset{t\to \infty }{\lim \inf }}{u}_i\right(t\left)\right\}⩾\varsigma ,i=1,2,\cdots ,5\text{.}$$ (3.10)

Theorem 3.9

If ${\mathcal{R}}_0>1$ , model (2.3) has at least one positive periodic solution which is uniformly persistent.

Proof

It follows from Lemma 3.7 and (Zhao et al., 2003, Thorem 3.1.1) that the solution of model (2.3) is uniformly persistent.

Furthermore, taking advantage of Zhao et al. (2003, Theorem 1.3.6), P has a fixed point $u^{\ast }\left(0\right)\in X_0$. Then, we see that $u_i^{\ast }\left(0\right)>0(i=1,2,3,4),u_5^{\ast }\left(0\right)⩾0$. We further prove that $u_5^{\ast }\left(0\right)>0$. Suppose not, if $u_5^{\ast }\left(0\right)=0$, form the last equation of model (2.3), we derive that

$$\frac{\mathrm{d}{u}_5^{\ast }}{\mathrm{d}t}⩾\mathrm{\Lambda }-a^{\ast }\left(t\right)u_5^{\ast }$$

with $u_5^{\ast }\left(0\right)=u_5^{\ast }\left(n\omega \right)=0,n=1,2,3\cdots$, where $a^{\ast }\left(t\right)=\mu +{\beta }_1\left(t\right)\frac{u_1^{\ast }}{N}+{\beta }_2\left(t\right)u_3^{\ast }$. Therefore, we have

$$u_5^{\ast }\left(n\omega \right)⩾e^{-{\int }_0^{n\omega }{a}^{\ast }\left({\tau }_1\right)\mathrm{d}{\tau }_1}\left(u_5{\left(0\right)}^{\ast }+\mathrm{\Lambda }{\int }_0^t{e}^{{\int }_0^{{\tau }_2}{a}^{\ast }\left({\tau }_1\right)\mathrm{d}{\tau }_1}\mathrm{d}{\tau }_2\right)>0,\forall t>0,$$ (3.11)

which yields a contradiction. Hence, $u_5^{\ast }\left(0\right)>0$ and $u^{\ast }\left(0\right)$ is a positive $\omega$-periodic solution of model (2.3). This completes the proof.

We next consider the special case of ${\beta }_1\left(t\right)={\beta }_1,{\beta }_2\left(t\right)={\beta }_2$. For simplicity, define

$$\begin{array}{c}\phi \left(a\right)≔\mu a+a{\gamma }_1+\upsilon ,\hfill \\ \varphi \left(a\right)≔(1-a)\left(\mu +\rho +{\gamma }_1\right),\hfill \\ \psi \left(a\right)≔\left(a\rho +\mu +{\gamma }_2\right){\gamma }_1+\left((1-a)\rho +\mu +\upsilon \right){\gamma }_2+{\mu }^2+\mu \rho +\upsilon \mu +\rho \upsilon ,\hfill \end{array}$$

where $a\in [0,1]$.

To find endemic equilibrium, we make the substitution $x=\frac{u_2}{N}$. Then,

$$\left\{\begin{array}{c}(1-p){\beta }_1\left(t\right)u_{5}x+(1-q){\beta }_2\left(t\right)u_5{u}_3-(\mu +\upsilon +{\gamma }_1)u_1=0,\hfill \\ \upsilon u_1+p{\beta }_1\left(t\right)u_{5}x+q{\beta }_2\left(t\right)u_5{u}_3-(\mu +\delta +{\gamma }_2)u_2=0,\hfill \\ \alpha u_2-{\mathit{cu}}_3=0,\hfill \\ {\gamma }_1{u}_1+{\gamma }_2{u}_2-\mu u_4-\rho u_4=0,\hfill \\ \mathrm{\Lambda }-\mu u_5-{\beta }_1\left(t\right)u_{5}x-{\beta }_2\left(t\right)u_5{u}_3+\rho u_4=0\text{.}\hfill \end{array}\right)$$ (3.12)

Since $\mathrm{\Lambda }-\mu N-\delta u_2=0$, By using some algebraic computations, we can obtain

$$\begin{array}{cc}{u}_1=\frac{x\mathrm{\Lambda }\left(\mu +\delta +{\gamma }_2\right)a_0}{\left(\delta x{\mathcal{R}}_0^{\mathrm{dir}}+\mu {\mathcal{R}}_0^{\mathrm{dir}}+\mu {\mathcal{R}}_0^{\mathrm{ind}}\right)\phi \left(p\right)\phi \left(q\right)\left(\delta x+\mu \right),}\hfill & u_2=\frac{\mathrm{\Lambda }x}{\mu +\delta x},\hfill \\ u_3=\frac{\alpha \mathrm{\Lambda }x}{c(\mu +\delta x)},\hfill & u_5=\frac{\mathrm{\Lambda }}{\mu {\mathcal{R}}_0+\delta {\mathcal{R}}_0^{\mathrm{dir}}x},\hfill \end{array}$$

where x is a positive real root of the following equation:

$$f\left(x\right)={\mathit{Ax}}^2+\mathit{Bx}+C=0,$$ (3.13)

where,

$$\begin{array}{cc}A=\hfill & {\mathcal{R}}_0^{\mathrm{dir}}\delta \phi \left(q\right)\left(\varphi \left(p\right)\delta +\psi \left(p\right)\right)>0,\hfill \\ B=\hfill & b_1{\mathcal{R}}_0^{\mathrm{dir}}+b_2{\mathcal{R}}_0^{\mathrm{ind}}+\delta \left(\mu +\rho \right)\phi \left(p\right)\phi \left(q\right)(1-{\mathcal{R}}_0^{\mathrm{dir}}),\hfill \\ C=\hfill & \mu \left(\mu +\rho \right)\phi \left(p\right)\phi \left(q\right)(1-{\mathcal{R}}_0),\hfill \end{array}$$

and

$$\begin{array}{c}{b}_1=\mu \phi \left(q\right)\left(\varphi \left(p\right)\delta +\psi \left(p\right)\right)>0,b_2=\mu \phi \left(p\right)\left(\varphi \left(q\right)\delta +\psi \left(q\right)\right)>0\text{.}\hfill \end{array}$$

If ${\bar{\mathcal{R}}}_0\le 1$, then ${\mathcal{R}}_0^{\mathrm{dir}}\le 1$, $C⩾0$ and $B>0$. It follows that Eqn. (3.13) has no positive real root. If ${\mathcal{R}}_0>1$, Eq. (3.13) has a unique real root $x^{\ast }$:

$$x^{\ast }=\frac{-B+\sqrt{B^2-4\mathit{AC}}}{2A}\text{.}$$

Hence model (2.3) has a unique endemic equilibrium $E^{\ast }=(u_1^{\ast },u_2^{\ast },u_3^{\ast },u_4^{\ast },u_5^{\ast })$ with

$$\begin{array}{c}{u}_1^{\ast }=\frac{x^{\ast }\mathrm{\Lambda }\left(\mu +\delta +{\gamma }_2\right)a_0}{\left(\delta x^{\ast }{\mathcal{R}}_0^{\mathrm{dir}}+\mu {\bar{\mathcal{R}}}_0\right)\phi \left(p\right)\phi \left(q\right)\left(\delta x^{\ast }+\mu \right)},u_2^{\ast }=\frac{\mathrm{\Lambda }{x}^{\ast }}{\mu +\delta x^{\ast }},\hfill \\ u_3^{\ast }=\frac{\alpha \mathrm{\Lambda }{x}^{\ast }}{c(\mu +\delta x^{\ast })},u_4^{\ast }=\frac{{\gamma }_1{u}_1^{\ast }+{\gamma }_2{u}_2^{\ast }}{\mu +\rho },u_5^{\ast }=\frac{\mathrm{\Lambda }}{\mu {\bar{\mathcal{R}}}_0+\delta {\mathcal{R}}_0^{\mathrm{dir}}{x}^{\ast }}\text{.}\hfill \end{array}$$ (3.14)

In a special case of $\delta =0$, if ${\bar{\mathcal{R}}}_0>1$, model (2.3) has a unique endemic equilibrium $E^{\ast }=(u_1^{\ast },u_2^{\ast },u_3^{\ast },u_4^{\ast },u_5^{\ast })$ with

$$\begin{array}{c}{u}_2^{\ast }=\frac{\mathrm{\Lambda }\left({\bar{\mathcal{R}}}_0-1\right)\left(\mu +\rho \right)\phi \left(q\right)\phi \left(p\right)}{\mu \left({\mathcal{R}}_0^{\mathrm{dir}}\phi \right(q\left)\psi \right(p)+{\mathcal{R}}_0^{\mathrm{ind}}\phi (p\left)\psi \right(q\left)\right)},\hfill \\ u_1^{\ast }=\frac{u_2^{\ast }(\mu +{\gamma }_2)\left({\mathcal{R}}_0^{\mathrm{dir}}\right(1-p\left)\phi \right(q)+{\mathcal{R}}_0^{\mathrm{ind}}(1-q\left)\phi \right(p\left)\right)}{{\bar{\mathcal{R}}}_0\phi \left(p\right)\phi \left(q\right)},\hfill \\ u_3^{\ast }=\frac{\alpha u_2^{\ast }}{c},u_4^{\ast }=\frac{{\gamma }_1{u}_1^{\ast }+{\gamma }_2{u}_2^{\ast }}{\mu +\rho },u_5^{\ast }=\frac{\mathrm{\Lambda }}{{\bar{\mathcal{R}}}_0\mu }\text{.}\hfill \end{array}$$ (3.15)

4. TB epidemics in Jiangsu, China via numerical simulations

4.1. TB epidemics in Jiangsu, China from 2009 to 2018

The monthly TB incident cases are collected from the Jiangsu provincial center for diseases control and prevention (CDC) (The reported tuberculosis cases in Jiangsu province, 2018). In Fig. 3(a), we show the local TB epidemic from 2009 to 2018. We can observe that a substantially decreasing trend in the TB incidences, dropped from some 4000 cases per month in 2009 to some 2000 cases per month in 2018.

The relative infectivity can be (preliminary) quantified by using the approach in Fine and Clarkson (1982) as well as adopted in Zhao et al. (2018). The relative infectivity can be easily calculated by using the ratio of the number of incidences of time $(t+1)$ to the number of incidences of time t, i.e., $Q_t={\mathrm{case}}_{t+1}/{\mathrm{case}}_t$. This Q appears to be a simplified version of quantifying the time-varying (effective) reproduction number by the serial interval approach as studied and implemented in Wallinga and Teunis, 2004, Fraser, 2007, Zhao et al., 2019. The relative infectivity of TB, $Q_t$, is quantified in Fig. 3(b).

In Fig. 3(c), we show the strong seasonality (Fine and Clarkson, 1982) in the TB incidence time series in the annualised epidemic curves. And in Fig. 3(d), we show the annualised relative infectivity to show the seasonality in the TB infectivity across years. We can find that the (relative) infectivity in February appeared to be dominant (or the highest) across different months.

4.2. Fitting and estimation results via numerical simulations

4.2.1. Statistical fitting framework

Based on the epidemic model (2.1), we compute the monthly number of reported cases, $Z_i$, of the i-th month (during the study period) as

$$\begin{array}{c}{Z}_i≔{\int }_{\mathit{i}\mathrm{-th}\mathrm{month}}\kappa {\gamma }_{2}T\mathit{dt},\hfill \end{array}$$ (4.1)

where $\kappa \in (0,1)$ is a constant scaling term for the number of TB cases. In other words, $\kappa$ represents a combined effect of the TB symptomatic rate and the reporting rate. Obviously, $Z_i$ denotes the theoretical monthly TB cases yielding from model (2.1).

On the other hand, we treat the observed (or reported) number of TB cases, $C_i$ for the i-th month, as a partially observed Markov process (POMP) (King et al., 2016), also know as the hidden Markov model (HMM) from the theoretical number of cases, i.e., $Z_i$ in Eqn. (4.1).

We adopt the Poisson-distributed priors for the $C_i$s such that all $C_i$s are assumed to follow Poisson distributions according to the theoretical outcomes, i.e., $Z_i$s (Zhao et al., 2018). In other words, the rate of Poisson distribution is a variable depending on $Z_i$, and the observed number of TB cases, $C_i$, is a random sample from the (predetermined) Poisson distribution in Eqn (4.2). Therefore,

$$\begin{array}{c}{C}_i\sim \mathrm{Poisson}(\mathrm{mean}=Z_i)\text{.}\hfill \end{array}$$ (4.2)

We denote $L_i(·)$ to be the likelihood function of the i-th month, which is the measurement of the “probability” of the observed $C_i$, given the theoretical number of cases being $Z_i$ under the Poisson distribution (Zhao et al., 2018, He et al., 2009, Lin et al., 2018).

Gathering all $L_i$s, the overall log-likelihood, denoted by l, for the whole TB incidences time series is given in Eqn (4.3).

$$\begin{array}{cc}l\left(\mathrm{\Theta }\right):\hfill & ={\displaystyle \sum _{i=1}^M}\ln \left[L_i\right(C_i|Z_0,\dots ,Z_i\text{;}\mathrm{\Theta })]={\displaystyle \sum _{i=1}^M}\ln [L_i\left(C_i\right|Z_i\text{;}\mathrm{\Theta }\left)\right],\hfill \end{array}$$ (4.3)

where $\mathrm{\Theta }$ is the parameter vector to be estimated. The term M denotes the total number of months during the study period, i.e., from 2009 to 2018. We apply the plug-and-play likelihood-based inference framework to estimate the maximum likelihood estimates (MLE) of $\mathrm{\Theta }$ (He et al., 2009, Lin et al., 2018, Ionides et al., 2006). The profile likelihood approach is implemented to inference the confidence intervals of the model parameters to be estimated (Ionides et al., 2006, Ionides et al., 2017). We use the fixed-time-step Euler-multinomial algorithm (Zhao et al., 2018, Lin et al., 2018) to simulate the epidemic model (2.1).

We consider that there are equivalent birth and death rate (by forcing $\mathrm{\Lambda }=\mu N=\mathrm{constant}$ in model (2.1)), and zero disease-induced mortality rate ($\delta =0$) in the whole study period, from 2009 to 2018. In this case, the number of the total population, N, is a constant, which, in Jiangsu, slightly changed from 78.1 million in 2009 to 80.5 million in 2018 (The reported tuberculosis cases in Jiangsu province, 2018).

We attempt to find the MLEs of both ${\mathcal{R}}_0^{\mathrm{dir}}$ and ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$ within biologically and clinically reasonable ranges by seeking for maximal value(s) of l in (4.3). And this ${\mathcal{R}}_0$ reconstruction approach allows us to project the TB epidemics in an intuitive manner. The projection are conducted by simulating the model (2.1) with MLEs of the parameters up to the end of 2019.

The model simulations are conducted by using the software R (version 3.6.3) (Team, 2013).

4.2.2. Fitting and estimation results

First of all, we show the parameters’ values used for the numerical simulation and sensitivity analysis for model (2.1) in Table 1 .

Table 1.

The summary table of model parameters’ values.

parameter	value	unit	statu
${\gamma }_1^{-1}={\gamma }_2^{-1}$	1.5	year	fixed
${\mu }^{-1}$	75	per year	fixed
$\mathrm{\Lambda }$	$\mu N$	person	fixed
p	0.05	per year	fixed
q	0.1	per year	fixed
$\alpha$	1	per case day	assumed
c	0.1	per day	assumed
$\kappa$	0.01	unit-free	fixed
$\rho$	0	per day	assumed
v	1	per day	assumed
${\beta }_1\left(t\right)={\beta }_2\left(t\right)$	time-varying	per day	to be estimated
N	$8\times {10}^7$	person	fixed
$S\left(0\right)$	0.15	unit-free	fixed
$T\left(0\right)$	$1\times {10}^{-3}$	unit-free	fixed
$T_e\left(0\right)$	$1\times {10}^{-3}$	unit-free	fixed
$R\left(0\right)$	$1-S\left(0\right)-T\left(0\right)-T_e\left(0\right)$	unit-free	fixed
$W\left(0\right)$	0.04	unit-free	assumed

In Fig. 4 (a)-(b), we show the MLEs of ${\mathcal{R}}_0^{\mathrm{dir}}$ and ${\mathcal{R}}_0^{\mathrm{ind}}$ of each month, respectively. And the annual average ${\mathcal{R}}_0$ is estimated of 1.13, with ${\mathcal{R}}_0^{\mathrm{dir}}$ of 0.35 (see Fig. 5 (a) for details). The ${\mathcal{R}}_0^{\mathrm{dir}}$ is estimated to be strictly less than one. We can find that the estimated annual trends in ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$ (Fig. 4(b)) are consistent with the patterns in the preliminary descriptive “infectivity” in Fig. 3(d). We estimated that the ${\mathcal{R}}_0^{\mathrm{ind}}$ in February is larger than one (estimated to be 6.9 in Fig. 5(b)), whereas those in other months are likely to below one.

Fig. 4.

The estimation of direct, ${\mathcal{R}}_0^{\mathrm{dir}}$, and indirect reproduction number, ${\mathcal{R}}_0^{\mathrm{ind}}$, and the model simulation and projection results. Panel (a) shows the maximal likelihood estimation (MLE) of ${\mathcal{R}}_0^{\mathrm{dir}}$. Panel (b) shows the MLEs of the ${\mathcal{R}}_0^{\mathrm{ind}}$ of each month. Panel (c) presents the model simulation results, the black dots are the observed number of incidence, the blue line is the model fitting result and the green dashed line is the model projection result. The shading areas represents the 95% credible intervals (CI). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 5.

(a) The profile likelihood of the direct basic reproduction number ${\mathcal{R}}_0^{\mathrm{dir}}$; (b) The profile likelihood of the indirect basic reproduction number, ${\mathcal{R}}_0^{\mathrm{ind}}$ in February as an example. The green dots are the random prior samples of different set of parameter values for further simulation purpose. The green curve is the smoothed (by the locally estimated scatterplot smoothing, LOESS) likelihood profile. The horizontal black dashed line is the 95% CI cutoff. The red triangle is the MLE of the parameter of interest. The two vertical red dashed lines indicate the lower and upper bounds of the 95% CI. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

In Fig. 4(c), we give the fitting results and projection to 2019. We find that a decreasing trend in the fitting results, which matched the trends in the observed incidence data. The projection is also likely to maintain these trends in 2019.

It is should be noted that the term ${\beta }_2$ is considered as a time-varying parameter such that the indirect transmission could also be time-varying. Hence, the ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$ reconstructed in Fig. 4(b) is the time-varying reproduction number.

Getting back to the basic reproduction number defined in (3.2), we agree that it should be in an autonomous setting that all model parameters are fixed. In this case, the term ${\beta }_2$ in (3.2) is the average of ${\beta }_2\left(t\right)$, i.e., annual average. Thus, the basic reproduction number, ${\mathcal{R}}_0$, in (3.2) is the annual average of the time-varying, which is estimated at 1.13 in Fig. 4.

In addition, in the special case of ${\beta }_1\left(t\right)={\beta }_1$ and ${\beta }_2\left(t\right)={\beta }_2$, since, in (3.4), ${\beta }_1$ and ${\mathcal{R}}_0^{\mathrm{dir}},{\beta }_2$ and ${\mathcal{R}}_0^{\mathrm{ind}}$ are all one-to-one mapping, the profile of fitted values of ${\beta }_1$ and ${\beta }_2$ can thus be directly derived from the estimates in Fig. 5 and other fixed parameters in Table 1. We consider the terms ${\mathcal{R}}_0^{\mathrm{dir}}$ and ${\mathcal{R}}_0^{\mathrm{ind}}$ appear easier to interpret and more biologically meaningful, and thus we choose to show the fitting values of ${\mathcal{R}}_0^{\mathrm{dir}}$ and ${\mathcal{R}}_0^{\mathrm{ind}}$ in Fig. 5.

Since the numerical simulation is conducted with the same complexity in the model structure, we can directly study the goodness-of-fit (in term of the likelihood) and the fitting errors. The goodness-of-fit and the error term analyses are demonstrated in Fig. 6 . We can find that the fitted values of the TB incidences are in line with the observations with the error terms (largely) following in a Normally distribution (Fig. 6(a)-(b)). And the mean percentage error is close to zero (Fig. 6(c)).

Fig. 6.

The matching between the observed and fitted values and the distribution of the fitting error terms, e.g., the differences between observed and fitted values. Panel (a) shows the (normalised) observations against the fits (dots), and the diagonal line represents the “$y=x$” line. Panel (b) shows the Normal quantile–quantile (QQ) plot of the fitting errors. Panel (c) shows the distribution of the percentage errors, i.e., the ratios of the errors over the observations. Panel (d) shows the distribution of the errors.

4.2.3. Sensitivity analysis and the trend change in the TB epidemic

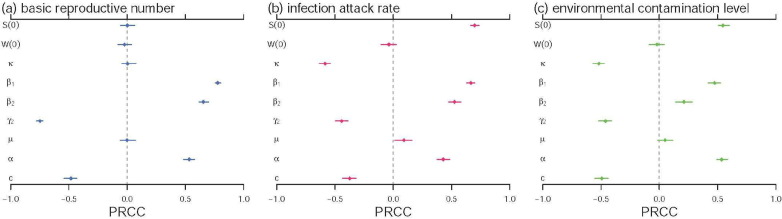
Following (Zhao et al., 2018, Zhao et al., 2018, Musa et al., 2019, Gao et al., 2016, Tang et al., 2016, Tang et al., 2016), we adopt the partial ranked correlation coefficient (PRCC) for the sensitivity analysis between the model outcomes and the parameters. The PRCCs of the ${\mathcal{R}}_0$, infection attack rate (IAR) and the environmental contamination level of the model (2.1) are estimated. The sensitivity analysis results are in Fig. 7 , and suggest that most of the model parameters are significantly associated with the TB infectivity, IAR and the environmental contamination, which should be given priorities in controlling the TB epidemics.

Fig. 7.

The partial rank correlation coefficients (PRCC) of basic reproduction number in panel (a), the infection attack rate (IAR) in panel (b) and the level of the environmental contamination in panel (c) against the model parameters. The $S\left(0\right)$ denotes the initial susceptible ratio. The $W\left(0\right)$ denotes the initial environmental contamination level. The dots are the estimated PRCCs, and the bars represent the 95% CIs. The ranges of model parameters are based on the values in Table 1 having a random perturbation with a coefficient of variation of 0.2.

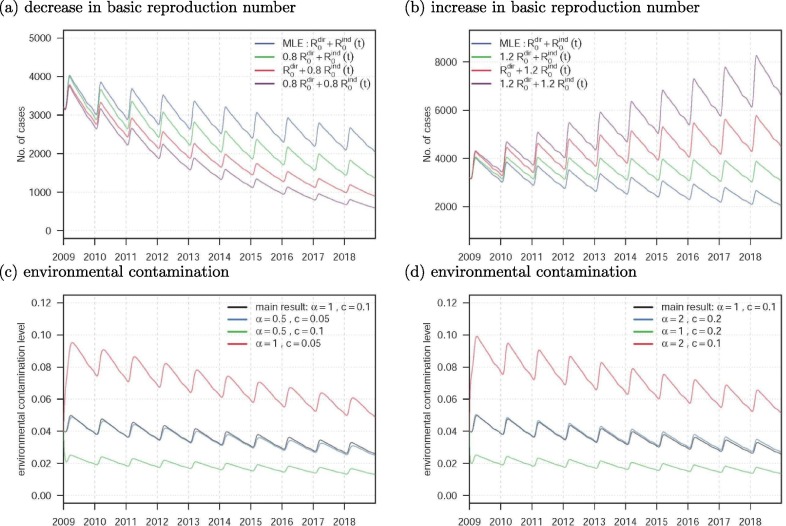
Based on the results of the sensitivity analysis above, we conduct the numerical simulations to present the changing dynamics of the TB epidemics and the environmental contamination levels with changes in the epidemiological parameters. Fig. 8 (a) and (b) show the trend changes in the TB epidemic with changes in the ${\mathcal{R}}_0^{\mathrm{dir}}$ and ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$, respectively. Fig. 8(c) and (d) show the trend changes in the environmental contamination levels with changes in the parameters $\alpha$ and c, respectively.

Fig. 8.

The numerical simulation results with the changes in epidemiological parameters. The panels (a) and (b) are the numbers of TB cases. The panels (c) and (d) are the levels of the environmental contamination. In panels (a) and (b), the blue lines are the same main results, by using the ${\mathcal{R}}_0$ MLEs, as in Fig. 4(c). In panels (c) and (d), the black lines are the same main results as in Fig. 4(c). Except for those indicated in the figure legends, all other model parameters and initial conditions are the same as in Table 1.

5. Concluding remarks

The main focus of this study is to investigate the effects of the contaminated environments on the TB transmission dynamics in Jiangsu, China analytically and numerically. Mathematically, we define the basic reproduction number ${\mathcal{R}}_0$ (cf. (3.2  ), and prove that ${\mathcal{R}}_0$ can be used to govern the threshold dynamics of the model: if ${\mathcal{R}}_0<1$, the unique DFE is globally asymptotic stable (cf. Theorem 3.4); while ${\mathcal{R}}_0>1$, there is at least one positive periodic solution and TB will persist uniformly (Theorem 3.9). Epidemiologically, we show that the cost of the contaminated environments affect the transmission dynamics of TB in Jiangsu, China in the following aspects:

• (i)  Based on the monthly TB incident cases counted by the Jiangsu CDC (cf. Fig. 3(a) ), the TB incidence time series has strong seasonality (cf. Fig. 3(c) ). And the annual average ${\mathcal{R}}_0$ is $1.13>1$, then from Theorem 3.9, we can conclude that the TB in Jiangsu persists under current circumstances. That is, the TB becomes an endemic disease and will persist in Jiangsu for a long time. And there is a long way to go to achieve the world-wide goal towards elimination of tuberculosis by 2050.

• (ii)  The annualised relative infectivity (cf. Fig. 3(d) ) shows that the relative infectivity in February is dominant across different months. This is consistent with the estimation of that ${\mathcal{R}}_0^{\mathrm{ind}}$ in February is 6.9 (cf. Fig. 5(b) ), whereas those in other months are likely to below one. This phenomenon seems to be the first reported case. For one of the possible explanations, we conjecture that this is induced by the travel or migration with the winter vacation and the Spring Festival, commonly started since mid-February of each year and lasted for about 20 days. During this period, a large number of people working or living outside of Jiangsu will return to their hometown, and the local CDC will increase the screening of tuberculosis for returning people. Moreover, due to population movements and increased exposure rates, the risk of tuberculosis transmission has increased significantly, and the resulting lagging effect will increase the number of cases in the next month (see Fig. 3(c) ). Although this has not yet been formally verified in public health filed, it is desirable in future studies. From the model fitting side, both of the surveillance reporting and the TB infectivity have similar effects on the number of TB incidences. This means it is difficult to disentangle the solo effect of both factor as the same time based on our model framework. We choose to set the surveillance reporting efforts, in term of $\kappa$ in Eqn (4.1), as a constant during the entire study period, i.e., 2009–2018, and estimate the TB infectivity, in term of ${\mathcal{R}}_0\left(t\right)$, as a time-varying function. If both ${\mathcal{R}}_0$ and $\kappa$ were set to be time-varying in the fitting procedure, the potential over-fitting problem as well as the estimation biases in both ${\mathcal{R}}_0$ and $\kappa$ would probably occur. This is largely due to the effects of ${\mathcal{R}}_0$ and $\kappa$ cannot be disentangled and thus not independent in our model structure. Although lack of supporting information or data, our model is still capable to capture the long-term TB epidemic in Jiangsu. We remark that more detailed information on quantifying the local TB surveillance and the changing dynamics of the de jure population and floating population would be very helpful to identifying more accurate TB infectivity estimates.

• (iii)  From the numerical results in Fig. 5, we find that merely controlling the changing dynamics of the TB indirect transmission, in term of the ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$, appears sufficient to successfully capture the long-term patterns in TB epidemics in Jiangsu. With ${\mathcal{R}}_0^{\mathrm{dir}}$ estimated strictly less than one, we remark that the TB epidemics are likely to be controlled, in term of ${\mathcal{R}}_0<1$, by effectively controlling the indirect transmission path. Also, Fig. 8 indicates that the control measures reduce the ${\mathcal{R}}_0^{\mathrm{ind}}\left(t\right)$ or ${\mathcal{R}}_0^{\mathrm{dir}}$ could effectively decrease the number of TB cases. This could be achieved by providing timely and effective treatment and maintaining a low environment contamination level. We further find that a lower virus shedding rate, $\alpha$, and a higher environmental clearance rate, c, lead to low level of environment contamination (Fig. 8) and ${\mathcal{R}}_0$ (Fig. 7), which could control the TB epidemic efficiently.

• (iv) From Fig. 7, the TB transmissibility and number of cases are positively associated with the effective transmission rates ${\beta }_1$ and ${\beta }_2$, as well as the virus shedding rate $\alpha$. The effective control efforts are suggested to focus on reducing the ${\beta }_1,{\beta }_2$ and $\alpha$. We also find that the recovery rates, ${\gamma }_1$ and ${\gamma }_2$, and environmental clearance rate, c, are negatively associated with the TB transmissibility and number of cases. Thus, increasing ${\gamma }_1$ and ${\gamma }_2$ are also likely to control the TB epidemics.

It is worthy to note that, increasing number of evidences support that the respiratory infections are primarily transmitted between people through respiratory droplets and contact routes World Health, 2020, Liu et al., 2020, Li et al., 2020, Huang et al., 2020). Recently, Gao et al. (2020) investigated the relative contributions of different transmission routes to a multi-route transmitted respiratory infection and found that all transmission routes can dominate the total transmission risk under different scenarios. In the present paper, we model the transmissions of the TB into two categories, one is direct, and the other is indirect, which is measure by $W\left(t\right)$ representing the effects of the contaminated environments. Our model (2.1) provides a straightforward method to evaluate the transmission efficiency of different transmission routes of TB.

In addition, the progress in controlling TB is, however, currently influenced by some major factors, such as multidrug resistant (MDR) (Dodd et al., 2016, Knight et al., 2019, Liu et al., 2019), ambient particulate air pollution (Liu et al., 2019, Peng et al., 2017, Liu et al., 2019), etc. The effects of MDR or air pollution on the transmission dynamics of TB in Jiangsu, China will be desirable in our future studies.

CRediT authorship contribution statement

Yongli Cai: Modelling, mathematical analysis, writing. Shi Zhao: Modelling, numerical analysis, writing. Yun Niu: Modelling, numerical analysis. Zhihang Peng: Modelling, mathematical analysis. Kai Wang: Modelling, mathematical analysis. Daihai He: Modelling, numerical analysis. Weiming Wang: Modelling, mathematical analysis, numerical analysis, Writing-Reviewing and Editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.