Generative-Discriminative Complementary Learning

Abstract

The majority of state-of-the-art deep learning methods are discriminative approaches, which model the conditional distribution of labels given inputs features. The success of such approaches heavily depends on high-quality labeled instances, which are not easy to obtain, especially as the number of candidate classes increases. In this paper, we study the complementary learning problem. Unlike ordinary labels, complementary labels are easy to obtain because an annotator only needs to provide a yes/no answer to a randomly chosen candidate class for each instance. We propose a generative-discriminative complementary learning method that estimates the ordinary labels by modeling both the conditional (discriminative) and instance (generative) distributions. Our method, we call Complementary Conditional GAN (CCGAN), improves the accuracy of predicting ordinary labels and is able to generate high-quality instances in spite of weak supervision. In addition to the extensive empirical studies, we also theoretically show that our model can retrieve the true conditional distribution from the complementarily-labeled data.

Introduction

Deep supervised learning has achieved great success in various applications such as visual recognition (Krizhevsky, Sutskever, and Hinton, 2012; He et al., 2015) and natural language processing (Kim, 2014). Despite the effectiveness of supervised classifiers, acquiring labeled data is often expensive and time-consuming. As a result, learning from weak supervision has been studied extensively in recent decades, including but not limited to semi-supervised learning (Kingma et al., 2014), multi-instance learning (Zhou et al., 2012), learning from side information (Hoffman, Gupta, and Darrell, 2016), and learning from data with noisy labels (Natarajan et al., 2013; Liu and Tao, 2016; Xia et al., 2019; Cheng et al., 2017).

In this paper, we consider a recently proposed weakly-supervised classification scenario, i.e., learning from complementary labels (Ishida et al., 2017; Yu et al., 2018). Unlike an ordinary label, a complementary label specifies a class that an input instance does not belong to. Given an instance from a class, it is laborious to choose the correct class label from many candidate classes, especially when the number of classes is relatively large or the annotator is not familiar with the characteristics of all candidate classes. However, it is less demanding and inexpensive to choose one of the incorrect class as a complementary label for an instance. For example, when an annotator is labelling an image containing an animal that she has never seen before, she can easily identify that this animal does not belong the usual animal classes he can see in daily life, such as, “not dogs”. In medical field, a doctor may not be able to identify the exact disease type given symptoms. However, he/she can easily obtain complementary labels denoting some disease types a patient does not belong to.

Existing complementary learning methods modified the ordinary classification loss functions to enable learning from complementary labels. Ishida et al. (2017) proposed a method that provides a consistent estimate of the classifier from complementarily-labeled data where the loss function satisfies a particular symmetric condition. However, this method only allows classification loss functions with certain non-convex binary losses for one-versus-all and pairwise comparison. Later, Yu et al. (2018) proposed to use the forward loss correction technique (Patrini et al., 2017) that learns the conditional, P_{Y |X}, from complementary labels, where X denote the input features and Y denote labels. Ishida et al. (2018) derived an unbiased estimator of the true classification risk with arbitrary loss functions from complementarily-labeled data.

To clarify the differences between learning with ordinary and complimentary labels, we define the notion of “effective sample size”, which is the number of instances with ordinary labels that carries the same amount of information as instances with complementary labels of a given size. Since the complementary labels are weak labels, they carry only partial information about the ordinary labels. Hence, the effective sample size n_l for complementary learning is much smaller than the given sample size n (i.e., n_l << n). Current methods for learning with complementary labels need a relatively large training set to ensure low variance for predicting ordinary label.

Although n_l is small under complementary learning settings, we can still use all samples with size n to estimate the instance distribution P_X. However, current complementary methods focus on modeling conditional P_{Y |X} and thus fail to account for information hidden in P_X, which is essential in complementary learning.

To improve the prediction performance, we propose a generative-discriminative complementary learning approach that learns both P_Y|X and P_X|Y in a unified framework. Our main contributions can be summarized as follows:

• We propose a Complementary Conditional Generative Adversarial Net (CCGAN), which simultaneously learns P_Y|X and P_X|Y from complementary labels. Because the estimate of P_X|Y benefits from P_X, it provides constraints on P_Y|X and helps reduce its estimation variance.

• Theoretically, we show that our CCGAN model is guaranteed to learn P_X|Y from complementarily-labeled data.

• Empirically, we conduct comprehensive experiments on benchmark datasets, including MNIST, CIFAR10, CIFAR100, and VGG Face; demonstrating that our model gives accurate classification prediction and generates high-quality images.

The code is at https://github.com/xuyanwu/ComplementaryGAN.

Related Works

Generative Adversarial Nets

Generative Adversarial Nets (GANs) are a class of implicit generative models learned by adversarial training (Goodfellow et al., 2014). With the development of new network architectures (e.g., (Brock, Donahue, and Simonyan, 2019)) and stabilizing techniques (e.g., (Miyato et al., 2018)), GANs generates high-quality images that are indistinguishable from real ones. Conditional GANs (CGANs) (Mirza and Osindero, 2014) extend the GAN models to generate images given specific labels, which can be used to model the class conditional P_X|Y (e.g., AC-GAN (Odena, Olah, and Shlens, 2017), Projection cGAN (Miyato and Koyama, 2018), and TAC-GAN (Gong et al., 2019)). However, training of CGANs requires ordinary labels for the images, which are not available under the complementary learning settings. To the best of our knowledge, our proposed CCGAN is the first conditional GAN that is trained with complementary labels. The most related works to us are the robust conditional GAN approaches that aim to learn a conditional GAN from labels corrupted by random noise (Thekumparampil et al., 2018; Kaneko, Ushiku, and Harada, 2018). However, our method generates better quality images and more accurate prediction, by utilizing complementary labels.

Semi-Supervised Learning

Under semi-supervised learning settings, we are provided a relatively small number of labeled data and plenty of unlabeled data. The basic assumption for the semi-supervised methods is that the knowledge on P_X gained from unlabeled data carries useful information for inferring P_Y|X. This principle has been implemented in various forms, such as co-training (Blum and Mitchell, 1998), generative modeling (Odena, 2016; Kumar, Sattigeri, and Fletcher, 2017), etc. Inspired by the commonalities between complementary learning and semi-supervised learning, i.e., more data are available to estimate P_X than P_Y|X; we propose to make use of P_X to help infer P_Y|X in complementary learning.

Background

In this section, we first introduce the concept of learning from so-called complementary labels. Then, we discuss a state-of-the-art discriminative complementary learning approach, Yu et al. (2018), which is the most relevant to our method.

Problem Setup

Let two random variables X and Y denote the features and the labels, respectively. The goal of discriminative learning is to infer a decision function (classifier) from independent and identically distributed training set ${\left\{{\mathbf{x}}_i,y_i\right\}}_{i=1}^n\subseteq \mathcal{X}\times \mathcal{Y}$ drawn from an unknown joint distribution P_XY, where $X\in \mathcal{X}={ℝ}^d$ and $Y\in \mathcal{Y}=\{1,\dots ,K\}$. The optimal function, f^∗, can be learned by minimizing the expected risk $R\left(f\right)={\mathbb{E}}_{(X,Y)\sim P_{XY}}\ell (f(X),Y)$, where $\mathbb{E}$ denotes the expectation and ℓ denotes a classification loss function. Because P_XY is unknown, we usually approximate R(f) using its empirical estimation $R_n(f)=\frac{1}{n}{\sum }_{i=1}^n\ell \left(f\left({\mathbf{x}}_i\right),y_i\right)$.

In the complementary learning setting, for each sample x, we are given only a complementary label $\overline{y}\in \mathcal{Y}\backslash y$ which specifies a class that x does not belong to. That is to say, our goal is to learn f that minimizes the classification risk R(f) from complementarily-labeled data ${\left\{{\mathbf{x}}_i,{\overline{y}}_i\right\}}_{i=1}^n\subseteq \mathcal{X}\times \mathcal{Y}$ drawn from an unknown distribution $P_{X\overline{Y}}$, where $\overline{Y}$ denote the random variable for complementary label. The ordinary loss function, ℓ(·,·), cannot be used since we do not have access to the ordinary labels (y_i’s). In the following, we explain how discriminative learning can be extended in such scenarios.

Discriminative Complementary Learning

Existing Discriminative Complementary Learning (DCL) methods modified the ordinary classification loss function ℓ to the complementary classification loss $\overline{\ell }$ to provide a consistent estimation of f. Various loss functions have been considered in the literature, such as one-vs-all ramp/sigmoid loss (Ishida et al., 2017), pair-comparison ramp/sigmoid loss (Ishida et al., 2017), and cross-entropy loss (Yu et al., 2018). Here we briefly review a recent method that modifies the cross-entropy loss for deep learning with complementary labels Yu et al. (2018). The general idea is to view the ordinary label Y, as a latent random variable. Suppose the classifier has the form f(X) = arg max_i∈[K] g_i(X), where g_i(X) is an estimation for P(Y = i|X). The loss function for complementary labels is defined as $\overline{\ell }(f(X),\overline{Y})=\ell \left(M^{\top }\mathbf{g},\overline{Y}\right)$, where g = (g₁(X),…,g_K(X))^⊤ and M is the transition matrix satisfying

$$P(\overline{Y}=j|X)=\sum _{i\ne j}\underset{M_{ij}}{\underbrace{p(\overline{Y}=j|Y=i)}}P(Y=i|X).$$ (1)

Ishida et al. (2017, 2018) assumed the uniform setting in which M takes 0 on diagonals and $\frac{1}{K-1}$ on non-diagonals. Yu et al. (2018) relaxed this assumption by allowing other values on non-diagonals and proposed a method to estimate M from data. It has been shown in (Yu et al., 2018) that the classifier ${\overline{f}}_n$ that minimizes the empirical estimation of $\overline{R}(f)$, i.e.,

$${\overline{R}}_n(f)=\frac{1}{n}\sum _{i=1}^n\overline{\ell }\left(f\left({\mathbf{x}}_i\right),{\overline{y}}_i\right),$$ (2)

converges to the optimal classifier f^∗ as n → ∞.

Proposed Method

In this section, we will present the motivation and details of our generative-discriminative complementary learning method. First, we demonstrate why generative modeling is valuable for learning from complementary labels. Second, we present our Complementary Conditional GAN (CCGAN) model that is trained using complementarily-labeled data and provide theoretical guarantees. Finally, we discuss several practical factors that are crucial for reliably training our model.

Motivation

It is guaranteed that existing discriminative complementary learning approaches lead to optimal classifiers, given sufficiently large sample size. However, due to the uncertainty introduced by the complementary labels, the effective sample size is much smaller than the sample size n. If we have access to samples with ordinary labels ${\left\{{\mathbf{x}}_i,y_i\right\}}_{i=1}^n$, we can learn the classifier f_n by minimizing R_n(f). Since knowing the ordinary labels is equivalent to having all the K − 1 complementary labels, we can also learn f_n with ordinary labels by minimizing the empirical risk

$${\overline{R}}_n^{\prime }(f)=\frac{1}{n(K-1)}\sum _{i=1}^n\sum _{k=1}^{K-1}\overline{\ell }\left(f\left({\mathbf{x}}_i\right),{\overline{\mathbf{y}}}_{ik}\right),$$ (3)

where ${\overline{\mathbf{y}}}_{ik}$ is the k-th complementary label for the i-th example. In practice, since we only have one complementary label for each instance, we are minimizing ${\overline{R}}_n(f)$ as shown in Eq. (2), rather than ${\overline{R}}_n^{\prime }(f)$. Note that ${\overline{R}}_n(f)$ approximates ${\overline{R}}_n^{\prime }(f)$ by randomly picking up one complementary label for the i-th example, which implies that the effective sample size is roughly n/(K − 1). In other words, although we provide each instance a complementary label, the accuracy of the classifier learned by minimizing ${\overline{R}}_n$ is close to that of a classifier learned with n/(K − 1) examples with ordinary labels.

Because the effective sample size is usually much smaller than the actual sample size, complementary learning resembles semi-supervised learning, where only a small proportion of instances are associated with ordinary labels. In semi-supervised learning, P_X can be estimated with more unlabeled samples compared to P_Y|X, which requires labels to estimate. Therefore, modeling P_X is beneficial because it allows us to take advantage of unlabeled data. This justifies the motivation of introducing a generative term in complementary learning. A natural way to utilize P_X is to model the class-conditional, P_X|Y. P_X imposes a constraint on P_X|Y indirectly since $P_X=\int P(X|Y=y)P(y)dy$. Therefore, a more accurate estimation of P_X will improve the estimation of P_X|Y and thus P_Y|X.

Complementary Conditional GAN (CCGAN)

Given the recent advances in generative modeling using (conditional) GANs, we propose to use conditional GAN to model P_X|Y in the paper. A conditional GAN learns a function G(Y, Z) that generates samples from a conditional distribution Q_X|Y, neural network is used to parameterize the generator function, and Z is a random samples drawn from a canonical distribution P_Z. To learn the parameters, we can minimize certain divergence between Q_X,Y and P_XY by solving the following optimization:

$$\begin{gathered} \underset{G}{\min }\underset{D}{\max }\underset{(X,Y)\sim P_{XY}}{\mathbb{E}}[\varphi (D(X,Y))] \\ +\underset{Z\sim P_Z,Y\sim P_Y}{\mathbb{E}}[\varphi (1-D(G(Z,Y),Y))], \end{gathered}$$ (4)

where ϕ is a function of choice and D is the discriminator.

However, the conditional GAN framework cannot be directly used for our purpose for the following two reasons: 1) the first term in Eq. (4) cannot be evaluated directly, because we do not have access to the ordinary labels. 2) the conditional GAN only generates X’s and does not infer the ordinary labels. A straightforward solution would be to generate (x, y) from the learned conditional GAN model and to train a separate classifier on the generated data. However, such two-step solution results in a sub-optimal performance.

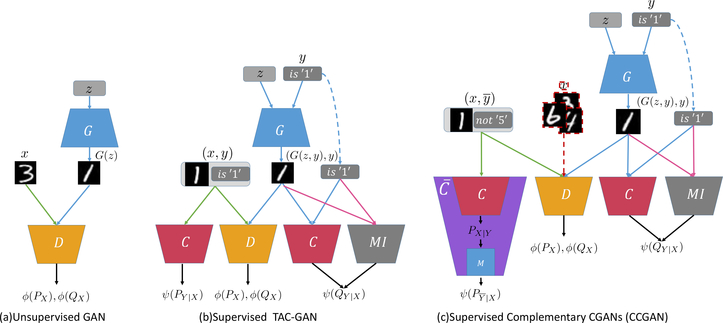
To enable generative-discriminative complementary learning, we propose a complementary conditional GAN (CCGAN) by extending the TAC-GAN (Gong et al., 2019) framework to deal with complementarily-labeled data. The model structures of GAN, TAC-GAN, and our CCGAN are shown in Figure 1. TAC-GAN decomposes the joint distributions as P_XY = P_Y|XP_X and Q_XY = Q_Y|XQ_X and match the conditional distributions and marginal distributions separately. The marginals P_X and Q_X are matched using adversarial loss (Goodfellow et al., 2014), and P_Y|X and Q_Y|X are matched by sharing a classifier with probabilistic outputs. However, P_Y|X is not accessible in a complementary setting since the ordinary labels are not observed. Therefore, P_Y|X and Q_Y|X cannot be directly matched as in TAC-GAN. Fortunately, we make use of the relation between P_Y|X and $P_{\overline{Y}|X}$ (Eq. (1) ) and propose a new loss matching P_Y|X and Q_Y|X in a complementary setting. Specifically, we learn our CCGAN using the following objective

$$\begin{array}{l}\begin{array}{l}\underset{G,C}{\min }\underset{D,C^{mi}}{\max }\underset{X\sim P_X}{\mathbb{E}}\varphi (D(X))\\ +\underset{{}_{Z\sim P_Z,Y\sim P_Y}}{\mathbb{E}}\varphi (1-D(G(Z,Y)))\end{array}\}ⓐ\\ +\underset{(X,\overline{Y})\sim P_{X\overline{Y}}}{\mathbb{E}}\ell (\overline{Y},\overline{C}(X))ⓑ\\ \begin{array}{l}+\underset{Z\sim P_Z,Y\sim P_Y}{\mathbb{E}}\ell (Y,C(G(Z,Y)))\\ +\underset{Z\sim P_Z,Y\sim P_Y}{\mathbb{E}}\ell \left(Y,C^{mi}(G(Z,Y))\right)\end{array}\}ⓒ,\end{array}$$ (5)

where ℓ is the cross-entropy loss, C is a function modeled by a neural network with softmax layer as the final layer to produce class probability outputs, $\overline{C}(X)=M^{\top }C(X)$, and C^mi is another function modeled by a neural network with class probability outputs. From the objective function, we can see that our method naturally combines generative and discriminative components in a unified framework. Specifically, the component ⓑ performs pure discriminative complementary learning on the complementarily-labeled data (only learns C), and the components ⓐ and ⓒ perform generative and discriminative learning simultaneously (learn both G and C).

Figure 1:

Model structure.

The three components in Eq. (5) correspond to the following three divergences: 1) component ⓐ corresponds to Jensen-Shannon divergence between P_X and Q_X, 2) component ⓑ represents KL divergence between $P_{\overline{Y}|X}$ and $Q_{\overline{Y}|X}^{\prime }$, and 3) component corresponds to KL divergence between $Q_{Y|X}^{\prime }$ and Q_Y|X, where $Q_{Y|X}^{\prime }$ is a conditional distribution of ordinary labels given features modeled by C and $Q_{\overline{Y}|X}^{\prime }$ is a conditional distribution of complementary labels given features implied by $Q_{Y|X}^{\prime }$ through the relation $Q_{\overline{Y}|X}^{\prime }=M^{\top }{Q}_{Y|X}^{\prime }$. The following theorem demonstrates that minimizing these three divergences in our objective can effectively reduce the divergence between Q_{Y X} and P_{Y X}.

Theorem 1 Let P_{Y X} and Q_{Y X} denote the data distribution and the distribution implied by our model, respectively. Let $Q_{Y|X}^{\prime }(Q_{\overline{Y}|X}^{\prime })$ denote the conditional distribution of ordinary (complementary) labels given features induced by the parametric model C. If M is full rank, we have

$$\begin{gathered} d_{TV}(P_{XY},Q_{XY})\le 2c_1\sqrt{d_{JS}(P_X,Q_X)} \\ +c_2{\Vert M^{-1}\Vert }_{\infty }\sqrt{d_{KL}(P_{\overline{Y}|X},Q_{\overline{Y}|X}^{\prime })} \\ +c_2\sqrt{d_{KL}(Q_{Y|X},Q_{Y|X}^{\prime })}, \end{gathered}$$ (6)

where d_TV is the total variation distance, d_JS is the Jensen-Shannon divergence, d_KL is the KL divergence, and c₁ and c₂ are two constants.

A proof of Theorem 1 is provided in Section S1 of the supplementary file. An illustrative figure that shows the relations between the quantities in Theorem 1 is also provided in Section S2 of the supplementary file.

Practical Considerations

Estimating Prior P_Y

In our CCGAN model, we need to sample the ordinary labels y from the prior distribution P_Y, which needs to be estimated from complementary labels. Let ${\overline{P}}_{\overline{Y}}={\left[P_{\overline{Y}}(\overline{Y}=1),\dots ,P_{\overline{Y}}(\overline{Y}=K)\right]}^{\top }$ be the vector containing complementary label probabilities and ${\overline{P}}_Y={\left[P_Y(Y=1),\dots ,P_Y(Y=K)\right]}^{\top }$ be true label probabilities. We estimate ${\overline{P}}_Y$ by solving the following optimization:

$$\begin{gathered} \underset{{\overline{P}}_Y}{\min }{\Vert {\overline{P}}_{\overline{Y}}-M^{\top }{\overline{P}}_Y\Vert }^2, \\ s.t.{\Vert {\overline{P}}_Y\Vert }_1=1\text{and}{\overline{P}}_Y[i]\ge 0. \end{gathered}$$ (7)

This is a standard quadratic programming (QP) problem and can be easily solved using a QP solver.

Estimating M

If the annotator is allowed to choose to assign either an ordinary label or a complementary label for each instance, the matrix M will be unknown because of the possible non-uniform selection of the complementary labels. In Yu et al. (2018), the authors provided an anchor-based method to estimate M, we also follow the same technique. Please refer to (Yu et al., 2018) for more details.

Incorporating Unlabeled Data

In practice, we may have access to additional unlabeled data. We can readily incorporate such unlabeled data to improve the estimation of the first term in Eq. (5), which further improves the learning of G through the second term in Eq. (5) and eventually improves the classification performance.

Experiments

To demonstrate the effectiveness of our method, we present a number of experiments examining different aspects of our method. After introducing the implementation details, we evaluate our methods on three datasets, including MNIST (LeCun and Cortes, 2010), CIFAR10, CIFAR100 (Krizhevsky, Nair, and Hinton), and VGGFACE2 (Cao et al., 2018). We compare classification accuracy of our CCGAN with the state-of-the-art Discriminative Learning (DCL) method (Yu et al., 2018) and show the capability of CCGAN to generate good quality class-conditioned images from complementarily-labeled data. In addition, ablation studies based on MNIST are presented to give a more detailed analysis of our method. To be notified, we also have the Inception Score and Fréchet Inception Distance (FID) to measure the generative performance of our model, the result is shown in S3.

Implementation Details

Label Generation

All the four datasets have ordinary class labels, which allows generating labels to evaluate our method. Following the procedure in (Ishida et al., 2017), the label for each image was obtained by randomly picking a candidate class and asking the labeler to answer “yes” or “no” questions. In this case, The candidate classes are uniformly assigned to each image, and therefore the transition matrix M satisfies M_i,j = 1/(K − 1), i ≠ j; M_i,j = 0, i = j. Also, data are usually biased, and the annotators also tend to hold biased choices based on their experience. Thus transition matrix M could be biased (Yu et al., 2018). For uniformed M we assume M is known. However, for biased M, we consider both cases when true M is given, and M needs to be estimated during training time. To be notified, when generating complementary data, we assume M is known.

Training Details

We implemented our CCGAN model in Pytorch. We trained our CCGAN model in an end-to-end strategy, which means the classifier and GAN discriminator share the common bottom to neck conventional layers except for the final fully-connected softmax layer as well as mutual information learner. To train our CCGAN model, we optimized the whole objective equation 5 using Adam (Kingma and Ba, 2014) with learning rate 2e − 4, β₁ = 0.0, β₂ = 0.999 for both D and G network, where we train 2 steps of D and 1 step of G in each iteration for 10,000 iteration in total. To train our baseline DCL model, we apply the same training strategy as (Yu et al., 2018) for all dataset. For the additional VGGFACE2 dataset, we apply the same training settings as CIFAR100. We adopted data augmentation for all datasets except MNIST, where we first resized all images to 32 × 32 resolution, employed random croppings to change the image into 28 × 28 and then applied zero-padding to turn the image back with 32 × 32 resolution.

MNIST

We first evaluate our model on MNIST, which is a handwritten digit recognition dataset that contains 60K training images and 10K testing images, with size 32 × 32. We chose Lenet-5 (LeCun and Cortes, 2010) as the network structure for the DCL method and the C network in our CCGAN. We employed the DCGAN network (Radford, Metz, and Chintala, 2015) as the backbone of our CCGAN. Due to the simplicity of MNIST data, the accuracy of learning is close to that of learning with ordinary labels if we use all 60K training samples. Therefore, we sample a subset of 6K images as our basic sampling set S for training.

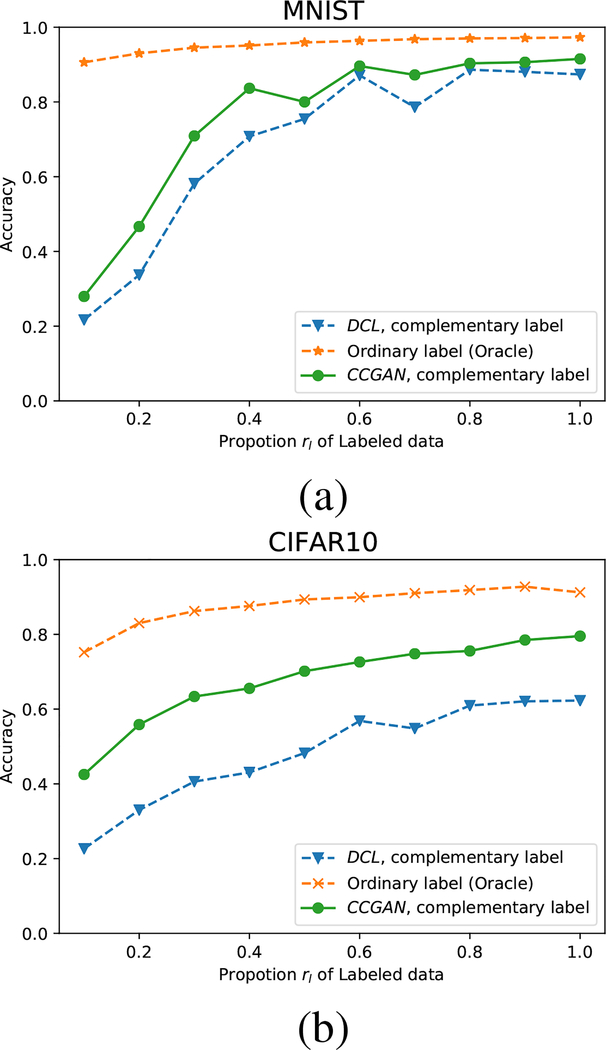
In the experiments, we evaluate all the methods under different sample sizes. Specifically, we randomly re-sampled subsets with r_l × 6K samples, where r_l = 0.1, 0.2,…, 1; and trained all the methods on these subsets. The classification accuracy was evaluated on the 10k test set. We report the results under the following three settings: 1) We only use samples with complementary labels, ignoring all ordinary labels, to train our model CCGAN and baseline DCL. 2) We also train ordinary classifier such that all labeled data are provided with ordinary labels (Oracle). This classifier is trained with the strongest supervision possible, representing the best achievable classification performance. The results are shown in Figure 2 (a).

Figure 2:

Test accuracy on (a) MNIST dataset and (b) CIFAR10 dataset. x axis represents the proportion r_l of labeled data in the training set S.

It can be seen from the results that our CCGAN method outperforms DCL under different sample sizes, and the gap increases as the sample size reduces. our method outperforms DCL by a large margin. The results demonstrate that generative-discriminative modeling is advantageous over discriminative modeling for complementary learning. Figure 3 (a) shows the generated images from TAC − GAN (Oracle) and our CCGAN. We can see that our CCGAN generates high-quality digit images, suggesting that CCGAN is able to learn P_X|Y very well from complementarily-labeled data.

Figure 3:

Synthetic results. (a)Mnist, (b)Cifar10, (c)Cifar100, (d)Vggface100

CIFAR10

We then evaluate our method on the CIFAR10 dataset, which consists of 10 classes of 32×32 RGB images, including 60K training samples and 10K test samples. We deploy ResNet18 (He et al., 2015) as the structure of the C network in our model. Since training GANs on the CIFAR10 dataset is unstable, we utilize the latest conditional structure Big-GAN (Brock, Donahue, and Simonyan, 2018) for our CCGAN backbone. If without mention, the following dataset experiments apply the same settings.

We evaluate all the methods following the same procedure used in the MNIST dataset. The results are shown in Figure 2 (b). Again our method consistently outperforms the DCL method for different sample sizes. Figure 3 (b) shows the generated images from TAC − GAN (Oracle) and our CCGAN. It can be seen that our CCGAN successfully learns the appearance of each class from complementary labels.

CIFAR100 and VGGFACE100

We finally evaluate our method on CIFAR100 and VGGFACE2 data, different from CIFAR10, CIFAR100 dataset contains 100 classes and each class has 500 images in average and 10.000 testing images of 100 classes in total. VG-GCAE2 is a large-scale face recognition dataset. The face images have large variations in pose, age, illumination, ethnicity, and profession. The number of images for each person (class) varies from 87 to 843, with an average of 362 images for each person. We randomly sampled 100 classes and constructed a dataset for evaluation of our method. We selected 80% data as the training set S and the rest 20% as the testing set. Since our CCGAN model can only generate fixed-size images, we re-scaled all training images into 32 × 32.

Because the number of classes is relatively large, the effective labeled sample size is approximately n/99, where n is the total sample size. In case of limited supervision, neither DCL nor our CCGAN can converge. Thus, we applied the complementary label generation approach in (Yu et al., 2018), which assumed only a small subset of candidate classes can be chosen as complementary labels. In specific, we randomly selected 10 candidate classes as the potential compelementary label each class, and assigned them with uniform probabilities.

We used the same evaluation procedures used in MNIST and CIFAR10. The classification accuracy is reported in Table 1. It can be seen that our method outperforms DCL by 5% when the proportion of labeled data is smaller than 0.3 and is slightly better than DCL when the proportion is larger than 0.5. Figure 3 (c) shows the generated images from TAC − GAN (Oracle) and our CCGAN. We can see that CCGAN generates images that are visually similar to the real images for each person.

Table 1:

This table shows the test accuracy on VGGFACE100 and CIFAR100 dataset.

Method╲rl	0.2	0.4	0.6	0.8	1.0
	VGGFACE100
Ordinary label (Oracle)	0.673	0.804	0.870	0.891	0.917
DCL	0.378	0.685	802	0.849	0.884
CCGAN	0.447	0.728	0.822	0.865	0.896
	CIFAR100
Ordinary label (Oracle)	0.439	0.804	0.870	0.891	0.917
DCL	0.252	0.452	0.561	0.609	0.651
CCGAN	0.320	0.520	0.571	0.632	0.660

Biased M training

According to (Yu et al., 2018), we also implement the biased transition matrix M setting. During the training time, we test two settings: 1) we assume true M used for generating data is known; 2) M can not be acquired and needs to be estimated. For the unknown M, we follow the same settings as (Yu et al., 2018) and apply the same anchor method to estimate M. The other training settings are the same as above experiments. The result is shown in Table 2.

Table 2:

This table shows the test accuracy on MNIST, CIFAR10, CIFAR100, and VGGFACE100 when M is biased.

Method╲rl	0.2	0.6	1.0	0.2	0.6	1.0
	True M			Esimated M
	MNIST
DCL	0.675	0.866	880	0.563	0.787	0.894
CCGAN	0.839	0.908	0.918	0.773	0.837	0.916
	CIFAR10
DCL	0.413	0.658	0.724	0.282	0.624	0.713
CCGAN	0.559	0.767	0.815	0.440	0.740	0.757
	CIFAR100
DCL	0.2814	0.582	663	0.176	0.381	0.574
CCGAN	0.320	0.621	0.664	0.206	0.445	0.589
	VGGFACE100
DCL	0.461	0.769	0.863	0.161	0.660	0.836
CCGAN	0.533	0.805	0.866	0.174	0.681	0.850

Ablation Study

Here we conduct ablation studies on MNIST to study the details and validate possible extensions of our approach.

Multiple Labels

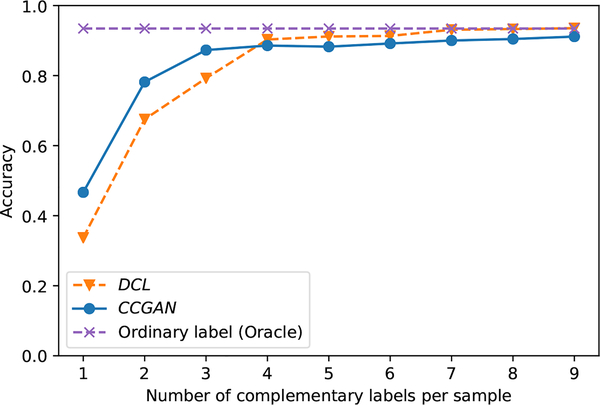
In this experiment, we give an intuitive strategy to verify the effectiveness of generative modeling for complementary learning. In ordinary supervised learning, discriminative models are usually preferred than generative models because estimating the high-dimensional P_X|Y is difficult. To demonstrate the importance of generative modeling in complementary learning, we propose to assign multiple complementary labels to each image and observe how the performance changes with the number of complementary labels. The classification accuracy is shown in Figure 4. We can see that the accuracy of our CCGAN and DCL both increases with the number of complementary labels. When the number of complementary labels per image is large, DCL performs better than our CCGAN because the supervision information is sufficient. However, in practice, the number of complementary labels for each instance is typically small and is usually one. In this case, the advantage of generative modeling is obvious, as demonstrated by the superior performance of our CCGAN compared to DCL.

Figure 4:

Test accuracy. x axis denotes number of assigned complementary labels per image. classifier trained on ordinary labeled data as the Oracle.

Semi-Supervised Learning

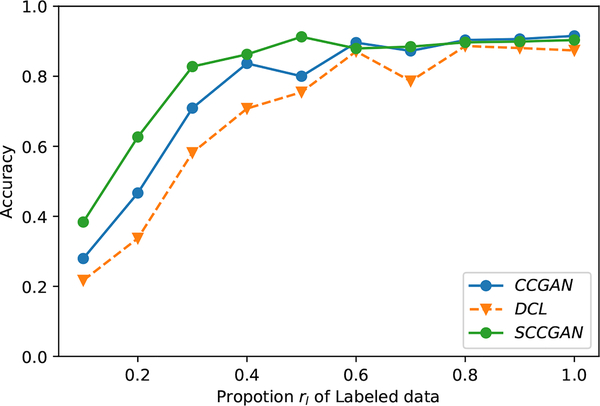
In practice we might have easier access to unlabeled data which can be incorporated into to our model to perform semi-supervised complementary learning. On the MNIST dataset, we used the additional 90% data as unlabeled data to improve the estimation of the first term in our objective Eq. (5). We denote the semi-supervised method as Semi-supervised complementary Conditional GAN(SCCGAN). The classification accuracy w.r.t. different proportion of labeled data is shown in Figure 5. We can see that SCCGAN further improves the accuracy over CCGAN due to the incorporation of unlabeled data.

Figure 5:

Test accuracy of SCCGAN

Conclusion

We study the limitation of complementary learning as a weakly supervised learning problem, where the effective supervised information is much smaller compared to the sample size. To address this problem, we propose a generative-discriminative model to learn a better data distribution, as a strategy to boost the performance of the classifier. We build a conditional GAN model (CCGAN) which learns a generative model conditioned on ordinary class labels from complementary labeled data, and unify the generative and discriminative modeling in one framework. Our method shows superior classification performance on several datasets, including MNIST, CIFAR10, and CIFAR100 and VGGFACE100. Besides, our model generates high-quality synthetic images by utilizing complementary labeled data. In addition, we give a theoretical analysis that our model can converge to true conditional distribution learning from complementarily-labeled data.