Buckling of an Epithelium Growing under Spherical Confinement

Summary

Many organs are formed through folding of an epithelium. This change in shape is usually attributed to tissue heterogeneities, for example, local apical contraction. In contrast, compressive stresses have been proposed to fold a homogeneous epithelium by buckling. While buckling is an appealing mechanism, demonstrating that it underlies folding requires measurement of the stress field and the material properties of the tissue, which are currently inaccessible in vivo. Here, we show that monolayers of identical cells proliferating on the inner surface of elastic spherical shells can spontaneously fold. By measuring the elastic deformation of the shell, we infer the forces acting within the monolayer and its elastic modulus. Using analytical and numerical theories linking forces to shape, we find that buckling quantitatively accounts for the shape changes of our monolayers. Our study shows that forces arising from epithelial growth in three-dimensional confinement are sufficient to drive folding by buckling.

Graphical Abstract

Highlights

• •A proliferating epithelium encapsulated in a hollow sphere spontaneously invaginates
• •Epithelial proliferation generates compressive stresses that deform the elastic shell
• •Coupling between stress and folding shape shows that folding arises from buckling
• •Epithelial elastic moduli are inferred from buckling theory and experiments

Force-driven buckling was proposed to cause epithelial folding. Trushko et al. test this hypothesis by measuring the force (or stress) arising during spontaneous folding of an epithelium grown in an elastic shell. Coupling between stress and folding shape provides evidence that folding occurs by buckling.

Introduction

Epithelium folding is essential for the formation of many organs, such as the gut during gastrulation and the central nervous system during neurulation (Davidson, 2012; Lecuit et al., 2011). Historically, morphogenesis through epithelium folding was studied using gastrulation of simple embryos (sea urchins and cnidarians) as models. In the early 20^th century, Rhumbler and Assheton discussed the mechanical processes by which epithelium could fold during gastrulation (Assheton, 1910; Rhumbler, 1902). They proposed that accumulation of stresses within the layer could lead to folding. The origin of these stresses could be growth under confinement or active contractile forces. Rhumbler and Assheton very well pictured that these contractile forces had to be local and polarized—occurring only on one face of the embryo—to fold the epithelium. By imaging how excised animal poles of embryos would invaginate in absence of compressive stresses of surrounding tissues, Moore and Burt showed that active contraction was an essential mechanism of folding (Moore and Burt, 1939). This polarized active contraction—now called apical constriction—was further showed to rely on the acto-myosin belt found at the apical surface of epithelial cells (Davidson, 2012; Harris, 2018; He et al., 2014; Lecuit and Lenne, 2007; Leptin, 1995; Leptin and Grunewald, 1990; Martin et al., 2009; Wang et al., 2012). Apical constriction is driven by the activation of myosin-II by the Fog pathway, downstream of Twist (Barrett et al., 1997; Kölsch et al., 2007; Müller and Wieschaus, 1996; Parks and Wieschaus, 1991). More generally, islets of more contractile cells can form domains within a growing mesenchyme and lead to its folding (Hughes et al., 2018). All active bending mechanisms rely on a subpopulation of cells that have specific mechanical properties within the tissue (more contractile, more rigid, or more motile) and that locally generate mechanical stresses. Following the impressive example of Rhumbler (Rhumbler, 1902), many studies showed that mechanical models of apical constriction could predict accurately the global shape of gastrulated embryos but also of individual cells (Driquez et al., 2011; Hočevar Brezavšček et al., 2012; Krajnc and Ziherl, 2015; Odell et al., 1980, 1981; Pouille and Farge, 2008; Rauzi et al., 2013; Štorgel et al., 2016; Streichan et al., 2018).

However, because they are local and are generated by a small number of cells, these forces may be too weak to deeply invaginate large tissues. Also, they must be counteracted by contractility of cells surrounding the invagination. Alternatively, compressive stresses arising from growth under confinement could fold epithelium by buckling without requiring heterogeneities or the generation of local stresses. Buckling is a bending instability occurring in elastic materials under compressive forces (Landau and Lifshitz, 1975). For example, a paper sheet lying on a table buckles when pushed inwards on opposite sides. This mechanism, while being implicit in Rhumbler and Assheton’s work (Assheton, 1910; Rhumbler, 1902), was best formulated by Rashevsky (Rashevsky, 1940): Embryos usually grow under the confinement of a protective elastic shell (Gilbert and Barresi, 2017), which could drive buckling of the ectoderm during gastrulation. While the role of this elastic shell in the gastrulation is under intense interest (Bailles et al., 2019; Münster et al., 2019), it is usually considered to be essential to gastrulation (Gilbert and Barresi, 2017). For example, the vitelline layer is essential to gastrulation in C. elegans (Schierenberg and Junkersdorf, 1992). Theoretical studies proposed that cell proliferation in confined geometries induce epithelium folding through buckling (Drasdo, 2000; Hannezo et al., 2014; Hočevar Brezavšček et al., 2012; Rauzi et al., 2015).

The shapes of many organs, for example, plant leaves (Liang and Mahadevan, 2009), villi in the mice gut (Shyer et al., 2013), and the Drosophila wing (Tozluoǧlu et al., 2019), are compatible with shapes resulting from buckling. In several of these examples, confinement is not generated by an external elastic shell but rather by surrounding tissues (smooth muscles in Shyer et al., [2013]) or heterogeneities within the tissue (Tozluoǧlu et al., 2019). Importantly, apical constriction and buckling are not mutually exclusive, and their added contributions were theoretically predicted to set the exact shape of cells and epithelium in many cases (Drasdo, 2000; Hočevar Brezavšček et al., 2012; Krajnc and Ziherl, 2015; Odell et al., 1981; Rauzi et al., 2013; Tozluoǧlu et al., 2019).

In all cases, it is however required to measure the mechanical stresses in the epithelium and its mechanical properties in order to evaluate the specific contribution of buckling to epithelium folding. Several techniques are available for measuring mechanical stresses in single cells and tissues (Roca-Cusachs et al., 2017). A first category relies on local elastic deformation of the substrate balancing the internal forces of the tissue or cells, such as traction force microscopy (Mandal et al., 2014). Another category relies on mechanical probes embedded into the tissue, such as oil droplets (Mongera et al., 2018) or mechanosensitive lipid probes (Colom et al., 2018). Finally, these forces can be inferred from the dynamics of tissue deformations during morphogenesis, with some assumptions (Etournay et al., 2015; Guirao et al., 2015). Many of these techniques require knowledge of the tissue’s material properties, which are often impossible to measure directly. In this study, we aimed at measuring compressive stresses within folding epithelium using elastic properties of an alginate capsule, into which an epithelial monolayer grows.

Results

Cell Encapsulation Recapitulates Epithelial Monolayer Folding under Confinement

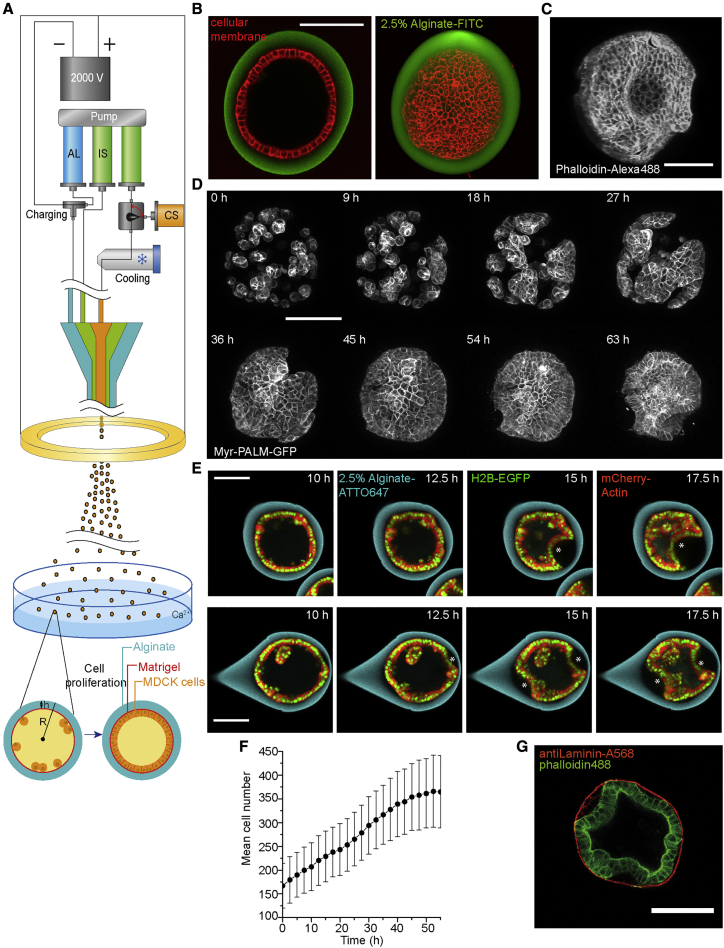
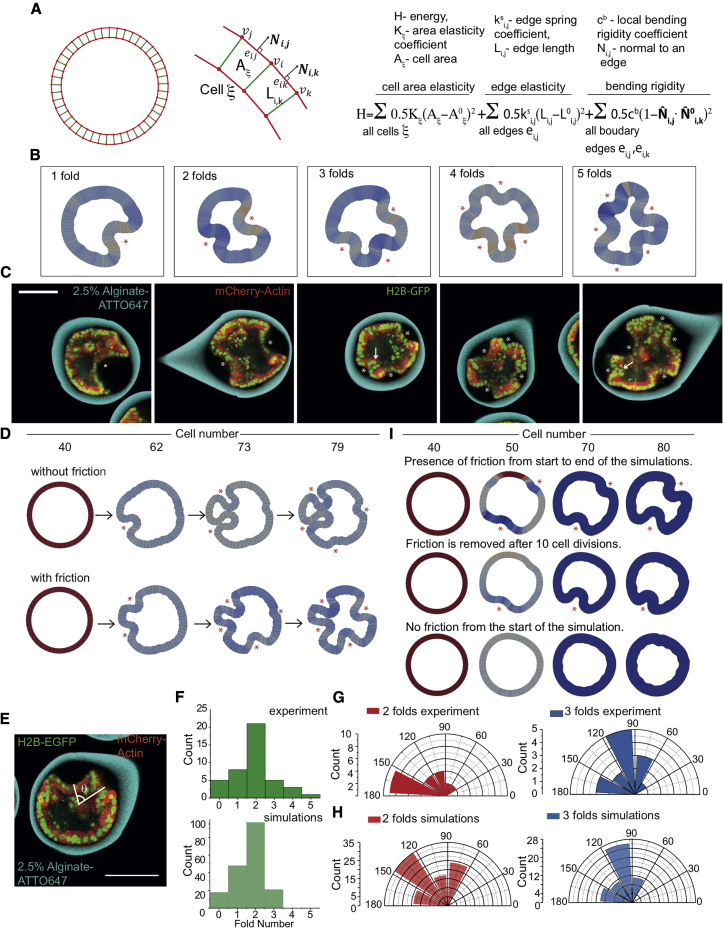
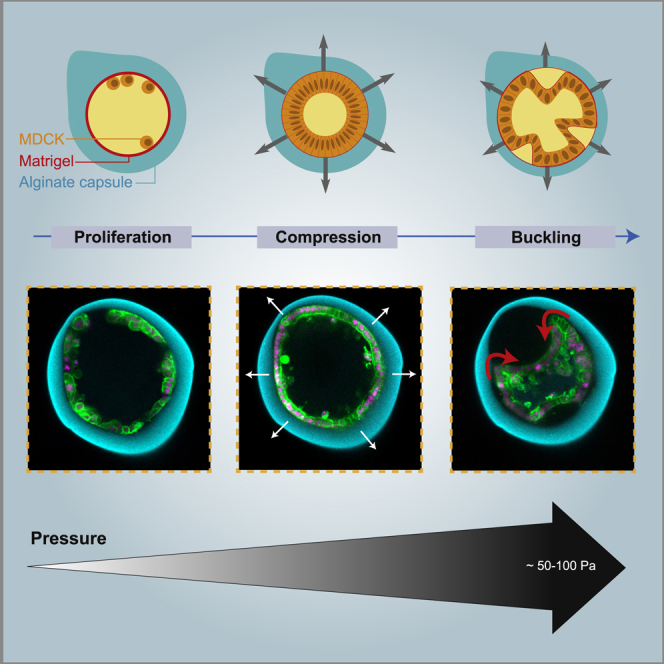
To directly test if mechanical stresses generated by proliferation can induce buckling of epithelia, we undertook an in vitro approach and studied the growth of a cell monolayer confined in a spherical shell. The spherical geometry presents several advantages over others: it is the one of the early embryos, and it does not have boundaries, such that all cells experience the same three-dimensional (3D) environment. Specifically, we encapsulated MDCK-II cells in hollow alginate spheres, hereon referred to as capsules. To form them, we used a 3D-printed microfluidic device to generate three-layered droplets. Their outer layer consisted of alginate, which underwent gelation in a 100 mM CaCl₂ solution (Figures 1A and S1 and STAR Methods) (Alessandri et al., 2016; Alessandri et al., 2013). The inner surface of the capsules was coated with a 3–4-μm thick layer of Matrigel to which cells adhered (Figures 1G and S1) (Alessandri et al., 2016) and on which they formed epithelial monolayers (Figure 1B).

Figure 1.

Characterization of Epithelium Growth and Folding in a Spherical Capsule

(A) Schematic of experimental setup (see also Figure S1).

(B) Left, confocal plane and right, maximum Z-projection of a fully formed MDCK spherical monolayer (Red, deep red CellMask, membrane and green, FITC-alginate, capsule).

(C) Maximum Z-projection of a fixed and folded MDCK monolayer stained with Phalloidin-Alexa488 (actin), respectively.

(D) Maximum projections of confocal planes of MDCK-Myr-PALM-GFP cells forming spherical epithelial monolayer that folds after 45 h.

(E) Confocal equatorial planes of 1-fold (top) and 2-fold (bottom) of epithelium. Asterisks indicate folds.

(F) Mean cell number per capsule over time; three experiments, n = 53 capsules; error bars are SDs.

(G) A confocal equatorial image of a folded MDCK II monolayer after fixed and immunostaining with antiLaminin-A568 (red, Matrigel) and phallodin-Alexa488 (green, actin). Scale bars, 100 μm.

Encapsulated cells were imaged using 3D time-lapse confocal microscopy. Time zero corresponds to the start of imaging, 24 h after capsule formation (STAR Methods), unless mentioned otherwise. Initially, MDCK-II cells were sparsely distributed on the capsule’s inner surface. Through proliferation, cells first formed clusters, which then merged into a monolayer (Figure 1D). Monolayers reached confluency at 8.8 ± 0.8 h (mean ± SEM, as in the rest of the text, unless noted, n = 54). Monolayers folded after 14.5 ± 0.8 h (n = 54) in approximately 80–90% of the capsules. In this process, a portion of the monolayer detached from the alginate shell and progressively bent inward (Figures 1C–1E; Video S1). Proliferation was unaffected by confluency or folding, as the cell number increased linearly with a rate of 3.6 ± 0.1 cells per hour (n = 54) for 55 h (Figure 1F), consistent with the established growth dynamics of MDCK cells (Soderberg et al., 1983). From these observations, we concluded that cell monolayers confined in a spherical shell can spontaneously fold.

Video S1. MDCK H2B-eGFP mCherry-Actin Monolayers Forming 1-fold (Left Panel) and 2-fold (Right Panel) Inside a 2.5% Alginate Capsules

Red channel is mCherry-actin, green channel is H2B-eGFP, and cyan is Alginate is labeled with ATTO647. Time-lapse is 2.5 h. Scale bar, 100 μm, related to Figure 1E.

Epithelial Monolayer Folding Is Due to Buckling

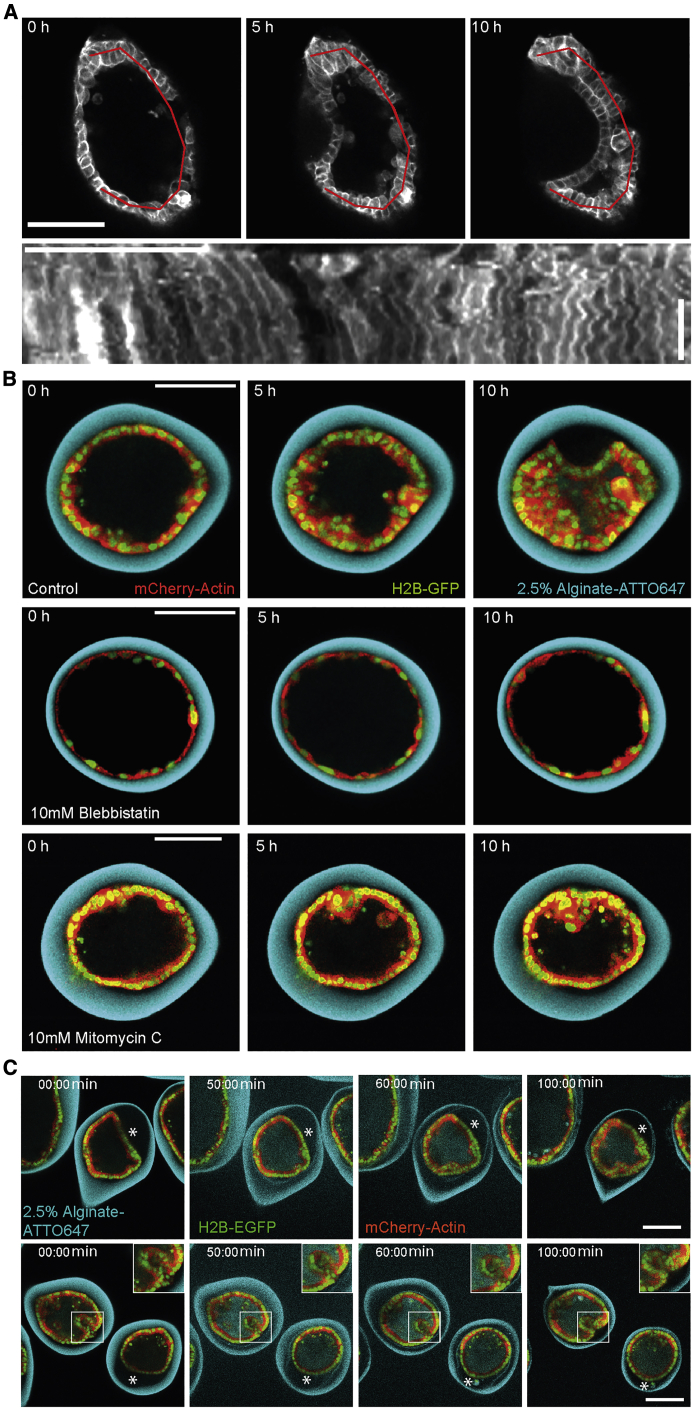
Before investigating in detail whether epithelium folding in our experiments was due to buckling, we checked whether other processes contributed to folding. First, monolayers of MDCK-II cells on micro-patterned substrates have been reported to form osmotically swelling domes by ionic pumping through the cell monolayer (Latorre et al., 2018). To sustain the osmotic pressure difference that grow the domes, the substrate needs to be impermeable to these ions, and the monolayer must have no holes. In our experiments, the monolayer remained sealed during folding, as evidenced by negligible fluorescein loss from the monolayer lumen (Figure S2). The exchange of volume between the lumen of the monolayer and its exterior during folding can be accounted for by the flux of water through the monolayer (Methods S1, Section 1). In contrast to the experiments in (Latorre et al., 2018), where polydimethylsiloxane (PDMS) was used as a substrate, alginate shells cannot maintain significant osmotic pressure differences: Alginate is highly permeable to small molecules, as we showed by fast fluorescein diffusion from the capsule exterior to its interior (Figure S2).

Second, in some morphogenetic processes, active cell flows induce sufficient stresses to fold epithelia (Etournay et al., 2015; Münster et al., 2019). In our assay, however, no large-scale collective cellular flows were observed (Figure 2A). Altogether, we concluded that none of these mechanisms explained monolayer folding in our assay, and we further investigated the possibility of epithelium buckling due to stresses by cell proliferation under confinement.

Figure 2.

Monolayer Folding is Due to Buckling

(A) Top; confocal equatorial planes of Myr-PALM-GFP-MDCK monolayer during folding. Time T = 0 corresponds to the beginning of folding. Bottom; Kymograph along the red line shown above 10 h post-folding. Time is towards the bottom (see arrow on the right). Timescale bar, 5 h.

(B) Confocal equatorial planes of MDCKII monolayers. Top, non-treated control; middle, application of 10 μM Mitomycin-C; bottom, application of 10 μM blebbistatin. T = 0 corresponds to cell confluency.

(C) Confocal equatorial planes of MDCKII monolayer relaxation due to capsule dissolution with alginate lyase. Asterisks highlight relaxation. Scale bars, 100 μm.

Finally, acto-myosin contractility can lead to folding, for example, through apical constriction or in presence of differences between basal and lateral tension (Sui et al., 2018). Since the apical side of our encapsulated monolayers faced the interior of capsules (Figure S3), apical constriction would rather oppose than promote folding in our system (Diaz-de-la-Loza et al., 2018; Krajnc and Ziherl, 2015; Lecuit and Lenne, 2007; Štorgel et al., 2016). We further investigated the role of acto-myosin contractility in folding by treating capsules with 10 μM blebbistatin to inhibit myosin II. In that case, cells did not detach from the alginate shell, and no fold emerged (Figure 2B; Video S2). This result was fully consistent with our recent work showing that contractility of epithelial cells was required to detach the cell monolayer encapsulated in alginate tubes (Maechler et al., 2019). In these alginate tubes, the epithelium detached but did not fold, and blebbistatin inhibited detachment. In those tubes, cell monolayers did not fold because cells were not confined, as they can grow along the tube axis almost indefinitely. We, however, wanted to test further if acto-myosin constriction was essential to folding in the spherical capsules after detachment.

Video S2. A Cell Monolayer Treated with 10 μM Blebbistatin

Red channel is mCherry-actin, green channel is H2B-eGFP, and cyan is Alginate is labeled with ATTO647. Time-lapse is 2.5 h. Scale bar, 100 μm, related to Figure 2B.

To bypass the effect of confinement, we blocked cell proliferation. To this end, we treated encapsulated epithelia with 10 μM Mitomycin C to block their proliferation at the time they reached confluency. After 10 h of Mitomycin treatment, no folds were observed, whereas epithelia were folded in control capsules (Figure 2B; Video S3). Over a longer time period, cell monolayers detached, tore, and reorganized but never folded (Figure S4). These results showed that when proliferation is blocked and contractility is not affected, monolayer detachment is observed, but not folding, supporting our previous findings that cell contractility is involved in detachment and not in folding (Maechler et al., 2019). It also shows that confinement is essential to folding.

Video S3. A Cell Monolayer Treated with 10 μM Mitomyocin C

Red channel is mCherry-actin, green channel is H2B-eGFP, and cyan is Alginate is labeled with ATTO647. Time-lapse is 2.5 h. Scale bar, 100 μm, related to Figure 2B.

To further check that confinement was essential, we dissolved capsules using alginate lyase immediately after monolayers reached confluency. In this case either, we could not observe monolayer folding (Figure 2C; Video S4). We concluded that confinement is essential for monolayer folding. Interestingly, if capsules were dissolved after folding, epithelia just detached or partially folded relaxed to a round shape, while fully folded epithelium only partially relaxed (Figure 2C). At the longer overnight timescale, fully formed folds almost fully relaxed. This suggested that epithelia were under compressive stresses during folding and supported the buckling hypothesis.

Video S4. Cell Monolayer Relaxation over Short Period of Time after Capsule Dissolution with Alginate Lyase Corresponding to the Top Panel of Figure 2C

Red channel is mCherry-actin, green channel is H2B-eGFP, and cyan is Alginate is labeled with ATTO647. Time-lapse is 15 s. Scale bar, 100 μm.

Measurements of Compressive Stresses Due to Monolayer Proliferation and Folding

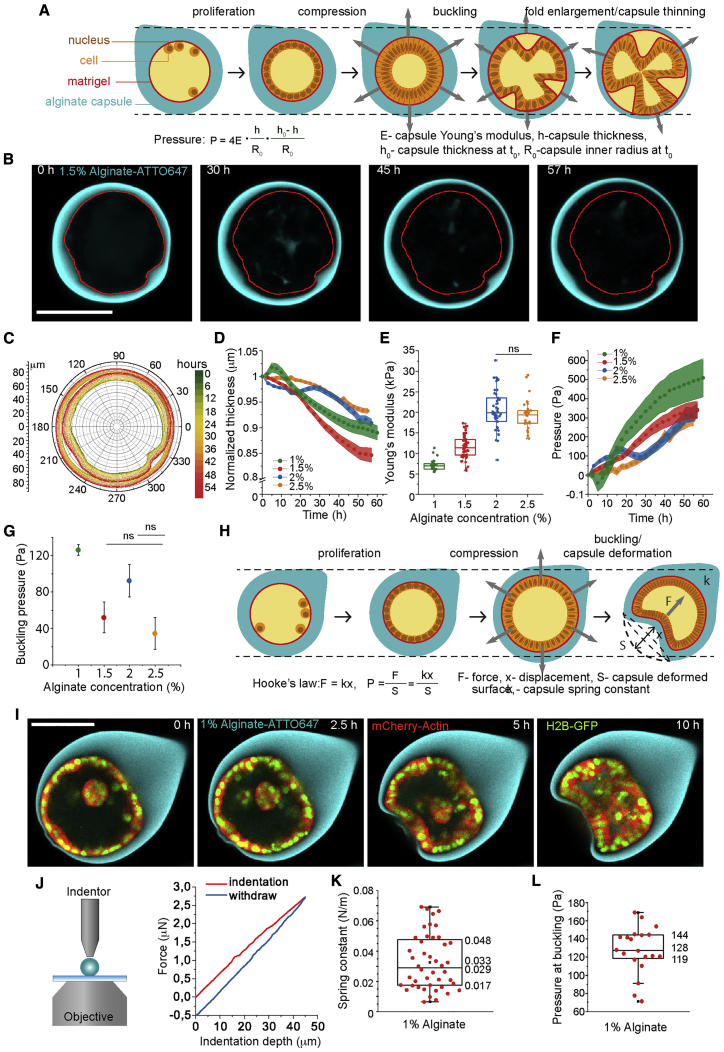
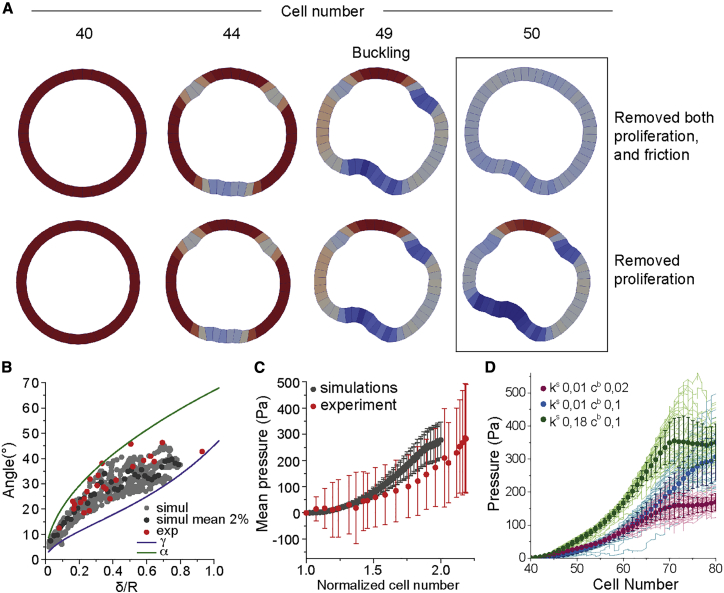
Since alginate is elastic, stresses caused by cell proliferation can be inferred from capsule deformations: The alginate shell undergoes expansion and thinning during proliferation (Figure 3A). Capsules without cells kept a constant wall thickness (Figure S5). To infer the effective pressure corresponding to these compressive stresses, we measured the average capsule radius and wall thickness in confocal images (Figures 3B–3D), and their elasticity modulus (Young’s modulus) by atomic force microscopy (AFM) (Figure 3E; STAR Methods), for four different alginate concentrations (1, 1.5, 2, and 2.5%, see STAR Methods; Figure S5). For all alginate concentrations, the pressure increased during approximately 55 h, reaching a maximal value of 300–400 Pa (Figure 3F). The proliferation rate being constant during the the first 40–50 h, we concluded that pressures below 300 Pa did not significantly affect the proliferation rate.

Figure 3.

Measurements of Compressive Stresses Due to Monolayer Proliferation and Folding

(A) Schematic of capsule thinning during epithelium proliferation.

(B) Confocal equatorial plane of thinning alginate capsule. Red contours correspond to the capsule inner perimeter at T = 0 h.

(C) Superimposed contours of inner and outer boundaries corresponding to different time points.

(D) Normalized mean capsule thickness as a function of time for different alginate concentrations.

(E) Young’s modulus (kPa) as a function of the alginate concentration measured by AFM. Respective Young moduli are: 1%, 7.1 ± 0.3 kPa (n = 25), 1.5%, 11.5 ± 0.4 kPa (n = 52), 2%, 20.7 ± 0.7 kPa (n = 46) and 2.5%, 19.5 ± 0.7 kPa (n = 29). Difference between 2% and 2.5% alginate is not statistically significant (ns) with two-tailed p value 0.7042.

(F) Evolution of pressure (Pa) within capsules over time during epithelium proliferation and for different alginate concentrations (see STAR Methods).

(G) Mean buckling pressure (Pa) for different alginate concentration. For (D), (F), and (G): 1% alginate, n = 22; for 1.5%, n = 35; for 2%, n = 25; for 2.5%, n = 53; error bars are SEM. Difference between 1.5% and 2% alginate, and between 2.5% and 1.5% are not statistically significant (ns) with two-tailed p values 0.1119 and 0.4909, respectively.

(H) Schematic of capsule invagination following epithelium folding.

(I) Confocal equatorial planes showing capsule invagination for 1% alginate capsule.

(J) Left, schematic of an indentation experiment with the FemtoTools indenter (see also Figure S5). Right, a representative plot of force with indentation depth.

(K) Box plot of spring constant for 1% alginate.

(L) Box plot of pressure at buckling (Pa) for 1% alginate capsule calculated from capsule deformation (see STAR Methods). Scale bars, 100 μm.

The pressure at folding measured stresses required for folding and was between 50 and 100 Pa for 1.5, 2, and 2.5% alginate concentration (Figure 3G). Thus, it did not significantly depend on the capsule stiffness. For 1%, however, the monolayer did not detach from the capsule shell upon folding in approximately 65% of the cases. Rather, the shell was pulled in by the folding monolayer (Figures 3H and 3I; Video S5), confirming that osmotic pressure was not at the origin of folding. We estimated the force exerted by cells onto 1% alginate shells by using Hooke’s law for the deformation of the capsule (Figure 3H). The effective spring constant (0.03 ± 0.003 N/m, n = 44) was measured using an FT-S100 indenter (FemtoTools, Buchs, Switzerland, see STAR Methods, Figures 3J, 3K, and S5). This value resulted in an average maximal deflection force of 1.8 ± 0.2 μN (n = 20), about a hundred times larger than the maximal force exerted by a single cell (Mandal et al., 2014). Dividing this value by the invagination area, we obtained a pressure of 128 ± 6 Pa (n = 20) (STAR Methods; Figure 3L), which is of the same order as for other alginate concentrations (Figure 3G).

Video S5. Deformation of a 1% Alginate Capsule over Time Resulting from MDCK H2B-eGFP mCherry-Actin Monolayer Buckling

Red channel is mCherry-actin, green channel is H2B-eGFP, and cyan is Alginate is labeled with ATTO647. Time-lapse is 2.5 h. Scale bar, 100 ?m, related to Figure 3I

Continuum Theory of the Buckling Transition Supports Buckling

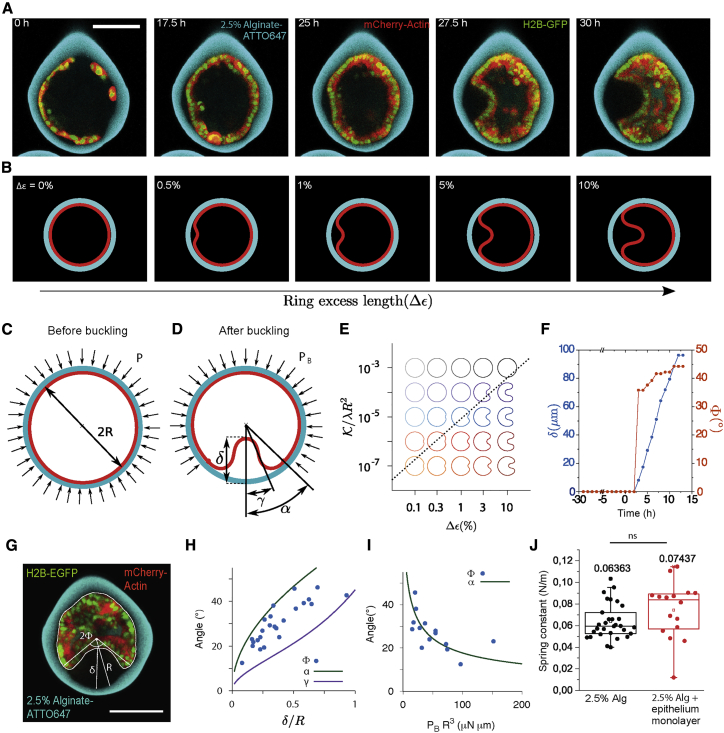
We theoretically determined the compressive stresses within the monolayer corresponding to the pressure at folding. To this end, we used a continuum description without cellular details. Cell monolayers are described as a circular elastic ring in two dimensions, reproducing the geometry in an equatorial confocal plane (Figures 4A and 4B; Methods S1, Section 2). Confinement is accounted for by restricting the cellular ring to a circular domain of radius R. If not confined, the ring is circular and has a radius r. If confined and r > R, then the ring is deformed, namely, compressed or bent. Two elastic parameters characterize its resistance to these deformations: the bending rigidity K and the compressional rigidity λ (Methods S1, Section 2). For r > R, confinement is achieved by a harmonic force of spring constant k, which represents the elasticity of the capsule. The ring shape is determined by minimization of the total energy, which is a combination of the bending, compression, and confinement energies (Methods S1, Section 2).

Figure 4.

Continuum Theory of the Buckling Transition and Comparison to Experimental Data

(A) Confocal equatorial planes of epithelial monolayer bending.

(B) Equilibrium shapes of a buckled elastic ring (red) under circular confinement (cyan) as a function of ring excess strain (Δε), calculated from continuum theory (see Figure 4B and Supplemental Information).(C) Schematic of a compressed elastic ring (red) under the pressure P of the confinement ring (cyan). (D) Schematic of a buckled elastic ring (red) under the pressure P_B of the confinement ring (cyan).

(E) Equilibrium shapes as a function of K /λR² and the excess strain Δε. The dashed line stands for the threshold given by Equation S25 in Method S1. List of parameters: K = 10⁻², k = 10⁵, R = 1, and λ varies from 10 to 10⁵.

(F) Experimental values of δ (n = 43 from 3 replicates) and Φ (n = 43 from 3 replicates) as a function of time. Time point 0 corresponds to the monolayer confluence.

(G) Experimental measurements of δ, Φ, R depicted on a confocal equatorial scan of a capsule with a buckled monolayer.

(H) Blue dots, experimental values of (Φ;δ), (n = 24, from 3 replicates). Solid lines; theoretical relations between δ and α (green) and δ and γ (purple) for the compressional rigidity 10 8.

(I) Blue dots, experimental values (Φ,P_B R³), n = 14, from (F). Only dots where δ was smaller than R were kept for the fit. Solid green line fits to the theoretical relation between α and P_BR³ giving K = 0.5 μN.μm.

(J) Spring constant values of 2.5% alginate capsules with (n = 17 from 2 replicates) and without (n = 31 from 3 replicates) a cell monolayer (see Figure S5). The difference is not statistically significant with two-tailed p value 0.5809.

In our theory, we captured monolayer size by the excess strain Δε = ΔL/2πR, where ΔL = 2π(r−R) is the excess length (Figure 4B). This system exhibits a first order buckling transition controlled by the excess strain Δε (Chan and McMinn, 1966; Lo et al., 1962) (Figure S6; Methods S1, Section 3). If the rigidity of the capsule is much higher than the one of the epithelium (λ/kR² < 1), the threshold excess strain at the transition can be deduced by comparing the energies in two limiting cases: a compressed unbuckled ring (Figure 4C) and an uncompressed buckled ring (Figure 4D). In the first case (Figure 4C), stationary rings accommodate Δε through compression, resulting in circular shapes. The local strain scales as ∼ Δε and the compressed ring length as ∼R, resulting in a compressive energy per unit length ΔE ∼ λRΔε² (Methods S1, Section 3). In the second case (Figure 4D), rings accommodate Δε through bending deformations. We estimated the energy of a buckled ring by splitting it into two parts: a folded segment and an undeformed ring segment (Figure 4D). The fold is characterized by its depth δ and its opening angle α (Figures 4D and S6). Minimizing the energy for this shape while keeping the total length constant yields α ∼ Δε^1/3 and δ ∼ RΔε^2/3 (Methods S1, Section 3). The fold average curvature scales as ∼ δ/(Rα)², and the folded segment length scales as ∼ Rα, resulting in a bending energy per unit length of the buckled ring ΔE ∼ KΔε^1/3/R (Methods S1, Section 3). The buckling transition occurs when the energies of both the constraint ring and the buckled ring are comparable, which happens for a threshold excess strain Δε_c ∼ (K/λR²)^3/5. This threshold depends on both the tissue material properties and the confinement geometry (Figure 4E; Methods S1, Section 3).

From this, the pressure at buckling can be determined. Below the threshold (Δε < Δε_c), the ring compression is stabilized by a uniform pressure P exerted by the confinement (Figure 4C). The energy associated with this pressure is ∼PR²Δε and equals the ring compression energy ΔE∼λRΔε², yielding P∼λΔε/R (Figure S6; Methods S1, Section 4). Hence, the pressure at the buckling transition P_buckling, when Δε ∼Δε_c,

$${\text{P}}_{\text{buckling}}\sim {\text{λ}}^{2/5}{\text{K}}^{3/5}/{\text{R}}^{11/5}{\text{P}}_{\text{buckling}}\sim {\text{λ}}^{2/5}{\text{K}}^{3/5}/{\text{R}}^{11/5}$$ (Equation 1)

depends only on the material properties of the monolayer and on the capsule geometry, but not on the capsule stiffness k (Figure S6), in agreement with our experimental observations (Figures 3G and 3K). Above the threshold (Δε>Δε_c), a uniform pressure P_B on the undeformed ring segment contributes to stabilization of the buckled ring (Figure 4D; Methods S1, Section 4).

We then tested this theory against experimental data. In order to do this, we aimed at comparing how the shape of folds depends on the pressure in the capsules with theoretical predictions. For this, we experimentally characterized the shape of single folds by their opening angle Φ, defined as the angle between the fold axis and the line connecting thelumen’s center to the epithelium detachment point and their depth δ (Figure 4G). We reasoned that since epithelia are adhering to the capsules, experimental Φ should be comprised between two extreme values defined theoretically in absence of adhesion: α, the opening angle; and γ, the inflexion angle (Figure 4D). We find that P_B can be expressed in terms of α and δ, and independent of λ (Chan and McMinn, 1966) (Figure S6; Methods S1, Section 4). Φ, δ, and P_B can be experimentally measured in capsules with a single fold. First, the sharp transition in experimental values of Φ and δ with time (Figure 4F) agrees with buckling being a first-order transition. Moreover, the dependence of Φ with δ is framed by the ones of α and γ with δ, fulfilling theoretical prediction with no other free parameter (Figure 4F), supporting that the folded monolayer’s shape emerges from buckling. Thus, the continuum theory of buckling correctly accounts for the shape of folds.

Next, we sought to test if our theory was accounting for the value of the buckling pressure. To test this, we estimated the elastic parameters K and λ of the monolayer. From the relation between α²/δ and P_B, we found for the bending rigidity K∼0.5 ± 0.2 μNμm (approximately 10⁻¹² J, Figure 3I). Given that the pressure at buckling is of the order of 100 Pa (Figures 3G and 3L), we estimated λ ≈ 0.1 N/m from Equation 1 (Table 1; Methods S1, Section 5). An independent experimental measure of λ can be deduced from rigidity differences between empty versus monolayer-filled capsules measured through capsule indentation (Figures 4J and S5), yielding λ = 0.15 ± 0.13 N/m (Table 1; Methods S1, Section 5) in agreement with the previous estimate. Also, previous measurements established that the Young modulus of cell monolayers was 20 kPa (Harris et al., 2012). Multiplying this value by the cell size, 10 μm, gives λ = 0.2 N/m, in agreement with our findings. Altogether, the agreement between continuum theory and experimental values of elastic parameters and buckling pressure supports that folding results from buckling.

Table 1.

Estimation of the Material Parameters of the Physical Model

E	Capsule Elastic Modulus	19.5 ± 0.7 kPa (n = 29)
Y	Capsule Poisson ratio	½
H	Capsule thickness	19.9 ± 0.4 μm (n = 54)
R	Capsule radius	97 ± 1 μm (n = 54)
${\mathcal{K}}^{cap}=E{h}^3/\left(12(1-{\upsilon }^2)\right)$	Capsule bending rigidity	17 ± 1 μNμm (n = 54)
${\text{λ}}^{cap}=Eh/(1-{\upsilon }^2)$	Capsule compressional rigidity	0.52 ± 0.02 μN/μm
$K^{cap}$	Capsule without tissues spring constant	0.064 ± 0.003 μN/μm (n = 30)
$K$	Capsule with tissues spring constant	0.074 ± 0.007 μN/μm (n = 16)
$\mathcal{K}$	Tissue bending rigidity	0.5 ± 0.2 μNμm
$\text{λ}$	Tissue compressional rigidity	0.15 ± 0.13 μN/μm
$\text{Δ}{\epsilon }_c$	Critical excess strain at the buckling transition	$\sim 0.1$
$P_{buckling}$	Pressure at the buckling transition	$\sim 100$Pa

Errors are SEM.

The Role of Adhesion and Proliferation in Buckling Studied by Numerical Simulations

The continuous equilibrium theory pictures well the experimental pressure and associated shapes of folds. This approach is appropriate, when dynamic processes, such as proliferation and friction/detachment from the capsule shell, occur on timescales that are slow in comparison with the elastic relaxation of the cell monolayer. To study the effects of these processes in a more general case, we numerically analyzed the monolayer dynamics inside alginate capsules using a two-dimensional (2D) vertex model (Hočevar Brezavšček et al., 2012; Merzouki et al., 2016; Merzouki et al., 2018; Rauzi et al., 2015). When simulations start, cells are characterized by a resting area A⁰ and a resting edge length L⁰ (Figure 5A; Methods S1, Section 6). Deviations from these values are penalized by harmonic spring energy terms with constants K and for the area and the length, respectively (Figure 5A; Methods S1, Section 6) (Brückner et al., 2017; Merzouki et al., 2016). In addition, large bending deformations of the monolayer are penalized by a harmonic spring energy term with constant c^b (Methods S1, Section 6). The cell elasticity K can be estimated by K ∼ λ/A₀ ∼ 10⁹ N/m³. As in the continuum theory, the monolayer is confined to a circular domain of radius R by a spring constant (Methods S1, Section 6). To simulate proliferation, at each iteration, one cell is selected to enter a growth phase (linear increase with time) that ends by division when the cell has increased two times its resting area. All other cells cannot enter growth or division until the growing cell has divided. We kept the other two elastic parameters and c^b undefined. Interestingly, we previously showed that when the division rate is faster than the mechanical relaxation time, circular epithelia spontaneously fold because gradient of stresses appear (Merzouki et al., 2018). However, this situation is most likely irrelevant to our MDCK cells, which have a division time of several tens of hours (Soderberg et al., 1983) and a mechanical relaxation time of a few tens of minutes (Harris et al., 2012; Wyatt et al., 2020).

Figure 5.

Numerical Simulations of Epithelial Growth and Buckling

(A) Theoretical model for numerical simulations.

(B) Representative ending shapes of simulations executed with different couples of (c^b,k^s). Asterisks show folds.

(C) Confocal equatorial planes of MDCK monolayer with 1–5-fold. Asterisks highlight folds. Arrows show high curved folds. Scale bar 100 μm.

(D) Top, shape evolution of a cell ring simulated without friction force. Bottom, shape evolution of the same cell ring simulated using the same sequence as on top, but with friction force F_NS = ${5.10}^{-3}\mu N$.

(E) Experimental measurement of the angle between consecutive folds, θ.

(F) Histogram of fold number for 2.5% alginate capsules (n = 43 from 3 replicates) and fold number obtained in silico for $\overline{k^s}/\overline{c^b}=0.1$ (n = 184 independent simulations).

(G) Angle distribution between consecutive folds for two (red, n = 21 from 3 replicates) and three (blue, n = 15 from 3 replicates) folds in 2.5% alginate capsules.

(H) Angle distribution between consecutive folds for two (red, n = 97 independent simulations) and three (blue, n = 63 independent simulations) folds obtained in silico for $\overline{k^s}/\overline{c^b}=0.1$.

(I) Top, shape evolution of a cell ring simulated with friction, F_NS = ${5.10}^{-3}\mu N$. Middle, shape evolution of a cell ring simulated with friction F_NS = ${5.10}^{-3}\mu N$ from the start, which then got removed after ten cell divisions. Bottom, shape evolution of a cell ring simulated without any friction.

Simulations started with 40 cells, similar to the cell number in a confocal section at confluency and ended when the cell number doubled. Simulations reproduced folding (Figures 5B and 5C; Video S6). However, at later times, the shapes of the folds differed from those observed experimentally; due to cell flows, the simulated folds exhibited narrow “neck regions” at their bases (Figure 5D). We reasoned that in experiments, cell adhesion to the Matrigel acts as an effective friction that suppressed cell flows (Figure 2A) and kept the bases wide. We found in our simulations that a friction force ${\text{F}}_{\text{NS}}\sim {5.10}^{-3}\text{μN}$ prevented lateral cell displacements on the capsule’s inner surface resulting in shapes resembling the experimental ones (Figures 1D and 5D; Video S6).

Video S6. Simulated Cell Monolayer Forming 1-, 2-, 3-, 4-, and 5-fold (from Left to Right, Respectively) Inside an Elastic Capsule (k_spring = 0.06 N/m)

Simulations were performed within the model parameters region matching the experimental fold number distribution. The normalized non-slipping force between the growing cell monolayer and the underlying capsule is FNS=10-2, which corresponds to FNS=O10-8N with K = 109 N/m³ and A₀ = 300 μm². The colors represent the cell’s aspect ratio (AR) = width/height. Red corresponds to high AR ≈ 1, where width ≈ height. Blue corresponds to elongated cells with low AR, where width ≪ height, related to Figure 5B.

Another consequence of friction was, on average, to produce more and deeper folds than without friction (Figure 5D). In the experiments, 2-fold is the most frequent case (50%) followed by 1-fold (20%) (Figure 5F). This is different from the continuum theory, where equilibrium shapes feature a single fold (Methods S1, Section 3). In case of 2-fold, angles between folds were between 150° and 180°, whereas in case of 3-fold, they were between 90° and 120° (Figures 5E and 5G). We thought that friction could prevent mechanical relaxation away from the fold. But when friction was removed at the onset of buckling, while cells were kept proliferating, no obvious change in the shape of folds was seen even if there were fewer folds (Figure 5I). We suspected that proliferation could counteract the expected relaxation after removal of friction. When friction and proliferation were both removed at the onset of buckling, a clear relaxation was observed when compared to the situation where only proliferation was stopped (Figure 6A). We concluded that proliferation, by sustaining growth of the folds, and friction, by hindering propagation of the relaxation, synergistically increased the number of folds.

Figure 6.

Numerical Simulations of Epithelial Relaxation upon Friction Removal

(A) Top, shape evolution of a cell ring simulated with friction, F_NS = ${5.10}^{-3}\mu N$, which was removed after ten cell divisions together with cell proliferation. Bottom, shape evolution of a cell ring simulated with friction, F_NS = ${5.10}^{-3}\mu N$, which was kept, however, while cell proliferation was removed after ten cell divisions.

(B) Angles as a function of δ/R obtained from experiments (red, n = 24 from 3 replicates), continuum theory (green and purple lines) and simulations (gray, n = 1,297 points from >100 independent simulations, and dark gray, n = 39 points averaged from the 1,297 points).

(C) Mean pressure as a function of cell number in experiments (n = 53 from 5 replicates) and in silico (n = 184 independent simulations); error bars are SDs.

(D) Pressure as a function of cell number of individual numerical simulations (solid lines; n = 41 per each pair of normalized parameters (c^b,k^s)) and mean pressure (dots; n = 41 per each pair of normalized parameters (c^b,k^s)) as a function of cell number for three different pairs of normalized parameters (c^b,k^s); error bars are SDs.

To fix the values of the elastic parameters ${\text{k}}^{\text{s}}$ and c^b, we computed the distributions of folds for various values and compared the distributions with the experimental distribution (Figure S7; Methods S1, Section 7). The distribution of fold number is similar to experiments only along the line $\overline{{\text{k}}^{\text{s}}}/\overline{{\text{c}}^{\text{b}}}=0.1$, where $\overline{{\text{k}}^{\text{s}}}=\frac{{\text{k}}^{\text{s}}}{{\text{KA}}^0}$ and $\overline{{\text{c}}^{\text{b}}}=\frac{{\text{c}}^{\text{b}}}{\text{K}{\left({\text{A}}^0\right)}^2}$ are normalized parameter used in simulations (Figures 5F and S7). Furthermore, along this line, the shape of folds obtained in our simulations matched the ones observed in our experiments and continuum theory, as seen from the agreement with the relation between Φ and δ (Figure 6B).

We wondered if this set of parameters could also match the pressure dynamics in capsules. The continuum theory predicts that the pressure after buckling decreases as the excess strain increases (Figure S6). Upon a continuous increase of the excess strain (as in growing monolayers), a sharp pressure drop should be observed at the onset of folding. Instead, in the experiments, the monolayer pressure typically grew continuously over time before and after buckling—only in 2% alginate capsules the pressure decreased after folding (Figure 3F). Similarly, in our simulations, pressure increased monotonically after buckling for $\overline{{\text{k}}^{\text{s}}}/\overline{{\text{c}}^{\text{b}}}=0.1$ (Figures 6C–6E). Away from this value, the pressure could drop after buckling (Figure S7; Methods S1, Section 8). We, thus, concluded that with the specific set of parameters that matches the experimental shape, number, and angular distributions of folds, we also reproduced the pressure dynamics observed in most experiments.

Discussion

In this study, we quantitatively showed that an epithelium growing under spherical confinement buckles due to the compressive stresses arising from cell proliferation. Importantly, in this case, all cells are mechanically similar, as theoretically proposed before (Hočevar Brezavšček et al., 2012; Rauzi et al., 2013). However, in other studies, folding was obtained by differential tensions between the apical and baso-lateral sides (Odell et al., 1981; Pouille and Farge, 2008; Rauzi et al., 2013; Streichan et al., 2018) or between the lateral, and the basal sides could drive the deformation (Sui et al., 2018), without the requirement of confinement and compressive forces. While our study does not exclude the importance of different contractile properties of the cells, it shows that forces required to fold the cell monolayer are in the range of micronewtons and cannot be generated by a small (<100) group of cells. In fact, in the MDCK cell monolayer, contractile forces were shown to flatten a buckled epithelium (Wyatt et al., 2020) rather than causing folding. As high as these forces are, the pressure necessary for epithelium buckling is at least five times lower than that required to hinder cell proliferation, which makes proliferation a potent mechanism for epithelium folding. In support of this, it was recently shown that heterogeneous growth in the Drosophila wing epithelium generates buckling of proliferating cells under the confinement of surrounding tissues (Tozluoǧlu et al., 2019). This supports that tissues with different growth rates can fold epithelia at different scales during organogenesis, as previously shown for the gut and the brain gyration (Savin et al., 2011; Tallinen et al., 2014).

Even if our theoretical analysis was done in 2D, whereas the real system is 3D, all the main conclusions emerging for this study are valid, starting with the buckling transition being still present in 3D. Besides this, qualitative features of our description are still valid in 3D, such as the presence of a single fold at equilibrium after the buckling transition or the buckling pressure being independent of the capsule rigidity. Other quantitative features should also be the same, because they are independent of dimensionality, such as the fold’s shape and the buckling pressure. Some features are expected to change with dimensionality, such as the specific values of the vertex model parameters, as well as the specific power-law relations derived in our theory.

Furthermore, while our study provides first estimates of the bending rigidity and the compressibility modulus of cell monolayers, it is difficult to estimate how these values would evolve with cell’s activity (proliferation and contractility) and cell’s mechanical parameters (elasticity and viscosity). The drug treatments commonly used to reduce cell’s proliferation, contractility, and elasticity turned out to be so drastic that we could not obtain a dose-response, precluding any quantitative assessment of the coupling between cell’s activity and macroscopic tissue parameters.

While our study does not unravel the mechanism of epithelium folding in embryos, it identifies buckling as a potential mechanism that drives enough forces to do so. Our study also identifies the importance of friction/adhesion to the shell surrounding the tissue to promote large deformations. This is consistent with recent reports that gastrulation only completes if adhesion to the vitelline membrane is not impaired in Drosophila embryos (Bailles et al., 2019; Münster et al., 2019). Most probably, buckling will complement apical constriction and other contractile mechanisms to drive folding in the embryo. These mechanisms are not exclusive to each other, and the relative contribution of each one may vary in different physiological conditions. For example, we previously identified that in our system, contractility of cells, together with the curvature of the alginate tube, was involved in releasing of adhesion but not in folding (Maechler et al., 2019). In the specific case of gastrulation, which our encapsulation assay intends to mimic, we imagine that apical constriction could set the position and the timing of the fold, and that buckling would drive the propagation of the invagination.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Anti-Laminin	Abcam	ab11575, RRID:AB_298179
Anti-Paxillin	Abcam	ab32084, RRID:AB_779033
Anti-E-cadherin	BD	610181, RRID:AB_39758
Anti-Ezrin	BD	610602, RRID:AB_397939
Anti-Occludin	Thermo Fisher	71-1500, RRID:AB_2533977
AlexaFluor 568 donkey anti-mouse	Invitrogen	A-11031, RRID:AB_144696,
AlexaFluor 568 donkey anti-rabbit	Invitrogen	A-11036, RRID:AB_143011
Chemicals, Peptides, and Recombinant Proteins
Formaldehyde solution	Sigma-Aldrich	F8775
MEM, no phenol red	Thermo Fisher	Cat#51200087
Glycine	Sigma-Aldrich	G8898
Gelatin 40-50% in H2O	Sigma-Aldrich	G7765
EDTA	Sigma-Aldrich	EDS
Saponin	Sigma-Aldrich	47036
PBS	Gibco	Cat#18912014
Phalloidin488	Thermo Fisher	A12379
Hoechst 33342	Invitrogen	H3570
DMEM	Gibco	Cat#0566016
Penicillin-Streptomycin	Gibco	Cat#15070063
Nonessential amino acids (NEAA) 100X	Gibco	Cat#11140050
FBS	Gibco	Cat#10270106
Alginate lyase	Sigma-Aldrich	A1603
Fluorescein (FITC)	Sigma-Aldrich	46955
Blebbistatin	Sigma-Aldrich	B0560
Mitomyocin C	Sigma-Aldrich	M4287
L-15 Medium (Leibovitz)	Sigma-Aldrich	L1518
Matrigel Matrix	Corning	354230
Low-melting agarose	Sigma-Aldrich	A9414
Alginate	FMS BioPolymer	Protanal LF200FTS
ATTO647N-amine	ATTO-TEC	AD647N-95
Fluoresceinamine	Sigma-Aldrich	201626
DMSO (anhydrous)	Invitrogen	Cat#D12345
Sulfo-NHS	Sigma-Aldrich	56485
EDC	Sigma-Aldrich	03449
MES	Sigma-Aldrich	3671
SDS 20% solution	Sigma-Aldrich	428018
Critical Commercial Assays
pLenti6.3/V5-DEST™Gateway™ Vector Kit	Invitrogen	Cat#V53306
Deposited Data
All Imaging raw data	Roux Lab	Trushko -> Data
Raw data and custom analysis codes	Mendeley Data	https://doi.org/10.17632/3vfxhr2m34.1
Experimental Models: Cell Lines
Madin-Darby Canin Kidney II (MDCK-II)	ECACC	Cat#00062107
MDCKII Myr-PALM-GFP	A gift from the lab of Dr. Mathieu Piel (Institut Curie, Paris, France)	N/A
MDCKII H2B-eGFP mCherry-Actin	A gift from the lab of Prof. Daniel J. Müller (BSSE, ETH Zurich, Switzerland)	N/A
MDCKII Myr-PALM-GFP H2B-mCherry	This paper	N/A
Recombinant DNA
H2B-mCherry	A gift from Robert Benezra (Memorial Sloan Kettering Cancer Center, Sloan Ketting Institute, New York, US)	Addgene plasmid #20972, RRID:Addgene_20972
pLenti6.3/V5-DEST containing C-terminal mCherry	This paper	N/A
Software and Algorithms
MATLAB	MATLAB	N/A
Fiji	https://fiji.sc/	N/A
ImageJ	ImageJ	N/A
SolidWorks	Dassault Systèmes	N/A
Illustrator CS6	Adobe	N/A
Origin	OriginLab Corp.	N/A
Imaris	Oxford Instrument	N/A
Other
Micro Hi-Res Plus 3D Printer	EnvisionTEC	N/A
Resin for 3D printer	EnvisionTEC	HTM 140 V2
PFA Tubing, 360 μm OD, 100 μm ID	IDEX	1932
Loctite EA M-31 CL	Henkel	N/A
Dremler 8000	Dremler	F0138000JF
Dremler Workstation (220)	Dremler	26150220AA
Pumps neMESYS (low pressure module V2)	Cetoni	N/A
Glass Syringes 10mL	Analytical Science	10MDR-LL-GT SGE
Bohlender PTFE Tubings 0.5 mm ID	Aldrich	Z609706
Copper ring, 21 mm OD	RadioSpare (RS)	Cat#367-6177
High Voltage DC Power Supply	Stanford Research	PS350
Glass-bottom dish	MatTek	P35G-1.0-14-C
Slide-A-Lyzer™ Dialysis cassette 10K 12-30mL capacity	Thermo Fisher	Cat#66456
Acrodisc Syringe Filter with Glass Fiber – 1um	Pall	4529
Micro-mechanical testing machine	FemtoTools	FT-FS1000
Microforce sensing probe	FemtoTools	FT-S100
Microscope LSM780	Carl Zeiss	N/A
Objective Plan-Apochromat 20x/0.8 M27	Carl Zeiss	420650-9902-000
Microscope LSM710	Carl Zeiss	N/A
Objective W Plan-Apochromat 20x×/1.0 DIC M27 75mm	Carl Zeiss	421452-9800-000

Resource Availability

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Aurélien Roux (aurelien.roux@unige.ch).

Data and code availability

The datasets/code generated during this study are available at Mendeley data https://doi.org/10.17632/3vfxhr2m34.1.

Experimental Model and Subject Details

Cell Culture and Generation of Cell Lines

Madin-Darby Canine Kidney II (MDCK-II) cells were cultured in DMEM supplemented with 1% (vol/vol) Penicillin-Streptomycin, 1% (vol/vol) nonessential amino acids (NEAA) 100X, and 10% (vol/vol) FBS in cell culture flasks (TPP) at 37 °C and 5% CO₂.

The cell line MDCK H2B-eGFP mCherry-Actin was a kind gift from the lab of Prof. Daniel J. Müller (BSSE, ETH Zurich, Switzerland). The cell line MDCK Myr-Palm-GFP, a kind gift from the lab of Dr. Matthieu Piel (Institut Curie, Paris, France), was used to generate the cell line MDCK Myr-Palm-GFP H2B-mCherry. The plasmid H2B-mCherry, a gift from Robert Benezra, was inserted into the pLenti6.3/V5-DEST vector (containing C-terminal mCherry) using the Gateway cloning system. Lentiviral particles were generated in HEK293T cells using third generation lentiviral packaging vectors and MDCK Myr-Palm-GFP cells were infected with pLenti-H2B-mCherry. After infection, cell clones expressing both markers were sorted by Fluorescence Activated Cell Sorting (FACS) using a Beckman Coulter MoFlo Astrios, and monoclonal cells with unchanged morphology and sufficient expression level of the transgenes was selected. Cell lines were regularly tested negative for contamination with mycoplasma.

Method Details

Microfluidic Device Fabrication

The microfluidic device was printed with EnvisionTEC Micro Hi-Res Plus 3D printer using the resin HTM 140 V2 (EnvisionTEC), with the following printing parameters (set automatically based on the resin used): burn-in range thickness 400 μm, base plate of 300 μm, and exposure time 3000 ms. The printed device was washed using ethanol and air dried using an air gun. A thin layer of PDMS (polydimethylsiloxane) at a ratio of 1:10 (curing agent: elastomer) was put on the cone of the chip with the help of a syringe needle and baked at 70 °C for 30 minutes and subsequently baked using a UV chamber for 10 minutes. To ensure hydrophobicity and reduce the diameter of the device tip, Bohlender PTFE tubing was used. The tubing was cut under a stereo binocular (Leica) using a scalpel to obtain a size of around 200 - 300 μm in length and glued on the tip of the microfluidic device with epoxyglue EA M-31CL (Loctite) and left to solidify for 1h at RT. To make the inlets, three 19-gauge stainless steel needles were cut into segments 1:5 cm long and polished using a Dremel 8000 WorkStation to avoid sharp edges. A small droplet of glue EA M-31CL was spread at the edges of the needles and they were inserted into the inlets of the devices, after which the glue was left to solidify for 24 hours at RT.

Device Operation and Cell Encapsulation

The working principle of the microfluidic device (MD) is explained in detail in (Alessandri et al., 2016). In brief, the system comprises the MD, three glass syringes connected to a pump (neMESYS) for flow rate control, a Matrigel cooling part, and both an Alginate charging part and a copper ring (21 mm OD, RadioSpare) connected to a High Voltage DC Power Supply (Stanford Research PS350). The MD consists of three coaxial cones inside which three different solutions are injected. The outermost cone contains alginate solution (AL), the intermediate cone contains 300 mM sorbitol solution (IS) and the innermost cone contains cells/Matrigel/sorbitol solution (CS) in a ratio of 2:1:2 (v/v), with a cell number in the range of 2∗10⁶. The AL and IS solutions are loaded into two syringes controlled by the pumps for injection into the MD. The CS is injected into a cooling part to maintain Matrigel liquid, and this part is connected to a third syringe containing sorbitol that pushes out CS into the MD. The flow rates are set to 45 mL/h, 45 mL/h and 30 mL/h for AL, IS and CS, respectively, ensuring droplet formation upon exiting the MD. Once connected to the pumps the MD is positioned 50 - 60 cm above the petri dish with a 100 mM CaCl2 solution for collection of capsules. To improve capsule shape and mono-dispersity of size an alginate charging part and copper ring, both connected to a high voltage (2000V) generator, are introduced. The alginate charging part is a glass T connector that on opposite sides of the T has a high voltage wire (coming from the generator) and a tubing containing AL that flows down the T. The HV wire is coupled to a silver wire (OD 1 mm) that crosses the T such that it is in contact with the alginate and charges the solution, after which the charged AL then flows into the MD. The copper ring is held below the tip of the MD at a distance of 0.5 cm and centered with respect to the MD tip. The charged formed droplets passing through the copper ring under electrical tension get deflected as they cross the ring, creating a shower-like jet that prevents capsule merging. Once formed inside the calcium bath, capsules are washed with DMEM and transferred to cell culture medium.

Fluorescent Labeling of Alginate

0.25 g Alginate was dissolved in 25 mL 0.1M MES pH 6.0 to get 1% Alginate solution. Next, 5 mg ATTO647N-amine or 13 mg Fluoresceinamine dissolved in 200 μL DMSO (anhydrous) was added into the tube with 25 mL 1% Alginate solution and let mix, rotating, for 10min. Next, 21.5 mg sulfo-NHS dissolved in 200 μL of 0.1 M MES pH 6.0 was added and let mix for 30 min. Finally, 24 mg EDC dissolved in 200 μL of 0.1 M MES pH 6.0 was added and let mix and react for overnight. After this, the labeled alginates solution was transferred to Slide-A-Lyzer™ dialysis cassette 10K 12–30mL capacity and let dialyze in milliQ water for 1 day and 1 night changing the water first twice every 2 h and then, last time, for overnight dialysis. After dialysis the labeled alginate was filtered with an Acrodisc syringe filter and keep it at 4 °C before use. The final alginate concentration was 0.5%.

To get 2.5%, 2%, 1.5% or 1% ATTO647N-labeled alginate solutions, to 10 mL milliQ water, with both 10 mL SDS 20% solution and 1 mL 0.5% ATTO647N alginate, 0.27 g, 0.165 g, 0.22 g, 0.11 g of alginate powder was added, respectively, and mixed overnight at room temperature. To get 2.5% FITC-labeled alginate solution, 10 mL milliQ water was mixed with 1 mL 0.5% FITC alginate, 0.25 g alginate powder and 10 μL SDS 20% solution, mixed overnight at room temperature. Before use the solutions were spun down at 48000 g for 30 min at 20 °C, after what alginate was filtered with a sterile glass fiber Acrodisc syringe filter.

Imaging

To maintain capsules in set positions for several days of time-lapse acquisitions, 20 - 25 capsules were selected 24 hours post cell encapsulation and embedded in 0.4% low-melting agarose (0.04 g in 10 mL) in a 35 mm MatTek glass-bottom dish. The agarose was left to solidify for 15 minutes and 2 mL of MEM containing no phenol red, supplemented with 1% (vol/vol) Penicillin-Streptomycin, 1% (vol/vol) non-essential amino acids (NEAA) 100X, 10% (vol/vol) FBS and 1% (vol/vol) GlutaMax were added. Live time-lapse confocal images of samples were obtained using inverted LSM780 microscope (Carl Zeiss) using the objective Plan-Apochromat 20x/0.8 M27 (FWD=0.55mm). During imaging, capsules were maintained at 37 °C with 5% CO2. For each capsule, 3D confocal Z-stacks with a range of 100 μm to 250 μm with 2 μm interval were acquired, and each capsule was imaged every 2. 5 – 3 h for 25 – 30 cycles using with definite focus (autofocus). For imaging of fixed samples, upright microscope LSM710 NLO was used with the objective W Plan-Apochromat 20x/1.0 DIC M27 75mm.

Immunostaining

Cell monolayers in capsules were fixed with warm 4% PFA in MEM, no phenol red (not PBS, to avoid dissolving alginate capsule) for 30 min at RT. Once fixed, capsules were washed with 100 mM Glycine and 1% Gelatin in MEM. Cells were permeabilized using 1% Gelatin/0.1% Saponin in PBS 100 mM Glycine and 0.5 mM EDTA for about 45 minutes at RT until capsules dissolved followed by cell washing with 100 mM Glycine and 1% Gelatin in MEM. Cells were then incubated with primary antibodies: anti-Laminin (1 : 200), anti-paxillin (1:250), anti E-cadherin (1:50), anti-Ezrin (1:50), anti-p120 catenin (1:50) and anti-occludin (1:50) diluted in 1X PBS 100 mM Glycine 0.5 mM EDTA overnight at 4 °C. Cell monolayers were washed 3 times with 1X PBS 100 mM Glycine and incubated with secondary antibody AlexaFluor 568 donkey anti-mouse or anti-rabbit (1:1000) for 1 hour at RT (diluted in 100 mM Glycine 1X PBS with 1% Gelatin, and counterstained for f-actin and nuclei using Phalloidin488 (1:40) and Hoechst 33342 (1:1000), respectively. Samples were rinsed 3 times with 1X PBS 100 mM Glycine.

Capsule Dissolution with Alginate Lyase

For high-temporal resolution experiment, cell monolayers in capsules were embedded in 0.4% agarose for imaging in a 35 mm glass-bottom dish. The MatTek dish was priced on the side with a 19G hot needle to introduce teflon tubing into the dish sterilely for alginate lyase (Sigma-Aldrich, ref. A1603) injection. The MatTek dish was mounted onto inverted LSM780 NLO microscope (Carl Zeiss) (section Imaging). The 1mL of PBS alginate lyase solution (20 units per 1mL of PBS) was added both after 1min of imaging and after 20 min of imaging, resulting in total amount of alginate lyase of 40 units in MatTek petri dish. The imaging was performed with microscope parameters mentioned in section Imaging. For each capsule, confocal equatorial planes were acquired with time interval of 15 s for 2 hours with definite focus (autofocus). For low-temporal resolution, the experiment was conducted as a high-temporal resolution with addition of medium alginate lyase solution giving final alginate lyase amount of 75 units in MatTek dish. The imaging of capsule equatorial planes was performed with time interval of 10 min for 19 hours and with definite focus (autofocus).

Fluorescein Diffusion Experiments

For fluorescein (FITC) diffusion from capsule exterior to its interior, cell monolayers in capsules were embedded in 0.4% agarose for imaging in a 35 mm glass-bottom dish. The MatTek dish was priced on the side with a 19G hot needle to introduce teflon tubing into the dish sterilely for FITC injection. The MatTek dish was mounted onto inverted LSM780 microscope (Carl Zeiss). Once imaging started, 10 μL of 10μg/ml medium FITC solution was added. The imaging was performed with microscope parameters mentioned in section Imaging. For each capsule, confocal equatorial planes were acquired with time interval of 10 s for 2 hours with definite focus (autofocus). For FITC diffusion from capsule interior to its exterior, cell monolayers in capsules were pre-incubated with FITC solution (100 μg/ml) for 2.5 hours followed by careful washing with medium. Then, cell monolayers in capsules were imbedded in 0.4% agarose for imaging. For each capsule, confocal equatorial planes were acquired with time interval of 10 min for 12 hours with definite focus (autofocus).

Blebbistatin and Mitomycin C controls

For Blebbistatin experiments, cell monolayers in capsules were embedded in 0.4% agarose for imaging, then 10 μM of Blebbistatin was added to capsules, after 1 hour of incubation at 37 °C with CO2 control, monolayers were imaged. For Mitomyocin C experiments, cell monolayers in capsules at the stage of confluence were incubated with 10 μM Mitomyocin C for 1 hour followed by washing with warm medium before imaging. The imaging conditions in both cases were as described in section Imaging.

Capsule Spring Coefficient Measurements

There were three types of indentation experiments: i) 1% empty alginate capsule indentation, ii) 2.5% empty alginate capsule indentation and iii) 2.5% alginate capsule with a formed cellular monolayer (48 h capsule post-formation). Capsules were transferred into glass-bottom Mattek petri dish with MEM containing no phenol red solution for empty capsules and L-15 Medium supplemented with 1% (vol/vol) Penicillin-Streptomycin, 1% (vol/vol) non-essential amino acids (NEAA) 100X, and 10% (vol/vol) FBS at 37 °C. The medium was changed every 2 h. Capsules were indented normally to the glass-bottom surface using micro-mechanical testing machine (FT-FS1000, FemtoTools) with indenter FT-S100. The indenter of the probe has flat silicon tip with a tip size of 50 μm by 50 μm with a force range ±100 μN and with resolution at 10 Hz 0.005 μN. For all capsule indentation experiments indentation parameters were step size 0.2 μm, speed 1 μm/s, force threshold 50 μN and signal record time 0.1 s, indentation depth was varying from 5 μm to 40 μm. The process of indentation was monitored by bright-field microscopy. To calculate capsule stiffness coefficient, the dependences of force versus indentation depth were plotted and the part of the indention was fitted with a linear fit.

Capsule AFM Indentation

Indentation measurements were performed at 37°C using a Nanowizard 4 AFM equipped with a Petri-dish heater (JPK Instruments) and an optical inverted microscope (Observer D1, Zeiss). Measurements were carried out using a PNP-TR-TL cantilevers (Nanoworld) with a nominal spring constant of 0.08 N/m after attaching a sphere of 5 μm diameter to the tip.

The force-indentation curves of Alginate capsules in concentration ranging from 1 – 2.5% were acquired then analyzed using the JPK data processing software (JPK Instruments, Germany) in which the cantilever approach curves are fitted with the Hertz and Sneddon modified model for a spherical indenter

$$F=\frac{E}{1-{\nu }^2}\left(\frac{R^2+r^2}{2}log\frac{R+r}{R-r}-Rr\right),$$ (Equation S1)

and,

$$\delta =\frac{R}{2}log\frac{R+r}{R-r},$$ (Equation S2)

where $F$ is the indentation force,$\delta$ is the indentation depth, $r$ is the indenter radius, $R$ is the radius of the circular contact area between indenter and sample, $\upsilon$ is the Poisson's ratio and is set to 0.5 and finally, $E$ is the apparent Young's modulus of the measured sample and is extracted from the fitted curve.

Quantification and Statistical Analysis

Capsule Pressure Calculated from Capsule Deformations

To calculate the buckling pressure from capsule thinning, confocal images at capsule equatorial planes were thresholded with Fiji to get black-white masks. Then, these masks were processed using a homemade MATLAB script that detected masks boundaries (Figure S5B), corrected for drifts (Figure S5C), and computed outer and inner capsule radii ($R_o(t,\theta )$ and $R_i(t,\theta )$, resp.) as a function of the polar angle θ with the origin at the inner capsule surface centroid (Figure S5D and S5E). At each polar angle θ, the capsule thickness

$$h\left(t,\theta \right)=R_o\left(t,\theta \right)-R_i\left(t,\theta \right),$$ (Equation S3)

was calculated from the capsule radii, and the capsule pressure $P(t,\theta )$ was approximated as

$$P\left(t,\theta \right)=\frac{4Eh(t,\theta )(R_i\left(t,\theta \right)-R_i\left(0,\theta \right))}{R_i{(t,\theta )}^2}$$ (Equation S4)

where $E$ corresponds to the capsule Young's modulus and $R_i(0,\theta )$, corresponds to the capsule inner radius at the start of imaging. For spherical geometries, Equation S4 corresponds to the theoretical relation between the inner pressure P and the geometrical deformations of a linear-elastic spherical shell with thickness h, radius R, Poisson ratio $\upsilon =0.5$ and that satisfies $h/R\ll 1$. For more details concerning the derivation of Equation S4, we refer the reader to (Landau and Lifshitz, 1975, Theory of elasticity) in the main text. For instance, the reported values in Figures S5F and S5G are the mean over the polar angle θ of the thickness given by Equation S3 and the pressure given by Equation S4, respectively.

Capsule Pressure Calculated from Capsule Bending

To calculate the buckling pressure from capsule bending deformations, the capsule boundary displacement was monitored on confocal scans at capsule equatorial planes. Since alginate capsules exhibit an elastic behavior and its spring constant $k$ was measured from indentation experiments, the maximal force $F_m$ was calculated according to Hooke's law:$F_m=k{x}_m$, where $x_m$ is a maximal capsule boundary displacement (see Figure 3 in the main text). To convert force to pressure, we use the formula $P=F_m/S$, where $S$ is the surface of the deformed capsule that was approximated by a spherical cap: $S=2\pi Rh$, where $R$ is the radius of the spherical cap and $h$ is the height of the spherical cap.

Fold Opening Angle and Fold Depth Calculation

Both the fold opening angle, 2α, and fold depth δ, were manually measured on the confocal scans of equatorial planes of the monolayers that exhibit one-fold buckling (see Figure 4G in the main text). The center of capsules was considered the centroid of capsule inner surface. The fold ends in contact with the capsule inner surface were considered the points where cell nuclei lied parallel to the capsule inner surface, and the angular distance between them defines the fold opening angle 2Φ (see Figure 4G in the main text). Fold depth δ was considered the maximum radial distance between the fold and the capsule inner surface (see Figure 4G in the main text). Fold opening angle and fold depth were measured over time for each capsule. The same folds at different time points were considered as independent.

Fold Number and Fold Angular Position Calculation

Fold number was measured from the confocal scans at equatorial planes of the monolayers that exhibit developed folds. The center of capsules was considered the centroid of inner capsule surface. To analyze fold position distribution, the angles in between adjacent folds were calculated (see definition of θ in Figure 5E). Angles θ larger than 180° were subtracted −360°.

Statistical Analysis

All statistical analyses for experimental data were performed in Origin (Origin Lab Corp., Northampton, MA, USA). For comparing two populations, two sample a t-test with Welch’s correction was used, at p < 0.05 two samples were assumed to be different. Error bars represent mean + SEM (Standard Error of the Mean) unless stated otherwise. Sample sizes are specified in figure legends.

Published: August 14, 2020