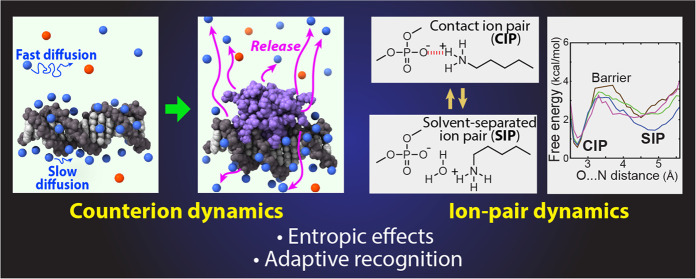
Conspectus
Molecular association of proteins with nucleic acids is required for many biological processes essential to life. Electrostatic interactions via ion pairs (salt bridges) of nucleic acid phosphates and protein side chains are crucial for proteins to bind to DNA or RNA. Counterions around the macromolecules are also key constituents for the thermodynamics of protein–nucleic acid association. Until recently, there had been only a limited amount of experiment-based information about how ions and ionic moieties behave in biological macromolecular processes. In the past decade, there has been significant progress in quantitative experimental research on ionic interactions with nucleic acids and their complexes with proteins. The highly negatively charged surfaces of DNA and RNA electrostatically attract and condense cations, creating a zone called the ion atmosphere. Recent experimental studies were able to examine and validate theoretical models on ions and their mobility and interactions with macromolecules. The ionic interactions are highly dynamic. The counterions rapidly diffuse within the ion atmosphere. Some of the ions are released from the ion atmosphere when proteins bind to nucleic acids, balancing the charge via intermolecular ion pairs of positively charged side chains and negatively charged backbone phosphates. Previously, the release of counterions had been implicated indirectly by the salt-concentration dependence of the association constant.
Recently, direct detection of counterion release by NMR spectroscopy has become possible and enabled more accurate and quantitative analysis of the counterion release and its entropic impact on the thermodynamics of protein–nucleic acid association. Recent studies also revealed the dynamic nature of ion pairs of protein side chains and nucleic acid phosphates. These ion pairs undergo transitions between two major states. In one of the major states, the cation and the anion are in direct contact and form hydrogen bonds. In the other major state, the cation and the anion are separated by water. Transitions between these states rapidly occur on a picosecond to nanosecond time scale. When proteins interact with nucleic acids, interfacial arginine (Arg) and lysine (Lys) side chains exhibit considerably different behaviors. Arg side chains show a higher propensity to form rigid contacts with nucleotide bases, whereas Lys side chains tend to be more mobile at the molecular interfaces. The dynamic ionic interactions may facilitate adaptive molecular recognition and play both thermodynamic and kinetic roles in protein–nucleic acid interactions.
Introduction
Formation of protein–nucleic acid complexes is crucial for gene regulation, transcription, translation, DNA repair, replication, and recombination, all of which are essential for life. Since the first crystal structures of protein–DNA and protein–RNA complexes were solved in the 1980s,1−4 thousands of structures have shown how proteins bind to nucleic acids. From these structures, as well as from prior thermodynamic studies,5,6 it became evident that electrostatic interactions between positively charged protein side chains and negatively charged phosphates play a major role in molecular association of proteins with nucleic acids. Structural bioinformatic studies confirmed that phosphates of nucleic acids are the most common interaction sites in protein–nucleic acid complexes.7,8 Backbone phosphates serve as anchor points for shape recognition of nucleic acids by proteins through steric and electrostatic interactions with basic side chains of proteins.
Ionic interactions at backbone phosphates have major impacts on the thermodynamics of protein–nucleic acid association. Figure 1 summarizes key factors that contribute to the change in free energy upon the molecular association (ΔG, referred to as the “binding free energy”). Coulomb interactions and hydrogen bonds between proteins and nucleic acids make enthalpic contributions to ΔG. The rearrangement of solvent and counterions upon the formation of intermolecular ion pairs (salt bridges) makes a major entropic contribution to ΔG.5,10,11 The highly negatively charged surfaces of DNA and RNA electrostatically attract and condense cations, whereas the ion condensation around proteins is typically less significant due to their lower charge density.5 The zone where counterions exist around a macromolecule is called the ion atmosphere. When proteins bind to nucleic acids and form a complex, charge neutralization via ion pairs between phosphates and basic side chains causes the release of counterions from the ion atmosphere around the molecular interfaces. Since the released ions gain freedom in a solution, the counterion release causes an increase in entropy. In some cases, the release of counterions makes the largest contribution to the binding free energy ΔG for protein–nucleic acid complexes.5,10,11 Dynamics of ion pairs involving protein side chains and nucleic acid backbone can also influence the entropic term in ΔG.12−14 Thus, ionic interactions at protein–nucleic acid interfaces make significant contributions to both enthalpic and entropic terms of the binding free energy.
Figure 1.
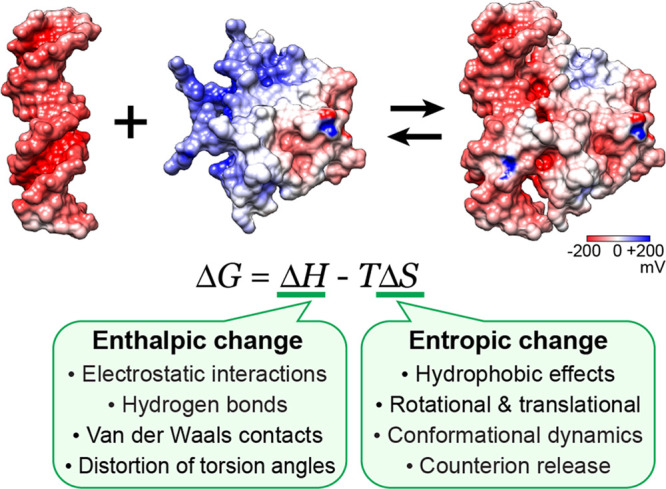
Key factors that influence the enthalpic (ΔH) and entropic (ΔS) terms of the binding free energy ΔG for formation of a protein–nucleic acid complex. The main factors of the entropic changes are (1) the hydrophobic effects that accompany a decrease in nonpolar surface areas exposed to the solvent, (2) rotational and translational restrictions of the interacting macromolecules, (3) conformational dynamics, and (4) counterion release. Empirical formulas for these entropic effects are given in ref (9). The structures of the MEF2A DNA-binding domain, a DNA duplex, and their complex (PDB 1EGW) are shown with surface electrostatic potentials.
In this Account, we provide a brief overview on ionic interactions and dynamics at protein–nucleic acid interfaces. The main focus is on experimental findings about the dynamics of ions and ion pairs involved in protein–nucleic acid association. There has been significant advancement in our understanding of the ionic interactions and their contributions to the thermodynamics of protein–nucleic acid association. Owing to the wealth of structural information, structural bioinformatics and other computational approaches have also provided insight into the dynamic properties of the ion pairs formed between proteins and nucleic acids. New knowledge about the ionic interactions at protein–nucleic acid interfaces help us understand the fundamental basis of protein–nucleic acid association involved in various biological processes.
Observation of Ion Condensation
How do ions surround biological macromolecules and interact with their charged moieties? Researchers have pursued this question for many decades since the discovery in 1888 of the Hofmeister series of ions that influence stability and solubility of proteins.15 In particular, nucleic acids have been a subject of extensive research on ionic interactions. In the 1950s and 1960s, ionic interactions of nucleic acids were investigated using electrophoretic,16 volumetric,17 conductometric,18 and dialysis equilibrium19 analyses. These methods allowed for characterizations of the ion–nucleic acid interactions and determination of relative affinities of ions for nucleic acids. In the 1970s and 1980s, 23Na nuclear magnetic resonance (NMR) was used to investigate the interactions between Na+ ions and DNA.20−22 The NMR studies showed that cations interact with DNA and undergo fast exchange between the free and DNA-bound states. In the 21st century, the physical presence of the ion atmosphere around DNA was confirmed with anomalous small-angle X-ray scattering (ASAXS) using heavy alkali metal ions such as Rb+.23−25 More recently, so-called “ion counting” methods that utilize atomic emission spectroscopy or mass spectrometry were developed for quantitative analysis of the ion atmosphere around DNA,26,27 RNA,27−29 and nucleosomes.30 The ion-counting methods can provide information about how many cations are condensed in the ion atmosphere and how many anions are excluded from the ion atmosphere.26 The quantitative information greatly advanced knowledge about ion–nucleic acid interactions.
Theoretical and computational studies also provided invaluable insights into ion condensation around nucleic acids. The counterion condensation theory by Manning presented the condition required for ion condensation and gave a simple analytical expression of the fraction of a counterion bound in the thermodynamic sense per polyion charge.31 Although Manning’s theory is useful for rod-shaped polyelectrolytes such as DNA, this theory is inapplicable to non-rod-shaped molecules such as folded RNA. Ion condensation around such molecules can be predicted from electrostatic potentials calculated with nonlinear Poisson–Boltzmann equations.32,33 However, this approach treats solvent as a continuum and does not necessarily provide accurate spatial distribution of ions around hydration shells of nucleic acids. Integral equation-based molecular solvation theory methods (e.g., 3D RISM)34−37 can provide more information on ion distribution in a close proximity to nucleic acids. Molecular dynamics calculations also provide accurate atomic details of ionic interactions of nucleic acids (e.g., refs (24, 35, and 38−44)). Appropriate empirical parametrizations are essential for the theoretical models to produce realistic views. There is a great need for quantitative experiments in order to validate computational predictions and to improve the theoretical models.
Remarkable progress to address this need has been made for some aspects of ion–nucleic acid interactions. Due to their quantitative nature, the ion-counting methods allowed examination and validation of existing theories on the ion atmosphere. Perhaps most importantly, the experiments confirmed that despite lacking solution correlations, the Poisson–Boltzmann approximation can account for the number of condensed cations around DNA or RNA with certain assumptions.26,29 Theoretical predications from 3D RISM were also validated.27 The ion-counting data also illuminated some theoretical limitations. For example, the Manning’s theory predicts that the balance between the numbers of the condensed cations and the excluded anions is independent of total salt concentration,5 but ion-counting data clearly showed that this prediction is not true.26 The ion-counting methods have facilitated advancement of research on ion condensation around nucleic acids.
Although the ion-counting methods are powerful, they do not provide any information about the spatial distribution and dynamic properties of counterions within the ion atmosphere. Even at high-resolution in crystal structures, the vast majority of counterions are unresolved, suggesting that they are highly mobile. Computational studies portrayed how ions could behave around nucleic acids. While the majority of the findings remain to be validated through experiments, both computational and experimental studies agree in that there are preferential sites for cations to dynamically interact with nucleic acids.36,42,45−49 For double-stranded DNA, cations were found to preferentially bind to the minor groove. How cations move and change locations within the ion atmosphere is not well understood.
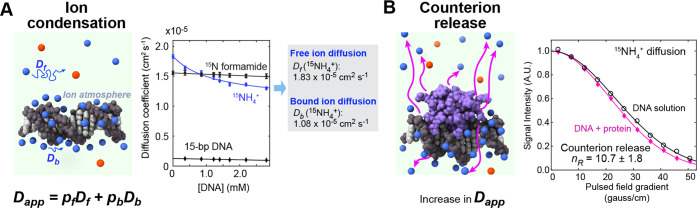
Recently, an NMR-based approach was developed to study the dynamic behavior of counterions in the ion atmosphere.50 In this approach, through pulsed field gradient (PFG) NMR experiments, apparent diffusion coefficients are measured for an ensemble of cations that undergo fast exchange between the free and nucleic acid-bound states. As indicated in Figure 2A, an apparent diffusion coefficient (Dapp) is given by a population average of the diffusion coefficient for the free ions (Df) and that for the macromolecule-bound ions (Db). The diffusion coefficients Df and Db can be determined from the dependence of Dapp on the concentration of the nucleic acid (Figure 2A). If the counterions are tightly bound to DNA, the diffusion coefficient Db should be almost equal to the diffusion coefficient of DNA. However, the bound ion diffusion coefficient Db for NH4+ ions within the ion atmosphere around a 15-bp DNA duplex was 10-fold larger than the diffusion coefficient of the DNA. In fact, ionic diffusion within the ion atmosphere was found to be only <2-fold slower than diffusion in the free state (i.e., Df/Db < 2). The mobility of counterions within the ion atmosphere should affect the entropic change arising from the release from the ion atmosphere and thereby should impact the binding free energy ΔG. Information on ionic diffusion both inside and outside the ion atmosphere is invaluable for us to better understand the thermodynamics of protein–nucleic acid association.
Figure 2.
Ion condensation around nucleic acid and counterion release upon protein–nucleic acid association. (A) Impact of ion condensation on ionic diffusion. Blue and red spheres represent cations and anions, respectively. The apparent diffusion coefficient, Dapp, for cations is given by a population average of the diffusion coefficients Df for the free ions and Db for the bound ions within the ion atmosphere. The Dapp data for NH4+ ions measured at various concentrations of a 15-bp DNA duplex are shown.50 The diffusion coefficients Df and Db can be determined from Dapp data at various concentrations of the nucleic acid. (B) NMR diffusion data showing the direct evidence of counterion release upon the Antp homeodomain–DNA association. Adapted from Pletka et al.50 with permission from Wiley-VCH.
Counterion Release upon Protein–Nucleic Acid Association
Upon formation of a protein–nucleic acid complex, some counterions in the ion atmosphere are released to the solvent, causing a significant entropic contribution to the binding free energy ΔG. Historically, this effect was assessed through an indirect approach using the salt concentration dependence of the association constant (Ka) for formation of the protein–nucleic acid complex.6,10 In this approach, the association constant Ka is measured at various salt concentrations, and the slope |∂ log Ka/∂ log [salt]| in a plot of log [salt] versus log Ka is interpreted as the number of counterions released upon protein–nucleic acid association. Record and co-workers originally used this approach to explain salt-concentration dependence of Ka for DNA-binding of oligo-lysine peptides, not folded proteins.51 Due to its simplicity and practical ease, this indirect approach gained popularity in research on DNA- and RNA-binding proteins as well.10 However, such applications to proteins have often been criticized in the theory community.52−55 This approach does not account for the impacts of changes in salt concentration on hydrophobic effects and some aspects of long-range electrostatic interactions between proteins and nucleic acids. These effects may be negligible for oligo-lysine peptide–DNA complexes but can significantly contribute to ΔG for larger protein–nucleic acid complexes. For example, the salt-concentration dependent Ka data for the HMG-box, TBP, and IHF proteins gave the estimated number of released counterions to be considerably smaller than the number of the protein–DNA ion pairs in the crystal structures.56−58 These proteins distort DNA through extensive hydrophobic interactions within the minor groove. The salt-concentration dependence of the association constant Ka can lead to erroneous interpretation with regard to the release of counterions because this indirect approach relies on simple assumptions that are not necessarily valid for proteins generally.
Obviously, direct observation of ions is more suited for investigating the release of counterions upon protein–nucleic acid association. Such a study to directly observe counterion release was reported recently.50 This observation was achieved through NMR-based measurements of ionic diffusion (Figure 2B). When some counterions are released upon protein–nucleic acid association, the apparent diffusion coefficient Dapp for the ensemble of cations increases because the population of the free ions increases and free ions diffuse more rapidly. The number of the counterions released can be determined from the apparent diffusion coefficients measured for solutions of the protein, the nucleic acid, and the protein–nucleic acid complex. This approach was used to observe the release of NH4+ ions upon the sequence-specific association of the Antp homeodomain (HD) with a 15-bp DNA duplex. For this system, it was found that 11 cations were released from DNA upon the protein–DNA association. In the crystal structure of the same complex, there are 9 ion pairs of phosphates and basic side chains with an interionic O···N distance being <6 Å. Additionally, one of the three basic side chains in the disordered tail, which is not resolved in the crystal structure, is known to interact with DNA.59 Thus, the diffusion-based method can accurately determine the number of cations released upon protein–nucleic acid association. This method will be useful particularly for systems involving disordered interfaces that electrostatically interact with DNA or RNA.
Through direct observation of ionic diffusion, one can also obtain information on the entropic change due to the counterion release.50 From the diffusion coefficients Df and Db for the ions in the free state and bound in the ion atmosphere, the entropic increase due to the counterion release can be calculated using the theoretical relationship between entropy and diffusion:60 ΔSrelease = kB ln(Df/Db) per ion. For example, if Db is small, the ions released from the ion atmosphere would gain more entropy, which should consequently increase the affinity for protein–nucleic acid association. It is reasonable that Df/Db depends on ion species, which might explain why binding affinities of proteins and nucleic acids depend on types of salt used in biochemical experiments. To test this possibility, investigations on diffusion of various ions are required. In principle, the release of alkali metal ions such as 7Li+, 23Na+, 87Rb+, and 133Cs+ ions can be detected with broadband NMR probe hardware that can generate a far stronger PFG than conventional probe hardware. Such investigations would further delineate the behavior of counterions and their roles in protein–nucleic acid association.
Contact Ion Pairs of Protein Side Chains and DNA or RNA Phosphates
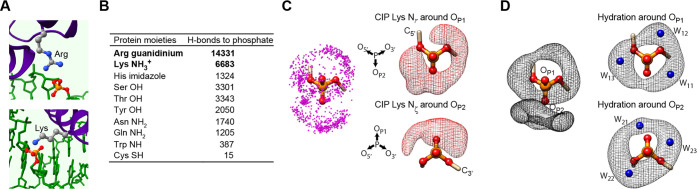
Electrostatic interactions and hydrogen bonds are crucial for protein–DNA/RNA association. Crystal structures of protein–nucleic acid complexes show ion pairs of phosphates and basic side chains that directly form intermolecular hydrogen bonds. This type of ion pair whose anionic and cationic moieties are in direct contact is referred to as a contact ion pair (CIP). Examples of CIPs at protein–nucleic acid interfaces are shown in Figure 3A. Surveying 3213 crystal structures at a resolution <2.5 Å deposited to Protein Data Bank, 34 379 hydrogen bonds were found between protein side chain and DNA or RNA phosphate moieties (Figure 3B). The majority (61%) of these hydrogen bonds are formed through CIPs of phosphates and arginine (Arg) or lysine (Lys) side chains.
Figure 3.
Electrostatic interactions between protein and nucleic acids via contact ion pairs (CIPs). (A) Ion pairs of Lys/Arg side chain and phosphate groups forming hydrogen bonds in PDB 2HDD. (B) CIPs with basic side chains are predominant in intermolecular hydrogen bonds between protein side chain and phosphate moieties of protein–nucleic acid complexes. The table lists the total numbers of hydrogen bonds between protein side chain and phosphate moieties found in 3213 crystal structures of protein–DNA or −RNA complexes solved at a resolution <2.5 Å.63 (C) Spatial distribution of Lys Nζ atoms forming a hydrogen bond to backbone phosphate in high-resolution (<2.0 Å) crystal structures.61 On the right-hand side, the probability density maps are shown separately for the Lys Nζ atoms contacting OP1 and for those contacting OP2. As a guide to the eye, C5′ and C3′ atoms are also shown with the backbone torsion angles of α = −50° and ζ = −114°, which are in a typical range for B-form DNA. (D) Probability density maps of hydration of water oxygen atoms around backbone phosphate in high-resolution (<2.0 Å) crystal structures.61 Six peaks in the probability density are indicated with blue spheres and annotated as defined by Schneider et al.62 Each probability density map represents an enclosure at a 90% probability.
Structural statistics of the ion pairs at the protein–nucleic acid interfaces provide insight into how the basic side chains and water compete for phosphate.61Figure 3C shows the spatial distribution of Nζ atoms of Lys side-chain NH3+ groups forming CIPs with DNA phosphates in high-resolution (<2.0 Å) crystal structures. As shown in Figure 3D, the probability density of hydration water around phosphates appears like two donut-shaped distributions: one donut-shaped distribution around the OP1 atom and the other around the OP2 atom of phosphate. The spatial distribution of Lys Nζ atoms that form CIPs with DNA phosphate considerably overlaps with the spatial distribution of water molecules around DNA phosphate, suggesting that the cationic moiety and water compete for the same surface of phosphates. Interestingly, Lys side-chain NH3+ ions at the hydration site W22 (Figure 3D) are rare, suggesting that the water molecule at this position is difficult to displace. In fact, the probability density of the water molecule at this site is highest,61,62 suggesting a high stability or occupancy of the hydration water molecule at this site. The competition between water molecules and the cationic side chains are relevant to the dynamics of the ion pairs at protein–DNA interfaces, as explained below.
Dynamics of Macromolecular Ion Pairs
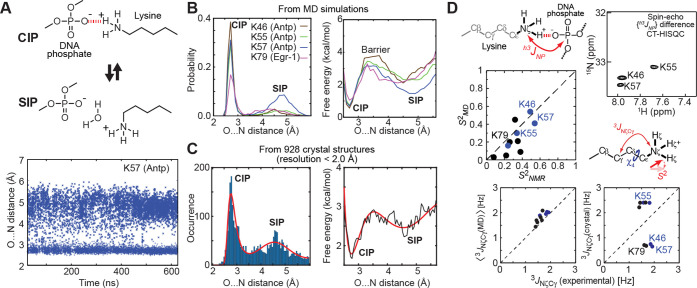
Crystal structures of protein–nucleic acid complexes may give an impression that the ion pairs at the molecular interfaces are relatively static. However, recent experimental and computational studies have revealed that the ion pairs are highly dynamic despite the simultaneous presence of strong electrostatic interactions and hydrogen bonds. Solution NMR studies of Arg and Lys side chains at the protein–DNA/RNA interfaces showed that basic side chains interacting with phosphate groups are generally more mobile than basic side chains interacting with nucleotide bases.12,59,64−68 This difference in mobility may be related to steric restriction and other interactions in the grooves compared with those with the phosphate. More importantly, however, the dynamic equilibria between the CIP state and the solvent-separated ion pair (SIP) enhance the mobility of basic side chains forming ion pairs with phosphates (Figure 4A).65,66 In the CIP state, a cation and an anion are in direct contact, whereas in the SIP state, water molecules intervene between the two ions.
Figure 4.
Dynamics of ion pairs of Lys side-chain NH3+ groups and backbone phosphates. (A) Transitions between the contact ion pair (CIP) state and the solvent-separated ion pair (SIP) state observed in molecular dynamics (MD) simulations. (B) Probability distribution and free-energy landscape (i.e., potential of mean force [PMF]) as a function of the O···N distance obtained from MD trajectories.65 (C) Histogram of the O···N distances for 3038 Lys NH3+–DNA phosphate ion pairs found in high-resolution (<2.0 Å) crystal structures.61 PMF obtained from this histogram is also presented. These data represent experimental evidence of SIP as a metastable state in electrostatic interactions. (D) NMR data supporting the CIP–SIP transitions.65 The h3JNP coupling data show the presence of the CIP states. The S2 and 3JNζCγ data show good agreement with those obtained from MD trajectories, suggesting that these ion pairs are as dynamic as seen in the MD simulations.
Molecular dynamics (MD) simulations for protein–DNA complexes showed that the dynamic transitions between the CIP and SIP states occur on a picosecond to nanosecond time scale for the ion pairs of Lys NH3+ and phosphate groups (Figure 4A).65 The probability distributions as a function of the O···N distance between the phosphate and NH3+ groups in the trajectories give the potentials of mean force as a free energy landscape (Figure 4B). The free-energy difference between the CIP and SIP states was ∼1 kcal/mol, and the energy barrier for a transition from the CIP state to the SIP state was ∼3 kcal/mol. The CIP–SIP energetics for the Lys NH3+–phosphate ion pairs were similar to those of various small ion pairs that had been studied using theoretical and computational approaches.69−75 It should also be pointed out that the Poisson–Boltzmann approximation and certain implicit solvation models predict the CIP state as the sole minimum and do not capture the SIP state.71 This represents a weakness of the continuum electrostatic models.
The statistical analysis of numerous high-resolution (<2.0 Å) crystal structures provides indirect but compelling evidence of the CIP–SIP equilibria.61 The histogram of interionic O···N distances between Lys NH3+ and phosphate groups clearly shows two major peaks corresponding to the CIP and SIP states (Figure 4C). The statistical data are consistent with the probability distribution of the CIP–SIP equilibria obtained from molecular dynamics simulations. Although the majority of these high-resolution crystal structures were solved using diffraction data at a temperature around 100 K, the CIP–SIP ensemble of each ion pair in crystals at the cryo-temperature should be similar to the ensemble immediately before conformational fluctuations cease at a temperature around 200 K during the flash cooling of crystals.76 The statistical distribution of interionic O···N distances for numerous crystal structures likely reflects a general trend in the free energy landscape of Lys NH3+–DNA phosphate ion pairs.
The presence of the dynamic equilibria between the CIP and SIP states was also supported by solution NMR data.12,65 The rapid transitions on a picosecond to nanosecond time scale are reflected in relatively small values of NMR order parameters (S2) for Lys NH3+ groups interacting with phosphates. At the same time, these Lys NH3+ groups exhibit a sizable magnitude of the hydrogen-bond scalar coupling between 15N and 31P nuclei (h3JNP), indicating the presence of the CIP states in solution (Figure 4D). The experimental data of S2 order parameters for Lys NH3+ groups and three-bond 15Nζ–13Cγ coupling constants (3JNζCγ) relevant to Lys side-chain χ4 torsion angles were consistent with corresponding parameters calculated from MD trajectories, but not with those calculated from single crystal structures (Figure 4D). These data suggest that the ion pairs at protein–DNA interfaces are actually as dynamic as observed in atomistic MD simulations.
Do the CIP–SIP equilibria play any roles in protein–nucleic acid interactions? Some potential roles have been suggested (Figure 5). Due to the CIP–SIP equilibria, the basic side chains interacting with phosphates retain high mobility and thereby do not suffer from a drastic decrease in side-chain conformational entropy upon binding.12,14 The same effect could occur for the phosphate backbone.77 Thus, the conformational flexibility through the CIP–SIP equilibria could entropically contribute to the thermodynamics of protein–nucleic acid association. The CIP–SIP equilibria may also facilitate molecular recognition.59,66 RNA and DNA are conformationally dynamic.78−80 Even while the sugar–phosphate backbone undergoes significant conformational fluctuations such as sugar-puckering, BI–BII transitions, or base-flipping, the CIP–SIP equilibria can allow proteins to adaptively recognize the conformationally dynamic nucleic acids (Figure 5). The dynamics of ion pairs at an atomic level may also be related to the kinetic properties of proteins at a molecular level.12 While nonspecifically associated with DNA, proteins move from one site to an adjacent site on DNA. In this process called sliding, ion pairs of basic side chains and phosphates must be transiently broken and recombined with another set of DNA phosphates when the protein settles at an adjacent site (Figure 5). For example, a homeodomain involves 6 CIPs; the time to simultaneously break the 6 CIPs is estimated to be 10–7 to 10–5 s. When all CIPs are broken, the protein molecule may be able to slide to an adjacent site more easily. A recent NMR study showed that the rate constant for a HoxD9 homeodomain to slide from a nonspecific site to an adjacent site is on the order of 105 to 106 s–1,81 which is comparable to the time required to simultaneously break all CIPs. Thus, the dynamic equilibria between the CIP and SIP states of ion pairs could be both thermodynamically and kinetically important for protein–nucleic acid interactions.
Figure 5.
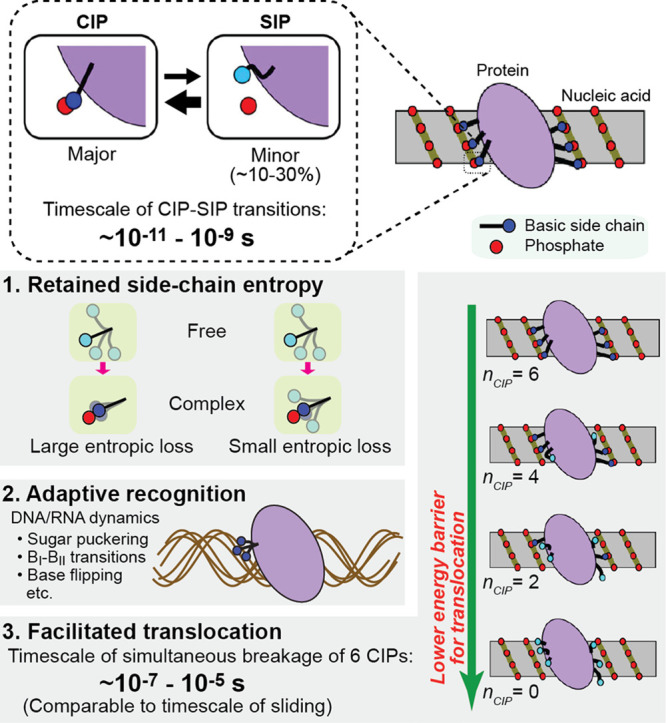
Potential roles of CIP–SIP equilibria at protein–nucleic acid interfaces. See the main text for details.
Arg versus Lys: Cationic Side Chains with Different Roles
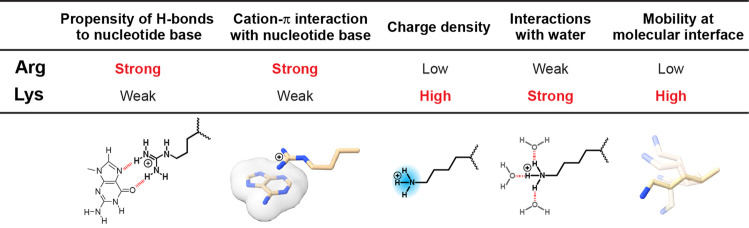
Arg and Lys side chains, both of which are positively charged at physiological pH, are crucial for electrostatic interactions with negatively charged nucleic acids. Interestingly, Arg and Lys appear to play considerably different roles in protein–nucleic acid association. Figure 6 summarizes the characteristic differences between the interfacial Arg and Lys side chains. Compared to Lys side chains, Arg side chains exhibit a stronger propensity to form hydrogen bonds to DNA/RNA bases.7,8 In fact, hydrogen bonds between Arg and guanine represent the most common type of protein side chain–DNA/RNA base interactions.7,8 Cation−π interactions with nucleotide base aromatic rings are also more common for Arg side chains.82,83 This is consistent with the results from quantum chemical calculations showing that cation−π interactions with aromatic rings are more stable for Arg than for Lys.83,84 Thus, Arg and Lys side chains seem to have different roles in base recognition by proteins.
Figure 6.
Differences in properties of the cationic moieties of Arg and Lys side chains. See the main text for details.
Interfacial Arg and Lys side chains appear to be different in mobility at protein–nucleic acid interfaces. This difference was revealed in NMR studies of basic side chains in the free and DNA/RNA-bound states.12,59,64−68 Interfacial Lys NH3+ groups were found to generally be more mobile than interfacial Arg guanidinium groups. The NMR studies also showed that the mobility of Arg side chains is more sensitive to interactions with nucleic acids and can more easily become rigid. This is partially due to a larger number of nitrogen atoms as hydrogen-bonding donors in Arg guanidinium groups than in Lys NH3+ groups. While the multiple hydrogen bonds could be favorable in terms of binding enthalpy, the stronger conformational restriction should cause substantial loss in conformational entropy for Arg side chains. In contrast, the Lys side chain possesses only a single ammonium group as a hydrogen-bonding donor and can adopt various conformations, without substantial loss in side-chain conformational entropy.66
Lys and Arg side chains differ in charge density and desolvation energy.85 The charge density of a Lys NH3+ group is higher than that of an Arg guanidinium group. The higher charge density of a Lys NH3+ group also means a stronger interaction with water’s dipole and, consequently, a higher desolvation energy. Structural bioinformatic investigations of protein–DNA complexes showed that the interactions with the DNA minor groove have a preference for Arg side chains over Lys side chains.85 This preference was attributed to lower desolvation energy for Arg side chains, because insertion into the narrow space of the minor groove requires desolvation.85 However, this preference for Arg could also be related to the different dynamic properties of Arg and Lys side chains. Insertion into the DNA minor groove might diminish the advantage of Lys in terms of side-chain conformational entropy, because the narrow space in the minor groove would not allow for its more usual wide conformational sampling.
Conclusions and Future Perspectives
In the past decade, there were significant advances in research on ionic interactions of biological macromolecules. Owing to the methodological progress, more quantitative information about ion condensation, counterion release, and macromolecular ion pairs has become available. The ionic interactions are highly dynamic and contribute to both enthalpic and entropic terms of the binding free energy for protein–nucleic acid complexes. The counterion release and the CIP–SIP equilibria contribute to the entropic term of the binding free energy. How ions behave around nucleic acids is better understood now. On the other hand, the behavior of ions around proteins remains to be delineated experimentally. Although Manning’s counterion condensation theory predicts that proteins do not condense counterions, the Poisson–Boltzmann equation predicts that proteins to some extent may also condense counterions.53,54 Some thermodynamic studies implicated the release of anions from the protein surface upon protein–DNA association.10,86 Recently developed methods can in principle allow investigations of counterions around proteins as well. Intermolecular ion pairs of protein side chains and phosphates undergo dynamic equilibria between CIP and SIP states. The recent experimental confirmation of the CIP–SIP equilibria represents an important milestone for understanding macromolecular electrostatic interactions and may illuminate a problem of continuum electrostatic models and relevant implicit solvation models, which do not predict the CIP–SIP equilibria.71 Implementation of knowledge of the CIP–SIP equilibria might improve computational approaches to investigate protein–nucleic acid interactions: for example, those for predicting the binding specificity of DNA-binding proteins (reviewed in ref (87)). Further experimental studies on ionic interactions will deepen our physicochemical understanding of proteins, nucleic acids, and their functions.
Acknowledgments
This work was supported by the National Institutes of Health (Grant R35-GM130326 to J.I.) and the Robert A. Welch Foundation (Grant H-0013 to B.M.P.). We thank Channing Pletka for editing the manuscript and Chuanying Chen for useful discussions.
Biographies
Binhan Yu is a Research Scientist at Department of Biochemistry and Molecular Biology, University of Texas Medical Branch. He received his Ph.D. in Biophysics from the National University of Singapore. He conducted postdoctoral research at Texas A&M University. His research interests are NMR spectroscopy and its applications to macromolecular interactions.
B. Montgomery Pettitt is the Robert A. Welch Distinguished University Professor of Chemistry in the Department of Biochemistry and Molecular Biology, University of Texas Medical Branch. He is also the Director of the Sealy Center for Structural Biology and Molecular Biophysics. He received his Ph.D. in Physical Chemistry from the University of Houston. He conducted postdoctoral research at the University of Texas at Austin and Harvard University. His research interests are theoretical and computational biophysics.
Junji Iwahara is a Professor of Department of Biochemistry and Molecular Biology, University of Texas Medical Branch. He received his Ph.D. in Biochemistry and Biophysics from the University of Tokyo. He conducted postdoctoral research at the University of California, Los Angeles, and at the National Institutes of Health. His research interests are biophysical chemistry of protein–DNA interactions.
The authors declare no competing financial interest.
References
- Aggarwal A. K.; Rodgers D. W.; Drottar M.; Ptashne M.; Harrison S. C. Recognition of a DNA operator by the repressor of phage 434: a view at high resolution. Science 1988, 242, 899–907. 10.1126/science.3187531. [DOI] [PubMed] [Google Scholar]
- Jordan S. R.; Pabo C. O. Structure of the lambda complex at 2.5 Å resolution: details of the repressor-operator interactions. Science 1988, 242, 893–899. 10.1126/science.3187530. [DOI] [PubMed] [Google Scholar]
- Otwinowski Z.; Schevitz R. W.; Zhang R. G.; Lawson C. L.; Joachimiak A.; Marmorstein R. Q.; Luisi B. F.; Sigler P. B. Crystal structure of trp repressor/operator complex at atomic resolution. Nature 1988, 335, 321–329. 10.1038/335321a0. [DOI] [PubMed] [Google Scholar]
- Rould M. A.; Perona J. J.; Soll D.; Steitz T. A. Structure of E. coli glutaminyl-tRNA synthetase complexed with tRNAGln and ATP at 2.8 Å resolution. Science 1989, 246, 1135–1142. 10.1126/science.2479982. [DOI] [PubMed] [Google Scholar]
- Manning G. S. Molecular theory of polyelectrolyte solutions with applications to electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978, 11, 179–246. 10.1017/S0033583500002031. [DOI] [PubMed] [Google Scholar]
- Record M. T.; Anderson C. F.; Lohman T. M. Thermodynamic analysis of ion effects on binding and conformational equilibria of proteins and nucleic-acids: Roles of ion association or release, screening, and ion effects on water activity. Q. Rev. Biophys. 1978, 11, 103–178. 10.1017/S003358350000202X. [DOI] [PubMed] [Google Scholar]
- Jones S.; Daley D. T.; Luscombe N. M.; Berman H. M.; Thornton J. M. Protein-RNA interactions: a structural analysis. Nucleic Acids Res. 2001, 29, 943–954. 10.1093/nar/29.4.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luscombe N. M.; Laskowski R. A.; Thornton J. M. Amino acid-base interactions: a three-dimensional analysis of protein-DNA interactions at an atomic level. Nucleic Acids Res. 2001, 29, 2860–2874. 10.1093/nar/29.13.2860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spolar R. S.; Record M. T. Jr. Coupling of local folding to site-specific binding of proteins to DNA. Science 1994, 263, 777–784. 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- Privalov P. L.; Dragan A. I.; Crane-Robinson C. Interpreting protein/DNA interactions: distinguishing specific from non-specific and electrostatic from non-electrostatic components. Nucleic Acids Res. 2011, 39, 2483–2491. 10.1093/nar/gkq984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Record M. T. Jr.; Zhang W.; Anderson C. F. Analysis of effects of salts and uncharged solutes on protein and nucleic acid equilibria and processes: a practical guide to recognizing and interpreting polyelectrolyte effects, Hofmeister effects, and osmotic effects of salts. Adv. Protein Chem. 1998, 51, 281–353. 10.1016/S0065-3233(08)60655-5. [DOI] [PubMed] [Google Scholar]
- Anderson K. M.; Esadze A.; Manoharan M.; Brüschweiler R.; Gorenstein D. G.; Iwahara J. Direct observation of the ion-pair dynamics at a protein-DNA interface by NMR spectroscopy. J. Am. Chem. Soc. 2013, 135, 3613–3619. 10.1021/ja312314b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen D.; Zandarashvili L.; White M. A.; Iwahara J. Stereospecific effects of oxygen-to-sulfur substitution in DNA phosphate on ion-pair dynamics and protein-DNA affinity. ChemBioChem 2016, 17, 1636–1642. 10.1002/cbic.201600265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandarashvili L.; Nguyen D.; Anderson K. M.; White M. A.; Gorenstein D. G.; Iwahara J. Entropic enhancement of protein-DNA affinity by oxygen-to-sulfur substitution in DNA phosphate. Biophys. J. 2015, 109, 1026–1037. 10.1016/j.bpj.2015.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofmeister F. Zur Lehre von der Wirkung der Salze. Naunyn-Schmiedeberg's Arch. Pharmacol. 1888, 24, 247–260. 10.1007/BF01918191. [DOI] [Google Scholar]
- Ross P. D.; Scruggs R. L. Electrophoresis of DNA. II. Specific interactions of univalent and divalent cations with DNA. Biopolymers 1964, 2, 79–89. 10.1002/bip.1964.360020111. [DOI] [Google Scholar]
- Skerjanc J.; Strauss U. P. Interactions of polyelectrolytes with simple electrolytes. III. The binding of magnesium ion by deoxyribonucleic acid. J. Am. Chem. Soc. 1968, 90, 3081–3085. 10.1021/ja01014a017. [DOI] [PubMed] [Google Scholar]
- Zubay G.; Doty P. Nucleic acid interactions with metal ions and amino acids. Biochim. Biophys. Acta 1958, 29, 47–58. 10.1016/0006-3002(58)90145-8. [DOI] [PubMed] [Google Scholar]
- Shapiro J. T.; Stannard B. S.; Felsenfeld G. The binding of small cations to deoxyribonucleic acid. Nucleotide specificity. Biochemistry 1969, 8, 3233–3241. 10.1021/bi00836a015. [DOI] [PubMed] [Google Scholar]
- Anderson C. F.; Record M. T. Jr.; Hart P. A. Sodium-23 NMR studies of cation-DNA interactions. Biophys. Chem. 1978, 7, 301–316. 10.1016/0301-4622(78)85007-8. [DOI] [PubMed] [Google Scholar]
- Bleam M. L.; Anderson C. F.; Record M. T. Relative binding affinities of monovalent cations for double-stranded DNA. Proc. Natl. Acad. Sci. U. S. A. 1980, 77, 3085–3089. 10.1073/pnas.77.6.3085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuben J.; Shporer M.; Gabbay E. J. The alkali ion-DNA interaction as reflected in the nuclear relaxation rates of Na and Rb. Proc. Natl. Acad. Sci. U. S. A. 1975, 72, 245–247. 10.1073/pnas.72.1.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R.; Mills T. T.; Kwok L. W.; Maskel G. S.; Millett I. S.; Doniach S.; Finkelstein K. D.; Herschlag D.; Pollack L. Counterion distribution around DNA probed by solution X-ray scattering. Phys. Rev. Lett. 2003, 90, 188103. 10.1103/PhysRevLett.90.188103. [DOI] [PubMed] [Google Scholar]
- Kirmizialtin S.; Pabit S. A.; Meisburger S. P.; Pollack L.; Elber R. RNA and its ionic cloud: solution scattering experiments and atomically detailed simulations. Biophys. J. 2012, 102, 819–828. 10.1016/j.bpj.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meisburger S. P.; Pabit S. A.; Pollack L. Determining the Locations of Ions and Water around DNA from X-Ray Scattering Measurements. Biophys. J. 2015, 108, 2886–2895. 10.1016/j.bpj.2015.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai Y.; Greenfeld M.; Travers K. J.; Chu V. B.; Lipfert J.; Doniach S.; Herschlag D. Quantitative and comprehensive decomposition of the ion atmosphere around nucleic acids. J. Am. Chem. Soc. 2007, 129, 14981–14988. 10.1021/ja075020g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebala M.; Giambasu G. M.; Lipfert J.; Bisaria N.; Bonilla S.; Li G.; York D. M.; Herschlag D. Cation-anion interactions within the nucleic acid ion atmosphere revealed by ion counting. J. Am. Chem. Soc. 2015, 137, 14705–14715. 10.1021/jacs.5b08395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebala M.; Bonilla S.; Bisaria N.; Herschlag D. Does cation size affect occupancy and electrostatic screening of the nucleic acid ion atmosphere?. J. Am. Chem. Soc. 2016, 138, 10925–10934. 10.1021/jacs.6b04289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebala M.; Herschlag D. Quantitative studies of an RNA duplex electrostatics by ion counting. Biophys. J. 2019, 117, 1116–1124. 10.1016/j.bpj.2019.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebala M.; Johnson S. L.; Narlikar G. J.; Herschlag D. Ion counting demonstrates a high electrostatic field generated by the nucleosome. eLife 2019, 8, e44993. 10.7554/eLife.44993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manning G. S. Limiting laws and counterion condensation in polyelectrolyte solutions. 3. An analysis based on mayer ionic solution theory. J. Chem. Phys. 1969, 51, 3249. 10.1063/1.1672502. [DOI] [Google Scholar]
- Draper D. E. A guide to ions and RNA structure. RNA 2004, 10, 335–343. 10.1261/rna.5205404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp K. A.; Honig B. Salt effects on nucleic acids. Curr. Opin. Struct. Biol. 1995, 5, 323–328. 10.1016/0959-440X(95)80093-X. [DOI] [PubMed] [Google Scholar]
- Beglov D.; Roux B. An integral equation to describe the solvation of polar molecules in liquid water. J. Phys. Chem. B 1997, 101, 7821–7826. 10.1021/jp971083h. [DOI] [Google Scholar]
- Giambasu G. M.; Luchko T.; Herschlag D.; York D. M.; Case D. A. Ion counting from explicit-solvent simulations and 3D-RISM. Biophys. J. 2014, 106, 883–894. 10.1016/j.bpj.2014.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. J.; Lynch G. C.; Pettitt B. M. Ion and solvent density distributions around canonical B-DNA from integral equations. J. Phys. Chem. B 2011, 115, 547–556. 10.1021/jp107383s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovalenko A.; Hirata F. Potentials of mean force of simple ions in ambient aqueous solution. I. Three-dimensional reference interaction site model approach. J. Chem. Phys. 2000, 112, 10391–10402. 10.1063/1.481676. [DOI] [Google Scholar]
- Andrews C. T.; Campbell B. A.; Elcock A. H. Direct comparison of amino acid and salt interactions with double-stranded and single-stranded DNA from explicit-solvent molecular dynamics simulations. J. Chem. Theory Comput. 2017, 13, 1794–1811. 10.1021/acs.jctc.6b00883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen A. A.; Draper D. E.; Pappu R. V. Molecular simulation studies of monovalent counterion-mediated interactions in a model RNA kissing loop. J. Mol. Biol. 2009, 390, 805–819. 10.1016/j.jmb.2009.05.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dans P. D.; Danilane L.; Ivani I.; Drsata T.; Lankas F.; Hospital A.; Walther J.; Pujagut R. I.; Battistini F.; Gelpi J. L.; Lavery R.; Orozco M. Long-timescale dynamics of the Drew-Dickerson dodecamer. Nucleic Acids Res. 2016, 44, 4052–4066. 10.1093/nar/gkw264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai C. L.; Chen C.; Ou S. C.; Prentiss M.; Pettitt B. M. Interactions between identical DNA double helices. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2020, 101, 032414. 10.1103/PhysRevE.101.032414. [DOI] [PubMed] [Google Scholar]
- Pasi M.; Maddocks J. H.; Lavery R. Analyzing ion distributions around DNA: sequence-dependence of potassium ion distributions from microsecond molecular dynamics. Nucleic Acids Res. 2015, 43, 2412–2423. 10.1093/nar/gkv080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savelyev A.; MacKerell A. D. Jr. Competition among Li+, Na+, K+, and Rb+ monovalent ions for DNA in molecular dynamics simulations using the additive CHARMM36 and Drude polarizable force fields. J. Phys. Chem. B 2015, 119, 4428–4440. 10.1021/acs.jpcb.5b00683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoo J.; Aksimentiev A. Competitive binding of cations to duplex DNA revealed through molecular dynamics simulations. J. Phys. Chem. B 2012, 116, 12946–12954. 10.1021/jp306598y. [DOI] [PubMed] [Google Scholar]
- Denisov V. P.; Halle B. Sequence-specific binding of counterions to B-DNA. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 629–633. 10.1073/pnas.97.2.629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giambasu G. M.; Case D. A.; York D. M. Predicting site-binding modes of ions and water to nucleic acids using molecular solvation theory. J. Am. Chem. Soc. 2019, 141, 2435–2445. 10.1021/jacs.8b11474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hud N. V.; Feigon J. Localization of divalent metal ions in the minor groove of DNA A-tracts. J. Am. Chem. Soc. 1997, 119, 5756–5757. 10.1021/ja9704085. [DOI] [Google Scholar]
- Hud N. V.; Feigon J. Characterization of divalent cation localization in the minor groove of the AnTn and TnAn DNA sequence elements by 1H NMR spectroscopy and manganese(II). Biochemistry 2002, 41, 9900–9910. 10.1021/bi020159j. [DOI] [PubMed] [Google Scholar]
- Hud N. V.; Schultze P.; Sklenar V.; Feigon J. Binding sites and dynamics of ammonium ions in a telomere repeat DNA quadruplex. J. Mol. Biol. 1999, 285, 233–243. 10.1006/jmbi.1998.2327. [DOI] [PubMed] [Google Scholar]
- Pletka C. C.; Nepravishta R.; Iwahara J. Detecting counterion dynamics in DNA-protein association. Angew. Chem., Int. Ed. 2020, 59, 1465–1468. 10.1002/anie.201910960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Record M. T. Jr.; Lohman M. L.; De Haseth P. Ion effects on ligand-nucleic acid interactions. J. Mol. Biol. 1976, 107, 145–158. 10.1016/S0022-2836(76)80023-X. [DOI] [PubMed] [Google Scholar]
- Fenley M. O.; Russo C.; Manning G. S. Theoretical assessment of the oligolysine model for ionic interactions in protein-DNA complexes. J. Phys. Chem. B 2011, 115, 9864–9872. 10.1021/jp204915y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogolari F.; Elcock A. H.; Esposito G.; Viglino P.; Briggs J. M.; McCammon J. A. Electrostatic effects in homeodomain-DNA interactions. J. Mol. Biol. 1997, 267, 368–381. 10.1006/jmbi.1996.0842. [DOI] [PubMed] [Google Scholar]
- Misra V. K.; Hecht J. L.; Sharp K. A.; Friedman R. A.; Honig B. Salt effects on protein-DNA interactions. The lambda cI repressor and EcoRI endonuclease. J. Mol. Biol. 1994, 238, 264–280. 10.1006/jmbi.1994.1286. [DOI] [PubMed] [Google Scholar]
- Stigter D.; Dill K. A. Binding of ionic ligands to polyelectrolytes. Biophys. J. 1996, 71, 2064–2074. 10.1016/S0006-3495(96)79405-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragan A. I.; Read C. M.; Makeyeva E. N.; Milgotina E. I.; Churchill M. E.; Crane-Robinson C.; Privalov P. L. DNA binding and bending by HMG boxes: energetic determinants of specificity. J. Mol. Biol. 2004, 343, 371–393. 10.1016/j.jmb.2004.08.035. [DOI] [PubMed] [Google Scholar]
- Holbrook J. A.; Tsodikov O. V.; Saecker R. M.; Record M. T. Jr. Specific and non-specific interactions of integration host factor with DNA: thermodynamic evidence for disruption of multiple IHF surface salt-bridges coupled to DNA binding. J. Mol. Biol. 2001, 310, 379–401. 10.1006/jmbi.2001.4768. [DOI] [PubMed] [Google Scholar]
- O’Brien R.; DeDecker B.; Fleming K. G.; Sigler P. B.; Ladbury J. E. The effects of salt on the TATA binding protein-DNA interaction from a hyperthermophilic archaeon. J. Mol. Biol. 1998, 279, 117–125. 10.1006/jmbi.1998.1743. [DOI] [PubMed] [Google Scholar]
- Nguyen D.; Hoffpauir Z. A.; Iwahara J. Internal motions of basic side chains of the Antennapedia homeodomain in the free and DNA-bound states. Biochemistry 2017, 56, 5866–5869. 10.1021/acs.biochem.7b00885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seki K.; Bagchi B. Relationship between entropy and diffusion: A statistical mechanical derivation of Rosenfeld expression for a rugged energy landscape. J. Chem. Phys. 2015, 143, 194110. 10.1063/1.4935969. [DOI] [PubMed] [Google Scholar]
- Yu B.; Pettitt B. M.; Iwahara J. Experimental evidence of solvent-separated ion pairs as metastable states in electrostatic interactions of biological macromolecules. J. Phys. Chem. Lett. 2019, 10, 7937–7941. 10.1021/acs.jpclett.9b03084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider B.; Patel K.; Berman H. M. Hydration of the phosphate group in double-helical DNA. Biophys. J. 1998, 75, 2422–2434. 10.1016/S0006-3495(98)77686-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu B.; Pletka C. C.; Iwahara J. NMR observation of intermolecular hydrogen bonds between protein tyrosine side-chain OH and DNA phosphate groups. J. Phys. Chem. B 2020, 124, 1065–1070. 10.1021/acs.jpcb.9b10987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baird-Titus J. M.; Thapa M.; Doerdelmann T.; Combs K. A.; Rance M. Lysine side-chain dynamics in the binding site of homeodomain/DNA complexes as observed by NMR relaxation experiments and molecular dynamics simulations. Biochemistry 2018, 57, 2796–2813. 10.1021/acs.biochem.8b00195. [DOI] [PubMed] [Google Scholar]
- Chen C. Y.; Esadze A.; Zandarashvili L.; Nguyen D.; Pettitt B. M.; Iwahara J. Dynamic equilibria of short-range electrostatic interactions at molecular interfaces of protein-DNA complexes. J. Phys. Chem. Lett. 2015, 6, 2733–2737. 10.1021/acs.jpclett.5b01134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esadze A.; Chen C.; Zandarashvili L.; Roy S.; Pettitt B. M.; Iwahara J. Changes in conformational dynamics of basic side chains upon protein-DNA association. Nucleic Acids Res. 2016, 44, 6961–6970. 10.1093/nar/gkw531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson T. A.; Botuyan M. V.; Kaplan B. E.; Rossi J. J.; Chen Y. Arginine side-chain dynamics in the HIV-1 rev-RRE complex. J. Mol. Biol. 2000, 303, 515–529. 10.1006/jmbi.2000.4143. [DOI] [PubMed] [Google Scholar]
- Zandarashvili L.; Iwahara J. Temperature dependence of internal motions of protein side-chain NH3+ groups: insight into energy barriers for transient breakage of hydrogen bonds. Biochemistry 2015, 54, 538–545. 10.1021/bi5012749. [DOI] [PubMed] [Google Scholar]
- Debiec K. T.; Gronenborn A. M.; Chong L. T. Evaluating the strength of salt bridges: a comparison of current biomolecular force fields. J. Phys. Chem. B 2014, 118, 6561–6569. 10.1021/jp500958r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fennell C. J.; Bizjak A.; Vlachy V.; Dill K. A. Ion pairing in molecular simulations of aqueous alkali halide solutions. J. Phys. Chem. B 2009, 113, 6782–6791. 10.1021/jp809782z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masunov A.; Lazaridis T. Potentials of mean force between ionizable amino acid side chains in water. J. Am. Chem. Soc. 2003, 125, 1722–1730. 10.1021/ja025521w. [DOI] [PubMed] [Google Scholar]
- Pettitt B. M.; Rossky P. J. Alkali-halides in water: Ion-solvent correlations and ion-ion potentials of mean force at infinite dilution. J. Chem. Phys. 1986, 84, 5836–5844. 10.1063/1.449894. [DOI] [Google Scholar]
- Resat H.; Mezei M.; McCammon J. A. Use of the grand canonical ensemble in potential of mean force calculations. J. Phys. Chem. 1996, 100, 1426–1433. 10.1021/jp951496n. [DOI] [Google Scholar]
- Rozanska X.; Chipot C. Modeling ion-ion interaction in proteins: A molecular dynamics free energy calculation of the guanidinium-acetate association. J. Chem. Phys. 2000, 112, 9691–9694. 10.1063/1.481604. [DOI] [Google Scholar]
- Thomas A. S.; Elcock A. H. Direct observation of salt effects on molecular interactions through explicit-solvent molecular dynamics simulations: differential effects on electrostatic and hydrophobic interactions and comparisons to Poisson-Boltzmann theory. J. Am. Chem. Soc. 2006, 128, 7796–7806. 10.1021/ja058637b. [DOI] [PubMed] [Google Scholar]
- Weik M.; Colletier J. P. Temperature-dependent macromolecular X-ray crystallography. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2010, 66, 437–446. 10.1107/S0907444910002702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karslake C.; Botuyan M. V.; Gorenstein D. G. 31P NMR spectra of oligodeoxyribonucleotide duplex lac operator-repressor headpiece complexes: importance of phosphate ester backbone flexibility in protein-DNA recognition. Biochemistry 1992, 31, 1849–1858. 10.1021/bi00121a038. [DOI] [PubMed] [Google Scholar]
- Ganser L. R.; Kelly M. L.; Herschlag D.; Al-Hashimi H. M. The roles of structural dynamics in the cellular functions of RNAs. Nat. Rev. Mol. Cell Biol. 2019, 20, 474–489. 10.1038/s41580-019-0136-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salmon L.; Yang S.; Al-Hashimi H. M. Advances in the determination of nucleic acid conformational ensembles. Annu. Rev. Phys. Chem. 2014, 65, 293–316. 10.1146/annurev-physchem-040412-110059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogg J. M.; Randall G. L.; Pettitt B. M.; Sumners W. L.; Harris S. A.; Zechiedrich L. Bullied no more: when and how DNA shoves proteins around. Q. Rev. Biophys. 2012, 45, 257–299. 10.1017/S0033583512000054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahu D.; Iwahara J. Discrete-state kinetics model for NMR-based analysis of protein translocation on DNA at equilibrium. J. Phys. Chem. B 2017, 121, 9548–9556. 10.1021/acs.jpcb.7b07779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rooman M.; Lievin J.; Buisine E.; Wintjens R. Cation-π/H-bond stair motifs at protein-DNA interface. J. Mol. Biol. 2002, 319, 67–76. 10.1016/S0022-2836(02)00263-2. [DOI] [PubMed] [Google Scholar]
- Wintjens R.; Lievin J.; Rooman M.; Buisine E. Contribution of cation-pi interactions to the stability of protein-DNA complexes. J. Mol. Biol. 2000, 302, 393–408. 10.1006/jmbi.2000.4040. [DOI] [PubMed] [Google Scholar]
- Kumar K.; Woo S. M.; Siu T.; Cortopassi W. A.; Duarte F.; Paton R. S. Cation-π interactions in protein-ligand binding: theory and data-mining reveal different roles for lysine and arginine. Chem. Sci. 2018, 9, 2655–2665. 10.1039/C7SC04905F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohs R.; West S. M.; Sosinsky A.; Liu P.; Mann R. S.; Honig B. The role of DNA shape in protein-DNA recognition. Nature 2009, 461, 1248–1253. 10.1038/nature08473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ha J. H.; Capp M. W.; Hohenwalter M. D.; Baskerville M.; Record M. T. Jr. Thermodynamic stoichiometries of participation of water, cations and anions in specific and non-specific binding of lac repressor to DNA. Possible thermodynamic origins of the “glutamate effect” on protein-DNA interactions. J. Mol. Biol. 1992, 228, 252–264. 10.1016/0022-2836(92)90504-D. [DOI] [PubMed] [Google Scholar]
- Liu L. A.; Bradley P. Atomistic modeling of protein-DNA interaction specificity: progress and applications. Curr. Opin. Struct. Biol. 2012, 22, 397–405. 10.1016/j.sbi.2012.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]