An ensemble learning approach for estimating high spatiotemporal resolution of ground-level ozone in the contiguous United States

Abstract

In this paper we integrated multiple types of predictor variables and three types of machine learners (neural network, random forest, and gradient boosting) into a geographically weighted ensemble model to estimate daily maximum 8-hr O₃ with high resolution over both space (at 1 km × 1 km grid cells covering the contiguous United States) and time (daily estimates between 2000 and 2016). We further quantify monthly model uncertainty for our 1 km × 1 km gridded domain. The results demonstrate high overall model performance, with an average cross-validated R² (coefficient of determination) against observations of 0.90, and of 0.86 for annual averages. Overall, model performance of the three machine learning algorithms was quite similar. The overall model performance from the ensemble model outperformed those from any single algorithm. The East North Central region of the United States had the highest R², 0.93, and performance was weakest for the western mountainous regions (R² of 0.86) and New England (R² of 0.87). For the cross-validation by season, our model had the best performance during summer, with an R² of 0.88. This study can be useful for the environmental health community to more accurately estimate the health impacts of O₃ over space and time, especially in health studies at intra-urban scale.

Graphical Abstract

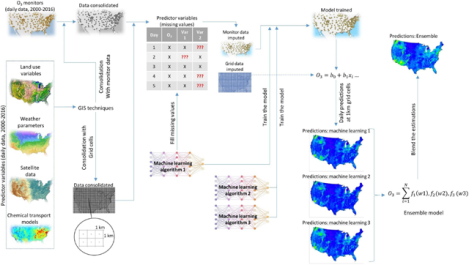
1. INTRODUCTION

Ground-level ozone (O₃) primarily results from photochemical reactions involving nitrogen oxides (NO_x = NO + NO₂) and volatile organic compounds (VOCs) in the presence of sunlight¹. The spatial variation of O₃ concentration is strongly linked to activity associated with land use and population. Emissions from motor vehicles, industrial sources, and electric generation are major sources of anthropogenic O₃ precursors^2,3. The formation of O₃ also depends on natural sources, which include biogenic (e.g., isoprene from vegetation) and abiotic (biomass burning and geogenic sources) emissions⁴. NO_x released from fertilized soils can also play an important role in the formation of O₃⁵. In urban areas, VOCs are often the limiting precursors for O₃ formation. In contrast, in non-urban areas, O₃ formation is often limited by NOx availability. The intra-urban variations of O₃ levels are also linked to the geographic variation in sources of O₃ precursors and oxidizing compounds^6,7.

Besides the variation of O₃ precursors, rates of O₃ formation are also sensitive to meteorological conditions, such as the temperature and solar radiation. Previous studies have shown that variations in O₃ trends are associated with differences in characteristic local weather patterns^8,9. Low precipitation, high temperature, and low wind speed favor O₃ formation and build-up^10,11. Relative humidity is negatively correlated with O₃ because cloudy days with precipitation tend to have lower actinic flux than clear sky days and therefore less photochemical activity. In addition, dry atmospheric conditions can cause drought stress and suppress stomatal O₃ uptake and contribute to the high warm season O₃¹².

Understanding the mechanisms related to O₃ formation is crucial for emissions control and for implementing public health policies as well as for modeling ozone concentrations. A large number of studies have demonstrated that O₃ is a major public health risk, affecting respiratory^13–15, cardiovascular^16–18, and nervous systems^19,20, as well as mortality. For example, Anenberg et al. (2010) estimated that surface O₃ is responsible for 0.7 ± 0.3 million deaths worldwide due to respiratory disease annually. In the United States, Fann et al. (2012) estimated 47,000 O₃-related deaths base solely on acute health effects. Other evidence suggests that O₃ modifiesthe health impacts of other air pollutants, including PM_2.5^23–25.

Modeling approaches to estimate O₃ concentrations over space and time have been developed to improve exposure characterization for health studies. These O₃ exposure models fall into several classes, including chemical transport model simulations, geostatistical interpolation approaches^26–28, land use regression models^29,30, source dispersion models³¹, models based on remote sensing technology^32,33, ensemble-based forecast³⁴, and, most recently, machine learning models^35–38. These various modeling approaches have different strengths and limitations that result in varying levels of exposure misclassification. The great advantage of machine learning is that these models can represent any kind of nonlinear relationships in which the variables from different data sources have complex interactions. This advantage is important for air pollution characterization, especially to model O₃ concentration, due to the complex nonlinear atmospheric mechanisms governing O₃ formation and transport.

Recently, ensemble learning approaches that integrate different techniques (e.g., land use, geostatistical, remote sensing, and source dispersion models) as well as different machine learning algorithms have been applied to improve air pollution characterization^39–42. Environmental scientists interested in the health effects of air pollution, including that of O₃, have explored exposure models based on these ensemble approaches in order to minimize residual exposure measurement errors (i.e., misclassification error) and improve the accuracy of epidemiological studies. However, ensemble-based models of air pollution are still very limited in terms of the following criteria: i) spatial or temporal resolution, ii) set of predictor variables, iii) machine learning approaches, and iv) model uncertainty. For example, most studies focus only on small regions^41,43, or annual averages; they also account for only a restricted number of predictors, including land use terms and remote sensing data⁴⁴, or consider only one machine learning method^42,45. Finally, most studies do not quantify the spatiotemporal variation in uncertainty in the predictions, which is important for assessing exposure measurement error. Several studies have addressed these limitations for some pollutants, including PM_2.5⁴⁶ and NO₂, but not yet for O₃. Our research addresses these gaps by integrating multiple types of predictor variables (including 169 variables representing land use, chemical transport simulations, weather, and remote sensing data) and three types of machine learners into an ensemble model to estimate daily maximum 8-hr O₃ with high resolution over space (at 1 km × 1 km grid cells covering the contiguous United States) and time (daily estimates between 2000 and 2016). We further quantify the spatial and temporal pattern of model uncertainty by predicting monthly standard deviation of the difference between daily monitored and predicted O₃ at 1 km × 1 km grid cells.

2. MATERIALS AND METHODS

2.1. Study design

This study was conducted in seven stages. First, we accessed multiple datasets that included daily maximum 8-hr O₃ concentrations at sites across the U.S. and the predictor variables for O₃, which included weather parameters, gridded output from chemical transport models, remote sensing observations, and land use variables. We obtained these data for the period between 2000 and 2016. The spatial area included the continental U.S (the 48 contiguous states and Washington D.C.). In the second stage, we applied GIS techniques to create a single data frame with O₃ observations and predictor variables at O₃ monitor locations and at 1 km² grid cells over the U.S.. In the third stage, we applied one machine learning algorithm to fill in missing values in the predictor variables consolidated in the previous stage. For model training in the fourth stage, we applied three machine learning algorithms to estimate O₃ concentration at observation site locations. In the fifth stage, we made daily (2000–2016) predictions of O₃ concentration at 1 km² spatial resolution over the U.S., using the same grid cells as consolidated in the second stage. We made three predictions, including one prediction for each one of the three machine learning models applied in the fourth stage. In the sixth stage, we employed an ensemble model to blend the O₃ estimations from the previous stage, which resulted in the final prediction. Finally, in the seventh stage, we performed cross-validation on withheld monitors to estimate the model performance from each of three machine learners separately, and from the ensemble model. We estimated model uncertainty by predicting monthly standard deviation at 1 km² grid cells based on the difference between model predictions and observations at site locations. Figure S1 shows the flowchart of our study design. In S2 we provide details on the first stage (data source). Details on stages 2–7 are provided below.

2.2. Consolidation of the dataset (second stage)

We used GIS techniques to consolidate all the data obtained, which includes 169 predictor variables, covering the contiguous U.S in 6,205 days (daily information during 2000–2016). In Table S1 we present the list of these predictors. Daily maximum 8-hr O₃ concentration and predictors used for training were consolidated at O₃ monitoring site locations and predictors were consolidated at the 1 km² grid cells over the U.S. Our study area encompassed 11,196,911 grid cells with a spatial resolution of 1 km × 1 km. Due to the high spatiotemporal resolution defined in our study, the size of the 169 predictor variables consolidated at grid cells was computationally intensive. The data has about 20 TB of information.

2.3. Machine learning approaches

We used three machine learning models in this study, including neural network, random forest, and gradient boosting. All three models attempt to model the complex relationship between the dependent variable and predictor variables with different algorithms. The details of these machine learning models can be found in Bishop (2006). Briefly random forests and gradient boosting are methods that use regression trees. In a regression tree, one first finds the best predictor, and best break point for that predictor, such that dividing the data at that break point explains the most variation of the outcome available for such a division. The process is repeated producing a series of splits in the subsequent subsets of the data. In a random forest, many (generally over 100) bootstrap samples of the data are chosen, and separate trees are fit in each sample. The predictions from the many trees (the forest) are then averaged to generate the prediction, in order to improve the performance by handling overfitting, reducing variance and using parallel (independent) classifiers⁴⁸. In gradient boosting, a tree with few splits is fit, and then another tree is fit to the residuals of the outcome. To allow more predictors to contribute, only part of the prediction of the second tree is added to the first, and the process is repeated. The key parameters in such approaches are the number of trees, the number of breaks in each tree, the fraction of the prediction of the next tree that is used (gradient boosting) the fraction of the covariates considered, etc. A neural network fits a model by taking the predictors as inputs into artificial neurons, that, like real neurons, fire when the weighted inputs reach a certain level. Their output goes into other layers of neurons, and ultimately, to a single prediction of output. Key parameters of such models are the number of layers and number of neurons. Importantly, given the large number of variables, all three methods use withheld monitoring sites as validation samples to avoid overfitting, and all three incorporate methods to give little or no weight to some variables. In the neural network, the weights given to input variables impacts on the hidden neurons can be near zero. In addition, we incorporated a lasso penalty into the neural network (lasso regularization to the neural network cost function) that can force variable weights to zero. Neural networks are able to model nonlinear relationship. It is very useful for modeling air pollution, which the underlying atmospheric dynamics are elusive, and variables have complex interactions^41,49. In gradient boosting and random forests, the size of each tree is chosen by cross-validation (10% of the monitors were held out and used for validation, and this step was repeated 10 times), and the shorter the trees the fewer variables can contribute (This process is described in section 2.3.2, and illustrated in Table S2)…

Given the differences among the machine learning models, where the model performance of different algorithms seems to vary by location and concentration⁵⁰, there is an interest in hybrid models instead of a single model, which the multiple approach would complement each other. The combination of the three machine learning models used in our study is described in section 2.4.

In our study, the random forest algorithm was applied to fill the missing values for predictors (Imputation process, third stage). For the model training (fourth stage) and predictions (fifth stage), we used the three machine learning algorithms. In the next sections, we describe these stages.

Finally, the analyses for the three machine algorithms were performed in R by using the H2O package. In S3 we provide the script used in the analyses.

2.3.1. Imputation (third stage)

Some of the predictors in our study (e.g., satellite measurements, weather variables and others) presented missing values at some locations and time. To predict O₃ concentrations across the contiguous U.S. and the entire study period, we used random forest to fill in the missing values.

The imputation was performed based on variables without missing values to predict each variable with missing values. For example, Aerosol Optical Depth (AOD) had more than 50% missing values. When AOD data were available, we used a random forest to train the model considering the variables in tables S1, including CMAQ, GEOS-Chem, land-use types, and meteorological variables (these variables have no missing values) as predictors. Then, we predicted the AOD missing values. As in the main models, the predictors for the imputation model included land use terms averaged over different spatial grids (1 km, 10km, etc.). The random forest depends on a number of hyper-parameters which we chose as detailed below.

2.3.2. Model training (fourth stage)

After imputing missing values, we standardized the dataset. Considering a variable “X”, data standardization was based on the X_ij – X_mean / X_std, where X_ij is the raw data of the variable “X” on day i in the site j; X_mean and X_std are the mean and standard deviation of variable “X”, respectively.

Using the dataset resulting from the standardization process, we trained the three machine learning models on all input variables standardized at monitor data, with parameters of each models selected by a search process. The performance of our machine learning algorithms depends on hyper parameters, which are listed in Table S2. As noted above these are chosen using a grid search process and a held out set of validation monitors. For random forests and gradient boosting these parameters included the depth of the tree, the number of trees, the subsample of covariates fit to each tree, and the learning rate. For neural networks, the hyper-parameters included the number of hidden layers, number of neurons per layer, learning rate and number of iterations through the data, and lasso penalty (i.e., L1 regularization). In Table S2 we show the parameters tuned for each machine learning model.

2.4. Predictions (fifth stage) and ensemble model (sixth stage)

After filling in missing values and interpolating data to 1 km grid cells, all predictor variables were available across the study area. Then, we used the trained models to predict daily maximum 8-hr O₃ concentration at each 1 km × 1 km grid cell in the contiguous U.S. for 6,205 days (daily information during 2000–2016). The predictions for each grid cell were based on values of predictors in neighboring grid cells. For example, for some land use terms 10 km averages were used as well as 1km averages.: As result, we obtained individual predictions for each one of the three machine learners (fifth stage).

To combine the three predictions, we used an ensemble model based on a geographically weighted generalized additive model (GAM). We used a geographically weighted approach to account for the spatially heterogeneous relationship, and the possibility that some learners fit better in particular parts of the country. To capture a better spatial variation of weights given to the different learners across the country, we regressed the monitored values against thin plate splines of latitude, longitude, and the interaction of those splines with a spline for the predicted concentrations for each learner. This allows the contribution of each learner in the final O₃ estimation to potentially depend on the O₃ concentration (i.e., non-linear response) and to have more weight in particular regions of the country. The equation below describes the ensemble model:

$$\widehat{O_3}=f_1\left(\mathit{\text{Locatio}}{n}_i,{\widehat{O_{3,nn}}}_{ij}\right)+f_2\left(\mathit{\text{Locatio}}{n}_i,{\widehat{O_{3,rf}}}_{ij}\right)+f_3(\mathit{\text{Locatio}}{n}_i,{\widehat{O_{3,gb}}}_{ij})$$

where f₁ denotes a thin plate spline for an interaction between location i and O₃ estimation from neural network (nn) at location i and at day j; and ${\widehat{O_{3,rf}}}_{ij}$ and ${\widehat{O_{3,gb}}}_{ij}$ stand for the same, but from random forest (rf) and gradient boosting (gb) at location i and at day j, respectively.”

2.5. Cross-validation (seventh stage)

We performed individual 10-fold cross validation for each one of the three models applied in this study – neural network, random forest, and gradient boosting. Here, we first divided the monitoring sites into 10 splits, and then we trained the models with 90% of the data and predicted O₃ concentration at the remaining 10% of the sites. The observations predictions at the excluded sample site were then compared. Finally, we assembled O₃ predictions from all 10 splits and then calculated R² (coefficient of determination), spatial R², and temporal R².

The cross-validation was also performed for different subsets of the dataset, which included a time-wise cross-validation (for the whole period), cross-validation by year, by region (9 regions), by season (summer, fall, winter, and spring), and population density (quartiles 1–4).

The temporal R² was calculated by regressing (using GAM model) ΔO_{3 measured} against ΔO_{3 predicted}, where ΔO₃ is the difference between O₃ value at site i at time t and annual mean of O₃ at site i. The spatial R² was calculated by regressing the annual mean O₃ at site i against the annual mean predicted O₃ at site i.

Finally, we estimated model uncertainty by calculating monthly standard deviation of the difference between daily monitored and predicted O₃ at 1 km × 1 km grid cells with monitors (sdO3_ij, where i represents the sites, and j is the month). Note that we quantified uncertainty for the monthly mean to increase the number of data points in the standard deviation calculation. Then we regressed (using GAM) sdO3_ij against the following predictors: elevation, surface reflectance, humidity, tree canopy, Normalized Difference Vegetation Index (NDVI) – an indicator of green vegetation, developed area coverage from the land used dataset, density of roads, year, month. We highlight that if there were more than one monitor in a grid cell we averaged them to get the grid cell measured and subtracted the grid cell prediction to get a single grid cell residual. For grid cells that have no monitors, we cannot directly estimate the error of prediction. We can approximate this, however, by treating some monitoring locations as if they did not have measurements, training the models on the remaining stations, making the predictions for the held out monitoring locations, and seeing what error we got. This was the 10-fold cross validation we did. We divided the monitors into 10 groups, and held out one successive group in turn, fit the models on the remaining 9 groups of monitors, and looked at the prediction error at the held out group.

3. RESULTS AND DISCUSSION

Table 1 shows the cross-validated R², RMSE (square root of the average value of the square of the residual), and slope from the ensemble model by year and for the entire period. For the individual models (neural network, random forest, and gradient boosting), we present only the cross-validated R². As mentioned above, all R² values were based on 10-fold cross-validation. The R² from the ensemble model varied by year from 0.889 to 0.920, with an average of 0.902, indicating good model performance. The Root Mean Square Error (RMSE) decreased significantly over the years. In 2000, the RMSE was 5.705 ppb; in 2016, it decreased to 3.579 ppb. The average RMSE was 4.550 ppb. Overall, model performance of the three machine learning algorithms was quite close. The overall model performance from the ensemble model outperformed that from any single algorithm.

Table 1 –

Cross-validation results by year

Year	Ensemble model						Neural Network	Random Forest	Gradient Boosting
	R2	RMSE (ppb)	Intercept	Slope	Spatial R2	Temporal R2	R2	R2	R2
2000	0.889	5.705	0.088	0.991	0.848	0.905	0.889	0.887	0.889
2001	0.892	5.517	0.254	0.992	0.845	0.911	0.889	0.889	0.892
2002	0.908	5.375	0.338	0.984	0.863	0.924	0.904	0.906	0.907
2003	0.897	5.244	0.126	0.988	0.837	0.917	0.894	0.895	0.896
2004	0.889	4.986	0.543	0.982	0.812	0.912	0.886	0.886	0.888
2005	0.901	5.090	0.228	0.991	0.845	0.921	0.898	0.898	0.900
2006	0.898	4.873	0.357	0.992	0.839	0.918	0.895	0.896	0.898
2007	0.903	4.731	0.284	0.998	0.889	0.916	0.902	0.900	0.902
2008	0.904	4.447	0.317	0.990	0.886	0.916	0.902	0.901	0.903
2009	0.899	4.196	0.032	0.996	0.862	0.915	0.897	0.897	0.899
2010	0.891	4.399	0.090	0.990	0.863	0.908	0.889	0.888	0.890
2011	0.902	4.296	0.009	0.997	0.847	0.921	0.901	0.899	0.902
2012	0.920	4.003	0.339	0.990	0.883	0.933	0.919	0.916	0.919
2013	0.907	3.787	1.049	0.973	0.879	0.921	0.904	0.904	0.907
2014	0.913	3.585	0.259	0.991	0.888	0.922	0.913	0.909	0.912
2015	0.919	3.538	0.447	1.005	0.894	0.926	0.914	0.915	0.918
2016	0.906	3.579	0.187	0.989	0.897	0.934	0.901	0.904	0.907
Overall (2000–2016)	0.905	4.668	0.654	0.985	0.862	0.916	0.904	0.896	0.900

Note: The slope and intercept were obtained from the linear regression model, which we regressed predicted O₃ against monitored O₃.

Tables S2–S4 show the cross-validated results by region, season, and population density, respectively. Model performance varied over the nine regions that we considered in this analysis (Table S3). The East North Central region had the highest R² (0.928) and the West North Central region had the lowest RMSE (3.699) among the nine regions. Performance was weakest, but still excellent, for the mountainous regions (0.862) and New England (0.867). For the cross-validation by season, our model had the best performance during summer, with a R² value equal to 0.885 (Table S4). For the cross-validation by population density, our results show relatively little variation, with the less populous locations (quartile 1, Table S5) having an R² equal to 0.888, while in areas with high population density (quartile 4, Table S3) the R² was 0.911. The similar performance in more rural areas with fewer monitors is an important result. Overall, the ensemble model stratified by region and season outperformed the three single machine learning. Importantly, the slope of the relationship between O₃ at held out monitors and predicted at those locations was essentially 1, and the intercept very close to zero. This indicates that there is no bias in the predictions of the ensemble model.

We used GAM to regress daily predictions of O₃ from each model against monitored O₃ (Figure S4). We applied a penalized spline function to assess the linearity of the association. The results from the ensemble model show that the relationship between predicted and monitored O₃ values has a good agreement, except for the highest concentration (above 120 ppb). Among the three learners, neural network presented the best relationship. The underprediction at high concentrations was worse for the random forest and then gradient boosting. Particularly on random forest, its key limitation is that the algorithm cannot predict very high pollution events outside the range encountered during training. In Figure 1, we show the density scatter plot of the annual O₃ predictions of the ensemble model versus the measured values.

Figure 1 –

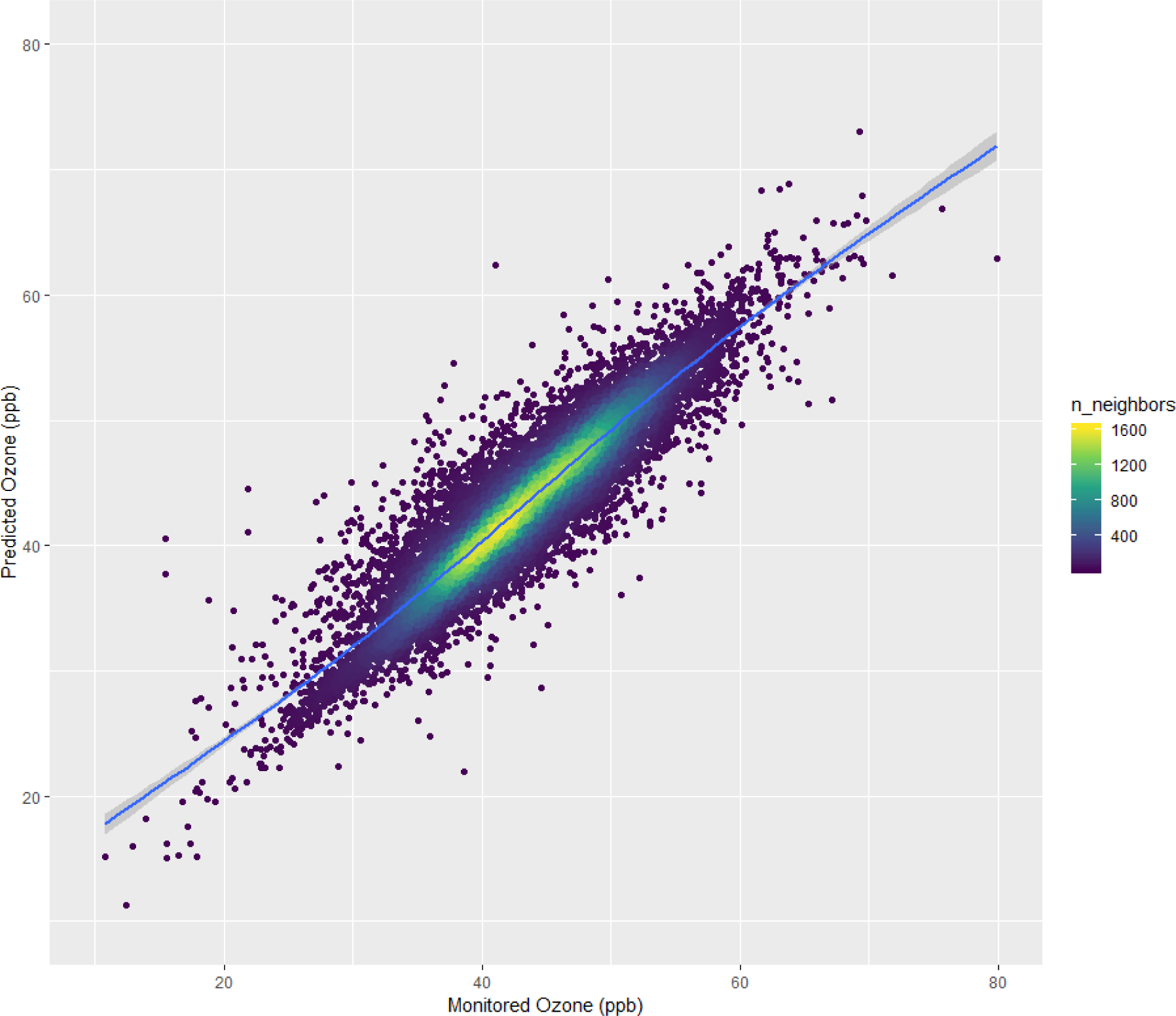
Density scatter plot of the annual predicted O₃ levels versus measured levels for the ensemble model.

Note 1: We regressed annual averaged predicted O₃ from ensemble model against annual averaged monitored O₃ using a GAM model with spline on the monitored O₃. Blue color represents 95% confidence interval.

Note 2: “n_neighbors” represents the density of points (O₃ sites) of the scatter plot.

Figure S5 presents the density distribution of error estimates (difference between estimated and observed values) from cross validation for each model. There was a difference in the error density among the three learning algorithms, with the neural network having the narrowest distribution, the random forest having a slightly wider distribution, and the gradient boosting having the widest distribution. We can see the improvement with the ensemble model in Figure S4, which shows higher density of monitors with errors closest to zero.

The relative contribution of predictor variables estimated by each machine learning algorithm is similar (Figure S6). The spatially weighted average of O₃ measurements at nearby monitoring locations (inverse distance weighted O₃ measurements at other locations) was the variable with the highest importance for the three models. Other variables identified as important by the three models are the O₃ estimates from CMAQ, total column O₃ from GEMS, spatiotemporally lagged O₃ measurements (1-day lag), and some meteorological variables (Figure S6).

We calculated the daily nationwide averages by averaging daily predictions at all 1 km×1 km grid cells (Figure S7). Our results show a relatively consistent annual pattern of O₃ concentration from 2000 to 2005. Between 2005 and 2010, there was a cycle of decrease and increase of O₃ levels. From 2010 to 2016, our results showed a decrease of O₃ concentrations, although the overall decrease was modest, at about 3ppb.

The spatial distribution of the predicted levels of the standard deviation of O₃ prediction error (uncertainty model) is illustrated in Figure 2. Overall, the model performed moderately well in the east coast and central region (including Texas, Oklahoma, Arkansas, Louisiana, Alabama, and Missouri). A difference in spatial patterns of the uncertainty is evident during the summer and spring seasons. Our results also showed that the model performance improved over the years (lower standard deviation in 2016 than in 2000 – Figure 2). We suggest that the improvement of the data input quality over the years was an important factor to improve the model performance over the years. Regarding the substantial level of uncertainty in the Southeast (especially in 2000), compared to the West, we highlight that more O₃ in the East is generated locally, while elsewhere there is more transport of O₃ from elsewhere. As emissions decline, background ozone in the Southeast (and East) become more important. Therefore, according to Travis et al. (2016)⁵¹ and Lin et al. (2017)⁵², here are two potential theories about the large error in the Southeast/East: i) O₃ produced locally has a nonlinear dependence with the predictors, which the model is unable to capture well. As emissions declined, local production also declined, and the model showed a better performance in 2008 and 2016; and, ii) GEOS-Chem has difficulty capturing O₃ in the Southeast, and that difficulty may propagate into our model. The reason for this difficulty has to do with uncertainty in NO_x emissions and in vertical mixing.

Figure 2 –

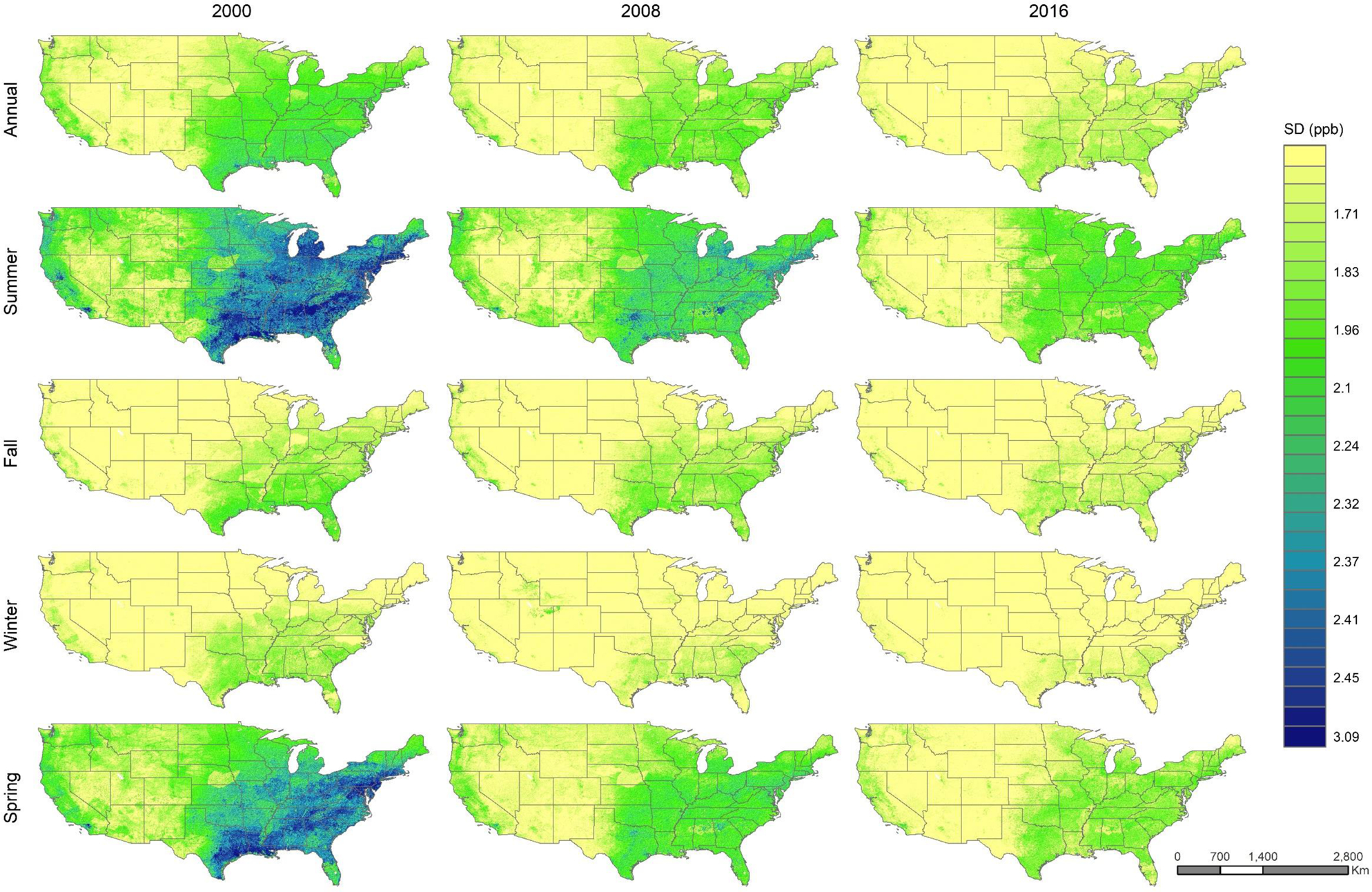
Spatial distribution of the standard deviation of the prediction error (SD) of O₃ by season.

Note: The seasons were defined as follows: summer (July – September), fall (October – December), winter (January – March), and spring (April – June).

Figure 3 shows the spatial distribution of ozone concentration (annual and seasonal) over the U.S. in three years, 2000, 2008, and 2016. Ozone levels varied significantly by season and regions. Overall, summer O₃ concentration decreased in most regions between 2000 and 2016, especially in Southeast. In contrast, annual O₃ concentrations have increased in the Northeast which is driven by increases in the fall and winter. Fall and winter were the seasons with the lowest O₃ concentration in most regions. In Figure S8, we illustrate the downscaled O₃ levels in the four highest populated cities in the USA (New York, Los Angeles, Chicago, and Houston) plus the city of Boston. Notably O₃ levels increased over time in New York, Chicago, and Boston, primarily by an increased geographic spread of the highest O₃ concentrations.

Figure 3 –

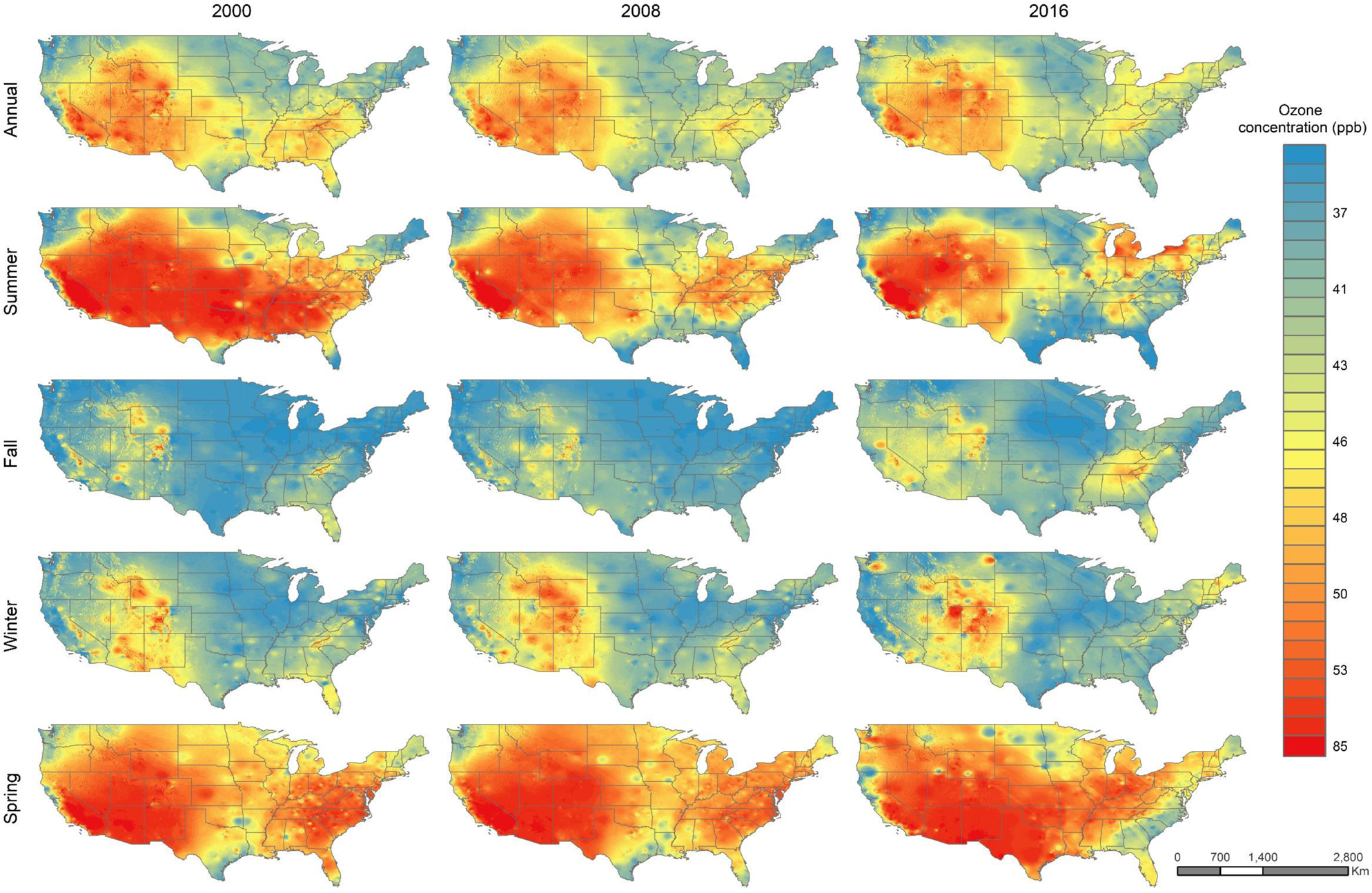
Spatial distribution of the predicted levels of O₃ by the ensemble model.

Note: The seasons were defined as follows: summer (July – September), fall (October – December), winter (January – March), and spring (April – June).

The three machine algorithms showed good performance in the explained concentration variance of O₃, with a R² values varying between 0.88 – 0.90 for the analysis stratified by year, 0.85 – 0.92 for the analysis stratified by region, and 0.84 – 0.88 for the analysis stratified by season. Overall, the ensemble model improved the performance of the three machine learning algorithms, especially when we look at the density distribution of error estimates, which is illustrated by Figure 5. The good performance of our models is explained by the range of predictors representing local source emissions and predictors of formation rate and quenching rate. Incorporating these predictors allowed us to define areas with certain types of pollution regimes based on emissions sources. The characterization of these areas improves the estimation of the spatial heterogeneity in pollution levels, while accounting for spatial autocorrelation (captured by the spatiotemporal terms) among observed values in neighboring areas. Taking that together in the models (emission sources + weather data + chemical transport and remote sensing data + land use and geographical data + temporal terms + spatial autocorrelation), it is possible to minimize within-region variability and maximize between-regional variability prediction values.

Our results showed that the model performs better in the East North Central region, while we observed weakest performance in New England and the mountainous regions. This spatiotemporal pattern in model performance is similar that reported in previous studies (Hogrefe et al. 2018 and Di et al. 2017). Our model had relatively good performance in areas with high population density. Differences in performance for highly populated areas and less urban regions were also reported previously⁹. Regarding the temporal variation, model performance was best in the summer season, whereas performance was weakest in winter. We suggest that the performance limitations during winter could be related to more heterogeneity and lower O₃ concentrations in winter and because almost 1/3 of the monitors across the U.S. do not operate in winter. The model performance issues for winter are in agreement with the previous study in the U.S. (for the period 2000–2012) based on a hybrid machine learning model using a neural network⁴². Di et al. 2017 reported the best performance for the fall season.

In addition to differences in performance over space and time, our three-machine learning models do not perform equally well at all concentration levels, especially for high concentration levels (Figure 1). The ensemble model minimized this limitation by combining the three base learners through a non-linear process and fit their contributions to vary over space and concentration. Di et al. (2019) found similar results in a recent ensemble modeling study for PM2.5.

As we mentioned before, an advantage of our machine learning algorithms is the possibility to rank the relative contribution of predictor variables. The variables classified as high importance can be used to create a more parsimonious model and provide insights on factors of importance for characterizing O₃ concentrations. Our analyses suggested four main variables with high importance, including the spatially weighted average of O₃ measurements at nearby monitoring locations, CMAQ predictions, GEMS total column O₃, and spatiotemporally lagged O₃ measurements with 1-day lag. Some meteorological variables were also important. These variables, especially the variables representing the spatio-temporal terms, reflects the influence of the regional and temporal sources when predicting local O₃ concentrations with high spatio-temporal resolution. These predictors with high importance improved the ability of our model to minimize within-region variability and maximize between-regional variability of O₃. This is consistent with the literature that have shown substantial contributions from spatiotemporal terms^31,33,54 and meteorological variables^3,9,12 when predicting ozone concentration.

As illustrated in Figure S7, daily nationwide averages of O₃ decreased somewhat from 2000 to 2016 in the U.S. We suggest that this temporal variation reflects a combination of emissions control^3,55 and meteorological conditions^3,56–58. The U.S. EPA trend report (https://gispub.epa.gov/air/trendsreport/2018/) indicates that the national average of the fourth highest daily maximum 8-hour O₃ concentration at monitors decreased from about 82 ppb in 2000 to about 69 ppb in 2016. In our analysis, we used a smoothed conditional means function and estimated that the national annual average daily maximum 8-hour ozone concentration decreased from about 42 ppb in 2000 to 39 ppb in 2016. The difference in trends for our annual metric and the fourth-highest-concentration metric in the EPA report are likely because the downward trends in summer O₃ concentrations are dampened by the relatively flat or increasing trends in winter O₃ concentrations in the annual average. Also, our estimates are for the entire U.S. on all days, including many areas and periods with low ozone concentrations and limited monitoring, whereas the EPA values are based on monitored locations concentrations alone. The downward temporal trend in O₃ concentrations observed in our analyses was also observed in previous study⁴².

The impact of meteorological conditions on O₃ concentration is also illustrated by Figure 3, which shows that summer and spring were the seasons with the highest O₃ levels. This is explained by the photochemical process related to O₃ formation. Primarily, O₃ is formed in the presence of sunlight through photochemical reactions involving NO_x and VOCs¹. Overall, low humidity, low precipitation, high temperature, and low wind speed favor O₃ formation^10,11. Our results show that O₃ concentration increased in numerous regions in the U.S. during the spring season over the study period (Figure 3). Previous studies have reported that the increases in O₃ concentrations in the western U.S. in spring during our study period may be associated with increased transport of O₃ from Asia associated with increased anthropogenic emissions in Asia (e.g., Lin et al., 2017; Cooper et al., 2012). We suggest that drier and hotter air between 2000 and 2016^56,59 may have also increased O₃ concentrations in the spring season. The increase in ozone in the Northeast region in the fall and winter seasons may reflect the influence of NO_x emission controls. Previous studies have suggested that areas where O₃ formation is NO_x-limited in summer may become VOC-limited in winter due to the lower photochemical activity and reduced biogenic VOC emissions in winter (Jacob et al., 1995; Martin et al, 2004; Simon et al., 2015). NO_x emission reductions that have reduced the relatively high summertime O₃ concentrations in the U.S. may therefore have led to some O₃ increases in winter (Simon et al., 2015). Model simulations under conditions of reduced NO_x emissions are consistent with the interpretation that NO_x emission reductions could have increased O₃ concentrations in winter and spring in some areas (e.g., Clifton et al., 2014; Simon et al., 2016).

Land use is another important factor linked to the spatial variation of O₃ concentration. In urban areas, traffic emissions and industrial activity are major sources of O₃ precursors and conditions tend to be NO_x-saturated. In non-urban areas, sources of O₃ precursors include emissions from vegetation (emissions of isoprene from vegetation), biomass burning, geogenic sources⁴, and fertilized soils⁵ and conditions tend to be NO_x-limited. Large spatial variability also exists in the effects of meteorological conditions on rates of O₃ formation. In Figure 10, we downscaled O₃ distribution in five major urban areas, including New York, Los Angeles, Chicago, Houston, and Boston. Intra-urban variations of O₃ levels are evident in Figure 10 and are due in part to the spatial variation of emission sources, such as vehicle NO_x emissions that can suppress O₃ concentrations under NO_x-saturated conditions^6,7.

Our study has some limitations. First, some monitoring sites did not operate during the entire study period and the spatial distribution of O₃ monitors in the continental U.S. is not homogeneous. The eastern United States and the western coast are the regions with most of the monitors. Consequently, the model performance varied over space and time, as shown in Tables 1 and 2. Second, the predictors used in our analyses have different spatial resolution, including resolution of 1, 10, and 32 km. To standardize the resolutions at 1 km, we interpolated the original data (when the resolution was different from 1 km). During this interpolation process, there is an residual error^28,60. Third, another residual error is related to the leap to predict over the entire domain based on fitting at the limited monitoring locations. We applied this approach based on an assumption defined in our study design. By leaving out monitoring sites, fitting the model with the remaining sites, and comparing the predictions to the observed values, we approximate the prediction error at held out locations. This relies on the assumption that the monitoring network has sites at enough locations with different characteristics to include the range of characteristics observed in the sites without monitoring. The monitoring network includes urban, suburban, and rural locations across the U.S. including both regulatory sites as well as CASTNET sites. This includes 2,279 monitoring locations during the period. Their land use characteristics and climate are predictor variables in the model, so we believe this is a reasonable assumption. Note that this limitation was imposed by the current monitoring network, and additional O₃ monitoring for sparsely covered areas and periods (e.g., winter) would help improve models in the future. Fourth, missing predictor values occurred at some sites and days, especially the predictors based on satellite remote sensing (e.g., AOD had more than 50% missing values, in Table S6 we present the list of variables sorted by percentage of missing values). We performed an imputation process using random forest to fill in the missing values. This process generates residual error as well, which can be interpreted based on the R² of the imputation model. We estimated the R² after comparing variables values before and after imputation at monitoring sites. The average R² was 0.88.

In this study we applied an ensemble learning approach to estimate high spatiotemporal resolution of O₃ across the continental U.S. The results indicate a high overall model performance, with an average R² of 0.902. We have also estimated model uncertainty in the O₃ prediction, which will allow futures studies to take into account exposure measurement error. Taken together, the results presented here can be useful for the environmental health community to more accurately estimate the health impacts of O₃ over space and time, especially in health studies at intra-urban scale.