Uncoupling gene expression noise along the central dogma using genome engineered human cell lines

Abstract

Eukaryotic protein synthesis is an inherently stochastic process. This stochasticity stems not only from variations in cell content between cells but also from thermodynamic fluctuations in a single cell. Ultimately, these inherently stochastic processes manifest as noise in gene expression, where even genetically identical cells in the same environment exhibit variation in their protein abundances. In order to elucidate the underlying sources that contribute to gene expression noise, we quantify the contribution of each step within the process of protein synthesis along the central dogma. We uncouple gene expression at the transcriptional, translational, and post-translational level using custom engineered circuits stably integrated in human cells using CRISPR. We provide a generalized framework to approximate intrinsic and extrinsic noise in a population of cells expressing an unbalanced two-reporter system. Our decomposition shows that the majority of intrinsic fluctuations stem from transcription and that coupling the two genes along the central dogma forces the fluctuations to propagate and accumulate along the same path, resulting in increased observed global correlation between the products.

INTRODUCTION

The genetic program responsible for the maintenance and operation of all living cells is executed by complex gene regulatory networks (1–4). These networks operate robustly under uncertainty in an inherently noisy environment (5–13). The various biochemical sources that contribute to gene expression noise have been broadly categorized as either being intrinsic or extrinsic (6,14–16). The collection of stochastic biochemical events that independently affect gene expression within a given cell are called ‘intrinsic’ or ‘local’ noise sources. These variations can propagate and accumulate throughout biochemical regulatory networks where the quantitative distributions of a network's constituent proteins appear correlated. However, even proteins originating from unconnected regulatory networks can show correlation. These correlations arise from the stochastic variations in the quantities of reactive species that indiscriminately interact with all genes and are referred to as ‘extrinsic’ or ‘global’ noise sources.

The categorical quantification of gene expression noise as being either intrinsic or extrinsic is intimately defined in the context of a synthetic two-reporter system (6,17). The standard two-reporter design includes two independently expressed genes absent of other regulations that produce measurable fluorescent proteins within a single cell. As both genes operate stochastically, their observed protein products exhibit variability. From a gene-centric perspective, the collection of stochastic sources that jointly contribute to the variability of both genes are said to be extrinsic, whereas the sources of noise that independently affect both genes are said to be intrinsic. The two-reporter experimental setup designed for decomposition of observed noise into extrinsic and intrinsic components has been used successfully to study noise contributed by global effects and gene-specific effects, as well as pathway-specific effects (4,6,18).

While this decomposition method can be useful, the proper application requires two identically regulated reporters with equal variance and mean expression (6,14,19). In this ideal scenario, a scatter plot of the resulting population forms around diagonal line with a slope of 1 (Supplementary Figure S1, left), and the observed noise can be partitioned into its extrinsic and intrinsic components. If the slope of this line is not 1, the intrinsic dispersion is calculated from the diagonal which is numerically wrong (Supplementary Figure S1, left, observed population). Researchers have used various methods to deal with this issue, but there are no commonly accepted and validated strategies. For example, a typical approach is to divide both reporters by their mean, which shifts the population to the diagonal, but the slope remains the same and the decomposition will still be incorrect.

To ease this constraint and accommodate the analysis of increasingly complex two-reporter designs, we introduce a generalized intrinsic dispersion framework. We define the generalized intrinsic noise as the normalized root mean square (RMS) distance from the two-dimensional, orthogonal regression line (Supplementary Figure S1, right). We apply this framework to custom architectures that decouple the production of two fluorescent proteins at the transcriptional, translational and post-translational levels. We utilize SpCas9:sgRNA_AAVS (20–22) to integrate these two-reporter gene cassettes and produce several monoclonal mammalian cells. We probe and unravel the intrinsic and extrinsic noise sources along the central dogma (23,24).

MATERIALS AND METHODS

Molecular cloning

Restriction enzymes, Q5 High-Fidelity 2X Master Mix (NEB, catalog #M0492) and T4 DNA Ligase (NEB, catalog #M0202S) were purchased from New England Biolabs. All primers were synthesized by Sigma Aldrich. PCR and Gel Purification was performed using PCR Purification kits (QIAGEN, catalog #28104) and QIAquick Gel extraction kits (QIAGEN, catalog #28704) according to manufacturers’ protocols. All intermediate and final plasmids were transformed into NEB-5alpha competent Escherichia coli (NEB, catalog #C2987H). For the assembly of all genetic constructs a donor plasmid flanked by ∼1 kb homology arms to the AAVS1 safe harbor locus (unpublished data) was used. Plasmid integrity was confirmed with direct Sanger sequencing, which was carried out by Genewiz, and restriction enzyme digestion. Bacterial culture media and agar were purchased from BD Biosciences (BD Biosciences, catalog #DF0446-07-5). Miniprep was performed using QIAprep Spin Miniprep kit (QIAGEN, catalog #27104).

Cell culture and monoclones selection

HCT116 cells were maintained at 37°C, 100% humidity and 5% CO₂. The cell line was maintained in Dulbecco's modified Eagle's medium (Invitrogen, catalog #11965-1181) which was supplemented with 10% Fetal Bovine Serum (Invitrogen, catalog #26140), 0.1 mM MEM non-essential amino acids (Invitrogen, catalog #11140-050) and 0.045 units/ml of Penicillin with 0.045 units/ml of streptomycin (Invitrogen, catalog #15140). When 50–90% confluent, the cells were passed by washing with Dulbecco's phosphate buffered saline (Mediatech, catalog #21-030-CM), then trypsinizing using 0.25% Trypsin with EDTAX4Na (Invitrogen, catalog #25200) and diluted in fresh medium.

For generation of the stable cell lines, 10 million human HCT116 cells were seeded onto a 10 cm petri dish. After 16 h, HCT116 cells were transiently transfected with 1 μg of circuit constructs and 9 μg of CMV-spCas9-t2a-mKate-U6-gRNA using jetPRIME as transfection agent. 48 hours later, puromycin was added to the final concentration of 2 μg/ml (ThermoFisher Scientific, catalog #A1113802). Selection lasted roughly two weeks and polyclonal stable cell lines were generated for each construct.

To generate monoclonal stable cell lines, flow cytometric sorting was performed at the UTD Flow Cytometry core facility using BD Aria Fusion flow cytometer. Single cells were grown in 96-well plates (Griener Bio-ONE, catalog #650101) using complete conditioned media. Conditioned media was prepared by harvesting media when fully confluent and passing it through a syringe filter (Fisher Scientific, catalog #50-202-072).

Flow cytometry measurements

For each cell line, ∼150 000 cells were seeded into one well of a 12-well cell culture treated plastic plate. After 24 h, the cells were trypsinized using 0.1 ml of 0.25% trypsin–EDTA. 0.9 ml of supplemented DMEM were added to neutralize the 0.25% trypsin–EDTA. The cell suspension was centrifuged at 1000 rpm for 5 min. After removal of the supernatant, the cell pellets were re-suspended in 0.5 ml of Dulbecco's phosphate buffered saline (Mediatech, catalog #21-030-CM). The cells were analyzed on a BD LSRFortessa flow analyzer. CFP was measured with a 445-nm laser and a 470/20 band-pass filter and mKate2 with a 561-nm laser, 600 emission filter and a 610/20 band-pass filter. A gate to SSC-width/SSC-area gates were first used to exclude doublets. Then, a FSC (forward scatter)/SSC (side scatter) gate was generated to select for live cell populations. All experiments were performed in triplicates.

Microscopy measurements

Fluorescence microscopy was carried out using an Olympus IX81 microscope in a Precision Control environmental chamber. The images were captured using a Hamamatsu ORCA-03 Cooled monochrome digital camera. The filter sets used were ET436/20× (excitation) and ET480/40 m (emission) for CFP, ET560/40× (excitation) and ET630/75 m (emission) for mKate. Slidebook was used to process and analyze the images. All images within a given experimental set were collected with the same exposure times and underwent identical processing.

RESULTS

Circuits and cell line engineering

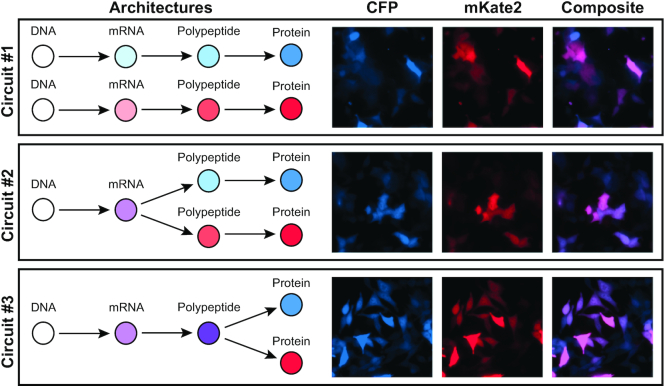
The panel of cell lines is comprised of a series of three engineered immortalized human colorectal carcinoma lines (HCT116), each consisting of custom synthetic gene cassettes that constitutively express a cyan fluorescent protein (CFP) and a red fluorescent protein (mKate2) (Figure 1). Specifically, the transcriptionally uncoupled ‘Circuit #1’ is comprised of two constitutive CMV promoters that each independently drive CFP and mKate2 expression. Both genes are separated by two cHS4 insulator sites to ensure transcriptional independence given their proximity and shared orientation (25,26). The translationally uncoupled ‘Circuit #2’ features a single CMV promoter driving the expression of a bicistronic transcript encoding both CFP and mKate2 that is separated by an internal ribosome entry site (IRES), thus allowing each ORF to be translated independently (27). Finally, the post-translationally uncoupled ‘Circuit #3’ again features a constitutive CMV promoter driving the expression of a bicistronic transcript, except the IRES motif is replaced by the T2A self-cleaving peptide motif (28). The T2A motif uncouples the co-expression of both reporters after their shared transcript is successfully transcribed and translated, allowing for independent protein folding for both CFP and mKate2. Additionally, both fluorescent reporter proteins are fused to a PEST peptide sequence that enhances protein degradation and reduce protein half-life.

Figure 1.

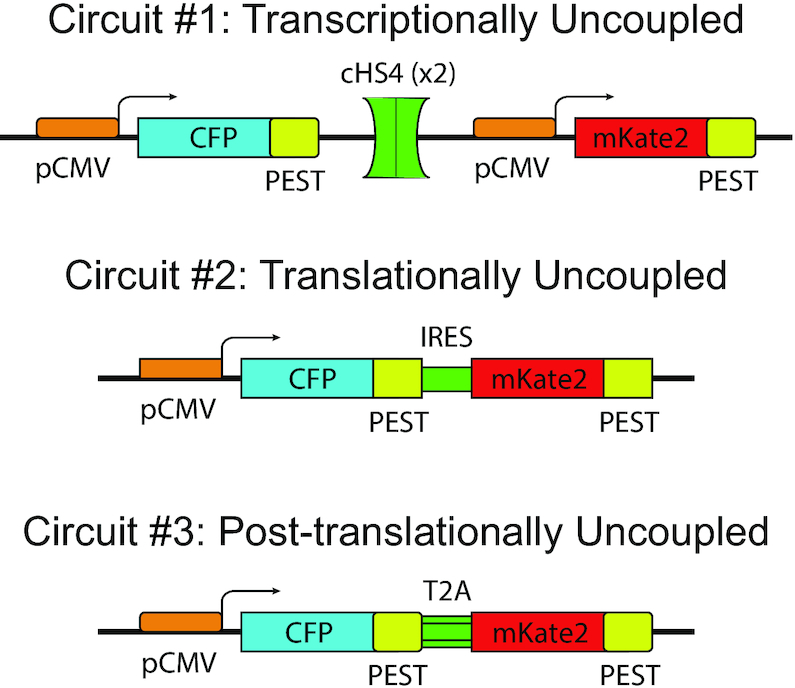
Gene circuits. The three synthetic gene circuits that couple the protein production process. The transcriptionally uncoupled circuit #1 produces CFP and mKate2 fluorescent proteins originating from two transcriptionally independently expressing genes separated by two insulating elements (cHS4). The translationally uncoupled circuit #2 produces both CFP and mKate2 fluorescent proteins originating from a single gene whose transcript contains two cistrons separated by an IRES element. The post-translationally uncoupled circuit #3 produces both CFP and mKate2 fluorescent proteins originating from a single translated polypeptide that self-cleaves into two functional proteins.

Each cassette was stably integrated into the adeno-associated safe harbor locus (AAVS1) using SpCas9 (29). To perform genomic integrations, we engineered donor strands using standard recombinant DNA cloning to enable homology-directed repair (HDR) integration via Cas9-induced double strand cleavage at the AAVS1 safe-harbor locus of HCT116 cells (30). The donor plasmids that contain the circuits were designed to be flanked by sequences homologous to the DNA surrounding the guide RNA (gRNA) target site of the AAVS1 locus (Supplementary Figure S2). Cells receiving the respective donor cassettes with the different configurations of the two-reporter system were selected by inclusion of a puromycin resistance gene in the donor cassette. Following co-transfection of the donor cassette plasmids with SpCas9 and the AAVS1-targeting sgRNA, cells remained under puromycin selection for two weeks. The surviving colonies were then sorted into single cells by FACS. The surviving clones were sequenced and evaluated for the constitutive two-reporter expression using fluorescence microscopy and flow cytometry; for each circuit, we isolated at least three monoclonal populations harboring the gene circuit.

Probing noise along the central dogma

The three circuits uncouple the output protein production at strategic locations as the DNA sequence information is passed through the central dogma (Figure 2, Supplementary Figures S3 and S4), allowing for the propagative effects of intrinsic and extrinsic noise to manifest differently. The stable cell line containing Circuit #1 independently expresses both reporter proteins at all stages ensured by the inclusion of the cHS4 insulator. In this mode of expression, both fluorescent proteins will be subjected to both extrinsic and intrinsic sources of noise within their own genes. In the case of Circuit #2, where cistrons of CFP and mKate2 share the same promoter and transcript, any sources of fluctuations that impinge either the promoter or transcript will be applied globally to both fluorescent proteins’ expression. The inclusion of the IRES element allows for the single transcript to interact with multiple ribosomes, thereby uncoupling the expression of both CFP and mKate2 at the translation stage by allowing intrinsic noise sources to independently affect CFP and mKate2 expression in addition to their shared extrinsic noise sources. Finally, the stable cell line containing Circuit #3, maintains the coupling of mKate2 and CFP through the translation stage of protein production by replacing the IRES element of Circuit #2 with a T2A element. Consequently, there is only one ribosome initiation site in which a single transcript will be translated into a single polypeptide containing both CFP and mKate2 proteins temporarily fused together with the T2A self-cleaving polypeptide. Upon complete translation, the T2A element will self-cleave, uncoupling the expression of CFP and mKate2 by allowing each protein to be subjected to independent fluctuations of post-translational processing.

Figure 2.

Fluorescence microscopy images of engineered stable cell lines. Co-expression of both CFP and mKate2 fluorescent proteins were observed in all monoclonal stable cells expressing circuits #1, #2 and #3 (top to bottom).

Evaluation of the two-reporter systems

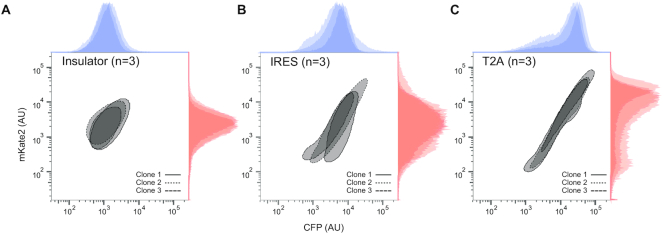
The function and genomic integration of the synthetic circuits was first evaluated by fluorescence microscopy of isogenic clones (Figure 2). Fluorescent microscopy confirmed successful integration of the reporter genes. In all three circuits, the majority of the cells show constitutive expression of both CFP and mKate2. Subsequently, flow cytometry measurements of the stable clones reveal marked differences in the pattern of the co-expressed proteins that is not readily apparent in the microscopy images (Figure 3).

Figure 3.

Flow cytometry assay of engineered stable cell lines. Flow cytometry assay demonstrated that the three circuit designs resulted in different fluorescent distributions, with circuit #1 being more oval (i.e. balanced intrinsic and extrinsic contributions) while circuits #2 and #3 having progressively larger extrinsic noises resulting to elongated profile.

To ensure the difference in reporter expression between each population are not due to differences in their transgene copy number, we evaluated the relative copy numbers of transgene among all transgenic cell lines (Supplementary Figure S5 and Supplementary Methods). Regarding the magnitude of expression for each individual reporter set, when the production of two proteins is segregated at the promoter level (Figure 3A) the average output is lower than the clones with shared promoter (Figure 3B and C, Supplementary Figure S6 and Table S1).

Furthermore, we observed that the clonal differences in Circuit #2 are most noticeable, as unlike the other two circuits, the slopes of each clone's co-expression are significantly different (Supplementary Figure S7). In other words, having co-expressed proteins that originate from a single bicistronic mRNA has the most pronounced effect on the relative production rate of the proteins. This potentially reflects the differences in the ribosome binding activity to the 5′ cap of the CFP versus the IRES of the mKate2.

Interestingly, our initial visual assessment of the flow cytometry data showed that the three circuit designs resulted in different fluorescent distributions, with circuit #1 being more ovular (i.e. balanced intrinsic and extrinsic contributions) while circuits #2 and #3 having progressively larger extrinsic contributions resulting in a more elongated profile. These results indicate that segregation at the polypeptide level and beyond may have the effect of widening the range of expression for both the co-expressed proteins (i.e. increased observed extrinsic noise and decreased observed intrinsic noise).

Errors-in-variables (EIV) modeling

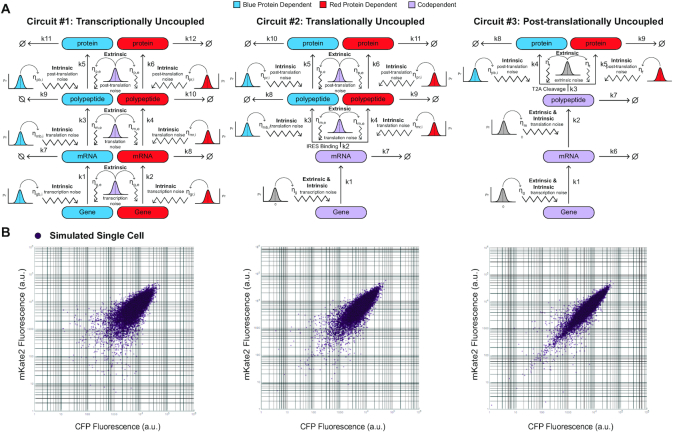
To investigate the effects of extrinsic and intrinsic noise within the central dogma in silico, we constructed three models that are representative of our gene circuits (Figure 4). In order to introduce noise, we follow an error-in-variables (EIV) (1,31) modeling approach (Supplemental Material, EIV Modeling of Extrinsic and Intrinsic Noise in Biological Systems) and tandemly add two noise sources throughout the kinetics of the central dogma. At each production stage, the protein precursor species are subjected to two sources of noise; an extrinsic noise, which additively perturbed the production kinetic parameters of both protein precursor species identically, and an intrinsic noise, which additively perturbed both protein precursor species independently. Procedurally, both intrinsic noise parameters within a given production stage are paired random sampling events from a Gaussian distribution with zero mean and a defined standard deviation in which two unique values perturb their respective protein precursors kinetic parameter independently. On the other hand, the single extrinsic noise parameter within a given production stage is a unique random sampling from a Gaussian distribution with zero mean and a defined standard deviation in which both kinetic parameters of each respective protein precursor are perturbed simultaneously and identically. The variance of each noise distribution is chosen to scale with the parameter it is perturbing such that the noise of the parameter, as measured by the coefficient of variation (CV), remains constant throughout the production stages of the simulation. For our simulations, we chose our intrinsic noise to generate a 20% coefficient of variation and our extrinsic noise to generate a 40% coefficient of variation about the parameter(s) they are affecting, respectively. Next, for each circuit model, we simulated 10 populations of 1000 cells and plotted the simulation results on a logarithmic scale. As shown in Figure 4B, our simulated data displayed comparable distribution patterns as the experimental ones, which become progressively more elongated as we transition from Circuit #1 to #3.

Figure 4.

Errors-in-variables (EIV) Modeling and simulation results. (A) Diagrammatic representation of error in variables ODE model of each synthetic architecture. Each random sampling of an error variable is indicated by a representative Gaussian distribution. The intrinsic noise sources at each production stage are sampled simultaneously, whereas the extrinsic noise sources are sampled once and applied to both noisy kinetic parameters within a given stage. The reaction species and sampling events that are solely responsible for the production of mKate2 or CFP are indicated in red and blue, respectively, whereas the reaction species and sampling events that are jointly responsible for the production of mKate2 and CFP are indicated in light purple. (B) Simulation results for the three architectures.

Generalized noise decomposition

Extrinsic and intrinsic noise have been empirically defined through the covariant expression of two genes being expressed in symmetric two-reporter systems (6). As such, the application of these definitions of noise are limited to proportionally expressed and equivalently varying reporter protein expressions and thus could not be directly applied on our gene circuits. As an example, an expression bias towards the protein downstream of the IRES motif in synthetic bicistronic transcripts is typically observed and can be seen in our cell lines containing Circuit #2 (32). Therefore, to accommodate for biases present in non-ideal two reporter systems in which the reporter genes of a two-reporter system are dissimilarly processed and/or regulated, we relaxed the mathematical definition of intrinsic noise as the normalized root mean square (RMS) distance from the orthogonal regression line of the two co-expressed reporter proteins rather than line of equal co-expression. Specific to the reporter proteins used in our constructs, our intrinsic noise quantifies the dispersion of the co-expression of mKate2 and CFP as the RMS distance to an orthogonally regressed line rather than the co-expression line of equality (for mKate2 and CFP). Finally, to enable the comparison between clones and architectures, we normalized the extrinsic and intrinsic noises using the total noise.

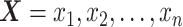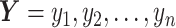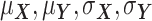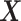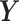Specifically, let and be the ordered sets of n observations of two fluorescent proteins produced from a two-reporter noise analyzing system. We denote as the sample means and sample standard deviations of and and 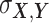as the covariance between 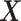and 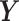. Using this notation, we adopted Elowitz's (6) extrinsic noise 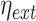definition, as

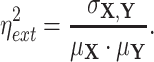Subsequently, we relax the assumptions that the variances and means of the two proteins are equal and accordingly define the generalized intrinsic noise, 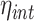, as the normalized root mean square (RMS) distance from the two-dimensional, orthogonal regression line. Using our notation, the orthogonal regression line is defined through the relationship

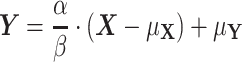where

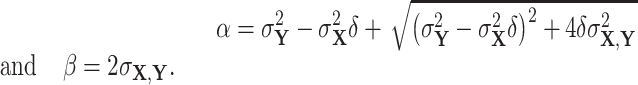Here, δ is defined as the ratio of the variances of errors in 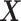or 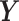, a quantity different than sample variances whose approximation is obtained through continual assessment of a single co-expression event. As our instrumental setup does not allow multiple measurements of a single event, we assume δ = 1. Next, the RMS distance is calculated as

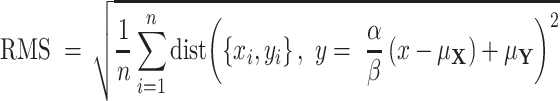which reduces to

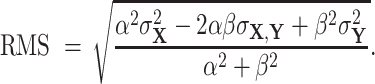Finally, the relaxed definition of intrinsic noise is obtained as

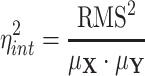and related to the extrinsic and total noise through the definition

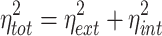Noise decomposition of the synthetic circuit

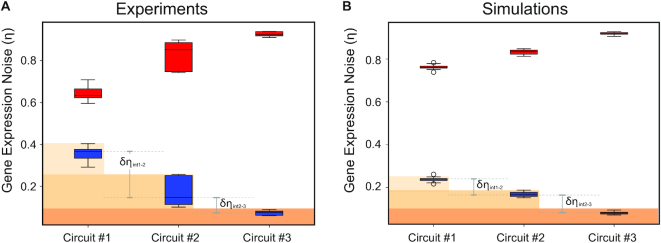
Both the engineered populations and their corresponding simulated populations were decomposed following the generalized noise decomposition method and enable clonal and architectural comparison through the normalization of intrinsic and extrinsic noise to the total noise. As shown in Figure 5A, as the two-fluorescent proteins become coupled through the production stages of the central dogma (from circuit #1 to circuit #3), the normalized intrinsic noise appears to decrease while the normalized extrinsic noise appears to increase. We validated the noise decomposition approach by adjusting the size of forward scatter (FSC) and side scatter (SSC) gates, which has been previously demonstrated (4,33–35) as a standard way to modulate noise levels in previous studies (Supplementary Figure S8).

Figure 5.

Apparent extrinsic and intrinsic noise. Extrinsic (red) and intrinsic (blue) noise values of three circuit designs. The box height indicates the 75% (top) and 25% (bottom) quantiles and the whiskers bound the upper and lower range of values observed. (A) Noise decomposition of the experimental data for the three circuit designs. (B) Noise decomposition of the simulated data for the three circuit designs. In both cases, the extrinsic noise appears to increase while the intrinsic noise appears to decrease as the two proteins become coupled (at transcription, translation, post-translation levels)

As a production step becomes coupled, two individual protein precursors susceptible to independent noise fluctuations are engineered to merge into a single precursor responsible for the eventual production of both proteins. Both biological sources of intrinsic and extrinsic remain present yet cannot be decoupled from a single measured output. This causes any intrinsic noise sources that would have affected both independent precursor species, had they been uncoupled, to only affect a single precursor. The resulting fluctuations propagate through the remaining production stages, causing an increase in the observed extrinsic fluctuations.

For additional insight regarding the propagation of intrinsic noise, we constructed a new set of stochastic simulations using intrinsic noise sources alone. In contrast to our EIV model where we simulate noise by sampling from Gaussian distributions, we opted to use Gillespie stochastic simulations to model the intrinsic noise impact (Supplementary Figure S9). From the transcriptionally uncoupled Circuit #1 simulation, we observe that any intrinsic noise sources that covary along the central dogma appear as extrinsic contributions, in accordance with the definition of intrinsic and extrinsic noise (Supplementary Figure S10A). As we couple the central dogma steps (in Circuits #2 and #3) we force the intrinsic and extrinsic contributions to manifest as a single noise source. Therefore, the downstream decoupled products covary, and as a result, the scatter plot further expands along the diagonal. This is consistent with the point that intrinsic noise is now being measured at the output (or observed) as extrinsic.

Importantly, if we consider the Circuit #3 simulations, the observed intrinsic noise is strictly from the post-translational step (i.e. the only step that is decoupled in this circuit), and all other sources of intrinsic noise upstream are being observed as extrinsic. Similarly, for Circuit #2 simulations, the observed intrinsic noise stems from both the translational and post-translational steps. Lastly, Circuit #1 represents noise contribution from transcriptional, translational and post-translational steps (Supplementary Figure S10B).

From the noise decomposition of the experimental measurements, we observe the lowest mean intrinsic noise value from Circuit #3 (Figure 5A, Circuit #3: relative intrinsic noise: 0.07, relative extrinsic noise: 0.93). For Circuit #2, we observe the mean intrinsic noise contribution from the translational on top of the post-translational steps (Figure 5A, Circuit #2: relative intrinsic noise: 0.18, relative extrinsic noise: 0.82). Lastly, Circuit #1, which represents noise contribution from transcriptional, translational and post-translational steps, we observe the highest mean intrinsic noise and lowest mean extrinsic noise (Figure 5A, Circuit #1 relative intrinsic noise: 0.36, relative extrinsic noise: 0.64). Interestingly, between the circuits we observe a significantly bigger difference between δη_int1–2 = 0.18 versus δη_int2–3 = 0.10.

Similar noise decomposition patterns were observed using the simulated datasets (Figure 5B). As an example (Supplementary Table S2), the means of relative intrinsic noise decreased from 0.24 (circuit #1) to 0.17 (circuit #2) and then 0.08 (circuit #3). Furthermore, the observation that the simulations show relatively fixed intrinsic noise differences between the circuits (δη_int1–2 = 0.07 and δη_int2–3 = 0.09) validates our decomposition approach as the artificial noise sources are balanced at each simulation step.

Taken together, the δη_int difference between the simulated and experimental data suggest that there are additional sources of (intrinsic) noise that we did not consider in the model (e.g. noise in RNA processing and trafficking). Moreover, the contrast between experiments and simulations shows that the majority of experimental intrinsic fluctuations stem from the transcription step.

DISCUSSION

Gene expression noise has wide-ranging implications, including its involvement in the generation of phenotypic heterogeneity in microorganisms, development and cellular differentiation in higher organisms, and the progression of disease (8,36–38). Herein, we experimentally unravel the noise sources along the central dogma using custom engineered genetic circuits stably integrated in human cells.

These circuits allow us to decompose and attribute noise to extrinsic (global) and intrinsic (local) sources and calculate the relative contributions of each. We note that our definition of intrinsic noise can be further generalized to quantify dispersion about any regression line, allowing for the decomposition of nonlinearly co-expressed systems when required. However, in these nonlinear systems, a redefinition of extrinsic noise would be required. To conclude, our results not only provide better understanding of pivotal biological processes, but also provide insights for pathway characterization (39–44) and a platform for engineering of custom genetic circuits that exploit noise sources (7,45–49).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

US National Science Foundation (NSF) CAREER [1351354]; NSF [1361355]; a Cecil H. and Ida Green Endowment; Eugene McDermott Graduate Fellows Program; University of Texas at Dallas. Funding for open access charge: Cecil H. and Ida Green Endowment, NSF.

Conflict of interest statement. None declared.