Sparse Sliced Inverse Regression Via Lasso

Abstract

For multiple index models, it has recently been shown that the sliced inverse regression (SIR) is consistent for estimating the sufficient dimension reduction (SDR) space if and only if $\rho =\text{lim}\frac{p}{n}=0$, where p is the dimension and n is the sample size. Thus, when p is of the same or a higher order of n, additional assumptions such as sparsity must be imposed in order to ensure consistency for SIR. By constructing artificial response variables made up from top eigenvectors of the estimated conditional covariance matrix, we introduce a simple Lasso regression method to obtain an estimate of the SDR space. The resulting algorithm, Lasso-SIR, is shown to be consistent and achieve the optimal convergence rate under certain sparsity conditions when p is of order o(n²λ²), where λ is the generalized signal-to-noise ratio. We also demonstrate the superior performance of Lasso-SIR compared with existing approaches via extensive numerical studies and several real data examples.

1. Introduction

Dimension reduction and variable selection have become indispensable steps for modern-day data analysts in dealing with the “big data,” where thousands or even millions of features are often available for only hundreds or thousands of samples. With these ultra high-dimensional data, an effective modeling strategy is to assume that only a few features and/or a few linear combinations of these features carry the information that researchers are interested in. One can consider the following multiple index model [Li, 1991]:

$$y=f\left({\mathit{\beta }}_1^{\tau }\mathit{x},{\mathit{\beta }}_2^{\tau }\mathit{x},\dots ,{\mathit{\beta }}_d^{\tau }\mathit{x},ϵ\right),$$ (1)

where x follows a p-dimensional elliptical distribution with mean zero and covariance matrix Σ, the β_i’s are unknown projection vectors, d is unknown but is assumed to be much smaller than p, and the error ϵ is independent of x and has mean 0. When p is very large, it is reasonable to further restrict each β_i to be a sparse vector.

Since the introduction of the sliced inverse regression (SIR) method (Li [1991]), many methods have been proposed to estimate the space spanned by (β₁, ⋯, β_d) with few assumptions on the link function f(·). Assume the multiple index model (1), the objective of all the SDR (Sufficient Dimension Reduction, Cook [1998]) methods is to find the minimal subspace $\mathcal{S}\subseteq {ℝ}^p$ such that $y⫫\mathit{x}|P_{\mathcal{S}}\mathit{x}$, where $P_{\mathcal{S}}$ stands for the projection operator to the subspace $\mathcal{S}$. When the dimension of x is moderately large, all the SDR methods, including SIR, are proven to be successful [Xia et al., 2002, Ni et al., 2005, Li and Nachtsheim, 2006, Li, 2007, Zhu et al., 2006]. However, these methods were previously known to work well when the sample size n grows much faster than the dimension p, an assumption that becomes inappropriate for many modern-day datasets, such as those from biomedical researches. It is important to have a thorough investigation of “the behavior of these SDR estimators when n is not large relative to p”, as raised by Cook et al. [2012].

Lin et al. [2015] made an attempt to address the aforementioned challenge for SIR. They showed that, under mild conditions, the SIR estimate of the central space is consistent if and only if ${\rho }_n\stackrel{def}{=}p/n$ goes to zero as n grows. Additionally, they showed that the convergence rate of the SIR estimate of the central space (without any sparsity assumption) is ρ_n. When p is greater than n, certain constraints must be imposed in order for SIR to be consistent. The sparsity assumption, i.e., the number of active variables s must be an order of magnitude smaller than n and p, appears to be a reasonable one. In a follow-up work, Neykov et al. [2016a] studied the sign support recovery problem of the single index model (d = 1), suggesting that the correct optimal convergence rate for estimating the central space might be $\frac{s\text{log}(p)}{n}$, a speculation that is partially confirmed in Lin et al. [2016]. It is shown that, for multiple index models with bounded dimension d and the identity covariance matrix, the optimal rate for estimating the central space is $\frac{ds+s\text{log}(p/s)}{n\lambda }$, where s is the number of active covariates and λ is the smallest non-zero eigenvalue of $var(\mathbb{E}[\mathit{x}|y])$. They further showed that the Diagonal-Thresholding algorithm proposed in Lin et al. [2015] achieves the optimal rate for the single index model with the identity covariance matrix.

The main idea.

In this article, we introduce an efficient Lasso variant of SIR for the multiple index model (1) with a general covariance matrix Σ. Consider first the single index model: y = f(β^τx,ϵ). Let η be the eigenvector associated with the largest eigenvalue of $var(\mathbb{E}[\mathit{x}|y])$. Since β ∝Σ⁻¹η, there are two immediate ways to estimate the space spanned by β. The first approach, as discussed in Lin et al. [2015], estimates Σ⁻¹ and η separately (see Algorithm 1). The second one avoids a direct estimation of Σ⁻¹ by solving the following penalized least square problem: ${\Vert \frac{1}{n}\mathit{X}{\mathit{X}}^{\tau }\mathit{\beta }-\mathit{\eta }\Vert }_2^2+\mu \Vert \mathit{\beta }{\Vert }_1$, where X is the p × n covariate matrix formed by the n samples (see Algorithm 2). However, similar to most L₁-penalization methods for nonlinear models, theoretical underpinning of this approach has not been well understood. Since these two approaches provide good estimates compared with earlier approaches (e.g.,Li [1991], Li and Nachtsheim [2006], Li [2007]) as shown in Lin et al. [2015] and Supplementary Materials, we set the two approaches as benchmarks for comparisons.

We note that an eigenvector $\widehat{\mathit{\eta }}$ of $\widehat{var}(\mathbb{E}[\mathit{x}|y])$, where $\widehat{var}(\mathbb{E}[\mathit{x}|y])$ is an estimate of the conditional covariance matrix $var(\mathbb{E}[\mathit{x}|y])$ using SIR [Li, 1991], must be a linear combination of the column vectors of X. Thus, we can construct an artificial response vector $\tilde{\mathit{y}}\in {ℝ}^n$ such that $\widehat{\mathit{\eta }}=\frac{1}{n}\mathit{X}\tilde{\mathit{y}}$, and estimate β by solving another penalized least square problem: $\frac{1}{2n}{\Vert \tilde{\mathit{y}}-{\mathit{X}}^{\tau }\mathit{\beta }\Vert }_2^2+\mu \Vert \mathit{\beta }{\Vert }_1$ (see Algorithm 3). We call this algorithm “Lasso-SIR”, which is computationally very efficient. In Section 3, we further show that the convergence rate of the estimator resulting from Lasso-SIR is $\frac{s\text{\hspace{0.17em}log}(p)}{n\lambda }$, which is optimal if s = O(p^1−δ) for some positive constant δ. Note that Lasso-SIR can be easily extended to other regularization and SDR methods, such as SCAD (Fan and Li [2001]), Group Lasso (Yuan and Lin [2006]), sparse Group Lasso (Simon et al. [2013]), SAVE (Cook [2000]), etc.

Connection to Other work Estimating the central space is widely considered as a generalized eigenvector problem in the literature [Li, 1991, Li and Nachtsheim, 2006, Li, 2007, Chen and Li, 1998]. Lin et al. [2016] explicitly described the similarities and differences between SIR and PCA (as first studied by Jung and Marron [2009]) under the “high dimension, low sample size (HDLSS)” scenario. However, after comparing their results with those for Lasso regression, Lin et al. [2016] advocated that a more appropriate prototype of SIR (at least for the single index model) should be the linear regression. In the past three decades, tremendous efforts have been put into the study of linear regression models y = x^τβ + ϵ for HDLSS data. By imposing the L₁ penalty on the regression coefficients, the Lasso approach [Tibshirani, 1996] produces a sparse estimator of β, which turns out to be rate optimal [Raskutti et al., 2011]. Because of apparent limitations of linear models, there are many attempts to build flexible and computationally friendly semi-parametric models, such as the projection pursuit regression [Friedman and Stuetzle, 1981, Chen, 1991], sliced inverse regression [Li, 1991], MAVE [Xia et al., 2002]. However, none of these methods work under the HDLSS setting. Existing theoretical results for HDLSS data mainly focus on linear regressions [Raskutti et al., 2011] and submatrix detections [Butucea et al., 2013], and are not applicable to index models. In this paper, we provide a new framework for the theoretical investigation of regularized SDR methods for HDLSS data.

The rest of the paper is organized as follows. After briefly reviewing SIR, we present the Lasso-SIR algorithm in Section 2. The consistency of the Lasso-SIR estimate and its connection to the Lasso regression are presented in Section 3. Numerical simulations and real data applications are reported in Sections 4 and 5. Some potential extensions are briefly discussed in Section 6. To improve the readability, we defer all the proofs and brief reviews of some existing results to the appendix.

2. Sparse SIR for High Dimensional Data

Notations.

We adopt the following notations throughout this paper. For a matrix V, we call the space generated by its column vectors the column space and denote it by col(V). The i-th row and j-th column of the matrix are denoted by V_i,* and V_*,j, respectively. For (column) vectors x and $\mathit{\beta }\in {ℝ}^p$, we denote their inner product 〈x, β〉 by x(β), and the k-th entry of x by x(k). For two positive numbers a, b, we use a ∨ b and a ∧ b to denote max{a, b} and min{a, b} respectively; We use C, C′, C₁ and C₂ to denote generic absolute constants, though the actual value may vary from case to case. For two sequences {a_n} and {b_n}, we denote a_n ≻ b_n and a_n ≺ b_n if there exist positive constants C and C′ such that a_n ≥ Cb_n and a_n ≤ C′b_n, respectively. We denote a_n ≍ b_n if both a_n ≻ b_n and a_n ≺ b_n hold. The (1, ∞) norm and (∞, ∞) norm of matrix A are defined as $\Vert A{\Vert }_{1,\infty }={\text{max}}_{1\le j\le p}{\sum }_{i=1}^p\left|A_{i,j}\right|$ and max_1≤i,j≤n∥A_i,j∥ respectively. To simplify discussions, we assume that $\frac{s\text{\hspace{0.17em}log}(p)}{n\lambda }$ is sufficiently small. We emphasize again that our covariate data X is a p × n instead of the traditional n × p matrix.

A brief review of Sliced Inverse Regression (SIR).

In the multiple index model (1), the matrix B formed by the vectors β₁,…,β_d is not identifiable. However, col(B), the space spanned by the columns of B is uniquely defined. Given n i.i.d. samples (y_i, x_i), i = 1, ⋯, n, SIR [Li, 1991] first divides the data into H equal-sized slices according to the order statistics y(i), i = 1,…,n. To ease notations and arguments, we assume that n = cH and $\mathbb{E}[\mathit{x}]=0$, and re-express the data as y_h,j and x_h,j, where h refers to the slice number and j refers to the order number of a sample in the h-th slice, i.e., y_h,j = y_(c(h-1)+j), x_h,_j = x_(c(h-1)+j) Here x_(k) is the concomitant of y_(k). Let the sample mean in the h-th slice be denoted by ${\overline{\mathit{x}}}_{h,\cdot }$, then $\Lambda \triangleq var(\mathbb{E}[\mathit{x}|y])$ can be estimated by:

$${\widehat{\Lambda }}_H=\frac{1}{H}\sum _{h=1}^H{\overline{\mathit{x}}}_{h,}{\overline{\mathit{x}}}_{h,.}^{\tau }=\frac{1}{H}{\mathit{X}}_H{\mathit{X}}_H^{\tau }$$ (2)

where X_H is a p×H matrix formed by the H sample means, i.e., ${\mathit{X}}_H=\left({\overline{\mathit{x}}}_{1,\cdot },\dots ,{\overline{\mathit{x}}}_{H,\cdot }\right)$. Thus, col(Λ) is estimated by $col\left({\widehat{\mathit{V}}}_H\right)$, where ${\widehat{\mathit{V}}}_H$ is the matrix formed by the top d eigenvectors of ${\tilde{\mathbf{\Lambda }}}_H$. The $col\left({\widehat{\mathit{V}}}_H\right)$ was shown to be a consistent estimator of col(Λ) under a few technical conditions when p is fixed [Duan and Li, 1991, Hsing and Carroll, 1992, Zhu et al., 2006, Li, 1991, Lin et al., 2015], which are summarized in the online supplementary file. Recently, Lin et al. [2015, 2016] showed that $col\left({\widehat{\mathit{V}}}_H\right)$ is consistent for col(Λ) if and only if ${\rho }_n=\frac{p}{n}\to 0$ as n → ∞, when the number of slices H can be chosen as a fixed integer independent of n and p when the dimension d of the central space is bounded. When x’s distribution is elliptically symmetric, Li [1991] showed that

$$\mathbf{\Sigma }col(\mathit{B})=col(\mathbf{\Lambda }),$$ (3)

and thus our goal is to recover col(B) by solving the above equation. It is shown in [Lin et al., 2015] that when ${\rho }_n\to 0,\widehat{col(\mathit{B})}={\widehat{\mathbf{\Sigma }}}^{-1}col\left({\widehat{\mathit{V}}}_H\right)$ consistently estimate col(B) where $\widehat{\Sigma }=\frac{1}{n}\mathit{X}{\mathit{X}}^{\tau }$ is the sample covariance matrix of X. However, this simple approach breaks down when ρ_n ↛ 0, especially when p ≫ n. Although stepwise methods [Zhong et al., 2012, Jiang and Liu, 2014] can work under HDLSS settings, the sparse SDR algorithms proposed in Li [2007] and Li and Nachtsheim [2006] appeared to be ineffective. Below we describe two intuitive non-stepwise methods for HDLSS scenarios, which will be used as benchmarks in our simulation studies to measure the performance of newly proposed SDR algorithms.

Diagonal Thresholding-SIR.

When p ≫ n, the Diagonal Thresholding (DT) screening method [Lin et al., 2015] proceeds by marginally screening all the variables via the diagonal elements of ${\widehat{\mathbf{\Lambda }}}_H$ and then applying SIR to those retained variables to obtain an estimate of col(B). The procedure is shown to be consistent if the number of nonzero entries in each row of Σ is bounded.

Matrix Lasso.

We can bypass the estimation and inversion of Σ by solving an L₁ penalization problem. Since (3) holds at the population level, a reasonable estimate of col(B) can be obtained by solving a sample-version of the equation with an appropriate regularization term to cope with the high dimensionality. Let ${\widehat{\mathit{\eta }}}_1,\cdots ,{\widehat{\mathit{\eta }}}_d$ be the eigenvectors associated with the largest d eigenvalues of ${\widehat{\mathbf{\Lambda }}}_H$. Replacing Σ by its sample version $\frac{1}{n}\mathit{X}{\mathit{X}}^{\tau }$ and imposing an L₁ penalty, we obtain a penalized sample version of (3):

$${\Vert \frac{1}{n}\mathit{X}{\mathit{X}}^{\tau }\mathit{\beta }-{\widehat{\mathit{\eta }}}_i\Vert }_2^2+{\mu }_i\Vert \mathit{\beta }{\Vert }_1$$ (4)

for some appropriate μ_i’s.

This simple procedure can be easily implemented to produce sparse estimates of β_i’s. Empirically it works reasonably well, so we set it as another benchmark to compare with. Since we later observed that its numerical performance was consistently worse than that of our main algorithm, Lasso-SIR, we did not further investigate its theoretical properties.

The Lasso-SIR algorithm.

First consider the single index model

$$y=f\left({\mathit{x}}^{\tau }{\mathit{\beta }}_0,\mathit{ϵ}\right).$$ (5)

Without loss of generality, we assume that (x_i,y_i), i = 1,…,n, are arranged in a way such that y₁ ≤ y₂ ≤ ⋯ ≤ y_n. Construct an n × H matrix M = I_H ⊗ 1_c, where 1_c is the c × 1 vector with all entries being 1. Then, according to the definition of X_H, we can write X_H = XM/c. Let $\widehat{\lambda }$ be the largest eigenvalue of ${\widehat{\Lambda }}_H=\frac{1}{H}{\mathit{X}}_H{\mathit{X}}_H^{\tau }$ and let $\widehat{\mathit{\eta }}$ be the corresponding eigenvector of length 1. That is,

$$\widehat{\lambda }\widehat{\mathit{\eta }}=\frac{1}{H}{\mathit{X}}_H{\mathit{X}}_H^{\tau }\widehat{\mathit{\eta }}=\frac{1}{nc}\mathit{X}\mathit{M}{\mathit{M}}^{\tau }{\mathit{X}}^{\tau }\widehat{\mathit{\eta }}.$$

Thus, by defining

$$\tilde{\mathit{y}}=\frac{1}{c\widehat{\lambda }}\mathit{M}{\mathit{M}}^{\tau }{\mathit{X}}^{\tau }\widehat{\mathit{\eta }}$$ (6)

we have $\widehat{\mathit{\eta }}=\frac{1}{n}\mathit{X}\tilde{\mathit{y}}$. Note that a key in estimating the central space col(β) of SIR is the equation η ∝ Σβ. If approximating η and Σ by $\widehat{\mathit{\eta }}$ and $\frac{1}{n}\mathit{X}{\mathit{X}}^{\tau }$ respectively, this equation can be written as $\frac{1}{n}\mathit{X}\tilde{\mathit{y}}\propto \frac{1}{n}\mathit{X}{\mathit{X}}^{\tau }\mathit{\beta }$. To recover a sparse vector $\widehat{\mathit{\beta }}\propto \mathit{\beta }$, one can consider the following optimization problem

$$\text{min}\Vert \mathit{\beta }{\Vert }_1,\text{\hspace{1em} subject to \hspace{1em}}{\Vert \mathit{X}\left(\tilde{\mathit{y}}-{\mathit{X}}^{\tau }\mathit{\beta }\right)\Vert }_{\infty }\le \mu ,$$

which is known as the Dantzig selector [Candes and Tao, 2007]. A related formulation is the Lasso regression, where β is estimated by the minimizer of

$${\mathcal{L}}_{\mathit{\beta }}=\frac{1}{2n}{\Vert \tilde{\mathit{y}}-{\mathit{X}}^{\tau }\mathit{\beta }\Vert }_2^2+\mu \Vert \mathit{\beta }{\Vert }_1.$$ (7)

As shown by Bickel et al. [2009], the Dantzig selector is asymptotically equivalent to the Lasso for linear regressions. We thus propose and study the Lasso-SIR algorithm in this paper.

There is no need to estimate the inverse of Σ in Lasso-SIR. Moreover, since the optimization problem (7) is well studied for linear regression models [Tibshirani, 1996, Efron et al., 2004, Friedman et al., 2010], we may formally “transplant” their results to the index models. Practically, we use the R package glmnet to solve the optimization problem where the tuning parameter μ is chosen using cross-validation.

Last but not least, Lasso-SIR can be easily generalized to the multiple index model (1). Let ${\widehat{\lambda }}_i,1\le i\le d$, be the d-top eigenvalues of ${\widehat{\mathbf{\Lambda }}}_H$ and $\widehat{\mathit{\eta }}=\left({\widehat{\mathit{\eta }}}_1,\cdots ,{\widehat{\mathit{\eta }}}_d\right)$ be the corresponding eigenvectors. Similar to the definition of the “pseudo response variable” for the single index model, we define a multivariate pseudo response $\tilde{\mathit{Y}}$ as

$$\tilde{\mathit{Y}}=\frac{1}{c}\mathit{M}{\mathit{M}}^{\tau }{\mathit{X}}^{\tau }\widehat{\mathit{\eta }}diag\left(\frac{1}{{\widehat{\lambda }}_1},\cdots ,\frac{1}{{\widehat{\lambda }}_d}\right).$$ (8)

We then apply the Lasso on each column of the pseudo response matrix to produce the corresponding estimate.

The number of directions d plays an important role when implementing Algorithm 4. A common practice is to locate the maximum gap among the ordered eigenvalues of the matrix ${\widehat{\mathbf{\Lambda }}}_H$, which does not work well under HDLSS settings. In Section 3, we show that there exists a gap among the adjusted eigenvalues ${\widehat{\lambda }}_i^a={\widehat{\lambda }}_i{\Vert {\widehat{\beta }}_i\Vert }_2$ where ${\widehat{\beta }}_i$ is the i-th output of Algorithm 4. Motivated by this, we estimate d according to the following algorithm:

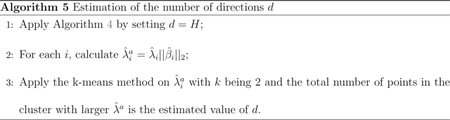
Remark 1. In another paper that the authors are preparing, it is shown that the Lasso-SIR algorithm works on the joint distribution of (X, Y) and is thus not tied to the single or multiple index models. We choose the single/multiple index models to have a clear representation of the central subspace $\mathcal{S}$, i.e., $\mathcal{S}=span\left\{{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_d\right\}$.

Remark 2. When dealing with real data, we suggest that the users employ quantile normalization to transform each covariate when X is not normally distributed. When p is too large and beyond our bound of $n=O(\sqrt{p})$, as required by our provided R-package (see Section 7 for its downloading information), the user can first conduct variable screening based on DT-SIR, which is also included in this package.

3. Consistency of Lasso-SIR

For simplicity, we assume that x ~ N(0, Σ). The normality assumption can be relaxed to elliptically symmetric distributions with sub-Gaussian tail; however, this will make technical arguments unnecessarily tedious and is not the main focus of this paper. From now on, we assume that d, the dimension of the central space, is bounded; thus we can assume that H, the number of slices, is a large enough but finite integer [Lin et al., 2016, 2015]. In order to prove the consistency, we need the following technical conditions:

• A1) There exist constants C_min and C_max such that 0 < C_min < λ_min(Σ) ≤ λ_max(Σ) < C_max;

• A2) There exists a constant κ ≥ 1, such that

• $0<\lambda ={\lambda }_d(var(\mathbb{E}[\mathit{x}|y])\le \dots \le {\lambda }_1(var(\mathbb{E}[\mathit{x}|y])\le \kappa \lambda \le {\lambda }_{max}(\Sigma );$

• A3) The central curve $\mathit{m}(y)=\mathbb{E}[\mathit{x}|y]$ satisfies the sliced stability condition.

Condition A1 is commonly imposed in the analyses of high-dimensional linear regression models. Condition A2 is merely a refinement of the coverage condition that is commonly imposed in the SIR literature, i.e., $rank(var(\mathbb{E}[\mathit{x}|y]))=d$. For single index models, there is a more intuitive explanation of condition A2. Since $rank(var(\mathbb{E}[\mathit{x}|y]))=1$, condition A2 is simplified to 0 < λ = λ₁ ≤ λ_mαx(Σ) which is a direct corollary of the total variance decomposition identity (i.e., $var(\mathit{x})=var(\mathbb{E}[\mathit{x}\left|y])+\mathbb{E}[var(\mathit{x}\right|y)]$). We may treat λ as a generalized SNR and A2 simply requires that the generalized SNR is non-zero. Condition A3 is a property of the central curve, or equivalently, a regularity condition on the link function f(·) and the noise ϵ introduced in Lin et al. [2015].

Remark 3 (Generalized SNR and eigenvalue bound). Recall that the signal-to-noise ratio (SNR) for the linear model y = β^τx + ϵ, where x ~ N(0, Σ) and ϵ ~ N(0,1), is defined as

$$SNR=\frac{E\left[{\left({\mathit{\beta }}^{\tau }\mathit{x}\right)}^2\right]}{\mathbb{E}\left[y^2\right]}=\frac{\Vert \mathit{\beta }{\Vert }_2^2{\mathit{\beta }}_0^{\tau }\Sigma {\mathit{\beta }}_0}{1+\Vert \mathit{\beta }{\Vert }_2^2{\mathit{\beta }}_0^{\tau }\Sigma {\mathit{\beta }}_0}.$$

where β₀ = β/∥β∥₂. A simple calculation shows that

$$\mathrm{var}(\mathbb{E}[\mathit{x}|y])=\frac{\Sigma \mathit{\beta }{\mathit{\beta }}^{\tau }\Sigma }{{\mathit{\beta }}_0^{\tau }\Sigma {\mathit{\beta }}_0\Vert \mathit{\beta }{\Vert }_2^2+1},$$

and

$$\lambda (\mathrm{var}(\mathbb{E}[\mathit{x}|y]))=\frac{{\mathit{\beta }}_0^{\tau }\Sigma \Sigma {\mathit{\beta }}_0\Vert \mathit{\beta }{\Vert }_2^2}{{\mathit{\beta }}_0^{\tau }\Sigma {\mathit{\beta }}_0\Vert \mathit{\beta }{\Vert }_2^2+1},$$

where $\lambda (var(\mathbb{E}[\mathit{x}|y]))$ is the unique non-zero eigenvalue of $var(\mathbb{E}[\mathit{x}|y])$. This leads to the following identity for the linear model:

$$\lambda (var(\mathbb{E}[\mathit{x}|y]))=\frac{{\mathit{\beta }}_0^{\tau }\Sigma \Sigma {\mathit{\beta }}_0}{{\mathit{\beta }}_0^{\tau }\Sigma {\mathit{\beta }}_0}SNR.$$

Thus, in a multiple index model we call λ, the smallest non-zero eigenvalue of $var(\mathbb{E}[\mathit{x}|y])$, the model’s generalized SNR.

Theorem 1 (Consistency of Lasso-SIR for Single Index Models). Assume that nλ = p^α for some α > ½ and that conditions A1–A3 hold for the single index model, $y=f\left({\mathit{\beta }}_0^{\tau }\mathit{x},ϵ\right)$, where β₀ is a unit vector. Let $\widehat{\mathit{\beta }}(\mu )$ be the output of Algorithm 3, then

$$\Vert P_{\widehat{\mathit{\beta }}}-P_{{\mathit{\beta }}_0}{\Vert }_F\le C_1\sqrt{\frac{s\text{ log}(p)}{n\lambda }}$$

holds with probability at least 1 – C₂ exp(−C₃ log(p)) for some constants C₂ and C₃.

When no sparsity on η is assumed, the condition α > 1/2 is necessary. This condition can be relaxed if a certain sparsity structure is imposed on η or Σ such that Σβ becomes sparse. Next, we state the theoretical result regarding the multiple index model (1).

Theorem 2 (Consistency of Lasso-SIR). Assume that nλ = p^α for some α > ½, where λ is the smallest nonzero eigenvalue of $var(\mathbb{E}[\mathit{x}|y])$, and that conditions A1–A3 hold for the multiple index model (1). Assume further that the dimension d of the central subspace is known. Let $\widehat{B}$ be the output of Algorithm 4, then

$$\Vert P_{\widehat{\mathit{B}}}-P_{\mathit{B}}{\Vert }_F\le C_1\sqrt{\frac{s\text{ log}(p)}{n\lambda }}$$

holds with probability at least 1 − C₂ exp(−C₃ log(p)) for some constants C₂ and C₃.

Lin et al. [2016] have shown that the lower bound of the risk $\mathbb{E}\Vert P_{\widehat{\mathit{B}}}-P_{\mathit{B}}{\Vert }_F^2$ is $\frac{s\text{ log}(p/s)}{n\lambda }$ when (i) d = 1, or (ii) d(> 1) is finite and λ > c₀ > 0. This implies that if s = O(p^1–δ) for some positive constant δ, the Lasso-SIR algorithm achieves the optimal rate, i.e., we have the following corollary.

Corollary 1. Assume that conditions A1–A3 hold. If nλ = p^α for some α > 1/2 and s = O(p^1−δ), then Lasso-SIR estimate $P_{\widehat{\mathit{B}}}$ achieves the minimax rate when (i) d =1, or (ii) d(> 1) is finite and λ > c₀ > 0.

Remark 4. Consider the linear regression y = β^τx + ϵ, where x ~ N(0, Σ), ϵ ~ N(0,1). It is shown in Raskutti et al. [2011] that the lower bound of the minimax rate of the l₂ distance between any estimator and the true β is $\frac{s\text{ log}(p/s)}{n}$ and the convergence rate of Lasso estimator ${\widehat{\mathit{\beta }}}_{Lasso}$ is $\frac{s\text{ log}(p)}{n}$. Namely, the Lasso estimator is rate optimal for linear regression when s = O(p^1–δ) for some positive constant δ. A simple calculation shows that $\lambda (var(\mathbb{E}[\mathit{x}|y]))~\Vert \mathit{\beta }{\Vert }_2^2$, if ||β||₂ is bounded away from ∞. Consequently,

$${\Vert P_{{\widehat{\mathit{\beta }}}_{Lasso}}-P_{\mathit{\beta }}\Vert }_F\le 4\frac{{\Vert {\widehat{\mathit{\beta }}}_{Lasso}-\mathit{\beta }\Vert }_2}{\Vert \mathit{\beta }{\Vert }_2}\le C\sqrt{\frac{s\text{log}(p)}{n\lambda (var(\mathbb{E}[\mathit{x}|y]))}}$$ (9)

holds with high probability. In other words, if we treat Lasso as a dimension reduction method (where d = 1 and the link function is linear), the projection matrix $P_{{\widehat{\mathit{\beta }}}_{Lasso}}$ based on Lasso is rate optimal. The Lasso-SIR has extended the Lasso to the non-linear multiple index models. This justifies a statement in Chen and Li [1998], stating that ”SIR should be viewed as an alternative or generalization of the multiple linear regression”. The connection also justifies a speculation in Lin et al. [2016] that ”a more appropriate prototype of the high dimensional SIR problem should be the sparse linear regression rather than the sparse PCA and the generalized eigenvector problem”.

Determining the dimension d of the central space is a challenging problem for SDR, especially for HDLSS cases. If we want to discern signals (i.e., the true directions) from noises (i.e., the other directions) simply via the eigenvalues $\widehat{{\lambda }_i}$ of ${\widehat{\Lambda }}_H$, i = 1,…, H, we face the problem that all these $\widehat{{\lambda }_i}$‘s are of order p/n, but the gap between the signals and noises is of order λ (≤ C_max). With the Lasso-SIR, we can bypass this difficulty by using the adjusted eigenvalues ${\widehat{\lambda }}_i^a={\widehat{\lambda }}_i\Vert {\widehat{\mathit{\beta }}}_i{\Vert }_2$, i = 1,…, H. To this end, we have the following theorem.

Theorem 3. Let ${\widehat{\mathit{\beta }}}_i$ be the output of Algorithm 4 for i = 1,…, H. Assume that nλ = p^α for some α > ½, s log(p) = o(nλ), and H > d, then, for some constants C₁,C₂ C₃ and C₄,

$${\widehat{\lambda }}_i^a\ge C_1\sqrt{\lambda }-C_2\sqrt{\frac{s\text{log}(p)}{n}},\text{ for }1\le i\le d,\text{ and}$$

$${\widehat{\lambda }}_i^a\le C_3\frac{\sqrt{p\text{log}(p)}}{n\lambda }\sqrt{\lambda }+C_4\sqrt{\frac{s\text{log}(p)}{n},}\text{ for }d+1\le i\le H,$$

hold with probability at least 1 − C₅ exp(−C₆ log(p)) for some constants C₅ and C₆.

Theorem 3 states that, if s log(p) ∨ (plog(p))^½ = o(nλ), there is a clear gap between signals and noise. The Lasso-SIR algorithm then provides us the rate optimal estimation of the central space. It can be easily verified that p^½ dominants s log(p) if s < p^½ and s log(p) dominants p^½ if s > p^½. The region s² = o(p) and the region p = o(s²) are often referred to as the “highly sparse” and “moderately sparse” regions [Ingster et al., 2010], respectively. These two scenarios should be treated differently in high dimensional SIR and SDR frameworks, just like what has been done in high dimensional linear regression (Ingster et al. [2010]).

4. Simulation Studies

4.1. Single index models

Let β be the vector of coefficients and let $\mathcal{S}$ be the active set; namely, ${\beta }_i=0,\forall i\in {\mathcal{S}}^c$. Furthermore, for each $i\in \mathcal{S}$, we simulated independently β_i ~ N(0,1). Let x be the design matrix with each row following N(0, Σ). We consider two types of covariance matrices: (i) Σ = (σ_i,j) where σ_ii = 1 and σ_i,j = ρ^|i–j|; and (ii) σ_ii = 1, σ_i,j = ρ when i, $j\in \mathcal{S}$ or i, $j\in {\mathcal{S}}^c$, and σ_i,j = 0.1 when $i\in \mathcal{S}$, $j\in {\mathcal{S}}^c$ or vice versa. The first one represents a covariance matrix which is essentially sparse and we choose ρ among 0, 0.3, 0.5, and 0.8. The second one represents a dense covariance matrix with ρ chosen as 0.2. In all the simulations, we set n = 1, 000 and let p vary among 100, 1,000, 2,000, and 4,000. For all the settings, the random error ϵ follows N(0, I_n). For single index models, we consider the following model settings:

• I$\mathit{y}=\mathit{x}\mathit{\beta }+\mathit{ϵ}\text{ where }\mathcal{S}=\{1,2,\cdots ,10\};$.
• II$\mathit{y}={(\mathit{x}\mathit{\beta })}^3/2+\mathit{ϵ}\text{ where }\mathcal{S}=\{1,2,\cdots ,20\};$.
• III$\mathit{y}=\text{sin}(\mathit{x}\mathit{\beta })*\text{exp}(\mathit{x}\mathit{\beta })+\mathit{ϵ}\text{ where }\mathcal{S}=\{1,2,\cdots ,10\};$.
• IV$\mathit{y}=\text{exp}(\mathit{x}\mathit{\beta }/10)+\mathit{ϵ}\text{ where }\mathcal{S}=\{1,2,\cdots ,50\};$.
• V$\mathit{y}=\text{exp}(\mathit{x}\mathit{\beta }+\mathit{ϵ})\text{ where }\mathcal{S}=\{1,2,\cdots ,7\}.$.

The goal is to estimate col(β), the space spanned by β. As in Lin et al. [2015], the estimation error is defined as $\mathcal{D}(\widehat{col(\mathit{\beta })}$, col(β)), where $\mathcal{D}(M,N)$, the distance between two subspaces M, $N\subset {\mathcal{R}}^p$, is defined as the Frobenius norm of P_M − P_N where P_M and P_N are the projection matrices associated with these two spaces. The methods we compared with are DT-SIR, matrix Lasso (M-Lasso), and Lasso. The number of slices H is chosen as 20 in all simulation studies. The number of directions d is chosen according to Algorithm 5. Note that both benchmarks (i.e., DT-SIR and M-Lasso) require the knowledge of d as well. To be fair, we use the $\widehat{d}$ estimated based on Algorithm 5 for both benchmarks. For comparison, we have also included the estimation error of Lasso-SIR assuming d is known. For each p, n, and ρ, we replicate the above steps 100 times to calculate the average estimation error for each setting. We tabulated the results for the first type of covariance matrix with ρ = 0.5 in Table 1 and put the results for other settings in Tables 4–7 in the online supplementary file. The average of estimated directions $\widehat{d}$ is reported in the last column of these tables.

Table 1:

Estimation error for the first type covariance matrix with ρ = 0.5.

	p	Lasso-SIR	DT-SIR	Lasso	M-Lasso	Lasso-SIR(Known d)	$\widehat{d}$
I	100	0.12 ( 0.02 )	0.47 ( 0.11 )	0.11 ( 0.02 )	0.19 ( 0.08 )	0.12 ( 0.02 )	1
	1000	0.18 ( 0.02 )	0.65 ( 0.14 )	0.15 ( 0.02 )	0.26 ( 0.02 )	0.18 ( 0.02 )	1
	2000	0.2 ( 0.02 )	0.74 ( 0.15 )	0.16 ( 0.02 )	0.3 ( 0.03 )	0.2 ( 0.02 )	1
	4000	0.23 ( 0.09 )	0.9 ( 0.17 )	0.18 ( 0.01 )	0.39 ( 0.09 )	0.23 ( 0.03 )	1
II	100	0.07 ( 0.01 )	0.6 ( 0.1 )	0.23 ( 0.03 )	0.27 ( 0.31 )	0.07 ( 0.01 )	1
	1000	0.12 ( 0.02 )	0.78 ( 0.11 )	0.31 ( 0.04 )	0.17 ( 0.02 )	0.12 ( 0.02 )	1
	2000	0.15 ( 0.02 )	0.86 ( 0.13 )	0.34 ( 0.05 )	0.2 ( 0.03 )	0.15 ( 0.02 )	1
	4000	0.2 ( 0.04 )	0.99 ( 0.15 )	0.37 ( 0.05 )	0.28 ( 0.06 )	0.19 ( 0.03 )	1
III	100	0.21 ( 0.03 )	0.55 ( 0.12 )	1.25 ( 0.19 )	0.26 ( 0.11 )	0.21 ( 0.03 )	1
	1000	0.28 ( 0.04 )	0.74 ( 0.14 )	1.32 ( 0.18 )	0.51 ( 0.04 )	0.27 ( 0.04 )	1
	2000	0.35 ( 0.17 )	0.87 ( 0.17 )	1.34 ( 0.14 )	0.66 ( 0.14 )	0.31 ( 0.05 )	1.1
	4000	0.46 ( 0.28 )	1 ( 0.25 )	1.33 ( 0.16 )	0.83 ( 0.22 )	0.39 ( 0.1 )	1.1
IV	100	0.46 ( 0.05 )	0.92 ( 0.09 )	0.78 ( 0.12 )	0.58 ( 0.06 )	0.45 ( 0.04 )	1
	1000	0.62 ( 0.22 )	1.07 ( 0.18 )	0.87 ( 0.11 )	0.78 ( 0.22 )	0.59 ( 0.04 )	1.1
	2000	0.71 ( 0.34 )	1.22 ( 0.26 )	0.89 ( 0.12 )	0.94 ( 0.31 )	0.59 ( 0.04 )	1.3
	4000	0.71 ( 0.26 )	1.3 ( 0.18 )	0.91 ( 0.13 )	1 ( 0.22 )	0.63 ( 0.04 )	1.2
V	100	0.12 ( 0.02 )	0.37 ( 0.1 )	0.42 ( 0.18 )	0.15 ( 0.02 )	0.12 ( 0.02 )	1
	1000	0.2 ( 0.03 )	0.55 ( 0.15 )	0.55 ( 0.22 )	0.41 ( 0.05 )	0.2 ( 0.05 )	1
	2000	0.38 ( 0.34 )	0.8 ( 0.29 )	0.6 ( 0.24 )	0.67 ( 0.27 )	0.29 ( 0.18 )	1.2
	4000	0.78 ( 0.51 )	1.22 ( 0.31 )	0.77 ( 0.25 )	1.06 ( 0.41 )	0.48 ( 0.31 )	1.5

The simulation results in Table 1 show that Lasso-SIR outperformed both DT-SIR and M-Lasso under all settings. The performance of DT-SIR has become worse when the dependence is stronger and denser. The reason is that this method is based on the diagonal threshold and is only supposed to work well for the diagonal covariance matrix. Overall, Algorithm 5 provided a reasonable estimate of d especially for moderate covariance matrix. When assuming d is known, the performances of both DT-SIR and M-Lasso are inferior to Lasso-SIR, and are thus not reported.

Under Setting I when the true model is linear, Lasso performed the best among all the methods, as expected. However, the difference between Lasso and Lasso-SIR is not significant, implying that Lasso-SIR does not sacrifice much efficiency without the knowledge of the underlying linearity. On the other hand, when the models are not linear (Case II-VI), Lasso-SIR worked much better than Lasso. We observed that Lasso performed better than Lasso-SIR for Setting V when ρ=0.8 (Supplemental Materials) or when the covariance matrix is dense. One explanation is that Lasso-SIR tends to overestimate d under these conditions while Lasso used the actual d. If assuming known d = 1, Lasso-SIR’s estimation error is smaller than that of Lasso.

The results, reported in the supplementary material, for the other values of ρ are similar to what we observed when ρ = 0.5. The Lasso-SIR performed the best when compared to its competitors.

4.2. Multiple index models

Let β be the p × 2 matrix of coefficients and $\mathcal{S}$ be the active set. Let x be simulated similarly as in Section 4.1, and denote z = xβ. Consider the following settings:

• VI$y_i={\left|z_{i2}/4+2\right|}^3*sgn\left(z_{i1}\right)+{ϵ}_i\text{ where }\mathcal{S}=\left\{1,2,\cdots ,7\right\}\text{ and }{\beta }_{1:4,1}=1,{\beta }_{5:7,2}=1,\text{ and\hspace{0.17em}}{\beta }_{i,j}=0\text{ otherwise;}$
• VII$y_i=z_{i1}*exp\left(z_{i2}\right)+{ϵ}_i\text{ where }\mathcal{S}=\left\{1,2,\cdots ,12\right\}\text{ and }{\beta }_{1:7,1},{\beta }_{8:12,2}~N(0,1),\text{ and }{\beta }_{i,j}=0\text{\hspace{0.17em}otherwise;}$
• VIII$y_i=z_{i1}*exp\left(z_{i2}+{ϵ}_i\right)\text{ where }\mathcal{S}=\left\{1,2,\cdots ,12\right\}\text{ and }{\beta }_{1:7,1},{\beta }_{8:12,2}~N(0,1),\text{ and }{\beta }_{i,j}=0\text{\hspace{0.17em}otherwise;}$
• IX$y_i=z_{i1}*{\left(2+z_{i2}/3\right)}^2+{ϵ}_i\text{ where }\mathcal{S}=\left\{1,2,\cdots ,12\right\}\text{ and }{\beta }_{1:8,1}=1,{\beta }_{9:12,2}=1\text{ and }{\beta }_{i,j}=0\text{\hspace{0.17em}otherwise.}$

For the multiple index models, we compared both benchmarks (DT-SIR and M-Lasso) with Lasso-SIR. Lasso is not applicable for these cases and is thus not included. Similar to Section 4.1, we tabulated the results for the first type covariance matrix with ρ = 0.5 in Table 2 and put the results for others in Tables 8–11 in the online supplementary file.

Table 2:

Estimation error for the first type covariance matrix with ρ = 0.5.

	p	Lasso-SIR	DT-SIR	M-Lasso	Lasso-SIR (Known d)	$\widehat{d}$
VI	100	0.26 ( 0.06 )	0.57 ( 0.15 )	0.31 ( 0.05 )	0.26 ( 0.05 )	2
	1000	0.33 ( 0.07 )	0.74 ( 0.17 )	0.62 ( 0.04 )	0.33 ( 0.07 )	2
	2000	0.36 ( 0.11 )	0.92 ( 0.18 )	0.73 ( 0.07 )	0.38 ( 0.08 )	2
	4000	0.44 ( 0.14 )	1.12 ( 0.25 )	0.87 ( 0.1 )	0.42 ( 0.09 )	2
VII	100	0.32 ( 0.04 )	0.67 ( 0.11 )	0.42 ( 0.04 )	0.32 ( 0.04 )	2
	1000	0.6 ( 0.28 )	0.93 ( 0.22 )	1.02 ( 0.2 )	0.66 ( 0.3 )	2.1
	2000	0.95 ( 0.44 )	1.18 ( 0.27)	1.35 ( 0.32 )	0.83 ( 0.35 )	2.3
	4000	1.17 ( 0.38 )	1.43 ( 0.31 )	1.47 ( 0.33 )	1.08 ( 0.33 )	2.1
VIII	100	0.29 ( 0.09 )	0.61 ( 0.11 )	0.34 ( 0.08 )	0.25 ( 0.03 )	2
	1000	0.37 ( 0.08 )	0.82 ( 0.14 )	0.69 ( 0.13 )	0.35 ( 0.07 )	2
	2000	0.54 ( 0.35 )	1 ( 0.25 )	0.92 ( 0.28 )	0.47 ( 0.22 )	2.2
	4000	0.88 ( 0.45 )	1.37 ( 0.26 )	1.27 ( 0.31 )	0.71 ( 0.37 )	2.5
IX	100	0.43 ( 0.06 )	0.74 ( 0.12 )	0.48 ( 0.05 )	0.43 ( 0.07 )	2
	1000	0.47 ( 0.09 )	0.91 ( 0.15 )	0.91 ( 0.05 )	0.48 ( 0.09 )	2
	2000	0.58 ( 0.23 )	1.11 ( 0.23 )	1.12 ( 0.16 )	0.5 ( 0.1 )	2.1
	4000	0.57 ( 0.18 )	1.25 ( 0.22 )	1.23 ( 0.1 )	0.56 ( 0.11 )	2

For the identity covariance matrix (ρ = 0), there was little difference between performances of Lasso-SIR and DT-SIR. However, Lasso-SIR was substantially better than DT-SIR in other cases. Under all settings, Lasso-SIR worked much better than the matrix Lasso. For the dense covariance matrix Σ₂, Algorithm 5 tended to underestimate d, which is worthy of further investigation.

The results, reported in the supplementary material, for the other values of ρ are similar to what we observed when ρ = 0.5. The Lasso-SIR performs the best when compared to its competitors.

There are other sparse inverse regression method, such as the Sparse SIR, given in Li and Nachtsheim [2006]. In Lin et al. [2015], we have shown that the DT-SIR outperforms this method. We thus did not include the numerical comparison. For the reason of completeness, we have included the numerical results of comparing Lasso-SIR and Sparse SIR in Section D of the online supplementary file, showing that Lasso-SIR is better than Sparse-SIR.

4.3. Discrete responses

We consider the following simulation settings where for the response variable Y is discrete.

1. $\mathit{y}=1(\mathit{x}\mathit{\beta }+\mathit{ϵ}>0)\text{ where }\mathcal{S}=\left\{1,2,\cdots ,10\right\};$

2. $\mathit{y}=1(exp(\mathit{x}\mathit{\beta })+ϵ>0)\text{ where }\mathcal{S}=\left\{1,2,\cdots ,7\right\};$

3. $\mathit{y}=1\left({(\mathit{x}\mathit{\beta })}^3/2+ϵ\right)\text{ where }\mathcal{S}=\left\{1,2,\cdots ,20\right\};$

4. Let z = xβ where $\mathcal{S}=\left\{1,2,\cdots ,12\right\}$, β is a p by 2 matrix with β_1:7,1, β _8:12,2 ~ N(0,1) and β_i,j = 0 otherwise. The response y_i is

   $$y_i=\{\begin{array}{ll}1,\hfill & \text{ if }{z}_{i1}+{ϵ}_{i1}<0,\hfill \\ 2,\hfill & \text{ if }{z}_{i1}+{ϵ}_{i1}>0\text{ and }{z}_{i2}+{ϵ}_{i2}<0,\hfill \\ 3,\hfill & \text{ if }{z}_{i1}+{ϵ}_{i1}>0\text{ and }{z}_{i2}+{ϵ}_{i2}>0,\hfill \end{array}$$

   where ϵ_i,j ~ N(0,1).

In settings X, XI, and XII, the response variable is dichotomous, and β_i ~ N(0,1) when $i\in \mathcal{S}$ and β_i = 0 otherwise. Thus the number of slices H can only be 2. For Setting XIII where the response variable is trichotomous, the number of slices H is chosen as 3. The number of direction d is chosen as H − 1 in all these simulations.

Similar to the previous two sections, we calculated the average estimation errors for Lasso-SIR (Algorithm 4), DT-SIR, M-Lasso, and generalized-Lasso based on 100 replications and reported the result in Table 3 for the first type covariance matrix with ρ = 0. 5 and the results for other cases in Tables 12–15 in online supplementary file. It is clearly seen that Lasso-SIR performed much better than DT-SIR and M-Lasso under all settings and the improvements were very significant. The generalized Lasso performed as good as Lasso-SIR for the dichotomous response; however, it performed substantially worse for Setting XIII.

Table 3:

Estimation error for the first type covariance matrix with ρ = 0.5.

	p	Lasso-SIR	DT-SIR	M-Lasso	Lasso
X	100	0.22 ( 0.03 )	0.66 ( 0.05 )	0.26 ( 0.03 )	0.2 ( 0.03 )
	1000	0.26 ( 0.04 )	1.21 ( 0.03 )	0.52 ( 0.03 )	0.28 ( 0.03 )
	2000	0.27 ( 0.03 )	1.33 ( 0.02 )	0.59 ( 0.02 )	0.29 ( 0.04 )
	4000	0.28 ( 0.04 )	1.39 ( 0.02 )	0.65 ( 0.03 )	0.3 ( 0.04 )
XI	100	0.32 ( 0.07 )	0.83 ( 0.07 )	0.6 ( 0.17 )	0.33 ( 0.07 )
	1000	0.43 ( 0.1 )	1.32 ( 0.02 )	1.07 ( 0.05 )	0.45 ( 0.09 )
	2000	0.45 ( 0.09 )	1.38 ( 0.01 )	1.15 ( 0.04 )	0.46 ( 0.09 )
	4000	0.49 ( 0.12 )	1.41 ( 0.01 )	1.2 ( 0.05 )	0.51 ( 0.12 )
XII	100	0.24 ( 0.03 )	0.63 ( 0.05 )	0.52 ( 0.35 )	0.22 ( 0.03 )
	1000	0.33 ( 0.03 )	1.18 ( 0.04 )	0.53 ( 0.03 )	0.32 ( 0.03 )
	2000	0.37 ( 0.05 )	1.3 ( 0.04 )	0.62 ( 0.03 )	0.35 ( 0.03 )
	4000	0.4 ( 0.04 )	1.38 ( 0.03 )	0.68 ( 0.03 )	0.39 ( 0.04 )
XIII	100	0.38 ( 0.06 )	1.09 ( 0.06 )	0.61 ( 0.05 )	1.07 ( 0.02 )
	1000	0.39 ( 0.07 )	1.79 ( 0.02 )	1.12 ( 0.05 )	1.08 ( 0.02 )
	2000	0.38 ( 0.07 )	1.91 ( 0.02 )	1.24 ( 0.04 )	1.09 ( 0.03 )
	4000	0.42 ( 0.07 )	1.98 ( 0.01 )	1.32 ( 0.03 )	1.1 ( 0.03 )

5. Applications to Real Data

Arcene Data Set.

We first apply the methods to a two-class classification problem, which aims to distinguish between cancer patients and normal subjects from using their mass-spectrometric measurements. The data were obtained by the National Cancer Institute (NCI) and the Eastern Virginia Medical School (EVMS) using the SELDI technique, including samples from 44 patients with ovarian and prostate cancers and 56 normal controls. The dataset was downloaded from the UCI machine learning repository (Lichman [2013]), where a detailed description can be found. It has also been used in the NIPS 2003 feature selection challenge (Guyon et al. [2004]). For each subject, there are 10,000 features where 7,000 of them are real variables and 3,000 of them are random probes. There are 100 subjects in the validation set.

After standardizing X, we estimated the number of directions d as 1 using Algorithm 5. We then applied Algorithm 3 and the sparse PCA to calculate the direction of β and the corresponding components, followed by a logistic regression model. We applied the fitted model to the validation set and calculated the probability of each subject being a cancer patient. We also fitted a Lasso logistic regression model to the training set and applied it to the validation set to calculate the corresponding probabilities.

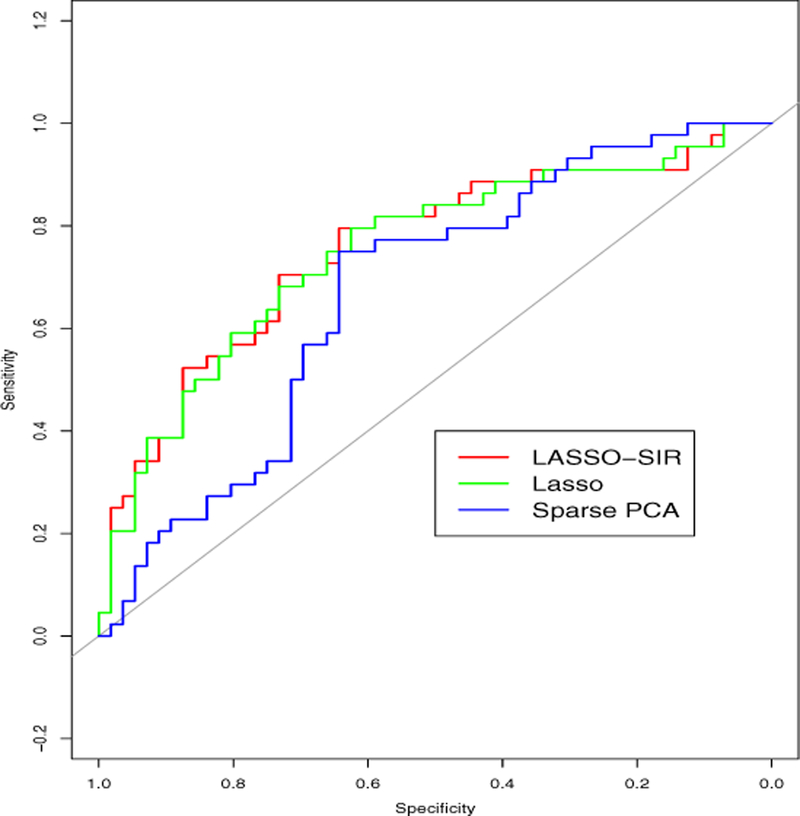
In Figure 1, we plot the Receiver Operating Characteristic (ROC) curves for various methods. Lasso-SIR, represented by the red curve, was slightly better than Lasso (insignificant) and the sparse PCA, represented by the green and blue curves respectively. The areas under these three curves are 0.754, 0.742, and 0.671, respectively.

Figure 1:

ROC curve of various methods for Arcene Data set.

HapMap.

In this section, we analyzed a data set with a continuous response. We consider the gene expression data from 45 Japanese and 45 Chinese from the international “HapMap” project (Thorisson et al. [2005],Thorgeirsson et al. [2010]). The total number of probes is 47,293. According toThorgeirsson et al. [2010], the gene CHRNA6 is the subject of many nicotine addiction studies. Similar toFan et al. [2015], we treat the mRNA expression of CHRNA6 as the response Y and expressions of other genes as the covariates. Consequently, the number of dimension p is 47,292, much greater than the number of subjects n=90.

We first applied Lasso-SIR to the data set with d being chosen as 1 according to Algorithm 5. The number of selected variables was 13. Based on the estimated coefficients β and X, we calculated the first component and the scatter plot between the response Y and this component, showing a moderate linear relationship between them. We then fitted a linear regression between them. The R-sq of this model is 0.5596 and the mean squared error of the fitted model 0.045.

We also applied Lasso to estimate the direction β. The tuning parameter λ is chosen as 0.1215 such that the number of selected variables is also 13. When fitting a regression model between Y and the component based on the estimated β, the R-sq is 0.5782 and the mean squared error is 0.044. There is no significant difference between these two approaches. This confirms the message that Lasso-SIR performs as good as Lasso when the linearity assumption is appropriate.

We have also calculated a direction and the corresponding components based on the sparse PCA [Zou et al., 2006]. We then fitted a regression model. The R-sq is only 0.1013 and the mean squared error is 0.093, significantly worse than the above two approaches.

Classify Wine Cultivars.

We investigate the popular wine data set which has been used to compare various classification methods. This is a three-class classification problem. The data, available from the UCI machine learning repository (Lichman [2013]), consists of 178 wines grown in the same region in Italy under three different cultivars. For each wine, the chemical analysis was conducted and the quantities of 13 constituents are obtained, which are Alcohol, Malic acid, Ash, Alkalinity of ash, Magnesium, Total Phenols, Flavanoids, Non-flavanoid Phenols, Proanthocyanins, Color intensity, Hue, OD280/OD315 of diluted wines, and Proline. One of the goals is to use these 13 features to classify the cultivar.

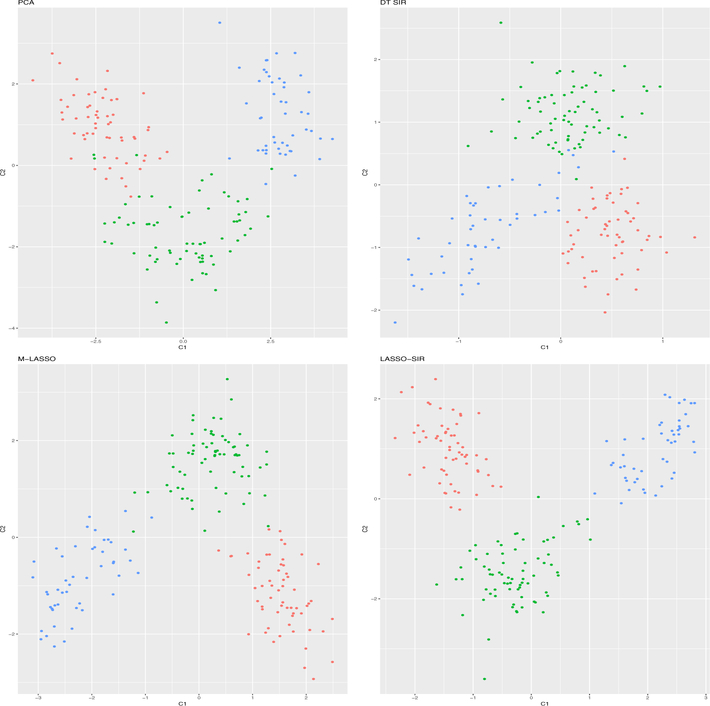
The number of directions d is chosen as 2 according to Algorithm 5. We tested PCA, DT-SIR, M-Lasso, and Lasso-SIR, for obtaining these two directions. In Figure 2, we plotted the projection of the data onto the space spanned by two components. The colors of the points correspond to three different cultivars. It is clearly seen that Lasso-SIR provided the best separation of the three cultivars. When using one vertical and one horizontal line to classify three groups, only one subject would be wrongly classified.

Figure 2:

We plotted the second component versus the first component for all the wines, which are labeled with different colors, representing different cultivars (1–red, 2–green, 3–blue). The four methods for calculating the directions are PCA, DT-SIR, M-Lasso, and Lasso-SIR from top-left to bottom-right. It is clearly seen that Lasso-SIR offered the best separation among these three groups.

6. Discussion

Researchers have made some attempts to extend Lasso to non-linear regression models in recent years (e.g.,Plan and Vershynin [2016], Neykov et al. [2016b]). However, these approaches are not efficient enough for SDR problems. In comparison, Lasso-SIR introduced in this article is an efficient high-dimensional variant of SIR [Li, 1991] for obtaining a sparse solution to the estimation of the SDR subspace for multiple index models. We showed that Lasso-SIR is rate optimal if nλ = p^α for some α > 1/2, where λ is the smallest nonzero eigenvalue of $var(\mathbb{E}[x|y])$. This technical assumption on n, λ, and p is slightly disappointing from the ultra-high dimensional perspective. We believe that this technical assumption arises from an intrinsic limitation in estimating the central subspace, i.e., some further sparsity assumptions on either Σ or $var(\mathbb{E}[x|y])$ or both are needed to show the consistency of any estimation method. We will address such extensions in our future researches.

Cautious reader may find that the concept of “pseudo-response variablee is not essential for developing the theory of the Lasso-SIR algorithm. However, by re-formulating the SIR method as a linear regression problem using the pseudo-response variable, we can formally consider the model selection consistency, regularization path and many others for multiple index models. In other words, the Lasso-SIR does not only provide an efficient high dimensional variant of SIR, but also extends the rich theory developed for Lasso linear regression in the past decades to the semi-parametric index models.

The R-package, LassoSIR, is available on CRAN (https://cran.r-project.org/package=LassoSIR).

A Appendix: Sketch of Proofs of Theorems 1, 2 and 3

We assume the condition A1) A2) and A3) hold throughout of the rest of the paper. In particular, the sliced stability condition A3) requires that H > d is a large enough but finite integer. We denote the SIR estimate of $\mathbf{\Lambda }=var(\mathbb{E}[x|y])$ by ${\widehat{\mathbf{\Lambda }}}_H=\frac{1}{H}{X}_H{X}_H^{\tau }$ (see e.g., (2)) and its eigenvector of unit length associated to the j-th eigenvalue ${\widehat{\lambda }}_j$ by ${\widehat{\mathit{\eta }}}_j$. To avoid unnecessary confusion, we assume that $\frac{s\text{log}(p)}{n\lambda }$ and $\frac{\sqrt{p}}{n\lambda }$ are sufficiently small. We call an event Ω happens with high probability if $\mathbb{P}\left({\Omega }^c\right)\le C_1\text{exp}\left(-C_2\text{log}(p)\right)$ for some absolute constants C₁ and C₂.

A.1. Assistant Lemmas

A.1.1. Concentration Inequalities

Lemma 1. Let d₁, …, d_p be positive constants. We have the following statements:

1. For p i.i.d. standard normal random variables x₁, …, x_p, there exist constants C₁ and C₂ such that for any sufficiently small a, we have

   $$\mathbb{P}\left(\left|\frac{1}{p}\sum _i{d}_i\left(x_i^2-1\right)\right|>a\right)\le C_1\text{ exp}\left(-\frac{p^2{a}^2}{C_2{\sum }_j{d}_j^4}\right).$$ (10)

2. For 2p i.i.d. standard normal random variables x_1;… ,x_p, y₁, ⋯ , and y_p, there exist constants C₁ and C₂ such that for any sufficiently small a , we have

$$\mathbb{P}\left(\left|\frac{1}{p}\sum _i{d}_i{x}_i{y}_i\right|>a\right)\le C_1\text{ exp}\left(-\frac{p^2{a}^2}{C_2{\sum }_j{d}_j^4}\right).$$ (11)

Proof. ii) is a direct corollary of i). We put the proof of i) in the supplementary materials.

A.1.2 Sine-Theta Theorem

Lemma 2 (Sine-Theta Theorem). Let A and A + E be symmetric matrices satisfying

$$\mathit{A}=\left[{\mathit{F}}_0,{\mathit{F}}_1\right]\left[\begin{array}{cc}{\mathit{A}}_0& 0\\ 0& {\mathit{A}}_1\end{array}\right]\left[\begin{array}{c}{\mathit{F}}_0^{\tau }\\ {\mathit{F}}_1^{\tau }\end{array}\right],\mathit{A}+\mathit{E}=\left[{\mathit{G}}_0,{\mathit{G}}_1\right]\left[\begin{array}{cc}{\mathbf{\Lambda }}_0& 0\\ 0& {\mathbf{\Lambda }}_1\end{array}\right]\left[\begin{array}{c}{\mathit{G}}_0^{\tau }\\ {\mathit{G}}_1^{\tau }\end{array}\right]$$

where [F₀, F₁] and [G₀, G₁] are orthogonal matrices. If the eigenvalues of A₀ are contained in an interval (a,b), and the eigenvalues of Λ₁ are excluded from the interval (a − δ, b + δ) for some δ > 0, then

$$\Vert {\mathit{F}}_0{\mathit{F}}_0^{\tau }-{\mathit{G}}_0{\mathit{G}}_0^{\tau }\Vert \le \frac{\text{min}\left(\Vert {\mathit{F}}_1^{\tau }\mathit{E}{\mathit{G}}_0\Vert ,\Vert {\mathit{F}}_0^{\tau }\mathit{E}{\mathit{G}}_1\Vert \right)}{\delta },$$

and

$$\frac{1}{\sqrt{2}}{\Vert F_0{F}_0^{\tau }-G_0{G}_0^{\tau }\Vert }_F\le \frac{\text{min}\left({\Vert F_1^{\tau }E{G}_0\Vert }_F,{\Vert F_0^{\tau }E{G}_1\Vert }_F\right)}{\delta }.$$

A.1.3. Restricted Eigenvalue Properties

We briefly review the restricted eigenvalue (RE) property, which was first introduced in Raskutti et al. [2010]. Given a set S ⊂ [p] = {1, …, p}, for any positive number α, define the set $\mathcal{C}(S,\alpha )$ as

$$\mathcal{C}(S,\alpha )=\left\{\theta \in {ℝ}^p|{\Vert {\theta }_{S^c}\Vert }_1\le \alpha {\Vert {\theta }_S\Vert }_1\right\}.$$

We say that a sample matrix XX^τ/n satisfies the restricted eigenvalue condition over S with parameter (α, κ) ϵ [1, ∞) × (0, ∞) if

$$\frac{1}{n}{\theta }^{\tau }X{X}^{\tau }\theta \ge {\kappa }^2\Vert \theta {\Vert }_2^2,\forall \theta \in \mathcal{C}(S,\alpha ).$$ (12)

If (12) holds uniformly for all the subsets S with cardinality s, we say that XX^τ/n satisfies the restricted eigenvalue condition of order s with parameter (α,κ). Similarly, we say that the covariance matrix Σ satisfies the RE condition over S with parameter (α, κ) if ∥Σ^½θ∥₂ ≥ κ∥θ∥ for all $\theta \in \mathcal{C}(S,\alpha )$. Additionally, if this condition holds uniformly for all the subsets S with cardinality s, we say that Σ satisfies the restricted eigenvalue condition of order s with parameter (α, κ). The following Corollary is borrowed from Raskutti et al. [2010].

Corollary 2. Suppose that Σ satisfies the RE condition of order s with parameter (α,κ). Let X be the p × n matrix formed by n i.i.d samples from N(0, Σ). For some universal positive constants a₁, a₂ and a_3; if the sample size satisfies

$$n>{\mathfrak{a}}_3\frac{{(1+\alpha )}^2{\text{max}}_{i\in [p]}{\Sigma }_{ii}}{{\kappa }^2}S\text{log}(p),$$

then the matrix $\frac{1}{n}X{X}^{\tau }$ satisfies the RE condition of order s with parameter $\left(\alpha ,\frac{\kappa }{8}\right)$ with probability at least 1 − a₁ exp (−a₂n).

It is clear that λ_min(Σ) ≥ C_min implies that Σ satisfies the RE condition of any order s with parameter $\left(3,\sqrt{C_{\text{min}}}\right)$. Thus, we have the following proposition.

Proposition 1. For some universal constants a₁, a₂ and a₃, if the sample size satisfies that n > a₁s log(p), then the matrix $\frac{1}{n}X{X}^{\tau }$ satisfies the RE condition for any order s with parameter $\left(3,\sqrt{C_{\text{min}}}/8\right)$ with probability at least 1 – a₂ exp (−a₃n).

A.1.4. The sliced approximation Lemma

Let $x\in {ℝ}^p$ be a sub-Gaussian random variable. For any unit vector $\beta \in {ℝ}^p$, let x(β) = 〈x, β〉 and $m(\beta )=\langle m,\beta \rangle =\mathbb{E}[x(\beta )|y]$. In order to get the deviation properties of the statistics var_H(x(β)), Lin et al. [2015] has introduced the sliced stable condition, i.e., the condition A3 in this paper. For the exact definition and more discussion, we refer to Lin et al. [2015].

Lemma 3. Let $x\in {ℝ}^p$ be a sub-Gaussian random variable. Assume that $\mathbb{E}[x|y]$ is sliced table with respect to y. For any unit vector $\beta \in {ℝ}^p$, let x(β) = 〈x, β〉 and $m(\beta )=\langle m,\beta \rangle =\mathbb{E}[x(\beta )|y]$, we have the following:

1. If var(m(β)) = 0, there exist positive constants C₁,C₂ and C₃ such that for any b and sufficiently large H, we have

   $$\mathbb{P}\left(va{r}_H(x(\beta ))>b\right)\le C_1\text{exp}\left(-C_2\frac{nb}{H^2}+C_3\text{log}(H)\right).$$
2. If var(m(β)) ≠ 0, there exist positive constants C₁,C₂ and C₃ such that, for any ν > 1, we have

   $$\left|va{r}_H(x(\beta ))-var(m(\beta ))\right|\ge \frac{1}{2\nu }var(m(\beta ))$$

   with probability at most

   $$C_1\text{exp}\left(-C_2\frac{nvar(m(\beta ))}{H^2{\nu }^2}+C_3\text{log}(H)\right).$$

   where we choose H such that H^ϑ > C₄ν for some sufficiently large constant C₄.

The following proposition is a direct corollary.

Proposition 2. There exist positive constants C₁,C₂ and C₃, such that

$${\Vert {\beta }^{\tau }{\Lambda }_H\beta -{\beta }^{\tau }var(\mathbb{E}[x|y])\beta \Vert }_2\ge \frac{1}{2\nu }{\beta }^{\tau }var(\mathbb{E}[x|y])\beta$$ (13)

with probability at most C₁ exp $\left(-C_2\frac{n\lambda }{H^2{\nu }^2}+C_3\text{log}(H)\right)$.

Proof. It follows from Lemma 3 and the fact that for any $\beta \in col(var(\mathbb{E}[x|y])),var(m(\beta )))\ge \lambda$. ◽

A.1.5. Properties of ${\widehat{\eta }}_j$ ‘s.

Proposition 3. Recall that ${\widehat{\mathit{\eta }}}_j$ is the eigenvector associated to the j-th eigenvalue of ${\widehat{\mathbf{\Lambda }}}_H,j=1,\dots ,H$. If nλ = p^a for some a > 1/2, there exist positive constants C₁ and C₂ such that

i) for j = 1, …, d, one has

$${\Vert P_{\Lambda }{\widehat{\mathit{\eta }}}_j\Vert }_2\ge C_1\sqrt{{\frac{\lambda }{\widehat{\lambda }}}_j}$$ (14)

ii) for j = d + 1, …, H, one has

$${\Vert P_{\Lambda }{\widehat{\mathit{\eta }}}_j\Vert }_2\le C_2\frac{\sqrt{p\text{ log}(p)}}{n\text{λ}}\sqrt{{\frac{\lambda }{\widehat{\lambda }}}_j}$$ (15)

hold with high probability.

Remark: This result might be of independent interest. In order to justify that the sparsity assumption for the high dimensional setting is necessary, Lin et al. [2015] have shown that for single index models, $\mathbb{E}\left[\angle \left({\eta }_1,{\widehat{\eta }}_1\right)\right]=0$ if and only if lim $\frac{p}{n}=0$. Proposition 3 states that the projection of $\sqrt{{\widehat{\lambda }}_j}{\widehat{\mathit{\eta }}}_j$, j = 1, …, d, onto the true direction is non-zero if nλ > p^a where a > 1/2.

Proof. Let x = z + w be the orthogonal decomposition with respect to $col(var(\mathbb{E}[x|y]))$ and its orthogonal complement. We define two p × H matrices Z_H = (z₁,,…, z_H,.) and W_H = (w₁,,…, w_H,) whose definition are similar to the definition of X_H. We then have the following decomposition

$${\mathit{X}}_H={\mathit{Z}}_H+{\mathit{W}}_H.$$ (16)

By definition, we know that ${\mathit{Z}}_H^{\tau }{W}_H=0$ and $y⫫\mathit{w}$. Let Σ₁ be the covariance matrix of w, then $W_H=\frac{1}{\sqrt{c}}{\Sigma }_1^{1/2}{E}_H$ where E_H is a p × H matrix with i.i.d. standard normal entries.

For sufficiently large ν₁ and a, Lemma 3 implies that

$${\Omega }_1=\left\{\omega |\left(1-\frac{\kappa }{2{\nu }_1}\right)\lambda \le {\lambda }_{\text{min}}\left(\frac{1}{H}{\mathit{Z}}_H^{\tau }{\mathit{Z}}_H\right)\le {\lambda }_{\text{max}}\left(\frac{1}{H}{\mathit{Z}}_H^{\tau }{\mathit{Z}}_H\right)\le \left(1+\frac{1}{2{\nu }_1}\right)\kappa \lambda \right\}$$ (17)

happens with high probability and Lemma 1 implies

$${\Omega }_2=\left\{\omega |{\Vert \frac{1}{H}{\mathit{W}}_H^{\tau }{\mathit{W}}_H-\frac{tr\left({\Sigma }_1\right)}{n}{\mathit{I}}_H\Vert }_F\le \mathfrak{a}\frac{\sqrt{p\text{ log}(p)}}{n}\right\}$$ (18)

happens with high probability.

For any ω ∈ Ω = Ω₁ ∩ Ω₂, we can choose a p × p orthogonal matrix T and an H × H orthogonal matrix S such that

$$\frac{1}{H}T{\mathit{Z}}_H(\omega )S=\left(\begin{array}{cc}{B}_1& 0\\ 0& 0\\ 0& 0\end{array}\right)\text{ and }\frac{1}{H}T{\mathit{W}}_H(\omega )S=\left(\begin{array}{cc}0& 0\\ B_2& B_3\\ 0& B_4\end{array}\right)$$ (19)

where B₁ is a d × d matrix, B₂ is a d × d matrix, B₃ is a d × (H − d) matrix and B₄ is a (p − 2d) × (H − d) matrix. By definition of the event ω, we have

$$\begin{gathered} \left(1-\frac{\kappa }{2{\nu }_1}\right)\lambda \le {\lambda }_{\text{min}}\left(B_1^{\tau }{B}_1\right)\le {\lambda }_{\text{max}}\left(B_1^{\tau }{B}_1\right)\le \left(1+\frac{1}{2{\nu }_1}\right)\kappa \lambda \\ {\Vert \left(\begin{array}{cc}{B}_2^{\tau }{B}_2& B_2^{\tau }{B}_3\\ B_3^{\tau }{B}_2& B_3^{\tau }{B}_3+B_4^{\tau }{B}_4\end{array}\right)-\frac{tr\left({\mathbf{\sum }}_1\right)}{n}{\mathit{I}}_H\Vert }_F\le \mathfrak{a}\frac{\sqrt{p\text{ log}(p)}}{n}. \end{gathered}$$ (20)

Proposition 3 follows from the linear algebraic lemma below:

Lemma 4. Assume that nλ = p^a for some a > ½. To avoid unnecessary confusion, we also assume that $\frac{\sqrt{p\text{ log}(p)}}{n\lambda }$ is sufficiently small. Let $M=\left(\begin{array}{cc}{B}_1& 0\\ B_2& B_3\\ 0& B_4\end{array}\right)$ be a p × H matrix, where B₁ is a d × d matrix, B₂ is a d × d matrix, B₃ is a d × (H − d) matrix and B₄ is a (p − 2d) × (H − d) matrix satisfying (20). Let ${\widehat{\mathit{\eta }}}_j$ be the eigenvector associated with the j-th eigenvalue ${\widehat{\lambda }}_j$ of MM^τ, j = 1, …, H. Then the length of the projection of ${\widehat{\mathit{\eta }}}_j$ onto its first d-coordinates is at least $C\sqrt{\frac{\lambda }{{\widehat{\lambda }}_j}}$ for j = 1, …, d and is most $C\frac{\sqrt{p\text{ log}(p)}}{n\lambda }\sqrt{\frac{\lambda }{{\widehat{\lambda }}_j}}$ for j = d +1, …, H.

Proof. Let us consider the eigen-decompositions of

$$Q_1\triangleq {\mathit{M}}^{\tau }\mathit{M}=\left(\begin{array}{cc}{\mathit{E}}_1& {\mathit{E}}_2\\ {\mathit{E}}_3& {\mathit{E}}_4\end{array}\right)\left(\begin{array}{cc}{\mathit{D}}_1& 0\\ 0& {\mathit{D}}_2\end{array}\right)\left(\begin{array}{cc}{\mathit{E}}_1^{\tau }& {\mathit{E}}_3^{\tau }\\ {\mathit{E}}_2^{\tau }& {\mathit{E}}_4^{\tau }\end{array}\right)$$

where D₁ (resp. D₂) is a d × d (resp. (H − d) × (H − d)) diagonal matrices satisfying that λ_min(D₁) ≥ λ_max(D₂). (20) implies that

$$\begin{gathered} \left(1-\frac{\kappa }{2{\nu }_1}\right)\lambda +\frac{tr\left({\mathbf{\sum }}_1\right)}{n}-\mathfrak{a}\frac{\sqrt{p\text{ log}(p)}}{n}\le {\lambda }_{\text{min}}\left(D_1\right) \\ \le {\lambda }_{\text{max}}\left(D_1\right)\le \left(1+\frac{1}{2{\nu }_1}\right)\kappa \lambda +\frac{tr\left({\mathbf{\sum }}_1\right)}{n}+\mathfrak{a}\frac{\sqrt{p\text{ log}(p)}}{n}. \end{gathered}$$

On the other hand, we could consider the eigen-decomposition of

$$Q_2\triangleq \left(\begin{array}{cc}{B}_1^{\tau }{B}_1+\frac{tr\left({\mathbf{\Sigma }}_1\right)}{n}{\mathit{I}}_d& 0\\ 0& \frac{tr\left({\mathbf{\Sigma }}_1\right)}{n}{\mathit{I}}_{H-d}\end{array}\right)=\left(\begin{array}{cc}{\mathit{F}}_1& 0\\ 0& {\mathit{F}}_2\end{array}\right)\left(\begin{array}{cc}{\mathit{D}}_1^{\prime }& 0\\ 0& {\mathit{D}}_2^{\prime }\end{array}\right)\left(\begin{array}{cc}{\mathit{F}}_1^{\tau }& 0\\ 0& {\mathit{F}}_2^{\tau }\end{array}\right)$$

where ${\mathit{D}}_1^{\prime }$ (resp. ${\mathit{D}}_2^{\prime }$) is a d × d (resp. (H − d) × (H − d)) diagonal matrices satisfying that ${\lambda }_{\text{min}}\left({\mathit{D}}_1^{\prime }\right)\ge {\lambda }_{\text{max}}\left({\mathit{D}}_2^{\prime }\right)$. (20) implies that

$$\frac{tr\left({\mathbf{\Sigma }}_1\right)}{n}-\mathfrak{a}\frac{\sqrt{p\text{log}(p)}}{n}\le {\text{λ}}_{\text{min}}\left({\mathit{D}}_2^{\prime }\right){\text{λ}}_{\text{max}}\left({\mathit{D}}_2^{\prime }\right)\le \frac{tr\left({\mathbf{\Sigma }}_1\right)}{n}+\mathfrak{a}\frac{\sqrt{p\text{log}(p)}}{n}.$$

Thus the eigen-gap is of order $\lambda -\mathfrak{a}\frac{\sqrt{p\text{log}(p)}}{n}$ (which is of order λ, since nλ = p^a for some α > 1/2). From (20), we know that ${\Vert Q_1-Q_2\Vert }_F\le C\frac{\sqrt{p\text{log}(p)}}{n}$. The Sine-Theta theorem (see e.g., Lemma 2) implies that

$${\Vert \left(\begin{array}{c}{\mathit{E}}_1\\ {\mathit{E}}_3\end{array}\right)\left(\begin{array}{cc}{\mathit{E}}_1^{\tau }& {\mathit{E}}_3^{\tau }\end{array}\right)-\left(\begin{array}{cc}{\mathit{I}}_d& 0\\ 0& 0\end{array}\right)\Vert }_F\le C\frac{\sqrt{p\text{log}(p)}}{n\text{λ}},$$ (21)

i.e., ${\Vert E_3{E}_3^{\tau }\Vert }_F\le C\frac{\sqrt{p\text{log}(p)}}{n\lambda }$. Similar argument gives us that ${\Vert E_2{E}_2^{\tau }\Vert }_F\le C\frac{\sqrt{p\text{log}(p)}}{n\lambda }$.

Let η be the (unit) eigenvector associated to the non-zero eigenvalue $\widehat{\lambda }$ of MM^τ. Let us write ${\eta }^{\tau }=\left({\eta }_1^{\tau },{\eta }_2^{\tau },{\eta }_3^{\tau }\right)$ where η₁, ${\eta }_2\in {ℝ}^d$ and ${\mathit{\eta }}_3\in {ℝ}^{p-2d}$. Let $\alpha =\left({\alpha }_1^{\tau },{\alpha }_2^{\tau }\right)$ where ${\alpha }_1=B_1^{\tau }{\eta }_1+B_2^{\tau }{\eta }_2\in {ℝ}^d$ and ${\alpha }_2=B_3^{\tau }{\eta }_2+B_4^{\tau }{\eta }_3\in {ℝ}^{H-d}$. It is easy to verify that $\alpha /\sqrt{\widehat{\lambda }}$ is the (unit) eigenvector associated to the eigenvalue $\widehat{\lambda }$ of M^τM and

$${\mathit{\eta }}_1=\frac{B_1}{\sqrt{\widehat{\lambda }}}\frac{{\alpha }_1}{\sqrt{\widehat{\lambda }}},{\mathit{\eta }}_2=\frac{B_2}{\sqrt{\widehat{\lambda }}}\frac{{\alpha }_1}{\sqrt{\widehat{\lambda }}}+\frac{B_3}{\sqrt{\widehat{\lambda }}}\frac{{\alpha }_2}{\sqrt{\widehat{\lambda }}},\text{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}}{\mathit{\eta }}_3=\frac{B_4}{\sqrt{\widehat{\lambda }}}\frac{{\alpha }_2}{\sqrt{\widehat{\lambda }}}.$$

If $\widehat{\lambda }$ is among the first d eigenvalues of M^τM, then ${\Vert {\alpha }_1/\sqrt{\widehat{\lambda }}\Vert }_2$ is bounded below by some positive constant. Thus ${\Vert {\mathit{\eta }}_1\Vert }_2\ge C\sqrt{\frac{\lambda }{\widehat{\lambda }}}$. If $\widehat{\lambda }$ is among the last H − d eigenvalues of M^τM, then ${\Vert {\alpha }_1/\sqrt{\widehat{\lambda }}\Vert }_2=O\left(\frac{\sqrt{p\text{log}(p)}}{n\lambda }\right)$. Thus ${\Vert {\mathit{\eta }}_1\Vert }_2\le O\left(\kappa \sqrt{\frac{\lambda }{\widehat{\lambda }}}\frac{\sqrt{p\text{log}(p)}}{n\lambda }\right)$. ◽

A.2. Sketch of Proof of Theorem 1

We only sketch some key points of the proof here and leave the details in the online supplementary files. Recall that for single index model $y=f\left({\beta }_0^{\tau }x,ϵ\right)$ where β₀ is a unit vector, we have denoted by $\widehat{\mathit{\eta }}$ the eigenvector of ${\widehat{\mathbf{\Lambda }}}_H$ associated to the largest eigenvalue $\widehat{\lambda }$. Let $\widehat{\mathit{\beta }}$ be the minimizer of

$${\mathcal{L}}_{\mathit{\beta }}=\frac{1}{2n}\Vert \tilde{\mathit{y}}-{\mathit{X}}^{\tau }\mathit{\beta }\Vert +\mu \Vert \mathit{\beta }{\Vert }_1,$$

where $\tilde{\mathit{y}}\in {ℝ}^n$ such that $\widehat{\mathit{\eta }}=\frac{1}{n}X\tilde{\mathit{y}}$. Let η₀ = Σβ₀, $\tilde{\eta }=P_{{\eta }_0}\widehat{\eta }$ and $\tilde{\mathit{\beta }}={\Sigma }^{-1}\tilde{\mathit{\eta }}\propto {\beta }_0$. Since we are interested in the distance between the directions of $\widehat{\mathit{\beta }}$ and β₀, we consider the difference $\mathit{\delta }=\widehat{\mathit{\beta }}-\tilde{\beta }$. A slight modification of the argument in Bickel et al. [2009] implies that, if we choose $\mu =C\sqrt{\frac{\text{log}(p)}{n\widehat{\lambda }}}$ for sufficiently large constant C, we have $\Vert \delta {\Vert }_2\le C_1\sqrt{\frac{s\text{ log}(p)}{n\widehat{\lambda }}}$ with high probability. The detailed arguments are put in the online supplementary file. The Proposition 3, Condition A1) and $\tilde{\beta }={\Sigma }^{-1}\tilde{\mathit{\eta }}$, imply that $C_1\sqrt{\frac{\lambda }{\widehat{\lambda }}}\le \Vert \tilde{\mathit{\beta }}{\Vert }_2\le C_2$ holds with high probability for some constants C₁ and C₂. Thus, we have

$${\Vert P_{\widehat{\mathit{\beta }}}-P_{{\mathit{\beta }}_0}\Vert }_F={\Vert P_{\widehat{\mathit{\beta }}}-P_{\tilde{\mathit{\beta }}}\Vert }_F\le 4\frac{\Vert \widehat{\mathit{\beta }}-\tilde{\mathit{\beta }}{\Vert }_2}{\Vert \tilde{\mathit{\beta }}{\Vert }_2}=4\Vert \mathit{\delta }{\Vert }_2/\Vert \tilde{\mathit{\beta }}{\Vert }_2\le C\sqrt{\frac{s\text{log}(p)}{n\lambda }}$$ (22)

holds with high probability. ◽

A.3. Proof of Theorem 2

Recall that ${\widehat{\mathit{\eta }}}_j$‘s are the (unit) eigenvectors associated to the j-th eigenvalues of ${\widehat{\mathbf{\Lambda }}}_H$, j = 1, …, d. We introduce the following notations,

$${\tilde{\mathit{\eta }}}_j=P_{\Lambda }{\widehat{\mathit{\eta }}}_j,{\tilde{\mathit{\beta }}}_j={\Sigma }^{-1}{\tilde{\mathit{\eta }}}_j\text{\hspace{1em} and }{\mathit{\gamma }}_j={\tilde{\mathit{\beta }}}_j/{\Vert {\tilde{\mathit{\beta }}}_j\Vert }_2.$$ (23)

Applying the argument in Theorem 1 on these eigenvectors, we have

$${\Vert {\widehat{\mathit{\beta }}}_j-{\widehat{\mathit{\beta }}}_j\Vert }_2\le C\sqrt{\frac{s\text{log}(p)}{n{\widehat{\lambda }}_j}}\text{ and }{\Vert P_{{\widehat{\mathit{\beta }}}_j}-P_{{\tilde{\mathit{\beta }}}_j}\Vert }_F\le C\sqrt{\frac{s\text{log}(p)}{n\lambda }}$$ (24)

for some constant C hold with high probability. Since we assume that d is fixed, if we can prove that

I) the lengths of ${\tilde{\mathit{\beta }}}_j$, j = 1, …, d, are bounded below by $C\sqrt{\frac{\lambda }{{\widehat{\lambda }}_j}}$

II) the angles between any two vectors of ${\tilde{\mathit{\beta }}}_j$, j = 1, …, d, are bounded below by some constant, hold with probability, then the Gram-Schmit process implies that ${\Vert P_{\widehat{B}}-P_B\Vert }_F\le C\sqrt{\frac{s\text{log}(p)}{n\lambda }}$ holds with high probability from (24). It is easy to verify that I) follows from the Proposition 3, the Condition A1) and the definition of ${\tilde{\mathit{\beta }}}_j\left(={\Sigma }^{-1}{\tilde{\mathit{\eta }}}_j\right)$, j = 1, …, d. II) is a direct corollary of the following two statements.

Statement A. The angles between any two vectors in ${\widehat{\mathit{\eta }}}_j$‘s, j = 1, …, d are nearly π/2. Since nλ = p^a for some a > 1/2, we only need to prove that

$$\left|\text{cos}\left(\angle \left({\tilde{\mathit{\eta }}}_j,{\tilde{\mathit{\eta }}}_j\right)\right)\right|\le C\frac{\sqrt{p\text{ log}(p)}}{n\text{λ}}$$ (25)

holds with high probability for any i ≠ j. Recall that we have the following decomposition X_H = Z_H + W_H. It is easy to see that $col\left({\mathit{Z}}_H\right)=col(var(\mathbb{E}[\mathit{x}|y]))$ and $\sqrt{n}cov{(w)}^{-1/2}{W}_H$ is identically distributed to a matrix, ε₁, with all the entries are i.i.d. standard normal random variables. Let us choose an orthogonal matrix T such that $\frac{1}{\sqrt{H}}T{\mathit{Z}}_H={\left({\mathit{A}}^{\tau },0\right)}^{\tau }$ and $\frac{1}{\sqrt{H}}T{\mathit{W}}_H={\left(0,{\mathit{B}}^{\tau }\right)}^{\tau }$ where A is a d × H matrix and B is a (p − d)× H matrix. Thus, $T{\widehat{\mathit{\eta }}}_j$ is the eigenvector of $\frac{1}{H}T{X}_H{X}_H^{\tau }{T}^{\tau }$ associated with the j-th eigenvalue ${\widehat{\lambda }}_j$, j = 1, …, d. If we have a) λ_min(AA^τ) ≥ λ, b) $\Vert P_{col\left(T{Z}_H\right)}\left(T{\widehat{\mathit{\eta }}}_j\right){\Vert }_2\ge C\sqrt{\frac{\lambda }{{\widehat{\lambda }}_j}}$ and c) $\Vert B^{\tau }B-\mu {\mathit{I}}_H{\Vert }_F\le C\frac{\sqrt{p\text{ log}(p)}}{n}$ for some scalar μ > 0, then the statement I is reduced to the following linear algebra lemma.

Lemma 5. Let A be a d × H matrix (d < H) with λ_min(AA^τ) = λ. Let B be a (p − d) × H matrix such that $\Vert B^{\tau }B-\mu I_H{\Vert }_F^2\le C\frac{\sqrt{p\text{log}(p)}}{n}$. Let ${\widehat{\mathit{\xi }}}_j$ be the j-th (unit) eigenvector of CC^τ associated with the j-th eigenvalue ${\widehat{\lambda }}_j$ where C^τ = (A^τ, B^τ) and ${\tilde{\mathit{\xi }}}_j$ be the projection of ${\widehat{\mathit{\xi }}}_j$ onto its first d-coordinates. If $\Vert {\tilde{\mathit{\xi }}}_j{\Vert }_2\ge C\sqrt{\frac{\lambda }{{\widehat{\lambda }}_j}}$, then for any i ≠ j,

$$\left|\text{cos}\left(\angle \left({\tilde{\mathit{\xi }}}_i,{\tilde{\mathit{\xi }}}_j\right)\right)\right|\le C\frac{\sqrt{p\text{log}(p)}}{n\text{λ}}.$$ (26)

Thus, ${\tilde{\mathit{\xi }}}_i$ ′s are nearly orthogonal if nλ = p^a for some a > ½.

Proof. Let ${\widehat{\mathit{\alpha }}}_j={\mathit{C}}^{\tau }{\widehat{\mathit{\xi }}}_j$, then ${\widehat{\mathit{\xi }}}_j=\frac{1}{{\widehat{\lambda }}_j}\mathit{C}{\mathit{\alpha }}_j$ and ${\widehat{\mathit{\xi }}}_j=\frac{1}{{\widehat{\lambda }}_j}\mathit{A}{\mathit{\alpha }}_j$. It is easy to see that $\Vert {\widehat{\mathit{\alpha }}}_j{\Vert }_2=\sqrt{{\widehat{\lambda }}_j}$ and $\Vert \mathit{C}{\widehat{\mathit{\alpha }}}_j{\Vert }_2\ge \sqrt{{\widehat{\lambda }}_j}$. Since ${\widehat{\mathit{\alpha }}}_j/\sqrt{{\widehat{\lambda }}_j}$ is also the (unit) eigenvector of

$${\mathit{C}}^{\tau }\mathit{C}={\mathit{A}}^{\tau }\mathit{A}+\mu \mathit{I}+\left({\mathit{B}}^{\tau }\mathit{B}-\mu \mathit{I}\right),$$

for any i ≠ j, we have

$$\begin{gathered} 0={\widehat{\mathit{\alpha }}}_j^{\tau }{\mathit{C}}^{\tau }\mathit{C}{\widehat{\mathit{\alpha }}}_i={\widehat{\mathit{\alpha }}}_j^{\tau }{\mathit{A}}^{\tau }\mathit{A}{\widehat{\mathit{\alpha }}}_j+\mu {\widehat{\mathit{\alpha }}}_j^{\tau }{\widehat{\mathit{\alpha }}}_i+{\widehat{\mathit{\alpha }}}_j^{\tau }\left({\mathit{B}}^{\tau }\mathit{B}-\mu \mathit{I}\right){\widehat{\mathit{\alpha }}}_{\mathit{I}} \\ ={\widehat{\lambda }}_j{\widehat{\lambda }}_{\mathit{I}}{\tilde{\mathit{\xi }}}_j^{\tau }{\tilde{\mathit{\xi }}}_{\mathit{I}}+{\widehat{\mathit{\alpha }}}_j^{\tau }\left({\mathit{B}}^{\tau }\mathit{B}-\mu \mathit{I}\right){\widehat{\mathit{\alpha }}}_{\mathit{I}}. \end{gathered}$$

Since $\Vert {\mathit{B}}^{\tau }\mathit{B}-tr(\Sigma ){\mathit{I}}_H{\Vert }_F\le C\frac{\sqrt{p\text{log}(p)}}{n}$ and $\Vert {\widehat{\mathit{\xi }}}_j{\Vert }_2\ge C\sqrt{\frac{\lambda }{{\widehat{\lambda }}_j}},\forall i\ne j$, we have

$$\left|\frac{{\xi }_j^{\tau }{\xi }_i}{{\Vert {\xi }_i\Vert }_2{\Vert {\xi }_j\Vert }_2}\right|\le C\left|{\widehat{\xi }}_j^{\tau }{\widehat{\xi }}_i\frac{{\widehat{\lambda }}_j^{1/2}{\widehat{\lambda }}_i^{1/2}}{\text{λ}}\right|=C\left|\frac{1}{\text{λ}}\frac{{\widehat{\mathit{\alpha }}}_j^{\tau }}{{\widehat{\lambda }}_j^{1/2}}\left({\mathit{B}}^{\tau }\mathit{B}-\mu \mathit{I}\right)\frac{{\widehat{\mathit{\alpha }}}_i}{{\widehat{\lambda }}_i^{1/2}}\right|\le C\frac{\sqrt{p\text{log}(p)}}{n\text{λ}}.$$

Note that a) follows from the Lemma 2, b) follows from Proposition 3 and c) follows from the Lemma 1. Thus statement A holds.

Statement B. The angles between any two vectors in ${\tilde{\mathit{\beta }}}_j$ ′s are bounded away from 0. Since ${\tilde{\mathit{\beta }}}_j={\Sigma }^{-1}{\tilde{\mathit{\eta }}}_j$, we only need to prove that there exists a positive constant ζ < 1 such that

$$\left|\frac{{\tilde{\mathit{\eta }}}_i^{\tau }{\Sigma }^{-1}{\Sigma }^{-1}{\tilde{\mathit{\eta }}}_i}{{\Vert {\Sigma }^{-1}{\tilde{\mathit{\eta }}}_i\Vert }_2{\Vert {\Sigma }^{-1}{\tilde{\mathit{\eta }}}_j\Vert }_2}\right|\le \zeta .$$ (27)

Let $\left({\tilde{\mathit{\eta }}}_1/\Vert {\tilde{\mathit{\eta }}}_1{\Vert }_2,\dots ,{\tilde{\mathit{\eta }}}_d/\Vert {\tilde{\mathit{\eta }}}_d{\Vert }_2\right)=\mathit{T}\mathit{M}$, where T is a p × d orthogonal matrix. Since ${\tilde{\mathit{\eta }}}_j/\Vert {\tilde{\mathit{\eta }}}_j{{\Vert }^{\prime }}_{2}s$ are nearly mutually orthogonal, we know that M^τM is nearly an identity matrix. Thus, by some continuity argument, the statement is reduced to the following linear algebra lemma.

Lemma 6. Let A be a p × p positive definite matrix such that C_min ≤ λ_min(A) ≤ λ_max (A) ≤ C_max for some positive constants C_min and C_max. There exists constant 0 < ζ < 1 such that for any p × d orthogonal matrix B, we have

$$\left|\frac{{\mathit{B}}_{*,i}^{\tau }{\mathit{A}}^{\tau }\mathit{A}{\mathit{B}}_{*,j}}{{\Vert \mathit{A}{\mathit{B}}_{*,i}\Vert }_2{\Vert \mathit{A}{\mathit{B}}_{*,j}\Vert }_2}\right|\le \zeta \forall i\ne j.$$ (28)

Proof. When d is finite, without loss of generality, we can assume that B is a p × 2 matrix. Note that the expression on the left side is invariant under orthogonal transformation of B. We can simply assume that B is a matrix with the last p – 2-rows consisting of all zeros. The result follows immediately based on basic calculation. ◽

A.4. Proof of Theorem 3

Recall that ${\widehat{\mathit{\eta }}}_i$ is the eigenvector associated with the i-th eigenvalue ${\widehat{\lambda }}_i$ of ${\widehat{\mathbf{\Lambda }}}_H$, ${\tilde{\mathit{\eta }}}_i=P_{\mathbf{\Lambda }}{\tilde{\mathit{\eta }}}_i$ and ${\tilde{\mathit{\beta }}}_i={\Sigma }^{-1}{\tilde{\mathit{\eta }}}_i$, i = 1, …, H (see e.g., (23)). The argument in Theorem 1 implies that, for any 1 ≤ i ≤ H,

$${\Vert {\widehat{\mathit{\beta }}}_i-{\widehat{\mathit{\beta }}}_i\Vert }_2\le C\sqrt{\frac{s\text{log}(p)}{n\widehat{\lambda }}}.$$ (29)

The Proposition 1 implies that

$${\Vert {\widehat{\mathit{\beta }}}_i\Vert }_2\ge C_1\sqrt{\frac{\text{λ}}{{\widehat{\lambda }}_i}},1\le i\le d\text{ and }{\Vert {\widehat{\mathit{\beta }}}_i\Vert }_2\le C_2\sqrt{\frac{\text{λ}}{{\widehat{\lambda }}_i}}\frac{\sqrt{p\text{ log}(p)}}{n\text{λ}},d+1\le i\le H.$$ (30)

The above two statements give us the desried result in Theorem 3. ◽