Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Oct 1.
Published in final edited form as: Drug Alcohol Depend. 2020 Aug 6;215:108208. doi: 10.1016/j.drugalcdep.2020.108208

Imprecise Action Selection in Substance Use Disorder: Evidence for Active Learning Impairments When Solving the Explore-Exploit Dilemma

Ryan Smith 1, Philipp Schwartenbeck 2, Jennifer L Stewart 1, Rayus Kuplicki 1, Hamed Ekhtiari 1; Tulsa 1000 Investigators†, Martin P Paulus 1
PMCID: PMC7502502  NIHMSID: NIHMS1619437  PMID: 32801113

Abstract

Background:

Substance use disorders (SUDs) are a major public health risk. However, mechanisms accounting for continued patterns of poor choices in the face of negative life consequences remain poorly understood.

Methods:

We use a computational (active inference) modeling approach, combined with multiple regression and hierarchical Bayesian group analyses, to examine how treatment-seeking individuals with one or more SUDs (alcohol, cannabis, sedatives, stimulants, hallucinogens, and/or opioids; N = 147) and healthy controls (HCs; N = 54) make choices to resolve uncertainty within a gambling task. A subset of SUDs (N = 49) and HCs (N = 51) propensity-matched on age, sex, and verbal IQ were also compared to replicate larger group findings.

Results:

Results indicate that: (a) SUDs show poorer task performance than HCs (p = .03, Cohen’s d = .33), with model estimates revealing less precise action selection mechanisms (p = .004, d = .43), a lower learning rate from losses (p = .02, d = .36), and a greater learning rate from gains (p = .04, d = .31); and (b) groups do not differ significantly in goal-directed information seeking.

Conclusions:

Findings suggest a pattern of inconsistent behavior in response to positive outcomes in SUDs combined with a tendency to attribute negative outcomes to chance. Specifically, individuals with SUDs fail to settle on a behavior strategy despite sufficient evidence of its success. These learning impairments could help account for difficulties in adjusting behavior and maintaining optimal decision making during and after treatment.

Keywords: Substance Use Disorders, Computational Modeling, Active Inference, Learning Rate, Explore-Exploit Dilemma, Directed Exploration

1. Introduction

Substance use disorders (SUDs) are a major public health risk. In the United States, lethal drug overdose is the leading cause of accidental deaths (Jones et al., 2013; Rudd et al., 2016). Risky behavior, and loss of career, relationships, and other sources of well-being in SUDs, is thought to derive in part from dysfunctional decision-making processes. Maladaptive decision-making has been associated with negative personal long-term outcomes in SUDs, including relapse (Passetti et al., 2008; Verdejo-Garcia et al., 2018). While evidence-based treatments are available, relapse rates are high, and patients often discontinue treatment (Connery, 2015; Hser et al., 2014). Consequently, it is crucial to better understand computational processes promoting maladaptive choices within SUDs to improve treatment retention/success and reduce relapse rates.

A growing behavioral literature suggests that SUDs show decision-making impairments associated with a number of factors, including a focus on short-term outcomes, poor choice flexibility, differential learning from rewards and punishments, and memory deficits. For example, opioid users are less likely to predict distal future events and more likely to continue selecting actions with short-term rewards but larger delayed punishments (implying impaired learning to avoid suboptimal choices; (Petry et al., 1998). When compared to healthy controls (HCs), opioid users also show reduced sensitivity to losses paired with greater responses to known risks (Ahn et al., 2014). Moreover, opioid users perform more poorly than HCs while learning to avoid punishment under high memory load (Myers et al., 2017) and higher ambiguity tolerance predicts prospective opioid use (Konova et al., 2019). Both opioid and stimulant (cocaine and/or amphetamine) users are less likely than HCs to stick to successful decision strategies and instead: (a) choose to switch responses even when a previous response has been rewarding (Myers et al., 2016); or (b) perseverate on responses independent of outcomes (Kanen et al., 2019). Similar difficulties in flexibly adjusting behavior following punishments have also been reported in other stimulant user samples ((Ersche et al., 2016; Ersche et al., 2011); but see (Kanen et al., 2019)). In contrast, stimulant users appear to exhibit heightened sensitivity to monetary reward (Ahn et al., 2014).

Individuals with multiple SUDs also show neuroimaging evidence of abnormalities during risky decision-making that appear consistent with behavioral evidence (Gowin et al., 2013). For example, a general blunting of neural responses in stimulant users has been observed across several brain regions (as well as consistent behavioral differences) in response to negative affective stimuli signaling threat and/or punishment (Hester et al., 2013; Stewart et al., 2014). These blunted responses could correspond to the reduced reflection on future outcomes and reduced sensitivity to action consequences observed behaviorally, and self-report measures also offer consistent evidence of lower sensitivity to punishment in stimulant users (as well as marijuana users; see (Simons and Arens, 2007; Simons et al., 2008)). Jointly, extant behavioral, neural, and self-report evidence thus suggests a pattern of reduced future thinking and a reduced ability to learn from negative outcomes in SUDs.

While these studies exemplify progress in identifying potentially meaningful differences, current understanding of several aspects of aberrant decision-making in SUDs remains incomplete. One area in which further investigation may be useful is how individuals with SUDs solve what is known as the explore/exploit dilemma, which has recently been highlighted as of potential importance in psychiatric disorders (Addicott et al., 2017; Linson et al., 2020). This dilemma arises in cases where decisions must first be taken to gather information about the environment, before exploiting knowledge of the environment to maximize reward. If an individual “over-exploits,” they will fail to learn better behavioral strategies (especially in a changing environment) – and subsequently develop strong habits for less adaptive choices. Over-exploration instead reflects an inefficient use of past experience to inform subsequent decision-making, and thus a suboptimal preference for information-seeking behavior. One factor determining the efficiency in using past experience is the rate at which individuals learn (i.e., update beliefs) about their environment after making a new observation. A higher learning rate will facilitate learning from negative and positive outcomes and induce a faster switch to exploitative behavior in a stable environment. One additional distinction concerns different explorative strategies. Specifically, individuals can simply act more randomly (“random exploration”) to sample the outcomes of different choices; or they can strategically seek out observations that are expected to provide the most useful information (“goal-directed exploration”; (Wilson et al., 2014)). Importantly, goal-directed exploration implies future-oriented cognition, in that behaviors are strategically chosen to gather information that would benefit future choices one will need to make.

There is a small, but emerging literature on explore/exploit dynamics in addiction. For example, nicotine smokers make fewer exploratory choices and evidence a higher learning rate (Addicott et al., 2012); moreover, more ingrained smoking habits are associated with greater cognitive effort when making exploratory choices (Addicott et al., 2014). Stimulant users make choices based primarily on recent outcomes (e.g., which could follow from an overly high learning rate (Harle et al., 2015)), while individuals with alcohol use disorders show fewer strategic exploratory decisions than HCs (Morris et al., 2016). This is consistent with current models of dopaminergic function suggesting that increases in dopamine promote (energetic) exploratory behavior, and that the chronic use of dopaminergic drugs reduces dopaminergic efficacy, therefore reducing exploration (Beeler et al., 2012). While informative, this body of work on addiction remains in its infancy, with only one or two studies for a given substance. Replication will be necessary, and it remains unclear whether effects are substance-specific or common across SUDs. Further, the distinction between directed and random exploration has not been thoroughly addressed. Reduced future thinking and learning from negative outcomes in SUDs both suggest reduced directed exploration, but this remains to be established.

Recent work in one area of computational neuroscience, active inference, has focused on how individuals make decisions to actively infer and learn about the structure of their environment, distinguishing different mechanisms that affect the explore/exploit trade-off (Schwartenbeck et al., 2019). These mechanisms include differences in random exploration, goal-directed exploration, separate learning rates for wins and losses, and sensitivity to information. Because this computational framework allows testing for differences in each of these separate mechanisms, we chose to employ this modeling approach to investigate potential differences in these computational mechanisms between HCs and SUDs when solving the explore/exploit dilemma – with the aim of better distinguishing the mechanisms that best account for sub-optimal exploratory behavior.

Participants from the Tulsa 1000 project (Victor et al., 2018), a prospective longitudinal cohort study of HCs and treatment-seeking individuals with substance, mood/anxiety, and eating disorders, completed a three-armed bandit task designed to assess explore/exploit behavior. The Tulsa 1000 has pre-specified exploratory and confirmatory subsamples; SUDs (N = 147) and HCs (N = 54) from the exploratory subsample were here extracted for analysis based on the presence versus absence of one or more SUD diagnoses (alcohol, cannabis, sedatives, stimulants, hallucinogens, and/or opioids). Based on the evidence for poor learning and future thinking in SUDs, we expected that, relative to HCs, SUDs would solve this dilemma sub-optimally and obtain less reward. Model-based analyses could disambiguate whether suboptimal performance in SUDs was due to greater random or directed exploration, greater learning rate for wins, lower learning rate for losses, and/or less sensitivity to new information – which could inform novel interventions more specifically targeting active learning strategies in SUDs. Between-group analyses were performed with all SUDs and HCs as well as subgroups propensity-matched on age, sex, and a measure of pre-morbid intelligence quotient (IQ) (SUDs: n = 49; HCs: n = 51). Based on prior work, we predicted that SUDs would exhibit lower directed exploration and lower learning rate for losses than HCs.

2. Methods

2.1. Participants

Participants were identified from the exploratory subsample (i.e., first 500 participants) of the Tulsa 1000 (T1000) (Victor et al., 2018), a prospective longitudinal cohort study recruiting subjects based on the dimensional NIMH Research Domain Criteria framework. The T1000 study included individuals 18–55 years old, screened on the basis of dimensional psychopathology scores: Patient Health Questionnaire (PHQ-9 (Kroenke et al., 2001)) ≥ 10, Overall Anxiety Severity and Impairment Scale (OASIS (Norman et al., 2006)) ≥ 8, and/or Drug Abuse Screening Test (DAST-10 (Bohn et al., 1991)) score > 3. HCs did not show elevated symptoms or psychiatric diagnoses. Participants were excluded if they: (a) tested positive for drugs of abuse via urine screen, (b) met criteria for psychotic, bipolar, or obsessive-compulsive disorders, or (c) reported history of moderate-to-severe traumatic brain injury, neurological disorders, severe or unstable medical conditions, active suicidal intent or plan, or change in medication dose within 6 weeks. Full inclusion/exclusion criteria are described in (Victor et al., 2018). The study was approved by the Western Institutional Review Board. All participants provided written informed consent prior to completion of the study protocol, in accordance with the Declaration of Helsinki, and were compensated for participation. clinicaltrials.gov identifier: #NCT02450240.

Participants were grouped based on DSM-IV or DSM-5 diagnosis using the Mini International Neuropsychiatric Inventory (MINI) (Sheehan et al., 1998). This analysis focuses on treatment-seeking individuals with SUDs (alcohol, cannabis, sedatives, stimulants, hallucinogens, and/or opioids) with or without comorbid depression and anxiety disorders (N = 147), and HCs with no mental health diagnoses (N = 54). Most SUDs were currently enrolled in a residential facility or maintenance outpatient program after completion of more intensive treatments (mean days abstinent = 92; SD = 56). Table 1 lists group demographics and symptom severity, whereas Table 2 lists diagnosis frequency within SUDs.

Table 1.

Descriptive Statistics (Means and Standard Deviations) for Demographic and Clinical Measures by Group

Full Sample HCs SUDs p
N= 54 147
Age 32.27 (11.35) 34.05 (9.17) 0.26
Sex (Male) 0.44 (0.50) 0.49 (0.50) 0.57
DAST 0.11 (0.37) 7.54 (2.22) <0.001
PHQ 0.80 (1.28) 6.58 (5.70) <0.001
OASIS 1.35 (1.94) 5.84 (4.63) <0.001
WRAT 63.53 (4.93) 58.47 (5.85) <0.001
Regular nicotine smoker* 8 (15%) 54 (37%) <0.001
Propensity Matched HCs SUDs p
N= 51 49
Age 32.35 (11.40) 32.25 (7.72) 0.96
Sex (Male) 0.45 (0.50) 0.55 (0.50) 0.32
DAST 0.12 (0.38) 7.57 (2.36) <0.001
PHQ 0.78 (1.30) 7.12 (5.19) <0.001
OASIS 1.31 (1.92) 6.98 (4.55) <0.001
WRAT 63.53 (4.93) 61.76 (5.06) 0.08
Regular nicotine smoker* 8 (16%) 18 (37%) <0.001
Open in a new tab
*

defined as >3650 lifetime cigarettes. DAST = Drug Abuse Screening Test. PHQ = Patient Health Questionnaire. OASIS = Overall Anxiety Severity and Impairment Scale. WRAT = Wide Range Achievement Test.

Table 2.

Lifetime DSM-IV/DSM-5 psychiatric disorders within SUDs

SUDs (n = 147) Propensity-Matched SUDs (n = 49)
Substance Use Disorders
Alcohol 56 (38%) 21 (43%)
Cannabis 58 (39%) 20 (41%)
Stimulants 105 (71%) 36 (73%)
Opioids 56 (38%) 25 (51%)
Sedatives 38 (26%) 14 (29%)
Hallucinogens 5 (3%) 2 (4%)
2+ Disorders 94 (64%) 34 (69%)
Alcohol Only 10 (7%) 4 (8%)
Cannabis Only 12 (8%) 7 (14%)
Stimulants Only 26 (18%) 7 (14%)
Opioids Only 8 (5%) 2 (4%)
Sedatives Only 0 (0%) 0 (0%)
Mood, Anxiety, Stress Disorders
Major Depressive 78 (53%) 30 (61%)
Generalized Anxiety 22 (15%) 9 (18%)
Social Anxiety 19 (13%) 8 (16%)
Panic 17 (12%) 7 (14%)
Posttraumatic Stress 23 (16%) 10 (20%)
2+ Disorders 46 (31%) 18 (37%)
Open in a new tab

Note:Stimulants = amphetamine, methamphetamine, and/or cocaine.

2.2. Procedure

Participants underwent an intensive assessment for demographic, clinical and psychiatric features. Here we focused on the clinical measures indicated above, as well as the Wide Range Achievement Test (WRAT), a common measure of premorbid IQ (Johnstone et al., 1996). This measure was included to account for group differences in task performance due to general cognitive ability. The complete list of assessments and references supporting their validity and reliability are provided in (Victor et al., 2018).

To assess our hypotheses about reduced information-seeking and altered learning rates in SUDs, we employed a commonly used three-armed bandit task to assess decision dynamics in the context of the explore/exploit dilemma (Zhang and Yu, 2013). This task consists of 20 blocks of 16 trials. Within each block, participants were informed that they could choose one of three bandits (slot machines), and that each bandit had a different probability of reward that was stable throughout the block. They were further informed that the probabilities changed at the start of each new block. They were not informed about the probabilities. Thus, with each block the participant started with no knowledge of these probabilities, and, to maximize reward, they needed to decide how many times to observe the outcomes of selecting each bandit (explore) before concluding they had sufficient information to consistently choose the bandit believed to have the highest reward probability (exploit). Reward rates were fixed for all bandits in each block, and were generated from a Beta (2,2) distribution prior to the start of data collection. Identical reward rates were used across participants, with pseudorandomized block order (see Figure 1).

Figure 1.

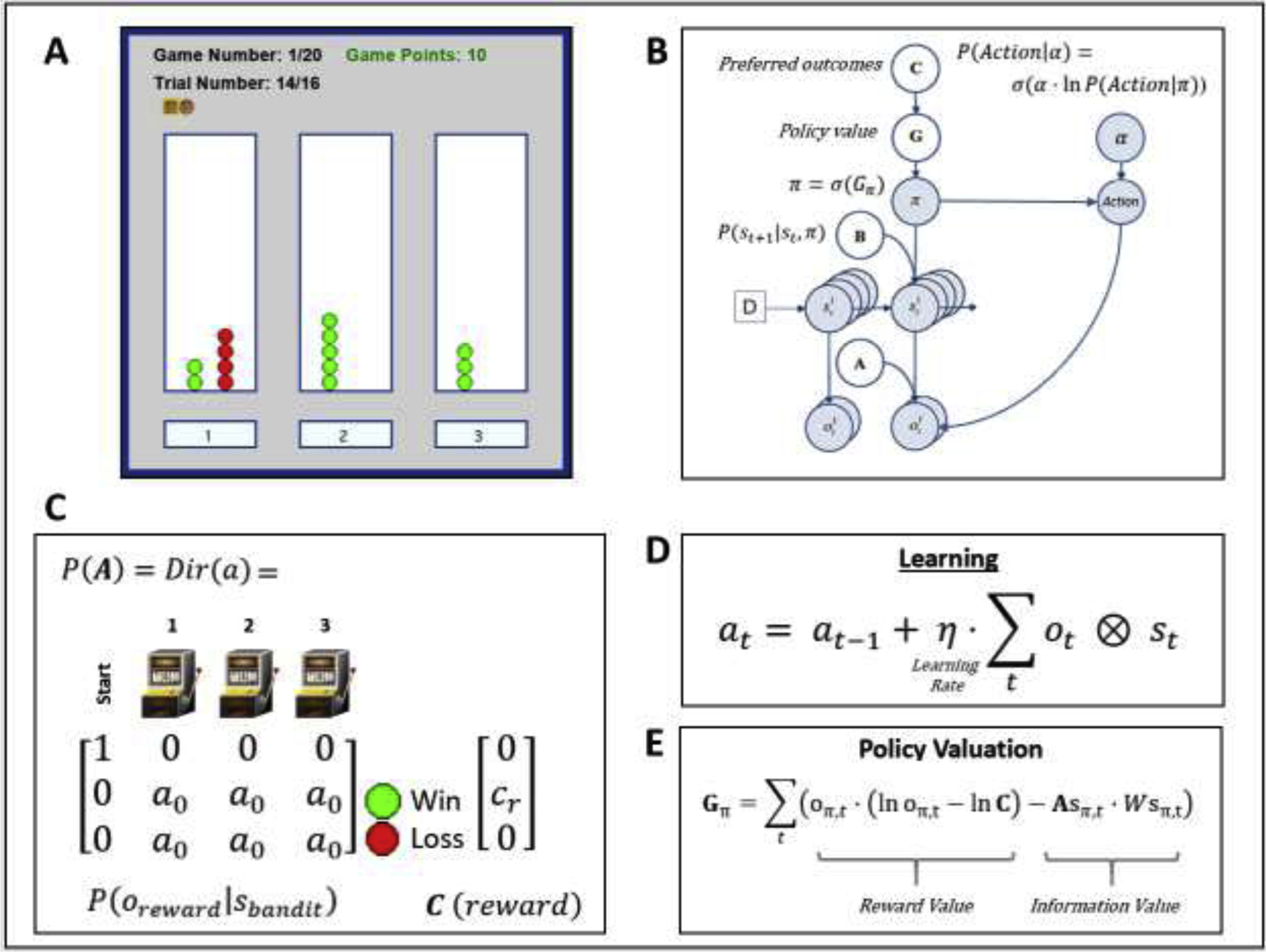
Figure 1.

Open in a new tab

(A) Illustration of the task interface (for each of three choices, green circle = win; red circle = loss). This task is designed to quantify how individuals switch between an “exploration” and “exploitation” strategy. Participants had to sample from 3 different choice options (lotteries) that had unknown probabilities of winning/losing, with the goal of maximizing reward. The optimal strategy is to start by “exploring” (trying all possible options) to gain information about the probability of winning for each lottery, and then begin “exploiting” after a few trials by repeatedly choosing the lottery with highest reward probability. Participants performed a total of 20 games with a known number of trials (16) per game – corresponding to 16 tokens that had to be assigned to one of the three lotteries of their choice (white panels on the left, middle and right sides of the interface). After placing each token, they earned 1 point if the token turned green or zero points if the token turned red. Each token decision lasted about 2 sec. After the button press, the chosen lottery became highlighted for 250ms, after which the token turned green or red to reveal the decision outcome. Participants were instructed to find the most rewarding lottery and maximize the points earned in each game. Participants were paid an additional $5 or $10 based on task performance. (B) Graphical depiction of the computational (Markov decision process) model used to model the task. Here, arrows indicate dependencies between variables such that observations (o) depend on hidden states (s), where this relationship is specified by the A matrix, and those states depend on both previous states (as specified by the B matrix, or the initial states specified by the D vector) and the sequences of actions (policies; π) selected by the agent. Here, D = [1 0 0 0]’, such that the participant always started in an undecided state at the beginning of each trial. The probability of selecting each policy in turn depends on the expected free energy (G) of each policy with respect to the prior preferences (C vector) of the participant. These preferences are defined as a participant’s log-expectations over observations. These C values are passed through a softmax function and correspond to log probabilities. For example, if cr = 4, this would indicate the expectation that observing reward is exp(4) ≈ 55 times more likely than observing no reward, exp(0) = 1. When actions are sampled from the posterior distribution over policies, randomness in chosen actions is controlled by an inverse temperature parameter (α), as depicted in the equation shown in the top right. (C) Depicts the A matrix learned by the agent (encoding probability of reward given each choice) and the C vector encoding the preference magnitude (cr value) for reward. Here, a0 values indicate the strength of baseline beliefs about reward probabilities at time t = 0, before observing the outcomes of any action. Dir(A) indicates a Dirichlet prior over the state-outcome mappings in A, such that higher baseline Dirichlet concentration parameter values (a0 values) encode greater confidence in reward probabilities – reducing the estimated value of seeking information. (D) Learning involves accumulating concentration parameters (a) based on outcomes observed after each choice of action. Learning rate is controlled by η as depicted in the displayed equation. Here ⊗ indicates the cross-product. (E) Policies are evaluated by G (lower G indicates a higher policy value), which can in this case be decomposed into two terms. The first term maximizes reward (as in a reinforcement learning model), by minimizing the divergence between predicted outcomes and rewarding outcomes. The second term maximizes information gain (goal-directed exploration) by assigning higher values to policies that are expected to produce the most informative observations (i.e., the greatest change in beliefs about reward probabilities; based on a novelty term, W:=12(a⊙(−1)−a0⊙(−1)), where ⊙ denotes element-wise power). For more details regarding the associated mathematics, see supplemental materials as well as (Da Costa et al., 2020; Friston et al., 2017b; Friston et al., 2017c).

2.3. Computational Modeling

To model task behavior, we adopted a Markov decision process (MDP) model commonly used within the active inference framework; for more details about the structure and mathematics of this class of models, see (Friston et al., 2017a; Friston et al., 2017c; Parr and Friston, 2017). We selected this approach because these models can test for differences in learning rates, random exploration, goal-directed exploration, and sensitivity to information (Schwartenbeck et al., 2019), each of which can contribute to explore/exploit decisions in distinct ways. Estimating these parameters for each individual is therefore useful to address how decision processes can lead to suboptimal behavior in SUDs as a result of suboptimal model parameter settings (Schwartenbeck et al., 2015).

For full modeling details and example simulations, see Supplementary Materials. The model is outlined in Table 3; important vectors, matrices, and equations are shown in Figure 1 and described in the legend. As described there, the model was defined by the choices (states and state transitions) available at each time point in the task, the observable outcomes of those choices (wins/losses), the choice-dependent reward probabilities, and the value of each possible outcome. There are several free model parameters that influence behavior: action precision (α), reward sensitivity (cr), learning rate (η), and insensitivity to information (a0). The action precision parameter controls the level of randomness in behavior. Those with lower values show less consistency in their choices when repeatedly placed in the same decision context. Put another way, they appear to be more uncertain about the best action to take. In explore-exploit tasks, this corresponds most closely to the construct of random exploration (i.e., choosing actions more randomly as a means of gathering information in the context of high uncertainty). The reward sensitivity parameter reflects how much an individual values a win. Importantly, as described in Supplementary Materials, because decision-making is based on a weighted tradeoff between reward value and the value of information, lower reward sensitivity values will lead individuals to place more value on information-seeking and promote greater goal-directed exploration. Learning rates quantify how much an individual’s beliefs about action outcomes change when experiencing each new win/loss. (i.e., influencing how quickly the value of information decreases over time). Insensitivity to information reflects baseline levels of confidence in beliefs about the probability of wins vs. losses for each choice (i.e., before making any observations). Higher insensitivity leads to reduced goal-directed exploration, because an individual sees less need to seek information a priori.

Table 3.

Computational model description

Model element General Description Model specification
ot One vector per category of possible observations. Each vector contains entries corresponding to possible p’bse, ablj stimuli for that category at time t. Possible observations for reward:

  1. Start

  2. Reward

  3. No reward


Possible observations for choice:

  1. Start

  2. Bandit 1

  3. Bandit 2

  4. Bandit 3
st A vector containing entries corresponding to the probability of each possible state that could be occupied at time t. Possible choice states:

  1. Start

  2. Bandit 1

  3. Bandit 2

  4. Bandit 3
A
P(ot|st)		 A matrix encoding the relationship between states and observations (one matrix per observation category).

  1. A reward probability matrix:

    P (oreward|schoice)

  2. An identity matrix for observed choice (entailing that participants had no uncertainty about the choice they made):

    P (ochoice|schoice)
a Dirichlet priors associated with the A matrix that specify beliefs about the mapping from states to observations. Learning corresponds to updating the concentration parameters for these priors after each observation, where the magnitude of the updates is controlled by a learning rate parameter q (see Supplementary Materials and Figure 1). Each entry for learnable reward probabilities began with a uniform concentration parameter value of magnitude a0, and was updated after each observed win or loss on the task. The learning rate η and a0 (which can be understood as a measure of sensitivity to new information; see Supplementary Materials) were fit to participant behavior.
B
P(st+1|st,π)		 A set of matrices encoding the probability of transitioning from one state to another given the choice of policy (π). Here policies simply include the choice of each bandit. Transition probabilities were deterministic mappings based on a participant’s choices such that, for example, P(sbandit 1|sstart’πbandit 1) = 1, and 0 for all other transitions, and so forth for the other possible choices.
C
lnP(o)		 One vector per observation category encoding the preference (reward value) of each possible observation within that category. The value of observing a win was a model parameter cr reflecting reward sensitivity; the value of all other observations was set to 0. The value of cr was fit to participant behavior. Crucially, higher cr values have the effect of reducing goal-directed exploration, as the probability of each choice (based on expected free energy Gπ) becomes more driven by reward than by information- seeking (see Supplementary Materials and Figure 1).
D
P(st=1)		 A vector encoding prior probabilities over states. This encoded a probability of 1 that the participant began in the start state.
π A vector encoding the probability of selecting each allowable policy (one entry per policy). The value of each policy is determined by its expected free energy (Gπ), which depends on a combination of expected reward and expected information gain. Actions at each time point are chosen based on sampling from the distribution over policies, π = σ(Gπ); the determinacy of action selection is modulated by an inverse temperature or action precision parameter α (see Supplementary Materials and Figure 1). This included 3 allowable policies, corresponding to the choice of transitioning to each of the three bandit choice states. The action precision parameter a was fit to participant behavior.
Open in a new tab

We estimated 10 different nested models, illustrated in Table 4, each with different choices of which model parameters were estimated. Based on our interest in goal-directed exploration, cr was always estimated. We then performed Bayesian model comparison (based on (Rigoux et al., 2014; Stephan et al., 2009)) to determine the best model. Variational Bayes (variational Laplace; (Friston et al., 2007)) was used to estimate parameter values that maximized the likelihood of each participant’s responses, as described in (Schwartenbeck and Friston, 2016).

Table 4.

Nested models

Parameter: α
(action
precision)		 cr
(reward sensitivity)		 η
(learning rate)		 α0
(insensitivity to information)
Default value if not estimated 4 (always estimated) (removed from model) 0.25
Prior means during estimation* 4 4 0.5 0.25
Model 1 Y Y N N
Model 2 Y Y Y N
Model 3 Y Y Y Y
Model 4 N Y Y Y
Model 5 N Y Y N
Model 6 N Y N N
Model 7 N Y N Y
Model 8 Y Y N Y
Model 9** Y Y Wins/Losses Y
Model 10 Y Y Wins/Losses N
Open in a new tab

Yindicates that a parameter was estimated for that model; Nindicates that a parameter was not estimated for that model.

*

Prior variance for all parameters was set to a precise value of 2−2 in order to deter over-fitting.

**

Winning model

2.4. Statistical Analyses

All analyses were performed in R. We used multiple regression analyses with each model parameter as the outcome variable and included age, sex, premorbid IQ, and group (SUDs versus HCs) as predictor variables. As indicated above, our participant data was sampled from the first 500 participants of the T1000 dataset, which was pre-specified as an exploratory subsample within an exploratory-confirmatory framework (i.e., with the second cohort of 500 participants reserved for confirmatory replication analyses; see (Victor et al., 2018)). As such, we set an exploratory p-value threshold of p ≤ .05, uncorrected. However, we note for reference that a Bonferroni corrected threshold for the 5 parameters in the winning model (see below) is p ≤ .01.

Table 1 demonstrates that SUDs exhibited lower premorbid IQ and higher depression/anxiety (PHQ/OASIS) symptoms than HCs. Table 2 illustrates that over half of SUDs met criteria for lifetime major depressive disorder (MDD), with almost half meeting criteria for two or more lifetime MDD, anxiety and/or stress disorders. We took three steps to help address these potential confounds. First, we reran analyses after propensity-matching (resulting in 51 HCs and 49 SUDs that did not differ significantly on age, sex or premorbid IQ; see Table 1). Second, we ran within-SUDs correlations between model parameters and each of the following to assess whether the direction of these relationships could provide an alternative interpretation of our results: (a) PHQ; (b) OASIS; and (3) premorbid IQ. Third, we ran post-hoc two-sample t-tests comparing individuals with vs. without MDD and with vs. without anxiety disorders.

We also ran a confirmatory parametric empirical Bayes (PEB) analysis (Friston et al., 2016), using standard MATLAB routines (see software note), computing group posterior estimates that incorporate posterior variances of individual-level parameter estimates when assessing evidence for group-level models with and without the presence of group differences. Aside from incorporating individual-level variance estimates, a further benefit of this type of hierarchical Bayesian analysis is that it is robust against concerns related to multiple comparisons (Gelman et al., 2012; Gelman and Tuerlinckx, 2000).

To assess relationships between model parameters and model-free metrics of task behavior, we calculated: (a) total number of wins and mean reaction times (RTs; trimmed using an iterative Grubbs test method to remove outliers until a distribution was found which contained no outliers at a threshold of p < .01; (Grubbs, 1969)); and (b) number of stays vs. shifts in bandit selection after win and loss outcomes. Next, we ran correlations between model parameters and each of these model-free metrics and performed two-sample t-tests to assess group differences. For strategy differences, we examined the first and second halves of the games separately (i.e., first 7 choices vs. final 8 choices) to assess periods wherein exploration vs. exploitation would be expected to dominate.

3. Results

Out of the 10 nested computational models we estimated (Table 4), the model including action precision, reward sensitivity, separate learning rates for wins and losses, and insensitivity to information was the best model (protected exceedance probability = 1). On average, this model accurately predicted true actions on 60% of trials (SD = 11%); SUDs = 59% (SD = 10%), HCs = 62% (SD = 12%). Average probability assigned to true actions by this model was .53 (SD = .1); SUDs = .52 (SD = .09), HCs = .56 (SD = .12). Note that chance accuracy = 1/3.

Table 5 presents group descriptive statistics for both samples, while Figure 2 depicts significant group differences in computational model parameters for the entire sample. Within the entire sample, SUDs exhibited (a) lower action precision (t = 2.9, p = .004), (b) higher learning rate for wins (t = 2.1, p = .02), and (c) lower learning rate for losses (t = 2.4, p = .02) than HCs. Groups did not differ in reward sensitivity or insensitivity to information. With respect to other predictors, higher age was linked to (a) higher reward sensitivity (t = 3.2, p = .002), (b) lower learning rate (t = 2.8, p = .007), and (c) less sensitivity to new information (t = 2.7, p = .008). Higher IQ was also linked to lower learning rate for losses (t = 2.7, p = .007). Table 5 indicates that group difference results for action precision and win/loss learning rates were also significant after propensity matching for age, sex, and premorbid IQ.

Table 5.

Model Parameters by Group (Means and Standard Deviations)

Full Sample HCs SUDs p* Cohen’s d
N= 54 147
Action Precision 2.59 (0.88) 2.18 (0.58) 0.004 0.43
Reward Sensitivity 4.43 (1.44) 4.26 (1.42) 0.85
Learning rate (Wins) 0.48 (0.12) 0.50 (0.13) 0.04 0.31
Learning rate (Losses) 0.42 (0.13) 0.38 (0.15) 0.02 0.36
Insensitivity to Information 0.76 (0.29) 0.81 (0.30) 0.27
Propensity Matched HCs SUDs p Cohen’s d
N= 51 49
Action Precision 2.60 (0.9) 2.17 (0.59) 0.005 0.57
Reward Sensitivity 4.38 (1.45) 4.37 (1.56) 0.98
Learning rate (Wins) 0.47 (0.12) 0.53 (0.12) 0.02 0.46
Learning rate (Losses) 0.41 (0.13) 0.34 (0.16) 0.01 0.52
Insensitivity to Information 0.77 (0.28) 0.84 (0.30) 0.26
Open in a new tab
*

within a linear model including Age, Sex, and WRAT scores

Figure 2.

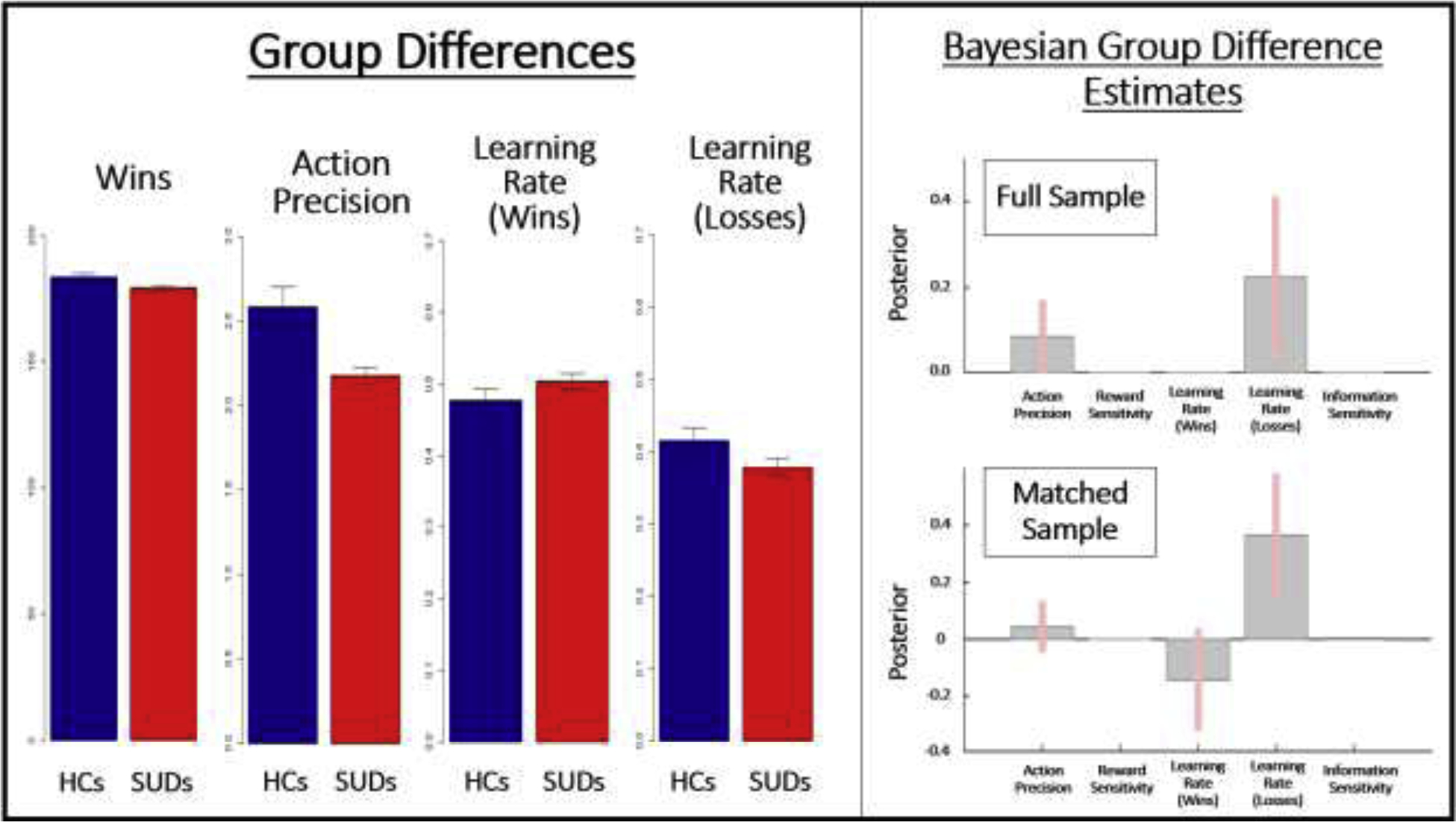
Figure 2.

Open in a new tab

Left: Means and standard errors for significant group differences in model-based and model-free measures. HCs = healthy controls, SUDs = substance use disorders. Data displayed is based on the full sample of 54 HCs and 147 individuals with SUDs. Right: Results of parametric empirical Bayes (PEB) analyses, showing the posterior means and variances for group difference estimates in the full and propensity-matched samples. These Bayesian group comparisons largely confirmed the mean group difference effects found in frequentist analyses; they also indicated a particularly pronounced group difference in the learning rate for losses when taking the individual posterior variances of parameter estimates into account. The model with the most evidence only retained the difference in these parameters, which is why other parameters have 0 values. Action precision, Reward Sensitivity, and Information Sensitivity values are in log-space. Learning Rate values are in logit-space.

Bayesian (PEB) analyses indicated that, in the full sample, the winning model provided positive evidence for the group difference in action precision (posterior probability = .81) and learning rate for losses (posterior probability = .88); the effect was stronger for the difference in learning rate (illustrated in Figure 2). If age, sex, and IQ were included in the model, only the difference in learning rate for losses was retained, and the evidence for this group difference became stronger (posterior probability = 1). In the propensity-matched sample, the winning model retained the group difference in learning rate for losses, with strong evidence (posterior probability = .97). It also included the group difference in action precision (weak evidence; posterior probability = .45) and learning rate for wins (positive evidence; posterior probability = .75).

Table 6 lists group descriptive statistics in model-free behavioral measures for both samples. Figure 2 indicates that SUDs achieved fewer wins than HCs, although groups did not differ in RTs or their use of win-stay/lose-shift strategies. However, during early trials, when exploratory behavior would be expected to dominate, SUDs in the propensity-matched sample made more lose/stay choices than HCs (t(91) = 2.23, p = .03, Cohen’s d = 0.45).

Table 6.

Model-Free Measures of Task Behavior by Group (Means and Standard Deviations)

Full Sample HCs SUDs p Cohen’s d
N= 54 147
Wins 183.59 (12.08) 179.33 (13.01) 0.03 0.33
Reaction Time 0.62 (0.25) 0.57 (0.26) 0.29
Win/Stay 136.54 (32.46) 130.20 (36.44) 0.26
Win/Shift 35.41 (28.04) 37.48 (29.51) 0.70
Lose/Stay 42.17 (26.54) 45.89 (30.22) 0.43
Lose/Shift 85.89 (28.01) 86.43 (32.10) 0.91
Propensity Matched HCs SUDs p Cohen’s d
N= 51 49
Wins 183.25 (12.34) 178.16 (13.60) 0.05 0.39
Reaction Time 0.62 (0.25) 0.54 (0.27) 0.15
Win/Stay 136.24 (32.75) 131.10 (38.92) 0.48
Win/Shift 35.47 (28.00) 35.63 (32.46) 0.98
Lose/Stay 41.43 (27.00) 52.45 (33.87) 0.08*
Lose/Shift 86.86 (28.47) 80.82 (34.30) 0.34
Open in a new tab
*

When only examining early trials in each game (i.e., first 7 choices), this difference was significant at p = 0.03.

Across all participants, faster RTs were associated with greater reward sensitivity (r = − .34, p < .001), higher learning rate for wins (r = −.26, p < .001), lower learning rate for losses (r = .30, p < .001), and less sensitivity to information (r = −.21, p = .003). A greater number of wins was associated with greater action precision (r = .27, p < .001) and greater reward sensitivity (r = .48, p < .001). For relationships between model parameters and win stay/shift vs. lose stay/shift strategies, see Supplementary Figure S2. As shown there: (a) higher action precision promoted greater numbers of stays in win trials; (b) higher learning rate for losses promoted shifts on loss trials (whereas learning rate for wins had the opposite influence); and (c) both higher reward sensitivity and lower sensitivity to information promoted stay behavior.

Within SUDs, we observed negative correlations between: (a) reward sensitivity and OASIS (r = −.19, p = .02); and (b) insensitivity to information and both OASIS (r = −.17, p = .04) and PHQ (r = −.18, p = .03). However, we note that these results did not survive correction for multiple comparisons. No relationships were observed between other parameters and clinical measures in SUDs, although premorbid IQ showed significant associations with learning rate for wins (r = .22, p = .01) and losses (r = −.25, p = .004). T-tests comparing SUDs with vs. without MDD (N = 78 vs. 69) revealed lower reward sensitivity in those with MDD (t = 3.17, p = .002), and marginally higher sensitivity to information in those with MDD (t = 2.0, p = .05). No differences were observed for other parameters. Comparisons between SUDs with vs. without anxiety disorders (N = 50 vs. 97) did not reveal any significant group differences.

4. Discussion

We used a computational framework that dissociated between goal-directed information seeking and random exploration, alongside differences in learning rates, to examine whether differences in these parameters could shed light on which of several possible computational failure modes best accounts for poor decision-making in SUDs when solving the explore/exploit dilemma. While SUDs won less often than HCs, reward sensitivity and insensitivity to information – both of which influence goal-directed exploration – did not differ between groups. In contrast, SUDs exhibited lower action precision, greater learning rate for rewards, and lower learning rate for losses than HCs – with Bayesian analyses finding the strongest evidence for the group difference in learning rate for losses.

Our finding that lower action precision was associated with fewer wins, and a greater number of shifts to a new choice after a win, suggest a failure of SUDs to settle on a behavior strategy despite sufficient evidence. This appears consistent with previous work suggesting that substance users are less likely than HCs to stick to successful decision strategies (Kanen et al., 2019; Myers et al., 2016). Future work will be necessary to better understand the possible bases of this difference (e.g., underconfidence, distractibility, reduced awareness, etc.). Our finding that, relative to HCs, individuals with SUDs show attenuated learning rate for losses also appears consistent with neural and self-report results suggesting diminished responses to negative stimuli in SUDs (i.e., under the assumption that learning about a stimulus is facilitated by stronger affective or salience-based responses to that stimulus; (Hester et al., 2013; Simons and Arens, 2007; Simons et al., 2008; Stewart et al., 2014)). This result, as well as the greater learning rate we observed for wins, also supports previous work in SUDs demonstrating a lower impact of large losses on future choices (opioid users; (Petry et al., 1998)), reduced sensitivity to losses (opioid users; (Ahn et al., 2014)), and difficulty avoiding punishment (opioid users; (Myers et al., 2017)).

Unlike our model-based results, standard model-free analyses of RTs and behavioral strategy revealed few significant group differences, which may be due to the fact that different computational strategies can lead to similar summary statistics. For example, if lose/stay behaviors decrease slowly over time – because learning after losses still occurs, but at a slower rate for some individuals than others – averaging lose/stay choices over trials may not capture this because the high early and low late trial values may cancel out (i.e., this is what motivated our further analysis restricted to early trials, which did reveal significant differences in lose/stay choices between groups). This contrasts with estimates of learning rate, which capture more complex dynamics in behavior over time that also account for other influences (e.g., exploratory drives). This highlights the potential utility of our computational approach in its ability to pick up on potentially important differences in the mechanisms whereby individuals with SUDs differ in decision-making from HCs. As discussed above, aside from fewer wins, the only significant model-free finding was that SUDs showed a greater number of lose/stay choices in early trials. This is consistent with our finding that individuals with SUDs learn more slowly from losses – hindering the ability to “lock on to” the most optimal choice during exploration. Together, our findings could be taken to suggest that, in the face of uncertainty, individuals with SUDs persist in making poor choices (at least in part) because they do not appropriately update their beliefs when drug use leads to negative consequences – and that, even in the face of positive outcomes, they fail to reliably adopt the actions that produce them.

While supportive of previous findings, this study was also distinct in using an active inference (active information-seeking) model to disambiguate different possible mechanisms that may be affected while solving the explore/exploit dilemma. In our computational model, lower reward sensitivity values and higher sensitivity to information both promote goal-directed exploration in different ways (i.e., sensitivity to information is more prominent in cases of high uncertainty), whereas low action precision promotes random exploration (which can reflect several factors, including simple computational noise; (Findling et al., 2019)). SUDs and HCs did not differ on either reward sensitivity or information sensitivity, suggesting no difference in the use of goal-directed information seeking. Random exploration may therefore be of greater relevance.

If our results can be replicated, it may be useful to explore the potential utility of designing interventions focused on facilitating attention to, and learning from, negative outcomes. Learning rates are thought to be modulated by estimates of environmental volatility – such that learning rates should be lower in more stable environments to avoid learning from random outcomes (Lawson et al., 2017; Mathys et al., 2014; Sales et al., 2019; Sutton and Barto, 1998). A lower learning rate for losses may indicate that SUDs believe losses are explained more by chance, as opposed to by a consistent relationship with their past behavior (i.e., unexpected losses are treated as noise instead of signal). As such, it would be helpful to test whether interventions focused on helping substance users more explicitly see poor outcomes as reliable consequences of their actions could help address this. One potential example could be treatments targeting poor emotion regulation strategies in SUDs (Gold et al., 2020; Kober, 2014; Richmond et al., 2020; Suzuki et al., 2020). For instance, in some cases a failure to learn from losses could be due to avoidant attention strategies in which negative outcomes tend to be ignored as a means of regulating negative affect. If so, interventions helping individuals to directly face negative affect and develop more adaptive emotion regulation strategies could be beneficial in targeting this mechanism.

This study is not without limitations. While we chose a particular modeling framework – motivated by the natural distinction between different forms of exploration and learning afforded by the active inference approach – other models could also be used to examine behavior. It is worth noting here that, if the goal-directed information-seeking component were removed from active inference, the resulting model would become a simple model-based reinforcement learning model. While we compared several nested models, we were also required to choose prior parameter values. However, correlations between parameters and RTs, as well as the model’s accuracy in predicting behavior, both support its validity. Finally, our SUD group was heterogenous – including various, often comorbid drugs of choice and combinations of lifetime emotional disorders. Through propensity-matching sub-groups and examining within-group depression/anxiety symptoms, we believe that this issue has been adequately addressed. Notably, while no differences in action precision or learning rates were seen in SUDs with vs. without comorbid depression/anxiety, those with MDD did show reduced reward sensitivity compared to those without MDD (consistent with previous literature, e.g., see (Katz et al., 2020); although note that, in this context, this could also be interpreted as indicating greater goal-directed information seeking).

In summary, sub-optimal explore/exploit decisions in SUDs appear to be due to both inconsistent choices (especially in the face of positive outcomes) and sub-optimal learning rates for rewarding vs. non-rewarding outcomes. These results may help explain the difficulty in adjusting to more adaptive patterns of behavior in SUDs. Future work should examine ways of facilitating substance users’ abilities to learn the relationships between poor choices and negative outcomes and perhaps ways of increasing consistency in healthy behaviors after reinforcing outcomes.

Supplementary Material

1
2

Highlights.

Decision-making mechanisms in substance use disorders (SUDs) remain poorly understood

We used computational modeling to better understand these mechanisms

SUD patients showed less precise action selection mechanisms than healthy subjects

SUD patients also learned slower from negative than positive outcomes

This could help explain continued patterns of maladaptive choices in SUDs

Acknowledgment:

The authors would like to thank Edda Bilek for her suggestions regarding the PEB analyses.

Funding: This work has been supported in part by The William K. Warren Foundation, the National Institute of Mental Health (K23MH112949 (SSK), K23MH108707 (RLA)), and the National Institute of General Medical Sciences Center Grant, P20GM121312.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Software Note: All model simulations and parametric empirical Bayes analyses were implemented using standard routines (spm_MDP_VB_X.m, spm_dcm_peb.m, spm_dcm_peb_bmc.m) that are available as Matlab code in the latest version of SPM academic software: http://www.fil.ion.ucl.ac.uk/spm/. Matlab code specifying the generative model of the three-armed bandit task is included here in the supplementary material (TAB_task_model.m).

Conflict of Interest: None of the authors have any conflicts of interest to disclose.

References

  1. Addicott MA, Baranger DA, Kozink RV, Smoski MJ, Dichter GS, McClernon FJ, 2012. Smoking withdrawal is associated with increases in brain activation during decision making and reward anticipation: a preliminary study. Psychopharmacology (Berl) 219(2), 563–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Addicott MA, Pearson JM, Froeliger B, Platt ML, McClernon FJ, 2014. Smoking automaticity and tolerance moderate brain activation during explore-exploit behavior. Psychiatry Res 224(3), 254–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Addicott MA, Pearson JM, Sweitzer MM, Barack DL, Platt ML, 2017. A Primer on Foraging and the Explore/Exploit Trade-Off for Psychiatry Research. Neuropsychopharmacology 42(10), 1931–1939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ahn WY, Vasilev G, Lee SH, Busemeyer JR, Kruschke JK, Bechara A, Vassileva J, 2014. Decision-making in stimulant and opiate addicts in protracted abstinence: evidence from computational modeling with pure users. Front Psychol 5, 849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Beeler JA, Frazier CR, Zhuang X, 2012. Putting desire on a budget: dopamine and energy expenditure, reconciling reward and resources. Front Integr Neurosci 6, 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bohn M, Babor T, Kranzler H, 1991. Validity of the Drug Abuse Screening Test (DAST-10) in inpatient substance abusers. Problems of drug dependence 119, 233–235. [Google Scholar]
  7. Connery HS, 2015. Medication-assisted treatment of opioid use disorder: review of the evidence and future directions. Harv Rev Psychiatry 23(2), 63–75. [DOI] [PubMed] [Google Scholar]
  8. Da Costa L, Parr T, Sajid N, Veselic S, Neacsu V, Friston K, 2020. ACTIVE INFERENCE ON DISCRETE STATE-SPACES – A SYNTHESIS. arXiv, 200107203v07202 [q-bio.NC] [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ersche KD, Gillan CM, Jones PS, Williams GB, Ward LH, Luijten M, de Wit S, Sahakian BJ, Bullmore ET, Robbins TW, 2016. Carrots and sticks fail to change behavior in cocaine addiction. Science 352(6292), 1468–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ersche KD, Roiser JP, Abbott S, Craig KJ, Muller U, Suckling J, Ooi C, Shabbir SS, Clark L, Sahakian BJ, Fineberg NA, Merlo-Pich EV, Robbins TW, Bullmore ET, 2011. Response perseveration in stimulant dependence is associated with striatal dysfunction and can be ameliorated by a D(2/3) receptor agonist. Biol Psychiatry 70(8), 754–762. [DOI] [PubMed] [Google Scholar]
  11. Findling C, Skvortsova V, Dromnelle R, Palminteri S, Wyart V, 2019. Computational noise in reward-guided learning drives behavioral variability in volatile environments. Nat Neurosci 22(12), 2066–2077. [DOI] [PubMed] [Google Scholar]
  12. Friston K, FitzGerald T, Rigoli F, Schwartenbeck P, Pezzulo G, 2017a. Active Inference: A Process Theory. Neural Computation 29, 1–49. [DOI] [PubMed] [Google Scholar]
  13. Friston K, Lin M, Frith C, Pezzulo G, Hobson J, Ondobaka S, 2017b. Active Inference, Curiosity and Insight. Neural Computation 29, 2633–2683. [DOI] [PubMed] [Google Scholar]
  14. Friston K, Mattout J, Trujillo-Barreto N, Ashburner J, Penny W, 2007. Variational free energy and the Laplace approximation. Neuroimage 34(1), 220–234. [DOI] [PubMed] [Google Scholar]
  15. Friston K, Parr T, de Vries B, 2017c. The graphical brain: Belief propagation and active inference. Network Neuroscience 1, 381–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Friston KJ, Litvak V, Oswal A, Razi A, Stephan KE, van Wijk BCM, Ziegler G, Zeidman P, 2016. Bayesian model reduction and empirical Bayes for group (DCM) studies. NeuroImage 128, 413–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gelman A, Hill J, Yajima M, 2012. Why We (Usually) Don’t Have to Worry About Multiple Comparisons. Journal of Research on Educational Effectiveness 5(2), 189–211. [Google Scholar]
  18. Gelman A, Tuerlinckx F, 2000. Type S error rates for classical and Bayesian single and multiple comparison procedures. Computational Statistics 15(3), 373–390. [Google Scholar]
  19. Gold AK, Stathopoulou G, Otto MW, 2020. Emotion regulation and motives for illicit drug use in opioid-dependent patients. Cogn Behav Ther 49(1), 74–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gowin JL, Mackey S, Paulus MP, 2013. Altered risk-related processing in substance users: imbalance of pain and gain. Drug Alcohol Depend 132(1–2), 13–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Grubbs F, 1969. Procedures for detecting outlying observations in samples. Technometrics 11(1), 1–21. [Google Scholar]
  22. Harle KM, Zhang S, Schiff M, Mackey S, Paulus MP, Yu AJ, 2015. Altered Statistical Learning and Decision-Making in Methamphetamine Dependence: Evidence from a Two-Armed Bandit Task. Front Psychol 6, 1910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hester R, Bell RP, Foxe JJ, Garavan H, 2013. The influence of monetary punishment on cognitive control in abstinent cocaine-users. Drug Alcohol Depend 133(1), 86–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hser YI, Saxon AJ, Huang D, Hasson A, Thomas C, Hillhouse M, Jacobs P, Teruya C, McLaughlin P, Wiest K, Cohen A, Ling W, 2014. Treatment retention among patients randomized to buprenorphine/naloxone compared to methadone in a multi-site trial. Addiction 109(1), 79–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Johnstone B, Callahan CD, Kapila CJ, Bouman DE, 1996. The comparability of the WRAT-R reading test and NAART as estimates of premorbid intelligence in neurologically impaired patients. Arch Clin Neuropsychol 11(6), 513–519. [PubMed] [Google Scholar]
  26. Jones CM, Mack KA, Paulozzi LJ, 2013. Pharmaceutical overdose deaths, United States, 2010. JAMA 309(7), 657–659. [DOI] [PubMed] [Google Scholar]
  27. Kanen JW, Ersche KD, Fineberg NA, Robbins TW, Cardinal RN, 2019. Computational modelling reveals contrasting effects on reinforcement learning and cognitive flexibility in stimulant use disorder and obsessive-compulsive disorder: remediating effects of dopaminergic D2/3 receptor agents. Psychopharmacology (Berl) 236(8), 2337–2358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Katz BA, Matanky K, Aviram G, Yovel I, 2020. Reinforcement sensitivity, depression and anxiety: A meta-analysis and meta-analytic structural equation model. Clin Psychol Rev 77, 101842. [DOI] [PubMed] [Google Scholar]
  29. Kober H, 2014. Emotion regulation in substance use disorders, in: Gross J (Ed.) Handbook of emotion regulation The Guilford Press, pp. 428–446. [Google Scholar]
  30. Konova AB, Lopez-Guzman S, Urmanche A, Ross S, Louie K, Rotrosen J, Glimcher PW, 2019. Computational Markers of Risky Decision-making for Identification of Temporal Windows of Vulnerability to Opioid Use in a Real-world Clinical Setting. JAMA Psychiatry. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kroenke K, Spitzer RL, Williams JB, 2001. The PHQ-9: validity of a brief depression severity measure. J Gen Intern Med 16(9), 606–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lawson R, Mathys C, Rees G, 2017. Adults with autism overestimate the volatility of the sensory environment. Nature Neuroscience 20, 1293–1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Linson A, Parr T, Friston KJ, 2020. Active inference, stressors, and psychological trauma: A neuroethological model of (mal)adaptive explore-exploit dynamics in ecological context. Behav Brain Res 380, 112421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mathys CD, Lomakina EI, Daunizeau J, Iglesias S, Brodersen KH, Friston KJ, Stephan KE, 2014. Uncertainty in perception and the Hierarchical Gaussian Filter. Front Hum Neurosci 8, 825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Morris LS, Baek K, Kundu P, Harrison NA, Frank MJ, Voon V, 2016. Biases in the Explore-Exploit Tradeoff in Addictions: The Role of Avoidance of Uncertainty. Neuropsychopharmacology 41(4), 940–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Myers CE, Rego J, Haber P, Morley K, Beck KD, Hogarth L, Moustafa AA, 2017. Learning and generalization from reward and punishment in opioid addiction. Behav Brain Res 317, 122–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Myers CE, Sheynin J, Balsdon T, Luzardo A, Beck KD, Hogarth L, Haber P, Moustafa AA, 2016. Probabilistic reward- and punishment-based learning in opioid addiction: Experimental and computational data. Behav Brain Res 296, 240–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Norman SB, Hami Cissell S, Means-Christensen AJ, Stein MB, 2006. Development and validation of an overall anxiety severity and impairment scale (OASIS). Depression and Anxiety 23(4), 245–249. [DOI] [PubMed] [Google Scholar]
  39. Parr T, Friston K, 2017. Working memory, attention, and salience in active inference. Scientific Reports 7, 14678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Passetti F, Clark L, Mehta MA, Joyce E, King M, 2008. Neuropsychological predictors of clinical outcome in opiate addiction. Drug Alcohol Depend 94(1–3), 82–91. [DOI] [PubMed] [Google Scholar]
  41. Petry NM, Bickel WK, Arnett M, 1998. Shortened time horizons and insensitivity to future consequences in heroin addicts. Addiction 93(5), 729–738. [DOI] [PubMed] [Google Scholar]
  42. Richmond JR, Tull MT, Gratz KL, 2020. The Roles of Emotion Regulation Difficulties and Impulsivity in the Associations between Borderline Personality Disorder Symptoms and Frequency of Nonprescription Sedative Use and Prescription Sedative/Opioid Misuse. J Contextual Behav Sci 16, 62–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Rigoux L, Stephan KE, Friston KJ, Daunizeau J, 2014. Bayesian model selection for group studies - revisited. Neuroimage 84, 971–985. [DOI] [PubMed] [Google Scholar]
  44. Rudd RA, Aleshire N, Zibbell JE, Gladden RM, 2016. Increases in Drug and Opioid Overdose Deaths--United States, 2000–2014. MMWR Morb Mortal Wkly Rep 64(50–51), 1378–1382. [DOI] [PubMed] [Google Scholar]
  45. Sales AC, Friston KJ, Jones MW, Pickering AE, Moran RJ, 2019. Locus Coeruleus tracking of prediction errors optimises cognitive flexibility: An Active Inference model. PLoS Comput Biol 15(1), e1006267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Schwartenbeck P, FitzGerald TH, Mathys C, Dolan R, Wurst F, Kronbichler M, Friston K, 2015. Optimal inference with suboptimal models: addiction and active Bayesian inference. Med Hypotheses 84(2), 109–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Schwartenbeck P, Friston K, 2016. Computational Phenotyping in Psychiatry: A Worked Example. eNeuro 3, ENEURO.0049–0016.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Schwartenbeck P, Passecker J, Hauser TU, FitzGerald TH, Kronbichler M, Friston KJ, 2019. Computational mechanisms of curiosity and goal-directed exploration. Elife 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Sheehan DV, Lecrubier Y, Sheehan KH, Amorim P, Janavs J, Weiller E, Hergueta T, Baker R, Dunbar GC, 1998. The Mini-International Neuropsychiatric Interview (M.I.N.I.): the development and validation of a structured diagnostic psychiatric interview for DSM-IV and ICD-10. The Journal of Clinical Psychiatry 59 Suppl 20, 22–33;quiz 34–57. [PubMed] [Google Scholar]
  50. Simons JS, Arens AM, 2007. Moderating effects of sensitivity to punishment and sensitivity to reward on associations between marijuana effect expectancies and use. Psychol Addict Behav 21(3), 409–414. [DOI] [PubMed] [Google Scholar]
  51. Simons JS, Dvorak RD, Batien BD, 2008. Methamphetamine use in a rural college population: associations with marijuana use, sensitivity to punishment, and sensitivity to reward. Psychol Addict Behav 22(3), 444–449. [DOI] [PubMed] [Google Scholar]
  52. Stephan KE, Penny WD, Daunizeau J, Moran RJ, Friston KJ, 2009. Bayesian model selection for group studies. Neuroimage 46(4), 1004–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Stewart JL, May AC, Poppa T, Davenport PW, Tapert SF, Paulus MP, 2014. You are the danger: attenuated insula response in methamphetamine users during aversive interoceptive decision-making. Drug Alcohol Depend 142, 110–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Sutton R, Barto A, 1998. Reinforcement Learning: An Introduction. [Google Scholar]
  55. Suzuki S, Mell MM, O’Malley SS, Krystal JH, Anticevic A, Kober H, 2020. Regulation of Craving and Negative Emotion in Alcohol Use Disorder. Biol Psychiatry Cogn Neurosci Neuroimaging 5(2), 239–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Verdejo-Garcia A, Chong TT, Stout JC, Yucel M, London ED, 2018. Stages of dysfunctional decision-making in addiction. Pharmacol Biochem Behav 164, 99–105. [DOI] [PubMed] [Google Scholar]
  57. Victor TA, Khalsa SS, Simmons WK, Feinstein JS, Savitz J, Aupperle RL, Yeh HW, Bodurka J, Paulus MP, 2018. Tulsa 1000: a naturalistic study protocol for multilevel assessment and outcome prediction in a large psychiatric sample. BMJ Open 8(1), e016620. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wilson R, Geana A, White J, Ludvig E, Cohen J, 2014. Humans use directed and random exploration to solve the explore-exploit dilemma. Journal of experimental psychology. General 143, 2074–2081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Zhang S, Yu AJ, 2013. Forgetful Bayes and myopic planning: Human learning and decision-making in a bandit setting. Advances in neural information processing systems, 2607–2615. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS1619437-supplement-1.docx (439.3KB, docx)
2
NIHMS1619437-supplement-2.m (4.7KB, m)

RESOURCES