Stochastic reaction networks in dynamic compartment populations

Significance

Many biochemical processes in living systems take place in compartmentalized environments, where individual compartments can interact with each other and undergo dynamic remodeling. Studying such processes through mathematical models poses formidable challenges because the underlying dynamics involve a large number of states, which evolve stochastically with time. Here we propose a mathematical framework to study stochastic biochemical networks in compartmentalized environments. We develop a generic population model, which tracks individual compartments and their molecular composition. We then show how the time evolution of this system can be studied effectively through a small number of differential equations, which track the statistics of the population. Our approach is versatile and renders an important class of biological systems computationally accessible.

Abstract

Compartmentalization of biochemical processes underlies all biological systems, from the organelle to the tissue scale. Theoretical models to study the interplay between noisy reaction dynamics and compartmentalization are sparse, and typically very challenging to analyze computationally. Recent studies have made progress toward addressing this problem in the context of specific biological systems, but a general and sufficiently effective approach remains lacking. In this work, we propose a mathematical framework based on counting processes that allows us to study dynamic compartment populations with arbitrary interactions and internal biochemistry. We derive an efficient description of the dynamics in terms of differential equations which capture the statistics of the population. We demonstrate the relevance of our approach by analyzing models inspired by different biological processes, including subcellular compartmentalization and tissue homeostasis.

Compartmentalization is inherent to all forms of life (1). By separating biochemical processes from their surroundings, compartments serve as spatial and functional building blocks that govern biological organization at different scales. At the subcellular level, for instance, networks of vesicles collectively regulate the delivery, sorting, and breakdown of molecular cargo (2, 3). At the tissue scale, cells themselves act as functional units, each executing its internal biochemical program while interacting with the surrounding cell population and environment. These and other forms of compartmentalization have in common that an emergent behavior or function is achieved through the collective dynamics of multiple interacting compartments, which are in complex interplay with their environment as well as the biochemical processes they carry. In many biological systems, the compartments as well as their molecular contents are present in low numbers, such that random fluctuations in their dynamics become important (4, 5). Thus, investigating the dynamical properties of compartmentalized systems, especially in the presence of random fluctuations, is an important task toward understanding living systems across different scales.

From a methodological perspective, stochasticity poses formidable challenges in the analysis of biochemical processes. Even in homogenous environments, the treatment of stochastic reactions is demanding, and a large body of literature has been devoted to addressing this subject (6–8). A few previous studies, however, have attempted to study stochastic reaction dynamics within compartmentalized systems. Notable examples include the work from refs. 9 and 10, where compartments correspond to fixed spatial entities (e.g., cells in a tissue), in which reactions take place and which exchange material, for instance, through diffusion. An advantage of these models is that they can be formulated as a concatenation of multiple homogeneous reaction systems and thus could be effectively analyzed using available techniques. On the downside, however, they cannot account for compartmental dynamics, for instance, due to cell division or apoptosis.

Among the few available approaches to combine reaction and compartmental dynamics, population balance equations (PBEs) are among the most prominent (11–13). In this context, PBEs describe the time evolution of the number density of a compartment population due to compartment interactions or internal compartment dynamics, which may stem from chemical reactions or material exchange. Despite their popularity and numerous applications across various fields of science (14–16), PBEs are most commonly found as integro-partial differential equations in mean-field form: Rather than the actual number density, they describe the expected number density in the thermodynamic limit (17). Correspondingly, information about mesoscopic fluctuations is necessarily lost.

The relevance of noise in biological systems has led to an increased interest in stochastic population balance modeling (12, 18, 19). A few recent elegant studies, for instance, show how cell proliferation can be coupled with stochastic cell internal dynamics (20, 21). Since the adoption of a stochastic number density severely complicates the mathematical treatment, results can be often achieved only by imposing tailored approximations and simplifying assumptions, or using costly Monte Carlo simulation. In summary, while stochastic population balance has generated important insights into different biological applications, a sufficiently general yet effective framework remains lacking.

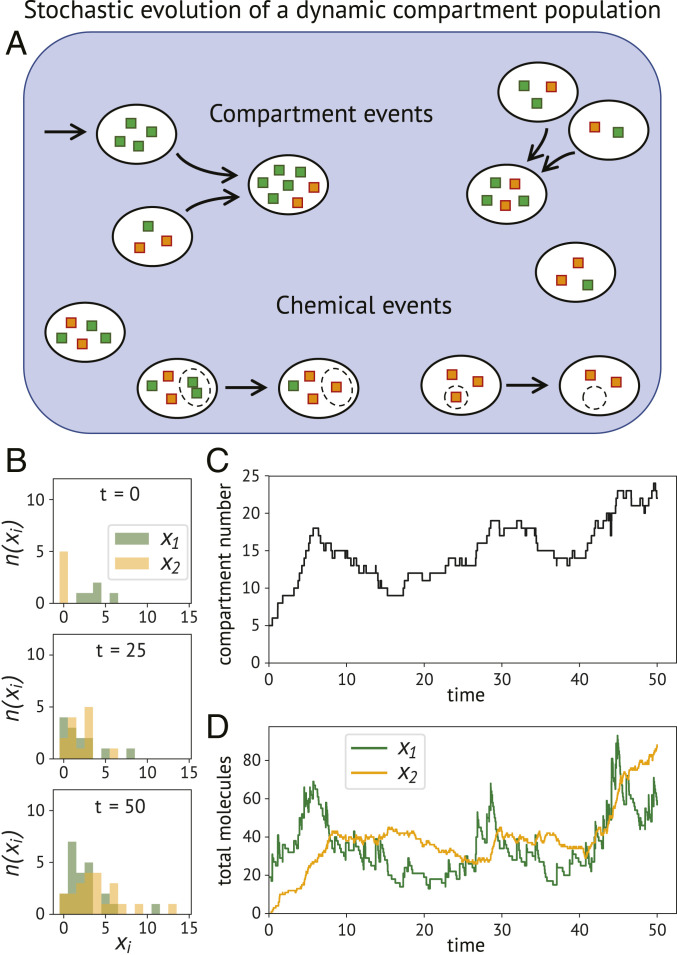
The goal of the present work is to develop a versatile and efficient approach to study stochastic biochemical processes in populations of dynamically interacting compartments. In particular, we consider both the compartments and the molecules inside them as discrete objects that can undergo arbitrary stochastic events, captured by a set of stoichiometric equations. This allows us to include interactions among distinct compartments such as compartment fusion or fission as well as chemical modifications inside each compartment (Fig. 1A). In contrast to population balance approaches, we describe the time evolution of a finite-size population of compartments and their molecular constituents in terms of counting processes. Based on this formalism, we then show how the population dynamics can be compactly expressed in terms of population moments. The obtained moment dynamics are themselves stochastic and therefore carry information not only about the average behavior of the population but also about its variability, as opposed to mean-field models. Using moment closure approximations, we derive a set of ordinary differential equations (ODEs), which reveal means and variances of these population moments in a very efficient manner. We demonstrate our approach using several case studies inspired by biological systems of different complexity.

Fig. 1.

Compartment population exhibiting chemical and compartmental dynamics. Compartment events alter the number of compartments in the population and, in general, also their content. Chemical events act only on the compartment contents, without changing the compartment number. (A) Schematic illustration of a simple example. This system is driven by an influx of compartments containing green molecules. The compartments can then randomly undergo binary fusion events. At the same time, the content of each compartment is subject to chemical modifications of two types: a bimolecular conversion of two green molecules into a yellow one, and a constant degradation of yellow molecules. (B–D) Output of one stochastic simulation of this specific model. (B) The marginals of the joint number distribution $n\left(x_1,x_2\right)$ are shown at three time points. (C) Stochastic trajectory of the total number of compartments in the population. The positive and negative updates are caused by intake and fusion events, respectively. (D) The trajectories of the total amount of molecules in the population are affected by the chemical events and compartment influx, but not by compartment fusion.

1. Theoretical Results

A. Stochastic Compartment Populations

We define a compartment population as a collection of $N$ distinct entities, each being associated with its own molecular state. The state of compartment $i$ is described by a discrete-valued, $D$-dimensional variable ${\mathbf{x}}_i=\left(x_{1,i},\dots ,x_{D,i}\right)\in \mathbb{X}\subseteq {\mathbb{N}}_0^D$. A single state variable $x_{d,i}$ typically represents the copy number of a particular chemical species present in compartment $i$, but may also be used to capture more coarse-grained compartment attributes such as cell types or vesicle identities. We consider the case where the population and their compartments are characterized by their molecular state only, while other physical properties such as location in space or shape are not taken into account. Thus, two compartments with the same molecular state $\mathbf{x}$ are identical and indistinguishable in our formalism. Correspondingly, we can characterize the population in terms of the number distribution function $n\left(\mathbf{x}\right)\in {\mathbb{N}}_0$, which counts the number of compartments that have content equal to $\mathbf{x}$ (Fig. 1B). The full state of the population is then given by the compartment number array $\mathbf{n}={\left(n_{\mathbf{x}}\right)}_{\mathbf{x}\in \mathbb{X}}$ with $n_{\mathbf{x}}=n\left(\mathbf{x}\right)$, which enumerates all compartment numbers within a single (and typically infinitely sized) structure of rank $D$. The state $\mathbf{n}$ can be understood as a multidimensional matrix, where the compartment number $n\left(\mathbf{x}\right)$ is found at index $\mathbf{x}$.

We next allow the compartment population to exhibit temporal dynamics. On the one hand, changes in the population may occur because compartments themselves undergo modifications and interact with one another. For instance, two compartments may fuse, or a compartment may exit the system. On the other hand, a compartment’s state may change due to chemical reactions among its molecules. Regardless of their specific nature, all chemical or compartment modifications can be expressed in terms of changes in the number compartment distribution $n\left(\mathbf{x}\right)$. Formally, we can describe those changes using stoichiometric equations of the form

$$\sum _{\mathbf{x}\in \mathbb{X}}{a}_{j,\mathbf{x}}\left[\mathbf{x}\right]\stackrel{\hspace{0.17em}}{\rightharpoonup }\sum _{\mathbf{x}\in \mathbb{X}}{b}_{j,\mathbf{x}}\left[\mathbf{x}\right],$$ [1]

where the symbol $\left[\mathbf{x}\right]$ denotes a compartment of content $\mathbf{x}$, and the nonnegative integers $a_{j,\mathbf{x}}$ and $b_{j,\mathbf{x}}$ are the stoichiometric reactant and product coefficients of transition $j$. Furthermore, we define the arrays ${\mathbf{a}}_j={\left(a_{j,\mathbf{x}}\right)}_{\mathbf{x}\in \mathbb{X}}$ and ${\mathbf{b}}_j={\left(b_{j,\mathbf{x}}\right)}_{\mathbf{x}\in \mathbb{X}}$, such that the population state $\mathbf{n}$ changes by $\mathrm{\Delta }{\mathbf{n}}_j={\mathbf{b}}_j-{\mathbf{a}}_j$ whenever transition $j$ occurs. We let $\mathcal{J}$ denote the set of all considered transitions. Using these definitions, we can express the state of the population at any time $t>0$ as

$$\mathbf{n}\left(t\right)=\mathbf{n}\left(0\right)+\sum _{j\in \mathcal{J}}\mathrm{\Delta }{\mathbf{n}}_j{R}_j\left(t\right),$$ [2]

with $R_j\left(t\right)$ as a counting process that counts the number of occurrences of transition $j$ up to time $t$ and $\mathbf{n}\left(0\right)$ as the initial configuration of the system. Note that, for compactness, time dependencies are dropped in our notation in the following, but the reader should keep in mind that both $\mathbf{n}\left(t\right)$ and $R_j\left(t\right)$ vary with time.

We next equip the counting processes $R_j\left(t\right)$ with instantaneous rate functions $h_j\left(t\right)$ for $j\in \mathcal{J}$, which govern how likely each compartment transition happens within an infinitesimal interval of time $\left(t,t+\mathrm{d}t\right]$. Throughout this work, we consider the rate functions to depend only on the current configuration of the population $\mathbf{n}\left(t\right)$, consistent with Markovian dynamics. It can then be shown that the counting processes $R_j\left(t\right)$ can be expressed as independent, time-transformed unit Poisson processes $U_j\left(t\right)$ such that

$$\mathbf{n}=\mathbf{n}\left(0\right)+\sum _{j\in \mathcal{J}}\mathrm{\Delta }{\mathbf{n}}_j{U}_j\left({\int }_0^t{h}_j\left(\mathbf{n}\left(s\right)\right)\mathrm{d}s\right).$$ [3]

Eq. 3 is known as the random time change representation (22). We can also write the stochastic evolution [2] of the population state in differential form as

$$\mathrm{d}\mathbf{n}=\sum _{j\in \mathcal{J}}\mathrm{\Delta }{\mathbf{n}}_j\mathrm{d}{R}_j,$$ [4]

where $\mathrm{d}{R}_j$ is the differential of the counting process $R_j$, and takes value 1 whenever a transition of type $j$ occurs at time $t$, and is zero otherwise.

B. Transition Classes

Eq. 4 represents a continuous time Markov chain formalism for stochastic compartment populations whose dynamics are governed by an arbitrary set of transitions $\mathcal{J}$. While this representation is very general, it is rather impractical, because, in most relevant situations, the set $\mathcal{J}$ encompasses infinitely many transitions. For instance, if two compartments of arbitrary size can fuse with each other, then an infinite number of transitions has to be introduced to model the interaction of all possible pairs of compartment contents. To address this problem, we introduce a specification of the transitions in terms of a finite set of transition classes, which represent generic rules by which compartments of arbitrary content can interact. In the case of compartment fusion, for instance, we could define a single transition class which transforms two compartments with content $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$ into a single compartment with content $\mathbf{x}+{\mathbf{x}}^{\prime }$, regardless of the specific value of $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$.

Formally, we define a transition class in two steps. First, we specify the general structure of a transition class $c$ by fixing the number of reactant compartments $r_c$ and the number of product compartments $p_c$ that are involved. For instance, in the case of compartment fusion, we would have $r_c=2$ and $p_c=1$. Throughout this work, we will restrict ourselves to the case $r_c,p_c\in \left\{\mathrm{0,1,2}\right\}$, but the following discussion holds true also for transitions involving more than two reactant or product compartments. We denote by ${\mathbf{X}}_c\in {\mathbb{X}}^{r_c}$ and ${\mathbf{Y}}_c\in {\mathbb{X}}^{p_c}$ the particular choice of reactant and product compartment contents that define a distinguishable instance of class $c$. Two transitions within a class are called distinguishable if they are associated with a different stoichiometry when expressed in the form [1]. In our settings, this practically means that, whenever $r_c$ or $p_c$ take value 2, we will count only pairs of ${\mathbf{X}}_c$ or ${\mathbf{Y}}_c$ that are combinatorially distinct, because the ordering of the compartments is physically irrelevant. In order to formally enumerate the distinct transitions within a class, we introduce a bijective mapping $j={\phi }_c\left({\mathbf{X}}_c,{\mathbf{Y}}_c\right)$ that assigns to each distinguishable choice of ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$ a unique index $j$ (and vice versa). This index $j$ refers to a specific stoichiometric equation of the form [1], whose stoichiometric arrays ${\mathbf{a}}_j^c$ and ${\mathbf{b}}_j^c$ take entries $a_{j,\mathbf{x}}^c={\sum }_{\mathbf{z}\in {\mathbf{X}}_c}{\delta }_{\mathbf{x},\mathbf{z}}$ and $b_{j,\mathbf{x}}^c={\sum }_{\mathbf{z}\in {\mathbf{Y}}_c}{\delta }_{\mathbf{x},\mathbf{z}}$, with the symbol $\delta$ denoting a Kronecker delta. In practice, the mapping ${\phi }_c$ can be made explicit by enumerating all of the possible contents ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$ without repeating indistinguishable instances. In the following, we will denote the image of ${\phi }_c$ by ${\mathcal{J}}_c$, which collects all of the transitions belonging to class $c$.

The second step in defining a transition class is the specification of a rate law that assigns a rate to each individual transition within the class as a function of its particular compartment contents ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$. This rate law can be defined in two parts. First, we introduce a probability per unit time for the reactant compartment(s) with content ${\mathbf{X}}_c$ to participate in a transition of class $c$, given the current state $\mathbf{n}$ of the population, that is,

$$\begin{array}{ll}\hfill & P\left({\mathbf{X}}_c\hspace{0.17em}\text{participating}\hspace{0.17em}\mathrm{during}\hspace{0.17em}\mathrm{d}t\mid \mathbf{n}\right)\hspace{0.17em}=\hfill \\ \hfill & \hspace{1em}=k_c{g}_c\left({\mathbf{X}}_c\right)w\left(\mathbf{n};{\mathbf{a}}_j^c\right)\mathrm{d}t,\hfill \end{array}$$ [5]

with $k_c\in {\mathbb{R}}^{+}$ being a content-independent rate constant and $g_c\left({\mathbf{X}}_c\right)$ being a nonnegative function which tunes the rate in terms of the reactant compartment content(s). Note that $g_c\left({\mathbf{X}}_c\right)$ must be symmetric in its arguments when $r_c=2$. The term $w\left(\mathbf{n};{\mathbf{a}}_j^c\right)$ is a population weight that takes into account all of the possible ways the current state $\mathbf{n}$ could realize a transition involving reactant compartments with content ${\mathbf{X}}_c$. In this work, we consider $w\left(\mathbf{n};{\mathbf{a}}_j^c\right)$ to be a combinatorial weight that reflects the physical indistinguishability of compartments having equal content. Thus, we set

$$w\left(\mathbf{n};{\mathbf{a}}_j\right)=\prod _{\mathbf{x}\in \mathbb{X}}\left(\genfrac{}{}{0.0pt}{}{n\left(\mathbf{x}\right)}{a_{j,\mathbf{x}}^c}\right),$$ [6]

which is akin to the mass action principle of standard stochastic reaction kinetics. Note that the binomials in Eq. 6 take a value different from 1 only when $\mathbf{x}\in {\mathbf{X}}_c$.

Finally, the second part of the rate law is a conditional probability ${\pi }_c\left({\mathbf{Y}}_c\mid {\mathbf{X}}_c\right)$ that describes how likely the reacting compartments of content ${\mathbf{X}}_c$ result in product compartments of content ${\mathbf{Y}}_c$. While this step might be generally of probabilistic nature, it can also be used to encode deterministic outcomes. For instance, coming back to the example of compartment fusion, the content of the product compartment is uniquely determined by fixing the contents of the two reactant compartments. Similarly to $g_c\left({\mathbf{X}}_c\right)$, we require ${\pi }_c$ to be symmetric in ${\mathbf{X}}_c$ or ${\mathbf{Y}}_c$ whenever either of those involves two compartments. In summary, Eq. 5 and the outcome distribution ${\pi }_c$ determine the propensity function of a specific transition $j$ of class $c$, that is,

$$h_{c,j}\left(\mathbf{n}\right)=k_c{g}_c\left({\mathbf{X}}_c\right)w\left(\mathbf{n};{\mathbf{a}}_j^c\right){\pi }_c\left({\mathbf{Y}}_c\mid {\mathbf{X}}_c\right),$$ [7]

which involves contents $\left\{{\mathbf{X}}_c,{\mathbf{Y}}_c\right\}={\phi }_c^{-1}\left(j\right)$. The rate law [7] provides a versatile definition, which allows us to equip a transition class with different physical properties, constraints, or selectivity. We emphasize that Eq. 7 can be parameterized entirely in terms of the involved contents ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$, such as illustrated for the examples in Table 1. Additional information on how chemical reactions can be described as compartment transition classes can be found in SI Appendix, section S1.

Table 1.

Several examples of population transition classes and the structure of their rate laws

Description	Stoichiometry	Propensity function
Compartment intake	$\varnothing \stackrel{h_I\left(\mathbf{n};\mathbf{y}\right)}{\rightharpoonup }\left[\mathbf{y}\right]$	$h_I\left(\mathbf{n};\mathbf{y}\right)=k_I{\pi }_I\left(\mathbf{y}\right)$
Compartment exit	$\left[\mathbf{x}\right]\stackrel{h_E\left(\mathbf{n};\mathbf{x}\right)}{\rightharpoonup }\varnothing$	$h_E\left(\mathbf{n};\mathbf{x}\right)=k_E{g}_E\left(\mathbf{x}\right)n\left(\mathbf{x}\right)$
Binary coagulation	$\left[\mathbf{x}\right]+\left[{\mathbf{x}}^{\prime }\right]\stackrel{h_C\left(\mathbf{n};\mathbf{x},{\mathbf{x}}^{\prime },\mathbf{y}\right)}{\rightharpoonup }\left[\mathbf{y}\right]$	$h_C\left(\mathbf{n};\mathbf{x},{\mathbf{x}}^{\prime },\mathbf{y}\right)=k_C{g}_C\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)\frac{n\left(\mathbf{x}\right)\left(n\left({\mathbf{x}}^{\prime }\right)-{\delta }_{\mathbf{x},{\mathbf{x}}^{\prime }}\right)}{1+{\delta }_{\mathbf{x},{\mathbf{x}}^{\prime }}}{\delta }_{\mathbf{y},\mathbf{x}+{\mathbf{x}}^{\prime }}$
Binary fragmentation	$\left[\mathbf{x}\right]\stackrel{h_F\left(\mathbf{n};\mathbf{x},\mathbf{y},{\mathbf{y}}^{\prime }\right)}{\rightharpoonup }\left[\mathbf{y}\right]+\left[{\mathbf{y}}^{\prime }\right]$	$h_F\left(\mathbf{n};\mathbf{x},\mathbf{y},{\mathbf{y}}^{\prime }\right)=k_F{g}_F\left(\mathbf{x}\right)n\left(\mathbf{x}\right){\pi }_F\left(\mathbf{y}|\mathbf{x}\right){\delta }_{{\mathbf{y}}^{\prime },\mathbf{x}-\mathbf{y}}$
Chemical reaction	$\left[\mathbf{x}\right]\stackrel{h_l\left(\mathbf{n};\mathbf{x},\mathbf{y}\right)}{\rightharpoonup }\left[\mathbf{y}\right]$	$h_l\left(\mathbf{n};\mathbf{x},\mathbf{y}\right)=k_l{g}_l\left(\mathbf{x}\right)n\left(\mathbf{x}\right){\delta }_{\mathbf{y},\mathbf{x}+\mathrm{\Delta }{\mathbf{x}}_l}$

We can now reformulate the general counting process model from Eq. 4 using the concept of transition classes. In particular, we associate a counter $R_{c,j}\left(t\right)$ with each transition $j\in {\mathcal{J}}_c$ within class $c$. Moreover, we introduce the total class transition counter ${\overline{R}}_c\left(t\right)={\sum }_{j\in {\mathcal{J}}_c}{R}_{c,j}\left(t\right)$, which corresponds to the cumulative number of events associated with class $c$ that happened until time $t$. The rate function of ${\overline{R}}_c\left(t\right)$ is given by the total propensity function $H_c\left(\mathbf{n}\right)={\sum }_{j\in {\mathcal{J}}_c}{h}_{c,j}\left(\mathbf{n}\right)$, which follows from the superposition theorem for Poisson processes (23). The propensity $H_c\left(\mathbf{n}\right)$ represents the probability per unit time of any event in class $c$ occurring, given the current state $\mathbf{n}$. Based on this, we can rewrite Eq. 4 as

$$\mathrm{d}\mathbf{n}=\sum _{c\in \mathcal{C}}\sum _{j\in {\mathcal{J}}_c}\mathrm{\Delta }{\mathbf{n}}_j^c\mathrm{d}{R}_{c,j},$$ [8]

$$=\sum _{c\in \mathcal{C}}\mathrm{\Delta }{\mathbf{n}}^c\mathrm{d}{\overline{R}}_c,$$ [9]

where $\mathcal{C}$ is a finite set of transition classes. Whenever a transition in class $c$ occurs ($\mathrm{d}{\overline{R}}_c=1$), the state $\mathbf{n}$ changes by a random state update $\mathrm{\Delta }{\mathbf{n}}^c$ with distribution $P\left(\mathrm{\Delta }{\mathbf{n}}^c=\mathrm{\Delta }{\mathbf{n}}_j^c\mid \mathbf{n}\right)=h_{c,j}\left(\mathbf{n}\right)/H_c\left(\mathbf{n}\right)$. The jump process representation in Eq. 9 is analytically convenient and, moreover, entails a natural strategy to perform stochastic simulations similar to Gillespie’s stochastic simulation algorithm (SSA) (24). Further details on how to perform stochastic simulations of the considered model are provided in SI Appendix, section S2.

C. Stochastic Moment Dynamics

Eq. 8 describes the stochastic evolution of the population state $\mathbf{n}$, under a considered set $\mathcal{C}$ of transition classes. Our goal is now to analyze the statistical properties of the population. In the context of stochastic population balance, compartment populations are typically studied based on the expected number distribution $⟨n\left(\mathbf{x}\right)⟩$, which reveals the average number of compartments in the population with content equal to $\mathbf{x}$. In principle, the dynamics of $⟨n\left(\mathbf{x}\right)⟩$ can be readily derived from Eq. 8 by taking the expectation on both sides of the equation. Unfortunately, however, this generates an infinite-dimensional system of equations which, in general, involves higher-order cross-correlations of the number distribution such as $⟨n\left(\mathbf{x}\right)n\left({\mathbf{x}}^{\prime }\right)⟩$ (14). As mentioned earlier, this problem is typically addressed either by neglecting these cross-correlations based on mean-field arguments or by resorting to approximate numerical schemes and Monte Carlo estimation.

To circumvent these problems, we use an alternative strategy to study the dynamics of the population. In particular, we focus on population moments, which capture summary statistics of the full population state $\mathbf{n}$, such as the total number of compartments in the population or the total number of molecules of a given type. Importantly, this will allow us to effectively access fluctuations in the dynamics of the population, while bypassing the difficulties encountered when dealing with the expected number distribution.

A moment associated with the population state $\mathbf{n}$ can be defined as

$$M^{\gamma }=\sum _{\mathbf{x}\in \mathbb{X}}{\mathbf{x}}^{\gamma }n\left(\mathbf{x}\right),$$ [10]

with ${\mathbf{x}}^{\gamma }={\prod }_{i=1}^D{x}_i^{{\gamma }_i}$ and $\gamma$ as a vector of nonnegative integer exponents. The sum ${\sum }_i{\gamma }_i$ sets the order of the moment $M^{\gamma }$. For instance, if ${\sum }_i{\gamma }_i=0$, then the moment corresponds to the total number of compartments present in the population, that is, $N=M^{\mathbf{0}}={\sum }_{\mathbf{x}}n\left(\mathbf{x}\right)$. Similarly, moments of order 1 represent the total amount—or mass—of a particular species, and so forth. It is important to keep in mind that the compartment number distribution $n\left(\mathbf{x}\right)$ is stochastic, and therefore each population moment will be stochastic as well (Fig. 1 C and D). In the following, our goal is to derive an equation which captures the stochastic moment dynamics.

We begin by studying how a single transition $j\in {\mathcal{J}}_c$ of transition class $c\in \mathcal{C}$ affects an arbitrary population moment. Assume that, right before the transition, the population is in configuration ${\mathbf{n}}^{-}$, and consider an associated moment $M^{\gamma ,-}$. When the transition happens, the moment instantaneously changes to

$$\begin{array}{ll}\hfill M^{\gamma ,+}& =\sum _{\mathbf{x}\in \mathbb{X}}{\mathbf{x}}^{\gamma }\left(n^{-}\left(\mathbf{x}\right)+\mathrm{\Delta }{n}_{j,\mathbf{x}}^c\right)\hspace{0.17em}=M^{\gamma ,-}+\sum _{\mathbf{x}\in \mathbb{X}}{\mathbf{x}}^{\gamma }\mathrm{\Delta }{n}_{j,\mathbf{x}}^c\hfill \\ \hfill & =M^{\gamma ,-}+\mathrm{\Delta }{M}_{c,j}^{\gamma },\hfill \end{array}$$ [11]

with $\mathrm{\Delta }{M}_{c,j}^{\gamma }$ as the net change of moment $M^{\gamma }$ due to transition $j$ of class $c$. Correspondingly, we can write the differential change of any population moment in point process notation

$$\mathrm{d}{M}^{\gamma }=\sum _{c\in \mathcal{C}}\sum _{j\in {\mathcal{J}}_c}\mathrm{\Delta }{M}_{c,j}^{\gamma }\mathrm{d}{R}_{c,j},$$ [12]

$$=\sum _{c\in \mathcal{C}}\mathrm{\Delta }{M}_c^{\gamma }\mathrm{d}{\overline{R}}_c,$$ [13]

where, in the second line, $\mathrm{\Delta }{M}_c^{\gamma }$ is a random jump update with distribution $P\left(\mathrm{\Delta }{M}_c^{\gamma }=\mathrm{\Delta }{M}_{c,j}^{\gamma }\mid \mathbf{n}\right)=h_{c,j}\left(\mathbf{n}\right)/H_c\left(\mathbf{n}\right)$, analogous to Eq. 9. Likewise, [13] is a continuous time jump process with discrete increments.

We finally remark that a useful distinction between transition classes can be made based on the moment updates $\mathrm{\Delta }{N}_c=\mathrm{\Delta }{M}_c^{\mathbf{0}}=p_c-r_c$ related to the total compartment number $N$. In particular, we will refer to any transition class that leaves the total number of compartments $N$ unchanged (i.e., $\mathrm{\Delta }{N}_c=0$) as a chemical event, since it exclusively modifies the compartment contents. All other cases are referred to as compartment events, since $\mathrm{\Delta }{N}_c\hspace{0.17em}\ne \hspace{0.17em}0$ for those transition classes.

D. Calculating Mean and Variance of the Population Moments

To effectively describe fluctuations in the population moments $M$, we derived ordinary differential equations that capture the time evolution of their average and variance. We show, in SI Appendix, section S3, that the expectation of an arbitrary population moment satisfies the equation

$$\frac{\mathrm{d}}{\mathrm{d}t}⟨M^{\gamma }⟩=\sum _{c\in \mathcal{C}}⟨\sum _{j\in {\mathcal{J}}_c}\mathrm{\Delta }{M}_{c,j}^{\gamma }{h}_{c,j}\left(\mathbf{n}\right)⟩,$$ [14]

where $⟨\cdot ⟩$ denotes the expectation operator. Note that, since the moment change $\mathrm{\Delta }{M}_{c,j}^{\gamma }$ is a constant for each $j\in {\mathcal{J}}_c$, the expectation could, in principle, be moved inside the second sum in [14]. In the latter form, however, the right-hand side (r.h.s.) of [14] involves infinite sums of moments of the number distribution $n\left(\mathbf{x}\right)$ itself, which defeats the purpose of a low-dimensional description in terms of population moments. Instead, we show that, under certain conditions, the sum ${\sum }_{j\in {\mathcal{J}}_c}\mathrm{\Delta }{M}_{c,j}^{\gamma }{h}_{c,j}\left(\mathbf{n}\right)$ can be expressed again as a function of a finite number of population moments, so that, after applying the expectation operator, Eq. 14 reduces to a self-contained system of differential equations. A sufficient condition for this to be the case is that 1) the function $g_c$ is a polynomial in ${\mathbf{X}}_c$ and 2) the conditional distribution ${\pi }_c$ has moments which are polynomials in ${\mathbf{X}}_c$ too (SI Appendix, section S4). In the present study, we will focus on systems which exhibit those two properties.

Analogously to Eq. 14 for the expected moment dynamics, we can derive differential equations for the expectation of a squared moment using the rules of stochastic calculus for counting processes (SI Appendix, section S5). In combination with [14], this allows us to study the expected behavior of a population moment as well as its variability across different realizations. This is an important difference from mean-field approaches, in which fluctuations in the number distribution and their corresponding moments are neglected.

We finally remark that the coupled ODE system resulting from Eq. 14 will not be closed, in general, since its r.h.s. may depend on higher-order moments. This problem can be addressed using moment closure approximations, where moments above a certain order are approximated by functions of moments up to that order (25). These approximation schemes typically rely on certain assumptions on the underlying process distribution and may give more or less accurate results depending on the details of the considered system (26). In our analyses, we found the multivariate Gamma closure as proposed in ref. 27 to give accurate results, and we will adopt this choice of closure in our case studies when needed (details in SI Appendix, section S6).

2. Case Studies

We next demonstrate our framework and the moment equation approach using several case studies inspired by biological systems at different scales. All simulations have been performed using the scientific computing language Julia (28). The code is publicly available at https://github.com/zechnerlab/StochasticCompartments.

A. Nested Birth–Death Process

We begin by considering a population of compartments with univariate content $x\in \left[0,\infty \right)$ and introducing a simplistic toy model defined by the four transition classes

$$\begin{array}{cccc}\hfill \varnothing & \stackrel{h_I\left(\mathbf{n};y\right)}{\rightharpoonup }\left[y\right]\hfill & \hfill & h_I\left(\mathbf{n};y\right)=k_I{\pi }_{Poiss}\left(y;\lambda \right)\hfill \\ \hfill \left[x\right]& \stackrel{h_E\left(\mathbf{n};x\right)}{\rightharpoonup }\varnothing \hfill & \hfill & h_E\left(\mathbf{n};x\right)=k_{E}n\left(x\right)\hfill \\ \hfill \left[x\right]& \stackrel{h_b\left(\mathbf{n};x\right)}{\rightharpoonup }\left[x+1\right]\hfill & \hfill & h_b\left(\mathbf{n};x\right)=k_{b}n\left(x\right)\hfill \\ \hfill \left[x\right]& \stackrel{h_d\left(\mathbf{n};x\right)}{\rightharpoonup }\left[x-1\right]\hfill & \hfill & h_d\left(\mathbf{n};x\right)=k_{d}xn\left(x\right),\hfill \end{array}$$ [15]

which are also illustrated in Fig. 2A. The first and second transition classes in [15] are, respectively, an intake transition class, where a new compartment enters the population with a Poisson-distributed content with mean-parameter $\lambda$, and a random-exit transition class, for which any compartment can leave the population with the content-independent exit rate $k_E$. According to our terminology, these first two transitions classes are compartment events, since they affect the number of compartments in the population, whereas the last two transition classes in [15] account for chemical modifications. The total propensities associated with [15] are found to be $H_I\left(\mathbf{n}\right)=k_I$, $H_E\left(\mathbf{n}\right)=k_{E}N$, $H_b\left(\mathbf{n}\right)=k_{b}N$, and $H_d\left(\mathbf{n}\right)=k_d{M}^1$. We start writing the stochastic differential equation (SDE) for the number of compartments $N$ in the form [13],

$$\mathrm{d}N=\mathrm{d}{\overline{R}}_I-\mathrm{d}{\overline{R}}_E,$$ [16]

which is affected only by the occurrence of compartment events, while the chemical birth–death events do not alter $N$. For the total population mass $M^1={\sum }_{x=0}^{\infty }xn\left(x\right)$, we can use [12] to find

$$\begin{array}{ll}\hfill \mathrm{d}{M}^1& =\sum _{y=0}^{\infty }\left(+y\right)\mathrm{d}{R}_{I,y}+\sum _{x=0}^{\infty }\left(-x\right)\mathrm{d}{R}_{E,x}\hfill \\ \hfill & \hspace{1em}+\sum _{x=0}^{\infty }\left(+1\right)\mathrm{d}{R}_{b,x}+\sum _{x=0}^{\infty }\left(-1\right)\mathrm{d}{R}_{d,x}.\hfill \end{array}$$ [17]

Note that the mass updates related to intake or exit events depend on the content of each specific transition, while, for birth or death events, they always take values $+1$ or $-1$, respectively. We can express Eq. 17 in the compact form [13] too, which equals

$$\mathrm{d}{M}^1=Y_I\mathrm{d}{\overline{R}}_I-X_E\mathrm{d}{\overline{R}}_E+\mathrm{d}{\overline{R}}_b-\mathrm{d}{\overline{R}}_d,$$ [18]

where we introduced the random variables $\mathrm{\Delta }{M}_I^1=Y_I$ with $P\left(Y_I=y\right)={\pi }_{Poiss}\left(y;\lambda \right)$ and $\mathrm{\Delta }{M}_E^1=-X_E$ with $P\left(X_E=x\mid \mathbf{n}\right)=n\left(x\right)/N$, which is a categorical distribution for the content of the compartment randomly exiting the system, found by evaluating $h_E\left(\mathbf{n};x\right)/H_E\left(\mathbf{n}\right)$. We can proceed to study the average trajectory for Eqs. 16 and 17 by using the result [14]. We obtain

$$\begin{array}{cc}\hfill \frac{\mathrm{d}⟨N⟩}{\mathrm{d}t}& =k_I-k_E⟨N⟩\hfill \\ \hfill \frac{\mathrm{d}⟨M^1⟩}{\mathrm{d}t}& =k_I\lambda -k_E⟨M^1⟩+k_b⟨N⟩-k_d⟨M^1⟩.\hfill \end{array}$$ [19]

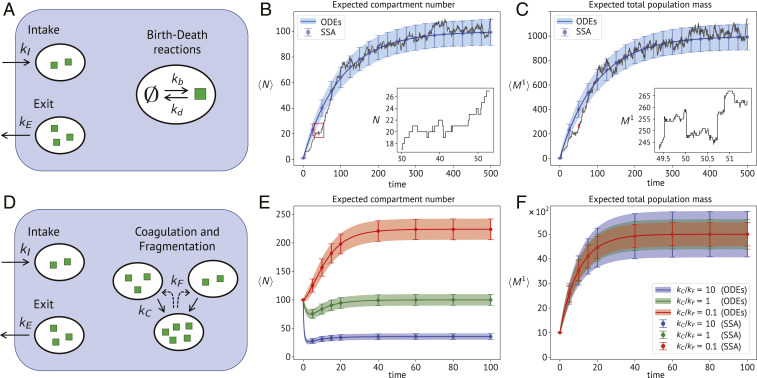
Not surprisingly, the evolution of $⟨N⟩$ is independent of that of $⟨M^1⟩$ because $N$ is just a birth–death process with constant rates $k_I$ and $k_E$. Conversely, the dynamics of the expected total mass $⟨M^1⟩$ depends on the expected number of compartments. Corresponding equations for the variance of $N$ and $M^1$ can be derived analogously (SI Appendix, section S7). In summary, this leads to a system of six coupled ODEs which can be integrated numerically to compute the exact mean and variance of $N$ and $M^1$, as shown in Fig. 2 B and C. Note that no moment closure approximation is required for this system.

Fig. 2.

Expected moment dynamics of compartment number and total mass for the nested birth–death model and the coagulation–fragmentation case study. Solutions obtained from moment equations (ODEs) are compared with Monte Carlo averages from stochastic simulations (SSA). Error bars and shaded areas correspond to 1 SD above and below the mean. (A) Schematic illustration of the nested birth–death system. (B and C) Moment dynamics for parameters $k_I=1$, $k_E=0.01$, $k_b=1$, and $k_d=0.1$. The content of new compartments is Poisson distributed mean $\lambda =k_b/k_d$. The superimposed black lines show one stochastic realization of Eqs. 16 and 17 in B and C, respectively. A small section (highlighted in red) is enlarged in Insets to illustrate the stochastic jump dynamics. (D) Schematic illustration of the coagulation–fragmentation model. (E and F) Expected moment dynamics for parameters $k_I$ = 10, $\lambda =50$, $k_E=0.1$, $k_F=5\cdot 10^{-3}$, and $k_C$ varying according to the ratios shown in the legend.

We next utilize the derived moment equations to investigate more closely how compartmental and chemical fluctuations affect the dynamics of the population. We first focus on the expected total mass at steady state, $⟨M_{\infty }^1⟩=\underset{t\to \infty }{lim}⟨M^1⟩$, for which we find

$$⟨M_{\infty }^1⟩=\frac{k_I}{k_E}\left[\frac{k_b}{k_d}\frac{1+\alpha \beta }{1+\alpha }\right],$$ [20]

where we introduced the dimensionless parameters $\alpha =k_E/k_d$ and $\beta =\lambda /\left(k_b/k_d\right)$. The term $k_I/k_E$ corresponds to $⟨N_{\infty }⟩$, the expected number of compartments at steady state, which follows from $N$ being a birth–death process (SI Appendix, section S7). The term in the square brackets corresponds to the steady-state average content per compartment, $⟨m_{\infty }⟩=⟨M_{\infty }^1⟩/⟨N_{\infty }⟩$. The latter coincides with the first moment of the normalized expected number distribution $P_{\infty }\left(x\right)=⟨n_{\infty }\left(x\right)⟩/⟨N_{\infty }⟩$, where we defined $⟨n_{\infty }\left(x\right)⟩=\underset{t\to \infty }{lim}⟨n\left(x\right)⟩$. We observe that setting $\beta =1$ in Eq. 20 gives $⟨m_{\infty }⟩=k_b/k_d$, since the intake distribution ${\pi }_{Poiss}\left(x;\lambda =k_b/k_d\right)$ now matches the stationary distribution of the chemical birth–death process of rates $k_b$ and $k_d$ occurring in each compartment. In other words, the content of newly arriving compartments is already at steady state, thus preserving Poissonian content statistics.

To study variations across compartment contents, we calculated the variance-to-mean ratio ${\sigma }_{\infty }^2/⟨m_{\infty }⟩$ of $P_{\infty }\left(x\right)$, where ${\sigma }_{\infty }^2$ is obtained from moment equations as ${\sigma }_{\infty }^2=⟨M_{\infty }^2⟩/⟨N_{\infty }⟩-{⟨m_{\infty }⟩}^2$ (SI Appendix, section S7). We find

$$\frac{{\sigma }_{\infty }^2}{⟨m_{\infty }⟩}=1+⟨m_{\infty }⟩\frac{\alpha }{2+\alpha }\frac{{\left(\beta -1\right)}^2}{{\left(1+\alpha \beta \right)}^2}.$$ [21]

The first contribution in [21] corresponds to Poissonian noise stemming from the chemical fluctuations inside each compartment. The second contribution is caused by compartmental fluctuations, generally leading to super-Poissonian statistics. However, when $\beta =1$, Poissonian noise is recovered due to the agreement of chemical and intake processes.

Note that, in this simple linear case study, $P_{\infty }\left(x\right)$ could be characterized also directly by taking the expectation on Eq. 8. We show, in SI Appendix, section S7, how closed-form analytical solutions can be obtained for this simple system under two special parameter configurations.

We want to point out that, while Eq. 21 reveals the fluctuations of the content across individual compartments, a similar analysis can be performed for the total population mass $M^1$. This is demonstrated in SI Appendix, section S7, where we show the evolution of $M^1$ for three different values of $\beta$ and compare it against a static population without compartmental dynamics (SI Appendix, Fig. S1). This analysis shows that compartmental events are typically the dominant source of total mass fluctuations in the considered model.

This simple case study serves to illustrate how the proposed framework can be used to study fluctuations in systems that exhibit both compartment and reaction dynamics. In the following, we will consider systems with more complex interactions.

B. Stochastic Model of a Coagulation–Fragmentation Process.

Coagulation–fragmentation processes form an important class of models to describe populations of interacting components (15), which have been used to study biological phenomena at different scales, including protein clustering (29), vesicle trafficking (30–32), or clone-size dynamics during development (33). Previously, these models have been analyzed mostly using mean-field approaches or forward stochastic simulation. In this case study, we will revisit coagulation–fragmentation systems using the proposed moment equation approach. For simplicity, we will consider again a univariate compartment content $x\in \left[0,\dots ,\infty \right)$, but we remark that multivariate scenarios can be handled analogously. We define a random coagulation class, where each pair of compartments is equally likely to fuse with rate $k_C$ (i.e., $g_C\left(x,x^{\prime }\right)=1$ in Table 1). Instead, we introduce a mass-driven fragmentation class, where a compartment undergoes a fragmentation event with rate $k_F{g}_F\left(x\right)=k_{F}x$ that is proportional to its content. For ${\pi }_F\left(y\mid x\right)$, we choose a uniform fragment distribution. The corresponding total class propensities read $H_C\left(\mathbf{n}\right)=k_{C}N\left(N-1\right)/2$ and $H_F\left(\mathbf{n}\right)=k_F{M}^1$ (SI Appendix, section S8). Moreover, we might consider that the population can exchange compartments with an external environment. In order to account for this, we can equip our model with an intake and an exit transition class, similarly to model [15]. Considering these four transition classes (Fig. 2D), the SDE for $N$ is

$$\mathrm{d}N=\mathrm{d}{\overline{R}}_I-\mathrm{d}{\overline{R}}_E-\mathrm{d}{\overline{R}}_C+\mathrm{d}{\overline{R}}_F,$$ [22]

because $\mathrm{\Delta }N$ is equal to $-1$ for any exit or coagulation event and $+1$ for intake or fragmentation. The SDE for the total mass $M^1$ of the compartment population assumes an even simpler form,

$$\mathrm{d}{M}^1=Y_I\mathrm{d}{\overline{R}}_I-X_E\mathrm{d}{\overline{R}}_E,$$ [23]

since coagulation and fragmentation events conserve mass. The random variables $Y_I$ and $X_E$ are defined like in the previous case study. For space considerations, the derivation of the moment equations is left to SI Appendix, section S8. In particular, since the considered system does not exhibit closed moment dynamics, we made use of the proposed Gamma closure as mentioned earlier. In Fig. 2 E and F, we plot the expected trajectories and fluctuations of $N$ and $M^1$ for different parameter settings and compare them to exact stochastic simulations. In all cases, we found very good agreement between both approaches. An analogous analysis of the expected second-order moment is provided in SI Appendix, Fig. S2. An interesting feature emerging from Fig. 2F is that the coagulation and fragmentation rates affect the variability of the total mass, but not its average behavior, which depends only on the intake and exit parameters. This happens because a larger coagulation rate implies that the same total mass has to be shared among fewer compartments, which causes the total population mass to exhibit larger fluctuations upon occurrence of the intake and exit events. This fact could not be captured by a mean-field treatment of a coagulation–fragmentation system, since fluctuations are necessarily lost in that case. Similar considerations hold true for the expected compartment number dynamics

$$\frac{\mathrm{d}⟨N⟩}{\mathrm{d}t}=k_I-k_E⟨N⟩-\frac{k_C}{2}\left(⟨N^2⟩-⟨N⟩\right)+k_F⟨M^1⟩,$$ [24]

where we point out the dependency on the second-order moment $⟨N^2⟩$. In a mean-field approximation, the coagulation term in Eq. 24 would simplify to $-\frac{k_C}{2}{⟨N⟩}^2$. Indeed, replacing $⟨N^2⟩$ with ${⟨N⟩}^2$ implies that $\text{Var}\left(N\right)=⟨N^2⟩-{⟨N⟩}^2=0$, thereby neglecting fluctuations in the compartment number. Additionally, the linear correction $k_C⟨N⟩/2$ in Eq. 24, which originates from the exact combinatorics of the possible compartment pairings, would be omitted too. Both of these approximations can lead to significant deviations when only a few compartments are present in the system. For more details on the validity of mean-field approximations in stochastic coagulation systems, the reader may refer to ref. 34.

C. Protein Expression Dynamics in a Cell Community

In our next case study, we apply our approach to analyze a population of compartments which are chemically coupled to each other. To this end, we consider a cell population of fixed size $N_0=100$, and we equip each cell (i.e., each compartment) with a protein expression network, as shown in Fig. 3A. Protein expression is described as a random telegraph process (35), where a binary gene variable can stochastically switch between an off state $\left(x_G=0\right)$ and on state $\left(x_G=1\right)$. The active state promotes the production of a protein at rate $k_P$. Furthermore, the protein is constantly degraded at rate $k_d^P$. We define the two-dimensional compartment content variable $\mathbf{x}=\left(x_G,x_P\right)\in \mathbb{X}=\left[\mathrm{0,1}\right]\times {\mathbb{N}}_0$. We account for a cell-to-cell communication mechanism where cells in the active state can promote inactive cells to switch on protein expression. Previous studies have described cell-to-cell communication by a stochastic diffusion mechanism that couples neighboring compartments on a lattice (10, 36) or, in the limit of fast diffusion, through a shared environment (37, 38). Similarly to the latter scenario, we consider that an active cell can interact with the same probability with any inactive cell in the population. Such communication mechanism can be captured by a bicompartmental transition class

$$\left[\mathbf{x}\right]+\left[{\mathbf{x}}^{\prime }\right]\stackrel{h_{\mathrm{c}\mathrm{o}\mathrm{m}}\left(\mathbf{n};\mathbf{x},{\mathbf{x}}^{\prime }\right)}{\rightharpoonup }\left[1,x_P\right]+\left[1,x_P^{\prime }\right],$$ [25]

where we made explicit in the r.h.s. that, upon this transition, both cells are in the active state (details in SI Appendix, section S9). The total class propensity for [25] equals

$$H_{\mathrm{c}\mathrm{o}\mathrm{m}}\left(\mathbf{n}\right)=k_{\mathrm{c}\mathrm{o}\mathrm{m}}{M}^{\mathrm{1,0}}\left(N_0-M^{\mathrm{1,0}}\right),$$ [26]

which reflects the fact that the global activation rate is proportional to the product of the number of active cells $M^{\mathrm{1,0}}$ and the number of inactive cells (i.e., $N_0-M^{\mathrm{1,0}}$) in the current configuration $\mathbf{n}$. Note that, in the considered model, all transition classes—including the communication events—are chemical transitions according to our definition, so that the number of compartments remains constant at its initial value $N_0$. We further remark that, while the communication class [25] only acts on the binary gene state $x_G$, similar transitions can be defined within our framework to capture also exchange of molecules between compartments.

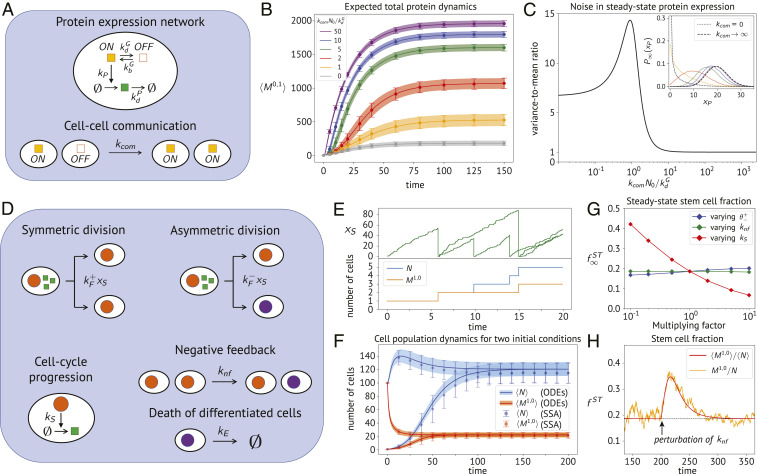
Fig. 3.

Moment dynamics and steady-state properties of the cell communication model and the stem cell system. (A) Schematic illustration of the reaction network and the cell–cell interaction mechanism in the cell communication model. The yellow square symbolizes the active gene state. The green square represents the expressed protein species. (B) Expected dynamics of the total protein mass $M^{\mathrm{0,1}}$ for different values of $k_{\mathrm{c}\mathrm{o}\mathrm{m}}$, with 1 SD above and below the mean. Lines and shaded areas correspond to the result of moment equations, while dots and error bars were obtained from averaging $10^3$ stochastic simulations. The population comprises $N_0=100$ cells, of which only one is in the active state at time 0. Parameters are set to $k_b^G=0.01$, $k_d^G=0.1$, $k_P=1$, and $k_d^P=0.05$. (C) Variance-to-mean ratio of the steady-state total protein mass, obtained by moment equations and plotted as a function of $k_{\mathrm{c}\mathrm{o}\mathrm{m}}{N}_0/k_d^G$. (Inset) The expected steady-state protein distribution in one cell, computed with stochastic simulations for the range of communication rates used in B. The dotted and dashed lines are analytical solutions, respectively, for no cell communication and infinitely fast communication (i.e., gene always active). (D) Schematic illustration of the stem cell model. Stem cells are indicated by an orange nucleus, and differentiated cells are indicated by a purple one. The green square represents a factor associated with cell cycle progression that induces stem cell division. The reference parameter values for E–H are set to $k_F^{+}=k_F^{-}=5\cdot 10^{-3}$, $k_S=10$, $k_{\mathrm{n}\mathrm{f}}=0.01$, and $k_E=0.05$. (E) (Upper) The accumulation-reset stochastic dynamics of $x_S$ in stem cells is shown for the initial transient of a single realization, starting with one stem cell. (Lower) The corresponding changes in total cell number and stem cell number. (F) Comparison of the expected dynamics for the total cell number $N$ (blue) and stem cell number $M^{\mathrm{1,0}}$ (orange) obtained from moment equations (ODEs) and stochastic simulations (SSA), for two different initial conditions. (G) Dependency of the steady-state stem cell fraction on variations of some model parameters around their reference values, computed from moment equations. (H) Robust dynamics of the stem cell fraction, upon applying a perturbation at time $t=200$ where $k_{\mathrm{n}\mathrm{f}}$ was suddenly downscaled by a factor of 5. In red, the expected stem cell fraction obtained from moment equations. In orange, one particular stochastic realization.

We are now interested in studying the protein expression dynamics in the cell population, as a function of the communication rate constant $k_{\mathrm{c}\mathrm{o}\mathrm{m}}$. To this end, we derived moment equations describing the averages and variances of the active cell number $M^{\mathrm{1,0}}$ and the total amount of proteins $M^{\mathrm{0,1}}$ (SI Appendix, section S9). In Fig. 3B, we plot the expected total protein dynamics $⟨M^{\mathrm{0,1}}⟩$ for different values of the communication rate $k_{\mathrm{c}\mathrm{o}\mathrm{m}}$. Similarly to the previous case studies, results obtained from exact SSA and the moment-based approach are in very good agreement with each other. Next, Fig. 3C illustrates the variance-to-mean ratio of the total protein amount at steady state as a function of the communication rate. This result has been obtained through moment equations, by computing $\text{Var}\left(M_{\infty }^{\mathrm{0,1}}\right)/⟨M_{\infty }^{\mathrm{0,1}}⟩$. We note how the noise initially increases with $k_{\mathrm{c}\mathrm{o}\mathrm{m}}$, peaks around $k_{\mathrm{c}\mathrm{o}\mathrm{m}}{N}_0/k_d^G=1$, and then soon starts declining toward Poissonian noise as the activation saturates. This can be appreciated also from Fig. 3C, Inset, which shows the shape of the normalized expected protein distribution in a cell, computed by SSA sampling. The distributions are in agreement with the theoretical predictions for the two limiting cases of absent and infinitely fast communication. In particular, for $k_{\mathrm{c}\mathrm{o}\mathrm{m}}\to \infty$, all cells in the population are constitutively maintained active, so that the protein levels are Poisson-distributed with mean $k_P/k_d^P=20$. When, instead, $k_{\mathrm{c}\mathrm{o}\mathrm{m}}=0$, each cell evolves independently, and the steady-state distribution is in agreement with the canonical telegraph model, whose analytical solution is known (35). We performed an analysis equivalent to Fig. 3 B and C for the expected number of active cells $⟨M^{\mathrm{1,0}}⟩$ (SI Appendix, Fig. S3). As can be seen from this application, moment equations provide an effective means to access the statistics of a compartment population for a wide range of parameters and identify interesting dynamical regimes with little computational effort.

D. Stem Cell Population Dynamics

In our last application, we aim to study a system involving a more complicated interplay between internal and compartmental dynamics. Specifically, we consider a model inspired by the proliferation and differentiation dynamics of stem cell populations (39, 40), as illustrated in Fig. 3D. While the regulatory mechanisms controlling cell differentiation are diverse and complex, we focus here on a minimal model to exemplify how our framework can be applied to problems of such kind. We consider that stem cells can undergo division events with two probabilistic outcomes: either a symmetric division, where both daughter cells are stem cells, or an asymmetric division, where one of the daughter cells differentiates. Cell cycle length distributions are typically peaked and nonexponential (41–43). To account for this, we couple the division rate of a stem cell to the dynamics of an internal molecular factor $x_S$ which stochastically increases over time at a constant rate $k_S$. More precisely, we consider the propensity of cell division to be proportional to the current abundance of $x_S$. Upon division, $x_S$ is reset to zero in both daughter cells, so that $x_S$ can be interpreted as a proxy for cell cycle progression. This is illustrated in Fig. 3E, where the dynamics of $x_S$ across a lineage is followed over multiple rounds of cell division along a stochastic realization. This accumulation-reset mechanism provides a simple strategy to account for peaked and nonexponential interdivision time distributions (SI Appendix, Fig. S4). Similar models of cell division have been considered in ref. 19, with the difference that the factor $x_S$ was considered to increase deterministically. Additionally, we introduce a negative feedback mechanism, which causes stem cells to differentiate at a rate that increases with their own abundance. For instance, such feedback could originate from mechanical cues due to cell crowding (44). To account for negative feedback in our model, we introduce a second-order compartment event, which mimics the interaction of a stem cell with the remaining stem cell population (SI Appendix, section S10). Finally, we assume that differentiated cells die or exit the system at a constant rate $k_E$. Formally, the cell content of the considered model is described by $\mathbf{x}=\left(x_G,x_S\right)\in \mathbb{X}=\left[\mathrm{0,1}\right]\times {\mathbb{N}}_0$, where the binary variable $x_G$ indicates whether a cell is either a stem cell ($x_G=1$) or a differentiated cell ($x_G=0$).

Our goal is to study the dynamics and the variability of the total cell number $N$ and the stem cell number $M^{\mathrm{1,0}}$ in the population. We remark that, in comparison to the previous case studies, the application of the moment equation method turns out to be more challenging for this model. This is because the total propensities of the division events depend on the second-order moment $M^{\mathrm{1,1}}={\sum }_{\mathbf{x}}{x}_G{x}_S$, which represents the total amount of $x_S$ in stem cells. In combination with the second-order feedback mechanism, this would lead to a large number of equations required to capture the full dynamics of all involved moments up to a certain order. Here we address this problem by combining the multivariate Gamma closure with a mean-field approximation, where correlations among certain population moments are neglected (SI Appendix, section S10).

In Fig. 3F, we plot the expected dynamics of the total number of cells and the number of stem cells starting from two different initial conditions (1 or 100 stem cells). Even though we used additional approximations, the moment dynamics are in relatively good agreement with the results obtained from stochastic simulations. Based on the moment equations, we next investigated how the steady-state stem cell fraction $f_{\infty }^{ST}=⟨M_{\infty }^{\mathrm{1,0}}⟩/⟨N_{\infty }⟩$ is affected by varying three different parameters of the model: the feedback rate $k_{\mathrm{n}\mathrm{f}}$, the rate $k_S$, and the ratio ${\theta }_{-}^{+}=k_F^{+}/k_F^{-}$, with $k_F^{+}+k_F^{-}$ held constant (Fig. 3G). Interestingly, we find that the stem cell fraction is largely robust against changes in the feedback strength $k_{\mathrm{n}\mathrm{f}}$ as well as the ratio of division rates ${\theta }_{-}^{+}$. In regard to the former, while changing $k_{\mathrm{n}\mathrm{f}}$ affects the number of stem cells present in the system (SI Appendix, Fig. S5), the relative propensity between symmetric and asymmetric divisions remains unaffected, thereby preserving the total stem cell fraction. This is further illustrated in Fig. 3H, which shows how the stem cell fraction returns to its set point upon perturbing $k_{\mathrm{n}\mathrm{f}}$. Instead, considering variations of ${\theta }_{-}^{+}$, the robustness of $f_{\infty }^{ST}$ seems to originate from the fact that the rates of symmetric divisions and feedback events compensate for each other. A more detailed analysis of the principles underlying the robustness properties of such models shall be performed in future work. This last application shows that, even though approximate, the moment equation approach provides valuable insights into the collective dynamics of cell populations.

3. Discussion

Compartmentalization of biochemical processes is a hallmark of living systems across different scales, from organelles to cell communities. Theoretical approaches which address the interplay between compartment and reaction dynamics are therefore of great relevance. In this work, we introduced a mathematical framework to model arbitrary compartmental and biochemical dynamics in a population of interacting compartments. Our approach relies on a fully stochastic treatment and is thus suitable to investigate the effect of mesoscopic fluctuations on compartmentalized biochemical systems. We have shown how the dynamics of a compartment population can be compactly described by ordinary differential equations, which capture means and variances of certain population moments, such as the compartment number or total molecular content. Therefore, this technique provides an analytical and computational means to efficiently access the statistical properties of the population, which would be costly to obtain using Monte Carlo simulation.

While the proposed approach is fairly general, it currently has a few limitations, which are worth addressing in the future. First, it relies on the availability of suitable moment closure approximations. In all our case studies, we found the Gamma closure to give accurate results, but different closures may be required for other types of systems. Second, we have focused on propensity functions that lead to self-contained moment dynamics, and we identified two sufficient conditions for this to be the case. While this entails a large class of systems, it will be interesting to extend our approach to more general rate laws, which are beyond these two conditions.

Our approach relies on a Markovian formalism, where the rate functions depend only on the current state of the population. However, coarse-grained events, such as cell division, can exhibit strong history dependencies. We have shown how memory effects can be included within our Markovian framework by coupling compartment events to internal processes or supplementary variables (45). For instance, in our last case study, we introduced an internal timer process which controls the rate of cell division, leading to peaked interdivision time distributions as observed experimentally (41). This strategy is similar to the work of ref. 46, where the authors have shown that a chemical system with molecular memory can be mapped onto an equivalent Markovian model.

In some of the presented case studies, we have shown how our framework can be used to track additional compartment properties in addition to their molecular content. For instance, compartments can be associated with distinct types or categories, each exhibiting different dynamical features. These categories could correspond to cell types or clusters of cells within different regions in a tissue. This could be particularly relevant for studying stochasticity in developmental systems, where cells originating from the same progenitors can commit to different fates and genetic programs in a spatiotemporal context.

Data Availability.

Derivations and additional information are provided in SI Appendix. The code used for simulations is available at GitHub, https://github.com/zechnerlab/StochasticCompartments.