Significance
Enzyme kinetic parameters are crucial for a quantitative understanding of metabolism, but traditionally have to be measured in laborious low-throughput assays. To solve this problem, the enzyme turnover number, kcat, can be estimated in vivo, but it is unclear whether in vivo estimates represent stable systems parameters that can be used for metabolic modeling. We present the data-driven estimation of in vivo kcats using proteomics and flux data of metabolic knock out strains of Escherichia coli. Our results show that in vivo kcats are stable parameters that can be used for metabolic modeling. We use the estimated in vivo kcats to parameterize metabolic models and show that model performance for gene expression predictions increases drastically compared to in vitro parameters.
Keywords: in vivo, turnover number, proteomics, kcat, gene knockout
Abstract
Enzyme turnover numbers (kcats) are essential for a quantitative understanding of cells. Because kcats are traditionally measured in low-throughput assays, they can be inconsistent, labor-intensive to obtain, and can miss in vivo effects. We use a data-driven approach to estimate in vivo kcats using metabolic specialist Escherichia coli strains that resulted from gene knockouts in central metabolism followed by metabolic optimization via laboratory evolution. By combining absolute proteomics with fluxomics data, we find that in vivo kcats are robust against genetic perturbations, suggesting that metabolic adaptation to gene loss is mostly achieved through other mechanisms, like gene-regulatory changes. Combining machine learning and genome-scale metabolic models, we show that the obtained in vivo kcats predict unseen proteomics data with much higher precision than in vitro kcats. The results demonstrate that in vivo kcats can solve the problem of inconsistent and low-coverage parameterizations of genome-scale cellular models.
Enzyme catalytic rates are crucial for understanding many properties of living systems like growth, proteome allocation, stress, and dynamic responses to perturbation. The turnover number of an enzyme, kcat, describes the maximal rate at which an enzyme’s catalytic site can catalyze a reaction. Knowledge of kcat has traditionally been a bottleneck in the quantitative understanding of cells, mainly because kcats have historically been obtained in labor-intensive, low-throughput in vitro assays. The substantial effort required for in vitro assays is likely the reason why, even in model organisms, only a small fraction of cellular enzymes has a measured kcat (1). Furthermore, in vitro kcat estimates for the same enzyme that are found in databases are frequently very inconsistent when different literature sources are compared (2), probably because different experimental protocols are used. Furthermore, in vitro conditions can miss important in vivo effects like posttranslational modifications, cellular crowding, or metabolite concentrations. The latter points hamper the utilization of in vitro kcats in genome-scale metabolic models.
In order to address the problems of low-throughput acquisition and in vivo−in vitro discrepancies, Davidi et al. (3) combined proteomics data and flux predictions to estimate in vivo turnover numbers based on apparent catalytic rate (kapp). Davidi et al. (3) integrated published Escherichia coli proteomics datasets with in silico flux predictions in multiple growth conditions and showed that the resulting maximum apparent catalytic rate (kapp,max) across growth conditions is significantly correlated with in vitro kcats. Thus, kapp,max has the potential to overcome the problem of inconsistent conditions, low coverage, and in vitro−in vivo discrepancies that hampers the use of in vitro kcats in large models of metabolism. However, it is unclear whether kapp,max is a stable system parameter that is robust to perturbation, and how much experimental procedures bias the estimation of kapp,max: Absolute proteomic quantification techniques are still suffering from high variation, and previous estimates of kcat were based on in silico flux predictions rather than 13C fluxomics data. Furthermore, kcat is expected to scale with growth rate (4). As many experimental conditions in the literature data used in Davidi et al. (3) resulted in low growth rates, the effective number of datasets contributing to kapp,max is low. Finally, if kapp,max is a useful estimator of in vivo kcat, it should improve the predictive capability of metabolic models on data that was not used to obtain kapp,max, that is, the performance on a test set.
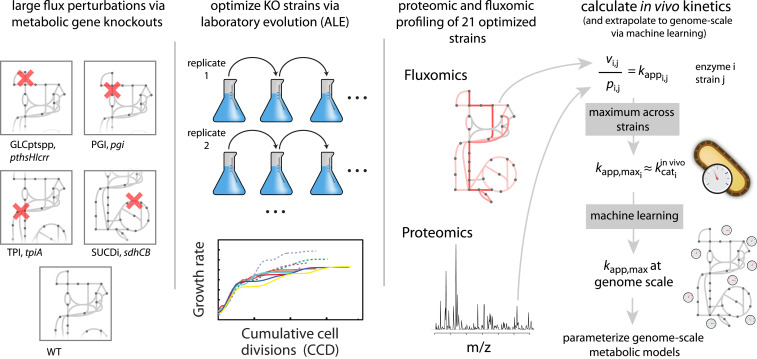
Here, we present an approach for estimating kcat in vivo (Fig. 1). We combined proteomic profiling with fluxomics data to estimate in vivo kcats in E. coli strains that have undergone strong physiological perturbations via knockout (KO) of metabolic genes. To obtain strains with high growth rates for which kapp approaches kapp,max, adaptive laboratory evolution (ALE) (5) was used on the metabolic KO strains. We profiled 21 strains, representing metabolic specialists with diverse flux profiles that are able to obtain high growth rates (6–9). With this data-driven approach, we show that in vivo kcats are stable and robust to genetic perturbations, and that they can be used in genome-scale models to obtain a high predictive performance for unseen protein abundance data.
Fig. 1.
Approach for obtaining kcat in vivo from metabolic specialists: KO of enzymes in central metabolism was followed by ALE to obtain 21 strains that had diverse flux profiles, while achieving high growth rates (6–9). Fluxomics and proteomics data were then integrated for the evolved strains to obtain the maximum kapp across the 21 strains (kapp,max) for each enzyme that could be mapped uniquely. The obtained kapp,max vector was then extrapolated to genome scale via supervised machine learning and used to parameterize genome-scale metabolic models. The resulting genome-scale models were then validated on unseen proteomics data.
Results
Quantifying In Vivo Kinetics in Metabolic Specialists.
In theory, kapp,max will approach kcat in vivo if a condition is found in which the respective enzyme is utilized at full efficiency. In order to achieve strong genetic perturbations of enzyme usage, we used gene KO strains for the phosphotransferase system (PTS) (ptsHIcrr; ref. 6), the phosphoglucose isomerase (pgi; ref. 8), triosephosphate isomerase (tpiA; ref. 7), and succinate dehydrogenase (sdhCB; ref. 9). As kapp increases with growth rate (4), we used KO strains that were optimized for growth on glucose minimal medium via ALE (6–9) experiments. In addition to these KO strains, we utilized a wild-type (WT) MG1655 strain that was subjected to ALE (6–10). As evolution is not a deterministic process, ALE endpoints differ in genotype, and we included a total of 21 strains that resulted from replicates of ALE experiments (i.e., four endpoint strains for ptsHIcrr, eight for pgi, four for tpiA, three for sdhCB, and two WT controls) and that were representative for the respective endpoint population. We subjected the selected strains to genome sequencing and used the resulting sequences as reference proteomes in liquid chromatography with tandem mass spectrometry (LC-MS/MS) proteomics (see Materials and Methods). Absolute quantification of biological duplicates was achieved via calibration to the UPS2 standard and the top3 metric (11, 12), which estimates protein abundance based on the average intensity of the three best ionizing peptides. Measured protein abundances show a median R2 of 0.91 between biological replicates, and a median number of 2,076 proteins were detected per strain (SI Appendix, Table S1). The obtained protein abundance vectors cluster by the genetic background of the strain used for ALE (SI Appendix, Fig. S1). This result indicates that protein levels have adjusted in a specific pattern to compensate for the respective gene KO (see refs. 6–9 for details on the transcript level).
Gene KO and ALE Cause Diversity in Enzyme Usage.
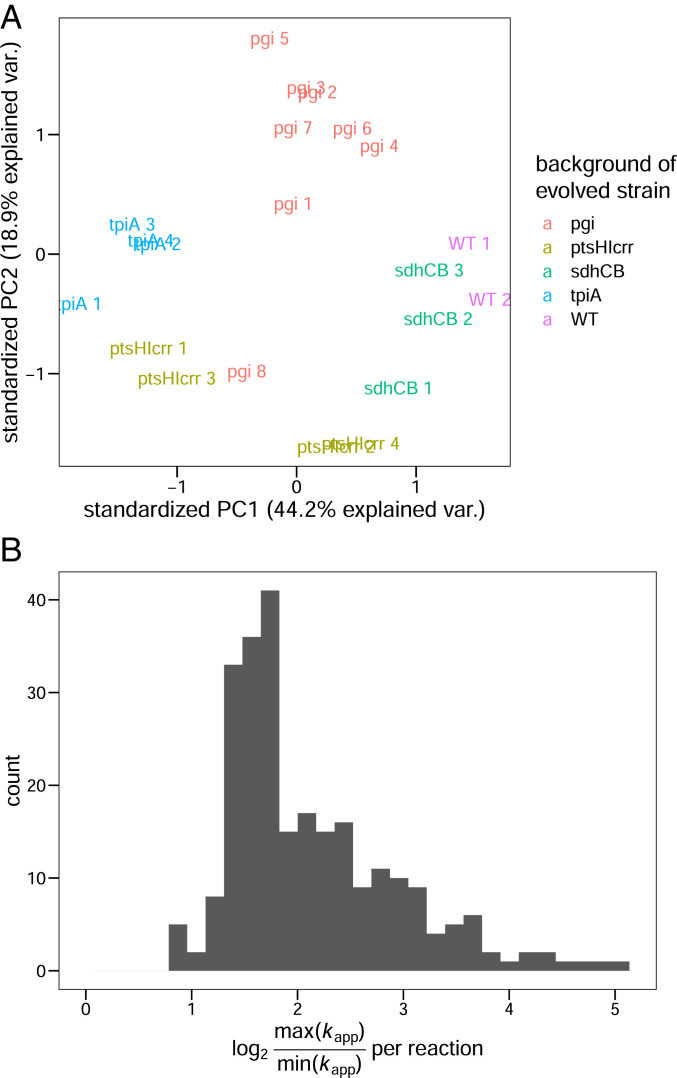
We integrated the measured protein abundances with 13C metabolic flux analysis (MFA) fluxomics data (6–9) to calculate apparent catalytic rates in the 21 strains as the ratio of flux and protein abundance. Like in Davidi et al. (3), we only calculated kapp for homomeric enzymes and reactions that are not catalyzed by multiple isoenzymes, to allow a specific mapping of proteins to reactions. This approach resulted in a median number of 258 enzymes per strain for which we were able to calculate kapp. The resulting apparent catalytic rates largely cluster by the genotype of the KO strain (Fig. 2A), confirming that enzyme usage was indeed perturbed by the respective KOs. Across the 21 strains, the maximum observed kapp of an enzyme is, on average, 4.4 times larger than the smallest observed kapp (Fig. 2B). This result indicates that considerable variation in enzyme usage was caused by the metabolic gene KO. To exclude the possibility that experimental variation causes this apparent diversity in enzyme usage, we compared the SD of kapp in biological replicates (mean on log10 scale = 0.07) to the SD measured across the 21 strains (mean on log10 scale = 0.18). We found that the variation caused by KOs and ALE is significantly larger than that caused by experimental variation (P < 2e-16, n1 = 5177, n2 = 311, Wilcoxon rank sum test).
Fig. 2.
Apparent catalytic rates cluster by genetic background and exhibit diversity across strains. (A) Data on kapp in each of the 21 strains projected onto the first two principal components. Only reaction−strain combinations for which kapp was available in all strains were used, resulting in 214 reactions used in the analysis. Data were centered and scaled before conducting principal component analysis. (B) Distribution of ranges of kapp across reactions. The log2 of the ratio between the highest and the lowest kapp per reaction is shown.
In Vivo Turnover Numbers Are Stable and Consistent.
We estimated in vivo kcat for a given enzyme as the maximum of kapp (kapp,max) in the 21 KO strains. This approach was similar to Davidi et al. (3), who estimated in vivo kcats as the maximum kapp over different growth conditions. Due to incomplete substrate saturation and backward flux, the apparent catalytic rate of an enzyme is smaller than the in vivo kcat. It is thus unclear whether kapp,max is a stable property of the system that can be used in metabolic models to give reliable predictions. Furthermore, absolute proteomics data and fluxomics data come with significant experimental uncertainties and biases that could prevent kapp,max from being useful in modeling applications.
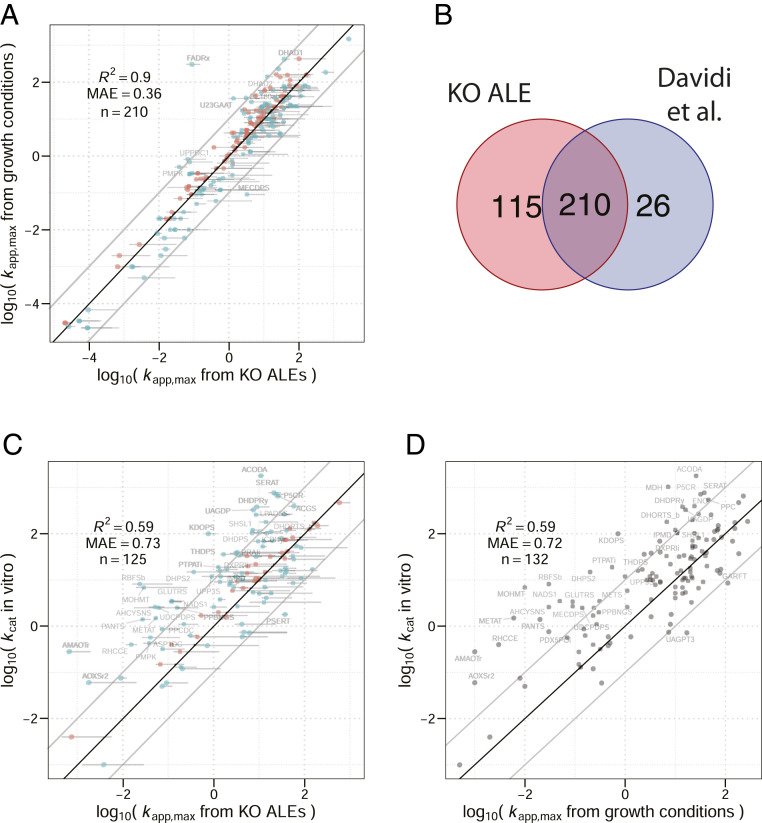
Even though our protocol perturbed enzyme kapp via gene KO and ALE, whereas Davidi et al. (3) used differences in growth conditions to achieve variation in enzyme usage, we found a very high agreement between kapp,max from the two sources (R2 = 0.9, Fig. 3A). We used a parametric bootstrap procedure to quantify the uncertainty in our kapp,max estimations (see Materials and Methods). We found that 42% (88 out of 210) of comparable values estimated by Davidi et al. (3) fall into the 95% CIs of the kapp,max values obtained in this study. A clear outlier is the reaction FAD reductase (FADRx; Fig. 3A). This discrepancy is caused by the different methods of flux estimation: While protein abundances of FAD reductase are relatively similar in the respective conditions for which the maximum kapp was measured [protein abundance is 2 times lower in Davidi et al. (3)], flux through the FADRx reaction in parsimonious flux balance analysis (FBA) (13) is 1,000 times higher than the flux estimated in 13C MFA.
Fig. 3.
Estimates of in vivo turnover numbers are consistent. (A) Comparison between kapp,max obtained from KO strains (this study) and kapp,max from growth conditions (3). MAE, mean absolute error. (B) Number of reactions for which kapp,max was obtained in KO strains (this study) and varying growth conditions (3). (C) Comparison between kapp,max obtained from KO strains and in vitro kcats. (D) Comparison between kapp,max obtained from KO strains and in vitro kcats (3). Horizontal lines are 95% CIs determined by 500 parametric bootstrap samples (see Materials and Methods). Points are marked red when the compared value falls into the 95% CI of kapp,max from KO strains and are colored blue if the compared value does not fall into the CI. Points are labeled with reaction IDs as given in the iJO1366 reconstruction (51) if the values differ by more than one order of magnitude. Data on kcat in vitro shown in C and D were taken from Davidi et al. (3) to allow for comparison between the studies. Davidi et al. (3) obtained this in vitro dataset from the Braunschweig Enzyme Database (BRENDA) (52) and utilized the maximal kcat in cases where multiple sources were available for the same enzyme.
It is worth noting that the mutations observed in the ALE strains are mostly regulatory in nature, with almost no structural changes in the homomeric enzymes examined in this study (see Dataset S1D and refs. 6–9 and 14 for details). One exception is the enzyme isocitrate dehydrogenase, which has shown a very high level of convergence for a coding sequence mutation (R395C) in seven out of the eight evolved pgi KO strains. We found no significant difference in kapp,max compared to the kapp,max of isocitrate dehydrogenase reported by Davidi et al. (3) (P = 0.28, n = 500, parametric bootstrap), suggesting that the structural mutation does not increase the in vivo catalytic efficiency.
In order to understand the relationship of kapp,max from KO strains with kcat in vitro, we compared kapp,max with a dataset of kcat in vitro that was compiled by Davidi et al. (3) for that purpose. This in vitro dataset originates from a variety of literature sources and thus varying assay conditions (3). While kapp,max from KO strains is very consistent with kapp,max from different growth conditions, the correlation with kcat in vitro is significantly lower (R2 = 0.59; Fig. 3C), and only 26% (32 out of 125) of the in vitro values fall into the 95% CIs of kapp,max. A similar low correlation with in vitro kcat was found in the kapp,max estimates published by Davidi et al. (3) (R2 = 0.59; Fig. 3D).
In summary, although we obtained kapp,max from a genetic perturbation rather than variation in growth conditions and used 13C fluxomics data instead of in silico flux, and despite proteomics and flux data being subject to significant noise, we found very high agreement between kapp,max from the two sources.
Using Machine Learning to Extrapolate to the Genome Scale.
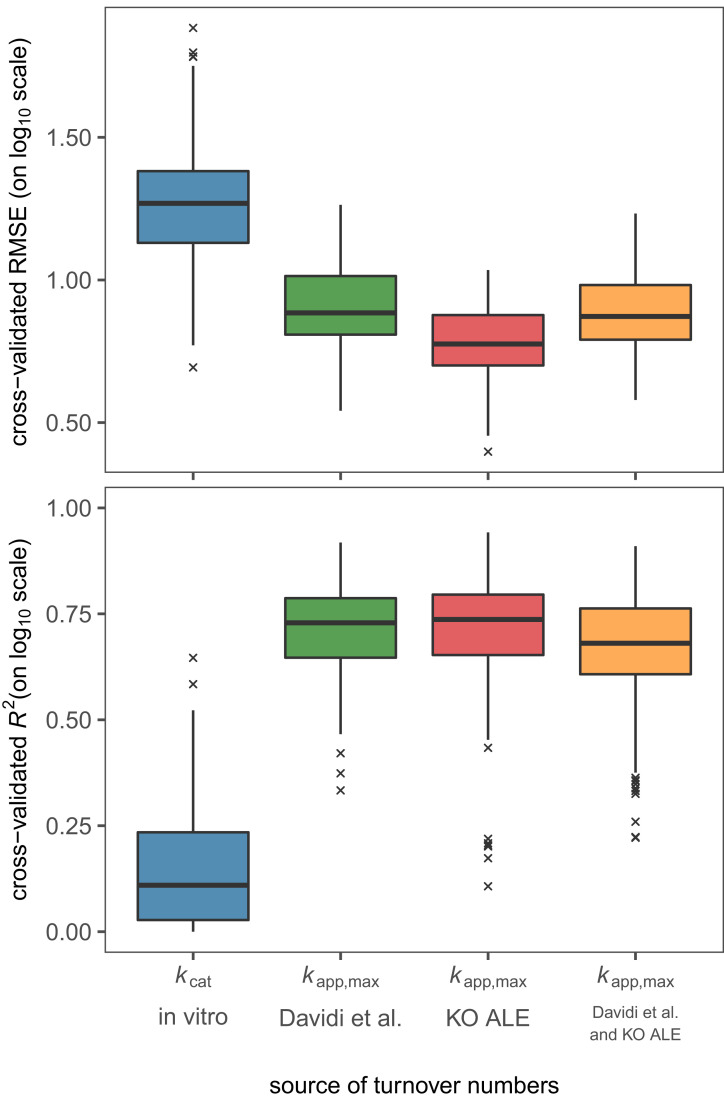
The problem of low coverage that is associated with kcat in vitro is also present in kapp,max: Not all protein abundance can be mapped to enzymes uniquely, and proteomics experiments still suffer from coverage issues. The final set of kapp,max values includes 325 enzymes (Fig. 3B). This coverage is 27% higher than that found in Davidi et al. (3), mostly because we used 13C fluxomics data that tends to have a higher sensitivity than the in silico method (parsimonious FBA; ref. 13) used by Davidi et al. (3). In order to validate the estimated in vivo turnover numbers in a genome-scale model that contains over 3,000 direction-specific reactions, we first needed to extrapolate the data to the genome scale. We used supervised machine learning on a diverse enzyme dataset (15) that includes data on enzyme network context, enzyme three-dimensional structure, and enzyme biochemistry to achieve this goal. An ensemble model of an elastic net, random forest, and neural network (15) showed good performance in cross-validation for the in vivo turnover numbers, where the highest performance was achieved for kapp,max that was obtained from the 21 KO strains (Fig. 4). Taking the maximum of kapp,max from this study and that of Davidi et al. (3) did not improve model performance, even though it resulted in the largest training set.
Fig. 4.
Performance of machine learning models on different sources of turnover numbers. The performance is estimated in five-times repeated five-fold cross-validation in elastic net, random forest, and a neural network (15) (see Materials and Methods). Data for kcat in vitro were taken from Heckmann et al. (15).
Validation of Turnover Numbers in Mechanistic Models.
The enzyme turnover number is a major determinant of gene expression levels, as it sets a lower limit on the enzyme concentration required to maintain a given flux. Turnover numbers are successfully used in genome-scale metabolic models to constrain metabolic fluxes by a limited cellular protein budget (16–18) or the balance of translation and dilution of proteins (19–21). The kapp,max obtained from diverse growth conditions was previously used successfully in genome-scale metabolic models, showing that the performance of protein abundance predictions of models using kapp,max was significantly higher than that of models using in vitro kcats (15). A major drawback of this analysis lies in the validation of the metabolic model which used data (22) that was also utilized in obtaining kapp,max (3), posing the risk of circular reasoning through data leakage. If kapp,max is a stable property of in vivo enzyme catalysis, it is expected to yield a high performance in metabolic models on unseen data; that is, kapp,max-based models should generalize well.
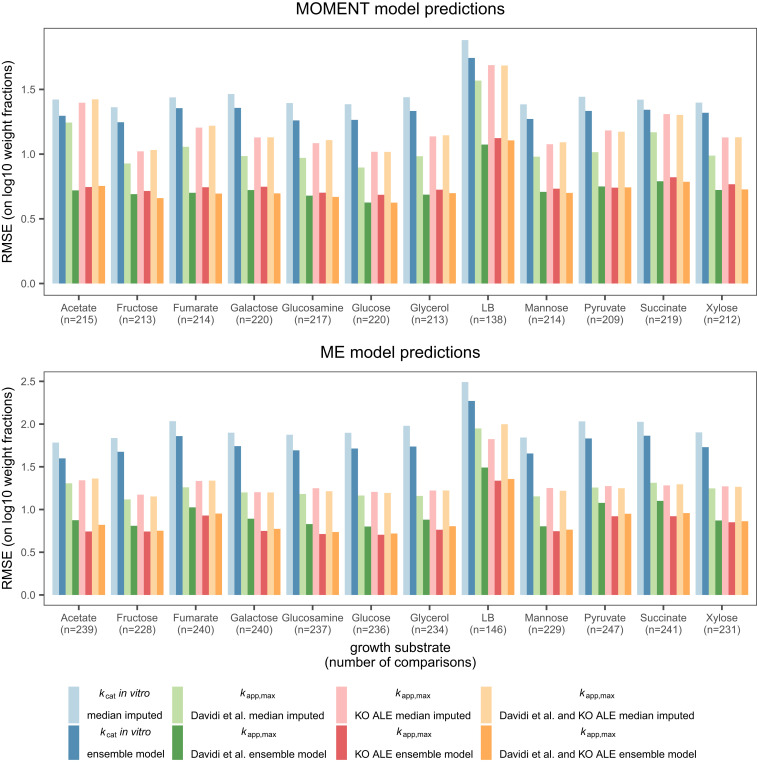
To test this hypothesis, we parameterized two genome-scale modeling algorithms of proteome-limited metabolism, a metabolic modeling with enzyme kinetics (MOMENT) model (16) and an integrated model of metabolism and macromolecular expression (ME model) (19), with kapp,max obtained from KO strains. We then used the model to predict enzyme abundance data under various growth conditions published by Schmidt et al. (22), a dataset that was not used to obtain kapp,max in this study. For comparison, we included model parameterization based on kcat in vitro, with kapp,max from Davidi et al. (3), and the maximum of kapp,max obtained in this study and that of Davidi et al. (3). We found that the performance of kapp,max from KO strains on the Schmidt et al. (22) data is very similar to that of Davidi et al. (3): The average root-mean-square error (RMSE) on log10 scale is 4% higher for the MOMENT model and 12% lower for the ME model, even though the Schmidt et al. (22) data were used to obtain kapp,max in Davidi et al. (3) (Fig. 5 and SI Appendix, Fig. S2). This good performance on unseen data confirms that in vivo kcat are stable against genetic perturbation and consistent across experimental protocols.
Fig. 5.
Performance of turnover number vectors in mechanistic models of proteome allocation. The MOMENT algorithm and an ME model were parameterized with different sources of turnover numbers [including Davidi et al. (3)]. Growth on different carbon sources was simulated with the two algorithms to predict relative protein weight fractions of metabolic enzymes. The protein abundance predictions were then compared to proteomics data in the respective growth condition published by Schmidt et al. (22) using the RMSE on log10 scale. Machine learning model predictions were based on the protocol introduced by Heckmann et al. (15), but all models were newly trained on the data produced in this study (Dataset S1).
We further found that kapp,max outperforms kcat in vitro in MOMENT and ME models across all growth conditions (Fig. 5). When comparing median-imputed kcat parameterizations to those using supervised machine learning, we found that machine learning reduces RMSE on log10 scale by 38% for kapp,max and 10% for kcat in vitro, confirming the utility of this approach (15).
Discussion
A large-scale characterization of the kinetic parameters that govern metabolism, termed the kinetome (1), has been a major hurdle in our quantitative understanding of cellular behavior (1, 23, 24). Previous efforts to use kcat, which represents a major fraction of the kinetome, at the genome scale either utilized in vitro data (16, 18) or fitted kinetic parameters to physiological data (4, 25, 26). While the parameterization with in vitro kcats can suffer from varying assay protocols, low throughput, and potentially missing in vivo effects, parameter fitting is frequently underdetermined and leads to nonunique solutions that cannot be expected to generalize well when used in new conditions. The use of proteomics data and flux predictions on homomeric enzymes (3), for which proteome abundances can be assigned uniquely, is a promising approach that could solve many shortcomings of in vitro data and fitting approaches. While it was shown that this approximation of in vivo kcat, kapp,max, exhibits a decent correlation with kcat in vitro, it is unclear whether kapp,max captures an upper bound on enzymatic rate that is stable with respect to genetic perturbations and consistent across experimental procedures. These properties are prerequisites for the application of kapp,max in metabolic models.
We found that in vivo turnover numbers that are obtained from KO strains are surprisingly consistent between very different protocols (Fig. 3). Specifically, the protocol we used to obtain kapp,max shows the following differences compared to that of Davidi et al. (3): 1) kapp is not perturbed by growth conditions, but by genetic KOs; 2) we used 13C MFA fluxomics data instead of in silico data from parsimonious FBA; 3) we utilized proteomics data that were obtained with a single LC-MS/MS protocol, avoiding batch effects; and 4) all data were obtained under batch growth that promotes high growth rates, increasing kapp (4). Given these differences in the two approaches to obtain kapp,max, the high agreement between the two methods indicates a high stability and consistency of in vivo kcats.
The high stability of in vivo kcats indicates that the adaptation of the strains during ALE does not lead to drastic increases in in vivo kcats. This hypothesis is supported by the relatively low number of convergent mutations in the coding regions of enzymes (Dataset S1D). Short-term metabolic evolution appears to be governed by changes in gene regulation, rather than changes in enzyme efficiencies, at least in the case of the homomeric enzymes investigated in this study.
Why does kapp,max exhibit a high consistency, where, in contrast, in vitro kcats often show a low agreement between different sources (2)? In the context of large metabolic models, in vitro kcats are typically obtained from hundreds of different publications that are collected in databases. Thus, it is usually not possible to obtain data that use uniform experimental protocols that mimic the in vivo situation of interest. In contrast, kapp,max is obtained from a small number of proteomics and flux datasets that were ideally obtained on the same instruments, thus avoiding batch effects. Furthermore, there is some indication that metabolite levels in vivo tend to saturate many enzymes (27). Such a high saturation might allow for conditions of high enzyme saturation to be found even with a relatively small number of system perturbations.
Some sources of uncertainty remain in the kapp,max values presented in this study. The 13C MFA data that we used were obtained for the endpoint populations of the respective ALE experiments (6–9), whereas we used clonal samples for proteomics experiments. While we chose clones that represented the most dominant mutations found in the endpoint populations, flux distributions could be affected by uncommon mutations. Furthermore, 13C MFA data can yield high coverage (28), but it still relies heavily on the quality of the underlying network model, which could bias analyses.
Because not all enzymes can be mapped to a reaction uniquely and proteomics data still suffer from incomplete coverage, kapp,max has a low coverage of the metabolic network and cannot be readily used in genome-scale models. Based on mechanistic knowledge of factors that shape enzyme turnover numbers (2, 29, 30), supervised machine learning was previously used successfully to extrapolate in vivo kcats to the genome scale (15). We find a slightly lower error in cross-validation on kapp,max obtained from KO strains compared to kapp,max from varying growth conditions (3); this slight increase in performance may lie in the increased size of the training set, as we were able to obtain 38% more kapp,max values due to the use of 13C MFA data. This finding is consistent with previously computed learning curves of kapp,max on the Davidi et al. (3) dataset that showed that a domain of diminishing returns in model performance is reached with respect to the size of the training set (15).
We find that metabolic models that are parameterized with the kapp,max values we obtained from KO strains lead to very good predictive performance on unseen proteomics data. This performance in mechanistic models supports the hypothesis that kapp,max indeed represents a stable property of the system, that is, kcat in vivo. Thus, kapp,max can enable genome-scale metabolic models that generalize well to unseen conditions.
While kinetic parameters remain difficult to obtain, the stable and consistent properties of in vivo kcats support the notion that these parameters can improve the predictive capabilities of metabolic models significantly, and thus enable better quantitative understanding of the cell. Finally, the high stability of in vivo kcats suggests that short-term metabolic evolution is governed by changes in gene expression, rather than adaptation at the level of enzyme kinetics.
Materials and Methods
Strain Genomic Sequencing.
Genomic DNA of ALE endpoint clones was isolated using bead agitation in 96-well plates as outlined previously (31). Paired-end whole-genome DNA sequencing libraries were generated with a Kapa HyperPlus library prep kit (Kapa Biosystems) and run on an Illumina HiSeq 4000 platform with a HiSeq SBS kit, 150 base pair reads. The generated DNA sequencing fastq files were processed with the breseq computational pipeline (version 0.32.0) (32) and aligned to an E. coli K12 MG1655 reference genome (33) to identify mutations. DNA sequencing quality control was accomplished using the software AfterQC (version 0.9.7) (34).
Clones were chosen in order to represent the high-frequency alleles found in the endpoint populations of the respective ALE experiments. DNA sequences were used to create reference proteomes for proteomics experiments described below.
Sample Preparation.
For each strain, 3 mL of culture was grown overnight at 37 °C with shaking in M9 medium (4 g of glucose L−1) (35) with trace elements (36), and then passed twice the following days in 15 mL of media at 37 °C from optical density (OD) 0.05 to 0.1 to OD 1.0 to 1.5. For the experiment, 100 mL of culture with initial OD600 (OD at a wavelength of 600 nm) = 0.1 was grown in flasks with stirring in a water bath at 37 °C. When cultures reached OD600 = 0.6, 40 mL of culture was collected and immediately put on ice. The cells were pelleted by centrifuge at 5,000 rpm at 4 °C for 20 min. Cell pellets were then washed with 20 mL of cold phosphate-buffered saline (PBS) buffer three times and centrifuged at 5,000 rpm for 20 min at 4 °C. Pellets were transferred into 1.5-mL microcentrifuge tubes and centrifuged at 8,000 rpm at 4 °C for 10 min. Remaining PBS buffer was removed, and pellets of proteomic samples were frozen at −80 °C.
Sample Lysis for Proteomics.
Frozen samples were immersed in a lysis buffer comprising 75 mM NaCl (Sigma Aldrich), 3% sodium dodecyl sulfate (Fisher Scientific), 1 mM sodium fluoride (VWR International, LLC), 1 mM β-glycerophosphate (Sigma Aldrich), 1 mM sodium orthovanadate, 10 mM sodium pyrophosphate (VWR International, LLC), 1 mM phenylmethylsulfonyl fluoride (Fisher Scientific), 50 mM Hepes (Fisher Scientific) pH 8.5, and 1× complete ethylenediaminetetraacetic acid-free protease inhibitor mixture. Samples were subjected to rapid mixing and probe sonication using a Q500 QSonica sonicator (Qsonica) equipped with a 1.6-mm microtip at amplitude 20%. Samples were subjected to three cycles of 10 s of sonication followed by 10 s of rest, with a total sonication time of 50 s.
Protein Abundance Quantitation.
Total protein abundance was determined using a bicinchoninic acid Protein Assay Kit (Pierce) as recommended by the manufacturer.
Peptide Isolation.
Six milligrams of protein was aliquoted for each sample. Sample volume was brought up to 20 mL in a solution of 4 M Urea + 50 mM Hepes, pH = 8.5. Disulfide bonds were reduced in 5 mM dithiothreitol (DTT) for 30 min at 56 °C. Reduced disulfide bonds were alkylated in 15 mM of iodoacetamide in a darkened room-temperature environment for 20 min. The alkylation reaction was quenched via the addition of the original volume of DTT for 15 min in a darkened environment at room temperature. Proteins were next precipitated from solution via the addition of 5 μL of 100% wt/vol trichloroacetic acid. Samples were mixed and incubated on ice for 10 min. Samples were subjected to centrifugation at 16,000 × g for 5 min at 4 °C. The supernatant was removed and sample pellets were gently washed in 50 μL of ice-cold acetone. Following the wash step, samples were subjected to centrifugation at 16,000 × g at 4 °C. The acetone wash was repeated, and the final supernatant was removed. Protein pellets were dried on a heating block at 56 °C for 15 min, and pellets were resuspended in a solution of 1 M Urea + 50 mM Hepes, pH = 8.5. The UPS2 standard (Sigma) was reconstituted as follows. Twenty milliliters of a solution of 4 M Urea + 50 mM Hepes, pH = 8.5 was added to the tube. The sample tube was subjected to vortexing and water bath sonication for 5 min each. The standard was subjected to reduction and alkylation using methods described above. The sample was next diluted in a solution of 50 mM Hepes, pH = 8.5 such that the final concentration of Urea was 1 M. Then 0.88 mg of the protein standard was spiked into each experimental sample, and samples were subjected to a two-step digestion process. First, samples were digested using 6.6 μg of LysC at room temperature overnight, shaking. Next, protein was digested in 1.65 μg of sequencing-grade trypsin (Promega) for 6 h at 37 °C. Digestion reactions were terminated via the addition of 3.3 μL of 10% trifluoroacetic acid (TFA), and were brought up to a sample volume of 300 μL of 0.1% TFA. Samples were subjected to centrifugation at 16,000 × g for 5 min and desalted with in-house-packed desalting columns using methods adapted from previously published studies (37, 38). Following desalting, samples were lyophilized, and then stored at −80 °C until further use.
LC-MS/MS.
Samples were resuspended in a solution of 5% acetonitrile (ACN) and 5% formic acid (FA). Samples were subjected to vigorous vortexing and water bath sonication. Samples were analyzed on an Orbitrap Fusion Mass Spectrometer with in-line Easy NanoLC (Thermo) in technical triplicate. Samples were run on an increasing gradient from 6 to 25% ACN + 0.125% FA for 70 min, then 100% ACN + 0.125% FA for 10 min. One milligram of each sample was loaded onto an in-house−pulled and −packed glass capillary column heated to 60 °C. The column measured 30 cm in length, with outer diameter of 360 mm and inner diameter of 100 mm. The tip was packed with C4 resin with diameter of 5 mm to 0.5 cm, then with C18 resin with diameter of 3 mm an additional 0.5 cm. The remainder of the column up to 30 cm was packed with C18 resin with diameter of 1.8 mm. Electrospray ionization was achieved via the application of 2,000 V to a T-junction connecting sample, waste, and column capillary termini. The mass spectrometer was run in positive polarity mode. MS1 scans were performed in the Orbitrap, with a scan range of 375 m/z to 1,500 m/z with resolution of 120,000. Automatic gain control (AGC) was set to 5 × 105, with maximum ion inject time of 100 ms. Dynamic exclusion was performed at 30-s duration. Top n was used for fragment ion isolation, with n = 10. The decision tree option was used for fragment ion analysis. Ions with charge state of 2 were isolated between 375 m/z and 1,500 m/z, and ions with charge states 3 to 6 were isolated between 600 m/z and 1,500 m/z. Precursor ions were fragmented using fixed Collision-Induced Dissociation. Fragment ion detection occurred in the linear ion trap, and data were collected in profile mode. Target AGC was set to 1 × 104.
Technical triplicate spectral data were searched against a customized reference proteome comprising the reference proteome of the respective strain (see above) appended to the UPS2 fasta sequences (Sigma) using Proteome Discoverer 2.1 (Thermo). Spectral matching and in silico decoy database construction was performed using the SEQUEST algorithm (39). Precursor ion mass tolerance was set to 50 parts per million. Fragment ion mass tolerance was set to 0.6 Da. Trypsin was specified as the digesting enzyme, and two missed cleavages were allowed. Peptide length tolerated was set to 6 to 144 amino acids. Dynamic modification included oxidation of methionine (+15.995 Da), and static modification included carbamidomethylation of cysteine residues (+57.021 Da). A false-discovery rate of 1% was applied during spectral searches.
Protein Abundance Estimation.
In order to estimate absolute protein abundance, the top3 metric was calculated for each protein as the average of the three highest peptide areas (11, 12). Robust linear regression (as implemented in the Modern Applied Statistics with S (MASS) package; ref. 40) was used to calibrate top3 with the UPS2 standard according to the following model to obtain the amount of loaded protein A:
In order to obtain abundance relative to cell dry weight (C), we use a constant ratio γ = 13.94 µmol⋅gDW−1 (41),
Calculation of kapp,max.
For each biological replicate, apparent catalytic rates kapp were calculated as the ratio of protein abundance and measured flux if 1) the protein abundance surpassed 50 pmol⋅gDW−1 and 2) the estimated flux was at least 4 times larger than the range of the 95% CI and larger than 100 fmol⋅gDW−1 h−1, and the 95% CI did not include zero, as defined in McCloskey et al. (28).
For each of the two biological replicates per strain, kapp,max was calculated as the maximum kapp,max across the 21 strains. Finally, the average kapp,max over the two replicates was calculated and used in the presented analyses.
Parametric Bootstrap for kapp,max.
We used a parametric bootstrap approach to estimate how experimental variability in proteomics and fluxomics data affects kapp,max. For each enzyme, we assumed protein abundance to be normally distributed with mean and SD estimated from the biological replicates for the respective enzyme. In cases where only one biological replicate was available due to lack of detection in the MS/MS, we imputed the missing SD with a linear regression of SD (on log scale) against mean abundance (on log scale) for all available enzymes. Variability in flux data for the respective reaction was also assumed to take a normal distribution, where we used the SD estimated in the MFA procedure that resulted from multiple MFA model reruns on biological triplicates (as described in refs. 6–9). For each reaction, 500 bootstrap samples were simulated based on the parameterized normal distributions of protein abundance and flux for that reaction, and these samples were used to calculate 95% CIs for kapp,max.
Machine Learning.
Turnover numbers were extrapolated to the genome scale using the machine learning approach published previously (15). In this supervised machine learning procedure, enzyme features on enzyme network context, enzyme structure, biochemical mechanism, and, in the case of kcat in vitro, assay conditions were utilized (15). These enzyme features were labeled with the kapp,max values estimated in this study, and an ensemble model of elastic net, random forest, and neural network was trained using the caret package (42) and h2o (43). The ensemble used an average of the predictions of the three individual models. Model hyperparameters were chosen in five-times repeated cross-validation (one repetition in the case of neural networks) based on the RMSE metric, as reported in Heckmann et al. (15). For the neural networks, random discrete search was used for optimization of hyperparameters (15).
MOMENT Modeling.
Validation of different turnover number vectors in the MOMENT model was conducted as described in Heckmann et al. (15). In the MOMENT algorithm, a flux distribution is computed that maximizes strain growth rate subject to constraints on the total protein budget of the cell (16). In order to constrain fluxes based on enzyme usage, the algorithm requires kcat parameters (16). Here, we use the respective vectors of kcat from different sources to parameterize MOMENT and thus to predict protein abundances that were experimentally determined by Schmidt et al. (22). The genome-scale metabolic model iML1515 (44) was used in the R (45) packages sybil (46) and sybilccFBA (47) to construct linear programming problems that were solved in IBM CPLEX version 12.7.
ME Modeling.
To complement the MOMENT-based validation of the computed turnover numbers, a similar validation approach was employed with the iJL1678b-ME genome-scale model of E. coli metabolism and gene expression (48). The ME model contains a detailed description of the cell’s gene expression machinery that is not contained in the MOMENT model. The kapps were mapped to iJL1678b-ME as previously described (15). However, the ME model kapps were adjusted due to a key difference that lies in the way that the MOMENT and ME model resource allocation models apply enzyme constraints. MOMENT accounts for each unique protein contained within a catalytic enzyme, whereas the ME model formulation accounts for the complete number of protein subunits in an enzyme. As a result, the macromolecular “cost” of catalyzing a reaction in the ME model is often notably higher than in MOMENT. To account for this, the kapps in the ME model were adjusted by scaling each kapp by the number of protein subunits divided by the number of unique proteins.
The ME model was solved in quad precision using the qMINOS solver (49) and a bisection algorithm (50) to determine the maximum feasible model growth rate, within a tolerance of of 10−12. All proteins in a solution with a computed synthesis greater than zero copies per cell were compared to experimentally measured protein abundances. Since the ME model accounts for the activity of many proteins outside of the scope of the kapp prediction method, only those that overlap with predicted kapps were considered.
Supplementary Material
Acknowledgments
This work was funded by the Novo Nordisk Foundation Grant NNF10CC1016517. We thank Dan Davidi and Douglas McCloskey for insightful discussions, Lars Nielsen for insightful comments on the manuscript, and Marc Abrams for proofreading the manuscript.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. A.C-B. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2001562117/-/DCSupplemental.
Data Availability.
Results of genome sequencing and mutation calling were deposited to ALEdb (aledb.org) as part of the “Central Carbon Knockout (CCK) project.” MS-based proteomic data can be found on the ProteomeXchange Consortium (http://proteomecentral.proteomexchange.org) with the dataset identifier PXD015344. Inferred protein abundances, MFA fluxes, and resulting kapps are available as Dataset S1A. Sets of kapp,max are available as Dataset S1B. A table of kcat in vitro and kapp,max extrapolated with machine learning models or the median is available as Dataset S1C. A mutation table of the strains used in this study is available as Dataset S1D. Source code in R and Python used for producing the analyses presented in this article is available in GitHub under https://github.com/SBRG/Kinetome_profiling. All study data are included in the article and SI Appendix.
References
- 1.Nilsson A., Nielsen J., Palsson B. O., Metabolic models of protein allocation call for the kinetome. Cell Syst. 5, 538–541 (2017). [DOI] [PubMed] [Google Scholar]
- 2.Bar-Even A.et al., The moderately efficient enzyme: Evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 50, 4402–4410 (2011). [DOI] [PubMed] [Google Scholar]
- 3.Davidi D.et al., Global characterization of in vivo enzyme catalytic rates and their correspondence to in vitro kcat measurements. Proc. Natl. Acad. Sci. U.S.A. 113, 3401–3406 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goelzer A.et al., Quantitative prediction of genome-wide resource allocation in bacteria. Metab. Eng. 32, 232–243 (2015). [DOI] [PubMed] [Google Scholar]
- 5.Sandberg T. E., Salazar M. J., Weng L. L., Palsson B. O., Feist A. M., The emergence of adaptive laboratory evolution as an efficient tool for biological discovery and industrial biotechnology. Metab. Eng. 56, 1–16 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McCloskey D.et al., Adaptive laboratory evolution resolves energy depletion to maintain high aromatic metabolite phenotypes in Escherichia coli strains lacking the phosphotransferase system. Metab. Eng. 48, 233–242 (2018). [DOI] [PubMed] [Google Scholar]
- 7.McCloskey D.et al., Adaptation to the coupling of glycolysis to toxic methylglyoxal production in tpiA deletion strains of Escherichia coli requires synchronized and counterintuitive genetic changes. Metab. Eng. 48, 82–93 (2018). [DOI] [PubMed] [Google Scholar]
- 8.McCloskey D.et al., Multiple optimal phenotypes overcome redox and glycolytic intermediate metabolite imbalances in Escherichia coli pgi knockout evolutions. Appl. Environ. Microbiol. 84, e00823-18 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McCloskey D.et al., Growth adaptation of gnd and sdhCB Escherichia coli deletion strains diverges from a similar initial perturbation of the transcriptome. Front. Microbiol. 9, 1793 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.LaCroix R. A.et al., Use of adaptive laboratory evolution to discover key mutations enabling rapid growth of Escherichia coli K-12 MG1655 on glucose minimal medium. Appl. Environ. Microbiol. 81, 17–30 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Silva J. C., Gorenstein M. V., Li G.-Z., Vissers J. P. C., Geromanos S. J., Absolute quantification of proteins by LCMSE: A virtue of parallel MS acquisition. Mol. Cell. Proteomics 5, 144–156 (2006). [DOI] [PubMed] [Google Scholar]
- 12.Ahrné E., Molzahn L., Glatter T., Schmidt A., Critical assessment of proteome-wide label-free absolute abundance estimation strategies. Proteomics 13, 2567–2578 (2013). [DOI] [PubMed] [Google Scholar]
- 13.Holzhütter H.-G., The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur. J. Biochem. 271, 2905–2922 (2004). [DOI] [PubMed] [Google Scholar]
- 14.McCloskey D.et al., Evolution of gene knockout strains of E. coli reveal regulatory architectures governed by metabolism. Nat. Commun. 9, 3796 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Heckmann D.et al., Machine learning applied to enzyme turnover numbers reveals protein structural correlates and improves metabolic models. Nat. Commun. 9, 5252 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Adadi R., Volkmer B., Milo R., Heinemann M., Shlomi T., Prediction of microbial growth rate versus biomass yield by a metabolic network with kinetic parameters. PLOS Comput. Biol. 8, e1002575 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Beg Q. K.et al., Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc. Natl. Acad. Sci. U.S.A. 104, 12663–12668 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sánchez B. J.et al., Improving the phenotype predictions of a yeast genome-scale metabolic model by incorporating enzymatic constraints. Mol. Syst. Biol. 13, 935 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lerman J. A.et al., In silico method for modelling metabolism and gene product expression at genome scale. Nat. Commun. 3, 929 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.O’Brien E. J., Lerman J. A., Chang R. L., Hyduke D. R., Palsson B. Ø., Genome-scale models of metabolism and gene expression extend and refine growth phenotype prediction. Mol. Syst. Biol. 9, 693 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yang L., Yurkovich J. T., King Z. A., Palsson B. O., Modeling the multi-scale mechanisms of macromolecular resource allocation. Curr. Opin. Microbiol. 45, 8–15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schmidt A.et al., The quantitative and condition-dependent Escherichia coli proteome. Nat. Biotechnol. 34, 104–110 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Davidi D., Milo R., Lessons on enzyme kinetics from quantitative proteomics. Curr. Opin. Biotechnol. 46, 81–89 (2017). [DOI] [PubMed] [Google Scholar]
- 24.van Eunen K., Bakker B. M., The importance and challenges of in vivo-like enzyme kinetics. Perspect. Sci. 1, 126–130 (2014). [Google Scholar]
- 25.Ebrahim A.et al., Multi-omic data integration enables discovery of hidden biological regularities. Nat. Commun. 7, 13091 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Khodayari A., Maranas C. D., A genome-scale Escherichia coli kinetic metabolic model k-ecoli457 satisfying flux data for multiple mutant strains. Nat. Commun. 7, 13806 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bennett B. D.et al., Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nat. Chem. Biol. 5, 593–599 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McCloskey D., Young J. D., Xu S., Palsson B. O., Feist A. M., Modeling method for increased precision and scope of directly measurable fluxes at a genome-scale. Anal. Chem. 88, 3844–3852 (2016). [DOI] [PubMed] [Google Scholar]
- 29.Heckmann D., Zielinski D. C., Palsson B. O., Modeling genome-wide enzyme evolution predicts strong epistasis underlying catalytic turnover rates. Nat. Commun. 9, 5270 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Davidi D., Longo L. M., Jabłońska J., Milo R., Tawfik D. S., A bird’s-eye view of enzyme evolution: Chemical, physicochemical, and physiological considerations. Chem. Rev. 118, 8786–8797 (2018). [DOI] [PubMed] [Google Scholar]
- 31.Marotz C.et al., DNA extraction for streamlined metagenomics of diverse environmental samples. Biotechniques 62, 290–293 (2017). [DOI] [PubMed] [Google Scholar]
- 32.Deatherage D. E., Barrick J. E., Identification of mutations in laboratory-evolved microbes from next-generation sequencing data using breseq. Methods Mol. Biol. 1151, 165–188 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Phaneuf P., SBRG/bop27refseq. Zenodo. 10.5281/zenodo.1301236. Accessed 28 August 2020. [DOI]
- 34.Chen S.et al., AfterQC: Automatic filtering, trimming, error removing and quality control for fastq data. BMC Bioinf. 18 (suppl. 3), 80 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sambrook J., Russell D. W., Molecular Cloning: A Laboratory Manual, (Cold Spring Harbor Laboratory Press, ed. 3, 2001). [Google Scholar]
- 36.Fong S. S.et al., In silico design and adaptive evolution of Escherichia coli for production of lactic acid. Biotechnol. Bioeng. 91, 643–648 (2005). [DOI] [PubMed] [Google Scholar]
- 37.Lapek J. D. Jr., Lewinski M. K., Wozniak J. M., Guatelli J., Gonzalez D. J., Quantitative temporal viromics of an inducible HIV-1 model yields insight to global host targets and phospho-dynamics associated with protein Vpr. Mol. Cell. Proteomics 16, 1447–1461 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rappsilber J., Ishihama Y., Mann M., Stop and go extraction tips for matrix-assisted laser desorption/ionization, nanoelectrospray, and LC/MS sample pretreatment in proteomics. Anal. Chem. 75, 663–670 (2003). [DOI] [PubMed] [Google Scholar]
- 39.Eng J. K., McCormack A. L., Yates J. R., An approach to correlate tandem mass spectral data of peptides with amino acid sequences in a protein database. J. Am. Soc. Mass Spectrom. 5, 976–989 (1994). [DOI] [PubMed] [Google Scholar]
- 40.Venables W. N., Ripley B. D., Modern Applied Statistics with S, (Springer, ed. 5, 2002). [Google Scholar]
- 41.Neidhardt F. C.et al., Escherichia coli and Salmonella: Cellular and Molecular Biology, (ASM Press, ed. 2, 1996). [Google Scholar]
- 42.Kuhn M., Others, caret package. J. Stat. Softw. 28, 1–26 (2008).27774042 [Google Scholar]
- 43.Candel A., Parmar V., LeDell E., Arora A., Deep Learning with H2O, (H2O.ai Inc., 2016). [Google Scholar]
- 44.Monk J. M.et al., iML1515, a knowledgebase that computes Escherichia coli traits. Nat. Biotechnol. 35, 904–908 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.R Core Team , R: A Language and Environment for Statistical Computing, (R Foundation for Statistical Computing, Vienna, Austria, 2017). [Google Scholar]
- 46.Gelius-Dietrich G., Desouki A. A., Fritzemeier C. J., Lercher M. J., Sybil—Efficient constraint-based modelling in R. BMC Syst. Biol. 7, 125 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Desouki A. A., sybilccFBA: Cost Constrained FLux Balance Analysis: MetabOlic Modeling with ENzyme kineTics (MOMENT), version 2.0.0. https://CRAN.R-project.org/package=sybilccFBA. Accessed 28 August 2020.
- 48.Lloyd C. J., et al., COBRAme: A computational framework for genome-scale models of metabolism and gene expression. PLoS Comput. Biol. 14, e1006302 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ma D.et al., Reliable and efficient solution of genome-scale models of metabolism and macromolecular expression. Sci. Rep. 7, 40863 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yang L.et al., solveME: Fast and reliable solution of nonlinear ME models. BMC Bioinf. 17, 391 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Orth J. D.et al., A comprehensive genome-scale reconstruction of Escherichia coli metabolism–2011. Mol. Syst. Biol. 7, 535 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Schomburg I.et al., BRENDA, the enzyme database: Updates and major new developments. Nucleic Acids Res. 32, D431–D433 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Results of genome sequencing and mutation calling were deposited to ALEdb (aledb.org) as part of the “Central Carbon Knockout (CCK) project.” MS-based proteomic data can be found on the ProteomeXchange Consortium (http://proteomecentral.proteomexchange.org) with the dataset identifier PXD015344. Inferred protein abundances, MFA fluxes, and resulting kapps are available as Dataset S1A. Sets of kapp,max are available as Dataset S1B. A table of kcat in vitro and kapp,max extrapolated with machine learning models or the median is available as Dataset S1C. A mutation table of the strains used in this study is available as Dataset S1D. Source code in R and Python used for producing the analyses presented in this article is available in GitHub under https://github.com/SBRG/Kinetome_profiling. All study data are included in the article and SI Appendix.