Excimer Intermediates en Route to Long-Lived Charge-Transfer States in Single-Stranded Adenine DNA as Revealed by Nonadiabatic Dynamics

Abstract

The ultrafast time evolution of a single-stranded adenine DNA is studied using a hybrid multiscale quantum mechanics/molecular mechanics (QM/MM) scheme coupled to nonadiabatic surface hopping dynamics. As a model, we use (dA)₂₀ where a stacked adenine tetramer is treated quantum chemically. The dynamical simulations combined with on-the-fly quantitative wave function analysis evidence the nature of the long-lived electronically excited states formed upon absorption of UV light. After a rapid decrease of the initially excited excitons, relaxation to monomer-like states and excimers occurs within 100 fs. The former monomeric states then relax into additional excimer states en route to forming stabilized charge-transfer states on a longer timescale of hundreds of femtoseconds. The different electronic-state characters is reflected on the spatial separation between the adenines: excimers and charge-transfer states show a much smaller spatial separation than the monomer-like states and the initially formed excitons.

Understanding the impact that light has on DNA,¹ for instance, as photodamage on the genetic code,² requires the characterization of the electronically excited states created upon light absorption as well as their time evolution beyond the Franck–Condon region. The collective excited state behavior of DNA depends on a number of structural and electronic interactions, which are often interrogated with time-resolved spectroscopy and theory.³⁻⁹ Stacking interactions between nucleobases is one important mechanism that affects the excited-state behavior of DNA versus isolated nucleobases and mononucleotides.^1,3,8,10,11 They cause the formation of delocalized exciton states upon UV absorption, influencing decay lifetimes strongly.⁶ Thus, while single nucleobases and mononucleotides return to the ground state mainly by internal conversion within hundreds of femtoseconds, polynucleotides live drastically longer.¹ Despite initial experimental controversy, it is also well accepted that base pairing also controls the excited-state dynamics of DNA. Early transient absorption experiments³ showed similar spectra of single- and double-stranded DNA polynucleotides; however, later measurements¹² found a significant decrease in the lifetime of the long-lived excited states via internal conversion in double-stranded (dA)_n·(dT)_n (70 fs) with respect to single-stranded (dA)_n (100–200 fs). Furthermore, it was found that the decay via vibrational cooling following internal conversion is slowed down in the double-stranded DNA.¹² A recent exciton model based on semiempirical electronic-structure calculations combined with trajectory surface hopping¹³ also identified long-lived excited states delocalized not only over intrastrand bases but also over interstrand bases in the double-stranded model, (dAdT)₁₀·(dTdA)₁₀. Additionally, it has been shown that base pairing further enhances photostability by provinding decay channels connected to hydrogen transfer between the nucleobases, especially in guanine-cytosine pairs.¹⁴

The photochemistry of DNA single strands of adenine has been particularly well studied. There is a consensus that upon photoexcitation two deactivation pathways operate: ultrafast internal conversion to the ground state and the formation of a long-lived excited state within 400 fs. However, the nature of the long-lived excited state has been subjected to different interpretations as to how many nucleobases are involved in the excitation and its amount of charge-transfer character. On the one hand, several transient absorption studies^{1,3,5,10−12,15−18} have suggested the formation of excited states with strong charge-transfer character, where the excitation is shared between neighboring bases, mainly facilitated by π stacking. These states have been also postulated after calculating reaction energy profiles of stacked adenines in different environments.^19,20 Furthermore, a quantum dynamics study of an isolated adenine dimer based on a simple vibronic model of four electronic states and six nuclear coordinates found an efficient transfer to charge-transfer states after 50 fs.²¹ On the other hand, several fluorescence up-conversion experiments along complementary exciton theory computations^4,22,23 attributed these long-lived excited states to Frenkel excitons, delocalized over several nucleobases. A recent transient absorption spectroscopy study²⁴ on DNA single strands of adenine revealed the internal conversion of the initial exciton states within 100 fs, followed by a decrease in the interbase distance along with an increase in charge-transfer character of the excitation, which is stabilized within 3 ps. Here, we strive to resolve this debate by using the hybrid quantum mechanics/molecular mechanics (QM/MM) method in combination with surface-hopping dynamics on a stacked adenine tetramer embedded in the full biological environment of a single-stranded (dA)₂₀ oligonucleotide.

In stacked DNA multimers, monomer-like excitations, excitons, charge-transfer states, and excimers can be formed after excitation (Figure 1). Monomer-like excitations imply that the excitation occurs mainly on a single nucleobase. Frenkel excitons are excitations where both electron–hole and excited-electron densities are delocalized over two or more nucleobases with no density exchange between different nucleobases. Charge-transfer states imply that electron–hole and excited-electron densities are entirely localized on different nucleobases. Finally, excimers consist of electron–hole and excited electron densities both delocalized over at least the same two nucleobases, as a result of density transfer between the nucleobases.

Figure 1.

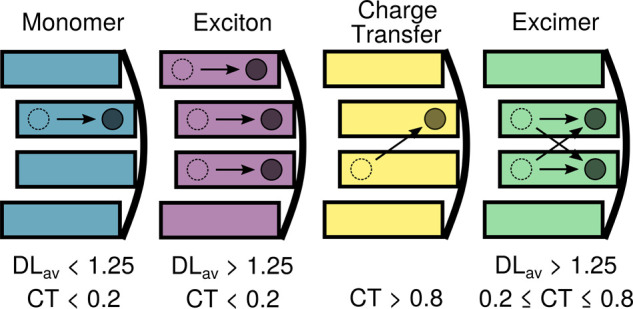
Pictorial representation of the excited states formed in a strand of four stacked adenines, represented by rectangles. The curved line is the backbone. Dashed, empty circles depict electron holes, and solid and filled circles depict excited electrons. To define the different types of excitations, thresholds for the average delocalization length (DL_av) and charge transfer (CT) descriptors are given.

Because it has been shown that upon excitation delocalized excitations over two, three, and four adenines are formed,⁹ our model will consider four stacked adenines in the QM region, while the rest of the system is treated classically. The different electronic states involved in the absorption process as well as in the subsequent nuclear dynamics are classified with the help of two descriptors based on the decomposition of the one-particle transition density²⁵⁻²⁸ among the four adenines: the average delocalization length, DL_av, and the charge-transfer number, CT (see Section 1 of the Supporting Information (SI) for further details). Thereby, the QM region is partitioned in a way such that each adenine represents a separate fragment. The DL_av is based on the arithmetic mean between the electron–hole and excited-electron participation ratios and indicates the number of adenines over which the hole and electron are on average delocalized. For example, if the hole is localized only on a single fragment and the electron is also localized on one (the same or a different) fragment, then there is only one adenine involved in either a hole or an electron, and hence the average gives DL_av = 1. The CT descriptor describes the fraction of excited electron (or hole) density transferred between different adenines. The combination of these two parameters, defining certain (somewhat arbitrary) thresholds, allows us to discriminate between the different states (Figure 1). The monomer-like states are excitations localized on a single nucleobase, so they are defined as DL_av < 1.25 and CT < 0.2. Excitons and excimers are associated with DL_av > 1.25, with the former also exhibiting small charge transfer (below 0.2) and the latter being a mixture between charge-transfer and local excitations (0.2 ≤ CT ≤ 0.8). The remaining charge-transfer states are defined by CT values >0.8.

The calculated absorption spectrum of a solvated (dA)₂₀ oligonucleotide (Figure 2) is based on an ensemble of 100 geometries obtained from a ground-state classical molecular dynamics simulation. For each of these geometries the vertical excitation energies are computed within an electrostatic embedding QM/MM scheme, with the QM region described at the CAM-B3LYP²⁹/def2-SV(P)³⁰ level of theory. Figure 2 compares the spectra calculated with four, six, and eight adenines in the QM region, with the latter taken from ref (9). All spectra are decomposed into monomer-like, exciton, excimer, and charge-transfer states.

Figure 2.

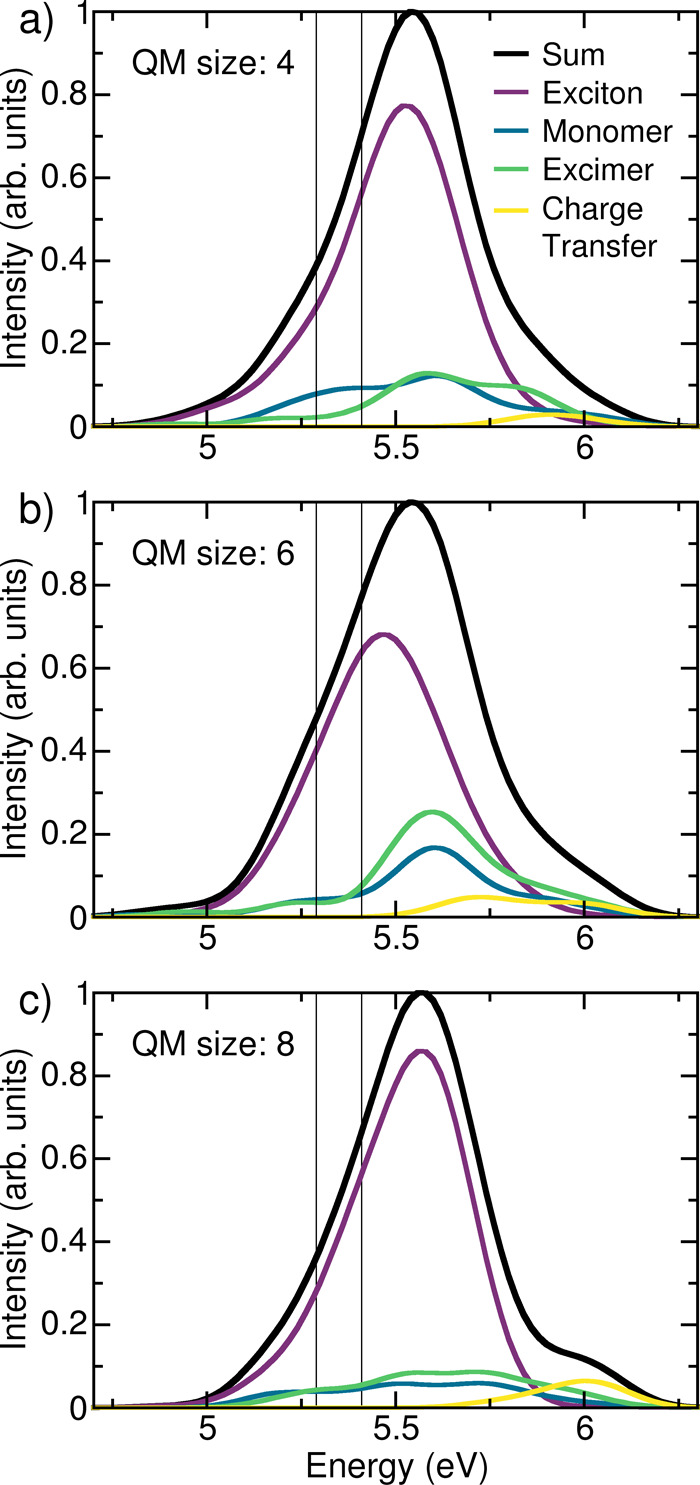
Absorption spectra of (dA)₂₀ with (a) four, (b) six, and (c) eight adenines included in the QM region and their decomposition into exciton, monomer-like, excimer, and charge-transfer states at the CAM-B3LYP/def2-SV(P) level of theory. The two vertical lines indicate the excitation window chosen for the dynamics. Panel (c) is convoluted from data taken from ref (9).

First, we focus on the effect of the size of the QM region. The influence of the edge nucleobases, the basis set, and the Tamm–Dancoff approximation³¹ is discussed in the SI (Figures S1 and S2). Reassuringly, the overall absorption spectrum is very similar in shape regardless of the size of the QM region. The absorption maximum is 5.54 eV for QM sizes four and six and 5.56 eV for QM size eight,⁹ which corresponds to a shift of about 0.7 eV with respect to the experimental spectrum.^3,16,24 As discussed in the literature⁹ and in the SI, better agreement in terms of energy can be obtained with a larger basis set, at the expense of considerable computational cost. Since the nature and electronic properties of the excited states are independent of the basis set, we refrain from using larger basis sets. The different electronic contributions are also not significantly affected by the QM size. The number of charge-transfer states is minor in all cases and important only at high energies. With eight QM bases, the shoulder at 6 eV presents a large contribution to the charge-transfer states, but this shoulder partially disappears and decreases its charge-transfer character with four or six QM bases. Monomer-like and excimer states are similarly present in all three spectra but in a much smaller contribution than the exciton states are, which dominate the absorption band regardless of QM size. While there are visible differences between the spectra calculated with different QM sizes, the qualitative picture of the absorption remains the same: The majority of the absorption stems from exciton states (68, 60, and 74% for four, six, and eight QM adenines, respectively), with larger contributions of monomer states (15, 14, and 9%) and excimers (14, 21, and 12%), while charge-transfer states absorb only a small amount (2, 4, and 4%). With the prospect of performing computationally demanding excited-state dynamics, we conclude that four QM adenines provide a qualitatively good description of the contributions to the absorption spectrum and represent a good compromise between accuracy and computational feasibility.

In order to investigate the time evolution of the solvated stacked tetramer, 100 trajectories were initialized from the eight lowest excited singlet states that comprise the energy window between 5.29 and 5.41 eV (Figure 2), which mimics the excitation energy of 4.65 eV employed experimentally^3,16,24 (after accounting for the 0.7 eV theoretical blue shift discussed above). The trajectories were propagated during 400 fs using the SHARC approach³² that relies on surface hopping.³³ The energies, gradients, and couplings underlying the SHARC trajectories are obtained from an electrostatic-embedding QM/MM calculation, where the QM region includes four nucleobases described at the CAM-B3LYP/def2-SV(P) level of theory (Figure S3), as in the absorption spectrum above. Further details can be found in the SI (Section S1).

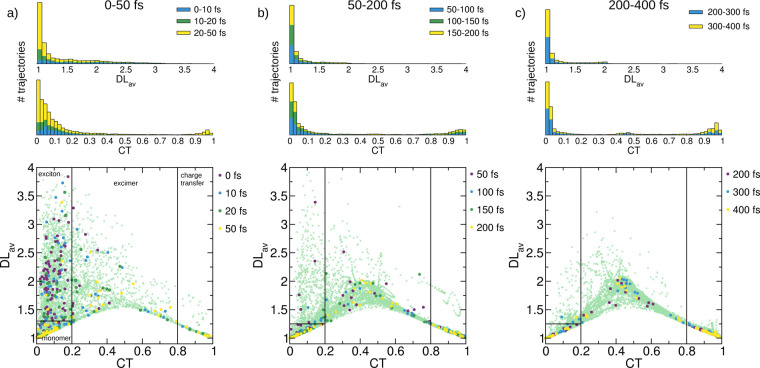
The time evolution of the CT and DL_av descriptors computed for the active state at each time step is shown in the bottom plots of Figure 3. The overall dynamics is broken into three main time intervals, 0–50, 50–200, and 200–400 fs, shown in Figure 3a–c, respectively. The values of CT vs DL_av are depicted for all trajectories at each time step (light-green crosses in the background), and specific points in time are emphasized with solid, larger circles. The thin black lines in the plot separate the areas classified as excitons, monomer-like, excimers, and charge-transfer states, as defined above. Histograms on the top indicate the number of trajectories with the respective descriptor value of CT and DL_av integrated over the whole time interval and are split in the intervals spanned by the indicated time points by the respective color of the points.

Figure 3.

Time evolution of CT and DL_av descriptors during the dynamics. Light-green crosses indicate all trajectories in the full specified time interval, and solid colored circles depict the trajectories at the given simulation time. The black lines indicate the areas defined as the exciton, monomer-like, excimer, and charge-transfer states, as detailed in the main text. The histograms on the top indicate the CT and DL_av contributions in the specified time interval and are separated by color in the respective intervals.

Because there are many dynamic effects at early times, we inspect the time steps at 0, 10, 20, and 50 fs (Figure 3a). Initially (palatinate circles, 0 fs), most states fall into the category of excitons, with few monomer-like and excimer states. However, after only 10 fs (dark-green circles), the number of monomer-like states as well as intermediate excimer-like states increases and the first charge-transfer states are formed. This behavior continues after 20 fs (light blue circles), with more charge-transfer states being formed. After 50 fs (yellow circles), only a few excitons can be seen and most of the trajectories exhibit monomer-like character. Several trajectories are in intermediate excimer states or already-formed charge-transfer states. The histograms show that the majority of the population has CT < 0.2, and only at later times a minority at high CT values emerge. While in the first 10 fs the values of DL_av are between 1 and 2.5, between 20 and 50 fs almost all of the population has a DL_av value below 1.25, indicating that it is composed of either a monomer-like or a charge-transfer state.

Between 50 and 200 fs (Figure 3b), the largest part of the population has a DL_av value of <1.25. The number of trajectories with high CT values (>0.8) keeps increasing. In addition, the population in intermediate excimer states is much higher than that in the previous 50 fs. Moreover, this intermediate states show a DL_av value of around 2 and a CT values of around 0.5, which indicates the formation of excimers not only as a transition between monomer-like and charge-transfer states (where lower DL_av values are expected) but also as a intermediate between excitons and charge-transfer states. Looking at the trajectories at specific points in time (50, 100, 150, and 200 fs), it can be seen that at 50 fs the vast majority of trajectories are in monomer-like states while only five trajectories are excitons. At 100 fs, most of the excitons have decreased their DL_av value and are thus converted to monomer-like or excimer states. The number of charge-transfer states is steadily increasing. After 150 fs, only one trajectory is left in an exciton state, although this is transitional to an intermediate excimer state. Indeed, after 200 fs several trajectories occupy the more stable excimer intermediate state with DL_av ≈ 2. The histograms show time evolution toward states with very small or very large CT numbers and small DL_av values, in agreement with a scenario dominated by monomer-like and charge-transfer states.

From 200 to 400 fs (Figure 3c), more stable excimers are being formed. At all times indicated (200, 300, and 400 fs), multiple trajectories are in a state with CT ≈ 0.5 and DL_av ≈ 2. The background, where all trajectories are depicted, reveals that the intermediate excimers split in two parts: one where DL_av stays below 1.75, which very rapidly evolves to charge-transfer states, and one where DL_av is above 1.75, forming stabilized, homogeneous excimers. The histograms show that there is now some population with CT between 0.4 and 0.5 and DL_av around 2. Thus, the exciton states have almost vanished and an increase in the number of intermediate states can be observed, while the number of charge-transfer states is steadily increasing.

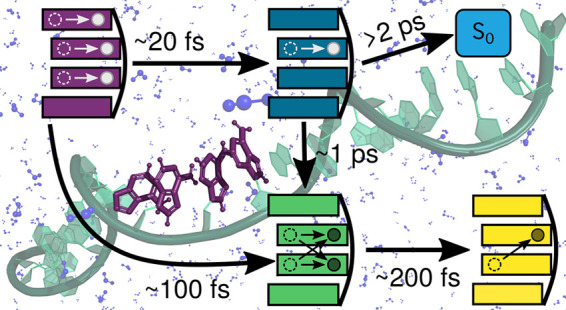
In order to quantify these observations, the populations of the respective states are plotted (thin lines) in Figure 4a and fitted (thick lines) to a kinetic model. On the basis of the initial oscillator strengths, a majority of the trajectories (80) are initialized in exciton states with a small number (11 and 9) starting from monomer-like and excimer states, respectively. The population of excitons readily decreases and decays completely after 100 fs, where only small fluctuations can be appreciated. Within the first 50 fs, a concomitant increase in monomer-like excitations can be observed, leading to the assumption that the initial exciton states will rapidly localize in order to form monomer-like states. Charge-transfer states are also populated almost from the beginning, although they do not increase as swiftly as the monomer-like states. One should note that the previous analysis does not differentiate between the two types of excimers detailed above: the intermediate excimer states arising in transition from a monomer-like state to a charge-transfer state and the more stabilized excimer state where both hole and electron density are delocalized over two nucleobases and exhibit the same amount of charge transfer and local excitations. Finally, five trajectories showed an S₁–S₀ energy gap below 0.1 eV, and they were hence assumed to deactivate to the ground state (see Figure S4 and Section S2 for more details).

Figure 4.

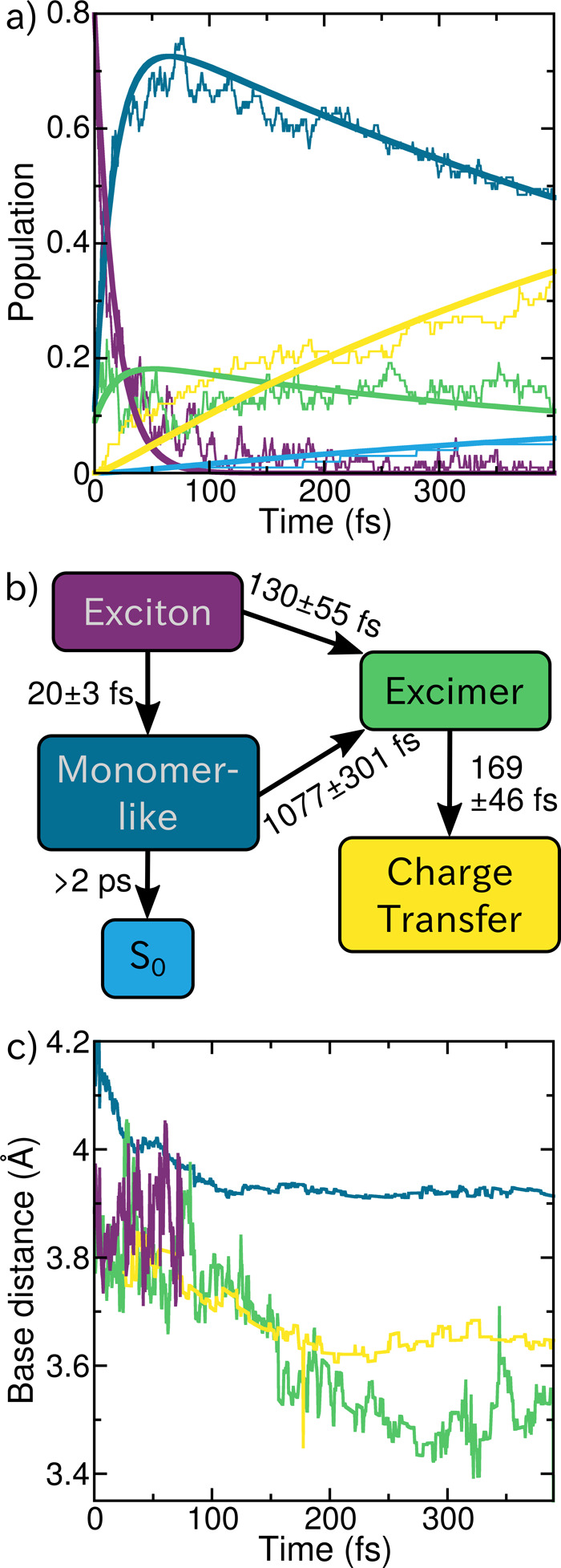
(a) Population traces (thin lines) of the fraction of trajectories in the different excited states as well as the ground state (light blue). The thick lines indicate the fitted kinetic model detailed in (b). (c) Evolution of the average distance between the nucleobases involved in the different excited states (average distance to the neighboring nucleobase for the monomer-like states).

On the basis of these observations, we propose the following kinetic model (Figure 4b). The initial excitons have two decay pathways: either very rapid formation of a monomer-like state with a time constant of 20 ± 3 fs or the formation of intermediate excimers with a time constant fitted to 130 ± 55 fs. Population in the monomer-like states bifurcates again into forming excimers or deactivating to the ground state. Both processes occur on longer time scales, with a time constant of 1077 ± 301 fs to convert to the excimer state. Due to the small number of trajectories deactivating to the ground state during the simulated time scale, we cannot provide a precise time constant, thus we state only a lower limit of 2 ps. Excimer states are then fitted to rather rapidly convert to charge-transfer states with a time constant of 169 ± 46 fs. This fitted model should be regarded cum grano salis because the analysis is based on our definition of the different states, and because we do not have exact diabatic states, thus fluctuations can be observed. However, we are able to map the complexity of the dynamics in a simplified model that conveys the main dynamical events.

The conclusions derived from our simulations agree well with recent experimental findings by Markovitsi and co-workers,²⁴ where they proposed four main time constants. In less than 100 fs they observed internal conversion among exciton states, which correlates well with the computed time constants of 20 and 130 fs for monomer-like and excimer state formation from the excitons, respectively. They assigned the second experimental time constant between 150 and 800 fs to the increasing charge-transfer character of the excited states.²⁴ Their time interval likely corresponds to our calculated time constants of 169 fs for charge-transfer state formation from excimers and 1077 fs for excimer formation from monomer-like states. As seen in Figure 3, these late excimer states present larger charge-transfer character than the early excimer states. The next experimental time frame was between 800 fs and 3 ps, when strong geometrical rearrangements take place, leading to the stabilization of charge-transfer states after 3 ps. Because we do not simulate such long time scales, we cannot observe the same rearrangements and charge-transfer state stabilization. However, looking at the time evolution of the separation between the bases involved in the excited states, as shown in Figure 4c, we can still monitor the early geometrical rearrangements occurring within the timescale of our excited-state dynamics. The earliest times of the dynamics (approximately the first 100 fs) are governed by the initial response of the system to the excitation, and therefore large fluctuations in the base separations are observed, particularly in the exciton states which dominate initially and dissapear with time. At later times, after 100–150 fs, the interbase distances to the monomer-like, excimer, and charge-transfer states all seem to be in a plateau found at different separation values. For the monomer-like states, the neighboring adenines are approximately 3.93 Å away, and the adenines involved in excitation with charge-transfer character are significantly closer to each other. In the charge-transfer states, the two involved bases are around 3.65 Å apart on average, and for excimer states the separation fluctuates more but remains constant at around 3.55 Å. The even further reduction of the interbase distance in excimer states results from the formation of a homogeneous dimer-like structure, where the charge transfer occurs from both adenines in both directions. We note that for these observations we need to keep in mind that the relaxation of the system due to the change in level of theory from the ground-state sampling (classical molecular dynamics) to the excited-state dynamics (QM/MM) is not taken into account quantitatively. The effect of additional QM/MM dynamics in the ground state on the base separation is discussed in Section S3. In any case, the fact that the base distances for the different excited states reaches a plateau at later points in the dynamics indicates that the observed reduction of spatial separation is in fact induced by the excited-state dynamics (Figures S5 and S6). Thus, our simulations illustrate the influence of the electronic-state character on the spatial separation of the nucleobases: compared to monomer-like states, charge-transfer character reduces the distance by approximately 0.28 and 0.38 Å for pure charge transfer and excimer states, respectively.

In conclusion, our calculations provide a rationalization of the ultrafast behavior of a single-stranded adenine oligonucleotide after photoabsorption. The time evolution of the initially excited states was investigated by hybrid QM/MM surface-hopping molecular dynamics combined with on-the-fly wave function analysis. The simulations evidenced how the initial exciton states quickly relax to monomer-like and excimer states on the way to the formation of charge-transfer states. Since it is known that adenine monomers undergo a very efficient S₁ → S₀ deactivation, the formation of monomer-like states might be an initial step in the nonadiabatic mechanisms favoring the photostability of DNA strands. Within hundreds of femtoseconds, the charge-transfer character increases steadily from the excimer states, leading to the formation of stabilized charge-transfer states. Our findings are consistent with the transient absorption study by Borrego-Varillas et al.,²⁴ lending further support to the proposed mechanism. Furthermore, we are able to observe a geometrical manifestation of larger charge-transfer character within 400 fs, as charge transfer and excimer states show a smaller spatial separation between the adenines compared to the distance of monomer-like states between neighboring bases. Finally, this study illustrates the usefulness of quantitative electronic-structure analysis to disentangle excited-state dynamics of multichromophoric systems, following the charge-transfer character and the averaged delocalization length descriptors.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c02193.

• Further computational details and additional results on the deactivation to the ground-state channel (PDF)

Author Present Address

^# Photonics Institute, Vienna University of Technology, Gußhausstraße 27-29, 1040 Vienna, Austria.

The authors declare no competing financial interest.