Chemistry in Quantum Cavities: Exact Results, the Impact of Thermal Velocities, and Modified Dissociation

Abstract

In recent years tremendous progress in the field of light–matter interactions has unveiled that strong coupling to the modes of an optical cavity can alter chemistry even at room temperature. Despite these impressive advances, many fundamental questions of chemistry in cavities remain unanswered. This is also due to a lack of exact results that can be used to validate and benchmark approximate approaches. In this work we provide such reference calculations from exact diagonalization of the Pauli–Fierz Hamiltonian in the long-wavelength limit with an effective cavity mode. This allows us to investigate the reliability of the ubiquitous Jaynes–Cummings model not only for electronic but also for the case of ro-vibrational transitions. We demonstrate how the commonly ignored thermal velocity of charged molecular systems can influence chemical properties while leaving the spectra invariant. Furthermore, we show the emergence of new bound polaritonic states beyond the dissociation energy limit.

Within the past few years, cavity-modified chemistry has gained popularity in the scientific community. This is due to several major breakthroughs in this emerging field of research.¹⁻⁶ For example, it was demonstrated that strong coupling in a cavity can be used to control reaction rates⁷⁻⁹ or strongly increase energy-transfer efficiencies.^10,11 In contrast to the usual studies in quantum optics,¹² where ultrahigh vacua and ultralow temperatures are employed, many of these results were obtained at room temperature with relatively lossy cavities. Furthermore, recently it was even reported that strong coupling can modify the critical temperature of superconducting materials.^13,14 These results nurture the hope of the technological applicability of cavity-modified chemistry and material science.

Despite these experimental successes, the basic principles of cavity-modified chemistry (also called polaritonic or QED chemistry^2,4,9,15) are still under debate.^4,16−21 Currently, much of our understanding is based on quantum-optical models that have been designed for single (or a dilute gas of) atomic systems, whereas approximate first-principles simulations for coupled matter–photon situations emerge only slowly.^15,22−29 We believe it is pivotal to validate these model approaches and approximate first-principles simulations with numerically exact reference calculations to obtain a detailed understanding of cavity-modified chemistry and to see the limits of the different approximations used. Eventually, one should reach a level of certainty as is the case in standard quantum chemistry.³⁰

This work provides such references by presenting an exact-diagonalization scheme for the Pauli–Fierz Hamiltonian of nonrelativistic quantum electrodynamics (QED) in the long-wavelength approximation for three interacting particles. Here, we report the first exact results for real, three-dimensional atoms/molecules coupled to one effective photon mode. To date, exact solutions were available only for model Hamiltonians within a cavity (e.g., 1D with soft-Coulomb interaction). As examples, we present results for the He atom and for HD+ and H₂⁺ molecular systems in a cavity. We highlight that the inclusion of the quantized photons makes the interpretation of the obtained spectra much richer and more involved; we discuss the level of accuracy of the ubiquitous Jaynes–Cummings model and demonstrate fundamental effects beyond this model, such as the formation of bound states beyond the dissociation energy limit as well as the influence of the thermal velocity for charged systems. The latter point is specifically interesting because it gives an indication why strong coupling has such an impact on chemistry at room temperature. Moreover, it suggests that current phenomenological models used to investigate collective-coupling effects are less reliable when applied to molecular systems.

The consistent quantum description of photons coupled to matter is based on QED,³¹⁻³³ which in its low-energy nonrelativistic limit is given by the Pauli–Fierz Hamiltonian.^33,34 For the case of optical and infrared wavelengths (dipole approximation) the Pauli–Fierz Hamiltonian in the Coulomb gauge can be further simplified^29,32,35 and then reads in atomic units

1

While the Pauli–Fierz quantum theory as well as nonrelativistic quantum mechanics are not relativistically covariant, for equilibrium properties (the focus of this work) and low-energy processes these theories have been proven to be highly accurate.⁴ Here N is the number of charged particles (electrons and nuclei/ions) with mass m_i and charge Z_i and p̂ = −i∇ is the nonrelativistic momentum. Further, M_pt photon modes with frequency ω_α are coupled to the matter with the coupling λ_α that contains the polarization vector and coupling strength of the individual modes. These couplings and frequencies are determined by the properties of the cavity. Further, q̂_α and p̂_α = −i∂/∂q_α are the photon displacement and conjugate momentum operators, respectively, and the total dipole operator is defined as 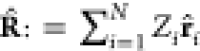. The inclusion of the quadrature of the dipole operator in the Hamiltonian, i.e., the dipole self-energy, is necessary for the stability of the light–matter system.³⁶

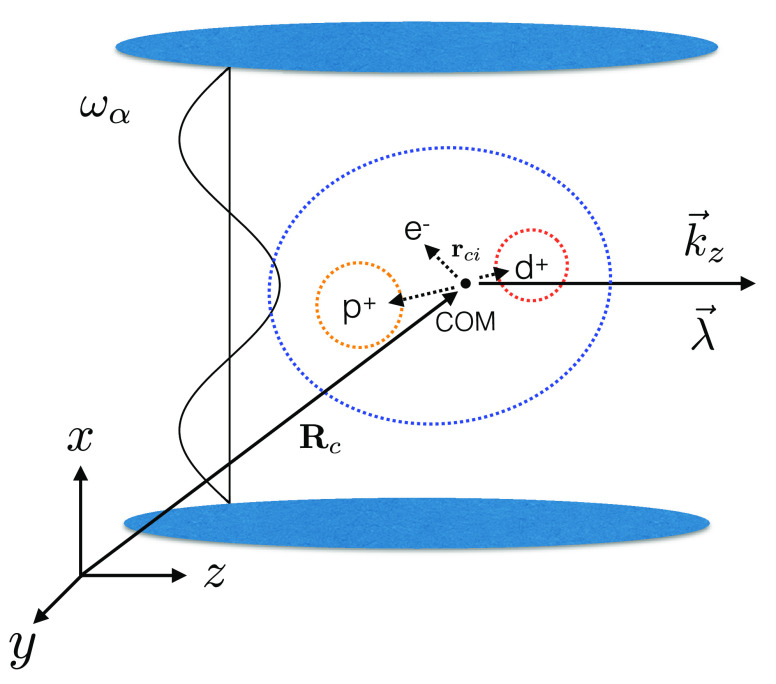
In the current work we will choose N = 3 and consider the standard case of a single-mode cavity, i.e. M_pt = 1, with polarization in the z direction (see Figure 1). To bring this numerically very challenging problem into a more tractable form we first re-express the Hamiltonian in terms of its center-of-mass (COM) coordinates r_ci = r_i – R_c, where the COM is given by 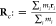. Next we can shift the COM contribution of the total dipole operator to the COM momentum by a unitary Power–Zienau–Woolley transformation (see section 1.1 of the Supporting Information). The resulting eigenvalue equation can be brought into the form

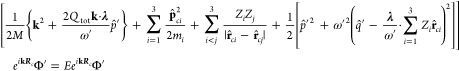2

where we made the wave function ansatz 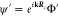. Here 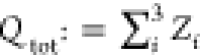is the total charge of the three-particle system and we have performed a photon-coordinate transformation such that the frequency of the cavity becomes dressed 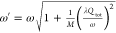. We already see that for charged systems, i.e., Q_tot ≠ 0, we get novel contributions from the coupling of the COM motion with the quantized field that are not taken into account in usual quantum-optical models.¹² Therefore, in contrast to the usual Schrödinger equation, we will be able to show that the COM motion (corresponding to the continuous quantum number k) has an influence on the bound states of the system. Such a contribution is to be expected, because moving charges will create a transversal electromagnetic field. Note that in our long-wavelength approximation this contribution appears only for charged systems. For the full (minimal-coupling) Pauli–Fierz Hamiltonian (i.e., beyond dipole approximation), small deviations are also expected for neutral systems.³³

Figure 1.

Schematics of the cavity–matter setup used here and exemplified for the HD+ molecule. We assume the relevant cavity mode polarized along the z-direction. The relative COM coordinates r_ci are given with respect to the COM R_c.

After separating off the COM coordinate with the above transformations, we can represent the three relative COM coordinates in terms of spherical–cylindrical coordinates,³⁷ i.e., r_ci(R, θ, ϕ, ρ, ψ, ζ). Here ζ ∈ ]–∞, ∞[, {R, ρ} ∈ [0, ∞[, and the radial coordinates obey {ϕ, ψ} ∈ [0, 2π[ and θ ∈ [0, π[. A detailed description of the spatial coordinate representation is given in section 1.3.1 of the Supporting Information. This allows us to express the wave function by

3

where D_m,k^l are the Wigner-D-matrices,³⁷ with variational coefficients C_l,m,n,k (see section 1.3.2 in the Supporting Information). Photons are represented in a Fock number basis |n⟩. Being formally exact, finite numerical precision is already indicated by the number of basis states N_l, N_m, and N_pt for the angular and photonic basis states. The radial wave function φ_k is represented numerically in perimetric coordinates on a 3D Laguerre mesh³⁷ of dimensionality N_matter. In practice, radial integrals are solved numerically by a Gaussian quadrature (see section 1.3.3 in the Supporting Information), whereas angular integrals are solved analytically. Corresponding numerical parameters are given in section 2.1 and convergence tests in section 2.2 of the Supporting Information. We note that for an uncoupled setup (i.e., λ = 0) m and l correspond to the usual magnetic and angular quantum number, respectively. In this case, the expansion of eq 3 becomes highly efficient because the Hamiltonian assumes a block diagonal shape and it can be solved for each pair m and l independently (reducing the dimension of the problem to 3).³⁷⁻³⁹ Further simplifications can be made based on the parity invariance of the uncoupled problem. For our coupled problem, however, these symmetries are broken. Yet, because of the choice of the polarization direction, we preserve cylindrical symmetry with respect to the lab frame, and it can be shown that ⟨Φ′_{l′,m′,n′}|H^′|Φ′_l,m,n⟩ = δ_m′,m⟨Φ′_{l′,m′,n′}|H^′|Φ′_l,m,n⟩. Hence, the coupling only mixes angular momenta and Fock states, which implies that the original 10-dimensional problem can be reduced to 6 dimensions. Different spin-states can be distinguished by (anti)symmetrization of the matter-only wave functions. This is possible because we have at most 2 indistinguishable particles for bound 3-body problems and the Pauli–Fierz Hamiltonian in the long-wavelength limit is spin-independent. Note that our exact diagonalization approach might also be suitable to investigate chiral cavities ab initio with only minor modifications. They offer promising perspectives to control material properties by breaking time reversal symmetry (unpublished results).

After having discussed how we exactly solve the problem of real systems coupled to the photons of an optical cavity numerically exactly, let us turn to the obtained results. As a first example we consider parahelium coupled to a cavity. We perform a scan of different frequencies, ω, centered around the 2S–2P resonance frequency ω_2S2P = 0.6 eV, with an imposed coupling of λ_2S2P = 0.027 (i.e., a coupling strength of g = 0.074 eV). To be consistent with the traditional quantum optics perspective, we kept 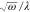constant for all calculations. This implies ω ∝ g, and thus, our dispersion relations scale with respect to the coupling strength g, which would be the natural parameter choice for the traditional Jaynes–Cummings (JC) model.⁴⁰ The first observation that can be made in the dispersion relation of Figure 2 is that the spectrum of the Pauli–Fierz Hamiltonian becomes more intricate when compared to the usual Schrödinger Hamiltonian. The reason being that to each matter excitation we get photon replica spaced by roughly the corresponding photon frequency. This can be best observed for small frequencies, where we see clusters of eigenenergies. In our case, we get 5 replica, where we have chosen the number of photon states N_pt = 6. However, in principle we would get infinitely many discrete replicas at higher energies, which is an indication of the photon continuum. Moreover, if we simulated many modes, one would observe a continuum of energies starting at the ground state.^22,33 This photon continuum is necessary to capture fundamental physical processes like spontaneous emission and dissipation,²² but it makes the identification of excited states difficult (in full QED they turn into resonances^31,33). That is why we have supplemented the energies in Figure 2 with their color-coded oscillator strengths. This allows us to associate the eigenenergies with large oscillator strengths to genuine resonances, i.e., they correspond to excited states with a finite line width. In a many-mode case the photon replica with smaller oscillator strength then constitute this line width.²² At the 2S–2P transition (indicated with a vertical line) we find a Rabi splitting Ω = 0.148 eV into the upper and lower polariton (indicated with two horizontal lines), which is of the order of Ω/ω_2S2P ≈ 0.24; hence, we are in the strong-coupling regime.¹² Furthermore, we have indicated the predictions from the ubiquitous JC model based on the bare 2S and 2P states with yellow crosses. Because this model was constructed for atomic transitions on resonance, it captures the Rabi splitting quite accurately, but for larger detuning parameters (i.e., off-resonance) it becomes less reliable (see also section 3.1 in the Supporting Information). The JC model also gives a good approximation to the multiphoton replicas. However, because the JC model takes into account only the 2S and 2P bare-matter states in our case, all the other excitations are not captured. At this point it becomes important to highlight that the considered strong-coupling situation is hard to engineer on the single-atom level, and usually the collective polarization of an ensemble of atoms or molecules is used to achieve a similar Rabi splitting.^3,5,6 In most cases the theoretical description of collective coupling is then based on simplified few-level approximations, such as the Jaynes–Cumming approximation. The above result shows that such a few-level approximation captures the basic behavior of the electronic 2S–2P transition for a single atom quite accurately and hence seems a good starting point for a collective-coupling model, e.g., the Dicke model for a dilute gas.¹² Yet, as discussed below, this can change when we consider more complex systems such as molecules.

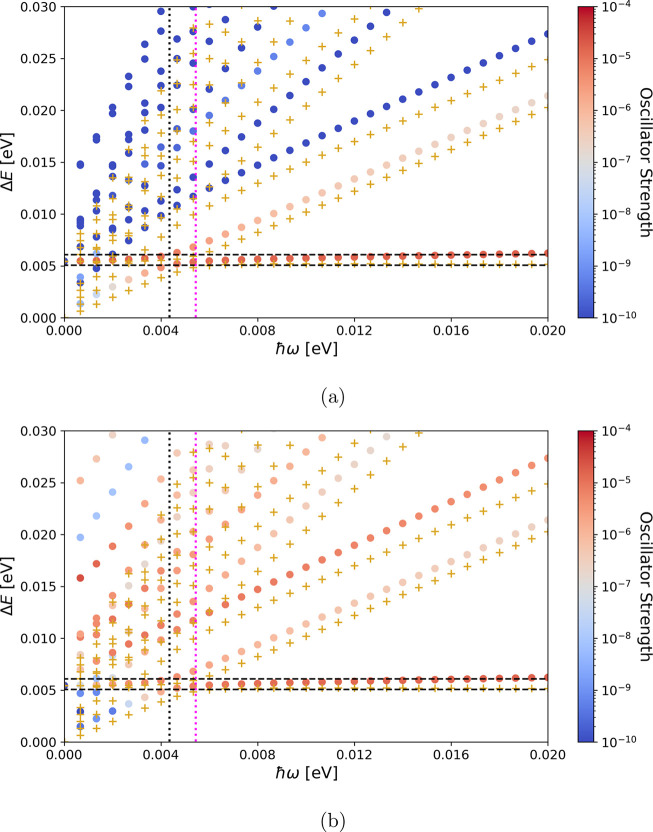
Figure 2.

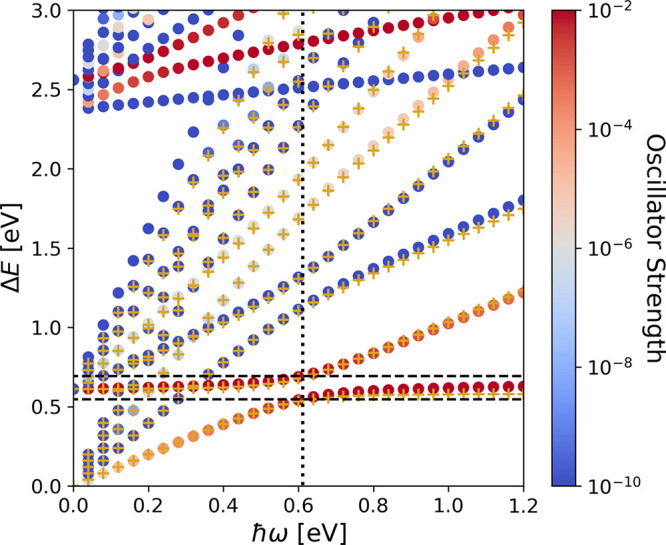
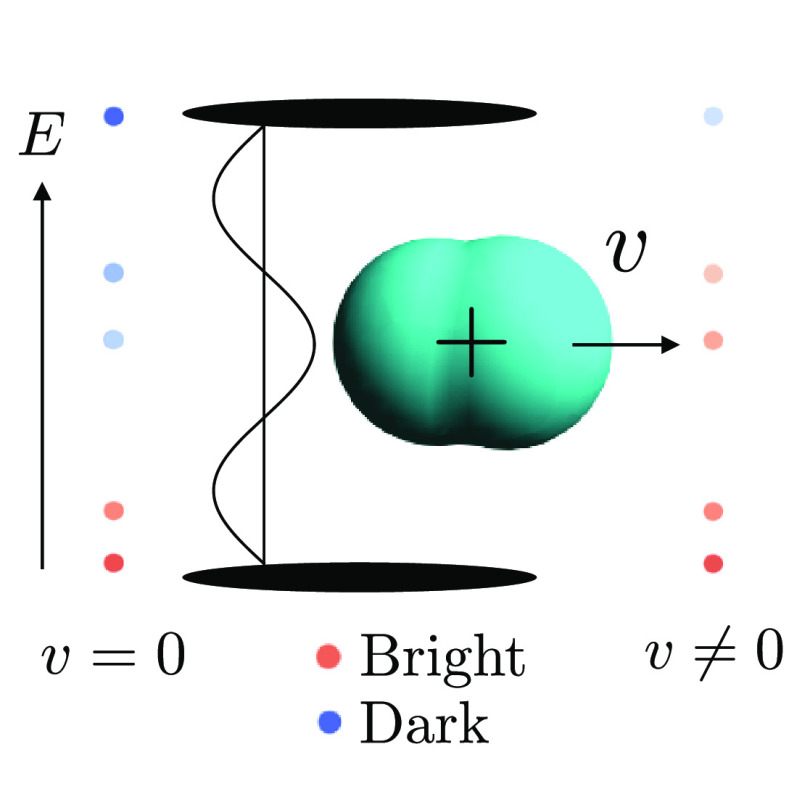
Rabi dispersion relation for parahelium in a cavity. The bright polaritonic states, located at the ΔE = E_2P – E_2S resonance frequency (vertical line) of the uncoupled system, are indicated by the two horizontal lines. They are associated with a high (red) dipole transition oscillatory strength, while corresponding dark many-photon replicas and improbable 2S – iS transitions have a small oscillator strength (blue). The yellow crosses (+) indicate energies derived from the JC model based on a 2S and 2P two-level approximation and using the respective parameters for the cavity detuning frequencies and photon mode numbers.

Let us switch from the atomic to the molecular case and consider transitions due to the nuclear motion. We here consider the HD+ molecule and the lowest ro-vibrational L0–L1 transition with a Rabi splitting of Ω = 0.1 × 10^–2 eV. A similar dispersion plot as previously given for He can be seen in Figure 3a. The first difference is that we now have two vertical lines. The black vertical line corresponds to the (now dressed) resonance frequency ω of the system. The charged molecule slightly shifts the frequency of the empty cavity. The JC model, which does not take into account this effect, predicts the resonance at the magenta vertical line. In the HD+ case, where we find the exact value Ω/ω ≈ 0.23, the JC model predicts instead a value of 0.28 with the a wrong Rabi splitting of 0.149 × 10^–2 eV. In addition, the JC model underestimates polaritonic energy levels for all evaluated cavity frequencies in the ro-vibrational regime. This relatively strong deviation is due to the missing dipole self-energy term in the JC model, and it highlights that few-level atomic quantum-optical models are in principle less reliable when applied to molecular systems (see also section 3.2 in the Supporting Information). As already anticipated in the theory part, the COM momentum in the z direction will have an influence on the eigenstates of HD+, because we consider a charged system. Indeed, while Figure 3a was calculated for zero momentum, in Figure 3b we see the dispersion plot for a finite COM kinetic energy 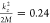× 10^–2 eV ∝ T = 28.66 K. Interestingly, the spectrum itself does not change, yet the eigenfunctions do change (additional information is provided in section 3.2 in the Supporting Information). Consequently, previously dark transitions (small oscillator strength, blue) become bright (large oscillator strength, red). Therefore, the absorption/emission spectra, which depend on the oscillator strength, get modified because of this COM motion and excitations to higher-lying states become more probable. Overall, the effect of the finite COM momentum appears to be strong for the infrared energy range. Note that we find similar results for H₂⁺, which are shown in section 3.3 in the Supporting Information. Because for realistic situations we will always have a thermal velocity distribution, these spectral modifications will become important. Specifically, when we think about chemical reactions, where the properties of charged subsystems are essential, these modifications could help to explain the so far elusive understanding of cavity-modified chemistry at room temperature. They suggest that the phenomenological models of collective strong coupling might not be accurate enough and do not account for all relevant aspects of cavity-modified chemistry in the infrared regime.

Figure 3.

(a and b) Rabi dispersion relation for HD+ in a cavity for COM motion E_kin = 0 and E_kin = 0.24 × 10^–2 eV, respectively. The bright polaritonic states at the dressed L0–L1 transition (vertical black line) are indicated by the two horizontal lines. The magenta vertical line shows the prediction of the JC model, which does not account for the net-charge frequency dressing. Dark (blue) and bright (red) states can be identified by corresponding dipole oscillator strengths. The yellow crosses (+) indicate energies derived from the JC model.

Another interesting result with relevance for polaritonic chemistry is the formation of bound polaritonic states below^41,42 and above the proton dissociation limit of H₂⁺ (see green region in Figure 4). Because we treat the nuclei/ions quantum-mechanically, we do not have to approximate the Born–Oppenheimer surfaces in our present approach for a simple picture of dissociation. Therefore, we can identify the dissociation energy limit and the emergence of novel bound polaritonic states based on the expectation value of the proton–proton distance and by variation of the finite numerical grid (see section 3.3 in Supporting Information). It is important to note that there are no dipole-allowed transitions to excited bound states available for the uncoupled case; that is, there are only S-type many-body eigenstates below the proton dissociation energy limit. Hence, if we couple to the cavity with a frequency close to the dissociation energy, e.g., ω = 2.15 eV and λ = 0.051, the Rabi model breaks down and no Rabi splitting is observed. Yet, while we find (dark) S-type states (blue dots) that follow the expected matter-only dissociation, multiple bright bound states (red dots) emerge, which can persist beyond the proton dissociation energy limit. These states, which are bright photon replicas of the bound matter-only S-states, employ the captured photons to bind the otherwise dissociating molecule. How strongly these states influence the molecular dissociation process has to be investigated in more detail in the future. It will depend also on whether they correspond to long-lived excited states or short-lived metastable states.

Figure 4.

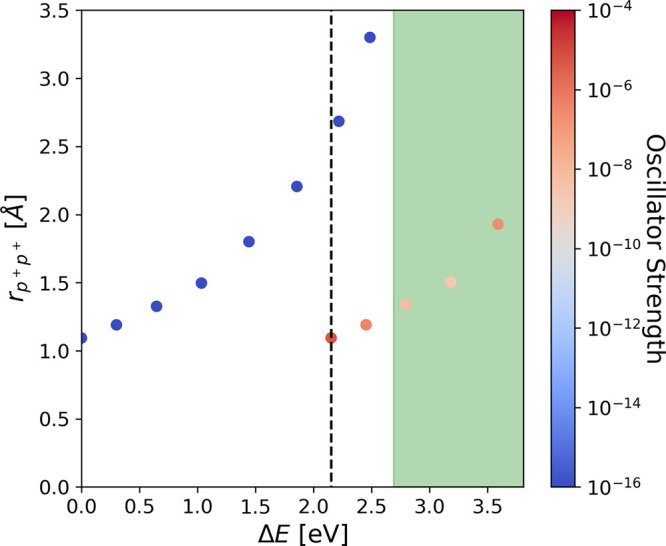
Quantized (i.e., bound) proton–proton distances for H₂⁺ with respect to ground-state energy differences ΔE and corresponding oscillator strength. The blue dots correspond to dressed bare matter states, whereas red dots indicate the emerging bright photon replicas, which are absent without a cavity. The cavity frequency is ω = 2.15 eV (dashed vertical line) with λ = 0.051 and zero COM motion. The green area indicates energy ranges beyond the p⁺-dissociation limit according to matter-only simulations.

In this work we have provided numerically exact references for cavity-modified chemistry and we have demonstrated that the thermal velocity has a direct impact on properties of charged systems, as well as the emergence of bound polaritonic states beyond the dissociation-energy limit. We have done so by an exact diagonalization of the Pauli–Fierz Hamiltonian for three particles and one mode in center-of-mass coordinates and used further symmetries to reduce the originally 10-dimensional problem to a 6-dimensional problem. We have shown that the resulting spectrum shows the onset of the photon continuum and hence is no longer obvious to interpret. Furthermore, for ro-vibrational transitions we have shown that the ubiquitous Jaynes–Cummings model is not very accurate and that for charged systems important properties like the oscillator strength are modified for nonzero center-of-mass motion. Because this can be connected to the thermal velocity, we found a so far neglected contribution for cavity-modified chemistry at a finite temperature. All these results highlight that at the interface between quantum optics and quantum chemistry well-established “common knowledge” is no longer necessarily applicable and that currently used quantum-optical models potentially require a further refinement when chemical properties are considered. To get a basic understanding of polaritonic chemistry and material science we need to revisit standard results and establish possibly new scientific facts, and numerically exact calculations of the basic QED equations are an integral part of this endeavor.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c01556.

• Theoretical and simulation details given with respect to COM separation, PZW transformation, observables, numerical representation, integration procedures, input parameters, and convergence tests; additional observables calculated for He, HD+, and H₂⁺ (PDF)

The authors declare no competing financial interest.