Primary motor cortical activity during unimanual movements with increasing demand on precision

Abstract

In functional magnetic resonance imaging (fMRI) studies, performance of unilateral hand movements is associated with primary motor cortex activity ipsilateral to the moving hand (M1_ipsi), in addition to contralateral activity (M1_contra). The magnitude of M1_ipsi activity increases with the demand on precision of the task. However, it is unclear how demand-dependent increases in M1_ipsi recruitment relate to the control of hand movements. To address this question, we used fMRI to measure blood oxygenation level-dependent (BOLD) activity during performance of a task that varied in demand on precision. Participants (n = 23) manipulated an MRI-compatible joystick with their right or left hand to move a cursor into targets of different sizes (small, medium, large, extra large). Performance accuracy, movement time, and number of velocity peaks scaled with target size, whereas reaction time, maximum velocity, and initial direction error did not. In the univariate analysis, BOLD activation in M1_contra and M1_ipsi was higher for movements to smaller targets. Representational similarity analysis, corrected for mean activity differences, revealed multivoxel BOLD activity patterns during movements to small targets were most similar to those for medium targets and least similar to those for extra-large targets. Only models that varied with demand (target size, performance accuracy, and number of velocity peaks) correlated with the BOLD dissimilarity patterns, though differently for right and left hands. Across individuals, M1_contra and M1_ipsi similarity patterns correlated with each other. Together, these results suggest that increasing demand on precision in a unimanual motor task increases M1 activity and modulates M1 activity patterns.

NEW & NOTEWORTHY Contralateral primary motor cortex (M1) predominantly controls unilateral hand movements, but the role of ipsilateral M1 is unclear. We used functional magnetic resonance imaging (fMRI) to investigate how M1 activity is modulated by unimanual movements at different levels of demand on precision. Our results show that task characteristics related to demand on precision influence bilateral M1 activity, suggesting that in addition to contralateral M1, ipsilateral M1 plays a key role in controlling hand movements to meet performance precision requirements.

INTRODUCTION

Unilateral hand movements are controlled by descending projections originating predominantly in the primary motor cortex (M1) of the contralateral hemisphere (M1_contra). In addition to this robust contralateral M1 activity, some neuroimaging studies have also reported modulation of activity in ipsilateral primary motor cortex (M1_ipsi) when movements are complex (Ehrsson et al. 2000; Kim et al. 1993; Rao et al. 1993; Uehara and Funase 2014; Verstynen et al. 2005). When examined with qualitatively similar movements that only differ in the demand on precision or force, there is evidence that increasing difficulty elicits corresponding parametric modulations in M1_ipsi recruitment (Buetefisch et al. 2014; Derosière et al. 2014; Sehm et al. 2010; Seidler et al. 2004; Winstein et al. 1997). However, since uncrossed descending projections from M1_ipsi are limited and are not thought to directly control hand movements (Soteropoulos et al. 2011), the functional significance of increased M1_ipsi activity during movements at higher levels of demand remains unclear.

Previous functional magnetic resonance imaging (fMRI) approaches investigating the effect of parametric increases in precision of hand movements have mainly measured the extent of activated voxels or the mean activation levels across voxels in a region (Boyd et al. 2009; Buetefisch et al. 2014; Seidler et al. 2004). While these studies provide evidence for M1’s involvement in task precision, a few possible confounding factors complicate interpretation of M1_ipsi activity. First, most fMRI studies using unimanual tasks lack the verification of a strictly unilateral execution during data acquisition, which may be problematic because bilateral upper extremity activity with increasing difficulty can contribute to observed bilateral M1 activation (Bütefisch et al. 2005). We previously demonstrated parametric modulation of M1_ipsi activity during electromyographically confirmed unimanual execution of a motor task, but electromyographic (EMG) data were collected intermittently during scanner silence and not throughout the task period (Buetefisch et al. 2014). Second, previous fMRI studies parametrically manipulating demand on precision focused on movements made with the dominant (right) hand, so it is unclear how hemispheric specialization for motor processes may influence M1_ipsi contributions to demand-dependent performance (Mutha et al. 2013; Sainburg and Kalakanis 2000; Serrien et al. 2006).

Investigating multivariate pattern activity in conjunction with univariate analyses has the potential to reveal complementary task-specific information from the spatial distribution of the blood oxygenation level-dependent (BOLD) responses (Haynes 2015). Representational similarity analysis (RSA) compares how the multivoxel patterns of activity in a brain region vary across features of interest (Kriegeskorte and Kievit 2013; Kriegeskorte et al. 2008). The advantage of RSA is that patterns of activity can be compared across different brain regions and tested against alternative computational models. RSA extracts relevant fine-grained information dissociable from mean activity across conditions (Coutanche 2013; Mur et al. 2009) and has been used to reveal representations underlying simple unimanual tasks involving finger presses, reaching, and grasping (Ejaz et al. 2015; Fabbri et al. 2016; Magri et al. 2019; Marneweck et al. 2018). Here, we attempt to apply the RSA approach to investigate complex movements in which task performance accuracy can vary across conditions.

In the present study, we combined standard univariate analysis with RSA to examine how the demand on the precision of a unimanual task may alter M1 BOLD activity and whether M1 patterns of activity are related to distinct movement components. We measured kinematics and used fMRI to examine M1 BOLD activity as participants performed right- or left-hand movements with a joystick to targets appearing in one of four different spatial locations on a visual display. Demand on precision is defined as the change in the precision requirements imposed by the task. We used a parametric increase in the target size (small, medium, large, extra large) across blocks to isolate demand on precision while keeping other important kinematic features that can vary with M1 activity (e.g., force, direction, frequency, amplitude, and activated muscles) similar across blocks (Barany et al. 2014; Fabbri et al. 2012; Kalaska 2009; Pool et al. 2013). Importantly, we recorded EMG activity from the extensor carpi ulnaris (ECU) muscles of both arms throughout the scanning session to confirm that participants did not exhibit any mirrored muscle activity in the nonperforming hand (Mayston et al. 1999; Sehm et al. 2010).

We hypothesized that increasing the target size would be associated with higher univariate BOLD activity and more dissimilar BOLD response patterns in both M1_contra and M1_ipsi. Furthermore, we hypothesized that models capturing demand-dependent aspects of the task, i.e., models based on task parameters that vary with demand on precision, would best explain M1 similarity patterns. For the current study, we recruited an older population of subjects given known age-dependent variation in neural responses in motor tasks and the potential relevance of the current results to understanding motor representations following stroke (Buetefisch 2015; Talelli et al. 2006, 2008; Ward 2015).

MATERIALS AND METHODS

Participants

Twenty-three healthy right-handed participants (15 women; mean age 63.3 ± 8.7 yr, age range 50–78 yr) fulfilled the following inclusion criteria and were included in the study: age between 50 and 80 yr, no neurological or psychiatric disorder, a normal neurological examination, no intake of central nervous system (CNS) active drugs, normal cognitive function as determined using the Repeatable Battery for the Assessment of Neuropsychological Status (RBANS) (Randolph et al. 1998), normal or corrected-to-normal vision, and the ability to give informed consent. A neurologist (C.M.B.) confirmed that no structural abnormalities or white matter disease were present on the structural MRI scans for any of the participants, and the Edinburgh inventory for handedness (Oldfield 1971) confirmed that all subjects were strongly right-handed. All participants provided written consent, and all procedures were approved by the Institutional Review Board at Emory University. On a separate day before the scanning session, each participant was trained on the task and achieved at least a 50% performance accuracy on the medium target size (see Experimental Task). One participant who subsequently exhibited <50% overall accuracy during scanning was excluded from all analyses.

Experimental Setup

Participants were placed supine in the MRI scanner with their head and neck padded with foam to minimize head motion. They were provided headphones for noise cancellation and to communicate with experimenters between scans. The participant’s performing hand rested on the base of an MRI-compatible joystick (Mag Design and Engineering, Redwood City, CA) with their thumb and middle finger free to manipulate the joystick. The joystick was secured on the participant’s lap with a strap around the waist. Soft padding was placed under the participant’s forearm to minimize involvement of proximal muscles while moving the joystick. The nonperforming arm rested at the subject’s side and was supported by pads (Fig. 1A).

Fig. 1.

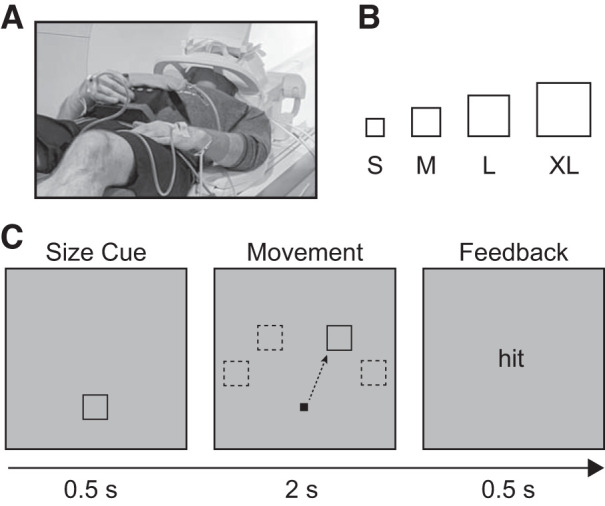
Task design. A: participants used an MRI-compatible joystick secured on their lap. Electromyogram (EMG) electrodes were placed on participants’ right and left extensor carpi ulnaris (ECU) muscles. B: target size conditions for the task [small (S): 1.4° × 1.4° visual angle; medium (M): 1.75° × 1.75° visual angle; large (L): 2.1° × 2.1° visual angle; extra large (XL): 2.45° × 2.45° visual angle]. C: each trial began with a size cuing the upcoming movement demand. After the precue, the target appeared in 1 of 4 possible locations (−60°, −30°, 30°, 60° relative to vertical meridian), after which the participants were instructed to use the joystick to move the cursor to the target as quickly and accurately as possible. If the cursor was inside the target 2 s after target presentation, participants received “hit” feedback; otherwise they received “miss” feedback.

Continuous EMG was recorded with the BrainAmp MR plus system (Brain Vision, LLC, Morrisville, NC) from both ECU muscles in the scanner, using MRI-compatible surface electrodes (Brain Vision, LLC, Morrisville, NC) placed 2 cm apart in a belly tendon montage. The ECU muscle was recorded because manipulating the joystick involved extensions and flexions of the hand. EMG signals were bandpass filtered (5 Hz to 1 kHz), amplified, digitized, sampled at a 5,000-Hz frequency, and stored for offline analysis. The recording software (BrainVision Recorder version 1.20; Brain Products GmbH, Gilching, Germany) collected trigger pulses from the scanner [repetition time (TR) = 2,000 ms] to synchronize the EMG recording with the task conditions.

Visual stimuli were back-projected onto a screen by an LCD projector with a frame rate of 60 Hz and viewed by participants through a mirror on top of the MR head coil. Stimuli were displayed and joystick positions were recorded using Presentation software (www.neurobs.com) Stimulus presentation was time-locked to the first trigger pulse from the scanner for every functional run.

Experimental Task

We used a block-design pointing task in which the task demand on precision increases parametrically as a function of target size (Buetefisch et al. 2014; Wischnewski et al. 2016). Decreases in target size result in longer movement times and less accurate movements, which is described by the index of difficulty (ID) term of Fitts’s Law (Fitts 1954). The targets were small (S; 1.4° × 1.4° visual angle, Fitts’s ID = 3.42), medium (M; 1.75° × 1.75° visual angle, Fitts’s ID = 3.09), large (L; 2.1° × 2.1° visual angle, Fitts’s ID = 2.83), or extra large (XL; 2.45° × 2.45° visual angle, Fitts’s ID = 2.61) squares presented in one of four possible locations on the screen (−60°, −30°, 30°, or 60° relative to the vertical meridian). Note that the increase in target size was not linear—as target size increases, the relative change in difficulty becomes smaller (i.e., the difference in Fitts’s ID between S and M is greater than that between M and L). Target sizes were chosen based on previous studies using a similar task with an older population so that participants could achieve an accuracy of >50% on each target size (Fig. 1B; Buetefisch et al. 2014).

Figure 1C shows the trial progression. Each trial began with a fixation square of the same size as the upcoming target, thereby providing advance information about target size. Following the fixation period (0.5 s), both the target and a cursor (0.6° × 0.6° visual angle) appeared for 2 s. The cursor position on the screen represented real-time veridical feedback about the joystick position. Participants were instructed to move the cursor from the start position to the target as quickly and as accurately as possible and then hold their final position until the target disappeared. Manipulating the joystick to reach the target required wrist extension/flexion movements of ~5° in addition to finger movements. An accurate movement (“hit”) was defined as originating from the start position at the center of the screen and resulting in an overlap between the center of the cursor and the target at the end of the 2-s movement period. Accordingly, a movement was recorded as inaccurate when the participant did not reach the target, failed to hold the cursor position within the target, or left the start position early. After each trial, participants were provided feedback (“hit” or “miss”) and instructed to relax their hand to allow the joystick to return passively to the start position.

Each 16-s task block consisted of four movement trials of the same target size, with pseudorandomly jittered intertrial intervals of 0.5, 1, 1.5, or 2 s. Targets appeared in each of the four possible locations once per block. The four-trial target order was determined from a predefined set of 12 sequences such that each block of the same target size had a unique ordering, and the same set of target orders was used across blocks of different target sizes. The purpose of this ordering scheme was to minimize differential effects of movement direction over the course of the experiment while still ensuring that each within-block movement direction could not be planned before target onset. Task blocks were interleaved with 9 s of rest. Each functional run contained three blocks of every target size (12 total blocks per run). Participants performed four runs with one hand (right or left) and then four runs with the other hand in counterbalanced order across participants. The position of the joystick was adjusted accordingly.

To independently define the M1 region of interest (ROI), we used a separate task in which participants repeatedly opened and closed either their right or left hand at ~1 Hz. Movement blocks of 10 s (5 per hand) alternated with resting blocks of 10 s. A visual display showing a right (left) arrow specified a right (left) hand movement block.

On a separate day before scanning, participants completed a training session to familiarize themselves with the pointing task and to minimize learning effects during the fMRI experiment. Participants performed up to three training runs of three blocks each (7 trials of the same target size per block) for both their right and left hands. Baseline performance was determined from the first training run for a given hand. Participants completed fewer than three training runs if they had 50% accuracy on the smallest target size or improved to >50% accuracy on the next largest target size that was at <50% accuracy at baseline. This training procedure was used to standardize the degree of learning across participants (and across hands) during training (Wischnewski et al. 2016).

Image Acquisition

Imaging data were acquired on a Siemens 3T Prisma scanner using a 64-channel head coil. For structural images, we collected a high-resolution T1-weighted scan using a magnetization-prepared rapid gradient echo (MPRAGE) sagittal sequence [voxel size = 0.8 × 0.8 × 0.8 mm³, repetition time (TR) = 2,400 ms, echo time (TE) = 2.24 ms, flip angle (FA) = 8°, field of view (FOV) = 256 × 256 mm²]. For fMRI images, BOLD contrast was measured with a T2*-weighted echoplanar gradient-echo imaging sequence (voxel size = 3.0 × 3.0 × 3.0 mm³, TR = 2,000 ms, TE = 27.0 ms, FA = 90°, FOV = 192 × 192 mm²). For each volume, 34 slices were acquired in interleaved order parallel to the anterior commisure-posterior commisure (AC-PC) plane for near whole brain coverage.

Data Analysis

Motor performance.

Accuracy was defined for each target size as the percentage of hits. Online cursor position data were analyzed for all trials (hits and misses), except for trials where the subject left the start position before the go signal (3% of trials were excluded across all subjects). Position data were first filtered using a second-order two-way Butterworth low-pass filter and differentiated to obtain velocities in the x- and y-axes. Movement onset was defined as the time the cursor extended 1.75° visual angle away from the start position in any direction. Reaction time (RT) was defined as the time from target presentation to movement onset, and movement time (MT) was defined as the time from movement onset to the time the cursor reached and remained in the target (MT was valid for hit trials only). Maximum velocity (MV) and number of velocity peaks (NVP) were determined from the tangential velocity of the combined x- and y-axis data. Finally, initial direction error (IDE) was calculated as the absolute difference between the movement direction of the cursor at maximum tangential velocity and the direction of the ideal straight-line path for the given target (Shabbott and Sainburg 2010). Since the distributions for RT, MT, MV, and IDE were not normal, the median values were computed for each condition, and the resulting medians were averaged across participants. The effect of task demand was analyzed for each of the behavioral measures with repeated-measures ANOVAs using within-subject variables of hand (right/left) and target size (S, M, L, XL), and post hoc comparisons between target sizes were conducted using Bonferroni–Holm-corrected t tests.

EMG.

The objective of the EMG analysis was to test whether the nonperforming hand was coactivated during the movement of the performing hand (i.e., “mirroring” the performing hand), which may increase BOLD activity in M1 ipsilateral to the performing hand. Absence of nonperforming hand activity was assumed when the mean EMG amplitude of the ECU muscle of the nonperforming hand during movement blocks was similar to that in resting blocks. EMG data for the nonperforming hand were first corrected for MR artifacts in BrainVision Analyzer 2 (version 2.1.2; Brain Products GmbH, Gilching, Germany) using the artifact subtraction method (Allen et al. 1998) with template drift detection and a sliding average calculation of 11 TR intervals (22 s). Next, data were downsampled to 1,000 Hz, baseline-corrected, rectified, and segmented into task (16 s) and rest (9 s) blocks. Mean EMG activity for the nonperforming hand was compared for task and rest blocks. A repeated-measures ANOVA with task period (movement/rest) and nonperforming hand (right/left) as factors was used to determine whether performing hand activity (i.e., during the task period or during the rest period) was related to changes in mean EMG amplitude of the nonperforming hand. The task blocks were further separated by target size (S, M, L, XL) to determine whether EMG activity varied as a function of task demand. For the task blocks, a second repeated-measures ANOVA was used to determine whether the within-subject variables of nonperforming hand (right/left) and target size block (S, M, L, XL) affected the mean EMG activity for the nonperforming hand. Since larger movements introduce additional MR artifacts that cannot be reliably corrected, EMG activity of the performing hand was not quantified.

Image preprocessing.

Data were preprocessed incorporating tools from AFNI (Cox 1996) and SPM12 (Friston et al. 2007) integrated within a Nipype workflow (Gorgolewski et al. 2011). Functional images were despiked, slice-time corrected (SPM), and realigned to the mean echo planar imaging (EPI) image to correct for head motion. EPI images were then coregistered to the participant’s high-resolution T1 scan. All ROI analyses were performed in individual subject space.

M1 region of interest analysis.

A first-level parametric statistical analysis was performed to determine the BOLD response in M1 for right- and left-hand movements at different levels of demand. Images were first smoothed with a 6-mm full-width half-maximum (FWHM) isotropic Gaussian kernel and high-pass filtered at 128 Hz. We used a standard general linear model (GLM) with eight regressors corresponding to each hand and target size combination. Onsets for each regressor of interest were modeled as a boxcar function of 16-s duration and convolved with the canonical hemodynamic response function (HRF). Noise regressors were estimated by applying principal component analysis on task-unrelated voxels, as implemented in the GLMdenoise toolbox (Kay et al. 2013). Including noise regressors in the design matrix improves signal-to-noise ratios and thus the reliability of estimates of the voxelwise BOLD response (β weights) used for univariate and representational similarity analyses (Charest et al. 2018; Kay et al. 2013).

For each hand and target size task regressor, we extracted the β weights in the voxels in right and left M1 ROIs. Right and left M1 ROIs were defined separately for each participant in individual subject space based on both anatomical and functional constraints. First, Brodmann’s areas (BA) 4a and 4p were anatomically defined from each participant’s high-resolution T1 scan using an automated parcellation scheme in Freesurfer (Destrieux et al. 2010; Fischl et al. 2004) and transformed into individual subject volumetric space. To identify the area within the anatomically defined M1 that is activated during hand movement, we performed a separate GLM for the hand localizer task, with data in individual subject space and smoothed using a 10-mm FWHM isotropic Gaussian kernel. We defined regressors of interest corresponding to each hand modeled as a boxcar function of 10-s duration and convolved with the canonical HRF. For each participant, we drew a 12-mm sphere around the coordinate in BA 4a/4p that was maximally activated in a left hand > right hand contrast for the right hemisphere or right hand> left hand contrast for the left hemisphere using the MarsBar toolbox (version 0.44; Brett et al. 2002) in SPM. These spheres were then restricted to only include voxels within the anatomically defined boundaries of BA 4a/4p.

The effect of precision demand on M1 ROI activation was analyzed using a repeated-measures ANOVA using the following within-subject variables: performing hand (right/left), M1 (contralateral/ipsilateral with reference to the performing hand), and target size (S, M, L, XL). Follow-up repeated-measures ANOVAs were used to investigate the effect of increasing target size on each performing hand/M1 hemisphere combination.

M1 representational similarity analysis.

The goal of RSA is to explore whether M1 reflects changes to demand on precision by testing explicit hypotheses about how a feature of interest (i.e., motor demand on precision) is represented in distributed activity patterns in an ROI. Importantly, RSA provides a measure of the spatial distribution of BOLD responses that is stable across different levels of overall activation (Diedrichsen and Kriegeskorte 2017; Kriegeskorte et al. 2008). β weight estimates for RSA were obtained from a first-level GLM performed on unsmoothed data in individual subject space. As with the M1 ROI analysis, there were eight task regressors corresponding to each hand and target size combination, as well as task-unrelated noise regressors estimated using GLMdenoise. Since the GLMdenoise approach uses cross-validation to determine optimal noise regressors for each participant, the GLM outputs one β weight per condition across all scanning runs (Kay et al. 2013). To ensure that the dissimilarities in response patterns were not due to differences in the overall BOLD response, the mean β weight estimates for each condition were subtracted from each voxel in the ROI.

RSA was performed using the RSA toolbox (Nili et al. 2014) and custom Matlab and Python scripts. We used the Mahalanobis distance to estimate the dissimilarity between multivariate voxel BOLD response patterns within an ROI for each pair of target size conditions. Each pairwise distance estimate (e.g., small vs. medium) corresponds to one cell in the representational dissimilarity matrix (RDM). The Mahalanobis distance is a more reliable way to calculate RDMs than correlation metrics or Euclidean distance because it accounts for differing noise levels across voxels and spatially correlated noise in nearby voxels (Walther et al. 2016). This weighting scheme is implemented by estimating the noise-covariance matrix from the residuals of the GLM.

Four BOLD RDMs corresponding to each hand (right/left) and hemisphere (M1_contra/M1_ipsi) combination were computed separately for each participant and then averaged. For visualization purposes, the mean BOLD RDMs were rank-transformed and normalized so that distance values were between 0 and 1. The BOLD RDMs are intended to provide a characterization of the overall trends in demand-related pattern activity. As noted above, this primary RSA was based on averaging across runs for each target size condition. In addition to this analysis, we explored whether a cross-validated approach could be applied to obtain an unbiased estimate with a meaningful zero point (Walther et al. 2016). To perform cross-validated RSA, we obtained β weight estimates separately for each run (without adding GLMdenoise regressors, which requires multiple runs to be modeled together), compared response estimates in each condition from one run to estimates from the remaining runs for all possible iterations, and averaged the resulting Mahalanobis distances. Note that in our experimental design, multiple target directions occurred within a block of trials and could not be disentangled, and though target orders completed for each target size were the same across the experiment, they were not balanced within each run (see Experimental Task). These differences in target direction could interfere with cross-validation.

To further assess the representational structure of the M1 ROIs, we performed a second-order Spearman rank correlation between the BOLD RDMs and different behavioral models for each participant. We focused on two fixed models and five behavioral models: the “target size” model assumes that pattern dissimilarity is determined by the task demand on precision for the different target sizes; this model captures the nonlinear difference in the Fitts’s ID between the different target sizes. The “non-demand” model assumes the opposite; that is, targets farther apart in size are more similar to each other. This served as a null model that should only correlate with the BOLD RDMs if task demand on precision has no effect. The five behavioral RDM models (accuracy, NVP, MV, RT, and IDE) were constructed for each participant based on their individual performance across right- and left-hand runs. A subject’s RDM was computed as the pairwise distances between the averaged values of each of the target size conditions. The resulting RDMs reflect ranked dissimilarity because we are interested in assessing the relative differences between performance at the different target sizes, rather than the overall difference in performance (for example, between the right and left hands).

For each of the four BOLD RDMs, we estimated the upper and lower bound of the noise ceiling (Nili et al. 2014). The upper bound is computed as the mean Spearman rank correlation between the single-subject BOLD RDMs and the averaged rank-transformed BOLD RDM, giving the maximum possible correlation that can be expected from a fixed model. The lower bound estimate is derived through a leave-one-subject-out procedure (to account for overfitting) in which each left-out subject’s RDM is compared with the average RDM of the remaining subjects, and the lower bound is the mean correlation across all iterations. The resulting noise ceiling estimates provide information about the intersubject variability and measurement noise in each of the BOLD RDMs, as well as a standard for assessing model performance. Note that for the behavioral models, the correlation can exceed the noise ceiling since each subject’s individual behavioral RDM could theoretically perfectly match their BOLD RDM.

In addition to assessing the relatedness between the single-subject RDMs and model RDMs, we sought to determine whether an individual’s RDMs for left and right M1 were correlated with each other. For right- and left-hand movements separately, we calculated the Spearman’s rank correlation between a subject’s left and right RDMs. All second-order correlations were tested for statistical significance against 0 using the one-sided Wilcoxon rank sum test, and all models were compared with each other using the two-sided Wilcoxon rank sum test (Wilcoxon 1945). All tests were corrected for multiple comparisons using the false discovery rate (FDR) correction (Benjamini and Hochberg 1995).

RESULTS

Motor Performance

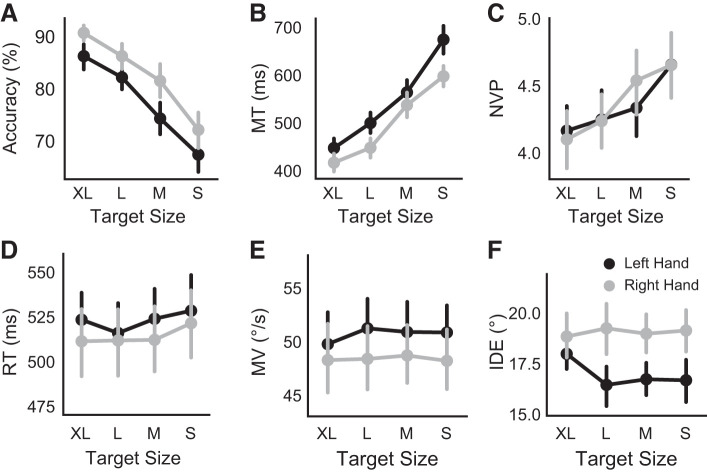
Figure 2, A and B, shows that accuracy decreased and MT increased with decreasing target size. This was similar for both hands. A 2 × 4 repeated-measures ANOVA with performing hand (right/left) and target size (S, M, L, XL) as factors showed significant main effects of hand (F_1,21 = 6.32, P = 0.02, ${\eta }_p^2$ = 0.035) and target size (F_1.90,40.01 = 46.89, P < 0.001, ${\eta }_p^2$ = 0.217, Greenhouse-Geisser correction ε = 0.635) on accuracy. The hand × target size interaction was not significant (F_3,63 = 0.64, P = 0.589, ${\eta }_p^2$ = 0.002). As expected, Bonferroni–Holm post hoc comparisons for both hands showed a significant decrease in accuracy when the target size decreased (XL > L > M > S, all P values <0.05 corrected). Though there was an overall main effect of hand favoring the right hand, performance accuracy at each target size was not different between the hands (all P values >0.05). Similarly, a 2 (hand) × 4 (target size) ANOVA revealed significant main effects of both hand (F_1,21 = 5.92, P = 0.023, ${\eta }_p^2$ = 0.04) and target size (F_1.81,38.07 = 92.06, P < 0.001, ${\eta }_p^2$ = 0.33, Greenhouse-Geisser correction ε = 0.604) on MT (accurate trials only), indicating longer MT for left hand movements and for smaller targets. Post hoc comparisons showed that MT significantly increased with decreasing target size (XL < L < M < S, all P values <0.05 corrected) and that the right-hand MT was significantly shorter than the left-hand MT for the S target size (t₂₁ = 3.24, P = 0.016). Overall, this indicates that, in the employed task, target sizes were sufficiently different to modulate both accuracy and MT, consistent with the criteria of Fitts’s law (Fitts 1954).

Fig. 2.

Motor performance showing the effect of task demand on precision (decreasing target size) and hand used (right or left) on accuracy (A), movement time (MT; hit trials only; B), number of velocity peaks (NVP; C), reaction time (RT; D), maximum velocity (MV; E), and initial direction error (IDE; F). Values are means; error bars indicate SE.

Similar to MT, there was an increase in NVPs for the smaller target sizes (F_2.32,48.81 = 19.12, P < 0.001, ${\eta }_p^2$ = 0.03, Greenhouse-Geisser correction ε = 0.77), indicative of more online adjustments during movement (Fig. 2C). There was no difference in NVPs between the right and left hands (F_1,21 = 0.71, P < 0.410, ${\eta }_p^2$ = 0.003). Post hoc comparisons showed that the NVPs significantly increased with decreasing target size (XL < L < M < S, all P values <0.05 corrected). As shown in Fig. 2, D–F, neither MV, RT, nor IDE varied with task demand on precision at the group level, as a 2 (hand) × 4 (target size) ANOVA showed no significant main effects or interactions for each measure. Together, the behavioral results indicate that accuracy, MT, and NVPs can be considered as demand-dependent behavioral features of the task, whereas MV, RT, or IDE are not demand dependent.

EMG

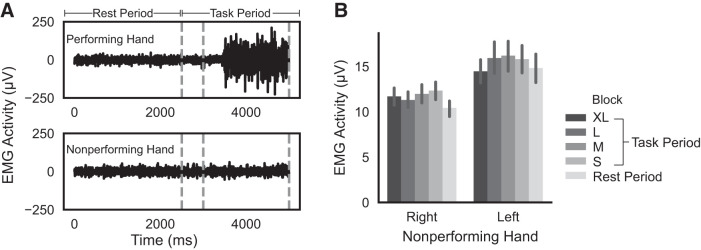
Four subjects’ EMG data were excluded from further analysis because of excessive artifacts or incomplete data. Figure 3A shows representative EMG traces during task performance, showing increases in EMG activity for the performing hand during task performance compared with rest. As shown in Fig. 3B, mean EMG activity for the nonperforming hand did not increase along with the performing hand (relative to the rest period, F_1,17 = 2.69, P = 0.119, ${\eta }_p^2$ = 0.003), and there was no significant difference in mean EMG activity of the nonperforming hand between right- and left-hand blocks (F_1,17 = 3.82, P = 0.067, ${\eta }_p^2$ = 0.045). Mean EMG activity for the nonperforming hand also did not depend on the target size of the task block (F_3,51 = 1.57, P = 0.207, ${\eta }_p^2$ = 0.002). Together, these results indicate it is unlikely that M1_ipsi activations were driven by differences in mirror activity in the nonperforming hand.

Fig. 3.

Electromyographic (EMG) activity in the nonperforming hand. A: example EMG traces during the rest period (between movement blocks of 4 trials) and task period for the performing and nonperforming hands. Performing hand activity was recorded but not analyzed for differences across blocks due to scanner artifacts related to changing hand position that could not be reliably corrected. B: mean EMG activity in the nonperforming hand as a function of nonperforming hand (right or left) and movement in the performing hand [i.e., to extra-large (XL), large (L), medium (M), or small (S) targets, or during rest].

Univariate Analysis of BOLD Responses

The primary aim of this study was to determine how task-related M1 activity varies with a parametric increase in motor demand on the precision of a strictly unilateral hand movement. We first performed a univariate ROI analysis in both left M1 (91.3 ± 26.1 voxels) and right M1 (86.1 ± 26.1 voxels) to assess whether overall M1 activation differed during movements across different target sizes, and whether this pattern was different for right- vs. left-hand movements. Consistent with a previous report (Buetefisch et al. 2014), we found that a decrease in target size was related to increased BOLD activity in M1_contra and M1_ipsi, and we extend previous results to show this activation increase occurs for movements made using either hand (Fig. 4). A 2 × 2 × 4 repeated-measures ANOVA with performing hand (right/left), M1 (contralateral/ipsilateral with reference to the performing hand), and target size (S, M, L, XL) as factors revealed statistically significant main effects of M1 (F_1,21 = 175.79, P < 0.001, ${\eta }_p^2$ = 0.498) and target size (F_3,63 = 12.91, P < 0.001, ${\eta }_p^2$ = 0.004). There was no significant main effect of hand (F_1,21 = 3.86, P = 0.063, ${\eta }_p^2$ = 0.014), and no significant interactions were found. Follow-up tests showed that for right-hand movements, M1_contra activity increased for smaller target sizes (F_3,63 = 4.95, P = 0.004, ${\eta }_p^2$ = 0.004). Activity in M1_ipsi also varied with target size for right-hand movements (F_3,63 = 3.21, P = 0.029, ${\eta }_p^2$ = 0.003), but the relationship was less clear: while M1_ipsi activity increased as target size decreased for the three largest targets (XL, L, and M), activity for the smallest target (S) was similar to that for the larger (XL and L) target sizes. For left-hand movements, both M1_contra and M1_ipsi showed a similar trend of increasing activity with smaller target size (M1_contra: F_1.96,41.13 = 4.95, P = 0.042, ${\eta }_p^2$ = 0.004, Greenhouse-Geisser correction ε = 0.653; M1_ipsi: F_3,63 = 10.06, P < 0.001, ${\eta }_p^2$ = 0.008). These results indicate that the motor demand on precision modulates overall activity in task-relevant M1_contra and M1_ipsi.

Fig. 4.

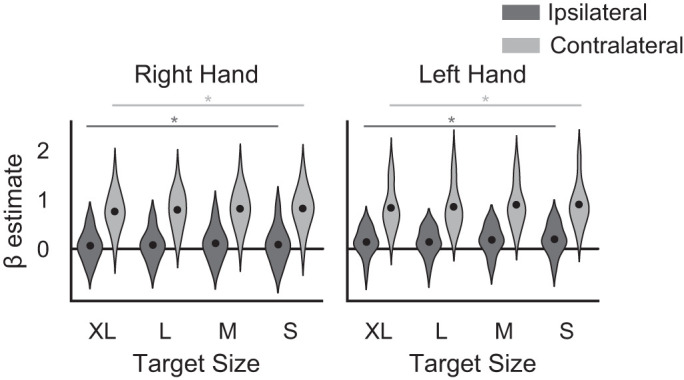
Violin plot of the overall β estimates of blood oxygen level-dependent (BOLD) activation levels in individually defined primary motor cortex (M1) regions of interest (ROIs) for right and left hands. Black dots show the mean estimate. *Significant main effect of target size for the given M1 ROI and hand used.

Representational Similarity Analysis of BOLD Responses

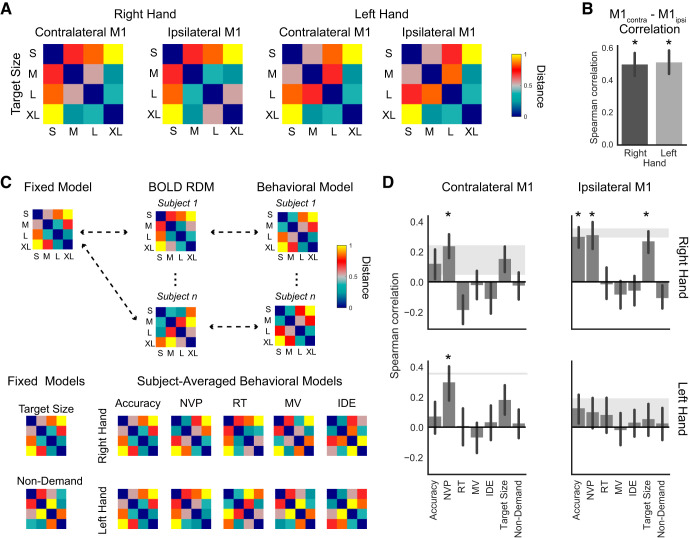
Figure 5A shows the rank-transformed and normalized subject-averaged BOLD representational dissimilarity matrix (RDM) corresponding to each hand (right/left) and M1 (M1_contra/M1_ipsi). Visual inspection of the RDMs provides initial evidence for a demand-like organizational structure: in each RDM, there is a parametric increase in dissimilarity when the smallest target (S) is compared with the larger three (M, L, and XL). That is, BOLD response patterns for movements during S target blocks were most similar to movements during the M target blocks and least similar to movements during the XL target blocks. Overall, the subject-averaged BOLD RDMs have a similar structure to a model of target size (Fig. 5C), which assumes the dissimilarity of the BOLD response pattern increases with decreasing target size. Despite this general organization, the RDMs do not have a strict correspondence with demand. For example, a representation based solely on the differences in the Fitts’s ID of the target size would predict the highest similarity to occur between the L and XL target blocks; instead, the M and XL target blocks show the highest similarity in each hand/region combination. A separate RSA using cross-validation showed no differences in mean distances (all t values <1.6, all P values >0.13), though this result may have been affected by imbalances in the order of target locations and participants’ variable motor performance across the separate runs (see materials and methods and discussion).

Fig. 5.

A: subject-averaged representational dissimilarity matrices (RDMs; rank-transformed and normalized) depicting group effect of blood oxygen level-dependent (BOLD) activity pattern variation with demand in contralateral (M1_contra) and ipsilateral M1 (M1_ipsi) for movements made with the right or left hand. Each RDM cell depicts the Mahalanobis distance between multivoxel response patterns for the given pair of target size conditions. B: Spearman correlations between individual subjects’ ipsilateral and contralateral RDMs *Correlation is significantly above chance, after false discovery rate (FDR) correction (Benjamini and Hochberg 1995). C: fixed models of target size and non-demand were compared with each subject’s BOLD RDM. For the behavioral models of accuracy, number of velocity peaks (NVP), reaction time (RT), movement velocity (MV), and initial direction error (IDE), a model RDM was computed separately for the right and left hands and compared with that individual’s BOLD RDM. D: Spearman correlations between BOLD RDMs and model RDMs in contralateral and ipsilateral M1 for movements made with the right or left hand. Gray-shaded area indicates the upper and lower bounds of the noise ceiling. *Correlation is significantly above chance, after FDR correction (Benjamini and Hochberg 1995).

The trend from the group-averaged RDMs showing similar organization for both M1_contra and M1_ipsi suggests that the representations of the different target size conditions in the two hemispheres might be related to each other. To test this, we correlated each subject’s RDM in M1_contra with their own M1_ipsi RDM, for right- and left-hand movements separately. As shown in Fig. 5B, the RDMs in the two M1 cortices were significantly correlated with each other for both right-hand (r = 0.503, Z = 242.0, P < 0.001) and left-hand movements (r = 0.517, Z = 247.0, P < 0.001). This suggests that the M1 BOLD response patterns to movements with differential demand on precision vary similarly in M1_contra and M1_ipsi, though the group-averaged RDMs are not identical across hemispheres for either right- or left-hand movements.

The overall organization of the group RDMs provides evidence for a demand-dependent representation in M1 while preparing for and executing movements with varying demands on precision; however, a more stringent analysis tests whether between-subject variation in the BOLD response patterns can be explained by simple models of motor demand or individual performance metrics. To do this, we computed the Spearman rank correlation between single-subject BOLD RDMs and each of seven model RDMs. Of the models, two were fixed models (target size and non-demand) and thus were the same for each subject, and five (accuracy, NVP, MV, RT, and IDE) were behavioral models computed for each subject from their task performance, separately for right- and left- hand blocks (Fig. 5C). Across subjects, the right-hand accuracy and NVP models showed a clear parametric variation with demand across subjects (mean Spearman rank correlation with target size: r = 0.597, Z = 249.0, P < 0.001 for accuracy, r = 0.424, Z = 237.5, P < 0.001 for NVP), the RT models showed a moderate variation with demand of borderline significance (r = 0.172, Z = 177.0, P = 0.052), and the MV (r = 0.003, Z = 120.5, P = 0.577) and IDE (r = 0.031, Z = 127.0, P = 0.502) models did not change systematically with demand. Similarly, for left-hand movements, the accuracy (r = 0.576, Z = 241.5, P < 0.001) and NVP (r = 0.301, Z = 200.5, P = 0.008) models were demand-dependent, whereas the RT (r = 0.098, Z = 143.5, P = 0.171), MV (r = −0.20, Z = 56.0, P = 0.989) and IDE (r = 0.033, Z = 129.5, P = 0.535) models were not. Note that MT was not included as a parameter for a model RDM because it could only be defined for correct trials, whereas the BOLD signal RDMs were based on the multivoxel response estimates of the entire movement block (which could include both correct and missed trials).

As shown in Fig. 5D, for right-hand movements, there were significant correlations between the BOLD RDM for M1_ipsi and the three models with clear demand-dependent variation (target size: r = 0.265, Z = 209.0, P = 0.003; accuracy: r = 0.295, Z = 226, P < 0.001, NVP: r = 0.306, Z = 209, P = 0.003), but not for the models unrelated to demand (RT: r = −0.013, Z = 112.5, P = 0.542; MV: r = −0.081, Z = 100.0, P = 0.805; IDE: r = −0.055, Z = 107.5, P = 0.732; non-demand: r = −0.104, Z = 87.0, P = 0.900). A comparison between all possible model pairs showed that the correlations for the target size, accuracy, and NVP models were each significantly greater than the correlations for the MV, IDE, and non-demand models (P values <0.05 after FDR correction for multiple comparisons). This provides supporting evidence that BOLD response patterns measured throughout the course of movement blocks are sensitive to the demand aspects of the task (target size, accuracy, NVP), and not to non-demand-dependent aspects (MV, IDE). For right-hand movements, a similar trend of correlations with the M1_contra BOLD RDM was observed, though only the NVP model reached statistical significance after FDR correction for multiple comparisons (r = 0.232, Z = 209.5, P = 0.003). Similarly, the NVP model was significantly correlated with the M1_contra BOLD RDMs for left-hand movements (r = 0.293, Z = 201.0, P = 0.008). In M1_ipsi, for left-hand movements, no model showed a significant correlation with the BOLD RDMs. The low number of stimulus conditions (four) for RSA and high intersubject variability of the RDMs, especially in M1_ipsi during left-hand movements (as indicated by the low noise ceiling), limit the interpretation of the significance of model correlations.

DISCUSSION

The main findings of the current study are that BOLD responses in contralateral and ipsilateral M1 during performance of a strictly unimanual task vary with increasing demand on the precision of task performance. In replication of our previous results (Buetefisch et al. 2014), the univariate analysis of BOLD responses showed an increase in M1_contra and M1_ipsi activation with increasing task demand on movement precision. Notably, we extend previous findings to show this increase applies not only for movements made with the dominant (right) hand, but for nondominant (left) hand movements as well. Additionally, we implemented improved in-scanner EMG recording methods to establish that the observed increased M1_ipsi activity is not attributable to differences in EMG activity of the nonperforming hand. To complement the univariate findings, RSA of the BOLD data provides initial supporting evidence that there is also distinct variation with task demand in the underlying response patterns, particularly in M1_ipsi during right-hand movements. Because the current task kept important kinematic variables (e.g., force, amplitude, and frequency) and participating muscle groups similar across movements to different target sizes, and controlled for strictly unimanual movements at the level of EMG activity, the univariate and RSA findings provide evidence that neural activity in M1 is modified in part by task features that vary with demand on precision.

Relating M1 BOLD Activity to Demand on Precision

The unimanual task used in the current study manipulated the demand on movement precision by changing the size of the to-be-reached target. Group-level behavioral performance showed that decreasing the target size resulted in a decrease in accuracy and increase in MT, in accordance with Fitts’s Law (Fitts 1954; Fitts and Peterson 1964). Unlike manipulating movement amplitude, the increase in MT associated with decreasing target sizes was associated with an increase in the number of online adjustments (as indexed by NVP) rather than a decrease in MV (Bootsma et al. 2004; Yang and Song 2015). Consistent with previous results, there were no significant differences in RT or IDE, likely due to presentation of a precue indicating the size of the upcoming target (Boyd et al. 2009; Munro et al. 2007). The target size precue allows for advance planning of desired trajectories appropriate for the relative end-point accuracy required, mitigating any demand-related differences after target onset (Harris and Wolpert 1998; Munro et al. 2007; Tanaka et al. 2006).

In replication of previous results, we found that greater demand on movement precision led to an overall increase in bilateral M1 BOLD activation during pointing movements (Alahmadi et al. 2015; Buetefisch et al. 2014; Ehrsson et al. 2000; Newton et al. 2005; Pool et al. 2013; Sehm et al. 2010; Verstynen et al. 2005). In extension of these results, we now demonstrate similar demand-dependent activation for movements made with either the right or left hand. Importantly, this increased activation during strictly unimanual task performance did not depend on explicitly manipulating movement parameters known to influence M1 population activity, such as force, amplitude, or movement frequency (Georgopoulos and Carpenter 2015; Kalaska 2009). In addition, EMG activity of the nonperforming hand was similar during rest and movement periods and did not vary with target size. Previously, we showed an absence of increased EMG activity in the nonperforming hand during the movement period, but in that study only the latter half of the movement that occurred during scanner silence (due to sparse sampling) could be recorded (Buetefisch et al. 2014). Here, we took advantage of improved in-scanner EMG recording and MR artifact correction techniques to confirm that there was no difference in nonperforming hand EMG activity throughout the entire task. Thus the increase in M1_ipsi activity with increasing demand on precision cannot simply be attributed to mirroring movements of the nonperforming hand (Bütefisch et al. 2005; Sehm et al. 2010).

Increased overall M1 activation for smaller targets could be a result of multiple interrelated mechanisms, including coding of more precise trajectories, recruitment of more motor cortical neurons, or changes to higher cognitive or attentional resources engaged (Boyd et al. 2009; Pool et al. 2013). Investigating the distributed pattern activity within a region with RSA provides a complementary approach that has the potential to uncover information content driving the behavioral differences independent of mean activation levels (Kriegeskorte and Kievit 2013; Kriegeskorte et al. 2008). We used RSA to explore how increasing the demand on precision may modulate M1 neural activity patterns by comparing patterns of M1 BOLD responses between blocks of movements to differently sized targets. Our results showed that similarity patterns within M1_contra and M1_ipsi vary when demand on precision is manipulated, providing support to the idea that the underlying neural computations within M1 are sensitive to demand-dependent task components (Serrien et al. 2006; Verstynen and Ivry 2011). The RDMs showed an increase in dissimilarity when the S target was compared with M, L, and XL targets; however, the overall representational structure was not a monotonic reflection of increasing demand (for example, in all comparisons, there was a higher similarity between M and XL targets than M and L).

To better understand the representational structure in M1, we compared each subject’s RDM to alternative models that tested competing hypotheses about demand-like representation or were based on individual subject performance. For right-hand movements, models that reflected changes in demand on precision (target size, accuracy, NVP) significantly correlated with the BOLD RDMs in M1_ipsi, whereas non-demand-dependent models (RT, MV, IDE, non-demand) did not show positive correlations with the BOLD RDMs. This finding is consistent with the results from the univariate analysis and provides additional evidence for demand-dependent representations in M1_ipsi, which may relate to preparing for movements that have different precision requirements and/or the associated kinematic variations in executing those movements (Gallivan et al. 2013; Georgopoulos and Carpenter 2015; Ifft et al. 2011). In M1_contra, only the NVP model significantly correlated with the BOLD RDMs. One possible explanation for this result is that variation with target size in M1_contra may largely reflect a greater reliance on visually based adjustments for movements to smaller targets during movement execution rather than preparing for movements with different demands (Bootsma et al. 2004). However, the unique contribution of the different demand-dependent features (e.g., target size, accuracy, movement time, NVPs) to shaping M1 response patterns cannot be disentangled from the present results.

M1_contra and M1_ipsi response patterns qualitatively showed a similar representational structure, yet differences emerged that point to distinct roles in controlling unimanual action. Across individuals, M1_contra and M1_ipsi representations of demand were correlated, which may be related to the report of demand-dependent differences in active interhemispheric inhibition between M1s (Wischnewski et al. 2016). There is some evidence that even though uncrossed descending projections are not involved in controlling ipsilateral movement (Soteropoulos et al. 2011), encoding of movement properties of strictly unilateral hand movements in M1_ipsi is similar to that of M1_contra (Bundy et al. 2018; Fujiwara et al. 2017; Ganguly et al. 2009; Haar et al. 2017). Here, we found different group-level correlations with the model RDMs depending on the hemisphere tested, suggesting that the source of ipsilateral activity patterns might be at least partially distinct from M1_contra, though this possibility needs to be explored in future work.

Comparison of Moving the Right and Left Hands

Differences in motor performance and BOLD activation found in the present study point to hemispheric asymmetries in how M1 contributes to the control of hand movements (Alahmadi et al. 2015; Haaland 2006; Hayashi et al. 2008; Pool et al. 2013; Serrien et al. 2006; van den Berg et al. 2011). Behaviorally, left-hand movements were slower and less accurate overall than right-hand movements, indicative of an added effort for moving with the nondominant hand (Vaughan et al. 2012). Though there were small hand-related differences in overall BOLD activation levels and group-level RDMs, the most noticeable difference between hands was in the BOLD RDM/model RDM comparison. In M1_ipsi, demand-dependent models were correlated with the BOLD RDMs for the right hand, but not the left (though this result may have been partially influenced by intersubject variability), which may relate to distinct specializations for motor control in the two hemispheres (Serrien et al. 2006). For example, the left hemisphere is thought to encode properties related to the specifying task dynamics, whereas the right hemisphere may preferentially encode spatial or sensory components of the movement (Yadav and Sainburg 2014). Thus the utility of M1_ipsi’s involvement in response to task demands may differ depending on which hemisphere is ipsilateral to the performing hand. Though this hypothesis remains to be tested, our results emphasize the value of measuring activity related to both nondominant and dominant hands for understanding the role of ipsilateral M1 in unimanual motor control.

Limitations and Conclusions

Increasing the demand on precision in our task was coupled with a decrease in performance accuracy. The advantage of this approach was that the demand on movement precision (target size) was manipulated while important kinematic features were matched across target size blocks. However, an inherent limitation in this block design is that we could not decouple successful from unsuccessful movements. Therefore, the effects of demand on precision could not be distinguished from the effects of worse motor performance and feedback error monitoring; our observed results may reflect a combination of these interacting processes (Cisek et al. 2003).

A key aim of the present study was to investigate M1 activity during strictly unilateral movements (as confirmed using EMG) made with either the right or left hand in which task performance accuracy could vary across conditions. Additionally, we sought to explore the utility of RSA to investigate the possibility of demand-like representations in M1 while at the same time keeping the experimental design consistent with previous investigations of motor demand on precision (Buetefisch et al. 2014). An important caveat to this approach is that the experimental design was not fully optimized for RSA: movements to four different directions were intermixed within each block, and the order in which these movements were completed was not balanced within each run. Similarly, motor performance could vary considerably both within blocks (i.e., different performance accuracies) and across runs (i.e., learning throughout the task). These design limitations may have interfered with the cross-validation approach by skewing the dissimilarity estimates obtained with cross-validation, which requires comparing BOLD activity across separate runs. Thus, though the presented RDMs are based on overall response estimates to avoid imbalances in the sequence of movement directions and individual motor performance across runs, the lack of cross-validation with this approach limits the reliability and therefore the conclusions that can be derived from the present RSA results (Walther et al. 2016). An additional drawback in using RSA with the present task was the low number of unique target sizes, which limits the ability to infer significant differences between the models through statistical inference (Nili et al. 2014). Nevertheless, when viewed in conjunction with the univariate results of increasing M1 activity with demand on precision, the exploratory results from the RDMs and model comparisons provide initial evidence that demand on precision is a relevant factor determining M1 activity patterns and highlight RSA as a promising tool. Future work that takes advantage of the cross-validated approaches and more condition-rich designs afforded by RSA and related analyses (e.g., separating effects of movements to different directions at different levels of demand) is necessary to further elucidate the nature of demand-like representations in M1 and to differentiate between competing representational models of demand on precision (Diedrichsen and Kriegeskorte 2017; Diedrichsen et al. 2011).

The participants in the present study were older adults, who are relatively understudied and serve as a more suitable group than younger adults to understand motor deficits in many patient populations (Talelli et al. 2008). Since we did not test younger individuals, we cannot determine how aging may have influenced the present pattern of results. Because older subjects have more variable motor performance, show altered kinematics in Fitts’s Law tasks (Ketcham et al. 2002; Seidler et al. 2010), and exhibit more widespread activation of motor regions, especially in the ipsilateral hemisphere (Michely et al. 2018; Seidler et al. 2010; Talelli et al. 2008), the present results should not be extrapolated to a younger population.

In summary, the current findings provide evidence that M1_ipsi is active during the execution of a strictly unimanual task and that demand on movement precision modulates BOLD activity in M1_contra and M1_ipsi. By combining standard univariate fMRI analysis techniques with multivoxel RSA, we found that overall M1_contra and M1_ipsi BOLD activation was higher during movements made to smaller, more demanding targets and that the dissimilarity between multivoxel M1 response patterns for different movements varied with target size.

GRANTS

This work was supported by National Institutes of Neurological Diseases and Stroke (NINDS) and National Institutes of Child Development and Health Grant R01NS090677. D.A.B. received support from the Emory University NIH/NINDS Training and Translational Research in Neurology Program Grant T32NS007480, Georgia StrokeNet, and American Heart Association Award 18POST34060183.

DISCLAIMERS

The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.A.B., K.P.R., K.S., and C.M.B. conceived and designed research; D.A.B., K.P.R., A.C., and I.V. performed experiments; D.A.B., K.P.R., and A.S. analyzed data; D.A.B., K.S., and C.M.B. interpreted results of experiments; D.A.B. prepared figures; D.A.B. drafted manuscript; D.A.B., K.S., and C.M.B. edited and revised manuscript; D.A.B., K.P.R., A.C., I.V., A.S., K.S., and C.M.B. approved final version of manuscript.