Hsp90 chaperones have an energetic hot‐spot for binding inhibitors

Abstract

Although Hsp90‐family chaperones have been extensively targeted with ATP‐competitive inhibitors, it is unknown whether high affinity is achieved from a few highly stabilizing contacts or from many weaker contacts within the ATP‐binding pocket. A large‐scale analysis of Hsp90α:inhibitor structures shows that inhibitor hydrogen‐bonding to a conserved aspartate (D93 in Hsp90α) stands out as most universal among Hsp90 inhibitors. Here we show that the D93 region makes a dominant energetic contribution to inhibitor binding for both cytosolic and organelle‐specific Hsp90 paralogs. For inhibitors in the resorcinol family, the D93:inhibitor hydrogen‐bond is pH‐dependent because the associated inhibitor hydroxyl group is titratable, rationalizing a linked‐protonation event previously observed by the Matulis group. The inhibitor hydroxyl group pK _a associated with the D93 hydrogen‐bond is therefore critical for optimizing the affinity of resorcinol derivatives, and we demonstrate that spectrophotometric measurements can determine this pK _a value. Quantifying the energetic contribution of the D93 hotspot is best achieved with the mitochondrial Hsp90 paralog, yielding 3–6 kcal/mol of stabilization (35–60% of the total binding energy) for a diverse set of inhibitors. The Hsp90 Asp93➔Asn substitution has long been known to abolish nucleotide binding, yet puzzlingly, native sequences of structurally similar ATPases, such as Topoisomerasese II, have an asparagine at this same crucial site. While aspartate and asparagine sidechains can both act as hydrogen bond acceptors, we show that a steric clash prevents the Hsp90 Asp93➔Asn sidechain from adopting the necessary rotamer, whereas this steric restriction is absent in Topoisomerasese II.

1. INTRODUCTION

The Hsp90 family of ATP‐dependent chaperones aid in the folding and stabilization of “client proteins”. Human Hsp90 paralogs include Hsp90α and Hsp90β in the cytosol, Grp94 in the endoplasmic reticulum (ER), and Trap1 in mitochondria. ¹ Many oncogenic proteins depend on Hsp90 for their stability, and consequently, Hsp90 has been targeted with ATP‐competitive inhibitors. ² Longstanding development efforts have yielded high affinity inhibitors from diverse structural classes, such as those based on geldanamycin, resorcinol, purine, pyrimidines, or azoles. ²

Fragment‐based drug discovery (FBDD) has produced compounds with high affinity for Hsp90. ³ A premise of FBDD is that energetic hotspots can be identified by analyzing the binding properties of diverse small molecules, and that key stabilizing contacts can then be integrated into a single compound that achieves high affinity. While the general success of FBDD suggests that energetic hot‐spots are a common feature of drug targets, ⁴ their exact energetic contributions are challenging to quantify. Structure‐based calculations are being developed to predict energetic hot‐spots. ⁵ , ⁶ , ⁷ Improvements in these computational methods will require benchmarks of experimentally validated hot‐spots and their associated energetic contributions.

The Hsp90 binding pocket has been described as having several distinct regions. For example, Taldone et al. identify Pocket A, which ATP and the majority of inhibitors contact, Pocket B, a hydrophobic pocket that is opened upon the binding of some inhibitors, and Pocket C, which is at the opening leading into these deeper pockets. ⁸ Each of these regions contains potentially important contacts for inhibitor binding. In Hsp90α, these are N51, D93, and T184 in Pocket A; L107 and F138 in Pocket B; and G97 and K58 in Pocket C. Areas in the vicinity of Pocket B have been subdivided into Sites 1, 2, and 3 which are distinguished by paralog‐specific conformations. ⁹ For example, PU‐H54, a Grp94 selective inhibitor, interacts with Site 1 in Hsp90α and Site 2 in Grp94. In Grp94 the movement of F199 allows access to a deeper hydrophobic area. ¹⁰ While paralog‐specific differences in residues and conformations are being utilized in attempts to create more selective inhibitors, it is not known how much each of these regions contributes to Hsp90 inhibitor binding affinity. Indeed, it is not known whether inhibitor affinity arises from a few energetically dominant contacts or from many widely distributed contacts.

Previous findings have yielded perplexing results about the impact of specific Hsp90 residues on the binding of both inhibitors and nucleotides. For example, the D93N substitution dramatically weakens nucleotide binding, ¹¹ which has been rationalized to arise from a loss of a hydrogen‐bond in which the nucleotide N6 amine group acts the proton donor and Asp93 acts as the hydrogen‐bond acceptor. ¹² This explanation is at best incomplete because asparagine and aspartate sidechains can both act as hydrogen‐bond acceptors. Asparagine and aspartate sidechains have identical hydrogen‐bonding energy as measured by helix‐capping stabilization. ¹³

Hsp90 is part of the GHKL superfamily, whose members (DNA gyrase, Hsp90, histidine Kinase, mutL) have similar ATP binding pockets. ¹⁴ Shortly after D93N in Hsp90α was shown to disrupt ATP binding, the homologous D73N variant of DNA gyrase B was found to abolish the binding of ATP and two classes of inhibitors: coumarins and cyclothialidines. ¹¹ , ¹⁵ However, in stark contrast, other GHKL family members, such as Topoisomerase II, have an asparagine (N99 in yeast numbering) at the equivalent position of D93. The seemingly disparate observations about influence of the D93 position for Hsp90 and the entire GHKL superfamily have contributed to difficultly in understanding which inhibitor contacts to Hsp90 provide the most energetic stabilization and whether the energetic influence of these contacts is conserved across the GHKL superfamily.

2. RESULTS

We questioned whether a large‐scale structural analysis could yield insights into whether certain regions of Hsp90 are critical to the binding of most inhibitors. The Hsp90 NTD readily crystalizes and as a result, over 200 NTD:inhibitor crystal structures are currently deposited in the PDB. We analyzed these crystal structures to quantify which types of inhibitor contacts are observed most frequently (Table S1). The D93 residue in Hsp90α stands out in this analysis. Figure 1a,b catalogs the frequency of direct and water‐mediated hydrogen bonds made between Hsp90 inhibitors and residues on the Hsp90α NTD. The D93 sidechain forms these two types of hydrogen‐bonds in 94.5% of the NTD:inhibitor crystal structures examined. All available NTD:inhibitor structures for Grp94, Trap1 and Hsp90β have an inhibitor hydrogen‐bond at the equivalent of D93 (Table S1).

FIGURE 1.

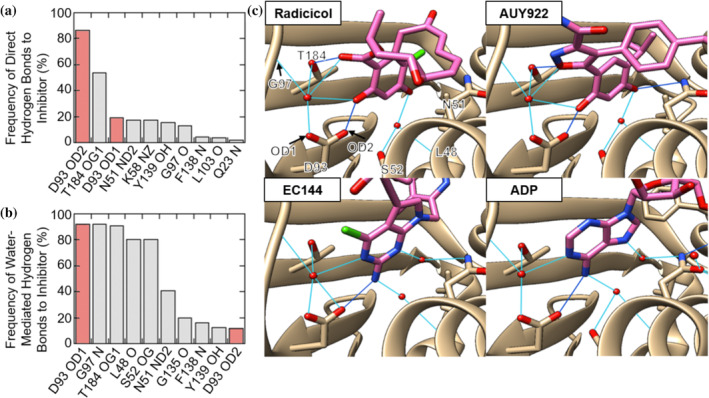
Hsp90α residues are rank‐ordered by their frequency of forming direct hydrogen‐bonds (a) and water‐bridged hydrogen bonds (b) to inhibitors. Data compiled from Table S1. The contacts on Hsp90α are listed as the single letter amino acid code, the residue number in the PDB and the name of specific atom contacted by IUPAC‐IUB rules. ²⁵ (c) Key residues involved in hydrogen bonding to radicicol (PDB: 4EGK), EC144 (PDB: 3NMQ), AUY922 (PDB: 2VCI), and ADP (PDB: 6GQ6). Direct hydrogen bonds are dark blue and water‐mediated bonds are light blue

Of the 200 Hsp90α structures examined only 11 inhibitors do not make a direct or water‐mediated hydrogen bond with D93. Of these, 8 are less than 300 Da in size and therefore likely are fragments from screening efforts. One of the remaining three inhibitors (Ligand ID: 592) binds near D93 but in an orientation not compatible with a D93 hydrogen bond. ¹⁶ Only two structures show inhibitors larger than 300 Da that do not contact D93 (Ligand IDs: YJX and IK9). These two inhibitors bind at Pocket B; a large hydrophobic pocket which is formed upon the binding of some inhibitors. ¹⁰ A roughly equal proportion of these structures show inhibitor hydrogen bonding with D93 through nitrogen‐ or oxygen‐associated hydrogens, 45% and 50%, respectively (Figure S1A). Further examination reveals that the nitrogen‐associated hydrogen‐bond donors are substituents of highly variable inhibitor scaffolds (Figure S1B). In contrast, the oxygen‐associated hydrogen‐bond donors are predominantly aromatic OH groups of resorcinol derivatives (Figure S1C).

Figure 1c shows examples of inhibitor hydrogen‐bonding to D93. The geometry of nitrogen‐associated hydrogen‐bond donors (ADP, EC144) is distinct from the resorcinols (radicicol, AUY922). However, in all cases the same group of residues on Hsp90α (D93, T184, G97) participates in the hydrogen‐bonding network. Indeed, Figure 1b shows that T184 and G97 make water‐mediated hydrogen‐bonds in approximately 90% of all Hsp90α:inhibitor structures. The consistency of the D93‐centered hydrogen bonding network despite the high structural and chemical diversity of Hsp90 inhibitors suggests that this region is critically important

2.1. Residue D93 is critical for the binding of highly diverse Hsp90 inhibitors

Inhibitor‐induced melting temperature (T _m) shifts of the Hsp90 NTD are frequently used as an indicator of inhibitor affinity. ¹⁷ Thermal shift assay (TSA) measurements were performed using a fluorescent dye that monitors the exposure of hydrophobic surface associated with unfolding of the Hsp90α NTD (Methods). Both inhibitors and ADP show concentration‐dependent increases in T _m (Figure S2). To compare many different inhibitors we evaluated T _m shifts (ΔT _m) at a single concentration of 50 μM. Figure 2 shows that the D93N variant has severely impaired inhibitor binding properties, as indicated by the smaller ΔT _m for all inhibitors.

FIGURE 2.

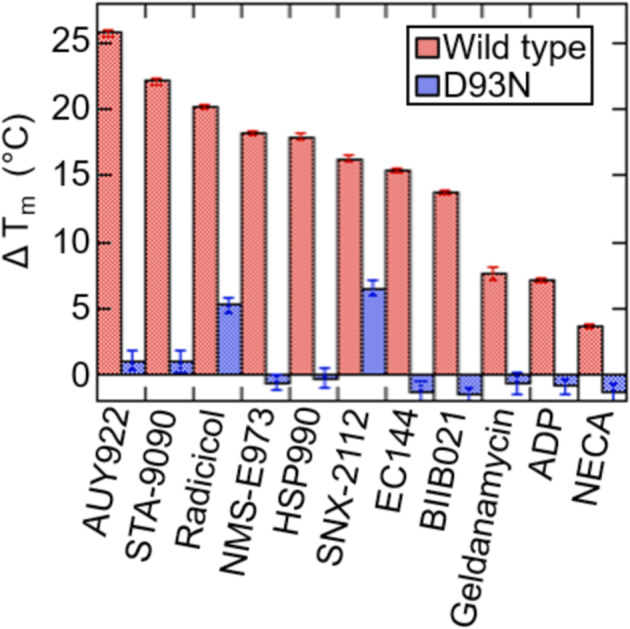
Measured changes in the Hsp90α NTD melting temperature upon addition of 50 μM inhibitor, 400 μM NECA, or 5 mM ADP with 5 mM MgCl₂. Error bars are the SEM of 3 measurements. Buffer conditions consist of 150 mM KCl, 50 mM HEPES, 2% DMSO v/v

We next sought a method to determine the specific energetic contribution of the D93 position in a wild‐type, full‐length Hsp90 dimer under the biologically relevant conditions in which the inhibitor is competing against ATP under turnover conditions. As described next, a discovery from the Matulis group provides this opportunity.

The Matulis group previously discovered that radicicol binding to Hsp90α NTD is associated with a linked protonation event and speculated that protonation of the D93 carboxyl group is responsible. ¹⁸ We can reproduce the pH‐dependent stabilization of the Hsp90α NTD by radicicol as measured by TSA (Figure 3) and observe similar pH‐dependent stabilization for Grp94 and Trap1. Importantly, we observe that this pH‐dependence is abolished for the D93N variant (Figure 3a) indicating that this residue is indeed the responsible group. A second resorcinol‐based inhibitor, AUY922 also shows an analogous, albeit weaker, pH dependence. We later show this difference in pH dependence is related to the pK _a of the hydroxyl group which contacts D93. In contrast, EC144, which is not a resorcinol‐family inhibitor, and ADP both show no significant pH dependence.

FIGURE 3.

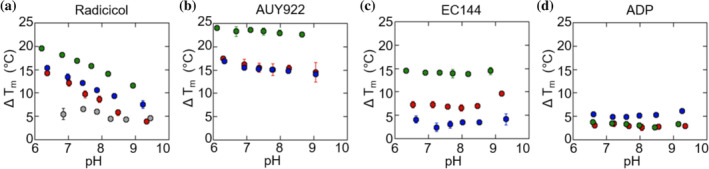
The pH‐dependence of inhibitor‐induced T_m shifts for Hsp90α (green), Grp94 (red) and Trap1(blue) NTD with 50 μM radicicol, AUY922 and EC144, and 1 mM ADP with 1 mM MgCl₂. Additionally, Hsp90α D93N (gray) is shown with 50 μM radicicol. Error bars are the SEM of 3 measurements. Buffer conditions are described in Methods section

2.2. Quantifying the energetic contribution of an inhibitor binding hot‐spot

The pH‐dependence of radicicol inhibition provides an opportunity to determine the energetic contribution of the D93 position in a wild‐type, full‐length Hsp90 dimer. ATPase inhibition measurements can quantify inhibitor affinity relative to ATP over a wide range of pH. The pH range used in these experiments was chosen to be as wide as possible while ensuring that the chaperone remains active in hydrolyzing ATP. Furthermore, while the chaperone may exhibit pH‐dependent changes in structure, the outcome of a competition experiment is sensitive only to the pH‐dependent affinity differences between ATP and inhibitor. Trap1 was used for this analysis due to its high activity relative to other Hsp90 paralogs. The D93 residue in Hsp90α corresponds to the D158 residue in Trap1.

Figure 4a shows that the radicicol IC₅₀ is strongly pH dependent. The Trap1 K _M for ATP is minimally pH dependent (Figure S3), demonstrating that the pH‐dependent radicicol inhibition is not due to pH‐dependent alterations in nucleotide affinity. Control experiments show that pH‐dependent inhibition by radicicol is also not due to an irreversible change to radicicol occurring at high pH (Figure S4). IC₅₀ values for radicicol, AUY922, and EC144 were measured over a wide pH range and converted into K _i values (Equations (2) and (3)). Figure 4b,c shows the strong pH‐dependence of radicicol, a modest pH‐dependence of AUY922, and a minimal pH‐dependence of EC144.

FIGURE 4.

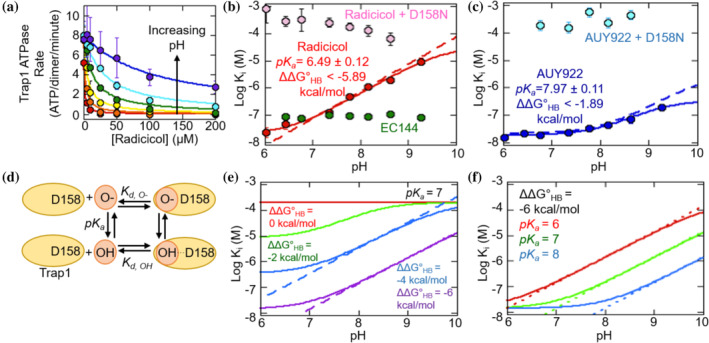
(a) IC₅₀ curves of radicicol for Trap1 at pH values between 6.02 and 9.27 (from low to high pH: red, orange, yellow, green, blue, violet). Measurements were performed with 1 mM ATP. Solid lines are fits with Equation (2). Error bars are the SEM for at least 2 measurements. (b) The pH‐dependence of radicicol inhibition with wild‐type and D158N Trap1 and of EC144 with wild‐type Trap1. The solid line is a fit to Equation (4). Error bars are the fitting error from at least 3 measurements. (c) The pH‐dependence of the Log Ki of AUY922 with wild‐type and D158N Trap1. The solid line is a fit to Equation (4). Error bars are the fitting error from Equation (2) for at least two measurements. (d) Scheme of the model for the pH‐dependence of radicicol binding. (e) Numerical simulations illustrating the influence of variable hydrogen‐bonding energy on pH‐dependent inhibition. Solid lines are calculated using Equation (4). Fixed parameters are K _d,O‐ at 2 × 10⁻⁴ M and pK _a at 7. (f) Numerical simulations illustrating the influence of variable inhibitor pK _a values on pH‐dependent inhibition. Solid lines are calculated using Equation (4). Fixed parameters are K _d,OH at 1.4 × 10⁻⁸ M and K _d,O‐ at 2 × 10⁻⁴ M

The pH‐dependent inhibition of radicicol and AUY922 is quantitatively consistent with a model that can evaluate the strength of the inhibitor hydrogen‐bonding to Trap1 (Figure 4d, Methods). This model has three parameters: the inhibitor binding affinity in the protonated state (K _d,OH); the deprotonated state affinity (K _d,O‐); and the pK _a of the inhibitor in the unbound state. Because the inhibitor can form a hydrogen donor to D158 only in the protonated state, the hydrogen‐bonding energy is given by ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}=-\text{RTln}\left(\frac{K_{d,\mathit{OH}}}{K_{d,O-}}\right)$. This calculation assumes that the measured K _i values represent an effective binding constant of the inhibitor under ATP turnover conditions.

Hallmarks of pH‐dependent hydrogen‐bonding are illustrated by the expected behavior for an inhibitor with a hydrogen‐bonding donor group pK _a of 7 and variable hydrogen‐bonding strength (Figure 4e). The log(K _i) values exhibit a linear phase above the inhibitor pK _a. In this regime, each pH unit increase is accompanied by a tenfold weakening of the K _i, reflecting the energetic penalty associated with a shifted pK _a. This telltale characteristic is observed for the radicicol experimental data (dashed lines, Figure 4b).

According to the coupled‐equilibria model used here (Figure 4d), inhibitors with different pK _a values will have different profiles of pH‐dependent inhibition. Figure 4f shows the expected behavior for an inhibitor with a fixed hydrogen‐bonding energy of −6 kcal/mol and variable pK _a values of 6, 7, and 8. Higher pK _a values result in a broader pH range over which the inhibitor is maximally effective. This behavior is evident in the comparison between the highly pH‐dependent inhibition by radicicol and the modestly pH‐dependent inhibition by AUY922 (Figure 4b,c).

Inhibition data for radicicol and AUY922 are fit well by the pH‐dependent hydrogen‐bonding model (Figure 4b,c). The fit provides predictions for the pK _a values for radicicol (6.49 ± 0.12) and AUY922 (7.97 ± 0.11). As discussed later, these pK _a values can be independently confirmed with spectrophotometric measurements. Chi‐square analysis shows the fit values of pK _a and K _d,OH are well‐defined by the radicicol K _i data (Figure S5a,b). In contrast, only a lower limit for K _d,O‐ can be determined with confidence (Figure S5b). As a consequence, the fitting can determine that radicicol hydrogen‐bonding provides at least −5.9 kcal/mol of stabilization. In the case of AUY922 the ${\mathrm{∆∆}G}_{\mathit{HB}}^o$ fitting is limited by its high pK _a value (Figure S5c,d).

To confirm that the pH‐dependent affinity is due to hydrogen‐bonding with the D93 equivalent of Trap1 (D158), we tested full length D158N in the ATPase assay. Consistent with observations from the Tsai lab, ¹⁰ we find that D158N is still ATPase active at high ATP concentrations and has a similar activity to wild‐type albeit with a 160‐fold diminished K _M (Figure S6). The D158N substitution abolishes pH‐dependent inhibition of radicicol and AUY922 (Figure 4b,c), demonstrating that this residue is indeed responsible for pH‐dependent inhibitor hydrogen‐bonding.

The D158N variant provides an opportunity to evaluate ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}$ by a method that is independent of the model and pH‐dependent fitting in Figure 4. Specifically, ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}$ can be calculated by comparing the K _i of an inhibitor with wild‐type and D158N Trap1 (Methods). With this method we find that radicicol and AUY922 have ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}$ values of −6.0 ± 0.4 and −6.2 ± 0.5 kcal/mol, respectively, consistent with the lower limits provided from the pH‐dependent fitting (Figure 4b,c). Table 1 reports ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}$ values for a variety of inhibitors and ATP. While ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}$ values show variability, inhibitor hydrogen‐bonding to D158 accounts for 35–60% of the total binding energy, with the exception of AUY922 measured by pH titration, which is limited by its high pK _a value, as discussed previously.

TABLE 1.

Energetic contribution of D158 to the binding of inhibitors

Ligand	${\mathbf{\Delta \Delta G}}_{\mathit{HB}}^{\mathbf{\text{o}}}$ (kcal/mol)	Percent of total binding energy
Radicicol (pH titration)	< −5.89	>53.1%
AUY922 (pH titration)	< −1.89	>17.0%
Radicicol	−5.97 ± 0.43	54.3% ± 4.1
AUY922	−6.19 ± 0.48	54.9% ± 4.3
HSP990	−5.73 ± 0.77	54.1% ± 6.6
STA‐9090	−4.06 ± 0.50	40.8% ± 5.4
EC144	−3.76 ± 0.23	37.1% ± 2.3
ATP	−3.29 ± 0.06	56.6% ± 1.1

Notes: Values for ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}$ are calculated as described in Methods. Measurements for the ${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}$ calculated using Trap1 D158N were performed at pH 6.02 for radicicol and AUY922 and pH 6.91 for HSP990, STA‐990, EC144 and ATP. The error values are propagated from IC₅₀ and K _M measurements.

2.3. The pK_a of a titrating hydroxyl group is critical to the effectiveness of resorcinol‐family inhibitors

The pH‐dependent hydrogen‐bond model (Figure 4d) demands that the different pH‐sensitivities of radicicol and AUY922 simply reflect a difference in the pK _a values of their hydrogen‐bonding donor groups. Therefore, we sought a method to measure these pK _a values.

Figure 5a depicts the phenolic moiety of radicicol and AUY922. Ionization of a phenolic hydroxyl group is expected to change the UV‐absorption spectra, such as those observed for tyrosine. ¹⁹ Indeed, radicicol and AUY922 both show large changes at specific wavelengths when the pH is changed (Figure 5b). For both radicicol and AUY922 the absorbance at a characteristic wavelength over pH can be fit to the titration of a single group (Figure 5c). In comparison EC144, an inhibitor without the resorcinol group, exhibits minimal pH‐dependent absorption changes. The measured pK _a values for the hydrogen‐bonding donor groups of AUY922 and radicicol are close to their predicted pK _a values from Figure 4. This independent validation of the pK _a values provides strong support of the pH‐dependent hydrogen‐bonding model described in Figure 4. Although the resorcinol group on radicicol contains two hydroxyl groups, the pH‐independent binding affinity for radicicol and AUY922 to D158N (Figure 4b,c) indicates that the energetically dominant group is the one proximal to D158.

FIGURE 5.

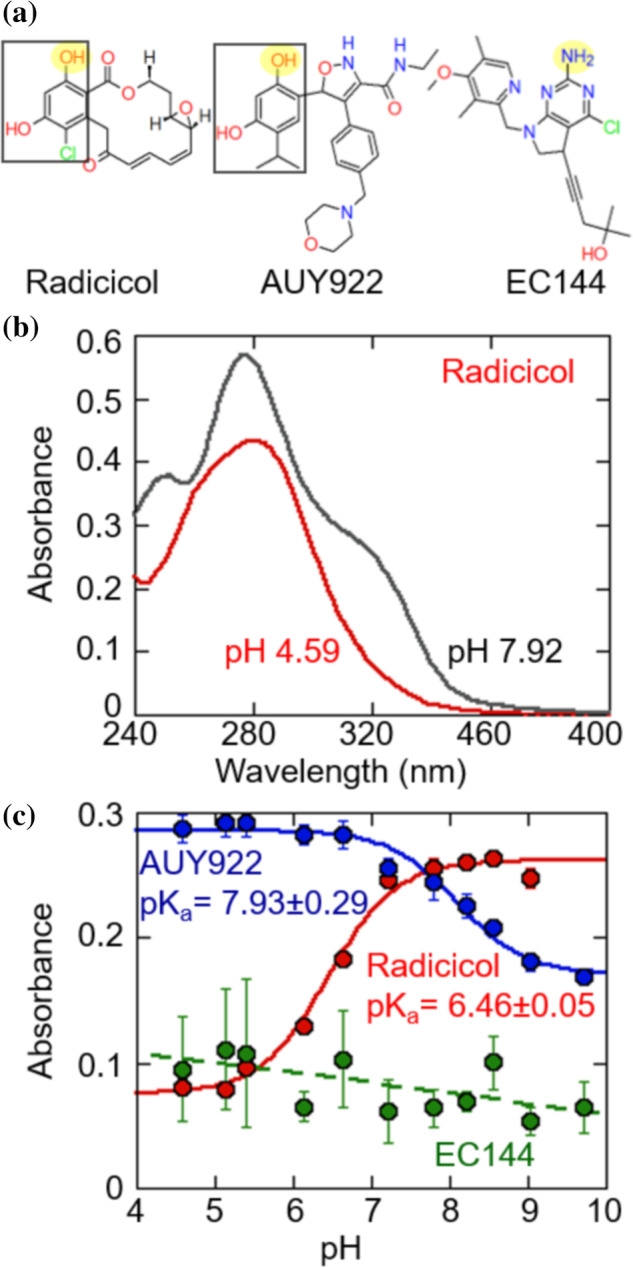
(a) Structures of radicicol, AUY922 and EC144. The resorcinol group of radicicol and AUY922 are indicated by black squares. The group which contacts D93 in crystal structures is highlighted in yellow. (b) Absorbance spectra of 100 μM radicicol. (c) The absorbance of radicicol (at 320 nm), AUY922 (at 302 nm) and EC144 (at 340 nm) versus pH. Solid lines are fit to the titration of a single group. Error bars are the SEM of three measurements

2.4. A steric clash prevents the D93N variant from hydrogen bonding with nucleotides and inhibitors

The D93N substitution has long been known to disrupt nucleotide binding. ¹¹ This observation appears inconsistent with the strong influence of hydrogen‐bonding because both the aspartate and asparagine sidechain can act as a hydrogen bond acceptor. However, as described next, a steric clash prevents the D93N asparagine from adopting the necessary rotamer in which it can act as a hydrogen bond acceptor for both nucleotides and inhibitors.

Figure 6a,b shows a high‐resolution crystal structure of an ATP analog bound to Hsp90α (PDB: 3T10, 1.24 angstrom resolution). The D93 carboxylate oxygen accepts a hydrogen bond from the nucleotide N6 amine group and from the backbone amide of G95. In contrast, for D93N the amide group will disrupt hydrogen bonding in both of its possible rotameric states. Rotamer 1 of D93N can form a backbone hydrogen‐bond to G95 but the amide group cannot act as a hydrogen bond acceptor to bound nucleotide (Figure 6c,d). Rotamer 2 of D93N is inaccessible due to a steric clash with the backbone of G95 (Figure 6e,f). Adding further energetic penalty, this rotamer also places the positively charged amide dipoles of asparagine and backbone in close proximity. Molecular dynamics further show that for D93N rotamer 2 is not accessed on the timescale of a 1 ns simulation (Figure S7). Similar steric and dipole‐related restrictions apply to gyrase B, where the binding of inhibitors of the coumarin and cyclothialidine family is disrupted by the D73N variant ¹⁵ (Figure S8).

FIGURE 6.

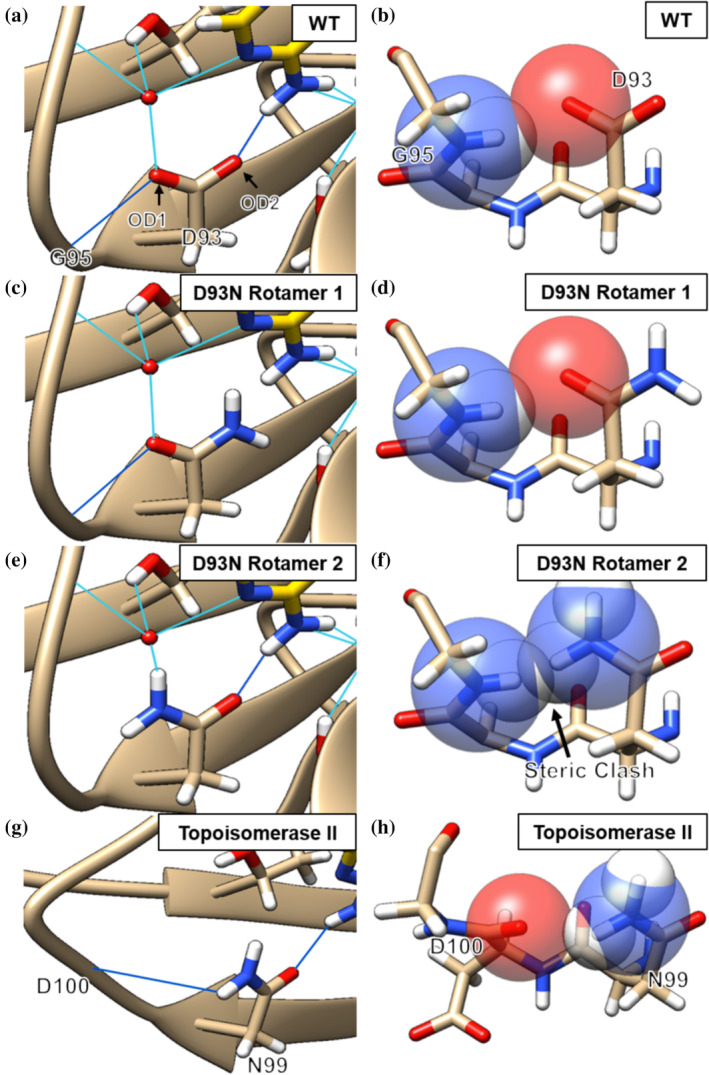
Hsp90α hydrogen bonding network for D93 (a, PDB: 3T10), modeled rotamers for D93N (c and e) and the N99 residue of Topoisomerase II (g, PDB: 4GFH). Water‐mediated bonds are in light blue and direct hydrogen bonds are in dark blue. (b) Hsp90α D93 is sterically allowed. (d) Rotamer 1 of D93N is sterically allowed but cannot act as a hydrogen‐bond acceptor to bound nucleotide or inhibitor. (f) Rotamer 2 is sterically disallowed with an atomic overlap of 0.8 Å. (h) The N99 residue of Topoisomerase II does not sterically clash with the backbone. Rotamer modelling was performed with Chimera

The role of sterics in preventing D93N from forming inhibitor or nucleotide hydrogen bonds, provides an explanation for the puzzling observation that the wild‐type sequence of S. cerevisiae Topoisomerase II has an asparagine (N99) at the equivalent position of D93 and yet still binds ATP. Inspection of this structure (Figure 6g,h) shows that Topoisomerase II has a longer loop that prevents a steric clash at N99 and positions the backbone carbonyl to allow hydrogen‐bonding between N99 and D100. By allowing the amide group of N99 to face away from the binding pocket, the carboxyl‐group is then able to hydrogen‐bond with the bound nucleotide.

3. DISCUSSION

While hotspots are a focal point in the development of novel and tighter binding ligands, their energetic contribution is difficult to quantify. Here we find that the D93 position on Hsp90‐family chaperones makes a dominant contribution to the binding affinity of highly diverse inhibitors. The central importance of the D93 position is evident in measurements of NTD stabilization from inhibitor binding (Figures 2 and 3) for cytosolic Hsp90, Trap1, and Grp94. Similarly, this position makes a dominant contribution to ATPase inhibition of full‐length Trap1 (Figure 4).

For Trap1, we determine that the D93 position contributes −3 to −6 kcal/mol of binding for diverse inhibitors (Table 1). As a comparison, benzenesulfonamide hydrogen‐bonding to T199 of carbonic anhydrase (CA) II contributes −1 to −2 kcal/mol whereas the Zn^II‐sulfonamide bond contributes −8 to −9 kcal/mol. ²⁰ The greater hydrogen‐bonding energy associated with D93 relative to T199 of carbonic anhydrase likely is due to the fact that D93 is at the center of a large network of hydrogen‐bonds (Figure 1) whereas T199 hydrogen‐bonding is restricted to the ligand and one surrounding residue. Interestingly, CA also exhibits pH‐dependent sulfonamide binding, and the pK _a of the responsible amino group, can also be measured spectrophotometrically. ²¹

Our findings clarify seemingly disparate observations about the specific influence of the D93 position within the larger GHKL superfamily. We find that steric restrictions prevent inhibitor hydrogen bonding to the D93N variant of Hsp90 (Figure 6e,f) and the equivalent variant of DNA Gyrase (Figure S7), whereas the relaxed steric environment of Topoisomerase II enables N99 to adopt the required rotamer (Figure 6g,h). Our results suggest that the Hsp90 energetic hot‐spot may also apply to the wider GHKL superfamily.

The finding that residue D93 is an energetic hotspot provides context for observations from the Matulis lab showing that a linked protonation event is associated with radicicol binding to Hsp90α. The pK _a we measured for the titration of free radicicol spectrophotometrically (6.46 ± 0.05) and by the fit to our linkage model (6.49 ± 0.12) match the pK _a value of 6.6 determined by Zubriene et al. via fitting ITC and TSA data to a linked protonation event. ¹⁸

The hydrogen‐bonding hydroxyl group of radicicol has a lower pK _a than AUY922 (Figure 5c) likely because chlorine is a better electron withdrawing group than isopropyl. In the design of resorcinol‐derived compounds the hydroxyl pK _a needs to be as high as possible to avoid losing binding affinity at neutral pH. We show that a simple spectrophotometric assay can be used to determine the resorcinol hydroxyl group pK _a value. This approach should be widely applicable because resorcinol‐based inhibitors comprise the approximately a third of all inhibitors for which there is a crystal structure (Figure S1).

Computational methods, such as ligand docking or hotspot identification, have become increasingly employed in the early stages of drug design. Experimental data can benchmark these computational methods. Therefore, we tested the hotspot identification program FTmap, and indeed find that it identifies the region around D93 as a hot‐spot (Figure S9). Thus, the solvent mapping procedure of FTmap coupled with the CHARMM forcefield energy function is sufficient to predict the Hsp90 hot‐spot solely based on the apo crystal structure. ⁷

Despite the fact that both ATP and inhibitors gain substantial binding energy though the Hsp90 hot‐spot, all the inhibitors tested were stabilized to a greater extent than compared to ATP (Table 1). Furthermore, despite the fact all the inhibitors form a hydrogen bond to D93, their degree of stabilization varies between 4 and 6 kcal/mol (Table 1). More work is needed to determine why different ligands extract different amounts of binding energy from the same hot‐spot.

4. EXPERIMENTAL PROCEDURES

4.1. Protein expression

All proteins were expressed in E. coli BL21 cells in pET151D vectors which contain a 6xHis‐tag and TEV cleavage site. Cells were grown in LB at 37°C and induced with 1 mM IPTG at an OD₆₀₀ between 0.6 and 0.8. Cells expressed overnight at 20°C. Proteins were first purified by Ni‐NTA affinity chromatography. After cleavage of the N‐terminal 6xHis‐tag proteins were further purified by anion exchange chromatography and size exclusion chromatography using a Superdex 200 column.

4.2. Thermal shift assay

Measurements were performed on a StepOnePlus^TM Real‐Time PCR System (Applied Biosystems). Protein unfolding was monitored by the fluorescence of Sypro Orange as the temperature was ramped at a rate of 0.3°C/min from 10 to 95°C. Experiment conditions consist of 5 μM Hsp90 paralog NTD, ×1 Sypro Orange, 2% v/v DMSO, 50 mM HEPES, Tris or CAPS, 150 mM KCl and, for experiments including ligands where concentrations are not stated to be otherwise, 50 μM inhibitor, 400 μM NECA or 1 mM ADP with matching MgCl₂ with Trap1 NTD or 5 mM ADP with matching MgCl₂ with Hsp90α NTD. Because the T _m measurements in Figures 2 and S2 are obtained from experiments with variable temperature, the pH values in these experiments will change (ranging from 6.5 to 7.1) over the experimental temperature range due to the temperature dependence of HEPES buffering.

To determine the T _m, the fluorescence data were fit to a Boltzmann sigmoidal curve, as described previously. ²² The relationship between the T _m of a protein and the total concentration of ligand can be fit by an equation which is based on the thermodynamic parameters of protein unfolding and ligand binding. ¹⁸

4.3. ATPase measurements

Measurements were performed on a Biotek plate reader. ATP hydrolysis rates were calculated from NADH turnover which was measured by the change in absorbance at 340 nm. Experiment conditions consist of 0.5 μM wild type Trap1 or 1.5 μM D158N Trap1, 150 mM KCl, 50 mM buffering agent, 400 μM NADH, 800 μM phosphoenolpyruvate (PEP), 50 units/mL pyruvate kinase, 50 units/mL lactate dehydrogenase, 0.75 mg/mL BSA, and 2% DMSO v/v and are performed at a set temperature of 42°C, which yields plate temperatures in the range of 37–41°C. ATP and MgCl₂ were maintained at stoichiometric concentrations. The buffer pH is reported as the measured pH at the assay temperature. For pH 6.0, the buffering agent is MES; for pH 6.4 HEPES; for pH 6.9, 7.5, 7.8, 8.2, and 8.7 Tris; and for pH 9.5 CAPS.

To determine the K _M, ATP concentrations were varied between 0 and 4 mM for wild‐type Trap1 or 0 and 80 mM for D158N Trap1. The ATPase rates at these varied concentrations of ATP were fit to a Michaelis–Menten equation:

$$\mathit{\text{ATPase rate}}=\frac{{\mathrm{k}}_{\mathit{cat}}\times \left[\mathit{\text{Trap}}1\right]\times \left[\mathit{ATP}\right]}{K_M+\left[\mathit{ATP}\right]}$$ (1)

To determine IC₅₀ values for inhibitors, ATPase rates were measured at a set concentration of ATP as inhibitor concentrations were varied between 0 and 200 μM. Rates were fit to a falling Langmuir where r ₀ is the ATPase rate without inhibitor:

$$\mathit{\text{ATPase rate}}=\frac{r_0}{1+\left(\frac{1}{{\mathit{IC}}_{5o}}\times \left[\mathit{\text{Inhibitor}}\right]\right)}$$ (2)

These IC₅₀ values were then converted to K _i values:

$$K_i=\frac{{\mathit{IC}}_{50}}{1+\frac{\left[\mathit{ATP}\right]}{K_M}}$$ (3)

The pH‐dependent K _i of radicicol and AUY922 were fit with a pH‐dependent hydrogen‐bonding model (Figure 4b), assuming that the K _i is a measure of effective binding affinity:

$$K_i=K_{d,\mathit{obs}}=\frac{1+\left(\frac{{10}^{-\mathit{pKa}}}{{10}^{-\mathit{pH}}}\right)}{\frac{1}{K_{d,\mathit{OH}}}+\frac{1}{K_{d,O-}}\times \left(\frac{{10}^{-\mathit{pKa}}}{{10}^{-\mathit{pH}}}\right)}$$ (4)

where K _d,OH and K _d,O‐ are the K _d of the protonated and deprotonated form of the ligand and pK _a is the pK _a of the free ligand at the group which hydrogen bonds with D158.

The hydrogen bonding energy of D158 was calculated using three separate equations:

$${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}=-\mathit{RT}\ln \left(K_{d,\mathit{OH}}/K_{d,O-}\right)$$ (5)

where the values for K _d,OH and K _d,O‐ are obtained from Equation (4).

$${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}=-\mathit{RT}\ln \left(K_{i,\mathit{WT}}/K_{i,D158N}\right)$$ (6)

where the values for K _i,WT and K _i,D158N are obtained from fitting IC₅₀ measurements to wild‐type and the D158N variant of Trap1 to Equation (3).

$${\mathrm{∆∆G}}_{\mathit{HB}}^{\mathrm{o}}=-\mathit{RT}\ln \left(K_{M,\mathit{WT}}/K_{M,D158N}\right)$$ (7)

Which is specifically for measuring the hydrogen bonding energy of D158 to ATP. The values for K _M,WT and K _M,D158N are obtained from Equation (1).

The average standard deviation of K _i measured at a specific pH value in Figure S5 is calculated via:

$$〈\sigma 〉=\frac{\sum _{i=1}^n{\sigma }_i}{n}$$ (8)

where 〈σ〉 is the average of the standard deviations, σ_i is the standard deviation of K _i measured at one pH value and n is the number of pH values at which K _i values were measured.

4.4. Spectrophotometric assay

Inhibitor UV absorbance profiles were measured from 240 to 500 nm using a Biotek plate reader. Experiment conditions consist of 100 μM inhibitor, ATPase buffer (150 mM KCl, 50 mM buffering agent at the previously listed pHs), and 2% DMSO v/v and were measured at 25°C.

4.5. Hydrogen bond analysis

Hydrogen bond analysis was carried out in Chimera using default geometric criteria, ²³ against a set of ligands bound to Hsp90α NTD listed on (Table S1). Direct hydrogen bonds are defined by any hydrogen bonds between the ligand and a group on Hsp90α. Water‐mediated hydrogen bonds are defined as two bonds: one between the ligand and a crystalized water and another between that same crystalized water and a group on Hsp90α.

4.6. Molecular dynamics

The structure of the mutant Hsp90α D93N was created from the WT structure (PDB: 3T0H) using Chimera's rotamer tool. The rotamer with the highest probability was chosen. The molecular dynamics simulations were performed using the GROMACS software package. ²⁴ For the simulation, the OPLS force field and explicit hydration with the SPC model were used. A cubic box was used as the unit cell, with all edges at least 1 nm away from the protein. Sodium ions were used to neutralize the protein. The structure was minimized using steepest descent minimization then equilibrated at 300 K for 100 ps each under an NVT then an NPT ensemble. The production simulation was 1 ns.

Supporting information

Table S1 PDB structures analyzed for Figure 1 and Figure S1. For each PDB the inhibitor's PDB ligand ID, molecular weight and class (as determined by the inhibitors structure near D93) are listed. Row 1 and 2 list

Figure S1 (A) Identity of the direct hydrogen bond donor atom to the D93 OD2 group of Hsp90 or, if no direct hydrogen bond is present, the atom that is closest to D93 OD2. (B) Classes of ligands which hydrogen bond to D93 OD2 with nitrogen, grouped based on the structure near this contact. Group 1 contains a fused 5 and 6‐member ring which are aromatic and nitrogen‐containing. This includes purines, indoles, indazoles, azaindazoles and pyrrolopyrimidine. Group 2 contains aromatic, nitrogen‐containing 6‐member rings and includes pyrimidine, aminopyridine and triazine. Group 3 contains carboxamides. Group 4 contains aminotriazoloquinazolines. Group 5 contains tetrahydroisoquinolinols (C) Classes of ligands which hydrogen bond to D93 OD2 with oxygen, grouped based on the structure near this contact. Group 1 contains resorcinols. Group 2 contains a fused 5 and 6‐member ring which are aromatic and nitrogen‐containing, including indoles and indazoles.

Figure S2 The ligand concentration dependence of melting temperature for wild‐type (A) and D93N (B) Hsp90α NTD. The solid lines come from the best fit of the data to the model from reference 18. Error bars are the SEM of 3 measurements. Buffer conditions consist of 150 mM KCl, 50 mM HEPES, 2% DMSO v/v. When ADP was the ligand titrated a matching concentration of MgCl2 was added.

Figure S3 The Log KM of ATP with WT Trap1 over pH. Buffer conditions described in Methods. Error bars are the SEM of at least 3 measurements.

Figure S4 Comparison of inhibitory power of radicicol that was incubated for one hour at pH 9.5, in red, to radicicol which was not, in blue. The pH for both conditions when measuring ATPase inhibition was 6.3. Error bars are the SEM of 2 measurements.

Figure S5 Chi‐square analysis of the fitting in Figure 4(e) and 4(f). Two fitting parameters are fixed while one is varied. The fixed parameters come from the best fit of Equation 4 to the data. For Radicicol (A, B, C) the fixed parameters are: pKa = 6.49; Kd,OH = 1.93*10–8 M; Kd,O‐ = 3.24*10–5 M. For AUY922 (D, E, F) the fixed parameters are: pKa = 7.97; Kd,OH = 1.82*10–8 M; Kd,O‐ = 3.34*10–7 M. The cut‐off shown by a dotted line is the average of the standard deviations of Ki measured at each specific pH, as described in Equation 8.

Figure S6 Michaelis–Menten curves for WT (blue) and D158N (Red) Trap1 at pH 6.9. The KM for WT and D158N Trap1 are 110.0 ± 19.0 and 17,907 ± 1,044 μM, respectively. Error bars are the SEM of 4 measurements.

Figure S7 Overlay of 101 frames of a 1 ns molecular dynamics simulation of apo D93N Hsp90α.

Figure S8 Gyrase B (gyrB) hydrogen bonding network for D73 (A, PDB: 4PRX) and modeled rotamers for D73N (B and C). Water‐mediated bonds are in light blue and direct hydrogen bonds are in dark blue. (D) GyrB D73 is sterically allowed. (E) Rotamer 1 of D73N is sterically allowed but cannot act as a hydrogenbond acceptor to bound nucleotide or inhibitor. (F) Rotamer 2 is sterically disallowed with an atomic overlap of 0.8 Å. Rotamer modelling was performed with Chimera.

Figure S9 Results from FTMap (https://ftmap.bu.edu/) for 5J2V. D93 is shown in spheres and solvent molecules are colored pink for clarity.

Hoxie RS, Street TO. Hsp90 chaperones have an energetic hot‐spot for binding inhibitors. Protein Science. 2020;29:2101–2111. 10.1002/pro.3933