MODELING MICROBIAL ABUNDANCES AND DYSBIOSIS WITH BETA-BINOMIAL REGRESSION

Abstract

Using a sample from a population to estimate the proportion of the population with a certain category label is a broadly important problem. In the context of microbiome studies, this problem arises when researchers wish to use a sample from a population of microbes to estimate the population proportion of a particular taxon, known as the taxon’s relative abundance. In this paper, we propose a beta-binomial model for this task. Like existing models, our model allows for a taxon’s relative abundance to be associated with covariates of interest. However, unlike existing models, our proposal also allows for the overdispersion in the taxon’s counts to be associated with covariates of interest. We exploit this model in order to propose tests not only for differential relative abundance, but also for differential variability. The latter is particularly valuable in light of speculation that dysbiosis, the perturbation from a normal microbiome that can occur in certain disease conditions, may manifest as a loss of stability, or increase in variability, of the counts associated with each taxon. We demonstrate the performance of our proposed model using a simulation study and an application to soil microbial data.

1. Introduction

Estimating the proportion of a population that belongs to a certain category—the relative abundance—is a problem spanning fields as broad as social science, population health and ecology. For example, researchers may be interested in estimating the proportion of low-income students who attend competitive higher-education institutions (Bastedo and Jaquette (2011)), child mortality rates in Sub-Saharan African regions (Mercer et al. (2015)), or the proportion of diseased leaf tissue in coastal grasslands (Parker et al. (2015)). In most of these settings, it is not possible to sample the entire population of interest, and it is necessary to estimate the true proportion based on a sample of individuals from the population. In this paper we consider the general problem of estimating the prevalence of a category within a population when the category labels of the observed individuals may be correlated.

While this problem is of broad interest, our method is particularly motivated by the ever-increasing number of studies of microbiomes. A microbiome is the collection of microscopic organisms (microbes), along with their genes and metabolites, that inhabit an ecological niche (Poussin et al. (2018)). Microbes live on and in the human body, and in fact, microbial cells may outnumber human cells (Sender, Fuchs and Milo (2016)). Because of this, the relative abundance of a microbe—or a taxon, which refers to a biological grouping of microbes—is a common marker of host or environmental health. For example, the species G. vaginalis has been found to correlate with symptomatic bacterial vaginosis (Callahan et al. (2017)); different genera of Cyanobacteria flourish in response to precipitation and irrigation runoff (Tromas et al. (2018)); and Parkinson’s disease has been associated with reduced levels of the family Prevotellaceae (Hill-Burns et al. (2017)). Accurate and precise estimation of microbial abundances is critical for disease diagnosis and treatment (Qin et al. (2014), Grice (2014), Gevers et al. (2014), Shi et al. (2015)).

A particularly challenging aspect of estimating microbial abundances is that the category labels of microbes are known to be correlated. Microbial communities are spatially organized, with a member of one taxon more likely to be observed close to the same taxon than close to a different taxon (Welch et al. (2016)). In this paper we argue that a correlated-taxon model is a natural approach to estimating relative abundances in this setting. It successfully explains the large number of unobserved taxa in many samples, as well as overdispersion in the abundance of observed taxa relative to models where the occurrences of individual microbes are uncorrelated.

An additional advantage of our method is that it provides a statistical framework for testing for dysbiosis. Dysbiosis describes a microbial imbalance, or a deviation from a healthy microbiome (Petersen and Round (2014), Hooks and O’Malley (2017)). In particular, the term is often used to refer to a change in the stability of a microbiome. For example, inflammatory bowel disease (IBD) has been associated with increases in the variability of the gut microbiome (Halfvarson et al. (2017)), and the microbiomes of IBD patients are often referred to as dysbiotic (Tamboli et al. (2004)). Unlike many methods for modeling relative abundances of microbial taxa, the method that we propose provides a natural framework for hypothesis testing for dysbiosis via the parameters of a heteroskedastic model for taxon abundances. Specifically, we can test whether the variability in a taxon’s counts is associated with some covariate of interest.

Our paper is laid out as follows. In Section 2, we review several existing regression models for microbial abundances. In Section 3, we propose our model, and discuss parameter estimation. We propose approaches for testing for differential abundance and differential variability in Section 4. In Section 5, we show via simulation that our hypothesis testing framework is valid, even with small sample sizes. We apply our method to data from a soil microbiome study in Section 6, and we close with a discussion of our method in Section 7. Software for implementing our model and hypothesis testing procedures is available in the R package corncob, available at github.com/bryandmartin/corncob and provided in Supplement A of the Supplementary Material (Martin, Witten and Willis (2020a)).

2. Literature review

Modeling of population proportions, or relative abundances, has a long history in the statistical literature, and includes basic methods such as z-tests for proportions, and logistic regression. However, modeling microbial abundance data brings with it a number of challenges. For example, the dynamic nature of the microbiome commonly gives rise to a large number of microbial taxa that are only present in a small number of samples, but are highly abundant when present (DiGiulio et al. (2015), Dethlefsen and Relman (2011)). Some microbes may be so rare that they consistently evade detection or are observed at low abundances in all samples (Sogin et al. (2006)). In addition, the number of taxa (typically on the order of thousands) is generally substantially less than the number of samples (typically less than one hundred). Finally, the number of counts that are observed in each sample may differ substantially, and thus the amount of information contained in each sample may differ.

Thus, we focus our literature review on models for microbial abundances. We broadly categorize these models into two approaches: jointly modeling multiple taxa, and modeling each taxon individually. While our proposal pertains to the latter, both approaches are common and each has its advantages and disadvantages, which we now review.

Jointly modeling multiple taxa is a popular approach because it represents the entire microbial community with a single model. However, since these communities are often very diverse (the total number of taxa is large), and different taxa exhibit differing levels of variability, a large number of parameters is typically needed to obtain a good model fit (Kurtz et al. (2015), Sankaran and Holmes (2017)). Hierarchical models of absolute abundances are often used to constrain the number of parameters (e.g., La Rosa et al. (2012), Holmes, Harris and Quince (2012), Chen and Li (2013), Sankaran and Holmes (2017), Cao, Zhang and Li (2017)). However, modeling the variance structure is challenging with few parameters (Sankaran and Holmes (2017)). Many joint taxon models make use of the log-ratio or centered log-ratio transformations to model relative abundances. However, these approaches typically cannot be applied to zero-valued observations (Aitchison (1986), McMurdie and Holmes (2014), Willis and Martin (2018)). Since many taxa are typically unobserved in each sample, these methods commonly make use of pseudo-counts to replace zeros, or incorporate a zero-inflation component into their model (Xia et al. (2013), Mandal et al. (2015), Li et al. (2018), Willis and Martin (2018)). In the case of pseudo-counts, parameter estimation depends on an arbitrarily chosen hyperparameter, while zero-inflated models may lack interpretability.

Because simultaneously modeling large numbers of microbial taxa is challenging, an alternative approach is to model individual taxa one-by-one. We further classify individual taxon models into models for observed relative abundances (the proportion of the observed counts that corresponds to the specific taxon), and models for absolute abundances (the number of observed counts of the taxon). A particularly common model for observed relative abundances is the beta distribution, which is a natural choice since it is supported on (0, 1). Zero-inflated beta regression models have been proposed to account for the large number of zeros often observed in microbial abundance data, corresponding to the absence of a taxon in a sample (Peng, Li and Liu (2016), Chen and Li (2016), Chai et al. (2018)). Nonparametric models for observed relative abundances (White, Nagarajan and Pop (2009), Segata et al. (2011)) and Gaussian models for transformed observed relative abundances (Morgan et al. (2012, 2015)) have also been proposed.

Another option is to model the absolute abundance of a taxon. Popular methods originally designed for RNAseq data, such as DESeq2 (Love, Huber and Anders (2014)) and EdgeR (Robinson, McCarthy and Smyth (2010)), make use of the negative binomial distribution. These models can be extended with random effects and a zero-inflation component to account for correlation across subjects and to model additional overdispersion of the counts (Zhang et al. (2017), Fang et al. (2016)). Alternative approaches to modeling absolute abundances include the use of transformations such as cumulative sum scaling (Wahba et al. (1995), Paulson et al. (2013)), trimmed mean of M-values (Robinson and Oshlack (2010), Law et al. (2014)) and ratio approaches (Sohn, Du and An (2015), Chen et al. (2018)).

All of the papers mentioned thus far focus on an association between mean abundance and covariates. In this paper, we propose a beta-binomial regression model for microbial taxon abundances. To the best of our knowledge, this is the first regression model that allows for an association between the variance of a taxon’s abundance and covariates, rather than only an association between the mean abundance and covariates. In addition, our model can accommodate the absence of a taxon in samples, variability in the total number of counts across samples and high variability in the observed relative abundances.

3. The beta-binomial regression model

3.1. A hierarchical model for microbial abundances

In this section, we present a beta-binomial regression model for microbial abundance data. While the beta-binomial model has been extensively studied in the statistics literature (Skellam (1948), Kleinman (1973), Williams (1975), Prentice (1986), McCullagh and Nelder (1989), Aerts et al. (2002), Dolzhenko and Smith (2014), Wagner, Riggs and Mikulich-Gilbertson (2015)), to our knowledge, we are the first to propose a regression framework that can link both discrete and continuous covariates to both a relative abundance parameter and a correlation/overdispersion parameter, as well as the first to apply this model to the analysis of microbial data. We summarize the notation and definitions defined in this section in Table 1.

Table 1.

The notation for the observed random variables, latent random variables and parameters of our proposed beta-binomial model. The subscript i refers to the i th sample. Notations are defined for each taxon

Notation	Definition
Yi,j	indicator that the j th read corresponds to the taxon of interest
Wi	observed counts, or observed absolute abundance, of the taxon of interest
Mi	sequencing depth, or total number of counts, across all taxa
Wi/Mi	observed relative abundance of the taxon of interest
Zi	latent relative abundance of the taxon of interest
μi	expected relative abundance of the taxon of interest
ϕi	overdispersion, or within-sample correlation of the taxon of interest

Suppose we have n samples of microbial communities, indexed by i = 1, …, n. Let M_i be the sequencing depth, or the number of total counts (or reads) across all taxa, in the ith sample. Let Y_i,j for j = 1, …, M_i be an indicator that the jth read corresponds to the taxon of interest. Therefore, $W_i={\sum }_{j=1}^{M_i}{Y}_{i,j}$ is the observed absolute abundance of the taxon of interest in the ith sample.

It is natural to consider the model

$$W_i\mid \left(Z_i,M_i\right)\sim \mathrm{Binomial}\left(M_i,Z_i\right),$$ (3.1)

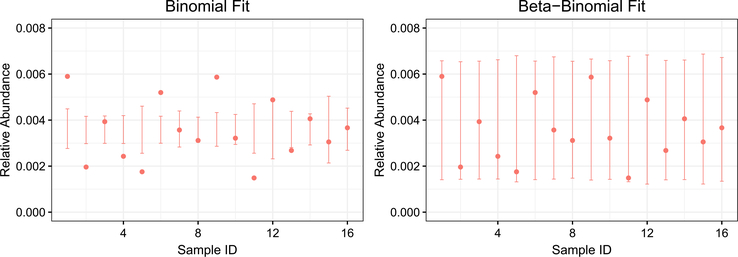
and to perform inference on Z_i, where Z_i is the probability of observing the taxon of interest in the ith sample. However, this model is insufficiently flexible to model microbial abundance data. For example, Figure 1 (left) shows 95% prediction intervals from a binomial model fit to the relative abundance of a strain of Rhizobium in 16 experimental replicates of sampling microbes in soil (see Section 6 for details). We see that the data are substantially overdispersed relative to the binomial model, which provides a very poor fit (see McMurdie and Holmes (2014) for further discussion on overdispersion of microbial abundance data).

Fig. 1.

The relative abundance of a strain of Rhizobium in 16 biological replicate samples in a soil microbiology study, and 95% prediction intervals based on a binomial model (left) and the proposed beta-binomial model (right). The data is clearly overdispersed relative to the binomial model, motivating the development of our beta-binomial model.

The overdispersion of the observed relative abundances compared to a binomial model motivates a more flexible model. We propose the following model:

$$W_i\mid \left(Z_i,M_i\right)\sim \mathrm{Binomial}\left(M_i,Z_i\right),$$ (3.2)

$$Z_i\sim \mathrm{Beta}\left(a_{1,i},a_{2,i}\right),$$ (3.3)

where $a_{1,i}\in {ℝ}_{+}$, $a_{2,i}\in {ℝ}_{+}$. In the model (3.2)–(3.3), Z_i is itself a random variable, representing the latent relative abundance of the taxon. As we will demonstrate, this hierarchical approach to modeling relative abundance is a major advantage of our approach.

Using the parameterization

$${\mu }_i=\frac{a_{1,i}}{a_{1,i}+a_{2,i}},$$ (3.4)

it can be shown that

$$\mathbb{E}\left(W_i\mid M_i\right)=M_i\times \mathbb{E}\left(Z_i\right)=M_i\times {\mu }_i.$$ (3.5)

Thus μ_i ∈ (0, 1) is the expected relative abundance of the taxon in the ith sample. In addition, using the parameterization

$${\varphi }_i=\frac{1}{a_{1,i}+a_{2,i}+1},$$ (3.6)

it can be shown that

$$\mathrm{Var}\left(W_i\mid M_i\right)=M_i\times {\mu }_i\times \left(1-{\mu }_i\right)\times \left(1+\left(M_i-1\right)\times {\varphi }_i\right).$$ (3.7)

The multiplicative factor (1 + (M_i − 1) × ϕ_i) is therefore the overdispersion of the absolute abundance of the taxon for the ith sample relative to a binomial random variable. Furthermore,

$$\mathrm{Corr}\left(Y_{i,j},Y_{i,j^{*}}\right)={\varphi }_i\text{for}1\le j<j^{*}\le M_i,$$ (3.8)

so ϕ_i can also be interpreted as the correlation between the taxon indicator variables within the ith sample (Prentice (1986)).

We then link the expected relative abundance, μ_i, and the overdispersion, ϕ_i, to covariates. We define link functions

$$g\left({\mu }_i\right)={\beta }_0+{\mathit{X}}_i^T\mathit{\beta },$$ (3.9)

$$h\left({\varphi }_i\right)={\beta }_0^{*}+{\mathit{X}}_i^{*T}{\mathit{\beta }}^{*},$$ (3.10)

where X_i, the ith row of the covariate matrix $\mathit{X}=\left[X_{ij}\right]\in {ℝ}^{n\times k}$, represents k covariates associated with μ_i; ${\mathit{X}}_i^{*}$, the ith row of the covariate matrix ${\mathit{X}}^{*}=\left[X_{ij}^{*}\right]\in {ℝ}^{n\times k^{*}}$, represents the k* covariates associated with ϕ_i; β = (β₁, …, β_k)^T; and ${\mathit{\beta }}^{*}={\left({\beta }_1^{*},\dots ,{\beta }_{k^{*}}^{*}\right)}^T$. X and X* may be identical, or they may be non- or partially-overlapping.

Throughout this paper, we choose the logit transformation for the link functions in (3.9) and (3.10), so that

$$g(x)\equiv h(x):=\log \left(\frac{x}{1-x}\right).$$

This link function is convenient as it is a bijection between [0, 1] and $ℝ$. Other choices for the link functions can be used as well, and the link functions for μ_i and ϕ_i need not be identical.

This hierarchical model has three key advantages over other approaches. First, the use of a beta random variable as a model for the binomial probability allows us to incorporate overdispersion. Second, the overdispersion parameter (rather than just the mean) can be modeled with covariates. As we will see in Section 6, this is a key advantage of our approach. Finally, our model makes direct use of the absolute abundance (W₁, …, W_n) and the total number of counts (M₁, …, M_n), rather than simply transforming these quantities into the observed relative abundance (W₁/M₁, …, W_n/M_n), which would amount to throwing away valuable information about the sequencing depth across in each sample. We show the 95% prediction intervals from a beta-binomial model for the soil microbiology study in Figure 1 (right).

3.2. Model fitting

Given n samples from the model (3.2)–(3.3), the log-likelihood is

$$\begin{gathered} \log L(\mathit{\theta }\mid \mathit{W},\mathit{M}) \\ =\sum _{i=1}^n\log \left[\left(\begin{array}{l}{M}_i\hfill \\ W_i\hfill \end{array}\right)\frac{B\left(a_{1,i}+W_i,a_{2,i}+M_i-W_i\right)}{B\left(a_{1,i},a_{2,i}\right)}\right] \\ =\sum _{i=1}^n\log \left[\left(\begin{array}{c}{M}_i\\ W_i\end{array}\right)\frac{B(\frac{e^{-{\beta }_0^{*}-{\mathit{X}}_i^{*T}{\mathit{\beta }}^{*}}}{1+e^{-{\beta }_0-{\mathit{X}}_i^T\mathit{\beta }}}+W_i,\frac{e^{-{\beta }_0^{*}-{\mathit{X}}_i^{*T}{\mathit{\beta }}^{*}}}{1+e^{{\beta }_0+{\mathit{X}}_i^T\mathit{\beta }}}+M_i-W_i)}{B(\frac{e^{-{\beta }_0^{*}-{\mathit{X}}_i^{*T}{\mathit{\beta }}^{*}}}{1+e^{-{\beta }_0-{\mathit{X}}_i^T\mathit{\beta }}},\frac{e^{-{\beta }_0^{*}-{\mathit{X}}_i^{*T}{\mathit{\beta }}^{*}}}{1+e^{{\beta }_0+{\mathit{X}}_i^T\mathit{\beta }}})}\right], \end{gathered}$$ (3.11)

where $\mathit{W}\in {ℝ}^n$, $\mathit{M}\in {ℝ}^n$, $\mathit{\beta }\in {ℝ}^k$, ${\mathit{\beta }}^{*}\in {ℝ}^{k^{*}}$, $\mathit{\theta }={\left({\beta }_0,{\mathit{\beta }}^T,{\beta }_0^{*},{\mathit{\beta }}^{*T}\right)}^T$, and B(·, ·) is the Beta function given by $B(x,y)={\int }_0^1{t}^{x-1}{(1-t)}^{y-1}dt$ for $x\in ℝ$ and $y\in {ℝ}_{+}$. We fit the model by maximum likelihood using the trust region optimization algorithm (Fletcher (1987), Nocedal and Wright (1999), Geyer (2015)), which has accelerated computation relative to a line search method.

In this iterative algorithm, a “trust region” is defined around the parameter estimate at each iteration. The algorithm then updates the parameter estimate by minimizing a second-order Taylor series expansion of the objective function, subject to the constraint that the solution is within the trust region. If a proposed update is infeasible (i.e., it is outside of the parameter space), then it is rejected and the trust region shrinks. The minimization of the objective function then repeats with the new constraint. If a proposed update is close to the boundary of the trust region, the trust region expands in the next iteration. We implement the trust algorithm for minimizing the negative log-likelihood using the R package trust (Geyer (2015)).

The log-likelihood is not concave in θ (see Appendix A), so trust region optimization does not guarantee convergence to the global minimum of the objective function. However, under mild conditions, the limit points of the trust algorithm are guaranteed to satisfy the first- and second-order conditions that are necessary for a local minimum (Fletcher (1987), Nocedal and Wright (1999)). We use multiple initializations and select the estimate that has the largest log-likelihood. In practice, there is little difference in the parameter estimates across initializations.

Each iteration of the trust region optimization algorithm makes use of the gradient and Hessian of (3.11). These are given in Appendix B for the case of logit link functions for g(·) and h(·) in (3.9) and (3.10).

4. Hypothesis testing

We now discuss inference on θ. We consider the null hypothesis that Aθ = b, where $\mathit{A}\in {ℝ}^{r\times \left(k+k^{*}+2\right)}$ has full row rank and r < k + k* + 2, $\mathit{b}\in {ℝ}^r$, and where θ is the parameter vector introduced in (3.11). Note that this general form for the null hypothesis allows us to test arbitrary subsets and linear combinations of the parameters within $\mathit{\theta }={\left({\beta }_0,{\mathit{\beta }}^T,{\beta }_0^{*},{\mathit{\beta }}^{*T}\right)}^T$. The Wald test statistic is

$${\widehat{T}}_{\text{Wald}}=n{(\mathit{A}\widehat{\mathit{\theta }}-\mathit{b})}^T{\left(\mathit{A}\widehat{\mathcal{I}}{(\widehat{\mathit{\theta }})}_n^{-1}{\mathit{A}}^T\right)}^{-1}(\mathit{A}\widehat{\mathit{\theta }}-\mathit{b}),$$ (4.1)

where

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\mathrm{argsup}}\log L(\mathit{\theta }\mid \mathit{W},\mathit{M})$$ (4.2)

and $\widehat{\mathcal{I}}{(\widehat{\mathit{\theta }})}_n$ is the observed Fisher information evaluated at $\widehat{\mathit{\theta }}$:

$$\widehat{\mathcal{I}}{(\widehat{\mathit{\theta }})}_n=-\frac{1}{n}\sum _{i=1}^n{\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}\log L(\mathit{\theta }\mid \mathit{W},\mathit{M})\right]}_{\mathit{\theta }=\widehat{\mathit{\theta }}}.$$ (4.3)

Algorithm 1.

Parametric Bootstrap Wald Test of H₀ : Aθ = b

Require: W, M, X, X*, a large integer B (e.g., B = 10,000)

1: Estimate $\widehat{\mathit{\theta }}$ and ${\widehat{\mathit{\theta }}}_0$ as in (4.2) and (4.5), respectively, with the trust region optimization procedure.

2: Compute ${\widehat{T}}_{\text{Wald}}$ as in (4.1) using A, b and $\widehat{\mathit{\theta }}$.

3: for b = 1, …, B do

4:   Simulate ${\tilde{\mathit{W}}}^b$ with elements ${\tilde{W}}_i^b$ drawn from a beta-binomial distribution with Mi draws and parameters ${\widehat{\mathit{\theta }}}_0$.

5:   Estimate ${\tilde{\mathit{\theta }}}^b$ as in (4.2) using ${\tilde{\mathit{W}}}^b$ and M with the trust region optimization procedure.

6:   Compute ${\widehat{T}}_{\text{Wald}}^b$ as in (4.1) using A, b and ${\tilde{\mathit{\theta }}}^b$.

7: Calculate the p-value: $$\widehat{p}\leftarrow \frac{1}{B+1}\left(1+\sum _{b=1}^B\mathbb{1}\left\{{\widehat{T}}_{\text{Wald}}^b\ge {\widehat{T}}_{\text{Wald}}\right\}\right).$$

8: return $\widehat{p}$

Under the null hypothesis that Aθ = b, we find empirically that ${\widehat{T}}_{\text{Wald}}$ is well-approximated by a ${\chi }_r^2$ distribution if n is large (Section 5.1). Alternatively, we can test Aθ = b using a likelihood ratio test statistic, defined as

$${\widehat{T}}_{\text{LRT}}=2\left(\log L(\widehat{\mathit{\theta }}\mid \mathit{W},\mathit{M})-\log L\left({\widehat{\mathit{\theta }}}_0\mid \mathit{W},\mathit{M}\right)\right),$$ (4.4)

where

$${\widehat{\mathit{\theta }}}_0=\underset{\mathit{\theta }:A\mathit{\theta }=\mathit{b}}{\mathrm{argsup}}\log L(\mathit{\theta }\mid \mathit{W},\mathit{M}).$$ (4.5)

When n is large and Aθ = b, we find that the distribution of ${\widehat{T}}_{\text{LRT}}$ is well-approximated by a ${\chi }_r^2$ distribution (Section 5.1).

In practice, we often do not have the sample size necessary to use the ${\chi }_r^2$ approximation. For this reason, we also implement a parametric bootstrap hypothesis testing procedure. Our parametric bootstrap Wald testing procedure is given in Algorithm 1; the parametric bootstrap likelihood ratio test procedure is provided in Appendix C.

For certain realizations of W, Wald-type inference is uninformative. For example, if k = k* = 1, ${\mathit{X}}_i={\mathit{X}}_i^{*}\in \{0,1\}$ for i = 1, …, n, and ${\sum }_{i:{\mathit{X}}_i=1}{W}_i=0$, then a parameter estimate diverges to −∞ (see Lemma D.1 in Appendix D for details). This limitation is not unique to our model, and hypothesis testing using Wald tests in the case of complete or quasi-complete separation in logistic regression is known to have the same issue (see Albert and Anderson (1984), Heinze and Schemper (2002), Heinze (2006) for further discussion). In this case, we instead use the likelihood ratio test to test hypotheses about β, such as β = 0. However, in this setting, even the likelihood ratio test does not provide a useful test of certain hypotheses about β*, such as β* = 0 (see Appendix D). Since it is often the case that a taxon is unobserved in certain experimental conditions, the default behaviour for our software in this setting is to return a test statistic of zero for Wald-type tests to indicate that inference is uninformative and the null hypothesis should not be rejected.

While (4.4) and Algorithms 1–2 hold for any A and b, they require solving (4.5). This may be difficult to do for certain A and b. In this case, an approximate solution could be obtained by maximizing the likelihood subject to a penalty on $\Vert A\mathit{\theta }-b\Vert$ by (e.g., see Fiacco and McCormick (1968), Ryan (1974)). Alternatively, approximating the distribution of (4.1) with a ${\chi }_r^2$ distribution does not require restricted maximum likelihood estimation.

In summary, we implement four hypothesis testing procedures: the Wald test, the likelihood ratio test, the parametric bootstrap Wald test and the parametric bootstrap likelihood ratio test. The Wald and likelihood ratio tests permit faster inference than the parametric bootstrap tests. However, the parametric bootstrap procedures successfully control Type 1 error in small sample sizes. We now demonstrate the performance of all of these hypothesis testing procedures in simulation.

5. Simulation study

We now investigate the performance of our approach, which we call count regression for correlated observations with the beta-binomial, or corncob, under simulation. We study the Type I error rate and the power when testing for both differential abundance and differential variability. We generate sequencing depths $M\in {ℝ}^n$ with elements M_i simulated from the empirical distribution of the observed sequencing depths in the data set discussed in Section 6, which ranges from 7821 to 58,655. We use sample sizes n ∈ {10, 30, 100} and a binary covariate $X_i=X_i^{*}=0$ for i = 1, …, n/2 − 1 and $X_i=X_i^{*}=1$ for i = n/2, …, n. We then simulate absolute abundances $\mathit{W}\in {ℝ}^n$ with elements W_i simulated under the data generating model (described below). The parameter values were selected by fitting corncob to the genus Thermomonas in the data set discussed in Section 6 so that simulated data are similar to what might be observed in a real-world experiment. For each simulation, we calculate 10,000 p-values using all four of the hypothesis testing procedures outlined in Section 4: the Wald test, the likelihood ratio test, the parametric bootstrap Wald test and the parametric bootstrap likelihood ratio test. We use 1000 bootstrap iterations for the parametric bootstrap testing procedures.

5.1. Type I error rate

We first confirm that corncob controls Type I error at the nominal level. We generate data using the beta-binomial model with logit link functions for mean and overdispersion, under three settings for β. In the first simulation setting, we test the null hypothesis $H_0:\left({\beta }_1,{\beta }_1^{*}\right)=(0,0)$. We generated model parameters by fitting a model to the genus Thermomonas without using soil amendment as a covariate, yielding parameters $({\tilde{\beta }}_0,{\tilde{\beta }}_1,{\tilde{\beta }}_0^{*},{\tilde{\beta }}_1^{*})=(-5.75,0,-5.24,0)$. In the second simulation setting, we test the null hypothesis $H_0:{\beta }_1^{*}=0$. We generated model parameters by fitting a model to the genus Thermomonas using soil amendment as a covariate for μ_i, yielding parameters $({\tilde{\beta }}_0,{\tilde{\beta }}_1,{\tilde{\beta }}_0^{*},{\tilde{\beta }}_1^{*})=(-5.36,-1.12,-5.69,0)$. In the third simulation setting, we test the null hypothesis H₀ : β₁ = 0. We generated model parameters by fitting a model to the genus Thermomonas using soil amendment as a covariate for ϕ_i, yielding parameters $({\tilde{\beta }}_0,{\tilde{\beta }}_1,{\tilde{\beta }}_0^{*},{\tilde{\beta }}_1^{*})=(-5.51,0,-5.38,0.70)$. For all three simulation settings, the null hypotheses are true, so we would expect p-values obtained from testing the null hypotheses to be uniformly distributed.

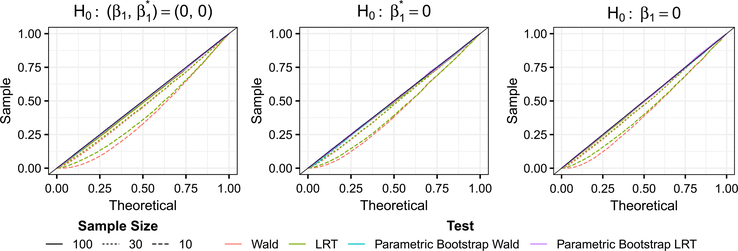
The results are shown in Figure 2. For sample sizes of 30 and 100, all testing procedures resulted in approximately uniform p-values, and Type I error is controlled. This suggests that for this experiment, a sample size of 30 is sufficient to approximate the distribution of the Wald and likelihood ratio test statistics using a χ² distribution.

Fig. 2.

Quantiles of p-values obtained from the Type I error rate simulation settings compared to quantiles of a Uniform(0, 1) distribution. We test the null hypotheses $H_0:\left({\beta }_1,{\beta }_1^{*}\right)=(0,0)$ (left), $H_0:{\beta }_1^{*}=0$ (middle) and H₀ : β₁ = 0 (right). A 45-degree line is shown (black). p-values were obtained using Wald (red), likelihood ratio (green), parametric bootstrap Wald (blue) and parametric bootstrap likelihood ratio (purple) tests. Sample sizes used were 10 (dashed), 30 (dotted) and 100 (solid). Quantiles of each test are shown in Table 2 in Appendix E.

Example quantiles from each of the simulation settings are shown in Table 2 in Appendix E. For a sample size of 10, only the parametric bootstrap procedures resulted in approximately uniform p-values and successful Type I error control. The p-values obtained using the Wald and likelihood ratio tests were anti-conservative, suggesting that for this experiment, a sample size of 10 is too small to approximate the distribution of the test statistics using a χ² distribution. Therefore, to obtain reliable inference, we recommend the parametric bootstrap procedure when n is smaller than 30.

5.2. Power

We now investigate the power of corncob to reject (i) the null hypothesis H₀ : β₁ = 0, as well as (ii) the null hypothesis $H_0:{\beta }_1^{*}=0$. We consider two cases: varying the value of β₁, and varying the value of ${\beta }_1^{*}$. For both settings, we generated model parameters by fitting a model to the genus Thermomonas using soil amendment as a covariate for μ_i and ϕ_i, yielding parameters $({\tilde{\beta }}_0,{\tilde{\beta }}_1,{\tilde{\beta }}_0^{*},{\tilde{\beta }}_1^{*})=(-5.17,-2.46,-5.13,-3.88)$. In the first case (Setting 4 in Figure 3), we set $\left({\beta }_0,{\beta }_1,{\beta }_n^{*},{\beta }_1^{*}\right)=({\tilde{\beta }}_0,c{\tilde{\beta }}_1,{\tilde{\beta }}_n^{*},{\tilde{\beta }}_1^{*})$ using c ∈ {0, 0.05, …, 1}. In the second case (Setting 5 in Figure 3), we set $\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\right)=({\tilde{\beta }}_0,{\tilde{\beta }}_1,{\tilde{\beta }}_0^{*},c{\tilde{\beta }}_1^{*})$ using c ∈ {0, 0.05, …, 1}.

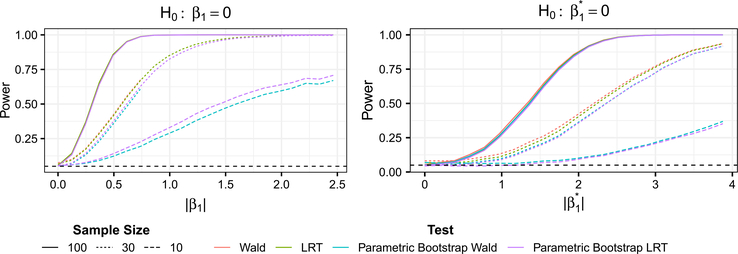
Fig. 3.

Power curves of p-values obtained from the power simulations. Setting 4 (left) tests H₀ : β₁ = 0. Setting 5 (right) tests $H_0:{\beta }_1^{*}=0$. A horizontal dashed line is shown at 0.05. p-values were obtained using Wald (red), likelihood ratio (green), parametric bootstrap Wald (blue) and parametric bootstrap likelihood ratio (purple) tests. Sample sizes used were 10 (dashed), 30 (dotted) and 100 (solid).

The results of the power analyses are shown in Figure 3. For both null hypotheses, all sample sizes, and all hypothesis testing procedures, the power increases as both the sample size and the magnitude of the coefficient being tested increases. For sample sizes of 30 and 100, there is little difference in power across the four testing procedures. This is not surprising, given that in the simulations in Section 5.1, all procedures performed similarly with sample sizes of 30 and 100. We do not show results for the procedures that rely on the asymptotic distribution of the test statistics for n = 10, as we saw in Section 5.1 that these procedures did not properly control Type I error.

6. Application to soil data

We now consider a study of the association between soil treatments and soil microbiome composition (Whitman et al. (2016)). In this experiment, there are three groups of soil treatments: no additions, biochar additions and fresh biomass additions. For each treatment group, multiple experimental replicates were taken at three time points: on the first day, after 12 days and after 82 days. The data include n = 119 samples with sequencing depths ranging from 8830 to 194,356. After quality control (as described in Whitman et al. (2016)), a total of 7770 operational taxonomic units were identified using the UPARSE workflow (Edgar (2013)), and taxonomy was assigned using reference databases. Using the assigned taxonomy, we aggregated counts to the genus level, giving 241 genera.

We are interested in applying our method to compare the microbiome of soil with no additions after 82 days (n = 15) to the microbiome of soil with biochar additions after 82 days (n = 16). We remove 13 genera for which the total number of counts in these 31 samples is zero. We apply corncob using soil addition as a covariate for μ_i and ϕ_i as in (3.9) and (3.10). We calculate p-values using the parametric bootstrap likelihood ratio test (Algorithm 2) with B = 10⁶ bootstrap iterations. We compare the results of corncob to those from DESeq2 (Love, Huber and Anders (2014)), EdgeR (Robinson, McCarthy and Smyth (2010)), metagenomeSeq (Paulson et al. (2013)) and a zero-inflated beta (ZIB) regression model (Peng, Li and Liu (2016)).

6.1. Detection of differential abundance

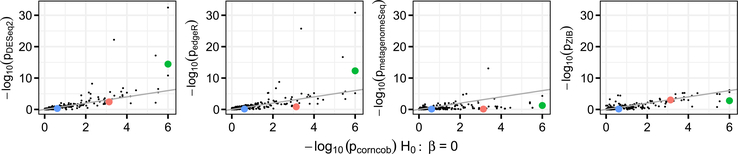
We first compare p-values obtained from testing for differential abundance across soil addition group. Roughly speaking, each of the approaches tests for a difference in abundance of a single taxon across conditions, although the details of the model used vary across methods. In the context of corncob, testing for differential abundance amounts to testing the null hypothesis H₀ : β = 0, using the notation defined in (3.9). Scatter plots of the negative log-10 p-values for each approach are shown in Figure 4.

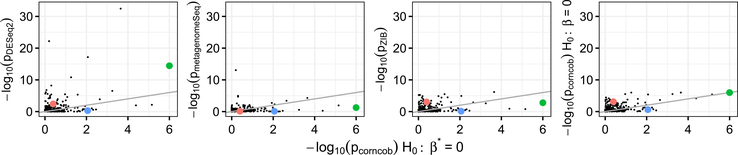
Fig. 4.

The negative log-10 p-values obtained by testing for differential abundance using corncob (H₀ : β = 0) compared to those from DESeq2 (left-most, Spearman’s correlation coefficient ρ = 0.854), EdgeR (middle-left, ρ = 0.783), metagenomeSeq (middle-right, ρ = 0.552) and ZIB (right-most, ρ = 0.705). A 45-degree line is shown. We see that the p-values are on a similar scale overall. Thermomonas (green), Flavisolibacter (red) and Myxococcus (blue) are further examined in Figure 6.

Overall, as p-values calculated using corncob decrease, so do those calculated using other approaches. We observe moderate to strong correlations across the different approaches, with Spearman’s correlation coefficients between the p-values obtained from corncob (H₀ : β = 0) and DESeq2, edgeR, metagenomeSeq and ZIB, respectively, of 0.854, 0.783, 0.552, 0.705. corncob calculated a lower p-value for 53.9%, 43.6%, 63.8% and 58.3% of genera compared to DESeq2, edgeR, metagenomeSeq and ZIB, respectively. Median p-values across all genera for corncob, DESeq2, edgeR, metagenomeSeq and ZIB are 0.273, 0.318, 0.297, 0.491 and 0.320, respectively. Therefore, while the p-values produced by corncob are on a similar scale to the other approaches, they may be higher or lower for any given taxon. While each of the approaches uses a different model and makes use of a different test statistic, they are all testing for some difference in the mean abundance of the taxon across the soil addition. Thus, it is unsurprising that the p-values are similar across the approaches.

6.2. Detection of differential variability

We now test for differences in the variability of the abundance of a single taxon across conditions, which we refer to as differential variability. Using corncob and the notation in (3.9)–(3.10), this amounts to testing the null hypothesis H₀ : β* = 0. As far as we know, corncob is the only approach that explicitly tests for differential variability. Thus, in this section, we investigate whether testing for differential variability allows us to identify new genera beyond what we identify when testing only for differential abundance.

We compare the results of testing for differential variability to the results of testing for differential abundance using the methods investigated in Section 6.1. Figure 5 shows scatter plots of the negative log-10 transformations of the p-values for testing differential abundance from DESeq2, metagenomeSeq, ZIB and corncob against the p-values for testing differential variability with corncob. We see from Figure 5 that there is only a weak association between the p-values for differential variability obtained using corncob and the p-values for differential abundance obtained using the other approaches. In particular, Spearman’s correlation coefficients are 0.127, 0.234, 0.132, 0.215 and 0.362 between corncob p-values for H₀ : β* = 0 and p-values from DESeq2, edgeR, metagenomeSeq, ZIB and corncob for H₀ : β = 0, respectively. We omit from Figure 5 the scatter plot comparing the corncob p-values for H₀ : β* = 0 to the edgeR p-values because the p-values from edgeR are similar to those from DESeq2. We conclude that applying corncob to test H₀ : β* = 0 leads to the discovery of a very different set of genera than those discovered by applying corncob or other approaches to test for differential abundance.

Fig. 5.

The negative log-10 p-values obtained by testing for differential variability using corncob (H₀ : β* = 0) compared to the negative log-10 p-values obtained by testing for differential abundance using DESeq2 (left-most, Spearman’s correlation coefficient ρ = 0.127), metagenomeSeq (middle-left, ρ = 0.132), ZIB (middle-right, ρ = 0.215) and corncob (H₀ : β = 0) (right-most, ρ = 0.362). A 45-degree line is shown. Thermomonas (green), Flavisolibacter (red) and Myxococcus (blue) are further examined in Figure 6. We omit a scatter plot showing p-values for edgeR (ρ = 0.234); results are similar to DESeq2.

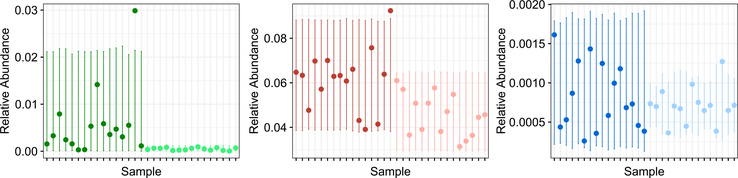
To obtain greater insight into the results shown in Figure 5, we consider the 3 highlighted genera, which we further investigate in Figure 6. The first, Thermomonas, has small p-values for both differential abundance (p = 1.00 × 10⁻⁶) and differential variability (p = 1.00 × 10⁻⁶) using corncob. The second, Flavisolibacter, has a small p-value for differential abundance (p = 7.44 × 10⁻⁴) and a large p-value for differential variability (p = 0.404). The third, Myxococcus, has a large p-value for differential abundance (p = 0.244) and a small p-value for differential variability (p = 8.83 × 10⁻³), so it would not be identified using the competing approaches (see Table 3 in Appendix F for p-values from all approaches). Figure 6 indicates a clear visual difference between genera that are identified as differentially abundant but not differentially variable, differentially variable but not differentially abundant, and both differentially abundant and differentially variable. Researchers can use corncob to distinguish between these three possibilities.

Fig. 6.

The observed relative abundances of the genera Thermomonas (left), Flavisolibacter (middle) and Myxococcus (right) in 31 soil samples. Each of these genera is highlighted in each panel of Figures 4 and 5. In each panel, the first 16 samples correspond to the biochar additions group (darker color), and the remaining 15 samples correspond to the no additions group (lighter color). 95% prediction intervals for the relative abundances from a corncob fit using soil addition as a covariate for μ_i and ϕ_i are shown. Using corncob to test H₀ : β = 0 and H₀ : β* = 0 indicates that Thermomonas is both differentially abundant (p = 1.00 × 10⁻⁶) and differentially variable (p = 1.00 × 10⁻⁶), Flavisolibacter is differentially abundant (p = 7.44 × 10⁻⁴) and not differentially variable (p = 0.404), and Myxococcus is differentially variable (p = 8.83 × 10⁻³) and not differentially abundant (p = 0.244). See Table 3 in Appendix F for p-values from all approaches.

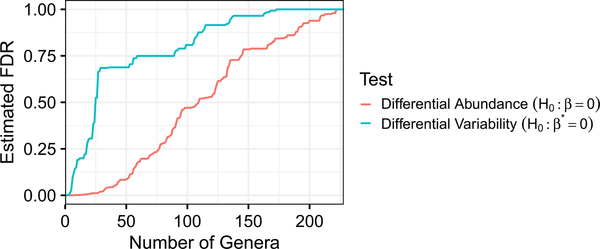
In practice, a data analyst will apply a multiple testing procedure to adjust the p-values for multiple comparisons, so we also investigative the number of genera identified as either differentially abundant or differentially variable after applying the Benjamini–Hochberg procedure (Benjamini and Hochberg (1995)) to the p-values obtained using corncob to test H₀ : β = 0 and H₀ : β* = 0. The results are shown in Figure 7. We see that for a given false discovery rate, in this data set we detect more genera as being differentially abundant than differentially variable; this can also be seen in the right-most panel of Figure 5. All code for performing this analysis is available in the supplementary materials available at github.com/bryandmartin/corncob_supplementary and provided in Supplement B of the Supplementary Material (Martin, Witten and Willis (2020b)).

Fig. 7.

The estimated false discovery rate using the Benjamini–Hochberg procedure, as a function of the number of genera identified as differentially abundant and differentially variable. For a given false discovery rate, we identify fewer genera that are differentially variable than differentially abundant.

7. Discussion

In this paper, we have proposed a beta-binomial regression model for abundance data. Our model extends existing beta-binomial models by allowing discrete and continuous covariates to be linked to both a relative abundance parameter and an overdispersion parameter. Our method is particularly well-suited to modeling microbial abundance data for a number of reasons. First, microbial taxa are commonly unobserved in many samples. For example, in the data set examined in Section 6, 34% of absolute abundances were zero. Our model can accommodate this without requiring a zero-inflation component or pseudocounts. Second, studies of microbial populations often have small sample sizes. Our simulation study in Section 5 suggests that our parametric bootstrap inference methods (Algorithms 1 and 2) give valid inference even with small samples. Third, the interpretation of μ_i as the expected relative abundance and of ϕ_i as the within-sample correlation of taxon labels (i.e., ${\varphi }_i=\mathrm{Corr}\left(Y_{ij}=Y_{i{j}^{\prime }}\right)$, see Section 3) are intuitive and complement ecological theory (Welch et al. (2016)). Finally, regression models for contrasting microbial populations commonly focus on differential abundance. By conducting inference about ϕ_i, our model is also able to identify differences in microbial populations associated with differential variability.

Many studies (e.g., see Gerber (2014), Faust et al. (2015), Zhou et al. (2015), among others) employ a longitudinal design to investigate the dynamics of microbial populations over time. To accommodate this setting, future work could incorporate random effects into (3.9) and (3.10).

Our proposed approach models a single taxon’s abundance. A limitation of this approach is that it does not enforce the compositionality constraint (i.e., the estimated expected relative abundances need not sum to 1 across all microbes in the population). Future work could consider a multivariate extension of our approach to enforce the compositionality constraint or incorporate between-taxon correlations.

All methods proposed in this paper are implemented in an R package available at github.com/bryandmartin/corncob and provided in Supplement A of the Supplementary Material (Martin, Witten and Willis (2020a)). Code to reproduce all simulations and data analyses are available at github.com/bryandmartin/corncob_supplementary and provided in Supplement B of the Supplementary Material (Martin, Witten and Willis (2020b)).

APPENDIX A: NONCONCAVITY OF THE BETA-BINOMIAL LOG-LIKELIHOOD

We show that (3.11) is not guaranteed to be concave in θ. Let n = 1, W ≡ W₁ = 15 and M ≡ M₁ = 2000. Suppose further that $\mathit{\theta }={\left({\beta }_0,{\beta }_0^{*}\right)}^T$. Let θ¹ = (−3 −5)^T and θ² = (−1 −5)^T. Then

$$\begin{gathered} \log L\left({\mathit{\theta }}^1\mid W_1,M_1\right)=-8.481, \\ \log L\left({\mathit{\theta }}^2\mid W_1,M_1\right)=-9.816, \\ \log L\left(0.5{\mathit{\theta }}^1+0.5{\mathit{\theta }}^2\mid W_1,M_1\right)=-\mathrm{9.251.} \end{gathered}$$

Therefore there exists θ¹, and θ² such that

$$\log L\left(0.5{\mathit{\theta }}^1+0.5{\mathit{\theta }}^2\mid \mathit{W},\mathit{M}\right)<0.5\log L\left({\mathit{\theta }}^1\mid \mathit{W},\mathit{M}\right)+0.5\log L\left({\mathit{\theta }}^2\mid \mathit{W},\mathit{M}\right),$$

which establishes that (3.11) is not concave in θ.

APPENDIX B: ANALYTIC EXPRESSIONS FOR THE GRADIENT AND HESSIAN

Let ${\gamma }_i=\frac{{\varphi }_i}{1-{\varphi }_i}$ for all i, and define $\psi (x)={\int }_0^{\infty }\left(\frac{e^{-t}}{t}-\frac{e^{-xt}}{1-e^{-t}}\right)dt$ for $x\in {ℝ}_{+}$ to be the digamma function, the derivative of the logarithm of the gamma function. Define Z_i = (1 X_i) and ${\mathit{Z}}_i^{*}=\left(1{\mathit{X}}_i^{*}\right)$ to be the design matrices for covariates associated with μ_i and ϕ_i, respectively, including intercept terms. Then the expression for the gradient of (3.11) is given by

$$\begin{gathered} \frac{\partial \log L(\mathit{\theta }\mid \mathit{W},\mathit{M})}{\partial \mathit{\beta }} \\ =\sum _{i=1}^n\{{\gamma }_i^{-1}{\mu }_i\left(1-{\mu }_i\right){\mathbf{Z}}_i[\psi \left(\frac{1-{\mu }_i}{{\gamma }_i}\right) \\ -\psi \left(M_i+\frac{1-{\mu }_i-W_i{\gamma }_i}{{\gamma }_i}\right) \\ +\psi \left(W_i+\frac{{\mu }_i}{{\gamma }_i}\right)-\psi \left(\frac{{\mu }_i}{{\gamma }_i}\right)]\}, \end{gathered}$$ (B.1)

$$\begin{gathered} \frac{\partial \log L(\mathit{\theta }\mid \mathit{W},\mathit{M})}{\partial {\mathit{\beta }}^{*}} \\ =\sum _{i=1}^n\left\{{\gamma }_i^{-1}{Z}_i^{*}\right[\psi \left(M_i+\frac{1}{{\gamma }_i}\right)-\psi \left(\frac{1}{{\gamma }_i}\right) \\ +({\mu }_i-1)\left(\psi \left(M_i+\frac{1-{\mu }_i-W_i{\gamma }_i}{{\gamma }_i}\right)-\psi \left(\frac{1-{\mu }_i}{{\gamma }_i}\right)\right) \\ +{\mu }_i\left(\psi \left(\frac{{\mu }_i}{{\gamma }_i}\right)-\psi \left(W_i+\frac{{\mu }_i}{{\gamma }_i}\right)\right)\left]\right\}. \end{gathered}$$ (B.2)

Let ${\psi }^{(1)}(x)=\frac{\partial }{\partial x}\psi (x)$ be the trigamma function. Define $Y_i={\left(Z_i^T\mathbf{0}\right)}^T\in {ℝ}^{k+k^{*}+2}$ and ${\mathit{Y}}_i^{*}={\left(\mathbf{0}{\mathit{Z}}_i^{*T}\right)}^T\in {ℝ}^{k+k^{*}+2}$. Then the expression for the Hessian of (3.11), H, is given by

$$\begin{gathered} \mathit{H}=\sum _{i=1}^n[c_{1,i}{\mu }_i^2{\left(1-{\mu }_i\right)}^2{\mathit{Y}}_i{\mathit{Y}}_i^T+c_{2,i}({\mu }_i\left(1-{\mu }_i\right){\mathit{Y}}_i{\gamma }_i{\mathit{Y}}_i^{*T} \\ +{\gamma }_i{\mathit{Y}}_i^{*}{\mu }_i\left(1-{\mu }_i\right){\mathit{Y}}_i^T)+c_{3,i}\left({\gamma }_i{\mathit{Y}}_i^{*}{\gamma }_i{\mathit{Y}}_i^{*T}\right) \\ +c_{4,i}\left({\mu }_i\left(1-{\mu }_i\right)\left(1-2{\mu }_i\right){\mathit{Y}}_i{\mathit{Y}}_i^T\right)+c_{5,i}\left({\gamma }_i{\mathit{Y}}_i^{*}{\mathit{Y}}_i^{*T}\right)], \end{gathered}$$

where

$$\begin{gathered} c_{1,i}=[{\psi }^{(1)}\left(M_i+\left(1-{\mu }_i-W_i{\gamma }_i\right)/{\gamma }_i\right)-{\psi }^{(1)}\left(\left(1-{\mu }_i\right)/{\gamma }_i\right) \\ +{\psi }^{(1)}\left(W_i+{\mu }_i/{\gamma }_i\right)-{\psi }^{(1)}\left({\mu }_i/{\gamma }_i\right)]{\gamma }_i^{-2}, \end{gathered}$$

$$\begin{gathered} c_{2,i}=[{\gamma }_i\left(\psi \left(M_i-\left({\mu }_i+W_i{\gamma }_i-1\right)/{\gamma }_i\right)-\psi \left(\left(1-{\mu }_i\right)/{\gamma }_i\right)\right)+{\gamma }_i(\psi \left({\mu }_i/{\gamma }_i\right) \\ -\psi \left({\mu }_i/{\gamma }_i+W_i\right))+\left({\mu }_i-1\right)({\psi }^{(1)}\left(\left(1-{\mu }_i\right)/{\gamma }_i\right) \\ -{\psi }^{(1)}\left(M_i-\left({\mu }_i+W_i{\gamma }_i-1\right)/{\gamma }_i\right))+{\psi }^{(1)}\left({\mu }_i/{\gamma }_i\right) \\ -{\psi }^{(1)}\left({\mu }_i/{\gamma }_i+W_i\right)]{\gamma }_i^{-3}, \end{gathered}$$

$$\begin{gathered} c_{3,i}=[2{\gamma }_i\psi \left(1/{\gamma }_i\right)+{\psi }^{(1)}\left(1/{\gamma }_i\right)-2{\gamma }_i\psi \left(M_i+1/{\gamma }_i\right)-{\psi }^{(1)}\left(M_i+1/{\gamma }_i\right) \\ +{\left({\mu }_i-1\right)}^2{\psi }^{(1)}\left(M_i-\left({\mu }_i+W_i{\gamma }_i-1\right)/{\gamma }_i\right) \\ -2{\gamma }_i\left({\mu }_i-1\right)\psi \left(M_i-\left({\mu }_i+W_i{\gamma }_i-1\right)/{\gamma }_i\right)-{\mu }_i^2{\psi }^{(1)}\left({\mu }_i/{\gamma }_i\right) \\ +{\mu }_i^2{\psi }^{(1)}\left({\mu }_i/{\gamma }_i+W_i\right)-{\left({\mu }_i-1\right)}^2{\psi }^{(1)}\left(\left(1-{\mu }_i\right)/{\gamma }_i\right) \\ +2{\gamma }_i\left({\mu }_i-1\right)\psi \left(\left(1-{\mu }_i\right)/{\gamma }_i\right)-2{\gamma }_i{\mu }_i\psi \left({\mu }_i/{\gamma }_i\right) \\ +2{\gamma }_i{\mu }_i\psi \left({\mu }_i/{\gamma }_i+W_i\right)]{\gamma }_i^{-4}, \end{gathered}$$

$$\begin{gathered} c_{4,i}=[\psi \left(\left(1-{\mu }_i\right)/{\gamma }_i\right)-\psi \left(M_i-\left({\mu }_i+W_i{\gamma }_i-1\right)/{\gamma }_i\right)+\psi \left({\mu }_i/{\gamma }_i+W_i\right) \\ -\psi \left({\mu }_i/{\gamma }_i\right)]/{\gamma }_i, \end{gathered}$$

$$\begin{gathered} c_{5,i}=[\psi \left(M_i+1/{\gamma }_i\right)-\psi \left(1/{\gamma }_i\right)+{\mu }_i\left(\psi \left({\mu }_i/{\gamma }_i\right)-\psi \left({\mu }_i/{\gamma }_i+W_i\right)\right) \\ +\left({\mu }_i-1\right)\left(\psi \left(M_i-\left({\mu }_i+W_i{\gamma }_i-1\right)/{\gamma }_i\right)-\psi \left(\left(1-{\mu }_i\right)/{\gamma }_i\right)\right)]{\gamma }_i^{-2}. \end{gathered}$$

APPENDIX C: PARAMETRIC BOOTSTRAP LIKELIHOOD RATIO TEST

We present Algorithm 2 to conduct a parametric bootstrap likelihood ratio test.

APPENDIX D: LIKELIHOOD RATIO TESTING WITH A ZERO-COUNT GROUP

We prove that testing the null hypothesis H₀ : β* = 0 results in a test statistic of zero under certain conditions. We first prove in Lemma D.1 that the log-likelihood of the model (3.2)–(3.3) is equal to zero under certain conditions. We use this to prove our main claim in Theorem D.2.

Algorithm 2.

Parametric Bootstrap Likelihood Ratio Test of H₀ : Aθ = b

Require: W, M, X, X*, a large integer B (e.g., B = 10,000)

1: Estimate $\widehat{\mathit{\theta }}$ and ${\widehat{\mathit{\theta }}}_0$ as in (4.2) and (4.5), respectively, with the trust region optimization procedure.

2: Compute ${\widehat{T}}_{\text{LRT}}$ as in (4.4) using W, M, $\widehat{\mathit{\theta }}$ and ${\widehat{\mathit{\theta }}}_0$.

3: for b = 1, …, B do

4:   Simulate ${\tilde{\mathit{W}}}^b$ with elements ${\tilde{W}}_i^b$ drawn from a beta-binomial distribution with Mi draws and parameters ${\widehat{\mathit{\theta }}}_0$.

5:   Estimate ${\tilde{\mathit{\theta }}}^b$ as in (4.2) using ${\tilde{\mathit{W}}}^b$ and M with the trust region optimization procedure.

6:   Estimate ${\tilde{\mathit{\theta }}}_0^b$ as in (4.5) using ${\tilde{\mathit{W}}}^b$ and the trust region optimization procedure.

7:   Compute ${\widehat{T}}_{\text{LRT}}^b$ as in (4.4) using ${\tilde{\mathit{W}}}^b$, M, ${\tilde{\mathit{\theta }}}^b$ and ${\tilde{\mathit{\theta }}}_0^b$.

8: Calculate the p-value: $$\widehat{p}\leftarrow \frac{1}{B+1}\left(1+\sum _{b=1}^B\mathbb{1}\left\{{\widehat{T}}_{\text{LRT}}^b\ge {\widehat{T}}_{\text{LRT}}\right\}\right).$$

9: return $\widehat{p}$

Lemma D.1. Consider the model (3.2)–(3.3) with parameters as in (3.4)–(3.6) and link functions as in (3.9)–(3.10) in the simplified setting with no covariates for μ_i, so that $\mathit{\theta }={\left({\beta }_0,{\beta }_0^{*},{\beta }^{*T}\right)}^T$. Suppose that ${\sum }_i{W}_i=0$. Then

$$\underset{{\beta }_0}{\sup }\log L(\mathit{\theta }\mid \mathit{W},\mathit{M})=0.$$

Proof. We write the log-likelihood

$$\begin{gathered} \log L(\mathit{\theta }\mid \mathit{W},\mathit{M}) \\ =\sum _{i=1}^n\log \left[\left(\begin{array}{l}{M}_i\hfill \\ W_i\hfill \end{array}\right)\frac{B(\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{-{\beta }_0}}+W_i,\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{{\beta }_0}}+M_i-W_i)}{B(\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{-{\beta }_0}},\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{{\beta }_0}})}\right]. \end{gathered}$$

Substituting W_i = 0, using the definition of B(·, ·), and taking the limit in β₀ gives

$$\begin{gathered} \underset{{\beta }_0\to -\infty }{\lim }\log L(\mathit{\theta }\mid \mathit{W},\mathit{M})=\underset{{\beta }_0\to -\infty }{\lim }\sum _{i=1}^n\log \left[\mathrm{\Gamma }\left(\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{{\beta }_0}}+M_i\right)\right] \\ +\log \left[\mathrm{\Gamma }\left(\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{-{\beta }_0}}+\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{{\beta }_0}}\right)\right] \\ -\log \left[\mathrm{\Gamma }\left(\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{-{\beta }_0}}+\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{{\beta }_0}}+M_i\right)\right] \\ -\log \left[\mathrm{\Gamma }\left(\frac{e^{-{\beta }_0^{*}-X_i^{*T}{\beta }^{*}}}{1+e^{{\beta }_0}}\right)\right] \\ =0 \\ \ge \underset{{\beta }_0}{\sup }\log L(\mathit{\theta }\mid \mathit{W},\mathit{M}), \end{gathered}$$

where the last inequality is because the log-likelihood associated with a discrete distribution cannot exceed 0.

Therefore,

$$\underset{{\beta }_0}{\sup }\log L(\mathit{\theta }\mid \mathit{W},\mathit{M})=\underset{{\beta }_0\to -\infty }{\lim }\log L(\mathit{\theta }\mid \mathit{W},\mathit{M})=0.$$

□

Theorem D.2. Consider the model (3.2)–(3.3) with parameters as in (3.4)–(3.6) and link functions as in (3.9)–(3.10). Assume that k = k* = 1 and $X_i=X_i^{*}\in \{0,1\}$ for i = 1, …, n. Suppose that ${\sum }_{i:X_i=0}{W}_i=0$ and ${\sum }_{i:X_i=1}{W}_i>0$. Then the likelihood ratio test statistic for testing the null hypothesis that ${\beta }_1^{*}=0$ is equal to 0.

Proof. Let L_i represent the likelihood of the ith sample, so that

$$\sum _{i=1}^n\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid W_i,M_i\right)\equiv \log L\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid \mathit{W},\mathit{M}\right).$$ (D.1)

We wish to show that the likelihood ratio test statistic

$$\begin{gathered} \underset{{\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}}{\sup }\sum _{i=1}^n\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid W_i,M_i\right) \\ -\underset{{\beta }_0,{\beta }_1,{\beta }_0^{*}}{\sup }\sum _{i=1}^n{L}_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}=0\mid W_i,M_i\right)=0. \end{gathered}$$ (D.2)

First, we notice that for all i, the parameters ${\beta }_0^{*}$ and ${\beta }_1^{*}$ enter the likelihood L_i(·) only though the term ${\beta }_0^{*}+{\beta }_1^{*}{X}_i$. This term is equal to ${\beta }_0^{*}$ for all i such that X_i = 0, and ${\beta }_0^{*}+{\beta }_1^{*}$ for all i such that X_i = 1. Similarly, the parameters β₀ and β₁ enter the likelihood L_i(·) only through the term β₀ for all i such that X_i = 0, and β₀ + β₁ for all i such that X_i = 1. Therefore, we can write the first term in (D.2) as the sum of two sub-problems,

$$\begin{gathered} \underset{{\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}}{\sup }\sum _{i=1}^n\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid W_i,M_i\right) \\ =\underset{{\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}}{\sup }\sum _{i:X_i=0}\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid W_i,M_i\right) \\ +\underset{{\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}}{\sup }\sum _{i:X_i=1}\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid W_i,M_i\right) \\ =\underset{{\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}}{\sup }\sum _{i:X_i=1}\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid W_i,M_i\right), \end{gathered}$$

where the last equality results from Lemma D.1. Similarly, we can write the second term in (D.2),

$$\begin{gathered} \underset{{\beta }_0,{\beta }_1,{\beta }_0^{*}}{\sup }\sum _{i=1}^n\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}=0\mid W_i,M_i\right) \\ =\underset{{\beta }_0,{\beta }_1,{\beta }_0^{*}}{\sup }\sum _{i:X_i=1}\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}=0\mid W_i,M_i\right). \end{gathered}$$

Thus, to show (D.2), it suffices to show that

$$\begin{gathered} \underset{{\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}}{\sup }\sum _{i:X_i=1}\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}\mid W_i,M_i\right) \\ -\underset{{\beta }_0,{\beta }_1,{\beta }_0^{*}}{\sup }\sum _{i:X_i=1}\log L_i\left({\beta }_0,{\beta }_1,{\beta }_0^{*},{\beta }_1^{*}=0\mid W_i,M_i\right)=0. \end{gathered}$$

This follows directly from the fact that the parameters ${\beta }_0^{*}$ and ${\beta }_1^{*}$ enter the likelihood L_i(·) only though the term ${\beta }_0^{*}+{\beta }_1^{*}$ for all i such that X_i = 1. This completes our proof of Theorem D.2. □

APPENDIX E: QUANTILES OF TYPE I ERROR RATE SIMULATIONS

We present Table 2 to display sample quantiles from the type I error rate simulations discussed in Section 5.1. We show the 5, 25, 50, 75 and 95% quantiles of each test.

Table 2.

The 5, 25, 50, 75 and 95% quantiles of p-values from the type I error rate simulations discussed in Section 5.1. The Wald and LRT procedures use a χ² distribution to approximate the distributions of the test statistics (4.1) and (4.4), respectively. The PB Wald and PB LRT procedures are the parametric bootstrap hypothesis testing procedures discussed in Algorithms 1 and 2, respectively

Null hypothesis	Sample size	Procedure	5%	25%	50%	75%	95%
(β1, β1*) = (0, 0)	10	Wald	0.002	0.089	0.329	0.647	0.929
		PB Wald	0.046	0.246	0.499	0.749	0.952
		LRT	0.013	0.132	0.360	0.655	0.929
		PB LRT	0.049	0.247	0.496	0.748	0.953
	30	Wald	0.027	0.202	0.453	0.713	0.941
		PB Wald	0.050	0.250	0.497	0.739	0.947
		LRT	0.035	0.213	0.458	0.716	0.941
		PB LRT	0.049	0.250	0.498	0.741	0.947
	100	Wald	0.039	0.234	0.485	0.738	0.947
		PB Wald	0.047	0.247	0.498	0.745	0.949
		LRT	0.042	0.238	0.486	0.738	0.947
		PB LRT	0.046	0.247	0.498	0.744	0.949
β1* = 0	10	Wald	0.006	0.124	0.381	0.688	0.934
		PB Wald	0.039	0.242	0.497	0.754	0.949
		LRT	0.014	0.146	0.393	0.689	0.934
		PB LRT	0.048	0.248	0.502	0.752	0.948
	30	Wald	0.031	0.212	0.472	0.735	0.949
		PB Wald	0.047	0.245	0.499	0.751	0.952
		LRT	0.035	0.215	0.473	0.735	0.949
		PB LRT	0.048	0.245	0.499	0.750	0.953
	100	Wald	0.045	0.244	0.487	0.740	0.947
		PB Wald	0.051	0.254	0.496	0.744	0.947
		LRT	0.047	0.245	0.488	0.740	0.947
		PB LRT	0.050	0.253	0.494	0.743	0.950
β1 = 0	10	Wald	0.002	0.123	0.387	0.685	0.935
		PB Wald	0.048	0.248	0.498	0.745	0.949
		LRT	0.015	0.157	0.401	0.687	0.935
		PB LRT	0.047	0.251	0.497	0.746	0.949
	30	Wald	0.030	0.216	0.470	0.740	0.953
		PB Wald	0.050	0.246	0.496	0.755	0.955
		LRT	0.037	0.221	0.472	0.741	0.953
		PB LRT	0.049	0.246	0.496	0.752	0.955
	100	Wald	0.044	0.24	0.492	0.747	0.952
		PB Wald	0.052	0.249	0.499	0.752	0.953
		LRT	0.048	0.242	0.492	0.746	0.952
		PB LRT	0.049	0.248	0.501	0.752	0.953

APPENDIX F: HYPOTHESIS TESTING RESULTS FOR EXAMPLE GENERA

We present Table 3 to display the results from the hypothesis tests conducted on the Thermomonas, Flavisolibacter and Myxococcus genera discussed in Section 6.2.

Table 3.

Results from the hypothesis tests conducted on the genera discussed in Section 6.2

Genus	Method	p-value
Thermomonas	corncob (H0 : β = 0)	1.00 × 10−6
	corncob (H0 : β* = 0)	1.00 × 10−6
	DESeq2	3.58 × 10−15
	edgeR	4.96 × 10−13
	metagenomeSeq	0.0543
	ZIB	0.00163
Flavisolibacter	corncob (H0 : β = 0)	0.000735
	corncob (H0 : β* = 0)	0.403
	DESeq2	0.00387
	edgeR	0.143
	metagenomeSeq	0.759
	ZIB	0.000941
Myxococcus	corncob (H0 : β = 0)	0.243
	corncob (H0 : β* = 0)	0.00871
	DESeq2	0.0018
	edgeR	0.0017
	metagenomeSeq	0.0016
	ZIB	0.0015