Sensitivity Analysis for Unmeasured Confounding in Meta-Analyses

Abstract

Random-effects meta-analyses of observational studies can produce biased estimates if the synthesized studies are subject to unmeasured confounding. We propose sensitivity analyses quantifying the extent to which unmeasured confounding of specified magnitude could reduce to below a certain threshold the proportion of true effect sizes that are scientifically meaningful. We also develop converse methods to estimate the strength of confounding capable of reducing the proportion of scientifically meaningful true effects to below a chosen threshold. These methods apply when a “bias factor” is assumed to be normally distributed across studies or is assessed across a range of fixed values. Our estimators are derived using recently proposed sharp bounds on confounding bias within a single study that do not make assumptions regarding the unmeasured confounders themselves or the functional form of their relationships with the exposure and outcome of interest. We provide an R package, EValue, and a free website that compute point estimates and inference and produce plots for conducting such sensitivity analyses. These methods facilitate principled use of random-effects meta-analyses of observational studies to assess the strength of causal evidence for a hypothesis.

1. Introduction

Meta-analyses can be indispensable for assessing the overall strength of evidence for a hypothesis and for precisely estimating effect sizes through aggregation of multiple estimates. Meta-analysis is often used not only for randomized trials, but also for observational studies. When the hypothesis of interest is about causation (e.g., of an exposure on a health outcome), evidence strength depends critically not only on the size and statistical uncertainty of the meta-analytic point estimate, but also on the extent to which these apparent effects are robust to unmeasured confounding (Shrier et al. 2007; Egger, Schneider, and Smith 1998; Valentine and Thompson 2013). However, when well-designed randomized studies do not exist because the exposure cannot be randomized, meta-analyses often include potentially confounded observational studies. Therefore, in practice, meta-analyses of observational studies are often met with concerns about the potential for unmeasured confounding to attenuate—or possibly even reverse the direction of—the estimated effects (e.g., Chung et al. 2014; Aune et al. 2011; Siri-Tarino et al. 2010 with critiques on the latter by Stamler (2010)). Yet such considerations rarely proceed beyond qualitative speculation given the limited availability of quantitative methods to assess the impact of unmeasured confounding in a meta-analysis.

Our focus in this article is therefore on conducting sensitivity analyses assessing the extent to which unmeasured confounding of varying magnitudes could have compromised the results of the meta-analysis. Existing sensitivity analyses for confounding bias or other internal biases in meta-analysis estimate a bias-corrected pooled point estimate by directly incorporating one or more bias parameters in the likelihood and placing a Bayesian prior on the distribution of these parameters (Welton et al. 2009; McCandless 2012). An alternative frequentist approach models bias as additive or multiplicative within each study and then uses subjective assessment to elicit study-specific bias parameters (Turner et al. 2009). Although useful, these approaches typically require strong assumptions on the nature of unmeasured confounding (e.g., requiring a single binary confounder), rely on the arbitrary specification of additive or multiplicative effects of bias, or require study-level estimates rather than only meta-analytic pooled estimates. Furthermore, the specified bias parameters do not necessarily lead to precise practical interpretations.

An alternative approach is to analytically bound the effect of unmeasured confounding on the results of a meta-analysis. To this end, bounding methods are currently available for point estimates of individual studies. We focus on sharp bounds derived by Ding and VanderWeele (2016) because of their generality and freedom from assumptions regarding the nature of the unmeasured confounders or the functional forms of their relationships with the exposure of interest and outcome. This approach subsumes several earlier approaches (Cornfield et al. 1959; Schlesselman’s 1978; Flanders and Khoury 1990) and, in contrast to Lin, Psaty, and Kronmal (1998) and certain results of VanderWeele and Arah (2011), does not make any no-interaction assumptions between the exposure and the unmeasured confounder(s).

This article extends these analytic bounds for single studies to the meta-analytic setting. Using standard estimates from a random-effects meta-analysis and intuitively interpretable sensitivity parameters on the magnitude of confounding, these results enable inference about the strength of causal evidence in a potentially heterogeneous population of studies. Broadly, our approach proceeds as follows. First, we select an effect size representing a minimum threshold of scientific importance for the true causal effect in any given study. Second, we use the confounded effect estimates from the meta-analyzed studies, along with simple sensitivity parameters, to make inference to the population distribution of true causal effects (the quantities of ultimate scientific interest). Last, we use this estimated distribution in turn to estimate the proportion of true causal effects in the population that are of scientifically meaningful size (i.e., those stronger than the chosen threshold). As we will discuss, the proportion of scientifically meaningful effect sizes in a meta-analysis is a useful characterization of evidence strength when the effects may be heterogeneous (Mathur and VanderWeele 2019). Conversely, we also solve for the sensitivity parameters on the bias that would be capable of “explaining away” the results of the meta-analysis by substantially reducing the proportion of strong causal effects. We also discuss sensitivity analysis for the pooled estimate of the mean effect.

If sensitivity analysis for unmeasured confounding indicates that only a small proportion of true causal effects are stronger than the chosen threshold of scientific importance, then arguably the results of the meta-analysis are not robust to unmeasured confounding in a meaningful way regardless of the “statistical significance” of the observed point estimate. To this end, we develop estimators that answer the questions: “In the presence of unmeasured confounding of specified strength, what proportion of studies would have true causal effects of scientifically meaningful size?” and “How severe would unmeasured confounding need to be ‘explain away’ the results; that is, to imply that very few causal effects are of scientifically meaningful size?” This approach to sensitivity analysis is essentially a meta-analytic extension of a recently proposed metric (the E-value) that quantifies, for a single study, the minimum confounding bias capable of reducing the true effect to a chosen threshold (VanderWeele and Ding 2017). We provide and demonstrate use of an R package (EValue) and a free website for conducting such analyses and creating plots.

2. Existing Bounds on Confounding Bias in a Single Study

Ding and VanderWeele (2016) developed bounds for a single study as follows. Let X denote a binary exposure, Y a binary outcome, Z a vector of measured confounders, and U one or more unmeasured confounders. Let

$${\text{RR}}_{XY|z}^c=\frac{P\left(Y=1|X=1,Z=z\right)}{P\left(Y=1|X=0,Z=z\right)}$$

be the confounded relative risk (RR) of Y for X = 1 versus X = 0 conditional or stratified on the measured confounders Z = z.

Let its true, unconfounded counterpart standardized to the population be

$${\text{RR}}_{XY|z}^t=\frac{{\sum }_{u}P\left(Y=1|X=1,Z=z,U=u\right)P(U=u|Z=z)}{{\sum }_{u}P(Y|X=0,Z=z,U=u)P(U=u|Z=z)}.$$

(Throughout, we use the term “true” as a synonym for “unconfounded” or “causal” when referring to both sample and population quantities. Also, henceforth, we condition implicitly on Z = z, dropping the explicit notation for brevity.) Define the ratio of the confounded to the true RRs as $B={\text{RR}}_{XY}^c/{\text{RR}}_{XY}^t$.

Let RR_Xu = P (U = u | X = 1) /P (U = u| X = 0). Define the first sensitivity parameter as RR_XU = max_u (RR_Xu); that is, the maximal RR of U = u for X = 1 versus X = 0 across strata of U. (If U is binary, this is just the RR relating X and U.) Next, for each stratum x of X, define a RR of U on Y, maximized across all possible contrasts of U:

$${\text{RR}}_{UY|X=x}=\frac{{\text{max}}_{u}P(Y=1|X=x,U=u)}{{\text{min}}_{u}P(Y=1|X=x,U=u)},x\in \{0,1\}.$$

Define the second sensitivity parameter as RR_UY = max(RR_UY|X=0, RR_UY|X=1). That is, considering both strata of X, it is the largest of the maximal RRs of U on Y conditional on X. Then, Ding and VanderWeele (2016) showed that when B ≥ 1, then B itself is bounded above by

$$B\le \frac{{\text{RR}}_{XU}\cdot {\text{RR}}_{UY}}{{\text{RR}}_{XU}+{\text{RR}}_{UY}-1}$$

and that when B ≤ 1, the same bound holds for 1/B. Thus, defining the “worst-case” bias factor as $B^{+}=\frac{{\text{RR}}_{XU}\cdot {\text{RR}}_{UY}}{{\text{RR}}_{XU}+{\text{RR}}_{UY}-1}$, a sharp bound the true effect is

$${\text{RR}}_{XY}^t\ge {\text{RR}}_{XY}^c/B^{+}.$$ (1)

This bound on the bias factor applies when examining the extent to which unmeasured confounding might have shifted the observed estimate ${\text{RR}}_{XY}^c$ away from the null. Thus, Equation (1) indicates that ${\text{RR}}_{XY}^t$ is at least as strong as a bound constructed by attenuating ${\text{RR}}_{XY}^c$ toward the null by a factor of B⁺. The factor B⁺ is larger, indicating greater potential bias, when U is strongly associated with both X and Y (i.e., RR_XU and RR_UY are large) and is equal to 1, indicating no potential for bias, if U is unassociated with either X or Y (i.e., RR_XU =1 or RR_UY = 1).

If the two sensitivity parameters are equal (RR_XU = RR_UY), then to produce a worst-case bias factor B⁺, each must exceed $B^{+}+\sqrt{B^{+}\left(B^{+}-1\right)}$ (which VanderWeele and Ding (2017) call the “E-value”). Thus, a useful transformation of B⁺ is the “confounding strength scale,” g, which is the minimum size of RR_XU and RR_UY under the assumption that they are equal:

$$g=B^{+}+\sqrt{B^{+}\left(B^{+}-1\right)}\iff B^{+}=\frac{g^2}{2g-1}.$$ (2)

If ${\text{RR}}_{XY}^c<1$ (henceforth the “apparently preventive case”), then Equation (1) becomes (Ding and VanderWeele 2016):

$${\text{RR}}_{XY}^t\le {\text{RR}}_{XY}^c\cdot \frac{{\text{RR}}_{XU}^{*}\cdot {\text{RR}}_{UY}}{{\text{RR}}_{XU}^{*}+{\text{RR}}_{UY}-1},$$

where ${\text{RR}}_{XU}^{*}={\text{max}}_u\left({\text{RR}}_{Xu}^{-1}\right)$, that is, the maximum of the inverse RRs, rather than the RRs themselves. Thus, B⁺ remains ≥ 1, and we have ${\text{RR}}_{XY}^t\ge {\text{RR}}_{XY}^c$.

Although these results hold for multiple confounders, in the development to follow, we will use a single, categorical unmeasured confounder for clarity. However, all results can easily be interpreted without assumptions on the type of exposure and unmeasured confounders, for instance by interpreting the relative risks defined above as “mean ratios” (Ding and VanderWeele 2016).

3. Random-Effects Meta-Analysis Setting

In this article, we use the aforementioned analytic bounds to derive counterparts for random-effects meta-analysis. Under standard parametric assumptions (Sutton et al. 2000), each of k studies measures a potentially unique effect size M_i, such that M_i ~_iid N(μ, V) for a grand mean μ and variance V. Let y_i be the point estimate of the ith study and ${\sigma }_i^2$ be the within-study variance (with the latter assumed fixed and known), such that $y_i|M_i~N\left(M_i,{\sigma }_i^2\right)$. Thus, marginally, $y_i~N\left(\widehat{\mu },V+{\sigma }_i^2\right)$.

Analysis proceeds by first estimating V via one of many possible estimators, denoted τ². Heterogeneity estimation approaches include, for example, maximum likelihood and restricted maximum likelihood as well as approaches proposed by Paule and Mandel (1982), Sidik and Jonkman (2005), Hartung and Makambi (2002), and Hedges and Olkin (1985); see Veroniki et al. (2015) for a review. We will denote an estimator of μ by ${\widehat{y}}_R$, which, for many estimators, will also be a function of τ². For example, a common approach is to use the maximum likelihood solutions for the two parameters¹:

$${\widehat{y}}_R=\frac{{\sum }_{i=1}^k{w}_i{y}_i}{{\sum }_{i=1}^k{w}_i},$$ (3)

$${\tau }^2=\text{ max}\left\{0,\frac{{\sum }_{i=1}^k{w}_i^2\left[{\left(y_i-{\widehat{y}}_R\right)}^2-{\sigma }_i^2\right]}{{\sum }_{i=1}^k{w}_i^2}\right\}.$$ (4)

The weights, w_i, are inversely proportional to the total variance of each study (a sum of the between-study variance and the within-study variance), such that $w_i=1/\left({\tau }^2+{\sigma }_i^2\right)$. Estimation can then proceed by first initializing ${\widehat{y}}_R$ and τ² to, for example, the weighted mean assuming τ² =0 and the method of moments estimators, respectively, and then by iterating between (3) and (4) to reach the maximum likelihood solutions (Veroniki et al. 2015). Other estimation procedures exist (see Veroniki et al. 2015 for a review), and our methods apply regardless of estimation procedure as long as: (1) ${\widehat{y}}_R$ and τ² are consistent and unbiased, asymptotically normal, and asymptotically independent; (2) the point estimates’ expectations are independent of their standard errors; and (3) there are approximately 10 or more meta-analyzed studies (see the online Appendix).

4. Main Results

Consider k studies measuring RRs with confounded population effect sizes on the log-RR scale, denoted M^c, such that M^c ~ N(μ^c, V^c). (Other outcome measures are considered briefly in Section 10.) For studies in which some confounders are measured and adjusted in analysis, we define M^c as the population effect sizes after adjusting for these measured confounders, but without adjusting for any unmeasured confounders. Let the corresponding true effects be M^t with expectation μ^t and variance V^t. Let ${\widehat{y}}_R^c$ be the pooled point estimate and ${\tau }_c^2$ be a heterogeneity estimate, both computed from the confounded study point estimates (e.g., from Equations (3) and (4)).

Consider the bias factor on the log scale, B* = log B, and allow it to vary across studies under the assumption that $B^{*}~N\left({\mu }_{B^{*}},{\sigma }_{B^{*}}^2\right)$, with B* independent of M^t. That is, we assume that the bias factor is independent of the true effects but not the confounded effects: naturally, studies with larger bias factors will tend to obtain larger effect sizes. For studies in which analyses conditioned on one or more measured confounders, B* represents additional bias produced by unmeasured confounding, above and beyond the measured confounders. Hence, studies with better existing control of confounding are likely to have a smaller value of B* than studies with poor confounding control. The normality assumption on the bias factor holds approximately if, for example, its components (RR_XU and RR_UY) are identically and independently log-normal with relatively small variance (Web Appendix). We now develop three estimators enabling sensitivity analyses.

4.1. Proportion of Studies With Scientifically Meaningful Effect Sizes as a Function of the Bias Factor

For an apparently causative RR (${\widehat{y}}_R^c>0$, or equivalently the confounded pooled RR is greater than 1), define p(q) = P(M^t > q) for any threshold q, that is, the proportion of studies with true effect sizes larger than q. Then a consistent estimator of p(q) is

$$\widehat{p}(q)=1-\mathrm{\Phi }\left(\frac{q+{\mu }_{B^{*}}-{\widehat{y}}_R^c}{\sqrt{{\tau }_c^2-{\sigma }_{B^{*}}^2}}\right),{\tau }_c^2>{\sigma }_{B^{*}}^2,$$

where Φ denotes the standard normal cumulative distribution function. In the special case in which the bias factor is fixed to μ_B* across all studies, the same formula applies with ${\sigma }_{B^{*}}^2=0$.

Many common choices of heterogeneity estimators, ${\tau }_c^2$, are asymptotically independent of ${\widehat{y}}_R^c$ (Web Appendix), an assumption used for all SEs in the main text. Results relaxing this assumption appear throughout the Web Appendix. An application of the delta method thus yields an approximate SE:

$$\widehat{\text{SE}}(\widehat{p}(q))\approx \sqrt{\frac{\widehat{\text{var}}\left({\widehat{y}}_R^c\right)}{{\tau }_c^2-{\sigma }_{B^{*}}^2}+\frac{\widehat{\text{var}}\left({\tau }_c^2\right){\left(q+{\mu }_{B^{*}}-{\widehat{y}}_R^c\right)}^2}{4{\left({\tau }_c^2-{\sigma }_{B^{*}}^2\right)}^3}}\cdot \varphi \left(\frac{q+{\mu }_{B^{*}}-{\widehat{y}}_R^c}{\sqrt{{\tau }_c^2-{\sigma }_{B^{*}}^2}}\right),{\tau }_c^2>{\sigma }_{B^{*}}^2,$$

where ϕ denotes the standard normal density function. (If ${\tau }_c^2\le {\sigma }_{B^{*}}^2$, leaving one of the denominators undefined, this indicates that there is so little observed heterogeneity in the confounded effect sizes that, given the specified bias distribution, V^t is estimated to be less than 0. Therefore, attention should be limited to a range of values of ${\sigma }_{B^{*}}^2$ such that ${\tau }_c^2>{\sigma }_{B^{*}}^2$. Also note that when $\widehat{p}(q)<0.15$ or >0.85, it is preferable to estimate inference using bias-corrected and accelerated bootstrapping [(Mathur and VanderWeele 2019)].)

For an apparently preventive RR (${\widehat{y}}_R^c<0$ or the confounded pooled RR is less than 1), define instead p(q) = P(M^t < q), that is, the proportion of studies with true effect sizes less than q. Then a consistent estimator is

$$\widehat{p}(q)=\mathrm{\Phi }\left(\frac{q+{\mu }_{B^{*}}-{\widehat{y}}_R^c}{\sqrt{{\tau }_c^2-{\sigma }_{B^{*}}^2}}\right),{\tau }_c^2>{\sigma }_{B^{*}}^2$$

with approximate SE:

$$\widehat{\text{SE}}(\widehat{p}(q))=\sqrt{\frac{\widehat{\text{var}}\left({\widehat{y}}_R^c\right)}{{\tau }_c^2-{\sigma }_{B^{*}}^2}+\frac{\widehat{\text{var}}\left({\tau }_c^2\right){\left(q-{\mu }_{B^{*}}-{\widehat{y}}_R^c\right)}^2}{4{\left({\tau }_c^2-{\sigma }_{B^{*}}^2\right)}^3}}\cdot \varphi \left(\frac{q-{\mu }_{B^{*}}-{\widehat{y}}_R^c}{\sqrt{{\tau }_c^2-{\sigma }_{B^{*}}^2}}\right),{\tau }_c^2>{\sigma }_{B^{*}}^2.$$

Because $\widehat{p}(q)$ ismonotonic in ${\sigma }_{B^{*}}^2$, the homogeneous bias case (i.e., ${\sigma }_{B^{*}}^2=0$) provides either an upper or lower bound on $\widehat{p}(q)$ (Table 1). We later return to the practical utility of these results.

Table 1.

Bounds on $\widehat{p}\left(q\right)$ provided by homogeneous bias with an apparently causative or preventive pooled effect.

	$q>{\widehat{y}}_R^t$	$q<{\widehat{y}}_R^t$
${\widehat{y}}_R^c>0$	Upper bound	Lower bound
${\widehat{y}}_R^c<0$	Lower bound	Upper bound

NOTE: ${\widehat{y}}_R^t$ estimates μ^t and is equal to ${\widehat{y}}_R^c-{\mu }_{B^{*}}$ for ${\widehat{y}}_R^c>0$ or ${\widehat{y}}_R^c+{\mu }_{B^{*}}$ for ${\widehat{y}}_R^c<0$.

4.2. Bias Factor Required to Reduce Proportion of Scientifically Meaningful Effect Sizes to Below a Threshold

Conversely, we might consider the minimum common bias factor (on the RR scale) capable of reducing to less than r the proportion of studies with true effect exceeding q. We accordingly define T(r, q) = B⁺ : P (M^t > q) = r to be this quantity, with B⁺ taken to be constant across studies. (Note that taking B⁺ to be constant does not necessarily imply that the unmeasured confounders themselves are identical across studies.) Then for an apparently causative RR, a consistent estimator for the minimum common bias capable of reducing to less than r the proportion of studies with effects surpassing q is

$$\widehat{T}(r,q)=\text{ exp}\left\{{\mathrm{\Phi }}^{-1}(1-r)\sqrt{{\tau }_c^2}-q+{\widehat{y}}_R^c\right\}$$

with approximate SE:

$$\widehat{\text{SE}}(\widehat{T}(r,q))=\text{ exp}\left\{\sqrt{{\tau }_c^2}\left({\mathrm{\Phi }}^{-1}(1-r)\right)-q+{\widehat{y}}_R^c\right\}\times \sqrt{\widehat{\text{var}}\left({\widehat{y}}_R^c\right)+\frac{\widehat{\text{var}}\left({\tau }_c^2\right){\left({\mathrm{\Phi }}^{-1}(1-r)\right)}^2}{4{\tau }_c^2}}.$$

For an apparently preventive RR, we can instead consider the minimum common bias factor (on the RR scale) capable of reducing to less than r the proportion of studies with true effect less than q, thus defining T(r, q) = B⁺ : P (M^t > q) = r. Then a consistent estimator is

$$\widehat{T}(r,q)=\text{ exp}\left\{q-{\widehat{y}}_R^c-{\mathrm{\Phi }}^{-1}(r)\sqrt{{\tau }_c^2}\right\}$$

with approximate SE:

$$\widehat{\text{SE}}(\widehat{T}(r,q))=\text{ exp}\left\{q-{\widehat{y}}_R^c-\sqrt{{\tau }_c^2}\left({\mathrm{\Phi }}^{-1}(r)\right)\right\}\times \sqrt{\widehat{\text{var}}\left({\widehat{y}}_R^c\right)+\frac{\widehat{\text{var}}\left({\tau }_c^2\right){\left({\mathrm{\Phi }}^{-1}(r)\right)}^2}{4{\tau }_c^2}}.$$

4.3. Confounding Strength Required to Reduce Proportion of Scientifically Meaningful Effect Sizes to Below a Threshold

Under the assumption that the two components of the common bias factor are equal as in Equation (2), such that g = RR_XU = RR_UY, the bias can alternatively be parameterized on the confounding strength scale. Consider the minimum confounding strength required to lower to less than r the proportion of studies with true effect exceeding q and accordingly define G(r, q) = g: P (M^t > q) = r. For both the apparently causative and the apparently preventive cases, an application of Equation (2) yields

$$\widehat{G}(r,q)=\widehat{T}(r,q)+\sqrt{{(\widehat{T}(r,q))}^2-\widehat{T}(r,q)}$$

with approximate SE:

$$\widehat{\text{SE}}(\widehat{G}(r,q))=\widehat{\text{SE}}(\widehat{T}(r,q))\cdot \left(1+\frac{2\widehat{T}(r,q)-1}{2\sqrt{\widehat{T}{(r,q)}^2-\widehat{T}(r,q)}}\right).$$

5. Practical Use and Interpretation

5.1. Interpreting $\widehat{p}(q)$

To conduct our first proposed sensitivity analysis, one first assumes a simple distribution on the amount of confounding bias in the meta-analyzed studies, leading to the specification of a pair of sensitivity parameters, μ_B* and ${\sigma }_{B^{*}}^2$. Then, one computes $\widehat{p}(q)$ to gauge the strength of evidence for causation if confounding bias indeed follows the specified distribution. As mentioned in Section 1, we consider the proportion of true effects above a chosen threshold of scientific importance because this metric characterizes evidence strength while taking into account the effect heterogeneity that is central to the random-effects meta-analysis framework. That is, a large proportion of true effect sizes stronger than a threshold of scientific importance in a meta-analysis (e.g., 70% of true effects stronger than the threshold RR = 1.10, i.e., q = log 1.10) suggests that, although the true causal effects may be heterogeneous across studies, there is evidence that overall, many of these effects are strong enough to merit scientific interest. If $\widehat{p}(q)$ remains large for even large values of μ_B*, this indicates that even if the influence of unmeasured confounding were substantial, a large proportion of true effects in the population distribution would remain of scientifically meaningful magnitude. Thus, the results of the meta-analysis might be considered relatively robust to unmeasured confounding.

5.2. How to Choose q, μ_B*, and ${\sigma }_{B^{*}}^2$ When Computing $\widehat{p}\left(q\right)$

The threshold q allows the investigator to flexibly define how much attenuation in effect size due to confounding bias would render a causal effect too weak to be considered scientifically meaningful. A general guideline might be to use q = log 1.10 as a minimum threshold for an apparently causative RR or q = log (1/1.10) ≈ log 0.90 for an apparently preventive RR. There is also an extensive interdisciplinary literature on how to choose such thresholds, as summarized elsewhere (Mathur and VanderWeele 2019). Because μ_B* and ${\sigma }_{B^{*}}^2$ are sensitivity parameters that are not estimable from the data, we would recommend reporting $\widehat{p}\left(q\right)$ for a wide range of values of μ_B* (including large values, representing substantial confounding bias) and with ${\sigma }_{B^{*}}^2$ ranging from 0 to somewhat less than ${\tau }_c^2$.

To provide intuition for what values of μ_B* and ${\sigma }_{B^{*}}^2$ might be plausible in a given setting, it can be useful to consider the implied range of bias factors across studies for a given pair of sensitivity parameters. For example, if μ_B* = log 1.20 and ${\sigma }_{B^{*}}^2=0.01$, so that the SD of the bias on the log scale is 0.10, these choices of sensitivity parameters imply that 95% of the studies have B (on the risk ratio scale) between exp(μ_B* − Φ⁻¹ (0.975) σ_B* = 0.98 and exp(μ_B*+ Φ⁻¹ (0.975 × σ_B*) = 1.46. This choice of sensitivity parameters may be reasonable, then, if one is willing to assume that studies very rarely (with approximately 2.5% probability) obtain point estimates that are inflated by more than 1.46-fold due to unmeasured confounding, and furthermore that studies very rarely obtain point estimates that are biased toward, instead of away from, the null (which requires B < 1). If, in contrast, an assessment of study design quality suggests that some studies in the meta-analysis might have more severely biased point estimates than the above bias distribution implies, then one might consider increasing μ_B* or ${\sigma }_{B^{*}}^2$. The choice of ${\sigma }_{B^{*}}^2$ can also be informed by the extent to which the meta-analyzed studies differ with respect to existing confounding control. When some studies have much better confounding control than others, then B* may vary substantially, so a larger ${\sigma }_{B^{*}}^2$ may be reasonable. When all studies adjust for similar sets of confounders and use similar populations, then a small ${\sigma }_{B^{*}}^2$ may be reasonable. In the Web Appendix, we consider the fidelity of assuming homogeneous bias (${\sigma }_{B^{*}}^2$ = 0) when in fact the bias is heterogenous, presenting quantitative summaries of the relative and absolute difference between the two.

Last, bounds achieved when ${\sigma }_{B^{*}}^2=0$ can provide useful conservative analyses. Table 1 shows that setting ${\sigma }_{B^{*}}^2=0$ yields either an upper or lower bound on $\widehat{p}\left(q\right)$, where the latter allows ${\sigma }_{B^{*}}^2>0$. The direction of the bound depends on whether ${\widehat{y}}_R^c$ is apparently causative or preventive and on whether q is chosen to be on the lower or upper tail of the bias-corrected pooled point estimate, defined as ${\widehat{y}}_R^t={\widehat{y}}_R^c-{\mu }_B^{*}$ for the apparently causative case and ${\widehat{y}}_R^t={\widehat{y}}_R^c+{\mu }_B^{*}$ for the apparently preventive case. For example, for ${\widehat{y}}_R^c>0$ and $q>{\widehat{y}}_R^c-{\mu }_B^{*}$, the ${\sigma }_{B^{*}}^2=0$ case provides an upper bound on $\widehat{p}\left(q\right)$. When concluding that results are not robust to unmeasured confounding, the analysis with ${\sigma }_{B^{*}}^2=0$ is therefore conservative in that fewer true effect sizes would surpass q under heterogeneous bias. For example, if we calculated $\widehat{p}\left(q=\text{ log }1.10\right)=0.15$ with μ_B* = log 1.20 and ${\sigma }_{B^{*}}^2=0$, then an analysis like this would yield conclusions such as: “The results of this meta-analysis are relatively sensitive to unmeasured confounding. Even a bias factor as small as 1.20 in each study would reduce to only 15% the proportion of studies with true RRs greater than 1.10, and if the bias in fact varied across studies, then even fewer studies would surpass this effect size threshold.”

5.3. Interpreting $\widehat{T}(r,q)$ and $\widehat{G}(r,q)$

In contrast to $\widehat{p}\left(q\right)$, the metrics $\widehat{T}(r,q)$ and $\widehat{G}(r,q)$ do not require specification of a range of sensitivity parameters regarding the bias distribution. Instead, they solve for the minimum amount of bias that, if constant across all studies, would “explain away” the effect in a manner specified through q (the minimum threshold of scientific importance) and r (the minimum proportion of true effects above q). That is, we might say that unmeasured confounding has, for practical purposes, “explained away” the results of a meta-analysis if fewer than, for example, 10% of the true effects are stronger than a threshold of RR 1.10, in which case we would set r = 0.10 and q log 1.10.

A large value of either $\widehat{T}(r,q)$ or $\widehat{G}(r,q)$ indicates that it would take substantial unmeasured confounding (i.e., a large bias factor as parameterized by $\widehat{T}(r,q)$ or a large strength of confounding as parameterized by $\widehat{G}(r,q)$ to “explain away” the results of the meta-analysis in this sense, and that weaker unmeasured confounding could not do so. Thus, the results may be considered relatively robust to unmeasured confounding. For example, by choosing q = log(1.10) and r = 0.20 and computing $\widehat{T}\left(r,q\right)\text{ = }2.50$ (equivalently, $\widehat{G}\left(r,q\right)=4.44$), one might conclude: “The results of this meta-analysis are relatively robust to unmeasured confounding, insofar as a bias factor of 2.50 on the RR scale (e.g., a confounder associated with the exposure and outcome by risk ratios of 4.44 each) in each study would be capable of reducing to less than 20% the proportion of studies with true RRs greater than 1.10, but weaker confounding could not do so.” On the other hand, small values of $\widehat{T}\left(r,q\right)$ and $\widehat{G}\left(r,q\right)$ indicate that only weak unmeasured confounding would be required to reduce the effects to a scientifically unimportant level; the meta-analysis would therefore not warrant strong scientific conclusions regarding causation.

5.4. How to Choose q and r When Computing $\widehat{T}\left(r,q\right)$ and $\widehat{G}\left(r,q\right)$

When computing $\widehat{T}\left(r,q\right)$ and $\widehat{G}\left(r,q\right)$, one can use the same effect size threshold q as discussed above for computing $\widehat{p}\left(q\right)$. When the number of studies, k, is large (e.g., ≥ 15), one might require at least 10% of studies (r = 0.10) to have effect sizes above q for results to be of scientific interest. For 10 ≤ k ≤ 15, one might select a higher threshold, such as r = 0.20 (thus requiring at least 20% of studies to have effects more extreme than, e.g., log 1.10). Of course, these guidelines can and should be adapted based on the substantive application. Furthermore, note that the amount of bias that would be considered “implausible” must be determined with attention to the design quality of the synthesized studies: a large bias factor may be plausible for a set of studies with poor confounding control and with high potential for unmeasured confounding, but not for a set of better-designed studies in which the measured covariates already provide good control of confounding.

6. Further Remarks on Heterogeneity

We operationalized “robustness to unmeasured confounding” as the proportion of true effects surpassing a threshold, an approach that focuses on the upper tail (for an apparently causative ${\text{RR}}_{XY}^c$) of the distribution of true effect sizes. Potentially, under substantial heterogeneity, a high proportion of true effect sizes could satisfy, for example, ${\text{RR}}_{XY}^t>1.10$ while, simultaneously, a nonnegligible proportion could be comparably strong in the opposite direction $\left({\text{RR}}_{XY}^t<0.90\right)$. Such situations are intrinsic to the meta-analysis of heterogeneous effects, and in such settings, we recommend reporting the proportion of effect sizes below another threshold on the opposite side of the null (e.g., log 1/1.20 ≈ log 0.80) both for the confounded distribution of effect sizes and for the distribution adjusted based on chosen bias parameters. For example, a meta-analysis that is potentially subject to unmeasured confounding and that estimates ${\widehat{y}}_R^c=\text{ log }1.15$ and ${\tau }_c^2=0.10$ would indicate that 45% of the effects ${\text{RR}}_{XY}^c$ surpass 1.20, while 13% are less than 0.80. For a common B* = log 1.10 (equivalently, g = 1.43 if considering worst-case bias), we find that $\left(1-\mathrm{\Phi }\left(\frac{\text{log }1.20-\text{ log }1.15+\text{ log }1.10}{\sqrt{0.10}}\right)\right)$ of the true effects surpass ${\text{RR}}_{XY}^c=1.20$, while 20% are less than ${\text{RR}}_{XY}^c=0.80$. More generally, random-effects meta-analyses could report the estimated proportion of effects above the null or above a specific threshold (along with a confidence interval for this proportion) as a continuous summary measure to supplement the standard pooled estimate and inference (Mathur and VanderWeele 2019). Together, these reporting practices could facilitate overall assessment of evidence strength and robustness to unmeasured confounding under effect heterogeneity.

7. Sensitivity Analysis for the Point Estimate

As discussed above, the proportion of effects stronger than a threshold can be a useful measure of evidence strength across heterogeneous effects in addition to pooled point estimate alone, and hence our sensitivity analysis techniques have emphasized the former. However, it is also possible to conduct sensitivity analysis on the pooled point estimate itself to assess the extent to which unmeasured confounding could compromise estimation of μ^t. The following development proceeds analogously to that of Section 4.

7.1. An Adjusted Point Estimate as a Function of the Bias Factor

For an apparently causative RR and a specified μ_B*, an unbiased estimate of the true mean, μ^t, is simply ${\widehat{y}}_R^t={\widehat{y}}_R^c-{\mu }_{B^{*}}$. For an apparently preventive RR, it is ${\widehat{y}}_R^t={\widehat{y}}_R^c+{\mu }_{B^{*}}$. Because these expressions consider the average true effect only, they do not involve bias correction of ${\tau }_c^2$, so are independent of ${\sigma }_{B^{*}}^2$. Since μ_B* is treated as fixed, we have $\text{var}\left({\widehat{y}}_R^t\right)=\text{ var}\left({\widehat{y}}_R^c\right)$, so inference on ${\widehat{y}}_R^t$ can use without modification the SE estimate for ${\widehat{y}}_R^c$ computed through standard meta-analysis of the confounded data. For example, Hartung and Knapp’s’s (2001) estimation approach yields

$$\widehat{\text{SE}}\left({\widehat{y}}_R^t\right)=\sqrt{\frac{{\sum }_{i=1}^k\frac{1}{{\tau }_c^2+{\sigma }_i^2}{\left(y_i^c-{\widehat{y}}_R^c\right)}^2}{(k-1){\sum }_{i=1}^k\frac{1}{{\tau }_c^2+{\sigma }_i^2}}},$$

where $y_i^c$ is the confounded log-RR estimate in the ith study.

7.2. Bias Factor and Confounding Strength Required to Shift the Point Estimate to the Null

One could instead consider the value of μ_B* that would be required to “explain away” the point estimate. That is, to completely shift the point estimate to the null (i.e., μ^t = 0, implying an average risk ratio of 1) would require ${\mu }_{B^{*}}={\widehat{y}}_R^c$. As in Section 4.3, the bias factor can be converted to the more intuitive confounding strength scale via Equation (2). Thus, the minimum confounding strength to completely shift the point estimate to the null is, for the apparently causative case:

$$\text{exp}\left({\widehat{y}}_R^c\right)+\sqrt{\text{exp}\left({\widehat{y}}_R^c\right)\left[\text{exp}\left({\widehat{y}}_R^c\right)-1\right]}.$$ (5)

Additionally, one can consider the confounding strength required to shift the confidence interval for ${\widehat{y}}_R^c$ to include the null; to do so, ${\widehat{y}}_R^c$ in the above expression would simply be replaced with the confidence bound closer to the null. (For the apparently preventive case, whether considering the point estimate or the confidence interval bound, each exponentiated term in Equation (5) would be replaced by its inverse.) As above, these measures do not describe heterogeneity. Thus, Equation (5) is in fact equivalent to VanderWeele and Ding (2017)’s E-value (as discussed in Section 2) applied directly to ${\widehat{y}}_R^c$, as illustrated in the next section.

8. Software and Applied Example

The proposed methods (as well as those discussed in Section 7) are implemented in an R package, EValue, which produces point estimates and inference for sensitivity analyses, tables across a user-specified grid of sensitivity parameters, and various plots. Descriptions of each function with working examples are provided in the Web Appendix and standard R documentation. A website implementing the main functions is freely available (https://mmathur.shinyapps.io/meta_gui_2/).

We illustrate the package’s basic capabilities using an existing meta-analysis assessing, among several outcomes, the association of high versus low daily intake of soy protein with breast cancer risk among women (Trock, Hilakivi-Clarke, and Clarke 2006). The analysis comprised 20 observational studies that varied in their degree of adjustment for suspected confounders, such as age, body mass index (BMI), and other risk factors. To obtain ${\tau }_c^2$ and $\widehat{\text{var}}\left({\tau }_c^2\right)$ (which were not reported), we obtained study-level summary measures as reported in a table from Trock, Hilakivi-Clarke, and Clarke (2006), treading odds ratios as approximate risk ratios given the rare outcome. This process is automated in the function EValue::scrape_meta. We estimated ${\widehat{y}}_R^c=\text{ log }0.82$, $\widehat{\text{SE}}\left({\widehat{y}}_R^c\right)=8.8\times {10}^{-2}$ via the Hartung and Knapp’s (2001) adjustment (whose advantages were demonstrated by IntHout, Ioannidis, and Borm (2014)), ${\tau }_c^2=0.10$ via the Paule and Mandel (1982) method, and $\widehat{\text{SE}}\left({\tau }_c^2\right)=5.0\times {10}^{-2}$.

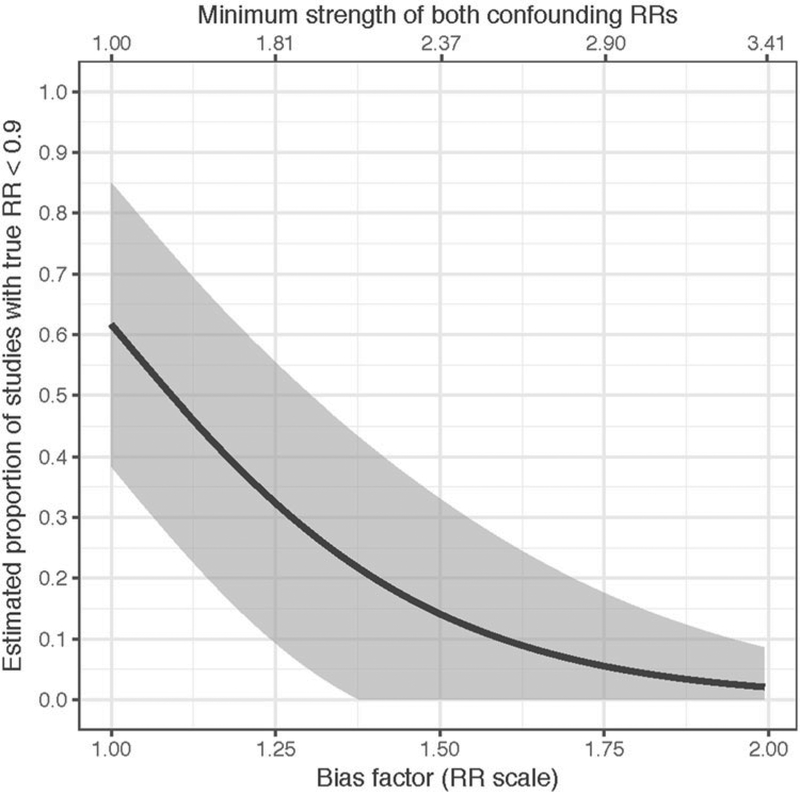
Figure 1 (produced by EValue::sens_plot) displays the estimated proportion of studies with true RRs < 0.90 as a function of either the bias factor or the confounding strength, holding constant ${\sigma }_{B^{*}}^2=0.01$. Table 2 (produced by EValue::sens_table) displays $\widehat{T}\left(r,q\right)$ and $\widehat{G}\left(r,q\right)$ across a grid of values for r and q. For example, only a bias factor exceeding 1.63 on the RR scale (equivalently, confounding association strengths of 2.64) could reduce to less than 10% the proportion of studies with true RRs < 0.90. However, variable bias across studies would reduce this proportion (see Table 1), and the confidence interval is wide.

Figure 1.

Impact of varying degrees of unmeasured confounding bias on proportion of true RRs < 0.90

Table 2.

$\widehat{T}\left(r,q\right)$ and $\widehat{G}\left(r,q\right)$ (in parentheses) for varying r and q.

r	q
	0.70	0.80	0.90
0.1	1.27 (1.85)	1.45 (2.25)	1.63 (2.64)
0.2	1.10 (1.44)	1.26 (1.84)	1.42 (2.19)
0.3		1.14 (1.55)	1.29 (1.89)
0.4		1.05 (1.28)	1.18 (1.64)
0.5			1.09 (1.41)

NOTE: Blank cells indicate combinations for which no bias would be required.

We now briefly illustrate the sensitivity analysis techniques for ${\widehat{y}}_R^c$ described in Section 7. For example, applying Equation (5) indicates that an unmeasured confounder associated with both soy intake and breast cancer by risk ratios of at least 1.72 could be sufficient to shift the point estimate $\left({\text{RR}}_{XY}^c=0.82\right)$ to 1, but weaker confounding could not do so (VanderWeele and Ding 2017). To reiterate the remarks made in Section 6 regarding heterogeneity, note that our proposed sensitivity analyses found $\widehat{G}(r=0.10,q=\text{ log }0.90)=2.64$. This is considerably larger than the E-value of 1.72 for the point estimate, demonstrating that even in the presence of unmeasured confounding strong enough to shift the point estimate to the null, more than 10% of the true RRs would nevertheless remain stronger than 0.90.

Other methods developed for a single study could similarly be applied to the meta-analytic point estimate, but they require specification of many more sensitivity parameters or make more assumptions about the underlying unmeasured confounder (e.g., Schlesselman’s 1978; Imbens 2003; Lin, Psaty, and Kronmal 1998; VanderWeele and Arah 2011). To apply these methods directly, we use a simplified form assuming that U is binary, that the prevalences P (U = 1 | X = 1, Z) = 0.65 and P (U = 1 | X = 0, Z) = 0.35 are in fact known, and that the relationship between U and Y is identical for X = 1 and X = 0. Under this more restrictive specification on unmeasured confounding, an application of Schlesselman’s (1978) method (or an application of a special case of Theorem 2 by VanderWeele and Arah (2011)) finds that such a confounder would exactly shift the point estimate to the null if were associated with both soy intake and breast cancer by risk ratios of 1.94.

9. Simulation Study

We assessed finite-sample performance of inference on $\widehat{p}\left(q\right)$ in a simple simulation study. While fixing the mean and variance of the true effects to μ^t = log 1.4 and V^t = 0.15 and the bias parameters to μ_B* = log 1.6 and ${\sigma }_{B^{*}}^2=0.01$, we varied the number of studies (k ∈ {15, 25, 50, 200}) and the average sample size N within each study (E[N] ∈ {300, 500, 1000}). The fixed parameters were chosen to minimize artifacts from discarding pathological samples with ${\tau }_c^2<{\sigma }_{B^{*}}^2$ or with truncated outcome probabilities due to extreme values of ${\text{RR}}_{XY}^c$; theoretically, $\widehat{p}\left(q\right)$ is unbiased regardless of these parameters. We set the threshold for a scientifically meaningful effect size at q = log 1.4 to match μ^t, such that, theoretically, 50% of true effects exceed q. We ran 1000 simulations for each possible combination of k and E[N], primarily assessing coverage of nominal 95% confidence intervals and secondarily assessing their precision (total width) and bias in $\widehat{p}(q=\text{ log }1.4)$ versus the theoretically expected 50%. Additionally, we assessed agreement between $\widehat{p}\left(q\right)$ and results obtained from an unconfounded meta-analysis (one in which all meta-analyzed studies adjust fully for confounding through stratification).

For each study, we drew N ~ Unif (150, 2E[N] − 150), using 150 as a minimum minimum sample size to prevent model convergence failures, and drew the study’s true effect size as M^t ~ N(μ^t, V^t). We simulated data for each subject under a model with a binary exposure (X ~ Bern(0.5)), a single binary unmeasured confounder, and a binary outcome. We set the two bias components equal to one another (g = RR_XU = RR_UY) and fixed P(U = 1|X = 1) = 1, allowing closed-form computation of

$$P(U=1|X=0)=\frac{\text{exp}\left(M^t\right)[1+(g-1)]-\text{ exp}\left(M^c\right)}{(g-1)\text{ exp}\left(M^c\right)}$$

as in Ding and VanderWeele (2016). Within each stratum X = x, we simulated U ~ Bern(P(U = 1|X = x)). We simulated outcomes as Y ~ Bern(exp{log 0.05 + log(g)U + M^tX}). Finally, we computed effect sizes and fit the random-effects model using the metafor package in R (Viechtbauer 2010), estimating ${\tau }_c^2$ per Paule and Mandel (1982) and $\widehat{\text{var}}\left({\widehat{y}}_R^c\right)$ with the Hartung and Knapp’s (2001) adjustment.

To compare results of our estimators to estimates from unconfounded meta-analyses, we also computed unconfounded effect sizes for each study using the Mantel–Haenszel risk ratio stratifying on U (Rothman, Greenland, and Lash 2008). (This approach is used only for theoretical comparison, since in practice we are concerned with confounders that are unmeasured and therefore cannot be incorporated in analysis.) We then meta-analyzed these unconfounded point estimates and estimated, with no adjustment for bias, the proportion of effects in the population stronger than q.

Results (Table 3) indicated approximately nominal performance for all combinations of k and E[N], with precision appearing to depend more strongly on k than E[N]. As expected theoretically, $\widehat{p}\left(q\right)$ was approximately unbiased. Compared to theoretical expectation, the proposed estimators appeared to perform slightly better than meta-analyses of unconfounded point estimates obtained through stratification on U. The latter method may have been compromised under strong confounding, which often induced zero cells in confounder-stratified analyses due to near collinearity of U with X and Y.

Table 3.

For varying numbers of studies (k) and mean sample sizes within each study (mean N), displays the estimated proportion $\left(\widehat{p}\left(q\right)\right)$ of true effects above RR = 1.4 with its bias versus theoretically expected 50% ($\widehat{p}\left(q\right)$ bias), coverage of 95% confidence intervals for $\widehat{p}\left(q\right)$ (CI coverage), and mean width of 95% confidence intervals (CI width).

k	Mean N	$\widehat{p}\left(q\right)$	$\widehat{p}\left(q\right)$ bias	CI coverage	CI width	${\widehat{p}}_{\text{MH}}$
15	300	0.530	0.030	0.970	0.575	0.585
25	300	0.533	0.033	0.965	0.459	0.582
50	300	0.527	0.027	0.975	0.316	0.572
200	300	0.528	0.028	0.917	0.154	0.568
15	500	0.523	0.023	0.981	0.522	0.558
25	500	0.527	0.027	0.982	0.409	0.561
50	500	0.522	0.022	0.973	0.283	0.554
200	500	0.523	0.023	0.945	0.140	0.553
15	1000	0.518	0.018	0.976	0.475	0.540
25	1000	0.516	0.016	0.983	0.370	0.537
50	1000	0.521	0.021	0.983	0.259	0.541
200	1000	0.515	0.015	0.971	0.129	0.536

NOTE: ${\widehat{p}}_{\text{MH}}$ is the estimated proportion of effects above RR = 1.4 in unconfounded analyses stratifying on U.

10. Discussion

This article develops sensitivity analyses for unmeasured confounding in a random-effects meta-analysis of an RR outcome measure. Specifically, we have presented estimators for the proportion, $\widehat{p}\left(q\right)$, of studies with true effect sizes surpassing a threshold and for the minimum bias, $\widehat{T}\left(r,q\right)$, or confounding association strength, $\widehat{G}\left(r,q\right)$, in all studies that would be required to reduce to below a threshold the proportion of studies with effect sizes less than q. Such analyses quantify the amount of confounding bias in terms of intuitively tractable sensitivity parameters. Computation of $\widehat{p}\left(q\right)$ uses two sensitivity parameters, namely the mean and variance across studies of a joint bias factor on the log-RR scale. Estimators $\widehat{T}\left(r,q\right)$ and $\widehat{G}\left(r,q\right)$ make reference to, and provide conclusions for, single sensitivity parameter, chosen as either the common joint bias factor across studies or the strength of confounding associations on the RR scale. These methods assume that the bias factor is normally distributed or fixed across studies, but do not make further assumptions regarding the nature of unmeasured confounding.

Assessing sensitivity to unmeasured confounding is particularly important in meta-analyses of observational studies, where a central goal is to assess the current quality of evidence and to inform future research directions. If a well-designed meta-analysis yields a low value of $\widehat{T}\left(r,q\right)$ or $\widehat{G}\left(r,q\right)$ and thus is relatively sensitive to unmeasured confounding, this indicates that future research on the topic should prioritize randomized trials or designs and data collection that reduce unmeasured confounding. On the other hand, individual studies measuring moderate effect sizes with relatively wide confidence intervals may not, when considered individually, appear highly robust to unmeasured confounding; however, a meta-analysis aggregating their results may nevertheless suggest that a substantial proportion of the true effects are above a threshold of scientific importance even in the presence of some unmeasured confounding. Thus, conclusions of the meta-analysis may in fact be robust to moderate degrees of unmeasured confounding.

We focused on RR outcomes because of their frequency in biomedical meta-analyses and their mathematical tractability, which allows closed-form solutions with the introduction of only one assumption (on the distribution of the bias factor). To allow application of the present methods, an odds ratio outcome can be approximated as an RR if the outcome is rare. If the outcome is not rare, the odds ratio can be approximately converted to an RR by taking its square root; provided that the outcome probabilities are between 0.2 and 0.8, this transformation is always within 25% of the true RR (VanderWeele 2017). Comparable sensitivity analyses for other types of outcomes, such as mean differences for continuous outcome variables, would require study-level summary measures (e.g., of within-group means and variances) and in some cases would yield closed-form solutions only at the price of more stringent assumptions. Under the assumption of an underlying binary outcome with high prevalence, such measures could be converted to log-odds ratios (Hasselblad and Hedges 1995) and then to RRs (Vander-Weele 2017) as described above (see VanderWeele and Ding 2017). It is important to note that, in circumstances discussed elsewhere (Tang 2000; Thorlund et al. 2011), RR outcomes can produce biased meta-analytic estimates. When such biases in pooled point estimates or heterogeneity estimators are likely, sensitivity analyses will also be biased.

For existing meta-analyses that report estimates of the pooled effect, the heterogeneity, and their SEs or confidence intervals, one could conduct the proposed sensitivity analyses using only these four summary measures (i.e., simply using existing summary statistics and without reanalyzing study-level point estimates). However, in practice, we find that reporting of ${\tau }_c^2$ and $\widehat{\text{var}}\left({\tau }_c^2\right)$ is sporadic in the biomedical literature. Besides their utility for conducting sensitivity analyses, we consider ${\tau }_c^2$ and $\widehat{\text{var}}\left({\tau }_c^2\right)$ to be inherently valuable to the scientific interpretation of heterogeneous effects. We therefore recommend that they be reported routinely for random-effects meta-analyses, even when related measures, such as the proportion of total variance attributable to effect heterogeneity (I²), are also reported. To enable sensitivity analyses of existing meta-analyses that do not report the needed summary measures, the R packages EValue and MetaUtility helps automate the process of obtaining and drawing inferences from study-level data from a published forest plot or table. The user can then simply fit a random-effects model of choice to obtain the required summary measures.

Our framework assumes that the bias factor is normally distributed or taken to be fixed across studies. Normality is approximately justified if, for example, log RR_XU and log RR_UY are approximately identically and independently normal with relatively small variance. Since RR_UY is in fact a maximum over strata of X and the range of U, future work could potentially consider an extreme-value distribution for this component, but such a specification would appear to require a computational, rather than closed-form, approach. Perhaps a more useful, conservative approach to assessing sensitivity to bias that may be highly skewed is to report $\widehat{T}\left(r,q\right)$ and $\widehat{G}\left(r,q\right)$ for a wide range of fixed values B*, including those much larger than a plausible mean.

An alternative sensitivity analysis approach would be to directly apply existing analytic bounds (Ding and VanderWeele 2016) to each individual study to compute the proportion of studies with effect sizes more extreme than q given a particular bias factor. This has the downside of requiring access to study-level summary measures (rather than pooled estimates). Moreover, the confidence interval of each study may be relatively wide, such that no individual study appears robust to unmeasured confounding, while nevertheless a meta-analytic estimate that takes into account the distribution of effects may in fact indicate that some of these effects are likely robust. As described in Section 7, one could also alternatively conduct sensitivity analyses on the pooled point estimate itself, but such an approach is naïve to heterogeneity: when the true effects are highly variable, a nonnegligible proportion of large true effects may remain even with the introduction of enough bias to attenuate the pooled estimate to a scientifically unimportant level (Mathur and VanderWeele 2019).

In summary, our results have shown that sensitivity analyses for unmeasured confounding in meta-analyses can be conducted easily by extending results for individual studies. These methods are straightforward to implement through either our R package EValue or website and ultimately help inform principled causal conclusions from meta-analyses.