Hidden dynamic signatures drive substrate selectivity in the disordered phosphoproteome

Significance

The discovery that more than 40% of the eukaryotic proteome is intrinsically disordered, and that these disordered segments are enriched in phosphorylation sites, suggests that conformational heterogeneity may be important to kinase selectivity. Indeed, phosphorylation prediction programs reliant on classic notions of conserved sequence information (i.e., “vertical information”) are only partially effective. We find that the conformational equilibrium of the phosphorylatable site, whose information is embedded in sequence-averaged energetic and structural properties of the protein (i.e., “horizontal information”), plays a major role in distinguishing phosphorylatable versus nonphosphorylatable sites. In fact, employing both horizontal and vertical information produces a state-of-the-art phosphorylation predictor, wherein the conformational equilibrium of the disordered chain is the dominant contributor.

Abstract

Phosphorylation sites are hyperabundant in the eukaryotic disordered proteome, suggesting that conformational fluctuations play a major role in determining to what extent a kinase interacts with a particular substrate. In biophysical terms, substrate selectivity may be determined not just by the structural–chemical complementarity between the kinase and its protein substrates but also by the free energy difference between the conformational ensembles that are, or are not, recognized by the kinase. To test this hypothesis, we developed a statistical-thermodynamics-based informatics framework, which allows us to probe for the contribution of equilibrium fluctuations to phosphorylation, as evaluated by the ability to predict Ser/Thr/Tyr phosphorylation sites in the disordered proteome. Essential to this framework is a decomposition of substrate sequence information into two types: vertical information encoding conserved kinase specificity motifs and horizontal information encoding substrate conformational equilibrium that is embedded, but often not apparent, within position-specific conservation patterns. We find not only that conformational fluctuations play a major role but also that they are the dominant contribution to substrate selectivity. In fact, the main substrate classifier distinguishing selectivity is the magnitude of change in local compaction of the disordered chain upon phosphorylation of these mostly singly phosphorylated sites. In addition to providing fundamental insights into the consequences of phosphorylation across the proteome, our approach provides a statistical-thermodynamic strategy for partitioning any sequence-based search into contributions from structural–chemical complementarity and those from changes in conformational equilibrium.

Phosphorylation is the most common posttranslational modification in eukaryotic proteomes (1, 2) and has been demonstrated to mediate key biological functions, including signaling (3), nutrient sensing (4), and protein conformational change (5). Despite the universal recognition of its importance, a significant gap in our knowledge has prevented a general mechanistic understanding of how phosphorylation mediates these processes. Specifically, many phosphorylation sites are contained within intrinsically disordered regions (IDRs) of proteins, which, due to their high sequence divergence, make it a challenge to identify phosphorylatable sites based on sequence comparisons with known sites. This knowledge gap is exacerbated by the fact that phosphorylation is both transient and reversible, producing a surprisingly low degree of consensus (6) between experimentally determined phosphorylation sites in several major databases: PhosphoELM (7), UniProt (8), and PhosphoSitePlus (9), resulting, understandably, in a concomitant degree of disagreement between phosphorylation site predictors (10–16) developed from these databases (6, 17).

Attempts to address this knowledge gap have typically involved the development of heuristics to augment the limited amount of experimentally annotated sequence sites. For example, the myriad substrates of cyclin-dependent protein kinases only appear to share a single Pro residue immediately C-terminal to the phosphorylated site (18). However, it was recognized early on that certain hydrophobic, acidic, or basic amino acid patterns were often found in the sequence neighborhood of a phosphorylation site (1, 10, 11). As a result, position-specific weight matrices were developed to identify motifs predictive of kinase-specific sites, achieving a moderate degree of success when leveraged with neural network algorithms (6, 19). However, the consensus pattern approach produced significant variability, limiting its utility as a prediction tool (6, 19).

Seminal work by Dunker and coworkers (11) revealed that phosphorylation correlates with surrounding intrinsic disorder, and explicit consideration of disorder resulted in an improved phosphorylation site predictor. Similarly, such a conformational energetic contribution was demonstrated by Elam et al. (20) to also involve conserved polyproline II (PII) propensity of the sequence elements surrounding the phosphorylation site. Both of these observations are suggestive of a distinct role for the conformational equilibrium of the potential substrate, not only in determining the overall function of the phosphorylated protein but also possibly in determining kinase specificity.

To test this hypothesis, we have developed a statistical thermodynamic framework that considers contributions to kinase selectivity driven either by direct recognition of sequence elements that are conserved at a particular sequence position (which we term “vertical information”) or by ensemble-averaged properties that are conserved along a sequence stretch (which we term “horizontal information”). Accounting explicitly for both types of information, “vertical” and “horizontal,” results in a predictor that exceeds performance relative to existing phosphorylation prediction methods. Indeed, our results show that the ensemble-averaged properties—equilibrium fluctuations that are encoded in horizontal information—dominate the contribution.

Furthermore, our results indicate that when averaged over the database the sequence neighborhoods of many Ser and Thr phosphorylation sites, specifically those containing Pro immediately C-terminal to the phosphorylated site (i.e., the +1 Pro sequence motif), are “energetically poised” near a conformational transition point, potentiating a phosphorylation-induced change in the dimensions of the disordered ensemble. This suggests a direct link between the conformational dimensions of the disordered substrate and its ability to be recognized and phosphorylated.

Results

Phosphorylation Equilibria Can Be Reflected by Two Types of Sequence Information.

Enrichment of disorder around phosphorylation sites has been noted previously (11), suggesting the possibility for widespread coupled folding–binding of the disordered substrate in order to become phosphorylated (Fig. 1, Top). If this is the case, it would be desirable to develop a strategy that accounts for the free energy change associated with narrowing or expanding the conformational ensemble (Fig. 1, blue box). This would involve selecting, from among the entire conformational ensemble, the subensemble wherein the residues that are recognized by the kinase are in the proper orientation for kinase recognition. For that subensemble, recognition and binding would then be based on classic notions of shape and chemical complementarity (Fig. 1, red box). Thus, the recognition of conformationally heterogeneous substrates by kinases can be viewed as being due to two distinct physical processes: a contribution arising from the energy difference between the substrate subensemble that can be phosphorylated and the subensemble that cannot and a contribution from the intrinsic ability of the kinase to recognize the substrate, a scenario that is captured by the equilibrium

$$S_{BI}\underset{K_{conf}}{\iff }{S}_{BC}+E\underset{K_{int}}{\iff }E{S}_{BC}.$$ [1]

In Expression 1, E is the kinase, S is the unphosphorylated substrate, and the subscripts BI and BC denote binding-incompetent and binding-competent conformations of the substrate. These equilibria are schematically depicted in Fig. 1. Importantly, the binding-competent and binding-incompetent thermodynamic states are agnostic as to the degree of structure present, only that a free energy barrier exists between the subensemble that can bind and be phosphorylated and the subensemble that cannot.

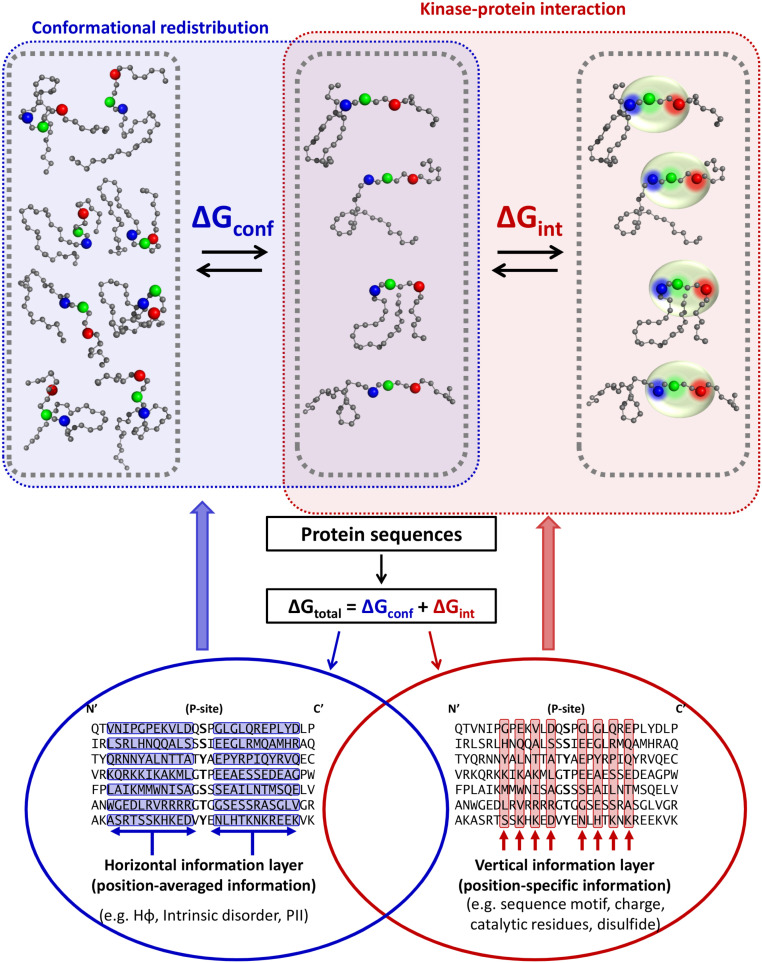
Fig. 1.

Horizontal and vertical protein sequence information reflected in the conformational and binding equilibria of kinase–substrate interaction. Cartoon of coupled equilibria (upper half) demonstrates a decrease of diversity in the substrate’s conformational ensemble mediated by horizontal information (blue box) necessary to position functional residues, mediated by vertical information (red box). Horizontal and vertical information are simultaneously encoded (lower half) in an amino acid sequence alignment. Black letters represent aligned sequences, with blue rows representing neighboring groups of amino acids exhibiting emergent biophysical properties and red columns representing conserved amino acids typically used for alignment and binding site identification. The central hypothesis of this work is that biological phosphorylation, and effective phosphorylation site prediction, critically depends on both types of information.

Expression 1 implies two free-energy contributions to protein phosphorylation: one from the organization of the intrinsically disordered substrate ensemble (i.e., ΔG_conf) and one from binding of the organized substrate to the kinase active site (i.e., ΔG_int). We hypothesize that these two contributions can be usefully separated and accessed in terms of quantifiable bioinformatics information (Fig. 1, red and blue circles).

In this scenario, both the substrate conformational ensemble and conserved recognition motif would encode the kinase specificity information, but the presence of two coupled equilibria might suggest two separate sources for this information. We define the ensemble-based information as “horizontal,” meaning regionally distributed across a sequence fragment (Fig. 1, blue circle), while the conserved motif is “vertical,” meaning that the residue positions are largely independent (Fig. 1, red circle). Importantly, the nature of these two types of information would suggest that horizontal information can be conserved even in the absence of significant vertical conservation.

Horizontal Sequence Information Encodes Conserved Conformational Equilibrium.

Our approach to accessing the residue-specific contributions to ΔG_conf encoded in the horizontal information is predicated on previous results from our group showing that proteins can be represented as sequences of thermodynamic environments (21–23) that capture the experimental conformational fluctuations (24) in both ordered (25) and disordered (26) ensembles. We also showed that the propensities of amino acids in these thermodynamic environments provide sufficient information to match unknown sequences to their environmental profiles (23) and that these profiles are conserved (25, 27, 28) (SI Appendix, Fig. S10). The importance of these earlier findings is that they directly demonstrate that hidden information about the stability of a chain (reported at each position) is nonetheless embedded within the sequence and can be accessed by comparing this horizontal information for diverse sequences, as schematically depicted in Fig. 1, Left.

Indeed, conservation of horizontal information may be even stronger than sequence conservation for some biological contexts, further motivating the combination of horizontal and vertical information. For example (Fig. 2A), conservation of the position-specific stability (29) among the members of the intrinsically disordered N-terminal domain of the glucocorticoid receptor family is high, while the amino acid conservation within the same domain is low (30). That such behavior seems to be a general feature of protein families (Fig. 2B) suggests that horizontal information is conserved to some degree even in the absence of amino acid conservation.

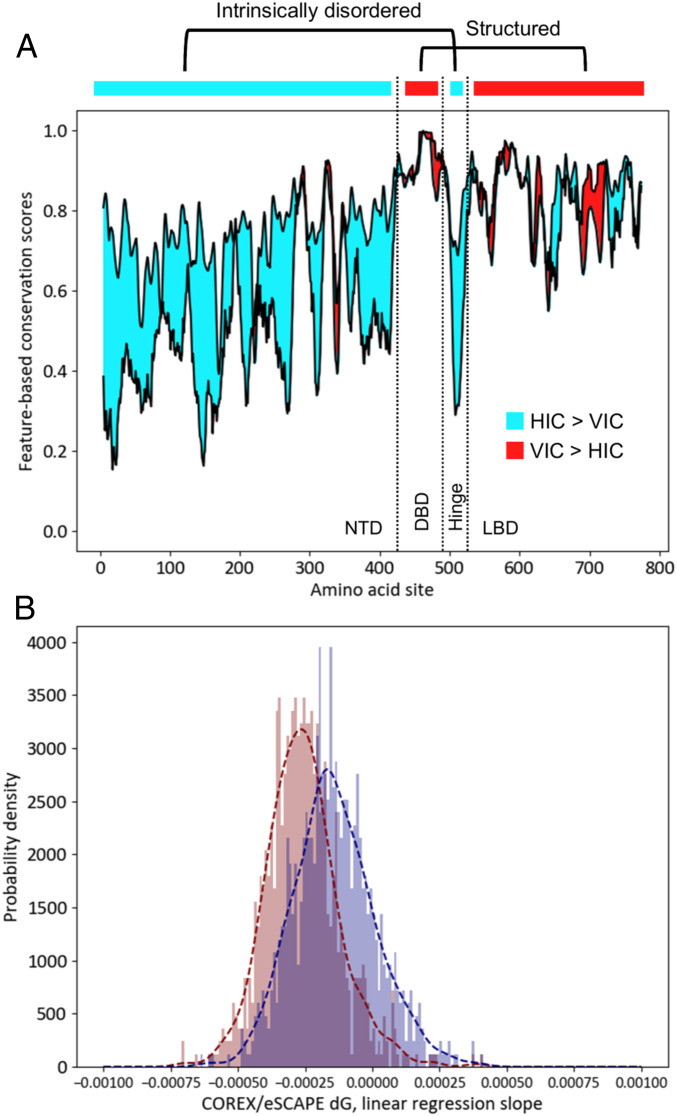
Fig. 2.

Horizontal information is more strongly conserved than vertical information in IDRs of protein families. (A) Difference between degrees of conservation of sequence and native-state free energy (ΔG, ref. 29) calculated for human glucocorticoid receptor (GR) and its orthologs (30). Cyan denotes regions where free energy conservation (HIC, horizontal information conservation) is stronger than sequence conservation (VIC, vertical information conservation), and red denotes the opposite. In human GR, the DNA binding domain (DBD) and the ligand binding domain (LBD) are structured, while the N-terminal domain (NTD) and hinge region are intrinsically disordered. Preponderance of cyan area demonstrates that horizontal information can be conserved when vertical information is not. (B) Coefficient of correlations between free energy and conservation score is calculated for ortholog alignments of 835 different transcription factors (30). Distribution of slope coefficients over many families show that sequence conservation (red) is more strongly correlated with calculated free energy, a property seen in A for a single family.

Vertical Sequence Information from Eukaryotic Phosphorylation Sites Is Distinguished Primarily by the Presence of +1 Pro.

The classic approach to identifying phosphorylatable substrates has been to use independent position-conserved information (i.e., vertical information). To characterize the vertical information component, we investigated amino acid sequence fragments of 29 residues centered on known Ser, Thr, and Tyr eukaryotic phosphorylation sites (Fig. 3A). Importantly, these sites are largely single phosphorylation sites within the window of the fragment. Immediately apparent from statistics of the human phosphoproteome is the abundance of Pro residues directly C-terminal to the annotated Ser or Thr phosphorylation site (Fig. 3 A and B). Using the presence or absence of +1 Pro to separate phosphorylated and nonphosphorylated sequences into four subclasses reveals substantial differences in amino acid conservation patterns.

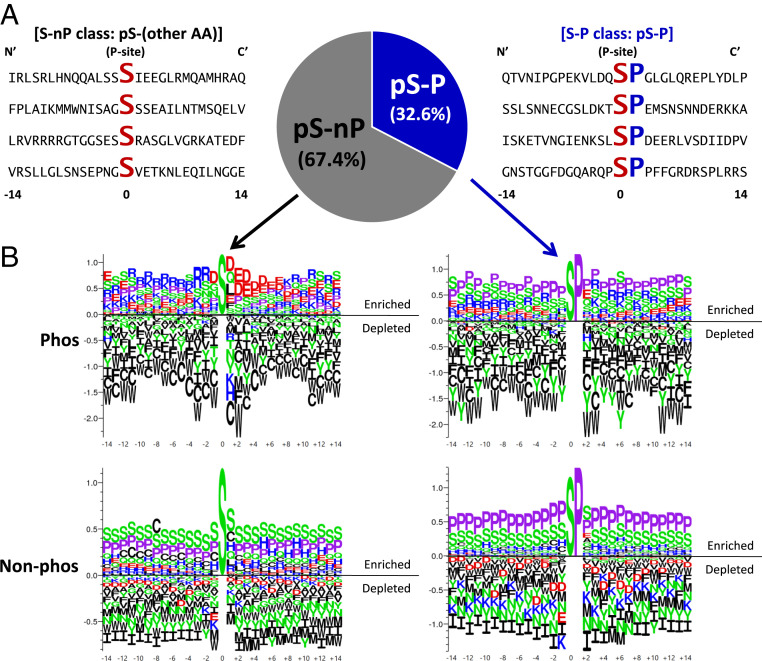
Fig. 3.

Proline residue at the +1 site (+1 Pro) of Ser phosphorylation sites defines a subclass of site (S-P) dependent on horizontal information. (A) Example 29-mer sequence neighborhoods centered on the phosphorylated Ser residue. Conserved Ser (S) and +1 Pro residues (P) are enlarged and bold. Frequencies of +1 Pro phosphorylation sites (S/T-P) make up one-third of all known human phosphorylated Ser. (B) Amino acid frequencies around S-P and S-nP demonstrate that S-P sites have little distinguishing sequence features as compared to nonphosphorylated sites with S-P dipeptide. (Top) Logos show enrichment/depletion patterns of amino acids around phosphorylated Ser sites. (Bottom) Logos show patterns around nonphosphorylated Ser sites. (Left) Logos show patterns where the Ser is immediately followed by amino acids other than Pro. (Right) Logos show patterns where the Ser is immediately followed by Pro (i.e., +1 Pro). Vertical scale indicates information content in bits. In all panels, aliphatic/nonpolar residues are colored black, prolines are lavender, polar residues are green, negatively charged side chains are red, and positively charged side chains are blue.

Focusing on Ser sites as examples, all subclasses are generally depleted in hydrophobic and aliphatic residues (Fig. 3B). All subclasses except for Ser/Thr phosphorylation sites without +1 Pro (S/T-nP) are enriched with Ser and Pro, implying enrichment of intrinsic disorder (SI Appendix, Fig. S1). In contrast, phosphorylated S/T-nP sites exhibit enrichment of positively charged amino acids Arg and Lys at positions N-terminal to the phosphorylation site and enrichment of negatively charged amino acids Asp and Glu at positions C-terminal to the site (Fig. 3 B, Top Left), distinguishing the sequence neighborhoods of phosphorylated and nonphosphorylated sites. Sites with +1 Pro (S/T-P) are more difficult to distinguish based on sequence conservation alone, although the phosphorylated sites appear to tolerate a certain amount of Glu (Fig. 3 B, Top Right) while the nonphosphorylated sites are depleted in all negatively charged side chains (Fig. 3 B, Bottom Right).

Surprisingly, when the presence of the +1 Pro is ignored, the sequence neighborhoods of Ser phosphorylation sites with +1 Pro (S-P) (Fig. 3 B, Top Right) are similar to those of nonphosphorylated S/T-nP sites (Fig. 3 B, Bottom Left), with both subclasses enriched in Pro, Ser, and Glu. This indicates that there is little conserved sequence information to locally distinguish a phosphorylated site from a nonphosphorylated one. Indeed, inspection of the logos suggests that Ser phosphorylation sites, for example, are especially depleted in aromatic amino acids (Fig. 3 B, Top) relative to nonphosphorylated sites (Fig. 3 B, Bottom). Simple positional conservation would report the absence of aromatics at all sites, but experimental results demonstrate that even single aromatic substitutions in an otherwise identical background could have large effects on denatured state properties (31).

Many classic examples of vertical information used in phosphorylation site prediction have been previously reported (10, 13, 14, 16), but we focus here on the special case of Ser and Thr sites with +1 Pro (noting Tyr shows no +1 sites) and demonstrate that this sequence motif, although not diagnostic by itself, is particularly useful in site prediction. Testing several residue types and locations in the neighborhood of known, mostly single, phosphorylation sites, the presence of +1 Pro is the single most informative position in differentiating subgroups from the complete dataset (SI Appendix, Fig. S2B). Thus, we can partition sites into five subclasses based on the presence or absence of the +1 Pro at Ser and Thr phosphorylatable sites: Ser phosphorylation sites with +1 Pro (S-P), Thr phosphorylation sites with +1 Pro (T-P), Ser phosphorylation sites without +1 Pro (S-nP), Thr phosphorylation sites without +1 Pro (T-nP), and Tyr phosphorylation sites (Y) (SI Appendix, Fig. S2 C and D). This grouping is supported by the observation that position-specific weight matrices constructed from these subclasses are more similar between S-P and T-P than between either S-nP and S-P or T-nP and T-P (SI Appendix, Fig. S2C). For consistency with previously published work from other researchers, we also considered the simpler three subclass grouping based only on the identity of the phosphorylatable residue (SI Appendix, Fig. S2D).

Embedded Differences in Conformational Tunability Define Phosphorylation Subclasses.

Accepted sequence heuristics exist that map expected conformational states of folded and disordered protein sequences to their PII propensity (20, 32), conformational stability (23, 26, 29, 33–36), or polarity and charge properties (37, 38). However, it is also possible that in addition to evolving with a particular average physical or functional property, phosphorylatable sequences also evolved a sensitivity of that property to regulatory perturbations (in this case, phosphorylation). To explore this issue, we chose to adopt the change in end-to-end distance and sequence compaction upon phosphorylation as proxies for the conformational sensitivity. Using distance calculations (32), and the method of Das and Pappu (37), we determined end-to-end distances (Fig. 4A) and mapped annotated phosphorylation sites to the charge-charge plots of the denatured state (Fig. 4C and Materials and Methods), respectively.

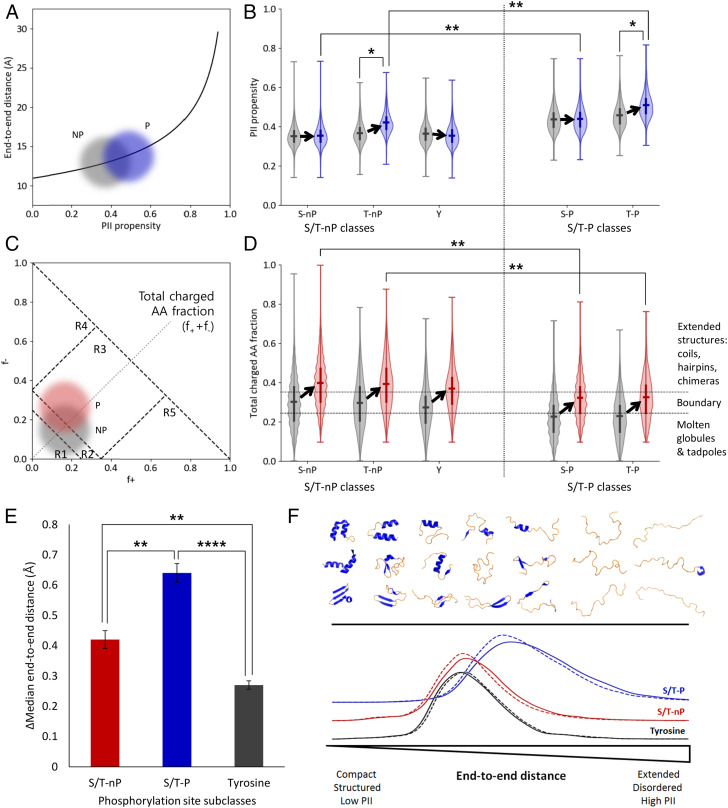
Fig. 4.

Phosphorylation sites containing +1 Pro (S/T-P) are energetically poised to respond to phosphorylation by local extension, mediated by charge and PII propensity. (A) Conceptual plot illustrating expected local end-to-end distance increase (32) due to phosphorylation of an ensemble distribution of 29-mer sequence fragments. Gray cloud represents nonphosphorylated sequences (NP) and blue cloud represents singly phosphorylated sequences (P). (B) Violin plots of ensemble distributions of sequence PII propensities (20) before (gray) and after (blue) phosphorylation. S/T-P classes in particular (the two rightmost pairs of distributions) exist in an extension range nearest the exponential increase in A. Significance bars demonstrate that the postphosphorylation ensembles of S/T-P occupy a very different conformational manifold than do the postphosphorylation ensembles of S/T-nP. (C) Conceptual plot illustrating expected charge change due to single phosphorylation (P) of a distribution of 29-mers. The numbered regions R1 through R5 represent conformational regimes as described in Das and Pappu (37). Note that the dashed diagonal line corresponds to the y axis in D. (D) Violin plots of ensemble distributions of sequence charge properties before (gray) and after (red) phosphorylation. Dotted horizontal lines represent conformational regimes as described in Das and Pappu (37). S/T-P sites (the two rightmost pairs of distributions) specifically exhibit a less unstructured conformational manifold prior to a phosphorylation event, and thus the Pro effectively buffers a conformational transition with an increased PII propensity. Significance bars demonstrate that the postphosphorylation ensembles of S/T-P occupy a very different conformational manifold than do the postphosphorylation ensembles of S/T-nP. Notably, the S/T-nP ensembles cross the boundary region, while the S/T-P ensembles do not. (E) S/T-P sites undergo the largest expected extension upon phosphorylation due to contributions from both extension (PII structure) and charge repulsion (see SI Appendix, Figs. S3–S6, in particular SI Appendix, Fig. S4). (F) Schematic summarizing local changes in the conformational ensemble upon phosphorylation. The top half represents an idealized conformational spectrum ranging from mostly folded (left side) with lower end-to-end distance to mostly disordered (right side) with higher end-to-end distance. Conformational change after the phosphorylation event is measured by end-to-end distance (bottom), mediated by PII propensity and charge interactions. Along this spectrum, tyrosine phosphorylation (black curve) exhibits the smallest population end-to-end distances, S/T-nP phosphorylation (red curve) exhibits intermediate distances, and S/T-P site phosphorylation exhibits the largest distances (blue curve). Dashed line: distribution before phosphorylation. Solid line: distribution after phosphorylation.*P < 0.05, **P < 0.01, ****P < 0.0001.

Distributions of the sequence properties for each of the five subclasses suggest not only that the computed dimensions of respective conformational ensembles are poised in statistically different regions, but that the pre- and postphosphorylation ensembles occupy different regions of conformational space identified by Das and Pappu (37), with the S/T-P ensembles being more similar to each other than are the S/T-nP ensembles (Fig. 4 B and D). In both cases, however, the pre- and postphosphorylated ensembles lie on opposite sides of critical boundaries. In other words, although individual cases vary from protein to protein, taken over the entire database the sequences evolved such that the local conformational ensembles are particularly sensitive to phosphorylation (Fig. 4C). Notably, the S/T-nP ensembles cross out of a critical boundary region identified by Das and Pappu (37) (Fig. 4D), while the S/T-P ensembles cross into this boundary region. However, the higher Pro content of these latter subclasses, which results in longer end-to-end distances, also results in an increased phosphorylation-induced sensitivity in end-to-end distance of the S/T-P relative at the S/T-nP (Fig. 4E), as both Fig. 4A and previous results would suggest (20, 39).

Phosphorylation Site Predictor That Uses Conformational Equilibrium of the Phosphorylatable Chain.

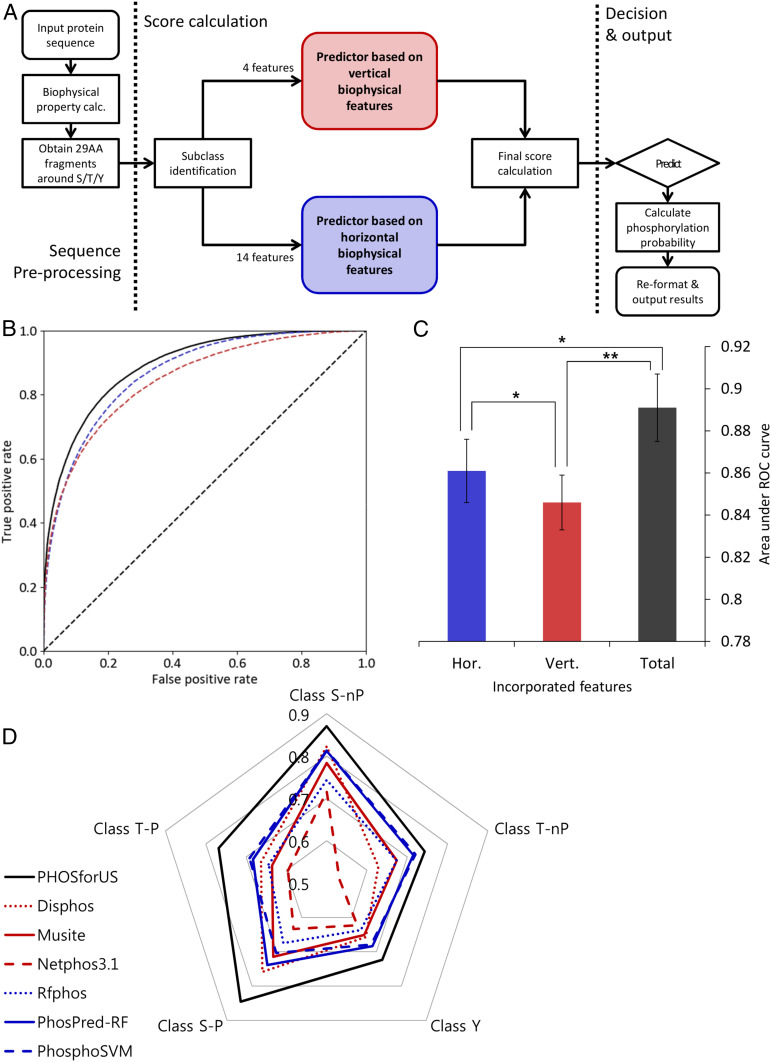
To explore the practical manifestations of our findings, the horizontal and vertical information were incorporated into a prediction method called PHOSforUS (Materials and Methods). Evaluation of the individual predictors with cross-validation demonstrates that all five subclass-specific predictors have significant predictive power for identifying annotated phosphorylation sites (Table 1). The horizontal and vertical information-specific predictors have similar performance, with the horizontal combination, including the position-specific COREX information (23, 26, 29, 33–35) contained in eScape, showing the best performance (Fig. 5B, blue curve). Although combining both horizontal and vertical information results in improved prediction accuracy relative to either alone (Fig. 5B, black curve), horizontal information consistently is more effective (as measured by area under the receiver-operating characteristics [ROC] curve [AUROC]) across subclasses than vertical information alone (Fig. 5C and SI Appendix, Figs. S7–S9 and Table S9). This result indicates that conformational equilibrium is the most important determinant as to whether a particular residue will be phosphorylated.

Table 1.

Subclass training performance of the PHOSforUS predictor

Subclass	Accuracy	Sensitivity	Specificity	Precision	F1	Matthews Correlation Coefficient	AUROC
Class S-P	0.795 ± 0.007	0.800 ± 0.007	0.789 ± 0.011	0.791 ± 0.010	0.796 ± 0.006	0.589 ± 0.014	0.883 ± 0.006
Class S-nP	0.838 ± 0.004	0.843 ± 0.010	0.832 ± 0.007	0.834 ± 0.005	0.838 ± 0.004	0.675 ± 0.007	0.919 ± 0.002
Class T-P	0.741 ± 0.015	0.768 ± 0.024	0.715 ± 0.017	0.729 ± 0.014	0.748 ± 0.016	0.484 ± 0.031	0.820 ± 0.015
Class T-nP	0.730 ± 0.007	0.735 ± 0.026	0.725 ± 0.018	0.728 ± 0.008	0.731 ± 0.011	0.460 ± 0.014	0.810 ± 0.007
Class Y	0.718 ± 0.018	0.717 ± 0.025	0.720 ± 0.024	0.719 ± 0.020	0.718 ± 0.019	0.437 ± 0.036	0.791 ± 0.015
Weighted average	0.803 ± 0.006	0.809 ± 0.013	0.796 ± 0.011	0.799 ± 0.008	0.804 ± 0.007	0.605 ± 0.013	0.885 ± 0.005

Fig. 5.

Architecture, training performance, and comparative effectiveness of the PHOSforUS predictor. (A) Simplified workflow of the PHOSforUS predictor algorithm. Biophysical properties of an arbitrary protein sequence are split into 29-mer fragments centered on Ser/Thr/Tyr residues. Five (or three) subclass-specific predictors are invoked, independently based on vertical (red) or horizontal (blue) information. Intermediate output is combined with gradient boost, and combination scores over a preset threshold are predicted as phosphorylated. (B) ROC of PHOSforUS constituent predictors. AUROC is indicated as a separate bar graph. (C) Performance of all subclasses of phosphorylation site are combined into a single curve. The combined predictor (Total, black) outperforms separate predictors based on vertical (Vert., red) or horizontal (Hor., blue) information. Notably, horizontal information significantly outperforms vertical information (C), demonstrating the importance of horizontal information. *P < 0.05, **P < 0.1. (D) Comparative effectiveness of protein phosphorylation site prediction by PHOSforUS. For five subclasses of phosphorylation site, PHOSforUS AUROC values meet or exceed those obtained on the identical data with six existing prediction tools.

Although several dozen prediction methods exist, six available tools were compared with PHOSforUS to assess the algorithm’s real-world performance (10, 11, 13–16). These methods were chosen because they were freely accessible and could handle the large datasets used for testing (Materials and Methods). Based on ROC curves the seven methods were broadly segregated into two groups, with the most effective group containing methods that either explicitly, or implicitly, incorporated disorder prediction information (Table 2). For all five site classes, PHOSforUS exhibited the highest AUROC values (Fig. 5D and Table 2).

Table 2.

Comparative analysis (AUROC) of PHOSforUS against currently used predictors

Subclass	PHOSforUS	Disphos	Musite	Netphos3.1	Rfphos	PhosPred-RF	PhosphoSVM
Class S-nP	0.871 ± 0.028	0.823 ± 0.028	0.783 ± 0.037	0.717 ± 0.044	0.744 ± 0.026	0.813 ± 0.034	0.814 ± 0.025
Class T-nP	0.743 ± 0.018	0.628 ± 0.018	0.674 ± 0.019	0.531 ± 0.042	0.674 ± 0.036	0.715 ± 0.029	0.720 ± 0.024
Class Y	0.724 ± 0.024	0.657 ± 0.024	0.651 ± 0.039	0.622 ± 0.022	0.637 ± 0.067	0.684 ± 0.022	0.678 ± 0.021
Class S-P	0.845 ± 0.046	0.758 ± 0.046	0.715 ± 0.030	0.633 ± 0.053	0.674 ± 0.032	0.738 ± 0.027	0.703 ± 0.054
Class T-P	0.768 ± 0.023	0.663 ± 0.023	0.635 ± 0.011	0.596 ± 0.033	0.644 ± 0.037	0.683 ± 0.023	0.692 ± 0.030
Weighted average	0.836 ± 0.021	0.767 ± 0.030	0.738 ± 0.032	0.665 ± 0.044	0.707 ± 0.032	0.769 ± 0.030	0.762 ± 0.018

The implications of this result are threefold. First, the prediction effectiveness of PHOSforUS is evidence that the conformational free energy of the ensemble around the phosphorylatable site is important for kinase recognition. Second, because PHOSforUS is trained on mostly single-site sequence fragments, information about the conformational equilibrium (i.e., fluctuations) of the single phosphorylation site is contained in the sequence neighborhood of that site. Third, because the +1 Pro can meaningfully segregate human phosphorylation sites, it is possible that phosphorylation site sequence logos (SI Appendix, Fig. S1) can in some cases also reflect evolutionary conservation of horizontal information, even in the absence of discernible sequence conservation at specific positions.

Discussion

Here we tested whether embedded horizontal information that captures the thermodynamics of a disordered chain plays a role in determining the ability of a substrate to be phosphorylated. Yet, phosphorylation can be considered as a specific case of a more general problem: how to identify the structural determinants of any biochemical reaction targeted to an intrinsically disordered site. Our proposed solution is to reformulate the problem of site prediction, whether structured or disordered, by couching it within a thermodynamic framework. In the case of a target site within a structured protein, such a framework is simplified by the existence of a stable unique native structure. In the case of intrinsic disorder, we employ a “thermodynamic proxy” due to the absence of accurate conformational ensemble modeling technology [although such technology is rapidly developing (40–43)].

In this work, we schematically represented the phosphorylation reaction and phosphorylation prediction in terms of two distinct processes with their corresponding free energies (Fig. 1). The “vertical” information is reflective of the classic static structural view of proteins and substrates, whereby the conserved sequence elements provide the scaffold for tight binding. In effect, the degree of conservation serves as a proxy for the energy of the interaction, a result that is consistent with the reported similarity in statistical vs. experimental energy changes observed within folded proteins (44).

Unique to the approach described here, however, is the explicit incorporation of “horizontal” information that specifically encodes the conformational free energy differences embedded along a sequence. Importantly, both types of information could be encoded by amino acid sequence and should be conserved in a substrate multiple sequence alignment (Fig. 1, circles), with a key difference being that the horizontal information is more diffuse and thus would be expected to be less conserved at individual positions using traditional alignment tools (45). This could be an indication of an evolutionary strategy that permits rapid testing of functional amino acid substitutions within a conserved disordered region. Support for the relevance of horizontal information comes from the direct comparison of subpredictor statistics, such as AUROC and accuracy, which reveals that horizontal features perform better than vertical features in every phosphorylation subclass (SI Appendix, Tables S4–S8).

The presence or absence of the +1 Pro is a key feature for subclass identification and for the effectiveness of PHOSforUS predictions. What is the biological function of a phosphorylated side chain followed by a Pro, and why is the +1 Pro motif common in eukaryotes and not prokaryotes? Although speculative, our results suggest the answer lies, at least in the case of single-site phosphorylation (which constitutes the majority of cases studied here), in the work that is done in the form of conformational extension upon phosphorylation. To appreciate this point, it must be remembered that there are at least two documented mechanisms for extension in a disordered ensemble: changes in charge mixing (Fig. 4C) (37, 38, 40) and changes in intrinsic PII propensity (Fig. 4A) (20, 32, 38, 39). Sequence logos (SI Appendix, Fig. S1) demonstrate that the second mechanism is likely to be associated with the S/T-P subclass.

We note that although charge and PII propensity are mechanisms for conformational change in ensembles of intrinsically disordered proteins, independent consideration of the effects of phosphorylation on each mechanism is unlikely to provide a complete understanding, as these two effects can be opposing. This issue is highlighted, for example, in Fig. 4D: In the absence of phosphorylation, S/T-P sequences would be expected to be more compact as most of these fall in the molten globule space, whereas the S/T-nP are expected to be less compact as they fall into boundary space. However, the computational results show the opposite, that the S/T-P are the more extended states to start with and then show the largest relative increase in end-to-end distance upon phosphorylation as well (Fig. 4 E and F and SI Appendix, Fig. S4).

To demonstrate this issue and assess the average local extension for these phosphorylated sequence fragments, we used the method of Tomasso et al. (32), which takes both charge and PII propensity into account. S/T-P single-phosphorylation-site subclasses show a significant local extension with expected postphosphorylation of more than 0.6 Å for a 29-mer (Fig. 4E). Notably, this extension is mediated by both charge and PII propensity (SI Appendix, Figs. S3–S6). Thus, singly phosphorylated S/T-P sites encode not only average structural properties but also the sensitivity of the conformational ensemble to the effects of phosphorylation. How nature employs this potential for switch-like behavior is likely to vary depending on the functional requirements of individual proteins, perhaps even mediating the sensitivity of liquid droplet formation in, for example, stress granule regulation in eukaryotes (46).

Importantly, the analysis presented here relates the phosphorylation of a residue to the conformational equilibrium around that specific site. In effect, our approach is reporting on local effects, and the success of this approach across the database of human proteins suggests that these local effects are both meaningful and predictive for a majority of cases. However, we note that although the vast majority of phosphorylatable sites in IDRs are composed of either isolated (i.e., single) or one other site (i.e., double) within a 29-amino-acid range (which forms the bulk of the sites used in the current analysis), it does not preclude the existence of other specific mechanisms that may modulate the conformational equilibrium. Indeed, it is well known that multisite phosphorylation is also employed by IDRs in a minority of cases, as has been reported for Sic1 (47), Ash1 (38), and the polymerase II carboxy-terminal domain (Pol II CTD) (48). This would seem to indicate that in addition to the local effects uncovered by our analysis, more global information about the protein can be determinative in modulating function for these proteins. For example, specific heptad repeats of CTD2′, which appear to modulate +1 Pro cis–trans ratios, can result in diverse outcomes, including chain compaction postphosphorylation (48), an outcome that is counter to the local expansion suggested with our analysis.

Thus, the cases of multisite phosphorylation in some proteins clarify an important aspect of this analysis and highlight an important caveat as well. Specifically, the current analysis examines the role of conformational equilibria within the disordered substrate toward phosphorylation, with the tacit assumption that these equilibria are partially determinative of whether a site is suitable for kinase recognition. There is no a priori reason, however, that the global conformational properties of the protein that determine its function should be the simple additive contribution of the individual local equilibria that are important for kinase recognition at each site. To the contrary, it is entirely reasonable, and has even been experimentally demonstrated (49, 50, 51), that proteins exploit competing local effects in different parts of a disordered chain in modulating overall global properties. It is interesting to note that, while purely speculative, the presence of thermodynamic frustration (i.e., competing energetic effects) in disordered sequences (52–54) is sufficient to enable a scenario wherein the overall global effect of a phosphorylation can be manifested in a way that is opposite to the local impact, although the validity of this claim awaits experimental demonstration. In any case, the fact that the approach described here identifies phosphorylatable sites based on the local conformational equilibrium around the phosphorylatable position, but does not capture the global compaction of a multiphosphorylatable protein (nor is it designed to), suggests that these are computationally, and perhaps functionally, separable phenomena. Indeed, clear experimental demonstration of the separation of local and distal effects has been reported for the CDK inhibitor p27^Kip1 protein system (51), where charge patterning outside the immediate sequence neighborhood of the single +1 Pro phosphorylation site can tune phosphorylation efficiency by up to twofold due to long-range electrostatic interactions.

Finally, in evaluating the significance of the thermodynamic framework and the dimensional analysis of the ensembles presented here, it is important to recognize that the horizontal information does not rely on the dimensions of the computed ensembles, which are only calculated after the fact. Instead, the horizontal information used in site prediction as in the case of the COREX data, thermodynamic in nature, and reports on the conformational free energy of the intrinsically disordered substrate, presumably reflecting the work done in redistributing the ensemble to one that is competent to interact with the kinase. This is important because detailed inspection of the individual phosphorylatable sites reveals that while there are clearly significant differences between the dimensions of the different ensembles (cf. Fig. 4), the distributions are broad and indicate that many counterexamples to ensemble expansion upon phosphorylation exist within the dataset. The fact that the approach reported here can nonetheless discriminate phosphorylatable from nonphosphorylatable sites indicates that the dimensions of the ensemble are secondary in importance, at least with regard to determining which sites will be phosphorylated.

Conclusion

We have shown that horizontally conserved information regarding the structure and energy of the conformational ensemble of a protein sequence plays a major role in determining which disordered sequences will be phosphorylated and how, on average, these ensembles will be affected by phosphorylation. Importantly, we note the approach presented here is not an atomistic statistical thermodynamic model that explicitly accounts for specific interactions and contributions of individual amino acids. Instead, we asked whether the hidden conformational free energy information, previously demonstrated to be embedded within all protein sequences, is sufficient to provide predictive information when sequence conservation is too low to render meaningful comparisons. Our ability to input a single amino acid sequence and predict the likelihood of single-site phosphorylation at Ser, Thr, and Tyr residues (Fig. 5) demonstrates the validity of our approach and supports our assertion that local conformational equilibria (or fluctuations) can affect (and in the case of phosphorylation, even dominate) the specificity of a biological process. Thus, in one key respect, our development of a state-of-the-art prediction algorithm can be viewed as a consequence (albeit highly desirable) of the more important biological finding, which demonstrates the critical role played by conformational equilibria in sensitizing intrinsically disordered sequences to functional regulatory changes.

Materials and Methods

Reference Dataset and Data Processing.

Canonical human protein sequences were obtained from SWISS-PROT (2018 December Release) (8), a manually curated subset of the UniProt database. Phosphorylation annotations were obtained from SWISS-PROT and PhosphoSitePlus (2018 December Release) (9). True positive sets were assembled from SWISS-PROT annotations and low-throughput (LTP) subset of PhosphoSitePlus. Sequence fragments of 29 amino acids (14 residues N-terminal and C-terminal relative to a central phosphorylation site) were extracted from these sets and subsequently divided into five subsets (S-P, S-nP, T-P, T-nP, and Y) based on the identity of the center residue and the presence of Pro as its C-terminal neighbor. For example, S-P denotes Ser as the phosphorylatable central residue with presence of the +1 Pro, while S-nP denotes any of the remaining 19 residues at the +1 position. To reduce information redundancy, a 50% maximum pairwise sequence similarity filter was applied to these subsets. True negative subsets were assembled in a similar way and sequences that shared more than 50% similarity to any phosphorylated sequence were removed to filter out false positives. Resulting statistics of these sets are shown in SI Appendix, Table S1.

For the comparative analysis, we constructed another positive set which contains none of the sequences already contained in the training set, and presumably minimal number of sequences in the training sets of existing phosphorylation predictors. From the PhosphoSitePlus high-throughput (HTP) subset, we removed sequences that show 50% similarity to any of sequences within SWISS-PROT, Phospho.ELM (7), and PhosphoSitePlus LTP datasets. From resulting positive set (statistics shown in SI Appendix, Table S1) and true negative set, we randomly sampled five testing sets with 100 positive sites and 100 negative sites to test predictor performances.

Visualizing Conservation of Vertical and Horizontal Information.

Orthologs of human proteins with DNA-binding transcription factor activity (Gene Ontology: 0003700) were obtained from the Orthologous Matrix (OMA) database (30). We selected ortholog groups with the number of members between 10 < n < 250 and downloaded multiple sequence alignments as archived in the database. A full list of the 835 ortholog groups we utilized can be found at https://github.com/bxlab/PHOSforUS.

Normalized local sequence conservation scores were calculated using the following procedure. The multiple sequence alignment (alignment size = n) was divided into small overlapping windows (window size = 5, step = 1). For each window, pairwise local alignment scores using BLOSUM62 matrix (55) were calculated between a reference sequence ($Se{q}_i$) and each of all other sequences within same ortholog group ($Se{q}_j$). This process was iterated using each of the sequences in the alignment as a reference sequence. Within each iteration, each pairwise score was divided by a maximum score attainable, which was defined as the case when a sequence which is identical to the reference was applied for pairwise comparison. Calculated pairwise scores were averaged to obtain a normalized local sequence conservation score (Eq. 2):

$$Scor{e}_{seq}=\frac{{{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^{n\left(noti\right)}\frac{BLOSUM(se{q}_i,se{q}_j)}{BLOSUM(se{q}_i,se{q}_i)}}{n(n-1)}.$$ [2]

Native-state free energy for each protein sequence was calculated using the eScape algorithm (ref. 29, https://best.bio.jhu.edu/eScape). For the same window we used for calculation of local sequence conservation score, we calculated local average and SD of free energy values. Horizontal conservation score was computed using the following Eq. 3:

$$Scor{e}_{Hor}=1-\frac{S{D}_{local}}{C_{\text{s}}}.$$ [3]

In this case, scaling coefficient ($C_{\text{s}}=$ 3.3 [kcal/mol]) was calculated from 10 different ortholog groups exhibiting high sequence conservation and structural stability (e.g., actin [ACTB] and rhodopsin [RHO] families). Resulting conservation scores are plotted in SI Appendix, Fig. S10A (glucocorticoid receptor/GCR), SI Appendix, Fig. S10B (actin), and SI Appendix, Fig. S10C (rhodopsin), respectively.

To observe its correlation with free energy, sequence conservation scores and horizontal conservation scores were normalized again with μ = 0 and SD = 1 (i.e., a Z-score). Linear correlations between average free energy and both conservation scores were calculated subsequently as SI Appendix, Fig. S10D. Binned distributions for slopes and correlation coefficients (for 835 correlations, one for each ortholog group) can be found in SI Appendix, Fig. S10 E and F, respectively.

Estimating End-To-End Distance of Phosphorylated and Nonphosphorylated Sequence Fragments.

Values for end-to-end distances $\overrightarrow{R}$ (Fig. 4E) were computed from Eq. 4, based on refs. 32, 56, and 57):

$$\overrightarrow{R}\cong R_0\cdot N^{\nu }\cdot \sqrt{6}.$$ [4]

In Eq. 4, N is the length of the sequence fragment (29 residues), R₀ is the hydrodynamic radius of a single amino acid (2.16 Å), and exponent v was defined as follows, incorporating the influence of PII propensity and net charge:

$$\text{ν}\left(f_{PII},\left|Q\right|\right)={\nu }_0+\alpha \cdot s\left(\right|Q\left|\right)+\text{β}\cdot (1-s\left(\right|Q\left|\right))\cdot \text{ln}(1-f_{PII}).$$ [5]

In Eq. 5, f_PII is the PII propensity, s(|Q|) is a sigmoid function parameterized by net charge and hydrodynamic radius (58), and α and β are scaling coefficients for the effects of net charge and polyproline propensity, respectively. Full details are given in SI Appendix.

Combining Horizontal and Vertical Information to Build a Phosphorylation Site Predictor.

Selected horizontal information was computed over a 29-residue window (SI Appendix) using properties contained within the AAindex database (59). Properties that were not classified as horizontal were considered vertical information. A naïve Bayes predictor (60, 61) trained on each individual property was used to assess predictive accuracy for each phosphorylation subclass (SI Appendix, Tables S4–S8), and the individual properties with highest information content were incorporated into the PHOSforUS prediction algorithm (SI Appendix, Tables S2 and S3). Horizontal properties included amino acid partition energies (62, 63), alpha helix frequencies (64), extended conformation (65, 66), and PII helix propensities (20), hinting at cooperative and noncooperative structure tendencies. Vertical properties included amino acid isoelectric point (67), molecular weight (68), volume (69), and side-chain average exposed surface area (70), all being characteristics independent of neighboring amino acids. Orthogonal information was incorporated from predicted thermodynamic properties (23, 26, 29, 33–35) using the eScape software (29), and this information was used to train a separate naïve Bayes predictor (SI Appendix).

The PHOSforUS algorithm consisted of three stages: sequence preprocessing, score calculation, and decision output (Fig. 5A). The first stage identifies the Ser, Thr, and Tyr residues as possible phosphorylation sites and computes the horizontal and vertical properties mentioned above for each site’s sequence neighborhood. The second stage routes each site to the appropriate subclass predictor and parameter set. Prediction scores from each individual horizontal, vertical, and thermodynamic property are combined using a Gradient Boost (61, 71) predictor (see details of predictor architecture in SI Appendix), resulting in a single value for the potential site. The third stage compares this single value to a predetermined threshold to predict the probability that the site is phosphorylated or nonphosphorylated. Thus, a confidence is attached to the binary phosphorylation prediction, making the prediction more interpretable to the researcher.

Data Availability.

All data necessary for replication, including amino acid sequences, associated protocols, code, and materials in the paper are freely and publicly available at GitHub, https://github.com/mcho22/PHOSforUS_figure_resource. The PHOSforUS software package and associated databases are freely available at GitHub, https://github.com/bxlab/PHOSforUS.