Abstract
The development of chemotherapeutic resistance resulting in tumor relapse is largely the consequence of the mechanism of competitive release of pre-existing resistant tumor cells selected for regrowth after chemotherapeutic agents attack the previously dominant chemo-sensitive population. We introduce a prisoner’s dilemma game theoretic mathematical model based on the replicator of three competing cell populations: healthy (cooperators), sensitive (defectors), and resistant (defectors) cells. The model is shown to recapitulate prostate-specific antigen measurement data from three clinical trials for metastatic castration-resistant prostate cancer patients treated with 1) prednisone, 2) mitoxantrone and prednisone and 3) docetaxel and prednisone. Continuous maximum tolerated dose schedules reduce the sensitive cell population, initially shrinking tumor burden, but subsequently “release” the resistant cells from competition to re-populate and re-grow the tumor in a resistant form. The evolutionary model allows us to quantify responses to conventional (continuous) therapeutic strategies as well as to design adaptive strategies. These novel adaptive strategies are robust to small perturbations in timing and extend simulated time to relapse from continuous therapy administration.
Keywords: Metastatic castration-resistant prostate, cancer, Competitive release, Evolutionary dynamics, Adaptive therapy, Chemotherapeutic resistance, Prisoner’s dilemma, Replicator dynamics, Evolutionary game theory, Adaptive control
1. Introduction
In his now classic 1961 study of competition for space between two species of barnacles in the intertidal zone off the Scottish coast, Connell (1961) discovered something interesting. The blue barnacles Balanus normally occupied the intertidal zone, while the brown barnacles Chthamalus occupied the coast above high tide. Despite the commonly held belief that each occupied their own niche because of different adaptations to local micro-conditions, Connell hypothesized that the colonization of the intertidal zone by Balanus was actually preventing Chthamalus from inhabiting this region. To test this, he removed the blue barnacles from the intertidal zone and tracked the subsequent penetration of Chthamalus into this region. He concluded that Chthamalus had undergone relief from competition with Balanus which allowed it to flourish where previously it could not. The point, he emphasized, was there was nothing inherent about the micro-environment of the intertidal zone that was preventing Chthamalus from occupying this region. It was simply the competition against a more dominant species that was holding it back. Without the presence of that species, Chthamalus happily claimed both zones as fundamental niches. Thus, the important notion of competitive release was formulated (see Grant (1972)). When two (or more) sub-species compete for the same resources, with one species dominating the other, if the dominant species is removed, this can provide the needed release from competition that can allow the less dominant species to flourish. The mirror image of competitive release is the related notion of character displacement developed by Brown and Wilson (1956) in which competition can serve to displace one or more morphological, ecological, behavioral, or physiological characteristics of two closely related species that develop in close proximity. These concepts are now well established as part of the overall framework of co-evolutionary ecology theory and play an important role in the evolution of chemotherapeutic resistance in cancer (Attolini and Michor, 2009; Enriquez-Navas et al., 2015; Greaves and Maley, 2012; Merlo et al., 2006).
Since co-evolution among competing clones and subclones is now a well established Nowell (1976) process in malignant tumors, the mechanism of competitive release should be expected to play a role and affect the chemotherapeutic strategies one might choose to eliminate or control tumor growth. Indeed, tumor relapse and the development of chemo-therapeutic resistance is now thought largely to be a consequence of the evolutionary mechanism of competitive release of pre-existing resistant cells in the tumor which are selected for growth after chemotherapeutic agents attack the subpopulation of chemo-sensitive cells which had previously dominated the collection of competing subpopulations. This concept, perhaps most forcefully advocated by Gatenby and collaborators Gatenby (2009), is gaining acceptance by clinicians. A recent (2012) systematic literature analysis of cancer relapse and therapeutic research showed that while evolutionary terms rarely appeared in papers studying therapeutic relapse before 1980 (< 1%), the language usage has steadily increased more recently, due to a huge potential benefit of studying therapeutic relapse from an evolutionary perspective Aktipis et al. (2011). Anticancer therapies strongly target sensitive cells in a tumor, selecting for resistance cell types and, if total eradication of all cancer cells is not accomplished, the tumor will recur as derived from resistant cells that survived initial therapy Perry (2008). It is argued by Gatenby (2009) that eradicating most disseminated cancers may be impossible, undermining the typical goal of cancer treatment of killing as many tumor cells as possible. The underlying assumption of this approach has been that a maximum cell-kill will either lead to a cure or, at worst, maximum life extension. Taking cues from agriculturists who have long abandoned the goal of complete eradication of pests in favor of applying insecticides only when infestation exceeds a threshold in the name of “control” over “cure,” there are those who advocate for a shift from the cure paradigm in cancer treatments to a control paradigm (Beckman et al., 2012; Gatenby, 2009).
1.1. The likelihood of pre-existing resistance
Pre-existing resistant cells should generally be present in all patients with late-stage metastatic disease (for single point mutations which confer resistance), a conclusion supported by probabilistic models (Bozic and Nowak, 2017) and from tumor samples taken prior to treatment (Kreuzer et al., 2003; Roche-Lestienne and Preudhomme, 2003) which have been reported for melanoma (Kemper et al., 2015), prostate cancer (Romanel et al., 2015), colorectal cancer (Diaz Jr et al., 2012; Laurent-Puig et al., 2014), ovarian cancer (Schwarz et al., 2015), and medulloblastoma (Morrissy et al., 2016). According to this view, treatment failure would not be due to evolution of resistance due to therapy, but rather the pre-existing presence of resistant phenotypes that are relatively sheltered from the toxic effects of therapy (Enriquez-Navas et al., 2015).
The likelihood of pre-existing resistance has important therapeutic implications. If we assume no pre-existing resistance, then most models predict maximum dose-density therapy will reduce the probability of resistance largely because this treatment minimizes the number of cell-divisions, thereby minimizing the risk of a mutation leading to acquired resistance (Enriquez-Navas et al., 2015). By contrast, in pre-existing resistance scenarios, the maximum dose-density therapy strategy lends itself to competitive release due to the evolutionary nature of tumor progression. Most pre-clinical efforts that aim to maximize the short-term effect of the drug on sensitive cells does not significantly affect the long-term control of cancer (Bozic and Nowak, 2017). This is because the phenomenon of competitive release can occur via the harsh selective pressure imposed by the tumor microenvironment after cancer therapies diminish the presence of the dominant (i.e. the chemo-sensitive) subpopulation. Additionally, the process of metastasis may allow a resistant subpopulation in the primary tumor to emerge elsewhere (Venkatesan and Swanton, 2016).
1.2. Leveraging the cost of pre-existing resistance
Pre-existing mutations that are responsible for conferring resistance may be associated with a phenotypic cost, or a reduced fitness, compared to the average fitness of the sensitive cell population (Gatenby et al., 2011; 2009). Even factoring in this fitness cost, deleterious mutations are still expected to be present in late-stage metastatic cancers (Bozic and Nowak, 2014). This cost can come in many ways, such as an increased rate of DNA repair, or an active pumping out of the toxic drug across cell membranes. All of these strategies use up a finite energy supply that would otherwise be available for invasion into non-cancerous tissues or proliferation. The rapid removal of chemo-sensitive cells during therapy releases the resistant population from unwanted competition and thereby permits unopposed proliferation of the resistant cell population. In contrast, the goal of an adaptive therapy is to maintain a stable tumor burden that permits a significant population of chemo-sensitive cells for the purpose of suppressing the less fit but chemo-resistant populations, consistent with the philosophy that it takes an evolutionary strategy to combat an evolving tumor (Venkatesan and Swanton, 2016). There is some evidence that adaptive therapies may be beneficial for a range of fitness cost (or lack thereof) and therapeutic sensitivity (Gallaher et al., 2018; Hansen et al., 2017).
A theoretical framework for these adaptive therapies first developed by Gatenby et al. (2009), leverages the notion that pre-existing resistance is typically present only in small population numbers due to a cost of resistance. This less fit phenotype is suppressed in the Darwinian environment of the untreated tumor but treatments that are designed to kill maximum numbers of cells remove the competition for the resistant population and ultimately select for that population during tumor relapse1 While the goal of an adaptive therapy (to capitalize on the competition resistant subpopulations incur through maintaining a stable sensitive cell population) has gained some level of acceptance, the ideal adaptive therapy schedule in practice, for different tumor types and growth rates is far from settled. Gatenby’s paper modulates dose density only, while stating that an ideal adaptive therapy would also modulate the drug, as well as the dose schedule (both dose and density) (Gatenby et al., 2009). Some of these evolutionary ideas were tested experimentally using mouse models with modulated dose strength and dose vacations designed to maintain a stable, controllable tumor volume (Enriquez-Navas et al., 2016; Seton-Rogers, 2016). This two-phase adaptive therapy involved an initial high-dose phase to treat the exponential growth of the tumor and a second phase designed for stable tumor control using a variety of strategies (such as decreasing doses or skipping doses when stability is achieved). Several spatial, agent-based computational models have modulated dose strength with respect to a threshold value of tumor size (a fraction of the original tumor burden) (Bacevic et al., 2017; Gallaher et al., 2018). Findings suggest that adaptive therapies based on evolutionary treatment strategies that maintain a residual population of chemo-sensitive cells may be clinically viable, and is currently extended to an on-going clinical trial (NCT02415621) which adaptively controls the on/off cycling of abiraterone (Cunningham et al., 2017). We refer the reader to similar approaches used in mitigating antibiotic resistance (Andersson and Levin, 1999; Gullberg et al., 2011).
With these advances in mind, the goal of this manuscript is to use the evolutionary framework introduced and advocated over the past 10 years (Bacevic et al., 2017; Cunningham et al., 2017; Gallaher et al., 2018; Gatenby, 2009; Gatenby et al., 2009) to mathematically model the important parameters of competitive release and use that framework to better understand therapeutic implications of the cost of developing resistance and to learn how to exploit competition between subpopulations. Here, we ignore clonal dynamics, mutations between subpopulations, and non-genetic (rapid, bidirectional) state transitions, to focus on the inter-subpopulation competition (Hoek and Goding, 2010; Pisco et al., 2013; Sharma et al., 2010). Specifically, we introduce a three-component replicator system with a prisoner’s dilemma payoff matrix (West et al., 2016b) to model the three relevant subclonal populations: healthy cells (H), sensitive cells (S), and resistant cells (R). We consider healthy cells as the surrounding non-neoplastic cells that do not contribute to the overall growth of the tumor, but nevertheless compete with neoplastic cells for space and resources. Using the nullcline information in a triangular phase plane representation of the nonlinear dynamics of the system, we first show the essential ingredients that render competitive release possible. Then, using the parameters that control selection pressure (hence relative growth rates) on the three subclonal populations, we attempt to maintain the tumor burden at low levels so that the resistant population does not reach fixation.
1.3. Retrospective analysis of metastatic castration-resistant prostate cancer
A recent retrospective analysis of tumor measurement data (PSA levels) from eight randomized clinical trials with metastatic castration-resistant prostate cancer (mCRPC) used a simple linear combination of exponentials model to estimate the growth and regression rates of disease burden over time (Wilkerson et al., 2017). In total, over 67% of patients were fit to models with a positive regrowth rate, indicating failure due to resistance. Prostate-specific antigen (PSA) measurement data for patients in each treatment silo (prednisone only, mitoxantrone and prednisone, docetaxel and prednisone) were obtained through the Project Data Sphere open data portal ((https://www.projectdatasphere.org), and we show that this model is able to adequately fit data for each treatment type with the additional capability of allowing us to track responses to conventional therapeutic strategies and design new adaptive strategies as the tumor evolves. The model can be used to test previously proposed adaptive therapies, but we propose a novel schedule utilizing quantitative tools from nonlinear dynamical systems theory which use the current global state of the nonlinear replicator system with respect to the nullcline curves of the equations as well as parameters controlling relative fitness levels of the competing sub-populations. The simulated chemotherapeutic strategies that we implement, based on tracking the phase-space structure of replicator system, are ones that can adapt on the same timescale as the inherent timescale of evolution of the subpopulations comprising the tumor, i.e. are as dynamic as the tumor. While this approach cannot be preplanned by the oncologist at the beginning of therapy like classical strategies, we provide discussion to explain how an evolutionary game theory model describing the fitness landscape (described below) is useful to understand the underlying features of a dynamical fitness landscape associated with a cost to resistance: a three-way prisoner’s dilemma. Specifically, the model indicates a boundary over which an adaptive therapy will cease to be effective. Our model focuses on cost to resistance, as opposed to specific mechanisms of resistance (i.e. hormone resistance, for example). This has the advantage in some ways as being agnostic to resistance mechanisms, but on the other hand, in this manuscript, we can not distinguish between different mechanisms: the analysis explores the effect of a fitness competition between subpopulations on the competitive release phenomenon. Three common therapies used in mCRPC do show that a fit of our model to prostate data lead to the emergence of a cost of resistance in a majority of patients, without pre-determining a value to the cost in the model a priori. Similarly, ref. Wilkerson et al. (2017) found that continuous administration of different therapies (i.e. different resistance mechanisms) is associated with slow tumor regrowth rates (i.e. a cost of resistance conferred to growth potential). We now describe the model.
2. Materials and methods
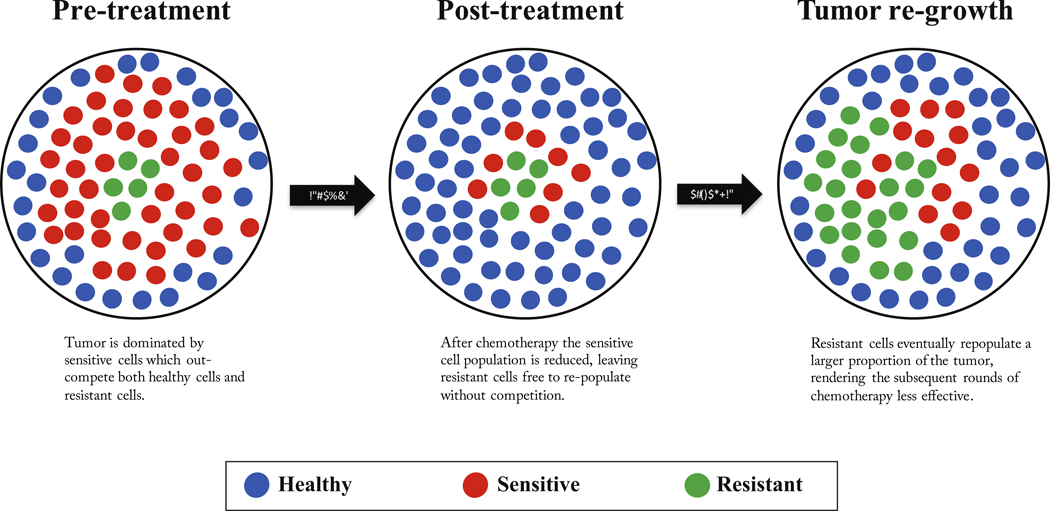
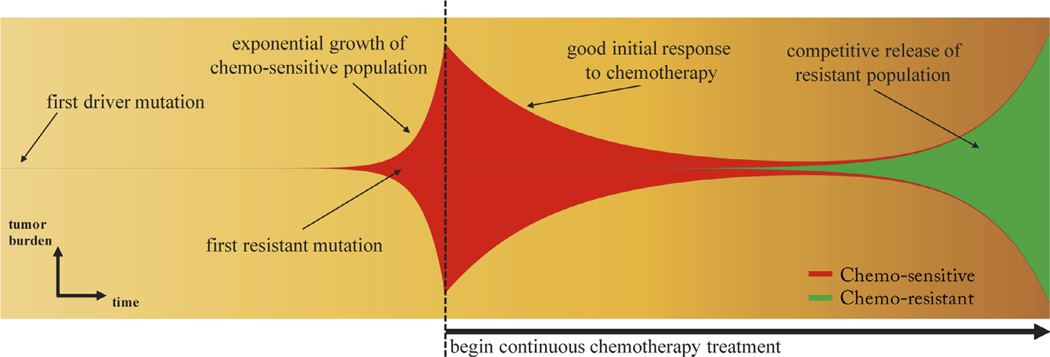
A schematic of a finite-population three component model (healthy, sensitive, resistant) of competitive release is shown in Fig. 1, where the tumor consisting of sensitive and resistant cells is competing with the surrounding healthy tissue. At diagnosis (see Fig. 1, left), the tumor is dominated by sensitive cells (red) which out compete the surrounding healthy population (blue) during unhindered tumor progression. A small portion of resistant cells (green) remains in small numbers, suppressed by the larger sensitive population. After several rounds of chemotherapy, the tumor shrinks, leaving the resistant population largely unaffected (Fig. 1, middle). Inevitably, the tumor relapses due to the small number of sensitive cancer cells remaining after therapy (Fig. 1, right). In the absence of competition from the dominant sensitive population, the resistant cells grow unhindered, rendering subsequent rounds of chemotherapy less effective. Subsequent application of identical therapies will have a diminished effect. Fig. 2 shows the process in a ‘Müller fishplot’, which we will use later to track the subclonal populations. This representation was first utilized in cancer to compare modes of clonal evolution in acute myeloid leukemia (see Ding et al. (2012)) and is particularly useful in computational models where every cell type can be tracked in time. A fishplot shows the tumor burden (vertical axis) over time (horizontal axis). The first resistant cell is assumed to arise from a single sensitive cell, undetectable by current methods of measurement. The schematic depicts unhindered tumor growth after the first driver mutation (Fig. 2, left) where the tumor grows exponentially before diagnosis, during which time a resistant mutation occurs (Fig. 2, middle). After diagnosis (dashed line), a regimen of continuous chemotherapy shows initial good response and tumor regression, but the resistant population grows back (although at a slower growth rate) unhindered by competition, leading to relapse (Fig. 2, right). Previously, a linear combination of exponentials model has been proposed to track the tumor quantity via prostate-specific antigen (PSA) measurement data (Carvalhal et al., 2010). The tumor quantity q(t) is a function of the exponential death rate of the sensitive cells, d. the exponential growth rate of the resistant cells, g, and the initial fraction of resistant cells, f (Bozic and Nowak, 2017). In this equation, q(t) is the tumour burden at time t in days, normalized to the PSA level at t = 0, (see Fig. 3, blue lines). The model can be written as follows:
| (1) |
Fig. 1. Schematic of competitive release in a tumor.
– (a) Prior to treatment, a tumor consists of a large population of sensitive cells (red) and a small population of less fit resistant cells (green) competing for resources with the surrounding healthy cells (blue); (b) Chemotherapy targets the sensitive population (middle), selecting for the less fit resistant population that thrives in the absence of competition from the sensitive population; (c) Upon regrowth, the tumor composition has larger numbers of resistant cells, rendering the subsequent rounds of treatment less effective.
Fig. 2. Clonal evolution of competitive release.
– A fishplot (sometimes known as a Müller plot), showing the tumor quantity (vertical axis) and composition (sensitive: red; resistant: green) over time (horizontal axis, left to right) with important events annotated. After first driver mutation (left), initial exponential growth of sensitive population occurs until diagnosis (dashed line). Continuous therapy targeting the chemo-sensitive population responds well with a decrease in tumor burden. In the absence of sensitive cells, the resistant population (existing in small numbers before the start of therapy) grows to become the dominant subpopulation at relapse, albeit typically with lower exponential growth rate due to the cost of resistance.
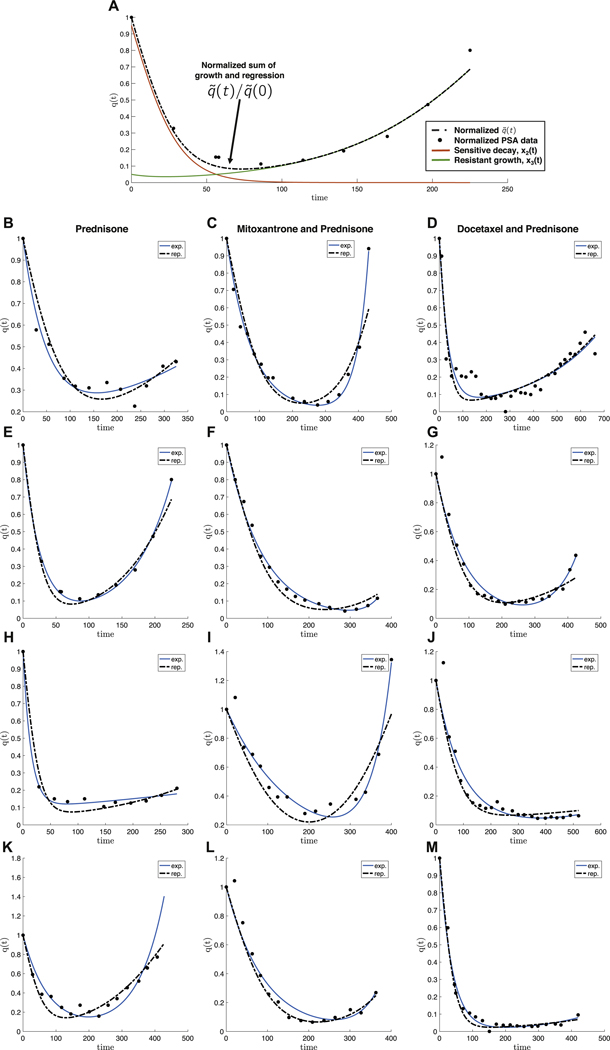
Fig. 3. Model fits of PSA measurement data for metastatic castration-resistant prostate cancer.
– Prostate-specific antigen (PSA) measurement data of four representative patients from three randomised clinical trials with metastatic castration-resistant prostate cancer. (A) A single patient data shown with model fit Eq. (4) of growing resistant population (green), decaying sensitive population (red), where the sum represents an overall initial good response and eventual relapse (q(t), dashed line). Left column: treatment with prednisone only Michaelson et al. (2013); middle column: treatment with mitoxantrone and prednisone Tannock et al. (2004); right column: treatment with docetaxel and prednisone Petrylak et al. (2015). PSA data is normalized by q(t = 0) (black dots). The data is fit using the exponential model (Eq. (1); blue curve) and the replicator model (Eqs. (2) and (3)). Each patient is fit reasonably well with both models. Data was fit by parameter sweep of cost (α − β, Eqs. (15) and (16), initial fractional resistance f and selection pressure w. Parameters used are α − β = [0.02, 0.07, 0.20, 0.00, 0.20, 0.00, 0.20, 0.03, 0.20, 0.01, 0.15, 0.19]; f = [0.20, 0.02, 0.09, 0.05, 0.03, 0.07, 0.10, 0.10, 0.09, 0.10, 0.03, 0.03]; w = [0.10, 0.20, 0.20, 0.30, 0.20, 0.10, 0.30, 0.15, 0.10, 0.15, 0.20, 0.20] for B − M respectively.
This model, shown to be a reasonably good description of the changing tumor size during therapy for colorectal, prostate, and multiple myeloma cancers, identifies the important parameters in competitive release: initial fractional resistance (f), and birth/death rates (g, d) for the resistant and sensitive populations, respectively. The model is used to fit prostate-specific antigen (PSA) measurement data from retrospective analysis of three randomized clinical trials with metastatic castration-resistant prostate cancer to estimate the growth (g) and regression (d) rates of disease burden over time. Four representative patients are chosen from the control arms of each randomized trial and shown in Fig. 3: treatment with prednisone only (Michaelson et al., 2013) (left column: Figs. 3B, E, H and K); treatment with mitox-antrone and prednisone (Tannock et al., 2004) (middle column: Figs. 3C, F, I and L) and treatment with docetaxel and prednisone Petrylak et al. (2015) (right column: Figs. 3D, G, J and M). PSA data and model fits are normalized by q (t = 0) (black dots) and exponential fits are shown in blue.
Despite the fact that the model (1) curve-fits data reasonably well (labeled “exp.” in Fig. 3), it contains no evolutionary information or concepts, a keystone principle behind competitive release. We also include in the Fig. 3 fits of our model presented here Eqs. (2) and (3) in red (labeled “rep.” in Fig. 3, where is given by Eq. (4), below). Our evolutionary model is able to capture similar trends as the exponential model of equations Eq. (1) but has the important property of allowing us to calculate cost of resistance associated with model fit. While each drug (columns) may have very different resistance mechanisms, ten of the twelve patients shown have a cost of resistance (α − β, described below). In the last section we will describe the dynamical phase portrait and implement adaptive strategies to capitalize on competition between resistant and sensitive subpopulations in order to maintain tumor control.
2.1. The replicator equation model
The dynamics of the fitness landscape of three competing cell types are described by the replicator equation (see Traulsen et al. (2005)), which is a deterministic birth-death process in which birth and death rates are functions of cell fitness, and cell fitness is a function of prevalence in the population. Each ith cell type (i = 1, 2, 3) competes according to Eq. (2), where x1, x2, x3 are the corresponding frequency of healthy (H), sensitive (S) and resistant (R) cells, respectively, such that .
| (2) |
| (3) |
Here, is the vector and (Ax)i is the ith element of vector Ax. The prevalence of each sub-population, xi, changes over time according to the changing population fitness, fi, as compared to the average fitness of all three populations . If the fitness of the sub-population is greater than the average fitness , that sub-population grows exponentially, whereas if it is less , it decays.
In order to directly compare results to previously published models of tumor quantity, q(t), during competitive release (i.e. Eq. (1)), the tumor quantity can be written as the sum of the resistant and sensitive tumor populations (x2, x3 respectively), ,
| (4) |
normalized by it’s initial condition, . This is shown in a schematic in Fig. 3A. These represent the same subpopulations shown in green (resistant) and red (sensitive) in Fig. 2.
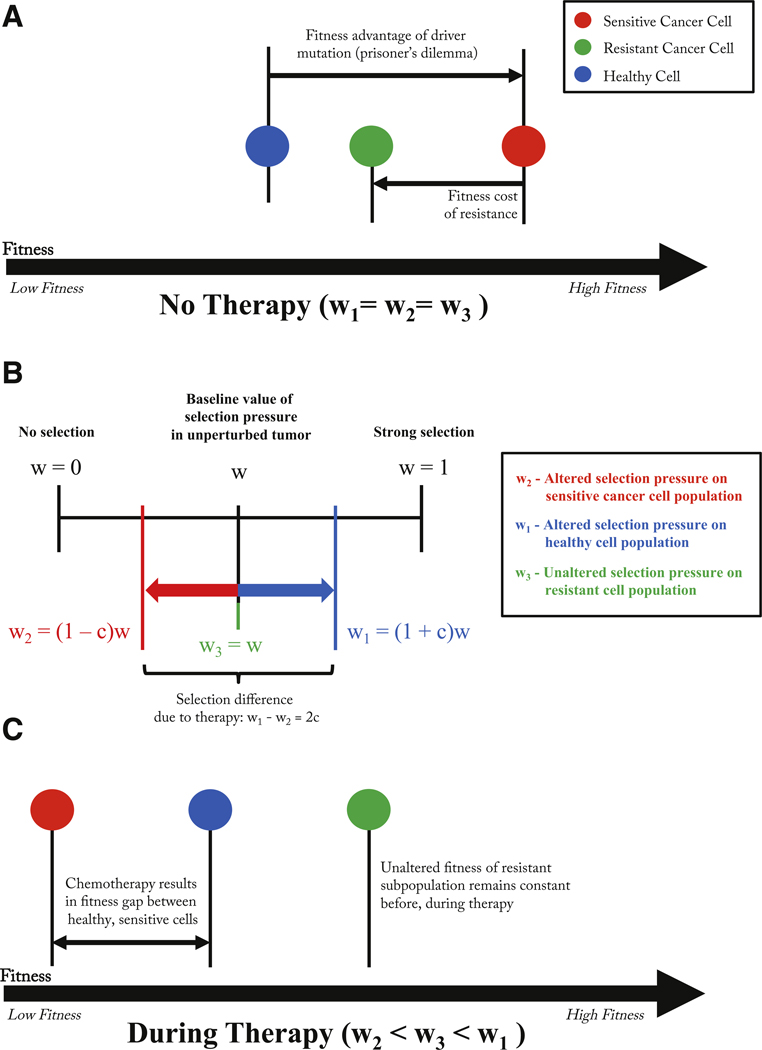
Before therapy, each subpopulation (healthy, chemo-sensitive, and resistant cells) the selection pressure is constant across all cell types (i.e. wi ≡ w, i = 1, 2, 3) at a level that represents the natural selection pressure the tumor environment imposes on the different subpopulations. These values discussed in the literature are typically small, in the range wi ≡ w ≈ 0, 1 – 0, 3, This is a weighting parameter between neutral dynamics (w = 0) and fitness-dependent dynamics (w = 1). Typically in replicator systems, this parameter scales out with time. In our model, we treat each subpopulation selection parameter independently. We implement chemotherapy in our model by changing the selection pressure parameters on each of the subpopulations of cells. Therapy can be administered at different doses (i.e. values of the drug concentration: c; 0 ≤ c ≤ 1). A higher value of c indicates a stronger dose of chemotherapy drug (described in more detail in West and Newton (2017)). This follows the schematic in Fig. 4 which depicts the change in the fitness landscape before and after therapy. In Fig. 3, dose concentration is assumed to be constant for a specific drug while patient-specific parameters are the selection pressure (w), cost of resistance (discussed below), and initial fraction of resistant cells (f). Values are altered as follows (see Fig. 4 for explanation of changing fitness landscape):
| (5) |
| (6) |
| (7) |
Fig. 4. Fitness landscape before and during therapy.
– (A) Before therapy, a driver mutation leads to a fitness advantage of the cancer cell (red) and a subsequent resistant-conferring mutation comes at a fitness cost (green). Parameters determined by the prisoner’s dilemma payoff matrix reflect these relative fitness differences. (B) Rather than change the elements of the game payoff matrix directly, the selection parameter is manipulated for healthy (increased) and cancer (decreased) subpopulations such that w1 − w2 = 2c. (C) Changes in wi results in a new relative fitness of each subpopulation during therapy. The fitness of the resistant population is unaffected by therapy’s selective pressure, but the healthy population is given an advantage over the chemo-sensitive population.
The fitness landscape (Eq. 3) is described in detail by the entries of the payoff matrix A,
| (8) |
where each pairwise cell-cell interaction is described by the row and column values, which are parameters in the fitness equation (3). The 3 × 3 payoff matrix is constructed as a standard prisoner’s dilemma matrix where healthy cells are the cooperators and sensitive/resistant cells are the defectors. In the absence of resistant cells, we describe in more detail the dynamics of the system and its relevance to tumor growth in the appendix. The key features are the Gompertzian growth of the cancer cell population which saturates at a lower overall population fitness level than the initial all healthy cell population. This necessitates the following inequalities of the payoff matrix below Eq. (8): h > a > j > b, l > a > n > o, and k > n > j > m, Note that these payoff entries remain constant before and during therapy: chemotherapy is viewed as affecting the selection balance among the three subpopulations. This is implemented in our model by a change in the selection pressure parameters only Eqs. (5)–(7). More discussion of why the prisoner’s dilemma matrix, which models the evolution of defection, is a useful paradigm for cancer can be found in West et al. (2016a,b) and the appendix.
2.2. The linearized system and the cost of resistance
An additional important feature of the payoff matrix is the notion of the cost of resistance which is highlighted in Fig. 4A. With no therapy, the sensitive cells exhibit fastest growth due to their higher fitness value relative to both the resistant population and the healthy population. The difference between the baseline fitness values of the sensitive cells and the resistant cells can be thought of as the ‘price paid’ by the resistant population to retain their resistance to toxins. This cost, in our model, is quantified as the difference in the (linearized) growth rates of the two populations (type 2: sensitive; type 3: resistant). Linearizing Eqs. (2) and (3), (which form a cubic nonlinear system if expanded out) gives rise to the sensitive-resistant uncoupled system:
| (9) |
| (10) |
with the growth parameters:
| (11) |
| (12) |
| (13) |
| (14) |
With no therapy, c = 0, we have:
| (15) |
| (16) |
We call the fitness cost of resistance the difference between these growth rates with no therapy, hence (α − β) = w(h − l), where we require h > l in the payoff matrix. However, the w parameter is patient-specific, allowing each patient a varied cost.
3. Results
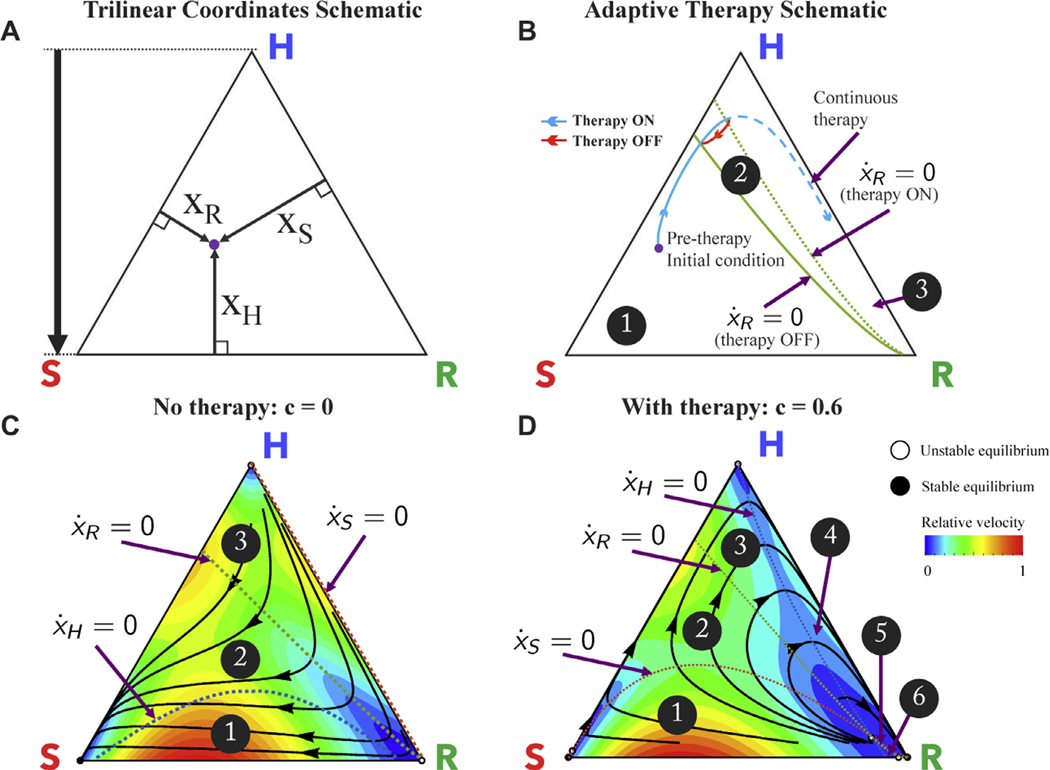
It is useful to view the nonlinear dynamical trajectories of the system using the trilinear coordinates shown in Fig. 5A, which gives a representation of the clonal phase space for every possible value of (Sandholm et al., 2012). The corners represent saturation of a single cell type (e.g. the top corner represents or all healthy cells). The healthy (H; top corner), sensitive (S; bottom left corner), and resistant (R; bottom right corner) populations compete according to Eq. (2) and follow trajectories shown (black) in Fig. 5C.
Fig. 5. Dynamic phase portraits before and during chemotherapy.
– (A) Trilinear coordinate phase space representation; (B) Schematic of proposed adaptive therapy concept using the resistant nullclines to determine therapy “on” and “off” times in order to trap the tumor in the controllable region 2, and reach approximate cycle that repeats back on itself in red. The continuous therapy is also plotted in dashed blue, for comparison. Two nullclines divide the triangle into 3 regions; region 1: for both therapy on and off; region 2: for therapy off and for therapy on; region 3: for both therapy on and off. (C) Before chemotherapy, the healthy (H), sensitive (S), and resistant (R) populations compete on a dynamical fitness landscape, with several solution trajectories shown (black) and the instantaneous relative velocity indicated by background color gradient (red to blue). All internal trajectories lead to tumor growth and eventual saturation of the sensitive population (bottom left corner). Each population nullcline (line of zero growth: ) is plotted: healthy (dashed blue), sensitive (dashed red), and resistant (dashed green). The nullclines divide the triangle into 3 regions. Region 1: Region 2: Region 3: ; (D) Chemotherapy alters the selection pressure to the disadvantage of chemo-sensitive cancer population and advantage of the healthy population (shown for c = 0.6, α = 0.020, β = 0.018, w = 0.1). In this case, the nullclines divide the triangle into 6 regions; Region 1: Region 2: Region 3: Region 4: Region 5: Region 6: ; Solution trajectories (black) show initial trajectory toward healthy saturation (triangle top) but eventual relapse toward resistant population (bottom right of triangle) upon passing the resistant nullcline.
Fig. 5C shows the complete dynamical information for untreated patient dynamics (c = 0, α = 0.020, β = 0.018, w = 0.1). All internal trajectories (black lines) lead to tumor growth and eventual saturation of the sensitive population (bottom left corner, “S”). Instantaneous relative velocity is indicated by background color gradient (blue to red). Subpopulation “nullclines,” the curves for which are shown for healthy (dashed blue), resistant (dashed green), and sensitive (dashed red). On one side there is positive growth ; on the opposite side negative growth . These nullclines delineate the phase space into three regions.
Likewise, Fig. 5D shows the complete dynamical information for the patient treated with chemotherapy (c = 0.6, α = 0.020, = 0.018, w = 0.1). Trajectories initially move away from the sensitive/resistant corners toward healthy, but subsequently relapse to the saturation of the resistant subpopulation. The phase space for treated dynamics is divided into six regions by the three nullclines.
An important detail emerges from the model: during treatment, the resistant nullcline is reached before the healthy nullcline (Fig. 5D). For example, a tumor with an initial diagnosis in region 2 (see Fig. 5D) can be expected to respond to treatment. The trajectory will follow along the black line towards the healthy corner (i.e. decreasing tumor quantity) until the trajectory passes over the nullcline for the resistant subpopulation (dashed green line; ) reaching region 3. Subsequently, the trajectory passes the healthy nullcline (dashed blue line; ) and the tumor relapses (), this time toward saturation of the resistant sub-population.
If the desire is to maintain treatment until the point of positive progression, this occurs when the trajectory is far past the resistant nullcline. Appearances (based on tumor burden) can be deceiving - while the tumor may appear to be responding, the overall state may be well past the point of no return, and the resistant population is preparing to re-populate.
3.1. Managing competitive release
Fig. 5B shows a schematic of the two resistant nullclines from 5 C and D (untreated: solid green line; treated: dashed green line) overlaid on the same phase portrait. From the initial condition (purple dot) treatment begins as the trajectory (solid blue line) approaches the nullcline, positive resistant growth can be avoided by a well-timed drug holiday (solid red line). Here, we propose an adaptive therapy with the goal of trapping the trajectory between the treated resistant nullcline and the untreated resistant nullcline, creating an orbit in a closed loop for a finite period of time to ‘steer’ tumor evolution in region 2 of Fig. 5B. We do this by altering the dose concentration parameter c (a parameter that can be accessed clinically) in Eq. (5) in an off-on (bang-bang) fashion, Eqs. (6) and (7) between the two resistant nullclines: the untreated nullcline from Fig. 5C and the treated nullcine from 5 D.
While all details of the ‘tumor phase space’ may not yet be directly measurable in the clinic, we propose that all successful adaptive therapies will operate in regions 1 and 2 in Fig. 5D; otherwise they ultimately will not be successful. In this way, meaningful insight is gained into the dynamics behind the cost to resistance, regardless of the mechanism of that resistance. Previous adaptive therapy schedules (described in the introduction; see (Bacevic et al., 2017; Cunningham et al., 2017; Enriquez-Navas et al., 2016; Gallaher et al., 2018)) have benefited from not crossing this “hidden” resistant nullcline. We now propose one example of an adaptive therapy schedule which actively captures and uses information from the dynamic phase space.
The simple control paradigm proposed to indirectly control the resistant population by systematically choosing when to administer therapy and when to give drug holidays. These holidays allow a sufficient number of sensitive cells to remain in order to suppress the resistant population. A continuous dose of therapy is administered until the treated nullcline is reached (see Fig. 5D, green dashed line). This is the starting point of positive growth for the resistant population (further therapy would result in ). A drug holiday is then imposed until the second nullcline is reached (see Fig. 5C, green dashed line). The sensitive population is allowed to regrow until it is large enough to suppress the resistant population once again (and when ). Therapy is administered to allow the tumor to cycle back and forth between the two nullclines. This bang-bang (on-off) strategy allows an extension of relapse times. We emphasize that the specific times we turn the therapy on and off in this bang-bang strategy cannot be pre-planned, but depend on the position of the trajectory in the tumor phase space as the disease evolves.
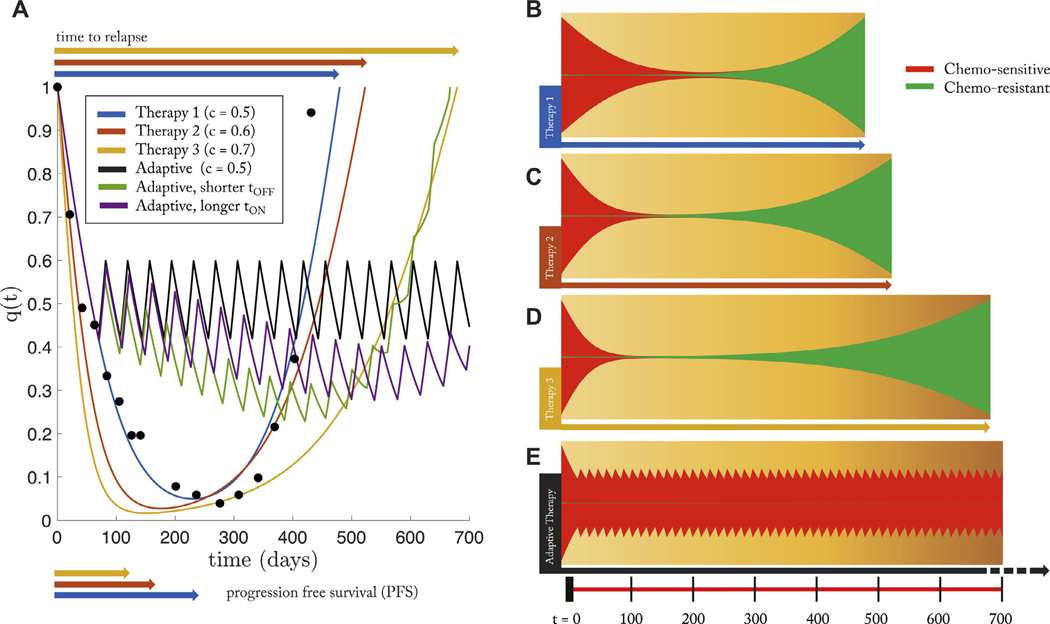
Next, we measure the success of this control paradigm compared to continuous treatment via two important measures of therapy effectiveness: progression free survival (PFS) and time to relapse. PFS is the time to which the patient has a measured response, before relapse of the tumor: shown in Fig. 6A, bottom. A more useful metric is “time to relapse,” where disease reaches initial state. Measuring the effectiveness of a chemotherapy schedule based on the killing rate or progression free survival alone are not sufficient predictive measures of long-term cancer control Bozic and Nowak (2017). PSA data from a single patient who relapsed due to treatment resistance (Fig. 3B) is replotted in Fig. 6A (black dots) along with the model best fit of continuous treatment (blue; therapy 1). Also shown are simulated new drugs with increased effectiveness of killing sensitive cells (red, yellow) simulated by increasing the effective dose concentration with identical patient-specific parameters (from the patient in Fig. 3B). Each increased dose corresponds to a slightly shorter PFS, but an increased time to relapse to the initial tumor burden. However, despite the increase in relapse times, none of these doses optimizes tumor control, as seen in the fishplots (Fig. 6, B,C,D). At the point of relapse to the initial tumor burden, the tumor is dominated by the presence of resistant subpopulations (green), rendering future treatments ineffective. Oftentimes, the effectiveness of a new chemotherapy drug is be determined by PFS times when drugs that have high killing rates of sensitive cells may have shorter times to progression and lower total tumor burden at all times (everything else equal). The figure clearly shows that all treatments have similar progression free times but with a greater range of relapse times (even though continuous treatment always eventually leads to relapse).
Fig. 6. The effect of dose on tumor relapse and progression free survival under continuous and adaptive therapy.
– (A) PSA data is from a single patient (see Fig. 3B) under continuous treatment (Mitoxantrone and Prednisone) is replotted (black dots) along with the best model fit (Eq. (2), (3)) in blue. Using identical patient parameters, continuous treatment of two “new”drugs with higher effectiveness (i.e. increased effective dose, c) is shown in red and yellow. Time to relapse significantly increases with increasing dose while the progression free survival shows marginal, but decreasing, difference. An adaptive therapy (see Fig. 5B) is also simulated (solid black line), showing an increased control over the tumor; Similar control paradigms were simulated with error in administration times: slightly shorter time on therapy (1 day; green) and slightly longer (1 day; purple). (B) The same four therapies are shown in a fish plot. Continous therapies show relapse to initial tumor size is dominated by chemo-resistant population (green). The adaptive therapy successfully suppressed the growth of the resistant population (bottom). Parameters used: α − β = 0.02; w = 0.10; f = 0.2.
Next, compare continuous treatments to the proposed control paradigm (solid black line) for identical initial conditions and identical drug dose. As seen in the fishplot (Fig. 6E), the resistant population (green) is suppressed during drug holidays, leading to an extended time without relapse. This adaptive technique is successful for two reasons. First, the drug holidays allow an adequate sensitive population size to suppress the growth of the lower-fitness resistant population. Second, the resistant population is never allowed to reach a positive growth under treatment , therefore cannot take over the tumor cell population. In order to test the robustness of this method, similar control paradigms were simulated with error in administration times: slightly shorter time on therapy (1 day; Fig. 6A; green) and slightly longer (1 day; Fig. 6A, purple). All else equal, it is better to err on the side of longer treatment on periods without decreasing off treatment time (purple).
4. Discussion
The chemotherapeutic scheduling strategies outlined in this paper cannot be pre-planned by the oncologist at the beginning of therapy like classical strategies (Norton and Simon, 1977), as they rely on significant decision making and continuous monitoring of the different subpopulations of cells that co-evolve as the tumor progresses. This means that the quality of the cell population monitoring system is crucial to the entire strategy, as has been pointed out in Fisher et al. (2015). There can be no adaptive tumor control strategy without continuous monitoring of the subpopulations as it is not the tumor burden that is of primary interest, but the heterogeneous balance of the subpopulations comprising the tumor. In addition, the information gleaned from a detailed monitoring system cannot be acted upon unless the various administered drugs are sufficiently targeted to act efficiently and exclusively on specific subpopulations. These two systems must be in place (sensing and actuating) in order to successfully shape the fitness landscape and steer a growth trajectory in a desired direction. We also want to emphasize a separate point, which is that it is not enough to know in detail the current state of the system in order to steer it successfully. One must also have a description of all possible nearby states of the system, both under therapeutic pressure and without therapy. Better yet is to have a global picture of all possible states of the system, with nonlinear nullcline information, as one would obtain by analyzing the full phase space of the entire system. With this information, one would know where to steer the system to get to a desired state, even if one does not know how to achieve this (clinically). In current state-of-the-art medical practice, such sophisticated sensor-actuator capability is not yet sufficiently developed as it is in many engineering contexts where versions of adaptive control theory are routinely used. Many similar challenges, and the necessary steps towards their implementation, present themselves in the ecology and pest control communities, and we point to Gould’s article (Gould, 1991) for a nice early overview. More recently, connections between the approaches developed in the past by ecologists and possible future strategies for oncologists have been discussed by Gatenby and collaborators (Gatenby and Brown, 2017). Other groups (Bratton et al., 2014; Ledzewicz and Schattler, 2002; Ledzewicz et al., 2017) have also developed highly mathematical approaches to tumor control from different points of view. Clearly not all of the clinical steps are in place to effectively test and implement many of the strategies that have been explored theoretically. Yet it is still important to continue to develop the kinds of mathematical models and computer simulations that would serve to identify the many possible schemes, parameter ranges, and sensitivities that could be tested via clinical trials that focus on adaptive therapies with the goal of suppression of potential evolution of resistance.
Acknowledgments
PKN gratefully acknowledges partial support from the Breast Cancer Research Foundation (BCRF) and the Jayne Koskinas & Ted Giovanis Foundation (JKTG) for Health and Policy. JW gratefully acknowledges support from the Physical Sciences Oncology Network (PSON) at the National Cancer Institute, U54CA193489.
Appendix A
To understand why the prisoner’s dilemma is a useful paradigm for tumor growth resulting from competing subpopulations, we focus on the 2 × 2 case only. The standard version of the prisoner’s dilemma payoff matrix (Nowak, 2006) in a 2 × 2 setting in which healthy cells compete with cancer cells is:
| (17) |
where the first row and column correspond to the payoffs associated with the cooperator (C) in the PD evolutionary game, and the second row and column correspond to the payoffs associated with the defector (D). In the simplest tumor growth paradigm in which a population of healthy cells competes with a population of cancer cells, the healthy cells are the cooperators, while the cancer cells are the defectors. In any mixed population , the fitness functions, , associated with the two subpopulations are:
| (18) |
which in component form yields:
| (19) |
| (20) |
while the average fitness of the total population is given by the quadratic form:
| (21) |
The average fitness of the healthy state is given by , while that of the cancerous state is given by , which minimizes the average fitness. Tumor growth is then modeled as a 2 × 2 evolutionary game governed by the replicator dynamical system:
| (22) |
| (23) |
It is straightforward to show:
| (24) |
with fixed points at . From this, we can conclude (using values from eqn (17)) that for any initial condition containing at least one cancer cell: , we have:
Condition (i) guarantees that the cancer cell population will saturate, while condition (ii) guarantees that the saturated state is sub-optimal, since . For these two reasons, the prisoner’s dilemma evolutionary game serves as a simple paradigm for tumor growth both in finite population models, as well as replicator system (infinite population) models (Traulsen et al., 2005; West et al., 2016a; 2016b; West and Newton, 2017). Note that the 2 × 2 system alone it not able to account for the evolution of resistance.
Footnotes
It is important to note that both high-dose, maximum tolerated dose schedules and low-dose, metronomic dose schedules have this cumulative goal of achieving maximum cell-kill over the course of many cycles of treatment
References
- Aktipis CA, Kwan VS, Johnson KA, Neuberg SL, Maley CC, 2011. Overlooking evolution: a systematic analysis of cancer relapse and therapeutic resistance research. PloS One 6 (11), e26100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson DI, Levin BR, 1999. The biological cost of antibiotic resistance. Curr. Opin. Microbiol 2 (5), 489–493. [DOI] [PubMed] [Google Scholar]
- Attolini CS-O, Michor F, 2009. Evolutionary theory of cancer. Ann. N. Y. Acad. Sci 1168 (1), 23–51. [DOI] [PubMed] [Google Scholar]
- Bacevic K, Noble R, Soffar A, Ammar OW, Boszonyik B, Prieto S, Vincent C, Hochberg ME, Krasinska L, Fisher D, 2017. Spatial competition constrains resistance to targeted cancer therapy. Nat Commun. 8 (1), 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckman R, Schemmarm G, Yeang C, 2012. Impact of genetic dynamics and single-cell heterogeneity on the development of personalized non-standard medicine strategies for cancer. Proc. Natl. Acad. Sci 109 (36), 14586–14591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bozic I, Nowak MA, 2014. Timing and heterogeneity of mutations associated with drug resistance in metastatic cancers. Proceedings of the National Academy of Sciences 111 (45), 15964–15968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bozic I, Nowak MA, 2017. Resisting resistance. Ann. Rev. Cancer Biol 1, 203–221. [Google Scholar]
- Bratton K, Ledzewicz U, Schattler H, 2014. Modeling and control of heterogeneous tumors under chemotherapy. Biomath Comm. 1 (1), 1–2. [Google Scholar]
- Brown WL, Wilson EO, 1956. Character displacement. Syst. Zool 5 (2), 49–64. [Google Scholar]
- Carvalhal GF, Daudi SN, Kan D, Mondo D, Roehl KA, Loeb S, Catalona WJ, 2010. Correlation between serum prostate-specific antigen and cancer volume in prostate glands of different sizes. Urology 76 (5), 1072–1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connell JH, 1961. The influence of interspecific competition and other factors on the distribution of the barnacle chthamalus stellatus. Ecology 42 (4), 710–723. [Google Scholar]
- Cunningham JJ, Zhang J, Brown JS, Gatenby RA, 2017. Integrating evolutionary dynamics into treatment of metastatic castrate-resistant prostate cancer. Nat. Commun 8 (1), 1816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaz LA Jr, Williams RT, Wu J, Kinde I, Hecht JR, Berlin J, Allen B, Bozic I, Reiter JG, Nowak MA, et al. , 2012. The molecular evolution of acquired resistance to targeted EGFR blockade in colorectal cancers. Nature 486 (7404), 537–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding L, Ley TJ, Larson DE, Miller CA, Koboldt DC, Welch JS, Ritchey JK, Young MA, Lamprecht T, McLellan MD, et al. , 2012. Clonal evolution in relapsed acute myeloid leukaemia revealed by whole-genome sequencing. Nature 481 (7382), 506–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enriquez-Navas PM, Kam Y, Das T, Hassan S, Silva A, Foroutan P, Ruiz E, Martinez G, Minton S, Gillies RJ, et al. , 2016. Exploiting evolutionary principles to prolong tumor control in preclinical models of breast cancer. Sci. Transl. Med 8 (327). 327ra24–327ra24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enriquez-Navas PM, Wojtkowiak JW, Gatenby RA, 2015. Application of evolutionary principles to cancer therapy. Cancer Res. 75 (22), 4675–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher A, Vazquez-Garcia I, Mustonen V, 2015. The value of monitoring to control evolving populations. Proc. Natl. Acad. Sci 112 (4), 1007–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallaher J, Enriquez-Navas PM, Luddy KA, Gatenby RA, Anderson AR, 2018. Spatial heterogeneity and evolutionary dynamics modulate time to recurrence in continuous and adaptive cancer therapies. Cancer Res. doi: 10.1158/0008-5472.CAN-17-2649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatenby RA, 2009. A change of strategy in the war on cancer. Nature 459 (7246), 508–509. [DOI] [PubMed] [Google Scholar]
- Gatenby RA, Brown J, 2017. The evolution and ecology of resistance in cancer therapy. Cold Spring Harb Perspect Med. doi: 10.1101/cshperspect.a033415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatenby RA, Gillies RJ, Brown JS, 2011. Of cancer and cave fish. Nat. Rev. Cancer (4), 237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatenby RA, Silva AS, Gillies RJ, Frieden BR, 2009. Adaptive therapy. Cancer Res. 69 (11), 4894–4903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gould F, 1991. The evolutionary potential of crop pests. Am. Sci 79, 496–507. [Google Scholar]
- Grant PR, 1972. Convergent and divergent character displacement. Biol. J. Linn. Soc 4 (1), 39–68. [Google Scholar]
- Greaves M, Maley CC, 2012. Clonal evolution in cancer. Nature 481 (7381), 306–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gullberg E, Cao S, Berg OG, Ilback C, Sandegren L, Hughes D, Andersson DI, 2011. Selection of resistant bacteria at very low antibiotic concentrations. PLoS Pathog. 7 (7), e1002158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen E, Woods RJ, Read AF, 2017. How to use a chemotherapeutic agent when resistance to it threatens the patient. PLoS Biol. 15 (2), e2001110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoek KS, Goding CR, 2010. Cancer stem cells versus phenotype-switching in melanoma. Pigment Cell Melanoma Res. 23 (6), 746–759. [DOI] [PubMed] [Google Scholar]
- Kemper K, Krijgsman O, Cornelissen-Steijger P, Shahrabi A, Weeber F, Song J-Y, Kuilman T, Vis DJ, Wessels LF, Voest EE, et al. , 2015. Intra-and inter-tumor heterogeneity in a vemurafenib-resistant melanoma patient and derived xenografts. EMBO Mol. Med 7 (9), 1104–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreuzer K-A, Le Coutre P, Landt O, Na I-K, Schwarz M, Schultheis K, Hochhaus A, Dorken B, 2003. Preexistence and evolution of imatinib mesylate-resistant clones in chronic myelogenous leukemia detected by a pna-based pcr clamping technique. Ann. Hematol 82 (5), 284–289. [DOI] [PubMed] [Google Scholar]
- Laurent-Puig P, Pekin D, Normand C, Kotsopoulos SK, Nizard P, Perez-Toralla K, Rowell R, Olson J, Srinivasan P, Le Corre D, et al. , 2014. Clinical relevance of kras-mutated subclones detected with picodroplet digital PCR in advanced colorectal cancer treated with anti-EGFR therapy. Clin. Cancer Res [DOI] [PubMed] [Google Scholar]
- Ledzewicz U, Schattler H, 2002. Optimal bang-bang controls for a two-compart-mental model in cancer therapy. J. Optim. Theory Appl 114 (3), 609–637 [Google Scholar]
- Ledzewicz U, Wang S, Schattler H, Andre N, Heng M, Pasquier E, 2017. On drug resistance and metronomic chemotherapy: a mathematical modeling and optimal control approach. Math. Biosci. Eng 14 (1), 217–235. [DOI] [PubMed] [Google Scholar]
- Merlo LM, Pepper JW, Reid BJ, Maley CC, 2006. Cancer as an evolutionary and ecological process. Nat. Rev. Cancer 6 (12), 924–935. [DOI] [PubMed] [Google Scholar]
- Michaelson MD, Oudard S, Ou Y-C, Sengelov L, Saad F, Houede N, Ostler P, Stenzl A, Daugaard G, Jones R, et al. , 2013. Randomized, placebo-controlled, phase iii trial of sunitinib plus prednisone versus prednisone alone in progressive, metastatic, castration-resistant prostate cancer. J. Clin. Oncol 32 (2), 76–82. [DOI] [PubMed] [Google Scholar]
- Morrissy AS, Garzia L, Shih DJ, Zuyderduyn S, Huang X, Skowron P, Remke M, Cavalli FM, Ramaswamy V, Lindsay PE, et al. , 2016. Divergent clonal selection dominates medulloblastoma at recurrence. Nature 529 (7586), 351–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norton L, Simon R, 1977. Tumor size, sensitivity to therapy, and design of treatment schedules. Cancer Treat. Rep 61 (7), 1307. [PubMed] [Google Scholar]
- Nowak MA, 2006. Evolutionary dynamics. Harvard University Press. [Google Scholar]
- Nowell PC, 1976. The clonal evolution of tumor cell populations. Science 194 (4260), 23–28. [DOI] [PubMed] [Google Scholar]
- Perry MC, 2008. The chemotherapy source book. Lippincott Williams & Wilkins. [Google Scholar]
- Petrylak DP, Vogelzang NJ, Budnik N, Wiechno PJ, Sternberg CN, Doner K, Bellmunt J, Burke JM, de Olza MO, Choudhury A, et al. , 2015. Docetaxel and prednisone with or without lenalidomide in chemotherapy-naive patients with metastatic castration-resistant prostate cancer (mainsail): a randomised, double-blind, placebo-controlled phase 3 trial. Lancet Oncol. 16 (4), 417–425. [DOI] [PubMed] [Google Scholar]
- Pisco AO, Brock A, Zhou J, Moor A, Mojtahedi M, Jackson D, Huang S, 2013. Non-darwinian dynamics in therapy-induced cancer drug resistance. Nat. Commun 4, 2467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roche-Lestienne C, Preudhomme C, 2003. Mutations in the abl kinase domain pre-exist the onset of imatinib treatment In: Seminars in Hematology, 40 Elsevier, pp. 80–82. [DOI] [PubMed] [Google Scholar]
- Romanel A, Tandefelt DG, Conteduca V, Jayaram A, Casiraghi N, Wetterskog D, Salvi S, Amadori D, Zafeiriou Z, Rescigno P, et al. , 2015. Plasma ar and abiraterone-resistant prostate cancer. Sci. Transl. Med 7 (312), 312re10–312re10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandholm W, Dokumaci E, Franchetti F, 2012. Dynamo: diagrams for evolutionary game dynamics. software. [Google Scholar]
- Schwarz RF, Ng CK, Cooke SL, Newman S, Temple J, Piskorz AM, Gale D, Sayal K, Murtaza M, Baldwin PJ, et al. , 2015. Spatial and temporal heterogeneity in high-grade serous ovarian cancer: a phylogenetic analysis. PLoS Med. (2), e1001789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seton-Rogers S, 2016. Chemotherapy: preventing competitive release. Nat. Rev. Cancer 16 (4). 199–199. [DOI] [PubMed] [Google Scholar]
- Sharma SV Lee DY Li B, Quinlan MP, Takahashi F, Maheswaran S, McDermott U, Azizian N, Zou L, Fischbach MA, et al. , 2010. A chromatin-mediated reversible drug-tolerant state in cancer cell subpopulations. Cell 141 (1), 69–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tannock IF, de Wit R, Berry WR, Horti J, Pluzanska A, Chi KN, Oudard S, Théodore C, James ND, Turesson I, et al. , 2004. Docetaxel plus prednisone or mitoxantrone plus prednisone for advanced prostate cancer. N. Engl. J. Med 351 (15), 1502–1512. [DOI] [PubMed] [Google Scholar]
- Traulsen A, Claussen JC, Hauert C, 2005. Coevolutionary dynamics: from finite to infinite populations. Phys. Rev. Lett 95 (23), 238701. [DOI] [PubMed] [Google Scholar]
- Venkatesan S, Swanton C, 2016. Tumor evolutionary principles: How intratumor heterogeneity influences cancer treatment and outcome In: American Society of Clinical Oncology educational book. American Society of Clinical Oncology. Meeting, 35, p. e141. [DOI] [PubMed] [Google Scholar]
- West J, Hasnain Z, Macklin P, Mason J, Newton P, 2016a. An evolutionary model of tumor cell kinetics and the emergence of molecular heterogeneity and gompertzian growth. SIAM Rev. 58 (4), 716–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West J, Hasnain Z, Mason J, Newton P, 2016b. The prisoner’s dilemma as a cancer model. Converg. Sci. Phys. Oncol 2 (3), 035002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West J, Newton P, 2017. Chemotherapeutic dose scheduling based on tumor growth rates provides a case for low-dose metronomic high-entropy therapies. Cancer Res. doi: 10.1158/0008-5472.CAN-17-1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkerson J, Abdallah K, Hugh-Jones C, Curt G, Rothenberg M, Simantov R, Murphy M, Morrell J, Beetsch J, Sargent DJ, et al. , 2017. Estimation of tumour regression and growth rates during treatment in patients with advanced prostate cancer: a retrospective analysis. Lancet Oncol. 18 (1), 143–154. [DOI] [PubMed] [Google Scholar]