Survival outcome prediction in cervical cancer: Cox models vs deep-learning model

Abstract

BACKGROUND

Historically, the Cox proportional hazard regression model has been the mainstay for survival analyses in oncologic research. The Cox proportional hazard regression model generally is used based on an assumption of linear association. However, it is likely that, in reality, there are many clinicopathologic features that exhibit a nonlinear association in biomedicine.

OBJECTIVE

The purpose of this study was to compare the deep-learning neural network model and the Cox proportional hazard regression model in the prediction of survival in women with cervical cancer.

STUDY DESIGN

This was a retrospective pilot study of consecutive cases of newly diagnosed stage I–IV cervical cancer from 2000–2014. A total of 40 features that included patient demographics, vital signs, laboratory test results, tumor characteristics, and treatment types were assessed for analysis and grouped into 3 feature sets. The deep-learning neural network model was compared with the Cox proportional hazard regression model and 3 other survival analysis models for progression-free survival and overall survival. Mean absolute error and concordance index were used to assess the performance of these 5 models.

RESULTS

There were 768 women included in the analysis. The median age was 49 years, and the majority were Hispanic (71.7%). The majority of tumors were squamous (75.3%) and stage I (48.7%). The median follow-up time was 40.2 months; there were 241 events for recurrence and progression and 170 deaths during the follow-up period. The deep-learning model showed promising results in the prediction of progression-free survival when compared with the Cox proportional hazard regression model (mean absolute error, 29.3 vs 316.2). The deep-learning model also outperformed all the other models, including the Cox proportional hazard regression model, for overall survival (mean absolute error, Cox proportional hazard regression vs deep-learning, 43.6 vs 30.7). The performance of the deep-learning model further improved when more features were included (concordance index for progression-free survival: 0.695 for 20 features, 0.787 for 36 features, and 0.795 for 40 features). There were 10 features for progression-free survival and 3 features for overall survival that demonstrated significance only in the deep-learning model, but not in the Cox proportional hazard regression model. There were no features for progression-free survival and 3 features for overall survival that demonstrated significance only in the Cox proportional hazard regression model, but not in the deep-learning model.

CONCLUSION

Our study suggests that the deep-learning neural network model may be a useful analytic tool for survival prediction in women with cervical cancer because it exhibited superior performance compared with the Cox proportional hazard regression model. This novel analytic approach may provide clinicians with meaningful survival information that potentially could be integrated into treatment decision-making and planning. Further validation studies are necessary to support this pilot study.

Globally, cervical cancer remains the most common gynecologic malignancy.¹ In 2012, more than one-half a million women were estimated to have been diagnosed with this disease. Because nearly one-third of the patients succumb to their disease within the first 5 years from diagnosis,² improvement in survival remains the ultimate treatment goal in the clinical setting. To this end, accurate prediction of survival is critical in precision medicine. Individual survival predictions are also important because they may provide clinicians a way to gauge treatment outcomes.

Traditionally, proportional hazard models have been used to estimate survival. Although it is possible to predict survival outcomes of individuals, these models typically have focused on differences in patient cohorts and not on survival prediction. Moreover, these approaches make linearity assumptions and thus cannot model the nonlinear relationships that may be present in a real-life setting, which reflects the complexity of biomedicine. Therefore, novel solutions that can include these potentially nonlinear variables are in great demand to predict individual survival accurately.

Recently, deep-learning frameworks based on multilayer perceptrons to predict individual survival based on clinicopathologic data have been developed.³ The utility of these frameworks have been examined in various settings related to translational and clinical medicine,^4–13 but the utility for survival prediction remains relatively understudied. With regards to survival analysis, deep-learning models, which is a class of machine learning models, can model automatically survival risks using nonlinear risk functions and to predict individual survival outcomes from learned representations.

Our previous preliminary study demonstrated that deep-learning models have superior accuracy for survival prediction in women with recurrent cervical cancer compared with the conventional analytic approaches.¹⁴ These results prompted us to conduct another pilot study to examine the performance of deep-learning neural network models in survival analysis for women with newly diagnosed cervical cancer. The objective of this study was to compare the performance of deep-learning neural network models with that of conventional Cox proportional hazard regression (CPH) models to predict survival in women with newly diagnosed cervical cancer.

Materials and Methods

Eligibility criteria

After Institutional Review Board approval was obtained at University of Southern California, a retrospective study was conducted to examine consecutive cases of newly diagnosed stage I–IV invasive cervical cancer that was diagnosed and managed at the Los Angeles County+University of Southern California Medical Center between January 2000 and December 2014. A previously established division database for cervical cancer was used to identify eligible cases.¹⁵ This study excluded cases with preinvasive cervical dysplasia, sarcoma, and metastatic tumors to the uterine cervix. Patients lacking clinicopathologic information at cervical cancer diagnosis were also excluded. Among eligible cases, patient demographics, vital signs, laboratory test results, tumor characteristics, treatment types, and survival outcomes were collected from medical records.

Clinical information

Patient demographics at cervical cancer diagnosis included age, race/ethnicity, body mass index (kilograms/square meter), and medical comorbidities (hypertension and beta-blocker use, diabetes mellitus, and hypercholesterolemia). Vital signs obtained at the initial cancer diagnosis included systolic and diastolic blood pressure and heart rate. In our practice, intake vital signs routinely are measured at all clinic visits. Vital signs are taken in an upright position after >10 minutes at rest. Laboratory test results at cervical cancer diagnosis included leukocyte count, hemoglobin level, and platelet count and blood urea nitrogen, creatinine, bicarbonate, and albumin levels.

Tumor characteristics included histologic subtype (squamous, adenocarcinoma, adenosquamous, and others) and cancer stage (I, II, III, and IV). Initial treatments after cervical cancer diagnosis included primary hysterectomy, systemic chemotherapy, and/or radiotherapy. For survival outcomes, progression-free survival (PFS) and overall survival (OS) were examined.

Study definition

Cancer stage was based on the 2014 International Federations of Gynecology and Obstetrics classification.¹⁶ PFS was defined as the time interval between initial cervical cancer diagnosis and the first disease recurrence/progression or death from cervical cancer. OS was defined as the time interval between initial cervical cancer diagnosis and death from any cause. Patients who were transferred to hospice for terminal cancer condition at the last follow-up evaluation were also recorded as death from cervical cancer, as previously described.¹⁷ This allocation was based on the rationale that time to death after hospice transfer is considerably short (approximately 3 weeks).¹⁸ Patients without these survival events at the last follow-up evaluation were censored.

Statistical consideration

The primary objective of this study was to compare the accuracy of survival prediction between the deep-learning neural network model and the conventional approach with the CPH model. The secondary objective of this study was to examine the clinicopathologic prognostic factors across the 2 analytic approaches.

To examine the study objective, the following subtasks were set: for patient i, given the medical features vector X_i, binary event indicator (censor variable) δ_i, predict patient’s survival (PFS/OS survival time prediction task). Regarding preprocessing, because the size of the dataset was relatively small, to train, cross-validate, and test the model properly, the whole dataset was split into 10 folds while preserving the percentage of data for censored patients and uncensored patients. We trained the models on 8 folds, validated it on another fold, and tested it on the remaining fold. We then tested the model 10 times to ensure that every fold had been tested.

To set the analytic approach for the deep-learning model, 3 groups of features set (FS) were examined (Table 1): FS1 represents patient baseline characteristics (20 features), including age, race/ethnicity, body mass index, vital signs, comorbidities, and pretreatment laboratory results; FS2 represents FS1 and tumor characteristics (20+16=36 features), including histologic type and cancer stage; FS3 represents FS2 and treatment type (36+4=40 features). The rational of this sequential split-grouping strategy is to examine the association between the extent of features and survival prediction in various analytic approaches.

TABLE 1.

Patient demographics (N = 768)

Features set 1 (20 features)	Measure	Features set 2,a n (%)	Measure	Features set 3,b n (%)	Measure
Age, yc	49 (41–58)	Histologic condition		Beta-blocker use
Race/ethnicity, n (%)		Squamous cell	578 (75.3)	No	710 (92.9)
White	64 (8.3)	Adenocarcinoma	137 (17.8)	Yes	54 (7.1)
Black	48 (6.3)	Adenosquamous	31 (4.0)	Primary hysterectomy
Hispanic	551 (71.7)	Other	22 (2.9)	No	559 (72.8)
Asian	101 (13.2)	Stage		Yes	209 (27.2)
Others	4 (0.5)	I	372 (48.7)	Radiotherapy
Body mass index, kg/m2c,d	28.0 (24.3–32.8)	IA1	91 (11.8)	No	297 (38.7)
Hypertension, n (%)e		IA2	21 (2.7)	Yes	471 (61.3)
No	569 (74.5)	IB1	160 (20.8)	Chemotherapy
Yes	195 (25.5)	IB2	100 (13.0)	No	699 (91.0)
Diabetes mellitus, n (%)e		II	167 (21.9)	Yes	69 (9.0)
No	654 (85.6)	IIA	30 (3.9)
Yes	110 (14.4)	IIB	136 (17.7)
Hypercholesterolemia, n (%)e		II NOS	1 (0.1)
No	701 (91.8)	III	156 (20.4)
Yes	63 (8.2)	IIIA	7 (0.9)
Vital signs at diagnosisc		IIB	149 (19.4)
Systolic blood pressure, mm Hg	125 (112–140)	IV	69 (9.0)
Diastolic blood pressure, mm Hg	72 (65–80)	IVA	11 (1.4)
Heart rate, beats/min	79 (70–89)	IVB	58 (7.6)
Laboratory testc		Unknown	4 (0.5)
White blood cell, ×109/L	8.3 (6.6–10.0)
Platelet, ×109/L	300 (244–451)
Hemoglobin, g/dL	12.3 (10.2–13.4)
Blood urea nitrogen, mg/dL	12.0 (9.0–15.0)
Creatinine, mg/dL	0.6 (0.5–0.8)
Bicarbonate, mEq/L	25 (23–27)
Albumin, g/dL	4.1 (3.7–4.4)

^aIncluded the demographics for features set 1 and the 16 listed tumor features

^bIncluded the demographics for features set 1, the 16 tumor features for features set 2, and the listed treatment features

^cData are given as median (interquartile range)

^dMissing 20 data

^eMissing 4 data.

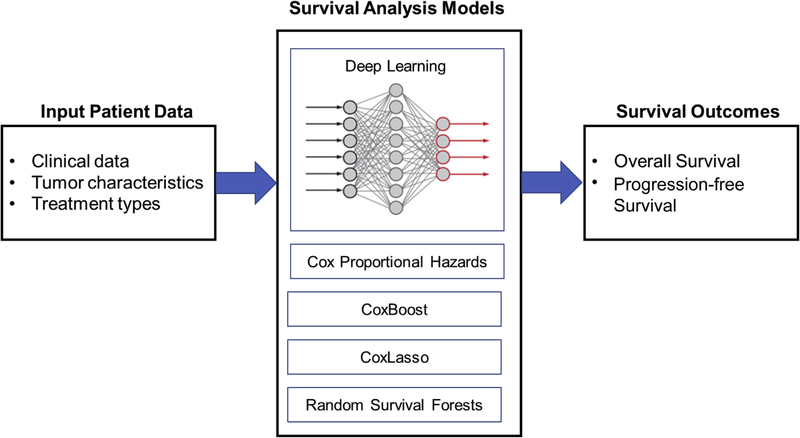
Our proposed deep-learning model has a hierarchic structure and uses fully connected feed-forward neural networks in the lower layers of the model and 2 subnetworks (fully connected layers) to optimize jointly the concordance index and mean absolute error evaluation metrics. In other words, our deep-learning model predicts both mean absolute error and concordance index by jointly optimizing the 2 subnetworks, each of which optimize these parameters separately. We compared baseline models (CPH,¹⁹ CoxLasso,²⁰ Random Survival Forest,²¹ and Cox Boost²²) to our proposed deep-learning model (Figure) on the provided dataset for 2 tasks (PFS/OS predictions) with 3 different sets of features (FS1–3). The results shown here are an average of 10 test folds (from cross validation) in terms of concordance index and mean absolute error.

FIGURE. Study schema for survival analysis.

Patient baseline characteristics were entered in various analytic models that included the deep-learning neural network model to examine survival outcome.

Mean absolute error is the absolute difference between the original survival time (ground truth) and the model’s predicted survival time measured in months. Lower mean absolute error means a better performing model. Concordance index can be interpreted as the fraction of all pairs of subjects whose predicted survival times are ordered correctly among all subjects that can actually be ordered. In other words, it is the probability of concordance between the predicted and the observed survival. Higher concordance index means better performing model.²³

Our proposed deep-learning model for survival analysis uses a subnetwork of deep neural networks with a single output node to estimate the survival risks h_θ(X_i) of patients i by the optimization of the negative log-partial likelihood function, which is measured by the concordance index score. In addition, our model uses another subnetwork of deep neural networks to minimize the mean absolute error between the actual survival time and the predicted survival time for individual patients. Thus, our proposed model jointly optimizes the concordance index score and mean absolute error simultaneously to accurately predict survival of individual patients.

CPH is a popular semiparametric model for survival analysis. It estimates the risk function h(X_i) of the event occurring (eg, died of cancer) for patient i based on observed covariates/features X_i with the use of a linear function: h(X_i) = X_iβ, where β is the coefficient of X_i.¹⁹ It measures the impact of the covariates and assumes that the log-hazard of every patient is a linear combination of the patient’s features.

In addition to standard CPH, other modeling variants such as CoxBoost²⁴ and CoxLasso²⁴ have been proposed in literature. Although these modeling approaches are not used frequently, we have included them for comparison to see how they perform with respect to proposed models. CoxBoost is a semiparametric survival model that is designed to handle high-dimensional datasets by fitting the Cox models with likelihood-based boosting for competing risks.²⁴ CoxLasso, a semiparametric survival model, is another variant of the Cox model and is regularized with the Lasso L1 penalty.^25–27 It treats the number of non-zero coefficients as a tuning parameter and simultaneously selects with the regularization parameter. Also, it fits a varying coefficient Cox model by kernel smoothing, with the aforementioned penalties. Random Survival Forest is a popular nonlinear machine learning model for survival analysis.²¹ It is used to estimate the risk function of patients. Random Survival Forest is a tree model that is based on the random forest method, and it can generate ensemble estimates for the cumulative hazard function.

For survival analysis that uses the multivariable CPH model in a conventional approach, conditional backward method was used to retain only the significant covariates with a probability value of <.05 in the final model.²⁸ All the covariates with a probability value of <.05 in the univariable analysis were entered in the initial model. This is due to relative small sample size and event number to avoid overfitting. Covariate selection and grouping was based on a priori criteria.^14,15 Magnitude of statistical significance was expressed with hazard ratios and 95% confidence intervals.

All statistical analyses were based on 2-tailed hypotheses, and a probability value of <.05 was considered statistically significant. For this study, the CPH models were implemented with the use of the CoxPHFitter function of Pythonpackage lifelines,²⁹ and the deep-learning models were implemented in Python with the use of the Keras deep learning package with tensor-flow backend.³⁰ The Statistical Package for Social Science software (version 24.0; IBM Corporation, Armonk, NY) was also used for conventional analyses other than deep-learning analysis. The Strengthening the Reporting of Observational Studies in Epidemiology guidelines were consulted when we outlined this retrospective cohort study.³¹

Results

There were 802 patients who had a diagnosis of cervical cancer. Among those, 34 patients who lacked vital signs at initial diagnosis were excluded, and the remaining 768 women were examined for the analysis. Patient demographics are shown in Table 1. The median age was 49 years, and most of the patients were Hispanic (71.7%). Most of the tumors were squamous histologic condition (75.3%) and stage I disease (48.7%). The median follow-up time of censored cases was 40.2 months (interquartile range, 16.7–69.9 months). There were 241 women who had recurrence or progression of disease and 170 deaths during the follow-up time.

The CPH model was compared with the deep-learning neural network model for PFS in FS3 (Table 2). The results were an average of 10-fold evaluation in terms of concordant index and mean absolute error. The deep-learning model had significantly better predictions compared with the CPH model, with >10-fold difference between the 2 analytic approaches (mean absolute error for CPH vs deep-learning: 316.2 vs 29.3). However, performance of the deep-learning model was similar when compared with other baseline models for PFS in FS3 (mean absolute error: 29.4 for CoxBoost, 28.8 for CoxLasso, 29.7 for Random Survival Forest, and 29.3 for deep-learning). Similar findings were observed for the results of concordance index (Table 2). Similar trends were observed in FS1 and 2 for mean absolute error and concordance index as in FS3 (Supplemental Table 1).

TABLE 2.

Comparison of Cox proportional hazard regression model vs deep-learning neural network model for survival (feature set 3)

Model	Concordance index,a mean±standard deviation	Mean absolute error,b mean±standard deviation
Progression-free survival (241 events)
Cox proportional hazard regression	0.784 ± 0.069	316.2 ± 128.3c
CoxBoost	0.783 ± 0.068	29.4 ± 4.0
CoxLasso	0.787 ± 0.066	28.8 ± 4.3
Random Survival Forest	0.766 ± 0.065	29.7 ± 4.3
Deep Learning	0.795 ± 0.066	29.3 ± 3.4
Overall survival (170 events)
Cox proportional hazard regression	0.607 ± 0.039	43.6 ± 4.3
CoxBoost	0.606 ± 0.039	37.2 ± 3.5
CoxLasso	0.606 ± 0.038	39.2 ± 2.4
Random Survival Forest	0.600 ± 0.054	33.4 ± 4.4
Deep Learning	0.616 ± 0.041	30.7 ± 3.6

Results of features sets 1 and 2 are shown in Supplemental Table 1.

^aA higher concordance index means better performing model

^bA lower mean absolute error means better performing model

^cConvergence failed: the Newton-Raphson algorithm was used for the estimation of the coefficients in the Cox model that was most likely the cause for this convergence failure.⁴⁵

The comparison was then made for OS in FS3 (Table 2). The deep-learning model outperformed all the other models. That is, the mean absolute error of the deep-learning model was the lowest among the tested analytic approaches (30.7 for deep-learning, 33.4 for random survival forest, 37.2 for CoxBoost, 39.2 for CoxLasso, and 43.6 for CPH). The performance of the CPH model was the lowest among the tested models. Similar findings were seen for the performance of concordance index (Table 2). Similar trends were observed in FS1 and 2 for mean absolute error and concordance index as in FS3 (Supplemental Table 1).

Next, performance of the deep-learning model was examined across the 3 FSs (Table 2 and Supplemental Table 1). Performance of the deep-learning model improved with more features in that the concordance index became larger as more features were added in the model (concordance index for PFS: 0.695 for FS1, 0.787 for FS2, and 0.795 for FS3, respectively). Similar trends were observed for OS (concordance index: 0.538 for FS1, 0.534 for FS2, and 0.616 for FS3, respectively).

Finally, clinicopathologic features that were associated with survival were compared between the CPH model and the deep-learning model. Specifically, results of the multivariable CPH models and the deep-learning model for FS3 were compared (Tables 3 and 4). The results of the deep-learning model validated the CPH model by demonstrating concordant clinicopathologic features for PFS in that vital signs (heart rate), laboratory test results (blood urea nitrogen, creatinine, and albumin), tumor characteristics (cancer stage and histologic type), and treatment type (hysterectomy and radiotherapy) were associated significantly with PFS in both analytic approaches. On the contrary, certain patient demographics (age, body mass index, race/ethnicity, and hypertension), laboratory test results (leukocyte count, platelet count, hemoglobin level, and bicarbonate level), and treatment factors (chemotherapy and beta-blocker use) were the significant covariates for PFS that were seen only in the deep-learning model, but not in the CPH models (10 features; Table 5).

TABLE 3.

Survival predictors in deep-learning model (feature set 3)

Progression-free survival		Overall survival
Features	P value	Features	P value
Hysterectomya	6.93E-69	Radiotherapya	8.04E-29
Albumina	2.53E-34	Whitea	4.25E-05
Hemoglobina	4.89E-32	Hispanica	6.27E-04
Stage IVBa	1.59E-27	Hysterectomya	2.19E-03
Stage IA1a	1.89E-27	Bicarbonatea	1.64E-02
Stage IB1a	8.61E-26	Stage IVBa	2.96E-02
Chemotherapya	2.33E-25	Heart ratea	3.17E-02
Stage IIIBa	4.09E-25	Blood urea nitrogena	4.33E-02
Heart ratea	5.16E-19	Black	5.42E-02
Plateleta	3.08E-17	Platelet	5.76E-02
Radiotherapya	1.14E-09	Age	6.83E-02
White blood cella	1.09E-08	Chemotherapy	7.07E-02
Creatininea	4.79E-08	Creatinine	7.62E-02
Blood urea nitrogena	1.78E-07	Stage IIIA	8.64E-02
Bicarbonatea	7.84E-07	White blood cell	1.05E-01
Agea	1.77E-05	Stage IVA	1.06E-01
Stage IVAa	5.83E-04	Body mass index	1.06E-01
Blacka	9.45E-04	Hypercholesterolemia	1.57E-01
Hispanica	1.00E-03	Diabetes mellitus	1.71E-01
Other histologic conditionsa	5.17E-03	Systolic blood pressure	1.80E-01
Stage IIBa	6.44E-03	Stage IIA	1.97E-01
Hypertensiona	1.30E-02	Asian	2.10E-01
Body mass indexa	1.61E-02	Diastolic blood pressure	2.40E-01
Beta-blocker usea	1.70E-02	Stage IA1	2.68E-01
Asiana	3.65E-02	Stage IIIB	2.91E-01
Adenocarcinomaa	4.80E-02	Other histologic conditions	3.01E-01
Hypercholesterolemia	1.22E-01	Stage IB1	3.58E-01
Stage IB2	2.78E-01	Beta-blocker	3.66E-01
Systolic blood pressure	2.94E-01	Squamous	4.08E-01
Squamous	3.92E-01	Adenocarcinoma	4.28E-01
Diastolic blood pressure	4.14E-01	Hypertension	4.49E-01
Diabetes mellitus	4.87E-01	Albumin	4.62E-01
Stage IIIA	5.38E-01	Stage IIB	4.74E-01
White	5.53E-01	Hemoglobin	4.98E-01
Adenosquamous	6.18E-01	Stage IB2	5.05E-01
Stage IIA	6.92E-01	Adenosquamous	5.54E-01

Covariates are listed based on the statistical significance.

^aSignificant covariates (P<.05). Results for features sets 1 and 2 are shown in Supplemental Tables 2 and 3.

TABLE 4.

Multivariable analysis for Cox proportional hazard regression models for survival

Features	Progression-free survival		Overall survival
	Hazard ratio (95% confidence interval)	P value	Hazard ratio (95% confidence interval)	P value
Histologic condition		.001a,b
Squamous cell	1
Adenocarcinoma	1.61 (1.12–2.32)	.011a
Adenosquamous	2.82 (1.45–5.44)	.002a
Other	1.77 (0.96–3.26)	.07
Stage		<.001a,b		<.001a,b
I	1		1
II	2.81 (1.77–4.46)	<.001a	1.80 (1.04–3.10)	.034a
III	5.15 (3.22–8.25)	<.001a	2.97 (1.75–5.02)	<.001a
IV	12.1 (7.49–19.4)	<.001a	10.2 (5.86–17.7)	<.001a
Primary hysterectomy
No	1		1
Yes	0.17 (0.10–0.31)	<.001a	0.26 (0.12–0.56)	.001a
Radiotherapy
No	1
Yes	0.24 (0.16–0.36)	<.001a
Laboratory test (per unit)
Platelet (×109/L)			1.002 (1.001–1.003)	.007a
Blood urea nitrogen (mg/dL)	1.02 (1.01–1.04)	.006a	1.03 (1.01–1.05)	.006a
Creatinine (mg/dL)	0.84 (0.72–0.98)	.024a	0.83 (0.71–0.98)	.024a
Albumin (g/dL)	0.59 (0.46–0.75)	<.001a	0.46 (0.35–0.62)	<.001a
Vital signs
Heart rate (bpm)	1.02 (1.01–1.03)	.001a	1.01 (1.01–1.02)	.021a

^aAll significant covariates (P<.05) on univariable analysis that are shown in Supplemental Table 4 were entered in the initial full model, and conditional backward method was used to retain only significant covariates (P<.05) in the final model

^bP value for interaction.

TABLE 5.

Summary of clinical-pathologic factors between Cox proportional hazard regression model and deep-learning model

Features	Progression-free survival			Overall survival
	Concordant	Deep-learning only	Cox proportional hazard regression only	Concordant	Deep-learning only	Cox proportional hazard regression only
Patient demographics	—	Age	—	—	—	—
	—	Body mass index	—	—	Race/ethnicity	—
	—	Race/ethnicity	—	—	—	—
	—	Hypertension	—	—	—	—
Vital signs	Heart rate	—	—	Heart rate	—	—
Laboratory test results	Blood urea nitrogen	White blood cell	—	Blood urea nitrogen	Bicarbonate	Platelet
	Creatinine	Platelet	—	—	—	Creatinine
	Albumin	Bicarbonate	—	—	—	Albumin
	—	Hemoglobin	—	—	—	—
Tumor characteristics	Cancer stage	—	—	Cancer stage	Radiotherapy	—
	Histology type	—	—	—	—	—
Treatment type	Hysterectomy	Chemotherapy	—	Hysterectomy	—	—
	Radiotherapy	Beta-blocker use	—	—	—	—

Blank space with indicates no feature.

For OS, the deep-learning model was concordant with the CPH model in that vital signs (heart rate), laboratory test results (blood urea nitrogen), tumor characteristics (cancer stage), and treatment type (hysterectomy) were associated significantly with OS in both analytic approaches. Contrary, certain clinicopathologic factors were significant only in the deep-learning model, but not in the CPH models (patient demographics with race/ethnicity, laboratory test results with bicarbonate level, and treatment type with radiotherapy). Moreover, there were 3 clinicopathologic factors that were significant only in the CPH model, but not in the deep-learning model (laboratory test results with platelet count, creatinine level, and albumin level; Table 5).

Comment

In this second pilot study, our analysis demonstrated that a deep-learning neural network model is superior to conventional linear regression modeling in survival prediction for women with newly diagnosed cervical cancer.

In a review of the previous literature, an increasing number of studies are integrating deep-learning models into analytic approaches in oncologic research. Most of these studies are related to either diagnostic work-up, such as radiographic image analysis and cytopathologic interpretation, or genomic/molecular analysis for biomarker discovery; studies that use deep-learning models for survival prediction in oncology patients remain limited to date. Specifically in the area of cervical cancer research, the utility of deep-learning has been used for interpretation of cervical cytologic testing,^32,33 human papillomavirus-related risk algorithm development,³⁴ colposcopy interpretation,³⁵ tumor tissue identification,^36,37 cervical cancer screening algorithm evaluation,³⁸ radiographic testing efficacy,^39,40 genomic analysis,^41,42 and early symptoms,⁴³ but there have been only a few studies that have examined oncologic outcome.^14,44

In an analysis of surgically treated women with early-stage cervical cancer (n=102), various deep-learning models were tested for 5-year OS prediction with the use of clinicopathologic features mainly from surgical-pathologic specimens.⁴⁴ Their main finding was that certain neural network algorithms are superior for survival prediction compared with conventional linear regression models. Because their study population was limited only to surgical cases, generalizability to other cervical cancer populations was not possible. In the current study, a larger number of unselected consecutive cases of women with cervical cancer, which included nonsurgical cases, were included for analysis, which provided more meaningful results for interpretation.

We previously have examined the performance of deep-learning neural network models in the prediction of survival of women with recurrent cervical cancer who have a limited life-expectancy (3 and 6 months).¹⁴ An enormous amount of data points (>5000) that included patient demographics, symptoms, vital signs, laboratory test results, tumor characteristics, and treatment types were time-sequentially examined after recurrence. The deep-learning model was compared with a linear regression model for survival prediction. The analysis found that the deep-learning model is superior to the CPH model to identify women with limited life-expectancy. Taken together, all 3 studies, which included the current study, have shown consistently that deep-learning neural network models may be useful analytic tools for survival prediction in women with cervical cancer, given its superior performance compared with the linear regression model.

Strengths of the deep-learning neural network model for survival analyses in oncology research are in the following threefold. First, as described earlier, this model exhibits an improved fit for variables with a nonlinear relationship, which is applicable when examining real-life factors. Unlike CPH and its variants, deep-learning approaches can model nonlinear risk functions that are present in survival data. Of note, in our previous study, we found that a number of clinical-laboratory factors demonstrated a nonlinear association with survival and implied that use of a neural network model would be more appropriate than a linear regression model in clinical medicine.¹⁴

Second, deep-learning models are able to not only automatically learn feature representations from raw clinical data without explicit feature engineering but also can fit censored survival data with the use of nonlinear risk functions. In other words, deep-learning models are powerful at learning nonlinear relationships that are present in the data, and they easily can handle censoring in survival data. Thus, selection bias because of the process of demographic grouping can be eliminated in the deep-learning model. For instance, there were several features that were not identified as survival predictors in the conventional analytic approach but were found to be significant prognosticators in the deep-learning model (Table 5). The ability to highlight these features without explicit feature engineering may represent an example of this benefit of deep-learning models.

Third, our study suggests that the performance of the deep-learning neural network model will perform better when large feature sets are used. The strength of the deep-learning model in handling large feature sets, because of its ability to learn feature representation, may be beneficial particularly in biomedical research because inclusion of many variables in conventional linear regression models may result in overfitting.

A limitation of deep-learning models is that these models are computationally expensive to train, and usually their predictions might be hard to interpret. For instance, in our analysis of OS, there were some features that were identified as significant prognostic factors only in the CPH model, but not in the deep-learning model (Table 5). Albumin level, for example, is a well-recognized prognostic factor in oncology patients that reflected general nutritional status, and our previous analysis of recurrent cervical cancer demonstrated that albumin level was the strongest predictor for limited life expectancy.¹⁴ Thus, the fact that this feature was not significant in the deep-learning model is a concern in terms of reliability of the modeling in the current study; further validation and model development are necessary to ensure the reliability of these deep-learning models.

In addition, the challenge and uncertainty in training the CPH models may result in much higher mean absolute error compared with other models. For example, when the coefficients of the CPH model for PFS prediction task were estimated, the model did not completely converge. One potential reason is the Newton-Raphson algorithm that was used in the estimation of coefficients in the CPH model: this likely caused convergence failure.⁴⁵ Last, mean absolute errors were similar between the deep-learning models and the other baseline models. One explanation of this observation is that the deep-learning model might need more fine-tuning for PFS prediction.

Another weakness of the current study is that the limited amount of data makes it challenging to train deep-learning models in our experiments. More investigation is needed to study the performance of deep-learning models in limited data settings. We examined only 40 features in the analysis, and there may be various confounders that were not examined. For example, performance status was not examined in the model but is known to be a prognostic indicator in oncology patients. Moreover, we examined features only at the initial cancer diagnosis; features after initial diagnosis were not assessed.

Although we likely examined one of the largest sample sizes among studies of this nature, the total number remains relatively small, which makes the analysis challenging in the deep-learning model. Follow-up time is also relatively short (<5 years), and there may be the possibility that late survival events were missed. Most of the study population was Hispanic, and generalizability to different population is not known.

The deep-learning neural network model is a new analytic tool that has been adopted recently in clinical decision-making, and its utility will be likely become more widespread in the near future. Our battery of pilot studies in cervical cancer (new diagnosis and recurrent disease) endorses the exploration of deep-learning approach, with promising results in survival analysis. This analytic approach is particularly useful in biomedicine where complexity and uncertainty exist; therefore, further study is warranted to establish its role in survival analysis. For future direction of study, an investigation of how to obtain feature importance scores directly from deep-learning models and how to provide clinically meaningful interpretations from deep-learning models will be of value.

AJOG at a Glance.

Why was this study conducted?

Cox proportional hazard regression models have been the mainstay of survival analyses for oncologic research based on assumptions of linear association; however, there are many clinicopathologic features that exhibit nonlinear correlations in clinical medicine.

Key findings

Deep-learning neural network models recently have been implemented as useful analytic approaches in biomedical research in the evaluation of nonlinear correlations. In this pilot study of women with cervical cancer, the deep-learning neural network model showed promising results and demonstrated higher performance, exhibiting lower mean absolute error and higher concordance index compared with the Cox proportional hazard regression models for survival analysis.

What does this add to what is known?

In the future, this novel analytic approach may have the potential to provide salient survival information that can assist clinicians via integration into the treatment decision-making process.