Predicting monoclonal antibody pharmacokinetics following subcutaneous administration via whole-body physiologically-based modeling

Abstract

Use of the subcutaneous (SC) route for administering monoclonal antibodies (mAbs) to treat chronic conditions has been hindered because of an incomplete understanding of fundamental mechanisms controlling mAb absorption from the SC site, and due to the limited translatability of preclinical studies. In this paper, we report on the development and evaluation of a whole-body physiologically-based model to predict mAb pharmacokinetics following SC administration. The circulatory model is based on the physiological processes governing mAb transport and includes two mAb-specific parameters representing differences in pinocytosis rate and the diffusive/convective transport rates among mAbs. At the SC administration site, two additional parameters are used to represent mAb differences in lymphatic capillary uptake and in pre-systemic clearance. Model development employed clinical intravenous (IV) plasma PK data from 20 mAbs and SC plasma PK data from 12 of these mAbs, as obtained from the literature. The resulting model reliably described both the IV and SC measured plasma concentration data. In addition, a metric based on the positive charge across the mAb’s complementarity determining region vicinity was found to positively correlate with the model-based estimates of the mAb-specific parameter governing organ/tissue pinocytosis transport and with estimates of the mAb’s SC lymphatic capillary clearance. These two relationships were incorporated into the model and accurately predicted the SC PK profiles of three out of four separate mAbs not included in model development. The whole-body physiologically-based model reported herein, provides a platform to characterize and predict the plasma disposition of monoclonal antibodies following SC administration in humans.

Introduction

Monoclonal antibodies (mAbs) are used in treating cancers, auto-immune, inflammatory and other diseases [1]. Between 2008 and 2019, the U.S. Food and Drug Administration (FDA) approved approximately 60 mAb-based treatments, 25 of which have involved subcutaneous (SC) delivery [2, 3]. The European Medicines Agency has approved 30 mAb products (including biosimilars) for SC administration since 2010 [4]. While SC delivery of mAbs for treating chronic diseases has significant advantages compared to intravenous (IV) administration [2, 5], it has been challenging to predict the variable absorption and delivery of mAbs following SC administration from preclinical experimental or modeling studies [6, 7].

For over 30 years, physiologically-based pharmacokinetic (PBPK) models have been applied to explore the disposition of mAbs for different applications, including inter-species scaling, guiding antibody engineering and predicting drug-drug interactions [8, 9]. In 1986, Covell et al. first applied a PBPK model to study the pharmacokinetics (PK) of an immunoglobulin G1 (IgG1) and antibody fragments in mice [10]. Baxter et al. scaled physiological parameters of mice to humans to predict clinical PK profiles of a mAb [11]. The influence of neonatal Fc receptor (FcRn) on mAb disposition was incorporated in a PBPK model by Ferl et al. [12] and by Garg and Balthasar [13]. In 2012, Shah and Betts reported a PBPK model platform for different species [14]. More recently, Glassman and Balthasar reported a comprehensive whole-body PBPK model to make priori predictions of the clinical PK of mAbs exhibiting target-mediated disposition [15], and Li and Balthasar applied this PBPK model framework to evaluate anti-FcRn therapy effects in humans [16].

Whole-body PBPK models and hybrid compartmental-PBPK models have been developed to describe and predict the absorption and SC PK of therapeutic proteins, including mAbs. In 2013, Zhao and coworkers coupled a compartment disposition model with a physiologically-based absorption model to quantify absorption process of mAbs after SC or intramuscular delivery [17]. Gill et al. developed a whole-body PBPK model for various protein drugs in humans [18], which represents SC tissues using model compartments that are linked to the circulatory system via blood flow and lymph flow anatomically. This model, however, does not account for FcRn-mediated recycling processes in the organ compartments, and requires previously determined values of the mAbs’ bioavailability. Offman et al. incorporated the lymphatic uptake pathway into a whole-body PBPK model for a peptide given subcutaneously [19]. More recently, Varkhede et al. developed a minimal PBPK model, composed of a two-compartment PK model and an expanded physiologically-based model of lymphatic system [20]. They also proposed that the isoelectric point (pI) of the mAb may be a predictor of its clearance and bioavailability following SC administration.

The above-mentioned models for SC absorption of mAbs have several limitations. The hybrid models ([17] and [20]), because of their compartmental components, are less suitable for preclinical to clinical translation, nor do they allow predictions of drug concentrations at sites of action. The previously published whole-body PBPK models ([18] and [19]) do not account for some important physiological processes involved with mAb transport, do not predict antibody SC bioavailability, and do not incorporate biophysical properties of the mAb to predict SC absorption and plasma PK.

In this study, we modified and extended the previous PBPK for IV administrated mAbs reported [15] to include a mechanistic representation of the pre-systemic degradation, trafficking and absorption of mAbs at the SC injection site. The model also incorporates a metric based on the local charge of the complementarity-determining regions of the mAb to explain differences among mAbs in organ transport processes, as well as degradation at the SC site. For each organ, the model represents transcapillary exchange using a two-pore transport theory and includes the sequential transit and processing of the mAb in the endosomal space of endothelial cells. The model for the central lymphatic system includes lumped lymph node and lymphatic vessel compartments, where the latter incorporates endothelial cell mAb processing. A peripheral sampling site is used to better reflect measured concentration in clinical studies. For the SC site model, both lymphatic capillary uptake and degradation processes are included. The mAb-specific model parameters were estimated using the whole body PBPK model and clinical intravenous (IV) plasma PK data from 20 mAbs and SC plasma PK data from 12 of these mAbs, as obtained from the literature. The model is used to predict bioavailability following SC administration, investigate the relative pathway specific contributions to systemic delivery from SC administration, and to examine, through sensitivity analysis, the role of key properties involved in SC absorption.

Methods

Clinical study data

Mean plasma concentrations following IV administration of the 20 mAbs listed in Table 1 and SC administration of 12 of these mAbs listed in Table 2 were digitized from figures reported in the cited publications. The molecular weights of these mAbs range from 1.42×10⁵ to 1.50×10⁵ g/mol. Data from most of the mAbs included results at multiple dose levels (see Tables 1 and 2). Dose normalization of PK data indicated no obvious non-linearity caused by target-mediated drug disposition. Mean plasma concentrations following the SC administration of another four mAbs (Omalizumab, Tildrakizumab, Ixekizumab, Lanadelumab) were also digitized from publications and used for further model evaluation as described below.

Table 1.

mAbs with plasma PK following IV administration. Also shown are the estimated drug-specific parameters (S_pino and S_diff-conv) determined using IV PK data for each mAb

mAb (abbreviation)	Molecular weight (g/mol ×105)	Dosing	Ref.	Spino (RSE%)	Sdiff-conv (RSE%)
Actoxumab (Act)	1.459	1–20 mg/kg	[67]	0.627 (5.2)	1.04 (5.7)
Adalimumab (Ada)	1.442	0.25–5 mg/kg	[68, 69]	1.19 (3.4)	1.24 (5.3)
Belimumab (Bel)	1.470	240mg	[70]	1.21 (2.6)	1.00 (10)
Canakinumab (Can)	1.452	1–3mg/kg; 600mg	[71]	0.868 (1.2)	1.15 (4.9)
Daclizumab (Dac)	1.426	200 mg; 400 mg	[72]	1.20 (1.3)	1.46 (6.6)
Enokizumab (Eno)	1.484	0.3–9 mg/kg	[73]	0.839 (2.7)	1.05 (4.7)
Figitumumab (Fig)	1.460	10 mg/kg; 20mg/kg	[74]	0.897 (2.1)	1.16 (7.6)
Gevokizumab (Gev)	1.452	0.01–3 mg/kg	[75]	0.833 (2.8)	0.823 (4.9)
GNbAC1 (GNb)	1.470	2 mg/kg; 6mg/kg	[76]	0.849 (11)	1.27 (9.6)
Golimumab (Gol)	1.469	100mg	[77]	2.14 (2.0)	1.49 (7.6)
Guselkumab (Gus)	1.436	0.03–10 mg/kg	[78]	1.43 (1.2)	1.89 (3.3)
Infliximab (Inf)	1.491	5 mg/kg	[79]	1.41 (3.4)	1.34 (9.7)
Mepolizumab (Mep)	1.492	250 mg	[80]	0.963 (2.4)	0.452 (13)
PAmAb (Pam)	1.500	1–40 mg/kg	[81]	1.13 (1.5)	0.640 (6.5)
Risankizumab (Ris)	1.456	200, 600, 1200mg	[82]	0.783 (3.2)	1.41 (5.9)
Siltuximab (Sil)	1.450	1–12 mg/kg	[83]	0.872 (11)	2.21 (5.6)
Tefibazumab (Tef)	1.476	10–20 mg/kg	[84]	1.23 (2.9)	1.62 (5.9)
Tralokinumab (Tral)	1.439	150 mg	[85]	0.936 (4.0)	0.630 (13)
Trastuzumab (Tras)	1.480	6mg/kg	[86]	1.16 (11)	0.822 (15)
Urtoxazumab (Urt)	1.446	0.1–3 mg/kg	[87]	0.742 (4.0)	0.981 (6.4)

Table 2.

mAbs with plasma PK following SC administration. Estimated drug-specific parameters ($C{L}_{\mathit{\text{LymCap}}}^{SC}$ and $S_{\mathit{\text{LymUpt}}}^{SC}$) in SC tissue site model using SC PK data are also shown for each mAb

mAb (abbreviation)	Dosing	Ref.	$C{L}_{\mathit{\text{LymCap}}}^{SC}$ (RSE%) (ml/day)	$S_{\mathit{\text{LymUpt}}}^{SC}$ (RSE%)
Adalimumab (Ada)	40 mg	[88]	0.957 (9.5)	0.166 (4.6)
Belimumab (Bel)	200, 240 mg	[70]	0.501 (15)	0.204 (3.9)
Canakinumab (Can)	150, 300 mg	[71]	0.798 (11)	0.220 (5.8)
Daclizumab (Dac)	50, 150, 300 mg	[72]	0.469 (17)	0.0904 (3.7)
Enokizumab (Eno)	1, 3, 9 mg/kg	[73]	0.441 (20)	0.301 (5.0)
Gevokizumab (Gev)	0.03, 0.3 mg/kg	[75]	0.732 (22)	0.130 (7.5)
Golimumab (Gol)	100 mg	[77]	2.72 (8.1)	0.193 (7.5)
Guselkumab (Gus)	10, 30, 100, 300 mg	[78]	3.66 (5.0)	0.283 (5.1)
Infliximab (Inf)	120 mg	[89]	0.950 (15)	0.262 (8.6)
Mepolizumab (Mep)	250 mg	[80]	0.700 (14)	0.272 (5.9)
Risankizumab (Ris)	18, 90, 300mg	[82]	1.38 (9.0)	0.217 (5.6)
Tralokinumab (Tral)	150, 300 mg	[85]	1.69 (7.4)	0.186 (5.2)

Model structure

The model builds upon that reported by Glassman and Balthasar to describe the PK of mAbs after IV administration [15]. A subcutaneous administration site and a central lymphatic system model were added to the model reported in [15], as depicted in Fig. 1. In addition, the model incorporates a two-pore formalism to describe vascular to interstitial exchange in each tissue as proposed by Li and Shah [21], along with a distinct peripheral blood sampling site.

Fig. 1.

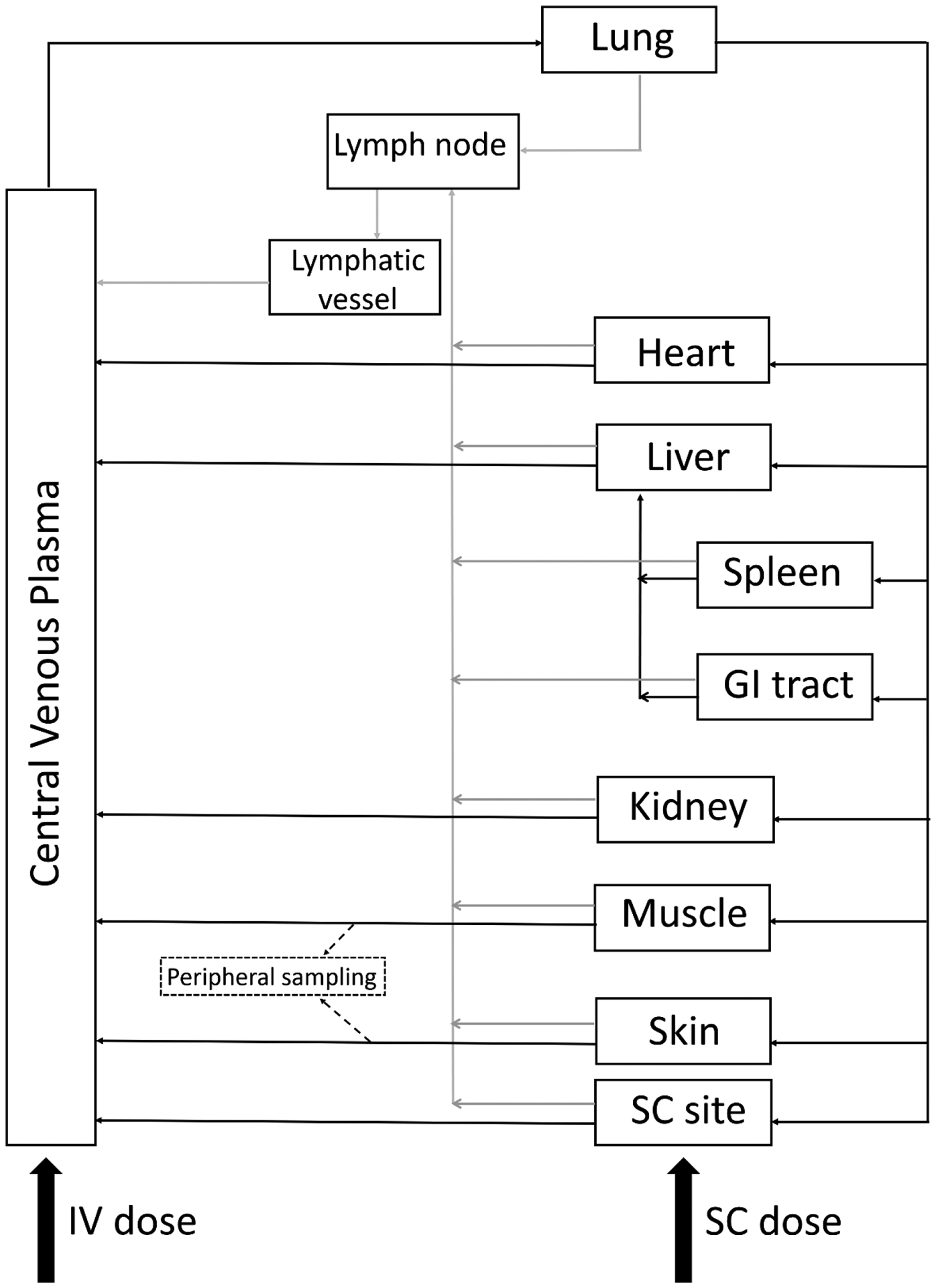
Schematic of the structure of the developed whole-body PBPK model for mAbs after IV or SC administration

Subcutaneous administration site

The model for the subcutaneous administration site is linked to the whole-body circulatory system through the SC administration site plasma flow (Q^SC) and lymph flow (L^SC). The subcutaneous tissue model is composed of the following spaces: plasma, endothelial, interstitial, lymphatic, and cell (see Fig. 2a). Following SC administration, the mAb distributes within the extracellular matrix (ECM) of SC tissue and exchanges with the blood capillaries and is transported to the local lymphatic capillaries before draining into the systemic venous plasma and central lymphatic system [22].

Fig. 2.

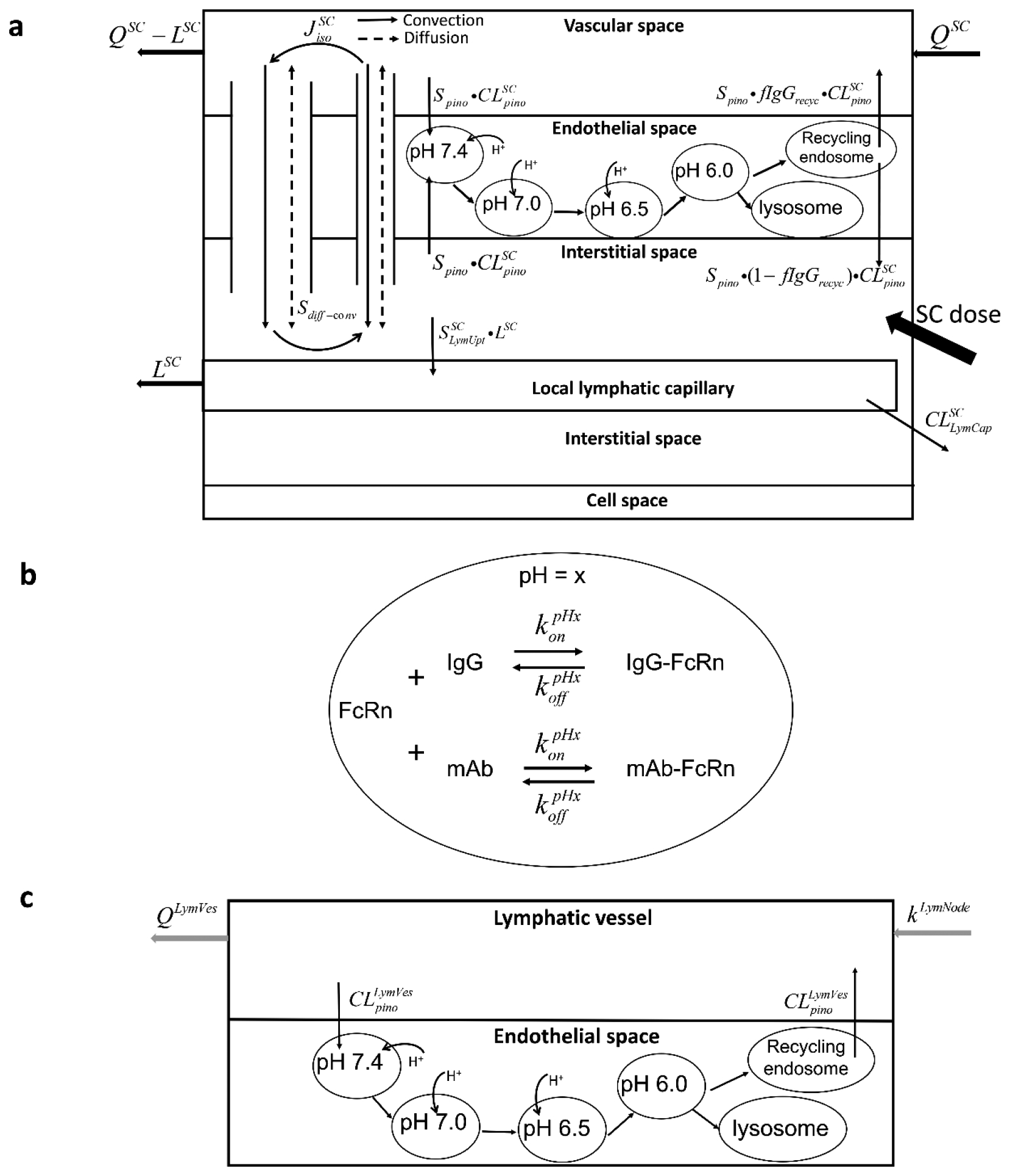
Schematic of the organ-level model. (a) of SC tissue, including vascular space, endothelial space (with endosomal sub-compartments), interstitial space and cells space. The SC dose was administrated into the interstitial space, from where mAbs can be drained into local lymphatic capillaries to enter the lymphatic system or be absorbed via blood perfusion. (b) of endosomal sub-compartments, representing the interaction of FcRn and IgG at a certain pH value (x). (c) of the lymphatic vessel, which is divided into lymph flow and lymphatic endothelial space

The predominant processes governing transport of IgG between the vascular and interstitial spaces are convection, diffusion and pinocytosis [23]. The work reported in [21] concluded that the transcapillary transport of therapeutic proteins (13 to 150 kDa) via convection and diffusion can be described using a two-pore model. Based on the model and results presented in [21, 24], the transport of 142–150 kDa mAbs could be described using a single (large) pore model. For generality and to allow for future extension, however, we have incorporated the two-pore model in this work (see Fig. 2a).

Exchange of IgG between the vascular and interstitial spaces also occurs via vascular endothelial pinocytosis followed by pH-dependent, FcRn-mediated endosomal processing [25]. To incorporate these mechanisms, we followed the approach in [15], which included separate, sequential pH-specific endosomal sub-compartments to represent this continuous endosomal processing. Based on the report in [26], we included four endosomal sub-compartments to represent early endosomal processing and sorting, each with a distinct pH value ranging from 7.4 to 6.0 (Fig. 2a). From the fourth sub-compartment, IgG is sorted into either a recycling endosome pool from which IgG is transported to the vascular and interstitial spaces, or into lysosome pool for proteolytic degradation (Fig. 2a).

Given these assumptions, and following Figs. 2a, the following equations can be written to describe the SC vascular space concentrations of endogenous IgG $\left(CIg{G}_{\mathit{\text{vasc}}}^{SC}\right)$ and administrated mAb $\left(CmA{b}_{\mathit{\text{vasc}}}^{SC}\right)$:

$$\begin{gathered} V_{\mathit{\text{vasc}}}^{SC}•\frac{\mathit{\text{dCIg}}{G}_{\mathit{\text{vasc}}}^{SC}}{dt}=Q^{SC}•CIg{G}_{\mathit{\text{vasc}}}^{\mathit{\text{Lung}}}-\left(Q^{SC}-L^{SC}\right)•CIg{G}_{\mathit{\text{vasc}}}^{SC} \\ -C{L}_{\mathit{\text{pino}}}^{SC}•CIg{G}_{\mathit{\text{vasc}}}^{SC}+fIg{G}_{\mathit{\text{recyc}}}•C{L}_{\mathit{\text{pino}}}^{SC}•{\mathit{\text{CIgFc}}}_{\mathit{\text{recyc}}}^{SC} \\ -P{S}_L^{SC}•\left(CIg{G}_{\mathit{\text{vasc}}}^{SC}-CIg{G}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_L}{e^{P{e}_L}-1}-P{S}_S^{SC}•\left(CIg{G}_{\mathit{\text{vasc}}}^{SC}-CIg{G}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_S}{e^{P{e}_s}-1} \\ -J_L^{SC}•\left(1-{\sigma }_L\right)•CIg{G}_{\mathit{\text{vasc}}}^{SC}-J_S^{SC}•\left(1-{\sigma }_S\right)•CIg{G}_{\mathit{\text{vasc}}}^{SC} \end{gathered}$$ (1)

$$\begin{gathered} V_{\mathit{\text{vasc}}}^{SC}•\frac{{\mathit{\text{dCmAb}}}_{\mathit{\text{vasc}}}^{SC}}{dt}=Q^{SC}•CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Lung}}}-\left(Q^{SC}-L^{SC}\right)•CmA{b}_{\mathit{\text{vasc}}}^{SC} \\ -S_{\mathit{\text{pino}}}•C{L}_{\mathit{\text{pino}}}^{SC}•CmA{b}_{\mathit{\text{vasc}}}^{SC}+S_{\mathit{\text{pino}}}•fIg{G}_{\mathit{\text{recyc}}}•C{L}_{\mathit{\text{pino}}}^{SC}•{\mathit{\text{CmAbFc}}}_{\mathit{\text{recyc}}}^{SC} \\ -S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•P{S}_L^{SC}•\left(CmA{b}_{\mathit{\text{vasc}}}^{SC}-CmA{b}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_L}{e^{P{e}_L}-1}-S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•P{S}_S^{SC}•\left(CmA{b}_{\mathit{\text{vasc}}}^{SC}-CmA{b}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_S}{e^{P{e}_s}-1} \\ -S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•J_L^{SC}•\left(1-{\sigma }_L\right)•CmA{b}_{\mathit{\text{vasc}}}^{SC}-S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•J_S^{SC}•\left(1-{\sigma }_S\right)•CmA{b}_{\mathit{\text{vasc}}}^{SC} \end{gathered}$$ (2)

The symbols for the model parameters and other concentration variables are defined in Table 3. The first lines of Eqs. (1) and (2) represent vascular perfusion of SC space, while the second lines reflect the uptake via pinocytosis and recycling pathway through vascular endothelial cells. The third lines in each equation represent the transport of IgG and mAb via diffusion through large and small pores driven by concentration differences $\left(CIg{G}_{\mathit{\text{vasc}}}^{sc}-CIg{G}_{\mathit{\text{inter}}}^{SC}\right)$ and $\left(CmA{b}_{\mathit{\text{vasc}}}^{SC}-CmA{b}_{\mathit{\text{inter}}}^{SC}\right)$, while the fourth lines describe convection through large and small pores. The values of the permeability surface area products ($P{S}_L^{SC}$ and $P{S}_S^{SC}$), Peclet numbers ($P{e}_L$ and $P{e}_S$), lymph flow ($J_L^{SC}$ and $J_S^{SC}$) and reflection coefficients (σ_L and σ_S) depend on mAb molecular weight as detailed below. Additional differences in exchange of mAbs relative to IgG were represented in Eq. (2) by scaling factors applied to pinocytosis (S_pino) and to the large and small pore diffusion and convention processes (S_diff-conv), following the approach in the IV PBPK model of [15]. These two drug-specific scaling factors were estimated for each mAb as described below.

Table 3.

Definitions of parameters and variables used in model equations

Parameter/variable	Unit	Definition
t	day	time
VPlasma	ml	Volume of central plasma compartment
CIgGPlasma	nM	Concentration of endogenous IgG in central plasma compartment
CmAbPlasma	nM	Concentration of administrated mAb in central plasma compartment
IgG0	nmol/day	Production rate of endogenous IgG
${}^a{V}_{\mathit{\text{vasc}}}^{\mathit{\text{Organ}}}$	ml	Volume of vascular space
$V_{\mathit{\text{inter}}}^{\mathit{\text{Organ}}}$	ml	Volume of interstitial space
$V_{\mathit{\text{endo}}}^{\mathit{\text{Organ}}}$	ml	Volume of endosomal space
$V_{\mathit{\text{endo}},sub}^{\mathit{\text{Organ}}}$	ml	Volume of endosomal sub-compartment
QOrgan	ml/day	Plasma flow
LOrgan	ml/day	Lymph flow
$CIg{G}_{\mathit{\text{vasc}}}^{\mathit{\text{Organ}}}$	nM	Concentration of endogenous IgG in vascular space
$CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Organ}}}$	nM	Concentration of administrated mAb in vascular space
$CIg{G}_{\mathit{\text{inter}}}^{\mathit{\text{Organ}}}$	nM	Concentration of endogenous IgG in interstitial space
$CmA{b}_{\mathit{\text{inter}}}^{\mathit{\text{Organ}}}$	nM	Concentration of administrated mAb in interstitial space
$CIg{G}_{pHx}^{\mathit{\text{Organ}}}$	nM	Concentration of free endogenous IgG in endosomal sub-compartment with pH = x of vascular endothelium
$CmA{b}_{pHx}^{\mathit{\text{Organ}}}$	nM	Concentration of free administrated mAb in endosomal sub-compartment with pH = x of vascular endothelium
${\mathit{\text{CIgFc}}}_{pHx}^{\mathit{\text{Organ}}}$	nM	Concentration of endogenous IgG-FcRn complex in endosomal sub-compartment with pH = x of vascular endothelium
${\mathit{\text{CmAbFc}}}_{pHx}^{\mathit{\text{Organ}}}$	nM	Concentration of administrated mAb-FcRn complex in endosomal sub-compartment with pH = x of vascular endothelium
$CIg{G}_{\mathit{\text{recyc}}}^{\mathit{\text{Organ}}}$	nM	Concentration of endogenous free IgG in recycling endosome of vascular endothelium
$CmA{b}_{\mathit{\text{recyc}}}^{\mathit{\text{Organ}}}$	nM	Concentration of endogenous free administrated mAb in recycling endosome of vascular endothelium
${\mathit{\text{CIgFc}}}_{\mathit{\text{recyc}}}^{\mathit{\text{Organ}}}$	nM	Concentration of endogenous IgG-FcRn complex in recycling endosome of vascular endothelium
${\mathit{\text{CmAbFc}}}_{\mathit{\text{recyc}}}^{\mathit{\text{Organ}}}$	nM	Concentration of administrated mAb-FcRn complex in recycling endosome of vascular endothelium
${\mathit{\text{CFcRn}}}_{pHx}^{\mathit{\text{Organ}}}$	nM	Concentration of FcRn in endosomal sub-compartment with pH = x of vascular endothelium
fIgGrecyc	-	IgG recycling fraction of IgG-FcRn complex back to vascular space
τ	day	IgG transit time through endosomal sub-compartments
$k_{on}^{pHx}$	nM−1day−1	Association rate constant between IgG and FcRn at pH = x
$k_{off}^{pHx}$	day−1	Dissociation rate constant between IgG and FcRn at pH = x
VLymCap	ml	Volume of local lymphatic capillaries
kLymNode	Day−1	Rate constant of mAb leaving lymph node
VLymVes	ml	Volume of lymphatic vessel compartment
QLymVes	ml/day	Lymph flow rate from lymphatic vessel compartment
AIGCLymNode	pmol	Amount of endogenous IgG in lymph node compartment
AmAbLymNode	pmol	Amount of administrated mAb in lymph node compartment
CIgGLymVes	nM	Concentration of endogenous IgG in lymphatic vessel compartment
CmAbLymVes	nM	Concentration of administrated mAb in lymphatic vessel compartment
CIgGLymCaP	nM	Concentration of endogenous IgG in local lymphatic capillary compartment
CmAbLymCap	nM	Concentration of administrated mAb in local lymphatic capillary compartment
σ	-	Lymph reflection coefficient
$C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Organ}}}$	ml/day	Pinocytosis rate of vascular endothelium
IVmAb(t)	pmol/day	Intravenous infusion rate of monoclonal antibodies
Dose	pmol	Subcutaneous dose of monoclonal antibodies
Spino	-	mAb specific pinocytosis transport rate scale factor
Sdiff–conv	-	mAb specific diffusion and convective transport scale factor
$C{L}_{\mathit{\text{LymCap}}}^{SC}$	ml/day	SC site lymphatic capillary mAb clearance
$S_{\mathit{\text{LymUpt}}}^{SC}$	-	SC site interstitial to lymphatic capillary mAb uptake scale factor
σS	−	Small pore vascular reflection coefficient
σL	−	Large pore vascular reflection coefficient
PeS	−	Peclet number of small pores
PeL	-	Peclet number of large pores
$P{S}_S^{\mathit{\text{Organ}}}$	ml/day	Permeability-surface area product of small pore of an organ
$P{S}_L^{\mathit{\text{Organ}}}$	ml/day	Permeability-surface area product of large of an organ
$J_{iso}^{\mathit{\text{Organ}}}$	ml/day	Circular isogravimetric flow of an organ
$J_S^{\mathit{\text{Organ}}}$	ml/day	Lymph flow through small pores of an organ
$J_L^{\mathit{\text{Organ}}}$	ml/day	Lymph flow through large pores of an organ

^aThe organs are listed in Table 4

In the endothelial space within each sub-compartment, the pH-dependent mass action between IgG and FcRn is modeled assuming pH specific association and dissociation rate constants ($k_{on}^{pHx}$ and $k_{off}^{pHx}$)as introduced in [15] (see Fig. 2b). In the endothelial sub-compartment for pH=7.4, the concentrations of $CIg{G}_{7.4}^{SC}$, $CIgF{c}_{7.4}^{SC}$, $CmA{b}_{7.4}^{SC}$ and ${\mathit{\text{CmAbFc}}}_{7.4}^{SC}$ can be described by the following equations:

$$\begin{gathered} \frac{{\mathit{\text{dCIgG}}}_{7.4}^{SC}}{dt}=\left(C{L}_{\mathit{\text{pino}}}^{SC}•CIg{G}_{\mathit{\text{vasc}}}^{SC}+C{L}_{\mathit{\text{pino}}}^{SC}•CIg{G}_{\mathit{\text{inter}}}^{SC}\right)/V_{\mathit{\text{endo}},sub}^{SC} \\ +k_{off}^{7.4}•{\mathit{\text{CIgFc}}}_{7.4}^{SC}-k_{on}^{7.4}•CIg{G}_{7.4}^{SC}•{\mathit{\text{CFcRn}}}_{7.4}^{SC}-\frac{1}{\tau }•CIg{G}_{7.4}^{SC} \end{gathered}$$ (3)

$$\frac{d{\mathit{\text{CIgFc}}}_{7.4}^{SC}}{dt}=k_{on}^{7.4}•CIg{G}_{7.4}^{SC}•{\mathit{\text{CFcRn}}}_{7.4}^{SC}-k_{off}^{7.4}•{\mathit{\text{CIgFc}}}_{7.4}^{SC}-\frac{1}{\tau }•{\mathit{\text{CIgFc}}}_{7.4}^{SC}$$ (4)

$$\begin{gathered} \frac{{\mathit{\text{dCmAb}}}_{7.4}^{SC}}{dt}=\left(S_{\mathit{\text{pino}}}•C{L}_{\mathit{\text{pino}}}^{SC}•CmA{b}_{\mathit{\text{vasc}}}^{SC}+S_{\mathit{\text{pino}}}•C{L}_{\mathit{\text{pino}}}^{SC}•CmA{b}_{\mathit{\text{inter}}}^{SC}\right)/V_{\mathit{\text{endo}},sub}^{SC} \\ +k_{off}^{7.4}•{\mathit{\text{CmAbFc}}}_{7.4}^{SC}-k_{on}^{7.4}•CmA{b}_{7.4}^{SC}•{\mathit{\text{CFcRn}}}_{7.4}^{SC}-\frac{1}{\tau }•CmA{\text{b}}_{7.4}^{SC} \end{gathered}$$ (5)

$$\frac{d{\mathit{\text{CmAbFc}}}_{7.4}^{SC}}{dt}=k_{on}^{7.4}•CmA{b}_{7.4}^{SC}•{\mathit{\text{CFcRn}}}_{7.4}^{SC}-k_{off}^{7.4}•{\mathit{\text{CmAbFc}}}_{7.4}^{SC}-\frac{1}{\tau }•{\mathit{\text{CmAbFc}}}_{7.4}^{SC}$$ (6)

The symbols for model parameters and concentration variables are defined in Table 3. The concentration of the FcRn receptor in this first endosomal sub-compartment $\left({\mathit{\text{CFcRn}}}_{pH7.4}^{SC}\right)$ is assumed to be constant at 3.3×10⁴ nM [15]. The first lines of Eqs. (3) and (5) represent uptake via pinocytosis of free IgG or free mAb from the SC site vascular and interstitial spaces, and the first two terms of the second lines of these equations reflect the interaction between FcRn and IgG. The second lines of Eqs. (3) and (5) represent the transit of IgG into the next sub-compartment. In Eqs. (4) and (6), the first two terms represent the interaction of IgG and FcRn and mAb-FcRn, while the last terms represent the transit of the IgG-FcRn and mAb-FcRn into the next sub-compartment.

The following equations described the corresponding concentrations for each species in endothelial sub-compartment for pH=7.0:

$$\frac{{\mathit{\text{dCIgG}}}_{7.0}^{SC}}{dt}=k_{off}^{7.0}•{\mathit{\text{CIgFc}}}_{7.0}^{SC}-k_{on}^{7.0}•CIg{G}_{7.0}^{SC}•{\mathit{\text{CFcRn}}}_{7.0}^{SC}+\frac{1}{\tau }•\left(CIg{G}_{7.4}^{SC}-CIg{G}_{7.0}^{SC}\right)$$ (7)

$$\frac{d{\mathit{\text{CIgFc}}}_{7.0}^{SC}}{dt}=k_{on}^{7.0}•CIg{G}_{7.0}^{SC}•{\mathit{\text{CFcRn}}}_{7.0}^{SC}-k_{off}^{7.0}•{\mathit{\text{CIgFc}}}_{7.0}^{SC}+\frac{1}{\tau }•\left({\mathit{\text{CIgFc}}}_{7.4}^{SC}-{\mathit{\text{CIgFc}}}_{7.0}^{SC}\right)$$ (8)

$$\frac{{\mathit{\text{dCmAb}}}_{7.0}^{SC}}{dt}=k_{off}^{7.0}•{\mathit{\text{CmAbFc}}}_{7.0}^{SC}-k_{on}^{7.0}•CmA{b}_{7.0}^{SC}•{\mathit{\text{CFcRn}}}_{7.0}^{SC}+\frac{1}{\tau }•\left(CmA{b}_{7.4}^{SC}-CmA{b}_{7.0}^{SC}\right)$$ (9)

$$\frac{d{\mathit{\text{CmAbFc}}}_{7.0}^{SC}}{dt}=k_{on}^{7.0}•CmA{b}_{7.0}^{SC}•{\mathit{\text{CFcRn}}}_{7.0}^{SC}-k_{off}^{7.0}•{\mathit{\text{CmAbFc}}}_{7.0}^{SC}+\frac{1}{\tau }•\left({\mathit{\text{CmAbFc}}}_{7.4}^{SC}-{\mathit{\text{CmAbFc}}}_{7.0}^{SC}\right)$$ (10)

$$\begin{gathered} \frac{d{\mathit{\text{CFcRn}}}_{pH7.0}^{SC}}{dt}=k_{off}^{7.0}•{\mathit{\text{CIgFc}}}_{7.0}^{SC}-k_{on}^{7.0}•CIg{G}_{7.0}^{SC}•{\mathit{\text{CFcRn}}}_{7.0}^{SC} \\ +k_{off}^{7.0}•{\mathit{\text{CmAbFc}}}_{7.0}^{SC}-k_{on}^{7.0}•CmA{b}_{7.0}^{SC}•{\mathit{\text{CFcRn}}}_{7.0}^{SC} \\ +\frac{1}{\tau }•\left({\mathit{\text{CFcRn}}}_{pH7.4}^{SC}-{\mathit{\text{CFcRn}}}_{pH7.0}^{SC}\right) \end{gathered}$$ (11)

The symbols for the concentration variables and model parameters are defined in Table 3. The first two terms of Eqs. (7)–(10) reflect the interaction of FcRn and IgG at pH = 7.0. The remaining terms in these equations represent the transit of IgG from the previous, to the next sub-compartment. In Eq. (11), the first two lines represent the interaction of FcRn with endogenous IgG and administrated mAb, and the third line reflects the transit through the FcRn pool. A similar set of equations (not shown) can be written for the endothelial sub-compartment for pH = 6.5.

For the endothelial sub-compartment with pH=6.0, the following equations apply:

$$\frac{{\mathit{\text{dCIgG}}}_{6.0}^{SC}}{dt}=k_{off}^{6.0}•{\mathit{\text{CIgFc}}}_{6.0}^{SC}-k_{on}^{6.0}•CIg{G}_{6.0}^{SC}•{\mathit{\text{CFcRn}}}_{6.0}^{SC}+\frac{1}{\tau }•\left(CIg{G}_{6.5}^{SC}-CIg{G}_{6.0}^{SC}\right)$$ (12)

$$\frac{d{\mathit{\text{CIgFc}}}_{6.0}^{SC}}{dt}=k_{on}^{6.0}•CIg{G}_{6.0}^{SC}•{\mathit{\text{CFcRn}}}_{6.0}^{SC}-k_{off}^{6.0}•{\mathit{\text{CIgFc}}}_{6.0}^{SC}+\frac{1}{\tau }•\left({\mathit{\text{CIgFc}}}_{6.5}^{SC}-{\mathit{\text{CIgFc}}}_{6.0}^{SC}\right)$$ (13)

$$\frac{{\mathit{\text{dCmAb}}}_{6.0}^{SC}}{dt}=k_{off}^{6.0}•{\mathit{\text{CmAbFc}}}_{6.0}^{SC}-k_{on}^{6.0}•CmA{b}_{6.0}^{SC}•{\mathit{\text{CFcRn}}}_{6.0}^{SC}+\frac{1}{\tau }•\left(CmA{b}_{6.5}^{SC}-CmA{b}_{6.0}^{SC}\right)$$ (14)

$$\frac{d{\mathit{\text{CmAbFc}}}_{6.0}^{SC}}{dt}=k_{on}^{6.0}•CmA{b}_{6.0}^{SC}•{\mathit{\text{CFcRn}}}_{6.0}^{SC}-k_{off}^{6.0}•{\mathit{\text{CmAbFc}}}_{6.0}^{SC}+\frac{1}{\tau }•\left({\mathit{\text{CmAbFc}}}_{6.5}^{SC}-{\mathit{\text{CmAbFc}}}_{6.0}^{SC}\right)$$ (15)

$$\begin{gathered} \frac{d{\mathit{\text{CFcRn}}}_{pH6.0}^{SC}}{dt}=k_{off}^{6.0}•{\mathit{\text{CIgFc}}}_{6.0}^{SC}-k_{on}^{6.0}•CIg{G}_{6.0}^{SC}•{\mathit{\text{CFcRn}}}_{6.0}^{SC} \\ +k_{off}^{6.0}•{\mathit{\text{CmAbFc}}}_{6.0}^{SC}-k_{on}^{6.0}•CmA{b}_{6.0}^{SC}•{\mathit{\text{CFcRn}}}_{6.0}^{SC} \\ +\frac{1}{\tau }•\left({\mathit{\text{CFcRn}}}_{pH6.5}^{SC}-{\mathit{\text{CFcRn}}}_{pH6.0}^{SC}\right) \end{gathered}$$ (16)

See Table 3 for the definition of the concentration variables parameter symbols. The last terms of Eqs. (12) and (14) represent free IgG and free mAb transported into lysosome for degradation. The last terms of Eqs. (13) and (15) represent the transport of FcRn-bound IgG and FcRn-bound mAb into recycling endosome.

The following equations describe the concentrations of IgG-FcRn $\left({\mathit{\text{CIgFc}}}_{\mathit{\text{recyc}}}^{SC}\right)$ and mAb-FcRn $\left({\mathit{\text{CmAbFc}}}_{\mathit{\text{recyc}}}^{SC}\right)$ in the recycling endosome pool:

$$\frac{d{\mathit{\text{CIgFc}}}_{\mathit{\text{recyc}}}^{SC}}{dt}=\frac{1}{\tau }•{\mathit{\text{CIgFc}}}_{6.0}^{SC}-C{L}_{\mathit{\text{pino}}}^{SC}•{\mathit{\text{CIgFc}}}_{\mathit{\text{recyc}}}^{SC}/V_{\mathit{\text{endo}},sub}^{SC}$$ (17)

$$\frac{d{\mathit{\text{CmAbFc}}}_{\mathit{\text{recyc}}}^{SC}}{dt}=\frac{1}{\tau }•{\mathit{\text{CmAbFc}}}_{6.0}^{SC}-S_{\mathit{\text{pino}}}•C{L}_{\mathit{\text{pino}}}^{SC}•{\mathit{\text{CmAbFc}}}_{\mathit{\text{recyc}}}^{SC}/V_{\mathit{\text{endo}},sub}^{SC}$$ (18)

where the second terms in Eqs. (17) and (18) represent the recycling of IgG-FcRn and mAb-FcRn into the vascular and interstitial spaces of the subcutaneous site.

From Fig. 2a, the following equations can be written to describe the interstitial concentrations of endogenous IgG $\left(CIg{G}_{\mathit{\text{inter}}}^{SC}\right)$ and administrated mAb $\left(CmA{b}_{\mathit{\text{inter}}}^{SC}\right)$:

$$\begin{gathered} V_{\mathit{\text{inter}}}^{SC}\frac{{\mathit{\text{dCIgG}}}_{\mathit{\text{inter}}}^{SC}}{dt}=\left(1-fIg{G}_{\mathit{\text{recyc}}}\right)•C{L}_{\mathit{\text{pino}}}^{SC}•{\mathit{\text{CIgFc}}}_{\mathit{\text{recyc}}}^{SC}-C{L}_{\mathit{\text{pino}}}^{SC}•CIg{G}_{\mathit{\text{inter}}}^{SC}-L^{SC}•CIg{G}_{\mathit{\text{inter}}}^{SC} \\ +P{S}_L^{SC}•\left(CIg{G}_{\mathit{\text{vasc}}}^{SC}-CIg{G}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_L}{e^{P{e}_L}-1}+P{S}_S^{SC}•\left(CIg{G}_{\mathit{\text{vasc}}}^{SC}-CIg{G}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_S}{e^{P{e}_s}-1} \\ +J_L^{SC}•\left(1-{\sigma }_L\right)•CIg{G}_{\mathit{\text{vasc}}}^{SC}+J_S^{SC}•\left(1-{\sigma }_S\right)•CIg{G}_{\mathit{\text{vasc}}}^{SC} \end{gathered}$$ (19)

$$\begin{gathered} V_{\mathit{\text{inter}}}^{SC}\frac{{\mathit{\text{dCmAb}}}_{\mathit{\text{inter}}}^{SC}}{dt}=S_{\mathit{\text{pino}}}•\left(1-fIg{G}_{\mathit{\text{recyc}}}\right)•C{L}_{\mathit{\text{pino}}}^{SC}•{\mathit{\text{CmAbFc}}}_{\mathit{\text{recyc}}}^{SC}-S_{\mathit{\text{pino}}}•C{L}_{\mathit{\text{pino}}}^{SC}•CmA{b}_{\mathit{\text{inter}}}^{SC}-S_{\mathit{\text{LymUpt}}}^{SC}•L^{SC}•CmA{b}_{\mathit{\text{inter}}}^{SC} \\ +S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•P{S}_L^{SC}•\left(CmA{b}_{\mathit{\text{vasc}}}^{SC}-CmA{b}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_L}{e^{P{e}_L}-1}+S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•P{S}_S^{SC}•\left(CmA{b}_{\mathit{\text{vasc}}}^{SC}-CmA{b}_{\mathit{\text{inter}}}^{SC}\right)•\frac{P{e}_S}{e^{P{e}_s}-1} \\ +S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•J_L^{SC}•\left(1-{\sigma }_L\right)•CmA{b}_{\mathit{\text{vasc}}}^{SC}+S_{\mathit{\text{diff}}-\mathit{\text{conv}}}•J_S^{SC}•\left(1-{\sigma }_S\right)•CmA{b}_{\mathit{\text{vasc}}}^{SC} \end{gathered}$$ (20)

The symbols for the concentration variables and model parameters are defined in Table 3. The initial concentration of mAb in SC interstitial space $\left(CmA{b}_{\mathit{\text{inter}}}^{SC}\left(0\right)\right)$ is $\mathit{\text{Dose}}/V_{\mathit{\text{inter}}}^{SC}$. In the first lines of these equations, the third term represents lymphatic transport of IgG or mAbs to the local lymphatic capillaries. Nearly first-order removal of IgG from SC administration site after a short stay was demonstrated in previous studies [27, 28], thus it is described using a constant SC site lymph flow (L^SC). The differences in lymphatic uptake of mAbs compared to IgG is modeled using a scaling factor $\left(S_{\mathit{\text{LymUpt}}}^{SC}\right)$ in Eq. (20). Other terms correspond to those in previous equations.

Compared to blood vessels, lymphatic capillaries possess larger gaps between endothelial cells, have greater vessel diameters, and do not have well-defined basement membranes [29]. Thus, lymphatic uptake is believed to be the major absorption process for subcutaneously delivered mAbs, considering their large molecular weight [2]. Degradation of mAbs occurs at the SC site interstitial space, local lymphatic capillaries and lymphatic vessels, via proteolytic enzymes and/or soluble and cell-membrane targets [25]. Without quantitative information on the relative contribution of different catabolic pathways at these sites [6], the model characterizes mAb degradation using a net clearance term $\left(C{L}_{\mathit{\text{LymCap}}}^{SC}\right)$ assigned to the local lymphatic capillary compartment (see Fig. 2a). The equations below describe the local SC lymphatic capillary concentrations of IgG $\left(CIg{G}^{\mathit{\text{LymCap}}}\right)$ and mAb $\left(CmA{b}^{\mathit{\text{LymCap}}}\right)$:

$$V^{\mathit{\text{LymCap}}}\frac{{\mathit{\text{dCIgG}}}^{\mathit{\text{LymCap}}}}{dt}=L^{SC}•CIg{G}_{\mathit{\text{inter}} }^{SC}-L^{SC}•CIg{G}^{\mathit{\text{LymCap}}}$$ (21)

$$V^{\mathit{\text{LymCap}}}\frac{{\mathit{\text{dCmAb}}}^{\mathit{\text{LymCap}}}}{dt}=S_{\mathit{\text{LymUpt}}}^{SC}•L^{SC}•CmA{b}_{\mathit{\text{inter}}}^{SC}-L^{SC}•CmA{b}^{\mathit{\text{LymCap}}}-C{L}_{\mathit{\text{LymCap}}}^{SC}•CmA{b}^{\mathit{\text{LymCap}}}$$ (22)

See Table 3 for the definition of the concentration variables parameter symbols. In the Eqs. (21) and (22), the first terms represent the lymph flow (L^SC) from the SC interstitial space and the second terms are lymph drainage into the lymph node. The last term in Eq. (22) is the first-order pre-systemic degradation of mAb with the clearance rate $C{L}_{\mathit{\text{LymCap}}}^{SC}$. In contrast, the degradation of endogenous IgG in SC site is assumed to be negligible given that it represents such a small fraction of the overall degradation of IgG from all the other organs and tissues.

Central lymphatic system model

The model used to describe the central lymphatic system is illustrated in Fig. 1. The lymph flow draining all organs and tissues is assumed to be collected in a lumped lymph node compartment. A single lymphatic vessel compartment (Fig. 2c) is used to represent all central lymphatic vessels (e.g. lymphatic trunks, thoracic duct, etc). Based on the previous confirmation of the existence of FcRn in lymphatic vessels [30, 31], FcRn-mediated protection of IgG in lymphatic vessel endothelium was also included in the model. The following equations describe the amount of IgG and mAb in the lymph node (Eqs. (23) and (23)) and their concentrations in the lymphatic vessel (Eqs. (25) and (26)) compartments:

$$\frac{{\mathit{\text{dAIgG}}}_{\mathit{\text{LymNode}}}}{dt}=\sum \left(1-\sigma \right)•L^{\mathit{\text{Organ}}}•CIg{G}_{\mathit{\text{inter}}}^{\mathit{\text{Organ}}}+L^{SC}•CIg{G}^{\mathit{\text{LymCap}}}-k^{\mathit{\text{LymNode}}}•AIg{G}^{\mathit{\text{LymNode}}}$$ (23)

$$\frac{{\mathit{\text{dAmAb}}}_{\mathit{\text{LymNode}}}}{dt}=\sum \left(1-\sigma \right)•L^{\mathit{\text{Organ}}}•CmA{b}_{\mathit{\text{inter}}}^{\mathit{\text{Organ}}}+L^{SC}•CmA{b}^{\mathit{\text{LymCap}}}-k^{\mathit{\text{LymNode}}}•AmA{b}^{\mathit{\text{LymNode}}}$$ (24)

$$\begin{gathered} V^{\mathit{\text{LymVes}}}\frac{{\mathit{\text{dCIgG}}}^{\mathit{\text{LymVes}}}}{dt}=k^{\mathit{\text{LymNode}}}•AIg{G}^{\mathit{\text{LymNode}}}-Q^{\mathit{\text{LymVes}}}•CIg{G}^{\mathit{\text{LymVes}}} \\ -C{L}_{\mathit{\text{pino}}}^{\mathit{\text{LymVes}}}•CIg{G}^{\mathit{\text{LymVes}}}+C{L}_{\mathit{\text{pino}}}^{\mathit{\text{LymVes}}}•{\mathit{\text{CIgFc}}}_{\mathit{\text{recyc}}}^{\mathit{\text{LymVes}}} \end{gathered}$$ (25)

$$\begin{gathered} V^{\mathit{\text{LymVes}}}\frac{{\mathit{\text{dCmAb}}}^{\mathit{\text{LymVes}}}}{dt}=k^{\mathit{\text{LymNode}}}•AmA{b}^{\mathit{\text{LymNode}}}-Q^{\mathit{\text{LymVes}}}•CmA{b}^{\mathit{\text{LymVes}}} \\ -S_{\mathit{\text{pino}}}•C{L}_{\mathit{\text{pino}}}^{\mathit{\text{LymVes}}}•CmA{b}^{\mathit{\text{LymVes}}}+S_{\mathit{\text{pino}}}•C{L}_{\mathit{\text{pino}}}^{\mathit{\text{LymVes}}}•{\mathit{\text{CmAbFc}}}_{\mathit{\text{recyc}}}^{\mathit{\text{LymVes}}} \end{gathered}$$ (26)

The symbols for the concentration variables and model parameters are defined in Table 3. The last terms of Eqs. (23) and (24) represent transit of IgG or mAb from the lymph node compartment, corresponding to the first terms of Eqs. (25) and (26). The second term of Eqs. (25) and (26) represent the transportation of IgG or mAb from lymphatic vessels. The equations for the transit and FcRn-mediated processing of IgG in endosomal sub-compartments follow those presented above for the SC endothelial space.

Central venous plasma

In the model, the central plasma compartment represents the systemic central venous pool, not including the vascular spaces in the organ compartments (Fig. 1) [32]. The endogenous IgG concentration $\left(CIg{G}^{\mathit{\text{Plasma}}}\right)$ in and mAb concentrations $\left(CmA{b}^{\mathit{\text{Plasma}}}\right)$ in central venous plasma can be written:

$$\begin{gathered} V^{\mathit{\text{Plasma}}}\frac{{\mathit{\text{dCIgG}}}^{\mathit{\text{Plasma}}}}{dt}=1000•IgG0+\left(Q^{\mathit{\text{Liver}}}-L^{\mathit{\text{Liver}}}\right)•CIg{G}_{\mathit{\text{vasc}}}^{\mathit{\text{Liver}}}+\left(Q^{\mathit{\text{Heart}}}-L^{\mathit{\text{Heart}}}\right)•CIg{G}_{\mathit{\text{vasc}}}^{\mathit{\text{Heart}}} \\ +\left(Q^{\mathit{\text{Kidney}}}-L^{\mathit{\text{Kidney}}}\right)•CIg{G}_{\mathit{\text{vasc}}}^{\mathit{\text{Kidney}}}+\left(Q^{\mathit{\text{Skin}}}-L^{\mathit{\text{Skin}}}\right)•CIg{G}_{\mathit{\text{vasc}}}^{\mathit{\text{Skin}}}+\left(Q^{\mathit{\text{Muscle}}}-L^{\mathit{\text{Muscle}}}\right)•CIg{G}_{\mathit{\text{vasc}}}^{\mathit{\text{Muscle}}} \\ +\left(Q^{SC}-L^{SC}\right)•CIg{G}_{\mathit{\text{vasc}}}^{SC}-Q^{\mathit{\text{Lung}}}•CIg{G}^{\mathit{\text{Plasma}}}+Q^{\mathit{\text{LymVes}}}•CIg{G}^{\mathit{\text{LymVes}}} \end{gathered}$$ (27)

$$\begin{gathered} V^{\mathit{\text{Plasma}}}\frac{{\mathit{\text{dCmAb}}}^{\mathit{\text{Plasma}}}}{dt}=\left(Q^{\mathit{\text{Liver}}}-L^{\mathit{\text{Liver}}}\right)•CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Liver}}}+\left(Q^{\mathit{\text{Heart}}}-L^{\mathit{\text{Heart}}}\right)•CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Heart}}} \\ +\left(Q^{\mathit{\text{Kidney}}}-L^{\mathit{\text{Kidney}}}\right)•CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Kidney}}}+\left(Q^{\mathit{\text{Skin}}}-L^{\mathit{\text{Skin}}}\right)•CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Skin}}}+\left(Q^{\mathit{\text{Muscle}}}-L^{\mathit{\text{Muscle}}}\right)•CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Muscle}}} \\ +\left(Q^{SC}-L^{SC}\right)•CmA{b}_{\mathit{\text{vasc}}}^{SC}-Q^{\mathit{\text{Lung}}}•CmA{b}^{\mathit{\text{Plasma}}}+Q^{\mathit{\text{LymVes}}}•CmA{b}^{\mathit{\text{LymVes}}}+\mathit{\text{IVmAb}}\left(t\right) \end{gathered}$$ (28)

Table 3 lists model parameter and variable definitions. In the above equations IgG0 represents the endogenous IgG production rate and IVmAb(t) is the rate of the intravenous infusion.

Peripheral sampling site

To better reflect the sampled peripheral venous mAb plasma concentration, especially for predictions at very early times immediately following IV administration, the model incorporates a separate peripheral sampling site compartment, following the approach reported in [33]. The peripheral sampling is composed of contributions from skin and muscle (Fig. 1) as follows: $CmA{b}^{\mathit{\text{peri}}·}=0.7•CmA{b}_{\mathit{\text{vasc}}·}^{\mathit{\text{Skin}}}+0.3•CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Muscle}}·}$, where CmAb^peri is the measured peripheral mAb concentration, $CmA{b}_{\mathit{\text{vasc}} }^{\mathit{\text{Skin}}}$ is the administrated mAb concentration in vascular space of skin and $CmA{b}_{\mathit{\text{vasc}}}^{\mathit{\text{Muscle }}}$ is the mAb concentration in muscle vascular space.

Models for other organs/tissues

The model structures of other organs and tissues are the same as those presented above for the subcutaneous tissue (Fig. 2a and Eqs. (1)–(20)). Since these organs do not receive direct administration of mAb, the distribution of mAb into local lymphatic capillaries is expected to be low due to significantly slower lymph flow relative to plasma. Thus, a local lymphatic capillary compartment for these organs was not included. The supplemental materials include the full set of equations for the complete model presented in this work.

Model parameters

Individual organs and tissues

Values for those model parameters that are related to the individual organs/tissues were fixed based on literature reported values for humans [11], including vascular volume $\left(V_{\mathit{\text{vasc}}}^{\mathit{\text{Organ}}}\right)$, interstitial volume $\left(V_{\mathit{\text{inter}}}^{\mathit{\text{Organ}}}\right)$, cell volume $\left(V_{\mathit{\text{cell}}}^{\mathit{\text{Organ}}}\right)$, plasma flow (Q^Organ) and lymph flow (L^Organ) (Table 4). The FcRn concentrations in liver and gastrointestinal tract, which are assumed constant, were assigned based on reported values obtained using quantitative Western blot [34], while the FcRn concentrations in all other organs $\left({\mathit{\text{CFcRn}}}_{7.4}^{\mathit{\text{Organ}}}\right)$ were fixed at 3.3×10⁴ nM as in [15] (see FcRn column in Table 4).

Table 4.

Fixed physiological parameters of individual organs/tissues specified in the whole-body PBPK model

Tissue	Vascular volume (ml)a $V_{\mathit{\text{vasc}}}^{\mathit{\text{Organ}}}$		Interstitial volume (ml)a $V_{\mathit{\text{inter}}}^{\mathit{\text{Organ}}}$	Cell volume (ml)a $V_{\mathit{\text{cell}}}^{\mathit{\text{Organ}}}$	Plasma flow (ml/day)a QOrgan	Lymph flow (ml/day)b LOrgan	FcRn (nM)c ${\mathit{\text{CFcRn}}}_{7.4}^{\mathit{\text{Organ}}}$	Vascular IgG clearance via pinocytosis (ml/day) $C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Organ}}}$	Endosomal volume (ml) $V_{\mathit{\text{endo}}}^{\mathit{\text{Organ}}}$
Lung	99.90	300.0		599.0	3.152×106 d	3463	3.300×104	3.306	0.01240
Heart	15.00	42.90		242.0	1.728×105	190.1	3.300×104	0.9927	0.003723
Liver	181.0	362.0		1270	1.152×106	1267	3.300×104	5.986	0.02245
Spleen	17.00	34.70		122.0	1.987×105	218.6	3.300×104	0.5744	0.002154
GI Tract	43.00	373.0		1730	6.739×105	741.3	4180	7.104	0.02664
Kidney	28.40	96.60		159.0	9.072×105	997.9	3.300×104	0.9397	0.003524
Muscle	700.0	4560		2.97×104	5.947×105	654.2	3.300×104	115.8	0.4343
Skin	462.0	2313d		6110	3.168×105	348.5	3.300×104	22.50	0.08438
SC site	0.6200	3.115		8.230	2952	3.240	3.300×104	0.03961	0.0001485

^aFrom Baxter et al [11].

^bAssumed to be 0.11 % of organ plasma flow, resulting in total prenodal lymph flow ~8000 ml/day as reported in [35].

^cFixed to whole-body load of FcRn concentration measured by Li et al. [34] or from Glassman et al [15].

Central venous and lymphatic systems

Total body plasma volume used in the model was 2750 ml, assuming a total blood volume of 5 L and hematocrit of 0.45. The sum of individual organ vascular volumes $\left(V_{\mathit{\text{vasc}}}^{\mathit{\text{Organ}}}\right)$ was subtracted from total plasma volume, yielding the volume of central venous plasma pool (V^Plasma = 1202 ml). The total plasma flow (Q^SC) was calculated as the sum of the individual organ/tissue plasma flows (3.152×10⁶ ml/day). Values of the parameters related to central venous system are listed in Table 5.

Table 5.

Fixed parameter values for central venous and lymphatic systems

Parameter (unit)	Value	Description	Ref.
Central venous
QPlasma (ml/day)	3.152×106	Plasma flow	(see text)
VPlasma (ml)	1202	Central plasma volume	(see text)
IgG0 (nmol/day)	1.540×104	Production rate of endogenous IgG	[41]
Central lymphatic
VLymNode (ml)	175.2	Volume of lymph node compartment	[35, 36]
QLymNode (ml/day)	4000	Post-nodal lymph flow	[35]
kLymNode (day−1)	23.83	Rate constant of mAb leaving lymph node	(see text)
VLymVes (ml)	11.35	Volume of lymphatic vessel compartment	[20, 37]
QLymVes (ml/day)	4000	Lymph flow rate from lymphatic vessel compartment	(see text)
σ	0.2	Lymph reflection coefficient	[14, 15]

Also listed in Table 5, are the values used for the parameters of the central lymphatic system. The model used a total number of lymph nodes in humans of 600 [35], with an average lymph node volume of 0.292 ml [20, 36]. Thus, the volume of the composite lymph node compartment in the model (V^LymNode) was calculated as 175.2 ml. After water reabsorption in lymph node, post-nodal lymph flow (Q^LymNode) is 4000 ml/day [35]. The transport of endogenous IgG and mAb in the lymph node are described by Eqs. (23) and (24), with a rate constant (k^LymNode), calculated as the ratio of Q^LymNode and V^LymNode , of 23.83 day⁻¹. The lymphatic vessel compartment includes the lymphatic trunks, thoracic duct and cysterna chyli. The volume of the lymphatic trunk was calculated as 0.94 ml, using a length of 30 cm and radius of 1 mm [37]. The volume of thoracic duct and cysterna chyli were determined to be 8.84 ml and 1.57 ml, respectively [20]. Thus, the volume of lymphatic vessels (V^LymVes) summed to 11.35 ml. The lymph flow rate through lymphatic vessel (Q^LymVes) was set at 4000 ml/day - the sum of the lymph flow from all organs/tissues. Finally, the reflection coefficient for lymph (σ) was set at 0.2 in the lymphatic vessel and used for all organs [14, 15].

Subcutaneous tissue site

The last row of Table 4 also lists values for parameters associated with the SC injection site. The interstitial space volume at the SC site $\left(V_{\mathit{\text{inter}}}^{SC}\right)$ was set as 3.115 ml based on the previous work [18], yielding a ratio of SC to skin interstitial volumes $\left(V_{\mathit{\text{inter}}}^{SC}/V_{\mathit{\text{inter}}}^{\mathit{\text{Skin}}}\right)$ of 0.00135. The same fraction was used for the other volumes of the SC site, yielding a SC site total volume and vascular volume of 11.97 ml and 0.6200 ml, respectively. Based on radiobelled IgG studies [27, 38], the baseline lymph flow from a SC injection site (L^SC) was determined to be 3.240 ml/day. As with the other organs and tissues, L^SC was also assumed to be 0.11 % of the SC plasma flow rate (Q^SC = 2952 ml/day). Based on lymphangiograms performed in control arms of subjects [28], the maximum spread of local lymphatic vessels from the injection site was fixed at 1.59 cm and the total length of lymphatic capillaries in a 1-cm annulus was 385 cm, resulting in a lymphatic capillary length of 612.15 cm. Assuming an average radius of 0.0274 mm [20, 37], the volume of the local lymphatic capillary compartment (V^LymCap) was calculated as 0.0144 ml.

Endosomal processing and two-pore transcapillary transport

The IgG-FcRn interaction rate constants ($k_{on}^{pHx}$ and $k_{off}^{pHx}$) and endosomal transit rate (τ) of IgG were fixed (see Table 6) at values used in the PBPK model in [15]. The FcRn binding affinity was fixed for all mAbs, because of the lack of information about the effect of Fv properties on FcRn binding (e.g., quantitative relationship between Fv positive charge and FcRn-IgG binding affinity at neutral pH). The transit time (τ) of IgG in the fourth endosomal sub-compartment was assumed to be 0.001875 day, the same as the previous transit steps. The volume of endosomal sub-compartment for each organ $\left(V_{\mathit{\text{endo}},sub}^{\mathit{\text{Organ}}}\right)$ was calculated as one fifth of its endosomal space $\left(V_{\mathit{\text{endo}},sub}^{\mathit{\text{Organ}}}=V_{\mathit{\text{endo}}}^{\mathit{\text{Organ}}}/5\right)$.

Table 6.

Fixed parameter values for endosomal processing and trans-capillary transport of mAbs

Parameter (unit)	Value	Description	Ref.
All organs, tissues and mAbs
τ (day)	0.001875	Transit time of IgG between endosomal sub-compartments	[15]
fIgGrecyc	0.7150	IgG recycling fraction of IgG-FcRn complex back to vascular space	[13]
$k_{on}^{6.0}$ (nM−1day−1)	13.42	Association rate constant between IgG and FcRn at pH = 6.0	[15]
$k_{on}^{6.5}$ (nM−1day−1)	1.354	Association rate constant between IgG and FcRn at pH = 6.5	[15]
$k_{on}^{7.0}$ (nM−1day−1)	0.6336	Association rate constant between IgG and FcRn at pH = 7.0	[15]
$k_{on}^{7.4}$ (nM−1day−1)	0	Association rate constant between IgG and FcRn at pH = 7.4	[15]
$k_{off}^{6.0}$ (day−1)	573.1	Dissociation rate constant between IgG and FcRn at pH = 6.0	[15]
$k_{off}^{6.5}$ (day−1)	573.1	Dissociation rate constant between IgG and FcRn at pH = 6.5	[15]
$k_{off}^{7.0}$ (day−1)	573.1	Dissociation rate constant between IgG and FcRn at pH = 7.0	[15]
$k_{off}^{7.4}$ (day−1)	0	Dissociation rate constant between IgG and FcRn at pH = 7.4	[15]
rS (nm)	4.440	Small pore radius	[21]
rL (nm)	22.85	Large pore radius	[21]
αS	0.9580	Fractional hydraulic conductance of small pores	[21]
αL	0.04200	Fractional hydraulic conductance of large pores	[21]
Adjusted for mAb MW (150 kDa IgG as an example); All organs and tissues
ae (nm)	4.810	Stokes Einstein radius	[21]
σS	0.9980	Small pore vascular reflection coefficient	[21]
σL	0.1800	Large pore vascular reflection coefficient	[21]
A/A0S	9.28×10−7	Fractional accessible pore size of small pore	[21]
A/A0l	0.3490	Fractional accessible pore size of large pore	[21]
PeS	9.820	Peclet number of small pores	[21]
PeL	4.480	Peclet number of large pores	[21]
Adjusted for mAb MW and individual organs and tissues (150 kDa IgG in liver as an example)
$P{S}_S^{\mathit{\text{Liver}}}$ (ml/day)	0.1560	Permeability-surface area product of small pores	[21]
$P{S}_L^{\mathit{\text{Liver}}}$ (ml/day)	97.61	Permeability-surface area product of large pores	[21]
$J_{iso}^{\mathit{\text{Liver}}}$ (ml/day)	481.5	Circular isogravimetric flow	[21]
$J_S^{\mathit{\text{Liver}}}$ (ml/day)	732.3	Lymph flow through small pores	[21]
$J_L^{\mathit{\text{Liver}}}$ (ml/day)	534.7	Lymph flow through large pores	[21]

The details involving calculation of the parameter value of the two pore model are presented in Li and Shah [21] and summarized below. The values for the four assigned parameters (r_S , r_L, α_S, α_L) related to pore radius and fractional hydraulic conductance of two-pore theory transportation are list in Table 6 [21]. Values for other parameters associated with the two-pore model for transcapillary transport depend on the MW of the mAb, the specific organ/tissue, or both. The Stokes Einstein radius in nm of each mAb was calculated as a_e = 0.0483·MW ^0.386 , with MW in g/mol. The vascular reflection coefficient of mAb through small pores (σ_S) and large pores (σ_L) were calculated:

$${\sigma }_S=1-0.8489•e^{-0.00004•MW},{\sigma }_L=0.000035•M{W}^{0.717}$$ (29)

The fractional accessible pore size of small pores (A/ A0_S) and large pores (A/ A0_L) were determined from the following equations [21]:

$$A/A{0}_S=0.2352•e^{-0.00008295•MW}+0.7767•e^{-0.00053095•MW}$$ (30)

$$A/A{0}_L=0.3429•e^{-0.00012175•MW}+0.6571•e^{-0.00000421•MW}$$ (31)

With these mAb specific parameter values, the Peclet number of small pores $\left(P{e}_S\right)$ and large pores $\left(P{e}_L\right)$ were calculated for each mAb as:

$$P{e}_S=\frac{\left(-X_J+{\alpha }_S\right)•\left(1-{\sigma }_S\right)•a_e•r_S{}^2}{X_P•\left(A/A{0}_S\right)•{\alpha }_S},P{e}_L=\frac{\left(X_J+{\alpha }_L\right)•\left(1-{\sigma }_L\right)•a_e•r_L{}^2}{X_P•\left(A/A{0}_L\right)•{\alpha }_L}$$ (32)

where X_P was fixed at 13197 nm³ and X_J was calculated to be 0.38 [21].

The organ-dependent permeability-surface area product of small pores $\left(P{S}_S^{\mathit{\text{Organ}}}\right)$ and large pores $\left(P{S}_L^{\mathit{\text{Organ}}}\right)$ can be calculated for each mAb as:

$$P{S}_S^{\mathit{\text{Organ}}}=\frac{X_P}{a_e}•\frac{A}{A{0}_s}•\frac{\left(1-{\alpha }_L\right)•L^{\mathit{\text{Organ}}}}{r_S{}^2},P{S}_L^{\mathit{\text{Organ}}}=\frac{X_P}{a_e}•\frac{A}{A{0}_L}•\frac{{\alpha }_L•L^{\mathit{\text{Organ}}}}{r_L{}^2}$$ (33)

where L^Organ is the organ lymph flow as given in Table 4. Finally, the circular isogravimetric flow, lymph flow through small and large pores for each organ/tissue and for each mAb can be calculated as:

$$J_{iso}^{\text{Organ }}=X_J•L^{\text{Organ }},J_S^{\mathit{\text{Organ}} }=\left(1-{\alpha }_L\right)•L^{\mathit{\text{Organ}}}-J_{iso}^{\mathit{\text{Organ}} },J_L^{\mathit{\text{Organ}} }={\alpha }_L•L^{\mathit{\text{Organ}} }+J_{iso}^{\mathit{\text{Organ}}}$$ (34)

Baseline values for endogenous IgG

Incorporating endogenous IgG allows the model to describe potential changes in serum IgG concentration due to pathophysiology conditions (e.g. autoimmune diseases). The endogenous IgG is produced in the central plasma pool at a constant rate (IgG0) of 1.54×10⁴ nmol/day, as determined in a previously reported IgG tracer kinetics study [28]. The baseline endogenous IgG concentration (CIgG^Plasma) in the plasma pool was reported as 12.1 mg/ml in [41]. The whole-body pinocytosis rate $\left(C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Total}}}\right)$ was estimated so as to achieve a steady state endogenous IgG concentration (CIgG^Plasma) of 12.1 mg/ml, assuming individual organ pinocytosis clearances $\left(C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Organ}}}\right)$ in proportion to the organ/tissue total volumes: $C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Organ}} }=\frac{V^{\mathit{\text{Organ}}·}}{V^{\mathit{\text{Total}}}}•C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Total}}}$. The endosomal volume of each organ $\left(V_{\mathit{\text{endo}}}^{\mathit{\text{Organ}}}\right)$ was calculated as reported in [16]: $V_{\mathit{\text{endo}}}^{\mathit{\text{Organ}}}=2•C{L}_{\mathit{\text{endo}}}^{\mathit{\text{Organ}}}•\tau$. Values of $C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Organ}}}$ and $V_{\mathit{\text{endo}}}^{\mathit{\text{Organ}}}$ for each organ are listed in Table 4.

Model parameter estimation: IV and SC studies

Prior to mAb administration, the model was simulated to reach steady state for all the endogenous IgG concentrations. The plasma concentration-time data for each of the 20 IV administered mAbs (Table 1) were used to estimate the drug specific parameters S_pino and S_diff-conv. For mAbs administered at different doses, the data were pooled to obtained a single set of estimates of S_pino and S_diff-conv for each mAb. The ADAPT software (version 5) [42] was used to obtain the maximum likelihood estimates for these parameters assuming an additive plus proportional error variance model. The Naïve pooled data (NPD) analysis application was employed for mAbs with pooled multiple dose data, and the individual estimation (ID) application was used for mAbs with a single dose.

For the 12 mAbs for which plasma concentration-time data were also available following SC as well as IV administration (Table 2), the subcutaneous site drug specific parameters $S_{\mathit{\text{LymUpt}}}^{SC}$and $C{L}_{\mathit{\text{LymCap}}}^{SC}$ were estimated. In the estimation involving each of these mAbs, the drug specific values for the parameters S_pino and S_diff-conv were fixed at their estimated values as obtained from their IV data. The maximum likelihood estimates of $S_{\mathit{\text{LymUpt}}}^{SC}$ and $C{L}_{\mathit{\text{LymCap}}}^{SC}$ were obtained using either the NPD or ID application in ADAPT, as described above for the IV data.

Model predicted bioavailability

Using the model with the drug-specific parameters values, the bioavailability for each of the 12 SC administered mAbs was determined. The model-based bioavailability was calculated as the total amount of the mAb dose absorbed through local SC lymphatic capillary space plus the total amount delivered via the SC site blood flow, divided by the SC dose. For the mAbs administered at different doses, bioavailability was calculated separately for each dose, with the average reported. Bioavailability was also calculated from the mean data for each mAb via noncompartmental analysis (NCA) using the in-house software.

Biophysical determinants of drug specific model parameters

A central goal of our work was to determine whether biophysical properties of mAbs, beyond MW, can be incorporated in a PBPK model to predict the pharmacokinetic characteristics of the different mAbs. Toward this end, we explored the relationships between the estimated drug-specific model parameters ($S_{\mathit{\text{LymUpt}}}^{SC}$ and $C{L}_{\mathit{\text{LymCap}}}^{SC}$ for SC, and S_pino and S_diff-conv for both IV and SC) and different biophysical characteristics of mAbs. Isoelectric point (pI) and five other in silico metrics calculated from the mAb variable domain structures were explored. The pI of each mAb was calculated with the Protein isoelectric point calculator using the mAb amino acid sequence [43]. Five other metrics, calculated using the TAP platform [44], characterize the length of the complementarity-determining regions (CDRs), charges in the CDRs (positive charge, PPC and negative charge, PNC), the surface hydrophobicity, and asymmetry in the net surface charges. Four mAbs (GNbAC1, PAmAb, Tefibazumab, Urtoxazumab) without available values for these metrics were excluded from this analysis.

Prediction of SC PK of other mAbs

The PBPK model incorporating the regression relationships based on biophysical properties identified above was used to predict the plasma PK of four additional mAbs not used in the model development (Omalizumab, Tildrakizumab, Ixekizumab, Lanadelumab). For each of these mAbs, model predictions were based on populations simulations (n=1000) of the PBPK model (SIM application in ADAPT), where the drug-specific parameters ($C{L}_{\mathit{\text{LymCap}}}^{SC}$, $S_{\mathit{\text{LymUpt}}}^{SC}$, S_pino and S_diff-conv) were assumed to follow a log normal distribution. The mean and standard deviations of these parameters in the simulation were based on the estimation results from the IV and SC data described above, as well as identified biophysical property regression relations.

Simulations and sensitivity analyses

For the SC mAbs, simulation analyses were also conducted to quantify the contribution to bioavailability from the lymphatic pathway and blood circulation. In addition, sensitivity analysis was performed using one of the SC mAbs (Golimumab) to quantify the influence of lymph flow on PK, by altering lymph flow by 0.1-, 0.5-, 10-, 100-fold of the original value.

Results

Intravenous pharmacokinetics

The total IgG clearance via pinocytosis in all the organs/tissues $\left(C{L}_{\mathit{\text{pino}}}^{\mathit{\text{Total}}}\right)$ was estimated to be 157.3 ml/day (relative standard errors, RSE% = 11.6) using the baseline endogenous IgG concentration of 12.1 mg/ml [41]. The ratio of simulated steady-state IgG organ interstitial concentration and plasma concentration was 0.41, which agrees with previous reported range of 0.1–0.5 in [23].

For each of the 20 IV mAbs, the values for the two estimated parameters, S_pino and S_diff-conv, are listed in the right two columns of Table 1 along with their percent relative standard errors. The results in Fig. 3 indicate that the model can predict the plasma PK of each of these 20 mAbs for the different doses administered, with R² ranging from 0.941 for Siltuximab to 0.998 for Belimumab. The parameters representing the mAb specific differences in tissue exchange via pinocytosis (S_pino) and diffusion/convection (S_diff-conv) were estimated with good precision as shown in Table 1. The estimates of S_pino range from 0.627 to 2.14, with a mean, median and standard deviation of 1.07, 0.949 and 0.337, respectively. While the estimates for S_diff-conv range from 0.452 to 2.21, with a mean, median and standard deviation of 1.18, 1.16 and 0.429, respectively. There was no significant correlation between S_pino and S_diff-conv among these 20 mAbs.

Fig. 3.

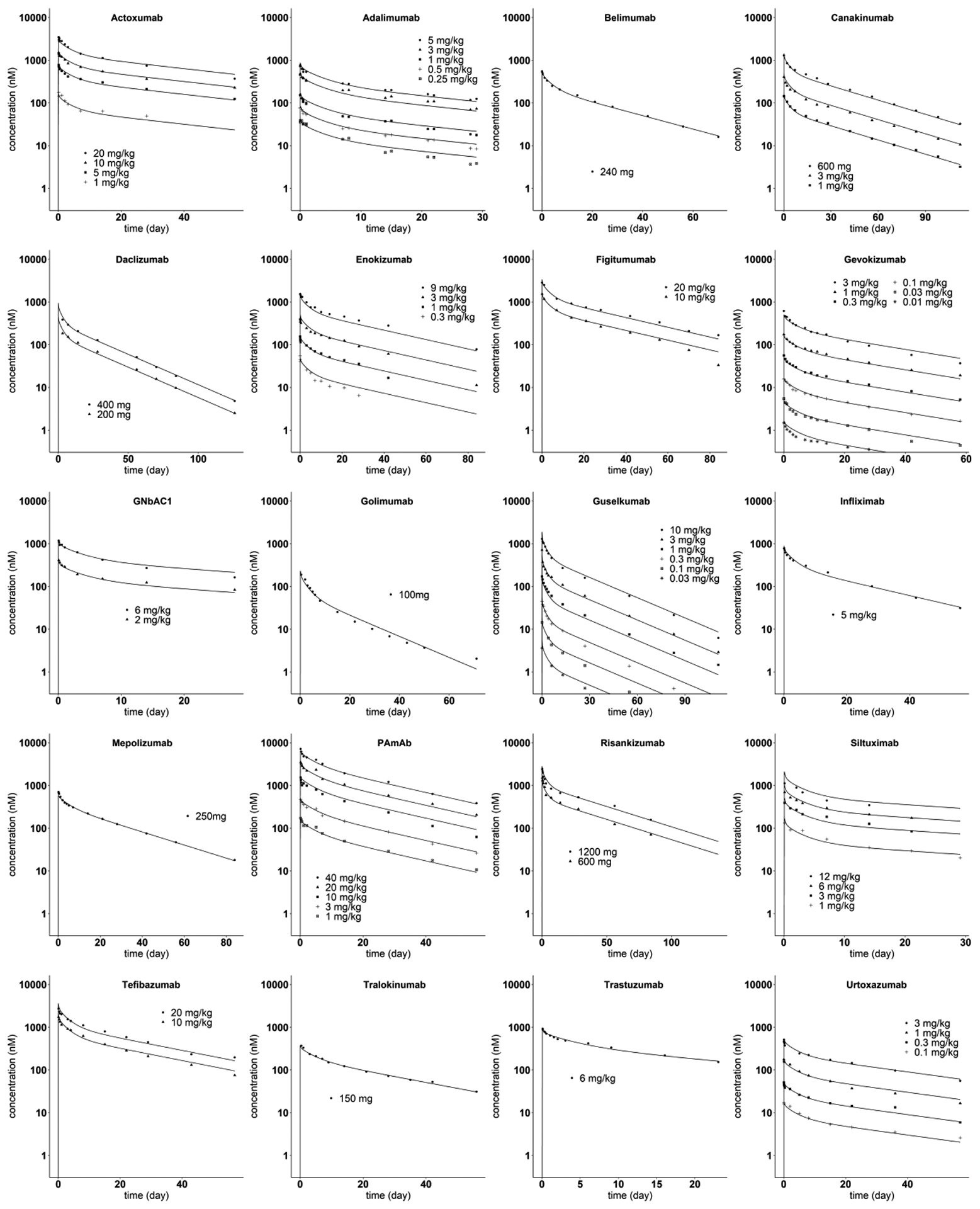
Model predicted and observed mAb plasma concentration versus time profiles after IV administration. The solid lines are model predictions. The symbols are digitized data from literature

Subcutaneous pharmacokinetics

The results of estimating the two SC site drug-specific parameters, $S_{\mathit{\text{LymUpt}}}^{SC}$ and $C{L}_{\mathit{\text{LymCap}}}^{SC}$, for each of the 12 SC administered mAb are listed in Table 2 (S_pino and S_diff-conv fixed at values obtained from the corresponding IV analysis), while the model predicted plasma concentration time course is shown with the measured plasma concentrations for each mAb in Fig. 4. The values of R² ranges from 0.948 for Daclizumab to 0.987 for Gevokizumab. As shown in Table 2, both $S_{\mathit{\text{LymUpt}}}^{SC}$ and $C{L}_{\mathit{\text{LymCap}}}^{SC}$ were estimated precisely. The value of estimated $C{L}_{\mathit{\text{LymCap}}}^{SC}$ ranges from 0.441 to 3.66, with a mean, median and standard deviation of 1.25, 0.874 and 0.998. The estimates of $S_{\mathit{\text{LymUpt}}}^{SC}$ are in the range of 0.0904 and 0.301, with a mean, median and standard deviation of 0.210, 0.211 and 0.0631, respectively.

Fig. 4.

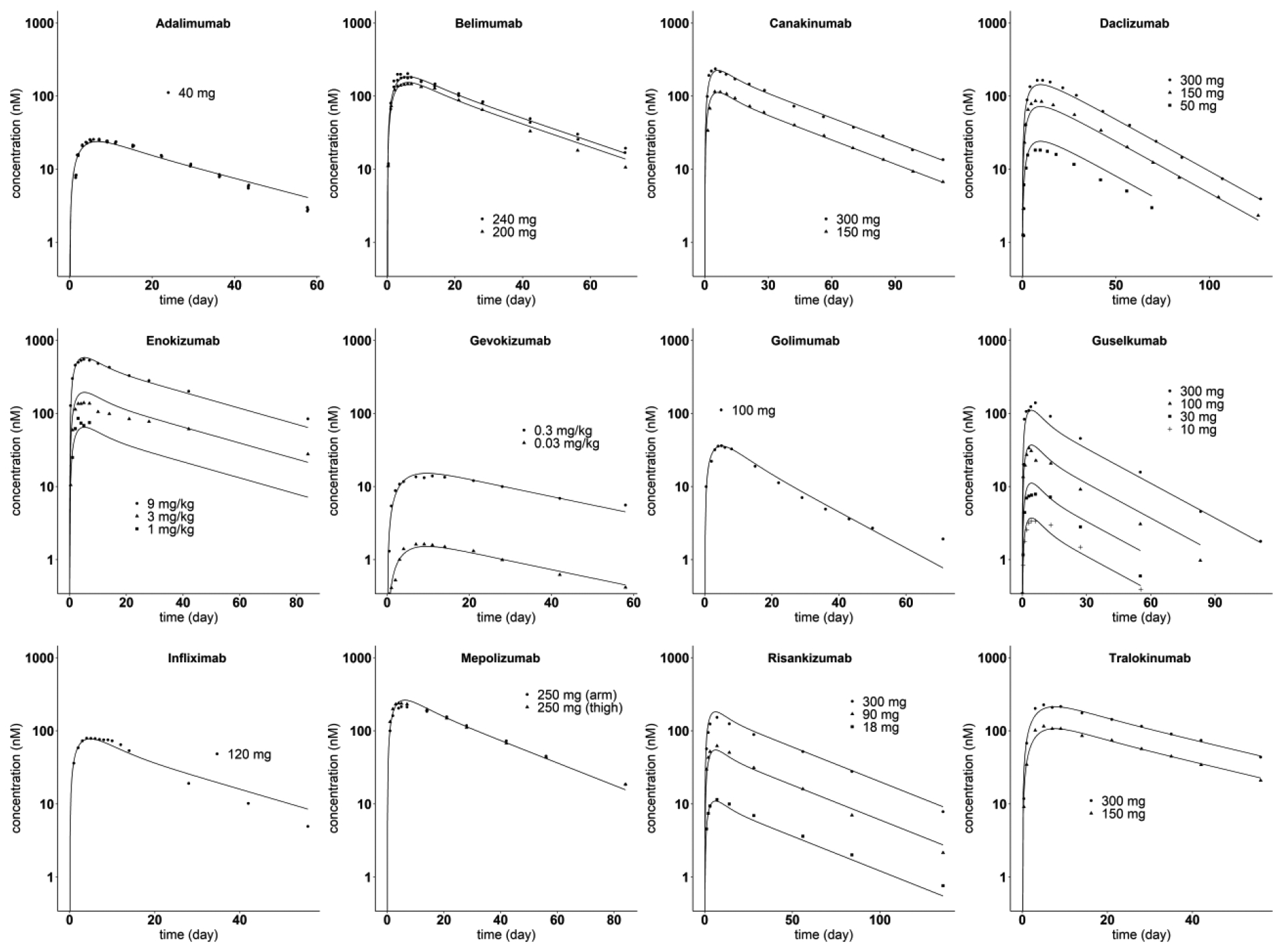
Model predicted and observed mAb plasma concentration versus time profiles after SC administration. The solid lines are model predictions. The symbols are digitized data from literature

The model-based prediction of bioavailability is plotted versus the NCA calculated value for each of the 12 mAbs in Fig. 5. As expected, these results are in good agreement (R² = 0.91), given that the PBPK model yielded good predictions of the plasma concentration-time data for each mAb as shown in Fig. 4.

Fig. 5.

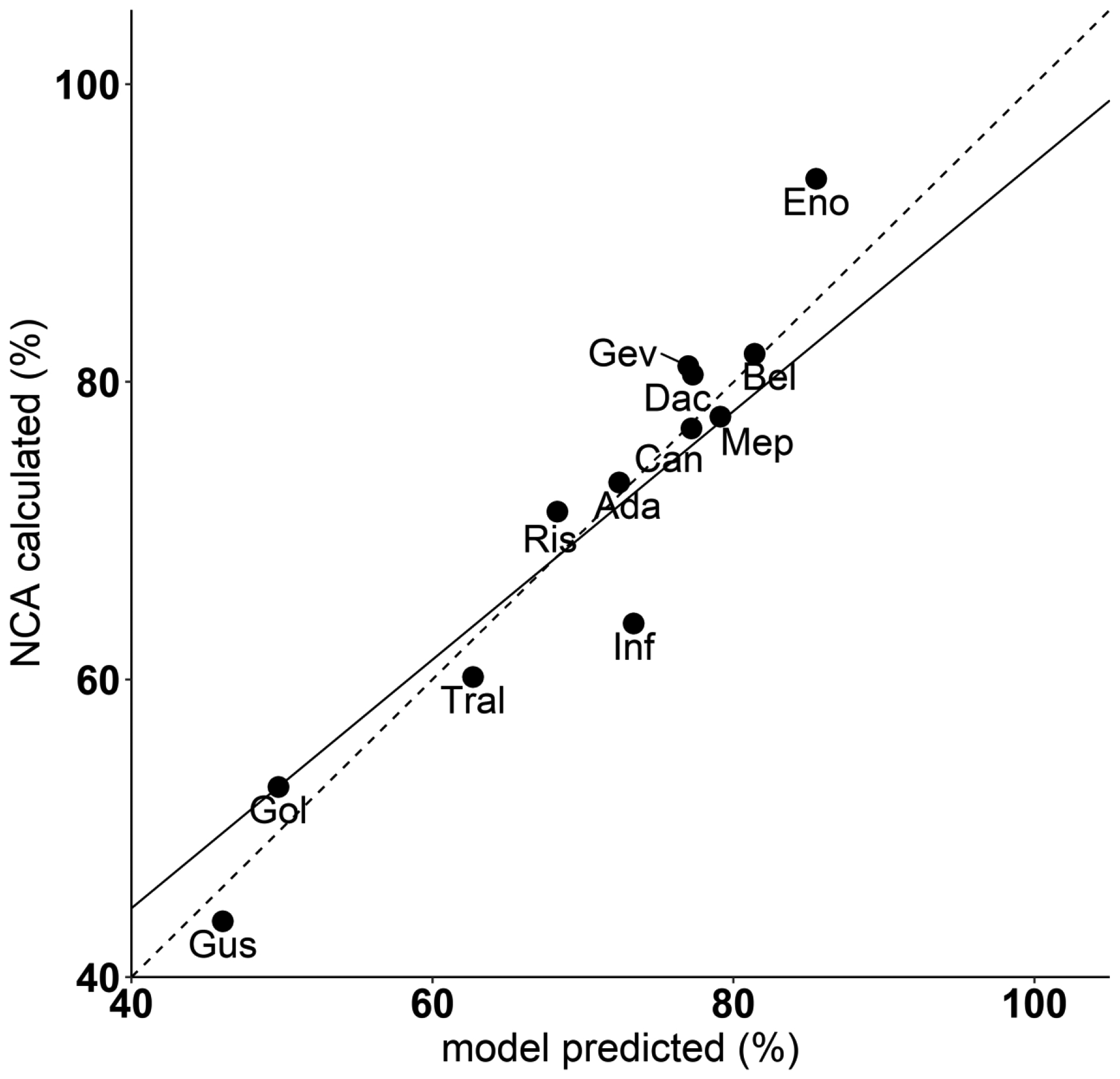
Linear correlation evaluation between NCA calculated bioavailability (%) and model predicted bioavailability (%). All mAbs with SC PK data are included. The solid line represents the regression line (R² = 0.91). The dashed line represents the hypothetical line of identity

The relationship between the observed SC PK characteristics bioavailability and T_max, and the estimated SC site model parameters $C{L}_{\mathit{\text{LymCap}}}^{SC}$ and $S_{\mathit{\text{LymUpt}}}^{SC}$ are shown in Fig. 6. Bioavailability is correlated with $C{L}_{\mathit{\text{LymCap}}}^{SC}$ (p < 0.0001) but not with $S_{\mathit{\text{LymUpt}}}^{SC}$, while T_max is correlated with $S_{\mathit{\text{LymUpt}}}^{SC}$ (p < 0.001) but not with $C{L}_{\mathit{\text{LymCap}}}^{SC}$.

Fig. 6.

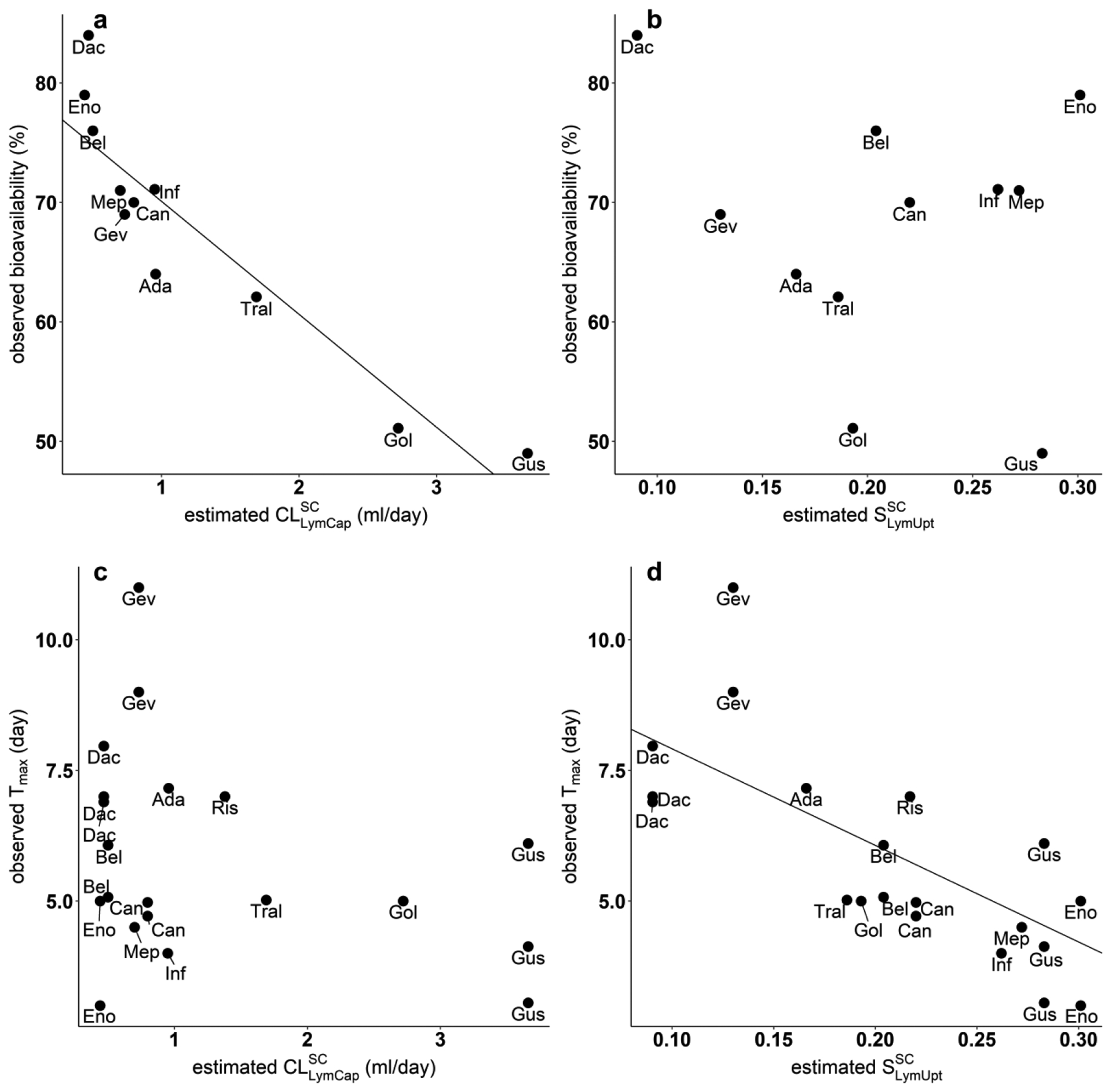
Correlation of observed SC PK characteristics versus estimated SC tissue model parameters. (a) Negative association between observed bioavailability (%) and estimated $C{L}_{\mathit{\text{LymCap}}}^{SC}$ (p = 6.77×10⁻⁰⁵). (b) No significant association between observed bioavailability (%) and estimated $S_{\mathit{\text{LymUpt}}}^{SC}$ (p = 0.547). (c) No significant association between observed T_max (day) and estimated $C{L}_{\mathit{\text{LymCap}}}^{SC}$ (p = 0.217). (d) Negative correlation between observed T_max (day) and estimated $S_{\mathit{\text{LymUpt}}}^{SC}$ (p = 0.000143).

Biophysical determinants of mAb SC absorption

The calculated values of the isoelectric points (pI) range from 6.36 to 7.37. There was no significant linear relation (results not shown) between pI and any of the four drug specific model parameters (S_pino , S_diff-conv , $C{L}_{\mathit{\text{LymCap}}}^{SC}$, $S_{\mathit{\text{LymUpt}}}^{SC}$). The linear correlation between four model estimated parameters and all five metrics provided in the TAP platform [44] were tested. The only two significant relations between model parameters and calculated metrics were between $C{L}_{\mathit{\text{LymCap}}}^{SC}$ and PPC (P=0.000362), S_pino and PPC (P=0.0013), as shown in Fig. 7. PPC metric ranges from 0 to 1.36 for each of the 12 mAbs. The resulting regression relationships are: $C{L}_{\mathit{\text{LymCap}}}^{SC}=0.51+2.13•PPC$ (R²=0.74, p=0.00036, residual standard error=0.539), S_pino = 0.89+0.72·PPC (R²=0.53, p = 0.0013, residual standard error = 0.256). By incorporating PPC into the PBPK model, the standard deviation of $C{L}_{\mathit{\text{LymCap}}}^{SC}$ decreases from 0.998 to 0.539, while the standard deviation of S_pino is reduced from 0.362 to 0.256. These results suggest that this model explains some of the differences in pinocytosis and SC lymphatic capillary clearance among the mAbs.

Fig. 7.

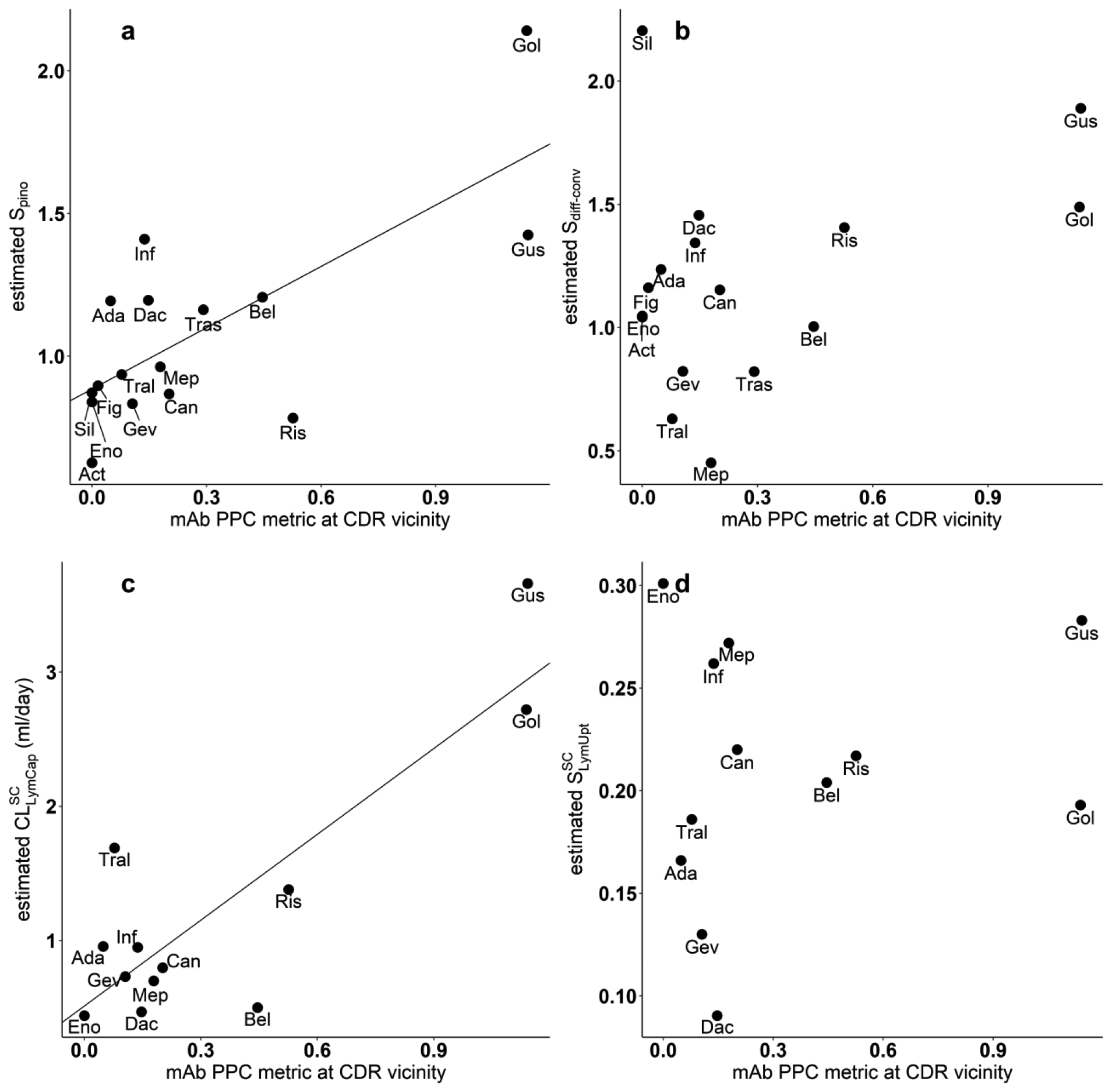
Correlation of estimated model parameters versus mAb PPC metric at CDR vicinity. (a) Positive association between estimated S_pino value and mAb PPC metric: S_pino = 0.89+0.72·PPC (R²=0.53, p = 0.0013, residual standard error = 0.256). (b) No significant association between estimated S_diff-conv value and mAb (p = 0.18). (c) Positive correlation between estimated $C{L}_{\mathit{\text{LymCap}}}^{SC}$ and mAb PPC metric: $C{L}_{\mathit{\text{LymCap}}}^{SC}=0.51+2.13•PPC$ (R²=0.74, p=0.00036, residual standard error=0.539). (d) No significant association between estimated $S_{\mathit{\text{LymUpt}}}^{SC}$ and mAb PPC metric (p = 0.549)

Model-based prediction of SC PK of other mAbs

The PBPK model incorporating the regression equations relating the mAb PPC metric and the model parameters S_pino and $C{L}_{\mathit{\text{LymCap}}}^{SC}$ was used to predict the plasma PK of the four mAbs (Omalizumab, Tildrakizumab, Ixekizumab, Lanadelumab) not used in the model development. Figures 8 and 9 show the resulting 5^th - 95^th percentile prediction intervals for Omalizumab (PPC = 0.015) and Tildrakizumab (PPC = 0), respectively, for two different SC doses in each case. Corresponding results are shown in Fig. 10 for Ixekizumab (PPC = 0.081) following one dose of 160 mg. For each of these three mAbs, the measured concentration-time profile is centered within the model predicted 5^th - 95^th percentile intervals.

Fig. 8.

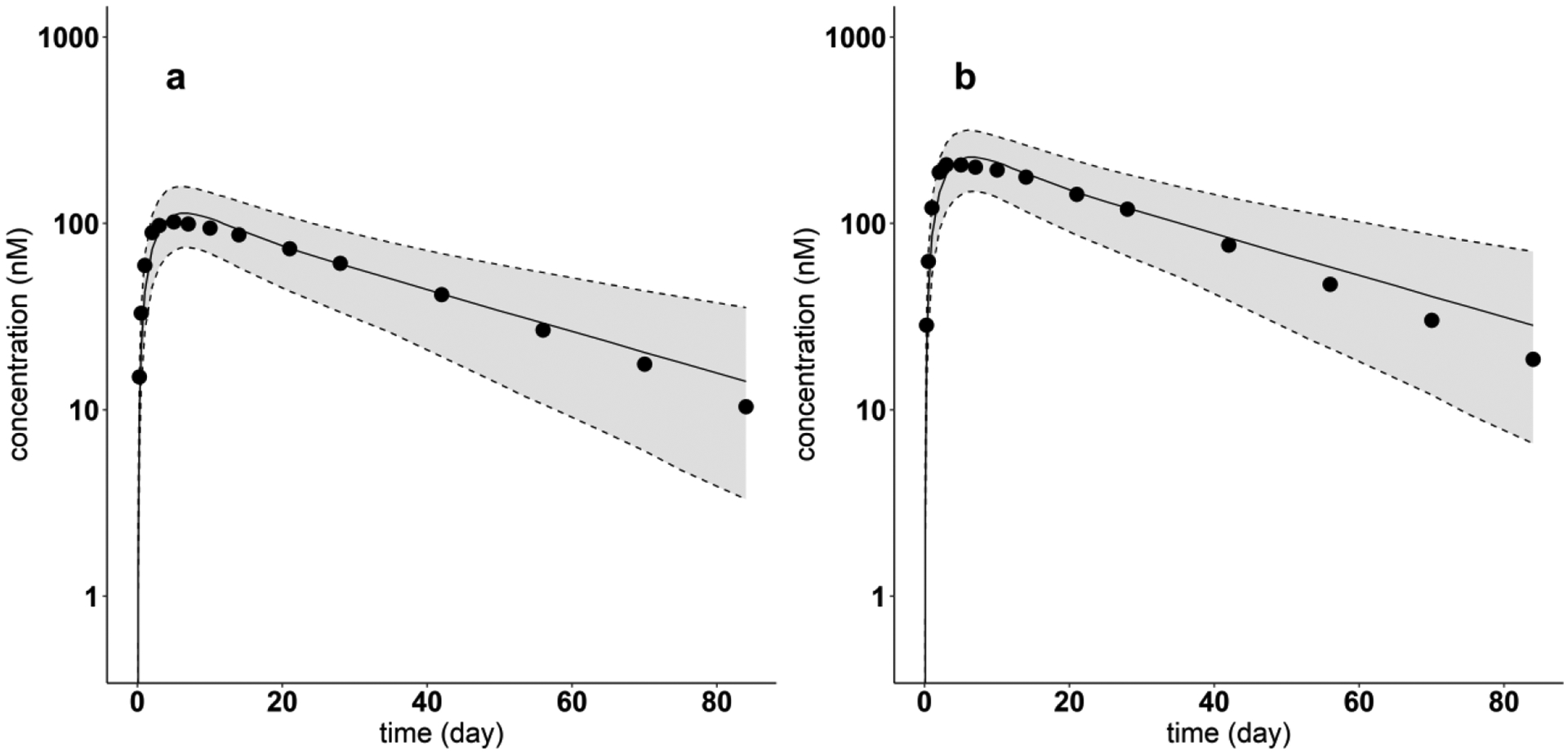
Model-predicted and digitized concentration versus time profiles of Omalizumab for each dose. Filled dots indicate digitized Omalizumab PK profiles from literature, after single SC dose of (a) 150 mg, (b) 300 mg. Solid lines show the predicted median. Dash lines indicate the predicted 5^th and 95^th percentiles. The shaded areas display the 5^th to 95^th percentile population simulation regions

Fig. 9.

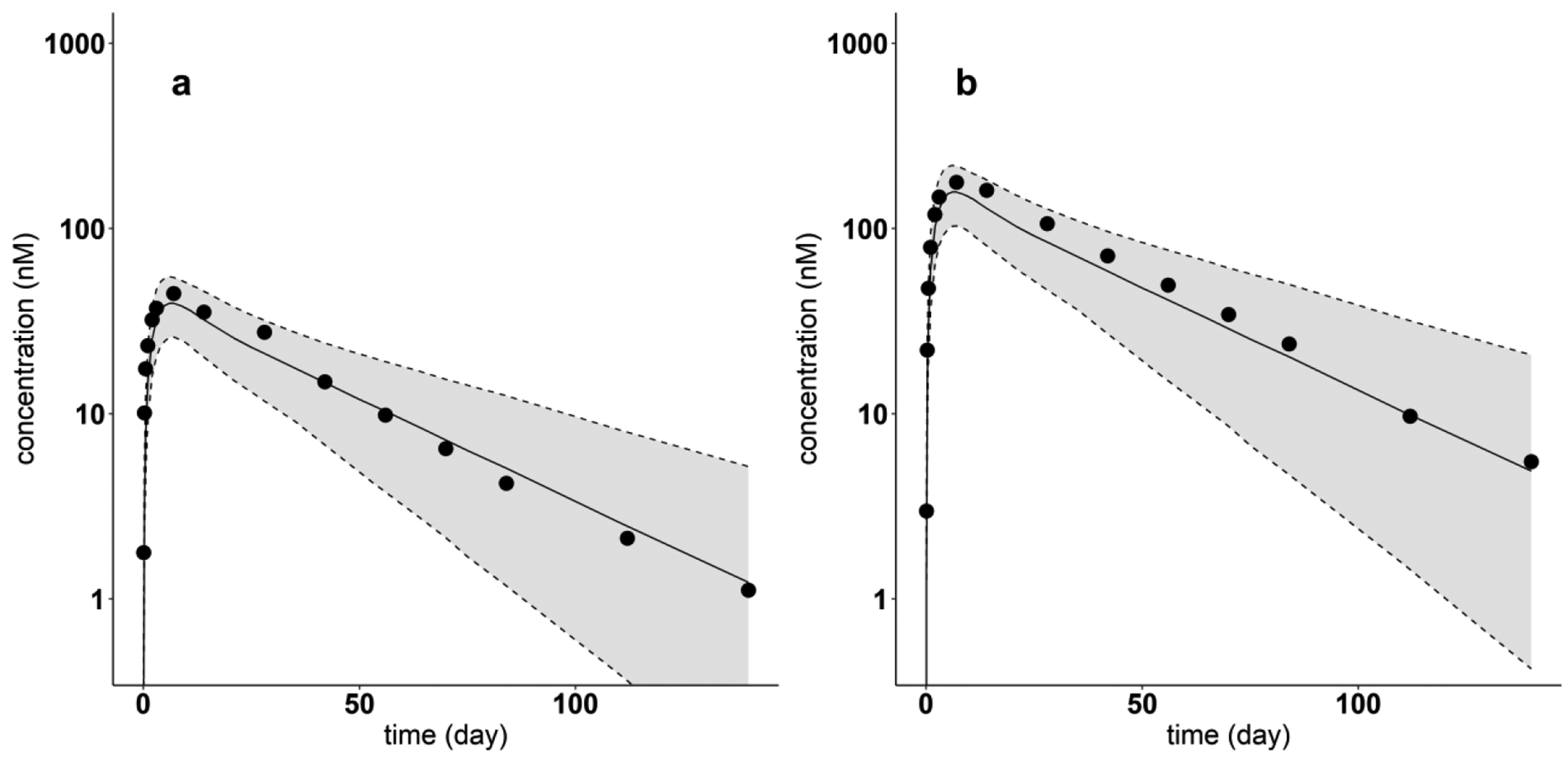
Model-predicted and digitized concentration versus time profiles for Tildrakizumab for each dose. Filled dots indicate digitized Tildrakizumab PK profiles from literature, after single SC dose of (a) 50 mg, (b) 200 mg. Solid lines show the predicted median. Dash lines indicate the predicted 5^th and 95^th percentiles. The shaded areas display the 5^th to 95^th percentile population simulation regions

Fig. 10.

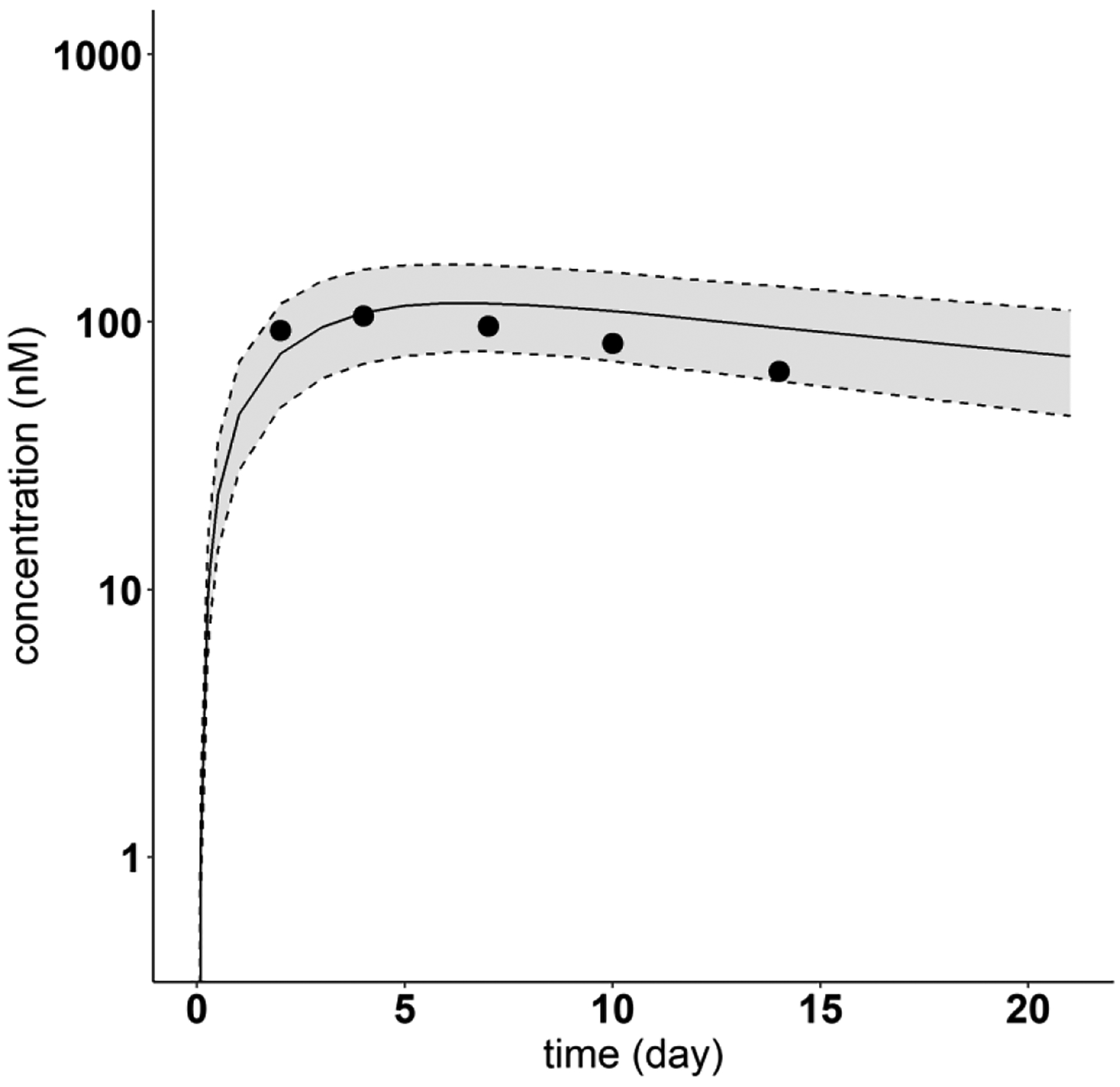
Model-predicted and digitized concentration versus time profiles for Ixekizumab. Filled dots indicate digitized Ixekizumab PK profiles from literature, after single SC dose of 160 mg. Solid lines show the predicted median. Dash lines indicate the predicted 5^th and 95^th percentiles. The shaded areas display the 5^th to 95^th percentile population simulation regions

When the model was used to predict the plasma PK of Lanadelumab (PPC = 2.48) at each of four different doses (from 7.8 mg to 249 mg), as shown in Fig. 11, the model underpredicted plasma concentrations of during the elimination phase. These results suggest that the value used for S_pino was likely over estimated based on the PPC regression equation (see Discussion).

Fig. 11.

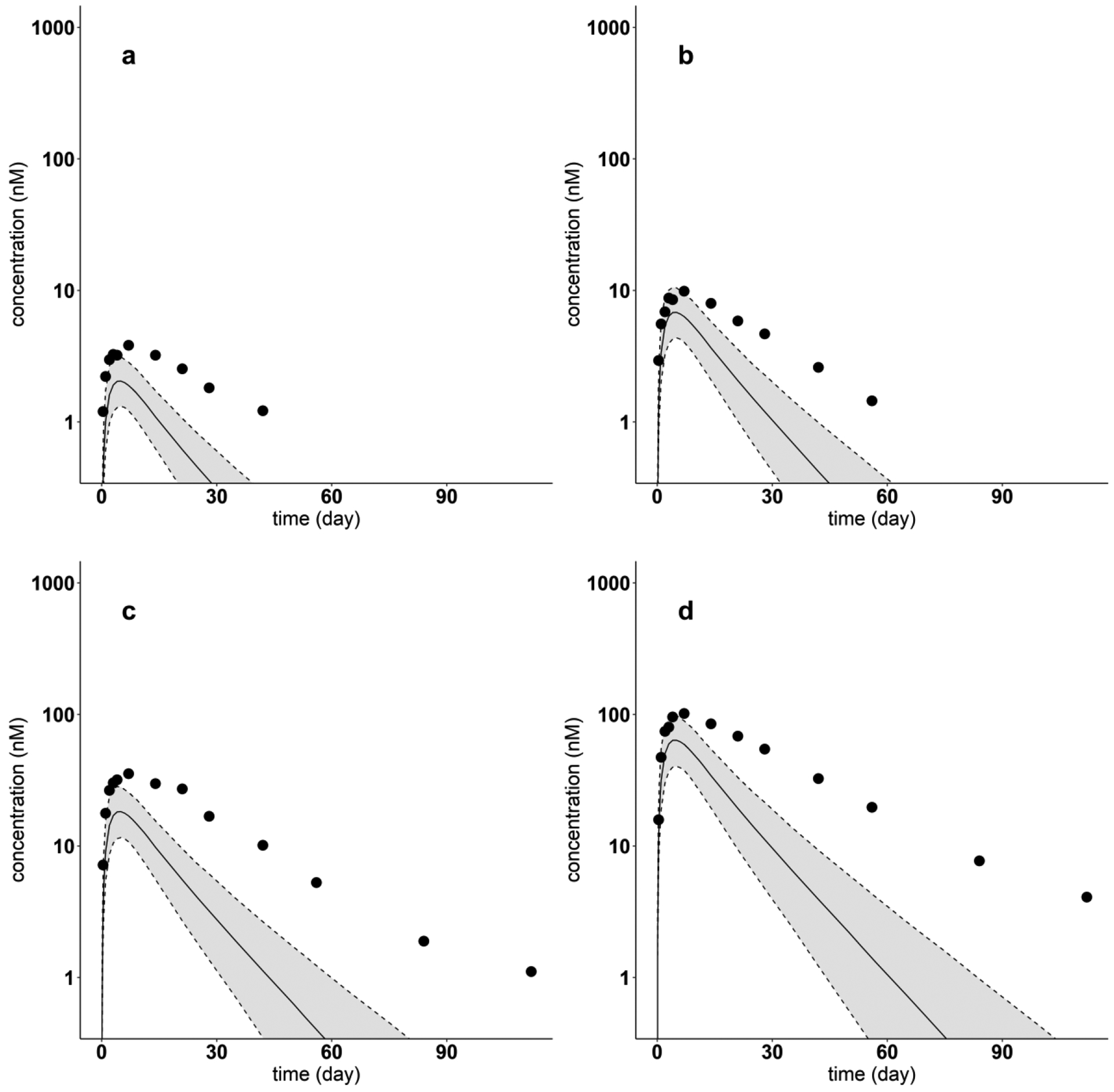
Model-predicted and digitized concentration versus time profiles for Lanadelumab for each dose. Filled dots indicate digitized Lanadelumab PK profiles from literature, after a single SC dose of (a) 7.8 mg, (b) 26 mg, (c) 71 mg, (d) 249 mg. Solid lines show the predicted median. Dash lines indicate the predicted 5^th and 95^th percentiles. The shaded areas display the 5^th to 95^th percentile population simulation intervals

Simulations and sensitivity analyses

Using the PBPK model, we compared the contributions to SC absorption attributable to the lymphatic pathway and the blood perfusion pathway, for each of the 12 mAbs. For these mAbs, the absorption through lymphatic pathway accounts for between 91.6 % to 99.0 % of the total amount of dose absorbed amount. This result showing the primary role of lymphatic uptake in the absorption of mAbs after SC dose is consistent with the previous studies in sheep [45] and other studies as reviewed in [25]. The PBPK model was also employed to predict the change of SC absorption rate over time. The SC absorption is essentially complete 25 days after SC injection (Fig. 12). The simulation in Fig. 12 also demonstrates the major contribution of the lymphatic system to absorption of subcutaneously administered mAbs using Golimumab as an example. From Fig. 12 the peak absorption rate via the lymphatic pathway is predicted to be of 72.2 nmol/day, compared to 4.53 nmol/day through blood perfusion.

Fig. 12.

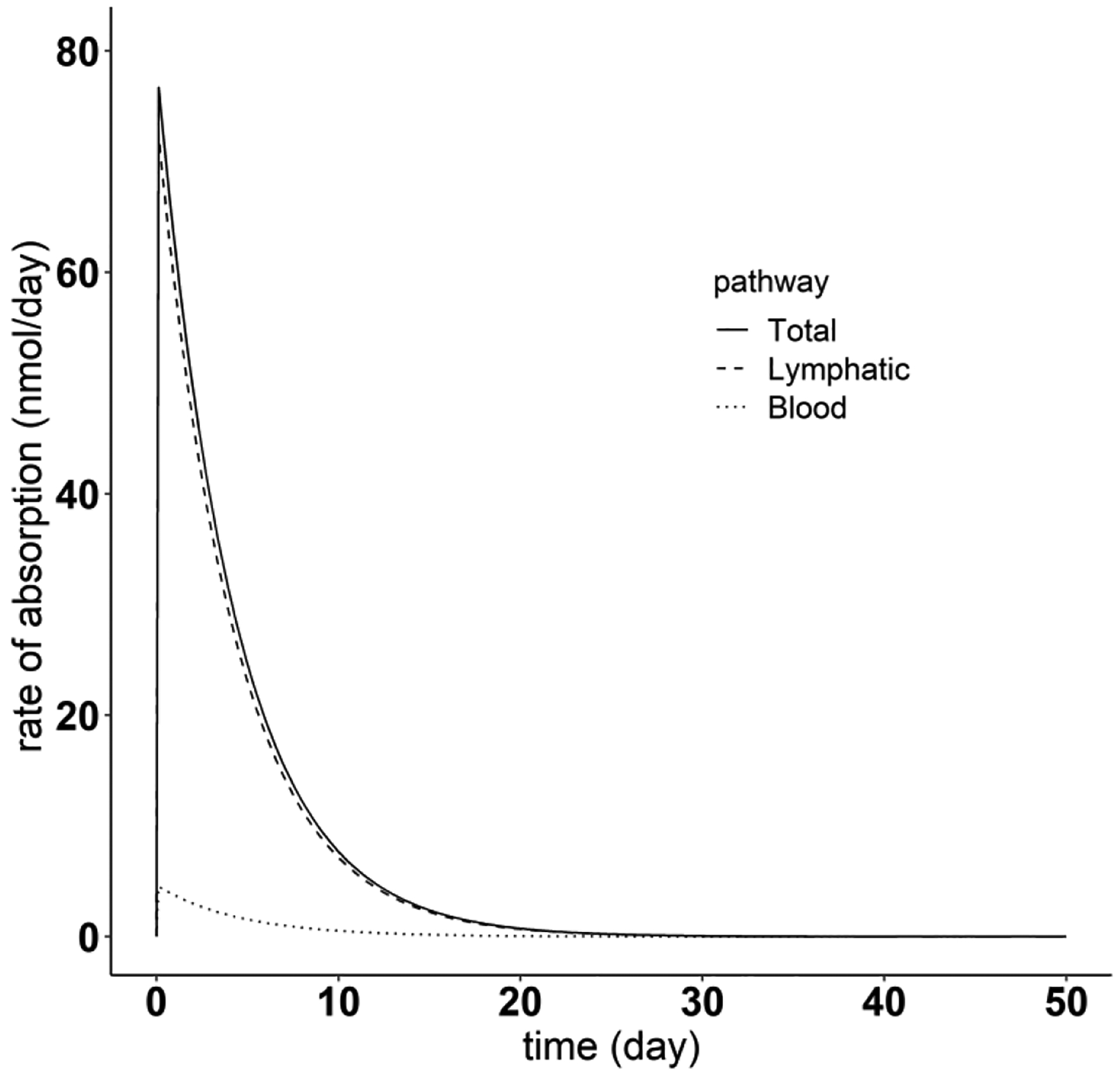
Simulation of absorption rate of different pathways after the SC dosing, using Golimumab as an example. The solid line represents the total absorption rate after SC administration. The dashed and dotted lines denote the mAb absorption rate through the lymphatic system and blood perfusion, respectively

The sensitivity analysis results shown in Fig. 13 illustrates the role of subcutaneous lymph flow (L^SC) on the plasma pharmacokinetics following SC administration of mAbs. For Golimumab, as an example, reducing lymph flow by 0.1- and 0.5-fold can significantly delay the SC absorption and decrease bioavailability to 5.79% and 31.1%, respectively, compared to 49.8% with the original lymph flow value. In contrast, increasing lymph flow (i.e. 10-fold difference) can facilitate the absorption of mAb, leading to greater absorption rate and larger bioavailability of 91.3%.

Fig. 13.

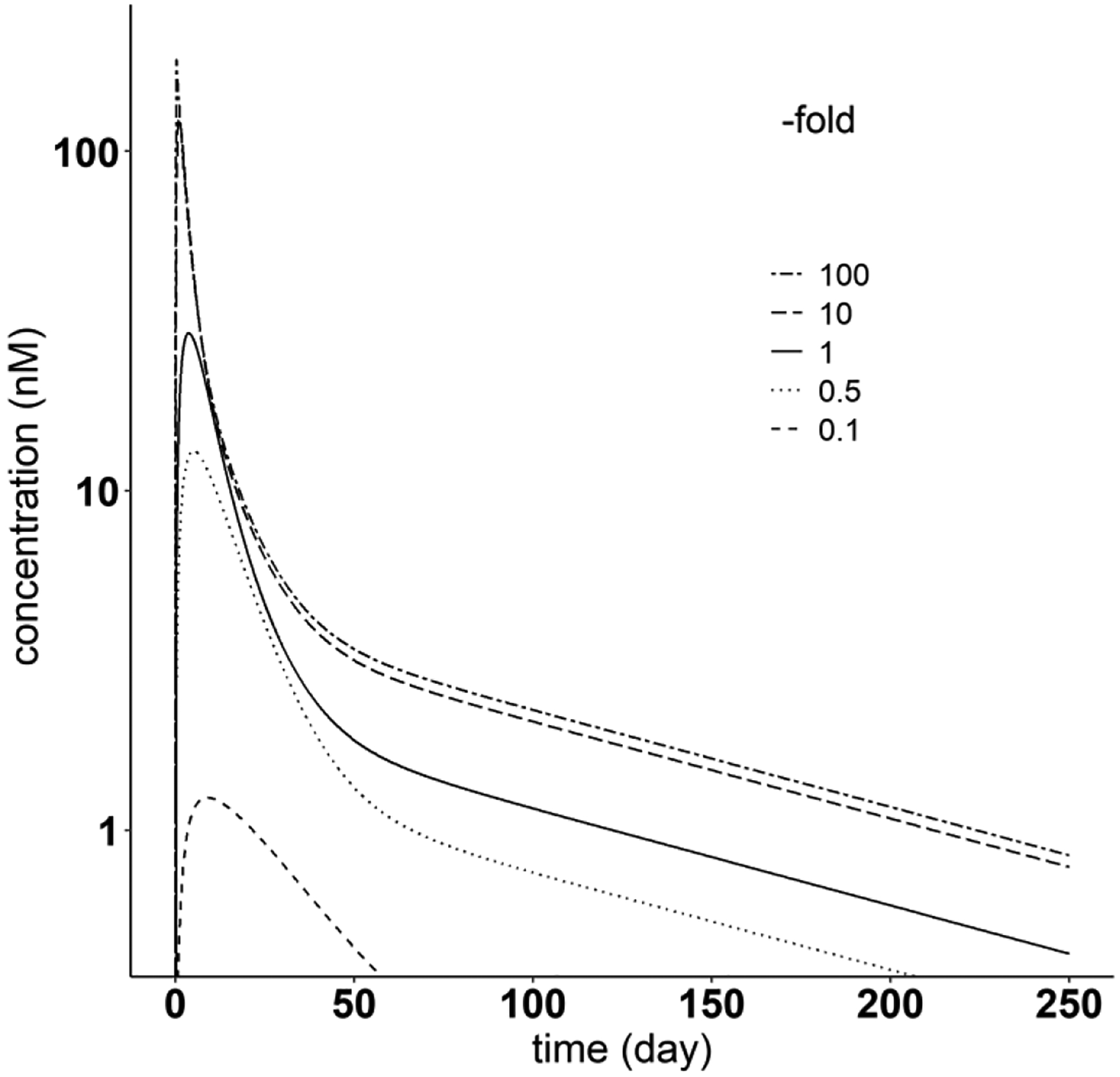
Sensitivity analysis of SC site lymph flow, using Golimumab as an example. The solid line represents the original Golimumab PK profile after SC administration. The two-dashed line, long-dashed line, dotted line and dashed line denote PK profiles after changing SC site lymph flow to 100-, 10-, 0.5- and 0.1-fold of the original parameter value (0.00225 ml/min), respectively

Discussion

In this work, a whole-body PBPK model is presented with the goal of predicting the clinical pharmacokinetics of mAbs following SC administration in humans. The model incorporates two mAb-specific parameters to represent differences in pinocytosis rate and the diffusive/convective transport rates among the mAbs. At the SC administration site, two additional parameters are used to represent differences in lymphatic capillary uptake and clearance among mAbs. The resulting model reliably predicted the bioavailability and T_max, as well as the overall plasma concentration time profile, of each of the 12 SC mAbs investigated. Further model-based investigation found that the mAb-specific differences in organ/tissue pinocytosis transport, as well as SC lymphatic capillary clearance could be explained, in part, based on the local charge of the complementarity-determining regions of the mAb (patches of positive charge metric), but not the antibody’s isoelectric point. The composite model’s predictive capability was evaluated through Monte Carlo simulations of the SC PK of another four mAbs not used in model development. Overall, this study provides a platform PBPK model to characterize and predict the plasma disposition of monoclonal antibodies following SC administration.

After SC administration, mAbs transverse the ECM to reach lymphatic capillaries or blood capillaries before absorption [2]. In our model, the ECM of the SC space was represented by a single homogenous interstitial compartment, with the transport and subsequent lymphatic uptake of the mAb expressed by a single term representing the mAb-specific interstitial to lymphatic capillary transport rate $\left(S_{\mathit{\text{LymUpt}}}^{SC}\cdot L^{SC}\right)$. Previous evidence suggests that the uptake of IgG from the depot following its SC administration is first-order [27, 38], further supporting the tissue-level model assumptions used in the SC model. While previous studies have investigated the pre-systemic degradation of biotherapeutics [46–48], quantitative information on local tissue catabolism/degradation is lacking [25]. Thus, in the model, the overall mAb clearance due to catabolism/degradation in the SC site and/or in the draining lymphatics was represented as a net clearance from the local lymphatic capillary space $\left(C{L}_{\mathit{\text{LymCap}}}^{SC}\right)$. Despite these simplifying assumptions, the model presented is qualitatively consistent with other studies reported in the literature. For example, the increase of lymph flow by massage or heat at the injection site has been shown to aid in the absorption of biotherapeutics [49, 50], which is consistent with the model sensitivity analysis results in Fig. 13. Also, the model prediction demonstrates the dominant role of the lymphatic system in the SC absorption (more than 90%), in line with experimental results in sheep [45]. The model predictions are also consistent with the central role of ECM transport and lymphatic uptake in determining the rate of mAb absorption (Fig. 6), as reported in preclinical and clinical studies using hyaluronidase to enhance the subcutaneous absorption [51–53]. In addition, the extent of SC absorption is largely determined by pre-systemic degradation $\left(C{L}_{\mathit{\text{LymCap}}}^{SC}\right)$, as identified by the correlation analysis (Fig. 6). This suggests that inhibiting pre-systemic elimination can increase SC bioavailability, which can be achieved by co-administration of protease inhibitors or via a dose saturation strategy, as mentioned in [2].

Various biophysical properties of mAbs have been considered in an effort to explain the substantial differences in PK behavior observed with different mAbs [54, 55]. Since the net charge of a mAb in vivo will influence its interaction with tissue components and/or targets, the antibody’s isoelectric point has been investigated as a determinant of its PK [55–57]. It has been reported, however, that differences in pI value of more than one unit are required to produce a detectable change in an antibody’s systemic clearance and tissue distribution [57–59]. In this study, the calculated pI values of the 12 mAbs examined range from 6.36 to 7.37. Given this narrow range it is not unexpected that we did not find a significant relationship between mAb pI value and any of the four mAb-specific model parameters.

It has been recently reported that the local charge of a mAb’s complementarity determining regions may impact the charge balance and clearance of these large molecules [56, 60, 61]. Since a mAb’s CDR directly contacts the antigen and mediates its binding, we investigated whether the positive charge of mAb CDR vicinity (PPC metric) could explain some of the differences observed in the four mAb-specific model parameters, and thus the variability in mAb PK behavior of the mAbs investigated. As shown in Fig. 7, we found that PPC could explain some of the inter-mAb differences in S_pino and $C{L}_{\mathit{\text{LymCap}}}^{SC}$, but not S_diff-conv or $S_{\mathit{\text{LymUpt}}}^{SC}$. Futher investigation with additional mAb over a range of PPC values is needed, however, to more fully evaluate these results.

The positive correlation found between mAb PPC and S_pino and between PPC and $C{L}_{\mathit{\text{LymCap}}}^{SC}$ can be understood as follows. Increased positive charge of CDR vicinity can lead to increased interaction between mAbs and cell membranes, which consist of negatively charged components such as heparin and sialic acid. This stronger binding then facilitates the entry of mAb into endothelial cells through pinocytosis, which is represented in the model by the mAb specific scale factor S_pino that alters the pinocytosis clearance. This result is consistent with the study of Datta-Mannan et al [61], in which they found that balancing charge in the CDR of humanized mAbs without changing pI can reduce mAb binding to cells, and thus decrease mAb clearance.

The PPC metric was also found to be positively correlated with the SC site pre-systemic mAb clearance $\left(C{L}_{\mathit{\text{LymCap}}}^{SC}\right)$. The pre-systemic degradation of mAbs can be mediated by proteases, as well as soluble and cell-membrane receptors [2]. With higher positive charge in the CDR vicinity, mAbs are more likely to be exposed to soluble or cell-surface targets with negative charge, which can lead to receptor-mediated uptake and degradation or the formation of immune complexes which will be cleared [62]. In a study in cynomolgus monkeys [63], it was reported that increasing the mAbs positive charge can lead to higher clearance at the administration site and to lower bioavailability, in line with our findings. In another report, Sharma et al found that extreme variable domain charges could result in faster mAb clearance [64].

It was also expected that the mAb-specific differences in the uptake rate from SC interstitial space to lymphatic capillaries, represented by the scaling factor $S_{\mathit{\text{LymUpt}}}^{SC}$ in the model, would correlate with PPC; but as shown in Fig. 7b, this is not the case. The rate-limiting step of SC absorption, mAb transport through ECM, is known to be effected by electrostatic interactions and steric exclusion [65]. Steric exclusion renders diffusion rate slower with increased content of hyaluronic acid in ECM and larger molecular weight of the drug, also with the possible influence of molecular shape [65]. Therefore, more positively charged mAbs would be expected to be transported within the ECM more slowly due to their increased interaction with tissue components [2]. However, the differences in some external and internal factors (e.g. steric exclusion, formulation, physical activity level, location of the SC injection, anesthesia) may obscure this relationship. As a result, any influence of positive charge of CDR vicinity of mAbs may not be detectable using the model.

Based on our modeling and the mAbs analyzed, the PPC metric did not correlate with the differences estimated in the mAb-specific model parameter related to diffusive/convective transport (S_diff-conv), suggesting that other non-charged based factors may be responsible for these differences. Also, the differences in S_diff-conv are beyond those due to the differences in mAb molecular weight, since the model incorporates the MW-based two-pore theory. Other factors not considered may influence the convective transport that depends on the difference between the hydrostatic pressure gradient and osmotic pressure gradient, such as structure of the capillary wall (e.g. diameter of paracellular pores) and physiological conditions of subjects [23, 66].

In developing the model presented in this report, pooled mean plasma mAb concentration-time profiles were used as obtained from more than 30 published literature reports. Thus, differences in these studies due to, for example, subject’s age, sex, weight, physiological state, as well as mAb formulation and administration site could not be incorporated as explanatory covariates. Instead the effects of these differences are represented as variability in the four estimated mAb-specific model parameters, thus resulting in an overestimation of the variability in these properties. Given the availability of only plasma mAb concentrations, we were unable to evaluate the ability of the model to predict organ/tissue PK.

In summary, in this study, we established a whole-body PBPK model for predicting mAb PK following SC delivery to support translational studies. Given its physiological basis, the developed model enables us to: (1) gain mechanistic insights of events determining mAb SC absorption and facilitate further optimization of SC delivery, (2) explain the influence on systemic PK by the alternation of antibody variable region, (3) support first-in-human translational studies for SC mAb administration. This model also provides the potential of predicting peripheral tissue concentration, which can guide the design of effective dosing ranges and strategies in mAb development process.