Emergence of anomalous dynamics in soft matter probed at the European XFEL

Significance

The European XFEL is a hard X-ray Free-Electron Laser (FEL) with pulse repetition rates in the megahertz regime. Thus, sample dynamics in the microsecond and submicrosecond regime can be accessed by means of X-ray photon correlation spectroscopy (XPCS). Application of XPCS at FEL sources has been challenged because of the intrinsic fluctuations of FELs and the radiation-induced sample heating and damage. In this work we demonstrate the unprecedented stability of the European XFEL and show the feasibility of microsecond XPCS on a model system. Nonlinear heating on microsecond timescales is observed reaching superheated water states that persist up to 100 μs. Our data indicate a violation of the Stokes–Einstein relation for nanoparticle diffusion at short times.

Abstract

Dynamics and kinetics in soft matter physics, biology, and nanoscience frequently occur on fast (sub)microsecond but not ultrafast timescales which are difficult to probe experimentally. The European X-ray Free-Electron Laser (European XFEL), a megahertz hard X-ray Free-Electron Laser source, enables such experiments via taking series of diffraction patterns at repetition rates of up to 4.5 MHz. Here, we demonstrate X-ray photon correlation spectroscopy (XPCS) with submicrosecond time resolution of soft matter samples at the European XFEL. We show that the XFEL driven by a superconducting accelerator provides unprecedented beam stability within a pulse train. We performed microsecond sequential XPCS experiments probing equilibrium and nonequilibrium diffusion dynamics in water. We find nonlinear heating on microsecond timescales with dynamics beyond hot Brownian motion and superheated water states persisting up to 100 μs at high fluences. At short times up to 20 μs we observe that the dynamics do not obey the Stokes–Einstein predictions.

Hard X-ray Free-Electron Laser (FEL) facilities based on self-amplified spontaneous emission (SASE) (1–4) have opened additional research directions during the last 10 y (5). For example, FEL facilities have successfully expanded structural biology by promoting femtosecond crystallography (6–9) and enabled nonlinear spectroscopies (10, 11). These machines hold great promise for exploring the onset of nonequilibrium processes via X-ray photon correlation spectroscopy (XPCS). At storage ring sources, XPCS is an established technique for studying dynamics in real time at atomic to nanometer length scales (12–15). Limited by the coherent X-ray flux and detector readout, dynamics between milliseconds and hours are typically probed in such XPCS experiments, covering, e.g., diffusion, sedimentation, gelation, and shear-induced dynamics in soft matter (16–20); domain wall dynamics in hard condensed matter (21, 22); surface dynamics (23); and dynamics in amorphous ices as well as network and metallic glasses (24–28).

At pulsed sources such as a hard X-ray FEL the accessible timescale in XPCS experiments is defined by the pulse repetition rate (29). Thus, repetition rates between 30 and 120 Hz at SACLA (the Spring-8-Å Compact Free-Electron Laser, Japan) and LCLS (Linac Coherent Light Source, United States) have enabled subsecond to second dynamics studies using XPCS (30–32). By tuning pulse lengths in the order of 10 to 100 fs or by introducing split-pulse systems, ultrafast dynamics ranging from femtoseconds to few nanoseconds can also be accessed. This has recently been shown in an X-ray speckle visibility spectroscopy (XSVS) on real-time molecular dynamics of liquid water (33) and in a double-shot XPCS study using a split-pulse device (34).

The unique pulse scheme at the European X-ray FEL (European XFEL) consists of trains of up to 2,700 pulses at a spacing of 222 ns that are generated every 100 ms (35) enabling the study of (sub)microsecond dynamics in X-ray experiments. Many phenomena in soft matter physics, biology, and nanoscience happen on this timescale. The submicrosecond and microsecond regime is the natural time of diffusion processes of nanoparticles and biological macromolecules in their native aqueous environment. A further prominent example is the folding kinetics of proteins that range from microseconds to seconds (36, 37). Understanding folding and misfolding kinetics and dynamics is essential to reveal protein function and its role for many diseases; however, accessing high-resolution structure on microsecond time has been challenging (38). While microsecond dynamics can be accessed by dynamic light scattering (DLS) (39), the length scales probed in DLS experiments typically exceed micrometers because of the large wavelength of visible light. Thus, (sub)microsecond XPCS using hard X-rays has the unique potential to measure structure and dynamics simultaneously at the relevant subnanometer length scale. In this study, we explore this timescale by studying dynamics of charge-stabilized colloidal nanoparticles as a model for nanoscale materials.

We show the results of a submicrosecond XPCS experiment at a hard X-ray free-electron laser. First, we demonstrate that the European XFEL provides in fact unprecedented beam stability by comparing speckle contrast from intra- and intertrain correlation functions. Second, we show the results of a sequential-mode XPCS experiment at an XFEL on charge-stabilized nanoparticles in an aqueous environment. We accessed the relevant time window in the range of microseconds, defined by the viscosity of water, and show that XPCS can be performed at the high-repetition rate XFEL without radiation damage. Third, we follow the transition from equilibrium to emerging nonequilibrium dynamics by driving this system toward superheated conditions using focused, high-fluence X-ray pulses.

Results

In XPCS experiments the sample dynamics are probed via the time correlation function

$$g_2\left(q,\tau \right)=\frac{⟨I\left(q,t\right)I\left(q,t+\tau \right)⟩}{{⟨I\left(q,t\right)⟩}^2},$$ [1]

from time series of speckle patterns. $I\left(q,t\right)$ denotes the scattered intensity at time $t$ and the modulus of the wave vector transfer $q=4\pi \sin \left(\theta /2\right)/\lambda$, the scattering angle $\theta$, and X-ray wavelength $\lambda$. The range of accessible lag times $\tau$ is given by the repetition rate and maximum number of pulses in a pulse train. The brackets in Eq. 1 denote an ensemble average over all equivalent times $t$ and detector pixels contained in the chosen wavevector range. Using the Siegert relation, the correlation function is given by

$$g_2\left(q,\tau \right)=1+\beta {\left|f\left(q,\tau \right)\right|}^2,$$ [2]

with the speckle contrast $\beta$. The intermediate scattering function $f\left(q,\tau \right)$ contains information about all of the dynamics of the sample. For a broad range of samples, $f\left(q,\tau \right)$ can be expressed by the Kohlrausch–Williams–Watts (KWW) function

$$f\left(q,\tau \right)=\exp \left(-{\left[\mathrm{\Gamma }\tau \right]}^{\gamma }\right).$$ [3]

Here, $\mathrm{\Gamma }\equiv \mathrm{\Gamma }\left(q\right)=1/{\tau }_c$ is the relaxation rate with the characteristic relaxation time ${\tau }_c$. The dynamics can by classified according to the exponent $\gamma$ and the $q$ dependence of $\mathrm{\Gamma }$; e.g., diffusion of particles results in $\gamma =1$ and $\mathrm{\Gamma }\propto q^2$ (Materials and Methods).

We measured series of X-ray speckle patterns from different nanoparticle samples at the single particles, clusters, and biomolecules & serial femtosecond crystallography (SPB/SFX) instrument at the European XFEL (40). Details on the sample preparation and experimental setup can be found in Materials and Methods. A sketch of the experiment is given in Fig. 1. During the experiment, the European XFEL delivered 120 pulses per train to the SPB instrument. The repetition rate within the train was 1.128 MHz, which results in the fastest accessible lag time of ${\tau }_0=886$ ns for XPCS.

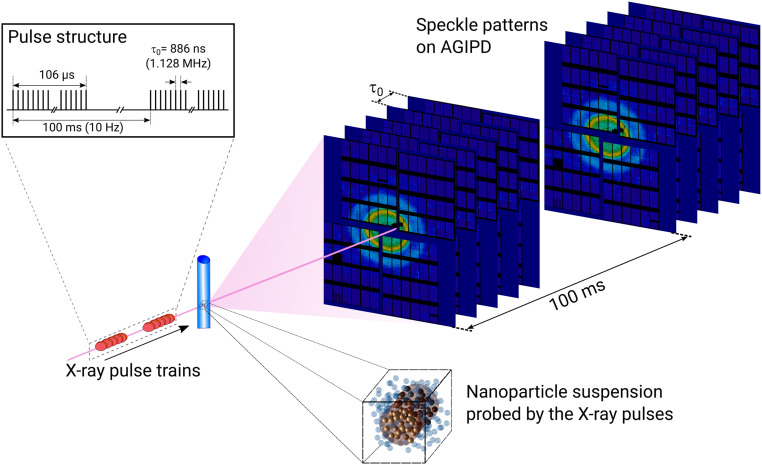
Fig. 1.

Sketch of the experiment at the SPB instrument of the European XFEL. The X-ray pulse trains scatter from the sample filled in quartz capillaries. The speckle patterns are recorded in small-angle scattering geometry 5.5 m downstream of the sample by the AGIPD detector. Each pulse train with 120 pulses was generated at 10-Hz repetition rate. Within the train, consecutive pulses were separated by ${\tau }_0=886$ ns (1.128 MHz). For clarity, only 5 instead of 120 speckle patterns per train are shown. The sample volume exposed to the X-ray pulses is schematically highlighted by the darker color.

Speckle Contrast and Coherence Properties.

The speckle contrast $\beta$ introduced in Eq. 2 is a crucial quantity for XPCS. It is proportional to the coherence properties of the X-ray beam, but is also affected by experimental parameters such as the detector pixel size and scattering geometry (41). At FEL sources the X-ray pulses have a superior degree of coherence (42–46), but shot-to-shot SASE fluctuations of intensity, pointing, beam size, and shape can significantly reduce the contrast obtained from $g_2$ functions (30–32), challenging the application of XPCS at FELs. The European XFEL makes use of a superconducting linear accelerator that is supposed to yield reduced fluctuations within pulse trains, enabling high-contrast megahertz XPCS experiments.

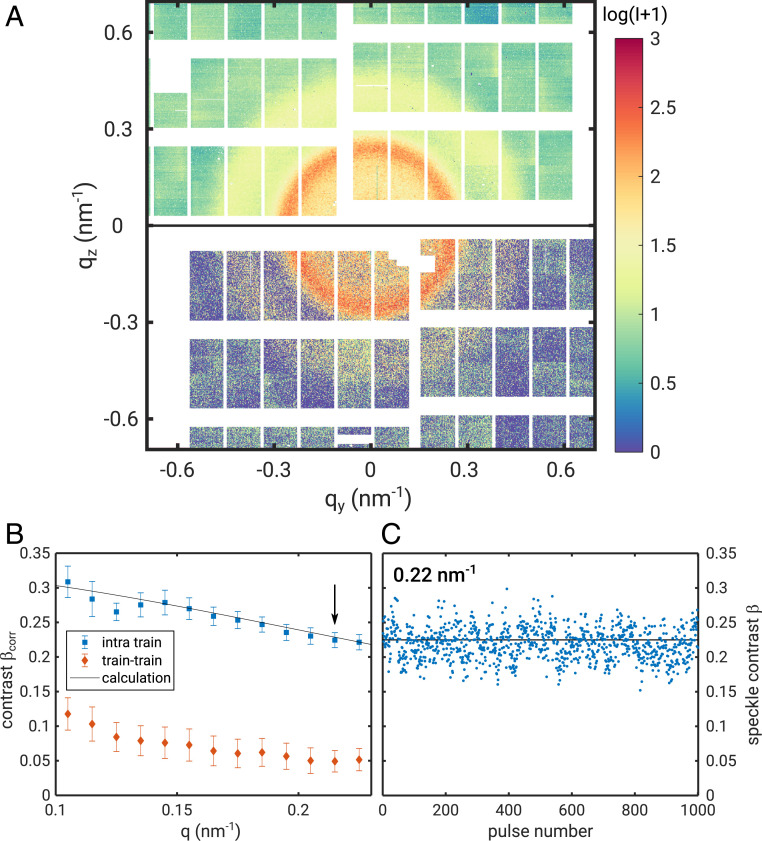
To benchmark the performance of the European XFEL on microsecond timescales, we compare the single-shot speckle contrast with the contrast obtained from correlations within pulse trains. Fig. 2A shows part of an averaged diffraction pattern (averaged over 400 trains) and of a single-shot speckle pattern taken from the static sample. The grainy appearance of the single-pulse pattern reflects the high degree of transverse coherence. $g_2$ functions have been calculated from different series of speckle patterns and analyzed following Eq. 2 to extract $\beta$. The results are shown in Fig. 2B for correlation functions taken in 1.128-MHz mode within the pulse trains (intratrain) and for a 10-Hz mode where only one pulse per train was generated by the accelerator. The intratrain speckle contrast is found to be between 0.2 and 0.3 and drops with $q$, because of the influence of longitudinal coherence length and speckle shape. This effect is modeled following ref. 43 by taking the experiment geometry, energy bandwidth of the X-rays, and beam properties into account (SI Appendix). The result is given by the black line in Fig. 2B which matches the data very well. In contrast, the intertrain correlations produce a significantly smaller value between 0.05 and 0.1. This lower value is indicative of slightly higher fluctuations between different pulse trains.

Fig. 2.

AGIPD images after dark and baseline correction and extracted speckle contrast from the static sample. (A) Scattering pattern averaged over 500 trains (Top) and single-shot speckle pattern (Bottom) from the static sample. White parts indicate masked pixels and blind regions between the AGIPD modules. The intensity scale is given in analog-to-digital unit (ADU) values (SI Appendix). One photon corresponds to 65 ADU. (B) Contrast ${\beta }_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$ from correlation function $g_2$ as a function of $q$ calculated within the train (intratrain) and between pulse trains (train–train). The solid line represents the calculated contrast (43). (C) Single-shot speckle contrast from 1,000 successive single pulses at $q=0.22\hspace{0.17em}{\mathrm{n}\mathrm{m}}^{-1}$ (arrow in B). The black line marks the average contrast of 0.225.

The contrast values obtained from the correlation functions are now compared to single-shot contrast values ${\beta }_s$ at a $q$ value of $q=0.22\hspace{0.17em}{\mathrm{n}\mathrm{m}}^{-1}$, indicated by the black arrow in Fig. 2B (see SI Appendix for details). Further analysis shows that the $g_2$ contrast is identical to the single-shot contrast. This is shown for $q=0.22\hspace{0.17em}{\mathrm{n}\mathrm{m}}^{-1}$ in Fig. 2C. It fluctuates around a mean value of 0.225 calculated from 500 pulse trains of 120 individual pulses. The variation of contrast is 7% (SI Appendix). Values reported for normal-conducting accelerator hard X-ray FEL sources with similar energy bandwidth fluctuate by more than 15% (45, 46). Our data thus indicate stable intratrain coherence properties without significant pointing fluctuations. Small fluctuations of coherence and pointing would already result in a significant loss in $g_2$ contrast with respect to the single-pulse value (31), e.g., as observed between the pulse trains.

Diffusion of Nanoparticles.

We have used this exceptional stability, the high peak, and average intensities at the European XFEL to study dynamics of small nanoparticles in the microsecond regime exploring increasing fluence values $H$. By focusing the X-ray pulses to $4.4\times 3.6\hspace{0.17em}\mathrm{\mu }{\mathrm{m}}^2$ and using different attenuators (see Materials and Methods for details), we obtain fluences between 1.3 and 56.8 mJ/${\mathrm{m}\mathrm{m}}^2$ per single pulse.

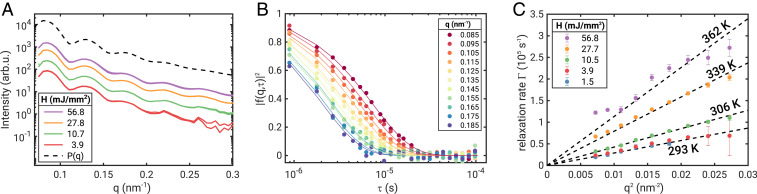
The resulting small-angle X-ray scattering profiles are shown in Fig. 3A. The oscillating curves perfectly resemble the form factor of spherical particles. Most importantly, apart from the overall intensity and lower statistics at large $q$ the curves do not differ, yielding the exact particle size and dispersity independently of the X-ray fluence. The best fit to the expression for a spherical particle form factor results in $R=69$ nm and a dispersity of $\mathrm{\Delta }R/R=0.045$ and is shown for comparison as well. We can thus exclude any influence of radiation damage on the size and shape of the nanoparticles.

Fig. 3.

Structure and dynamics of dilute nanoparticle dispersion. (A) Intensity as a function of wavevector transfer $q$ for different fluences $H$. The vertical offset indicates the intensity variation with fluence. For each $H$ several runs were performed at different sample spots whose $I\left(q\right)$ match each other within the statistical accuracy. The dashed line shows the calculated form factor of spherical particles with $R=69$ nm and $\mathrm{\Delta }R/R=0.045$. (B) Square modulus of the intermediate scattering function obtained from the correlation function $g_2$ via Eq. 2 for different $q$ values. The data were measured at $H=27.7$ mJ/${\mathrm{m}\mathrm{m}}^2$ with a single-pulse train. (C) Relaxation rates for different fluences $H$ as a function of $q^2$. The dashed lines are fits of Eq. 4 to the data with the temperature as the only free parameter.

In Fig. 3B intermediate scattering functions $|f\left(q,\tau \right){|}^2=\left(g_2-1\right)/\beta$ from a single-pulse train are shown for $H=27.7$ mJ/${\mathrm{m}\mathrm{m}}^2$ as a function of $q$. Results for $H=3.9$ mJ/${\mathrm{m}\mathrm{m}}^2$ and $g_2$-functions average over 500 trains are shown in SI Appendix. The $g_2$ functions are modeled by an exponential as described in Eqs. 2 and 3. All functions can be well described by a single and simple exponential decay ($\gamma =1$) and show a faster decorrelation at larger $q$, which is expected for diffusive dynamics. The $q$ dependence of the correlation rate $\mathrm{\Gamma }$ is shown in Fig. 3C. At low fluences, the relaxation rate follows the $q^2$ behavior of diffusive dynamics as described by Eq. 4 with temperature as the only free parameter. The viscosity of water was calculated for different temperatures using $\eta \left(T\right)$ expressions from the literature (47). Here, the data at low $H$ are well explained assuming the nanoparticles diffuse in water at 293 K, i.e., the actual temperature in the experimental hutch. These observations unambiguously prove that sequential-mode XPCS can be performed without influence of radiation damage at a high-repetition rate XFEL. Upon increasing $H$ to 10.5 and 27.7 mJ/${\mathrm{m}\mathrm{m}}^2$, the relaxation still follows the $\mathrm{\Gamma }\propto q^2$ behavior; however, the dynamics are faster compared to the low fluences. This change of the relaxation rates is reversible and can be modeled with a higher temperature as shown in Fig. 3C. This suggests an effective increase of temperature over the pulse train as a consequence of fast heating due to exposure to the previous X-ray pulses. Due the fast megahertz repetition rate, the temperature of water in the illuminated volume increases steadily during the pulse train with only a minimum of heat dissipation (29). For the highest fluence studied of $H=56.8$ mJ/${\mathrm{m}\mathrm{m}}^2$ we observe a further increase of $\mathrm{\Gamma }$, suggesting an even higher effective temperature. Furthermore, we observe deviations from the simple $q^2$ dependence at low and high q values. This may indicate the onset of nonequilibrium dynamics at high X-ray fluences, but may also stem from the averaging over all pulses (and all temperatures) in the pulse train and thus motivates the following more detailed, pulse-resolved analysis.

Microsecond X-Ray–Induced Heating.

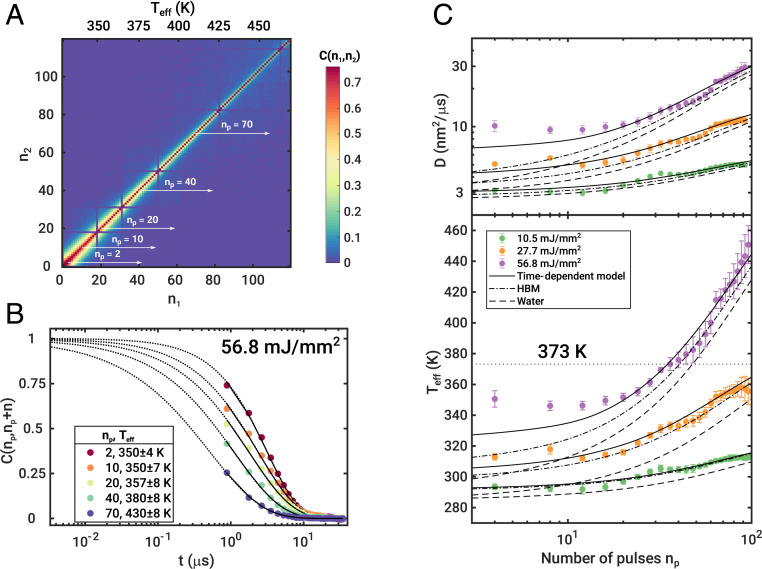
The results discussed so far are based on correlation functions averaged over 120 pulses. However, beam-induced heating can influence dynamics on a pulse-to-pulse basis. This is visualized by the instantaneous correlation function $C\left(q,t_1,t_2\right)$ (see Materials and Methods for details) shown in Fig. 4A for $H=56.8$ mJ/${\mathrm{m}\mathrm{m}}^2$ and $q=0.125\hspace{0.17em}{\mathrm{n}\mathrm{m}}^{-1}$. With progressing experimental time within the pulse train $t_e=n{\tau }_0$, with the pulse number $n$ in the train, the correlated region in $C$ becomes narrower perpendicular to the $t_1=t_2$ diagonal. This is a fingerprint of a speedup of the sample dynamics (48). For comparison, the instantaneous correlation function at low fluences shows no change of dynamics during the pulse train (see SI Appendix for $H=3.9$ mJ/${\mathrm{m}\mathrm{m}}^2$). To quantify this effect, correlation functions $C\left(q=0.125{\text{nm}}^{-1},n_p,n_p+n\right)$ have been extracted for different $n_p$ (white arrows in Fig. 4A). Here, $n_p$ denotes the first pulse number for which the correlation is computed (SI Appendix); e.g., for $n_p=10$ the correlation function is shown from pulse 10 onward with the first data point representing the correlation between pulses 10 and 11, so that the first 10 pulses act as pump pulses. The results are shown in Fig. 4B. With growing $n_p$, the correlation functions drop earlier; i.e., the dynamics become faster. The extracted $C\left(n_p,n_p+n\right)$ were modeled with Eq. 3 using speckle contrasts fixed to the values reported above (Fig. 2) and allowing for contrast variations within the error bars.

Fig. 4.

Steady sample heating. (A) Instantaneous correlation function $C\left(n_1,n_2\right)=C\left(n_p,n_p+n\right)$ at $q=0.125\hspace{0.17em}{\mathrm{n}\mathrm{m}}^{-1}$ and $H=56.8$ mJ/${\mathrm{m}\mathrm{m}}^2$ averaged over 500 pulse trains. (B) Correlation functions $C\left(n_p,n_p+n\right)$ for $n_p$ as indicated. The sequences are marked in A by white arrows. $T_{\mathrm{e}\mathrm{ff}}$ was calculated from the extracted diffusion constants. (C) Diffusion coefficient $D$ (Top) and temperature $T_{\mathrm{e}\mathrm{ff}}$ (Bottom) as function of pulse number in the pulse train $n_p$ for different $H$. The oscillating features for $n_p>30$ stem from the modulation of pulse intensities in the pulse train (SI Appendix). The black lines represent the time-dependent heating model, the dashed-dotted lines the HBM model, and the dashed lines the heating of water as solvent only. The boiling temperature of water at $p=1$ bar is given by the horizontal dotted line.

We find that the correlation functions are slightly stretched; i.e., $\gamma <1$ for the two highest fluences (SI Appendix, Figs. S12–S15). The resulting relaxation rates are shown in SI Appendix, Fig. S9 and the corresponding diffusion coefficients can be extracted. The corresponding effective temperatures were calculated as described before and are shown in Fig. 4C for the three highest fluences showing beam-induced heating (Fig. 3C). Here, $T_{\mathrm{e}\mathrm{ff}}$ represents an average over the pulses used for calculation of the correlation functions (typically dominated by the first four to six subsequent pulses with $C>0$) which is reflected by the error bars. Most interestingly, for $n_p\gtrsim 36$ at the highest fluence studied ($H=56.8$ mJ/${\mathrm{m}\mathrm{m}}^2$) we find $T_{\mathrm{e}\mathrm{ff}}>373$ K, i.e., the boiling point of water at 1 bar. With further increasing $n_p$ the effective temperature rises to $T_{\mathrm{e}\mathrm{ff}}\approx 445$ K. The subunity exponent ($\gamma <1$) is most likely a consequence of the nonstationary temperature in the probed volume. The effective temperature changes with each X-ray pulse and the correlation times for different temperatures are averaged so that the correlation functions effectively broaden, resulting in $\gamma <1$ (SI Appendix). An eventual influence of particle exchange due to thermophoresis (49) can be neglected since the diffusion time is in the range of microseconds and thus not significantly faster than the total probe time so that only few colder particles could reach the probed volume. Since the dynamics of the nanoparticles remain diffusive ($\mathrm{\Gamma }\propto q^2$) for $n_p>20,H>27.7$ mJ/${\mathrm{m}\mathrm{m}}^2$, we conclude to observe particle motion in a nonequilibrium, superheated state.

The intratrain temperature increase was first calculated based on conventional absorption models (see SI Appendix for details) (29–32, 43). Therein, the energy of the absorbed photons is converted into heat, resulting in an increase of temperature which drops subsequently due to heat flow on a timescale given by the volume and the thermal properties of the sample. As the diffusion coefficient is typically dominated by the solvent properties, we model first the temperature increase of water. Due to the megahertz repetition rate used in this experiment, its temperature has not equilibrated before the next pulse hits the sample, leading to an effective heating of the solvent. The result is shown in Fig. 4C by the dashed lines. However, as can be seen water heating alone cannot describe the data for all fluences. Therefore, we need to include the heating of the particles. Typically, the temperature increase of the nanoparticles is larger than for water because of the higher absorption of X-rays, but relaxes on a faster timescale. This leads to the case of a particle which is effectively hotter than the environment and thus transfers heat to the surrounding water volume. Consequently, the particle experiences a higher apparent solvent temperature than expected from the solvent heating only, in particular inside the solvent volume where the particle moves between two pulses. In the literature, this is typically described by the model of hot Brownian motion (HBM), especially for laser-heated nanoparticles in a solvent (50). Therein, an effective diffusion coefficient is obtained, replacing $T$ and $\eta$ by effective values $T_{\mathrm{H}\mathrm{B}\mathrm{M}}$ and ${\eta }_{\mathrm{H}\mathrm{B}\mathrm{M}}$ in Eq. 5. The results are given in Fig. 4C by the dashed-dotted lines. While it provides in general larger values for $D$ and $T_{\mathrm{e}\mathrm{ff}}$, it still underestimates the experimental data. Therefore, we explicitly calculated the time evolution of the temperatures of water and the nanoparticles together with the convective heat transfer from the particles to the surrounding water in a third time-dependent model (SI Appendix). The resulting diffusion coefficients and effective temperatures are given by the solid black lines in Fig. 4C, representing the temperature averaged over the pulses used for calculation of $\mathrm{\Gamma }$ and thus $T_{e\mathit{ff}}$. As can be seen from Fig. 4C we can (especially for high values of $H$) identify two heating regimes. First, the temperature increases after the first pulse and stays then constant up to $n_p\approx 20$. This immediate increase of the effective temperature is not well explained by the water model, hot Brownian motion, or the time-dependent model. Second, for $n_p\gtrsim 20$ the temperature increases steadily, reaching superheated states, which is very well reflected by the time-dependent model. We interpret this discrepancy at low $n_p$ values as a breakdown of the Stokes–Einstein relation (Materials and Methods and Eq. 5) at high X-ray fluences and short times. The dynamics of the particles are faster than expected, which is reflected in a higher effective temperature and thus a lower viscosity $\eta \left(T\right)$ of water based on the Stokes–Einstein relation. Note that our time-dependent model provides in general a better match than the temperatures calculated for diffusion of hot particles in a colder solvent (50) (SI Appendix), so that temperature differences between the particles and the solvent alone cannot explain the deviation.

Discussion

First, our results demonstrate the feasibility of microsecond XPCS at the European XFEL. The speckle contrast analysis shows that the European XFEL provides X-ray pulses with negligible intratrain shot-to-shot fluctuations. Such stable intratrain properties illustrate the unprecedented performance of hard X-ray FEL sources with superconducting accelerators and their suitability to perform sequential-mode XPCS experiments.

Second, we performed a microsecond XPCS experiment on water-based soft matter at the European XFEL. By tuning the fluence of the X-ray pulses we were able to measure equilibrium and nonequilibrium dynamics of silica nanoparticles dispersed in water, making use of the exceptional intratrain stability and without impact of radiation damage. As the timescale of thermal relaxation of many soft matter systems is of the same order of magnitude as the repetition rate of the European XFEL, XPCS-type pump–probe experiments become feasible on the microsecond timescale. Unlike studies at storage rings using fast diodes (51), or new detector developments (52), the superior average coherent flux and exceptional intratrain stability enable real-time microsecond XPCS experiments over a broad range of length scales ranging from the nanoscale—as shown here—to molecular and atomic length scales.

Third, we found nonlinear heating during a pulse train. For high fluences, we observe a broadening of the $g_2$ function by $\gamma <1$ due to fast heating. The temperature increase over the pulse train could be modeled taking heat relaxation of the solvent and convective heat transfer between the colloidal particles and the solvent into account. For high fluences, the temperature was found to increase immediately and remained constant up to ∼$n_p=20$. The time-dependent heating model as well as temperatures calculated for diffusion of hot nanoparticles still underestimate the measured effective temperature. This suggests a breakdown of the Stokes–Einstein relation at short timescales and large $\mathrm{\Delta }T$, where the nanoparticles move faster than expected from their and the solvent temperature. This clearly motivates theory and simulation studies focusing on heat transfer at the nanoscale to fully understand the emergence of nonequilibrium dynamics of liquids and soft matter. With increasing $n_p$, the heat transfer from the particles to the surrounding water volume combined with the absorption of X-ray photons by water leads to a steady increase of the probed temperature. At the highest fluence value studied, the sample reached superheated conditions before the solvent started to boil, as has been observed in liquid microjets (53, 54). Heating of water to temperatures above the boiling point by exposure to laser pulses was reported to happen on picosecond timescales using water microjets (55). We can thus assume that the temperature increase in our sample happens immediately, at least some orders of magnitude faster than our intrinsic time resolution of 886 ns. Remarkably, the sample showed still diffusive dynamics over the whole pulse train. This indicates that the sample was in a nonequilibrated, but still liquid state at least for timescales up to 100 $\mathrm{\mu }$s.

Materials and Methods

Samples.

We used silica nanoparticles as a dried powder (static sample) and dispersed in water (dynamic sample) as a sample. The static sample was a commercially available dispersion of silica particles in water (Sigma-Aldrich; Ludox TMA 420859). It consisted of particles with a radius of $R_{\text{stat}}=15$ nm. The size dispersity was $\mathrm{\Delta }{R}_{\text{stat}}/R_{\text{stat}}\approx 0.1$. The dispersion was dried to obtain a powder as a static sample for coherence characterization.

The dynamic sample was tailor-made so that its relaxation time is in the microsecond range, matching the time structure of the European XFEL (Experimental Setup). Colloidal silica nanoparticles were synthesized by the modified Stöber method (56, 57). Briefly, 20.4 g of tetraethyl orthosilicate (TEOS) diluted with 80 mL of absolute ethanol was added under vigorous stirring to the solution containing 400 mL of absolute ethanol and 30 mL of ammonium hydroxide (28 to 30 wt%). After stirring for 24 h at room temperature, the reaction was stopped and the colloidal suspension was concentrated using a rotational evaporator. Subsequently, the dispersion was dialyzed in ultrapure water (for about 1 wk with daily change of dialysis water) to obtain an aqueous suspension of silica nanoparticles. The nanoparticles had a radius of $R_{\text{dyn}}=69$ nm with a size dispersity of $\mathrm{\Delta }{R}_{\text{dyn}}/R_{\text{dyn}}\approx 0.045$. A concentration of 0.9 vol% was used to neglect particle–particle interactions. For instance, the expected relaxation time of these particles due to Brownian motion is about ${\tau }_B=32\hspace{0.17em}\mathrm{\mu }$s at $q=0.1\hspace{0.17em}{\mathrm{n}\mathrm{m}}^{-1}$ (Diffusive and Nonequilibrium Dynamics with XPCS), which fits well to the accessible $q$ and time range.

Experimental Setup.

The experiment was performed at the SPB/SFX instrument of the European XFEL (40). The X-ray energy was set to 9.3 keV and a mean pulse energy of 1.5 to 2 mJ which corresponds to about $10^{12}$ photons per pulse at pulse lengths of about 50 fs was obtained. The beam was focused by a Kirkpatrick–Baez mirror system (58) to about $4.4\times 3.6\hspace{0.17em}\mathrm{\mu }{\mathrm{m}}^2$ at the sample position. The quartz capillaries (0.7 mm diameter and 10 $\mathrm{\mu }$m wall thickness) containing the samples were placed in a custom-made holder. Speckle patterns were collected with the Adaptive Gain Integrating Pixel Detector (AGIPD) 1 M detector (59, 60) placed 5.5 m downstream the sample position in an evacuated flight path. To tune the number of photons per pulse hitting the sample, silicon plates of different thicknesses were inserted to the beam path upstream of the sample.

Typically, 500 to 1,000 pulse trains were measured from each sample. The trains consisted of a series of 120 pulses separated by 886 ns (1.128-MHz repetition rate) and were separated by 0.1 s (10 Hz). The sample was moved to a fresh spot between two subsequent pulse trains.

Diffusive and Nonequilibrium Dynamics with XPCS.

The $q$ dependence of the relaxation rate $\mathrm{\Gamma }$ introduced in Eq. 1 is connected to the type of dynamics, e.g., $\mathrm{\Gamma }\propto q^2$ for diffusive dynamics and $\mathrm{\Gamma }\propto q^1$ reflects ballistic motion. The exponent $\gamma$ is related to the distribution of relaxation times in the probed volume; $\gamma =1$ is found for most diffusive systems, while $\gamma <1$ may indicate heterogeneous dynamics and $\gamma >1$ suggests flow gradients in the scattering volume or stress-dominated dynamics.

For diffusion of nanoparticles in a solvent, the relaxation rate is given by

$$\mathrm{\Gamma }=D{q}^2,$$ [4]

with the Stokes–Einstein diffusion constant for spherical particles

$$D=k_{\mathrm{B}}T/\left(6\pi \eta R\right),$$ [5]

with Boltzmann’s constant $k_{\mathrm{B}}$, temperature $T$, viscosity $\eta$, and particle radius $R$.

To access nonequilibrium dynamics, e.g., dynamical heterogeneities or effects of waiting times, multitime correlation functions, such as the instantaneous correlation function

$$C\left(q,t_1,t_2\right)\hspace{0.17em}=\hspace{0.17em}\frac{{⟨I_p\left(q,t_1\right)I_p\left(q,t_2\right)⟩}_{\psi }}{{⟨I_p\left(q,t_1\right)⟩}_{\psi }{⟨I_p\left(q,t_2\right)⟩}_{\psi }},$$ [6]

are typically studied (48, 61–63). ${⟨\cdot ⟩}_{\psi }$ denotes the average over pixels within the same momentum transfer $q\pm \mathrm{\Delta }q$. It correlates every speckle pattern from an XPCS series with each other. Typically, $C$ is represented in the two-dimensional $t_1-t_2$ space. $C$ measures the time evolution of the intensity autocorrelation function $g_2\left(q,\tau \right)$ along the absolute experimental time $t_e=\left(t_1+t_2\right)/2$ for a delay time $\tau =|t_2-t_1|$. In the case that the dynamics do not change with $t$, the time average of $C_{\mathrm{I}}$ is equal to $g_2$ via $g_2\left(q,\tau \right)={⟨C\left(q,t_1,\tau \right)⟩}_{t_1}$. For easier interpretation, the notation $C\left(n_p,n_p+n\right)$ was used, with $C\left(n_p,n_p+n\right)=C\left(n_1,n_2\right)\equiv C\left(q,n_p{\tau }_0,\left[n_p+n\right]{\tau }_0\right)$. Furthermore, $C$ has been averaged over all studied pulse trains.

Data Availability.

Some study data from this article are available.