Exploring the landscape of model representations

Significance

Physical phenomena can often be described by surprisingly few order parameters. Unfortunately, it is challenging to identify these essential degrees of freedom. Here we develop a statistical physics framework for exploring the landscape of order parameters, or coarse-grained representations, for a microscopic protein model. We employ Monte Carlo methods to statistically characterize this landscape. We define metrics assessing the intrinsic quality of each representation for preserving the configurational information and large-scale motions of the underlying microscopic model. Interestingly, these metrics are anticorrelated in low-resolution representations. Moreover, below a critical resolution, a phase transition qualitatively distinguishes superior and inferior representations. Finally, we relate our work to recent approaches for clustering graphs and detecting communities in networks.

Abstract

The success of any physical model critically depends upon adopting an appropriate representation for the phenomenon of interest. Unfortunately, it remains generally challenging to identify the essential degrees of freedom or, equivalently, the proper order parameters for describing complex phenomena. Here we develop a statistical physics framework for exploring and quantitatively characterizing the space of order parameters for representing physical systems. Specifically, we examine the space of low-resolution representations that correspond to particle-based coarse-grained (CG) models for a simple microscopic model of protein fluctuations. We employ Monte Carlo (MC) methods to sample this space and determine the density of states for CG representations as a function of their ability to preserve the configurational information, $I$, and large-scale fluctuations, $\mathcal{Q}$, of the microscopic model. These two metrics are uncorrelated in high-resolution representations but become anticorrelated at lower resolutions. Moreover, our MC simulations suggest an emergent length scale for coarse-graining proteins, as well as a qualitative distinction between good and bad representations of proteins. Finally, we relate our work to recent approaches for clustering graphs and detecting communities in networks.

Introduction

Remarkably simple models explain many physical phenomena (1). This is clearly true of thermodynamic models for macroscopic systems (2). It is also true of simulation models for soft materials, such as polymers and proteins. While atomistic models provide exquisite detail, they are often computationally intractable. Moreover, unnecessary atomic details tend to obscure basic physical insight. Consequently, simulations of soft materials often adopt simplified, coarse-grained (CG) models that provide much greater computational efficiency and more transparent insight (3, 4).

Just as thermodynamic models rely upon identifying appropriate order parameters (1, 2), one expects the success of a CG model will critically hinge upon the quality of the CG representation, i.e., the degrees of freedom the CG model retains. However, it is often difficult to discern the essential degrees of freedom for complex phenomena. Historically, researchers have generally relied upon physical intuition to determine CG representations (5). For instance, generic bead-spring models of polymers often represent each monomer with a single sphere (4). More recent studies have proposed various methods for optimizing the representation of CG models for specific chemical systems (6–18).

Unfortunately, it is quite nontrivial to directly assess the intrinsic quality of a CG representation since the performance of a CG model will generally reflect various approximations introduced, e.g., when parameterizing its potential (5). Consequently, there remain many basic questions regarding the choice of CG representations. For instance, it is often far from obvious whether there exist significant distinctions between good and bad representations. Moreover, assuming such distinctions exist, it remains unclear whether good representations share certain common features or whether they are easy to find. These questions are also of considerable importance for the closely related problem of identifying order parameters or collective variables for accelerating, analyzing, and interpreting calculations with high-resolution models (19). Even more generally, these basic questions are of fundamental importance for developing reduced models for the large datasets that are relevant to, e.g., modern materials science (20).

In this work, we develop and apply a statistical physics framework for addressing these questions. Rather than optimizing the CG representation according to some specific metric, we seek to explore and characterize the entire landscape of representations (21). As an instructive case study, we start from a simple microscopic model of protein conformational fluctuations. There are an essentially infinite variety of ways to represent the protein in CG detail. Each representation corresponds to a different set of order parameters for characterizing the fluctuations of the underlying microscopic model. In particular, we consider representations that replace connected atomic groups with discrete CG particles. We introduce quantitative metrics for assessing the intrinsic quality of each representation. We employ Monte Carlo (MC) simulations to sample the space of representations and estimate a density of states quantifying the number of representations with a given quality. Interestingly, this density of states suggests the emergence of a phase transition distinguishing good and bad representations beyond a certain characteristic resolution. Finally, we also relate this work to research on community detection in complex networks.

Results

Microscopic Model.

We adopt the Gaussian network model (GNM) as a simple microscopic model of protein fluctuations about a single equilibrium conformation (22, 23). The GNM describes a protein as an isotropic network of $n$ atoms, each corresponding to the $\alpha$ carbon of an amino acid residue. The reduced potential for the GNM is $u\left(\text{q}\right)=\frac{1}{2}{\text{q}}^{†}\mathit{\kappa }\text{q}$, where ${\text{q}}^{†}=\left(q_1,\dots ,q_n\right)$ specifies the displacements of the $n$ atoms from their equilibrium positions, while $\mathit{\kappa }$ is a symmetric matrix that connects nearby atoms with linear springs and determines the corresponding covariance matrix, $\text{c}\propto {\mathit{\kappa }}^{-1}$. The equilibrium distribution is then $p\left(\text{q}\right)\propto \exp \left[-\beta u\left(\text{q}\right)\right]$, where $\beta$ is the inverse temperature. Despite its simplicity, the GNM has proven remarkably useful for investigating functional motions in proteins and biological complexes (24).

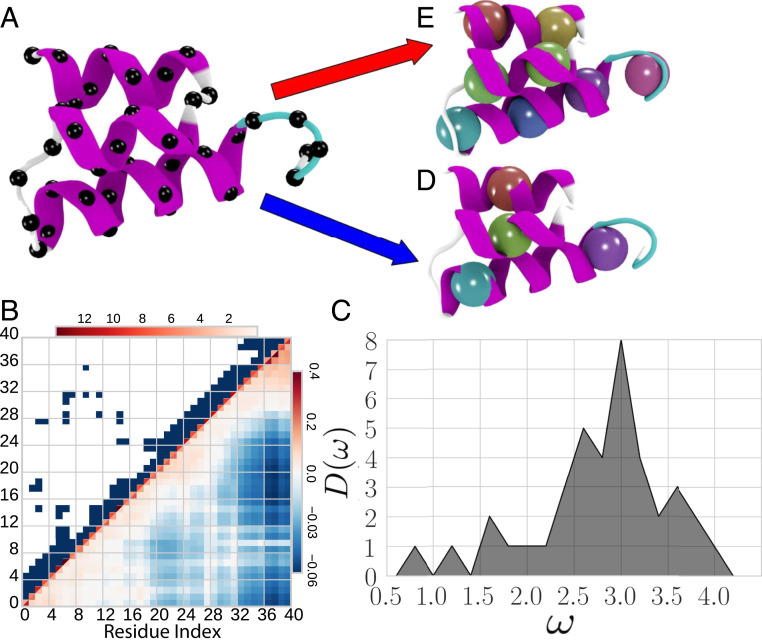
In the following, we primarily focus on the small helical protein 2ERL, although SI Appendix indicates that our conclusions are robust with respect to variations in the protein sequence, structure, and size. Fig. 1A presents the equilibrium structure of 2ERL, while Fig. 1 B and C present $\mathit{\kappa }$, $\text{c}$, and the corresponding vibrational density of states. We consider two metrics for characterizing the microscopic model: 1) the information content, $h\propto \ln det\mathit{\kappa }$, determines the protein-dependent contribution to the configurational entropy of the microscopic GNM (25) and quantifies the information stored in its equilibrium distribution (26) and 2) the vibrational power, $\sigma \propto \mathrm{T}\mathrm{r}\hspace{0.5em}\text{c}$, quantifies the magnitude of conformational fluctuations sampled by the protein. Note that $h$ emphasizes high-frequency motions, while $\sigma$ emphasizes biologically important, low-frequency motions (24). Materials and Methods and SI Appendix describe the model and metrics in greater detail.

Fig. 1.

Characterization of the model protein 2ERL. (A) Cartoon representation of the equilibrium folded structure with black spheres indicating $\alpha$ carbons. (B) Intensity plots of the upper and lower halves of the symmetric connectivity, $\mathit{\kappa }$, and covariance, $\text{c}\propto {\mathit{\kappa }}^{-1}$, matrices. (C) Vibrational densities of states for the high resolution GNM of 2ERL. (D and E) CG representations with spheres representing the location of the CG sites for block maps with $N$ = 4 and 8 sites, respectively. Figure employed VMD (66).

Characterizing and Sampling Representations.

There exist many ways to represent the microscopic model in reduced detail. We codify each representation in terms of a mapping, $\text{M}$, that specifies the CG configuration $\text{Q}=\left(Q_1,\dots ,Q_N\right)$ for $N$ CG particles, or sites, as a function of the microscopic coordinates, i.e., $\text{M}:\text{q}\to \text{Q}=\text{M}\left(\text{q}\right)$ (27). For simplicity, we assume that 1) this mapping corresponds to partitioning the $n$ atoms into $N$ disjoint groups of $R=n/N$ connected atoms and 2) each CG coordinate corresponds to the mass center for the associated atomic group. For example, Fig. 1 D and E illustrate the block map, which partitions the protein sequence into $N$ contiguous fragments of $R$ consecutive residues and associates a site with each fragment.

Given the microscopic equilibrium ensemble, $\text{M}$ determines a mapped ensemble with the distribution $P\left(\text{Q};\text{M}\right)=\int \text{d}\mathrm{q}p\left(\text{q}\right)\delta \left(\text{Q}-\text{M}\left(\text{q}\right)\right)$. The covariance matrix for the CG coordinates in this mapped ensemble is ${\text{C}}_{\text{M}}=\text{M}\mathrm{c}{\text{M}}^{†}\propto {\text{K}}_{\text{M}}^{-1}$ (25). Importantly, the information content, $H\left(\text{M}\right)\propto \ln det{\text{K}}_{\text{M}}$, and vibrational power, $\mathrm{\Sigma }\left(\text{M}\right)\propto \text{Tr}\hspace{0.5em}{\text{C}}_{\text{M}}$, within the mapped ensemble are functions of $\text{M}$. We quantitatively assess each CG representation, $\text{M}$, based upon the fraction of information, $I\left(\text{M}\right)=H\left(\text{M}\right)/h$, and vibrational power, $\mathcal{Q}\left(\text{M}\right)=\mathrm{\Sigma }\left(\text{M}\right)/\sigma$, that are preserved in the mapped ensemble. While many metrics may prove useful, $I$ and $\mathcal{Q}$ exemplify metrics that emphasize high-frequency, localized motions and low-frequency, global motions, respectively. Importantly, these metrics directly assess the quality of the CG representation and can be analytically calculated for the GNM (25).

We seek to explore the landscape of CG mappings and to investigate the thermodynamics of selecting maps. Accordingly, we define an energy function $\mathcal{E}\left(\text{M}\right)\propto I\left(\text{M}\right)$ or $\mathcal{E}\left(\text{M}\right)=1-\mathcal{Q}\left(\text{M}\right)$ and perform MC simulations that sample maps according to a canonical distribution, ${\mathcal{P}}_{\text{M}}\propto e^{-{\beta }_{\mathcal{E}}\mathcal{E}\left(\text{M}\right)}$, at a conjugate inverse temperature, ${\beta }_{\mathcal{E}}$. Starting from the block map, the simulations diffuse through mapping space by swapping atoms between pairs of CG sites, while ensuring that each site remains connected. Each move is accepted or rejected based upon a Metropolis criterion ensuring detailed balance (28). Given the maps sampled at a wide range of conjugate temperatures, we estimate densities of states that quantify the number of maps with a given information content, $\mathrm{\Omega }\left(I\right)$, and spectral quality, $\mathrm{\Omega }\left(\mathcal{Q}\right)$.

Densities of States.

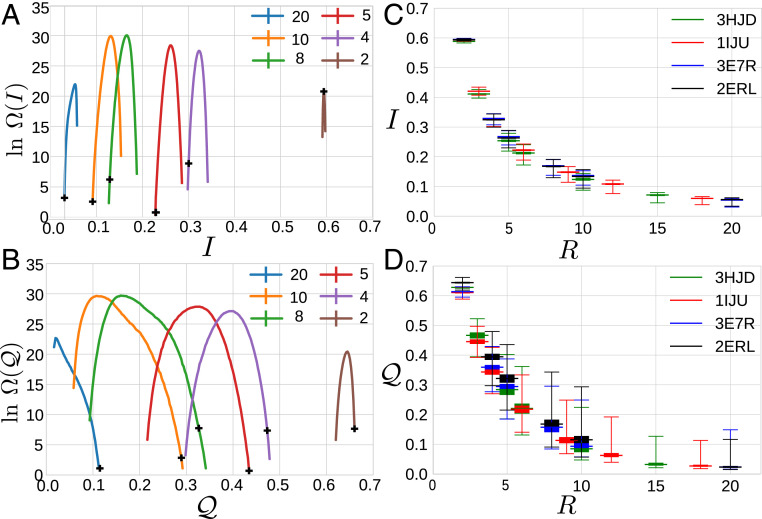
Fig. 2 presents the natural logarithm of the resulting density of states, $\ln \mathrm{\Omega }$, for different degrees of coarsening, $R$. Since $\ln \mathrm{\Omega }$ exhibits pronounced peaks for each $R$, each resolution is characterized by a very large number of typical maps with a characteristic information content, $I$, and spectral quality, $\mathcal{Q}$. As expected, the characteristic values for $I$ and $\mathcal{Q}$ systematically decrease with increased coarsening, although they decrease less rapidly than might be naïvely expected. For instance, when each site represents two atoms, i.e., $R=2$, typical representations preserve ∼60% of the information and vibrational power present in the microscopic ensemble. Interestingly, $\ln \mathrm{\Omega }\left(I\right)$ is similarly narrow at each resolution $R>2$. In contrast, $\ln \mathrm{\Omega }\left(\mathcal{Q}\right)$ becomes increasingly broad with coarsening. In particular, at a given resolution, there exist rare mappings that provide significantly higher spectral quality than typical maps.

Fig. 2.

Statistical analysis of mapping space. (A and B) The natural logarithm of the density of states, $\ln \mathrm{\Omega }$, quantifying the number of maps, $\text{M}$, with given information content, $I$, or spectral quality, $\mathcal{Q}$, for 2ERL at varying degrees of coarsening, $R=n/N$, indicated by the colors of the legend. The black crosses indicate $I$ and $\mathcal{Q}$ for the block map at each resolution. (C and D) Box plots indicating the mean (widest bar), extrema (top and bottom bars), and the 25 and 75% quantiles (shaded box) characterizing these densities of states for 2ERL (black) and for three other small proteins.

Fig. 2 C and D present box plots summarizing these statistics as a function of resolution for 2ERL and three other small proteins. The $I$ distributions are not only narrow but also almost identical for different proteins. Thus, the information content depends strongly upon resolution but appears relatively insensitive to the details of the mapping or the particular proteins. In contrast, the $\mathcal{Q}$ distributions are much broader, demonstrate greater protein dependence, and demonstrate long tails toward relatively high spectral quality. Certain proteins and certain resolutions appear particularly amenable for preserving the low-frequency motions of the microscopic model.

The crosses in Fig. 2 A and B indicate $I$ and $\mathcal{Q}$ for the block map at each resolution. When compared to typical representations, the block map tends to exhibit relatively low $I$ and relatively high $\mathcal{Q}$. Due to the simplicity and symmetry of the 2ERL structure, the block map provides nearly minimal $I$ and maximal $\mathcal{Q}$ at almost every resolution for this protein. For some proteins and resolutions, though, block maps do not optimize either metric but instead exhibit more typical values of $I$ and $\mathcal{Q}$.

Optimal Representations.

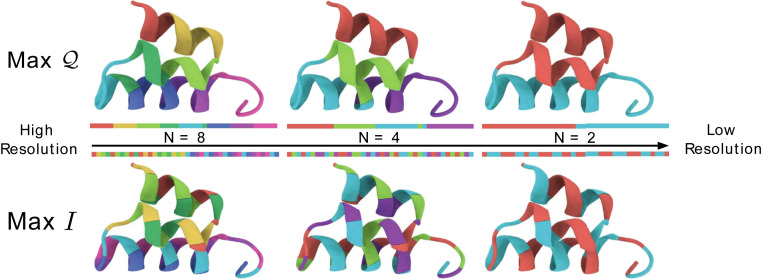
Fig. 2 indicates that $I$ and $\mathcal{Q}$ are not equivalent measures of model quality. Fig. 3 illuminates the difference between these two metrics by comparing the representations of 2ERL that maximize $\mathcal{Q}$ and $I$ at various resolutions. SI Appendix presents analogous comparisons for several additional proteins. Representations that maximize the spectral quality, $\mathcal{Q}$, preserve low-frequency fluctuations by grouping atoms into densely packed sites that move coherently. Accordingly, the block map generally has relatively high spectral quality and, in the case of 2ERL, even maximizes $\mathcal{Q}$ at certain resolutions. In contrast, representations that maximize the information content, $I$, form sites by grouping atoms that are distributed across the protein in order to preserve high-frequency motions. Because these high-frequency motions are usually localized and often physically uninteresting in soft materials, we focus on the spectral quality, $\mathcal{Q}$, in the remainder of this work.

Fig. 3.

Maps that maximize $\mathcal{Q}$ (Top) and $I$ (Bottom) among maps with $N$ = 8, 4, or 2 sites. The ribbon and line diagrams are colored to indicate the atoms that are grouped together in the three-dimensional structure and in the one-dimensional amino acid sequence, respectively. Figure employed VMD (66).

Apparent Phase Transition.

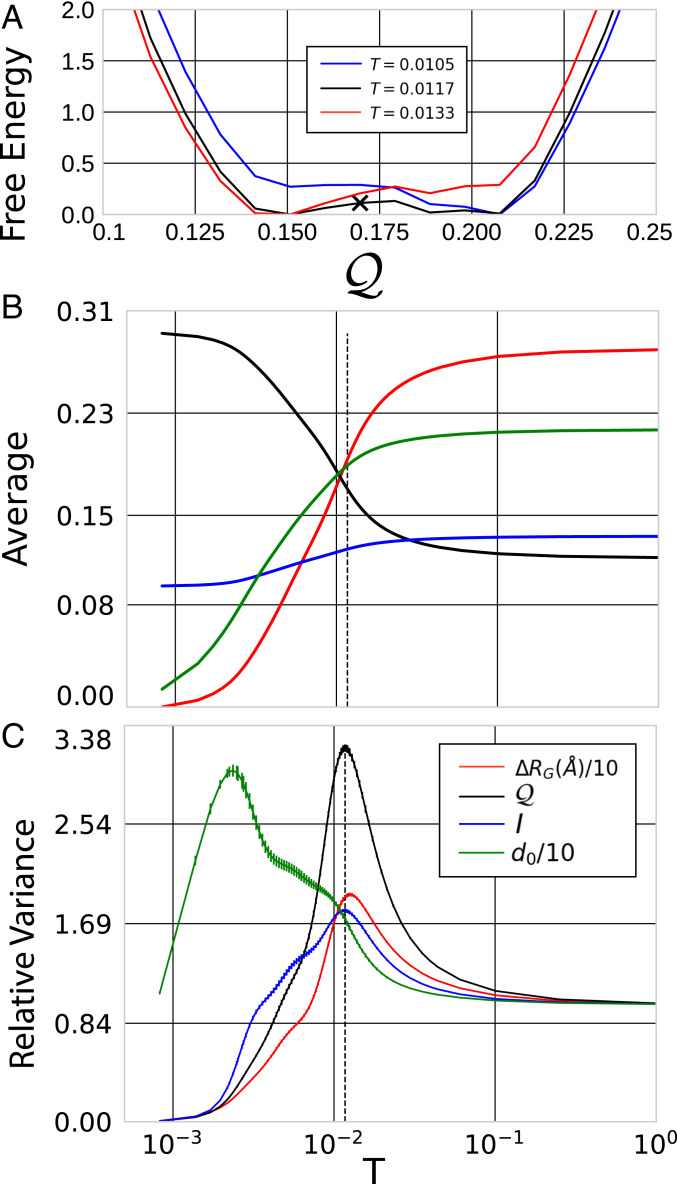
Given a mechanical model for a finite physical system with energy $E$, an inflection point in the corresponding density of states, $\mathrm{\Omega }\left(E\right)$, implies the existence of a first-order phase transition (29–31). Interestingly, the densities of states, $\mathrm{\Omega }\left(\mathcal{Q}\right)$, in Fig. 2B also exhibit inflection points at sufficiently coarse resolutions, which suggest the existence of analogous phase transitions in the space of CG representations. In order to characterize these transitions, we define a dimensionless free energy, ${\beta }_{\mathcal{Q}}F\left(\mathcal{Q};{\beta }_{\mathcal{Q}}\right)=-\ln \mathcal{P}\left(\mathcal{Q};{\beta }_{\mathcal{Q}}\right)$, where $\mathcal{P}\left(\mathcal{Q};{\beta }_{\mathcal{Q}}\right)$ is the probability of sampling a map $\text{M}$ with spectral quality $\mathcal{Q}$ at the inverse temperature ${\beta }_{\mathcal{Q}}$ that is conjugate to $\mathcal{E}\left(\text{M}\right)=1-\mathcal{Q}\left(\text{M}\right)$. Similarly, we define averages and variances as a function of the temperature $T_{\mathcal{Q}}={\beta }_{\mathcal{Q}}^{-1}$. Fig. 4 characterizes the suggested transition in the space of maps for $N=4$ site representations of 2ERL.

Fig. 4.

Characterization of the apparent transition for $N=4$ site representations of 2ERL. (A) The dimensionless free energy, ${\beta }_{\mathcal{Q}}F$, at the transition temperature (black) and at temperatures above (red) and below (blue) the transition. The black X indicates the separatrix, ${\mathcal{Q}}_{*}$, for which $\mathcal{P}\left(\mathcal{Q}<{\mathcal{Q}}_{*}\right)=1/2$ at the transition temperature. (B and C) The averages and variances, respectively, for several metrics. The metric $d_0\left(\text{M}\right)$ quantifies the difference in the atomic groups defined by the map, $\text{M}$, and the ground state map, ${\text{M}}_0$, while ${\text{R}}_{\text{G}}\left(\text{M}\right)$ quantifies the compactness of the associated atomic groups. For convenience, we have shifted ${\text{R}}_{\text{G}}$ such that $\mathrm{\Delta }{\text{R}}_{\text{G}}\left(\text{M}\right)$ vanishes as $T_{\mathcal{Q}}\to 0$ and have normalized variances relative to their $T_{\mathcal{Q}}\to \infty$ limit. Error bars estimate statistical uncertainty. The dashed vertical line indicates the transition temperature, which is defined by the variance peak in $\mathcal{Q}$. T denotes the fictitious temperature, $T_{\mathcal{Q}}$, conjugate to $\mathcal{E}\left(\text{M}\right)$ = 1- $\mathcal{Q}\left(\text{M}\right)$.

Fig. 4A demonstrates that at the transition temperature the free energy surface features two shallow minima, corresponding to maps with relatively high and low $\mathcal{Q}$. These minima are separated by a relatively small barrier, as might be expected for a weak first-order transition in a small system. The black cross indicates the separatrix, which is estimated based upon equal population for the two states. Fig. 4B demonstrates that near this transition the spectral quality increases and the information content decreases, as expected. Fig. 4C demonstrates that the variance in these metrics also peaks at or near this transition (32). In particular, we define the transition temperature by the variance peak for $\mathcal{Q}$.

Fig. 4 B and C also present two additional metrics characterizing this transition. For each resolution, $R=n/N$, we define the ground state map, ${\text{M}}_0$, as the $N$-site map with maximum spectral quality. We define the distance, $d_0$, of a map $\text{M}$ from ${\text{M}}_0$, based upon the variation of information (VI) (33), which quantifies the dissimilarity of the corresponding atomic partitions, i.e., $d_0\left(\text{M}\right)=\text{VI}\left(\text{M},{\text{M}}_0\right)$. Additionally, we define ${\text{R}}_{\text{G}}\left(\text{M}\right)$, by the average gyration radius of the partitioned atomic groups in the equilibrium protein conformation. Fig. 4 B and C demonstrate that the sampled maps become more compact and also more similar to ${\text{M}}_0$ at the observed transition. Interestingly, the variance in $d_0$ peaks at a noticeably lower temperature, which indicates considerable variation among the clusterings of maps with high spectral quality. Nevertheless, SI Appendix demonstrates that these metrics correlate quite well with the spectral fitness.

Consequently, Fig. 4 demonstrates that this transition in the space of representations bears consider similarity to a physical phase transition between different phases of matter. Moreover, this transition suggests a qualitative distinction between good and bad representations of a protein at a given resolution. In particular, good maps are characterized by compact sites that ensure high spectral quality and by quantitatively similar partitions of atoms.

Global Perspective.

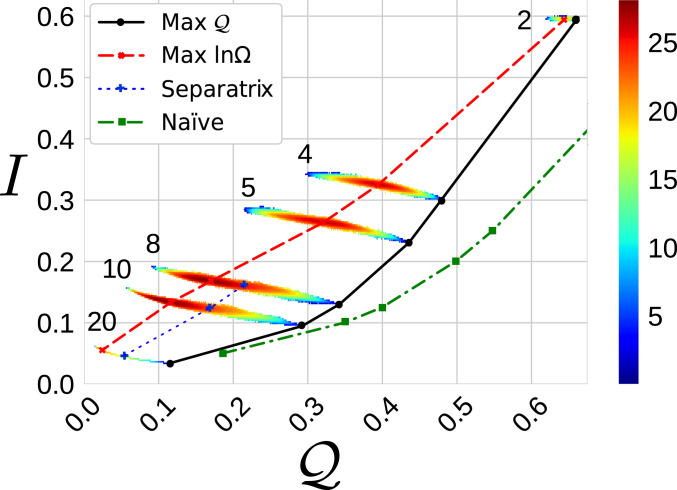
Fig. 5 provides a broader perspective on the space of representations by presenting an intensity plot of the natural logarithm of the joint density of states, $\ln \mathrm{\Omega }\left(\mathcal{Q},I\right)$ for CG representations of 2ERL. In particular, this two-dimensional density of states indicates the correlation between $\mathcal{Q}$ and $I$. While $\mathcal{Q}$ and $I$ are essentially uncorrelated for the highest-resolution CG representations, they become highly anticorrelated for lower resolutions. As noted above, at a given resolution, the CG representations sample a fairly narrow range in $I$ but a much broader range in $\mathcal{Q}$. For comparison, the green curve indicates, for each resolution, the maximum possible spectral fitness, ${\mathcal{Q}}_{max}$, which would be achieved if the $N$-site CG representation perfectly preserved the $N-1$ lowest vibrational frequencies of the atomic model, as well as a naïve scaling expectation for the information content $I=1/R$. Fig. 5 demonstrates that the CG representations almost always preserve more information than might be naïvely expected. Moreover, the best maps achieve ∼80% of ${\mathcal{Q}}_{max}$.

Fig. 5.

Global perspective on mapping space for 2ERL. The heat map colors indicate the magnitude of the 2D ln densities of states, $\ln \mathrm{\Omega }\left(\mathcal{Q},I\right)$, for CG maps with resolutions $R$ = 2, 4, 5, 8, 10, and 20. The dashed red and solid black curves indicate the maxima of $\ln \mathrm{\Omega }$ and $\mathcal{Q}$, respectively, at each resolution. The dashed-dotted green curve presents a naïve estimate of the expected information content at each resolution, i.e., $N/n$, and the optimal spectral quality, ${\mathcal{Q}}_{N;max}$, which corresponds to reproducing perfectly the $N-1$ lowest vibrational frequencies of the high-resolution model. The dotted blue curve and crosses indicate the separatrices of transitions that are observed at sufficiently low resolutions.

The blue crosses in Fig. 5 indicate the separatrices for the transitions that are observed at lower resolutions. In the case of 2ERL, we only observe these transitions for resolutions grouping at least eight residues per site, corresponding to approximately two turns of an $\alpha$ helix. SI Appendix presents $\ln \mathrm{\Omega }\left(\mathcal{Q}\right)$ for six additional proteins of up to 72 amino acid residues with varying secondary structures and topologies, which suggest that these trends are quite common among proteins. In almost every case, the densities of states indicate the onset of a phase transition past a certain threshold resolution, which suggests a characteristic length scale for coarse-graining these proteins.

Relation to Networks.

The process of determining CG representations for molecular systems bears striking similarity to clustering or detecting communities in complex networks. The GNM makes this analogy particularly transparent. The GNM defines an interaction network for a single protein by connecting nearby residues with linear springs. The protein residues correspond to the nodes of the network (or, equivalently, to the vertices of a graph) that are connected by edges corresponding to linear springs. The curvature of the GNM potential, $\kappa$, corresponds to the graph Laplacian, $L$, which specifies the edges of the protein interaction network (34). The process of grouping atoms into CG sites then corresponds to clustering nodes in a graph or defining communities in a network.

Consequently, the present work bears considerable similarity to several leading approaches for clustering and community detection (35, 36). For instance, SI Appendix demonstrates that the spectral quality, $\mathcal{Q}$, of a CG representation is quite correlated with the modularity (37), which quantifies the strength of the corresponding communities based upon the fraction of edges connecting the nodes within each cluster. Thus, the ground state representation that maximizes $\mathcal{Q}$ should be quite similar to the clustering obtained in simulations of Potts models that optimize the modularity (38, 39). The present work is also related to spectral clustering approaches that, e.g., partition nodes according to the lowest eigenvalues of $L$ (40, 41) or that identify communities based upon the stability of random walks on the graph (42, 43).

However, the present work bears two crucial distinctions with respect to prior investigations of network communities. First, while many prior studies have sought a single clustering that achieves a specific objective (38, 40, 42) or an ensemble of graphs with certain characteristics (44, 45), we have focused on the space of representations for a single GNM, which corresponds to an ensemble of clusterings for a single graph (46). Second, and more importantly, the process of coarse-graining does not simply correspond to grouping nodes but rather to the process of viewing the fluctuations of an underlying microscopic model for a physical system through a particular coarse lens. This physical process corresponds to a rigorous thermodynamic projection that renormalizes the underlying microscopic potential (47), such that the resulting effective springs connecting CG sites vary in strength and even in sign (25, 48).

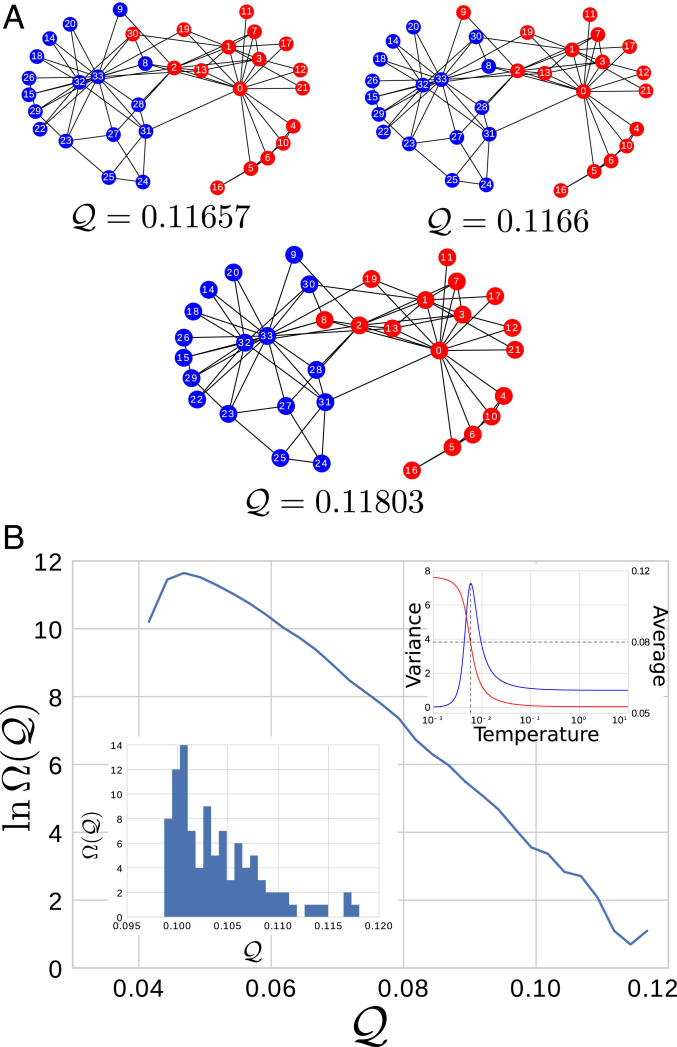
Accordingly, it is intriguing to apply the physical coarse-graining process to Zachary’s karate club network (49, 50), which is illustrated in Fig. 6. Zachary’s karate club provides a particularly simple archetype of networks considered by community detection algorithms and is known to have two meaningful communities. We defined a corresponding GNM by defining $\mathit{\kappa }$ as the graph Laplacian of the network. In this case, we can exhaustively enumerate all representations of the GNM since the network includes only 34 nodes with local connections. Fig. 6A presents the three CG representations that maximize $\mathcal{Q}$. Indeed, the ground state representation of the GNM corresponds to the known communities, while the first two excited state representations correspond to very similar clusterings. Fig. 6B presents the density of states, $\mathrm{\Omega }\left(\mathcal{Q}\right)$, for two-site representations of this GNM. Interestingly, a similar phase transition is also observed between good and bad representations of the GNM for Zachary’s karate club network.

Fig. 6.

Coarse-graining the GNM defined by Zachary’s karate club network. (A) The $N=2$ CG map with optimal spectral quality (${\mathcal{Q}}_{2;max}$ = 0.11803), as well as the first two excited states with slightly lower spectral quality. (B) $\ln \mathrm{\Omega }\left(\mathcal{Q}\right)$. (Lower Left Inset) The spectra for the first 100 maps. (Upper Right Inset) As a function of conjugate temperature, the average spectral quality (red curve, right scale) and the corresponding variance (blue curve, left scale), which has been normalized relative to its ${\beta }_{\mathcal{Q}}\to 0$ limit. The vertical line in Upper Right Inset indicates the transition temperature, while the horizontal line indicates the corresponding mean.

Conclusions

We have presented a statistical thermodynamic formalism and computational investigation of the landscape of CG representations for physical systems. In this first investigation, we adopted the GNM as a high-resolution model since it provides a qualitatively useful description of protein fluctuations and is amenable to theoretical analysis. We considered CG representations that are both linear and local since we defined CG coordinates as linear combinations of the atomic coordinates for connected groups. By employing an analytic coarse-graining of the GNM (25), we quantitatively and exactly assessed the intrinsic quality of CG representations without introducing any approximations, e.g., due to approximating the interactions between CG particles.

The present work focused on characterizing CG representations according to two metrics, $I$ and $\mathcal{Q}$, which quantify the ability of the CG representation to preserve the information and large-scale fluctuations, respectively, contained in the microscopic ensemble. A priori, one might anticipate that these metrics would both prove useful for optimizing CG representations. Our numerical studies demonstrate that both $I$ and $\mathcal{Q}$ decrease in a similar fashion with coarsening for typical maps. However, while $I$ appears relatively insensitive to the details of the CG representation or the protein, $\mathcal{Q}$ appears more sensitive to variations in representation and protein structure. Furthermore, these metrics appear uncorrelated for high-resolution representations but become highly anticorrelated for low-resolution representations. Representations that maximize $I$ feature loosely connected sites that preserve the information associated with the many localized and, thus, relatively informative high-frequency vibrations. Conversely, representations that maximize $\mathcal{Q}$ correspond to densely connected sites that preserve few low-frequency vibrations.

These considerations explain why block maps that group residues consecutively in sequence tend to be information-poor but provide a good description of low-frequency fluctuations. This intuition also underlies the connection between principal component analysis and the renormalization group (51), as well as current strategies for optimizing CG representations (6, 13) and order parameters (52, 53). In particular, SI Appendix demonstrates that $\mathcal{Q}$ is (anti-) correlated with the objective function, ${\chi }^2$, which is minimized in the essential dynamics coarse-graining methodology for determining good CG representations (7). Moreover, our estimates for $\mathrm{\Omega }\left({\chi }^2\right)$ indicate that similar phase behavior would be observed if ${\chi }^2$ were adopted as a metric for characterizing CG representations. Since $\mathcal{Q}$ emphasizes the large-magnitude, low-frequency motions that define the essential dynamics subspace of the mapped covariance matrix (54), we expect $\mathcal{Q}$ is representative of many metrics employed to identify coherent structural domains in proteins.

Quite generally, one expects that physical models of soft materials will often demonstrate relatively few low-frequency motions that correspond to important physical transitions and comparatively many high-frequency modes that correspond to uninteresting localized motions. In other words, most of the information contained in high-resolution models describes uninteresting noise, while a comparatively small fraction of the information describes interesting physics. For this reason, physical models are often “sloppy” in the sense of predicting large-scale phenomena that are insensitive to most of the parameters defining the model (55, 56). Moreover, these results suggest that it may be unwise to optimize representations of physical systems by naïvely maximizing their information content. Similarly, it may be unwise to optimize CG representations for backmapping to atomic resolution, i.e., for reintroducing high-resolution details into low-resolution structures. Rather, it is important to consider the physical variables of interest when determining the CG representation of a particular system.

Most interestingly, our numerical results suggest the emergence of a characteristic resolution for coarse-graining proteins. For relatively high resolutions, all CG representations are qualitatively similar. Below this characteristic resolution, a phase transition indicates a qualitative distinction between good and bad representations that becomes increasingly significant with further coarsening. Good representations reflect similar partitions of atoms into spatially compact, highly modular sites with relatively many stabilizing intrasite interactions.

In the case of 2ERL, this phase transition first emerges in $N=5$ site representations for which $R=8$ amino acids are grouped into each CG site. Fig. 3 indicates that just below this critical resolution, the ground state map represents each of the two small helices with distinct sites, while splitting the larger helix into contiguous fragments. This suggests that the critical resolution corresponds to the emergence of distinct, modular subunits that are stabilized by many internal interactions with relatively few interactions between different subunits. It also indicates that the details of this transition may depend somewhat upon the specific interactions included in the microscopic model. In the extreme limit that the microscopic GNM only includes nearest-neighbor interactions along the backbone, then only block maps are allowed, and no phase transition will be observed. However, SI Appendix demonstrates that similar transitions and critical resolutions are observed when the length scale defining interactions in the microscopic GNM is either decreased or increased by 30%. Thus, our findings appear fairly robust with respect to variations in the microscopic model.

Additionally, our work also highlights the similarity between the selection of CG representations for physical systems and recent work in clustering and detecting communities in complex networks (35). In particular, our work bears striking similarity to a variety of spectral approaches based upon the eigenvalues of the graph Laplacian (40–43). Importantly, though, the process of coarse-graining the microscopic GNM reweights the edges of the reduced graph to reflect the effective interactions at the CG resolution. Interestingly, this physical coarse-graining approach identifies the known communities for an archetypal network. Consequently, the present landscape approach may prove fruitful for considering ensembles of clusterings of a single graph (46) and for characterizing the effective interactions between communities. Conversely, the tools developed for community detection may prove useful for developing CG representations of physical systems (15, 16).

In closing, we note several promising directions for future work. First of all, future studies should further investigate the sensitivity of the observed phase transition and critical resolution to protein size and structure. Moreover, while the present work assumed that each CG particle corresponded to an equal number of atoms, we anticipate that it may be fruitful to relax this assumption. Similarly, while the present work considered linear, local CG representations, future studies should consider more general nonlinear, nonlocal order parameters. Additionally, we anticipate further exploring the relation to network community detection in future studies. Finally, it would be most interesting to extend this approach to simple model potentials with multiple metastable states (57) and, ultimately, to more realistic potentials that allow for folding–unfolding transitions (58). In this case, the quality of a given CG representation may vary among these metastable states (17, 59, 60). Nevertheless, we hope that this first study provides a useful framework for systematically constructing representations of complex physical systems.

Materials and Methods

High-Resolution Model.

The GNM represents a protein as a network of $n$ atoms with linear springs connecting nearby atoms. The dimensionless GNM potential is $u\left(\text{q}\right)=\frac{1}{2}{\text{q}}^{†}\mathit{\kappa }\text{q}$ where the dimensionless configuration ${\text{q}}^{†}=\left(q_1,\dots ,q_n\right)$ specifies the displacement of the atoms from equilibrium, and ^† denotes the transpose. The present approach can be readily adopted for anisotropic network models (61) or for quasiharmonic approximations to more general nonlinear models (62). The symmetric matrix, $\mathit{\kappa }$, corresponds to the graph Laplacian (34) for a protein interaction network that is formed by representing each atom with a vertex and introducing edges between nearby atoms. Because the protein is connected, the null space of $\mathit{\kappa }$ is spanned by a single vector corresponding to uniform translation of all $n$ atoms. Consequently, we consider matrix inverses and determinants in the complementary image space.

We employ the ProDy server to determine $\mathit{\kappa }$ for the high-resolution GNM (63). This GNM treats the $n\hspace{0.17em}\alpha$ carbons associated with the $n$ residues of the protein and includes interactions between each pair of $\alpha$ carbons that are within a cutoff of $R_c$ = 7.5 Å.

The (dimensionless) excess configurational entropy, $s$, of the GNM is

$$s=-\int \hspace{0.17em}\text{d}\mathrm{q}\hspace{0.5em}p\left(\text{q}\right)\ln \left[L^{n}p\left(\text{q}\right)\right]=\left(n-1\right)s_0-\frac{1}{2}\ln t_{\mathit{\kappa }},$$ [1]

where $s_0=\frac{1}{2}\left(1+\ln \left[2\pi /\beta L^2\right]\right)$ is a protein-independent constant, while $t_{\mathit{\kappa }}=n^{-1}det\mathit{\kappa }$ is the number of spanning trees for the protein interaction network (34). Consequently, we define $h=h\left(\mathit{\kappa }\right)=\frac{1}{2}\ln t_{\mathit{\kappa }}$ as the nontrivial information in the high-resolution model. Additionally, we consider the mass-weighted fluctuations about the equilibrium configuration:

$$\sigma =⟨\sum _{i=1}^{n}m{q}_i^2⟩={\text{Tr}}_{n}m\text{c}={\beta }^{-1}\sum _{i=1}^{n-1}{\omega }_i^{-2},$$ [2]

where $\text{c}={\left(\beta \mathit{\kappa }\right)}^{-1}$ is the covariance matrix describing correlated fluctuations, the angular brackets denote an equilibrium average according to $p\left(\text{q}\right)$, and ${\omega }_i>0$ is the $i^{\mathrm{t}\mathrm{h}}$ vibrational frequency. For simplicity, we assume that all atoms have equal mass, $m$.

Coarse Representation.

We codify CG representations with a mapping, $\text{M}$, that specifies the CG configuration, $\text{Q}=\left(Q_1,\dots ,Q_N\right)$, as a function of the microscopic configuration, $\text{Q}=\text{M}\left(\text{q}\right)$. We consider mappings that partition the $n$ atoms into $N$ mutually disjoint subsets, $\left\{S_1,\dots ,S_N\right\}$, each of which contains $R=n/N$ atoms that form a connected subgraph of the high-resolution protein interaction network, i.e., the bonds of the GNM must connect the atoms within each site. We associate a CG site, $I$, with each atomic group, $S_I$, and we define the CG coordinate, $Q_I$, by the mass center of the atomic group.

The mapping, $\text{M}$, along with the microscopic configuration distribution, $p\left(\text{q}\right)$, determines the configuration distribution for the mapped ensemble:

$$P\left(\text{Q};\text{M}\right)=\int \hspace{0.17em}\text{d}\mathrm{q}\hspace{0.5em}p\left(\text{q}\right)\hspace{0.5em}\delta \left(\text{Q}-\text{M}\left(\text{q}\right)\right)\propto \exp \left[-\frac{1}{2}\beta {\text{Q}}^{†}{\text{K}}_{\text{M}}\text{Q}\right],$$ [3]

where ${\text{K}}_{\text{M}}^{-1}=\text{M}{\mathit{\kappa }}^{-1}{\text{M}}^{†}$ for the maps we consider (25). The excess entropy of the mapped ensemble is

$$S\left(\text{M}\right)=-\int \hspace{0.17em}\text{d}\mathrm{Q}\hspace{0.5em}P\left(\text{Q};\text{M}\right)\ln \left[L^{N}P\left(\text{Q};\text{M}\right)\right],$$ [4]

$$=\left(N-1\right)s_0-\frac{1}{2}\ln T_{{\text{K}}_{\text{M}}},$$ [5]

where $T_{\text{K}}=N^{-1}det\text{K}$. Accordingly, $H=H\left(\text{M}\right)=\frac{1}{2}\ln T_{{\text{K}}_{\text{M}}}$ quantifies the nontrivial information preserved in the mapped ensemble. We also consider the mass-weighted fluctuations in the mapped ensemble:

$$\mathrm{\Sigma }\left(\text{M}\right)=⟨\sum _{I=1}^{N}M{Q}_I^2⟩={\text{Tr}}_{N}M{\text{C}}_{\text{M}}=k_{B}T\sum _{I=1}^{N-1}{\mathrm{\Omega }}_I^{-2},$$ [6]

where ${\text{C}}_{\text{M}}=\text{M}\mathrm{c}{\text{M}}^{†}$, $M=mn/N$ is the CG mass, and ${\mathrm{\Omega }}_I>0$ is the $I^{\mathrm{t}\mathrm{h}}$ vibrational frequency of the CG model.

Metrics for Characterizing Representations.

We consider two metrics for quantitatively assessing the quality of a CG representation. We define the information quality

$$I=I\left(\text{M}\right)=H\left(\text{M}\right)/h=\ln T_{{\text{K}}_{\text{M}}}/\ln t_{\mathit{\kappa }}$$ [7]

as the fraction of information preserved by the mapping. We define the spectral quality

$$\mathcal{Q}=\mathcal{Q}\left(\text{M}\right)=\mathrm{\Sigma }\left(\text{M}\right)/\sigma =\sum _{I=1}^{N-1}{\mathrm{\Omega }}_I^{-2}/\sum _{i=1}^{n-1}{\omega }_i^{-2}$$ [8]

as the fraction of vibrational power preserved by the CG representation. Both metrics satisfy $0\le I,\mathcal{Q}\le 1$, vanish in the limit $N\to 0$, and equal unity only in the limit $N=n$.

Fig. 4 considers two additional metrics: 1) Given the folded structure of a protein, we define the physical size of a CG site as the three-dimensional radius of gyration for the $\alpha$ carbons that are grouped into the site. We define the radius of gyration, ${\text{R}}_{\text{G}}\left(\text{M}\right)$, for the map, $\text{M}$, as the average gyration radius of the corresponding sites. 2) Given the ground state map, ${\text{M}}_0$, which maximizes $\mathcal{Q}$, we define the distance of a map, $\text{M}$, from the ground state as $d_0\left(\text{M}\right)=\text{VI}\left(\text{M},{\text{M}}_0\right)$, where $\text{VI}$ is the variation of information (33), which is a distance metric commonly employed for distinguishing clusterings on graphs and is explicitly defined in SI Appendix.

Exploring Representations.

We employ MC simulations to sample the space of connected CG maps at different resolutions, $R$. These simulations treat the CG mapping, $\text{M}$, as the microstate and employ a dimensionless energy function $\mathcal{E}=\mathcal{E}\left(\text{M}\right)=1-\mathcal{Q}\left(\text{M}\right)$ or $2H\left(\text{M}\right)$ to define an equilibrium Boltzmann distribution:

$${\mathcal{P}}_{\text{M}}\propto \exp \left[-{\beta }_{\mathcal{E}}\mathcal{E}\left(\text{M}\right)\right],$$ [9]

where ${\beta }_{\mathcal{E}}$ is the conjugate inverse temperature. Starting from a map defined by $N$ connected atomic subgroups, i.e., $\text{M}=\left\{S_1,\dots ,S_N\right\}$, we consider two move sets for generating a new trial map, ${\text{M}}^{\prime }$. Both move sets select a pair of sites $S_I,S_J\in \text{M}$ that are replaced with a new pair of sites, $S_I^{\prime }$ and $S_J^{\prime }$, while leaving the remaining $N-2$ sites unchanged. 1) The swap-based move set swaps a pair of atoms between the two sites, i.e., one atom is moved from site $I$ to site $J$, while a second atom is moved from site $J$ to site $I$. 2) The site-based move set merges the two sites to form a supersite $S_{IJ}=S_I\cup S_J$ of $2R$ atoms and then partitions $S_{IJ}$ into two new sites, $S_I^{\prime }$ and $S_J^{\prime }$, each of which contains $R$ atoms. Both move sets require that the resulting sites $S_I^{\prime }$ and $S_J^{\prime }$ are connected subgraphs of the high-resolution protein interaction network. Note that we employed the swap-based move set to exhaustively enumerate the set of maps for Zachary’s karate club. It is possible that the swap-based move set is not ergodic under certain conditions, although we have obtained numerically identical results with the less restrictive site-based move set. In cases that the move set is not ergodic, our results strictly apply to the subset of mapping space that is reachable from the block map.

The restriction to connected maps significantly reduces the size of mapping space but also complicates sampling. Operationally, given a connected map, $\text{M}$, and a specific move set, we first determine the number, $C_{\text{M}}$, of connected maps that can be reached in one move from $\text{M}$. We then select one of these connected maps, ${\text{M}}^{\prime }$, according to a uniform probability distribution and determine the number of maps, $C_{{\text{M}}^{\prime }}$, that can be reached in one move from ${\text{M}}^{\prime }$. We accept or reject the move $\text{M}\to {\text{M}}^{\prime }$ according to the acceptance probability (28)

$$\text{Acc}\left(\text{M}\to {\text{M}}^{\prime }\right)=\frac{C_{\text{M}}}{max\left\{C_{\text{M}},C_{{\text{M}}^{\prime }}\right\}}min\left\{1,{\mathcal{P}}_{{\text{M}}^{\prime }}/{\mathcal{P}}_{\text{M}}\right\}.$$ [10]

Because in general, $C_{\text{M}}\hspace{0.17em}\ne \hspace{0.17em}{C}_{{\text{M}}^{\prime }}$, a prefactor is necessary to preserve detailed balance, although other prefactors are possible.

We performed MC simulations using either energy function $\mathcal{E}$ = $1-\mathcal{Q}$ or $2H$ at a range of positive and negative conjugate (inverse) temperatures, ${\beta }_{\mathcal{E}}$. Given the CG maps, $\text{M}$, sampled from these MC simulations, we employed the multistate Bennett acceptance ratio method to estimate their statistical weights for various energy functions and conjugate temperatures (64, 65). We estimated the density of states for each energy function $\mathcal{E}$ from the ${\beta }_{\mathcal{E}}\to 0$ limit of these statistical weights.

Data Availability.

Software, Python notebooks, and text data files have been deposited in http://www.datacommons.psu.edu with DOI 10.26208/139c-8x65.