Thermodynamic and kinetic design principles for amyloid-aggregation inhibitors

Significance

Developing effective strategies against human disorders linked with amyloid aggregation, including Alzheimer’s and Parkinson’s diseases, has proven to be difficult. A major reason is that traditional drug-discovery methods are poorly suited to deal with complex reaction networks such as those in involved in the aggregation process. It therefore remains challenging to identify suitable targets for drug development. To overcome this difficulty, we lay out here a general theory for inhibition of protein aggregation into amyloid fibrils, which uncovers quantitative thermodynamic and kinetic design principles to guide the rational search and optimization of effective inhibitors of fibril formation.

Abstract

Understanding the mechanism of action of compounds capable of inhibiting amyloid-fibril formation is critical to the development of potential therapeutics against protein-misfolding diseases. A fundamental challenge for progress is the range of possible target species and the disparate timescales involved, since the aggregating proteins are simultaneously the reactants, products, intermediates, and catalysts of the reaction. It is a complex problem, therefore, to choose the states of the aggregating proteins that should be bound by the compounds to achieve the most potent inhibition. We present here a comprehensive kinetic theory of amyloid-aggregation inhibition that reveals the fundamental thermodynamic and kinetic signatures characterizing effective inhibitors by identifying quantitative relationships between the aggregation and binding rate constants. These results provide general physical laws to guide the design and optimization of inhibitors of amyloid-fibril formation, revealing in particular the important role of on-rates in the binding of the inhibitors.

The aggregation of peptides and proteins into amyloid fibrils is key in many phenomena, ranging from the formation of functional machineries in biology to the production of novel nanomaterials. Recent interest in this process has come from the realization that this protein-aggregation process is intimately linked to a range of human conditions, from Alzheimer’s disease to type 2 diabetes (1–6). Inhibition of protein aggregation into amyloid fibrils thus represents a major strategy for the development of effective pharmacological interventions against protein-misfolding diseases (7–24). Traditionally, inhibition strategies have focused either on blocking the production of aggregation-prone peptides and proteins or on promoting the degradation of their amyloid products (7). Recent attempts have instead concentrated on altering or delaying the aggregation process itself, which is typically achieved using compounds that bind noncovalently to different types of protein species during the aggregation reaction (8–10). Examples of such compounds include small drug-like molecules (23–28), molecular chaperones (29–31), antibodies (32, 33), and nanoparticles (34). Initially, such kinetic inhibitors were designed with the generic goal of delaying amyloid formation (15–21). It has now been recognized, however, that the cytotoxicity linked to amyloid-fibril aggregation is not attributable to a single species. Instead, the gamut of species accessible during aggregation contribute differently to toxicity (30, 35–38). Equally importantly, it has also been established that the aggregation reaction is a complex nonlinear kinetic process in which aggregating proteins can act simultaneously as the reactants, products, intermediates, and catalysts of the reaction (39–46). This coupling between different aggregation steps makes it difficult to estimate the overall effects of interventions aimed at affecting the population balance of specific species. Thus, successful inhibition strategies must build on a detailed mechanistic understanding of the aggregation reaction network and the manner in which it is affected by inhibitors (9). Despite this importance, the fundamental physical principles that underlie inhibition of protein aggregation into amyloid fibrils remain poorly understood. In particular, it remains challenging to establish a quantitative connection between inhibitor binding to aggregating species and the resulting inhibitory effect and, hence, between thermodynamics and kinetics in protein-aggregation inhibition.

To address this limitation, we present a general theory of inhibition of amyloid formation. We formulate the problem in terms of a master equation for aggregation kinetics in the presence of inhibitors that bind one or more of the aggregating species. We derive explicit integrated rate laws to such dynamic equations for compounds that preserve the structure of the aggregation-reaction network, i.e., that do not modify the final form of the analytical solution. The kinetics of inhibited aggregation can therefore be interpreted in terms of effective rate parameters, which in practice provide a clear strategy to determine the mechanistic effect of specific inhibitors from experimental data. Moreover, our framework uncovers general thermodynamic and kinetic constraints on effective inhibition by quantifying the effect of an inhibitor explicitly in terms of the aggregation rate constants and binding parameters, including binding affinities. These simple physical principles will likely facilitate the design, search, and optimization of effective inhibitors of pathological protein aggregation.

Aggregation Kinetics in the Presence of an Inhibitor

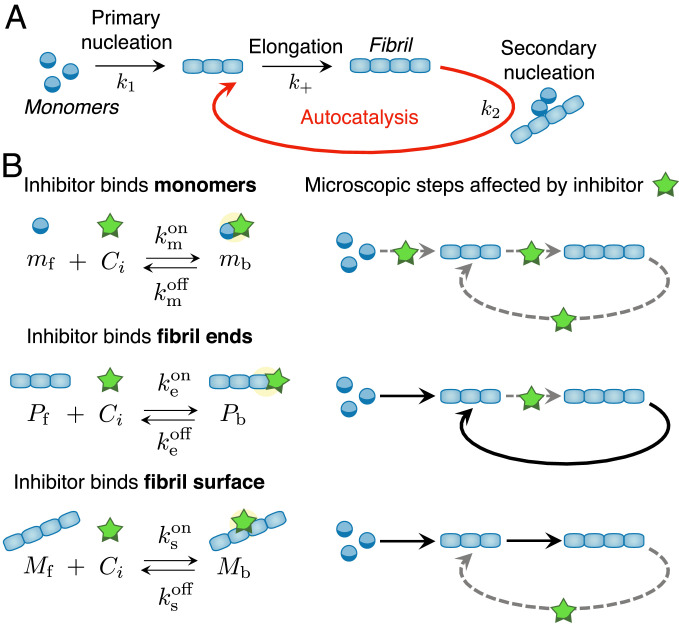
Dealing with the heterogeneous and transient mixture of species involved in protein aggregation has proved challenging. In the absence of inhibitors, progress has come from applying the methodologies of chemical kinetics, well established for simple chemical transformations, to protein-aggregation processes (39–45). In particular, the discovery of integrated rate laws for the aggregation kinetics has provided key insights into the specific molecular steps of amyloid-fibril formation from the analysis of experimental data (Fig. 1A) (39–45). Initially, the smallest aggregates form directly from soluble monomers through primary nucleation (40). Fibrils grow by elongation, i.e., the addition of individual monomers at the aggregate ends (40). In many cases, including the aggregation of A$\beta$42 (43), rapid proliferation of aggregates can be promoted by existing fibrils in a process termed surface-catalyzed secondary nucleation (43–48). In this process, new fibrils nucleate through the interaction of monomers with the surfaces of existing fibrils. Fibrils thus act as catalysts of the aggregation reaction.

Fig. 1.

Microscopic mechanisms of protein aggregation and possible inhibition pathways. (A) Schematic representation of the microscopic steps of protein aggregation into fibrillar structures. (B, Left) Potential target species during protein aggregation and associated binding rate constants. (B, Right) Schematic diagrams showing the microscopic steps that are targeted by the inhibitor.

Within this chemical kinetics approach, the combined effect of these different microscopic steps on the overall aggregation kinetics is captured by means of a master equation for key experimentally accessible observables, including the free monomer concentration $m\left(t\right)$ and the number or mass concentrations of fibrils, denoted with $P\left(t\right)$ and $M\left(t\right)$, respectively (see SI Appendix, section S1.1 for a derivation) (39–44):

$$\frac{\mathrm{\text{d}}P\left(t\right)}{\mathrm{\text{d}}t}=k_{1}m{\left(t\right)}^{n_1}+k_{2}m{\left(t\right)}^{n_2}M\left(t\right),$$ [1a]

$$\frac{\mathrm{\text{d}}m\left(t\right)}{\mathrm{\text{d}}t}=-2k_{+}m\left(t\right)P\left(t\right)=-\frac{\mathrm{\text{d}}M\left(t\right)}{\mathrm{\text{d}}t}.$$ [1b]

Here, $k_{+}$, $k_1$, and $k_2$ are the rate constants for filament elongation, primary nucleation, and surface-catalyzed secondary nucleation. The exponents $n_1$ and $n_2$, respectively, are the reaction orders of primary and secondary nucleation with respect to the concentration of free monomers (see SI Appendix, section S1.1 and refs. 48–52 for details on the physical interpretation of reaction orders). Eq. 1a captures the total rate of formation of new aggregates by primary and secondary nucleation. Eq. 1b describes the consumption of monomers, which occurs mainly by fibril elongation. Since monomers are either free or part of aggregates, the total concentration of monomers in the system, $m_{\mathrm{t}\mathrm{o}\mathrm{t}}$, is conserved at all times, i.e., $m\left(t\right)+M\left(t\right)=m_{\mathrm{t}\mathrm{o}\mathrm{t}}$.

Eqs. 1a and 1b yield sigmoidal-type kinetics for fibril mass concentration (Fig. 2). Integrated rate laws describing this behavior have been obtained previously using self-consistent methods, such as in refs. 41, 42, and 53 (SI Appendix, section S1.2):

$$\frac{M\left(t\right)}{m_{\mathrm{t}\mathrm{o}\mathrm{t}}}=1-\exp \left(-\frac{{\lambda }^2}{2{\kappa }^2}\left(e^{\kappa t}-1\right)\right).$$ [2]

The underlying idea of this method is to use the linearized solution to Eq. 1 as the starting point of an iterative fixed-point scheme that yields self-consistent solutions of increasing accuracy. Eq. 2 is obtained after one step of this procedure and by keeping only the dominant exponential growing term in the linearized solution. The convergence of the fixed-point scheme is ensured when the elongation rate is fast compared with the rate of the primary- and secondary-nucleation pathways, an assumption that is satisfied in practice, as discussed in SI Appendix, section S1.1. Eq. 2 reveals that only two key rate parameters control the time course of aggregation: $\lambda =\sqrt{2k_{+}{k}_1{m}_{\mathrm{t}\mathrm{o}\mathrm{t}}^{n_1}}$ and $\kappa =\sqrt{2k_{+}{k}_2{m}_{\mathrm{t}\mathrm{o}\mathrm{t}}^{n_2+1}}$ (SI Appendix, section S1.2).* These are combined rates describing aggregate proliferation through primary and secondary nucleation, respectively. Expressions such as Eq. 2 provide a useful means to interpret protein-aggregation experiments in terms of the underlying microscopic steps from global fitting of measured aggregation curves (54).

Fig. 2.

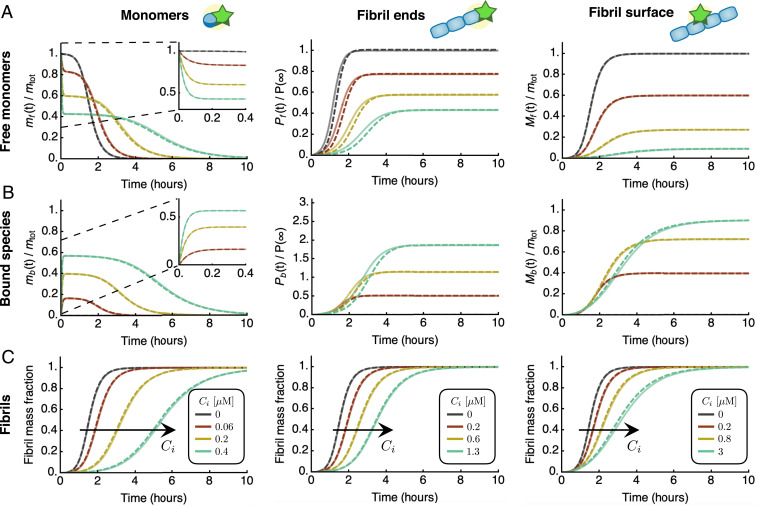
Integrated rate laws for protein aggregation in the presence of inhibitors. Characteristic kinetic profiles for free species (A), bound species (B), and fibril mass concentration (C) in the presence of an inhibitor that binds free monomers (left column), fibrils ends (middle column), or fibril surfaces (right column). Dashed lines are the analytical integrated rate laws (see SI Appendix, section S2 for explicit expressions), which are in excellent agreement with numerical simulations of Eq. 3 (solid lines). The curves were generated using typical rate parameters for amyloid-forming systems; here, the parameters correspond to experimentally measured rates for in vitro aggregation of the A$\beta$42 peptide of Alzheimer’s disease (43): $m_{\mathrm{t}\mathrm{o}\mathrm{t}}=3\mu$M, $k_{+}=3\times 10^6{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_1=10^{-4}{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_2=8\times 10^3{\mathrm{M}}^{-2}{\mathrm{s}}^{-1}$, $n_1=n_2=2$, $K_{\times }=0.3\mu {\mathrm{M}}^{-1}$, $k_{\times }^{\mathrm{on}}=1.3\times 10^{-2}{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$; and $C_i=0.06,0.2,0.4\mu$M (A); $C_i=0.2,0.6,1.3\mu$M (B); and $C_i=0.2,0.8,3\mu$M (C). Dark grey curves are without inhibitor.

Within the framework of Eq. 1 an inhibitor can affect protein aggregation kinetics by binding 1) free monomers, 2) fibril ends, or 3) fibril surface sites; these species correspond to the three fields: $m\left(t\right)$, $P\left(t\right)$, and $M\left(t\right)$ (Fig. 1B and SI Appendix, section S1.3) (8, 29). This description may be generalized to account for inhibitor binding to additional target species, including, e.g., transient oligomers (55). We describe the effect of inhibitors on aggregation using a master equation by introducing species for the monomer concentration, the number and mass concentrations of fibrils that are either active (“free”; subscript “f”) or deactivated due to the binding to inhibitor molecules (“bound”; subscript “b”). In our model, bound species are unable to participate in the aggregation process.^† We denote the binding and unbinding rates of the inhibitor to the respective species as $k_{\times }^{\mathrm{on}}$ and $k_{\times }^{\mathrm{off}}$, respectively, where $\times$ is a placeholder that can refer to monomers ($\times =\mathrm{m}$), fibrils ends ($\times =\mathrm{e}$), or fibril surface sites ($\times =\mathrm{s}$). By binding to its target, the inhibitor affects the population balance of free and bound species, thereby influencing the rates of the different aggregation processes in which these species are involved.

The time course of the aggregation reaction in the presence of an inhibitor is captured by the following kinetic equations for the free species, as an extension of Eq. 1:

$$\begin{array}{ll}\hfill \frac{\mathrm{\text{d}}{P}_{\mathrm{f}}\left(t\right)}{\mathrm{\text{d}}t}& =k_1{m}_{\mathrm{f}}{\left(t\right)}^{n_1}+k_2{m}_{\mathrm{f}}{\left(t\right)}^{n_2}{M}_{\mathrm{f}}\left(t\right)\hfill \\ \hfill & \hspace{1em}-k_{\mathrm{e}}^{\mathrm{on}}{P}_{\mathrm{f}}\left(t\right)C_i\left(t\right)+k_{\mathrm{e}}^{\mathrm{off}}{P}_{\mathrm{b}}\left(t\right),\hfill \end{array}$$ [3a]

$$\begin{array}{ll}\hfill \frac{\mathrm{\text{d}}{m}_{\mathrm{f}}\left(t\right)}{\mathrm{\text{d}}t}& =-2k_{+}{m}_{\mathrm{f}}\left(t\right)P_{\mathrm{f}}\left(t\right)\hfill \\ \hfill & \hspace{1em}-k_{\mathrm{m}}^{\mathrm{on}}{m}_{\mathrm{f}}\left(t\right)C_i\left(t\right)+k_{\mathrm{m}}^{\mathrm{off}}{m}_{\mathrm{b}}\left(t\right),\hfill \end{array}$$ [3b]

$$\frac{\mathrm{\text{d}}{M}_{\mathrm{f}}\left(t\right)}{\mathrm{\text{d}}t}=2k_{+}{m}_{\mathrm{f}}\left(t\right)P_{\mathrm{f}}\left(t\right)-k_{\mathrm{s}}^{\mathrm{on}}{M}_{\mathrm{f}}\left(t\right)C_i\left(t\right)+k_{\mathrm{s}}^{\mathrm{off}}{M}_{\mathrm{b}}\left(t\right),$$ [3c]

where $C_i\left(t\right)$ denotes the concentration of free inhibitor. The equations for the bound species read:

$$\frac{\mathrm{\text{d}}{m}_{\mathrm{b}}\left(t\right)}{\mathrm{\text{d}}t}=k_{\mathrm{m}}^{\mathrm{on}}{m}_{\mathrm{f}}\left(t\right)C_i\left(t\right)-k_{\mathrm{m}}^{\mathrm{off}}{m}_{\mathrm{b}}\left(t\right),$$ [3d]

$$\frac{\mathrm{\text{d}}{P}_{\mathrm{b}}\left(t\right)}{\mathrm{\text{d}}t}=k_{\mathrm{e}}^{\mathrm{on}}{P}_{\mathrm{f}}\left(t\right)C_i\left(t\right)-k_{\mathrm{e}}^{\mathrm{off}}{P}_{\mathrm{b}}\left(t\right),$$ [3e]

$$\frac{\mathrm{\text{d}}{M}_{\mathrm{b}}\left(t\right)}{\mathrm{\text{d}}t}=k_{\mathrm{s}}^{\mathrm{on}}{M}_{\mathrm{f}}\left(t\right)C_i\left(t\right)-k_{\mathrm{s}}^{\mathrm{off}}{M}_{\mathrm{b}}\left(t\right).$$ [3f]

To derive Eq. 3, we have further assumed that the amount of target species (monomers, fibril ends, or fibril surface sites) deactivated by the inhibitor can be calculated by considering independent binding events on the different sites. The binding rate is thus proportional to the concentration of free species and the concentration of free inhibitor $C_i\left(t\right)$.

Integrated Rate Laws for Inhibited-Aggregation Kinetics

To understand how an inhibitor influences aggregation in terms of the underlying rate parameters, we derived explicit analytical solutions to Eq. 3 by exploiting the same self-consistent scheme and approximations utilized to obtain Eq. 2 (SI Appendix, section S1.2). Strikingly, for all modes of inhibition, we find that the integrated rate law for $M\left(t\right)$ in the presence of an inhibitor has the same functional form as in the absence of the inhibitor, Eq. 2 (Fig. 2 and SI Appendix, Eqs. S60, S77, and S96):

$$\frac{M\left(t\right)}{m_{\mathrm{t}\mathrm{o}\mathrm{t}}}=1-\exp \left(-\frac{{\lambda }_{\mathrm{eff}}^2}{2{\kappa }_{\mathrm{eff}}^2}\left(e^{{\kappa }_{\mathrm{eff}}t}-1\right)\right).$$ [4]

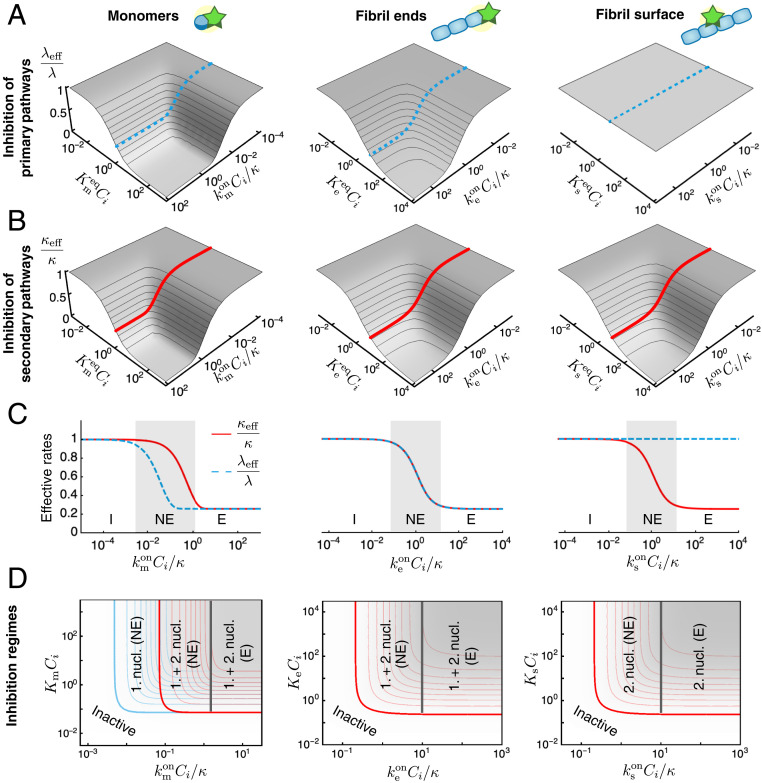
As a key result of the assumptions made here, we find that the structure of the reaction network of aggregation is preserved in the presence of inhibitors. This conclusion is true irrespective of the speed and magnitude of inhibitor binding, i.e., the rates of association and dissociation relative to the rate of aggregation. Consequently, in the presence of inhibitors the rate couplings $\lambda$ and $\kappa$ in Eq. 2 are replaced in Eq. 4 by effective rates, ${\lambda }_{\mathrm{eff}}$ and ${\kappa }_{\mathrm{eff}}$, which depend in characteristic ways on the kinetic parameters of aggregation and inhibitor binding. The functional dependence of ${\lambda }_{\mathrm{eff}}$ and ${\kappa }_{\mathrm{eff}}$ depends on which aggregating species are targeted (Fig. 3 A and B): 1) an inhibitor that binds the surface of fibrils may reduce the secondary-nucleation rate, hence affecting only $\kappa$; 2) an inhibitor that binds fibril ends may lower the rate of elongation, affecting $\lambda$ and $\kappa$ equally; or 3) an inhibitor that binds monomers may reduce the rates of all steps of aggregation, affecting both $\lambda$ and $\kappa$, although in general by different amounts.

Fig. 3.

Thermodynamic and kinetic design principles for protein aggregation inhibitors. (A and B) Effective rates of aggregation in the presence of an inhibitor. (A) The parameter ${\lambda }_{\mathrm{eff}}/\lambda$ describes the extent of inhibition on the primary aggregation pathways. (B) The parameter ${\kappa }_{\mathrm{eff}}/\kappa$ describes the effect on the secondary pathways. These effective rates depend in characteristic ways on two combined parameters: a dimensionless binding rate $k_{\times }^{\mathrm{on}}{C}_i/\kappa$ and dimensionless binding constant $K_{\times }{C}_i$. Dashed and solid lines in A and B indicate sample inhibitor-response curves as a function of $k_{\times }^{\mathrm{on}}{C}_i/\kappa$ at constant $K_{\times }{C}_i$. (C) Depending on the rate of inhibitor binding to its target, $k_{\times }^{\mathrm{on}}{C}_i$, compared with the overall rate of aggregation ($\kappa$), we distinguish different inhibition regimes: inactive (I) ($k_{\times }^{\mathrm{on}}{C}_i\ll \kappa$), nonequilibrium inhibition (NE) ($k_{\times }^{\mathrm{on}}{C}_i\simeq \kappa$), and equilibrium inhibition (E) ($k_{\times }^{\mathrm{on}}{C}_i\gg \kappa$). For fixed $K_{\times }$, maximal inhibition is obtained in the equilibrium regime. The extent of maximal inhibition depends solely on $K_{\times }{C}_i$. The plots in C correspond to the dashed and solid lines shown in A and B, respectively. (D) Schematic phase diagram summarizing possible inhibition regimes for an inhibitor that binds to monomers, fibril ends, or fibril surfaces. These phase diagrams are top views of the plots in A and B, i.e., contour plots of ${\lambda }_{\mathrm{eff}}/\lambda$ (blue) and ${\kappa }_{\mathrm{eff}}/\kappa$ (red) (SI Appendix, Fig. S1). Contour lines in A–C are shown in intervals of 0.1. Plots of ${\kappa }_{\mathrm{eff}}/\kappa$ and ${\lambda }_{\mathrm{eff}}/\lambda$ are generated using the expressions in SI Appendix, Table S2 for the same parameters as in Fig. 2.

The Interplay between Kinetics and Thermodynamics Generates a Rich Inhibition-Phase Behavior

We have calculated explicit expressions for the effective rates ${\lambda }_{\mathrm{eff}}$ and ${\kappa }_{\mathrm{eff}}$, which are summarized in SI Appendix, Table S2. These expressions reveal that, in the case when the inhibitor binds aggregate ends or surface sites, ${\lambda }_{\mathrm{eff}}/\lambda$ and ${\kappa }_{\mathrm{eff}}/\kappa$ are controlled only by two dimensionless parameters: 1) a normalized binding rate $k_{\times }^{\mathrm{on}}{C}_i/\kappa$ and 2) a dimensionless binding constant $K_{\times }\hspace{0.17em}{C}_i$, where $K_{\times }=k_{\times }^{\mathrm{on}}/k_{\times }^{\mathrm{off}}$ is the equilibrium binding constant. Based on these kinetic and thermodynamic parameters, we can distinguish three primary regimes of inhibition: 1) no inhibition ($k_{\times }^{\mathrm{on}}{C}_i\ll \kappa$), 2) nonequilibrium inhibition ($k_{\times }^{\mathrm{on}}{C}_i\simeq \kappa$), and 3) equilibrium inhibition ($k_{\times }^{\mathrm{on}}{C}_i\gg \kappa$). When the inhibitor binds the target species slowly compared with the characteristic timescale of aggregation ($1/\kappa$), the effective rates ${\lambda }_{\mathrm{eff}}/\lambda$ and ${\kappa }_{\mathrm{eff}}/\kappa$ are close to 1 and the inhibitor is kinetically inactive. In the opposite limit, when inhibitor binding is fast compared with aggregation, we can invoke preequilibrium for the binding of the inhibitor to the target species (SI Appendix, sections S1.4 and S1.5). We term this regime equilibrium inhibition, since the effective rate parameters are determined in this limit solely by the dimensionless binding constant $K_{\times }\hspace{0.17em}{C}_i$ (SI Appendix, Table S1):

$$\frac{{\lambda }_{\mathrm{eff}}}{\lambda }={\left(\frac{1}{1+K_{\mathrm{m}}{C}_i}\right)}^{\frac{n_1+1}{2}}{\left(\frac{1}{1+K_{\mathrm{e}}{C}_i}\right)}^{\frac{1}{2}},$$ [5a]

$$\frac{{\kappa }_{\mathrm{eff}}}{\kappa }={\left(\frac{1}{1+K_{\mathrm{m}}{C}_i}\right)}^{\frac{n_2+1}{2}}{\left(\frac{1}{1+K_{\mathrm{e}}{C}_i}\right)}^{\frac{1}{2}}{\left(\frac{1}{1+K_{\mathrm{s}}{C}_i}\right)}^{\frac{1}{2}}.$$ [5b]

Thus, effective inhibition necessarily requires sufficiently high binding affinity, i.e., sufficiently low dissociation constant (${\left(K_{\times }\right)}^{-1}\ll C_i$) and fast binding to the target ($k_{\times }^{\mathrm{on}}{C}_i\gg \kappa$). An interesting intermediate nonequilibrium inhibition regime emerges when the inhibitor binding rate to its target is comparable to the characteristic rate of aggregation $\kappa$. In this case, weaker inhibition is observed compared with the equilibrium limit. At fixed binding affinity, the maximum possible extent of inhibition is obtained in the equilibrium regime. Our explicit expressions for ${\lambda }_{\mathrm{eff}}/\lambda$ and ${\kappa }_{\mathrm{eff}}/\kappa$ interpolate smoothly between these limiting regimes (Fig. 3C).

In the case when the inhibitor binds monomers, an additional dimensionless parameter $\lambda /\kappa$ emerges as the ratio of the proliferation rates through primary and secondary pathways. Since $\lambda \ll \kappa$, on the basis of this parameter, we can distinguish two further nonequilibrium inhibition regimes. When $\lambda \ll k_{\mathrm{m}}^{\mathrm{on}}{C}_i\simeq \kappa$, we observe a nonequilibrium inhibition regime where both primary and secondary nucleation are affected. However, when $\lambda \simeq k_{\mathrm{m}}^{\mathrm{on}}{C}_i\ll \kappa$, the inhibitor affects primary nucleation only but binds monomers too slowly to be able to interfere with the secondary-nucleation process (Fig. 3D, first column).

Our theory may be extended to inhibitors that bind multiple species simultaneously. In this case, we find that the effects of the individual modes of inhibition on $\lambda$ and $\kappa$ combine multiplicatively (SI Appendix, section S2.4).

Physical Design Principles for Effective Inhibitors and Illustrative Examples on Experimental Data

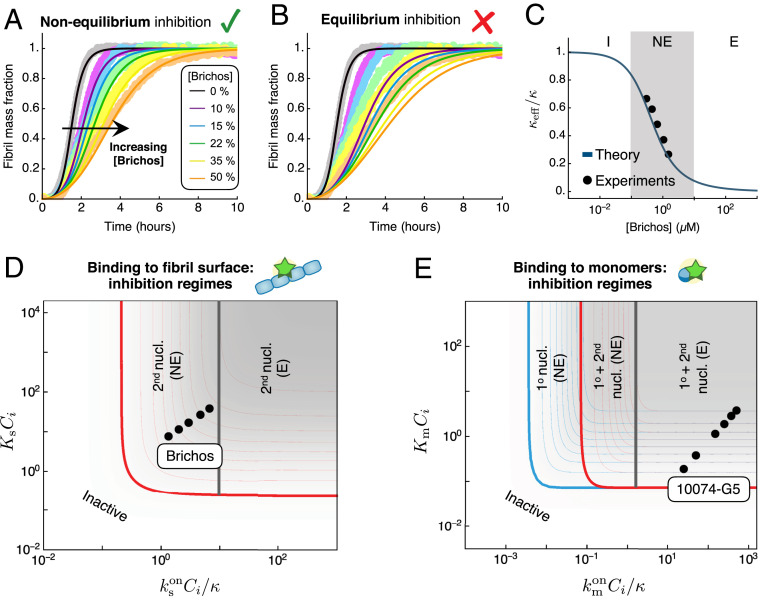
Our work carries important implications for the design of potential protein-aggregation inhibitors, by revealing that specific combinations of the thermodynamic and kinetic parameters determine the effectiveness of a compound to inhibit protein aggregation. The expressions for the effective rates of inhibited aggregation, ${\lambda }_{\mathrm{eff}}/\lambda$ and ${\kappa }_{\mathrm{eff}}/\kappa$, allow us to construct phase diagrams for the possible inhibition regimes (Fig. 3D and SI Appendix, Fig. S1). These diagrams, which have kinetic and thermodynamic axes, provide precise strategies to optimize inhibition. For instance, in the case of an inhibitor that binds monomers, increasing the parameter $k_{\mathrm{m}}^{\mathrm{on}}{C}_i/\kappa$ can turn an inhibitor of primary nucleation into an effective inhibitor of both primary- and secondary-nucleation pathways (Fig. 3D, first column). Systematically characterizing different compounds on phase diagrams such as in Fig. 3D provides a strategy for optimizing the efficacy of inhibitors of protein aggregation not only with respect to their binding affinity but also in terms of their binding kinetics. We now illustrate this principle by considering the example of the inhibition of A$\beta$42 aggregation by two compounds, Brichos (30) and 10074-G5 (56), which selectively target different aggregating species.

Kinetic models of protein filament formation are uniquely effective for yielding information about the microscopic mechanisms of aggregation from the analysis of experimental reaction profiles (54). Thus, the integrated rate law obtained in this work provides a systematic framework for establishing the mechanism of action of unknown inhibitors on aggregation. We have applied this approach to experimental data on the inhibition of A$\beta$42 aggregation by the human Brichos domain, a molecular chaperone that has been shown to bind the surface of A$\beta$42 fibrils (29, 30). The rates of binding and dissociation of Brichos to/from the surface of A$\beta$42 fibrils have been measured independently from the aggregation kinetics using surface plasmon resonance (30): $k_{\mathrm{s}}^{\mathrm{on}}=5.1\times 10^4\hspace{0.17em}{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{s}}^{\mathrm{off}}=2.1\times 10^{-3}\hspace{0.17em}{\mathrm{s}}^{-1}$, with a corresponding binding constant of $K_{\mathrm{s}}=2.4\times 10^7\hspace{0.17em}{\mathrm{M}}^{-1}$. Thus, using these parameters, we can predict kinetic traces of A$\beta$42 aggregation in the presence of increasing concentrations of Brichos using our analytical solution without free parameters. The resulting aggregation profiles, shown in Fig. 4A, are in excellent agreement with the experimental data, highlighting the power of our approach. Interestingly, a comparison between the rate of Brichos binding and the timescale of aggregation yields $k_{\mathrm{s}}^{\mathrm{on}}{C}_i/\kappa \simeq 1.3$ (for $C_i=0.3\hspace{0.17em}\mu$M), revealing that Brichos binds the surface of amyloid fibrils relatively slowly compared with aggregation. Indeed, the kinetic profiles predicted using the equilibrium model (Eq. 5) do not capture the data (Fig. 4B). Moreover, a comparison between the effective $\kappa$ and our theoretical prediction (SI Appendix, Eq. S61 and Fig. 4C) confirms that the inhibition of A$\beta$42 by Brichos falls in the nonequilibrium regime (Fig. 4D).

Fig. 4.

Application to the inhibition of A$\beta$42 aggregation. (A) Experimental data for the aggregation of 3 $\mu$M A$\beta$42 in the presence of increasing concentrations of Brichos, a molecular chaperone that binds amyloid fibrils (30) ($C_i=0.1,0.15,0.22,0.35,0.5$ A$\beta$42 molar equivalents). The experimental data are compared with the theoretical prediction of our integrated rate law (solid lines). The theoretical prediction for inhibited curves has no fitting parameters: the rate constants of aggregation are extracted from a fit of the aggregation curve in the absence of inhibitor ($k_{+}=3\times 10^6\hspace{0.17em}{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_2=8.2\times 10^4\hspace{0.17em}{\mathrm{M}}^{-2}{\mathrm{s}}^{-1}$, $k_1=1.1\times 10^{-4}\hspace{0.17em}{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$), and the effect of the inhibitor is predicted using the experimentally measured binding and dissociation rates ($k_{\mathrm{s}}^{\mathrm{on}}=5.1\times 10^3\hspace{0.17em}{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{s}}^{\mathrm{off}}=2.1\times 10^{-4}\hspace{0.17em}{\mathrm{s}}^{-1}$) (30). (B) Experimental data are compared with the theoretical prediction assuming equilibrium binding (Eq. 5) of Brichos with binding constant $K_{\mathrm{s}}=k_{\mathrm{s}}^{\mathrm{on}}/k_{\mathrm{s}}^{\mathrm{off}}=2.4\times 10^7\hspace{0.17em}{\mathrm{M}}^{-1}$. (C) Effective ${\kappa }_{\mathrm{eff}}/\kappa$ as a function of Brichos concentration and comparison with our theoretical prediction (SI Appendix, Table S2) (solid line). (D) Location of Brichos (30) in the phase diagram of possible inhibition regimes for an inhibitor binding fibril surface sites. The points correspond to the following concentrations of Brichos: $C_i=0.1,0.15,0.22,0.35,0.5$ molar equivalents. (E) Location of 10074-G5, a small molecule that binds A$\beta$42 monomers (56), in the phase diagram of possible inhibition regimes. The points correspond to the following inhibitor concentrations: $C_i=\mathrm{1,2,6,10,15,20}\mu$M for $1\mu$M A$\beta$42.

As a further example, we consider the inhibition of A$\beta$42 by the small molecule 10074-G5 {biphenyl-2-yl-(7-nitro-benzo[1,2,5]oxadiazol-4-yl)-amine}, which has recently been shown to inhibit aggregation likely by binding to and sequestering A$\beta$42 monomers (56). The binding rate constants of 10074-G5 to monomers have been measured using biolayer interferometry as $k_{\mathrm{m}}^{\mathrm{on}}=8.5\times 10^3\hspace{0.17em}{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$ and $k_{\mathrm{m}}^{\mathrm{off}}=4.7\times 10^{-2}\hspace{0.17em}{\mathrm{s}}^{-1}$ (56), allowing us to place 10074-G5 in the phase diagram of possible inhibition regimes (Fig. 4E). These results can inform future drug-discovery efforts for inhibitors that bind monomers, suggesting that it is important to find compounds that bind monomers with faster on-rates.

Summary and Outlook

In this work, we have developed a kinetic theory of protein-aggregation inhibition. This theory offers quantitative answers to questions such as: 1) Which aggregating species should one bind to in order to suppress most effectively aggregation? 2) Which binding rates and binding affinities should be optimized? and 3) Given a lead compound, which is the best optimization strategy? Our theory has allowed us to analyze quantitatively experimental data of aggregation inhibition outside of the conventional limiting regime where inhibitor binding is assumed to be fast compared with aggregation (equilibrium regime). Moreover, our work identifies a universal timescale ($1/\kappa$) to use as a ruler for developing compounds that bind specific aggregating species. These findings could guide the design and optimization of potent inhibitors of protein aggregation by combining our theoretical framework with independent measurements of kinetics and thermodynamics of binding, which, in many cases, are available from experimental methods such as surface plasmon resonance, biolayer interferometry, and microfluidics. (29, 30, 56).

The flexibility of the master equation formalism for amyloid-fibril formation allows one to include in the future other microscopic mechanisms, such as inhibition against surface-induced aggregation (57, 58) or inhibition of intermediate oligomers (55). Moreover, although our results specifically apply to protein fibrils, the strategy could be extended to other types of protein aggregates that are relevant in different contexts, including, for instance, the production and formulation of therapeutic proteins. General kinetic frameworks have been established to describe the variety of aggregation mechanisms that therapeutic proteins can experience under different stresses (59, 60), which often involve different microscopic steps with respect to the model discussed in this work. However, in analogy with amyloid-fibril formation, kinetic models can unravel the effect of excipients on individual microscopic events and specific protein species (61). We envision therefore that the strategy described in this work could be applied in the future to guide the design of therapeutic molecules against other types of protein aggregates.

Data Availability.

All study data are included in the article and SI Appendix.