Differential response to cytotoxic therapy explains treatment dynamics of acute myeloid leukaemia patients: insights from a mathematical modelling approach

Abstract

Disease response and durability of remission are very heterogeneous in patients with acute myeloid leukaemia (AML). There is increasing evidence that the individual risk of early relapse can be predicted based on the initial treatment response. However, it is unclear how such a correlation is linked to functional aspects of AML progression and treatment. We suggest a mathematical model in which leukaemia-initiating cells and normal/healthy haematopoietic stem and progenitor cells reversibly change between an active state characterized by proliferation and chemosensitivity and a quiescent state, in which the cells do not divide, but are also insensitive to chemotherapy. Applying this model to 275 molecular time courses of nucleophosmin 1-mutated patients, we conclude that the differential chemosensitivity of the leukaemia-initiating cells together with the cells’ intrinsic proliferative capacity is sufficient to reproduce both, early relapse as well as long-lasting remission. We can, furthermore, show that the model parameters associated with individual chemosensitivity and proliferative advantage of the leukaemic cells are closely linked to the patients’ time to relapse, while a reliable prediction based on early response only is not possible based on the currently available data. Although we demonstrate with our approach, that the complete response data is sufficient to quantify the aggressiveness of the disease, further investigations are necessary to study how an intensive early sampling strategy may prospectively improve risk assessment and help to optimize individual treatments.

1. Introduction

Acute myeloid leukaemia (AML) describes a group of malignant stem cell disorders, in which functional blood cells are rapidly replaced by malignant blasts. Owing to the acquisition of multiple genetic and epigenetic aberrations in haematopoietic stem and progenitor cells, those cells lose their ability to finally differentiate, which is frequently combined with an increase of their proliferative potential. These changes induce a competitive advantage and the malignant cells ultimately outcompete normal haematopoiesis. Clinically, the expansion of the malignant cells results in an acute and, if not immediately treated, fatal haematopoietic insufficiency. Whole-exome sequencing of large numbers of AML samples showed an extensive mutational heterogeneity between different patients with an average of five mutations in genes that are recurrently mutated [1]. The patient-specific mutational profile combined with other cytogenetic measurements at the time of diagnosis is used to categorize the patients into different risk-groups according to the European leukemia net (ELN) recommendations [2]. This categorization supports decisions about suitable treatment strategies.

Although treatment options have improved over the last decades, the prognosis for AML patients is still unsatisfactory. While 35–40% of patients under the age of 60 are cured, older patients have a significantly worse prognosis with less than 10% surviving after 5 years [3]. Whereas allogeneic haematopoietic cell transplantation is often the only curative approach, this option is not available to all patients and conveys its own specific risks, such as graft-versus-host disease. Therefore, the standard primary treatment for AML still consists of intensive chemotherapy including an induction therapy followed by a period of consolidation therapy. Chemotherapies are administered in a cyclic manner with usually 7 days of treatment followed by a treatment free interval. Induction and consolidation therapy include about five cycles of treatment. Cytarabine combined with an antracyclin are the most frequently used chemotherapeutic drugs in AML. These chemotherapies are highly cytotoxic, especially when applied in high doses. In particular, they act unspecifically, i.e. not only affecting the malignant but also all other dividing cells, therefore, often leading to severe side effects. Even after successful primary therapy about half of the patients relapse. Those relapses represent a major challenge in AML treatment as they are both, hard to predict and difficult to treat. Therefore, the time point of relapse is a critical measure reflecting the severity of the subsequent disease course.

About 30% of all AML patients present with a mutation of the nucleophosmin 1 (NPM1) gene, thereby forming one of the largest AML subgroups sharing a common characteristic mutation [1]. NPM1 mutations typically result in a dislocation of the protein from the nucleus, reducing its tumour supressive function [4]. Clinically, the NPM1 mutation is associated with a good response to AML induction therapy and a favourable prognosis [5]. Over the last years, polymerase chain reaction (PCR)-based quantification of NPM1 mRNA (relative to a suitable control gene, such as ABL) has been established as a surrogate measure of leukaemia abundance, especially for the detection of minimal residual disease levels.

In a recent study, we could show that monitoring NPM1 dynamics are closely linked to the long-term outcome in NPM1-mutated (NPM1-mut) AML patients [6]. Therefore, we argue that it is beneficial to incorporate measures about the individual disease dynamics in the process of clinical decision-making in order to further improve personalized treatment adaptation. Technically, the assessment of molecular disease dynamics is realized by monitoring the leukaemic burden in AML patients during and after therapy. However, the quantitative assessment of leukaemic markers is challenging as the abundance of those mutations does not necessarily correlate with the disease load. Some mutations in genes, such as in DNMT3A and TET2 are known as preleukaemic mutations that can persist during complete remission [7], while others are germ line associated, such as RUNX1 and GATA2 [8]. Mutations in genes like FLT3-ITD and NRAS are frequently lost upon relapse. Stable lesions recommended by the ELN for measurable residual disease (MRD) monitoring are the NPM1 mutations and gene fusions such as RUNX1-RUNX1T1,CBFB-MYH11 and PML-RARA [9]. As the measurement of mutated NPM1 (relative to the reference gene ABL) is now included in clinical routine and these values can be used as a surrogate for leukaemic burden, it is possible to track the molecular disease dynamics for these patients with high accuracy.

To gain further insights in the molecular mechanisms and individual differences in disease dynamics, mathematical models are a powerful tool, as was already shown for several diseases, such as cancer in general [10], chronic myeloid leukaemia (CML) [11–13], Alzheimer’s disease [14,15] and Parkinson’s disease [16,17]. Existing models of AML either address properties of the leukaemic cells [18–20] or focus on the mechanisms of the disease in general [21–23]. However, so far none of these models has been specifically tailored to account for individual patients’ molecular disease dynamics and to correlate these with achievement of remission or relapse. Such a model would allow us to quantitatively study the course of disease and factors influencing it in silico and to facilitate predictions on the relapse risk.

Earlier studies demonstrated that a mathematical model of haematopoietic stem cell (HSC) organization, which assumes a reversible switch between two functional states of HSC (i.e. a proliferative, active and a quiescent state), is able to consistently reproduce a number of experimental and clinical phenomena [24–26]. Translating this concept into the leukaemia context proved to be predictive, especially for the case of CML. Here, the theoretical analysis of the interaction between the cell cycle status of leukaemic cells and the effects of tyrosine kinase inhibitors allowed the quantitative predict ion of individual long-term disease dynamics [27] as well as the potential for tyrosine kinase inhibitor dose de-escalation and, therefore, side-effect reduction [13]. Based on these insights, we here apply the same concept to capture the treatment dynamics of AML. In particular, we investigate the question of whether the leukaemic reduction during chemotherapy can be mimicked without directly integrating any assumptions of a differential cytotoxic effect on leukaemic cells.

In the present study, we intentionally use a simple two-compartment approach to mathematically model disease and treatment dynamics in AML. We explicitly consider a chemotherapy effect operating on all actively cycling cells, independent of their mutation status. It is our main objective to test whether such a simple model description, i.e. considering an unspecific therapeutic cell kill together with an increased cell cycle activity of malignant cells, is sufficient to consistently describe the individual patient dynamics as observed in a large cohort of patients. To do so, we fit the model individually to each molecular time course of n = 275 NPM1-mut AML patients. We further investigate the ability of the model to estimate patients relapse times as a measure of the severity of disease, as well as to improve risk stratification and predict relapse.

2. Methods

2.1. Patient data

We used quantitative PCR (qPCR) NPM1 time courses of n = 275 patients from the AML Registry of the University Hospital Dresden Carl Gustav Carus and two phase 3 trials of the Study Alliance Leukemia (SAL), namely AML2003 (NCT00180102) and AML60+ (NCT00180167). All patients gave written informed consent to participate in the study in accordance with the Declaration of Helsinki. Specifically we selected patients from this cohort, according to the following selection criteria: NPM1-mutated AML subtype, available therapy information and at least three NPM1 measurements (more details and a flow chart can be found in the electronic supplementary material, S2). Bone marrow aspirates were taken at irregular time points, usually at diagnosis and during primary therapy, with additional measurements during follow-up and at relapse. NPM1 quantification was processed as described in [28], quantifying the amount of NPM1-mut transcripts relative to the amount of transcripts of the reference gene ABL in the bone marrow samples. As there were two different platforms used for PCR-quantification (i.e. Lightcycler480 and Taqman 7500, both with 5’-nuclease assays) a correction factor between the two values was estimated and applied to ensure comparability between measurements (for details see the electronic supplementary material, S1). In total, 69 patients presented with a molecular relapse and 57 patients did not reach remission. The median age was 53 years (range: 20–79). The median number of NPM1 measurements per patients was five (range: 3–21). The medium number of therapy cycles received was four (range: 1–10). Measurements below the detection limit of 0.001% NPM1/ABL (i.e. the lower limit of detection of the method) were handled as 0.001%. All measurements after allogeneic stem cell transplantation were removed from the dataset, as this treatment has a major effect on the disease dynamics and is not part of this analysis.

Patients were only included in our analysis of the accuracy of relapse time estimation if they did not reach remission at all, reached remission and relapsed within two years, or presented with later measurements confirming sustained remission during the entire 2 years.

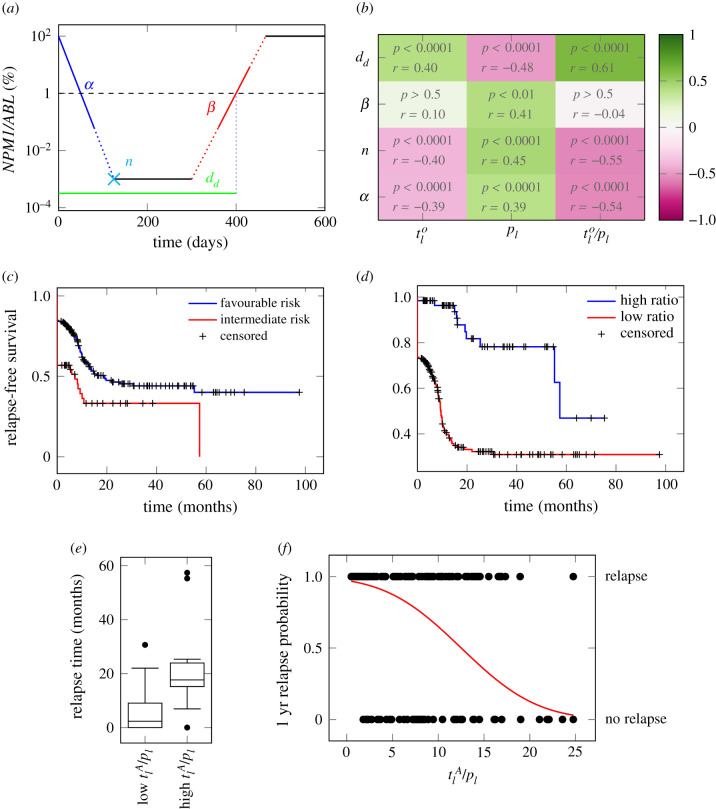
We recently suggested different quantitative characteristics to describe a patients’ molecular time course (in [6]). These are: the elimination slope (α, quantifying the decrease of the leukaemic burden during primary treatment), the minimal NPM1/ABL level after primary treatment (induction + consolidation) within nine months after treatment start (termed n), the maximum slope during molecular relapse (β, quantifying the speed of relapse outgrowth) and the time of molecular relapse (d) (for explanation see figure 3a; electronic supplementary material, S3). We defined molecular relapse as the approximated time point when the NPM1/ABL ratio exceeds the relapse threshold of 1% (following the suggestion in [28]). This time was approximated using a linear interpolation between the last point below the threshold and the first one above.

Figure 3.

(a) Schematic overview of an NPM1 time course. α: elimination slope during primary therapy [log10% d⁻¹]; n: minimal NPM1 level after primary treatment within nine months after treatment start [log10%]; β: the maximum slope during relapse phase [log10% d⁻¹]; d: time until molecular relapse [days]. (b) Spearman correlation coefficients between the fitted parameters (i.e. leukaemic activation $t_l^A$, leukaemic proliferation p_l and their ratio) and the patients molecular time course characteristics with adjusted p-values. (c) Relapse-free survival for intermediate and favourable ELN risk groups. p < 0.01 (logrank-test). HR = 1.86. (d) Relapse-free survival for high and low ratio of leukaemic activation and leukaemic proliferation ($t_l^A/p_l$) as estimated by the mathematical model with a threshold between high and low of 18. p < 0.0001 (logrank-test). HR = 5.47. (e) Boxplot for the comparison of the molecular relapse times of patients with high (n = 116) or low (n = 10) ratio of leukaemic activation and leukaemic proliferation ($t_l^A/p_l$) as estimated by the mathematical model with a threshold between high and low of 18. p < 0.0001 (U-test). (f) One year relapse probability (sigmoid function) as estimated by a logistic regression. Corresponding patient data (•) indicate the 1 year relapse status (relapse/no relapse) depending on the ratio of the two fitted parameters ($t_l^A/p_l$).

The whole dataset used for the present analyses is available as the electronic supplementary material, (PatientData1.csv with all patient-specific information; PatientData2.csv with NPM1/ABL measurements).

2.2. The mathematical model

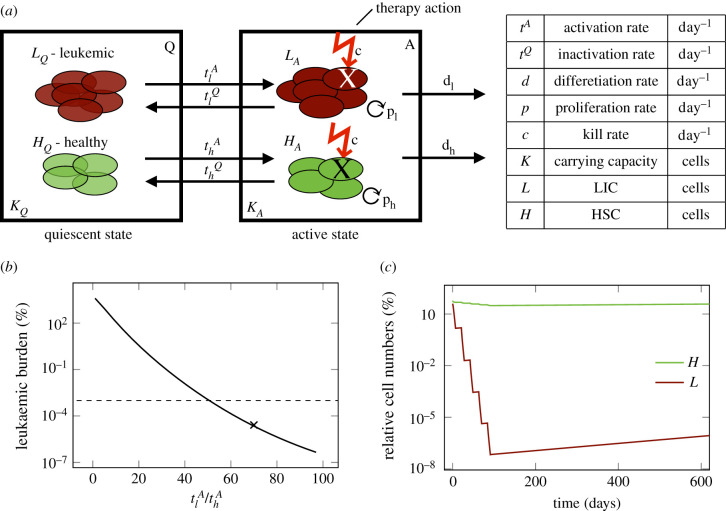
We developed a mathematical model describing the HSC dynamics in the bone marrow of AML patients (figure 1a). Because AML dynamics are largely driven by a pool of leukaemia-initiating cells, we restrict our model to the stem cell dynamics (cf. [19]). Similar to the general modelling concept applied for healthy haematopoiesis and CML [11,24], we consider two stem cell states with different proliferative activity, i.e. quiescent and proliferating cells. Cells in these two states are assumed to differentially respond to chemotherapy. While quiescent cells, both leukaemic (L_Q) and healthy (H_Q), are considered insensitive to S-phase specific drugs, activated leukaemic (L_A) and healthy cells (H_A) are targeted by those substances. Assuming a finite (stem cell-niche related) carrying capacity for both states (K_Q/A) (describing the distinct micro-environments of the two different states, for which we make the simplifing assumption of a 1 : 1 ratio) [29] the transition between the states is modelled as a function of the number of cells in the target state. Additionally, assuming different transition rates between the states for leukaemic ($t_{Q/A}^l$) and healthy ($t_{Q/A}^h$) cells, the following system of ordinary differential equation (ODEs) describes the change of the number of cells (H_Q/L_Q) in quiescent state Q over time (t):

$$\frac{\text{d}{H}_Q}{\text{d}t}=t_h^Q\cdot (1-\frac{L_Q+H_Q}{K_Q})\cdot H_A-t_h^A\cdot (1-\frac{L_A+H_A}{K_A})\cdot H_Q$$ 2.1

and

$$\frac{\text{d}{L}_Q}{\text{d}t}=t_l^Q\cdot (1-\frac{L_Q+H_Q}{K_Q})\cdot L_A-t_l^A\cdot (1-\frac{L_A+H_A}{K_A})\cdot L_Q.$$ 2.2

Figure 1.

(a) Schematic overview of the mathematical model describing the dynamics of leukaemia-initiating cells (LIC), L and healthy stem cells (HSC), H in the bone marrow of an AML patient. (b) Leukemic burden after therapy depending on the ratio of leukaemic activation to healthy activation $t_l^A/t_h^A$. Dashed line shows detection limit for clinically measured leukaemic burden. For x the time course is shown in figure 1c. (c) Time course of leukaemic and healthy cell numbers relative to the numbers at diagnosis with a $t_l^A/t_h^A=70$.

The cell numbers (H_A/L_A) in active state A are additionally influenced by the proliferation of the active cells with rate p_h/l, and by their dependency on the total amount of cells in the current state, modelled by the carrying capacity K_A. Furthermore, active cells can leave the stem cell state with a differentiation rate d_h/l or they can be targeted by chemotherapy with a constant kill rate c during treatment. The cyclic chemotherapy administration is realized in the model by a fixed chemotherapy kill rate, which can be switched on and off. These assumptions lead to the following model description in the active state A:

$$\begin{array}{rl}\frac{\text{d}{H}_A}{\text{d}t}& =t_h^A\cdot (1-\frac{L_A+H_A}{K_A})\cdot H_Q-t_h^Q\cdot (1-\frac{L_Q+H_Q}{K_Q})\cdot H_A\\ & +(\hspace{0.17em}{p}_h\cdot (1-\frac{L_A+H_A}{K_A})-c-d_h)\cdot H_A\end{array}$$ 2.3

and

$$\begin{array}{rl}\frac{\text{d}{L}_A}{\text{d}t}& =t_l^A\cdot (1-\frac{L_A+H_A}{K_A})\cdot L_Q-t_l^Q\cdot (1-\frac{L_Q+H_Q}{K_Q})\cdot L_A\\ & +(\hspace{0.17em}{p}_l\cdot (1-\frac{L_A+H_A}{K_A})-c-d_l)\cdot L_A.\end{array}$$ 2.4

The complete model describes the competition between healthy and leukaemic cells, in which the leukaemic cells would progressively outcompete the healthy cells if left untreated. The leukaemic burden, which is the main readout of the model, is calculated as the relative fraction of leukaemic cells in both states with respect to the overall number of all cells in these states, i.e.

$$\text{leuk. burden}[\text{\%}]=\frac{L_A+L_Q}{H_A+H_Q+L_A+L_Q}\times 100\text{\%}.$$ 2.5

The leukaemic burden is directly compared to the patient’s NPM1/ABL measurements, thereby making the simplifying assumption that the NPM1/ABL ratio in the unsorted bone marrow aspirates sufficiently approximates the relative frequency of leukaemic cells within the respective stem cell compartments.

To compare model results with the data, all values below the detection limit of the qPCR method of 0.001% were set to this limit (left-censoring). As it is common to have NPM1/ABL ratios of up to 1000%, because of the higher abundance of the NPM1 transcript compared to the reference gene [30,31] the percentage of leukaemic cells from the model was increased by a factor of 100 to translate them into the NPM1/ABL ratio and make the model results comparable with the measurements. This scaling factor does not influence the overall model behaviour.

2.3. Model parameters

Most values for the model parameters were taken from the literature (see below) and treated as constant values for all patients. To account for patient-heterogeneity, we compared several models with different choices of the free parameters and evaluated them with respect to an optimal fitting to the respective data. Using Akaike’s information criterion (AIC, which considers both the quality of the fit as well as the number of free parameters) as well as the identifiability of the parameters to be fitted to the data, (see the electronic supplementary materials, S4 and figures S1 and S5), we identified that the leukaemic proliferation rate p_l (reflecting the aggressiveness of the leukaemic clone) and the leukaemic activation rate $t_l^A$ (reflecting the individual chemosensitivity) represent the best choice for a minimal but optimal model parametrization.

The transition rate of leukaemic cells into quiescence ($t_l^Q$) was kept constant for all patients and was set to 0.002 d⁻¹. It was obtained by fitting the model to all patient time courses multiple times, each time with a different inactivation rate to find the globally best fitting rate. The other model parameters were set to plausible values based on available literature data.

• —Chemotherapeutic kill rate (c) was kept constant to ensure identifiability of the fitted parameters. It was set to 0.99 d⁻¹ to account for the high total leukaemic cell kill, as reported for an in vivo mouse study [32]. An analysis of different values for c showed nearly no dependence on the choice of this parameter. Only much smaller kill rates result in inferior model fits (see the electronic supplementary material, figure S6C).
• —Proliferation rate of healthy cells (p_h) was set to once every 25 days. It was estimated that healthy haematopoietic stem cells divide once every 30 days [33]; but as the actual proliferation rate in the model depends on the niche space in the current state and hence this rate would only be reached for an empty state, the rate was set to this higher value. Model results showed no qualitative dependence on the choice of this parameter (see the electronic supplementary material, figures S6A and S7).
• —Stem cell differentiation rate (d_h/l) was set to the value of the proliferation rate without influence of the capacity (1/30 d⁻¹) for both leukaemic and healthy cells.
• —Activation rate for healthy cells ($t_h^A$) was set to 0.01 d⁻¹ and the inactivation rate ($t_h^Q$) to 0.2 d⁻¹, based on the functions for these values from the original model [11].
• —Carrying capacities for each state (K_A/Q) were based on the value of 10⁵ cells as previously described [11], which is about a factor 10 smaller than actual stem cell numbers in a patient’s bone marrow. An analysis of different carrying capacities, showed that a smaller capacity for the active state results in slightly inferior model fits, whereas other values had no impact (electronic supplementary material, figure S6B).

The competitive advantage of leukaemic cells compared to healthy cells originates from their increased proliferative potential [34,35], which is represented in the model as an increased leukaemic proliferation rate of up to once every 5 days.

When fitting the model to patient data, the leukaemic activation rate ($t_l^A$) and the leukaemic proliferation rate (p_l) were estimated by minimizing the weighted log-likelihood, where negative NPM1/ABL measurements were double weighted to account for the possibility of these values being far below the detection limit. Differences between values were calculated on the log10 scale. For all patients, 100 random starting points were generated for fitting to eliminate the dependence on the start value and to increase the probability of reaching the global minimum. In order to avoid overfitting, we assessed the identifiability of the fitted parameters using the profile likelihood (see [36] for details). In the corresponding likelihood landscape in the electronic supplementary material, figure S1, it is shown that the identifiability is given for both free parameters.

For an additional, easier interpretable measure of goodness of fit the mean absolute error (MAE) was estimated by computing the mean divergence of the model from the measurements for each patient fit on the log10 scale.

2.4. Statistical analysis

General bivariate correlations were quantified using the Spearman rank correlation coefficient (ρ). p-values for multiple pairwise correlations were adjusted using Bonferroni correction. To specifically measure the agreement between relapse times estimated with the model and estimated from the clinical data we applied the Lin’s concordance correlation coefficient (ρ_c). The (Mann–Whitney) U-test was applied to compare rank distributions (i.e. shift in the medians) of two independent groups of patients. The Kaplan–Meier method was used for relapse-free survival analysis, using the time until recurrence/death. The logrank-test was applied to compare the survival of two independent groups. A cox regression was conducted for hazard ratio (HR) estimation. The threshold of the parameter ratio to discriminate between the two groups was determined by maximizing the HR with the additional requirement of at least 10 target events (i.e. relapse) in each group. Odds ratios were determined by logistic regression. Identifiability of the model parameters was assessed using the profile likelihood approach, as described in detail in [36]. The likelihood landscape is derived by estimating the profile likelihood for all parameter combination. The 95% confidence intervals (CI) for the model parameters were derived following the likelihood-based CI definition by Meeker & Escobar [37].

All analyses were done with Matlab R2018b (The MathWorks, Inc., 1994–2018). The source code is available from the authors on request.

3. Results

3.1. Reduction of leukaemic burden can be modelled without assuming a different chemotherapeutic kill effect on normal and leukaemic cells

In order to reproduce the molecular dynamics of AML, we developed a mechanistic mathematical model of the competition of leukaemic and healthy stem cells in the bone marrow. This modelling approach is in line with earlier works in which a minimal, two-compartment model of HSC organization was applied to describe various phenomena such as stem cell competition, ageing and leukaemia [11,13,24,25,38,39]. The model describes two functional states between which the cells can reversibly transit depending on the capacity in the target state. While in the ‘active state’ the cells proliferate and can potentially differentiate, they stay inactive in the ‘quiescent state’ (figure 1a). Both healthy HSCs and leukaemia-initiating cells (LICs) can adopt each state. However, while their transition dynamics between the two states differ, leukaemic and normal cells are competing for shared resources (such as limited niche space). The parameters for the healthy cells were taken from the literature as described in Material and methods. The routinely used chemotherapeutics D-arabinosyl cytosine (AraC) and Daunorubicin effect all dividing cells during S-phase equally [40]. Therefore, our first question to be answered was, whether it is possible to assume an equal cell kill on both active HSCs and LICs during chemotherapy and still achieve a leukaemic clearance. Therefore, we defined all parameters for the leukaemic cells to be the same as for the healthy ones, while only the leukaemic activation rate ($t_h^A$) was increased systematically. Figure 1b shows the leukaemic burden at the end of five chemotherapy cycles depending on the assumed value of leukaemic activation. The figure indicates that an elimination of the measurable leukaemic burden (for a detection limit at 10${\hspace{0.17em}}^{-3}\text{\%}$) can be consistently explained even without differences in the chemo-induced kill rate if an elevated activation of leukaemic cells by a factor of 50 is assumed compared to healthy cells. The exemplary time course in figure 1c confirms the rapid decline of leukaemic cells during therapy, while the healthy cells stay at a high level. This adheres to the general concept that leukaemic cells are almost constantly proliferating without periods of extended quiescence and reflects the typical leukaemic phenotype [41]. It shows further that this model is able to reproduce a broad bandwidth of treatment-induced reduction of leukaemic burden (reaching from 1 to 6 log-reduction), which is also confirmed in different AML patients during chemotherapy [31].

3.2. A simple mechanistic model is able to mimic the molecular dynamics of most NPM1-mut AML patients

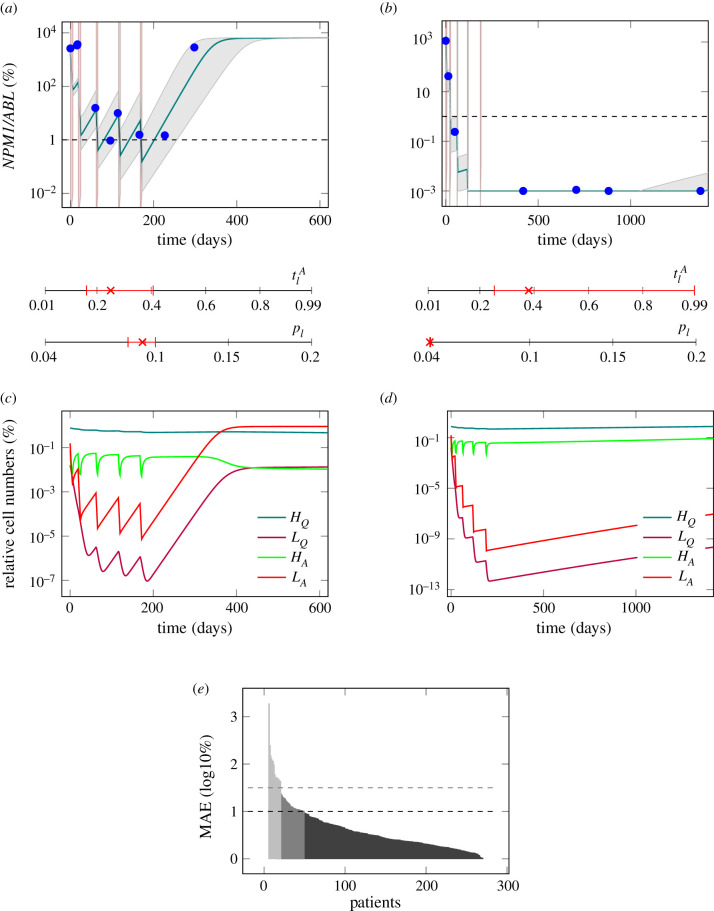
After having demonstrated the general ability of the model to mimic the leukaemic reduction during therapy we analysed whether the model can also account for the interpatient-variability in treatment response and dynamic behaviour. For this analysis, 1567 NPM1/ABL measurements of 275 patients with a median number of five measurements per patient were available. We assessed the ability of the model to reflect a large variety of time courses, including remission (n = 149), unresponsiveness to therapy (n = 57) and relapse cases (n = 69). Therefore, we adjusted the individual activation rate of leukaemic cells $t_l^A$, as well as the individual leukaemic proliferation rate p_l for each patient’s time course of leukaemic burden to find a patient specific parameter combination that optimally describes the individual disease dynamics, while all other parameters were kept constant. In figure 2a,b, there are two examples of fitted patient time courses along with the 95% CI for the optimal fit. These examples illustrate that the model reproduces the characteristic time course of AML patients presenting with either a molecular relapse or a sustained molecular remission. Although both patients received very similar chemotherapies it can be seen that for the relapsing patient the NPM1 burden is not eliminated after the therapy (figure 2a), while for the other patient (figure 2b) the value is below the detection limit. Hence, the slightly higher leukaemic activation ($t_l^A$) and the lower leukaemic proliferation (p_l) are sufficient to explain the difference between relapse and sustained remission. Furthermore, we observed, that a high leukaemic activation rate is linked to a fast decline of leukaemic burden during therapy, an effect which is illustrated clearly by the good responding patient in figure 2b. Therefore, we conclude that this rate estimate can be interpreted as a measure for the patient’s individual chemosensitivity. Also, we observed, that a high leukaemic proliferation rate is linked to fast leukaemic regrowth, which can be seen in the poorly responding patient in figure 2a. From this, we conclude that the estimated leukaemic proliferation rate provides a measure of the tumour intrinsic aggressiveness.

Figure 2.

(a) Model fit to the data (PatientID = 104) and 95% confidence interval (CI) of an example patient suffering a relapse. $\text{Mean absolute error}(MAE)=$ $0.6\hspace{0.17em}\text{log}10\text{\%}$. (b) Model fit to the data (PatientID = 3137) and 95% CI of an example patient staying in long time remission. $\text{MAE}=0.04\hspace{0.17em}\text{log}10\text{\%}$. The red shaded regions are the times of treatment. The red marks indicate the fitted parameter values for the leukaemic activation ($t_l^A$) and the leukaemic proliferation (p_l) with their corresponding 95% CI. (c) Time courses of cell numbers relative to the total cell numbers at diagnosis of model fit to patient from plot (a). (d) Time courses of cell numbers relative to the total cell numbers at diagnosis of model fit to patient from plot (b). H_Q, quiescent HSCs, L_Q, quiescent leukaemic stem cells (LSCs), H_A, active HSCs, L_A, active LSCs. (e) MAE in log10% for all patient fits as a measure of goodness of fit. Black dashed line indicates threshold for quantitatively good fitting patients. Grey dashed line indicates threshold for qualitatively good fitting patients. For all patients with higher MAE the fit was poor.

Looking in more detail how the different cell populations within our model respond to the treatment (figure 2c,d), one observes that the difference between a good and a poor therapy response is within the leukaemic cell population, with the good responder showing steeper decline during therapy as well as slower regrowth afterwards. In the poor responder the number of leukaemic cells in the model also drops to a vanishingly low proportion of their initial numbers during treatment. Nonetheless, a relapse occurs within a few months, because of the fast regrowth. Furthermore, a decrease of the net proliferation rate during leukaemic regrowth after chemotherapy can be observed (as the curves (L_A and L_Q) flatten after an exponential growth phase around 350 days after diagnosis). This observation agrees with a recent study by Akinduro et al. where the authors analysed the growth of AML cells after transplant in a mouse model [42]. The high number of quiescent HSCs is also in accordance with experimental data, as it was recently shown that in a leukaemic mouse bone marrow HSCs were mostly in a quiescent state [43]. This mechanism is also referred to as ‘self-protection’ by which HSCs avoid environmental effects in the quiescent state [44].

The quality of the individual fits was evaluated using the MAE of each model fit, which corresponds to the average residual between model fits and available data points on the log10 scale. We observed that fits with a MAE of up to 1 could quantitatively describe the patient’s course of disease. Hence, at least 227 of the 275 patients can be sufficiently described by the individual model fits (figure 2e). Patients with an average error of up to 1.5 log could still be qualitatively described (n = 260).

Looking more closely at the 15 patients in which the model could not optimally fit to the time course data, it becomes clear that for most of them (10) the model as it is cannot account for the strong leukaemic reduction found in the data (example patient in the electronic supplementary material, figure S3A). For two of the patients the very fast regrowth is not reproducible with the model and for three patients a chemo-resistance arises during treatment of a relapse, which is not yet captured by our current model (both can be seen in example patient in the electronic supplementary material, figure S3B).

Taken together, we could show that the proposed simple model is indeed able to reproduce most of the molecular behaviour of NPM1-mut AML patients, which can now be used to analyse the molecular characteristics of the course of disease.

3.3. The model parameters are closely linked to time course characteristics

Based on the patient individual model fits we obtain a pair of model parameters (leukaemic activation rate $t_l^A$ and leukaemic proliferation rate p_l) for each specific patient time course (distribution of the parameters in the cohort can be found in the electronic supplementary material, figure S2). In order to investigate how these model parameters correlate with typical, clinically relevant characteristics of the NPM1/ABL dynamics, we perform a systematic correlation analysis. For a quantitative description of the relevant NPM1/ABL time course characteristics, we use a parametrization based on the elimination slope (α), the minimal NPM1 level after primary treatment (induction + consolidation) within nine months after treatment start (n), the maximum slope during relapse phase (β) and the time until molecular relapse (d_d) (see figure 3a, [6]). Figure 3b provides a summary of pairwise comparisons between the individually fitted model parameters and the characteristics of treatment response. Generally, for all characteristics but the relapse slope β, a significant correlation with a correlation coefficient of up to 0.6 was found. Furthermore, the leukaemic activation ($t_l^A$) and leukaemic proliferation (p_l) are conversely correlated with all described time course characteristics. This means that later molecular relapse is linked to increased leukaemic activation, but decreased leukaemic proliferation. This supports the earlier conclusion, that the leukaemic activation is a measure for chemosensitivity, whereas the leukaemic proliferation provides a measure for the aggressiveness of the disease. Furthermore, this anti-correlation with the time course characteristics suggests that the ratio between the two parameters ($t_l^A$/p_l) reflects a good measure for the overall severity of the patient’s individual course of disease.

From a clinical perspective, it is most important to know whether and when a patient will relapse or not, and to estimate the chance for relapse-free survival. Using the approximated time point of molecular relapse as a surrogate for haematological relapse (including irresponsiveness), we studied whether a division into high and low ratio of estimated leukaemic activation and leukaemic proliferation (i.e. $t_l^A/p_l$; threshold at $t_l^A/p_l=18$, determined by maximizing the difference between both groups, details in Material and methods) can improve the current ELN risk stratification (stratifying into high and low risk). Figure 3c,d supports the notion that both variables are indeed correlated with relapse-free survival. However, the differences in the Kaplan–Meier plots indicate that this effect is considerably more pronounced using the ratio of leukaemic activation and proliferation. Comparing the HR between the two stratifications further supports this impression (HR_ratio = 5.5 (95% CI: 2.8 to 10.4); HR_ELN = 1.9 (95% CI: 1.2; 2.8)). A clear difference in the time of relapse can be seen, when directly comparing the molecular relapse times of the high and the low parameter groups (figure 3e). Patients with a high parameter ratio $t_l^A/p_l$ tended to relapse in median 15.3 months later. Moving away from the division into two risk groups, we apply a logistic regression approach to estimate to which extent the estimated ratio ($t_l^A/p_l$) correlates with the probability to relapse within the first year after diagnosis (figure 3f). The odds ratio of 1.17 (95% CI: 1.11 to 1.22) indicates that an increase in the ratio by 5 units more than doubles the chance of experiencing a relapse within the first year. However, the nearly linear relationship between the ratio ($t_l^A/p_l$) and the relapse risk indicates that the ratio $t_l^A/p_l$ alone cannot reliably predict relapse for a particular patient, although it can be useful in combination with other measures to improve risk prediction.

3.4. Clinically relevant characteristics can be estimated using the mathematical model

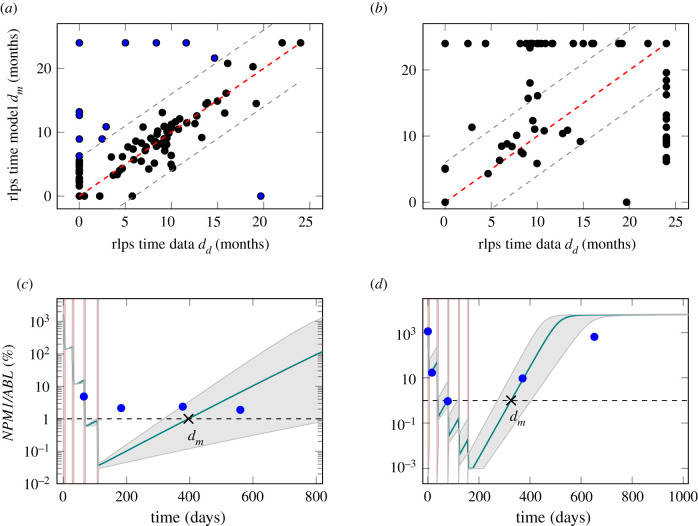
In the clinical context, the time of molecular relapse is a highly relevant measure. For this reason, we compared the molecular relapse time approximated from the data (d_d, definition can be found in Material and methods) with the estimated molecular relapse time predicted by the model (d_m). Figure 4a shows the corresponding scatter plot for all patients for which a relapse time within 2 years could be approximated (n = 175). As expected, there is a good accordance for most patients, while only for 13 out of the 175 patients (7%) the estimated molecular relapse time from the model diverges more than half a year from the molecular relapse time approximated from the data. The mean divergence for all patients is 1.9 months. However, the larger differences for some patients raises the question of why the model is incapable of mimicking their course of disease.

Figure 4.

(a) Scatter plot for the comparison of the molecular relapse time approximated from the patient data d_d and the molecular relapse time estimated from the fitted model d_m for each patient. ρ_c = 0.90. Perfect accordance is indicated with dashed red line. Grey dashed line indicates divergence by half a year. Points with divergence larger than half a year are marked blue. (b) Scatter plot for the comparison of the molecular relapse time estimated from the fitted model to the first nine months d_m of the patients and the molecular relapse time approximated from the data of these patients d_d. ρ_c = 0.37. (c) Example fit (PatientID = 3751) and 95% CI for a patient where the model is not able to capture the molecular course of disease. Dashed line shows remission/relapse threshold. d_d is 0 days (no remission reached), d_m is 396 days. (d) Example fit (PatientID = 3621) and 95% CI for a patient where the sparseness of data points makes it impossible to reliably approximate the molecular relapse time. Dashed line shows remission/relapse threshold. d_d is 0 days (no remission reached), d_m is 326 days.

Studying the 13 critical patients more closely it appears that the model is insufficient to describe at least six of them for technical reasons, i.e. very fast regrowth, very high chemosensitivity or stable tumour levels, that are not depicted in the model (see example in figure 4c). To explain a stable tumour level over a longer time (as in the example patient), an additional intrinsic leukaemic suppression (such as an immunological component) would be necessary in the model. For the other seven patients with poor accordance of the relapse times, it is the sparsity of the available measurements that limits a reliable approximation of the relapse times from the data. For the example patient in figure 4d, the measurements suggest that a remission could not be reached, but it is conceivable that the tumour burden decreases further during the time of therapy. Therefore, it is very likely that a temporary remission occurs at the end of therapy, as suggested by the model fit. However, just from the available data both conclusions cannot be excluded. Therefore, it is possible that the estimated relapse time from the fit is closer to the true relapse time than the approximation from the data. Hence, we conclude that the model, although not able to perfectly describe every single course of disease, might indeed harbour additional information about the true course between available measurements.

3.5. Predicting the relapse time based on the early time course is not reliable

We could show that the ratio $t_l^A/p_l$ is correlated to the approximated time of molecular relapse and suggested that the model can help to estimate the particular time point of molecular relapse occurrence. Moving a step further, we raise the question of whether an early (and clinically even more relevant) prediction of the relapse behaviour can be made with comparable precision. From a clinical perspective, nine months after treatment start is a time point when a decision about future treatment options for a particular patient is still relevant. We chose this time point as a cut-off until which the models were fitted, given there are at least three data points within this time period (n = 89). Figure 4b compares the relapse times predicted by the model based on these truncated time courses with the approximated relapse time from the complete data. It appears that reliable model predictions cannot be achieved for the majority of cases. In fact, for more than 40% of the patients the divergence is more than six months and the mean difference over all patients is 6.6 months. This visualization indicates that a reliable prediction of relapse occurrence cannot be achieved if only sparse measurements during the initial treatment response during the first nine months of treatment are considered. However, it cannot be excluded from our current study that additional diagnostic parameters together with close-meshed short term time course data convey more information for better predictions.

4. Discussion

In this study, we have developed and validated a simple mechanistic, mathematical model that is able to correctly reflect the individual molecular disease dynamics of NPM1-mut AML patients treated with cytotoxic drugs. As the model describes AML treatment response as the result of the competition between more proliferative leukaemic and less proliferative healthy stem cells, we can use this model to functionally analyse the underlying mechanisms and contribute to the understanding of AML remission and relapse. In particular, we explicitly assume that both healthy and leukaemic stem cells can be in a quiescent and chemotherapy-insensitive state, while they are equally targeted by chemotherapeutics if they are in an actively cycling state. Based on these assumptions, we addressed the question of how the individually fitted model parameters for each patient are linked to clinically relevant measures, such as the approximated time of molecular relapse.

The dynamics of AML pathogenesis and treatment have attracted several modelling approaches. However, few models explicitly address the competitive imbalance between leukaemic and healthy haematopoiesis, and nearly none are validated with large patient cohorts. To our knowledge, only a study by Stiehl et al. [45] follows a similar competitive approach in which the time after induction therapy is considered. However, this model focuses only on the time after therapy, starting always with a state in which no leukaemic cells are detectable. Thereby, patient-specific differences in their therapy response and treatment regimen are neglected. Considering earlier clinical findings [28], as well as our patient-specific analysis, this restriction to homogeneous treatment response limits the generalizability of this modelling approach.

The overall agreement between measured patient time courses and the optimally adapted model dynamics allows us to conclude that our model captures a set of features that are characteristic for the response of AML patients to cytotoxic treatment. Most importantly, this correspondence ensures us that the general notion of haematopoietic or leukaemic stem cells reversibly changing between states of differential proliferative activity and chemosensitivity, can also be applied in the context of AML. Strikingly, we did not even assume a different chemotherapeutic effect for dividing cells, irrespective of whether they are leukaemic or healthy cells. This reflects the mechanism of action inherent to S-phase specific drugs which effects all dividing cells. From our model estimates we conclude that the unregulated and strongly increased activation of leukaemic cells into the cell cycle is sufficient to describe a preferential targeting of this population and to explain the typical remission behaviour. And although NPM1-mut AML is more chemosensitive than other AML subtypes [46], the model could be transferred, as also unresponsiveness to treatment can be captured by the model. Furthermore, our simplistic model provides additional explanations for other phenomena observed in AML, which are not explicitly included in the model set-up. One of these phenomena is that the leukaemic proliferation rate decreases during regrowth [42]. This can be explained with the limitation of the proliferation by the available stem cell niche capacity. During leukaemic expansion the niche is rapidly filling, leading to a decreased proliferation. Another phenomenon is the high number of quiescent HSCs in AML [43], which can be explained by the fast activation of leukaemic cells into the active state. Therefore, the limited niche capacity is rapidly populated by leukaemic cells, pushing the healthy cells to stay quiescent. This is also in agreement with findings by Miraki-Moud et al. who showed that bone marrow failure in AML is not caused by depleting HSC numbers but impairing their differentiation [47]. Another phenomenon is the increased proportion of active cells within the leukaemic bulk in patients with a good therapy response compared to a poor therapy response [48] (electronic supplementary material, figure S4). This can be explained by the link between high leukaemic activation and a high chemosensitiviy. The higher leukaemic activation leads to more active leukaemic cells, which can be more easily killed by the treatment.

Furthermore, we could show that the two individually fitted model parameters, namely the leukaemic activation rate and the leukaemic proliferation rate, are closely linked to the patients’ time course characteristics, e.g. the elimination slope, the NPM1 burden after primary treatment and the time of molecular relapse. As the leukaemic proliferation is assumed to be a measure for the tumour aggressiveness, we expected to see a close link with the relapse slope β. However, only a weak correlation was found. The reason for this can be found in the imprecise estimation of the relapse slope on the basis of too sparse data, as the strong correlation (ρ = 0.97) with the relapse slope estimated from patients’ model time courses suggests. The leukaemic activation rate, which is assumed to be a measure for the patient’s chemosensitivity has a less clear impact on the time course, as it has medium influence on all characteristics, except for the relapse slope. In general, we found, that both parameters combined as a ratio show the closest link to the time course characteristics. Using this ratio of leukaemic activation and proliferation from the model to separate the patients into two groups (high and low estimated ratio) improves the risk stratification into favourable and intermediate risk patients compared to the ELN scheme (figure 3d). This supports our previous claim, that the close monitoring of molecular disease markers and incorporation of the molecular disease dynamics in risk stratification schemes will improve assessment of the severity of the patients’ AML [6].

Nonetheless, the inability of the model to reproduce all patients’ time courses shows that the model lacks some further regulations that cannot be neglected for some patients. Likely candidates for such a regulation could be the immune response, as suggested by an increased activity of natural killer cells in patients with longer relapse free survival [49], the emergence of new leukaemic clones at relapse with possibly different properties than the clone at diagnosis [50,51], the differences in cellularity found in AML bone marrow [52] or the ability of AML blast cells to de-differentiate [53].

When using the model to predict the individual patient’s time of relapse based on the measurements of the first nine months, the accuracy was rather limited. Therefore, we reason that individual predictions of relapse times are only possible with a high level of uncertainty, which is of limited value for individual patients. Most prominently, it is the above-mentioned inability of fitting some of the patients’ time courses, which in most cases results from the sparseness of the data and the individual measurement error, that render it difficult to obtain a suitable approximation of the patients’ molecular relapse time. A stringent MRD monitoring, as proposed by Rautenberg et al. [54], would help to overcome these shortcomings in the future. To our understanding, such an improvement of the time course data will allow better model fits and can contribute to better relapse predictions for AML patients.

In conclusion, we showed that the fitted parameters of a simple mathematical AML treatment model can consistently describe individual time course characteristics in the majority of the analysed patients. Furthermore, the model contributes to a better understanding of the complex dynamics and mechanisms of AML treatment. Finally, we showed that such a model-based understanding can further improve the classification of disease severity and risk predictions.

Ethics

The study was approved by the ethical board of the Medical Faculty of the TU Dresden (EK98032010).

Data accessibility

This article has no additional data.

Authors' contributions

H.H. developed the mathematical model, carried out the statistical analyses and drafted the manuscript. I.R. and I.G. gave regular feedback during all analyses and helped draft the manuscript. C.T. and M.B. conceived and designed the study, coordinated the clinical data collection and critically reviewed the manuscript. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

C.T. is CEO and co-owner of AgenDix GmbH, a company performing molecular diagnostics. Other authors declare that they have no conflict of interest.

Funding

This work was supported by the BMBF within the HaematoOPT project of the e:Med initiative (grant no. 031A424A).