Learning probabilistic neural representations with randomly connected circuits

Significance

We present a theory of neural circuits’ design and function, inspired by the random connectivity of real neural circuits and the mathematical power of random projections. Specifically, we introduce a family of statistical models for large neural population codes, a straightforward neural circuit architecture that would implement these models, and a biologically plausible learning rule for such circuits. The resulting neural architecture suggests a design principle for neural circuit—namely, that they learn to compute the mathematical surprise of their inputs, given past inputs, without an explicit teaching signal. We applied these models to recordings from large neural populations in monkeys’ visual and prefrontal cortices and show them to be highly accurate, efficient, and scalable.

Abstract

The brain represents and reasons probabilistically about complex stimuli and motor actions using a noisy, spike-based neural code. A key building block for such neural computations, as well as the basis for supervised and unsupervised learning, is the ability to estimate the surprise or likelihood of incoming high-dimensional neural activity patterns. Despite progress in statistical modeling of neural responses and deep learning, current approaches either do not scale to large neural populations or cannot be implemented using biologically realistic mechanisms. Inspired by the sparse and random connectivity of real neuronal circuits, we present a model for neural codes that accurately estimates the likelihood of individual spiking patterns and has a straightforward, scalable, efficient, learnable, and realistic neural implementation. This model’s performance on simultaneously recorded spiking activity of >100 neurons in the monkey visual and prefrontal cortices is comparable with or better than that of state-of-the-art models. Importantly, the model can be learned using a small number of samples and using a local learning rule that utilizes noise intrinsic to neural circuits. Slower, structural changes in random connectivity, consistent with rewiring and pruning processes, further improve the efficiency and sparseness of the resulting neural representations. Our results merge insights from neuroanatomy, machine learning, and theoretical neuroscience to suggest random sparse connectivity as a key design principle for neuronal computation.

The majority of neurons in the central nervous system know about the external world only by observing the activity of other neurons. Neural circuits must therefore learn to represent information and reason based on the regularities and structure in spiking patterns coming from upstream neurons, in a largely unsupervised manner. Since the mapping from stimuli to neural responses (and back) is probabilistic (1–3) and the spaces of stimuli and responses are exponentially large, neural circuits must be performing a form of statistical inference by generalizing from the previously observed spiking patterns (4–7). Nevertheless, circuit mechanisms that may implement such probabilistic computations remain largely unknown.

A biologically plausible neural architecture that would allow for such probabilistic computations would ideally be scalable and could be trained by a local learning rule in an unsupervised fashion. Current approaches satisfy some, but not all of the above properties. Top-down approaches suggest biologically plausible circuits that solve particular computational tasks but often rely on explicit “teaching signals” or do not even specify how learning could take place (8–14). It is widely debated how a teaching signal could reach each neuron at the correct time and be interpreted properly (also known as the credit assignment problem). Notably, an architecture designed for a particular task will typically not support other computations, as observed in the brain. Lastly, current top-down models relate to neural data on a qualitative level, falling short of reproducing the detailed statistical structure of neural activity across large neural populations. In contrast, bottom-up approaches grounded in probabilistic modeling, statistical physics, or deep neural networks can yield concise and accurate models of the joint activity of neural populations in an unsupervised fashion (15–27). Unfortunately, these models are difficult to relate to the mechanistic aspects of neural circuit operation or computation because they use architectures and learning rules that are nonbiological or nonscalable.

A neural circuit that would learn to estimate the probability of its inputs would merge these two approaches: rather than implementing particular tasks or extracting specific stimulus features, computing the likelihood of the input gives a universal “currency” for the neural computation of different circuits. Such circuits could be used and reused by the brain as a recurring motif, in a modular and hierarchical manner for a variety of sensory, motor, and cognitive contexts, as well as for feature learning. This would remove the need for many specialized circuits for different computations. Consequently, it would facilitate the adoption of new functions by existing brain circuitry and may serve as an evolutionary principle for creating new modules that communicate and interact with the old ones. The idea that the brain computes the probability of its inputs is supported by evidence of responses to novel inputs or events (28, 29) and has been explored in different contexts such as the hippocampal (30), olfactory (31), and visual (32) systems, as well as in the role of dopamine (33).

Here, we present a simple and highly flexible neural architecture based on spiking neurons that can efficiently estimate the surprise of its own inputs, thus generalizing from input history in an assumption-free and parsimonious way. This feed-forward circuit can be viewed as implementing a probabilistic model over its inputs, where the surprise of its current input is explicitly represented as the membrane potential of an output (readout) neuron. The circuit is trained by adjusting the connections leading into the output neuron from a set of intermediate neurons, which serve as detectors of random features of the circuit’s input. Unlike many models of neuronal networks, this model relies on local learning in a shallow network, and yet, it provides superior performance to state-of-the-art algorithms in estimating the probability of individual activity patterns for large real neural populations. Furthermore, the synaptic connections in the model are learnable with a rule that is biologically plausible and resolves the credit assignment problem (34), suggesting a possible general principle of probabilistic learning in the nervous system.

Results

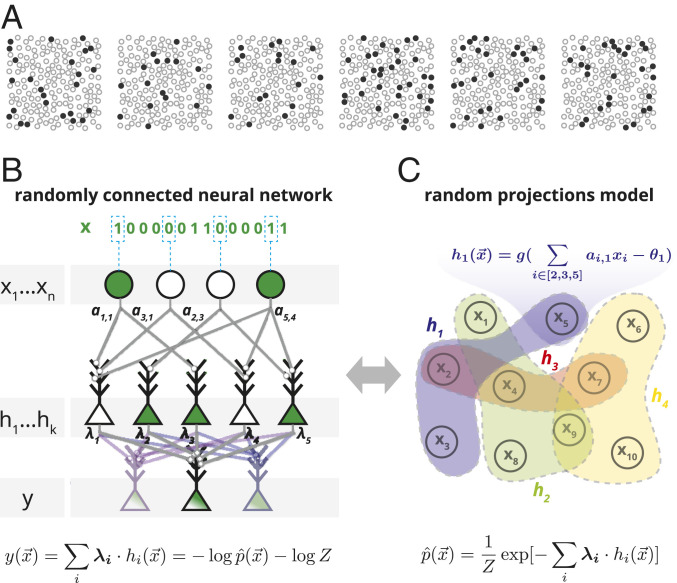
We consider the joint activity of large groups of neurons recorded from the visual and prefrontal cortices of macaques. Fig. 1A shows examples of activity patterns of 169 neurons, discretized into 20-ms time windows, from the prefrontal cortex of an awake behaving monkey at different times during a classification task. Notably, individual activity patterns would typically not repeat in the course of the experiment or even in the lifetime of an organism—even if we observed the neural activity for a hundred years, we would encounter at most $\sim 2^{37}$ patterns out of a possible $2^{169}$. Therefore, a neural circuit receiving these patterns as inputs cannot rely on counting them and must learn their statistical structure or otherwise fit a model in order to generalize to new, previously unseen, patterns. A neural circuit that estimates the surprise associated with observing a pattern would assess how the new pattern conforms with previously observed patterns, thus generalizing from past inputs without making additional assumptions. In mathematical terms, structure in the input patterns implies that some patterns are more likely to appear than others. This can be described in terms of a probability distribution over input patterns $p\left(\overrightarrow{x}\right)$, where $\overrightarrow{x}$ is a binary pattern representing the firing (one) or silence (zero) of each neuron in the population in a given time bin. The generic notion of surprise of observing an input pattern $\overrightarrow{x}=101100\dots$ appearing with probability $p\left(\overrightarrow{x}\right)$ is then given by $-\log p\left(\overrightarrow{x}\right)$ (35).

Fig. 1.

A randomly connected neural network, equivalent to an RP model, that learns to generalize from observed inputs to compute the surprise of novel inputs. (A) Examples of six neural population activity patterns at different time points, recorded from 169 neurons in the monkey prefrontal cortex while performing a visual classification task (plotted locations were chosen at random and do not correspond to actual spatial locations). (B) Architecture of a random feed-forward neural circuit based on spiking neurons that can learn to respond with the surprise of its input patterns, $x_1\dots x_n$. The input neurons are connected to an intermediate layer of neurons, $h_i$, with randomly selected synaptic weights $a_{ij}$, which then project to an output neuron with synaptic weights ${\lambda }_i$. After learning ${\lambda }_i$, the membrane potential of the output neuron $y\left(\overrightarrow{x}\right)$ will compute $-\log \widehat{p}\left(x_1\dots x_n\right)-\log Z$, an unnormalized estimate of the surprise, $-\log p\left(x_1\dots x_n\right)$, of the joint input. Note that the same layer of randomly projecting hidden neurons can be reused to simultaneously compute multiple probabilistic models for different output neurons (light color) (SI Appendix, Fig. S9A). (C) The circuit in B is equivalent to a probabilistic model over randomly weighted cliques of neurons, learned by reweighing their contributions, or the maximum entropy model based on random nonlinear statistics of the input.

Fig. 1B illustrates the architecture of a simple and shallow circuit, which can learn to respond to input patterns by computing their surprise. Each of these neurons computes a weighted sum of its inputs and responds with a spike (“1”) if the sum crosses the cell’s threshold. These binary neurons are approximations of real neurons, where synaptic inputs induce a change to the membrane potential that triggers a spike when it crosses a threshold. In the circuit, the input neurons $\left\{x_j\right\}$ are randomly connected to the neurons in an intermediate layer $\left\{h_i\right\}$, with randomly selected weights $\left\{a_{i,j}\right\}$ and so each of the $h_i$’s computes a nonlinear random projection (RP) of the input given by $h_i=g\left({\sum }_j{a}_{i,j}{x}_j-{\theta }_i\right)$ where $g\left(\right)$ is a threshold function and ${\theta }_i$ is the neuron’s threshold, which we set to a fixed value for all neurons (SI Appendix). These intermediate-layer neurons, each serving the role of a feature detector in the input layer, are then connected to a readout neuron, $y$, with weights ${\lambda }_i$. The specific values of ${\lambda }_i$ thus determine the function that the readout neuron computes based on the projections. The sum of inputs to the readout neuron, or its “membrane potential,” is then given by

$$y\left(\overrightarrow{x}\right)=\sum _i{\lambda }_i\cdot g\left(\sum _{j=1}^n{a}_{i,j}{x}_j-{\theta }_i\right).$$ [1]

This membrane potential can also be interpreted as $y\left(\overrightarrow{x}\right)=-\log \widehat{p}\left(\overrightarrow{x}\right)-\log Z$, where $\widehat{p}\left(x\right)$ corresponds to an internal model of the inputs:

$$\widehat{p}\left(\overrightarrow{x}\right)=\frac{1}{Z}\exp \left[-\sum _i{\lambda }_i\cdot g\left(\sum _{j=1}^n{a}_{i,j}{x}_j-{\theta }_i\right)\right],$$ [2]

and $Z$ is a normalization factor (or partition function). The membrane potential $y\left(\overrightarrow{x}\right)$ thus reflects an unnormalized model of the input distribution or the surprise of the joint inputs, $-\log \widehat{p}\left(x_1,x_2,\dots ,x_n\right)$, up to an additive factor. This factor can be compensated for by learning a bias to the readout neuron’s voltage or its spiking threshold that would give a normalized value of the surprise (SI Appendix has a discussion of possible normalization mechanisms and implementations). We are thus seeking the ${\lambda }_i$’s for which the distribution of inputs $p\left(\overrightarrow{x}\right)$ and the internal model $\widehat{p}\left(\overrightarrow{x}\right)$ are as similar as possible. Since these are probability distributions, the distance between them is naturally captured by their relative entropy or Kullback–Leibler divergence and can be minimized by finding the ${\lambda }_i$’s that would maximize the likelihood assigned to inputs by the readout neuron based on its history of input statistics. We recall that Eq. 2 is the well-known Boltzmann distribution (36), offering an alternative interpretation of the function that this circuit computes: given a set of K random functions of the input, i.e., the $h_i$’s, find the minimal model that is consistent with the expected values of these functions. This is then the most unstructured description of the data or the maximum entropy distribution based on the chosen RPs (37). Yet another interpretation is that this is a mixture model, reweighting of activity of random cliques or assemblies of neurons (38). Whichever interpretation one may like, the result is a circuit whose synaptic weights ${\lambda }_i$ correspond to the model parameters, and such models can be trained from a set of examples using standard numerical gradient descent-based approaches (39).

The randomly connected neural circuit we described for estimating the surprise is therefore a mechanistic implementation of the probabilistic model based on RPs illustrated in Fig. 1C and Eq. 2. Importantly, since the output neuron responds with a single bit, we propose that the surprise is reflected by its membrane voltage or internal state; the spiking output of the neuron would thus reflect whether its surprise has crossed a threshold. Critically, training this RP model requires only changing the synaptic weights ${\lambda }_i$ to the output neuron, using a process that requires no extra information about the projections other than that they are sufficiently informative about the input patterns. Thus, the connectivity $a_{i,j}$ could be predetermined (evolved) or learned by a separate process (feature selection). This simple design, where the process of selecting the features is distinct from the process of learning how to combine them, results in a convex optimization problem in which updating synaptic weights to the output neuron does not depend on updating of the rest of the circuit—sidestepping the credit assignment problem. Importantly, although the connectivity $a_{i,j}$ could be optimized or learned by a separate process (more below), purely random connectivity already results in a powerful and flexible probabilistic representation.

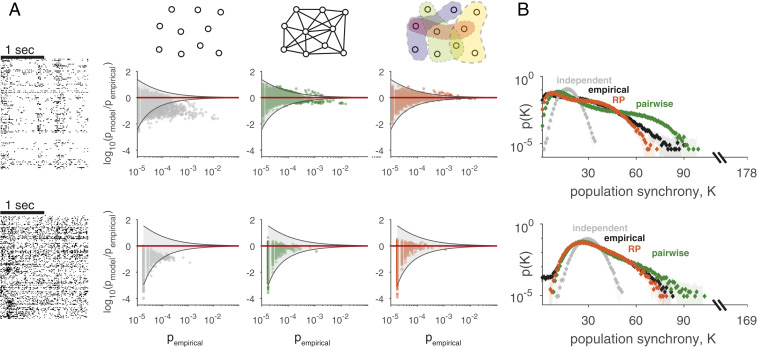
The RP model gives an excellent description of the joint activity patterns of large groups of cortical neurons and generalizes from training samples to estimate the likelihood of test data: Fig. 2A shows a short segment of spiking patterns of the jointly recorded population activity of 178 neurons from the macaque monkey visual cortex (V1/V2) under anesthesia while moving gratings were presented in the neurons’ receptive fields and a segment of 169 neurons from the prefrontal cortex while the monkey performed a visual discrimination task. We first evaluated the models on smaller groups of neurons (70 cells from the visual cortex and 50 cells from the prefrontal cortex), where we can directly test the validity of the model because individual activity patterns still repeat. We found that models using 2,000 RPs (fit on training data) were highly accurate in predicting the frequency of individual population activity patterns in test data. These populations were strongly correlated as a group, which is reflected by the failure of an independent model that ignores correlations (Fig. 2 A, Left): many of its predicted frequencies were outside the 99% CI for pattern frequencies (gray funnel), with errors commonly being one or two orders of magnitude. In contrast, maximum entropy models that use pairwise constraints (17, 18, 40) were considerably better (Fig. 2 A, Center), and RP models were superior with a smaller number of parameters (compared with the pairwise models). For the entire populations of 178 and 169 neurons, where individual activity patterns were so rare that they did not repeat during the experiment, we evaluated how closely models predict summary statistics of the experimental data. RP models were highly accurate in predicting synchrony (23) in the experimental data (Fig. 2B and SI Appendix, Fig. S4C) and high-order correlations (SI Appendix, Fig. S1), which the RP models were not built explicitly to capture.

Fig. 2.

RP models accurately predict the probability of population activity patterns. (A) Accuracy of different population models in capturing the frequencies of individual population activity patterns in test data from 70 neurons in the monkey visual cortex (Upper) or 50 neurons from the monkey prefrontal cortex (Lower): we compare likelihood ratio of models and test data for an independent model (Left), pairwise maximum entropy model (Center), and RP model (Right). Gray funnels denote 99% CIs of the likelihood ratio resulting from sampling fluctuations. (B) Probability of observing the simultaneous activation of K neurons (population synchrony) in a population of 178 neurons from the primate visual cortex (Upper) and 169 neurons from the primate prefrontal cortex (Lower) in test data and model predictions.

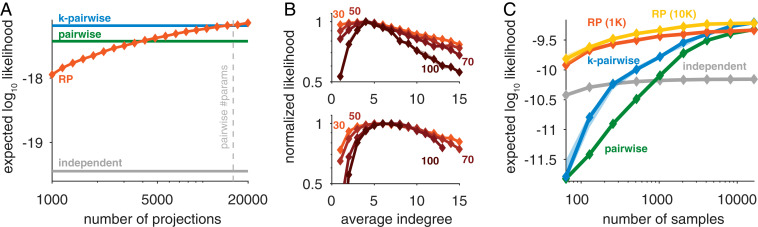
Randomly connected circuits have been successfully used in computational models of neural function, such as classification (11, 41, 42), associative memory (43), and novelty detection (31). More broadly, random projections have been effective for signal reconstruction (44–46). Here, in addition to superior performance, random connectivity also allows for greater flexibility of the probabilistic model: since the projections in the model are independent samples of the same class of functions, we can simply add projections (corresponding to adding intermediate $h_i$ neurons in a randomly connected circuit) to improve the accuracy of the model. This allows using as many or as few projections as required, in contrast to pairwise and higher-order correlation-based models that are difficult to scale to very large populations (22, 47). Indeed, the RP models improve monotonically with the number of projections and become on par with or better than state-of-the-art models, but with fewer parameters (23), as reflected by both the likelihood of test data of large populations (Fig. 3A and SI Appendix, Fig. S2A) and direct comparisons in small networks (SI Appendix, Fig. S2C). In our experimental data, we found that capturing activity patterns from the prefrontal cortex generally required fewer RPs than patterns from the visual cortex (SI Appendix, Fig. S5A). Since each RP corresponds to a parameter in the probabilistic model, it is important to select fewer projections than training data or risk overfitting (SI Appendix, Fig. S2A).

Fig. 3.

Scalability, optimal sparseness, and efficiency of the RP models. (A) Expected likelihood of RP models for held-out data of individual population activity patterns of 178 neurons in the visual cortex (SI Appendix, Fig. S2A) as a function of the number of projections used in the model (trained using 100,000 samples). Plotted values are median model performance over random choices of projections and divisions of train/test data (error bars are smaller than the marker size) (SI Appendix, Fig. S2D shows a zoomed-in version). (B) Performance of RP models (expected likelihood normalized to a maximum value of one) with different average indegrees (number of incoming connections) of the intermediate neurons, for the visual cortex (Upper) and for prefrontal cortex (Lower), each trained using 100,000 input activity patterns. Different curves denote different sizes of input populations, as denoted on each curve. (C) Expected likelihood of RP trained on population activity patterns of 100 neurons from the monkey visual cortex (SI Appendix, Fig. S2B) as a function of the number of samples in the training data, for RP models using 1,000 RPs (RP 1K), 10,000 RPs (RP 10K), pairwise, k-pairwise, and independent models.

The performance of the RP models has very little variance for different randomly chosen sets of projections (SI Appendix, Fig. S2D), reflecting that the exact sets of RPs used in each model are unimportant and can be replaced. Different choices of generating the RPs $a_{i,j}$ had little effect on the model performance (SI Appendix, Fig. S3A), and RP models using other classes of random functions we tested were inferior to those using Eq. 1 (SI Appendix, Fig. S3B). When applied to noise-corrupted activity patterns, the surprise predicted by RP models increased in proportion to the magnitude of the noise (SI Appendix, Fig. S6).

We found that for populations of different sizes, RP models were most accurate when the projections were sparse in terms of the number of $a_{i,j}$ weights that were not zero, corresponding to neural circuits with a low average “indegree” of their intermediate layer. Thus, sparseness, which has been suggested as a design principle for neural computation (42, 48), emerges in the RP models as their optimal operational regime. The optimal average indegree value ranged between $\sim 4$ for the prefrontal cortex to $\sim 7$ for the visual cortex and was surprisingly independent of the number of neurons in the population (Fig. 3B). Interestingly, these results are consistent with theoretical predictions and anatomical observations in the rat cerebellum (41) and the fly mushroom body (49).

A particularly important quality of the RP models, which is of key biological relevance, is their accuracy in learning the probabilities of input patterns from a severely undersampled training data. This would affect how quickly a neural circuit could learn from examples an accurate representation of its inputs. Fig. 3C shows large differences in the performance of pairwise maximum entropy and RP models (SI Appendix, Fig. S2E), when the sample size is of only a few hundred samples. Pairwise-based models (and even more so triplet-based models, etc.) fail for small training sets because estimating pairwise correlations with limited samples is extremely noisy when the input neurons are mostly silent. In contrast, the linear summation in the random functions of the RP models means that they are estimated much more reliably with a small number of samples (SI Appendix, Fig. S3B). As a result, even when the neural code can be captured equally well by the RP and pairwise models, the RP model often requires fewer samples to obtain the same performance (Fig. 3C and SI Appendix, Fig. S2B).

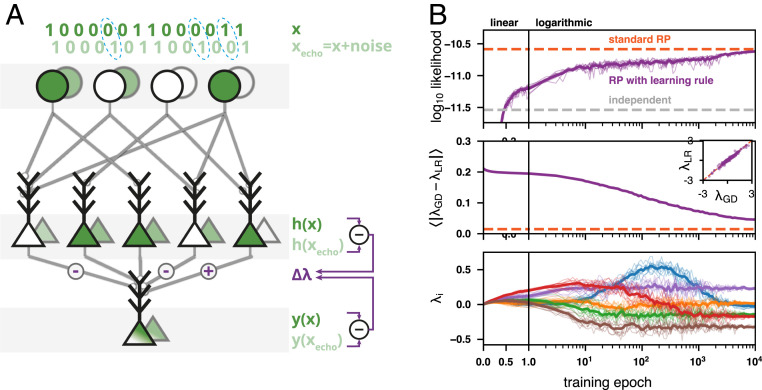
The RP models we presented thus far were trained using standard numerical algorithms based on incremental updates (39), which are nonbiological in terms of the available training data and the computations performed during learning. As we demonstrate below, we can find learning rules for RP models that are simple, biologically plausible, and local. While other biologically inspired learning rules may exist, the one we present here is particularly interesting since noise in the neural circuit is the key feature of its function. Our local learning rule relies on comparison of the activity induced in the circuit by its input $\overrightarrow{x}$ with the activity induced by a noisy version of the input. This “echo” pattern, ${\overrightarrow{x}}_{echo}$, would result from weak and independent noise that may affect each of the input neurons $\left\{x_i\right\}$, such that $\overrightarrow{x}$ and ${\overrightarrow{x}}_{echo}$ would differ by 1 to 2 bits on average (SI Appendix has details). Both $\overrightarrow{x}$ and ${\overrightarrow{x}}_{echo}$ are each propagated by the circuit’s feed-forward connectivity and may result in different activation of the intermediate neurons. If an intermediate neuron is activated only in response to the input but not by the noisy echo, its synapse to the output neuron is strengthened (Fig. 4A); when the converse is true, the synapse is weakened. The updates are scaled by the ratio of the output neuron’s membrane potential $y$ in response to the input and its noisy echo. This is concisely summarized in a single learning rule for each of the synapses connecting to the output neuron:

$$\frac{\partial {\lambda }_i}{\partial t}=\exp \left[\frac{y\left(\overrightarrow{x}\right)-y\left({\overrightarrow{x}}_{echo}\right)}{2}\right]\left(h_i\left(\overrightarrow{x}\right)-h_i\left({\overrightarrow{x}}_{echo}\right)\right),$$ [3]

and so, the change in synaptic weights depends only on the pre- and postsynaptic activity generated by the most recent input and its echo. This implies that the neural circuit responds with the surprise of its input while simultaneously updating its internal model to account for this input, which also means it can naturally adapt to changing statistics of the input distribution.

Fig. 4.

A local biologically plausible learning rule (LR) for the RP models based on neural noise gives highly accurate models. (A) An LR that trains a circuit to respond with the surprise of its input activity patterns by comparing the response to the input pattern (foreground) with the response to a weakly noisy echo of the input pattern (background). Each synaptic weight is modified according to the differences in activity in the presynaptic neuron, scaled by the relative membrane potentials of the output neuron. (B) RP model trained with the LR and standard gradient descent (GD) on population activity patterns of 100 neurons by repeatedly presenting epochs of the same 100,000 activity patterns. Bold curves denote average over 10 realizations of learning, each plotted in lighter color. (Top) Mean log likelihood of test data under the model (dashed orange: model trained with standard GD; dashed gray: independent model). (Middle) Mean difference in synaptic weights between the LR and standard GD (dashed orange: average difference across multiple realizations of standard GD). Inset shows final values of the individual synaptic weights when learned with the LR vs. standard GD. (Bottom) Example of six individual synaptic weights as they are modified across training epochs. For clarity, the plot uses a linear scale on the x axis for the first epoch and a logarithmic scale afterward.

The learning rule induces synaptic weight changes that implement a stochastic gradient descent on the RP model weights. In contrast to classical gradient descent-based methods, which apply the gradient of the likelihood of training data (Materials and Methods), the rule we present here is a biological implementation of stochastic gradient descent on the minimum probability flow (50) objective function (SI Appendix has details and derivation). In this implementation, the neural noise crucially allows the neural circuit to compare the surprise of observed activity patterns with that of unobserved ones, where the goal is to decrease the former and increase the latter. Although the learning rule is an adaptation of a convex optimization method, its form is similar to that of noise-perturbation methods for reinforcement learning (51, 52), which also rely on comparing between the circuits’ response to clean and noisy signals. Unlike the traditional roles of noise in computational learning theory for avoiding local minima (53, 54) or finding robust perturbation-based solutions (10), here it is the central component that actively drives learning. While the echo mechanism underlying the learning rule resolves the issues of locality and credit assignment, which are the two major obstacles to biological plausibility of learning deep neural networks, its exact implementation details are not fully addressed here (SI Appendix has some conceptual ideas) and remain a topic for future work.

Neural circuits trained using the learning rule of Eq. 3 reached a performance close to that of identical circuits (i.e., the same RPs) trained with the nonbiological standard gradient descent approach (Fig. 4 A, Top), with closely matching synaptic weights (Fig. 4 B, Middle). Notably, training the model for a single epoch already yielded a performance significantly higher than the independent model. These models also accurately captured high-order correlations (SI Appendix, Fig. S7A) and the distribution of population synchrony (SI Appendix, Fig. S7B). When trained with severely undersampled data, the performance of RP models trained with the learning rule was comparable with that of the standard pairwise model (SI Appendix, Fig. S7C).

The RP model can be further improved in terms of both its performance and biological realism by training it using Eq. 3 while periodically discarding projections with a low value of $\left|{\lambda }_i\right|$ and replacing them with new projections that were selected either randomly (SI Appendix, Algorithm 1) or in such a way that maximizes their predictive contribution (SI Appendix, Algorithm 2). In the equivalent neural circuit, this corresponds to pruning weak synapses to the output neuron (as reported by ref. 55) and creating new connections to previously unused parts of the circuit. We found that this simple pruning and replacement of synapses resulted in more compact models, where the performance increases primarily when the model has few projections (Fig. 5A and SI Appendix, Fig. S8A). The pruning, in effect, adapts the RPs to the statistics of the input by retaining those that are more informative in predicting the surprise. Although each intermediate neuron still computes a random function, the set of functions observed after training is no longer drawn from the initial distribution but is biased toward the informative features. As a result, the intermediate units that are retained have lower firing rates and are more decorrelated from each other (Fig. 5B and SI Appendix, Fig. S8B). Thus, when neural circuits learn to compute the surprise of their inputs, pruning weak synapses would result in a more efficient, sparse, and decorrelated activity as a side effect.

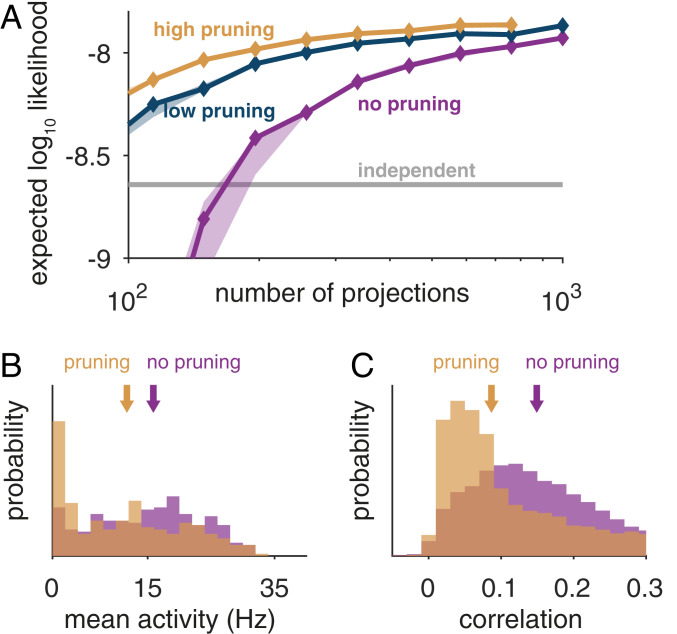
Fig. 5.

Improved RP models using synaptic pruning and replacement. (A) Expected log likelihood of RP models trained with the local learning rule on population activity patterns of 70 neurons from the monkey visual cortex (similar results for the prefrontal cortex are in SI Appendix, Fig. S8A) while periodically pruning weak synapses and replacing them with new randomly chosen projections. Curves denote the performance of models trained with different total average number of replacements per synapse (low: two; high: eight). (B) Average firing rates and (C) Pearson correlations of intermediate units $h_i$ in models trained with the learning rule with (orange) or without (purple) pruning and replacement; arrows denote median values.

Discussion

The RP models suggest a simple, scalable, efficient, and biologically plausible unsupervised building block for neural computation, where a key goal of neural circuits is to generalize from past inputs to estimate the surprise of new inputs. We further presented an autonomous learning mechanism that allows randomly connected feed-forward circuits of spiking neurons to use structure in their inputs to estimate the surprise. These neural circuits can be interpreted as implementing probabilistic models of their inputs that are superior to state-of-the-art probabilistic models of neural codes, while providing greater flexibility and simple scaling to large populations. Our biologically plausible learning rule reweights the connections to an output neuron to maximize the predictive contributions of intermediate neurons, each serving as a random feature detector of the input activity. Relying on noise as a key component, it is a completely local process that operates continuously throughout the circuit’s normal function and corresponds to a stochastic gradient descent implementation of a known machine learning algorithm. Neural circuits trained this way exhibit various properties similar to those observed in the nervous system: they perform best when sparsely connected and show sparse and decorrelated activity as a side effect of pruning weak synapses.

Therefore, the RP model gives a unified solution for three key questions, which have mostly been studied independently of one another: 1) a network architecture that can learn to compute the likelihood of its own inputs; 2) a statistical model that accurately captures the spiking patterns of very large networks of neurons in the cortex, using little training data; and 3) a shallow network design that allows for a biologically plausible learning rule based on noise.

The estimation of surprise that underlies the RP model also suggests an alternative interpretation to common observations of neural function: feature selectivity of cells would correspond to responding strongly to a stimulus that is surprising based on the background stimulus statistics, and neural adaptation would signify a change in surprise based on the recently observed stimuli (56). While we focused here on shallow and randomly connected circuits, the local scope of learning in these models also implies they would work in other neural architectures, including deeper networks with multiple layers or networks lacking a traditional layered structure. In particular, we speculate that this would be compatible with networks where the intermediate connectivity is adjusted by a separate process such as back propagation in deep neural networks. Importantly, relying on the existing random connectivity as random feature detectors simplifies and accelerates the learning process, and the emerging representations are efficient and sparse (16, 25, 48) without explicitly building this into the model.

The RP model also naturally integrates into Bayesian theories of neural computation: because learning involves only modifying the direct connections to an output neuron, multiple output neurons that receive inputs from the same intermediate layer can each learn a separate model over the stimuli. This could be accomplished if each readout neuron would modify its synapses based on some teaching signal only when particular input patterns or conditions occur, thus giving a probabilistic model for new inputs, conditioned on the particular subset of training ones. Thus, comparing the outputs of the readout neurons would give, for example, a Bayes-optimal classifier at the cost of a single extra neuron per input category (SI Appendix, Fig. S9A). Dopamine, which has already been implicated in learning mechanisms and the prediction of outcomes (57, 58), would be one possible candidate for such a teaching signal that selectively switches learning on and off based on external outcomes.

While randomly connected architectures have been used as a general basis for learning (59), we have found that they have especially attractive properties when applied to the neural code: the sparseness of projections, decorrelated representation by intermediate neurons, the reusable set of RPs, and the robustness of the model. The emergence of this set is both surprising and appealing, especially because they were neither required nor actively sought for in the design of the model. Each of these features has been suggested as a “design principle” of the neural code before, but here, we show their joint emanation in the responses of cortical populations—using statistical models that capture population response patterns and without using classical approaches for characterizing them. The similarity in the model’s parameters for visual and prefrontal cortex recordings suggests that the RP model captures some universal properties of the structure of the code of large neural populations. Particularly interesting are the optimal values of the indegree of the projections (a hyperparameter of the model), which generalize across datasets.

Finally, we reiterate that other, possibly more accurate, biological implementation of the models we presented may exist. The learning rule, noise-driven echo patterns, and pruning of projections are all specific suggestions of how the RP model may be implemented in the brain. In particular, the exact biological implementation of the echo patterns was not fully addressed here. Other local learning mechanisms (e.g., ref. 12) can potentially achieve the same goal, utilizing the power of shallow networks. A more detailed biological implementation of these models could also address the impact and potential role of recurrent connections, which we speculate may aid in making predictions about surprise in a dynamically changing environment.

Materials and Methods

Experimental Data.

We tested our models on extracellular recordings from neural populations of the prefrontal and early visual cortices of macaque monkeys. All experimental procedures conformed to the National Research Council’s Guide for the Care and Use of Laboratory Animals (60) and were approved by the New York University Animal Welfare Committee. For recordings from the visual cortex, we implanted 96-channel microelectrodes arrays (Utah arrays; Blackrock Microsystems) on the border of the primary and secondary visual cortices (V1 and V2) of macaque monkeys (Macaca nemestrina) such that the electrodes were distributed across the two areas. Recording locations were chosen to yield overlapping receptive fields with eccentricities around $5^{○}$ or less. During the experiment, monkeys were anesthetized with sufentanil citrate (4 to 6 $\mathrm{\mu }$g/kg per hour) and paralyzed with vecuronium bromide (Norcuron; 0.1 mg/kg per hour), while drifting sinusoidal gratings were presented monocularly on a CRT monitor (61, 62). Recordings from the prefrontal cortex were obtained by implantation of 96-channel Utah arrays in the prearcuate gyrus (area 8Ar) of macaque monkeys (Macaca mulatta). During the experiments, monkeys performed a direction discrimination task with random dots (63, 64). Neural spike waveforms were saved online (sampling rate, 30 kHz) and sorted offline (Plexon Inc.). Throughout the paper, we use the term “units” to refer to both well-isolated single neurons and multiunits. Models were fitted in each case to the population activity during all trials, regardless of their difficulty level (for the prefrontal recordings), and over all stimulus-induced activity, regardless of the gratings direction or size (in the V1 and V2 data).

Data Preprocessing.

Neural activity patterns were discretized using 20-ms bins. Models were trained on randomly selected subsets of the recorded data (training set), the number of samples of which is described in each case in the text. The remaining data were used to evaluate the model performance (held-out test set).

Construction of RPs.

The coefficients $a_{i,j}$ in the RPs $h_i=g\left({\sum }_{j=1}^n{a}_{i,j}{x}_j\right)$ underlying the RP models were randomly set, using a two-step process. First, we used a predetermined sparseness value to decide the average number of nonzero values (indegree) for each projection, picked them randomly and independently with probability $p=\frac{\text{indegree}}{n}$ (where n is the total number of neurons in the input layer), and set the remaining coefficients to zero. The values of the nonzero elements were then drawn from a Gaussian distribution $a_{i,j}\sim N\left(\mathrm{1,1}\right)$. The models were not sensitive to different variants of the selection process of $a_{i,j}$ (SI Appendix, Fig. S3A).

In the results shown in the text, we used indegree values in the range of four to seven (Fig. 3B shows the effect of different indegree values on the model performance) and set $g$ to be a threshold function (SI Appendix, Fig. S3B shows other choices of random functions).

Although the threshold ${\theta }_i$ of each individual projection neuron can be tuned separately, in the results shown in the text we used a fixed threshold value of $0.1\cdot indegree$ for models trained on the prefrontal cortex and $0.05\cdot \text{indegree}$ for models trained on the visual cortex. The models were not sensitive to changes in these values.

Training Probabilistic Models with Standard Gradient Descent.

We trained the probabilistic models by seeking the parameters ${\lambda }_i$ that would minimize the Kullback–Leibler divergence between the model $\widehat{p}\left(\overrightarrow{x};\overrightarrow{\lambda }\right)$ and the empirical distribution $p_{emp}\left(\overrightarrow{x}\right)$. This is equivalent to maximizing the log likelihood of

$$L\left(\overrightarrow{\lambda }\right)=\sum _{\overrightarrow{x}}{p}_{emp}\left(\overrightarrow{x}\right)\log \widehat{p}\left(\overrightarrow{x};\overrightarrow{\lambda }\right),$$

which is a concave function whose gradient is given by

$$G\left(\overrightarrow{\lambda }\right)={⟨\overrightarrow{h}\left(\overrightarrow{x}\right)⟩}_{p_{emp}}-{⟨\overrightarrow{h}\left(\overrightarrow{x}\right)⟩}_{\widehat{p}\left(\overrightarrow{x};\overrightarrow{\lambda }\right)}.$$ [4]

We found the values ${\lambda }_i$ that maximize the likelihood by iteratively applying the gradient (Eq. 4) with Nesterov’s accelerated gradient descent algorithm (65). We computed the empirical expectation in Eq. 4 (left-hand term) by summing over the training data and the expectation over the parameters ${\overrightarrow{\lambda }}^{\left(j\right)}$ by summing over synthetic data generated from $\widehat{p}\left(x;{\overrightarrow{\lambda }}^{\left(j\right)}\right)$ using Metropolis–Hasting sampling.

For each of the empirical marginals ${⟨h_i\left(\overrightarrow{x}\right)⟩}_{p_{emp}}$, we used the Clopper–Pearson method to estimate $\left({⟨h_i\left(\overrightarrow{x}\right)⟩}_p|{⟨h_i\left(\overrightarrow{x}\right)⟩}_{p_{emp}}\right)$: the distribution of possible values for the real marginal given the empirical observation. We set the convergence threshold of the numerical solver such that each of the marginals in the model distribution falls within a CI of one SD under this distribution, from its empirical marginal. After learning the parameters of the different models, we normalized them using the Wang–Landau algorithm (66) in order to compute the likelihood of the test data given the model.

We compared the RP model with the independent model, the pairwise maximum entropy model, and the k-pairwise maximum entropy model. The independent model is the maximum entropy model constrained over the mean activities $⟨x_i⟩$, which treats neurons as independent encoders. The pairwise maximum entropy model (17) is the probability distribution with maximum entropy constrained over

$$⟨x_i⟩\text{and}⟨x_i{x}_j⟩.$$

The k-pairwise model (23) uses the same constraints as the pairwise model, adding $n+1$ synchrony constraints:

$$⟨x_i⟩\text{and}⟨x_i{x}_j⟩\text{and}⟨{\sum }_i{x}_i=K⟩.$$

We learned the parameters of the pairwise and k-pairwise models with the same numerical solver used to learn the RP model and the parameters of independent model by using its closed-form solution. The code used to train the models is publicly available (67) as an open-source MATLAB toolbox: https://orimaoz.github.io/maxent_toolbox/.

Markov Chain Monte Carlo (MCMC) Sampling.

Synthetic data sampled from the probabilistic models (used in Fig. 2B and SI Appendix, Figs. S1, S4C, and S7 A and B) were generated using Metropolis–Hastings sampling, where $n$ proposal bit flips were made between samples ($n$ denoting the number of bits in the pattern). The first 10,000 samples were discarded (“burn-in”), and every subsequent 1,000th sample was used in order to reduce sample autocorrelations.

Training RP Models with the Learning Rule.

We trained the RP models with the learning rule by iteratively applying the gradient in Eq. 3:

$$\mathrm{\Delta }\overrightarrow{\lambda }=-\eta \exp \left[\frac{y\left({\overrightarrow{x}}^{\left(t\right)}\right)-y\left({\overrightarrow{x}}_{echo}^{\left(t\right)}\right)}{2}\right]\left(\overrightarrow{h}\left({\overrightarrow{x}}^{\left(t\right)}\right)-\overrightarrow{h}\left({\overrightarrow{x}}_{echo}^{\left(t\right)}\right)\right),$$

where ${\overrightarrow{x}}^{\left(t\right)}$ is the joint input to the circuit at time $t$, and $\overrightarrow{h}\left({\overrightarrow{x}}^{\left(t\right)}\right)$ are the concatenated responses of the intermediate neurons $h_1\dots h_k$ (in the text). We note that $h$ and $y$ can be written in vector form using a matrix $A$ consisting of the synaptic weights $a_{i,j}$:

$\overrightarrow{h}\left({\overrightarrow{x}}^{\left(t\right)}\right)=g\left(A\cdot {\overrightarrow{x}}^{\left(t\right)}-\overrightarrow{\theta }\right)$ and $y\left({\overrightarrow{x}}^{\left(t\right)}\right)={\overrightarrow{\lambda }}^T\overrightarrow{h}\left({\overrightarrow{x}}^{\left(t\right)}\right)$.

Training was performed over multiple epochs, with the same training data presented on each epoch and ${\overrightarrow{x}}_{echo}^{\left(i\right)}$ randomly chosen from the training data in each step. The learning rate $\eta$ was set at 0.005 at the first epoch and gradually scaled to 0.00005 in the last epoch, and it was normalized by a running average of the gradient norm for numerical stability.

Training Models with Synaptic Pruning and Replacement.

To train models with synaptic pruning and replacement, we applied the learning rule with the training data for 10 epochs with decreasing learning rate and then discarded the five projections whose learned values ${\lambda }_i$ were closest to zero. We then replaced these discarded projections with new ones either randomly (SI Appendix, Algorithm 1) or in such a way that would maximize the mismatch between the model and the training data (SI Appendix, Algorithm 2). This process was repeated until the desired numbers of projections were replaced. The performance of these models was not sensitive to different numbers of epochs used or discarded projections.

RP Model.

Code for training the RP model, as well as other models such as pairwise and k-pairwise, is available in the form of a MATLAB toolbox and can be obtained from https://orimaoz.github.io/maxent_toolbox/.

The software can be download in binary form (for 64-bit Windows, MacOS, or Linux) and directly installed as a toolbox for MATLAB. A specific example of using the toolbox to train an RP model is at https://orimaoz.github.io/maxent_toolbox/maxent_example.html#4.

Learning Rule.

MATLAB code demonstrating the learning rule can be obtained from GitHub (https://github.com/orimaoz/rp_learning_rule).

This code makes use of the matlab_toolbox described above.

Data Availability.

The datasets and a sample script that trains an RP model on the data are available in the Kiani Lab repository (https://www.cns.nyu.edu/kianilab/Datasets.html).