Significance
Imagine you are deciding between two goods: A is simple but inexpensive, B is luxurious but more costly. Introducing a less advantageous option (e.g., lower quality than A, same price) should not alter your choice between A and B. However, this principle is often violated; three classic biases known as “decoy effects” have been identified, each describing a stereotyped choice pattern in the presence of irrelevant information. Through behavioral testing in human participants and computer simulations, we show that these decoy effects are special cases of a wider principle, whereby stimulus value information is encoded in a relative, rather than an absolute, format. This work clarifies the origin of three behavioral phenomena that are widely studied in psychology and economics.
Keywords: decision-making, cognition, human behavior, consumer choice
Abstract
Human decisions can be biased by irrelevant information. For example, choices between two preferred alternatives can be swayed by a third option that is inferior or unavailable. Previous work has identified three classic biases, known as the attraction, similarity, and compromise effects, which arise during choices between economic alternatives defined by two attributes. However, the reliability, interrelationship, and computational origin of these three biases have been controversial. Here, a large cohort of human participants made incentive-compatible choices among assets that varied in price and quality. Instead of focusing on the three classic effects, we sampled decoy stimuli exhaustively across bidimensional multiattribute space and constructed a full map of decoy influence on choices between two otherwise preferred target items. Our analysis reveals that the decoy influence map is highly structured even beyond the three classic biases. We identify a very simple model that can fully reproduce the decoy influence map and capture its variability in individual participants. This model reveals that the three decoy effects are not distinct phenomena but are all special cases of a more general principle, by which attribute values are repulsed away from the context provided by rival options. The model helps us understand why the biases are typically correlated across participants and allows us to validate a prediction about their interrelationship. This work helps to clarify the origin of three of the most widely studied biases in human decision-making.
The best decisions are made by focusing on information that is relevant for the choice. When deliberating among more than two options (“multialternative” choices), this means ignoring those alternatives that are inferior or unavailable. Thus, the choice between two consumer goods should not be affected by the introduction of an unaffordable third option, and preferences between two electoral candidates should not change when a third contender with more dubious merit enters the race. This normative principle, which is enshrined in the axiom of regularity (1, 2), is of great interest to behavioral scientists because it is robustly violated by humans (3–5), monkeys (6), and other animals including amphibians (7), invertebrates (8), and, apparently, even unicellular organisms (9). Where choice alternatives are characterized by two value dimensions (e.g., the price and quality of a product, or the likeability and competence of a political candidate), the introduction of an irrelevant distracter item to the choice set leads to rich and stereotyped biases in decision-making. A major research goal in psychology and economics has been to identify a simple and elegant computational principle that can explain the biases provoked by an irrelevant “decoy” stimulus (10).
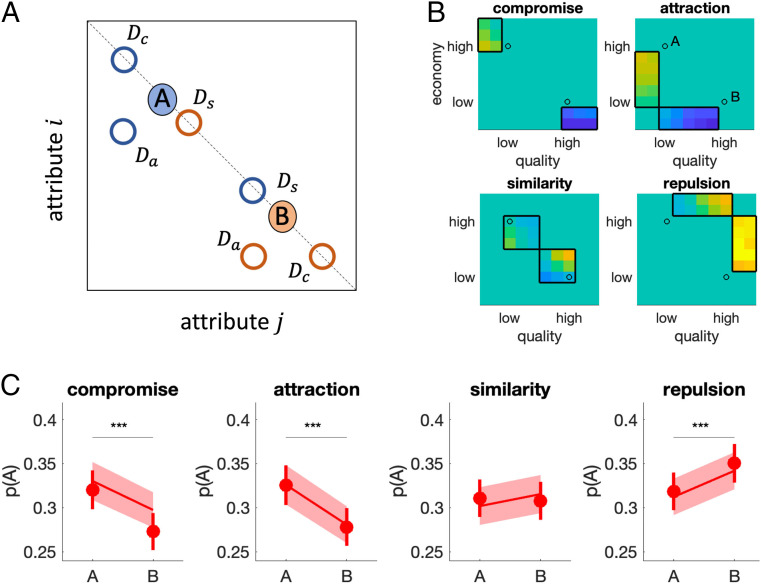
The literature has focused on three decoy effects that can arise during ternary (three-way) choice among alternatives characterized by two independent and equally weighted attributes. The phenomena are illustrated in Fig. 1A. Consider a consumer choosing among three products that are each characterized by dimensions (attributes) of quality and economy. The axes in Fig. 1A are scaled such that these attributes are perfect substitutions, in that the consumer will forego one unit of one attribute for one unit of the other. Two target items A and B lie on the line of iso-preference, which is perpendicular to the identity line. In other words, A is less expensive but lower quality than B, such that the consumer should be indifferent between these options. The empirical phenomena describe how preferences may be biased toward either A or B as a function of a third “decoy” item D that lies on or below the iso-preference line. The consensus view states that a bias toward A can be provoked by the inclusion of a decoy that it dominates, that is, where A (but not B) is equivalent or superior on both dimensions (the attraction effect); that a bias toward A occurs in the presence of a more extreme decoy which is superior in quality but more expensive than A, making A the “compromise” option (the compromise effect); and that a bias toward A is incurred by a decoy which is similar to B in price and quality (the similarity effect) (Fig. 1A).
Fig. 1.
Decoy effects. (A) Illustration of the attraction, compromise, and similarity effects. A and B denote two equally preferred stimuli; A is strong on attribute but weak on attribute and vice versa for B. The introduction of decoy stimuli (rings; denoted , and ) can bias preferences toward either A or B. The color of each ring signals the direction of the bias, for example, for blue rings, A is preferred. Stimuli falling on the dashed line are iso-preferred. (B) Illustration of the chosen locations in decoy space for , , , and (boxes) and the blue−yellow color scale relative preference for target A over B (warmer colors) or vice versa (colder colors) at each location. Black circles indicate the locations of targets A and B. (C) Average choice share for target A as a function of decoy location. Red dots are human data, and shaded lines are model fit of adaptive gain model (see below). Bars/shaded area signal SEM *** indicates P < 0.001.
These three phenomena have been a major object of study in psychology and behavioral economics for several decades, and, in particular, since the 2001 landmark study that proposed the first unified computational account of the three classic decoy effects (11). Since then, there has been a proliferation of empirical results and a plethora of computational explanations, including models that rely on loss aversion (12), pairwise normalization (13), attentional weighting (14–17), lateral inhibition (14), associative biases (15), power-law transformation of attribute values (15), sampling from memory (18, 19), or various other forms of reference-dependent computation (20–23). However, there has been a notable lack of consensus about the computational principles that give rise to decoy effects (10). There are a number of potential reasons for this, but here we focus on one limitation of past studies: Most have tested for decoy effects by selecting fixed attribute values for , , and and calculating for each the relative choice share (RCS) for target items A and B, with relative deviations from choice equilibrium signaling a bias indicative of the successful detection of a decoy effect. However, reducing the dimensionality of the data in this way (i.e., to six data points) makes it harder to distinguish theoretical accounts, as many models may mimic one another in successfully capturing the phenomena, so that comparisons among models are reduced to questions of a priori plausibility and parsimony. Relatedly, what defines a “decoy” of each class is typically left largely to the discretion of the researcher, who is free to choose a priori the values for , and —that is, the space over which the attraction, compromise, or similarity might occur. This, coupled with the fact that the effects are often studied in small participant cohorts, using diverse stimulus materials—consumer choices, text-based vignettes, or perceptual judgments (24)—has led to disagreement over the provenance and reliability of the three effects (25–28).
Here, we address these issues by conducting a large-scale (n > 200), incentive-compatible study in which we systematically map the decoy influence across attribute space, calculating the for each decoy with attribute values and . This allows us to explore the dimensionality of the data, with a view to asking whether a single principle can explain the ensemble of reported decoy effects. We find that a remarkably simple model, which draws on a computational framework that we have described previously (22), can capture the full decoy influence (RCS) map. Critically, the model suggests that the three canonical decoy effects are not, in fact, distinct phenomena but fall naturally out of previously described dynamics of attraction and repulsion of decision values toward and away from a reference value given by the mean of available options.
Results
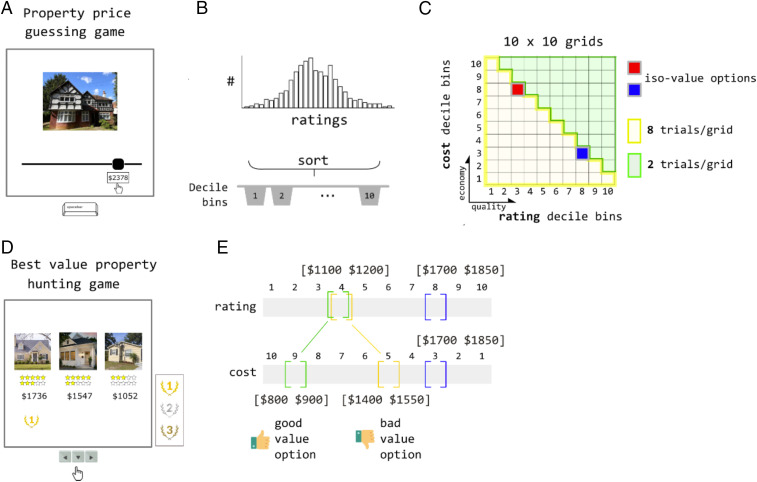
Human participants (n = 233) performed an online real estate valuation and choice game in which they decided which of three residential properties was being offered for the “best deal,” that is, for the most attractive price given its quality. In an initial (valuation) phase, participants provided their best guess of the monthly rental value for each of 500 residential properties (based on an exterior photograph; Fig. 2A). We assumed that this reported dollar value estimate is proportional to the subjectively estimated quality of the property for that participant. Inconsistent ratings were discarded, and remaining properties were binned into deciles by estimated value (Fig. 2B). This allowed us to construct choice sets for the subsequent (decision) phase consisting of three houses of known quality (attribute ) that are being rented for an independently varied monthly cost (attribute ). Using the valuation phase data, two target items were sampled with fixed price/quality ratio: one low-quality/low-cost item (the “low” item A) and one high-quality/high-cost item (the “high” item B). The third item (D) was sampled exhaustively from across the full attribute space in 10 quality × 10 economy bins (i.e., including both inferior and superior decoys; Fig. 2 C–E). Participants indicated both their first choice and then, from the remaining two items, their second choice (Fig. 2D). Measuring ranked preference in this way allowed us to chart the influence of all decoys, including superior decoys, on the RCS for A and B. Financial incentives were offered for making decisions that were consistent with their initial estimates. For all analyses, we included only participants for whom the probability that they were responding randomly was less than 0.001 (binomial test; leaving n = 189). More details about the task are provided in Methods.
Fig. 2.
Task and analysis pipeline. (A) Participants first played a “property price guessing game.” On each trial, they estimated the monthly rental value (in dollars) of a residential property, using a sliding scale. (B) After discarding properties with inconsistent responses, ratings were sorted into deciles for each participant. (C) These bins were used to select stimuli for targets A and B (deciles 3 and 8 of estimated ratings; red and blue squares), and decoy stimuli. Each choice task stimulus was created by matching a property with a given decile estimated value (quality; attribute ) to a new rental price (economy; attribute ) on a 10 × 10 grid. Eight property/price combinations were generated for each cell in the grid that lies below the diagonal (yellow cells), and two property/price combinations were generated for each cell above the diagonal (green cells). (D) Participants then played a “best value property hunting game” in which they were asked to rank three stimuli according to their economy/quality trade-off. A star rating system was used as a reminder of their previous price estimation judgment. (E) Illustration of how the initial rating and cost were paired to create good value options (above the diagonal; green), poor value options (below the diagonal, yellow), and iso-valued options (here a target option; blue).
Traditional Decoy Analysis.
We began by adopting the standard approach from previous studies that have focused on the RCS for , , and (Fig. 1). To calculate relative preference for the “low” item A over the “high” item B, we first defined portions of the influence map that corresponded to the traditionally defined positions of attraction, compromise, and similarity decoys (Fig. 1B). We also included an additional decoy set that we called “repulsion” decoys : These were mirror-symmetric to the attraction decoys but located in the upper triangle of the influence map where the decoy was the objectively best option (i.e., a set of “superior” decoys). We then calculated the RCS for , , , and , each defined with respect to target A and target B as shown in Fig. 1C. The strength of each effect is defined as the difference in RCS for each decoy set defined with respect to targets A and B.
Our first and most general observation was that, despite the careful sampling of targets that were matched in price/quality ratio according to participants’ responses in the valuation phase, and despite the incentives offered for consistent responding, participants exhibited a bias toward the “high” item B (average RCS of ∼0.7) over the “low” item A (perhaps because the ratings task focused attention on quality; see Methods). This additive bias notwithstanding, decoys still had a robust influence on choices, with clear attraction (t188 = 4.74, P < 0.001) and compromise (t188 = 6.31, P < 0.001) effects all significant and in the expected direction, as well as a repulsion effect (t188 = 3.45, P < 0.001). On average, the presence of attraction, compromise, or repulsion decoys shifted preferences from A to B by about 3 to 5% (Fig. 1C). However, the similarity effect was not significant (P = 0.65) in this dataset. Despite some strong past evidence for the similarity effect (29, 30), we are not alone in finding weak or absent effects for this decoy (19, 31).
A Map of Decoy Influence.
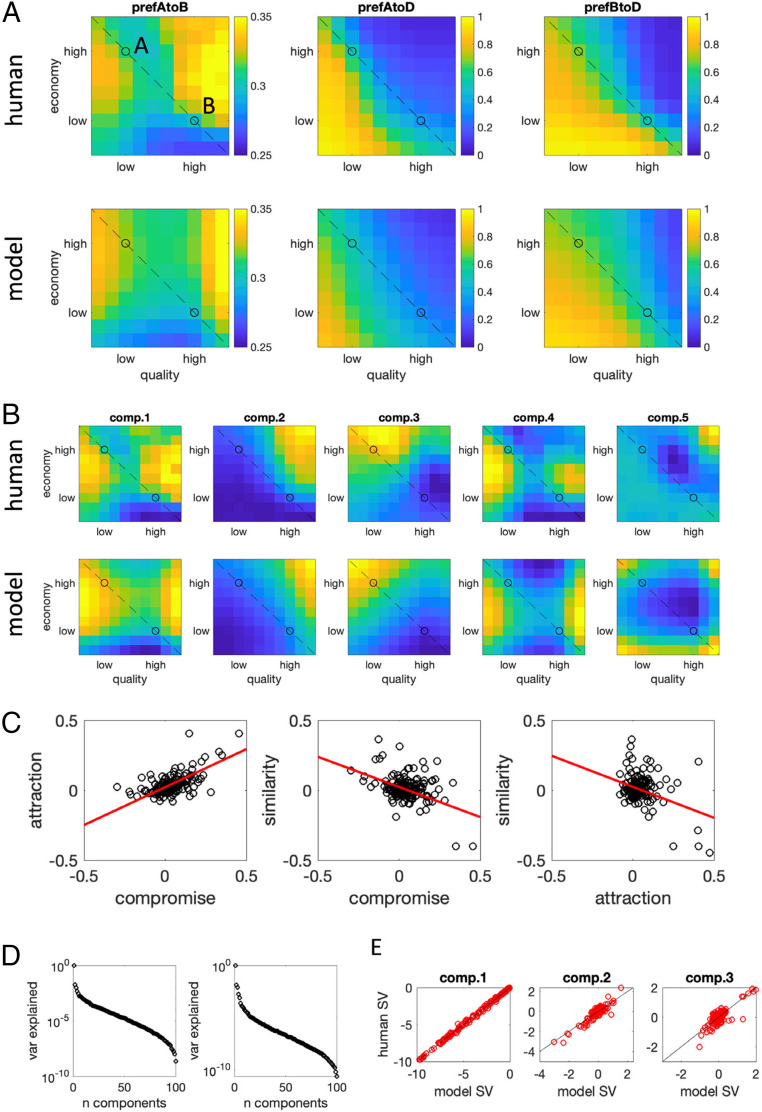
Our major goal in this project was to go beyond the conventional approach and plot the full map of decoy influence on choices between the two primary targets. This is shown in Fig. 3. Visual inspection reveals that the map has rich structure beyond the traditional decoy locations (Fig. 3 A, Top Left). Relative preferences for A and B seem to be driven by a dynamic of attraction and repulsion that depends on the position of the decoy with respect to each target stimulus. Robust “attraction” effects (whereby the presence of a decoy that is dominated by A shifts preferences toward A) were mirrored by strong “repulsion” effects (whereby a decoy that dominates A shifts preferences toward B). Attraction and repulsion were observed for both targets in approximate symmetry. We note, in passing, that, qualitatively, our results also appear consistent with a “decoy distance effect” (13, 20), whereby more eccentric decoys generate stronger effects.
Fig. 3.
(A) Decoy influence map showing for A over B (Left), A over D (Middle), and B over D (Right). (Top) The human data and (Bottom) the same data for the simulated model. The dashed line signals iso-preference, and the black circles are the targets A and B. (B) First five components obtained from SVD of the RCS for A vs. B. (Top) The human data and (Bottom) the model. (C) Correlations between the attraction, compromise, and similarity effects. Each dot is a single participant, red lines illustrate best linear fit; the decoy estimate is calculated as the difference between the RCS for given decoy with respect to targets A and B. (D) The variance (var) explained by each component obtained by SVD for (Left) the humans and (Right) the model. Note that the y axis is on a log scale; the data are dominated by the first component in both cases. (E) Correlation between singular values (SV) for components 1 to 3 between the human and the best-fitting model; each dot is a single participant, black lines illustrate best linear fit . For components 1 to 3, this correlation was very high.
Using an exhaustive range of decoy locations allowed us to use dimensionality reduction approaches to examine the (potentially distinct) factors from which the map of decoy influence is composed. We used singular value decomposition (SVD) to identify factors contributing to the map of preference for A > B and calculate the variance explained by these factors. We plot the first five factors identified in Fig. 3 B, Top. The first factor accounted for of the variance in the data, suggesting that there is a single explanatory variable that drives decoy effects across participants (Fig. 3D; note the log scale on the y axis). This is consistent with previous reports that attraction, compromise, and similarity decoys exhibit stereotyped correlations across the cohort (30, 31). Indeed, using the definitions in Fig. 1A, we plotted the correlations in influence between , , and and found that they mirrored those previously reported (31). Specifically, we observed a positive association between the attraction and compromise effects (r = 0.72, P < 0.001) and a negative relation between the similarity effect and both compromise (r = −0.59, P < 0.001) and attraction (r = −0.46, P < 0.001) effects (note that the latter correlations were observed despite the fact that, in our data, the similarity effect was, on average, nonsignificant). These are shown in Fig. 3C.
Computational Modeling.
Next, we sought to identify the simplest possible model that can reproduce the full decoy map. We note that, in previous studies, dynamic models (in which information is accumulated over time) have been able to jointly capture the attraction, compromise, and similarity effects (11, 15, 17, 32, 33), as well as accounting for other phenomena, such as the effect of time pressure on decoy decisions (34). Nevertheless, in the interests of parsimony, we focus instead on a different class of “static” model that has been used to predict decoy effects, which describes contextual biases as arising from normalization among populations of neurons. This modeling focus was informed by recent simulation work suggesting that adaptive gain control might offer a unifying explanation for choice biases (22), as well as the recent proposal of related models for decoy phenomena involving logistic (21, 35), pairwise (13), or recurrent (35, 36) normalization.
This class of model draws on a tradition proposing that decision biases occur when stimulus information is divisively normalized by the local context (37, 38),
| [1] |
where is a small regularization constant. In one successful variant of this model, this normalization is also “recurrent”; that is, it overweights the focal item’s contribution to normalization (35, 36). Thus, the subjective utility of attribute of item is computed by divisively normalizing the attribute value of attribute of item by both the mean of all three items and itself,
| [2] |
The adaptive gain model mentioned above proposes that the focal item is evaluated relative to the context mean via a sigmoidal nonlinearity or equivalent (22, 39),
| [3a] |
Thus, for each attribute, the utility of each target is given by a logistic function with slope whose inflection point is the mean value of all items (plus a bias ). The parameters and can potentially vary across attributes. We note, in passing, the resemblance with another account that deploys a logistic function for normalization (21). Connecting these models, we note that Eq. 3a is equivalent to a form of the recurrent divisive normalization model in which the values are exponentiated prior to normalization (see SI Appendix, Fig. S1 for a detailed comparison between AG and RDN),
| [3b] |
In each case, the utility of target is a weighted sum of its attributes and , and the final decision is made by passing the utilities of all three rival stimuli through a softmax function to make a ternary choice,
| [4] |
| [5] |
In addition to the softmax temperature , the model potentially has four free parameters of interest: the slope and inflection points and of the logistic function in Eq. 3a, and the weighting parameter in Eq. 4.
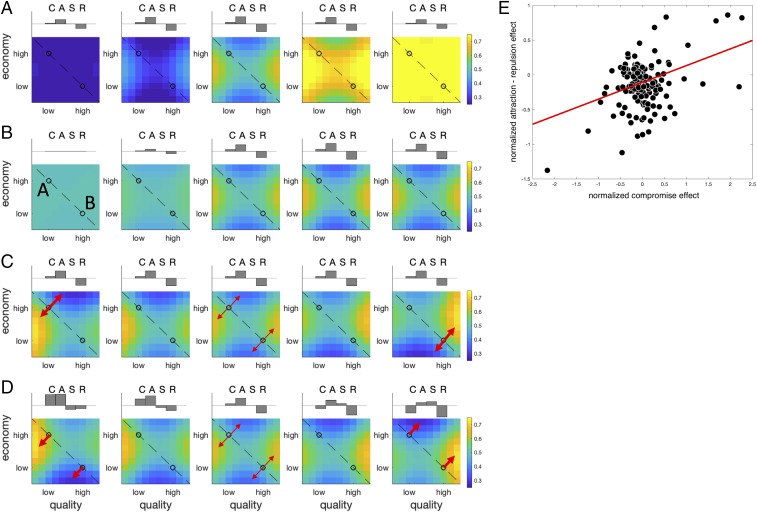
We begin with the adaptive gain model, exploring the effects of manipulating the parameters on the predicted decoy influence map in Fig. 4 (see SI Appendix, Table S1 for a full description of the parameters used). This figure shows how the model can systematically account for not only the pattern observed in the current study but also those from previous (and potentially contradictory) papers. In Fig. 4A, we show the effect of manipulating the parameter . This simply shows how we can tip the balance of responding from A to B according to the relative weight given to each attribute. In Fig. 4B, with now fixed to 0.5 (equal weighting of attributes), we show how the decoy effects grow in strength with . Above each plot, the relative positive or negative strengths of the compromise (C), attraction (A), similarity (S), and repulsion (R) effects are shown in a bar plot. As can be seen, the attraction and repulsion effects grow as grows, including a weak compromise effect but no similarity effect. Fig. 4C shows the influence of varying while and are fixed. This has the effect of shifting the relative strength of the attraction/repulsion effect for targets A and B. For example, when , the attraction/repulsion effects are strongest for the target A, whereas, when , they are strongest for B (red arrows). However, because these effects cancel out symmetrically, this does not affect the overall RCS for , , , or . Finally (Fig. 4D), varying brings about an asymmetric distortion whereby either attraction effects are stronger (i.e., below the iso-preference line) or repulsion effects are stronger (in the superior decoy portion of space). In addition to varying the relative strength of attraction and repulsion, this allows the compromise effect to vary from positive to negative, as described in previous studies; it allows a weak similarity effect to emerge. Combinations of all of these factors give the model systematic flexibility to account for a wide range of observed effects.
Fig. 4.
(A) Effect of varying the parameter from low (Left) to high (Right). The parameters used to generate each plot are shown in SI Appendix, Table S1. This parameter controls the relative preference for low price/quality to high price/quality items. (B) The effect of varying the parameter from high to low. This parameter controls whether A and B are equally preferred, or whether there is decoy-like distortion. (C) The effect of varying the difference of bias terms from negative (Left) to positive (Right). Varying this difference alters whether the maximal distortion occurs proximal to target A (Left) or target B (Right). (D) The effect of varying the sum of bias terms from negative (Left) to positive (Right). Varying this difference alters whether the maximal distortion occurs for inferior decoys (Left) or superior decoys (Right). Red arrows in C and D highlight directions of repulsion, with arrow width schematically representing the strength of the effect. The dashed line in A–D signals iso-preference, and the black circles are the targets A and B. (E) Correlation between the compromise effect and the relative strength of attraction vs. repulsion in the human data. Each dot is a participant; the red line is the best fitting linear trend.
Interestingly, the simulations shown in Fig. 4D allow us to make a prediction about the human data. As seen in the bar plots accompanying each predicted influence map, when and are both negative, the compromise effect is positive, and attraction is stronger than repulsion. By contrast, when and are both positive, the compromise effect is negative, and the repulsion effect is stronger than attraction. The model thus predicts that, on average, in the human data, there will be a correlation between the (signed) compromise effect and the relative magnitude of attraction vs. repulsion. This is plotted in Fig. 4E, and, as can be seen, this prediction holds for the data we collected (r = 0.57, P < 0.001). Of note is that this effect was driven both by a positive correlation between the compromise effect and the strength of repulsion and by the correlation between compromise and attraction effects described above (r = 0.43, P < 0.001).
In fact, to fully account for the distortions observed in the human dataset, we also need to vary , to account for the fact that participants overweighted quality relative to price during the decision phase. Fitting this five-parameter model to human data, we can fully recreate the decoy effects observed in this study using both traditional (Fig. 1) and novel (Fig. 3) analysis methods. Specifically, the model captured almost exactly the pattern of traditional decoy effects, in terms of the relative impact on RCS of , , and , as well as the repulsion decoy (red shaded lines in Fig. 1C; see also Fig. 3 A, Lower). The model reproduced the pattern of preferences for target A > target B qualitatively and quantitatively across the decoy space. Further, when we applied SVD to the model data generated under the best-fitting parameterization for each participant, the first five components that emerged were nearly identical to those for humans, and the first model component explained 97% of the variance (Fig. 3D). When we plotted the estimated singular values for the first three components for humans and the best-fitting model, we found them to be very tightly correlated (Fig. 3E). The model also displayed the same pattern of positive association between attraction and compromise effect (r = 0.86) and negative association between the similarity and attraction (r = −0.85) and similarity and compromise effects (r = −0.94) as the human data. In other words, the model captures the human data very closely, both at the individual and the aggregate level.
Model Comparison.
Finally, we compared our model to a broad space of alternative accounts based on normalization, that is, those that assume the value of each target (on each attribute) is encoded relative to its competitors. We note that fitting response times was not possible in the current project, due to the ranking procedure used to elicit preferences, precluding the comparison of dynamic models. We thus began by comparing the adaptive gain model to the vanilla and recurrent divisive normalization models described in Eqs. 1 and 2. A different class of contextual normalization model uses the range (rather than the average) of values being encoded on a given trial to normalize an imperative stimulus,
| [6] |
where corresponds to the difference between highest and lowest values of attribute across all stimuli (target or decoy) in the trial, and is a scaling term (20, 40).
We compared the fit of each of the candidate normalization accounts to adaptive gain in a direct model comparison exercise. To achieve this, we used Bayesian model selection on cross-validated model evidence. Cross-validation involved estimating model parameters from one-half of the trials (by comparing fits to preferences between target items A and B, as well as preferences between target and decoys) and computing log-likelihoods from the held-out trials. This comparison revealed that the exceedance probability for the adaptive gain model over each of the models, vanilla divisive normalization, recurrent divisive normalization, and range normalization, was 0.99, providing decisive evidence for the former over each of the latter.
However, to compare our model to a broader range of competitors, we also devised and fit a more flexible model which encompassed a large space of possible normalization schemes. This “grandmother” model could capture the encoding scheme proposed by the four models introduced above, along with a number of other “hybrid” models (see Methods). The model had the general form
| [7] |
where
| [8] |
We focus on free parameters , , and , which respectively encode the tendency to engage in asymmetric weighting of the evaluated (recurrent) item , the tendency to normalize with respect to the mean vs. range , and the extent to which inputs are compressed before being transduced . Further explanations, including derivations of adaptive gain and other normalization models nested within this account, are provided in SI Appendix.
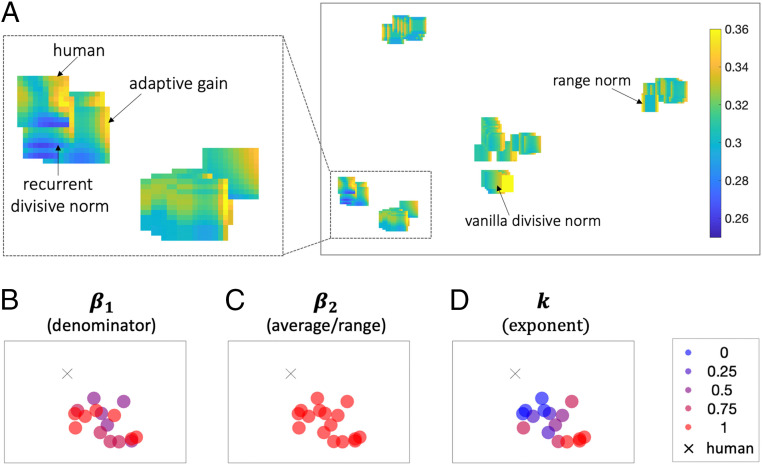
Fitting the grandmother model to human data revealed the different patterns of decoy influence predicted by variations of the general coding scheme. We used the t-distributed stochastic neighbor embedding (t-SNE) visualization technique (41) to calculate relations among the resulting decoy influence maps from 125 variations of the grandmother model, encompassing five stepwise levels of the parameters , , and . The adaptive gain, vanilla, and recurrent divisive normalization and range normalization models were nested within the grandmother model (see SI Appendix, Table S2 for parameterizations). In the resulting embedding plot (Fig. 5A), neighboring maps reflect models that produce relatively similar patterns of decoy influence (and vice versa for distant points). In Fig. 5 B–D, the points are colored according to levels of , , and , revealing the human data are neighbored by maps generated by models with high values of parameters and , that is, those that resemble the adaptive gain model.
Fig. 5.
Embedding space for normalization models of decoy effects. (A) The t-distributed stochastic neighbor visualization of the maps of decoy influence produced by different variants of the grandmother model. Each map represents a variant of the grandmother model positioned in two-dimensional space such that models with similar decoy influence patterns are nearby, while models with more different decoy patterns are farther apart. Heat maps illustrate decoy influence. (B–D) Each model-produced decoy map is denoted as a dot and color coded to indicate parameter value: (B) , (C) , or (D) . Human data are represented with a cross.
We note that the precise value of parameter , which interpolates between models implementing logistic and linear divisive normalization, is less important for fitting human data. This implies that the model is equally well fit with an exponentiated implementation of recurrent divisive normalization (, such as the adaptive gain model, Eqs. 3a and 3b) and with a power transform implementation of recurrent divisive normalization , where inputs are transformed with a power parameter prior to normalization (see SI Appendix, Eq. S4 for derivation and SI Appendix, Fig. S4 for the shape of the transfer function). We note that this formulation is conceptually analogous to a form of recurrent divisive normalization in which values are power transformed (as in ref. 35),
| [9] |
Indeed, Bayesian model selection reveals that this model fits the data equally as well as the adaptive gain model (exceedance probability for recurrent divisive normalization featuring a power transform = 0.49), suggesting that our dataset cannot arbitrate between an exponential and power transform. For completeness, we also fit another model implementing a flavor of normalization similar to power recurrent divisive normalization but differing substantially in its assumptions for how inputs are parsed, pairwise normalization (13, 42). Power recurrent divisive normalization and pairwise normalization were equally preferred by Bayesian model selection on cross-validated model evidence (exceedance probability for pairwise normalization = 0.48).
One additional question which arises from our modeling exercise is whether the adaptive gain model fits better than the full grandmother model after appropriate penalization for complexity. A failure to do so would imply the existence of a “hybrid” normalization solution that fits the human data even better, presumably involving some combination of parameters that has yet to be described in the literature. To assess this, we performed Bayesian model selection on complexity-penalized model fit metrics (Bayesian information criterion) which revealed that the exceedance probability for the normalization scheme favored by our empirical data, the adaptive gain model, over the grandmother model is 0.97, offering evidence against a hybrid solution.
Discussion
Decoy effects have been studied for decades, but substantial controversy has surrounded their replicability, their interrelationship, and their computational origins. The current work sheds light on these debates by gathering and analyzing a large-scale dataset that systematically maps the influence of a decoy stimulus across both the inferior and superior locations of multiattribute space. Conducting our analysis in a conventional fashion, we broadly replicate past studies, in that we find strong attraction effects, strong compromise effects, and a weaker similarity effect (not significant in our dataset). As in previous studies, the three decoy effects are correlated across the cohort, with a positive relationship observed between attraction and compromise, and a negative relationship between those two and the strength of the similarity effect (31, 32). This finding implies that three decoy phenomena have a single cause, and, indeed, previous dynamic models (in which information is accumulated over time) have been able to capture the three discrete effects with a single set of parameters (11, 15, 17, 32, 33). Here, we use dimensionality reduction on the full decoy influence map to confirm that, indeed, there is a single component that explains the vast majority (∼95%) of the variance in decoy influence, suggestive of a single computational origin for these biases.
To understand the computational origin of decoy effects, we chose to model our data with a framework based on divisive normalization. We made this choice because the normalization model offers a simple, parsimonious account of contextual biases in decision-making based on a rich, neurobiologically grounded tradition in the cognitive sciences (13, 21, 36–38). In particular, it allowed us to systematically measure the influence of various candidate computational steps on the predicted decoy map, providing an interpretable mapping from model to data (Fig. 4). On this basis, we were able to establish (for example) that normalization occurs relative to the average of the available values (via a sigmoidal gain function) rather than to the lower end (via a concave gain function) as proposed in some previous models (SI Appendix, Fig. S1). This characteristic sigmoidal shape of the transfer function may be approximated by transforming inputs via a power term in recurrent divisive normalization (35, 36).
Overall, out of the models tested here, evidence favored a model that we have previously called the adaptive gain model (22, 39). This account is closely related to other models involving recurrent divisive normalization, especially those proposing that values are nonlinearly transformed beforehand, as well as being very similar to another model known as the logistic model of subjective value (21). We draw the reader’s attention to the close correspondence between qualitative features of model and human performance displayed in Fig. 3, and, in particular, the close correspondence achieved after decomposition of the decoy map into linear components using SVD (Fig. 3B). The adaptive gain model even predicted a potentially counterintuitive relationship between the decoy effects: that, when the compromise effect is positive, attraction should dominate over repulsion (and vice versa), a prediction that was satisfied in the data.
We acknowledge, however, that the “static” models tested here abstract over the process by which information is accumulated dynamically to a decision bound. A more complete attempt to model the decision process would involve fitting the data with models based on the sequential sampling framework. It was beyond the scope of the current project, in particular, as our task involved a sequential ranking approach that was not suited to modeling decision latencies. However, we do note, in passing, that the pattern of decoy influence did not vary qualitatively for fast and slow trials, suggesting that, in our dataset, decision latencies are not indicative of distinct profiles of information acquisition and processing over time (SI Appendix, Fig. S2). Nevertheless, we hope that, in future studies, the full decoy influence map will help arbitrate among dynamic models of contextual decision biases.
Under the adaptive gain control framework described here, decoy effects occur because of contextual biases arising when each target item is transduced via a logistic function whose inflection point lies at the mean of all three items, including the decoy. For example, the “attraction” effect thus occurs because, when the decoy is lower in value than item A, the inflection point is lower than item A, and so A lies at the steepest portion of the sigmoidal gain function and is thus “overvalued” or repulsed away from this mean point. The precise converse occurs when the decoy is higher in value than A, as well as for B. We have previously shown how exactly this mechanism can, in principle, account for a range of decision biases arising in the presence of distracters, across perceptual, cognitive, and economic domains (22).
Whereas the attraction effect tends to be highly robust and consistent across participants, the compromise effect and similarity effect tend to be more idiosyncratic, with a high proportion of participants showing effects which are inverted with respect to the canonical form. For example, in previous studies, only a minority of participants show all three effects (numerically) in the expected direction (for example, only 23% in ref. 26; we find a comparable figure of 22%). Indeed, the similarity effect did not reach statistical significance in our dataset. In our model, the compromise and similarity effects occur when attractive and repulsive processes are asymmetric due to differential weighting or biasing of the two attributes, causing attraction effects (and their converse for superior decoys) to warp and/or “spill over” into locations where compromise and similarity decoys are typically tested. In other words, the fragile nature of the compromise and similarity effects might be, at least in part, due to heterogeneity in the asymmetric way each attribute is coded or transformed, which, in turn, might (for example) be due to differing choices concerning stimulus materials. A systematic unpicking of ways in which different classes of stimulus material (e.g., numerical values in distinct ranges, perceptual stimuli such as rectangles, and vignettes) are encoded, and thus why decoy effects may or may not have emerged in previous studies, is beyond the scope of our research project here. However, our simulations suggest that a relatively low-dimensional encoding model may be sufficient to capture this variation and thus to pinpoint the source of variation in previous studies.
This work thus explains decoy effects as a manifestation of a broader phenomenon whereby inputs are compressively normalized by their context in both space and time. As alluded to above, this principle has been previously proposed to explain phenomena as diverse as confirmatory biases in sequential sampling of perceptual information, low-level perceptual biases such as the tilt illusion, central tendency effects in summary statistical perception, and conflict effects in control tasks. Our previous work has considered a variant of this model whereby encoding gain is controlled by the tuning envelope of a population of feature-selective neurons (22). There, as in this manuscript, we demonstrate that contextual biases may arise because decisions are repulsed away from the contextual expectation. The brain may have evolved the type of normalization scheme proposed here because it promotes efficient neural coding (43, 44).
Methods
Participants.
A total of 358 US-based participants were recruited via the platform Amazon Mechanical Turk to participate in a three-phase study. All participants took part in the first phase (ratings task), and those who passed a performance threshold (n = 231; see below) were invited to join the second and third parts of the study in separate testing sessions (choice task). Of these, 189 met our criteria for inclusion in the analysis, namely, P < 0.001 of responding randomly during the choice task (binomial test). Phases 2 and 3 (choice task) were identical; phase 3 simply allowed us to gather more data (n = 149 completed both phases 2 and 3). Data were collected in two distinct batches. In the first batch, we paid participants $4 for completing each phase, in addition to a performance-based bonus of up to $20 for the second and third parts of the study (a maximum payment of $32). To reduce the dropout rate, in the second batch, the base payment was increased to $5, and the bonuses were increased to $12 and $18 in the second and third phases, respectively (a maximum payment of $45). All participants gave informed consent to participate by completing an online consent form. The study was approved by the University of Oxford Medical Sciences Division Research Ethics Committee (Ethics Approval Reference: R50750).
Task.
The first phase of the study (ratings task) was introduced as a “property rental price guessing game.” The task involved estimating the market rental price of residential real estate by viewing an exterior image of the property. On each trial, an image of a property was shown along with a horizontal slider for a maximum of 60 s. The task was to guess the market rental price of the property, that is, the dollar amount that an average person would be willing to pay per month to rent it, and to indicate it by moving a button over a slider. The slider ranged from $0 to $2,500, and the initial value of the button was randomized on each trial. We presented a total of 250 unique house images, each presented twice in randomized order (for a total of 500 trials per participant). The 250 houses had been selected to have the lowest average choice variability in a pilot study involving 30 distinct participants and a larger set of properties (n = 450), conducted before the main experiment.
We also used ratings from the pilot dataset to include/exclude participants. After phase 1, we correlated the 250 ratings for each participant against the average ratings obtained from the pilot study. Participants with a Spearman’s rank correlation of <0.7 were excluded; others (n = 231) were invited to progress to the choice task. We introduced phases 2 and 3 as a “best-value property hunting game.” Here, participants were told to imagine that they were a real estate agent recommending to a client the best-valued house offered from us—a fictitious real estate company. On each trial, three properties (i.e., choice alternatives) were displayed for a maximum of 60 s on left, central, and right positions on the screen. Underneath each image, we displayed an allocated rental cost (in dollars) and a number of stars (see below). The number of stars was proportional to value given in the ratings task, and merely served as a reminder; in piloting, we found that this improved choice consistency. Participants were informed that the property images were a subset of those that they had viewed in phase 1, and that that the stars were related to the ratings they had offered. The task was to press three keyboard buttons (left, down, and right arrow buttons) to indicate their ordered preference from the best-valued house to the worst-valued house. Participants were explicitly instructed that the best-valued house was the one with the highest market value but the lowest allocated rental price. At the end of each block, participants were told how many trials’ recommendations were correct, given their initial ratings. The bonus payment at the end of each phase was proportional to their accuracy.
Unbeknownst to participants, the options were carefully selected for each participant, to allow us to test our hypotheses of interest. First, for each participant, we filtered out the 90 properties with the highest rating variability, that is, the highest absolute deviance between the two ratings. Second, the remaining 160 properties were binned into quality deciles (attribute ) on the basis of each participant’s ratings and could be associated with an allocated rental cost that was drawn uniformly from within the range of dollar values that defined each decile (attribute ). This allowed us to select, on each trial, the three stimuli that differed on two dimensions: two targets A and B, and a decoy stimulus. Target A was always a property drawn from the third decile of quality (i.e., rating) and the eighth decile of economy (i.e., the third decile of cost); target B was always drawn from the eighth decile of quality and the third decile of economy (i.e., the eighth decile of cost). The decoy stimulus was sampled exhaustively from the full attribute space. Thus, targets A and B were equally valued options, and the decoy stimulus could be either superior or inferior in value. Participants completed a total of 530 trials in the second part of the study. The third part constituted an additional 530 trials of the same task.
Model Fitting and Comparison.
Models provided predictions about probabilities of choosing option A over B, which allowed us to compute model likelihoods on each trial, which were then used for model fitting. For parameter estimation, we used the Global Search function from the MATLAB Optimization Toolbox. Equations for the models are given in the Computational Modeling and Model Comparison sections. Derivations of special case models from the Grandmother model are in SI Appendix.
For the t-SNE plot, we fit 125 variations of the grandmother model, by varying and in five steps between 0 and 1, and in five steps between 0.001 and 1, in addition to four additional constrained parameterizations of the grandmother model that result in the vanilla divisive normalization, recurrent divisive normalization, adaptive gain, and range normalization models (SI Appendix, Table S2). We specified the hyperparameter perplexity, which controls the number of expected close neighbors, following guidelines in the literature to balance the trade-off between perplexity and the Kullback–Leibler divergence (45). A zoomed-out version of Fig. 5 B–D visualizing the parameters of all 129 models is available in SI Appendix, Fig. S3.
Supplementary Material
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2005058117/-/DCSupplemental.
Data Availability.
Anonymized Matlab files of data have been deposited in Open Science Framework (https://osf.io/U6BR3).
References
- 1.Block H. D., Marschak J., “Random orderings and stochastic theories of response” (Cowles Foundation Discussion Paper 66, Yale University, 1959). [Google Scholar]
- 2.Rieskamp J., Busemeyer J. R., Mellers B. A., Extending the bounds of rationality: Evidence and theories of preferential choice. J. Econ. Lit. 44, 631–661 (2006). [Google Scholar]
- 3.Huber J., Payne J. W., Puto C., Adding asymmetrically dominated alternatives: Violations of regularity and the similarity hypothesis. J. Consum. Res. 9, 90–98s (1982). [Google Scholar]
- 4.Simonson I., Choice based on reasons: The case of attraction and compromise effects. J. Consum. Res. 16, 158–174 (1989). [Google Scholar]
- 5.Tversky A., Elimination by aspects: A theory of choice. Psychol. Rev. 79, 281–299 (1972). [Google Scholar]
- 6.Parrish A. E., Evans T. A., Beran M. J., Rhesus macaques (Macaca mulatta) exhibit the decoy effect in a perceptual discrimination task. Atten. Percept. Psychophys. 77, 1715–1725 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lea A. M., Ryan M. J., SEXUAL SELECTION. Irrationality in mate choice revealed by túngara frogs. Science 349, 964–966 (2015). [DOI] [PubMed] [Google Scholar]
- 8.Shafir S., Intransitivity of preferences in honey bees: Support for comparative evaluation of foraging options. Anim. Behav. 48, 55–67 (1994). [Google Scholar]
- 9.Latty T., Beekman M., Irrational decision-making in an amoeboid organism: Transitivity and context-dependent preferences. Proc. Biol. Sci. 278, 307–312 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Turner B. M., Schley D. R., Muller C., Tsetsos K., Competing theories of multialternative, multiattribute preferential choice. Psychol. Rev. 125, 329–362 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Roe R. M., Busemeyer J. R., Townsend J. T., Multialternative decision field theory: A dynamic connectionist model of decision making. Psychol. Rev. 108, 370–392 (2001). [DOI] [PubMed] [Google Scholar]
- 12.Tsetsos K., Usher M., Chater N., Preference reversal in multiattribute choice. Psychol. Rev. 117, 1275–1293 (2010). [DOI] [PubMed] [Google Scholar]
- 13.Landry P., Webb R., Pairwise normalization: A theory of multi-attribute choice. SSRN Electron. J. 10.2139/ssrn.2963863. [DOI]
- 14.Hotaling J. M., Busemeyer J. R., Li J., Theoretical developments in decision field theory: Comment on Tsetsos, Usher, and Chater (2010). Psychol. Rev. 117, 1294–1298 (2010). [DOI] [PubMed] [Google Scholar]
- 15.Bhatia S., Associations and the accumulation of preference. Psychol. Rev. 120, 522–543 (2013). [DOI] [PubMed] [Google Scholar]
- 16.Tsetsos K., Chater N., Usher M., Salience driven value integration explains decision biases and preference reversal. Proc. Natl. Acad. Sci. U.S.A. 109, 9659–9664 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Trueblood J. S., Brown S. D., Heathcote A., The multiattribute linear ballistic accumulator model of context effects in multialternative choice. Psychol. Rev. 121, 179–205 (2014). [DOI] [PubMed] [Google Scholar]
- 18.Bhui R., Gershman S. J., Decision by sampling implements efficient coding of psychoeconomic functions. Psychol. Rev. 125, 985–1001 (2018). [DOI] [PubMed] [Google Scholar]
- 19.Noguchi T., Stewart N., In the attraction, compromise, and similarity effects, alternatives are repeatedly compared in pairs on single dimensions. Cognition 132, 44–56 (2014). [DOI] [PubMed] [Google Scholar]
- 20.Soltani A., De Martino B., Camerer C., A range-normalization model of context-dependent choice: A new model and evidence. PLOS Comput. Biol. 8, e1002607 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rigoli F., Reference effects on decision-making elicited by previous rewards. Cognition 192, 104034 (2019). [DOI] [PubMed] [Google Scholar]
- 22.Li V., Michael E., Balaguer J., Herce Castañón S., Summerfield C., Gain control explains the effect of distraction in human perceptual, cognitive, and economic decision making. Proc. Natl. Acad. Sci. U.S.A. 115, E8825–E8834 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Natazon P., Random choice and learning. J. Polit. Econ. 127, 419–457 (2019). [Google Scholar]
- 24.Trueblood J. S., Brown S. D., Heathcote A., Busemeyer J. R., Not just for consumers: Context effects are fundamental to decision making. Psychol. Sci. 24, 901–908 (2013). [DOI] [PubMed] [Google Scholar]
- 25.Trueblood J. S., Multialternative context effects obtained using an inference task. Psychon. Bull. Rev. 19, 962–968 (2012). [DOI] [PubMed] [Google Scholar]
- 26.Trueblood J. S., Brown S. D., Heathcote A., The fragile nature of contextual preference reversals: Reply to Tsetsos, Chater, and Usher (2015). Psychol. Rev. 122, 848–853 (2015). [DOI] [PubMed] [Google Scholar]
- 27.Frederick S., Lee L., Baskin E., The limits of attraction. J. Mark. Res. 51, 487–507 (2014). [Google Scholar]
- 28.Yang S., Lynn M., More evidence challenging the robustness and usefulness of the attraction effect. J. Mark. Res. 51, 508–513 (2014). [Google Scholar]
- 29.Mellers B. A., Biagini K., Similarity and choice. Psychol. Rev. 101, 505 (1994). [Google Scholar]
- 30.Tversky A., Features of similarity. Psychol. Rev. 84, 327 (1977). [Google Scholar]
- 31.Berkowitsch N. A., Scheibehenne B., Rieskamp J., Rigorously testing multialternative decision field theory against random utility models. J. Exp. Psychol. Gen. 143, 1331–1348 (2014). [DOI] [PubMed] [Google Scholar]
- 32.Noguchi T., Stewart N., Multialternative decision by sampling: A model of decision making constrained by process data. Psychol. Rev. 125, 512–544 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Usher M., McClelland J. L., Loss aversion and inhibition in dynamical models of multialternative choice. Psychol. Rev. 111, 757–769 (2004). [DOI] [PubMed] [Google Scholar]
- 34.Pettibone J. C., Testing the effect of time pressure on asymmetric dominance and compromise decoys in choice. Judgm. Decis. Mak. 7, 513–523 (2012). [Google Scholar]
- 35.Daviet R., “Methods for statistical analysis and prediction of discrete choices” in PhD/Doctoral dissertation, (University of Toronto, Toronto, ON, Canada, 2018). [Google Scholar]
- 36.Webb R., Glimcher P. W., Louie K., The normalization of consumer valuations: Context-dependent preferences from neurobiological constraints. Manage. Sci., 1–33 (2019). [Google Scholar]
- 37.Louie K., Khaw M. W., Glimcher P. W., Normalization is a general neural mechanism for context-dependent decision making. Proc. Natl. Acad. Sci. U.S.A. 110, 6139–6144 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Carandini M., Heeger D. J., Normalization as a canonical neural computation. Nat. Rev. Neurosci. 13, 51–62 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cheadle S. et al., Adaptive gain control during human perceptual choice. Neuron 81, 1429–1441 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bushong B., Rabin M., Schwartzstein J., A model of relative thinking. https://www.hbs.edu/faculty/Publication%20Files/relativethinkingJune2020_b56e6a49-723b-4cfa-aa4c-b517690c8087.pdf (2020).
- 41.van der Maaten L., Hinton G. E., Visualizing Data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008). [Google Scholar]
- 42.Daviet R., Webb R., A double decoy experiment to distinguish theories of dominance effects. 10.2139/ssrn.3374514. [DOI]
- 43.Summerfield C., Tsetsos K., Do humans make good decisions? Trends Cogn. Sci. 19, 27–34 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Summerfield C., Tsetsos K., “Rationality and efficiency in human decision-making” in The Cognitive Neurosciences VII, Gazzaniga M., Ed. (MIT Press, 2020), pp. 427–438. [Google Scholar]
- 45.Cao Y., Wang L., Automatic selection of t-SNE perplexity. arXiv:1708.03229 (2017). Accessed 10 December 2019.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Anonymized Matlab files of data have been deposited in Open Science Framework (https://osf.io/U6BR3).