Abstract
Estimates of plastic inputs into the ocean are orders of magnitude larger than what is found in the surface waters. This can be due to discrepancies in the sources of plastic released into the ocean but can also be explained by the fact that it is not well-known what the most dominant sinks of marine plastics are and on what time scales these operate. To get a better understanding on possible sources and sinks, an inverse modeling methodology is presented here for a Lagrangian ocean model, estimating floating plastic quantities in the Mediterranean Sea. Field measurements of plastic concentrations in the Mediterranean are used to inform parametrizations defining various sources of marine plastics and removal of plastic particles because of beaching and sinking. The parameters of the model are found using inverse modeling, by comparison of model results and measurements of floating plastic concentrations. Time scales for the sinks are found, and likely sources of plastics can be ranked in importance. A new mass balance is made for floating plastics in the Mediterranean: for 2015, there is an estimated input of 2100–3400 tonnes, and of plastics released since 2006, about 170–420 tonnes remain afloat in the surface waters, 49–63% ended up on coastlines, and 37–51% have sunk down.
Introduction
It is currently not well-known what happens with plastics once they end up in the marine environment. Studies have shown that only a fraction of plastics which are expected to enter the oceans remains afloat in the surface water. The total mass of floating plastics in the global ocean has been estimated to be from 93–236 thousand tonnes1 to at least 269 thousand tonnes.2 This is significantly different from the total input estimates into the marine environment, which range from 4.8–12.7 million tonnes per year from coastal population3 to 1.15–2.41 million tonnes from rivers only.4 This does not take into account the other possible sources resulting from activities such as fishing, aquaculture, and shipping.5
One can investigate different environmental compartments where the remainder of plastics might reside, such as shorelines. Another possibility is the deep ocean and marine sediments: the biofilm formed by micro- and macro-organisms6,7 and fecal pellets8 can cover plastic particles, increasing the average density and therefore induce sinking. Plastic particles might be present in biota: for example, zooplankton, fish, or birds.8−10 Oxidation caused by UV-exposure can make polymers more brittle, enhancing the fragmentation of plastics in the environment:11 particles might become too small to measure using conventional techniques.
Estimates have been made in which environmental compartments the marine plastics are likely to reside. Marine sediments are likely to contain a major percentage of plastics, for example, more than 90% of microplastics in terms of numbers for a global scenario,12 with abundances of about 4 orders of magnitude higher per unit volume of sediment than that found in surface waters in the oceanic gyres.13 Other studies cite the possibility that shorelines store the majority of plastics14 and that coastal fluxes possibly dominate mass fluxes to the sea bottom.15
In this paper, a framework is presented to close the plastic mass budget, by combining the strength of numerical models and in situ measurements.16 Models allow us to estimate plastic concentrations continuously over time on a large spatial domain, but there are still a number of unknowns regarding processes that affect the dispersal of marine debris.17 Measurements of plastic concentrations as obtained by, for example, neuston net trawls give us more reliable information at a given instance at a specific location. However, these are expensive to carry out and can be prone to high variation due to a relatively small area covered, high heterogeneity of plastic concentrations,18 and presence of waves.19 By using an inverse modeling approach, the best of modeling and observations is combined.
Here, parameters in a numerical model governing sources and sinks of marine plastics are estimated using observed plastic concentrations in surface waters. A Bayesian framework is used, where prior information can be specified for the parameters based on previous (experimental) findings. After the posterior step is done, the estimated parameters are used to quantify where and in which environmental compartments most of the marine plastics are expected to reside. Here, we choose to focus on the Mediterranean, which is an interesting test case because of two reasons. First of all, numerical studies and field measurements suggest that there are no stable plastic retention areas in the basin because of variability of the surface currents,20 making it important to take time-varying processes into account. Second, a large number of field studies measuring plastic concentrations are available, providing valuable information that can be used to train numerical models. We choose to focus on two major sinks of plastics: sinking down of plastics and plastics ending up on coastlines (beaching). Other sinks, such as fragmentation, degradation, and ingestion of plastics by animals are neglected, based on the assumption that the removal rates of these sinks are likely at least an order of magnitude smaller.
Methods
Lagrangian Framework and Forcing
In the Lagrangian framework presented here, virtual particles represent floating plastics. The OceanParcels Lagrangian ocean analysis framework21 is used to calculate the movement of floating plastic within a given velocity field. Trajectories are integrated using a Runge-Kutta 4 scheme. The velocity field is derived from E.U. Copernicus Marine Service Information reanalysis data for the Mediterranean currents at a 1/16° resolution22 and hindcast data for the Stokes drift at a 1/24° resolution,23 both spanning the years 2006–2016. Like other Lagrangian modeling studies,5,24 it is assumed that the plastic particles move just below the water surface and hence do not experience a direct wind drag.
The effects of subgrid-scale phenomena such as submesoscale eddies are parametrized using a zeroth-order Markov model,25 with a constant tracer diffusivity K. While some experimental estimates have been done estimating this diffusivity parameter,26 it is difficult to determine an appropriate value also because it will vary spatially.27 Here, three different (constant) values for K are used, namely K = 1 m2/s, K = 10 m2/s, and K = 100 m2/s, to determine the sensitivity to this parameter.
The number of virtual particles should be large enough for the results to be statistically significant. First, a baseline simulation is done with about 1.2 million particles. A certain percentage of plastic particles will disappear from the surface water over time because of sinking and particles ending up on coastlines. A time threshold at which 99.9% of the plastic particles in the baseline simulation are removed was determined to be approximately 50 days. Subsequent simulations were done with about 7.2 million particles, where particles were removed well above this threshold (after 180 days) (see the Supporting Information S4).
The beaching of particles is parametrized using a model presented later in this paper. Particles should therefore not move from mesh cells belonging to the ocean onto land cells because of other processes, such as interpolation errors or Stokes drift. This is ensured by pushing particles back toward the closest ocean cell when they have ended up on the land, identical to what is done by Delandmeter and Sebille.21
Area of Interest and Field Measurements Used
The area studied here is the Mediterranean. The high spatio-temporal variability of the currents in this basin causes that there are no known plastic retention areas.20 In order to get a better picture of the flow field, the time-mean surface currents over 2006–2016 have been plotted as vectors in Figure 1. In the same figure, locations of the measurements used here are plotted for which references are shown in the legend. Two types of measurements are used here (Table 1): manta trawl or neuston net samples reported in terms of abundance (counts per square kilometer, n/km2) and in terms of mass (grams per square kilometer, g/km2). A majority of the measurements were taken in the western basin of the Mediterranean. There are much fewer measurements in the eastern basin, which are mainly found in front of the coast of Turkey and Israel.
Figure 1.
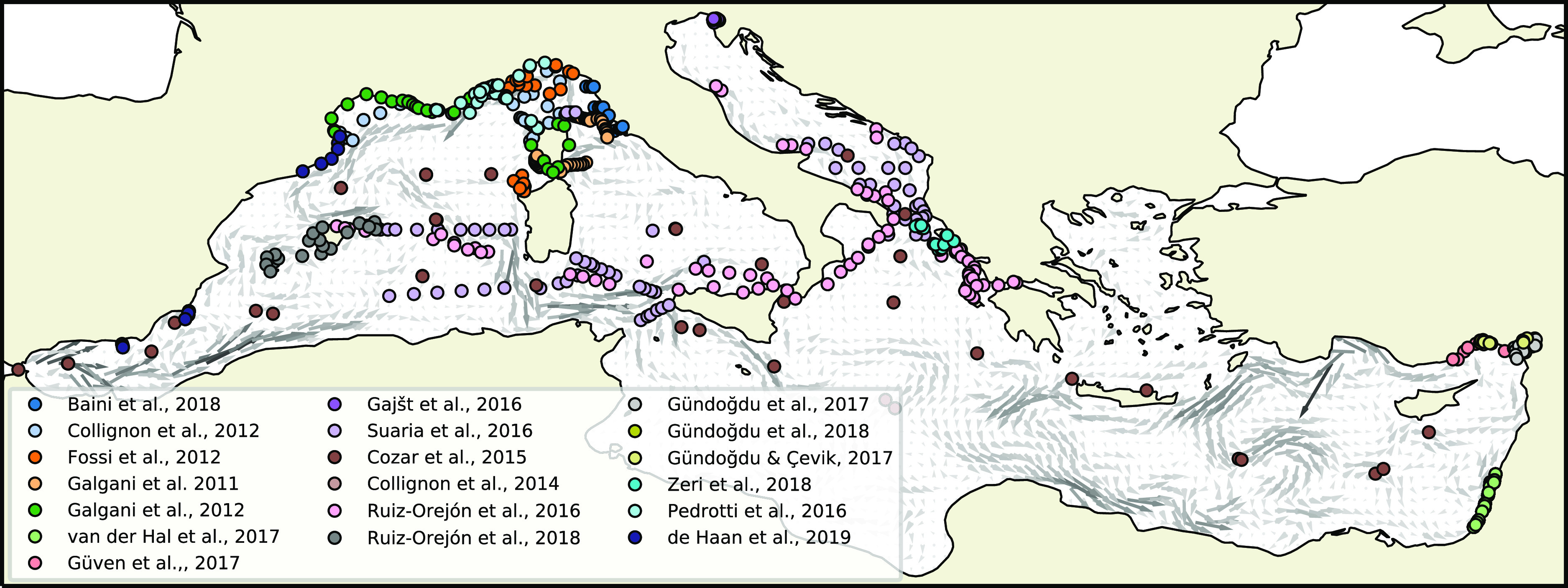
Available plastic measurements used here (colored dots) and the time-mean surface currents over 2006–2016 (grey arrows).
Table 1. Data Used of Plastic Concentration Measurements in the Mediterranean.
| reference | n/km2 | g/km2 | sampling year | size classes measured |
|---|---|---|---|---|
| Collignon et al.28 | √ | 2010 | <5 mm | |
| Collignon et al.29 | √ | 2011–2012 | <5 mm, > 5 mm | |
| Cózar et al.20 | √ | √ | 2013 | <5 mm, > 5 mm |
| Fossi et al.30 | √ | 2011 | <5 mm | |
| Gajšt et al.31 | √ | √ | 2012–2014 | <5 mm, > 5 mm |
| Galgani (2011) (unpublished)32 | √ | √ | 2011 | <5 mm, > 5 mm |
| Galgani (2012) (unpublished)32 | √ | √ | 2012 | <5 mm, > 5 mm |
| Gündoğdu and Çevik33 | √ | 2016 | <5 mm | |
| Gündoğdu et al.34 | √ | 2016–2017 | <5 mm | |
| Güven et al.9 | √ | 2015 | <5 mm | |
| de Haan et al.35 | √ | √ | 2015 | <5 mm, > 5 mm |
| van der Hal et al.36 | √ | 2013–2015 | <5 mm, > 5 mm | |
| Pedrotti et al.18 | √ | 2013 | <5 mm, > 5 mm | |
| Ruiz-Orejón et al.37 | √ | √ | 2011–2013 | <5 mm, > 5 mm |
| Ruiz-Orejón et al.38 | √ | √ | 2014 | <5 mm, > 5 mm |
| Suaria et al.39 | √ | √ | 2013 | <5 mm, > 5 mm |
| Zeri et al.40 | √ | 2014–2015 | <5 mm |
Two types of correction factors are used for the measurements: one for wind-induced vertical mixing and one accounting for different measured particle sizes. For wind-induced vertical mixing, the correction factor from Kukulka et al.41 is used (see the Supporting Information S1).
We want to account for all plastic particle sizes which are larger than the mesh size of the neuston nets. If the data are available, measurements of microplastics (<5 mm) and macroplastics (>5 mm) are combined. If the data are given for <5 mm only, a correction factor is used. This correction factor is calculated from the available measurements reporting both size classes. In terms of abundance, a correction factor of 1.14 (standard deviation: 0.14) was calculated. In terms of mass, only measurements are used where both microplastics and macroplastics were reported, so no correction factor is necessary in this case. Table 1 presents the size classes reported for each study.
The model output and measurements are transformed to a log10 scale for comparison. Measured values of plastic concentrations span multiple orders of magnitude. Not transforming the data would lead to high outliers dominating the inverse modeling process, while discrepancies at lower concentrations are just as relevant as those at higher concentrations.
As shown by de Haan et al.,35 replicate samples taken of plastic concentrations reveal a lot of variability. This variability was calculated on a specific length and time scale using an empirical variogram (see the Supporting Information S1). The model used here has a spatial resolution of 1/16° and a temporal resolution of one day. The variance of the measurements at this length and time scale, denoted by γ, is γn = 0.1376 (units: [log10(n/km2)]2) for the abundance measurements and γm = 0.2201 (units: [log10(g/km2)]2) for the mass measurements. When comparing the model output to the observations, this variance is used to specify the measurement uncertainty because fluctuations on the length and time scales smaller than these are not resolved by the model.
Sources of Plastics
Different release scenarios for plastics entering the marine environment are considered here. In modeling studies, the sources of marine plastics are often divided into different classes. In one recent example for a global scenario,5 59.8% was estimated to come from the coastal population (<50 km from the coastline), 12.1% from inland population by riverine transport, 17.9% from fisheries, 1.3% from aquaculture, and 8.9% from shipping. Because the proportions for the Mediterranean might be significantly different, we make no such assumption here. Instead, the model selects the appropriate fractions of input waste such that there is a good fit of the model with the observed plastic concentrations, consistent with their error estimates. The model can select from three major possible plastic sources as shown in Figure 2, which were estimated to be the biggest sources of pollution in Lebreton et al.5
Figure 2.
Sources of marine plastics used in the model. The amount of virtual particles released from each source is proportional to the magnitude of the source as plotted here. Virtual particles released from rivers can directly be expressed in terms of mass; the other sources are defined in terms relative to the riverine input.
First, the input from rivers is considered, using the results from Lebreton et al.4 In Figure 2, the yearly waste is plotted using green circles, where only rivers estimated to release more than 0.2 tonnes of plastic per year are shown. In the model, monthly estimates of plastic emissions are used for all rivers available. In Lebreton et al.,4 lower, mid, and upper estimates for the riverine plastic input were given. This is represented in our model by including a parameter varying from −1 to 0 to 1, corresponding to the lower, mid, and upper estimates, respectively. The parameter is allowed to vary continuously in the phase space, and linear interpolation is used to determine the riverine output for intermediate values. The input from rivers is given instantaneously at the river mouth, and possible delayed response due to, for example, transport in the river itself42,43 is not taken in account.
Another possible source of marine plastics is fishing activity (shown in blue in Figure 2). Data for the fishing intensity were obtained from the global fishing watch.44 These data are based on the automatic identification system installed on vessels. This system has not been equally present on fishing vessels over the years, and no data were available from before 2012. It was therefore decided to assume a constant fishing intensity over the years, based on the years 2012–2016.
Finally, land-based mismanaged plastic waste (MPW) from coastal population is considered (shown in red in Figure 2 for 2010). The MPW density was estimated by overlaying population density data45 with the estimated MPW per capita per country.3 The estimated population density data are available from 2000 to 2020 in increments of 5 years. It is linearly interpolated to estimate the population density at a given moment of time. The number of particles released along the coast is proportional to the MPW production within 50 km, similar to that reported by Jambeck et al.3
Input of plastics from the Atlantic is neglected here. In the study by Cózar et al.,20 a plastic concentration of 159 g/km2 was reported inside the Strait of Gibraltar. Taking the width of the strait, and the mean surface current which was calculated to be 0.55 m/s, would theoretically lead to about 40 tonnes of plastic per year. Because this is small compared to the previously mentioned sources and as it would require a separate model to estimate how this source varies over time, it is not taken in account here.
Parametrization of Plastic Particle Properties
Each virtual particle in the Lagrangian framework represents a certain abundance (n) and mass (g) of plastic particles, similar to the super-individual approach used for microbial modeling.46 The concentration of plastics in n/km2 and g/km2 is calculated by taking a weighted kernel density estimate47 of all virtual particles, weighted by the total abundance or total mass of plastic particles inside the virtual particle.
Initially, the abundance and mass of plastic particles inside the virtual particle depends on the particle’s source because one source might contribute more to the total plastic pollution compared to the other. Over time, the abundance and mass of the virtual particle are modified by sinks acting upon it. It is for example assumed that the collection of plastics inside the virtual particle has a constant probability of beaching over time when it is nearby the coast. This leads to an exponential reduction of the abundance and mass of the virtual particle on a certain time scale τbeach.
This Lagrangian approach, which assigns an abundance and weight to the virtual particles, allows for a relatively quick evaluation of different parameter sets compared to a continuum approach with a plastic tracer concentration. Another benefit is that it is easy to use reanalysis data sets for the forcing fields which have already been assimilated with observational data.
Two sinks of plastic particles are considered: beaching and sinking. Each sink has its own fraction defining what percentage of the plastics is still floating and not taken away by the sink, denoted by fbeach and fsink, respectively. The weight of the virtual particle is the product of the weight at its source (wsource) with these different factors
| 1 |
where wsource can
be expressed in mass (wsource,m) or in
abundance (wsource,n); the same holds
for the particle weight (wptcl,m or wptcl,n). The value of wsource depends on which of the three sources the particle comes
from; this source is kept track of for each particle during the simulation.
For riverine sources, there is an estimate available of their individual
pollution per month in tonnes:4wsource,m can directly be calculated. The rest
of the sources is expressed in terms relative to the riverine sources,
to convert these to tonnes as well. This leads to two parameters in
the model defining the source ratios: Spop:riv and Sfis:riv, where the subscripts pop,
riv, and fis denote the sources from coastal population, rivers, and
fisheries, respectively. A prior probability density function needs
to be defined for these parameters in the Bayesian framework used
here. Bounds for the prior, defined in terms of the 99.7th percentile
of a Gaussian distribution, are set to enable a very wide range of
possibilities (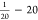 ), such that each source can contribute
at most to 95% of the total mass. This easily captures the possible
release scenarios mentioned in the previous section.5
), such that each source can contribute
at most to 95% of the total mass. This easily captures the possible
release scenarios mentioned in the previous section.5
For the total abundance of particles emitted by different sources, no estimates could be found. In order to express wptcl,n in terms of abundance (n), a linear fit through the origin is made of the modeled (unitless) concentrations versus the measured concentrations (see also van Sebille et al).1 The slope of this fit is used to assign abundances (n) to wptcl,n of the virtual particles, allowing us to calculate the density field in terms of n/km2.
One possible sink of floating plastics not taken into account here is fragmentation and degradation of plastics. Fragmentation eventually leads to particles being smaller than the detection limit (here: neuston net mesh size). This likely acts on a significantly longer time scale (order of years) than beaching and sinking of particles. In a study by Song et al.,11 polyethylene pellets, the material which forms the majority of plastics found in the Mediterranean,18,39 were subjected to 12 months of UV exposure and 2 months of mechanical abrasion. It was estimated that this might translate to more than 4 years in the natural environment. This weathering resulted in a volume loss of about 10% and produced about 20 fragments per polyethylene pellet. Photochemical oxidation might also play a direct role in plastic degradation, converting plastic polymers into carbon dioxide and dissolved organic carbon. In a study by Ward et al.48 it was reported that this process might play a role on decadal time scales. Both processes are unlikely to have a significant effect on the results presented here because their removal rates are expected to be at least an order of magnitude smaller than what is necessary for a mass balance: see the Supporting Information S6 for a detailed discussion. Nevertheless, taking fragmentation and degradation in account might be a next step for future modeling studies.
Another sink not taken into account is the presence of plastics in biota. To our knowledge, the total amount of plastics in biota has not been quantified thoroughly yet. In a study by Booth et al.12 the total amount of plastics in fish was estimated to be about 6 orders of magnitude lower than the amount of plastics in the surface water; hence, we neglect this possible sink.
The goal of this work is to have a surface mass balance: particles are removed once they start sinking down, and only surface measurements are used to infer the model parameters. The water column and marine sediments therefore need not be taken into account as separate sinks.
Sinks of Plastics
The parametrization of sinks is kept simple in order to avoid the problem from becoming too underdetermined (i.e. multiple sets of parameters fitting the data equally well). Time scales define how quickly particles are removed from the surface water because of the different sinks, with the goal of having a first-order estimation on their influence.
Beaching
The process of beaching takes place in the mesh cell adjacent to the land, which will be referred to as the coastal cell. It is assumed that plastic particles have a constant probability of beaching when inside this coastal cell. The cumulative probability of beaching for a set of plastic particles will follow an exponential distribution as a function of time that the particles spend in the coastal cell, denoted by tcoast
| 2 |
where τbeach is the time scale on which beaching occurs. The value for τbeach is one of the parameters which is estimated in the inverse modeling process. The larger the time scale τbeach, the longer the particles will remain in the water. This beaching time scale should be interpreted as a time at which particles remain permanently on the coastline (e.g. due to burial) and are not washed back to sea anymore.
For drifter buoys, the beaching time scale is calculated to be about 76 days (see the Supporting Information S2). However, floating plastic particles do not necessarily behave like drifter buoys close to the shore. Therefore, the prior probability density function for τbeach is defined on the log10 of the values to cover a wide range of possibilities (101 to 103 days), with the beaching time scale for the drifter buoys being approximately at the mode of the prior probability density function (102 days).
Sinking
For the sinking of particles, a similar approach is used as for beaching of particles, where a time scale τsink determines how quickly plastic particles are removed from the surface water. A majority of plastics is buoyant: the fraction of initially nonbuoyant plastics is defined as Psink,0. Because of the formation of a biofilm, initially buoyant particles can start sinking down. Similar to that reported by Fazey and Ryan,6 the probability that particles sink because of biofouling is modeled using a logistic function, where over time, the growing biofilm will increase the sinking probability
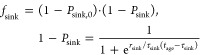 |
3 |
where tage is the age of the particle, τsink is a time scale when 50% of the initially buoyant particles will have sunk, and rsink is the inverse rate at which this happens (i.e. the slope of the logistic function at the inflection point) in terms of days. As a first-order approximation, sinking is assumed to be permanent: the effects of potential oscillations in the water column due to fouling/defouling49 are assumed to be small.
Data from Fazey and Ryan6 are used to estimate parameter bounds for the priors governing the biofouling process. The prior should cover a wide range of values because differences in the fouling process can be induced by factors such as the particle size used in the experiment, the material, tethered versus free-floating samples, and differences in fouling communities for different geographical regions. The prior probability density function of τsink is defined on the log10 of the value to cover a wide range of possibilities. The lower bound is set to the lowest fouling time found in Fazey and Ryan6 of 2 weeks. The upper bound is set to a value of 1 year, which is much longer than the experimentally found fouling times, to allow for possible differences in the fouling behavior as described above. For rsink, bounds on the prior are set to the smallest and largest values calculated using the reported experimental data (3–15 days). The initial fraction of positively buoyant plastic particles is estimated by computing the fraction of polymers produced with a density lower than water.50 Because it is not known for all materials whether it will float or sink (e.g. the “other materials” category, or polystyrene, which often appears in its foamed version), this information is used to estimate a lower and upper bound on the initial sinking fraction (0.17–0.44).
Inverse Modeling
Parameters governing the sources and sinks are estimated using an inverse modeling approach: parameters are chosen such that the model fit is consistent with the observed plastic concentrations, while trying to adhere to the prior parameter bounds specified in the previous sections.
There is relatively little information available on what kind of distribution is the most suitable for the prior information. In most cases, there are only point estimates available for possible parameter values as obtained from previous modeling studies or laboratory experiments. These estimates might differ for our modeling scenario because of different geographical and environmental conditions. However, we do want to use these estimates as prior knowledge because they tell us at least what orders of magnitude we should look at. We choose Gaussian prior distributions here and assume Gaussian statistics for the model and measurement errors. This allows us to formulate the problem as a least-squares problem, which is computationally much less costly than using Monte Carlo methods (see the Supporting Information S3). The cost function of the least-squares problem to be minimized as a function of the model parameters m is defined as51
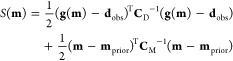 |
4 |
The first term on the right hand side is the mismatch between the modeled plastic concentrations g(m) and the observations dobs, weighted by the measurement covariance matrix CD. The last term is the deviation of m from the prior mprior, weighted by the covariance matrix defining uncertainty of the prior model parameters CM. This term is derived from assuming Gaussian prior distributions. It has the benefit of acting as a regularization term, which can help for solving ill-posed problems.52 Both CD and CM are diagonal matrices: it is assumed that there is no correlation between the measurements. The diagonal entries of CD contain the small-scale measurement variance presented before (γn = 0.1376, γm = 0.2201). Bounds on the model parameters as mentioned in the text are used for the entries in CM.
The cost function is minimized by linearizing the forward model around an estimate for the parameters m and iteratively updating the parameters using a quasi-Newton method (see the Supporting Information S3).
Results and Discussion
Parameter Estimation
Results are presented here for the simulation with a tracer diffusivity of K = 10 m2/s, which was calculated to be the most appropriate value for the grid resolution used here.15,53 See the Supporting Information S4 for further details, along with a discussion on the sensitivity of the results to the value of K and entries of CD and CM.
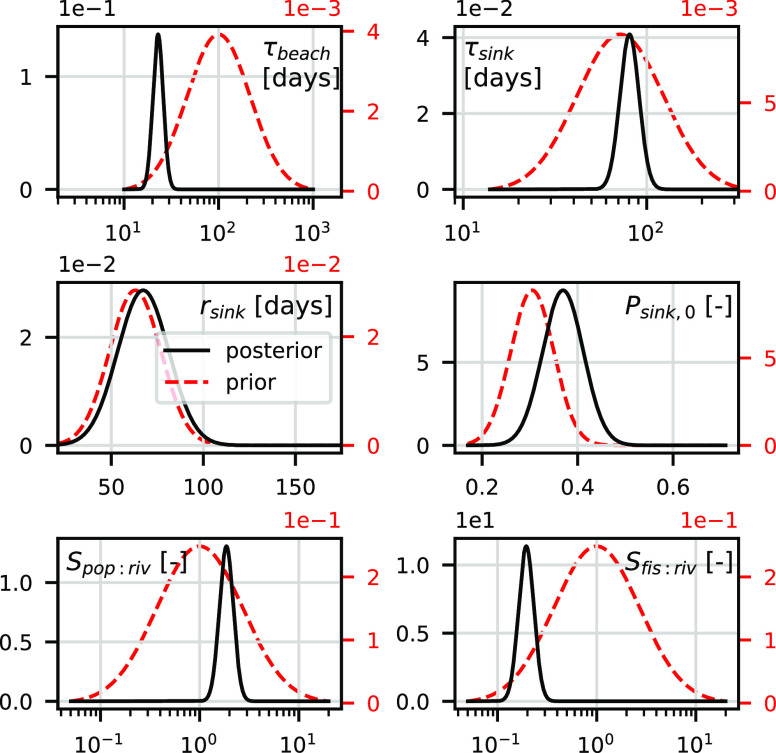
Figure 3 shows the probability density function of the prior and the updated (posterior) estimates for each parameter. The most likely value of the posterior for τbeach is 24 days. This is lower than the τbeach estimated for drifter buoys (76 days). The reason may be that floating plastic particles are more severely influenced by wave action compared to the (drogued) drifters. The most likely estimate for τsink is approximately 81 days. This is a bit higher than the estimates found in Fazey and Ryan6 ranging from 17 to 66 days for polyethylene samples. One explanation could be that the Mediterranean is relatively oligotrophic,54 causing slow growth of the biofilm. For rsink, there is not much difference between the prior and posterior. The available data do not seem to contain much information about this parameter (see the Supporting Information S4 for further discussion). For Psink,0, the most likely estimate is 0.36. This corresponds well to the estimated value by Lebreton et al.,14 where 65.5% of all polymers is expected to be positively buoyant (i.e. Psink,0 = 0.345).
Figure 3.
Prior (red dashed lines, right y-axes) and posterior (black solid lines, left y-axes) probability density functions for the estimated parameters defining sources and sinks of floating plastic particles. For probability density functions plotted using a logarithmic x-axis, parameters were defined in terms of the log10 of the values.
The inverse model suggests that most plastics are likely to originate from coastal population: the most likely value specifies about 1.9 times the total riverine input. This is slightly lower than the value range (3.2–17.6) calculated by Lebreton et al.5 for a global scenario. Fisheries are expected to emit less plastics: the most likely value specifies about 0.2 times the total riverine input. This is at the lower end of the global scenario range (0.2–4.9).5 In terms of percentages, 61% of marine plastics in the Mediterranean originates from coastal population, 32% from rivers, and 6% from fisheries according to the most likely posterior estimates.
The inverse model finds the low-end estimate of the riverine input given by Lebreton et al.4 to be the most likely (see the Supporting Information S4). Scatter plots of the modeled versus measured plastic concentrations can also be found here S5, where it can be seen that correlation between the model and measurements is somewhat low. This is difficult to overcome with the highly variable water surface measurements used here. Recommendations to address this in the future are given in the outlook.
Mass Balance
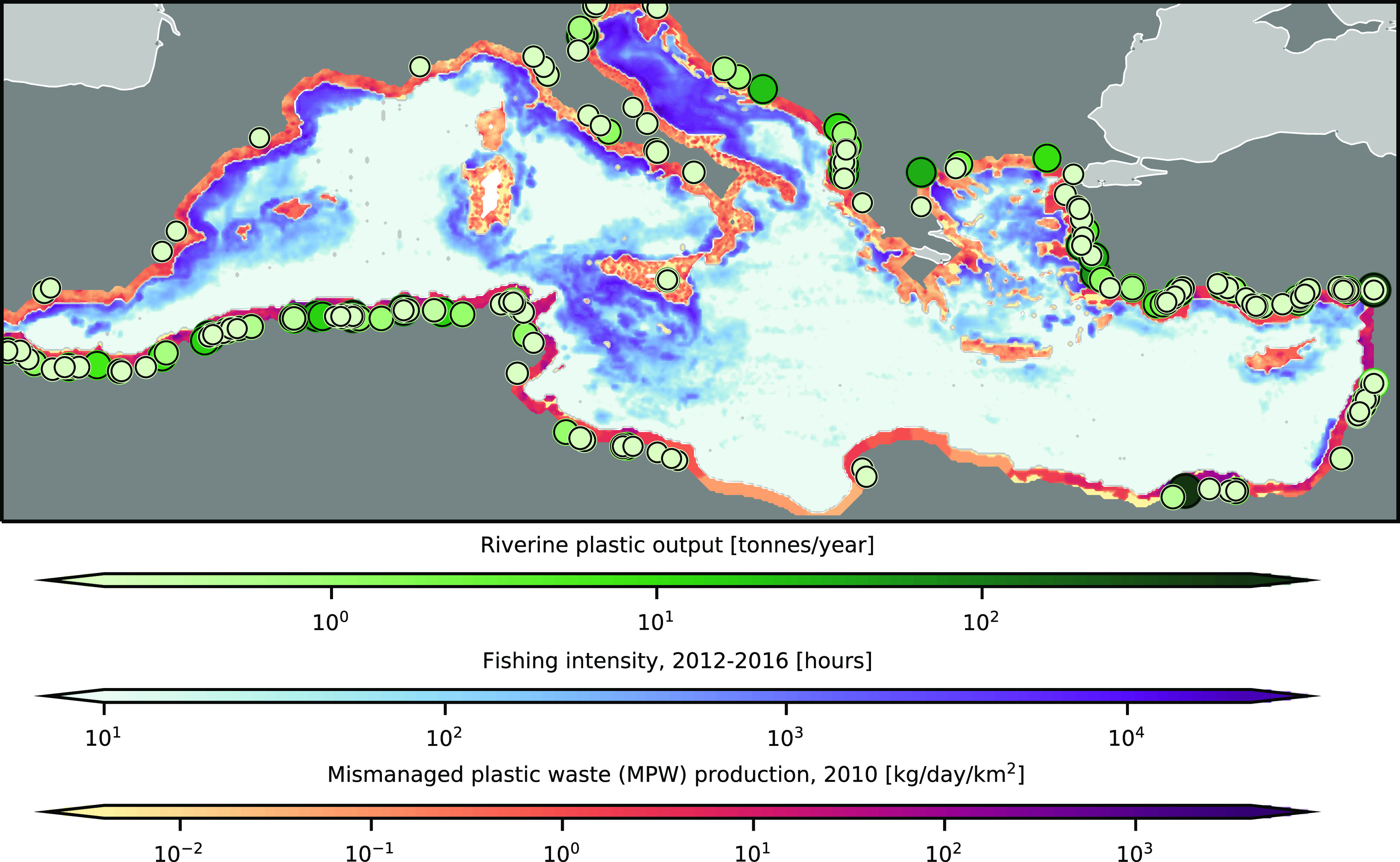
The posterior parameter estimates as obtained using the observational data can be plugged into the model. The now calibrated model is used to create a map where plastics are removed from the surface water. The resulting fluxes due to beaching and sinking are shown for the most likely estimates in Figure 4. Please note that the beaching fluxes are given in terms of the amount entering the coastal cells of the model, that is per unit area. By this way, no assumptions have to be made about the coastal length inside the cells.
Figure 4.
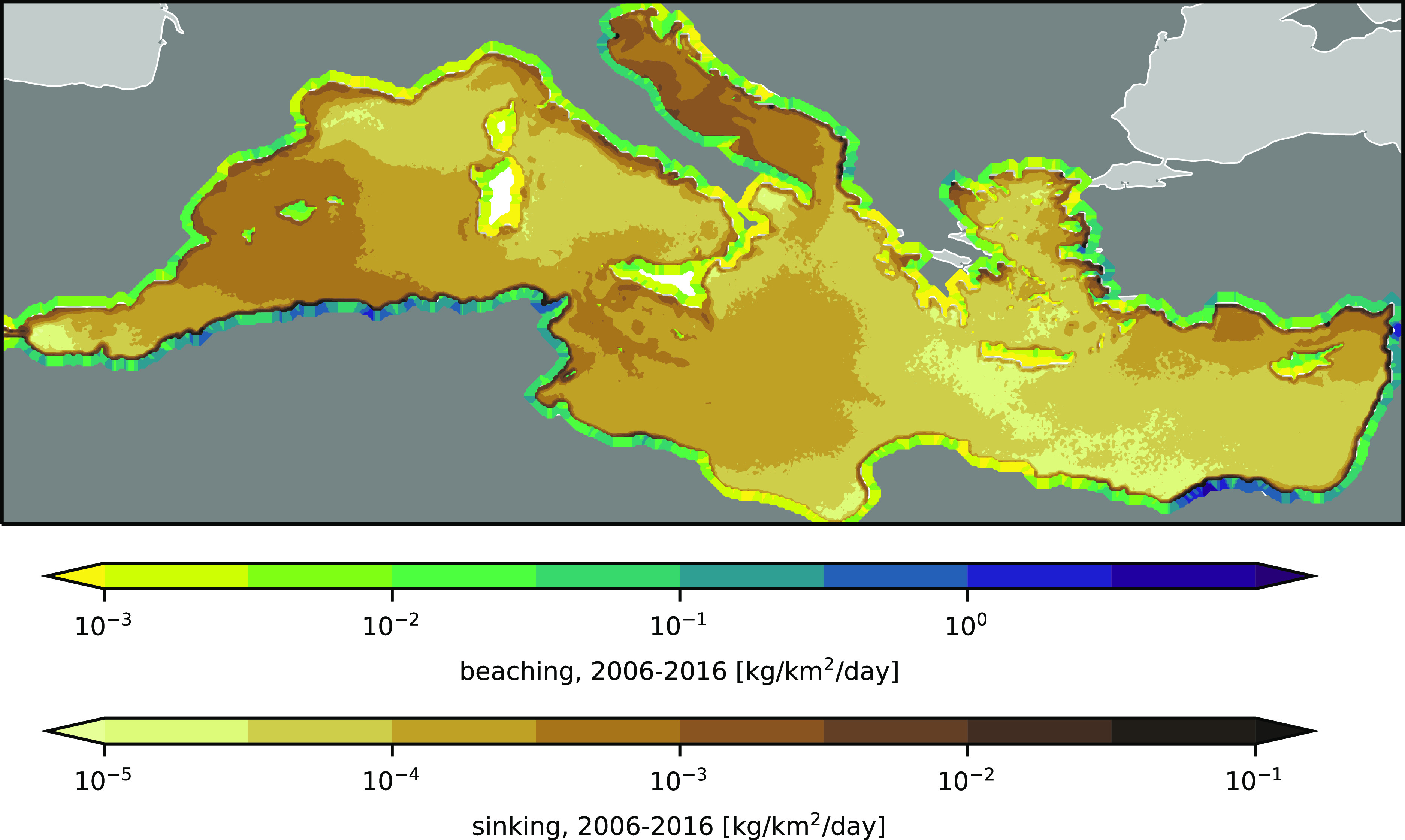
Locations in the Mediterranean where beaching and sinking of plastic particles are expected to occur, calculated over 2006–2016. Beaching fluxes are given for the coastal grid boxes (1/16 by 1/16°); hence, no assumptions are made about coastal segment lengths or widths (i.e. coastal lengths contained in the grid boxes will vary, the map does not represent fluxes per stretch of beach in kg/km/day directly).
Some beaches which appear to be heavily polluted are located along the North African coast, areas with high estimated amounts of MPW.3 Another area is the eastern coast of the Mediterranean. A significant amount of plastics is predicted to be emitted at the coast of Egypt, with predominant eastward currents following the coastlines. Other major sources of plastics are thought to be the Seyhan and Ceyhan rivers in Turkey, where coastlines in the vicinity are predicted to be heavily polluted as well. Adding to the various sources of plastics, many surface currents end in the eastern basin because of downwelling (Figure 1), enhancing the problem at these locations. Patterns of beaching are different on islands depending on which side one looks at: for example, more beaching is estimated on the western face of Sardinia and the northern face of Crete which was also reported in the observations.55
The highest fluxes of sinking of more than 1 kg/km2/day occur just next to the coast, where the nonbuoyant plastics immediately sink down. Further away from the coast, the fluxes are significantly less. In the centre of the Adriatic Sea, relatively high sinking fluxes are predicted of more than 1 g/km2/day. In the western basin, there is a large area around the Balearic Islands spanning the Algerian to the Spanish coast with relatively high sinking fluxes of 0.1–1 g/km2/day in the open water. Some qualitative similarities can be observed when comparing with the previous modeling study from Liubartseva et al.,15 which also found high sinking fluxes around the Balearic Islands, the western coast of the Adriatic, south of the Ionian Sea, and the southern coast of Turkey. However, we find higher sinking fluxes in the Gulf of Lion compared to its surroundings and high sinking fluxes along the Eastern Adriatic coast and between Tunisia and Sicily.
There is an estimated total plastic input of about 25,600 tonnes over 2006–2016 (2500 tonnes for the last complete model year 2015). The floating mass stays relatively constant during the simulation, while the sinks keep taking up mass introduced to the basin. Approximately, 54% of all plastics eventually ends up on coastlines, and 45% starts sinking down. The most likely estimate for the total floating mass in 2015 ranges from 110 to 190 tonnes. This has a small caveat: the model misses some variance compared to the measurements, and because model output is produced on a log10 scale, this results in a underestimation of the total mass (see the Supporting Information for further discussion S5). Correcting this missing variance leads to an estimate of 190–340 tonnes of floating plastics. This is somewhat lower than the estimate by Cózar et al.,20 where it was estimated to be 756–2969 tonnes.
The numbers presented above are for the most likely posterior estimates. We can also estimate the posterior covariance matrix (see the Supporting Information S3), allowing us to estimate likely mass balance ranges using Monte Carlo sampling. For 2015, this results in a total plastic input in the range of 2100–3400 tonnes; a floating mass of 170–420 tonnes; 1200–1900 tonnes of plastics beaching (49–63%); and 900–1500 tonnes of plastics sinking (37–51%), all reported in terms of the 95% confidence interval (80 samples).
Given the results presented here, it seems likely that at least for the Mediterranean, previous estimates of plastics entering the marine environment (>100,000 tonnes3,15) are too high. The observed floating plastic concentrations could, in these cases, only be explained by having much lower time scales for the sink terms than estimated here. The estimated beaching time scale for floating plastics is already lower than the one calculated for drifter buoys. While the sinking time scale could in theory be lower than the estimated 12 weeks, it is very unlikely that it will fall much below the minimum 2 weeks reported in experimental studies.6 We do not expect that sinks neglected here such as fragmentation and degradation of plastic could explain a large part of the discrepancy because time scales of these processes are expected to be relatively high. See the Supporting Information S6 for a detailed discussion. Using the approach from Jambeck et al.3 and the same conversion rates of MPW to marine debris (15–40%, 50 km radius), we get a plastic input into the Mediterranean water of about 340,000–910,000 tonnes for 2015. Our estimated plastic input from coastal population (1100–2300 tonnes for 2015) would correspond to a conversion rate of 0.05–0.10%, which is about 2 orders of magnitude lower. Neuston net measurements missing the larger plastic pieces could explain some of this discrepancy, which should be quantified in the future. We do not expect that this will explain all of the discrepancy, however: in the study by Lebreton et al.,5 it was found that in the North Pacific accumulation zone, 92% of the megaplastics category (>50 cm) consists of fishing nets, ropes, and lines, which are more likely attributed to fishing related activities than land-based MPW.
Outlook
In this work, inverse modeling was used to calibrate parameters governing sources and sinks of floating plastics in the Mediterranean, by making use of neuston net observations of plastic concentrations. The mass balance of floating plastics resulting from this calibrated model is presented, which gives us an insight into where we expect most plastics to enter and leave the surface water.
A major step which needs to be taken in future work is ensuring that there is enough reliable data to inform the model and making sure there is good correlation between the model and measurements. Here, the correlation is somewhat low because of the high measurement variability, which is further discussed in the Supporting Information S5.
Observed plastic concentrations are highly variable as discussed earlier in this text (see, for example, the study by de Haan et al.35 and the Supporting Information S1). Measurement variability is further increased by the fact that different sampling campaigns might have slightly different methodologies. The Mediterranean features highly dynamic currents, making it relatively difficult to model plastic concentrations accurately compared to a domain with a more steady-state structure, like the accumulation zones in the subtropical gyres.1
We can look at including more types of measurements, such as observations from beaches, marine sediments, particle size distributions, and possibly data of plastic ingestion by animals. Some of these measurements are of a more cumulative nature, such as plastics gathered in sediment traps over time. Perhaps, this could alleviate some of the high temporal variability, allowing for more accurate comparison of the model output against observational data, helping to constrain the model parameters more accurately. Furthermore, this can result in a better understanding of the sinks neglected here such as fragmentation, degradation, and ingestion. We expect that these processes have a minor influence on the total mass balance (see Supporting Information S6 for a detailed discussion). However, how particle sizes evolve over time because of degradation and fragmentation might be important to consider when extending the model to consider size-dependent processes.
Decreasing the mismatch of the model with respect to the measurements will also involve making the model more complex. Only three parameters define the magnitude and ratio of the different plastic sources. In future work, the number of sources could be extended, and the local uncertainty in the input could be taken into account spatially, for example, correcting the errors in the estimated MPW per country. The output from individual rivers could be estimated more accurately on smaller temporal scales, possibly taking into account variations on outflow and precipitation. Extending the amount of parameters defining the sources makes the problem more underdetermined however. This means it will be necessary to have more accurate prior knowledge or more measurement data and/or reduced measurement errors.
For some parameters, spatial and temporal variability is likely important to be considered in the future. Biological productivity in the Mediterranean has temporal variability (e.g. seasonal blooms) and spatial variability (e.g. productivity related to upwelling).56 This likely influences the sinking time scale of plastics and could be taken into account in the future by using data from biochemistry models. Similarly, coastlines along the basin vary in type, which might influence the beaching time scale. Spatial variability could be taken in account by estimating whether a beach is more “rocky” or “sandy”. On the other hand, a parameter like Psink,0 might remain relatively constant both spatially and temporally, assuming that the types of plastics discarded in different countries are relatively similar.
Some larger plastic objects, like fishing nets, might not be captured by the neuston net measurements used to calibrate the model. The input in terms of mass might therefore in reality be larger than that estimated here. It might be a good idea to combine data used here with visual observations of litter as for example done by Eriksen et al.57 to account for the larger plastic items, if the mass of these objects could be estimated.
In future work, nonlinear effects caused by washing away of particles from beaches, defouling of particles, and different forcing for different particle sizes and shapes can be taken into account by using a more elaborate data-assimilation scheme. This would also allow for better separation of the effects of primary and secondary sources of plastics.58 As a final point, this work can be extended to other geographical regions where measurements are available.
Acknowledgments
This work is part of the ”Tracking Of Plastic In Our Seas” (TOPIOS) project, supported through funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 715386). Simulations were carried out on the Dutch National e-Infrastructure with the support of SURF Cooperative (project no. 16371 and 2019.034).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.0c01984.
Measurement corrections and variance; beaching time scale estimate; inverse modeling implementation; parameter estimation sensitivity study; model-measurement scatter plots and mass correction factor; and which sinks are neglected and why? (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- van Sebille E.; Wilcox C.; Lebreton L.; Maximenko N.; Hardesty B. D.; Van Franeker J. A.; Eriksen M.; Siegel D.; Galgani F.; Law K. L. A global inventory of small floating plastic debris. Environ. Res. Lett. 2015, 10, 124006. 10.1088/1748-9326/10/12/124006. [DOI] [Google Scholar]
- Eriksen M.; Lebreton L. C.; Carson H. S.; Thiel M.; Moore C. J.; Borerro J. C.; Galgani F.; Ryan P. G.; Reisser J. Plastic Pollution in the World’s Oceans: More than 5 Trillion Plastic Pieces Weighing over 250,000 Tons Afloat at Sea. PloS One 2014, 9, 1–15. 10.1371/journal.pone.0111913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jambeck J. R.; Geyer R.; Wilcox C.; Siegler T. R.; Perryman M.; Andrady A.; Narayan R.; Law K. L. Plastic waste inputs from land into the ocean. Science 2015, 347, 768–771. 10.1126/science.1260352. [DOI] [PubMed] [Google Scholar]
- Lebreton L. C.; Van Der Zwet J.; Damsteeg J. W.; Slat B.; Andrady A.; Reisser J. River plastic emissions to the world’s oceans. Nat. Commun. 2017, 8, 1–10. 10.1038/ncomms15611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebreton L.; Slat B.; Ferrari F.; Sainte-Rose B.; Aitken J.; Marthouse R.; Hajbane S.; Cunsolo S.; Schwarz A.; Levivier A.; Noble K.; Debeljak P.; Maral H.; Schoeneich-Argent R.; Brambini R.; Reisser J. Evidence that the Great Pacific Garbage Patch is rapidly accumulating plastic. Sci. Rep. 2018, 8, 1–15. 10.1038/s41598-018-22939-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazey F. M. C.; Ryan P. G. Biofouling on buoyant marine plastics: An experimental study into the effect of size on surface longevity. Environ. Pollut. 2016, 210, 354–360. 10.1016/j.envpol.2016.01.026. [DOI] [PubMed] [Google Scholar]
- Lobelle D.; Cunliffe M. Early microbial biofilm formation on marine plastic debris. Mar. Pollut. Bull. 2011, 62, 197–200. 10.1016/j.marpolbul.2010.10.013. [DOI] [PubMed] [Google Scholar]
- Cole M.; Lindeque P.; Fileman E.; Halsband C.; Goodhead R.; Moger J.; Galloway T. S. Microplastic Ingestion by Zooplankton. Environ. Sci. Technol. 2013, 47, 6646–6655. 10.1021/es400663f. [DOI] [PubMed] [Google Scholar]
- Güven O.; Gökdağ K.; Jovanović B.; Kıdeyş A. E. Microplastic litter composition of the Turkish territorial waters of the Mediterranean Sea, and its occurrence in the gastrointestinal tract of fish. Environ. Pollut. 2017, 223, 286–294. 10.1016/j.envpol.2017.01.025. [DOI] [PubMed] [Google Scholar]
- van Franeker J. A.; Blaize C.; Danielsen J.; Fairclough K.; Gollan J.; Guse N.; Hansen P. L.; Heubeck M.; Jensen J. K.; Le Guillou G.; Olsen B.; Olsen K. O.; Pedersen J.; Stienen E. W.; Turner D. M. Monitoring plastic ingestion by the northern fulmar Fulmarus glacialis in the North Sea. Environ. Pollut. 2011, 159, 2609–2615. [DOI] [PubMed] [Google Scholar]
- Song Y. K.; Hong S. H.; Jang M.; Han G. M.; Jung S. W.; Shim W. J. Combined Effects of UV Exposure Duration and Mechanical Abrasion on Microplastic Fragmentation by Polymer Type. Environ. Sci. Technol. 2017, 51, 4368–4376. 10.1021/acs.est.6b06155. [DOI] [PubMed] [Google Scholar]
- Booth A. M.; Kubowicz S.; Beegle-Krause C.; Skancke J.; Nordam T.; Landsem E.; Throne-Holst M.; Jahren S.. Microplastic in global and Norwegian Marine Environments: Distributions, Degradation Mechanisms and Transport, 2017. Vol. M-918.
- Woodall L. C.; Sanchez-vidal A.; Paterson G. L. J.; Coppock R.; Sleight V.; Calafat A.; Rogers A. D.; Narayanaswamy B. E.; Thompson R. C. The deep sea is a major sink for microplastic debris. R. Soc. Open Sci. 2014, 1, 1–8. 10.1098/rsos.140317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebreton L.; Egger M.; Slat B. A global mass budget for positively buoyant macroplastic debris in the ocean. Sci. Rep. 2019, 9, 12922. 10.1038/s41598-019-49413-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liubartseva S.; Coppini G.; Lecci R.; Clementi E. Tracking plastics in the Mediterranean: 2D Lagrangian model. Mar. Pollut. Bull. 2018, 129, 151–162. 10.1016/j.marpolbul.2018.02.019. [DOI] [PubMed] [Google Scholar]
- Maximenko N.; Corradi P.; Law K. L.; Van Sebille E.; Garaba S. P.; Lampitt R. S.; Galgani F.; Martinez-Vicente V.; Goddijn-Murphy L.; Veiga J. M.; Thompson R. C.; Maes C.; Moller D.; Löscher C. R.; Addamo A. M.; Lamson M. R.; Centurioni L. R.; Posth N. R.; Lumpkin R.; Vinci M.; Martins A. M.; Pieper C. D.; Isobe A.; Hanke G.; Edwards M.; Chubarenko I. P.; Rodriguez E.; Aliani S.; Arias M.; Asner G. P.; Brosich A.; Carlton J. T.; Chao Y.; Cook A.-M.; Cundy A. B.; Galloway T. S.; Giorgetti A.; Goni G. J.; Guichoux Y.; Haram L. E.; Hardesty B. D.; Holdsworth N.; Lebreton L.; Leslie H. A.; Macadam-Somer I.; Mace T.; Manuel M.; Marsh R.; Martinez E.; Mayor D. J.; Le Moigne M.; Molina Jack M. E.; Mowlem M. C.; Obbard R. W.; Pabortsava K.; Robberson B.; Rotaru A.-E.; Ruiz G. M.; Spedicato M. T.; Thiel M.; Turra A.; Wilcox C. Toward the Integrated Marine Debris Observing System. Front. Mar. Sci. 2019, 6, 447. 10.3389/fmars.2019.00447. [DOI] [Google Scholar]
- van Sebille E.; Aliani S.; Law K. L.; Maximenko N.; Alsina J. M.; Bagaev A.; Bergmann M.; Chapron B.; Chubarenko I.; Cózar A.; Delandmeter P.; Egger M.; Fox-Kemper B.; Garaba S. P.; Goddijn-Murphy L.; Hardesty B. D.; Hoffman M. J.; Isobe A.; Jongedijk C. E.; Kaandorp M. L. A.; Khatmullina L.; Koelmans A. A.; Kukulka T.; Laufkötter C.; Lebreton L.; Lobelle D.; Maes C.; Martinez-Vicente V.; Morales Maqueda M. A.; Poulain-Zarcos M.; Rodríguez E.; Ryan P. G.; Shanks A. L.; Shim W. J.; Suaria G.; Thiel M.; van den Bremer T. S.; Wichmann D. The physical oceanography of the transport of floating marine debris. Environ. Res. Lett. 2020, 15, 023003. 10.1088/1748-9326/ab6d7d. [DOI] [Google Scholar]
- Pedrotti M. L.; Petit S.; Elineau A.; Bruzaud S.; Crebassa J. C.; Dumontet B.; Martí E.; Gorsky G.; Cózar A. Changes in the floating plastic pollution of the mediterranean sea in relation to the distance to land. PloS One 2016, 11, 1–14. 10.1371/journal.pone.0161581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiBenedetto M. H. Non-breaking Wave Effects on Buoyant Particle Distributions. Front. Mar. Sci. 2020, 7, 148. 10.3389/fmars.2020.00148. [DOI] [Google Scholar]
- Cózar A.; Sanz-Martín M.; Martí E.; González-Gordillo J. I.; Ubeda B.; gálvez J.; Irigoien X.; Duarte C. M. Plastic accumulation in the mediterranean sea. PloS One 2015, 10, 1–12. 10.1371/journal.pone.0121762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delandmeter P.; van Sebille E. The Parcels v2.0 Lagrangian framework: new field interpolation schemes. Geosci. Model Dev. 2019, 12, 3571–3584. 10.5194/gmd-12-3571-2019. [DOI] [Google Scholar]
- Simoncelli S.; Fratianni C.; Pinardi N.; Grandi A.; Drudi M.; Oddo P.; Dobricic S.. Mediterranean Sea Physical Reanalysis (CMEMS MED-Physics) [Data set], 2019.
- Korres G.; Ravdas M.; Zacharioudaki A.. Mediterranean Sea Waves Hindcast (CMEMS MED-Waves) [Data set], 2019.
- Macias D.; Cózar A.; Garcia-gorriz E.; González-Fernández D.; Stips A. Surface water circulation develops seasonally changing patterns of floating litter accumulation in the Mediterranean Sea. A modelling approach. Mar. Pollut. Bull. 2019, 149, 110619. 10.1016/j.marpolbul.2019.110619. [DOI] [Google Scholar]
- van Sebille E.; Griffies S. M.; Abernathey R.; Adams T. P.; Berloff P.; Biastoch A.; Blanke B.; Chassignet E. P.; Cheng Y.; Cotter C. J.; Deleersnijder E.; Döös K.; Drake H. F.; Drijfhout S.; Gary S. F.; Heemink A. W.; Kjellsson J.; Koszalka I. M.; Lange M.; Lique C.; MacGilchrist G. A.; Marsh R.; Mayorga Adame C. G.; McAdam R.; Nencioli F.; Paris C. B.; Piggott M. D.; Polton J. A.; Rühs S.; Shah S. H. A. M.; Thomas M. D.; Wang J.; Wolfram P. J.; Zanna L.; Zika J. D. Lagrangian ocean analysis: Fundamentals and practices. Ocean Model. 2018, 121, 49–75. 10.1016/j.ocemod.2017.11.008. [DOI] [Google Scholar]
- Okubo A. Oceanic diffusion diagrams. Deep-Sea Res. Oceanogr. Abstr. 1971, 18, 789–802. 10.1016/0011-7471(71)90046-5. [DOI] [Google Scholar]
- Rühs S.; Zhurbas V.; Koszalka I. M.; Durgadoo J. V.; Biastoch A. Eddy Diffusivity Estimates from Lagrangian Trajectories Simulated with Ocean Models and Surface Drifter Data-A Case Study for the Greater Agulhas System. J. Phys. Oceanogr. 2017, 48, 175–196. 10.1175/jpo-d-17-0048.1. [DOI] [Google Scholar]
- Collignon A.; Hecq J.-H.; Glagani F.; Voisin P.; Collard F.; Goffart A. Neustonic microplastic and zooplankton in the North Western Mediterranean Sea. Mar. Pollut. Bull. 2012, 64, 861–864. 10.1016/j.marpolbul.2012.01.011. [DOI] [PubMed] [Google Scholar]
- Collignon A.; Hecq J.-H.; Galgani F.; Collard F.; Goffart A. Annual variation in neustonic micro- and meso-plastic particles and zooplankton in the Bay of Calvi (Mediterranean-Corsica). Mar. Pollut. Bull. 2014, 79, 293–298. 10.1016/j.marpolbul.2013.11.023. [DOI] [PubMed] [Google Scholar]
- Fossi M. C.; Panti C.; Guerranti C.; Coppola D.; Giannetti M.; Marsili L.; Minutoli R. Are baleen whales exposed to the threat of microplastics? A case study of the Mediterranean fin whale (Balaenoptera physalus). Mar. Pollut. Bull. 2012, 64, 2374–2379. 10.1016/j.marpolbul.2012.08.013. [DOI] [PubMed] [Google Scholar]
- Gajšt T.; Bizjak T.; Palatinus A.; Liubartseva S.; Kržan A. Sea surface microplastics in Slovenian part of the Northern Adriatic. Mar. Pollut. Bull. 2016, 113, 392–399. 10.1016/j.marpolbul.2016.10.031. [DOI] [PubMed] [Google Scholar]
- Gerigny O.; Brun M.; Tomasino C.; Lacroix C.; Kerambrun L.; Galgani F.. Évaluation du Descripteur 10 ”Déchets Marins” en France Métropolitaine. Rapport Scientifique Pour l’évaluation 2018 au Titre de la DCSMM (ministère de l’environnement), Rapport interne IFREMER/CEDRE, 2018; p 349.
- Gündoğdu S.; Çevik C. Micro- and mesoplastics in Northeast Levantine coast of Turkey: The preliminary results from surface samples. Mar. Pollut. Bull. 2017, 118, 341–347. [DOI] [PubMed] [Google Scholar]
- Gündoğdu S.; Çevik C.; Ayat B.; Aydoğan B.; Karaca S. How microplastics quantities increase with flood events? An example from Mersin Bay NE Levantine coast of Turkey. Environ. Pollut. 2018, 239, 342–350. 10.1016/j.envpol.2018.04.042. [DOI] [PubMed] [Google Scholar]
- de Haan W. P.; Sanchez-Vidal A.; Canals M. Floating microplastics and aggregate formation in the Western Mediterranean Sea. Mar. Pollut. Bull. 2019, 140, 523–535. 10.1016/j.marpolbul.2019.01.053. [DOI] [PubMed] [Google Scholar]
- van der Hal N.; Ariel A.; Angel D. L. Exceptionally high abundances of microplastics in the oligotrophic Israeli Mediterranean coastal waters. Mar. Pollut. Bull. 2017, 116, 151–155. 10.1016/j.marpolbul.2016.12.052. [DOI] [PubMed] [Google Scholar]
- Ruiz-Orejón L. F.; Sardá R.; Ramis-Pujol J. Floating plastic debris in the Central and Western Mediterranean Sea. Mar. Environ. Res. 2016, 120, 136–144. 10.1016/j.marenvres.2016.08.001. [DOI] [PubMed] [Google Scholar]
- Ruiz-Orejón L. F.; Sardá R.; Ramis-Pujol J. Now, you see me: High concentrations of floating plastic debris in the coastal waters of the Balearic Islands (Spain). Mar. Pollut. Bull. 2018, 133, 636–646. 10.1016/j.marpolbul.2018.06.010. [DOI] [PubMed] [Google Scholar]
- Suaria G.; Avio C. G.; Mineo A.; Lattin G. L.; Magaldi M. G.; Belmonte G.; Moore C. J.; Regoli F.; Aliani S. The Mediterranean Plastic Soup: Synthetic polymers in Mediterranean surface waters. Sci. Rep. 2016, 6, 1–10. 10.1038/srep37551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeri C.; Adamopoulou A.; Bojanić Varezić D.; Fortibuoni T.; Kovač Viršek M.; Kržan A.; Mandic M.; Mazziotti C.; Palatinus A.; Peterlin M.; Prvan M.; Ronchi F.; Siljic J.; Tutman P.; Vlachogianni T. Floating plastics in Adriatic waters (Mediterranean Sea): From the macro- to the micro-scale. Mar. Pollut. Bull. 2018, 136, 341–350. 10.1016/j.marpolbul.2018.09.016. [DOI] [PubMed] [Google Scholar]
- Kukulka T.; Proskurowski G.; Morét-Ferguson S.; Meyer D. W.; Law K. L. The effect of wind mixing on the vertical distribution of buoyant plastic debris. Geophys. Res. Lett. 2012, 39, 1–6. 10.1029/2012gl051116. [DOI] [Google Scholar]
- van Emmerik T.; Schwarz A.. Plastic debris in rivers. WIREs Water 2020, 7. 10.1002/wat2.1398 [DOI] [Google Scholar]
- Castro-Jiménez J.; González-Fernández D.; Fornier M.; Schmidt N.; Sempéré R. Macro-litter in surface waters from the Rhone River: Plastic pollution and loading to the NW Mediterranean Sea. Mar. Pollut. Bull. 2019, 146, 60–66. 10.1016/j.marpolbul.2019.05.067. [DOI] [PubMed] [Google Scholar]
- Kroodsma D. A.; Mayorga J.; Hochberg T.; Miller N. A.; Boerder K.; Ferretti F.; Wilson A.; Bergman B.; White T. D.; Block B. A.; Woods P.; Sullivan B.; Costello C.; Worm B. Tracking the global footprint of fisheries. Science 2018, 359, 904–908. 10.1126/science.aao5646. [DOI] [PubMed] [Google Scholar]
- SEDAC; CIESIN—Center for International Earth Science Information Network—Columbia University; FAO—United Nations Food and Agriculture Programme; CIAT—Centro Internacional de Agricultura Tropical . Gridded Population of the World, Version 3 (GPWv3): Population Count Grid, 2015.
- Hellweger F. L.; Bucci V. A bunch of tiny individuals - Individual-based modeling for microbes. Ecol. Modell. 2008, 220, 8–22. 10.1016/j.ecolmodel.2008.09.004. [DOI] [Google Scholar]
- Guillamón A.; Navarro J.; Ruiz J. M. Kernel density estimation using weighted data*. Commun. Stat. Theor. Methods 1998, 27, 2123–2135. 10.1080/03610929808832217. [DOI] [Google Scholar]
- Ward C. P.; Armstrong C. J.; Walsh A. N.; Jackson J. H.; Reddy C. M. Sunlight Converts Polystyrene to Carbon Dioxide and Dissolved Organic Carbon. Environ. Sci. Technol. Lett. 2019, 6, 669–674. 10.1021/acs.estlett.9b00532. [DOI] [Google Scholar]
- Kooi M.; Nes E. H. v.; Scheffer M.; Koelmans A. A. Ups and Downs in the Ocean: Effects of Biofouling on Vertical Transport of Microplastics. Environ. Sci. Technol. 2017, 51, 7963–7971. 10.1021/acs.est.6b04702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bond T.; Ferrandiz-mas V.; Felipe-sotelo M.; van Sebille E. The occurrence and degradation of aquatic plastic litter based on polymer physicochemical properties : A review. Crit. Rev. Environ. Sci. Technol. 2018, 48, 685–722. 10.1080/10643389.2018.1483155. [DOI] [Google Scholar]
- Tarantola A.Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM, 2005. [Google Scholar]
- Tikhonov A. N. On the solution of ill-posed problems and the method of regularization. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. [Google Scholar]
- Neumann D.; Callies U.; Matthies M. Marine litter ensemble transport simulations in the southern North Sea. Mar. Pollut. Bull. 2014, 86, 219–228. 10.1016/j.marpolbul.2014.07.016. [DOI] [PubMed] [Google Scholar]
- Stambler N. In The Mediterranean Sea: Its History and Present Challenges; Goffredo S., Dubinsky Z., Eds.; Springer: Netherlands, Dordrecht, 2014; pp 113–121. [Google Scholar]
- Karkanorachaki K.; Kiparissis S.; Kalogerakis G. C.; Yiantzi E.; Psillakis E.; Kalogerakis N. Plastic pellets, meso- and microplastics on the coastline of Northern Crete: Distribution and organic pollution. Mar. Pollut. Bull. 2018, 133, 578–589. 10.1016/j.marpolbul.2018.06.011. [DOI] [PubMed] [Google Scholar]
- Macias D. M.; Garcia-gorriz E.; Stips A. Productivity changes in the Mediterranean Sea for the twenty-first century in response to changes in the regional atmospheric forcing. Front. Mar. Sci. 2015, 2, 79. 10.3389/fmars.2015.00079. [DOI] [Google Scholar]
- Eriksen M.; Lebreton L. C.; Carson H. S.; Thiel M.; Moore C. J.; Borerro J. C.; Galgani F.; Ryan P. G.; Reisser J. Plastic Pollution in the World’s Oceans: More than 5 Trillion Plastic Pieces Weighing over 250,000 Tons Afloat at Sea. PloS One 2014, 9, 1–15. 10.1371/journal.pone.0111913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browne M. A. In Marine Anthropogenic Litter; Bergmann M., Gutow L., Klages M., Eds.; Springer, 2015; pp 229–244. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.