Summary
The activity of neurons of the medial posterior parietal area V6A in macaque monkeys is modulated by many aspects of reach task. In the past, research was mostly focused on modulating the effect of single parameters upon the activity of V6A cells. Here, we used Generalized Linear Models (GLMs) to simultaneously test the contribution of several factors upon V6A cells during a fix-to-reach task. This approach resulted in the definition of a representative “functional fingerprint” for each neuron. We first studied how the features are distributed in the population. Our analysis highlighted the virtual absence of units strictly selective for only one factor and revealed that most cells are characterized by “mixed selectivity.” Then, exploiting our GLM framework, we investigated the dynamics of spatial parameters encoded within V6A. We found that the tuning is not static, but changed along the trial, indicating the sequential occurrence of visuospatial transformations helpful to guide arm movement.
Subject Areas: Neuroscience, Behavioral Neuroscience, Biocomputational Method
Graphical Abstract
Highlights
-
•
The parietal cortex integrates a variety of sensorimotor inputs to guide reaching
-
•
GLM disentangled the effect of various reaching parameters upon cell activity
-
•
V6A neurons were not functionally clustered, but characterized by mixed selectivity
-
•
Spatial selectivity was dynamic and reached its peak during the movement phase
Neuroscience; Behavioral Neuroscience; Biocomputational Method
Introduction
The ability to integrate and filter in a flexible way the multitude of sensory stimuli coming from inside and outside the body relies on associative cortices. How these computations occur at single neuron and population levels is still an unsolved problem. It is well accepted that the information is distributed in neural networks, with single cells modulated by many parameters at the same time, in a non-linear way. Thus, the actual view is that neuronal activity is characterized by what has been called “mixed selectivity” (Johnston et al., 2019; Parthasarathy et al., 2017; Fusi et al., 2016; Rigotti et al., 2013). According to this hypothesis, just a minority of cells would be strongly modulated by a specific factor, whereas most of them would code for combinations of different features.
The associative cortices, like the posterior parietal cortex (PPC), include a variety of multimodal associative areas whose neurons are modulated by a plethora of different factors (Binkofski and Buccino, 2018, Galletti and Fattori, 2018, Gamberini et al., 2020). Within macaque PPC area V6A, located in the anterior bank of parieto-occipital sulcus, (Galletti et al., 1999), is a higher-order visuomotor area modulated by visual signals coming from the whole visual field and somatic signals coming from the upper limbs (Gamberini et al., 2011, 2018), as well as by oculomotor signals related to gaze position and eye movement (Galletti et al., 1995; Kutz et al., 2003 Breveglieri et al., 2012). V6A neurons are also strongly modulated by reaching movements, both during action preparation and execution (Bosco et al., 2010, 2015, 2016; Fattori et al., 2001, 2005, 2009; Hadjidimitrakis, 2017; Santandrea et al., 2018) and attentional shifts (Galletti et al., 2010, see also Fattori et al., 2017; Galletti and Fattori, 2018 for reviews). In addition to single parameters, in some of the previous V6A studies the influence of pairwise parameters has also been studied, as for instance, target and gaze positions (Marzocchi et al., 2008), target position and visual condition (Bosco et al., 2010), target and initial hand positions (Hadjidimitrakis et al., 2017), etc. Recently, Bosco et al. (2019) used a novel dimensionality reduction method (dPCA) to extract from V6A information about a number of different modulating signals (visual condition, target position, wrist orientation, grip type), obtaining a compact view of the population activity. However, the authors did not address the question of whether all parameters were encoded in single cells, in separate subpopulations, or were distributed through the whole network.
To our knowledge, no comprehensive work has yet tried to correlate V6A single-cell activity with a full set of modulating variables concurrently acting upon the same neuron during the execution of the same task. Because of the multimodal nature of V6A, we expected that its neurons are characterized by “mixed selectivity.” Moreover, given the sensorimotor transformations occurring in this area, we also expected that the influence of spatial parameters changes over time. To test our hypotheses, we first uncoupled different parameter contributions at single-cell level, and then we moved to population level to study the dynamics of these contributions.
Among the mathematical probabilistic models, the family of Generalized Linear Models (GLM) offers a valid statistical framework to check how a variable of interest (i.e., the neural activity) is explained by several features or “regressors.” As the Poisson distribution is the most appropriate to model single-cell activity (see Transparent Methods), we used a Poisson GLM to study the effect on neuronal activity of the many factors that are known to modulate V6A. We collected spiking activity of V6A neurons and gaze positions during a delayed reaching task, and then fitted neural activity of a single cell with eye-related and reaching-related parameters. Our analysis allowed us to represent activity modulations of each cell with a set of weights that we named “functional fingerprint.” Across the population, units were not clustered in homogeneous groups according to their fingerprints, but were distributed in a functional continuum, suggesting that V6A is characterized by “mixed selectivity.” Influences of spatial parameters were not static but changed through space and time, indicating the occurrence of visuospatial transformations helpful to guide movement.
Results
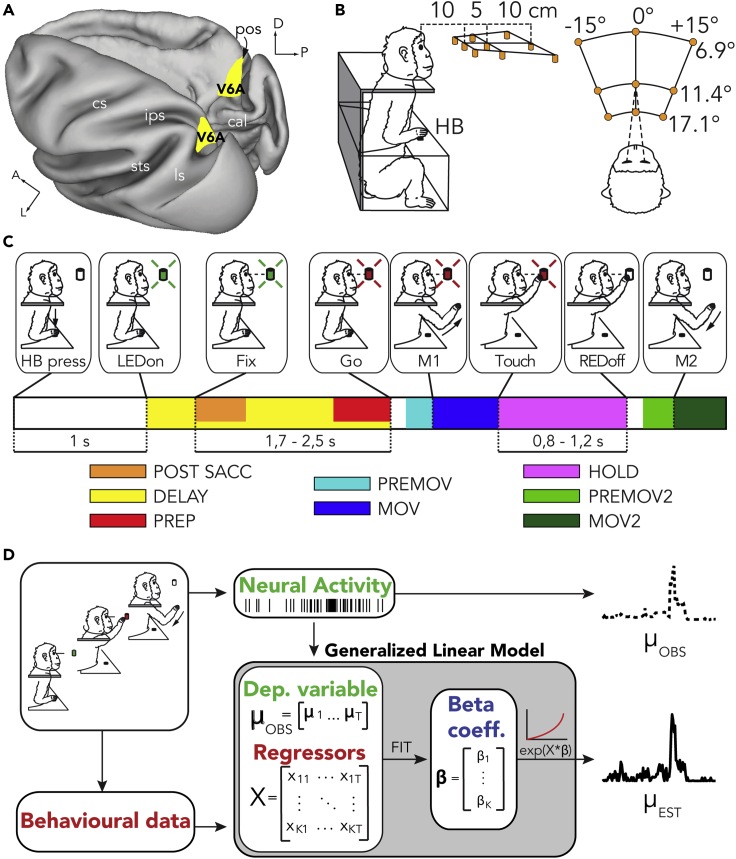
Single-cell activity was extracellularly recorded from area V6A (see Figure 1A) while two monkeys (M1 and M2) performed an instructed delay reaching task toward nine targets placed at eye level (Figure 1B). The monkey pressed a home button (HB) to begin the trial. As illustrated in the temporal sequence in Figure 1C, one of the nine LEDs lit up green and the monkey had to fixate it. After a variable delay, when the LED changed color from green to red, the animal was required to perform a hand movement to reach and press the LED and hold it until the LED turned off. After that, the animal returned the hand to the initial position, pressed the HB to receive liquid reward, and a new trial began.
Figure 1.
Anatomical Localization of Area V6A, Experimental Design, and Mathematical Model
(A) Three-dimensional reconstruction of macaque brain. Dorsal view of the left hemisphere and medial view of the right hemisphere showing area V6A in yellow (Galletti et al., 1999). cal, calcarine sulcus; cs, central sulcus; ips, intraparietal sulcus; ls, lunate sulcus; pos, parieto-occipital sulcus; sts, superior temporal sulcus; D, dorsal; P, posterior; A, anterior; L, lateral.
(B) Experimental setup. Reach movements were performed in darkness toward 1 of 9 LEDs (orange) arranged over a panel mounted at eye level in front of the monkey. Spatial coordinates of targets are indicated as vergence and version angles with respect to the eyes. HB: Home Button.
(C) Task sequence. From left to right: trial start (HB press), target appearance (LEDon), fixation onset (end of saccade, Fix), go signal (Go), start of the arm movement (M1), touch and holding of the target (Touch), LED switch-off (REDoff) return movement (M2). Color bar below the drawings illustrate the epochs considered in the model. DELAY epoch overlaps with POSTSACC and PREP.
(D) Schematic representation of the Generalized Linear model. Behavioral data are used to build the matrix of regressors (X, independent variables). Recorded neural activity is used to build the vector of μOBS (dependent variable). X and μOBS are used to fit the model and estimate the vector of beta coefficients (β). μEST can be reconstructed with X and the estimated β passing through an exponential function.
Our dataset consisted of cells that were recorded for 10 correct trials for each of the 9 targets (N = 181; 64 from M1, 117 from M2; see Figure S1 for the recording sites). To reduce sources of noise we performed a 1-way ANOVA (factor: epoch; levels: 8) on mean firing rates within epochs of interest (for more details see Transparent Methods) to identify task-related cells. The entire neural population resulted modulated, i.e., the mean firing rates differed significantly for at least one epoch, with no exceptions. Furthermore, we selected the cells according to the goodness-of-fit of our model (see below). Spikes were counted in 40 ms bins, and all trials were concatenated tip to tail in a unique vector for each cell that represented the dependent variable. In the GLM context a dependent variable is explained with a combination of independent variables called “regressors” or “features” in this article (Figure 1D). Each independent variable was a vector of the same length of the dependent variable. The regressors were organized in blocks. EYE POSITION block contained information about the average gaze position discretized in a 3D grid for each bin (see Transparent Methods); EYE SPEED/DIR block contained information about the velocity and the direction of eye movements; POSTSACC, FIX, PREP, PREMOV, MOV, HOLD, PREMOV2, and MOV2 were blocks that contained spatiotemporal information about the sequence of behavioral epochs occurring along the task (see Figure 1C for the temporal sequence of the task and Transparent Methods for details). We refer to these blocks of regressors as “extrinsic.” The SPIKEHISTORY block contained information about firing activity of the neuron in the previous 200 ms. We refer to it as “intrinsic” block. For each cell, we first selected the most relevant regressors with LASSO regularization technique. This first step led us to retain on average 90 ± 20 (standard deviation) regressors over ≃150 across the entire population (non-zero beta coefficients estimated by LASSO). Then, for each cell, we built several Poisson GLMs: a complete model that included all the selected regressors, 10 nested models in which we removed each time a different block of extrinsic regressors, 1 nested model removing the intrinsic block of regressors (extrinsic-only model), and 1 nested model removing all the extrinsic blocks of regressors (intrinsic-only model). All the models were cross-validated, and reported results are relative to the test datasets never seen by the no-LASSO-regularized models during the fitting (see Transparent Methods). To discard the units for which the model failed to capture neural modulations, we chose to select only the cells for which pseudo-R2 of the complete model reached at least 0.05, a criterion used in literature (Goodman et al., 2019; see Transparent Methods). As a result, 50/64 (78%) M1 units and 65/117 (56%) M2 units met this criterion and were retained for further analyses. For selected cells, pseudo-R2 was 0.102 [0.073, 0.147] (median [25th, 75th percentile]). To evaluate the influence of the different parts of our model (blocks of regressors) on neural activity, we first calculated for each nested model a relative pseudo-R2 that compared its goodness of fit with the complete model goodness of fit. We then adopted a metric that we called “w-value” (1 – relative pseudo-R2) directly proportional to the weight (i.e., the importance) of each block of regressors on the fitting of the complete model. Each w-value ranged from 0 (no influence of the removed block of regressors on spiking activity) to 1 (greatest influence of the block of regressors; see Transparent Methods for further details). The set of the 10 extrinsic w-values functionally qualifies each cell and represents what we called “functional fingerprint”.
Analysis at Single-Cell Level
Figure 2 shows data of two different example neurons (A, B). The column plots in the bottom part of the figure represent the “functional fingerprint” of cells shown in A and B, respectively. The first neuron (Figure 2A) showed strong changes in the discharge during the PREMOV and MOV epochs (light and dark blue, Figure 2A top), whereas during the other time epochs little or no effects were observed. In fact, the firing rate (dashed line) suddenly increased in PREMOV (just before the onset of arm movement) and remained high throughout the whole movement phase. A few motor-related parameters (linked to PREMOV and MOV epochs) explained most of cell modulation (highest columns, Figure 2A bottom). In the column plot, we marked with asterisks the blocks that resulted the most important to explain the neural activity from our analysis (see Transparent Methods).
Figure 2.
Examples of Single-Cell Activity
(A and B) (A) Neuron showing a marked selectivity for somato-motor components of the task; (B) a neuron with a mixed selectivity for several parameters. (Top) Plots are arranged according to the spatial position of targets over the panel (rows for different depths; columns for different directions, see Figure 1B). Recorded (μOBS, dashed line) and predicted (μEST, black continuous line) averaged firing rates (bin width: 40 ms). In each plot, data relative to the 10-fold validation sets are averaged across trials for each of the nine targets and aligned on movement onset (time “<0>”). Colors represent the epochs considered in the model. (Bottom) Bars show the weights (w-values) of the 10 extrinsic blocks of regressors (the “functional fingerprints” of the neurons) on the neural activity. Asterisks indicate most important w-values for each cell (their sum reaches at least 85% of the sum of all w-values of the cell, see Transparent Methods).
The neuron reported in Figure 2B had more complex modulations. It showed a clear preference for far positions and a peak in the activity when the animal reached them. Indeed, starting from the beginning of fixation, cell discharge was remarkably higher for far positions than for the others. Moreover, for far positions, it increased just before the movement onset (PREMOV) and reached a peak after it (MOV). On the contrary, for intermediate positions the neural activity was generally low, and even lower for near positions. Interestingly, during the epochs of major activity for far positions (PREMOV and MOV), the neuron was almost completely inhibited when the animal gazed and reached near positions. The “functional fingerprint” (Figure 2B bottom) shows the mixed selectivity of this cell, with six regressor blocks that significantly influence cell discharge (mainly PREMOV, MOV, HOLD, but also EYE POSITION, PREP, and MOV2).
It is worth noting that the “functional fingerprint” does not provide information about the spatial tuning of the unit, because it accounts for the overall influence of different parameters upon cell discharge (averaging the effect of parameters in different spatial positions) rather than accounting for changes in cell discharge according to the spatial position. Indeed, the functional fingerprint of cell in Figure 2A is much more selective (only a few parameters do influence cell discharge) than the one of cell in Figure 2B, even if the spatial selectivity of cell in Figure 2B is strikingly higher than the spatial selectivity of cell in Figure 2A.
Population Analysis
To understand how the functional properties were encoded in the V6A population, we further analyzed the results obtained cell by cell at population level. As described above, for each recorded neuron, we calculated 10 w-values, one for each of the extrinsic blocks of regressors. We first checked whether these w-values across the population were consistent between the two animals (Figures 3A and 3B; medians and intervals in Table S1). Despite some differences for single blocks (such as PREMOV that was higher in M1 than M2 or MOV and HOLD values that were slightly lower), the overall distribution of the median values of each block of regressors was consistent (Kolmogorov-Smirnov test, p = 0.6751). Figure 3A shows that in both animals the extrinsic regressors with higher w-values were EYE POSITION, MOV, and HOLD (median values for M1 + M2: 0.018, 0.015, and 0.016 respectively). Data of M1 and M2 pooled together are shown in Figure S2. The distribution of w-values sorted separately for each block of regressors showed that just a few cells in both animals had very high w-value, whereas the remaining cells (the large majority) showed gradually descending values (Figure 3B). It is possible to identify an elbow that splits the curve in two parts (see Transparent Methods). On average, the dividing point corresponded to the 90% ± 5% of the population (mean and standard deviation across all blocks and the two animals). In other words, focusing on each regressor, only a few cells (10%) were well modulated by that parameter, whereas most of the cells (the remaining 90%) showed mild or low modulations.
Figure 3.
Extrinsic Regressors' Weights across the Population
(A) Boxplot of w-values for each block of regressors across the population for the two animals separately. In each box, the central white mark represents the median, while the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points discarding outliers (MATLAB function: boxplot).
(B) W-values are plotted in ascending order for each block of regressors. Solid and empty arrows indicate the elbow of the curves for M1 and M2, respectively.
(C) Representation of the neural population (a dot for each cell) using the first three principal components (PCs) of the principal-component analysis (PCA) performed on the 10 extrinsic w-values. Dots take different combinations of three colors according to their w-values for the three most important regressor blocks (black for EYE POSITION, blue for MOV, pink for HOLD). Bull's-eyes indicated by solid and empty arrows represent the example neurons showed in Figures 2A and 2B respectively.
(D) Histogram showing the minimum number of extrinsic regressors' blocks (w-values) necessary for each cell to reach at least the 85% of its extrinsic w-values total sum (see Transparent Methods). Solid and empty arrows indicate where example neurons of Figures 2A and 2B, respectively fall.
Because each cell is described with a unique vector of w-values (functional fingerprint), to visualize this multidimensional data and investigate whether a functional structure does exist, we performed a principal-component analysis (PCA) on the extrinsic w-values (Figure 3C). No definite clustering of the data emerged from this analysis: the majority of cells were grouped together, with some outlier, sparse units. We tried to apply the most common clustering techniques (such as K-means and hierarchical clustering; see Transparent Methods), but any attempt failed to identify a segregation in our data.
To visually check whether there was a trend within the population, we colored in Figure 3C the dots according to cell modulations. For graphical purposes, we chose only the three main blocks of regressors (EYE POSITION, MOV, HOLD). Given the three pure colors associated with each of the three regressors (black, blue, and purple, respectively, see color code in Figure 3), each neuron (dot) was colored with a mixture of these colors based on its series of w-values (i.e., with a linear combination of colors weighed with the three w-values). The resulting colors of the outlier cells were similar to three pure ones, and thus they were the most selective for these parameters, whereas the majority of cells showed a combination of the three colors. For instance, the unit of Figure 2A, with high w-values for PREMOV and MOV, is located outside the central cloud of points in Figure 3C (bull's-eye indicated by filled arrow) and almost purely blue. On the contrary, the unit of Figure 2B is located in the central part of the principal components' (PCs') space and is colored according to its “mixed modulation” nature (Figure 3C, bull's-eye indicated by empty arrow). The gradual transition from one color to another across the dots is in accordance with the continuum of the w-values distributions (see Figure 3B).
To study cell selectivity for one block of regressors (versus non-selectivity, i.e., mixed selectivity), beyond the three main ones considered in Figure 3C, we computed how many blocks really matter for explaining the neural activity. Because of the variability both in the distribution and in the absolute values in the functional fingerprints, we adopted an adaptive threshold that took into account the cell total sum of w-values (see Transparent Methods). This procedure allowed us to calculate that, on average, that each cell was significantly modulated by 4.2 (±1.3) blocks of regressors (mean and standard deviation). Figure 3D shows the distribution across the entire population. Units on the left of the histogram were more selective (less parameters were needed to explain neural modulations), whereas units on the right were characterized by more complex and mixed modulations. In accordance with what has been already discussed, the example units of Figure 2 fell in opposite parts of the histogram: indeed, the cell of Figure 2A (filled arrow), more selective, with three modulating blocks of regressors, is in the left part; the cell of Figure 2B (empty arrow), with six modulating blocks, in the right part. As we partially expected, although V6A cells typically showed mixed selectivity, we never observed a “totally mixed” selectivity (i.e., cells with 8–9 important blocks).
Spatial and Temporal Correlation Analysis
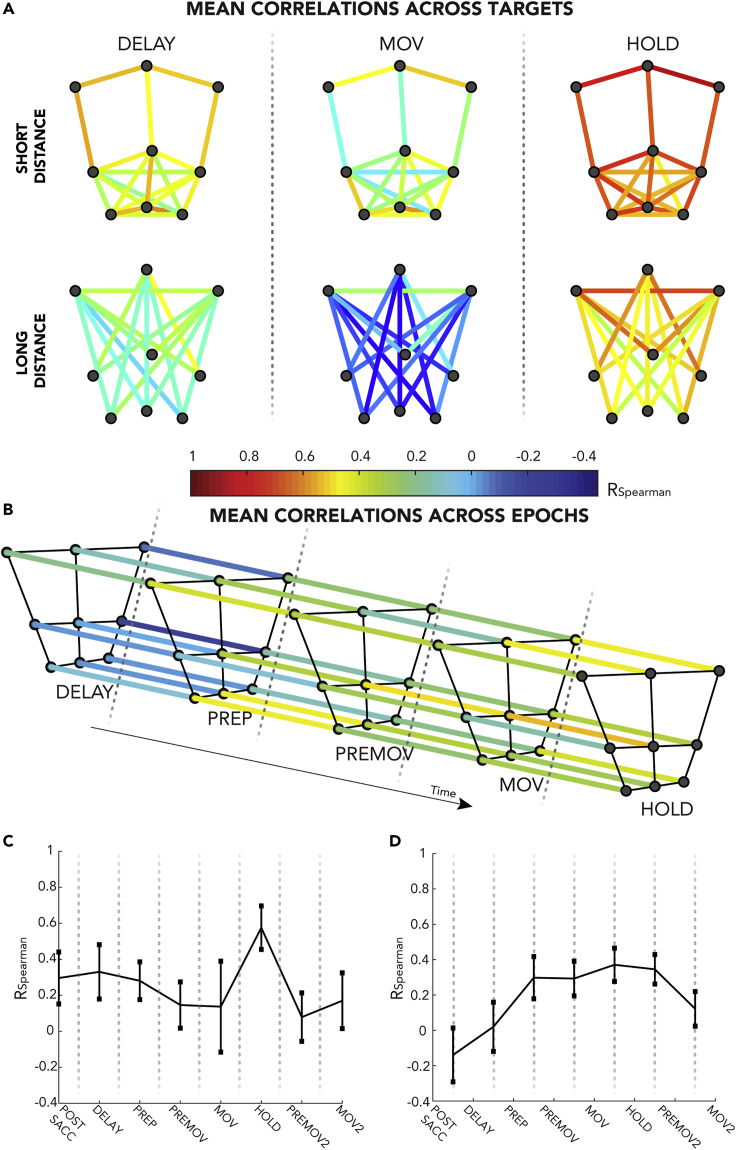
Up to here, we focused on the neural modulations explained by each block of regressors. However, our population analysis based on w-values did not give any direct indications about the spatial tuning, although it is known that area V6A is strongly influenced by direction and depth during reaching task (Fattori et al., 2017, 2005; Hadjidimitrakis et al., 2014, 2019; Battaglia-Mayer et al., 2000). To study the dynamics (or the lack of) of the spatial selectivity at population level, we extracted information about changes in the beta coefficients (i.e., the modulations captured by the model) performing a correlation analysis, similarly to recent studies (e.g., Zhang et al., 2017). Population activity for each target position and for each epoch can be expressed by a vector of beta coefficients extracted from the GL (generalized linear) complete models (one beta for each cell). In the graphs of Figures 4A and 4B, each node represents a target position. The colors of the edges represent the strength of the correlation between the two beta vectors of two different positions within the same epoch (Figure 4A) or between the two beta vectors of the same position across two subsequent epochs (Figure 4B). For a simpler interpretation, these results are averaged and summarized by the plots in Figures 4C and 4D.
Figure 4.
Spatial and Temporal Correlations between Beta Coefficients
(A) Correlations between beta coefficients of the population of different target positions within the same epoch. In the graphs, nodes represent the nine targets (see Figure 1B). Edges represent the correlation coefficient between beta coefficients of two different positions. Three panels show the three main epochs (DELAY, MOV. and HOLD). Top: edges link targets at short distance, bottom: edges for targets at long distances. Note that target positions are altered for graphical purposes. For a general trend across the task, see (C), and for details about the other epochs, see Supplementary Material.
(B) Correlations between beta coefficients of the population of the same target across subsequent epochs. In the graphs, nodes represent the nine targets (see Figure 1B). Edges represent the correlation coefficient between beta coefficients of two different epochs. The figure shows only the epochs of the central part of the task. For a general trend across the task, see (D).
(C) Mean correlation between beta coefficients of different target positions within the same epoch. Same data as in (A), but all pairwise correlations between targets are averaged. Error bars indicate the standard deviation.
(D) Mean correlation between beta coefficients of the same target across subsequent epochs. Same data as in (B), but pairwise correlations between epochs are averaged. Error bars indicate the standard deviation.
Figure 4A shows the correlations between two different positions within the same epoch. The three panels (DELAY, MOV, and HOLD) display the three epochs that resulted to be the most important ones after merging the data of the two animals (highest median w-values, see Figure S2/Table S1 and, for the other epochs, Figure S3). Moreover, for graphical purposes, we split all the pairwise correlations (36 edges) in two graphs for each epoch based on the physical distance between the linked nodes (top: short distance ≤ 10 cm, bottom: long distance >10 cm). We found differences among these epochs: HOLD was characterized by correlation coefficients generally higher than the others (0.58 ± 0.12, mean ± standard deviation), MOV had lower values (0.14 ± 0.25), and DELAY showed an intermediate strength in correlation (0.33 ± 0.15). Thus, the strength of spatial correlations (i.e., how similar population activity is between two different targets) varied along the trial. These fluctuations are shown in Figure 4C. In the figure, the plot represents the averaged correlation for all epochs (the three presented in Figure 4A and the remaining, presented in Figure S3). The peak of the plot corresponds to HOLD epoch, confirming what we already observed in Figure 4A (higher correlations). It is noteworthy that, within each epoch, there are huge differences in the strength of correlations depending on the physical distance of the two linked nodes (targets). Indeed, for all the three epochs in Figure 4A, within the same panel (epoch), bottom graphs (higher distances) show lower correlations than the upper ones (lower distances). This decrease in correlation strength with the increase of distance is highly significant (linear correlation, r = [-0.78; −0.91; −0.70], p ≃ [10−8; 10−14; 10−6] for DELAY, MOV and HOLD respectively; we observed the same effect in the remaining epochs, data not shown).
To study the changes in regression coefficients in a spatial-independent manner, we also correlated the two beta vectors of the same position across two subsequent epochs. This allowed to study the temporal evolution of the population encoding (Figure 4B). The figure displays only the epochs that represent the central part of the task, whereas Figure 4D shows the mean correlation values along the whole task. High correlation values indicate a stable pattern of population activity between two epochs (i.e., the neural activity for the same target is similar across the two epochs). At the beginning of the trial, the correlations were negative or near to 0, whereas they reached a sort of plateau with higher values as the task progressed (see Figure 4D).
Spike History Influence
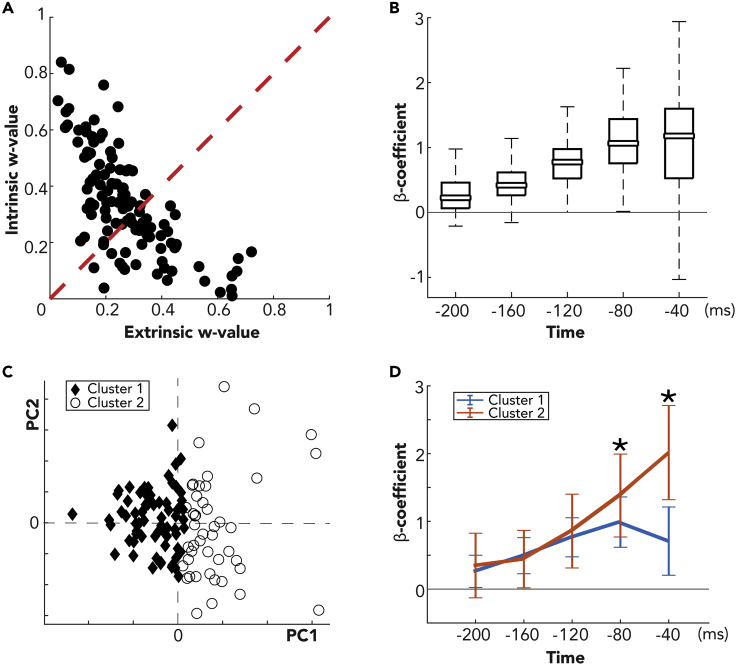
Until now, the analyses were focused on the extrinsic regressors. To also study the contribution on the fitting of the intrinsic part of the model, we compared the intrinsic w-value with the extrinsic w-value for each cell (Figure 5A). The scatterplot shows that a significant number of neurons (71/115, 62%) lied above the diagonal, that is, the w-value for the intrinsic part of the model was higher than that for the extrinsic part. It is remarkable that the spike history, represented in the model by only 5 regressors over a total of ≃150, predicted better the spiking activity than all the other variables in about 60% of cells. This is in accordance with the complex associative nature of area V6A (see Discussion). As the regressors have been normalized in the range [0,1] independently for each cell before the fitting, we extracted from the complete models the 5 beta coefficients relative to the spike history (1 for each time lag, see Transparent Methods) and directly compared them across the population (Figure 5B). Positive beta coefficients meant an excitatory effect of the spike history on the spiking activity, whereas negative values represented inhibition. Influence on neural activity of −200 ms and −160 ms time lags were low. More recent spiking events had on average greater effect. The most recent time lag (−40 ms) showed a broad distribution ranging from inhibition to the strongest excitatory effects. From a visual inspection of its probability distribution (data not shown), the existence of two peaks was evident, which could indicate two different clusters of cells within the population. To confirm this intuition, we ran a K-means clustering algorithm with 100 replicates to find a stable partition into the two clusters (i.e., a local minimum of the function, see Transparent Methods). We also tried to look for a greater number of clusters, but the three common techniques (elbow, gap statistics, and silhouette) we used to choose the optimal number failed to converge. We performed a PCA to reduce the dimensionality of our data points from 5-dimesional space (i.e., five spike history betas for each cell) to a 2-dimensional space (i.e., the first two PCs that explained the 86% of the variance) to represent the clusters in a Cartesian plane (Figure 5C). The two clusters included 70/115 (61%) and 45/115 (39%) units of the population, respectively.
Figure 5.
Influence of Spike History on Neural Activity
(A) Extrinsic w-value versus intrinsic w-value (data from M1 and M2 merged). Each dot represents a cell. For dots above the diagonal, spiking activity is predicted better by the intrinsic part of the model rather than the extrinsic one (i.e., the spike history fits better neural data than extrinsic regressors). x axis: w-value for the extrinsic part of the model. y axis: w-value for the intrinsic part.
(B) Boxplot of spike history beta coefficients in the full model across population. The model includes previous cell neural activity with five different time lags (−200, −160, −120, −80, −40 ms) and estimates a beta coefficient for each lag. For more details about the box plot, see Figure 3A.
(C) Representation of the neural population (a symbol for each cell) using the first two PCs of the PCA performed on the five spike history beta coefficients. Cells are divided in two clusters running a K-means clustering algorithm on the five spike history beta coefficients.
(D) Mean of the five spike history beta coefficients grouping the cells in the two clusters. Error bars represent the standard deviation, and asterisks indicate significant different distributions of beta coefficients between the clusters (t test, p < 0.05).
Note that, even if the clustering algorithm had been run on the original betas, the two clusters were almost perfectly separated according to the value of the first PC. From a visual inspection of PCA loadings (data not shown), it turned out that this PC carried information almost exclusively about the beta of the most recent bin confirming its relevance in driving clustering. Thus, the two clusters identified automatically by the algorithm corresponded to the two peaks observed at a glance. We did not find any correlation between the clusters and the two animals (chi-squared test on the ratios, p = 0.61). Conversely, we did find that, whereas the first cluster is equally distributed with about 50% of cells above and under the diagonal of the scatterplot in Figure 5A, the units of the second cluster lied mainly above the diagonal (75%). This higher influence of spike history on the model for this cluster is coherent with its higher beta coefficients (see below).
Figure 5D shows means and standard deviations for the five spike history betas within each cluster. The regression coefficients distributions were overlapping and not significantly different (t test, p > 0.05) for −200, −160, and −120 ms time lags. They were significantly different (t test, p < 0.05) for the −80 ms time lag, even if the error bars still partially overlapped and they finally differed (t test, p < 0.05) and did not overlap for the most recent (−40 ms) time lag, the one that drove the clustering. To sum up, whereas the first cluster had a mild excitatory modulation for the recent spike history (−120, −80 and −40 ms) that decreased for the previous time lags (−200 and −160 ms), the second cluster had a higher excitatory effect that increased almost linearly for the more recent two to three time lags. Note that inhibitory effects (negative betas in the Figure 5B, especially for −40 ms lag) sporadically observed for some cells did not constitute a significant trend in the population. Indeed, they almost completely disappeared computing the standard deviation (as in Figure 5D) instead of considering the boxplots (as in Figure 5B).
Discussion
In this study, we defined how different factors that modulated V6A cells are encoded at single-cell level by disentangling them with Poisson GLM. Our model inferred the dependence of activity pattern of each cell from several factors presented together. We obtained a “functional fingerprint” of each cell, which is the ensemble of factors (and their weights) modulating single cell's discharge (see the two example neurons in Figure 2). Present analyses revealed the virtual absence of units modulated by only one parameter. Indeed, on average, units were selective for four different regressor blocks, supporting the view of a mixed selectivity encoding in V6A. Next, we moved to the population level to study how neurons encoded spatial parameters along the trial. We found that spatial correlations were higher for neighboring positions and during hold epoch, whereas temporal correlations were higher and stable from movement preparation to target holding epoch. All these results taken together are coherent with the proposed role of V6A in sensorimotor transformations underlying eye-hand coordination in reaching and grasping.
Mixed Selectivity in V6A
The PPC is implicated in reach-to-grasp movements that are tightly coordinated in space and time. This functionality requires to integrate different inputs (either resulting from internal computation or from sensory information system). An open question is how all these parameters (visuospatial and somatic) are mixed together to guide coherent behavior. A recent work (Bosco et al., 2019) tried to uncouple contributions of visual information, target position, wrist orientation, and grip type in V6A during reach-to-grasp tasks using a demixed PCA technique (Kobak et al., 2016). The authors did separate the contributions of different parameters, but they did not explore how information was mixed at single cell level, a critical step in understanding the sensorimotor transformation, that is addressed by the present work. Theoretically, the encoding process of many inputs could occur following two hypotheses: (1) the area hosts separate, homogeneous groups of cells, each one of them carrying information mainly about one particular feature (or fixed combinations of them), but covering as a whole the encoding of many different features or (2) alternatively, each cell of the area mixes information relative to many different features in what is called “mixed selectivity” (Fusi et al., 2016). As demonstrated in this work, V6A contains only very few cells strongly modulated by a specific parameter, whereas most of them are mildly modulated by many factors. Indeed, the shape of w-values distributions for single blocks of regressors (see Figure 3B) across the population shows a few very high values and a gradual decrease toward 0. In particular, for every block of regressors considered, we found an elbow that splits the curve in two parts (highest values versus gradual descent). The shape of this distribution is very similar to that observed by Malik et al. (2015). The authors developed a measure that quantifies the tuning of a neural signal to relevant behavioral variables and found that the distribution of this measure in the motor cortex neural population could be well approximated with the generalized Pareto distribution. This means that regardless of how the strength of tuning is calculated (w-value here or Modulation Depth in Malik, 2015) and which cortical area is considered, only few cells are strongly modulated for one parameter, the majority of them showing a very low and continuous decreasing modulation. Similar results were found by Raposo et al. (2014) in rat PPC where they directly tested the hypothesis of the existence of cell types (or categories) within their population. They demonstrated the random distribution of features in what they defined a “category-free” population highlighting the possibility for a single network to respond the evolving demands of decision-making. From a functional point of view, in associative areas, we can hypothesize that the selective units receive specialized inputs from other areas and then they spread (working like a distribution hub) the information to neighboring cells. Mixed selectivity is demonstrated to be computationally efficient (Fusi et al., 2016) and less prone to errors than pure selectivity even when both forms of selectivity use the same number of spikes (Johnston et al., 2019). Neurons with mixed selectivity compute the information in a mixed way with a complexity that increases with the distance from the source of the inputs. This hypothesis is in accordance with computational models proposed for both parietal and other associative cortices (Barak et al., 2013; Rigotti et al., 2010; Pouget and Snyder, 2000; Zipser and Andersen, 1988).
Thus, the hypothesis of a full mixed selectivity seems to be more appropriate to describe V6A. Notably, Zhang et al. (2017) found that the AIP (anterior intraparietal area) area is characterized by what they called “partial mixed selectivity”: among the tested movement parameters, body parts (shoulder or hand) are encoded in two functionally segregated sub-populations within which the other parameters are mixed. In our case, none of the parameters considered in the present work leads to such a segregation, but they are randomly distributed across the population. Future studies should address this issue to investigate whether a similar encoding of effectors is present in area V6A (as in AIP) or whether this area is invariant to body part. The area AIP and the dorsolateral visual stream are more responsible for a finer control of hand configuration during grasping, whereas V6A and the dorsomedial visual stream are active for fast visuospatial computations in reach-to-grasp actions (Galletti and Fattori, 2018), so we do not expect such a clear-cut segregation between body parts.
The Importance of Eye and Arm Movement Signals Is Reflected in Mixed Selectivity
Eye-related signals, in particular gaze position signals in 3D space, strongly modulate the activity of V6A neurons (Breveglieri et al., 2012, 2014; Galletti et al., 1995; Hadjidimitrakis et al., 2011), whereas saccadic eye movements have a weaker influence (Battaglia-Mayer et al., 2000, Kutz et al., 2003). Indeed, in the “functional fingerprints”, EYE-POSITION had high w-values, whereas EYE SPEED/DIR showed extremely low values. We found transient post-saccadic modulations just after the beginning of fixation (POST SACC block of regressors) and tonic activity all along fixation (DELAY block of regressors, see below for a further Discussion). Relevance of eye position in V6A during reaching has a functional purpose given the pivotal role of V6A in visuomotor transformation. Retinotopic mapping together with eye position can support the reference frame transformation from eye- to body-centered frame, required to unfold reach movement (Andersen et al., 1985, McGuire and Sabes, 2011). Another example of activity strictly dependent on eye position signals is the one showed by V6A neurons with visual receptive field that remains stable in space regardless of eye movements (“real-position” cells; Galletti et al., 1993, Galletti et al., 1995). It is noteworthy that POST SACC and DELAY could contain information related not only to maintaining the fixation but also modulations due to planning activity or spatial attention. Unluckily, our task did not allow us to disentangle the contributions on neural activity of these processes. Beside the high influence of eye signals, we found that the early phase of arm movement, movement execution, and arm holding also strongly modulate the activity of V6A cells (high w-values of PREMOV, MOV, and HOLD blocks of regressors in Figure 3A). This is coherent with the visuomotor nature of area V6A and its involvement in coordination of reaching movements.
A Dynamic Representation of Visuospatial Information
To investigate how the neural population is spatially tuned along the trial, we performed a correlation analysis on the beta coefficients (Zhang et al., 2017). First, we computed all the correlations between different targets within a fixed epoch. For all the epochs considered, we found that target spatial positions close one to another were linked by higher correlations than farthest positions because, as expected, differences in population activity increased, increasing the distance. This trend is consistent with a gain field mechanism that typically plays an important role in multisensory integration, sensorimotor transformations, action planning, and visual stability (Morris et al., 2013, 2019; Salinas and Sejnowski, 2001).
From a temporal point of view, overall correlations fluctuate along the trial. PREMOV (Figure S3) and MOV (Figure 4C) were characterized by low correlation values because cells were more spatially selective during the arm movement or just before it, than in other periods of the task. The strongest correlations characterized the HOLD epoch, so the activity was less differentiated between different targets. This could be caused by the similar hand shape and wrist orientation used in the reaching task that can elicit similar responses in the cells sensitive to these parameters (Breveglieri et al., 2018, 2016). Furthermore, as V6A encodes target position, target information is no longer required in hold phase (because the target has already been reached), so it is plausible that some cells tuned for the goal of action were no longer selective during this epoch.
Intermediate correlations were present during DELAY period. This can be explained by two opposite trends: somatosensory inputs of the static position of the arm during HB pressing were the same across all trials and positions eliciting similar somatosensory discharges in many neurons, whereas activity is differentiated by spatial attention, motor planning, and gaze fixation toward different targets. Then, we computed the correlations between the same target across subsequent epochs (Figures 4B and 4D). In the first part of the trial, the activity of the population changed rapidly (low or negative correlations) to reach a pattern of activation sustained from the early phases of the movement up to the end on the hold epoch (higher correlations). The results therefore support a switch from a visual code to a more motor-related one or, alternatively, the superimposition of motor-related and proprioceptive information with previous underlying visual-related inputs. Similar results were recently found in V6A using a decoding analysis; the authors reported an evolution of visuo-to-motor coding during the execution of reaching and grasping (Filippini et al., 2017,2018). Moreover, the stability of the correlations found in most epochs is reminiscent of the stability of a mixed body/hand reference frame found in V6A (Hadjidimitrakis et al., 2020, Piserchia et al., 2017). Dynamic processing in PPC is controversial with some works reporting stationary or not-stationary encoding of information (Astrand et al., 2015; Crowe et al., 2010; Meyers et al., 2008). A certain grade of stability in encoded information, useful in state estimation and error correction, is coherent with the implication of V6A in the process of comparing the desired position of moving limb with the actual movement (Fattori et al., 2017, Medendorp and Heed, 2019).
Separate Subpopulations Differently Process Past Activity
We showed that the spike history (intrinsic block of regressors) explained neural activity better than the extrinsic part of the model (see intrinsic w-values versus extrinsic w-values in Figure 5A). This can be due to the result of the complex internal processes of the area (Takahashi et al., 2017). Notice that the spike history was only indirectly related to the ongoing task and behavior, and, thus, it could account for neural modulations caused by uncontrolled parameters (and so not directly included in the model as regressors). These modulations may be either internal (for instance, general state of attention or local circuitry) or external (e.g., kinematics and kinetics or fatigue) to the brain. Among these hypothetical contributions, attentional modulations known to affect V6A activity (Caspari et al., 2018, 2015; Ciavarro et al., 2013; Galletti et al., 2010) likely play a central role, but our task did not allow to disentangle it from other processes.
We then wondered whether contribution of past activity was different moving away from actual time. It turned out that two separable classes of neurons were present according to the importance of past activity: a first population with an increasing positive influence approaching current time and a second population where the past activity influence had quite constant and generally lower values. A possible explanation for these different patterns could be a functional difference between the two types of cells. Neurons with a ramp-like activity pattern, i.e., the first type, are common in PPC, and such activity could support progressive sensorimotor transformations. The second type, less modulated by past activity, could be part of an online control network, working as comparator between expected and actual movement (Medendorp and Heed, 2019; Fattori et al., 2017). Firing rates in this case could reflect faster transient activity like afferent feedback signals from the premotor cortex (found in V6A, see Passarelli et al., 2011; Gamberini et al., 2009). The possibility that the PPC works as a state estimator with an internal forward model constantly updated by different sensory inputs (Medendorp and Heed, 2019) makes the existence of different subpopulations with different functions plausible. However, further studies are needed to elucidate their functions.
Limitations and Future Directions
The task used in the present work (fix-to-reach) allowed us to study the effect on cell discharge of brief saccadic eye movement to foveate the target, eye position, arm-movement preparation, direction and extent of arm movement, and spatial position of the extended arm in the peripersonal space. Our task (with the visual target and movement target being the same, see Transparent Methods) does not allow to study separately the effects of spatial attention and motor planning, although both factors are known to strongly influence the activity of many V6A cells, in the same way we are aware that the attentional effect could be included in the eye position signals (Breveglieri et al., 2014, Fattori et al., 2017, Galletti et al., 2010). Due to the high variable timing of these processes between one cell and another, traces of their modulations were taken into account by few blocks of regressors (POST SACC, DELAY, and PREP; see above).
We did not record reaching kinematics during the task; therefore our model does not incorporate movement regressors that can describe arm position and joints rotation. As somatosensory cells are present in V6A (Breveglieri et al., 2002), future works could enhance our actual GLM with arm movement descriptors to test how finely this area is involved in the control of arm movements. Finally, recent imaging studies have found the putative human homolog of area V6A in the anterior part of the superior parieto-occipital cortex (Pitzalis et al., 2013, Tosoni et al., 2015). GLM methods could be applied also to multivoxel analysis helping to study dynamics of activations and separating different contributions of task parameters. This analysis on human V6A could confirm analogies between human SPL and monkey allowing a direct transfer of our accumulated knowledge on animal model to the deepening of human pathologies related to visuospatial processing performed by PPC (Gamberini et al., 2020).
Another interesting outcome of the analysis here presented could be the selection of the areas more suitable to extract information about specific parameters in the fast-growing BMI (brain-machine interfaces) field. Alternatively, the functional fingerprints could be used to feed a decoder with only the units more selective to the features of interest with a great computational advantage.
To summarize, we analyzed in detail many different parameters known to modulate area V6A during a reaching task. We fitted several GLMs for each cell to explain neural modulations. From these models, we computed the weight that each feature has on the cells to extract information about the population activity. Our results suggest that V6A encodes reaching parameters in a “mixed” fashion, with single cells that form a continuous functional spectrum and with no evidence of any segregation.
Limitations of the Study
Our task required the monkey to fixate the reaching target, thus we were not been able to decouple the effect of spatial attention and planning on cell activity. In addition, no kinematic data were recorded during the experiment, thus our model did not include such information that could have shed light on how finely V6A neurons track reaching movements.
Resource Availability
Lead Contact
Further information and request for resources should be directed to and will be fulfilled by the Lead Contact, Matteo Filippini (matteo.filippini7@unibo.it).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
The dataset and code supporting the current study are available from the lead contact upon reasonable request.
Methods
All methods can be found in the accompanying Transparent Methods supplemental file.
Acknowledgments
We thank Prof. Giuliano Galimberti (Dept. of Statistical Sciences, University of Bologna, Italy) and “Statistics Clinic” service of the University of Bologna; Rossella Breveglieri, Kostas Hadjidimitrakis, Annalisa Bosco, Federica Bertozzi, and Giulia Dal Bo’ for their help in the recordings; Lauretta Passarelli, Massimo Verdosci, and Francesco Campisi for technical assistance; and Michela Gamberini for anatomical reconstructions.
Funding: This work was supported by Ministero dell’Università e della Ricerca (Italy, PRIN2017-2017KZNZLN) and by Fondazione Cassa di Risparmio in Bologna, Bando Ricerca 2018/0373.
Author Contributions
S.D. and F.E.V. conceived the statistical model and performed the analysis. S.D., F.E.V., M.F., P.F., and C.G. interpreted the results. S.D. and F.E.V. wrote the original draft. P.F. provided funding and facilities. C.G. and M.F. supervised the project. All authors contributed to editing the manuscript.
Declaration of Interests
The authors declare no competing interests.
Published: October 23, 2020
Footnotes
Supplemental Information can be found online at https://doi.org/10.1016/j.isci.2020.101616.
Contributor Information
Matteo Filippini, Email: matteo.filippini7@unibo.it.
Patrizia Fattori, Email: patrizia.fattori@unibo.it.
Supplemental Information
References
- Andersen R.A., Essick G.K., Siegel R.M. Encoding of spatial location by posterior parietal neurons. Science. 1985;230:456–458. doi: 10.1126/science.4048942. [DOI] [PubMed] [Google Scholar]
- Astrand E., Ibos G., Duhamel J.R., Ben Hamed S. Differential dynamics of spatial attention, position, and color coding within the parietofrontal network. J. Neurosci. 2015;35:3174–3189. doi: 10.1523/JNEUROSCI.2370-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barak O., Rigotti M., Fusi S. The sparseness of mixed selectivity neurons controls the generalization–discrimination trade-off. J. Neurosci. 2013;33:3844–3856. doi: 10.1523/JNEUROSCI.2753-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosco A., Breveglieri R., Filippini M., Galletti C., Fattori P. Reduced neural representation of arm/hand actions in the medial posterior parietal cortex. Sci. Rep. 2019;9:936. doi: 10.1038/s41598-018-37302-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosco A., Breveglieri R., Hadjidimitrakis K., Galletti C., Fattori P. Reference frames for reaching when decoupling eye and target position in depth and direction. Sci. Rep. 2016;6:21646. doi: 10.1038/srep21646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosco A., Breveglieri R., Reser D., Galletti C., Fattori P. Multiple representation of reaching space in the medial posterior parietal area V6A. Cereb. Cortex. 2015;25:1654–1667. doi: 10.1093/cercor/bht420. [DOI] [PubMed] [Google Scholar]
- Battaglia-Mayer A., Ferraina S., Mitsuda T., Marconi B., Genovesio A., Onorati P., Lacquaniti F., Caminiti R. Early coding of reaching in the parietooccipital cortex. J. Neurophysiol. 2000;83:2374–2391. doi: 10.1152/jn.2000.83.4.2374. [DOI] [PubMed] [Google Scholar]
- Binkofski F., Buccino G. Section III. The Parietal Lobe and Brain Networks for Action and Perception. In: Vallar G., Coslett H.B., editors. The Parietal Lobe, Volume 151. 1st ed. Elsevier; 2018. pp. 467–480. [Google Scholar]
- Bosco A., Breveglieri R., Chinellato E., Galletti C., Fattori P. Reaching activity in the medial posterior parietal cortex of monkeys is modulated by visual feedback. J. Neurosci. 2010;30:14773–14785. doi: 10.1523/JNEUROSCI.2313-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breveglieri R., De Vitis M., Bosco A., Galletti C., Fattori P. Interplay between grip and vision in the monkey medial parietal lobe. Cereb. Cortex. 2018;28:2028–2042. doi: 10.1093/cercor/bhx109. [DOI] [PubMed] [Google Scholar]
- Breveglieri R., Bosco A., Galletti C., Passarelli L., Fattori P. Neural activity in the medial parietal area V6A while grasping with or without visual feedback. Sci. Rep. 2016;6:28893. doi: 10.1038/srep28893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breveglieri R., Galletti C., Bò G.D., Hadjidimitrakis K., Fattori P. Multiple aspects of neural activity during reaching preparation in the medial posterior parietal area V6A. J. Cogn. Neurosci. 2014;26:878–895. doi: 10.1162/jocn_a_00510. [DOI] [PubMed] [Google Scholar]
- Breveglieri R., Hadjidimitrakis K., Bosco A., Sabatini S., Galletti C., Fattori P. Eye position encoding in three-dimensional space: integration of version and vergence signals in the medial posterior parietal cortex. J. Neurosci. 2012;32:159–169. doi: 10.1523/JNEUROSCI.4028-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breveglieri R., Kutz D.F., Fattori P., Gamberini M., Galletti C. Somatosensory cells in the parieto-occipital area V6A of the macaque. Neuroreport. 2002;13:2113–2116. doi: 10.1097/00001756-200211150-00024. [DOI] [PubMed] [Google Scholar]
- Caspari N., Arsenault J.T., Vandenberghe R., Vanduffel W. Functional similarity of medial superior parietal areas for shift-selective attention signals in humans and monkeys. Cereb. Cortex. 2018;28:2085–2099. doi: 10.1093/cercor/bhx114. [DOI] [PubMed] [Google Scholar]
- Caspari N., Janssens T., Mantini D., Vandenberghe R., Vanduffel W. Covert shifts of spatial attention in the macaque monkey. J. Neurosci. 2015;35:7695–7714. doi: 10.1523/JNEUROSCI.4383-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciavarro M., Ambrosini E., Tosoni A., Committeri G., Fattori P., Galletti G. rTMS of medial parieto-occipital cortex interferes with attentional reorienting during attention and reaching tasks. J. Cogn. Neurosci. 2013;25:1453–1462. doi: 10.1162/jocn_a_00409. [DOI] [PubMed] [Google Scholar]
- Crowe D.A., Averbeck B.B., Chafee M.V. Rapid sequences of population activity patterns dynamically encode task-critical spatial information in parietal cortex. J. Neurosci. 2010;30:11640–11653. doi: 10.1523/JNEUROSCI.0954-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fattori P., Breveglieri R., Bosco A., Gamberini M., Galletti C. Vision for prehension in the medial parietal cortex. Cereb. Cortex. 2017;27:1149–1163. doi: 10.1093/cercor/bhv302. [DOI] [PubMed] [Google Scholar]
- Fattori P., Breveglieri R., Marzocchi N., Filippini D., Bosco A., Galletti C. Hand orientation during reach-to-grasp movements modulates neuronal activity in the medial posterior parietal area V6A. J. Neurosci. 2009;29:1928–1936. doi: 10.1523/JNEUROSCI.4998-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fattori P., Kutz D.F., Breveglieri R., Marzocchi N., Galletti C. Spatial tuning of reaching activity in the medial parieto-occipital cortex (area V6A) of macaque monkey. Eur. J. Neurosci. 2005;22:956–972. doi: 10.1111/j.1460-9568.2005.04288.x. [DOI] [PubMed] [Google Scholar]
- Fattori P., Gamberini M., Kutz D.F., Galletti C. “Arm-reaching” neurons in the parietal area V6A of the macaque monkey. Eur. J. Neurosci. 2001;13:2309–2313. doi: 10.1046/j.0953-816x.2001.01618.x. [DOI] [PubMed] [Google Scholar]
- Filippini M., Breveglieri R., Hadjidimitrakis K., Bosco A., Fattori P. Prediction of reach goals in depth and direction from the parietal cortex. Cell Rep. 2018;23:725–732. doi: 10.1016/j.celrep.2018.03.090. [DOI] [PubMed] [Google Scholar]
- Filippini M., Breveglieri R., Akhras M.A., Bosco A., Chinellato E., Fattori P. Decoding information for grasping from the macaque dorsomedial visual stream. J. Neurosci. 2017;37:4311–4322. doi: 10.1523/JNEUROSCI.3077-16.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fusi S., Miller E.K., Rigotti M. Why neurons mix : high dimensionality for higher cognition. Curr. Opin. Neurobiol. 2016;37:66–74. doi: 10.1016/j.conb.2016.01.010. [DOI] [PubMed] [Google Scholar]
- Galletti C., Fattori P. The dorsal visual stream revisited: stable circuits or dynamic pathways? Cortex. 2018;98:203–217. doi: 10.1016/j.cortex.2017.01.009. [DOI] [PubMed] [Google Scholar]
- Galletti C., Breveglieri R., Lappe M., Bosco A., Ciavarro M., Fattori P. Covert shift of attention modulates the ongoing neural activity in a reaching area of the macaque dorsomedial visual stream. PLoS One. 2010;5:e15078. doi: 10.1371/journal.pone.0015078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galletti C., Fattori P., Kutz D.F., Gamberini M. Brain location and visual topography of cortical area V6A in the macaque monkey. Eur. J. Neurosci. 1999;11:575–582. doi: 10.1046/j.1460-9568.1999.00467.x. [DOI] [PubMed] [Google Scholar]
- Galletti C., Battaglini P., Fattori P. Parietal neurons encoding spatial locations in craniotopic coordinates. Experimental brain research. 1993;96:221–229. doi: 10.1007/BF00227102. [DOI] [PubMed] [Google Scholar]
- Galletti C., Battaglini P.P., Fattori P. Eye position influence on the parieto-occipital area PO (V6) of the macaque monkey. Eur. J. Neurosci. 1995;7:2486–2501. doi: 10.1111/j.1460-9568.1995.tb01047.x. [DOI] [PubMed] [Google Scholar]
- Gamberini M., Passarelli L., Fattori P., Galletti C. Structural connectivity and functional properties of the macaque superior parietal lobule. Brain Struct. Funct. 2020;225:1349–1367. doi: 10.1007/s00429-019-01976-9. [DOI] [PubMed] [Google Scholar]
- Gamberini M., Dal Bò G., Breveglieri R., Briganti S., Passarelli L., Fattori P., Galletti C. Sensory properties of the caudal aspect of the macaque’s superior parietal lobule. Brain Struct. Funct. 2018;223:1863–1879. doi: 10.1007/s00429-017-1593-x. [DOI] [PubMed] [Google Scholar]
- Gamberini M., Galletti C., Bosco A., Breveglieri R., Fattori P. Is the medial posterior parietal area V6A a single functional area? J. Neurosci. 2011;31:5145–5157. doi: 10.1523/JNEUROSCI.5489-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamberini M., Passarelli L., Fattori P., Zucchelli M., Bakola S., Luppino G., Galletti C. Cortical connections of the visuomotor parietooccipital area V6Ad of the macaque monkey. J. Comp. Neurol. 2009;513:622–642. doi: 10.1002/cne.21980. [DOI] [PubMed] [Google Scholar]
- Goodman J.M., Tabot G.A., Lee A.S., Suresh A.K., Rajan A.T., Hatsopoulos N.G., Bensmania S. Postural representations of the hand in the primate sensorimotor cortex article postural representations of the hand in the primate sensorimotor cortex. Neuron. 2019;104:1000–1009.e7. doi: 10.1016/j.neuron.2019.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadjidimitrakis K., Ghodrati M., Breveglieri R., Rosa M.G.P., Fattori P. Neural coding of action in three dimensions: task- and time-invariant reference frames for visuospatial and motor-related activity in parietal area V6A. J. Comp. Neurol. 2020 doi: 10.1002/cne.24889. [DOI] [PubMed] [Google Scholar]
- Hadjidimitrakis K., Bakola S., Wong Y.T., Hagan M.A. Mixed spatial and movement representations in the primate posterior parietal cortex. Front. Neural Circuits. 2019;13:15. doi: 10.3389/fncir.2019.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadjidimitrakis K., Bertozzi F., Breveglieri R., Galletti C., Fattori P. Temporal stability of reference frames in monkey area V6A during a reaching task in 3D space. Brain Struct. Funct. 2017;222:1959–1970. doi: 10.1007/s00429-016-1319-5. [DOI] [PubMed] [Google Scholar]
- Hadjidimitrakis K., Bertozzi F., Breveglieri R., Bosco A., Galletti C., Fattori P. Common neural substrate for processing depth and direction signals for reaching in the monkey medial posterior parietal cortex. Cereb. Cortex. 2014;24:1645–1657. doi: 10.1093/cercor/bht021. [DOI] [PubMed] [Google Scholar]
- Hadjidimitrakis K., Breveglieri R., Placenti G., Bosco A., Sabatini S.P., Fattori P. Fix your eyes in the space you could reach: neurons in the macaque medial parietal cortex prefer gaze positions in peripersonal space. PLoS One. 2011;6:e23335. doi: 10.1371/journal.pone.0023335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston W.J., Palmer S.E., Freedman D.J. Nonlinear mixed selectivity supports reliable neural computation. PLoS Comput. Biol. 2019;16:e1007544. doi: 10.1371/journal.pcbi.1007544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobak D., Brendel W., Constantinidis C., Feierstein C.E., Kepecs A., Mainen Z.F., Qi X.L., Romo R., Uchida N., Machens C.K. Demixed principal component analysis of neural population data. Elife. 2016;5:e10989. doi: 10.7554/eLife.10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutz D.F., Fattori P., Gamberini M., Breveglieri R., Galletti C. Early- and late-responding cells to saccadic eye movements in the cortical area V6A of macaque monkey. Exp. Brain Res. 2003;149:83–95. doi: 10.1007/s00221-002-1337-9. [DOI] [PubMed] [Google Scholar]
- Malik W., Hochberg L., Donoghue J., Brown E. Modulation depth estimation and variable selection in state- space models for neural interfaces. IEEE Trans. Biomed. Eng. 2015;62:570–581. doi: 10.1109/TBME.2014.2360393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marzocchi N., Breveglieri R., Galletti C., Fattori P. Reaching activity in parietal area V6A of macaque: eye influence on arm activity or retinocentric coding of reaching movements? Eur. J. Neurosci. 2008;27:775–789. doi: 10.1111/j.1460-9568.2008.06021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuire L.M.M., Sabes P.N. Heterogeneous representations in the superior parietal lobule are common across reaches to visual and proprioceptive targets. J. Neurosci. 2011;31:6661–6673. doi: 10.1523/JNEUROSCI.2921-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medendorp W.P., Heed T. State estimation in posterior parietal cortex: distinct poles of environmental and bodily states. Prog. Neurobiol. 2019;183:101691. doi: 10.1016/j.pneurobio.2019.101691. [DOI] [PubMed] [Google Scholar]
- Meyers E.M., Freedman D.J., Kreiman G., Miller E.K., Poggio T. Dynamic population coding of category information in inferior temporal and prefrontal cortex. J. Neurophysiol. 2008;100:1407–1419. doi: 10.1152/jn.90248.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris A.P., Krekelberg B. A stable visual world in primate primary visual cortex. Curr. Biol. 2019;29:1471–1480.e6. doi: 10.1016/j.cub.2019.03.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris A.P., Bremmer F., Krekelberg B. Eye-position signals in the dorsal visual system are accurate and precise on short timescales. J. Neurosci. 2013;33:12395–12406. doi: 10.1523/JNEUROSCI.0576-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parthasarathy A., Herikstad R., Bong J.H., Medina F.S., Libedinsky C., Yen S.C. Mixed selectivity morphs population codes in prefrontal cortex. Nat. Neurosci. 2017;20:1770–1779. doi: 10.1038/s41593-017-0003-2. [DOI] [PubMed] [Google Scholar]
- Passarelli L., Rosa M.G., Gamberini M., Bakola S., Burman K.J., Fattori P., Galletti C. Cortical connections of area V6Av in the macaque: a visual-input node to the eye/hand coordination system. J. Neurophysiol. 2011;31:1790–1801. doi: 10.1523/JNEUROSCI.4784-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piserchia V., Breveglieri R., Hadjidimitrakis K., Bertozzi F., Galletti C., Fattori P. Mixed Body/Hand Reference Frame for Reaching in 3D Space in Macaque Parietal Area PEc. Cerebral cortex. 2017;27:1976–1990. doi: 10.1093/cercor/bhw039. [DOI] [PubMed] [Google Scholar]
- Pitzalis S., Sereno M.I., Committeri G., Fattori P., Galati G., Tosoni A., Galletti C. The human homologue of macaque area V6A. NeuroImage. 2013;82:517–530. doi: 10.1016/j.neuroimage.2013.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouget A., Snyder L.H. Computational approaches to sensorimotor transformations. Nat. Neurosci. 2000;3(Suppl):1192–1198. doi: 10.1038/81469. [DOI] [PubMed] [Google Scholar]
- Raposo D., Kaufman M., Churchland A. A category-free neural population supports evolving demands during decision-making. Nat. Neurosci. 2014;17:1784–1792. doi: 10.1038/nn.3865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M., Barak O., Warden M.R., Wang X., Nathaniel D., Miller E.K., Fusi S. The importance of mixed selectivity in complex cognitive tasks. Nature. 2013;497:585–590. doi: 10.1038/nature12160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M., Rubin D.B.D., Wang X., Fusi S. Internal representation of task rules by recurrent dynamics: the importance of the diversity of neural responses. Front. Comput. Neurosci. 2010;4:1–29. doi: 10.3389/fncom.2010.00024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E., Sejnowski T.J. Gain modulation in the central nervous system: where behavior, neurophysiology, and computation meet. Neuroscientist. 2001;7:430–440. doi: 10.1177/107385840100700512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santandrea E., Brev R., Bosco A., Galletti C., Fattori P. Preparatory activity for purposeful arm movements in the dorsomedial parietal area V6A : beyond the online guidance of movement. Sci. Rep. 2018;8:6926. doi: 10.1038/s41598-018-25117-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K., Best M.D., Huh N., Brown K.A., Tobaa A.A., Hatsopoulos N.G. Encoding of both reaching and grasping kinematics in dorsal and ventral premotor cortices. J. Neurosci. 2017;37:1733–1746. doi: 10.1523/JNEUROSCI.1537-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosoni A., Pitzalis S., Committeri G., Fattori P., Galletti C., Galati G. Resting-state connectivity and functional specialization in human medial parieto-occipital cortex. Brain Struct. Funct. 2015;220:3307–3321. doi: 10.1007/s00429-014-0858-x. [DOI] [PubMed] [Google Scholar]
- Zhang C.Y., Aflalo T., Revechkis B., Rosario E.R., Ouellette D., Pouratian N., Andersen R.A. Partially mixed selectivity in human posterior parietal association cortex. Neuron. 2017;95:697–708.e4. doi: 10.1016/j.neuron.2017.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zipser D., Andersen R.A. A back-propagation programmed network that simulates response properties of a subset of posterior parietal neurons. Nature. 1988;331:679–684. doi: 10.1038/331679a0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The dataset and code supporting the current study are available from the lead contact upon reasonable request.