Examining Factors Affecting Reading and Math Growth and Achievement Gaps in Grades 1–5: A Cohort-Sequential Longitudinal Approach

Abstract

Despite focused efforts, achievement gaps remain a problem in the America’s education system, especially those between students from higher and lower income families. Continued work on reducing these gaps benefits from an understanding of students’ reading and math growth from typical school instruction and how growth differs based on initial proficiency, grade, and demographic characteristics. Data from 5,900 students in Grades 1–5 tested in math and reading at six points across two years were analyzed using cohort-sequential latent growth curve models to determine longitudinal growth patterns. Results indicated that students with low initial proficiency grew more quickly than students with higher proficiency. However, after two school years their achievement remained below average and well below that of students with higher initial proficiency. Demographic characteristics had small but significant effects on initial score and growth rates.

Efforts to close achievement gaps have been a priority for America’s education system for decades. Just since 2000, major initiatives such as the No Child Left Behind legislation and the Race to the Top program have focused considerable federal resources on students with low achievement. Despite these and many other state and local efforts, achievement gaps remain apparent between higher and lower income students and to some extent between White and ethnic minority students (Reardon, 2011; Reardon & Portilla, 2016). Indeed, the most recent evidence suggests that achievement gaps based on household income are present at the beginning of kindergarten and change little over time (Reardon, 2013; Reardon & Portilla, 2016). The factors that initiate and maintain achievement gaps likely are multi-faceted and systemic, reaching far beyond the classroom door. However, a better understanding of the patterns of growth that characterize and differentiate student achievement across time can help education researchers to identify malleable factors that may be responsive to efforts to reduce achievement gaps and reveal critical periods when interventions aimed at narrowing achievement gaps are more likely to be successful. Studies of typical instruction also can shed light on the extent to which progress is being made in closing achievement gaps and when these gaps are more likely to widen or narrow. Documenting growth trajectories in the absence of researcher-introduced interventions increases our knowledge about the pattern of effects of typical instruction on student achievement. These insights can spur new research on ways to help raise the achievement of struggling students and inform policy discussions around achievement gaps.

Much of the research on student growth rates in reading and math has been conducted using either nationally representative longitudinal datasets such as the Early Childhood Longitudinal Survey (ECLS; e.g., Judge & Watson, 2011; Reardon & Galindo, 2009; Reardon & Portilla, 2016; von Hippel, Workman, & Downey, 2018) or longitudinal data from annual state assessments of reading and math conducted in the spring of each grade (e.g. Clotfelter, Ladd, and Vigdor, 2012; Schulte, Stevens, Elliott, Tindal, & Nese 2016). Other researchers have used cross-sectional data from the norming samples of standardized assessments to provide effect sizes for growth from spring of one grade through spring of the next grade (Bloom, Hill, Black, & Lipsey, 2008; Scammacca, Fall, & Roberts, 2015). These studies provide valuable information about how much growth occurs from the end of one grade to the end of the following grade.

However, studies that track student growth at multiple time points across more than one academic year (i.e., beginning, middle, and end of grade) and allow for examination of both within-year and between-year growth are rare. As school districts have adopted practices such as universal screening and periodic universal progress monitoring using norm-referenced, vertically scaled assessments, more data are becoming available that include beginning, mid-year, and endof-year assessments. Because these assessments measure growth on a continuous, equal-interval vertical scale within and across grades, they provide more precise information on students’ growth over time than other types of measures (von Hippel et al., 2018). In this study, we examine data from vertically scaled measures of reading and math to analyze the effects of initial achievement level, demographic characteristics, and grade on student growth and achievement gaps across the 2015–2016 and 2016–2017 academic years for students in Grades 1–5.

Effect of Initial Level of Achievement on Academic Growth

More than 30 years of research has been conducted to determine the effect of students’ initial level of achievement on their pattern of academic growth over time. Perhaps the most well-known growth pattern is the “Matthew effect” that education researchers began to explore in the 1980s (Stanovich, 1986; Walberg, Strykowski, Rovai, & Hung, 1984; Walberg & Tsai, 1983). The Matthew effect proposes that students who start out with high achievement will grow at a faster pace than students who start out with low achievement, leading to an ever-widening gap between high and low achievers (in other words, the rich get richer—a contextomy of a saying in the Gospel of Matthew). The hypothesized mechanism by which the gap widens involves inter-relations between motivation, exposure, and skill level. According to the Matthew effect, students with high reading or math skills are more motivated to engage in and benefit more from reading or math activities, resulting in greater exposure to reading and math concepts that then foster growth in those skills at an accelerated pace. Meanwhile, students with poorer skills are less motivated to practice and benefit less from reading or math instruction, giving them less exposure to new vocabulary words, math concepts, and other math and reading concepts over the course of the school year, leading to less skill development. As a result, students with low initial achievement fall further behind and those with higher initial achievement race further ahead, widening achievement gaps.

Patterns of growth in reading.

Given its memorable name and intuitive appeal, the Matthew effect has been a popular topic in education research. However, as early as the mid-1990s, research findings disputed its existence in reading (Shaywitz et al., 1995). In a review of studies of reading growth in students in Grades 1–6, Pfost, Hattie, Dörfler, and Artelt (2014) found evidence supporting the Matthew effect in 23% of 78 results reported in studies conducted in the U.S. and abroad. The studies that supported the Matthew effect tended to be those examining decoding speed and efficiency and those using highly reliable measures. More recent findings from longitudinal research have been equivocal. Data from students in early elementary school have supported the Matthew effect in reading (McNamara, Scissons, & Gutknecth, 2015). However, longitudinal studies of late elementary and middle school students have not, showing instead that students with different levels of reading achievement maintained their relative standing over time (Baumert, Nagy, & Lehmann, 2012; Schulte et al., 2016). This pattern of stable differences was evident in 26% of the 78 sets of results that Pfost et al. reviewed.

A compensatory pattern of growth, in which achievement gaps narrowed over time, occurred in 42% of the 78 reading studies that Pfost et al. (2014) reviewed. Because this pattern tended to appear in studies where reading measures had floor or ceiling effects, measurement error may be one reason for the reduction in gaps over time. The compensatory pattern also may be tied to developmental stage, with low-achieving children in the early primary grades being more likely to catch up as they benefit from instruction and master basic skills. However, researchers have found differences in pace of growth by high and low initial achievers that produced a compensatory pattern. Rambo-Hernandez and McCoach (2015) determined that students with high initial achievement grew more slowly in reading than students with average achievement across Grades 3–6. In a study of students in high-poverty schools, Huang, Moon, and Boren (2014) reported that high achievers in kindergarten grew at a slower rate in reading skills than low achievers.

Patterns of growth in math.

As with reading, researchers have studied growth trajectories in math to determine if the pattern aligns with the Matthew effect, the compensatory pattern, or a pattern of stable differences over time. Using data from ECLS:K, Morgan, Farkas, and Wu (2009) tracked math growth from kindergarten through Grade 5. Results indicated that math achievement for students with low levels of math proficiency in the fall and spring of kindergarten grew at the slowest rate through Grade 5 compared to students with low proficiency in fall or spring only and students with average or better math proficiency in kindergarten. These results remained true even when SES, race, and gender were included in the models. The magnitude of the difference between students with low kindergarten math achievement and students with adequate or better kindergarten math achievement was two standard deviations at the end of fifth grade, a finding that supports the Matthew effect. Studies examining the predictive effect of low math achievement in early elementary grades on later math proficiency have shown that students with low initial achievement grow more slowly through later elementary grades than students with higher initial achievement (Hansen, Jordan, & Rodrigues, 2017; Lu, 2016). In particular, lower-achieving students have demonstrated difficulty in gaining fractions knowledge in later grades (Fuchs et al., 2015; Hansen et al., 2017; Resnick et al., 2016). Math growth among students with learning disabilities also has been shown to be slower than among typical students, leading to math achievement gaps that either widened or were maintained over time (Jordon, Kaplan, & Hanich, 2002; Shulte & Stevens, 2015; Wei, Lenz, & Blackorby, 2012). Other longitudinal studies of math achievement in late elementary and middle school students have shown that students maintained their relative standing in the achievement distribution over time (Baumert et al., 2012). In a systematic review of 35 studies of longitudinal math achievement among students with math disabilities and difficulties, Nelson and Powell (2018) determined that students with low achievement typically did not close the gap with students with higher achievement over time. Some studies showed a pattern of stable differences in achievement and others showed widening gaps in performance.

Summary of patterns of growth in reading and math.

The research conducted to this point on patterns of math and reading growth for students differing in their level of initial achievement is inconclusive regarding the ways in which achievement gaps change over time. One possible explanation for the differences seen in these studies is the assessments used to measure growth. Studies that explored growth patterns in students in kindergarten through Grade 3 often used data from national longitudinal surveys such as ECLS. Beginning in Grade 3, students are tested annually using state assessments of reading and math and researchers have used the resulting data to track growth patterns from that point. However, no studies have examined student’s growth in math and reading across multiple time points using the same assessment in Grades 1–5, leaving open the question of the role of measurement differences on the observed growth patterns. Additionally, the effect of multiple student characteristics on growth has not often been explored within the same analytical models in the research conducted to date. Doing so likely will provide additional insight into the ways in which these factors interact, especially when the measure is held constant across grades.

Effect of Grade Level on Academic Growth

Another important factor to consider in understanding how patterns of growth relate to efforts to reduce achievement gaps is the ways in which the magnitude of normative reading and math growth change over time as students advance through the elementary grades. Previous research has reported declining annual growth rates in reading and math across Grades 1–5. Using data from normative samples of students from several standardized achievement tests, Bloom et al. (2008) determined that effect sizes for growth from spring of one grade to spring of the following grade decreased markedly in size as students advanced through school. In reading, students grew on average by 1.52 SDs from spring of kindergarten to spring of Grade 1, but only 0.40 SDs from spring of Grade 4 to spring of Grade 5. Annual growth in math also trended downward from 1.14 SDs for spring of kindergarten to spring of Grade 1 to 0.56 SDs for spring of Grade 4 to spring of Grade 5. Scammacca et al. (2015a) reported similar results when looking at the growth of students in the bottom quartile of the normative distributions of standardized reading and math tests. These results suggested that achievement gaps among younger students may be more likely to diminish over time than those among older students because more academic growth occurs in the early primary grades than in later grades.

Longitudinal studies also have documented the deceleration of growth rates as students progress through elementary school. Cameron, Grimm, Steele, Castro-Schilo, and Grissmer (2015) examined growth rates in two nationally representative longitudinal datasets from kindergarten through Grade 8. They concluded that students grew quickly through Grade 3, but growth in both reading and math then slowed. Lee (2010) analyzed longitudinal and cross-sectional data from nationally representative samples of students in K-12 and determined that their rate of growth slowed by 1–4% of a standard deviation per year, with reading growth decelerating to a greater extent than math. Effect sizes for math and reading growth declined each year with a similar trajectory and magnitude as that reported by Bloom et al. (2008).

Effects of Socioeconomic Status and Race or Ethnicity on Growth

Much recent attention has focused on achievement gaps based on socioeconomic status (SES), with evidence suggesting that these gaps have expanded over the past several decades and are present prior to the beginning of formal schooling (Reardon, 2011, 2013). Children from low SES families have shown lower initial achievement and a slower growth rate across many studies. For example, using data from ECLS:K, Aikens and Barbarin (2008) found differences in initial reading proficiency in kindergarten between low SES and more affluent students and that the gap expanded through Grade 3. Examining data from both the ECLS:K and the National Longitudinal Survey of Youth, Cameron et al. (2015) found that low SES was associated with slower growth in reading and math. Burnett and Farkas (2009) found a particularly strong effect for family SES on the math achievement of children age 9 and younger that faded out in children ages 10–14 when analyzing data from the Children of the National Longitudinal Survey of Youth.

Historically, achievement gaps based on race and ethnicity have been the focus of much attention, with inequality in available educational opportunities based on segregation of neighborhoods viewed as one cause. Recent evidence suggests that the achievement gaps between racial groups are narrowing (Reardon, 2013). However, gaps do remain and the effect of race and ethnicity on academic growth continues to be an important research question. In particular, gaps between White and Hispanic students have become of increasing interest as the Hispanic population in many states increases. Researchers have reported differences of a half standard deviation or more in math scores and more than a third of a standard deviation in reading scores between Hispanic and non-Hispanic White students in upper elementary grades (Phillips & Chin, 2004; Reardon & Galindo, 2009). Compared to White students, researchers have documented lower reading and math proficiency among Hispanic children at the beginning of kindergarten (Reardon & Galindo, 2009).

However, when researchers controlled for SES, some studies showed minimal differences in initial achievement and growth rate between Hispanic and White students. In Clotfelter et al.’s (2012) longitudinal analysis of state assessment data, Hispanic students had lower reading and math achievement in primary grades but caught up to White students of similar SES and parent education by Grade 5. Reardon and Portilla (2016) investigated changes in the magnitude of reading and math achievement gaps based on SES and race and ethnicity between 1998 and 2010. They concluded that differences between White and Hispanic students and between lower and higher SES students at Grade 4 have narrowed significantly over time. However, they asserted that these changes likely reflected improvements in school readiness at kindergarten entry for low SES and Hispanic students rather than progress from instruction after that point. Their conclusions underscore the importance of modeling these demographic characteristics together with initial proficiency level in reading and math to develop a better understanding of the factors that affect academic growth.

The Need for Additional Research on Growth Patterns

Despite the research described above, many questions remain unanswered about the effects of initial status and student SES and race or ethnicity on growth in reading and math and the implications of findings for reducing achievement gaps. More information is needed from models that include all of these variables and estimate their effects on reading and math achievement in the same students using the same measure over time. Much of the research cited above looked at only one factor (i.e., demographic characteristics or initial status) without taking account of the effect of others. Additionally, given the nature of available datasets, researchers have been able to explore questions about reading and math growth primarily from the end of one school year to the end of the next. Patterns of growth and factors that affect those patterns rarely have been explored at multiple time points within and across academic years. The longitudinal datasets used in many previous studies also are dated, meaning that results from more current datasets tracking patterns of growth and the factors that affect growth rates are needed to provide insight into the effectiveness of current typical school instruction for reducing achievement gaps.

Models of within- and across-year growth in the absence of researcher-introduced interventions also can provide more information on the ways in which current instructional practices may be funneling resources to students with low initial achievement in an effort to reduce achievement gaps, resulting in a faster pace of growth in BAU comparison groups than has been observed in the past. Lemons, Fuchs, Gilbert, and Fuchs (2012) presented evidence that typical instruction has improved over time, resulting in shrinking treatment effects in five randomized control trials of the same instructional intervention conducted over nine years. A meta-analysis of reading interventions from 1980–2012 found that publication year was a statistically significant predictor of effect size, with more recent studies having smaller effects (Scammacca, Roberts, Vaughn, & Steubing, 2015). These findings should not be surprising as requirements for evidence-based instruction mean that today’s BAU instruction oftentimes was the treatment in yesterday’s randomized control trial.

This Study

Due to the need for additional research documenting the patterns of academic growth and changes in achievement gaps over time, we acquired a dataset from a large, diverse school district containing two years of reading and math scores for students in Grades 1–5 and sought to answer the following research questions:

1. How do rates of growth in reading and math in Grades 1–5 vary depending on the student’s initial level of achievement?

2. Do demographic characteristics predict students’ initial status or growth rate?

3. How do effect sizes for growth differ across time for students in Grades 1 to 5?

We expected these research questions to provide additional insights into issues surrounding achievement gaps by illuminating the patterns of academic growth seen based on typical instruction in reading and math across the elementary grades. To address these research questions, we analyzed data from reading and math assessments administered at six time points across two grades. The assessments were conducted in the fall, winter, and spring of each school year, for a total of six observations in each of four cohorts that we followed for two years.

Research Design

This study utilized a cohort-sequential design, with cohorts of students who were in Grades 1–4 in 2015–2016 followed into the next academic year, when they were in Grades 2–5. A cohort-sequential design provides the opportunity to study student growth longitudinally across the elementary grades by linking the cohorts and determining if there is a common growth trajectory over time (Duncan & Duncan, 1994; Duncan, Duncan, & Strycker, 2006). It is a useful solution to the problems of cost, attrition, and delay in producing findings that occur in longitudinal research that involves following individuals for a lengthy period of time in order to study patterns of growth or change. A typical longitudinal design for examining growth in reading and math across Grades 1–5 would require following Grade 1 students for more than five years, from fall of Grade 1 through spring of Grade 5. In contrast, using a cohort-sequential longitudinal design requires following overlapping cohorts of students in these grades for only two years each. The overlap from these cohorts allows for linking their data across time, providing the ability to test for the existence of a single developmental trajectory across cohorts for the time span of interest. If a common trajectory is found, the results of the data analysis allow for conclusions to be drawn concerning the entire developmental period covered by the cohorts in a conceptually similar way as if a single cohort had been followed for the entire period. A comparison of results from a true longitudinal design and a cohort-sequential design used to study changes in alcohol use showed no significant differences in model parameter estimates (Duncan et al., 2006). Although not a commonly used research design, the cohort-sequential approach has been used to study topics such as developmental trends in illicit substance use (Duncan et al., 2006), executive function (Lee, Bull, & Ho, 2013), fluid and crystalized intelligence (McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002), and self-concept (Cole et al., 2001). This design is ideally suited to the present study because of the relatively large sample size available for each cohort and the similarity in the cohorts based on their attendance at schools in the same district, two conditions associated with improved model fit (Duncan et al., 2006).

Data from the cohort-sequential design were analyzed for reading and math using latent growth curve (LGC) models to determine the nature of student growth over two school years and the ways in which initial achievement, SES, and race or ethnicity affected reading and math growth. Gender differences were not anticipated, but gender also was included in the LGC models to explore possible effects. Initial achievement was operationalized as the quartile of the student’s score at Time 1 (the beginning-of-year testing occasion in the first year of the student’s participation). Quartile was used because the sample was not of sufficient size to make meaningful comparisons by decile and exact percentile ranks were not available in the data set that we obtained from the district. LGC models have been widely used to study development because they allow researchers to test for between-student differences in growth trajectories. These differences are at the heart of this study’s purpose, making cohort-sequential LGC models a suitable approach to addressing our research questions. In addition, standardized mean difference effect sizes were calculated for growth for each grade and for the two-grade period to aid in interpreting the results of the models.

Method

Participants

All participants were students enrolled in Grades 1–4 in the 2015–2016 academic year and Grades 2–5 in the 2016–2017 academic year across 18 K-5 elementary schools in one large, diverse school district in Texas. The district encompasses 589 square miles and includes schools in both urbanized and rural areas. Assessment and demographic data from approximately 6,800 students were received. Most students were of White (53%) or Hispanic (40%) ethnicity. Therefore, sufficient data were not available to operationalize race or ethnicity in a way that compared additional groups. About 35% of students received free or reduced-price lunch, which we used as a proxy for low SES because additional data on family income could not be obtained from the district. Less than 10% of students had special education status and 8.3% had limited English proficiency, meaning that these demographic variables could not be included in the analyses due to insufficient sample sizes in each cohort. However, students with special education status and limited English proficiency remained in the dataset. See Table 1 for a full breakdown of participant demographic characteristics.

Table 1.

Participant Demographic Characteristics

	Grade 1–2		Grade 2–3		Grade 3–4		Grade 4–5		Total
	n	%	n	%	n	%	n	%	n	%
Male	868	51.5%	915	52.5%	852	50.5%	833	50.1%	3468	51.2%
American Indian/Alaskan Native	4	0.2%	1	0.1%	5	0.3%	3	0.2%	13	0.2%
Asian	20	1.2%	22	1.3%	21	1.2%	25	1.5%	88	1.3%
Black/African-American	29	1.7%	26	1.5%	42	2.5%	33	2.0%	130	1.9%
Hispanic	708	42.0%	694	39.8%	651	38.6%	672	40.4%	2725	40.2%
Native Hawaiian/Pacific Islander	0	0.0%	1	0.1%	2	0.1%	4	0.2%	7	0.1%
Two or more races	46	2.7%	60	3.4%	46	2.7%	50	3.0%	202	3.0%
White	877	52.1%	939	53.8%	919	54.5%	877	52.7%	3612	53.3%
Free or reduced lunch	588	36.3%	564	33.8%	545	33.6%	550	34.5%	2247	34.5%
Special education	168	10.0%	158	9.1%	172	10.2%	155	9.3%	653	9.6%
Limited English proficiency	156	9.3%	144	8.3%	113	6.7%	151	9.1%	564	8.3%

Measures

Renaissance STAR Assessments.

The Renaissance STAR Reading Enterprise and STAR Math Enterprise are norm-referenced assessments designed for students in Grades 1–12 (Renaissance Learning, 2016a, 2016b). The intended uses of the assessments are to identify students in need of reading or math intervention and to monitor the progress of all students. Both assessments are computer-adaptive tests. Students complete a three-item practice session the first time they take STAR Reading and Math to learn how to use the computer interface. Items in the practice session are intended to be easy enough for students with low-level reading or math skills to answer correctly. The first test item presented following the practice session the first time a student takes the assessment is a below-grade level item that nearly all students will answer correctly. For future assessments, the first item is selected based on prior assessment results and is below the student’s ability level on the prior assessment. The items that follow depend on student’s response to the prior item and are selected using what Renaissance Learning (2016a) terms a “proprietary approach somewhat more complex than the simple Rasch maximum information IRT model” (p. 10). As a result, the difficulty of the items varies depending on the student’s ability and not on their grade level, making ceiling effects less likely.

Scores on both STAR Reading and Math are reported as Renaissance Scale Scores. These scores are on vertical (or growth) scales, meaning that the scales estimate ability levels across Grades 1–12 on a continuous metric and that growth can be measured on the same scale across these grades, with changes in scores representing the same amount of growth across the entire scale. To calculate the Renaissance Scale Score, the Renaissance STAR software first uses maximum likelihood estimation to locate a student on the Rasch ability scale and then converts this location to a Scale Score. Scale Scores are norm-referenced and range from 0 to 1400. Norms are based on a nationally representative sample of students in Grades 1–12. Scale scores for Reading and Math cannot be compared to each other as the two measures were not normed to a common growth scale.

Renaissance STAR Reading Enterprise.

STAR Reading consists of 34 multiple-choice items that most students complete in less than 25 minutes. Items have time limits that vary from 45 to 120 seconds depending on the item type and student’s grade. These time limits were set based on latencies observed during the norming process and are intended to give students adequate time to respond while controlling total testing time. According to Renaissance Learning (2016a), the item bank includes approximately 5,000 items. These items measure reading skills at the word level (including phonics, word reading, and vocabulary) and the text level (reading passages followed by comprehension items) and incorporate both literary and expository text. Specific skills tested on any single administration of STAR Reading depend on the student’s ability level as determined by the student’s correct or incorrect response to prior items. Students who have demonstrated mastery of basic skills are tested on higher-level skills.

Internal consistency reliability for STAR Reading for students in Grades 1–5 ranged from .93 - .95 when examined across 100,000 students per grade. Test-retest reliability for Grades 1–5 ranged from .82 - .89 across samples of 300 students per grade who were tested a second time within 8 days of their initial assessment using a set of items that excluded items from the initial test. Renaissance Learning also gathered evidence for the validity of STAR Reading in studies where students also were assessed with other norm-referenced reading assessments. The resulting correlation coefficients were meta-analyzed to provide validity coefficients across studies by grade. The coefficients were .70 for Grade 1 and .78 (SE=.001) for Grades 2–5.

Renaissance STAR Math Enterprise.

In STAR Math, students respond to 34 items with a time limit of three minutes per item; the average overall testing time is 20 minutes (Renaissance Learning, 2016b). The time limit per item was selected based on response latencies recorded during the norming process that averaged less than one minute per item. Nearly all students in the norming sample responded in less than three minutes per item. The item bank contains more than 4,000 items that assess skills that include counting, operations, equations, fractions, algebraic thinking, base ten operations, ratios, geometry, measurement, and statistics. As with STAR Reading, the specific skills tested on any single administration of STAR Math depend on the student’s ability level as demonstrated by correct or incorrect responses to prior items.

Renaissance Learning (2016b) reported internal consistency reliability for STAR Math for students in Grades 1–5 as ranging from .90 - .94 in samples of 1,500 or more students per grade. Test-retest reliability averaged .91 across nearly 7,400 students. In a meta-analysis of correlations between STAR Math and other norm-referenced mathematics assessments, the average correlation ranged from .56 for students in Grade 1 to .72 for students in Grade 5. The standard errors for the average correlations were .01 for Grades 1 and 2 and .001 for Grades 3–5.

Procedure

Both the STAR Reading and STAR Math were administered district-wide at three points each school year. The average number of calendar days between test administrations ranged from 114 to 135. See Table S1 in the online supplement for the means and standard deviations for the days between testing occasions for each measure and grade. Teachers administered the assessments using the procedures provided by Renaissance Learning. Students who were absent on the day of testing were tested on a subsequent day.

Results

The nature of LGC models and the cohort-sequential research design used in this study allowed for addressing our first two research questions within a single analysis. The reading and math LGC model results were used to determine how rates of growth in reading and math varied depending both on the student’s initial level of achievement and demographic characteristics. Effect sizes for growth were calculated within grades for the overall sample and across two academic years for each cohort to explore our third research question regarding the factors that differentiate the magnitude of growth in reading and math. Descriptive statistics for all students by grade for each time point are provided in Table 2. Descriptive statistics disaggregated by initial status (quartile of the students’ Year 1 beginning-of-year score in the normative sample), ethnicity, and SES are available in the online supplement, Tables S2–S4.

Table 2.

Descriptive Statistics for Renaissance STAR Reading and Math Scores by Grade

	Grade 1			Grade 2			Grade 3			Grade 4			Grade 5
	Mean	SD	N	Mean	SD	N	Mean	SD	N	Mean	SD	N	Mean	SD	N
Reading BOY	88.88	82.52	1532	236.73	131.39	3240	383.10	151.09	3170	436.52	171.58	2545	616.22	210.46	1572
Reading MOY	159.71	113.29	1532	324.03	140.70	3240	451.15	162.50	3170	512.07	183.89	2545	675.89	220.39	1572
Reading EOY	246.54	125.72	1532	394.25	142.31	3240	511.70	170.74	3170	566.50	195.99	2545	729.05	232.78	1572
Math BOY	288.85	88.33	1526	432.52	84.68	3241	545.71	81.22	3178	591.57	89.54	2872	706.64	80.59	1565
Math MOY	384.64	79.61	1526	502.39	83.82	3241	608.95	77.52	3178	648.15	86.31	2872	743.07	83.48	1565
Math EOY	449.29	75.94	1526	559.60	79.28	3241	655.43	79.45	3178	691.73	85.14	2872	765.60	80.53	1565

Missing Data

Given the two-year cohort sequential design and the nature of our research questions, we included students in the models if they had reading and math scores at the first time point (which determined their initial level of achievement) and at least one time point in Year 2. In total, 5,912 students had reading and math scores at Time 1. Of these students, 85.4% had reading and math scores at all six time points. In exploring missing data patterns, we found no evidence to suggest that likelihood of having missing data was systematically associated with initial status, grade, SES, or ethnicity. Rather, missing data likely resulted from students entering the school district after the first testing time point or exiting the district after that time point. Patterns of missing scores indicated that nearly all students who missed a testing time point also missed all subsequent testing time points and students who missed Time 1 testing had continuous scores from the later time points following when they were first tested. Given that the data represent participation in typical school instruction rather than an experimental intervention, differential attrition and non-random missingness are not as significant of a concern as they would be in an experimental design.

Data Analysis

To address our research questions, we analyzed the data using LGC models (Duncan et al., 2006; McArdle & Epstein, 1987; Muthén, 2004; Preacher, Wichman, MacCallum, & Briggs, 2008). Because the Renaissance STAR assessments are vertically scaled, scores from students in Grades 1–5 could be included in the same models. The dataset and the cohort-sequential research design presented complexities that required an analytical approach to the LGC model that could accommodate clustering at the school level (students within schools) as well as the multiple groups consisting of the overlapping cohorts. As a result, we implemented an aggregated analysis model (Muthén & Satorra, 1995; Stapleton, 2013) in which the standard errors and chi-squared statistics are adjusted for clustering and model parameters are estimated at the student level rather than the school (cluster) level. This approach was appropriate because our primary interest was in understanding growth at the student level rather than the school level while accounting for the dependence in the data that results from nesting students within schools (Stapleton, 2013). All models were run in MPlus v8.0 (Muthén & Muthén, 2017) using a TYPE = COMPLEX specifier for the model and full-information maximum likelihood (FIML) estimation to accommodate missing data.

As a first step in addressing Research Questions 1 and 2, we estimated unconditional models to determine the overall intercept and slope of math and reading scores across Grades 1–5 and the overall fit of the models to the data. Next, covariates were added to the models to determine the effects of initial status (defined as the quartile of a student’s score in Renaissance STAR’s normative sample at Time 1) in math and reading and demographic characteristics on the latent math and reading slopes and intercepts. Growth in reading and math across Grades 1–5 was not constrained to be linear. Rather, slope loadings for the first and last time points were fixed in order to identify the model and slope loadings for the second through fifth time points were freely estimated (Duncan et al., 2006). Model fit was evaluated using the Comparative Fit Index (CFI; Hu & Bentler, 1990), and the Root Mean Square Error of Approximation (RMSEA; Browne & Cudeck, 1993) using criteria of CFI ≥ .95 and RMSEA ≤ .08 as minimum standards for acceptable fit.

To address our third research question, effect sizes for each growth within each grade were calculated based on the raw data using means, standard deviations, sample sizes, and correlations between scores at each pair of testing occasions. These data were used to compute Hedges’s g and its standard error. Effect sizes by grade also were calculated for disaggregated groups by ethnicity and SES. To better understand the way in which initial achievement level impacts achievement gaps over the two-year period, effect sizes also were calculated by Time 1 quartile for each cohort. The standard deviation for all participants was used in calculating effect sizes for all disaggregated groups to avoid inflating the effect size due to within-group homogeneity yielding smaller standard deviations for the disaggregated group than for the overall sample.

Unconditional Cohort Sequential Latent Growth Curve Models

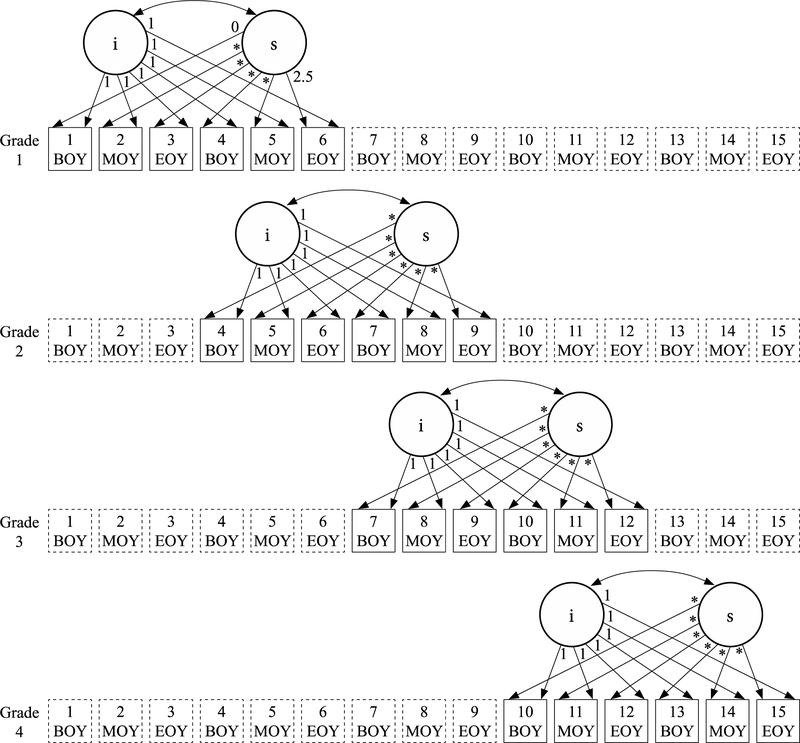
The first step in estimating a latent growth curve model is to estimate an unconditional model. This model represents within-individual growth over time and does not include any covariates. A good fit for the unconditional model is required before a conditional model with covariates can be estimated. The unconditional models for reading and math were estimated with latent means, variances, and covariances constrained as equal across cohorts to determine the overall fit of the model (Duncan et al., 2006). The models are based on scores at six time points for the four cohorts in Grades 1–4 in Year 1 and Grades 2–5 in Year 2. Figure 1 is a depiction of the model showing which of the 15 total time points across Grades 1–5 were represented by each cohort in the cohort-sequential design. Each cohort contributed data from three time points that overlap with the cohort before them, three that overlap with the cohort that follows them, or both (in the case of the Grade 2 and Grade 3 cohorts). The overlapping data allows for the linking of the cohorts to estimate a single growth trajectory across Grades 1–5.

Figure 1.

The unconditional cohort-sequential latent growth curve model.

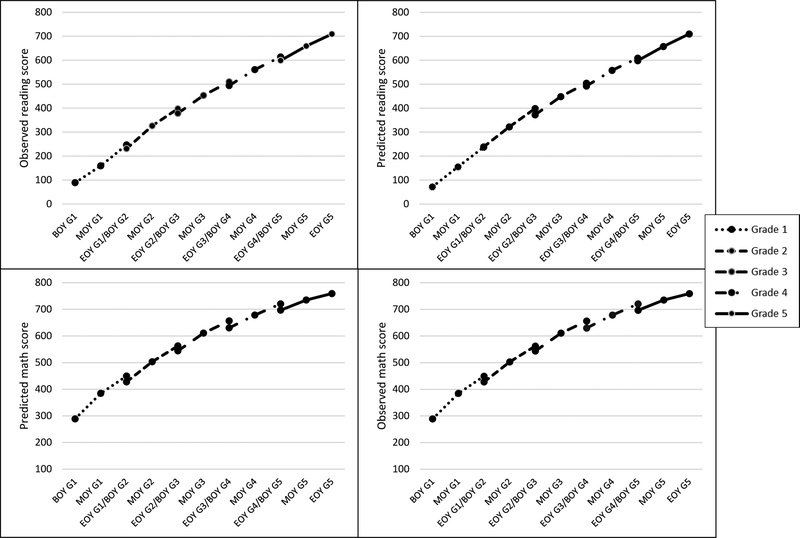
To improve model fit, residuals were freely estimated for the beginning-of-year time point for data for all six time points in the math model and in the first three time points only in the reading model; the remaining residuals were fixed as equal. The resulting models had good fit for both reading (CLI = .99; RMSEA = .06, 90% CI = .06 - .07) and math (CLI = .99; RMSEA = .06, 90% CI = .06 - .07). Given the large sample size, the chi-squared tests of fit for both unconditional models were statistically significant (χ² (56) = 366.97, p < .001 for reading; χ² (57) = 429.09, p < .001 for math). Because only the first and last slope loadings were fixed in the unconditional model, the developmental curve for the longitudinal growth trend (based on the freely estimated loadings for the remaining time points) was allowed to be non-linear and assume the shape that provided the best fit to the data. As shown in Figure 2, the shape of the developmental trends in reading and math based on the model-predicted means were non-linear and quite similar to the shape of the developmental trend based on the actual means. This correspondence and the fit of the unconditional model with equality constraints across cohorts indicates that the cohort-sequential LGC model likely provides a true representation of the longitudinal growth curve and that the cohorts are members of the same longitudinal population (Duncan et al., 2006).

Figure 2.

Observed and predicted growth curves based on mean reading and math scores across cohorts.

Not surprisingly, the mean slopes were statistically significant for both reading and math, showing that significant growth in both math and reading occurred between Grades 1 and 5. The statistically significant and negative covariance between the latent intercept and slope estimated in the unconditional model in math indicated that students with lower scores at Time 1 grew at a faster rate over time than students with higher scores at Time 1. The covariance between the latent intercept and slope was negative but not significantly different from zero in the reading model. The variances of the latent means and intercepts in both math and reading were statistically significant, meaning that between-student differences existed in initial status and growth over time that might be explained by introducing covariates into the models. See Table 3 for the parameter estimates for the unconditional math and reading LGC models.

Table 3.

Parameters for the Unconditional Cohort Sequential Latent Growth Curve Models in Reading and Math

	Mean	SE	p	Variance	SE	p
Reading Intercept	142.42	8.75	***	14057.56	1076.07	***
Reading Slope	99.87	3.20	***	992.15	78.02	***
Math Intercept	290.40	7.91	***	5876.45	404.64	***
Math Slope	106.53	1.90	***	245.49	29.13	***
	Unstandardized Covariances			Standardized Covariances
	B	SE	p	β	SE	p
Reading Intercept/Slope	−243.54	215.89	ns	−.07	.06	ns
Math Intercept/Slope	−531.84	80.69	***	−.44	.05	***

^***p<.001

Conditional Latent Growth Curve Models

To attempt to explain the inter-individual differences found in the unconditional models and to address our research questions, covariates were added to the math and reading models as predictors of the latent slopes and intercepts. In the resulting conditional math and reading models, we included students’ quartile at Time 1 (fall of Year 1) based on the Renaissance STAR’s normative sample for the reading and math assessments. Quartile was coded 0 = 25^th percentile and below, 1 = 26^th-50^th percentile, 2 = 51^st-75^th percentile, 3 = above the 75^th percentile. Although we were interested in quartile at Time 1 as a predictor of slope (growth over time), it was included as a predictor of intercept as well in order to improve model fit. Other covariates included in the models as predictors of the slopes and intercepts were gender (0 = male), ethnicity (0 = White), and free or reduced lunch (FRL) status as a proxy for SES (0 = did not receive FRL). The models were run first with all covariates predicting the slope and intercept. Next, covariates with coefficients where p ≥ .10 were dropped from the models one at a time starting with the covariate with the smallest coefficient until all remaining covariates had p values below .10, following a procedure similar to that used by Duncan et al. (2006). We do not consider covariates with coefficients where p ≥ .05 to be statistically significant predictors of the latent intercept or slope. However, we retained these covariates in the models in an attempt to explain as much variance as possible in the latent intercepts and slopes. Math quartile was included in the reading model and reading quartile in the math model to determine if math quartile predicted the reading intercept (and vice-versa) and how initial status in one area affected growth (slope) in the other.

The final conditional model for reading had excellent fit (CLI = .99; RMSEA = .06, 90% CI = .05 - .06), as did the conditional model for math (CLI = .99; RMSEA = .05, 90% CI = .05 - .06). As with the unconditional models, the chi-squared tests of fit for the conditional models were statistically significant for both reading (χ² (145) = 732.20, p < .001) and math (χ² (146) = 676.14, p < .001). See Table 4 for coefficients, standard errors, and p values for all covariates included in the conditional models. The percentage of variance accounted for in the latent reading and math intercepts and slopes varied. For the latent reading intercept, r² values ranged from .73 (Grade 1 cohort) to .88 (Grade 4 cohort). For the latent reading slope, r² ranged from .08 (Grade 2 cohort) to .19 (Grade 2 cohort). In the math model, the percentage of variance accounted for in the latent intercept was similar across cohorts, r² = .90 to .91, but varied for the latent slope, with r² values ranging from .25 (Grade 4 cohort) to .47 (Grade 1 cohort).

Table 4.

Standardized Parameters for the Cohort Sequential Latent Growth Curve Models in Reading and Math

		Grade 1–2			Grade 2–3			Grade 3–4			Grade 4–5
		β	SE	p	β	SE	p	β	SE	p	β	SE	p
Reading intercept	Reading quartile	.79	.02	***	.92	.01	***	.92	.02	***	.96	.01	***
	Math quartile	.11	.02	***	ns	--	--	.04	.02	.08	ns	--	--
	Gender	.05	.02	**	.01	.01	.09	ns	--	--	ns	--	--
	Ethnicity	−.03	.02	.08	ns	--	--	ns	--	--	ns	--	--
	SES	ns	--	--	ns	--	--	.04	.01	**	.06	.03	*
Reading slope	Reading quartile	−.26	.07	***	−.33	.04	***	−.26	.05	***	−.10	.05	*
	Math quartile	.34	.04	***	.25	.04	***	.19	.04	***	.24	.04	***
	Gender	ns	--	--	ns	--	--	ns	--	--	ns	--	--
	Ethnicity	−.13	.03	***	−.10	.03	***	−.07	.03	**	−.08	.03	***
	SES	−.22	.03	***	−.12	.02	***	−.18	.04	***	−.19	.05	***
Math intercept	Reading quartile	.14	.02	***	.05	.02	***	.10	.01	***	ns	--	--
	Math quartile	.88	.02	***	.92	.02	***	.88	.02	***	.95	.01	***
	Gender	ns	--	--	ns	--	--	−.03	.01	**	ns	--	--
	Ethnicity	ns	--	--	ns	--	--	ns	--	--	ns	--	--
	SES	ns	--	--	ns	--	--	−.03	.01	**	ns	--	--
Math slope	Reading quartile	.20	.04	***	.24	.05	***	.15	.03	***	.41	.04	***
	Math quartile	−.76	.05	***	−.79	.05	***	−.61	.03	***	−.60	.07	***
	Gender	−.12	.02	***	−.07	.03	*	ns	--	--	−.13	.03	***
	Ethnicity	−.17	.03	***	−.10	.02	***	−.06	.03	*	−.06	.03	*
	SES	−.20	.04	***	−.09	.03	**	ns	--	--	−.10	.03	***
Co-variances	Reading slope/intercept	−.18	.07	ns	−.51	.05	***	−.55	.06	***	−.45	.08	***
	Math slope/intercept	ns	--	--	−.28	.13	*	−.39	.10	***	−.44	.11	***

^*p < .05;

^**p ≤ .01;

^***p ≤ .001; paths where p ≥ .10 were dropped from model

Initial status.

Inverse relations were evident between math quartile at the beginning of Year 1 and math slope as well as reading quartile at the beginning of the Year 1 and reading slope, with the effect of initial status being larger in math than in reading. Standardized coefficients ranged from −.10 to −.33 for reading and −.60 to −.79 for math. Additionally, inverse relations between intercept and slope were found in both models (with standardized coefficients ranging from −.18 to −.55 for reading and −.28 to −.44 for math; in the Grade 1 cohort the coefficient was non-significant). These findings mean that students with lower scores at Time 1 grew at a faster rate over two school years than those with higher initial scores. However, math quartile was a positive predictor of reading slope and reading quartile was a positive predictor of math slope, indicating that students who started out with greater proficiency in one domain tended to grow at a somewhat faster rate in the other domain.

Demographic variables.

The three demographics variables included in the models had small effects on math and reading slopes and, to a more limited extent, intercepts. SES had the largest and most consistent effect on slope of growth in math and reading. Standardized coefficients ranged from −.12 to −.22 for the effect of SES on reading growth and −.09 to −.20 for math growth, though SES was not a significant predictor of reading slope in the Grade 3 cohort. The negative coefficients indicated that students of lower SES grew more slowly than higher SES students. Low SES was associated with lower reading intercept in the Grade 3 (β = −.04) and Grade 4 (β = −.06) cohorts and lower math intercept in the Grade 3 cohort (β = −.03), indicating that low SES students in these grades started out with weaker reading and math skills.

Being of an ethnicity other than White was associated with slower growth in reading, with standardized coefficients ranging from −.07 to −.13, and math, with coefficients ranging from −.06 to −.17. Ethnicity was not a significant predictor of math or reading intercept, indicating that students of all ethnicities had similar levels of initial achievement. Gender had a very small but statistically significant effect on reading intercept in the Grade 1 cohort (β = .05), with girls having higher intercepts, but no effect on reading slope. Gender had a significant effect on math intercept in the Grade 3 cohort only (β = −.03), with boys having higher intercepts. However, gender predicted math slope in the Grade 1, 2, and 4 cohorts, with boys growing more quickly (β = −.07 to −.13).

Effect Sizes for Within- and Across-Grade Growth

Effect sizes were calculated for growth in each grade for all students across cohorts. As expected based on previous research, effect sizes decreased as students progressed through elementary school. The effect size for reading growth declined from g = 1.37 in Grade 1 to g = 0.50 in Grade 5. In math, growth declined from g = 1.93 to g = 0.73. Effect sizes for within-year growth indicated that more growth occurred from the start of the year to mid-year than from mid-year to end-of-year time points, particularly in math. See Table 5 for effect sizes by grade.

Table 5.

Effect Sizes by Grade

	BOY-MOY		MOY-EOY		BOY-EOY
	g	SE	g	SE	g	SE
Grade 1 Reading	.65	.02	.72	.02	1.37	.03
Grade 1 Math	1.13	.03	.83	.02	1.93	.04
Grade 2 Reading	.64	.01	.50	.01	1.14	.01
Grade 2 Math	.83	.01	.70	.01	1.54	.02
Grade 3 Reading	.43	.01	.36	.01	.78	.01
Grade 3 Math	.79	.01	.59	.01	1.36	.02
Grade 4 Reading	.42	.01	.28	.01	.69	.01
Grade 4 Math	.64	.01	.51	.01	1.14	.02
Grade 5 Reading	.28	.01	.23	.01	.50	.02
Grade 5 Math	.44	.02	.27	.02	.73	.02

Effect sizes by initial status.

In order to examine the magnitude of math and reading growth based on students’ initial level of achievement, we calculated effect sizes separately for students in each cohort based on the quartile of their score at Time 1. These effect sizes represent their growth within and across their two academic years of participation in the study. Based on the findings of the LGC model, we expected that effect sizes for growth over time would be larger for students who were in the bottom quartiles of the normative distribution at Time 1 than for students with average to above-average proficiency at Time 1. This pattern generally held for reading (except for Grade 1) and tended to occur in Year 1 more often than Year 2 for each cohort. The differences were larger and more consistent in math than reading. In the Grade 1 and Grade 2 cohorts, the difference in effect sizes for two years of math growth for students in the lowest quartile compared to those in the highest quartile exceeded 1 SD in favor of students with lower initial achievement. See Table S5 in the online supplement for effect sizes by initial status.

Effect sizes by demographic variables.

Effect sizes in reading for the first half of Grade 1 differed by 0.26 SD between students of higher and lower SES. In later grades, differences in reading growth between lower and higher SES students were smaller in magnitude. Differences in growth between White students and students of other ethnicities followed a similar pattern, with the largest differences seen in Grade 1. Reading growth was 0.41 SD greater across Grade 1 for students with higher SES, but differences across Grades 2–4 ranged from 0.14 to 0.10 SD and no difference was found in Grade 5. For White students compared to students of other ethnicities, reading growth was 0.28 SD greater in Grade 1. That difference narrowed to 0.12 in Grade 2, and ranged from 0.04 to 0.09 in Grades 3–5.

In math, differences in the magnitude of growth favored students of higher SES across Grades 1 and 2 by 0.16 SD, but were 0.05 or less for older students. Growth differed most for White students and students of other ethnicities in Grades 1 and 4, amounting to 0.10 SD more growth for White students in Grade 1 and 0.11 SD in Grade 4. In other grades, the gap in magnitude of math growth was small, amounting to 0.05 SD or less. Table S6 in the online supplement contains the effect sizes for reading and math growth by SES and ethnicity.

To determine the extent to which membership in demographic groups overlapped with initial status, we examined the percentage of students in the lowest quartile at Time 1 that had low SES and that were of an ethnicity other than White. Results of chi-squared tests indicated statistically significant disproportionality of membership in the lowest quartile for reading by students of low SES and non-White ethnicity in each grade. However, no statistically significant differences in proportionality of membership in the lowest quartile for math was found based on SES or ethnicity for any grade. See Table S7 in the online supplement for the demographic characteristics of students in each quartile at Time 1.

Discussion

Given the evidence that achievement gaps have persisted despite concerted efforts to ameliorate them, our objective in undertaking this study was to describe the pattern of students’ growth in math and reading across Grades 1–5 in order to aid researchers and practitioners in better understanding when these gaps appear and how they may change over time. By documenting the effectiveness of typical instruction and factors that relate to differences in effectiveness, we also intended to contribute to the research on ways to ameliorate achievement gaps. Effect sizes for typical growth based on students’ initial achievement level can aid researchers in understanding the effect sizes that interventions for these students need to achieve to raise achievement for students with low levels of reading and math skills. To that end, we investigated how students’ initial level of achievement, SES, and ethnicity affected growth.

Effects of Initial Status on Reading and Math Growth

Our first research question sought to determine the ways in which rates of growth in reading and math varied for students who started out in the lowest quartile. This line of inquiry related to previous research documenting three patterns of growth: a) the Matthew effect, in which gaps widen over time between students with higher and lower initial achievement; b) a compensatory pattern, in which gaps between these groups narrow over time; and c) a pattern of stable differences that maintains achievement gaps over time. Findings from the LGC model indicated that initial status predicted growth pace in both math and reading. Students who started the year with scores in the lower quartiles grew at a more rapid rate across the school year than students with higher initial scores.

Pattern of reading growth.

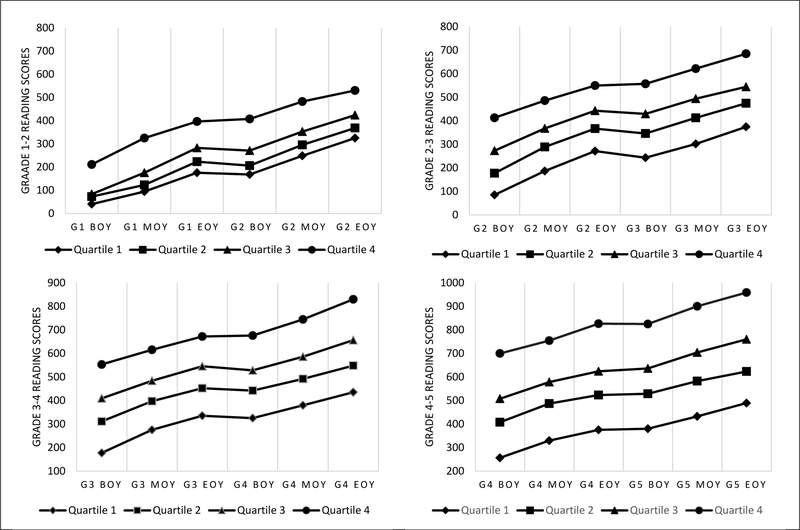
Despite the accelerated pace of reading growth of students with low initial achievement, the increase was not sufficient to raise their achievement to meet that of average students after two years of instruction. The mean reading scores for students in Quartile 1 indicated that they did move out of the bottom quartile, with end of Grade 2 average scores near the 45^th percentile, end of Grade 3 near the 35^th percentile, end of Grade 4 near the 30^th percentile, and end of Grade 5 slightly above the 25^th percentile. However, based on these results, achievement gains for older students with low initial scores did not close the gap for them as much as for younger students. Figure 3 depicts the trajectory of reading scores over time for students in each quartile. Despite faster growth, the mean end-of-year reading score in Year 1 for students who started out in Quartile 1 was below the beginning-of-year mean score for students in Quartile 4. These differences worsened for older students; by Grade 4, students who began the year with reading scores in Quartile 1 ended the year with lower reading scores than the beginning-of-year scores for students in Quartiles 2, 3, and 4. After two school years, students whose initial scores were in Quartile 1 had lower reading scores than those achieved after only one school year by students with higher initial scores.

Figure 3.

Mean reading scores by Time 1 quartile.

Although the accelerated pace of growth for students with low initial achievement seen in our findings showed some alignment with the compensatory pattern of growth, the magnitude of the differences in reading scores between groups after one and two years of instruction suggested the predominant pattern was one of stable differences that maintained achievement gaps over time. Pfost et al.’s (2014) review of longitudinal studies of reading growth noted that measures of reading skills affected by floor and ceiling effects and measures they rated as lower in quality were more likely to show decreasing patterns of differences than measures without these limitations. Because the Renaissance STAR tests are computer-adaptive and norm-referenced, they are less prone to ceiling and floor effects. The tests have been rated as having “convincing evidence” for their reliability and validity by the National Center on Intensive Intervention (2018). As a high-quality measure, results from the Renaissance STAR reading may be more sensitive to detecting a pattern of stable differences between students with low and high initial achievement. Shulte et al. (2016) also found a pattern of stable differences in reading among older elementary students using a high-quality measure. In their study, students with learning disabilities grew at a faster pace in reading compared to general education students from Grades 3 to 5, but significant differences in achievement remained evident. Our findings are similar in that the accelerated growth of students with low achievement did not produce a compensatory effect that was sufficient to produce a meaningful reduction in the achievement gap.

Studies that have found a compensatory pattern, such as Rambo-Hernandez and McCoach (2015) and Huang et al. (2014), showed that slower growth among students with high achievement was a factor in reducing the gap. Although students in the highest quartile in our study did grow more slowly than students in the lowest quartile, the difference was not of sufficient size to allow the lower-achieving students to close the gap to a meaningful extent. One reason for the difference in findings is the way in which low achievement was defined. Huang et al.’s low-achieving students scored on average at the 16^th percentile at the end of kindergarten; Most of the lower-achieving students in Rambo-Hernandez and McCoach scored at or above the 16^th percentile. In the present study, students in the lowest quartile in each grade had an average score that was below the 10^th percentile. As a result, it appears that a compensatory pattern of growth may be less likely to occur among students with such low initial reading scores.

Patterns of math growth.

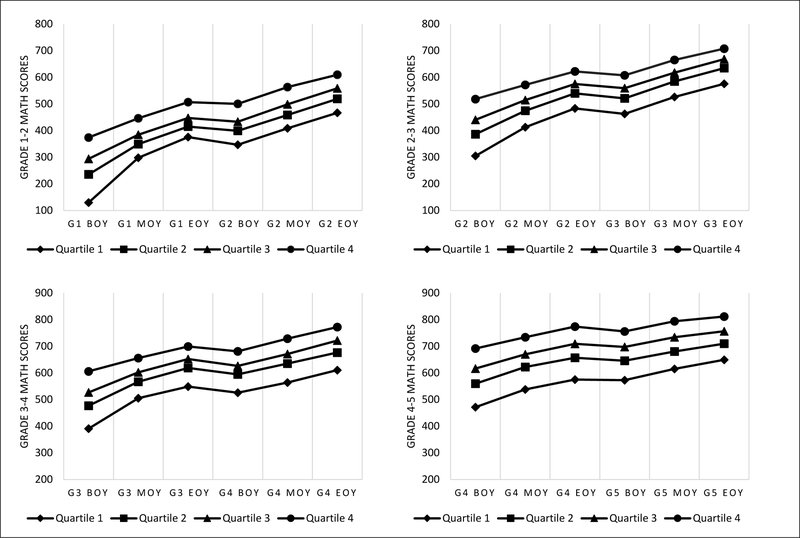
As with reading, the pattern of growth in math showed that students with low initial achievement remained well below their classmates with higher initial achievement despite having faster rates of growth. End of Grade 2 mean scores for Quartile 1 students neared the 33^rd percentile, end of Grade 3 neared the 40^th percentile, end of Grade 4 neared the 33^rd percentile, and end of Grade 5 neared the 23^rd percentile. As shown in Figure 4, at the end of Year 1, Quartile 1 students in all grades had mean math scores that were below the beginning-of-year scores for students in Quartile 4. At the end of two years of instruction, students who were in Quartile 1 in Year 1 had lower math scores than students in Quartile 4 after one year of instruction. As with reading, the gap widened for older students. Students in Quartile 1 at the start of Grades 3 and 4 had scores after two years that were lower than those of students in Quartiles 2, 3, and 4 after one year.

Figure 4.

Mean math scores by Time 1 quartile.

As in reading, our findings regarding growth in math for students with low initial achievement conformed to a pattern of stable differences. This pattern was found in many of the studies in Nelson and Powell’s (2018) review of research on achievement gaps in math, where achievement gaps were maintained over time. However, some longitudinal studies of math growth over time have found that students with math difficulties grow at a slower rate in the elementary grades than students with average or better math skills (Jordan et al., 2002; Morgan et al., 2009; Shulte & Stevens, 2015; Wei et al., 2012). The difference in our findings for rate of growth may be related to the way in which math disabilities were defined in the samples in these studies. We defined low-achieving students based on their scores at the beginning of two years of instruction rather than using a diagnosis of math disability. Fuchs et al. (2015) found that fourth-grade students with low initial achievement grew at a rapid rate when provided with a fractions intervention. However, their results indicated that the achievement gap widened over the three-year period of their study because the performance of typical-achieving fourth-grade students increased year-over-year with the introduction of an improved BAU curriculum. The schools in the district that supplied the data for our study, like many across the country, also provided interventions intended to raise the achievement of students with low initial scores. Thus, our results and those of Fuchs et al. demonstrated that even with intervention and a faster rate of growth, catching up with their classmates may be increasingly difficult for students with low initial achievement.

Differences in math and reading results.

Although we did not pose a research question regarding differences in patterns of growth and initial status in math and reading, the results of the two models presented some interesting comparative results. In discussing these findings, it is important to note that the scoring scale for the STAR Reading and STAR Math assessments are not equivalent. Thus, no direct comparison of mean scores or of the latent intercepts can be made across the two tests. However, latent slopes and predictors in the two models can be compared. In doing so, it is clear that initial status had a more pronounced influence on math growth than on reading growth. The coefficients for the predictive effects of math quartile on math slope were considerably larger than those for the effect of reading quartile on reading growth. Differences in effect sizes for growth between students in the lowest quartile and those in the highest quartile also were greater for math than for reading. Gender, which was included as a predictor in both models, had a statistically significant (though small) effect only on math growth, favoring boys in all but one cohort. Finally, the percentage of variance accounted for in the math slope (25%−47%) was considerably larger than for the reading slope (8%−19%). In considering these findings, we are cautious about offering definitive interpretations. Bailey, Duncan, Watts, Clements, and Sarama (2018) noted that longitudinal analyses like the present study often find stronger correlations between early and later achievement and between reading and math skills than is seen in experimental studies that control for confounding variables. These differences and the role of math achievement in predicting reading achievement and vice-versa merit further investigation in experimental contexts.

Effect of Demographic Characteristics on Initial Status and Growth

Given previous research that has documented achievement gaps based on race/ethnicity and SES, our second research question addressed the role of these demographic characteristics in predicting students’ initial scores (intercept) and rate of growth (slope) in math and reading. The LGC models indicated that demographic variables had small effects on students’ initial reading and math scores and pace of growth over two years of instruction. Like Clotfelter et al. (2012), we found small effects for ethnicity when SES was included as a covariate. Low SES was a significant predictor of lower Time 1 scores in reading in Grades 3 and 4 and predicted pace of growth in reading in all but Grade 3. In math, low SES predicted lower Time 1 scores only for Grade 3 and had a small effect on growth in math over time across all grades. Our findings are similar to Cameron et al. (2015), who also found that low SES predicted slower growth in reading and math. Burnett and Farkas (2009) reported a stronger negative effect for low SES on math scores in children under age 10 than was found in our data. However, their models did not include initial status or other demographic variables. Findings from studies such as Reardon and Portilla (2016) that included initial status showed that it had a larger role in achievement than SES, as was found in our study. However, it can be difficult to disentangle the effect of SES from the effect of low initial status on later achievement. We encountered this difficult in examining reading in our dataset, where students with low SES were over-represented in the lowest quartile at Time 1 in reading (though not in math).

The small effects for gender indicating that boys grew at a faster rate than girls in math in Grades 1, 2, and 4 were unexpected. Recent studies on gender differences in math achievement in the U.S. generally have shown that girls and boys have similar levels of math achievement in the elementary grades and have pointed to psychosocial factors such as attitude toward math and math anxiety to explain the disparity in the number of men and women who pursue advanced coursework in math and math-related careers (Geary et al., 2019; Gunderson, Ramirez, Levine, & Beilock, 2012). However, our findings suggest that examining math achievement scores over time for gender differences in pace of growth may be warranted. It may be that girls and boys arrive at equality in math achievement through growth that follows differing patterns. If our findings replicate to other datasets, these patterns may indicate opportunities for educators to shape girls’ attitudes toward math for the better.

Differences in Effect Sizes Across Grades

Our third research question focused on investigating differences in effect sizes based on grade level. Effect sizes for each grade indicated that growth in both reading and math is reduced in magnitude with each advancing grade. This finding held true when looking at effect sizes across all levels of initial status and all demographic groups. Effect sizes were consistently smaller as students advanced, and effect sizes for reading shrunk more quickly than those for math. These findings echo those from other longitudinal studies that also have indicated that the pace of growth slows in elementary school, with reading growth slowing more than math growth (Baumert et al. 2012; Cameron et al., 2015; Lee, 2010). Cameron et al. suggested that the pattern results from a rapid acquisition of foundational skills in early grades followed by a slower process of building knowledge on that foundation in later grades. The pace of reading growth may slow as students move from learning to read in the primary grades to reading to learn content knowledge in upper elementary grades and beyond. Lee (2010) noted that math concepts become increasingly complex as students progress through school, taking more time to master and potentially explaining the slowing pace of growth. A convincing explanation for the difference in trajectories of reading growth compared to math growth has not been offered by the researchers who have studied these patterns. However, our findings add support to the literature suggesting that grade level is one important context to consider when interpreting the magnitude of treatment effects from instructional programs (Bloom et al., 2012; Scammacca et al., 2015a). Programs focused on younger students likely will have larger effects than those for older students as a result of the slowed pace of growth among students of all ability levels.

Interestingly, the magnitude of the effect sizes for growth in each grade and the differences in the magnitude of effects for growth based on initial status differs from previous research based on cross-sectional calculations of growth based on the normative samples of standardized assessments. Two studies have reported effect sizes computed in this way for growth over one calendar year for students in Grades 1–5. Bloom et al. (2008) reported effect sizes for the mean of the distribution from seven reading and math assessments. Scammacca et al. (2015a) reported that effect sizes for students at the 10^th and 25^th percentiles and at the median from five reading assessments and four math assessments. Effect sizes from the two publications were similar and Scammacca et al. found that effect sizes were roughly equivalent across the ability distribution. However, the effect sizes for reading and math in each grade in both studies were somewhat smaller than those calculated in this study. In most cases, the effect sizes were within the 95% confidence intervals reported by Bloom et al. and Scammacca et al. The difference in findings may result from the use of cross-sectional data versus longitudinal data here. Additionally, both Bloom et al. and Scammacca et al. computed effect sizes based on one calendar year of growth (from spring of one grade to spring of the following grade). Therefore, their effect sizes included summer, when some learning loss may have occurred. However, additional longitudinal research using a nationally representative sample of students is needed to bring clarity to the magnitude of effects from typical instruction in reading and math.

Implications for Research

Given that students with low initial math and reading scores remained below the 40^th percentile after two years of instruction and supplemental intervention, more research is needed to develop interventions that can produce greater acceleration of growth. In particular, students in Grades 3 and 4 who score in the bottom quartile at the beginning of the school year require strong doses of reading and math interventions if they are to emerge from the bottom third of the normative distribution. The effect sizes for growth over time in our results can inform research regarding the magnitude of effects that need to be observed from these interventions to improve reading and math skills enough to begin closing achievement gaps.

Our findings on the faster growth pace of students with low initial status add to the growing literature (Fuchs et al., 2015; Lemons et al., 2012; Scammacca et al., 2015b) on the ways in which BAU instruction and school-provided interventions have evolved to provide a more efficacious comparison condition to experimental interventions. Given that schools must provide evidence-based instruction, researchers testing a new intervention against a BAU intervention are often actually comparing alternative treatments—testing two competing approaches to remediation rather than testing the effect of additional instruction, as was more often the case in decades past. Indeed, as Vaughn et al. (2016) pointed out, the treatment versus comparison contrast is better framed as a contrast between school-provided and researcher-provided intervention. When possible, researchers should request data on student growth in the year or two before their study begins to determine a baseline for growth in the absence of their intervention. Acquiring baseline data provides additional options for analyzing results from treatment studies to determine if the new intervention is more effective than the remediation efforts in place under BAU instruction.

Additionally, researchers should document the instructional practices in the BAU condition and assess the extent to which instruction in the treatment conditions varies from the comparison condition as part of assessing fidelity of implementation of the treatment (Roberts, Scammacca-Lewis, Fall, & Vaughn, 2017). By doing so, researchers can determine which elements of the treatment differentiate it from BAU and which are common to both, highlighting what aspects of the treatment might account for larger effects if such effects are observed. Using the same observation tool to document instructional practices allows researchers to measure both adherence to the experimental treatment’s protocol and the distinctive aspects of the treatment compared to BAU instruction. Examples of taking this approach to monitoring fidelity exist in the literature (e.g. Denton et al., 2010; Fogerty et al., 2014; Wolgemuth et al., 2014).

Implications for Practice

The results of this study of reading and math growth patterns can inform school policymakers and practitioners as well. Our results suggest that low-performing students may benefit from the universal screening, repeated progress monitoring, and interventions provided to them. The district that provided the data requires that schools deliver interventions to students with low proficiency as determined in part by the results of the Renaissance STAR assessments. However, district leaders do not prescribe a specific program or curriculum that schools must use. Therefore, the accelerated growth seen among students with low initial status may represent an indicator of effectiveness across programs and curriculum. Although this study was observational in nature and did not compare the effects of screening, progress monitoring, and intervention to the absence of these instructional practices, to the extent that our results generalize to other districts with similar practices, the data indicated that these efforts may play a part in accelerating growth for struggling students.

Despite screening, progress monitoring, and intervention, however, the data showed that at the end of one and two school years, large differences in proficiency remained between students who started out in the bottom quartile and those who started out with higher achievement. The fact that low achievement relative to norms persisted over two years for Quartile 1 students despite intervention provides evidence for the magnitude by which efforts to close achievement gaps must accelerate growth for these students.

Limitations to Address in Future Research

The primary limitation of our findings is that they represent a single school district. Data from other districts that implement Renaissance STAR or similar triannual assessment programs should be analyzed in the future to determine if the parameters reported here replicate with students in other districts. In particular, analyzing data from districts with greater racial and ethnic diversity and with a larger percentage of students with special education status and English language learner status would allow for additional covariates to be included in the LGC models and for percentile rank at Time 1 to be defined with greater specificity.

Additionally, regression to the mean—the tendency for scores at the high and low end of the distribution at one time point to be closer to the mean at a later time point—remains a threat to the validity of our findings regarding the growth rates of students with high and low initial status. Given that the Renaissance STAR assessments are vertically scaled computer-adaptive assessments, ceiling effects are less likely to limit our findings for high-achieving students. However, measurement error exists in every assessment and always presents a limitation to the validity of results. Assessing growth using other standardized, vertically scaled measures at multiple points across multiple academic years would provide information on the extent to which the results replicate when different assessments are used.

Conclusion

Our findings underscore the reality that achievement gaps, particularly between students of higher and lower SES, continue to plague the U.S. education system. Students who enter elementary grades with low achievement remain well behind typical and high-achieving students despite learning at faster rates, particularly in the upper elementary grades. Interventions may accelerate growth, but do not appear to be powerful enough presently to result in raising their achievement to that of average students. As researchers continue to work to develop, implement, and evaluate new approaches to helping these students catch up to their peers, further study of the magnitude of growth observed from typical instruction can help to benchmark the gains that are needed to see real progress.

Educational Impact and Implications Statement.

The present study determined that students who start out the school year with very low scores on math and reading assessments gain knowledge and skills at a faster pace that students who start with higher scores. However, the lower-scoring students do not grow at a rapid enough pace to catch up to their higher-scoring peers. As a result, achievement gaps are maintained over time. Efforts to raise the achievement of struggling students will need to involve educational interventions that accelerate growth to a much greater degree to make progress in closing achievement gaps.