Improving External Validity of Epidemiologic Cohort Analyses: A Kernel Weighting Approach

SUMMARY

For various reasons, cohort studies generally forgo probability sampling required to obtain population representative samples. However, such cohorts lack population-representativeness, which invalidates estimates of population prevalences for novel health factors only available in cohorts. To improve external validity of estimates from cohorts, we propose a kernel weighting (KW) approach that uses survey data as a reference to create pseudo-weights for cohorts. A jackknife variance is proposed for the KW estimates. In simulations, the KW method outperformed two existing propensity-score-based weighting methods in mean-squared error while maintaining confidence interval coverage. We applied all methods to estimating US population mortality and prevalences of various diseases from the non-representative US NIH-AARP cohort, using the sample from US-representative National Health Interview Survey (NHIS) as the reference. Assuming that the NHIS estimates are correct, the KW approach yielded generally less biased estimates compared to the existing propensity-score-based weighting methods.

1. INTRODUCTION

Large-scale long-term epidemiological cohorts are the gold standard of epidemiologic study design. Assembling cohort studies has become more difficult in developed countries because of increasing costs and declining response rates (Morton et al., 2006; Nohr et al., 2006), often due to concerns about confidentiality, respondent burden, and invasiveness of biological samples. To optimize resources, new epidemiological cohorts are being assembled within integrated health care systems that have electronic health-records and a large pre-existing base of volunteers to recruit, such as the UK Biobank in the UK National Health Service (Collins, 2012). Unfortunately, cohorts consist of participants who are not randomly selected and therefore generally are not representative of the target population. For example, many epidemiologic cohorts are subject to “healthy volunteer effects” (Pinsky et al., 2007), usually resulting in lower estimates of disease incidence and mortality in the cohorts than in the general population. For example, the estimated all-cause mortality rate in the UK Biobank was only half that of the UK population (Fry et al., 2017), and it is not representative of the UK population with regard to many sociodemographic, physical, lifestyle, and health-related characteristics.

In contrast to epidemiological cohorts, population-based household surveys are designed to generate nearly unbiased estimates of population quantities. They employ probability sample designs, such as stratified multi-stage cluster sampling, to select samples. The resulting samples, when appropriately weighted by the survey weights that adjust for differential sampling rates, nonresponse, and differences from known census population values, can closely represent the target population and therefore are less susceptible to selection bias and coverage issues that can occur in cohorts. Design-based variance estimation accounts for correlation induced by the homogeneity of participants from the same sampled geographic areas. On the contrary, cohorts are often recruited from a single, or a few geographic areas, and the intra-cluster correlation is either ignored or poorly considered in the analyses, leading to underestimated variances.

Applying probability sampling as done in surveys to assemble cohorts substantially increases costs (LaVange et al., 2001; Duncan, G. J., 2008). There is fractious debate between epidemiologists and statisticians about the value of population-representativeness when assembling cohorts (Little, 2010; Keiding & Louis, 2016; Ebrahim & Smith, 2013). This debate focuses on the value of population-representativeness for estimating association parameters such as regression coefficients. The critical role of population-representativeness for estimating population means and disease prevalences has been widely accepted (Duncan, G. J., 2008; Stuart, 2010). Improving population representativeness of cohort studies has received little attention by biostatisticians or epidemiologists (except Powers et. al. 2017), although is related to assessing external validity of randomized trials (Stuart et al., 2001).

More recently in survey research there has been literature investigating the use of propensity-score weighting methods to improve the representativeness of nonprobability samples, by using probability-based survey samples as external references (Elliott & Valliant, 2017). This work is mainly due to the increase in popularity of web-based surveys that use nonprobability samples (Baker et al., 2013; Kennedy et al., 2016). Two major propensity-score-based pseudo-weighting methods have been studied: 1) inverse propensity-score or odds weighting (IPSW) methods (Elliott & Valliant, 2017; Valliant & Dever, 2011); and 2) propensity score adjustment by subclassification (PSAS) (Lee & Valliant 2009). The IPSW methods, using propensity scores to estimate participation rates of nonprobability sample units, can correct bias under the true propensity models, but they are sensitive to the propensity model specification (Lee et al., 2010). Moreover, the IPSW methods can produce highly variable estimates due to extreme weights (Stuart 2010). Compared to the IPSW methods, the PSAS method uses the propensity score as a measure of similarity and thus is less sensitive to model misspecifications. In addition, the PSAS method avoids extreme weights (Rubin 2001), and therefore yields less variable estimates. However, the PSAS method is less effective at bias reduction (Valliant & Dever, 2011) because of the key assumption that nonprobability sample units represent equal numbers of population units within subclasses. Moreover, the measure of similarity of propensity scores is ad-hoc with limited guidance and justification for forming the subclasses.

In this paper, we propose a kernel-weighting (KW) method to estimate population means or prevalences from nonprobability samples. The KW method uses the propensity score as the measure of similarity, as does the PSAS method, and therefore is less sensitive to model misspecification while avoiding the extreme weights of the IPSW method. In addition, the KW method relaxes the key PSAS assumption above by fractionally (not equally) distributing the survey sample weights to the nonprobability sample units according to their similarity, which may reduce more bias. By using the kernel smoothing technique, the KW method avoids the ad-hoc formation of subclasses needed by the PSAS method. Jackknife variance estimators are proposed for all three methods that account for variability due to geographic clustering, differential pseudo-weights, and estimation of the propensity scores. Throughout the paper the nonprobability sample will be the sample from the cohort, for which we want to improve its population representativeness.

The paper is outlined as follows. We first review the IPSW and PSAS methods, and then describe the proposed KW approach, and the jackknife variance estimator. Justification for consistency of KW estimates of finite population means is given. We use simulations to study the finite sample bias and variance of the IPSW, PSAS and KW estimators of disease prevalence in the population under both correctly specified and misspecified propensity models, with attention paid to the effects of extreme weights. We also use simulations to compare the performance of the jackknife and the naïve Taylor linearization variance estimators, and the sensitivity of the KW estimation using different kernel functions and bandwidth selection methods. We compare the three pseudo-weighting methods by estimating disease prevalences and mortality rates in the US National Institutes of Health-American Association of Retired Persons (NIH-AARP) cohort, using the 1997 US National Health Interview Survey (NHIS), which has a probability sample as the reference.

2. METHODS

2.1. Sample Designs and Weighting Methods in Survey Research

Multistage stratified cluster sampling is a common sample design for national household surveys, such as the NHIS in the US (Korn & Graubard, 1999). For this type of sample design, the target population of the survey is initially divided into primary sampling units (PSUs) that are usually geographical-based units such as counties, cities, or parts of cities. The PSUs are grouped into strata, often according to PSU-level demographic characteristics, e.g., proportion of African-Americans or population size. At the first stage of sampling, PSUs are randomly selected from each stratum. At the second and further stages, stratification and cluster sampling (e.g., sampling households) can be used to ultimately sample individuals within the sampled PSUs. At each stage, the units (clusters or individuals) can be sampled with different selection probabilities. The sampling weight for each survey participant is the inverse of the product of the stage-specific selection probabilities. Typically, sampling weights must be adjusted for undercoverage (e.g., persons in long-term care institutions in NHIS) and for non-response (NCHS, 2000). The final sample weights can be considered as the number of individuals in the target population represented by the survey participant.

Unlike probability samples, non-probability samples do not have formal sample weights assigned to the study participants. Two types of propensity-score-based weighting methods have been developed to create a set of pseudo-weights for nonprobability samples to improve the representativeness: the IPSW (Valliant & Dever, 2011) and PSAS (Lee & Valliant 2009) methods. Both methods use a probability sample as a reference. The selection processes for the probability sample and for the nonprobability sample are treated as being independent. The IPSW method models the representation (i.e., pseudo-selection probabilities) of the participants in the nonprobability sample as a function of a set of variables and uses the reciprocal of the pseudo-selection probabilities as the pseudo-weights for the participants. The PSAS method distributes survey sample weights to the nonprobability sample units according to their similarity. We caution that propensity scores are used in the PSAS and IPSW methods to create pseudo-weights to improve the representativeness of the nonprobability sample. We note that this use differs from the traditional use of propensity scores to control for confounding in observational studies (Rosenbaum & Rubin, 1983) or adjust for nonresponse bias in probability samples (Czajka et al., 1992).

2.1.1. Inverse of Propensity Score Weighting (IPSW)

Suppose there are two samples selected from the same target finite population (FP) with size N: a non-probability cohort (s_c) with n_c individuals, and a reference probability-based survey sample (s_s) with n_s individuals. The individual i ∈ s_s has a sample weight, denoted by d_i. The goal is to estimate the cohort participation probability, P(r ∈ s_c|x_r), i.e., the probability for cohort unit r being included in the cohort given the observed covariates x_r. Following Valliant & Dever (2011), a logistic regression for the propensity score

$$\text{log}\left\{\frac{p\left(x_r\right)}{1-p\left(x_r\right)}\right\}=\alpha +{\beta }^T{x}_r,\text{ for} r\in \left\{s_c{\cup }^{*}{s}_s\right\},$$ (2.1.1)

is fitted to the combined cohort and weighted survey sample, where the propensity score p(x_r) is the likelihood of r ∈ s_c conditional on the cohort and weighted survey sample, and x_r is a vector of observed covariates for r ∈ {s_c ∪* s_s}. The notation ∪* represents the combination of the two samples that allows people to be selected in both cohort and survey. Denote the estimates of regression coefficients as ${\widehat{\beta }}_w$ where the subscript w indicates that the survey samples weights are used to estimate β in the propensity model (2.1.1). The P(r ∈ s_c|x_r) is then estimated by the odds $\frac{\widehat{p}\left(x_r, {\widehat{\beta }}_w\right)}{1-\widehat{p}\left(x_r, {\widehat{\beta }}_w\right)}$, with $\widehat{p}\left(x_r, {\widehat{\beta }}_w\right)$ being the estimated propensity score. The corresponding pseudo-weight is the inverse of estimated odds:

$$w_r^{\mathit{\text{IPSW}}}=\frac{1-\widehat{p}\left(x_r,{\widehat{\beta }}_w\right)}{\widehat{p}\left(x_r,{\widehat{\beta }}_w\right)}, r\in s_c.$$ (2.1.2)

When the population size is much greater than the cohort size, one can simply use $w_r^{\mathit{\text{IPSW}}}={\widehat{p}}^{-1}\left(x_r,{\widehat{\beta }}_w\right)$ (Valliant & Dever, 2011). The IPSW estimator of the target finite population mean or prevalence of variable y (i.e., $\overline{Y}=N^{-1}{\sum }_{k=1}^N{y}_k$) is ${\widehat{\overline{Y}}}^{\mathit{\text{IPSW}}}=\frac{{\sum }_{r\in s_c}{w}_r^{\mathit{\text{IPSW}}}\cdot y_r}{{\sum }_{r\in s_c}{w}_r^{\mathit{\text{IPSW}}}}$.

2.1.2. Propensity Score Adjustment by Subclassification (PSAS)

Unlike the IPSW method, the PSAS method fits the logistic regression model (2.1.1) to the combined cohort and unweighted survey sample (Lee & Valliant, 2009) to estimate propensity scores. The resulting estimates of the regression coefficients and the propensity score are denoted as $\widehat{\beta }$ and $\widehat{p}\left(x_r,{\widehat{\beta }}_w\right)$, respectively. Instead of estimating the participation probability for each cohort unit, the PSAS method uses the estimated propensity scores to measure the similarity of participants in the cohort and the survey samples with regard to their covariate values. Specifically, the combined sample is first sorted by the estimated propensity score $\widehat{p}\left(x_r,{\widehat{\beta }}_w\right)$ and then partitioned into G subclasses. There are multiple ways to form the subclasses. For example, Cochran (1968) recommended using quintiles to form G = 5 subclasses. Units within subclasses have similar propensity scores. The key assumption is that all cohort units within a subclass represent the same number of population units. The pseudo-weight for r ∈ s_c is computed as the sum of survey sample weights divided by the total number of cohort units within the subclass, denoted by $w_r^{\mathit{\text{PSAS}}}$. Note $w_r^{\mathit{\text{PSAS}}}$ is the same for all cohort units within subclasses but differs across subclasses. The PSAS estimator of $\overline{Y}$ is ${\widehat{\overline{Y}}}^{\mathit{\text{PSAS}}}=\frac{{\sum }_{r\in s_c}{w}_r^{\mathit{\text{PSAS}}}\cdot y_r}{{\sum }_{r\in s_c}{w}_r^{\mathit{\text{PSAS}}}}$.

Compared to PSAS, the IPSW method has less bias when the propensity model is correctly specified (Valliant & Dever, 2011). However, IPSW can produce extreme weights, which can inflate variances of the weighted estimators. In contrast, PSAS creates equal pseudo-weights for cohort units within subclasses and therefore is less likely to produce extreme weights. Although the efficiency of the estimators is improved, the bias of the PSAS estimators may increase due to using less specific sample weights. More subclasses (e.g., G = 10–20 suggested by Lunceford & Davidian, 2004) can be formed to achieve greater bias reduction, but it can reduce efficiency and does not have a general-purpose justification. In the next section, we propose a new weighting approach to reduce bias and increase efficiency of the estimators, without ad-hoc choice of G in forming subclasses.

2.2. The Proposed Kernel Weighting Method

In this section, we propose a kernel weighting (KW) approach to create pseudo-weights for the cohort by using a probability survey sample as a reference. Analogous to the PSAS method, KW uses propensity scores to measure the similarity of the covariate distributions between the cohort and the survey samples. Accordingly, the logistic regression (2.1.1) is fitted to the combined cohort and unweighted survey sample. The estimated propensity score for i ∈ s_s and j ∈ s_c are denoted by $\widehat{p}\left(x_i^{\left(s\right)}, \widehat{\beta }\right)$and $\widehat{p}\left(x_j^{\left(c\right)}, \widehat{\beta }\right)$, with the superscripts (s) and (c) denoting that unit i and unit j are in the survey and in the cohort, respectively.

For i ∈ s_s, we compute the (signed) distance of its estimated propensity score from each j ∈ s_c, $d\left(x_i^{\left(s\right)}, x_j^{\left(c\right)}\right)=\widehat{p}\left(x_i^{\left(s\right)}, \widehat{\beta }\right)-\widehat{p}\left(x_j^{\left(c\right)}, \widehat{\beta }\right)$, which ranges from −1 to 1. We apply a kernel function centered at zero to smooth the distances. The closer to zero the distance is, the more similar the pair of units is with respect to the covariates, and accordingly the KW method assigns a larger portion of the survey sample weight d_i to the cohort unit j based on the kernel weight:

$$k_{ij}=\frac{K\left(d\left(x_i^{\left(s\right)}, x_j^{\left(c\right)}\right)/h\right)}{{\sum }_{j\in s_c}K\left(d\left(x_i^{\left(s\right)}, x_j^{\left(c\right)}\right)/h\right)}, j\in s_c,$$ (2.2.1)

where K(·) is a zero-centered kernel function (Epanechnikov, 1969) (e.g. uniform, standard normal, or triangular density), and h is the bandwidth corresponding to the selected kernel function (see Section 3.5 for discussion of various bandwidth selection methods). Note that ${\sum }_{j\in s_c}{k}_{ij}=1$ and k_ij ∈ [0, 1]. The larger the k_ij is, the more similar the propensity scores are between cohort unit j and survey unit i.

Finally, the KW pseudo-weight $w_j^{KW}$ for j ∈ s_c, is a sum of the survey sample weights, ${\left\{d_i\right\}}_{i\in s_s}$, that are weighted by the cohort unit j’s kernel weights, ${\left\{k_{ij}\right\}}_{i\in s_s}$, given by

$${\text{w}}_j^{KW}={\sum }_{i\in s_s}{k}_{ij}\cdot d_i$$ (2.2.2)

Note that the sum of the cohort KW pseudo-weights equals the sum of survey weights, that is, ${\sum }_{j\in s_c}{w}_j^{KW}={\sum }_{i\in s_s}{d}_i$ (see Appendix A). Furthermore, the KW estimators of population means or prevalences are design consistent, under regularity conditions (Theorem 1). Also note that PSAS is a special case of the KW method, with a uniform kernel function in each subclass of estimated propensity scores, assuming that cohort units within subclasses represent equal numbers of population units. In contrast, the KW method relaxes the key PSAS assumption by assigning various portions of the survey weights to the cohort units according to the similarity of covariates considered in the propensity model.

Theorem 1. (See Web Appendix A for a proof).

Suppose, in the superpopulation, the variable of interest y has an expectation E(y) = μ < ∞, where E denotes the expectation with respect to the joint distribution of y and covariates x. Assume that the cohort and the survey sample are selected from a finite population (a simple random sample from a superpopulation) and the distributions of the estimated propensity scores are well overlapping between the two samples. If the following conditions are satisfied:

1. for the kernel function K(u), ∫K(u)du = 1, sup_u |K(u)| < ∞, and lim_{|u| → ∞}|u| · |K(u)| = 0;

2. for the bandwidth h = h(n_c), h → 0, but n_c · h → ∞ as n_c → ∞;

3. exchangeability, E{y|p(x), cohort} = E{y|p(x), survey} = E{y|p(x)};

4. bounded second moment, E(y²) < ∞; and

5. bounded survey sample weights, w_i < R for some $R\in {ℝ}_{>0}$, i ∈ s_s;

then the KW estimator of the population mean ${\widehat{\overline{Y}}}^{KW}=\frac{{\sum }_{j\in s_c}{w}_j^{KW}\cdot y_j}{{\sum }_{j\in s_c}{w}_j^{KW}}\to \mu$ in probability as the finite population size N → ∞, the survey sample size n_s → ∞, the cohort sample size n_c → ∞, with $\frac{n_c}{N}=O\left(1\right)$.

In practice, if a cohort or a survey sample includes only specific subgroups of people in the population (e.g. a women’s health cohort), then both samples should be constrained to the same subgroup. Otherwise, the estimated propensity scores of the two samples may not overlap well for important covariates, which can lead to unreliable pseudo-weight estimates (Stuart 2011; Stürmer et al., 2010). We recommend checking on the extent of overlap of the propensity scores used to compute the pseudo-weights from the IPSW, PSAS, and KW methods. Another issue is the covariate selection for Model (2.1.1). Following Stuart (2010), we suggest including as many variables that could be related to the unknown selection scheme of the cohort, as possible. All cohort selection-related variables that are common to both samples and their two-way interactions might be initially included in the model. Model selection criteria such as a stepwise procedure (D’Agostino, 1998) with Akaike information criteria (AIC) can be applied to obtain a final model.

2.3. Jackknife Variance Estimation

The naïve Taylor-linearization (TL) variance estimation method (Ch. 6, Wolter, 1985) may underestimate the variance of pseudo-weighted estimates due to ignoring the variability from estimating the pseudo-weights for the cohort. To improve variance estimation, we propose a jackknife method to account for all sources of variability (Ch. 2.5, Korn & Graubard, 1999).

The detailed steps of the leave-one-out jackknife (JK) variance estimation are described in Web Appendix B. Briefly, we leave out one PSU in the survey sample or one study center in the cohort, and assign replicate weights for the remaining sample. Then we re-estimate propensity scores by weighting the observations with the JK replicate weights, and calculate replicate pseudo-weights accordingly. The population mean is estimated for each replicate. Notice that compared to Lee & Valliant (2009), our jackknife variance includes extra replicates from leaving out PSUs in the survey sample to take account of the clustering of the survey sample. The simulation results showed that the coverage probabilities using our jackknife variance were approximately nominal (see Section 3.3). The jackknife method can be applied to all three weighting methods (Web Appendix B). For KW, the same bandwidth estimated from the original sample is used for each jackknife replicate (Korn & Graubard, 1999, Page 88).

3. SIMULATION STUDIES

3.1. Generating the Finite Population

Simulation details are in the Web Appendix C. Briefly, we generated a finite population of M = 3,000 clusters, with each cluster composed of 3,000 units (a total finite population size of N = 9,000,000). We used data from the 2015 American Community Survey (ACS) to generate covariates for race/ethnicity, age, sex, household income (hh_inc), and urban/rural area (urb). We also generated a continuous environmental factor (Env) that was positively predictive of disease status y for the finite population. The disease status y (1 for presence and 0 for absence) was generated by a Bernoulli distribution with mean $\mu =\frac{e^{\mathit{\gamma }v}}{1+e^{\mathit{\gamma }v}}$, where γ = (−5, 0.5, −1, 0.3, 0.1)^T with the intercept of −5, and the variables in vector v were age (=1 if 10–19 yrs; =2 if 20–29 yrs; =3 if 30–39 yrs; =4 if 40–49 yrs; =5 if 50–59 yrs; =6 if >=60 yrs), sex (1 = male and 0 = female), Hisp (1=Hispanic and 0= otherwise), Env, and an interaction between age and Env. All covariates and disease variable y were generated to have a positive intra-cluster correlation. The disease prevalence in the finite population was $\overline{Y}=9.59\%$.

3.2. Sampling from the Finite Population to Assemble the Survey Sample and Cohort

We conducted two-stage cluster sampling to select the cohort and the survey sample independently to ensure that the true propensity models for all three methods (IPSW, PSAS, and KW) had the same functional form. This sample design enabled us to form a fair comparison among the three methods because each of them would achieve the greatest bias reduction under the same true propensity model.

A survey sample of n_s = 1,500 individuals (150 clusters of each 10 individuals) was selected by two-stage cluster sampling. At the first stage, 150 clusters were sampled by probability proportional to size (PPS) sampling, with the measure of size (MOS) for finite population unit k defined by

$${\sum }_{k\in u_{\alpha }}{q}_k^b,$$

where μ_α is the set of individuals from the α-th cluster for α = 1, …,M; $b\in {ℝ}_{>0}$; and

$$q_k=\text{exp}\left({\beta }_0+\beta x_k\right),$$ (3.2.1)

where β₀ = 0, β = (β₁, β₂, β₃, β₄) = (0.3, −0.4, 0.7, 0.7), and the vector of covariates x_k included x_k,1 = age, x_k,2 = hh_inc, x_k,3 = Env, and x_k,4 = z (a substitute of μ; see Web Appendix C for further details). At the second stage, 10 individuals were selected by PPS sampling within each sampled cluster with MOS of $q_k^b$. The final sampling weight (i.e., the reciprocal of the selection probability) for population unit k was $\frac{{\sum }_{k=1}^N{q}_k^b}{n_s\cdot q_k^b}$. Using this MOS implies that clusters and individuals with larger values of q_k (older people with lower household income, higher environmental exposure, and larger probability of having disease) were sampled at higher rates to form the survey sample.

A cohort sample of size n_c = 11,250 people (75 clusters of each 150 individuals) was sampled independently using a similar two-stage PPS design but with different MOS’s in the PPS sampling at stages one and two, given as ${\sum }_{k\in u_{\alpha }}{q}_k^a$ and $q_k^a$, respectively, $a\in {ℝ}_{<0}$. As such, clusters and individuals with smaller q_k were sampled at higher rates in the cohort.

Under the two-stage PPS sampling described above, the true propensity models fitted to the combined sample of cohort and weighted survey sample (used by the IPSW method), and to the combined sample of cohort and the unweighted survey sample (used by the PSAS and KW methods), were logit{p(x_r)} = ω + a · β^Tx_r and logit{p(x_r)} = ω* + (a – b) · β^Tx_r respectively, for r ∈ s_c ∪* s_s, where ω and ω* were the intercepts (Web Appendix D). Note that both models had the same functional form of the covariates x. This ensures that, the IPSW and KW methods would result in unbiased estimation under the same true PS model. Otherwise, a simulation could result in unbiased estimation from one method, but not the other. The constants a and b allowed for different rates of over/under-sampling in the cohort versus the survey. For example, surveys can oversample racial/ethnic minority subpopulations, but cohorts often grossly undersample such subpopulations. The higher the value of |a − b|, the larger difference in the propensity-score (covariate) distributions would be between the cohort and the survey. Results with |a − b| = 1.5(a = −1 and b = 0.5) are presented in Figure 1, and Web Tables 3–4 in Web Appendix F, and results under an extreme case |a − b| = 3.7 are presented in Table 1.

Figure 1.

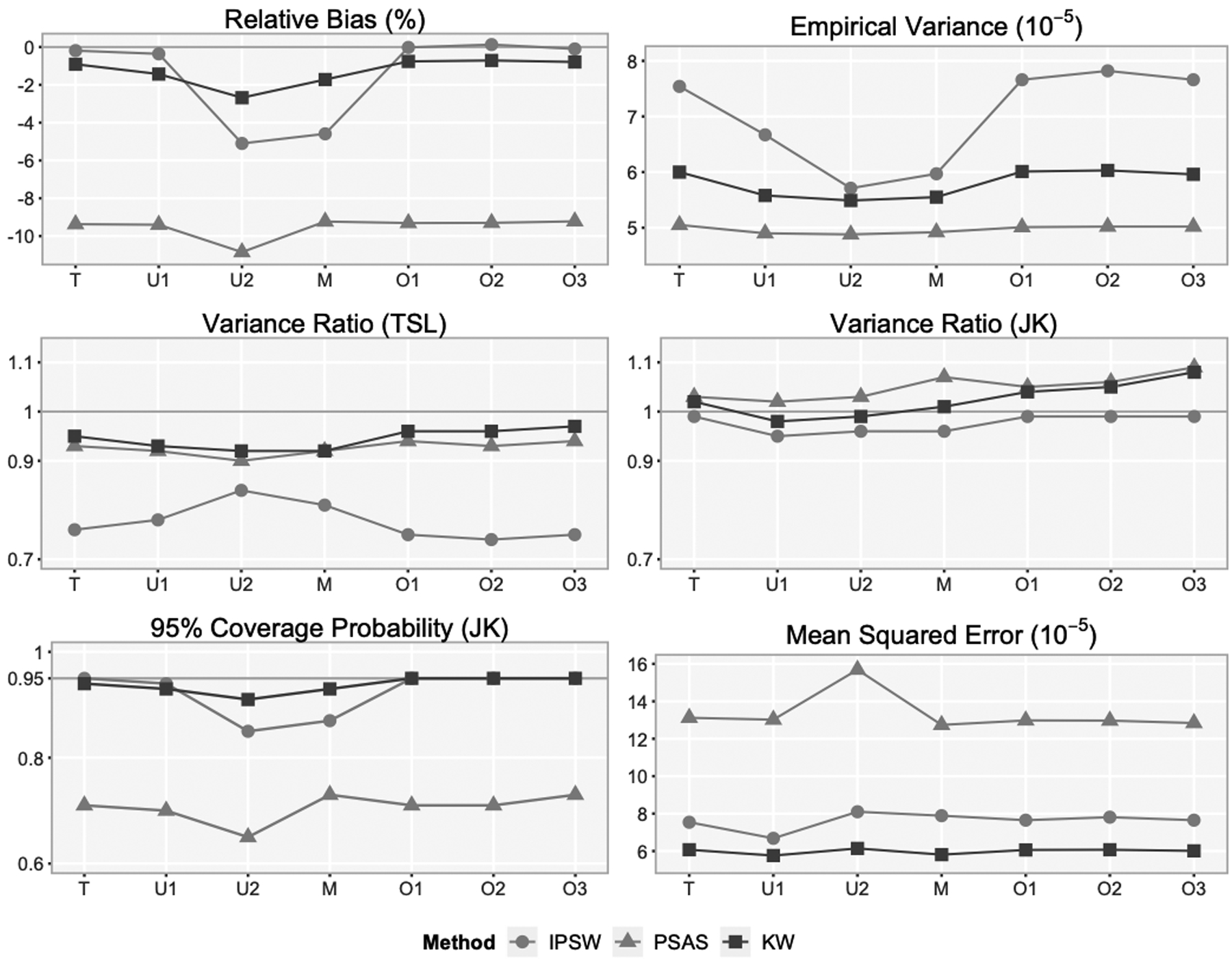
Simulation results from 1,000 simulated cohorts and survey samples with each cohort and survey sample fitted to the correct propensity model and six misspecified propensity models†.

†The true model (T) is logit{p(x)} ~ age, hh_inc, Env, z. The misspecified models are underfitted model (U1) logit{p(x)} ~ age, Env, z; underfitted model (U2) logit{p(x) ~ ag, Env; model (M) logit{p(x)} ~ age, Env, Hisp, sex; overfitted model (O1) logit{p(x)} ~ age, hh_inc, Env, z, Hisp; overfitted model (O2) logit{p(x)} ~ age, hh_inc, Env, z, Hisp, sex; and overfitted model (O3) logit{p(x)} ~ age, hh_inc, Env, z, urb.

Table 1.

Simulation results from 1,000 simulated cohorts and survey samples with the true propensity model fitted to each cohort and survey sample under extreme selection probabilities.

Method	%RB	V (× 10−5)	MSE (× 10−5)	VR (TL)	VR (JK)	CP (JK)
CHT	−71.02	1.17	465.26	0.21	NA	NA
SVY	−0.69	8.36	8.40	1.06	1.06	0.95
IPSW	7.60	392.29	397.24	0.29	1.56	0.88
PSAS	−35.16	5.88	119.60	0.90	1.78	0.09
KW	−6.85	33.31	37.59	0.97	2.40	0.96

3.3. Evaluating Criteria

We compared the KW estimates of the population disease prevalence $\left(\overline{Y}\right)$ with 1) the survey estimates (SVY), which were approximately unbiased, 2) the unweighted naïve cohort estimates (CHT) ignoring the sample designs, 3) the IPSW estimates, and 4) the PSAS estimates. The IPSW method used the inverse of estimated odds as the pseudo-weights. The PSAS method used quintiles of estimated propensity scores to form subclasses. For the KW method, the kernel was the symmetric triangular density on (-3, 3) with the bandwidth selected by Silverman’s Rule (see Web Appendix E); other kernel functions and bandwidths performed similarly (see Section 3.5, and Web Appendix F).

We used relative bias (%RB), empirical variance (V), mean squared error (MSE) of the estimators, defined by $\%\text{RB}=\frac{1}{B}{\sum }_{b=1}^B\frac{{\widehat{\overline{Y}}}^{\left(b\right)}-\overline{Y}}{\overline{Y}}100\%$, $\text{V}=\frac{1}{B-1}{{\sum }_{b=1}^B\left\{{\widehat{\overline{Y}}}^{\left(b\right)}-\frac{1}{B}{{\sum }_{b=1}^B\widehat{\overline{Y}}}^{\left(b\right)}\right\}}^2$, and $\text{MSE}=\frac{1}{B}{{\sum }_{b=1}^B\left\{{\widehat{\overline{Y}}}^{\left(b\right)}-\overline{Y}\right\}}^2$, respectively, to evaluate the performance of the prevalence estimators, where B = 1,000 is the number of simulations, ${\widehat{\overline{Y}}}^{\left(b\right)}$ is the estimate of the prevalence obtained from the b-th simulated samples.

For each mean estimator, we evaluated two variance estimators, i.e., the naive TL estimator and the JK estimator using the variance ratio (VR), and coverage probabilities (CP) of the corresponding 95% confidence intervals, defined by $VR=\frac{\frac{1}{B}{\sum }_{b=1}^B{\widehat{v}}^{\left(b\right)}}{V}$, and $CP=\frac{1}{B}{\sum }_{b=1}^{B}I\left(\overline{Y}\in C{I}^{\left(b\right)}\right)$ respectively, where ${\widehat{v}}^{\left(b\right)}$ is the variance estimate of ${\widehat{\overline{Y}}}^{\left(b\right)}$, and $C{I}^{\left(b\right)}=\left({\widehat{\overline{Y}}}^{\left(b\right)}-1.96\sqrt{{\widehat{v}}^{\left(b\right)}}, {\widehat{\overline{Y}}}^{\left(b\right)}+1.96\sqrt{{\widehat{v}}^{\left(b\right)}}\right)$ is the 95% confidence interval from the b-th simulated samples.

3.4. Results under Correctly Specified and Six Misspecified Propensity Models

The naïve cohort prevalence was biased by −42.48% (Web Table 3 in Web Appendix F). Figure 1 shows the results under the correctly specified propensity model (Model T) and six misspecified models. The KW estimates tended to have the smallest mean squared error and maintained the nominal coverage probability the best. Although IPSW removed slightly more bias than KW when all variables correlated with both sample selection and the outcome y were included in the model, the estimates were much more variable. The bias reduction and variance of the IPSW estimates were very sensitive to propensity model specification. The PSAS estimates had the smallest variance, but also the smallest bias reduction. The jackknife variance estimates were approximately unbiased for all three methods. The naïve TL method underestimated the variances of the IPSW estimates by 16%-26%, and the variances of the PSAS or KW estimates by <10%.

Models U1 and U2 were incorrectly under-fitted: Model U1 did not include hh_inc that was uncorrelated with disease status y, while Model U2 also excluded z that was highly predictive of y. The bias of all three pseudo-weighted estimates under Model U1 were very close to the bias under Model T (the true model) respectively. However, the empirical variance of the IPSW estimate was dramatically reduced because the missing variable hh_inc was uncorrelated with the outcome y (similar to the findings in Stuart, 2010). Also, the empirical variances of the KW and PSAS estimates were slightly smaller under Model U1 than the variances under Model T. In contrast, under Model U2 with missing z, all three estimates had higher biases but smaller variances, especially the IPSW estimate.

Model M did not include the highly predictive variable z along with hh_inc that were in Model T, but added two extra variables, being Hispanic and sex, which were predictive of y. Comparing results under Model U2 and M, we observed that adding additional predictors of the outcome y in the under-fitted model reduced, but did not eliminate, the bias. Adding these extra variables increased the variance of the IPSW estimate but did not affect the variances of the PSAS and KW estimates.

Models O1, O2, and O3 were incorrectly over-fitted, including unnecessary variables. Model O1 and O2 had one (being Hispanic) and two (sex and being Hispanic) additional predictors of y, respectively. Model O3 included on extra variable (urb) unrelated to y. Under these three models, the bias reduction was similar for all three estimates compared to the bias reduction under the true model respectively. However, adding extra variables resulted in higher variance of the IPSW estimates. Though the variances of the PSAS and KW estimates did not increase, the jackknife variance estimates were slightly inflated when the propensity model included covariate(s) unrelated to the propensity modeling or the outcome variable.

3.5. Results under Extreme Selection Probabilities

As noted in Section 3.2, we changed values of a and b to −2.5 and 1.2, respectively so that the cohort was an extremely non-representative sample of the finite population. Some of the selection probabilities for the cohort sample were close to zero due to extremely small $q_k^a$ (Section 3.2). For example, the minimum selection probability was as small as 7.44 × 10⁻¹², corresponding to an extremely large weight. Such large weights increased the variability of the pseudo-weighted estimates (Table 1). As a result, the IPSW estimate had an inflated variance, and the largest MSE among the three pseudo-weighted estimates. In contrast, the KW estimate had much smaller MSE than the others. The variances for all three estimates were overestimated by the jackknife method due to small sample bias that was likely induced mainly by highly variable weights.

3.6. Choice of Kernel and Bandwidth

We compared the KW estimates using two kernel functions: (1) a standard normal density kernel, and (2) a truncated triangular density kernel with support on (-3, 3) (see Web Table 4 in Web Appendix F). For either kernel function, the bandwidth was selected assuming a standard normal density kernel function using five methods: Silverman method (Silverman, 1986), Scott method (Scott, 1992), unbiased cross-validation (Scott & Terrell, 1987), biased cross-validation (Scott & Terrell, 1987), and Sheather & Jones’ method (Sheather & Jones, 1991). Our results were consistent with the existing literature (Terrell & Scott, 1985; Jones et al. 1996): the Silverman’s and Scott’s methods tend to give larger bandwidths than the other three. Based on our simulation results, either of these two methods is recommended because the other methods tend to result in smaller bandwidths that increase the empirical variance and inflate the jackknife variance estimation due to more variable pseudo-weights across replicates. With the same bandwidth, we observed that the standard normal density kernel, compared to the triangular density kernel, resulted in smaller bias but larger variances of the KW estimates. This is because the standard normal density kernel uses more extreme values for the distances than the truncated triangular density kernel. Hence, the combination of triangular density kernel and Silverman’s bandwidth appears to behave the best with regard to its overall mean squared error reduction.

4. DATA ANALYSIS: The NIH-AARP Cohort Study

We estimated (1) prevalence of eight self-reported diseases, (2) prospective nine-year rates of all-cause mortality and (3) all-cancer mortality for people aged 50 to 71 using the US National Institutes of Health and the American Association of Retired Persons (NIH-AARP) Diet and Health Study. These prevalences and mortalities were also available in the US National Health Interview Survey (NHIS), serving as the gold standard that allowed us to examine how much bias in the NIH-AARP estimates can be corrected by the pseudo-weighting methods in practice.

The NIH-AARP cohort recruited 567,169 AARP members from 1995–1996, aged 50 to 71 years, who resided in California, Florida, Pennsylvania, New Jersey, North Carolina, or Louisiana, or in metropolitan Atlanta, Georgia, and Detroit (NIH-AARP, 2006) in the US. The NIH-AARP cohort is linked with Social Security Administration Death Match File and National Death Index (NDI) (NCHS 2013) by standard record linkage methods up to 2011 (NIH-AARP 2006), providing mortality and cause of death ascertainment. AARP members were mailed questionnaires, but only 17.6% returned questionnaires, raising further questions about the representativeness of the NIH-AARP cohort for the US population.

For the reference survey, we used the NHIS, a cross-sectional household interview survey of the civilian noninstitutionalized US population. To make the two samples comparable, we chose the contemporaneous 1997 NHIS respondents aged 50 to 71 years (9,306 participants). The 1997 NHIS has a multistage stratified cluster sample design (see Section 2.1) with 339 strata with each consisting of two sampled PSUs (NCHS, 2000). NHIS was also linked to NDI through 2006 for mortality information (NCHS 2009). All the links were treated as true and no linkage error were considered in this analysis.

After harmonizing variables between NIH-AARP and NHIS, the distribution of common variables and variables of interests are described in Web Tables 5–6 of Web Appendix F. Table 2 shows the distribution of selected variables. Of note is the importance of self-reported health status, a variable often excluded in epidemiologic analyses as being a proxy for disease, but which turns out to be strongly predictive of the propensity to be selected in NIH-AARP versus NHIS. This is expected because cohorts often recruit healthier people (Pinsky et al., 2007; Fry et al., 2017).

Table 2.

Distribution of selected common variables in NIH-AARP and NHIS

	NIH-AARP (1995–96)			NHIS (1997)
	n	%		n	%	weighted n	Weighted %
Total	529708	100.00		9306	100.00	49761895	100.00
Age in years
50–54	69207	13.07		2637	28.34	15064732	30.27
55–59	117417	22.17		2091	22.47	11480359	23.07
60–64	148726	28.08		1861	20.00	9995586	20.09
65–69	174567	32.96		1944	20.89	9474745	19.04
70–71	19791	3.74		773	8.31	3746473	7.53
Sex
Male	314269	59.33		4059	43.62	23528092	47.28
Female	215439	40.67		5247	56.38	26233803	52.72
Health Status (Self-reported)
Excellent	87439	16.51		1922	20.65	10947894	22.04
Very good	191114	36.08		2708	29.10	15042319	30.06
Good	182621	34.48		2790	29.98	14711767	29.65
Fair	58741	11.09		1326	14.25	6588584	13.27
Poor	9793	1.85		560	6.02	2471331	4.97

We used a stepwise procedure based on the AIC to choose the propensity model fitted to the combination of the NIH-AARP cohort and unweighted NHIS sample, which initially included all main effects of five common demographic characteristics (age, sex race/ethnicity, etc.), three lifestyle factors (smoking status, physical activities, and body mass index [body weight (kg)/height (m) squared]), self-reported health status, and 31 two-way interactions. Web Table 7 in Web Appendix F shows the final model estimated by fitting the propensity model with (for IPSW) and without (for PSAS and KW) NHIS sample weights. Note that all the following analyses used the model described in Web Table 7.

Figure 2 plots the distributions of the estimated propensity score on the logit scale in the unweighted NIH-AARP cohort, and the three pseudo-weighted NIH-AARP cohorts by the IPSW, PSAS and KW methods, compared to the sample-weighted NHIS sample. The percentage of overlapped propensity scores in the data from NHIS and NIH-AARP exceeded 99.9%. All three pseudo-weighted distributions of propensity scores were close to the weighted NHIS sample, among which KW was the closest, followed by IPSW with some right-skewness, and PSAS with excess kurtosis. Because the KW and PSAS methods fitted a propensity model to the unweighted sample, their estimated propensity scores were close to 1 due to the predominance of cohort units in the combined cohort-survey sample. In contrast, the IPSW method used the propensity model to estimate NIH-AARP cohort membership in the combined cohort and the weighted NHIS sample (representing the underlying US population), resulting in small propensities and thus large pseudo-weights.

Figure 2.

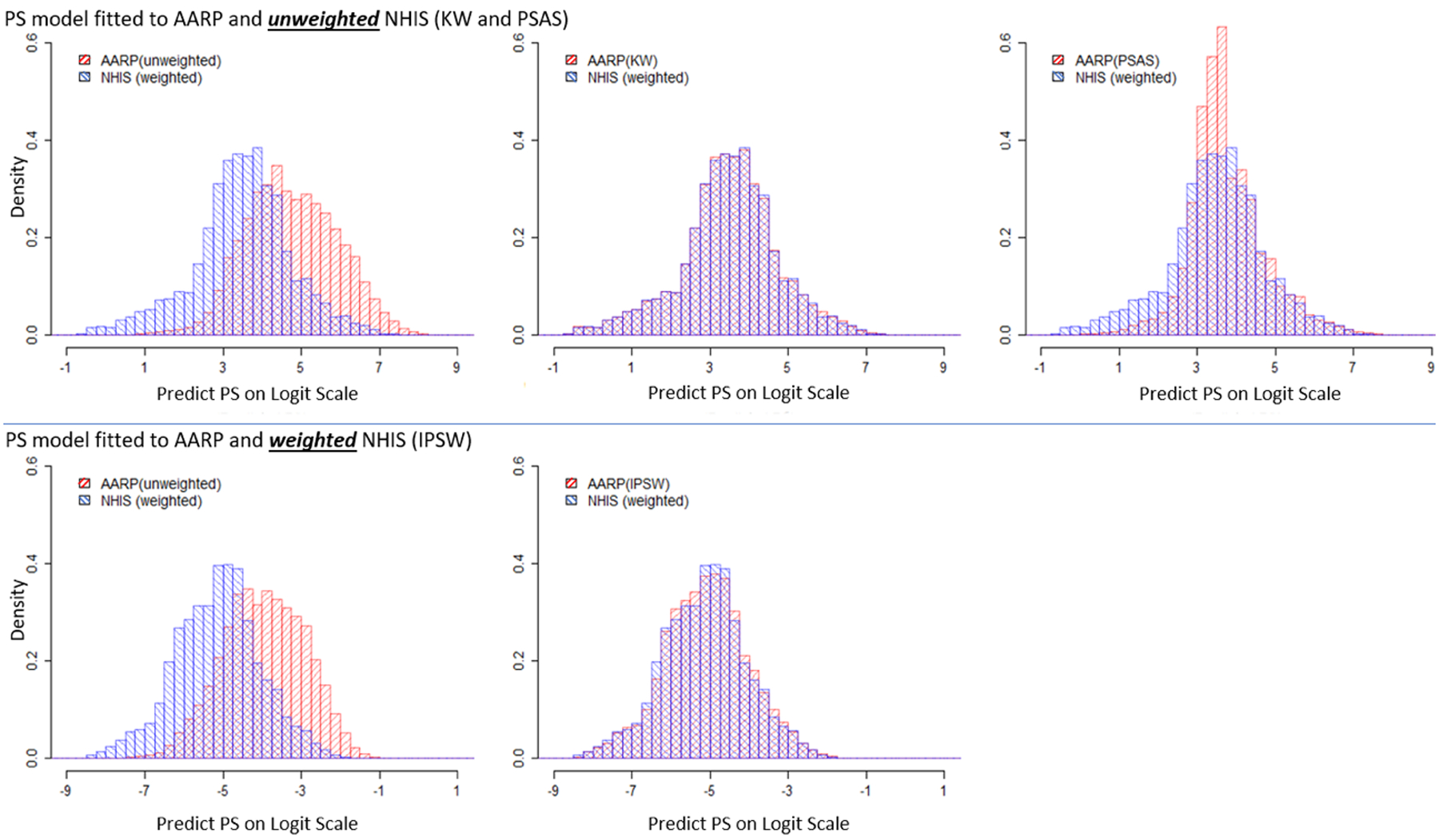
Comparison of Distributions of Estimated Propensity Scores on Logit Scale

We used the relative difference from the NHIS estimates $\left({\overline{Y}}^{\mathit{\text{NHIS}}}\right):\%RD=\left(\widehat{\overline{Y}}-{\overline{Y}}^{\mathit{\text{NHIS}}}\right)/{\overline{Y}}^{\mathit{\text{NHIS}}}\cdot 100\%$, and the percent of bias reduction from the naïve NIH-AARP estimates $\left({\widehat{\overline{Y}}}^{\mathit{\text{AARP}}}\right):\%BR=\left({\widehat{\overline{Y}}}^{\mathit{\text{AARP}}}-\widehat{\overline{Y}}\right)/\left({\widehat{\overline{Y}}}^{\mathit{\text{AARP}}}-{\overline{Y}}^{\mathit{\text{NHIS}}}\right)\cdot 100\%$ to evaluate the performance of the estimators, where $\widehat{\overline{Y}}$ is one of the IPSW, PSAS, and KW estimates. Of the eight self-reported diseases (Table 3), the naïve NIH-AARP cohort disease prevalence estimates were biased on average by ~44%, assuming the NHIS estimates as the truth. All three weighting methods removed roughly half the bias across the eight diseases. The KW method removed slightly more bias than the IPSW and PSAS methods, including a ~88% bias reduction for colon cancer, and ~79% bias reduction for prostate cancer. However, for all three methods, there was little bias reduction for stroke, and the bias increased for emphysema, possibly due to lack of covariates predictive of cohort membership, or accuracy of self-reported disease status (e.g., measurement errors).

Table 3.

Estimated population prevalences of eight self-reported diseases at baseline using four methods^†

Self-reported Disease	${\overline{Y}}^{\mathit{\text{NHIS}}}\left(\%\right)$	%RD				%BR
		NIH-AARP	IPSW	PSAS	KW	IPSW	PSAS	KW
Diabetes	10.48	−12.70	−12.48	−17.64	−8.94	1.74	−38.86	29.61
Emphysema	3.61	−24.03	−29.79	−25.03	−28.25	−23.99	−4.16	−17.55
Stroke	3.78	−43.61	−45.87	−47.05	−42.85	−5.18	−7.89	1.75
Heart Disease	7.25	94.05	45.13	43.41	46.09	52.01	53.84	50.99
Stroke or Heart Disease	9.89	55.54	19.72	18.25	20.84	64.49	67.13	62.48
Breast Cancer (Female)	3.44	38.53	16.19	21.51	17.75	57.98	44.19	53.92
Colon Cancer	0.69	31.52	3.91	5.91	3.88	87.61	81.24	87.69
Prostate Cancer (Male)	2.10	54.00	18.05	11.80	11.50	66.58	78.15	78.70
Average		44.25	23.89	23.83	22.51	46.00	46.16	49.12

^†The propensity model included nine main effects of age, sex, race/ethnicity, marital status, education, BMI, smoking, physical activities, and self-reported health status, as well as 31 interactions. Please refer to Web Table 7 in Web Appendix F. The estimates closest to the corresponding NHIS estimates are in bold.

Because self-reported diseases had potential measurement errors, we also examined nine-year all-cause mortality as it was obtained from linkage of NIH-AARP (and NHIS) to the National Death Index (NDI) (Table 4). Surprisingly, the naive NIH-AARP estimate of nonage-specific all-cause mortality had only ~9% bias. However, stratifying mortality by age revealed that the NIH-AARP estimates had a ~25% bias in each age group, which was reduced to 18% by KW (26% bias reduction), the most reduction among the three methods. Thus, the all-cause mortality was confounded by the age distribution: NIH-AARP oversampled older people (Table 2), which artificially inflated its overall mortality rate and offset the lower age-specific mortality in the cohort.

Table 4.

Estimated all-cause nine-year mortality, and all-cancer mortality (overall, and by subgroups) using four methods^†

	${\overline{Y}}^{\mathit{\text{NHIS}}}\left(\%\right)$	%RD				%BR
Group		NIH-AARP	IPSW	PSAS	KW	IPSW	PSAS	KW
ALL-CAUSE NINE-YEAR MORTALITY
Overall	13.67	−9.21	−16.9	−15.37	−15.51	−83.81	−66.91	−68.39
50–54	6.27	−22.64	−19.6	−23.87	−18.00	13.28	−5.44	20.50
55–59	9.71	−26.03	−20.6	−22.22	−18.90	20.77	14.63	27.37
60–64	15.66	−27.28	−22.5	−21.47	−19.95	17.68	21.29	26.87
64+	24.09	−25.09	−18.7	−17.95	−17.07	25.57	28.44	31.95
Average		25.26	20.3	21.38	18.48	19.45	15.36	26.83
ALL-CANCER NINE-YEAR MORTALITY
Overall	5.41	48.25	35.86	35.34	33.98	25.67	26.76	29.57
50–54	2.83	41.76	41.63	32.13	40.87	0.31	23.05	2.13
55–59	3.92	47.11	42.12	40.92	42.56	10.59	13.14	9.65
60–64	6.80	23.69	21.10	20.40	20.63	10.90	13.88	12.88
64+	8.61	35.37	28.48	26.30	26.31	19.48	25.64	25.62
Average		36.98	33.33	29.94	32.59	9.86	19.05	11.86
Male	6.56	44.47	32.13	29.38	29.63	27.76	33.94	33.37
Female	4.38	69.74	42.38	46.14	42.16	39.24	33.85	39.55
Average		57.11	37.25	37.76	35.90	34.77	33.88	37.14
50–54, male	3.47	23.28	25.96	18.96	26.79	−11.48	18.58	−15.05
55–59, male	5.36	14.23	22.24	16.24	22.82	−56.21	−14.09	−60.30
60–64, male	7.41	22.85	30.98	31.37	30.88	−35.57	−37.30	−35.17
64+, male	10.78	18.40	21.70	22.83	21.39	−17.93	−24.08	−16.26
50–54, female	2.23	65.31	67.15	53.00	63.91	−2.82	18.85	2.15
55–59, female	2.67	97.87	77.42	84.58	77.83	20.89	13.58	20.47
60–64, female	6.22	19.41	13.37	13.08	12.91	31.13	32.60	33.50
64+, female	6.84	44.75	34.37	34.08	33.67	23.20	23.84	24.75
Average		38.26	36.65	34.27	36.27	4.22	10.44	5.20

^†The propensity model included nine main effects of age, sex, race/ethnicity, marital status, education, BMI, smoking, physical activities, and self-reported health status, as well as 31 interactions. Please refer to Web Table 7 in Web Appendix F. The estimates closest to the corresponding NHIS estimates are in bold.

The results for all-cancer nine-year mortality differed from all-cause mortality (Table 4). The KW estimate had lowest bias for the overall all-cancer mortality (30% bias reduction). When stratifying cancer mortality by age, the PSAS method had slightly more bias reduction, and when stratifying by sex, the KW method reduced more bias. When we categorized mortality by age and sex, different weighting methods removed the most bias in different categories without any clear patterns, including the naïve NIH-AARP estimates having the least bias in three of the categories. Part of the reason was the small sample sizes of all-cancer deaths by age and sex in the NHIS sample. In addition, cancer mortality was not as well predicted as all-cause mortality from the covariates in the propensity model, thereby reducing the effectiveness of bias correction for all three weighting methods.

5. DISCUSSION

We proposed the KW approach to improve external validity of cohort analyses, using a representative survey sample as a reference of the target population. In brief, the KW approach produces a pseudo-weight for each cohort member in 3 steps: (1) estimate the propensity score for each unit in the combined sample, (2) compute the portion of the sample weight d_i for the survey unit i to be assigned to the cohort unit j by a kernel weight k_ij in equality (2.2.1), and (3) create the pseudo-weight for cohort unit j as the sum of the survey weights, weighted by the kernel weight k_ij. The sum of the cohort pseudo-weights equals the sum of survey weights. The KW method provides a consistent estimate of population mean/prevalence under the true propensity model and some standard assumptions. Unlike the naïve TL method, our jackknife variances account for all sources of variability in creating pseudo-weights. We applied these methods to reduce bias in prevalence estimates from the NIH-AARP cohort using the weighted 1997 NHIS sample as the reference. The KW method generally removed more bias than the IPSW or PSAS method, illustrating the potential benefits of the method. In a few cases, we found that small samples or possibly lack of factors predictive of cohort membership and outcome diseases could increase bias, illustrating practical limitations.

In our simulations, the KW estimates had smaller mean squared errors and better confidence interval coverages than the IPSW and PSAS estimates under both properly- and mis-specified propensity models that we considered. The IPSW estimates had the lowest bias among the three pseudo-weighted estimates when the propensity model was properly specified. However, the IPSW method tended to produce extreme weights that inflate variances, as noted previously (Stuart, 2010). Furthermore, the bias reduction and variance of the IPSW estimator can be sensitive to propensity model specification. PSAS is a special case of the KW method, with a uniform density kernel function in each subclass of estimated propensity scores that generally oversmoothed the pseudo-weights. Thus, PSAS tends to produce the least variable weights, resulting in the smallest variances, but also the least bias reduction (also noted by Valliant & Dever, 2011).

The naïve TL variances worked well for the KW and PSAS estimates but failed for the IPSW estimates. The naïve TL method substantially underestimated the variance of the IPSW estimates by ignoring variability due to estimating propensity scores. Since the IPSW method fits the propensity model to the combined sample of cohort and weighted survey sample, the estimated model coefficients and propensity scores can have large variance due to variable survey sample weights as well as the naturally high variability among cohort weights of 1 and the survey weights (Li et al., 2011). In contrast, the PSAS and KW methods fit a propensity model to the unweighted sample, which yields less variable estimates of the coefficients and propensity scores. Jackknife variance estimation is recommended for the IPSW estimates.

For the NIH-AARP cohort, the KW method reduced bias by 49% on average for estimating the prevalences of eight self-reported diseases (3% more than IPSW and PSAS methods). For nine-year nonage-specific all-cause mortality, the naïve cohort estimate had the smallest bias. However, mortality is strongly confounded by age. For age-specific mortality rates, the KW estimates had a greater averaged bias reduction (27%) than the IPSW (19.45%) and PSAS (15.36%) estimates. Thus, the better performance of the naïve cohort estimator for nonage-specific mortality was caused by disproportionately older volunteer recruitment in the NIH-AARP cohort.

For overall nine-year all-cancer mortality, KW reduced bias the most (~30% reduction). But when stratifying on key confounders (age and sex), no one method worked best for all categories, and PSAS had slightly higher averaged bias reduction than the other two methods across the eight age by sex categories. This result could be due to small sample bias (few cancer deaths in each age by sex category of NHIS sample) or the lack of factors predictive of all-cancer mortality in the propensity model.

All three weighting methods assume the final weights of the probability survey sample are the inverse of true inclusion probabilities from the finite population. However, ideal survey weights are likely unachievable due to imperfect undercoverage and nonresponse adjustments. The accuracy of the survey weights may affect the bias reduction of the IPSW method because this method fits the propensity model using the weighted survey sample. On the contrary, the KW and PSAS methods might be less sensitive to accuracy of the survey sample weights because they fit the propensity model using the unweighted survey sample.

The KW method was developed to reduce bias when estimating population prevalence of outcome variables available in cohorts but not in surveys, such as novel molecular or genetic risk factors. In our data example, we purposely selected outcome variables available in both cohort and survey, allowing us to quantify the relative bias by assuming the survey estimates as the gold standard. However, survey estimates can vary from the truth due to sampling errors, and non-sampling errors such as undercoverage and nonresponse bias. Unfortunately, there is no census of reported diseases in the US.

Although further investigation is needed, our simulations provide guidance for choosing propensity model predictors, the kernel function, and bandwidth for using the KW method. For the propensity model, Stuart (2010) suggests including all variables that may be associated with treatment assignment and the outcomes to reduce bias, but for small samples, it is useful to prioritize variables related to the outcome to control the variance (Brookhart et al., 2006). Our simulations agree that adding extra predictors that are associated with the outcome to the propensity model reduces bias, but at a cost of increasing variance. We suggest that the propensity models aim for maximal bias reduction by including all variables distributed differently in the cohort and the survey sample, all significant interaction terms, and all variables predictive of the outcome. Then, to control variance, we found that the triangular kernel effectively removed the influence of extreme imprecisely estimated weights for the KW method. Finally, we found that the Silverman and Scott bandwidth selection methods provided bias reduction yet controlled variance in our simulations.

Although the KW method outperformed the existing IPSW and PSAS methods, it has limitations. All propensity-score based methods require overlapping distributions of covariates between the cohort and survey sample. The amount of bias reduction depends on how well the propensity model predictors predict the outcome. If the propensity model is poorly fitted, the KW estimates can be more biased than naïve cohort estimates. Furthermore, including all known variables in the propensity model may not suffice for meaningful bias reductions. Further research is needed for developing propensity model selection and model diagnostics to identify situations when the KW method might increase bias.

There is much room for future research in improving representativeness of cohorts. First, other similarity measures, such as Mahalanobis distance or linear propensity score (Stuart, 2010), could be considered. Future research may explore how distance measures affect the performance of the proposed KW method. Second, weight adjustment methods such as weight trimming (Lee et al., 2010), and weight smoothing (Beaumont, 2008) may improve the performance of the KW method. Third, the KW method could be extended to epidemiologic studies involving sampling within cohorts (e.g. nested case-control, case-cohort, or general two-phase sampling (Li et al., 2016)). Fourth, although this paper focuses on estimating means and prevalences, the methods are needed to estimate general regression or risk models. For instance, due to potential unrepresentativeness of a cohort, the absolute risk estimates obtained from the naïve cohorts may not be generalizable to the population. We hope that this work will increase the attention paid to improving external validity of cohort analyses (e.g. Powers et. al. 2017), with the goal of developing reliable methodology and software for medical researchers.