Significance
Do animals encode statistical information about visual patterns the same way as humans do? If so, humans’ superior visual cognitive skills must depend on some other factors; if not, the nature of the differences can provide hints about what makes human learning so versatile. We provide a systematic comparison of automatic visual learning in humans and honey bees, showing that while bees do extract statistical information about co-occurrence contingencies of visual scenes, in contrast to humans, they do not automatically encode conditional information. Thus, acquiring implicit knowledge about the statistical properties of the visual environment may be a general mechanism in animals, but the richer representation developed automatically by humans might require specific probabilistic computational faculties.
Keywords: Apis mellifera, human visual cognition, insect cognition, unsupervised learning, internal representation
Abstract
The ability of developing complex internal representations of the environment is considered a crucial antecedent to the emergence of humans’ higher cognitive functions. Yet it is an open question whether there is any fundamental difference in how humans and other good visual learner species naturally encode aspects of novel visual scenes. Using the same modified visual statistical learning paradigm and multielement stimuli, we investigated how human adults and honey bees (Apis mellifera) encode spontaneously, without dedicated training, various statistical properties of novel visual scenes. We found that, similarly to humans, honey bees automatically develop a complex internal representation of their visual environment that evolves with accumulation of new evidence even without a targeted reinforcement. In particular, with more experience, they shift from being sensitive to statistics of only elemental features of the scenes to relying on co-occurrence frequencies of elements while losing their sensitivity to elemental frequencies, but they never encode automatically the predictivity of elements. In contrast, humans involuntarily develop an internal representation that includes single-element and co-occurrence statistics, as well as information about the predictivity between elements. Importantly, capturing human visual learning results requires a probabilistic chunk-learning model, whereas a simple fragment-based memory-trace model that counts occurrence summary statistics is sufficient to replicate honey bees’ learning behavior. Thus, humans’ sophisticated encoding of sensory stimuli that provides intrinsic sensitivity to predictive information might be one of the fundamental prerequisites of developing higher cognitive abilities.
Humans exhibit the most sophisticated cognitive behavior in the known animal kingdom (1–3). Our superior cognitive competence relies crucially on the ability to develop complex internal representations of the relations, structure, and physical rules defining the environment including our personal experience, and this ability requires a continuous unsupervised statistical learning (4). For example, in the auditory domain, 8-mo-old infants already demonstrate automatic extraction of co-occurring speech sounds from continuous auditory streams, thereby helping segmentation and eventually the development of language comprehension (5). In the visual domain, a number of studies in adults, 8-mo-old babies, and even newborns reported similar faculties potentially helping in extracting meaningful objects by identifying constant feature co-occurrence within complex visual scenes (6–9). In addition, humans become sensitive automatically not only to co-occurrences of features but also to predictivity of one feature on another, as well as embeddedness of smaller complex features in a larger one (10). Computational models demonstrated that human results can be captured best by assuming the existence of a sophisticated probabilistic learning mechanism in the brain (11), which indeed would be powerful enough to support the development of higher cognitive processes (12).
Humans’ high-level cognition is intimately related to our dominant sensory modality, vision, but there are other members of the animal kingdom with a lower level of brain complexity that nevertheless possess a well-developed visual system and demonstrate sophisticated behaviors, relying on object recognition and internal representations, such as landmark-based navigation. A notable example is the honey bee (Apis mellifera), one of the best-studied invertebrate models both for learning mechanisms and visual processing (13–17) that, despite the size of their nervous system, exhibits impressive abilities to recognize complex visual patterns (18–24). The honey bee’s recognition system is based on spatial configurations (18, 19, 23, 25, 26) that allow both fine discrimination among similar visual objects, such as human faces (21, 22), and efficient object recognition despite perceptual modifications, such as rotations (27). In addition, bees demonstrate high-level performance in categorization tasks based not only on perceptual regularities (15, 28, 29) but also on abstract relations, showing capacity to manipulate relational concept learning, such as “above/below” (30–34) or numerosity (35–42).
Given these impressive abilities of the bees to detect relations and recognize complex visual objects, there are three naturally arising questions: 1) Do honey bees extract information automatically without dedicated reinforcement about the statistical structure of the visual environment as humans do? 2) If so, do they extract the same kind of statistical information? 3) During the extraction process, do bees also rely on mechanisms that best capture probabilistic learning? Clear answers to these questions would provide information about the emergence of complex internal representations that are the basis of higher cognitive capacities. Investigating similarities and differences between how humans and honey bee encode intrinsically the underlying structure of complex visual scenes would provide insights regarding both the minimum requirement for sophisticated internal visual representations, and toward some of the critical characteristics of humans unsupervised learning mechanisms that might strongly contribute to our supreme cognitive skills.
To investigate these questions, we carried out a systematic comparison of honey bee and human behavior with a modified version of the classic visual statistical learning studies performed previously with adults and 8-mo-old infants (7, 8). While studies of the original human statistical learning paradigm employed an unsupervised framework, such that participants experienced sensory information without task specification or feedback, formal testing of honey bees requires a type of appetitive conditioning to permit experimental access (14, 43, 44). Therefore, we developed a supervised visual statistical learning paradigm, in which the supervised task has no bearing on the implicit learning of the significant higher-order statistical features of the input. Using this paradigm, we tested whether earlier human unsupervised learning results found with statistical structures of different complexity (7, 8) are evidenced both in humans and honey bees. Specifically, we asked to what extent humans and bees extracted individual shape frequencies, as well as joint probabilities (probability of two shapes to appear in a given spatial arrangement in a set of scenes; i.e., co-occurrence frequencies of shape pairs), and conditional probabilities of shapes (probability that shape B appears in a given relative position to shape A, whenever A is presented within a scene; i.e., predictability between shapes of a shape pair) without being specifically trained to do it. We also explored the possible computational model of learning that could capture the honey bee behavior, and compared how this model measured up against the probabilistic model attributed to statistical learning in humans.
Results
Human Baseline Experiments: Previous Unsupervised Statistical Learning Results Persist in a Supervised Learning Paradigm.
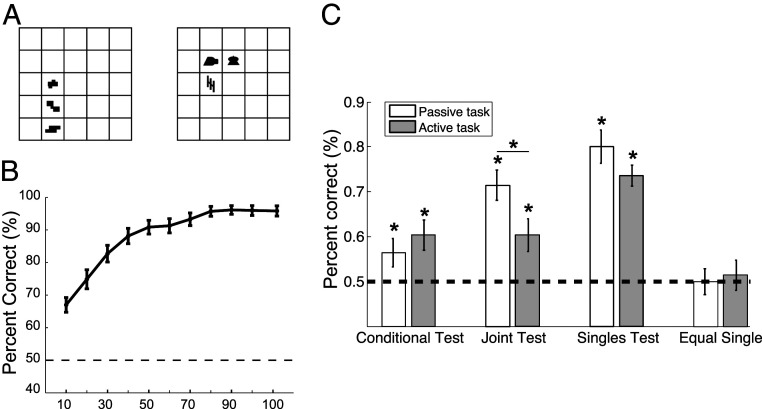
In a set of experiments, we tested whether the supervised learning set-up we employed with honey bees would interfere with humans’ performance reported in earlier unsupervised statistical learning tasks (7, 8). In particular, we assessed the effect of an explicit but unrelated task on the emergence of internal representations capturing statistical contingencies within the presented visual scenes. The stimuli in this experiment were composed of black shapes appearing in a grid in various spatial arrangements as customarily used in visual statistical learning experiments. At the beginning of the experiment, the abstract shapes were arbitrarily separated into two sets—labeled “Target” and “Distractor”—and, in each trial, these sets were used to generate a Target and a Distractor scene on the two sides of the screen in a counterbalanced manner (Fig. 1A). The participants of the experiment were randomly separated into two conditions, “passive” and “active.” During the familiarization phase, participants in the passive condition were told to simply pay attention to the upcoming scenes on the two sides of the screen because they would be asked questions after exposure. This is the exact instruction participants received in an earlier statistical learning study (7). In contrast, participants of the active condition were told prior to the familiarization that one of the two scenes in each trial would be Target, while the other would be Distractor, and they had to choose the Target scene. Participants in the active condition received no further specification about what Target or Distractor was, but they were provided a feedback about the correctness of their choice after each trial. In the two conditions, unbeknownst to the participants and unrelated to their main task (i.e., scene discrimination) in the active condition, shape co-occurrences and their spatial interrelations within each scene of a given trial were controlled by various statistical rules identical to those used in earlier unsupervised studies (7, 8). In particular, certain shape pairs could co-occur in a fixed spatial relationship with a higher chance (i.e., with higher joint probability) or one shape could perfectly predict the occurrence of another shape next to it (i.e., higher conditional probability) or simply just appear more often (higher appearance frequency) (see Materials and Methods for details).
Fig. 1.
Results of the human visual statistical learning experiments under passive and active conditions. (A) Illustration of a typical display presented in a trial of the familiarization phase during the human statistical learning experiments. In the active condition, one of the two scenes (a grid with its shape arrangement) was the Target, the other was the Distractor, and the participant learned to choose the Target across multiple trials with feedback. During the passive condition, the participant just inspects the two scenes for 6 s without a task. (B) Human discrimination performance in the active condition during familiarization. Average performance was computed in 10-trial bins, except for the last bin, which contained 12 trials. (C) Comparing human learning of conditional-, joint-, and single-element statistics in the passive and the active conditions after the familiarization session. The y axis shows average fraction of correct responses across subjects. Learning effects remained highly significant in the active condition, albeit with a significant reduction in learning the joint statistics (joint test). Chance performance in the control condition (equal single) indicates that the observed learning effects are specific and not due to general improvement due to increased overall familiarity. In B and C, dashed horizontal line shows chance performance, error bars represent SEM. (mean ± SEM). *P < 0.05.
Participants demonstrated a significant learning in choosing the Target scene correctly during familiarization in the active condition (P < 0.001) with a steady, almost linear improvement in the first part of the session, which saturated at a high, but not perfect level of performance in the last third of the trials (Fig. 1B). During the test phase following the familiarization, participants were tested for their sensitivity to the statistical contingencies in a two-alternative forced choice paradigm. In each trial of the test, they had to choose between two shapes or shape pairs the more familiar one. The shapes or pairs of a given trial always came from the same pool (Target or Distractor), but they differed with respect to their appearance frequencies, joint probabilities, or conditional probabilities. We confirmed that using this altered paradigm, regardless of whether they performed the supervised task in the active condition or just observed scenes in the passive condition, participants exhibited the same preferences during the tests as reported in an earlier visual statistical learning study (7). In particular, participants chose significantly more often the stimulus with higher frequency (singles test)/probability (joint test)/predictability (conditional test) as more familiar during the tests (Fig. 1C; see SI Appendix, Table S1 for statistics). Thus, the participants became automatically sensitive to frequency differences of individual shapes, the frequency of co-occurrences of shape combos in a given spatial relation (joint probability of shape pairs), and the strength of predictability between shapes (the conditional probability of shape pairs) in both conditions. We also confirmed that participants correctly performed at chance in the control test, when they assessed the relative frequency of shapes appearing equally often during familiarization (Fig. 1C, equal singles, and SI Appendix, Table S1). Thus, an easy, irrelevant task that could be solved merely by learning the class memberships of a few shapes in the two inventory sets did not hinder the inherent unsupervised processes that made participants acquire implicit knowledge of the underlying structure of the visual scenes, including both Targets and Distractors (SI Appendix).
Exp. 1: Honey Bees Become Sensitive to Shape Co-Occurrence Statistics in a Similar Fashion to Humans When Exposed to Moderately Complex Visual Scenes.
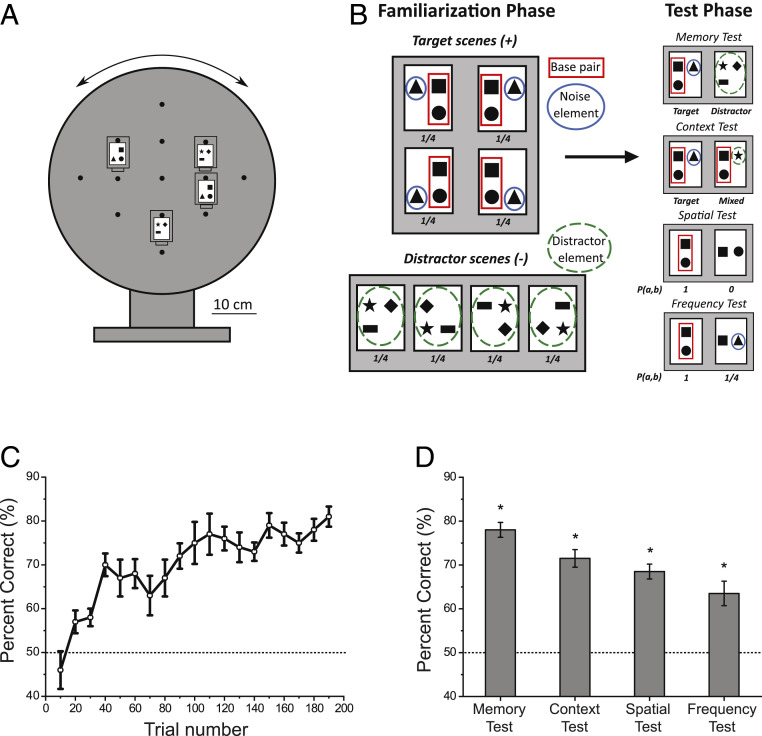
To relate human and honey bee statistical learning abilities, we tested bees (n = 10) with the design of Exp. 1 of the original adult (7) and infant studies (8) on spatial statistical learning, which we modified according to the active human baseline experiment presented above. During training, the bees performed 190 trials of a simple discrimination task with feedback between multishape Target and Distractor scenes presented on a rotating training platform (Fig. 2A). We used multiple three-element scenes varying between trials where the Target scenes consisted of a “base pair” of shape elements always appearing in a fixed spatial arrangement, while the third “noise” element could take one of four possible positions relative to the base pair within a 2 × 2 invisible grid (Fig. 2B). The Distractor scenes also employed three shape elements, but in a randomly arranged configuration. Specifically, for each bee, four scenes were randomly selected from the pool of the possible scenes with all combinations of shapes while taking special care that that no two scenes would present any of the two participating shapes in the same spatial relationship or in the same position. In each trial, the bee saw at a distance the Target and Distractor stimuli appearing simultaneously and in a random relative position on the training device. They had to select and land on the Target scene rather than on the Distractor scene in order to receive a reward (sucrose) instead of a punishment [quinine (43)] feedback (Materials and Methods). This task could potentially be solved simply by discriminating between a few shapes used in the Target vs. Distractor scenes without information about the relative configuration of the shapes.
Fig. 2.
The set-up, design, and results of Exp. 1 with honey bees. (A) The schematic picture of the experimental apparatus. In each trial, two scenes (a Target and a Distractor example) were chosen and two copies of these scenes were attached onto 4 randomly chosen positions of the available 13 options on a rotating wheel, which was subsequently turned by a random angle. Under each picture, there was a tray with either a positive or a negative reinforcement. (B, Left) The Target and Distractor visual stimuli of Exp. 1 chosen for one bee. (Right) Representative examples of the target (Left) and distracter stimuli (Right) in the four test types conducted in Exp. 1. Numbers under stimuli report relative frequencies of occurrence. Red and blue solid and green dashed outlines are only for informed viewing and were not presented in the original stimuli. (C) Mean improvement of performance during familiarization across trials in Exp. 1. (D) Average performance in the four tests of Exp. 1. Dashed line signals chance performance, error bars show SEM; *P < 0.05.
In the test session following the familiarization phase, we tested without reinforcement which statistical properties of the Target scenes were coded in the bees’ internal representation. This experiment had four objectives and correspondingly, four types of tests (Fig. 2B). First, to establish a baseline learning rate of these visual stimuli in bees, we compared choice preference for intact, rewarded shape triplets (Target scene) seen during practice over equally often experienced but unrewarded triplets (Distractor scene). This memory test provided a calibration in terms of the maximum level of expected performance in the subsequent tests. Second, we tested the bee’s preference for an intact Target scene considering the same scene but with the noise element replaced with a shape used for the Distractor scenes. This context test establishes whether the results of the memory test are simply due to memory traces of trials with rewarded Targets against visually very different Distractors during the practice, or the bees can actually transfer that knowledge to a novel situation, where the two proposed alternative stimuli share the same salient part, the base pair of a target scene. In the remaining two tests, we investigated bees’ ability to base their preference on the fine statistical structure of the base pair part of the target practice scenes rather than on the reward status of a whole Target scene over Distractor scenes. In the third spatial test, we examined whether bees encoded the spatial relationship between the two elements of the consistent base pair, or if the appearance of the two shapes in any configuration would suffice to induce preference. Finally, in the fourth frequency test, we measured whether bees could make a distinction between high spatially co-occurring fragment of the rewarded Target stimuli (the base pairs) compared to a low spatially co-occurring fragment (one shape from the base pair together with the noise shape), which they experienced less frequently by a factor of four during training as a part of the Target scene. This is a direct equivalent of the adult and infant tests showing frequency-based chunk coding in humans (7, 8). The order of the four tests represents an increasing difficulty of the underlying task. Each bee performed the memory test first followed by the other three tests in random order. There was no effect of test ordering on the results.
The training results show that honey bees efficiently learned the simple discrimination task between rewarded (Target) and punished (Distractor) scenes (Fig. 2C). Discrimination performance showed a steady and significant increase from a low performance to about 80% correct responses by completing the 190 training trials (generalized linear mixed-model [GLMM]: n = 10 bees, z = 6.99, P < 0.001) (Fig. 2C). The results reveal a similarity to the human baseline experiment in a task that could be solved simply by learning no more than a single shape in the Target stimuli, and thus did not require developing any implicit knowledge about the underlying structure of the scenes. Nevertheless, the four tests conducted after the training provided an unequivocal and strong support for the view that bees developed an implicit and sophisticated representation of the statistical structure of the multielement abstract training scenes, as they showed a significantly stronger preference for the more likely combination of shapes in all four tests (Fig. 2D).
Specifically, in the memory test, bees preferred the original Target scene compared to the Distractor scene significantly above chance expectation (generalized linear model [GLM]: n = 10, 78.0 ± 1.7%; z = 7.42, P < 0.001) (Fig. 2D), matching their performance at the end of the training session. The bees also demonstrated in the context test that they memorized all three shapes composing the scenes as they preferred a true Target scene over a Distractor scene composed of the base pair and a Distracter scene element replacing the noise element (n = 10; 71.5 ± 2.0%; z = 5.87; P < 0.001) (Fig. 2D). In the spatial test, bees demonstrated a high sensitivity for spatial relations and constancy within variable scenes (n = 10; 68.5 ± 1.7%; z = 0.15, P < 0.001) (Fig. 2D). Importantly, bees showed this behavior in a situation, which was independent of the trained reward value, since they had to choose between scenes with the same two shapes of the base pair relying solely on the correct rather than incorrect spatial arrangement. Finally, in the frequency test, honey bees showed a clear preference for base pairs over the base-shape/noise-shape combo that also appeared many times during the learning phase, but four times less often than the base pair (n = 10; 68.5 ± 1.7% of correct choices; z = 0.15, P < 0.001). This finding is compatible with the adult and infant results showing sensitivity to co-occurrence frequencies of shape pairs in humans (7, 8). It is also the same result we obtained in the joint test of the human baseline experiment in this study in a very similar experimental set-up. Since neither of the features necessary to perform above chance in the last two tests were required to learn the original discrimination task, honey bees exhibited the same learning behavior as humans. They automatically extracted and used the statistical information of co-occurrences and shape frequencies in the visual input beyond what was minimally sufficient for solving the task in which they were engaged.
Exp. 2: Unlike Humans, Honey Bees Do Not Become Sensitive to Conditional Statistics between Co-Occurring Shapes When Exposed to Moderately Complex Visual Scenes.
After establishing a basic similarity between human and honey bee visual statistical learning in Exp. 1, we explored in Exp. 2 whether this similarity holds at the next level of complexity. Human adults and infants are very good at automatically extracting and using the predictability of one visual feature by another one (i.e., conditional probability relations among features) even in cases when the co-occurrence statistics (joint probability of those features) are uniform and can provide no help in the task (7, 8). It is much less clear which nonhuman species possess similar capacities. Various animals, such as zebra finches (44), domestic chicks (45), rats (46), and cotton top tamarins (47) demonstrated sensitivity to statistical distribution of events in sequential learning studies. However, due to inadequate controls when making comparisons between different studies, it is an open question whether those animals learned transitional probabilities based on relative predictability (strength of condition probabilities) or just temporal co-occurrence frequencies (joint probability of two subsequent events) (48).
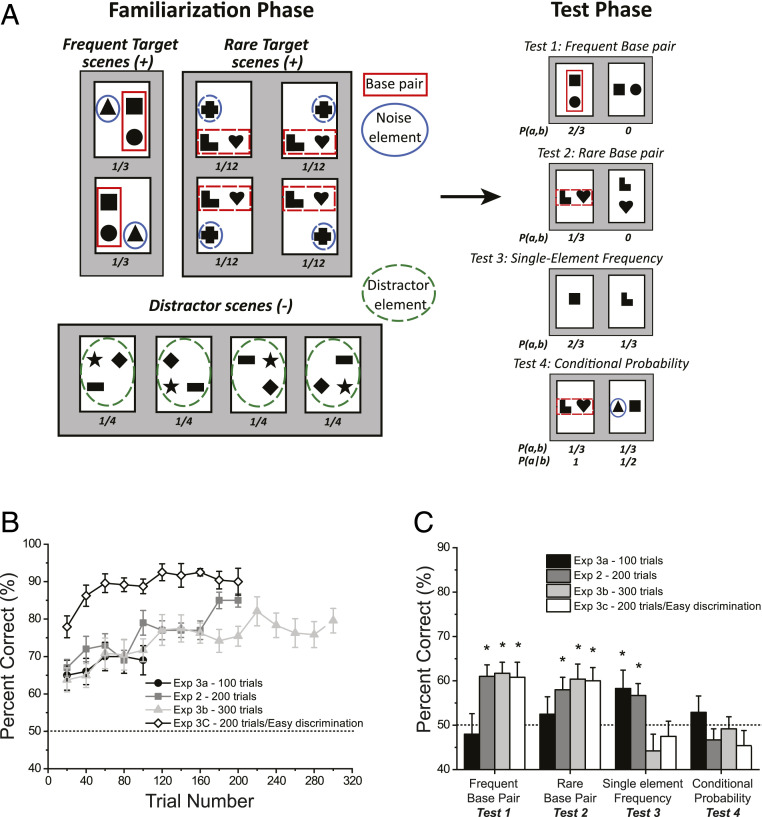
To investigate whether the animal model of the honey bee become automatically sensitive to relative predictability of spatial patterns (i.e., to true conditional probabilities), we tested a separate group of bees (n = 15) with the modified supervised version of Exps. 2 and 3 of the infant study on spatial statistical learning (8), which was equivalent to the conditional test of the human baseline experiments in the present study. The training and test design was the same as in Exp. 1, but the statistical structure of the training stimuli and the tests were different (Materials and Methods). The Target and Distractor training scenes were composed of three elements from a pool of nine rather than six different shapes as in Exp. 1 (Fig. 3A). Similar to Exp. 1, four Distractor scenes contained three distracter shapes in a random spatial arrangement. In this experiment, the statistical structure of the Target scenes had to provide shape pairs that were equal in terms of co-occurrence probabilities, but strongly different in terms of predictability (i.e., shape conditional probabilities). To achieve this, we applied the principle used in Exps. 2 and 3 of the previous infant study (8) and in the human baseline experiment of the present study. We used two sets of shape triplets in the Target pool for generating two types of Target scenes for the familiarization period: High-frequency Target scenes and low-frequency Target scenes that appeared four times less often than the high-frequency ones. The two types of scenes were composed of two different base pairs, where the elements were in a stable spatial relation and a noise element that could take different positions (Fig. 3A). In addition, there were only two distinctive high-frequency target scenes and four low-frequency target scenes. The result of this construction is that a base pair from the low-frequency scenes appeared exactly the same number of times as the “frequency-balanced pair” that was composed of one base-pair shape and the corresponding noise shape from the high-frequency scenes. At the same time, while the shapes in the low-frequency base–base pair always appeared together in the same configuration, this was not true for the “frequency-balanced” base-shape/noise-shape combo, since the noise element could take another relative position. Thus, the joint probability (co-occurrence) of the two pairs was equated, but in terms of the conditional probabilities (predictability), the low-frequency base pair had a twofold advantage over the combo pair.
Fig. 3.
The design and results of Exps. 2 and 3a–c with honey bees. (A, Left) The Target and Distractor visual stimuli. (Right) Representative examples of the Target (Left) and Distracter stimuli (Right) in the four test types in Exp. 2. Numbers under stimuli report relative frequencies of occurrence. Red and blue solid and green dashed outlines were not presented in the original stimuli. (B) Mean improvement of performance during familiarization across Exps. 2 and 3a–c. (C) Average performance in the four tests (x axis) across Exps. 2 and 3a–c (see legend). Dashed line signals chance performance, error bars show SEM; *P < 0.05.
Similarly to Exp. 1, following the training (200 trials), during in which bees performed a reinforced discrimination task between Target and Distractor scenes, the bees were subjected to four different tests performed in a random order. In Exp. 2, however, all four tests evaluated familiarity with fractions of the rewarded target scenes (Fig. 3A). The first two tests corresponded to the spatial test of Exp. 1, and they measured whether the bees had learned the fixed spatial relation of the two shapes within both the high-frequency base pair and the low-frequency base pair. These were the frequent base-pair test and the rare base-pair tests (tests 1 and 2). Test 3, called the single-element frequency test, evaluated if the bees became sensitive to the differences in appearance frequency of individual shapes during familiarization. In this test, one individual shape of the high-frequency base pair versus one from the low-frequency base pair were presented, and bees were expected to choose the high-frequency shape. Test 4 was the conditional probability test, in which the bees had to choose between the rare base pair (from the low-frequency scenes) and a “frequency-balanced nonbase pair” composed of one element of a frequent base pair and the noise element of the frequent scene in the relation seen in one of the two high-frequency scenes (Fig. 3A). This is the crucial test of sensitivity to conditional probabilities, a direct equivalent of the adult and infant tests showing predictability-based chunk coding in humans (7, 8) and of the human baseline experiment of the present study.
Despite the increase in task complexity due to the larger number of shapes used, bees showed a significant learning in the Target/Distractor discrimination task during the familiarization phase (GLMM: n = 15; z = 6.44, P < 0.001), and achieved above 70% performance after 200 training trials (Fig. 3B, dark gray). Moreover, the bees also showed a significantly stronger preference to the correct spatial arrangements for both the frequent (GLM: n = 15; 61.0 ± 2.6%; z = 3.78, P < 0.001) and for the rare base pairs (n = 15; 58.0 ± 2.8%; z = 2.76, P = 0.006) in tests 1 and 2 (Fig. 3C, dark gray). The bee’s performance with the frequent and rare base pairs was not significantly different (z = 1.41, P = 0.16). This indicates that even with more base pairs and uneven presentation numbers, bees have no problem remembering specific configural information and utilizing them in novel decisions. In the third, single-element frequency test, the bees showed significantly higher preference to the frequent shape (n = 15; 56.7 ± 2.7%; z = 2.07, P = 0.04) (Fig. 3C, dark gray). However, in the fourth conditional probability test, honey bees showed no preference for the more predictable base pairs over the frequency-balanced nonbase pairs (n = 15; 46.7 ± 2.5%; z = 1.15, P = 0.25) in contrast to the human baseline results (Fig. 3C, dark gray). In sum, while honey bees showed clear evidence of acquiring the statistical structure of the visual stimuli in terms of the underlying individual frequency and pair structure of the scenes, they did not show evidence of a capacity to use the predictability of shapes as quantified by conditional probabilities between elements of a co-occurring shape pair.
Exps. 3a–c: The Length of Exposure and Shape Distinctiveness Strongly Modulate the Visual Statistics Honey Bees Incorporate in Their Internal Representation.
The inability to handle conditional probabilities in Exp. 2 might be either a true feature of honey bees visual learning or it can be a confound due to increased task complexity. Two possible confounding reasons why learning does not occur are either that a participant had not received enough opportunity to get familiar with the stimuli, or that the stimuli were too hard to differentiate. To investigate these two possible confounds, we conducted three additional experiments, each with an independent set of bees. In Exp. 3a–c, we manipulated exposure time and stimulus similarity. First, we reran Exp. 2 twice without any modifications, except for changing the number of familiarization trials from 200 to 100 (Exp. 3a) and to 300 (Exp. 3b) to see whether more or less exposure changes the bees’ learning pattern of the statistical structure of the scenes. Second, we repeated Exp. 2 with 200 trials, but replaced the composite distractor scenes consisting of three shapes with a single distinctive achromatic pattern (Exp. 3c). This last modification strongly increased the discriminability of the Target and Distractor scenes while leaving intact the underlying structure of the Target scenes under investigation.
Fig. 3 B and C shows the results of these experiments together with those of Exp. 2 for comparison. The familiarization results indicate two notable effects. First, changing the exposure time from 100 to 200 and to 300 trials revealed similar learning curves in the early part of familiarization (first 100 trials; comparing Exp. 3a and Exp. 2: z = 1.33, P = 0.19; comparing Exp. 3b and Exp. 2: z = 0.40, P = 0.97). At the same time, more exposure led to higher performance, but only to a certain degree, as the average performance plateaued at around 80% correct response rate after 200 trials and did not improve further. Nevertheless, at the end of both 200 trials and 300 trials, bees performed significantly better on the Target/Distractor scene discrimination than after 100 familiarization trials (last 25 trials; comparing Exp. 3a and Exp. 2: z = 3.59, P < 0.001; comparing Exp. 3b and Exp. 2: z = 5.40, P < 0.001).
A second notable effect is that simplifying the discrimination task by providing more distinguishable Target and Distractor stimuli had a significant improving effect on the bees’ performance both immediately at the beginning of the familiarization after just 25 trials (first 25 trials; comparing Exp. 3a and Exp. 3c: z = 2.79, P = 0.005; comparing Exp. 2 and Exp. 3c: z = 2.97, P = 0.003; comparing Exp. 3b and Exp. 3c: z = 3.34, P < 0.001), and at the end of the 200-trial session (last 25 trials; comparing Exp. 2 and Exp. 3c: z = 2.30, P = 0.02; comparing Exp. 3b and Exp. 3c: z = 3.47, P < 0.001). Nevertheless, even in this condition after a faster early improvement in performance, a clear saturation is evident at a high (90%) but not perfect level (Fig. 3B). In sum, both complexity and length of exposure significantly affected bees’ performance in the discrimination task in an expected manner.
The key question of how these respective length and similarity manipulations influence the learning of the underlying structure of the visual scenes can be answered by interpreting the test results (Fig. 3C). Performances in the 100-, 200-, and 300-trial versions of the experiment indicate a remarkable transformation in the honey bees’ internal representation as the number of training trials increases. With 100 trials, neither the frequent nor rare base pairs in their right spatial configuration were reliably preferred over the wrong configuration by the honey bees (test 1: 48.0 ± 4.6%, z = 0.65, P = 0.52; test 2: 52.5 ± 3.9%, z = 0.77, P = 0.44) (Fig. 3C). However, the bees significantly preferred the frequent single elements over the rare ones (test 3: 58.3 ± 4.1%, z = 2.57, P = 0.01) (Fig. 3C). As training extended to 200 trials, the base pairs were gradually learned so that test 1 and 2 reached a significant level (test 1: 61.0 ± 2.6%, z = 3.78, P < 0.001; test 2: 58.0 ± 2.8%, z = 2.76, P = 0.006) (Fig. 3C), and for frequent base pairs, also elevated significantly above the performance recorded after 100 trials (test 1: z = 3.03, P = 0.002) (Fig. 3C). In contrast, while the single-element frequency results (test 3) remained significant, the performance outcome did deteriorate slightly (test 3: 56.7 ± 2.7%, z = 2.07, P = 0.04).
By reaching 300 training trials, both tests 1 and 2 reached a saturated level of significant performance (test 1: 61.7 ± 2.5%, z = 3.58, P < 0.001; test 2: 60.4 ± 3.4%, z = 3.20, P = 0.001), in case of test 1, significantly above the performance found after 100 trials (z = 3.02, P = 0.003). In contrast with this increase in performance with pairs (tests 1 and 2), the performance with individual shapes measured by the single-element frequency test (test 3) showed a strong negative change with more learning. Specifically, performance in test 3 after 300 training trials fell back to a nonsignificant level (test 3: 44.2 ± 3.8%, z = 1.80, P = 0.07). This performance was significantly below the level found with either 100 or 200 training trials (test 3: comparing Exp. 3a and Exp. 3b: z = 3.09, P = 0.002; comparing Exp. 2 and Exp. 3b: z = 2.57, P = 0.01). These results indicate a shift from simple element-frequency based internal representation to a representation based more on larger consistent chunks or underlying configurations of the scenes.
Regarding the effect of task difficulty, we also found that across the four test measures, the 300-trial experiment with standard Distractor stimuli (Exp. 3b) produced results that were indistinguishable statistically across the four tests from those found in the 200-trial experiment with simplified Distractor stimuli (Exp. 3c) (test 1: 60.8 ± 3.4%, z = 0.19, P = 0.85; test 2: 60.0 ± 3.0%, z = 0.37, P = 0.71; test 3: 47.5 ± 3.4%, z = 0.82, P = 0.41) (Fig. 3 B and C). This suggests that, while more exposure is required for good performance with a more challenging version of the discrimination task, the developing underlying representation seems to follow a remarkably similar transformation.
Importantly, under no condition did honey bees show evidence of sensitivity to conditional relationships (test 4) (Fig. 3C), suggesting that they were not able to extract this kind of information automatically (Exp. 3a: 52.9 ± 3.7%, z = 1.16, P = 0.25; Exp. 2: 46.7 ± 2.5%, z = 1.15, P = 0.25; Exp. 3b: 49.2 ± 2.7%, z = 0.26, P = 0.80; Exp. 3c: 45.4 ± 3.4%, z = 1.42, P = 0.16).
Computational Analyses: Honey Bees’ Learning Behavior Can Be Captured by a Counting-Based Rather than by a Probabilistic Learning Model.
Since our behavioral results only indicate the existence of differences in the statistical properties memorized between bees and humans, we used modeling to clarify what significance, if any, can be attributed to the finding that honey bees apparently do not encode automatically predictivity relations of their sensory input. As capturing human statistical learning requires a probabilistic chunk-learning model (PC) (11), our rationale was to test if the same model can explain the bee behavioral results, and alternatively, if a simpler model known to be insufficient to capture human learning would be adequate for replicating the learning behavior of the bees. The results of these tests would inform us as to whether bees and humans use different computational approaches during automatic unsupervised learning from sensory input of complex visual scenes.
In an earlier study, a combined behavioral-modeling analysis was performed to investigate what type of computation might capture human visual statistical learning (11). Five different computational models were selected ranging from storing simple memory traces, to collecting various summary statistics of the input, to compute probabilistic internal representation of those inputs in pairwise associative or probabilistic chunk-learning (PC) manner. These models were tested with the visual input of a set of increasingly complex human visual learning studies. Similarity of the learning results between models and humans were used to conclude on what type of learning humans might use. The result of the study was univocal: As the complexity of the learning tasks increased, models gradually failed to follow the pattern of human learning, and eventually only the PC learning model replicated all of the human results (11).
We followed Orbán et al.’s (11) strategy with the data obtained with the honey bees in the present study and focused on two models (Materials and Methods). The first is the improved version of the model that successfully captures human behavior: A PC learner model, which searches for the most parsimonious inventory (set of most likely chunks generating the scenes in a modular manner) to represent, store, and interpret the stream of appearing scenes. Conceptually, this algorithm develops a generative internal model of the outside world, which can then be used for solving any subsequent task, such as a familiarity judgment or a preference choice (11). The second model is a combination of the two counting-based summary statistics models that were also tested in Orbán et al. (11) study, and have been shown not to follow human behavior when learning more complex scene information. These two counting models enumerate how many times particular shapes and combinations of two shapes, respectively, occurred within the scenes during familiarization, and determine familiarity or choice preference during the test based on the magnitude of the obtained statistics. Following earlier reports finding that as learning duration increases, honey bees shift from elemental associations to compound associations (26, 49), we combined these two models into a single counting-based summary statistics model (CB), in which the shape-based counting model comes online early, and then it gradually gives way to the pair-based counting model (see SI Appendix for details). Conceptually, this model is equivalent to a fragment-based associative memory model or trace model, that keeps track of the co-occurrences of various subsets of elements (low-complexity features, such as individual shapes and shape-pair fragments) to form an internal model in order to guide further decisions (50, 51).
We implemented respective models and trained each with the same input sequences in the same order employed for the bees’ and humans’ experiments. For the CB model, each input scene was represented simply with a set of variables, each indicating, in a binary manner (0/1), whether a particular shape was observable in the present scene. The developing internal representation consisted of the tallies of all of the individual shapes and shape-pairs that occurred in the individual scenes summed across the entire training session. Choices during the test were made based on the relative strength of these tallies. For the PC model, two sets of variables were used to represent each scene: One indicating, in a binary manner, the presence/absence of individual shapes in the given scene, and the second set coding the position of these shapes (by 2D vectors). The internal representation of the PC model consisted of a set of “chunks,” where chunks could be any fixed configuration of arbitrary number of shapes (also encoded by presence/absence and relative position) that emerged during the training through probabilistic learning as the best set to capture the description of the previously experience scenes (Materials and Methods and SI Appendix). The behaviors of the two learning models were then examined by conducting all of the test trials with the scenes used in the behavioral tests and with the same decision model, but with the respective internal representation developed by the two models (SI Appendix).
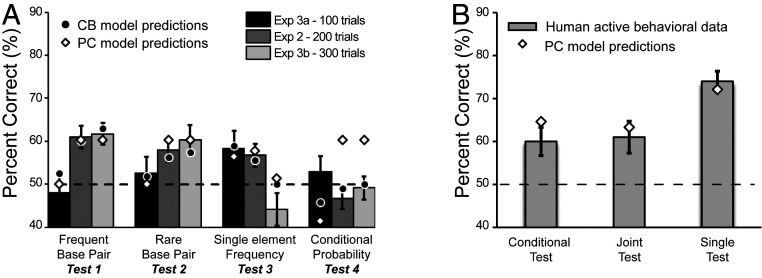
The simulation results showed a clear double dissociation: While the PC model followed human behavior but could not replicate the honey bee behavior, the CB model, which is known to be inadequate for modeling human learning under more complex conditions, adequately captured the honey bee behavior (Fig. 4). The failure of the PC model to reproduce the honey bee results was not a result of insufficient parametrization, but a direct consequence of the characteristics of the learning model as can be appreciated intuitively by inspecting the stimulus structure and the evolution of performance with increased training. Specifically, the significant preference for the frequent shapes and shape pairs in tests 1 to 3 after the first 200 training trials means that the PC model must already be sensitive to differences in element frequencies and in pair frequencies between the frequency-balanced and rare base pairs during the trials of the conditional test (test 4). Due to the joint effects of these two sensitivities, therefore, the conditional test must yield a strong preference for the frequency-balanced pairs over rare base pairs if probabilistic chunking were at work. In contrast, the CB model is not sensitive to conditional probabilities, while it can follow the shift in sensitivity from single shapes to shape pairs frequencies, thus replicating the empirical results with honey bees. These computational analyses reveal that the difference found between humans and honey bees with respect to the automatic treatment of predictive information available in the sensory input implies fundamentally different unsupervised learning mechanisms used by the two species.
Fig. 4.
The ability of CB and PC models to replicate honey bee’s and human behavioral data. (A) Bars show the bee’s results in the four tests of Exp. 2, filled circles and empty diamonds depict the choice probabilities computed by the CB and the PC models, respectively. The extent of familiarization was modeled by the length of the input in the PC model, and by the capacity parameters in the CB model. Both models followed the behavioral data similarly in the first three tests, but the PC model also learned by necessity the conditional contingencies while, in agreement with the honey bees’ behavior, the simple CB model could not. (B) Bars show the human behavioral result in the active statistical learning task and diamonds depict the choice probabilities obtained by the PC model (empty diamonds). The model’s predictions follow the behavioral data in all three test conditions. Error bars represent SEM, while dashed horizontal line indicate chance performance.
Discussion
In the present study, we systematically explored the statistical properties of complex visual scenes that honey bees can implicitly learn and compared these abilities to those of humans within the same experimental paradigm. Such a comparative approach has been highly successful in the past for understanding how similar cognitive challenges are solved by different species varying both in their evolutionary history and their brain computational capacities (3, 52–56). In the domain of visual perception and cognition in particular, the existence intriguing similarities between vertebrates and some invertebrate species of higher-level visual processes, such as the use of spatial configuration to facilitate object recognition (18, 25, 57–59) or the sensitivity to some visual illusions (60, 61), prompted a reevaluation of the required complexity of the underlying mechanisms. Importantly, while our study is grounded in the domain of vision, it investigates domain-general characteristics of implicit statistical learning, and our results are largely independent of how actual features are processed neurally in the visual modality by the two species.
Earlier studies using classic or operant conditioning showed that bees are capable of a wide range of nonelementary associative learning. These include negative patterning (configural processing of A+, B+, and compound AB− stimuli) (14, 62–64), visual categorization (grouping objects based on shared properties) (14, 15, 25, 29, 65), relational concept learning based on notions, such as “above,” “same,” or “larger” (32, 34), and even sophisticated numerical abilities (38, 39, 66). However, these studies were all conducted in a supervised setting with explicit training, and thus they did not clarify what bees learn naturally and automatically when they are simply confronted with a novel scene. With our method, we were able to show that honey bees automatically extract various relational information and recognize consistent visual fragments without being explicitly trained to do so, after simply being exposed to a large set of structured visual scenes. This is a remarkable evidence in an invertebrate species of such implicit learning, narrowing the gap between widely separated parts of the animal kingdom with respect to the ability to spontaneously develop sophisticated internal representations of the underlying structure of their environment as it was observed in humans. Moreover, the present study could also address our main question: Is there a significant difference between the resulting internal representation developed by humans and bees and if so, what is the nature of this difference?
In order to answer this question, we transcended earlier results obtained by explicit training that demonstrated learning and generalization of complex visual patterns in bees (18–20, 23–25) in three additional aspects beyond the fact that we obtained our results by implicit learning. First, the bees were confronted with a harder task and required to make stronger generalizations than in previous studies due to a more variable training set and test trials, in which the target and distractor stimuli both strongly diverged from the trained pattern (e.g., in overall configuration), while only subtly differing from each other (e.g., in appearance frequency). Second, we investigated the effects of exposure duration and task difficulty on performance to gain insights into the learning mechanism used by the bees. Third, we used multiple statistically defined test measures concurrently, so that we could identify the limits and trade-offs of implicit learning in bees and compare those systematically and computationally to human learning.
Our results show that the internal representation the bees developed to solve the simple Target–Distractor dissociation during training allowed them to also pass successfully a number of harder novel tests that required more abstract generalization. First, similar to Exp. 1 in Stach et al. (23), we found that bees could correctly choose the Target stimulus over a Distractor differing only in one component of the display, even when the component was not a simple orientated line but a complex shape (Exp. 1, context test). Second, bees were sensitive to the spatial arrangement of the abstract shape components even within a fragment of the full display (Exp. 1, spatial test; Exp. 2, rare and frequent base-pair test). Third, bees encoded frequencies of appearance for both pairs and single elements (Exp. 1, frequency test; Exp. 2, single-element frequency test). These results indicate that bees used a far more sophisticated internal representation than a simple matching template of the configuration capturing the entire input stimulus (17, 20, 26, 67). Remarkably, this internal representation emerged automatically without any targeted training, much akin to human unsupervised learning of internal representations reported with both adults and infants (7, 8).
However, we also found the limits of what bees could implicitly learn. Specifically, under no experimental condition we could find bees learning involuntarily the predictability between two elements as defined by their conditional probability. Although this null result could potentially be an artifact of an insufficient experimental design with excessively hard tests or a result of chance, the outcome of the control experiments (Exps. 3a–c) render these explanations unlikely for two reasons. First, the computed Bayes factor (BF) for the conditional probability test with the longest training substantially favoring the “no-learning” hypothesis over “learning” (Exp. 3b: BF = 3.35), and this makes the chance for a type II error slim. Second, both major components of complexity (exposure duration and task difficulty) have been modulated close to the extremes over the various control experiments in order to simplify the task, yet these manipulations failed to uncover any effect on learning conditional probabilities. It is, therefore, improbable that further extension of exposure time or simplification of the task would yield markedly different results.
One additional reason why bees would be unable to perform well in the conditional test might be that they could not discriminate the shapes sufficiently for learning the conditional relations. However, this alternative can be ruled out on two counts. First, shapes similar to the ones used in the present study were demonstrated as perfectly discriminable by bees in previous studies (31, 68) (Materials and Methods). Second, the visual conditions of the test stimuli in our study were kept constant, and only learning conditions were varied across the three experiments, more specifically, the very same shapes in the very same configurations were used in Exps. 1, 2, and 3. Bees performed equally well across experiments in most of the tests, including the joint probability tests with two shapes in the test scene. Since there was sufficient visual information to perform in all tests of Exp. 1, and in tests 2 and 3 in Exp. 2, the same visual information must be sufficient to perform the conditional test 4 in Exp. 2. Consequently, an explanation based on a limitation of low-level feature discrimination can be excluded.
It is important to clarify that our result does not imply that bees cannot learn conditional relations of events. Various earlier studes reported that under explicit differential conditioning, bees showed examples of nonelemental learning, such as negative patterning (A+, B+, AB−) or bidirectional discrimination (AB+, CD+, AC−, BD−) that are examples of acquiring conditional relations (14, 62–64). Bees could also use conditional rules to navigate a maze following symbols (69) or to decide between two rules (add or subtract one element), depending on the stimuli color (39). However, our results suggest that when engaged in a simple discrimination task that involves complex visual patterns, bees build up an internal representation that does not naturally and automatically encompass conditional contingencies of the patterns.
The failure of learning conditional probabilities is in agreement with earlier findings showing that during training for transitive inference rule (if A > B and B > C, then A > C), bees could learn correctly the premise pairs only when they were explicitly trained to the premises in uninterrupted, consecutive blocks of trials. When forced to handle more camouflage due to experiencing all pair relations essentially in a simultaneous manner in shorter and interspersed blocks of trials, bees failed to perform correctly the rule of transitivity (14, 65). The overall conclusion of these studies was that even in conditions where bees performed well with the premise pairs, they did not truly learn transitivity, but rather combined recency effects with associative strengths of pair learning. Bees can thus only perform complex tasks when they are trained to do it explicitly (e.g., in case of conditional probabilities) or when their training protocol allows them to derive satisfactory responses based on their simpler learning (e.g., in the case of learning the premise pairs during the transitivity study). Nevertheless, these simpler solutions that bees use to solve complex visual problems could be inspirational for developing efficient artificial intelligence systems with reduced computational resources to do the same (70–73), and provide insights into how larger brains automatically perform such tasks.
We found that with increasing exposure during training, the bees’ performance improved, and their internal representation shifted steadily from focusing on element frequencies to co-occurrence frequencies. This is similar to the findings that with increased exposure time, bees shift from associating elements of a compound S+ stimulus with the reward to associating the compound itself with the reward (49). Thus, in the light of more experience with newly introduced statistics of their environment, honey bees naturally transform their internal representation to capture progressively more complex statistics of the input.
In addition, we also found that simplifying the task (Exp. 3c) promoted earlier emergence of configural representation based on co-occurrences. At first sight, this might look similar to the finding that adjusting the color of the component shapes to be more similar promotes more configural learning (49). However, there is a subtle but important difference between the two experimental designs: In Giurfa et al.’s (49) color experiment, the adjustment of colors directly influenced the stimulus to be learned and tested, whereas in our case, only the task became easier by adjusting the complexity of the Distractor stimulus, yet the coding of the physically unchanged Target stimuli shifted earlier from elementary to compound representation. In other words, while Giurfa et al. showed a direct effect of manipulating the stimulus on learning, we showed an indirect effect through manipulating only the task. This means that learning in bees is a complex context-dependent process, in which the nature of the internal representation is determined by both the stimuli and the task involved in the experiment.
Regarding our key question about the similarity between human and honey bee learning, we found that the present results of honey bee’s learning performance can be sufficiently well captured by a simple model that learns CB summary statistics, specifically the most prominent individual and co-occurring shape-pairs of the scenes. This is in contrast with human behavior, which in similar tasks requires a more complex model, for example a PC learner model to be correctly replicated (11). It is instrumental to realize that human performance in the various tests changed only slightly when the protocol of the experiment switched from passive observation to active discrimination (Fig. 1). This suggests that the internal representation responsible for human results, which included coding for conditional probabilities, emerged largely automatically and it was independent of the particulars of the discrimination task. Automaticity of encoding conditional probabilities is supported by earlier findings that adults and 8-mo-old infants are equally sensitive to such statistics of the visual scenes (8). Unfortunately, such a comparison between active and passive protocols is not available with the bees. Therefore, we cannot completely rule out that the reinforcement learning protocol used in our experiments shaped learning and the internal representation in bees more powerfully than in humans, and that bees would show some sensitivity to conditional relations under more natural exploration of their environment.
While lack of automatic sensitivity to predictive information is one explanation of our results, a possible alternative is that the discrepancy between bees and humans exists at the stage of handling the task rather than at encoding. In this scenario, bees can encode conditional probabilities of the input, but in a substantively novel task situation (test), they do not utilize this information because the plain frequency difference weighted more in their decision in the context of a generalization test.
Nevertheless, given the present results, we posit that automatic extracting of conditional information is not a fundamental component of honey bee’s visual learning, and it occurs only when it is promoted by a dedicated reinforcement scheme. We propose that, as a consequence of this, humans and honey bees use different types of learning to encode their visual environment that lead to different internal representations. While simple discrimination, recognition, and a number of other basic tasks can be equally well solved with the two strategies, important differences could emerge in complex tasks. Based on the recently established prominence of probabilistic computation in the brain (74), we speculate that, combined with various other relevant factors, the richer internal representation that humans build automatically and the underlying probabilistic learning mechanism could potentially be one of the key components that led to the emergence of humans’ superior cognitive abilities.
Materials and Methods
Human Learning Experiment.
For the human learning experiment, 142 healthy volunteers (96 females, average age 22.08 y) with normal or corrected-to-normal vision participated in the experiment after giving informed consent. All procedures were approved by the Ethics Committee for Hungarian Psychological Research.
Stimuli.
Twenty individual abstract black shapes on white background were used in the experiment. Each trial consisted of two 5 × 5 black grids appearing side-by-side on the display and each grid contained a set of three shapes always in neighboring positions on the grid, but in various configurations. Stimuli were presented on a 27-inch Samsung Syncmaster S27B550 color monitor from a viewing distance of 1 m, so that the extent of the grid was 16.4 visual degrees. For each subject, half of the shapes were randomly assigned to the Target and Distractor categories, respectively. In addition, in each category, the shapes were organized into one frequent and two rare base pairs and four individual elements, and these were the building block of the sets of three shapes presented in the grids. Base pairs consisted of two shapes always appearing together in a fixed spatial relation in the grid. The frequent base pairs appeared in the display 2.6 times more often across trials than the rare pairs did. An individual element could appear in any adjacent position relative to the base pair in the grid so that visual segmentation of the pair and the single element was not possible (Fig. 1A). Twenty-eight unique three-shape scenes containing one base pair and one single shape with varying absolute position of the shapes across scenes were created separately from both the Target and Distractor categories. Scenes were further composed so that based on the co-occurrence of the single shapes and the frequent base pairs, there were two so called “frequency-balanced nonbase pairs” composed of one shape from the base pair and the single shape. These were pairs that had the same joint probabilities as the rare base pairs but much lower conditional probabilities. Indeed, while these nonbase pairs appear as often as the rare base pairs during familiarization, both shapes composing the nonbase pairs could also appear with a different relationship, which was not the case for the base pair by definition, where the two shapes always appeared together in a fixed spatial relationship. The arrangement of such rare, frequent, and frequency-based pairs allows systematic tests of sensitivity to co-occurrence and conditional probabilities, and it was used extensively in earlier studies (7, 8). The underlying statistical structure created by the co-occurrence of the shapes was exactly the same in the Target and Distractor categories but based on two nonoverlapping shape inventories.
Procedure.
Each experiment consisted of two phases: Familiarization and test. During the familiarization phase, a presentation trial started with a fixation cross appearing in the middle of the screen for 1 s. Next, two scenes (one Target and one Distractor scene) were simultaneously presented for 6 s on the left and right side of the screen equally distanced from the center (Fig. 1A), followed by a blank intertrial screen presented for 1 s. During familiarization, each unique scene in a category was presented 4 times, resulting in a total of 112 presentation trials (15 min). The presentation order of the scenes was randomized for every category and the left–right appearance of the two categories was counterbalanced. Participants were assigned to one of two tasks conditions prior to the familiarization phase. In the passive task condition, participants were instructed to pay attention to the sequence of the scenes so that they would be able to answer some simple questions after the familiarization phase. Participants received no information about the structure of the scenes. In the active task condition, participants were asked to choose in each presentation trial the Target scene by pressing the left or right arrow keys on their keyboard after the scenes disappeared. Every trial was followed by feedback about the correctness of their choice showing either the word “correct” in green or the word “incorrect” in red in the middle of the screen for 1 s. Participants received no further information about the structure of the scenes beyond the existence of the two categories.
A test phase followed familiarization with three or two temporal two-alternative forced-choice tasks conducted in a fixed order. First, in the conditional test, a rare base pair and a frequency-balanced nonbase pair were shown sequentially for 2 s centered in the grid and with 1-s blank separating them. Participants had to press a key “1” or “2,” depending on which of the two pairs they judged to be more familiar based on the familiarization scenes. The test trials were based on two rare base pairs and two frequency-balanced nonbase pairs in each category (Target and Distractor). Both base pairs were presented once with each of the two frequency-balanced nonbase pairs of the same category resulting in eight test trials in total. As the base pairs and nonbase pairs had the same co-occurrence frequencies (joint probabilities: P = 0.21), only the difference in conditional probabilities (base pairs: P = 1.0, nonbase pairs P = 0.75) could be utilized to choose between the pairs. Test trials were individually randomized, and the order of presentation of the base pairs and nonbase pairs was counterbalanced within a test session for each participant. In the second test, the single test, participants had to choose between two single shapes shown centrally the one, which was seen more frequently during familiarization. For both categories, the test contained two frequent shapes (P = 0.57) and six rare shapes (P = 0.21), which were organized to create eight fully randomized and counterbalanced test trials. Four test trials compared two frequent shapes with two rare shapes (singles test), and the remaining four rare shapes were used in four additional test trials with no correct answer (equal single test). This resulted in a total of 16 single test trials for each participant. In each trial of the third test, the joint test, participants had to choose the more familiar one between a rare base pair and a low frequency accidental pair shown sequentially with the same presentation times as in the conditional tests. For each category, two accidental pairs with low co-occurrence frequency were chosen from the scenes (joint probability: P = 0.036) and compared to two rare base pairs (joint probability: P = 0.21) resulting in four test trials for each category.
Honey Bee Learning Experiment.
Experimental set-up and general procedure.
All experiments were conducted with free-flying honey bees (A. Mellifera). The bees were individually recruited from a gravity sucrose feeder and trained to visit our testing apparatus, a vertical circular screen that could be rotated to disrupt positional learning. The gray Plexiglas screen (50 cm in diameter) allowed to attached at various spatial locations gray Plexiglas hangers (6 × 8 cm) presenting the visual stimuli on top of small horizontal landing platforms. During familiarization, trials were collected in runs (i.e., in a string of trials lasting until the bee was satiated and returned to the hive). In each run, one combination of Target and Distractor stimuli was used. In each trial, two copies of the Target and Distractor stimuli were presented simultaneously, making a total of four visual stimuli located on the rotating screen (Fig. 2A). The two target scenes were supplied with a 10-µL drop of sucrose solution (50%, 1.8 M), while the two Distractor scenes were provided with a 10-µL drop of quinine solution (60 mM) on the landing platforms associated with the visual stimuli. A choice was scored either as correct or incorrect each time a bee landed on one of the platforms associated with a Target or a Distractor stimulus, respectively. When a bee made a correct choice, it was collected onto a Plexiglas spoon providing 50% sucrose solution and placed behind an opaque barrier 1 m away from the screen, while the stimulus positions were changed, and the platforms cleaned and refilled. When a bee made an incorrect choice, it tasted the bitter quinine solution and then it was allowed to continue making choices until a correct choice was made, at which point, the same procedure as in the case of a correct choice was followed. When the bee was absent from the experimental set-up, the hangers were cleaned with 20% ethanol, a new combination of Target and Distractor stimuli were attached to the hangers at random locations, and the screen was rotated to further disrupt specific location learning. This course of actions was repeated until the prespecified number of familiarization trials was reached. After the familiarization processing was completed, the testing procedure started, which consisted of four tests sessions and reinforcement trials between the sessions. Each test session consisted of 20 successive trials that were in the same format as during familiarization, except that they were not reinforced (water drops were provided on the landing platforms). The choices of the bees during these trials were also recorded. Between each test session, the bees were given 10 refreshing trials with the stimuli used for the familiarization phase and with reinforcers to assure that the bees’ motivation was kept at a high level. The bees were individually identified through small painted color dots on the thorax. Only one bee was present at any one time at the apparatus to avoid social learning.
Stimuli.
Both Target and Distractor stimuli in Exp. 1 were scenes composed of three achromatic (black) shapes elements with the dimension of the entire scene being 6 × 8 cm (width × height). Six shapes were used in the experiment, each with 2 cm of maximum extent: A triangle, a square, a circular disk, a five-arm star, a diamond, and a rectangle. These shapes were perfectly resolvable by honey bees (see, e.g., refs. 31, 68), since they subtended a visual angle of 22° at the typical bee decision distance (∼5 cm), which is well above the resolution of the bee’s eye (3°) (75). For each bee, the shapes used for the Target or the Distractor scenes were randomly assigned from the pool of shapes, and the spatial relation and composition of the base pairs were randomly selected. This yielded four unique Target and four Distractor scenes for each bee that were also different across bees. Thus, the shapes and their location within each base pair were different across bees. For each trial of a bee, one Target and one Distractor scene was selected and two copies of each were attached to random positions on the rotating testing apparatus. Since Exps. 2 and 3a–c tested more complex statistical relationships, two additional target scenes (implementing low- and high-frequency pairs) were required; thus, three additional shapes were added to the pool with the same maximum extent: an orthogonal cross, a heart figure, and an L-shape with 1-cm line width. In addition, in Exp. 3c, we used a simplified Distractor scene: A simple achromatic pattern matching in overall size but strongly differing in appearance from all other scenes in the experiments.
Statistical Analyses.
Human responses were coded correct (1) or incorrect (0) depending on their choice in the two-alternative forced-choice trials. Each bee’s choice was scored as correct (1) or incorrect (0) according to whether the bee landed on the platform associated with the Target or Distractor scenes, respectively. To maintain compatibility between the findings, human and bee performance were analyzed with the same statistical method after this initial coding step. Specifically, performances during the familiarization were analyzed with GLMM [R software, v3.3.2 (R Development Core Team), lme4 package (76)]. This statistical method was used instead of a classic ANOVA analysis since it is better suited for the binomial structure of our data. The dependent variable consisting of binary choices (correct or incorrect) for each human/bee and the GLMM models were fitted assuming a binomial distribution with a logit link function. The choice number was included as a fixed factor while individual participant/bee was considered as a random factor to account for the repeated measurement design. Performances during the tests (proportion of correct test choices; a single value for each participant or bee) were analyzed with GLM with a binomial error structure. These models only included the intercept term to test for a significant difference between the mean recorded proportion of correction choices and the theoretical chance level (P = 0.5). Comparison of performances between experiments were performed by adding the experimental group as a fixed factor in the respective GLMM (familiarization phase) and GLM models (testing phase). Significance of the fixed effect was tested using likelihood ratio tests.
Computational Modeling.
The PC model was based on the parametric BCL model described in Orbán et al. (11). The task of the BCL is to infer the probability of various competing inventories (set of chunks) based on the familiarization scenes, and find the most likely inventory that would generate/explain the entire set of scenes by evoking a subset of the inventory’s chunks to capture each scene. The best inventory is the one that can explain all of the scenes to their fullest (with the highest probability) based on its chunks. In this model, the selected best inventory represents the internal model of the outside world that is used in a composite manner to explain any occurring scene. We extend the original BCL model by allowing the number of latent (hidden) variables (i.e., chunks) to be unbounded but assuming that only a finite number of latents could be used to describe any set of observed variables (scenes) (77). The nonparametric version of this model was implemented using the Indian Buffet Process (77) as a prior on the link matrix, which defines the latent variable-observed variable connections.
See SI Appendix for implementational details of the different computational models.
Supplementary Material
Acknowledgments
We thank Gergo Orbán and Richard Aslin for useful discussion. This work was supported by the Women in Science International Rising Talent award, Toulouse 3 University, the CNRS, and the Grants by the Office of Naval Research N62909-19-1-2029, NIH R21 HD088731, and the Australian Research Council DP130100015/DP160100161.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1919387117/-/DCSupplemental.
Data Availability.
All study data are included in the article and SI Appendix.
References
- 1.Penn D. C., Holyoak K. J., Povinelli D. J., Darwin’s mistake: Explaining the discontinuity between human and nonhuman minds. Behav. Brain Sci. 31, 109–130, discussion 130–178 (2008). [DOI] [PubMed] [Google Scholar]
- 2.Premack D., Human and animal cognition: Continuity and discontinuity. Proc. Natl. Acad. Sci. U.S.A. 104, 13861–13867 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shettleworth S. J., Modularity, comparative cognition and human uniqueness. Philos. Trans. R. Soc. Lond. B Biol. Sci. 367, 2794–2802 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Aslin R. N., Newport E. L., Statistical learning: From acquiring specific items to forming general rules. Curr. Dir. Psychol. Sci. 21, 170–176 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Saffran J. R., Aslin R. N., Newport E. L., Statistical learning by 8-month-old infants. Science 274, 1926–1928 (1996). [DOI] [PubMed] [Google Scholar]
- 6.Bulf H., Johnson S. P., Valenza E., Visual statistical learning in the newborn infant. Cognition 121, 127–132 (2011). [DOI] [PubMed] [Google Scholar]
- 7.Fiser J., Aslin R. N., Unsupervised statistical learning of higher-order spatial structures from visual scenes. Psychol. Sci. 12, 499–504 (2001). [DOI] [PubMed] [Google Scholar]
- 8.Fiser J., Aslin R. N., Statistical learning of new visual feature combinations by infants. Proc. Natl. Acad. Sci. U.S.A. 99, 15822–15826 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kirkham N. Z., Slemmer J. A., Johnson S. P., Visual statistical learning in infancy: Evidence for a domain general learning mechanism. Cognition 83, B35–B42 (2002). [DOI] [PubMed] [Google Scholar]
- 10.Fiser J., Aslin R. N., Encoding multielement scenes: Statistical learning of visual feature hierarchies. J. Exp. Psychol. Gen. 134, 521–537 (2005). [DOI] [PubMed] [Google Scholar]
- 11.Orbán G., Fiser J., Aslin R. N., Lengyel M., Bayesian learning of visual chunks by human observers. Proc. Natl. Acad. Sci. U.S.A. 105, 2745–2750 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tenenbaum J. B., Kemp C., Griffiths T. L., Goodman N. D., How to grow a mind: Statistics, structure, and abstraction. Science 331, 1279–1285 (2011). [DOI] [PubMed] [Google Scholar]
- 13.Srinivasan M. V., Honey bees as a model for vision, perception, and cognition. Annu. Rev. Entomol. 55, 267–284 (2010). [DOI] [PubMed] [Google Scholar]
- 14.Giurfa M., Behavioral and neural analysis of associative learning in the honeybee: A taste from the magic well. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 193, 801–824 (2007). [DOI] [PubMed] [Google Scholar]
- 15.Avarguès-Weber A., Deisig N., Giurfa M., Visual cognition in social insects. Annu. Rev. Entomol. 56, 423–443 (2011). [DOI] [PubMed] [Google Scholar]
- 16.Menzel R., The honeybee as a model for understanding the basis of cognition. Nat. Rev. Neurosci. 13, 758–768 (2012). [DOI] [PubMed] [Google Scholar]
- 17.Dyer A. G., The mysterious cognitive abilities of bees: Why models of visual processing need to consider experience and individual differences in animal performance. J. Exp. Biol. 215, 387–395 (2012). [DOI] [PubMed] [Google Scholar]
- 18.Avarguès-Weber A. et al., Does holistic processing require a large brain? Insights from honeybees and wasps in fine visual recognition tasks. Front. Psychol. 9, 1313 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Avarguès-Weber A., Dyer A. G., Ferrah N., Giurfa M., The forest or the trees: Preference for global over local image processing is reversed by prior experience in honeybees. Proc. Biol. Sci. 282, 20142384 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dyer A. G., Griffiths D. W., Seeing near and seeing far; behavioural evidence for dual mechanisms of pattern vision in the honeybee (Apis mellifera). J. Exp. Biol. 215, 397–404 (2012). [DOI] [PubMed] [Google Scholar]
- 21.Dyer A. G., Neumeyer C., Chittka L., Honeybee (Apis mellifera) vision can discriminate between and recognise images of human faces. J. Exp. Biol. 208, 4709–4714 (2005). [DOI] [PubMed] [Google Scholar]
- 22.Dyer A. G., Rosa M. G. P., Reser D. H., Honeybees can recognise images of complex natural scenes for use as potential landmarks. J. Exp. Biol. 211, 1180–1186 (2008). [DOI] [PubMed] [Google Scholar]
- 23.Stach S., Benard J., Giurfa M., Local-feature assembling in visual pattern recognition and generalization in honeybees. Nature 429, 758–761 (2004). [DOI] [PubMed] [Google Scholar]
- 24.Zhang S., Srinivasan M. V., Zhu H., Wong J., Grouping of visual objects by honeybees. J. Exp. Biol. 207, 3289–3298 (2004). [DOI] [PubMed] [Google Scholar]
- 25.Avarguès-Weber A., Portelli G., Benard J., Dyer A., Giurfa M., Configural processing enables discrimination and categorization of face-like stimuli in honeybees. J. Exp. Biol. 213, 593–601 (2010). [DOI] [PubMed] [Google Scholar]
- 26.Stach S., Giurfa M., The influence of training length on generalization of visual feature assemblies in honeybees. Behav. Brain Res. 161, 8–17 (2005). [DOI] [PubMed] [Google Scholar]
- 27.Dyer A. G., Vuong Q. C., Insect brains use image interpolation mechanisms to recognise rotated objects. PLoS One 3, e4086 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Benard J., Stach S., Giurfa M., Categorization of visual stimuli in the honeybee Apis mellifera. Anim. Cogn. 9, 257–270 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Wu W., Moreno A. M., Tangen J. M., Reinhard J., Honeybees can discriminate between Monet and Picasso paintings. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 199, 45–55 (2013). [DOI] [PubMed] [Google Scholar]
- 30.Avarguès-Weber A., Dyer A. G., Combe M., Giurfa M., Simultaneous mastering of two abstract concepts by the miniature brain of bees. Proc. Natl. Acad. Sci. U.S.A. 109, 7481–7486 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Avarguès-Weber A., Dyer A. G., Giurfa M., Conceptualization of above and below relationships by an insect. Proc. Biol. Sci. 278, 898–905 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Avarguès-Weber A., Giurfa M., Conceptual learning by miniature brains. Proc. Biol. Sci. 280, 20131907 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Avarguès-Weber A., d’Amaro D., Metzler M., Dyer A. G., Conceptualization of relative size by honeybees. Front. Behav. Neurosci. 8, 80 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Howard S. R., Avarguès-Weber A., Garcia J., Dyer A. G., Free-flying honeybees extrapolate relational size rules to sort successively visited artificial flowers in a realistic foraging situation. Anim. Cogn. 20, 627–638 (2017). [DOI] [PubMed] [Google Scholar]
- 35.Dacke M., Srinivasan M. V., Evidence for counting in insects. Anim. Cogn. 11, 683–689 (2008). [DOI] [PubMed] [Google Scholar]
- 36.Gross H. J. et al., Number-based visual generalisation in the honeybee. PLoS One 4, e4263 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Howard S. R., Avarguès-Weber A., Garcia J. E., Greentree A. D., Dyer A. G., Surpassing the subitizing threshold: Appetitive-aversive conditioning improves discrimination of numerosities in honeybees. J. Exp. Biol. 222, jeb205658 (2019). [DOI] [PubMed] [Google Scholar]
- 38.Howard S. R., Avarguès-Weber A., Garcia J. E., Greentree A. D., Dyer A. G., Numerical ordering of zero in honey bees. Science 360, 1124–1126 (2018). [DOI] [PubMed] [Google Scholar]
- 39.Howard S. R., Avarguès-Weber A., Garcia J. E., Greentree A. D., Dyer A. G., Numerical cognition in honeybees enables addition and subtraction. Sci. Adv. 5, eaav0961 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Howard S. R., Avarguès-Weber A., Garcia J. E., Greentree A. D., Dyer A. G., Symbolic representation of numerosity by honeybees (Apis mellifera): Matching characters to small quantities. Proc. Biol. Sci. 286, 20190238 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Giurfa M., Honeybees foraging for numbers. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 205, 439–450 (2019). [DOI] [PubMed] [Google Scholar]
- 42.Bortot M., Stancher G., Vallortigara G., Transfer from number to size reveals abstract coding of magnitude in honeybees. iScience 23, 101122 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Avarguès-Weber A., de Brito Sanchez M. G., Giurfa M., Dyer A. G., Aversive reinforcement improves visual discrimination learning in free-flying honeybees. PLoS One 5, e15370 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen J., Ten Cate C., Zebra finches can use positional and transitional cues to distinguish vocal element strings. Behav. Processes 117, 29–34 (2015). [DOI] [PubMed] [Google Scholar]
- 45.Santolin C., Rosa-Salva O., Vallortigara G., Regolin L., Unsupervised statistical learning in newly hatched chicks. Curr. Biol. 26, R1218–R1220 (2016). [DOI] [PubMed] [Google Scholar]
- 46.Toro J. M., Trobalón J. B., Statistical computations over a speech stream in a rodent. Percept. Psychophys. 67, 867–875 (2005). [DOI] [PubMed] [Google Scholar]
- 47.Hauser M. D., Newport E. L., Aslin R. N., Segmentation of the speech stream in a non-human primate: Statistical learning in cotton-top tamarins. Cognition 78, B53–B64 (2001). [DOI] [PubMed] [Google Scholar]
- 48.Santolin C., Saffran J. R., Constraints on statistical learning across species. Trends Cogn. Sci. (Regul. Ed.) 22, 52–63 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Giurfa M., Schubert M., Reisenman C., Gerber B., Lachnit H., The effect of cumulative experience on the use of elemental and configural visual discrimination strategies in honeybees. Behav. Brain Res. 145, 161–169 (2003). [DOI] [PubMed] [Google Scholar]
- 50.Thompson R. F., In search of memory traces. Annu. Rev. Psychol. 56, 1–23 (2005). [DOI] [PubMed] [Google Scholar]
- 51.Menzel R., Searching for the memory trace in a mini-brain, the honeybee. Learn. Mem. 8, 53–62 (2001). [DOI] [PubMed] [Google Scholar]
- 52.Emery N. J., Clayton N. S., Comparative social cognition. Annu. Rev. Psychol. 60, 87–113 (2009). [DOI] [PubMed] [Google Scholar]
- 53.Roitblat H. L., von Fersen L., Comparative cognition: Representations and processes in learning and memory. Annu. Rev. Psychol. 43, 671–710 (1992). [DOI] [PubMed] [Google Scholar]
- 54.Chittka L., Jensen K., Animal cognition: Concepts from apes to bees. Curr. Biol. 21, R116–R119 (2011). [DOI] [PubMed] [Google Scholar]
- 55.Nieder A., Honey bees zero in on the empty set. Science 360, 1069–1070 (2018). [DOI] [PubMed] [Google Scholar]
- 56.Chittka L., Niven J., Are bigger brains better? Curr. Biol. 19, R995–R1008 (2009). [DOI] [PubMed] [Google Scholar]
- 57.Avarguès-Weber A., Face recognition: Lessons from a wasp. Curr. Biol. 22, R91–R93 (2012). [DOI] [PubMed] [Google Scholar]
- 58.Chittka L., Dyer A., Cognition: Your face looks familiar. Nature 481, 154–155 (2012). [DOI] [PubMed] [Google Scholar]
- 59.Sheehan M. J., Tibbetts E. A., Specialized face learning is associated with individual recognition in paper wasps. Science 334, 1272–1275 (2011). [DOI] [PubMed] [Google Scholar]
- 60.Howard S. R., Avarguès-Weber A., Garcia J., Stuart-Fox D., Dyer A. G., Perception of contextual size illusions by honeybees in restricted and unrestricted viewing conditions. Proc. Biol. Sci. 284, 20172278 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tuthill J. C., Chiappe M. E., Reiser M. B., Neural correlates of illusory motion perception in Drosophila. Proc. Natl. Acad. Sci. U.S.A. 108, 9685–9690 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Buatois A., Laroche L., Lafon G., Avarguès-Weber A., Giurfa M., Higher-order discrimination learning by honeybees in a virtual environment. Eur. J. Neurosci. 51, 681–694 (2020). [DOI] [PubMed] [Google Scholar]
- 63.Deisig N., Lachnit H., Giurfa M., Hellstern F., Configural olfactory learning in honeybees: Negative and positive patterning discrimination. Learn. Mem. 8, 70–78 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Schubert M., Lachnit H., Francucci S., Giurfa M., Nonelemental visual learning in honeybees. Anim. Behav. 64, 175–184 (2002). [Google Scholar]
- 65.Benard J., Giurfa M., A test of transitive inferences in free-flying honeybees: Unsuccessful performance due to memory constraints. Learn. Mem. 11, 328–336 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Giurfa M., An insect’s sense of number. Trends Cogn. Sci. (Regul. Ed.) 23, 720–722 (2019). [DOI] [PubMed] [Google Scholar]
- 67.Dyer A. G., Howard S. R., Garcia J. E., Through the eyes of a bee: Seeing the world as a whole. Anim. Stud. J. 5, 97–109 (2016). [Google Scholar]
- 68.Lehrer M., Campan R., Generalization of convex shapes by bees: What are shapes made of? J. Exp. Biol. 208, 3233–3247 (2005). [DOI] [PubMed] [Google Scholar]
- 69.Zhang S. W., Bartsch K., Srinivasan M. V., Maze learning by honeybees. Neurobiol. Learn. Mem. 66, 267–282 (1996). [DOI] [PubMed] [Google Scholar]
- 70.Cope A. J. et al., Abstract concept learning in a simple neural network inspired by the insect brain. PLoS Comput. Biol. 14, e1006435 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Cyr A., Avarguès-Weber A., Thériault F., Sameness/difference spiking neural circuit as a relational concept precursor model: A bio-inspired robotic implementation. Biol. Inspired Cognit. Archit. 21, 59–66 (2017). [Google Scholar]
- 72.Kleyko D., Osipov E., Gayler R. W., Khan A. I., Dyer A. G., Imitation of honey bees’ concept learning processes using vector symbolic architectures. Biol. Inspired Cognit. Archit. 14, 57–72 (2015). [Google Scholar]
- 73.Vasas V., Chittka L., Insect-inspired sequential inspection strategy enables an artificial network of four neurons to estimate numerosity. iScience 11, 85–92 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Pouget A., Beck J. M., Ma W. J., Latham P. E., Probabilistic brains: Knowns and unknowns. Nat. Neurosci. 16, 1170–1178 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Giurfa M., Vorobyev M., Kevan P., Menzel R., Detection of coloured stimuli by honeybees: Minimum visual angles and receptor specific contrasts. J. Comp. Physiol. A 178, 699–709 (1996). [Google Scholar]
- 76.Bates D., Mächler M., Bolker B., Walker S., Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48 (2015). [Google Scholar]
- 77.Wood F., Griffiths T., Ghahramani Z., “A non-parametric Bayesian method for inferring hidden causes” in Proceedings of the Conference on Uncertainty in Artificial Intelligence, Dechter R., Richardson T., Eds. (AUAI Press, 2006), Vol. 22, pp. 536–543. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and SI Appendix.