Genetic nurturing, missing heritability, and causal analysis in genetic statistics

Significance

Correlation between genotypes and phenotypes can be produced by genetic nurturing, namely the effect of parents’ genotypes on their offspring’s phenotypes through the parents’ phenotypes. Population subdivision and assortative mating can give rise to correlations between genotypes and phenotypes similar to those due to genetic nurturing. Variances and correlations may not reveal causal relationships in the presence of these complexities. We analyze mechanistic models of genetic nurturing, population subdivision, and assortative mating and compare these with results obtained within the framework of modern causal analysis. Our results clarify statistical signals emanating from correlations between nontransmitted alleles and offspring phenotypes and reveal difficulties with standard linear models in the interpretation of heritability, in particular, the concept of missing heritability.

Abstract

Genetic nurturing, the effect of parents’ genotypes on offspring phenotypes through parental phenotypic transmission, can be modeled in terms of gene–culture interactions. This paper first uses a simple one-locus, two-phenotype gene–culture cotransmission model to compute the effect of genetic nurturing in terms of regression of children’s phenotypes on transmitted and nontransmitted alleles. With genetic nurturing, interpreting heritability and hence the meaning of “missing heritability” becomes problematic. Other factors, for example, population subdivision and assortative mating, generate similar signals to those of genetic nurturing, namely, correlation between parents’ nontransmitted alleles and children’s phenotypes. Corrections must be made for these to isolate the signal of genetic nurturing. Finally, a unified causal framework is constructed for genetic nurturing, population subdivision, and assortative mating. Causal and noncausal paths from transmitted and nontransmitted alleles to children’s phenotypes are identified and investigated in the presence of genetic nurturing, population subdivision, and assortative mating. Using causal analysis, assumptions made in inferring direct and indirect effects are then clarified and evaluated in a broader causal context.

The nature vs. nurture problem is fundamental to most human sciences. History is replete with disastrous human suffering caused by malevolent use of positions taken regarding this problem. In the second half of the 20th century, after the modern evolutionary synthesis, researchers in human behavior started to incorporate simple models from statistical genetics, in the process extending such concepts as heritability beyond their original function. The notion of heritability was first introduced by Lush (1) in 1937 in animal breeding to predict the effectiveness of artificial selection. From the 1960s, people such as Arthur Jensen (2) and others used an estimate known as “broad sense heritability” as a statistical measure of genetic determination in research into human behavior. Their high heritability estimates for IQ led to a genetic deterministic view of human intelligence (3, 4). These estimates were often based on studies of twins reared together and apart (5) or on other correlations between relatives. However, such estimates of broad heritability cannot disentangle gene-by-environment interactions from purely genetic effects (6–9).

The debates of the 1970s led Cavalli-Sforza and Feldman (10) to construct generative models of cultural and genotypic transmission from which one could assess the contribution of vertical cultural transmission to phenotypic variation. They showed that such cultural transmission could lead to inflated estimates of genetic heritability.

Correlations between relatives continued to be the primary tool for estimation of the genetic contribution to phenotypic variance throughout the 1970s and 1980s (3, 4, 11, 12), although the importance of cultural transmission in inflating such correlations was recognized by several investigators (7, 13–17). Analysis of the model constructed by Cavalli-Sforza and Feldman (10) showed that parents’ phenotypes, if transmitted through vertical cultural transmission, could have strong effects on correlations between relatives. This approach was used, and the results confirmed, by Cloninger et al. (13–15) and also by Morton and coworkers in Hawaii (17).

In the past 10 y, with the growing popularity of genome-wide association studies (GWAS), heritability has been estimated from data by accumulating the variance explained by millions of single-nucleotide polymorphisms (SNPs) and in general SNP heritability is lower than earlier estimates based on correlations between relatives. This inconsistency is known as “missing heritability” (18, 19) and represents an important conundrum in human statistical genetics. Different factors can contribute to this inconsistency and we divide them into two categories: genetic factors and demographic factors. Genetic factors include too few SNPs (20–22) and complex genetic interactions [linkage disequilibrium, epistasis (23), etc.]. Demographic factors include cultural transmission (19, 22, 24), population subdivision (25), and assortative mating (24). Both categories can contribute to missing heritability and their relative importance can vary from trait to trait. Historically, barring a few exceptions, researchers have focused primarily on genetic factors.

Recently, Kong et al. (26) found substantial correlation between parents’ nontransmitted alleles and children’s phenotypes. They suggested that this correlation could be generated by the effect of parents’ phenotypes, which are influenced by parents’ genotypes, on children’s phenotypes. This sequence, from parents’ genotypes to parents’ phenotypes to children’s phenotypes, was called “genetic nurturing.” Subsequent studies connected genetic nurturing to the missing heritability problem (27–29). These studies appear to be closely related to the original model of Cavalli-Sforza and Feldman (10) and its generalization by Feldman et al. (8). Here we propose a simple extension of these models and show how vertical cultural transmission can lead to genetic nurturing. This affects the linear regressions that have been used to separate the contributions to phenotypes by nature and nurture, and we show how it affects our understanding of the missing heritability problem. We also explore how population subdivision and assortative mating, which are common for many traits in humans (30, 31), can generate correlation between nontransmitted alleles and children’s phenotype. A natural next step is to analyze how these different factors could produce such a correlation in a causal framework, which can help expose the nature–nurture conundrum (32–35), in the presence of complex population dynamics and possible confounding factors. Thus, we propose a unified causal framework for genetic nurturing, population subdivision, and assortative mating, which extends to nonlinear cases such as the path analysis approach used by Kong et al. (26). We also examine the approach they used to estimate direct genetic effects and make corrections for assortative mating.

A Model with Cultural Transmission

Genetic nurturing (26) entails that parents’ genotypes can have an indirect effect on children’s phenotypes by influencing parents’ phenotypes. This implies that children’s phenotypes will be determined by both children’s genotypes and parents’ phenotypes, where the influence of parents’ phenotypes occurs via vertical cultural transmission. Cavalli-Sforza and Feldman (10) proposed a quantitative genetic model incorporating vertical cultural transmission and showed that the heritability could be overestimated if there was vertical cultural transmission. However, for quantitative traits, it is very difficult to analyze the mathematical dynamics of a trait’s distribution. To address this issue and develop some theoretical understanding of the genetic nurturing effect, we construct a discrete trait model based on Cavalli-Sforza and Feldman (10) and show how the genetic nurturing effect can be included in the model.

We consider one diploid locus with two alleles, $A_1$ and $A_2$. Each genotype can be one of two phenotypic variants represented by bar and nonbar. Thus the six pheno-genotypes can be written as $\overline{A_i{A}_j}$ and $A_i{A}_j$ with $i,j=\mathrm{1,2}$. The probability of a child being bar is determined by the parents’ phenotypes and the child’s genotype. To be specific, denote by $X_{ch}$ the phenotypic state of the child, which is 1 for bar and 0 for nonbar; $G_{ch}$ the genotypic state of the child, which is 1 for $A_1{A}_1$, 2 for $A_1{A}_2$, and 3 for $A_2{A}_2$; ${\epsilon }_{G_{ch}}$ the contribution of the child’s genotype when its genotype is $G_{ch}$; and $g\left(y,x\right)$ the contribution of a parent’s phenotype when the parent’s phenotype is $x$ and the child’s genotype is $y$. Then we have

$$P\left(X_{ch}=1|G_{ch},X_p,X_m\right)={\epsilon }_{G_{ch}}+g_{\left(G_{ch},X_p\right)}+g_{\left(G_{ch},X_m\right)},$$ [1]

where $g_{\left(y,x\right)}=a_{y}I\left(x=1\right)+b_{y}I\left(x=0\right)$, with $I\left(\cdot \right)$ the index function, and $X_p$ and $X_m$ stand for the phenotypic states of the father and mother, respectively.

Since we can always move the common part of $a$ and $b$ into $\epsilon$, we reduce the number of parameters by specifying for $y=\mathrm{1,2,3}$,

$$a_y-b_y=e_y;2b_y+{\epsilon }_y=c_y.$$ [2]

Table 1 describes this model, where

$$\begin{array}{cc}\hfill & P\left(X_{ch}=1|G_{ch},X_p,X_m\right)\hspace{0.17em}=\hfill \\ \hfill & \hspace{1em}\hspace{1em}{c}_{G_{ch}}+e_{G_{ch}}\left[I\left(X_p=1\right)+I\left(X_m=1\right)\right].\hfill \end{array}$$ [3]

We denote the frequency of the bar phenotype with genotype $y$ at generation $n$ by $x_y^n$, the allele frequency of $A_1$ by $p$, and the allele frequency of $A_2$ by $q=1-p$. Without selection and assortative mating, the population is in Hardy–Weinberg equilibrium and $p$ does not change. The frequencies of the six pheno-genotypes $\overline{A_1{A}_1},A_1{A}_1,\overline{A_1{A}_2},A_1{A}_2,\overline{A_2{A}_2},A_2{A}_2$ are $p^2{x}_1,p^2\left(1-x_1\right),2pq{x}_2,2pq\left(1-x_2\right),q^2{x}_3,q^2\left(1-x_3\right)$, respectively.

Table 1.

Transmission table

	$A_1{A}_1$	$A_1{A}_2$	$A_2{A}_2$
$\overline{A_i{A}_j}\times \overline{A_k{A}_h}$	${\epsilon }_1+2a_1=c_1+2e_1$	${\epsilon }_2+2a_2=c_2+2e_2$	${\epsilon }_3+2a_3=c_3+2e_3$
$\overline{A_i{A}_j}\times \hspace{0.17em}{A}_k{A}_h$	${\epsilon }_1+a_1+b_1=c_1+e_1$	${\epsilon }_2+a_2+b_2=c_2+e_2$	${\epsilon }_3+a_3+b_3=c_3+e_3$
$A_i{A}_j\times \overline{A_k{A}_h}$	${\epsilon }_1+a_1+b_1=c_1+e_1$	${\epsilon }_2+a_2+b_2=c_2+e_2$	${\epsilon }_3+a_3+b_3=c_3+e_3$
$A_i{A}_j\times A_k{A}_h$	${\epsilon }_1+2b_1=c_1$	${\epsilon }_2+2b_2=c_2$	${\epsilon }_3+2b_3=c_3$

The first row shows the child’s genotype; the first column represents parents’ pheno-genotypes, and the entries represent the child’s probability of having the bar phenotype conditioned on child’s genotype (first row) and parents’ phenotypes (first column).

Now consider the evolution under random mating. On the one hand, the probability of being bar for $A_1{A}_1$ in generation $n+1$ is $x_1^{n+1}$. On the other hand, it equals $c_1+2e_1{P}_1^n$, where $P_1^n$ represents the probability that one of the parents (say, the mother) in generation $n$ has the bar phenotype given that the child’s pheno-genotype is $\overline{A_1{A}_1}$. Since the child’s genotype is $A_1{A}_1$, the mother’s genotype has to be $A_1{A}_i$, where allele $i$ has probability $p$ being 1 and probability $q$ being 2. Since the probabilities of being bar for $A_1{A}_1$ and $A_1{A}_2$ in generation $n$ are $x_1^n$ and $x_2^n$, we have $P_1^n=p{x}_1^n+q{x}_2^n$. Thus, $x_1^{n+1}=2e_{1}p{x}_1^n+2e_{1}q{x}_2^n+c_1$. Corresponding recursions for $x_2$ and $x_3$ can be derived, and we have

$$\begin{array}{cc}\hfill x_1^{n+1}& =2e_{1}p{x}_1^n+2e_{1}q{x}_2^n+c_1;\hfill \\ \hfill x_2^{n+1}& =e_{2}p{x}_1^n+e_2{x}_2^n+e_{2}q{x}_3^n+c_2;\hfill \\ \hfill x_3^{n+1}& =2e_{3}q{x}_3^n+2e_{3}p{x}_2^n+c_3.\hfill \end{array}$$ [4]

The globally stable equilibrium of Eq. 4 (SI Appendix, section A), denoted by $\left(x_1,x_2,x_3\right)$, is $\left(x_1,x_2,x_3\right)=\left(\frac{B_1}{A},\frac{B_2}{A},\frac{B_3}{A}\right)$ with

$$\begin{array}{cc}\hfill A& =1-e_2-2e_{1}p-2e_{3}q+2e_1{e}_2{p}^2+2e_2{e}_3{q}^2\hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+4e_1{e}_{3}pq;\hfill \\ \hfill B_1& =\left(1-e_2-2e_{3}q+2e_2{e}_3{q}^2\right)c_1+2e_{1}q\left(1-2e_{3}q\right)c_2\hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+2e_1{e}_2{q}^2{c}_3;\hfill \\ \hfill B_2& =e_{2}p\left(1-2e_{3}q\right)c_1+\left(1-2e_{3}q\right)\left(1-2e_{1}p\right)c_2\hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+e_{2}q\left(1-2e_{1}p\right)c_3;\hfill \\ \hfill B_3& =2e_3{e}_2{p}^2{c}_1+2e_{3}p\left(1-2e_{1}p\right)c_2+\left(1-e_2-2e_{1}p\right.\hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left.2e_1{e}_2{p}^2\right)c_3.\hfill \end{array}$$ [5]

Regression Analysis

We regress the child’s phenotype $X_{ch}$ on alleles transmitted from the parents to the child and alleles not transmitted to the child. Let the number of $A_2$ in parental alleles transmitted to the child be $N_{pa}^t\in \left\{\mathrm{0,1,2}\right\}$ and the number of $A_2$ in parental alleles not transmitted to the child be $N_{pa}^n\in \left\{\mathrm{0,1,2}\right\}$. Then, since $N_{pa}^t$ and $N_{pa}^n$ are independent random variables, we can write the regression equation

$$X_{ch}={\beta }_1{N}_{pa}^t+{\beta }_2{N}_{pa}^n+\delta ,$$ [6]

where ${\beta }_1=\frac{Cov\left(X_{ch},N_{pa}^t\right)}{Var\left(N_{pa}^t\right)};{\beta }_2=\frac{Cov\left(X_{ch},N_{pa}^n\right)}{Var\left(N_{pa}^n\right)}$, and $\delta$ is the sum of the intercept and the residual. Calculation of these expressions is shown in SI Appendix, section B, and we obtain

$$Var\left(N_{pa}^t\right)=2pq;$$ [7a]

$$Var\left(N_{pa}^n\right)=2pq;$$ [7b]

$$Cov\left(X_{ch},N_{pa}^t\right)=2pq\left[p\left(x_2-x_1\right)+q\left(x_3-x_2\right)\right];$$ [7c]

$$\begin{array}{ll}\hfill Cov\left(X_{ch},N_{pa}^n\right)& =2pq\left[p\left(p{e}_1+q{e}_2\right)\left(x_2-x_1\right)\right.\hfill \\ \hfill & \hspace{1em}\hspace{1em}+\left.q\left(p{e}_2+q{e}_3\right)\left(x_3-x_2\right)\right].\hfill \end{array}$$ [7d]

Then the coefficients in Eq. 6 are

$${\beta }_1=\frac{Cov\left(X_{ch},N_{pa}^t\right)}{Var\left(N_{pa}^t\right)}=p\left(x_2-x_1\right)+q\left(x_3-x_2\right);$$ [8a]

$$\begin{array}{cc}\hfill {\beta }_2& =\frac{Cov\left(X_{ch},N_{pa}^n\right)}{Var\left(N_{pa}^n\right)}=p\left(p{e}_1+q{e}_2\right)\left(x_2-x_1\right)\hfill \\ \hfill & +q\left(p{e}_2+q{e}_3\right)\left(x_3-x_2\right).\hfill \end{array}$$ [8b]

If the transmission process is purely genetic, that is, $e$s are zero, we have ${\beta }_2=0$, and ${\beta }_1=p\left(c_2-c_1\right)=q\left(c_3-c_2\right)$, which corresponds to the classical average effect in Falconer and Mackay (36) and the regression slope in Lynch and Walsh (ref. 37, pp. 65–67). With cultural transmission, i.e., nonzero $e$s, ${\beta }_1$ still has the familiar form 8a due to independence of transmitted and nontransmitted alleles. However, the frequencies $x_1,x_2,x_3$ will be complicated expressions in $e$s and $c$s shown in Eq. 5, and ${\beta }_2$ will not be zero. We can understand this result more clearly from the way parents’ nontransmitted alleles influence children’s phenotypes. The nontransmitted alleles are included in parents’ genotypes, which affect parents’ phenotypes, and thus influence children’s phenotypes by cultural transmission ($e$s). When the cultural transmission pathway (genetic nurturing pathway) is absent ($e$s$\hspace{0.17em}=0$), there is no influence of nontransmitted alleles.

Kong et al. (26) assumed that both the transmitted and nontransmitted alleles participate in genetic nurturing, which is also the case in our model. Since the transmitted alleles influence the parents’ phenotypes, as do the nontransmitted alleles, they calculated the direct effect [$\delta$ in Kong et al.’s (26) paper] by subtracting the regression coefficients of nontransmitted alleles from those of the transmitted alleles. In our model, the corresponding quantity is ${\beta }_1-{\beta }_2$, which represents the direct genetic effect when the parents’ phenotypes have the same effect on different children’s genotypes. To show this, we assume $c$s are linear, i.e., $\left(c_1,c_2,c_3\right)=\left(c,c+d,c+2d\right)$, and $e$s are the same, i.e., $\left(e_1,e_2,e_3\right)=\left(e,e,e\right)$. Using Eqs. 8 and 5 we then have

$${\beta }_1=p\left(x_2-x_1\right)+q\left(x_3-x_2\right)=\frac{d}{1-e}$$ [9a]

and

$${\beta }_2=e{\beta }_1=\frac{ed}{1-e},$$ [9b]

which implies

$${\beta }_1-{\beta }_2=\left(1-e\right){\beta }_1=d.$$ [9c]

Although ${\beta }_1$ and ${\beta }_2$ do not constitute “total” and “indirect” effects due to the confounding of grandparents’ phenotypic effects, their difference $d$ is exactly the direct genetic effect. This analysis can be extended to cases with arbitrary $c$s and the same $e$, but it fails when $e$s are different. This is because the genetic nurturing influences the regression in two ways: First, as shown above, it incorporates the nontransmitted alleles. Second, it influences the equilibrium frequency of the bar phenotype for each genotype, which makes it difficult to extract the direct genetic effect, as claimed by Kong et al. (26). (For more detailed analysis, see A Unified Causal Framework for Genetic Nurturing, Population Subdivision, and Assortative Mating and SI Appendix, sections E and J.) We will see in the next part that this observation also leads to an interesting view of the missing heritability problem.

Missing Heritability?

The missing heritability problem (18) arises when the heritability calculated from regression on alleles is lower than the heritability calculated from correlations between relatives. As pointed out by Cavalli-Sforza and Feldman (10), the latter heritability can be overestimated if there is vertical cultural transmission. To quantify this in our model, we regress the child’s phenotype on the parental phenotypes. The parent–offspring phenotype covariance (SI Appendix, section C) can be written

$$Cov\left(X_{ch},X_p+X_m\right)={\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2,$$ [10]

where

$${\mathrm{\Delta }}_1=2pq{\beta }_1^2;$$ [11a]

$$\begin{array}{cc}\hfill {\mathrm{\Delta }}_2& =2p\left(p{e}_1+q{e}_2\right)\left(p{x}_1+q{x}_2\right)\left[1-\left(p{x}_1+q{x}_2\right)\right]\hfill \\ \hfill & +2q\left(p{e}_2+q{e}_3\right)\left(p{x}_2+q{x}_3\right)\left[1-\left(p{x}_2+q{x}_3\right)\right]\hfill \end{array}.$$ [11b]

(Note that for convenience, we use the sum of the parental phenotypic values rather than their average.) Note that the additive genetic variance calculated by regression on transmitted alleles is $V_A=Var\left(N_{pa}^t\right){\beta }_1^2=2pq{\beta }_1^2={\mathrm{\Delta }}_1,$ and ${\mathrm{\Delta }}_2$ is always positive. Thus the missing heritability can be explained qualitatively by $Cov\left(X_{ch},X_p+X_m\right)-V_A={\mathrm{\Delta }}_2>0$. More formally, let $j_1=p{x}_1+q{x}_2;j_2=p{x}_2+q{x}_3$, which gives

$$\frac{{\mathrm{\Delta }}_1}{{\mathrm{\Delta }}_2}=\frac{pq{\left(j_1-j_2\right)}^2}{p\left(p{e}_1+q{e}_2\right)j_1\left(1-j_1\right)+q\left(p{e}_2+q{e}_3\right)j_2\left(1-j_2\right)}$$ [12]

In the parameter region where $\frac{{\mathrm{\Delta }}_1}{{\mathrm{\Delta }}_2}\ll 1$, the heritability estimated from regression on alleles is much smaller than the heritability estimated from correlations between relatives. This seems to explain the missing heritability problem. However, our analysis raises two problems in interpreting missing heritability, which render it meaningless in the context of cultural transmission. First, the genetic nurturing effect entails that the additive genetic variance computed from GWAS and that computed from correlations between relatives both depend on the equilibrium frequencies ($x_i$s), which depend on both $c$s and $e$s. This is true even in the case where $e$s are all the same and $c$s are linear. In this case, from Eq. 9a, we have ${\mathrm{\Delta }}_1=\frac{2pq{d}^2}{{\left(1-e\right)}^2}$, and calculation of $Cov\left(X_{ch},X_p+X_m\right)$ shows that this also depends on $d$ and $e$. (For details, see SI Appendix, section D.) Thus the so-called “missing heritability problem” is generated by comparing two quantities, neither of which is purely genetic. Second, although cultural transmission can contribute to missing heritability, the absence of missing heritability does not imply that cultural transmission is weak or absent. There exist parameter regions where cultural transmission is relatively strong but the two heritability estimates are roughly the same. (For detailed analysis and examples, see SI Appendix, section D.) Given these two issues, the dichotomy of nature and nurture simply does not apply in the systems with genetic nurturing and vertical cultural transmission.

Population Subdivision and Assortative Mating

Population subdivision and assortative mating can have profound effects on the missing heritability (24, 25). It is then interesting to compare statistical signals generated by population subdivision and assortative mating with that of genetic nurturing. Kong et al. (26) made a correction for assortative mating. Here we use a simple one-locus, two-allele purely genetic model to show how population subdivision and assortative mating can generate a signal similar to that of genetic nurturing, namely, the correlation between parents’ nontransmitted alleles and children’s phenotypes. We also examine how Kong et al. (26) corrected for assortative mating.

The Effect of Population Subdivision.

Consider a metapopulation $H$ which includes $k$ subpopulations, denoted by $H_1,\dots ,H_k$. The relative sizes of the subpopulations are denoted by ${\alpha }_1,\dots ,{\alpha }_k$, respectively. Again we assume there are two alleles, $A_1$ and $A_2$, and two phenotypes, bar and nonbar. The probability of being bar is genetically determined and is $c_1$ for $A_1{A}_1$, $c_2$ for $A_1{A}_2$, and $c_3$ for $A_2{A}_2$. Hardy–Weinberg equilibrium is assumed for each subpopulation and the frequencies of $A_1$ and $A_2$ in population $i$ are assumed to be $p_i$ and $q_i$. The frequencies of $A_1$ and $A_2$ in the metapopulation are thus $p={\alpha }_1{p}_1+\cdots +{\alpha }_k{p}_k$ and $q={\alpha }_1{q}_1+\cdots +{\alpha }_k{q}_k$, respectively. The genotype frequencies for $A_1{A}_1,A_1{A}_2,A_2{A}_2$ are then ${\sum }_{i=1}^k{\alpha }_i{p}_i^2,2{\sum }_{i=1}^k{\alpha }_i{p}_i{q}_i,{\sum }_{i=1}^k{\alpha }_i{q}_i^2$, respectively, which we denote by $u,2v,w$. Set $x_i=c_1{p}_i^2+2c_2{p}_i{q}_i+c_3{q}_i^2$ and $x={\sum }_{i=1}^k{\alpha }_i{x}_i$, which represent, respectively, the frequencies of bar in each subpopulation and the metapopulation. We now study how subpopulation structure may mimic genetic nurturing.

First, we regress the child’s phenotype on alleles transmitted and alleles not transmitted to the child (in the metapopulation). We again denote the child’s phenotypic value by $X_{ch}$, which is 1 for the bar phenotype and 0 for the nonbar phenotype. Let the numbers of the father’s and mother’s transmitted $A_2$ alleles be $\left(N_p^t,N_m^t\right)$ and the numbers of the nontransmitted $A_2$ alleles be $\left(N_p^n,N_m^n\right)$. The regression is then

$$X_{ch}={\beta }_1\left(N_p^t+N_m^t\right)+{\beta }_2\left(N_p^n+N_m^n\right)+\delta ,$$ [13]

where ${\beta }_1$ and ${\beta }_2$ are the regression coefficients and $\delta$ is the sum of the intercept and the residual.

Using the law of total variance we can calculate the covariances among $N_p^t,N_m^t,N_p^n,N_m^n$ and $X_{ch}$ (SI Appendix, section F) and obtain

$$\begin{array}{cc}\hfill Cov\left(N_A^a,N_B^b\right)& =pq-v;\hfill \\ \hfill Cov\left(X_{ch},N_m^n\right)& =Cov\left(X_{ch},N_p^n\right)=\sum _{i=1}^k{\alpha }_i{q}_i{x}_i-qx;\hfill \\ \hfill Cov\left(X_{ch},N_m^t\right)& =Cov\left(X_{ch},N_p^t\right)=\sum _{i=1}^k{\alpha }_i{q}_i{x}_i-qx\hfill \\ \hfill & +\sum _{i=1}^k{\alpha }_i{p}_i{q}_i\left[p_i\left(c_2-c_1\right)+q_i\left(c_3-c_2\right)\right],\hfill \end{array}$$ [14]

where $N_A^a$ and $N_B^b$ are two different elements of the set $\left\{N_p^t,N_m^t,N_p^n,N_m^n\right\}$. Denote ${\sum }_{i=1}^k{\alpha }_i{q}_i{x}_i-qx$ by $K_1$ and ${\sum }_{i=1}^k{\alpha }_i{p}_i{q}_i\left[p_i\left(c_2-c_1\right)+q_i\left(c_3-c_2\right)\right]$ by $K_2$. Then from multivariate regression analysis (SI Appendix, section F), we obtain

$$\begin{array}{cc}\hfill {\beta }_1& =\frac{K_{1}v+K_2\left(2pq-v\right)}{\left(4pq-3v\right)v};\hfill \\ \hfill {\beta }_2& =\frac{K_{1}v-K_2\left(2pq-2v\right)}{\left(4pq-3v\right)v};\hfill \end{array}$$ [15]

and

$${\beta }_1-{\beta }_2=\frac{K_2}{v}.$$ [16]

Thus, when a population is subdivided, the nontransmitted alleles will also be correlated with the phenotype and the regression coefficient ${\beta }_2$ will in general not be zero. This correlation is generated by differences among allele frequencies in subpopulations. Both $K_1$, the covariance of probabilities being bar among subpopulations, and $pq-v$, the variance of allele frequencies among subpopulations, will be nonzero when such differences exist. This means that even in the purely genetic case, population subdivision may generate correlation between children’s phenotypes and nontransmitted alleles, which is considered by Kong et al. (26) as the signal of genetic nurturing. Thus, a correction must be made if we want to separate the genetic nurturing effect from that of population subdivision.

The Effect of Assortative Mating.

Assortative mating can be viewed as a special kind of population subdivision, namely, division into assorting groups, and an analysis similar to the above can be applied with assortative mating. Again we have alleles $A_1$ and $A_2$ with phenotypes bar and nonbar. The frequencies of $A_1$ and $A_2$ are $p$ and $q$. The probabilities of a child being bar if its genotype is $A_1{A}_1,A_1{A}_2,A_2{A}_2$ are, respectively, $c_1,c_2,c_3$. In each generation, we assume a proportion $r$ of individuals mate assortatively based on phenotype and the remaining individuals mate randomly. Denote the genotype frequencies of $A_1{A}_1,A_1{A}_2,A_2{A}_2$ in generation $n$ by $P^n,2Q^n,R^n$, respectively. Since the proportion of bar in each genotype is fixed, we need only analyze the genotype frequency dynamics, and since $P^n+Q^n=p;R^n+Q^n=q$ and $p$ and $q$ do not change, there is only one free variable. Thus, we need only to solve the recursion for one of $P^n,Q^n,R^n$; here we focus on the recursion for $Q^n$, namely

$$\begin{array}{cc}\hfill Q^{n+1}& =\left(1-r\right)pq+\left\{\frac{\left(P^n{c}_1+Q^n{c}_2\right)\left(R^n{c}_3+Q^n{c}_2\right)}{{\left[P^n{c}_1+2Q^n{c}_2+R^n{c}_3\right]}^2}\right.\times \hfill \\ \hfill & \left.\left(r{P}^n{c}_1+2r{Q}^n{c}_2+r{R}^n{c}_3\right)\right\}\hfill \\ \hfill & +\left\{\frac{\left[P^n\left(1-c_1\right)+Q^n\left(1-c_2\right)\right]\left[R^n\left(1-c_3\right)+Q^n\left(1-c_2\right)\right]}{{\left[P^n\left(1-c_1\right)+2Q^n\left(1-c_2\right)+R^n\left(1-c_3\right)\right]}^2}\right.\hfill \\ \hfill & \times [\left.r{P}^n\left(1-c_1\right)\right\}\hfill \\ \hfill & +\left.2r{Q}^n\left(1-c_2\right)+r{R}^n\left(1-c_3\right)\right].\hfill \end{array}$$ [17]

In SI Appendix, section G, we prove that there is a unique globally stable fixed point for the dynamical system 17. Assuming the equilibrium genotype frequencies are $\left(u,2v,w\right)$, we can use a regression analysis similar to that used for population subdivision. Let

$$\begin{array}{cc}\hfill & \alpha =\left[p\left(c_2-c_3\right)-q\left(c_2-c_1\right)\right]v+pq\left(c_3-c_1\right);\hfill \\ \hfill & \beta =\left(c_3+c_1-2c_2\right)\left(q_1+q_2\right)+2\left(c_2-c_1\right);\hfill \\ \hfill & \overline{x}=E\left(X_{ch}\right)=u{c}_1+2v{c}_2+w{c}_3.\hfill \end{array}$$ [18]

We can then compute the covariances among $N_p^t,N_m^t,N_p^n,N_m^n$ and $X_{ch}$ (SI Appendix, section H); namely,

$$\begin{array}{cc}\hfill & Cov\left(N_A^a,N_B^b\right)=\frac{r{\alpha }^2}{\overline{x}\left(1-\overline{x}\right)}.;\hfill \\ \hfill & Cov\left(X_{ch},N_m^n\right)=Cov\left(X_{ch},N_p^n\right)=\alpha ;\hfill \\ \hfill & Cov\left(X_{ch},N_m^t\right)=Cov\left(X_{ch},N_p^t\right)=\beta Cov\left(N_A^a,N_B^b\right)=\frac{r{\alpha }^2\beta }{\overline{x}\left(1-\overline{x}\right)}.\hfill \end{array}$$ [19]

Comparing these results with those of the population subdivision model, we see that in the assortative mating model,

$$\begin{array}{ll}\hfill K_1& =Cov\left(X_{ch},N_m^n\right)=\beta \left(pq-v\right);\hfill \\ \hfill K_2& =Cov\left(X_{ch},N_m^t\right)-Cov\left(X_{ch},N_m^n\right)=\alpha \left[1-\frac{r\alpha \beta }{\overline{x}\left(1-\overline{x}\right)}\right],\hfill \end{array}$$

which, together with Eq. 16, gives the regression coefficients. As a special case of population subdivision, assortative mating can also generate a similar signal to that of genetic nurturing and should be corrected for in computations of correlations. Kong et al. (26) do make the correction and we agree with their conclusion that the effect of assortative mating is relatively weak. However, there may be a problem with their model assumptions. To be specific, when assumption VI in their supplementary material section “Estimating the confounding effects induced by assortative mating” is translated into our model, it amounts to assuming $Cov\left(N_p^t,N_p^n\right)$ and $Cov\left(N_m^t,N_m^n\right)$ are zero while $Cov\left(N_p^t,N_m^t\right)$, $Cov\left(N_p^n,N_m^n\right)$, $Cov\left(N_p^t,N_m^n\right)$, $Cov\left(N_m^t,N_p^n\right)$, $Cov\left(N_p^t,N_m^t\right)$, and $Cov\left(N_p^n,N_m^n\right)$ are not zero. From our analysis this appears unreasonable since these covariances should all be the same.

A Unified Causal Framework for Genetic Nurturing, Population Subdivision, and Assortative Mating

In previous sections, we proposed a mechanistic model for genetic nurturing and showed how population subdivision and assortative mating could mimic genetic nurturing. We followed Kong et al. (26) and used a linear regression (i.e., path analysis or structural equation model [SEM]) method for mediation analysis. We showed that this method works well in the linear setting but becomes problematic in the nonlinear case. Fortunately, traditional structural mediation analysis and separation of total effect into direct effect and indirect effect can be naturally extended to the nonlinear setting using $do$ calculus and counterfactuals in causal analysis (38). Further, causal analysis provides powerful techniques for analyzing different causal effects and the influence of confounding factors (39, 40), which can also help frame the mismatch between causality and statistics used in the nature–nurture discussion, such as variance (6) and correlation. We therefore employ causal analysis in constructing a semi-Markovian causal model (Fig. 1) for genetic nurturing, population subdivision, and assortative mating (details in SI Appendix, section J). Using this unified causal framework, we show that the correlations between nontransmitted alleles and the phenotype under genetic nurturing, population subdivision, and assortative mating represent different pathways in the causal diagram. We also analyze different effects of transmitted alleles and clarify when the analysis by Kong et al. (26) of genetic nurturing works and when it fails.

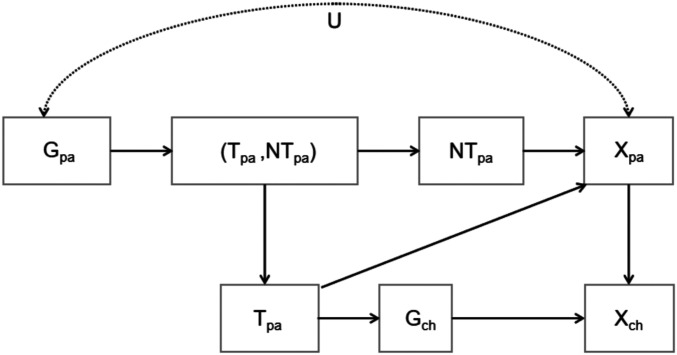
Fig. 1.

A unified causal diagram for genetic nurturing, population subdivision, and assortative mating.

In Fig. 1, $G_{pa}=\left(G_m,G_p\right)$ and $G_{ch}$, respectively, represent the parents’ and the child’s genotypes, $T_{pa}=\left(T_m,T_p\right)$ represents the alleles transmitted from the parents, and $N{T}_{pa}=\left(N{T}_m,N{T}_p\right)$ represents the alleles not transmitted from the parents. $X_{pa}=\left(X_m,X_p\right)$ and $X_{ch}$ represent the parents’ and the child’s phenotypes. The parents’ genotypes and phenotypes are confounded by $U$ and are thus connected by the bidirectional arc in Fig. 1. We study the effects of transmitted alleles and nontransmitted alleles.

In the causal diagram of Fig. 1, the “total effect” of changing transmitted alleles from $T_{pa}=x$ to $T_{pa}=y$ on the child’s phenotype can be represented by $P\left(X_{ch}|do\left(T_{pa}=y\right)\right)-P\left(X_{ch}|do\left(T_{pa}=x\right)\right)$, in which case the quantity corresponding to the regression coefficient ${\beta }_1$ will be $P\left(X_{ch}|T_{pa}=y\right)-P\left(X_{ch}|T_{pa}=x\right)$; the total effect of changing nontransmitted alleles from $N{T}_{pa}=x$ to $N{T}_{pa}=y$ on the child’s phenotype can be represented by $P\left(X_{ch}|do\left(N{T}_{pa}=y\right)\right)-P\left(X_{ch}|do\left(N{T}_{pa}=x\right)\right)$, in which case the quantity corresponding to the regression coefficient ${\beta }_2$ will be $P\left(X_{ch}|N{T}_{pa}=y\right)-P\left(X_{ch}|N{T}_{pa}=x\right)$. The relationships among these quantities and the path-specific effects corresponding to the “direct effect” and the “indirect effect” in Kong et al.’s (26) paper are analyzed in detail below.

Before doing the analysis, we address a key problem for the identification of different effects in Fig. 1, namely, the definition of $P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)$. This quantity is not always well defined because the parents’ genotypes are automatically determined when the transmitted alleles and nontransmitted alleles are known. Thus, to use causal analysis, we must define this probability $P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)$ when $G_{pa}$ is not compatible with $T_{pa},N{T}_{pa}$. If the confounding factor $U$ in Fig. 1 is known, then this quantity is just ${\sum }_{U}P\left(X_{pa}|T_{pa},N{T}_{pa},U\right)P\left(U|G_{pa}\right)$; otherwise, some prior knowledge of $U$ is needed. Table 2 lists the symbols used throughout our application of the causal analysis, while Table 3 lists the analogous symbols used in the cultural transmission model.

Table 2.

Symbols used in causal analysis

Notation	Meaning
$G_{ch}$	The child’s genotype
$G_m$	The mother’s genotype
$G_p$	The father’s genotype
$G_{pa}$	The parents’ genotypes, denoted by $\left(G_m,G_p\right)$
$X_{ch}$	The child’s phenotype
$X_m$	The mother’s phenotype
$X_p$	The father’s phenotype
$X_{pa}$	The parents’ phenotypes, denoted by $\left(X_m,X_p\right)$
$X_{mm}$	The mother’s mother’s phenotype
$X_{mp}$	The mother’s father’s phenotype
$X_{mpa}$	The mother’s parents’ phenotypes, denoted by $\left(X_{mm},X_{mp}\right)$
$X_{pm}$	The father’s mother’s phenotype
$X_{pp}$	The father’s father’s phenotype
$X_{ppa}$	The father’s parents’ phenotypes, denoted by $\left(X_{pm},X_{pp}\right)$
$T_m$	Alleles transmitted from the mother to the child
$T_p$	Alleles transmitted from the father to the child
$T_{pa}$	Alleles transmitted from the parents to the child,
	denoted by $\left(T_m,T_p\right)$
$N{T}_m$	Alleles not transmitted from the mother to the child
$N{T}_p$	Alleles not transmitted from the father to the child
$N{T}_{pa}$	Alleles not transmitted from the parents to the child,
	denoted by $\left(N{T}_m,N{T}_p\right)$

Table 3.

Matching symbols in the two models

Notation in cultural transmission model	Corresponding representation in the unified causal model
$c_1$	$P\left(X_{ch}=1|G_{ch}=A_1{A}_1,X_{pa}=\left(\mathrm{0,0}\right)\right)$
$c_1+e_1$	$P\left(X_{ch}=1|G_{ch}=A_1{A}_1,X_{pa}=\left(\mathrm{1,0}\right)\hspace{0.17em}\mathrm{o}\mathrm{r}\hspace{0.17em}\left(\mathrm{0,1}\right)\right)$
$c_1+2e_1$	$P\left(X_{ch}=1|G_{ch}=A_1{A}_1,X_{pa}=\left(\mathrm{1,1}\right)\right)$
$c_2$	$P\left(X_{ch}=1|G_{ch}=A_1{A}_2,X_{pa}=\left(\mathrm{0,0}\right)\right)$
$c_2+e_2$	$P\left(X_{ch}=1|G_{ch}=A_1{A}_2,X_{pa}=\left(\mathrm{1,0}\right)\hspace{0.17em}\mathrm{o}\mathrm{r}\hspace{0.17em}\left(\mathrm{0,1}\right)\right)$
$c_2+2e_2$	$P\left(X_{ch}=1|G_{ch}=A_1{A}_2,X_{pa}=\left(\mathrm{1,1}\right)\right)$
$c_3$	$P\left(X_{ch}=1|G_{ch}=A_2{A}_2,X_{pa}=\left(\mathrm{0,0}\right)\right)$
$c_3+e_3$	$P\left(X_{ch}=1|G_{ch}=A_2{A}_2,X_{pa}=\left(\mathrm{1,0}\right)\hspace{0.17em}\mathrm{o}\mathrm{r}\hspace{0.17em}\left(\mathrm{0,1}\right)\right)$
$c_3+2e_3$	$P\left(X_{ch}=1|G_{ch}=A_2{A}_2,X_{pa}=\left(\mathrm{1,1}\right)\right)$

Here for simplicity, we assume X =1 for bar phenotype and X =0 for nonbar phenotype.

Fortunately, for genetic nurturing, population subdivision, and assortative mating, the required prior knowledge exists. For population subdivision and assortative mating, since the effect is purely genetic, we have $P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)=P\left(X_{pa}|T_{pa},N{T}_{pa}\right)$. For genetic nurturing, $U$ represents the grandparents’ phenotypic influence. Denote the mother’s parents’ phenotypes by $X_{mpa}=\left(X_{mm},X_{mp}\right)$ and the father’s parents’ phenotypes by $X_{ppa}=\left(X_{pm},X_{pp}\right)$. Then

$$\begin{array}{cc}\hfill & P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)\hfill \\ \hfill & =\sum _{\genfrac{}{}{0ex}{}{X_{mpa},}{X_{ppa}}}P\left(X_{pa}|T_{pa},N{T}_{pa},X_{mpa},X_{ppa}\right)P\left(X_{mpa},X_{ppa}|G_{pa}\right),\hfill \end{array}$$ [20]

which can be calculated if data from the grandparents’ generation are given. If these data are not given (which we assume in this paper), we may assume that the population is at equilibrium under random mating, in which case

$$\begin{array}{cc}\hfill & P\left(X_{pa}|T_{pa},N{T}_{pa},X_{mpa},X_{ppa}\right)\hfill \\ \hfill & =P\left(X_m|T_m,N{T}_m,X_{mpa}\right)P\left(X_p|T_p,N{T}_p,X_{ppa}\right);\hfill \\ \hfill & P\left(X_{mpa},X_{ppa}|G_{pa}\right)=P\left(X_{mpa}|G_m\right)P\left(X_{ppa}|G_p\right).\hfill \end{array}$$ [21]

Each term on the right-hand side of [21] can be calculated using data from the parents’ generation. For example, we may assume $P\left(X_{mpa}=x|G_m=g\right)=P\left(X_{pa}=x|G_{ch}=g\right)$, where $x$ is a vector of two phenotypes and $g$ is a genotype. ($P\left(X_m|T_m,N{T}_m,G_m\right)$ and $P\left(X_p|T_p,N{T}_p,G_p\right)$ can be defined similarly.)

Now, since $P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)$ is defined and identifiable, we are now able to calculate the effects of nontransmitted alleles ($N{T}_{pa}$) on the child’s phenotype ($X_{ch}$). $N{T}_{pa}$ has one front-door (causal) path (we denote this by path 1; for definition of front-door path, see SI Appendix, section J) to $X_{ch}$,

$$N{T}_{pa}\to X_{pa}\to X_{ch},$$

and three backdoor (noncausal) paths (denoted by paths 2, 3, and 4; for definition of backdoor path, see SI Appendix, section J) to $X_{ch}$,

$$\begin{array}{ll}\hfill & N{T}_{pa}\leftarrow \left(T_{pa},N{T}_{pa}\right)\to T_{pa}\to G_{ch}\to X_{ch};\hfill \\ \hfill & N{T}_{pa}\leftarrow \left(T_{pa},N{T}_{pa}\right)\to T_{pa}\to X_{pa}\to X_{ch};\hfill \\ \hfill & N{T}_{pa}\leftarrow \left(T_{pa},N{T}_{pa}\right)\leftarrow G_{pa}\leftrightarrow X_{pa}\to X_{ch}.\hfill \end{array}$$

Following refs. 40–42, in the causal diagram Fig. 1, $P\left(X_{ch}|do\left(N{T}_{pa}\right)\right)$ can be given by

$$\begin{array}{cc}\hfill & P\left(X_{ch}|do\left(N{T}_{pa}\right)\right)=\sum _{\genfrac{}{}{0ex}{}{\genfrac{}{}{0ex}{}{G_{pa}}{T_{pa}}}{X_{pa}}}\left\{P\left(G_{pa}\right)P\left(T_{pa}|G_{pa}\right)\right.\times \hfill \\ \hfill & \left.P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)P\left(X_{ch}|T_{pa},X_{pa}\right)\right\}.\hfill \end{array}$$ [22]

Thus the total effect of changing from $N{T}_{pa}=x$ to $N{T}_{pa}=y$ given by $P\left(X_{ch}|do\left(N{T}_{pa}=y\right)\right)-P\left(X_{ch}|do\left(N{T}_{pa}=x\right)\right)$ can be calculated using Eq. 22. In the population subdivision and assortative mating case, since there is no effect of the parental phenotypes, the edge $X_{pa}\to X_{ch}$ (in Fig. 1) and paths 1, 3, and 4 vanish, so $P\left(X_{ch}|G_{ch},X_{pa}\right)=P\left(X_{ch}|G_{ch}\right)$. This automatically gives $P\left(X_{ch}|do\left(N{T}_{pa}\right)\right)=P\left(X_{ch}\right)$ and $P\left(X_{ch}|do\left(N{T}_{pa}=y\right)\right)-P\left(X_{ch}|do\left(N{T}_{pa}\right)=x\right)=0$, which means there is no causal effect of the nontransmitted alleles on the child’s phenotype. However, because of the existence of the active backdoor path 2, $P\left(X_{ch}|N{T}_{pa}\right)\hspace{0.17em}\ne \hspace{0.17em}P\left(X_{ch}\right)$ and $P\left(X_{ch}|N{T}_m=y\right)-P\left(X_{ch}|N{T}_{pa}=x\right)$ is not zero in general. To be specific, population subdivision and assortative mating introduce correlation between allele frequencies and (assorting) groups so that $N{T}_{pa}$ contains group information. As a result, $P\left(T_{pa}|N{T}_{pa}=y\right)$ and $P\left(T_{pa}|N{T}_{pa}=x\right)$ will generally not be the same and $P\left(X_{ch}|N{T}_{pa}=y\right)-P\left(X_{ch}|N{T}_{pa}=x\right)={\sum }_{T_{pa}}\left[P\left(T_{pa}|N{T}_{pa}=y\right)-P\left(T_{pa}|N{T}_{pa}\right)=x\right]P\left(X_{ch}|T_{pa}\right)$ will not be zero in general, which explains the correlation between the nontransmitted alleles and the child’s phenotype when there is population subdivision or assortative mating despite there being no causal path between these two quantities.

For genetic nurturing, $G_{pa}$ and $X_{pa}$ are confounded due to the influence of the grandparents’ phenotypes. In a random mating population, paths 2 and 3 are deactivated because under random mating, $P\left(T_{pa}|N{T}_{pa}\right)=P\left(T_{pa}|do\left(N{T}_{pa}\right)\right)=P\left(T_{pa}\right)$. Thus, $P\left(X_{ch}|N{T}_{pa}\right)$ is influenced by paths 1 and 4, with $P\left(X_{ch}|do\left(N{T}_{pa}\right)\right)$ representing the effect of path 1. This means that in the genetic nurturing case, $P\left(X_{ch}|N{T}_{pa}=y\right)-P\left(X_{ch}|N{T}_{pa}=x\right)$, which corresponds to ${\beta }_2$ in the previous section (Eqs. 6 and 8b), is in general not a suitable representation of the effect of the nontransmitted alleles. The correlation between the nontransmitted alleles and the child’s phenotype is in general not zero, but is a result of both genetic nurturing and confounding between the parents’ genotypes and phenotypes. This confounding, in the genetic nurturing case, is due to the grandparents’ phenotypic influence. [Kong et al. (26) did not take account of the grandparents’ influence or genetic nurturing’s influence on pheno-genotype frequencies; they therefore artificially deactivated path 4, which allowed their regression to work.]

Now we consider the effect of transmitted alleles. It is easy to see that there are four paths from $T_{pa}$ to $X_{ch}$, namely, two front-door paths (denoted by path $1^{\prime }$ and path $2^{\prime }$)

$$\begin{array}{ll}\hfill & T_{pa}\to G_{ch}\to X_{ch};\hfill \\ \hfill & T_{pa}\to X_{pa}\to X_{ch},\hfill \end{array}$$

and two backdoor paths (denoted by path $3^{\prime }$ and path $4^{\prime }$)

$$\begin{array}{ll}\hfill & T_{pa}\leftarrow \left(T_{pa},N{T}_{pa}\right)\to N{T}_{pa}\to X_{pa}\to X_{ch};\hfill \\ \hfill & T_{pa}\leftarrow \left(T_{pa},N{T}_{pa}\right)\leftarrow G_{pa}\leftrightarrow X_{pa}\to X_{ch}.\hfill \end{array}$$

From the analyses in refs. 40–42, $P\left(X_{ch}|do\left(T_{pa}\right)\right)$ is given by

$$\begin{array}{cc}\hfill & P\left(X_{ch}|do\left(T_{pa}\right)\right)=\sum _{\genfrac{}{}{0ex}{}{\genfrac{}{}{0ex}{}{G_{pa}}{N{T}_{pa}}}{X_{pa}}}\left\{P\left(G_{pa}\right)P\left(N{T}_{pa}|G_{pa}\right)\right.\times \hfill \\ \hfill & \left.P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)P\left(X_{ch}|T_{pa},X_{pa}\right)\right\}\hfill \end{array}$$ [23]

Similarly as in the above analysis of nontransmitted alleles, with population subdivision or assortative mating, only path $1^{\prime }$ is activated, and $P\left(X_{ch}|do\left(T_{pa}\right)\right)=P\left(X_{ch}|T_{pa}\right).$ With genetic nurturing, path $3^{\prime }$ vanishes while paths $1^{\prime }$, $2^{\prime }$, and $4^{\prime }$, which jointly contribute to $P\left(X_{ch}|T_{pa}\right)$, are activated. Also $P\left(X_{ch}|T_{pa}\right)$ represents the joint effect of causal paths $1^{\prime }$ and $2^{\prime }$. As for the nontransmitted alleles, because of the confounding of the parents’ genotypes and phenotypes, which introduces a backdoor path $4^{\prime }$, $P\left(X_{ch}|T_{pa}=y\right)-P\left(X_{ch}|T_{pa}=x\right)$, corresponding to ${\beta }_1$ (Eqs. 6 and 8a), is in general not a suitable representation of the total effect of the transmitted alleles. [Again Kong et al. (26) ignore path $4^{\prime }$, which allows their regression method to work.]

Nonetheless, the total effect of the transmitted alleles can be calculated using the do operator. Since there are two causal paths in this case, it is interesting to identify the path-specific effects. In mediation analysis, the path-specific effects of paths $1^{\prime }$ and $4^{\prime }$ are called “natural direct effect” and “natural indirect effect,” respectively. The total effect of changing from $T_{pa}=x$ to $T_{pa}=y$ can then be partitioned to into these two effects. Following refs. 43 and 44, the natural direct and natural indirect effects can be calculated as follows:

Natural direct effect:

$$\begin{array}{cc}\hfill & \sum _{\genfrac{}{}{0ex}{}{\genfrac{}{}{0ex}{}{G_{pa}}{N{T}_{pa}}}{X_{pa}}}\left\{P\left(G_{pa}\right)P\left(N{T}_{pa}|G_{pa}\right)P\left(X_{pa}|T_{pa}=x,N{T}_{pa},G_{pa}\right)\right.\hfill \\ \hfill & \hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\times \left.\left[P\left(X_{ch}|T_{pa}=y,X_{pa}\right)-P\left(X_{ch}|T_{pa}=x,X_{pa}\right)\right]\right\};\hfill \end{array}$$ [24]

Natural indirect effect:

$$\begin{array}{cc}\hfill & \sum _{\genfrac{}{}{0ex}{}{\genfrac{}{}{0ex}{}{G_{pa}}{N{T}_{pa}}}{X_{pa}}}\left\{P\left(G_{pa}\right)P\left(N{T}_{pa}|G_{pa}\right)P\left(X_{ch}|T_{pa}=y,X_{pa}\right)\right.\times \hfill \\ \hfill & \left.\left[P\left(X_{pa}|T_{pa}=y,N{T}_{pa},G_{pa}\right)-P\left(X_{pa}|T_{pa}=x,N{T}_{pa},G_{pa}\right)\right]\right\}.\hfill \end{array}$$ [25]

Kong et al. (26) also make this separation and called them direct effect and indirect effect, respectively. They also use the difference between regression coefficients for the transmitted alleles and the nontransmitted alleles to represent the direct effect of transmitted alleles. However, as we have shown above, their estimates of the total effects of the transmitted and nontransmitted alleles, represented by $P\left(X_{ch}|T_{pa}=y\right)-P\left(X_{ch}|T_{pa}=x\right)$ and $P\left(X_{ch}|N{T}_{pa}=y\right)-P\left(X_{ch}|N{T}_{pa}=x\right)$, respectively, are biased due to the confounding of the parents’ phenotypes and genotypes. Thus, we need to analyze the relationships among the following three quantities:

• 1)The difference between the total effects of the transmitted alleles and the nontransmitted alleles, represented by

$$\begin{array}{cc}\hfill & \left[P\left(X_{ch}|do\left(T_{pa}=y\right)\right)-P\left(X_{ch}|do\left(T_{pa}=x\right)\right)\right]\hfill \\ \hfill & -\left[P\left(X_{ch}|do\left(N{T}_{pa}=y\right)\right)-P\left(X_{ch}|do\left(N{T}_{pa}=x\right)\right)\right].\hfill \end{array}$$ [26]

• 2)Kong et al.’s (26) estimates of direct effect, represented by

$$\begin{array}{cc}\hfill & \left[P\left(X_{ch}|T_{pa}=y\right)-P\left(X_{ch}|T_{pa}=x\right)\right]\hfill \\ \hfill & -\left[P\left(X_{ch}|N{T}_{pa}=y\right)-P\left(X_{ch}|N{T}_{pa}=x\right)\right].\hfill \end{array}$$ [27]

• 3)Path 1-specific causal effects, the natural direct effect in our causal diagram (Fig. 1), represented by

$$\begin{array}{cc}\hfill & \sum _{\genfrac{}{}{0ex}{}{\genfrac{}{}{0ex}{}{G_{pa},}{N{T}_{pa},}}{X_{pa}}}\left\{P\left(G_{pa}\right)P\left(N{T}_{pa}|G_{pa}\right)P\left(X_{pa}|T_{pa}=x,N{T}_{pa},G_{pa}\right)\right.\hfill \\ \hfill & \hspace{0.17em}\hspace{1em}\hspace{1em}\times \left.\left[P\left(X_{ch}|T_{pa}=y,X_{pa}\right)-P\left(X_{ch}|T_{pa}=x,X_{pa}\right)\right]\right\}.\hfill \end{array}$$ [28]

These three quantities will be the same (for proof, see SI Appendix, section J) if there exist $F_1,F_{1\prime },F_2$ such that for $y=\left(y_m,y_p\right)$ and $x=\left(x_m,x_p\right)$

$$\begin{array}{cc}\hfill & P\left(X_m|T_m,N{T}_m=y_m,G_m\right)\hfill \\ \hfill & \hspace{1em}\hspace{1em}-P\left(X_m|T_m,N{T}_m=x_m,G_m\right)=F_1\left(X_m,y_m,x_m\right);\hfill \end{array}$$ [29]

$$\begin{array}{cc}\hfill & P\left(X_m|T_m=y_m,N{T}_m,G_m\right)\hfill \\ \hfill & \hspace{1em}\hspace{1em}-P\left(X_m|T_m=x_m,N{T}_m,G_m\right)=F_1\left(X_m,y_m,x_m\right);\hfill \end{array}$$ [30]

$$\begin{array}{cc}\hfill & P\left(X_p|T_p,N{T}_p=y_p,G_p\right)\hfill \\ \hfill & \hspace{1em}\hspace{1em}-P\left(X_p|T_p,N{T}_p=x_p,G_p\right)=F_{1^{\prime }}\left(X_p,y_p,x_p\right);\hfill \end{array}$$ [31]

$$\begin{array}{cc}\hfill & P\left(X_p|T_p=y_p,N{T}_p,G_p\right)\hfill \\ \hfill & \hspace{1em}\hspace{1em}-P\left(X_p|T_p=x_p,N{T}_p,G_p\right)=F_{1^{\prime }}\left(X_p,y_p,x_p\right);\hfill \end{array}$$ [32]

$$\begin{array}{cc}\hfill & P\left(X_{ch}|T_{pa}=y,X_{pa}\right)\hfill \\ \hfill & \hspace{1em}\hspace{1em}-P\left(X_{ch}|T_{pa}=x,X_{pa}\right)=F_2\left(X_{ch},y,x\right).\hfill \end{array}$$ [33]

Obviously, this assumption of additivity is exactly what the SEM and that of Kong et al. (26) assume. However, there are two problems. First, even when this assumption holds and the direct effect is estimated properly, their estimate of the total effect and the indirect effect is biased (SI Appendix, section J). Second, when this assumption is violated, as in the general case of the model defined by Table 1, these three quantities will not be the same. Thus, using the difference between total effects of the transmitted and nontransmitted alleles to estimate the direct effect of the transmitted alleles may be problematic.

Discussion

In this paper, we propose a simple generative model of cultural transmission and study the effects of including population subdivision and assortative mating in the model. Four main issues are addressed. First, the cultural transmission model gives a quantitative explanation of genetic nurturing that can be compared with that of Kong et al. (26). Second, we show how the notion of heritability from traditional statistical genetics is inadequate under this simple setting. Third, we show how population subdivision and assortative mating can generate signals similar to genetic nurturing and examine Kong et al.’s method (26) for correction of assortative mating. Finally, we propose a unified causal diagram for genetic nurturing, population subdivision, and assortative mating. Two statistical signals are used for our analysis: the difference between heritability estimated from GWAS and that estimated from pedigrees and the nonnegligible correlation between parents’ nontransmitted alleles and children’s phenotypes. Here we discuss the meaning of these two signals in a more general context.

For the first signal, represented by the missing heritability, we show in our gene–culture coevolution model, that heritability is an ill-defined notion and fails to decompose the total variance into nature and nurture. In addition, this failure, which is reflected in the missing heritability problem, has to be considered in the broader context of other problems, since it can be caused by both genetic and demographic factors, whose importance can vary from trait to trait. For example, having too few SNPs may produce missing heritability in height and body mass index (21, 22), while for social and behavioral traits, cultural transmission can be an important factor. However, even for height and body-mass index (BMI), it is not easy to exclude confounding cultural factors, such as diet, that can be vertically transmitted. In our analysis, when genetic nurturing exists, we find parameter regions where cultural transmission is not negligible, but the two estimates of heritability are roughly the same; this can be easily extended to the cases where parents’ phenotypes and genotypes are confounded by factors other than genetic nurturing. Thus, when vertical cultural transmission is potentially involved, heritability will not be a meaningful statistic.

Second, we show that genetic nurturing, population subdivision, and assortative mating can contribute to a second signal, namely, the correlation between parents’ nontransmitted alleles and children’s phenotypes. We also show that the method Kong et al. (26) used to correct for assortative mating entails restrictive assumptions. Using the causal diagram in Fig. 1, we see that the scenario is more complex when genetic nurturing coexists with population subdivision or assortative mating. When genetic nurturing coexists with population subdivision, $P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)$ can be defined similarly for each subpopulation. The difference between this case and genetic nurturing without population subdivision is that paths 2, 3, and $3^{\prime }$ will be activated. With genetic nurturing in the case of assortative mating, there is an added complication due to the additional source of confounding between the parents’ genotypes and phenotypes; prior information about this confounding is needed for $P\left(X_{pa}|T_{pa},N{T}_{pa},G_{pa}\right)$ to be well defined.

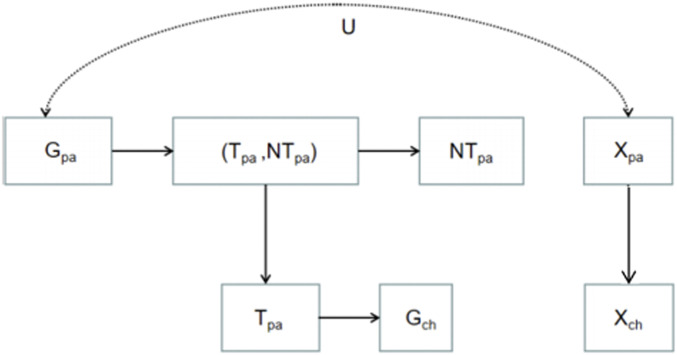
In our unified causal diagram (Fig. 1), the correlation between the parents’ nontransmitted alleles ($N{T}_{pa}$) and the child’s phenotype ($X_{ch}$) can arise from two different classes of paths: either through $T_{pa}$ (paths 2 and 3) or not through $T_{pa}$ but through $X_{pa}$ (paths 1 and 4). The paths through $T_{pa}$ can be tested and possibly corrected using linkage disequilibrium (LD). The path through $X_{pa}$, either causal or noncausal, implies the influence of parents’ phenotypes. Here we emphasize two points. First, although in the two-allele, two-phenotype model, we assumed that the parents’ phenotypes and that of the child referred to the same trait, in our causal diagram they could refer to different traits that have a causal relationship. In this case there will be “cultural influence” instead of “cultural transmission” but the whole causal diagram and all of the analysis will still be valid. Second, although without prior information about confounding the different effects cannot be calculated, confounding factors other than genetic nurturing between the parents’ phenotypes and genotypes can still produce correlation between the nontransmitted alleles and the child’s phenotype if the pathway from $X_{pa}$ to $X_{ch}$ is activated, even when there is no genetic basis for the phenotypes. Path 4 still exists even if $N{T}_{pa}\to X_{pa}$, $T_{pa}\to X_{pa}$, and $G_{ch}\to X_{ch}$ do not exist, see Fig. 2. (In principle, we should also include $G_{ch}\leftrightarrow X_{ch}$ in Fig. 2 since the genotypes and phenotypes are confounded in the parents’ generation. However, adding this will not activate any path, so we neglect it for simplicity.) In this case the correlation generated by the parental phenotypic influence and genotype–phenotype confounding will be an indicator of pure cultural influence or cultural transmission.

Fig. 2.

A potential causal diagram where $N{T}_{pa}$ and $X_{ch}$ are correlated due to pure cultural transmission.

Although our causal diagram unifies genetic nurturing, population subdivision, and assortative mating and can be extended qualitatively to more general cases of linkage disequilibrium and parental influences, it does not exhaust all potential mechanisms that could generate correlation between nontransmitted alleles and children’s phenotypes. Recent findings by Mostafavi et al. (45) that polygenic scores, which are computed under additive assumptions on allelic variances, are not portable among population groups with the same apparent genetic ancestry are relevant in the context of our analysis. They attribute their result to factors such as genetic nurturing (i.e., indirect genetic affects) and assortative mating studied here, as well as varying levels of environmental variance and genotype-by-environment interactions.

The correlation between parents’ nontransmitted alleles and children’s phenotypes is a signal of demographic or social influences, which can include parental phenotypic influence (genetic nurturing as a special case), linkage disequilibrium (population subdivision as a special case). (Confounding between $G_{pa}$ and $X_{ch}$ without referring to $X_{pa}$ can also contribute to such correlation, but in reality will be less likely.) More knowledge of the potential confounding factors is needed if we want to distinguish between these mechanisms more precisely.

Lewontin (ref. 6, p. 409) pointed out the pitfalls in inferring causality from variance statistics, including heritability derived from familial analyses: “The analysis of causes in human genetics is meant to provide us with the basic knowledge we require for correct schemes of environmental modification and intervention. Together with a knowledge of the relative frequencies of different human genotypes, a knowledge of norms of reaction can also predict the demographic and public health consequences of certain massive environmental changes. Analysis of variance can do neither of these because its results are a unique function of the present distribution of environment and genotypes.” Lewontin’s admonition, made 46 y ago, remains pertinent today with respect to SNP heritability derived from GWAS. Inference of causality from the relationships among statistical signals, including correlations and variances, remains extremely difficult.

Data Availability.

All study data are included in this article and SI Appendix

Change History

September 1, 2021: Figure 2 has been updated. The text of this article has been updated; please see accompanying correction for details.