Abstract
Introduction
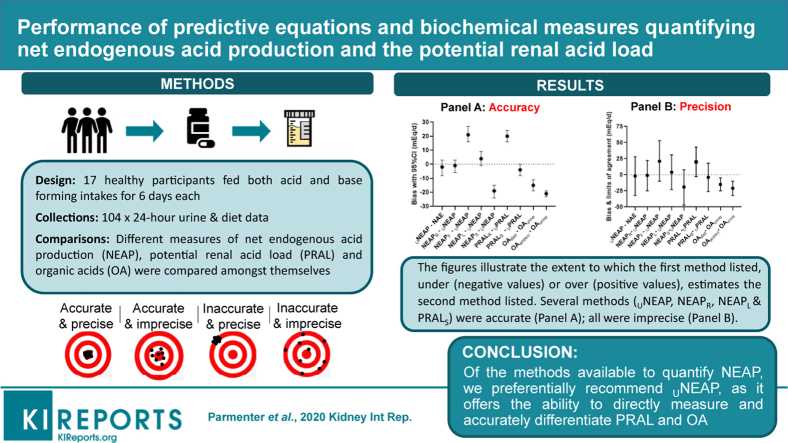
A limited number of studies have assessed the accuracy and precision of methods for determining the net endogenous acid production (NEAP) and its components. We aimed to investigate the performance of methods quantifying the diet dependent acid–base load.
Methods
Data from metabolic balance studies enabled calculations of NEAP according to the biochemical measures (of net acid excretion [NAE], urinary net endogenous acid production [UNEAP], and urinary potential renal acid load [UPRAL]) as well as estimative diet equations (by Frassetto et al., Remer and Manz, Sebastian et al., and Lemann) that were compared among themselves in healthy participants fed both acid and base forming diets for 6 days each.
Results
Seventeen participants (mean ± SD age, 60 ± 8 years; body mass index, 23 ± 2 kg/m2) provided 102 twenty-four-hour urine samples for analysis (NAE, 39 ± 38 mEq/d [range, −9 to 95 mEq/d]). Bland-Altman analysis comparing UNEAP to NAE showed good accuracy (bias, −2 mEq/d [95% confidence interval {CI}, −8 to 3]) and modest precision (limits of agreement, −32 to 28 mEq/d). Accurate diet equations included potential renal acid load (PRAL) by Sebastian et al. (bias, −4 mEq/d [95% CI, −8 to 0]) as well as NEAP by Lemann et al. (bias, 4 mEq/d [95% CI, −1 to 9]) and Remer and Manz (bias, −1 mEq/d [95% CI, −6 to 3]).
Conclusions
Researchers are encouraged to collect measures of UPRAL and UNEAP; however, investigators drawing conclusions between the diet-dependent acid–base load and human health should consider the limitations within all methods.
Keywords: accuracy, acid–base balance, net endogenous acid production, potential renal acid load, precision
Graphical abstract
Acid–base balance in the body requires that NEAP equals NAE. NEAP is the net combination of noncarbonic (i.e., fixed) acids produced from endogenous metabolic processes and acids ingested in the diet, minus the acids that are neutralized or buffered by noncarbonic dietary and endogenous base supplies.1 Carbonic acids are excreted by the lungs as carbon dioxide and do not contribute to NEAP.1 The noncarbonic or mineral compounds of cations (potassium, calcium and magnesium) in fruits and vegetables and anions (sulphate and phosphorus) in all foods release base (e.g., bicarbonate) and acid (e.g., hydrogen), respectively, upon metabolism.1 In addition, fruits and vegetables also contain noncarbonic nonmineral organic acids (OAs) and the human body endogenously generates OA.1 Collectively, the sum of acids and bases released from diet-derived compounds of cations and anions produces the PRAL; when added to total noncarbonic OA, this is considered an individual’s NEAP.1
NEAP can be measured through biochemical analysis of urine or estimated by dietary intake equations. Urine is the choice of biofluid for analysis because it is the route of fixed acid–base excretion.1 In early studies, NAE was measured as the ammonium and titratable acid content of urine minus bicarbonate,2,3 and to this day this method remains the criterion standard for measuring NEAP.4 However analysis of relevant cations and anions in urine elucidates the UPRAL,5 and if total urinary OA is added, this equals UNEAP, which is another method for calculating NAE. NAE, UNEAP, and UPRAL measurements are not generally available, and therefore several estimative equations using anthropometric measures and nutrient quantities of cations and anions derived from dietary intake have been developed to predict NEAP and its variables. Each equation estimates NEAP slightly differently, and like urinary measures, they are generally estimated using 24-hour data. As it stands, equations currently used in research (Table 1) include those by Frassetto et al. (NEAPF),6 Remer and Manz (PRAL and NEAPR),7,8 Sebastian et al. (PRALS and NEAPS),9 Manz et al. (OAanthro),10 Kleinman and Lemann (OAdiet),11 and a model attributed to Lemann (NEAPL).11, 12, 13
Table 1.
Estimative dietary equations and urinary measures of net endogenous noncarbonic acid production and its determinants (potential renal acid load and organic acids)
| Equation | Formula |
|---|---|
| NEAPF, mEq/d | = (0.91 × protein in g/d) − (0.57 × potassium in mEq/d) + 21 |
| NEAPR, mEq/d | = PRAL + OAanthro |
| NEAPL, mEq/d | = PRAL + OAdiet |
| NEAPS, mEq/d | = PRALS + OAdiet |
| PRAL, mEq/d | = ([0.488 × protein in g/d] + [0.0366 × phosphorus in mg/d]) − ([0.0205 × potassium in mg/d] + [0.0263 × magnesium in mg/d] + [0.0125 × calcium in mg/d]) |
| PRALS, mEq/da | = ([0.75 × sulphate] + [0.63 × phosphorus]) − ([0.80 × potassium] + [0.25 × calcium] + [0.32 × magnesium]) (all in mEq/d) |
| OAanthro, mEq/d | = body surface area × 41 / 1.73 |
| Body surface area, m2 | = 0.007184 − height (cm)0.725 − weight (kg)0.425 |
| OAdiet, mEq/d | = 32.9 + (0.15 × [{potassium} + {calcium × 2} + {magnesium × 2} – {phosphorus × 1.8}]) (all in mmol/d) |
| UPRAL, mEq/d | = ([sulphate × 2] + [phosphorus × 1.8]) − (potassium + [magnesium × 2] + [calcium ×2]) (all in mmol/d) |
| UNEAP, mEq/d | = UPRAL + total urine organic acid (both in mEq/d) |
| NAE, mEq/d | = titratable acid + ammonium − bicarbonate (all in mEq) |
NAE, net acid excretion; NEAP, net endogenous acid production estimated by dietary records where NEAPR pertains to the equation by Remer and Manz,7 NEAPF to the equation by Frassetto et al.,6 NEAPL to a model attributed to Lemann,11, 12, 13 and NEAPS to the equation by Sebastian et al.9; PRAL, potential renal acid load estimated by dietary intake where PRAL is the equation by Remer and Manz7 and PRALS pertains to the equation by Sebastian et al.9; UNEAP, net endogenous acid production determined by urine analysis; UPRAL, potential renal acid load determined by urine analysis; OA, organic acids where OAanthro pertains to the anthropometric estimate by Manz et al.10 and OAdiet to the estimative equation by Kleinman and Lemann.11
Prior to using PRALS, when converting mmol of phosphorus to mEq, 1.8 is used as the conversion factor.
Clinical and epidemiologic studies routinely rely on estimates of the diet-dependent acid–base load to investigate potential relationships to human health and disease.14,15 However, a limited number of studies have evaluated the accuracy and precision of estimates of PRAL, NEAP, and their contributors. The accuracy of a measurement is how close a result comes to the true value. Precision refers to how well measurements agree with each other in multiple tests. Metabolic balance studies, where measurements are repeated for days or weeks, are one of the types of investigations suited for this kind of statistical analysis. While NEAPR and NEAPF have been evaluated against NAE,6, 7, 8,16 the accuracy and precision of NEAPS and NEAPL has not been evaluated. Moreover, PRAL, PRALS, NEAPR, NEAPS, NEAPL, and NEAPF as well as their dietary mineral and OA estimates have not been evaluated for accuracy and precision against their respective UNEAP components and an assessment of UNEAP against NAE is needed. Consequently, we investigated the performance of published methods for determining the diet-dependent acid–base load.
Methods
The authors used data from their previously published and unpublished work conducted as part of metabolic balance studies.6,17,18 All subjects signed informed consent to participate in these studies and the use of previously collected deidentified data was approved by the University of the Sunshine Coast Human Ethics committee (E/16/070). Participant records were retrieved from studies conducted at the University of California San Francisco. Only participants with NAE, UNEAP, and dietary data collected during both acid- and base-forming diets were included. The University of California San Francisco Clinical Research Centre studies were conducted between 1987 and 1992, with the diets prepared by the metabolic research kitchen. To change diets from acidic to basic, or vice versa, all diets were supplemented with mineral salts of potassium bicarbonate. Data were retrieved from records where dietary NEAP intake was maintained constant for ≥6 consecutive days with a minimum washout phase of 3 days between the acid and base diets. Analytical methods used by this laboratory for measures of UNEAP have been previously reported in detail; NAE was calculated as the sum of the excretion rates of titratable acid and ammonium minus the excretion rate of bicarbonate.19,20 For this investigation, dietary estimates and urinary equations were computed according to Table 1. All studies used for the present analysis predate ClinicalTrials.gov.
Statistical analysis was completed using Microsoft Excel professional edition (Microsoft Corp, Redmond, WA) and the statistical programming language R (version 3.5.0).21 The averaged result for each individual during each diet period was used in the analyses. The accuracy and precision of dietary estimates to predict urinary outputs was evaluated by Bland–Altman analysis for repeated measures data where the true value varies,22 except in the instance of protein, sulphate, phosphorus, magnesium, and calcium, because these nutrients were consumed at a constant rate during both periods and were consequently evaluated by Bland–Altman analysis for repeated measures data where the true value was constant.23 A Shapiro–Wilk test with a significance level of 0.05 was used to determine if the differences were normally distributed. In the instances where the differences failed this test (i.e., they were not normally distributed) a nonparametric version of the Bland–Altman analysis was implemented. The nonparametric implementation used the median of the differences to estimate the bias and the 2.5% and 97.5% quantiles to estimate the lower and upper limits, respectively. The cases bootstrap method was used to compute 95% CIs for the median and lower and upper limits. This method is preferred because it is robust to outliers and it does not make any assumptions about the underlying distribution of the data. A similar methodology has been implemented in a related study estimating glomerular filtration rate.24 For our purposes, a priori limits of agreement for NEAP were set at ±20 mEq because this would permit a reasonably precise measure. The degree of agreement was also evaluated for urinary measures of acid excretion tested by different techniques, wherever appropriate, for which Bland–Altman analysis was also used. The results from all participants were used and retained in all analyses (n = 17).
Results
Data were available for 17 healthy participants (mean ± SD age, 60 ± 8 years; body mass index, 23 ± 2 kg/m2) providing 102 24-hour urine samples for analysis. The nutrient intake of participants and their urinary excretion of analytes relevant to NEAP are shown in Table 2. The range of NAE was wide (−9 to 95 mEq/d) and a paired t test showed a significant difference of 72 mEq/d (95% CI, 63–81 mEq/d), t16 = 17.0, P < 0.0001, between the base (3 ± 8 mEq/d) and acid (75 ± 12 mEq/d) intake periods. Bland–Altman analysis of UNEAP against NAE showed good accuracy with modest precision (Table 3). Bland–Altman analysis of dietary NEAP equations found only estimates of NEAPR and NEAPL were accurate yet both were imprecise (limits of agreement > ±20 mEq/d of the bias). When individual dietary PRAL and OA equations (which add together to compute NEAP) were assessed, PRAL but not PRALS overestimated UPRAL while both OAanthro and OAdiet underestimated OAurine. Similarly, when individual dietary cations and anions (which add together to compute PRAL) were analyzed, they were deemed inaccurate in predicting their respective urinary counterparts. Moreover, visual inspection of the Bland–Altman plots revealed that the true bias and precision of some of the equations appears to vary throughout differing intakes of dietary acid and base, which has implications for equation validity. To this end, out of all the equations, the accuracy and precision of NEAPR (compared with UNEAP) appeared most stable (Bland–Altman plots shown Supplementary Figures S1–S6).
Table 2.
Measures of net endogenous acid production, potential renal acid load, and single determinants of net acid excretion
| Variable | Value |
|---|---|
| Dietary intake | |
| Energy, Kcal/d | 2164 ± 211 (1731 to 2547) |
| NEAPR, mEq/d | 35 ± 37 (–30 to 75) |
| NEAPF, mEq/d | 58 ± 26 (9 to 92) |
| NEAPL, mEq/d | 41 ± 30 (13 to 73) |
| NEAPS, mEq/d | 17 ± 30 (–35 to 45) |
| PRAL, mEq/d | –5 ± 37 (–70 to 32) |
| PRALS, mEq/d | –29 ± 37 (92 to 4) |
| OAdiet, mEq/d | 46 ± 7 (38 to 59) |
| OAanthro, mEq/d | 40 ± 2 (35 to 44) |
| Sulphatedieta, mEq/d | 28 ± 3 (22 to 33) |
| Proteindietb, mEq/d | 51 ± 5 (41 to 60) |
| Phosphorusdieta, mEq/d | 37 ± 4 (30 to 44) |
| Potassiumdieta, mEq/d | 82 ± 37 (39 to 154) |
| Magnesiumdieta, mEq/d | 5 ± 0 (4 to 5) |
| Calciumdieta, mEq/d | 7 ± 1 (6 to 8) |
| Urinary excretion | |
| NAE, mEq/d | 39 ± 38 (–9 to 95) |
| UNEAP, mEq/d | 37 ± 39 (–38 to 94) |
| UPRAL, mEq/d | –25 ± 42 (–103 to 30) |
| OAurine, mEq/d | 61 ± 7 (48 to 77) |
| Sulphateurine, mEq/d | 34 ± 3 (28 to 40) |
| Phosphorusurine, mEq/d | 67 ± 8 (50 to 83) |
| Potassiumurine, mEq/d | 87 ± 43 (40 to 176) |
| Magnesiumurine, mEq/d | 17 ± 3 (13 to 22) |
| Calciumurine, mEq/d | 21 ± 9 (7 to 49) |
NAE, net acid excretion; NEAP, net endogenous acid production estimated by dietary records where NEAPR pertains to the equation by Remer and Manz,7 NEAPF to the equation by Frassetto et al.,6 NEAPL to a model attributed to Lemann,11, 12, 13 and NEAPS to the equation by Sebastian et al.9; PRAL, potential renal acid load estimated by dietary intake where PRAL is the equation by Remer and Manz,7 and PRALS pertains to the equation by Sebastian et al.9UNEAP, net endogenous acid production determined by urine analysis; UPRAL, potential renal acid load determined by urine analysis; OA, organic acids where OAanthro pertains to the anthropometrical estimate by Manz et al.,10 and OAdiet to the estimative equation by Kleinman and Lemann.11
Adjusted for intestinal absorption using multipliers specified in PRALS.
Adjusted for intestinal absorption using multipliers specified in PRAL.
Table 3.
Comparison of estimative dietary equations and urinary measures of net endogenous acid production, potential renal acid load, and single determinants of net acid excretion (sulphate, phosphate, potassium, magnesium, calcium, and organic acids)a,b
| Methods compared | Bland–Altman analysis |
|||
|---|---|---|---|---|
| Methodology | Bias (95% CI) | Lower limit of agreement (95% CI) | Upper limit of agreement (95% CI) | |
| UNEAP vs. NAE, mEq/d | Standard | –2 (–8, 3) | –32 (–46, –24) | 28 (20, 41) |
| NEAPR vs. NAE, mEq/d | Nonparametric | –2 (–15, 5) | –25 (–27, –20) | 16 (13, 16) |
| NEAPF vs. NAE, mEq/d | Standard | 19 (13, 25) | –14 (–27, –6) | 51 (44, 65) |
| NEAPL vs. NAE, mEq/d | Standard | 2 (–3, 7) | –27 (–40, –20) | 31 (24, 43) |
| NEAPS vs. NAE, mEq/d | Standard | –22 (–27, –16) | –51 (–64, –44) | 8 (1, 20) |
| NEAPR vs. UNEAP, mEq/d | Standard | –1 (–6, 3) | –25 (–36, –18) | 22 (15, 33) |
| NEAPF vs. UNEAP, mEq/d | Standard | 21 (16, 27) | –10 (–24, –3) | 53 (46, 67) |
| NEAPL vs. UNEAP, mEq/d | Standard | 4 (–1, 9) | –23 (–34, –16) | 31 (25, 43) |
| NEAPS vs. UNEAP, mEq/d | Standard | –19 (–24, –15) | –47 (–58, –40) | 8 (1, 19) |
| PRAL vs. UPRAL, mEq/d | Standard | 20 (16, 24) | –3 (–14, 3) | 43 (36, 54) |
| PRALS vs. UPRAL, mEq/d | Standard | –4 (–8, 0) | –26 (–36, –20) | 18 (12, 29) |
| OAdiet vs. OAurine, mEq/d | Nonparametric | –15 (–19, –11) | –25 (–27, –23) | –5 (–8, 5) |
| OAanthro vs. OAurine, mEq/d | Standard | –21 (–23, –19) | –32 (–37, –29) | –10 (–13, –5) |
| Sulphatedietc vs, Sulphateurine, mEq/d | Nonparametric | –7 (–8, –4) | –11 (–11, –9) | 0 (–3, 0) |
| Proteindietd v Sulphateurine, mEq/d | Nonparametric | 16 (14, 21) | 11 (10, 12) | 26 (23, 27) |
| Phosphorusdietc vs. Phosphorusurine, mEq/d | Standard | –30 (–32, –27) | –44 (–51, –40) | –15 (–19, –8) |
| Potassiumdietc vs. Potassiumurine, mEq/d | Standard | –6 (–9, –3) | –23 (–31, –18) | 12 (7, 19) |
| Magnesiumdietc vs. Magnesiumurine, mEq/d | Standard | –12 (–13, –11) | –17 (–20, –15) | –7 (–9, –5) |
| Calciumdietc vs. Calciumurine, mEq/d | Standard | –14 (–17, –11) | –33 (–43, –27) | 5 (–1, 15) |
NAE, net acid excretion; NEAP, net endogenous acid production estimated by dietary records where NEAPR pertains to the equation by Remer and Manz,7 NEAPF to the equation by Frassetto et al.,6 NEAPL to a model attributed to Lemann,11, 12, 13 and NEAPS to the equation by Sebastian et al.9; PRAL, potential renal acid load estimated by dietary intake where PRAL is the equation by Remer and Manz,7 and PRALS pertains to the equation by Sebastian et al.9UNEAP, net endogenous acid production determined by urine analysis; UPRAL, potential renal acid load determined by urine analysis; OA, organic acids where OAanthro pertains to the anthropometrical estimate by Manz et al.,10 and OAdiet to the estimative equation by Kleinman and Lemann.11
The bias indicates the extent to which the first method listed in the methods column, under (negative values) or over (positive values) estimates the second method listed and so on.
ll participants were used in all analyses and no data points were removed.
Adjusted for intestinal absorption using multipliers specified in PRALS.
Adjusted for intestinal absorption using multipliers specified in PRAL.
Discussion
In this 2-period, 2-condition metabolic balance study, our investigation reports for the first time a complete comparative analysis of methods for determining NEAP. Among the estimative equations, NEAPR and NEAPL accurately estimated both NAE and UNEAP while PRALS accurately estimated UPRAL. We then compared UNEAP to NAE and found that each method accurately determined the other. While NAE has been used historically as the criterion standard, out of all the methods available to measure NEAP we preferentially recommend UNEAP because it offers the ability to directly measure and accurately differentiate PRAL and OA. In addition, NAE is a labor-intensive method requiring a research laboratory to perform, while measures of UNEAP can be sent to a commercial laboratory. Our findings will be useful to investigators conducting clinical or epidemiologic studies that examine potential relationships between the diet-dependent acid–base load and human health and disease,14 exercise performance,25 or space flight applications.15
In this study, we used dietary equations to estimate NEAP and found that a number of these calculations accurately predicted their equivalent biochemical measure. In line with previous reports, we found that NEAPR accurately estimated NEAP,7,16 and for the first time it was observed that NEAPL did as well. However, we were surprised that PRAL and OAanthro inaccurately estimated UPRAL and OAurine, respectively; however, they added together to yield NEAPR, which accurately estimated both NAE and UNEAP. Likewise, OAdiet inaccurately estimated OAurine; however, when it was added to PRAL to yield NEAPL, this equation also accurately estimated both NAE and UNEAP. In contrast we observed that PRALS accurately estimated UPRAL; however, when it is added to OAdiet to yield NEAPS, this equation inaccurately estimated both NAE and UNEAP because of an inaccurate estimate of OA. Overall, the implications are that the use of differing predictive equations in clinical and epidemiologic studies likely results in differences in estimates of absolute NEAP between cohorts. Given our findings, resolving estimates of OA should remain a priority issue of NEAP nutrition research, but optimizing estimative equations to best elucidate OA is a contentious issue.13 Body surface area may be more useful in children than in adults because of their relatively greater change in body surface area as they grow compared with adults. Attempts to revise the OA equations are advised to consider the effects of fruit and vegetable–specific OAs, body surface area, and the varying production of endogenous acids in addition to possible further factors that may be significant predictors. As it stands, direct measurements of OA are best.
This study is the first to compare NAE against UNEAP using Bland–Altman statistics. In 1966, Lennon et al. reported that NAE correlated (r = 0.94) with NEAP determined by biochemical analysis, with a mean difference between the 2 measures of −1 ± 12 mEq/d (P = 0.70), indicating that both methods accurately measure the same quantity.2 Lennon et al. determined NEAP as the sum of urinary sulphate plus OAs minus the amount of base absorbed intestinally from the diet, which was measured as the difference between the amount of cations and anions present in the food consumed by the study participants less the amount excreted in their feces.2 Our study reports consistency between NAE and NEAP determined by urinary analysis alone (i.e., UNEAP), with a mean difference (Bland–Altman bias) of −2 mEq/d (95% CI, −8 to 3) and consequently, approximately 50 years on, our findings corroborate the report of Lennon et al.2 However, using Bland–Altman statistics we also report the relationship between NAE and UNEAP to be modestly imprecise (limits of agreement, −32 to 28 mEq), with application only for group estimates. We suggest that the imprecision between UNEAP and NAE is a consequence of known quantification errors/issues in the measurement of NAE or UNEAP.26
While NAE certainly remains a valid marker of NEAP, UNEAP offers the ability to directly measure and differentiate PRAL and OA, and consequently provides several advantages to the investigator conducting research on acid–base nutritional biochemistry. To elaborate, current research suggests that a chronic intake of acid derived from the PRAL may contribute to detrimental health outcomes while a chronic intake of food-specific OA from fruits and vegetables may contribute to health protection.27 This is indicated by findings of Krupp et al.5 who reported that higher diastolic blood pressure was more strongly associated with UPRAL than NAE, and Remer et al.,27 who found that increasing UPRAL but not NAE was associated with reduced diaphyseal bone mass and bone size in children. Both groups suggest that this may have been because NAE quantifies within it the food-specific portion of OA, which may contain beneficial components for blood pressure and bone health, and, as a result, relationships with NAE may have been attenuated. Such findings highlight the necessity to distinguish between the forms of acid intake in NEAP research. To facilitate this, accurate measures of the PRAL, OA, and NEAP are essential and can be achieved by measuring UNEAP.
Our study calculated urinary and dietary NEAP using the average measure of multiple days, while NEAP tends to be traditionally calculated from urine or diet records measured over 1 day5,8 or averaged over 2 days.28 Consequently, our results likely reflect a more accurate estimate of true NEAP than is typically obtained in standard research. This increases our confidence in the estimates and allows insight into the performance of each equation under optimized conditions. We also set our a priori limits of agreement to ±20 mEq because we believe that within these limits it would be reasonable to infer that the equations are fairly precise; none of the equations were found to be precise within these confines. Given that the collections of dietary intake and urinary output were completed under metabolic ward conditions, this indicates that there is room for improvement within the existing formula. However, given the inherent complexity of acid–base biochemistry, we may not be able to improve upon the current models. Although, NEAPR was precise within limits of agreement of ±25 mEq (when compared with either NAE or UNEAP), and so too did PRALS predict UPRAL within these limits. Moreover, NEAPL and UNEAP precisely measured NAE within ±30 mEq. As the question of what constitutes a reasonable limit of agreement is one of researcher judgement, other groups may believe that within ±30 mEq is a good enough measure to infer that these equations are precise. To this end, we maintain that the data illustrate a degree of imprecision across these techniques, although all in all they are not far from perfection.
As indicated, our study examined NEAP under metabolic ward or steady state conditions wherein the participants consume the same quantity of true NEAP day in and day out. In epidemiologic studies or the like, NEAP tends to be quantified in free living, non–steady state conditions, where participants consume varying quantities of NEAP from day to day. Measurements from diets that change daily may deviate from true NEAP because it is thought that acid production may differ from acid excretion. However, research previously conducted by members of the current investigation found that NEAPR as estimated from single 24-hour weighed food diaries, under non–steady state conditions, accurately estimated 24-hour NAE, implying that single-day measures might be considered accurate for measures of NEAP in free living groups of indiviudals.16 However, it is likely that NEAP intake fluctuates widely in free living populations on a day to day basis, and studies examining the relationship between NEAP and human health and disease are possibly better designed to use data measured over multiple days (e.g., perhaps ≥3 days, including a weekend day) in order to begin approximating an individual’s habitual NEAP intake. Indeed, any impact of NEAP on human health is plausibly chronic and dose dependent. While we saw accurate estimates of intake derived from weighed meals in the current study, investigators are cautioned that intake estimates calculated from other dietary collection techniques (such as food frequency questionnaires, food recalls, or nonweighted food diaries), are highly likely to decrease measurement accuracy because of known error in these methods; such strategies should be deployed and interpreted with caution. As an aside, substitute measures of NEAP, such as the use of urine pH, only yield valid results when 24-hour urine is collected; spot tests are known to be highly inaccurate and we, as others, do not recommend their use.29, 30, 31, 32
A unique strength of this research is that we examined the accuracy and precision of NEAP measurement methodologies over a wide range of intake (−9 to 95 mEq/d) which is typically observed in clinical and epidemiologic studies. In doing so, we observed that the true accuracy and precision of some of the equations appears to vary throughout differing intakes of dietary acid and base, which has implications for equation validity.23 The reason(s) for this variability in accuracy and precision are less clear; however, it can be observed that the dietary estimates certainly appear to be more stable in comparison to UNEAP than NAE (Supplementary Figures S1 and S2). One reason for this variability in accuracy may be related to endogenous OA production, wherein the body regulates the production of OA in response to a high or low dietary base intake.33 Thus, as NEAP intake becomes more extreme, the accuracy of the dietary equations may moderate as the equations do not factor for the internal regulation of OA. The overall implications are that researchers are best off using equations that better maintain accuracy and precision estimates, such as that displayed by NEAPR (compared with UNEAP). However, the most useful technique to measure the diet’s acid–base load should certainly also accurately differentiate PRAL and OA, and as it stands UNEAP is best positioned to accomplish this goal. That said, it is also of importance that excreted NEAP (i.e., NAE and UNEAP) is an indirect measure for true internal NEAP and its thought that one may not necessarily equal the other during times of elevated acid loads, as the body modulates utilization of fixed buffer reserves to titrate NEAP, causing true NEAP to progressively deviate from excreted NEAP.1,34 Another interesting point is that in this study we intervened with salts of potassium bicarbonate; as such, we are unable to infer from our data whether the accuracy and precision of the NEAP equations are the same when interventions of other acid- or base-forming nutrients or their combinations are consumed. However, most of the variation in NAE is thought to be explained by the ratio of protein to potassium,6 so it is possible that the equations perform somewhat similarly when different interventions are used.
In conclusion, a range of estimative equations and biochemical indices were found to accurately measure the diet-dependent acid–base load. Among the estimate equations, NEAPR, NEAPL, and PRALS displayed good agreement to their biochemical equivalent and are best applied for group estimates in future research. However, the direct measurement of NEAP in 24-hour urine samples offers several advantages for the researcher or laboratory with the capacity to do so. In particular, of the biochemical methods available to measure NEAP (i.e., NAE and UNEAP) we preferentially recommend UNEAP because it offers the ability to directly measure and differentiate PRAL plus OA. However, investigators wishing to draw conclusions between the diet-dependent acid–base load and human health and disease should consider the limitations within all methods.
Disclosure
All the authors declared no competing interests.
Acknowledgments
BHP is supported by an Australian Government Research Training Program Stipend Scholarship. AS passed away before this article was complete, and he has been added as an author in honor of his involvement with this research and in memory of his contributions to the field.
Footnotes
Figure S1. Bland–Altman plots comparing diet-derived estimates of NEAP against 24-hour urinary NAE for (A) NEAPR, (B) NEAPF, (C) NEAPL, and (D) NEAPS. Accuracy and precision were assessed using Bland–Altman analysis for repeated measures data where the true value varies. All participants were used in all analyses and no data points were removed. NAE, net acid excretion; NEAP, net endogenous acid production estimated by dietary records where NEAPR pertains to the equation by Remer and Manz,7 NEAPF to the equation by Frassetto et al.,6 NEAPL to a model attributed to Lemann,11, 12, 13 and NEAPS to the equation by Sebastian et al.9
Figure S2. Bland–Altman plots comparing diet-derived estimates of NEAP against 24-hour UNEAP for (A) NEAPR, (B) NEAPF, (C) NEAPL, and (D) NEAPS. Accuracy and precision were assessed using Bland–Altman analysis for repeated measures data where the true value varies. All participants were used in all analyses and no data points were removed. UNEAP, urinary net endogenous acid production; NEAP, net endogenous acid production estimated by dietary records where NEAPR pertains to the equation by Remer and Manz,7 NEAPF to the equation by Frassetto et al.,6 NEAPL to a model attributed to Lemann,11, 12, 13 and NEAPS to the equation by Sebastian et al.9
Figure S3. Bland–Altman plots comparing diet-derived estimates of PRAL against 24-hour UPRAL for (A) PRAL and (B) PRALs. Accuracy and precision were assessed using Bland–Altman analysis for repeated measures data where the true value varies. All participants were used in all analyses and no data points were removed. UPRAL, urinary potetnial renal acid load; PRAL, potential renal acid load estimated by dietary records where PRAL is the equation by Remer and Manz7 and PRALS pertains to the equation by Sebastian et al.9
Figure S4. Bland–Altman plots comparing diet-derived estimates of OA against 24-hour OAurine for (A) OAanthro and (B) OAdiet. Accuracy and precision were assessed using Bland–Altman analysis for repeated measures data where the true value varies. All participants were used in all analyses and no data points were removed. OAurine, urinary organic acid; OA, organic acids where OAanthro pertains to the anthropometrical estimate by Manz et al.,10 and OAdiet to the estimative equation by Kleinman and Lemann.11
Figure S5. Bland–Altman plots comparing diet-derived estimates of NEAP determinants against their equivalent 24-hour urinary biomarker (A) estimated dietary protein compared with urinary sulphate, (B) estimated dietary sulphate compared with urinary sulphate, (C) estimated dietary phosphate compared with urinary phosphate, (D) estimated dietary calcium compared with urinary calcium, (E) estimated dietary magnesium compared with urinary magnesium, and (F) estimated dietary potassium compared with urinary potassium. All dietary estimates were adjusted for intestinal absorption using multipliers specified in PRAL except for sulphate, which was determined using multipliers specified in PRALS. Accuracy and precision were assessed using Bland–Altman analysis for repeated measures data. All participants were used in all analyses and no data points were removed. PRAL, potential renal acid load estimated by dietary records where PRAL pertains to the equation by Remer and Manz7 and PRALS to the equation by Sebastian et al.9
Figure S6. Bland–Altman plot comparing 24-hour UNEAP against 24-hour urinary NAE. Accuracy and precision assessed using Bland–Altman analysis for repeated measures data where the true value varies. All participants were used in all analyses and no data points were removed. NAE, net acid excretion; UNEAP, urinary net endogenous acid production.
Supplementary Material
References
- 1.Poupin N., Calvez J., Lassale C. Impact of the diet on net endogenous acid production and acid–base balance. Clin Nutr. 2012;31:313–321. doi: 10.1016/j.clnu.2012.01.006. [DOI] [PubMed] [Google Scholar]
- 2.Lennon E.J., Lemann J., Litzow J.R. The effects of diet and stool composition on the net external acid balance of normal subjects. J Clin Invest. 1966;45:1601–1607. doi: 10.1172/JCI105466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Relman A.S., Lennon E.J., Lemann J. Endogenous production of fixed acid and the measurement of the net balance of acid in normal subjects. J Clin Invest. 1961;40:1621–1630. doi: 10.1172/JCI104384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ikizler H.O., Zelnick L., Ruzinski J. Dietary acid load is associated with serum bicarbonate but not insulin sensitivity in chronic kidney disease. J Ren Nutr. 2016;26:93–102. doi: 10.1053/j.jrn.2015.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Krupp D., Shi L., Remer T. Longitudinal relationships between diet-dependent renal acid load and blood pressure development in healthy children. Kidney Int. 2014;85:204–210. doi: 10.1038/ki.2013.331. [DOI] [PubMed] [Google Scholar]
- 6.Frassetto L.A., Todd K.M., Morris R.C. Estimation of net endogenous noncarbonic acid production in humans from diet potassium and protein contents. Am J Clin Nutr. 1998;68:576–583. doi: 10.1093/ajcn/68.3.576. [DOI] [PubMed] [Google Scholar]
- 7.Remer T., Manz F. Estimation of the renal net acid excretion by adults consuming diets containing variable amounts of protein. Am J Clin Nutr. 1994;59:1356–1361. doi: 10.1093/ajcn/59.6.1356. [DOI] [PubMed] [Google Scholar]
- 8.Remer T., Dimitriou T., Manz F. Dietary potential renal acid load and renal net acid excretion in healthy, free-living children and adolescents. Am J Clin Nutr. 2003;77:1255–1260. doi: 10.1093/ajcn/77.5.1255. [DOI] [PubMed] [Google Scholar]
- 9.Sebastian A., Frassetto L.A., Sellmeyer D.E. Estimation of the net acid load of the diet of ancestral preagricultural Homo sapiens and their hominid ancestors. Am J Clin Nutr. 2002;76:1308–1316. doi: 10.1093/ajcn/76.6.1308. [DOI] [PubMed] [Google Scholar]
- 10.Manz F., Vecsei P., Wesch H. Renal acid excretion and renal molar load in healthy children and adults. Monatsschr Kinderheilkd. 1984;132:163–167. [PubMed] [Google Scholar]
- 11.Kleinman J.G., Lemann J., Jr. Acid production. In: Maxwell M.H., Kleeman C.R., Narins R.G., editors. Clinical Disorders of Fluid and Electrolyte Metabolism. McGraw Hill; New York, New York: 1987. pp. 159–173. [Google Scholar]
- 12.Lennon E.J., Lemann J., Jr Influence of diet composition on endogenous fixed acid production. Am J Clin Nutr. 1986;21:451–456. doi: 10.1093/ajcn/21.5.451. [DOI] [PubMed] [Google Scholar]
- 13.Frassetto L.A., Shi L., Schloetter M. Established dietary estimates of net acid production do not predict measured net acid excretion in patients with Type 2 diabetes on Paleolithic-Hunter-Gatherer-type diets. Eur J Clin Nutr. 2013;67:899–903. doi: 10.1038/ejcn.2013.124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Akter S., Nanri A., Mizoue T. Dietary acid load and mortality among Japanese men and women: The Japan Public Health Center-based Prospective Study. Am J Clin Nutr. 2017;106:146–154. doi: 10.3945/ajcn.117.152876. [DOI] [PubMed] [Google Scholar]
- 15.Zwart S.R., Rice B.L., Dlouhy H. Dietary acid load and bone turnover during long-duration spaceflight and bed rest. Am J Clin Nutr. 2018;107:834–844. doi: 10.1093/ajcn/nqy029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Parmenter B.H., Slater G.J., Frassetto L.A. Accuracy and precision of estimation equations to predict net endogenous acid excretion using the Australian food database. Nutr Diet. 2017;74:308–312. doi: 10.1111/1747-0080.12324. [DOI] [PubMed] [Google Scholar]
- 17.Sebastian A., Harris S.T., Ottaway J.H. Improved mineral balance and skeletal metabolism in postmenopausal women treated with potassium bicarbonate. N Engl J Med. 1994;330:1776–1781. doi: 10.1056/NEJM199406233302502. [DOI] [PubMed] [Google Scholar]
- 18.Frassetto L., Morris R.C., Sebastian A. Potassium bicarbonate reduces urinary nitrogen excretion in postmenopausal women. J Clin Endocrinol Metab. 1997;82:254–259. doi: 10.1210/jcem.82.1.3663. [DOI] [PubMed] [Google Scholar]
- 19.Kurtz I., Maher T., Hulter H.N. Effect of diet on plasma acid–base composition in normal humans. Kidney Int. 1983;24:670–680. doi: 10.1038/ki.1983.210. [DOI] [PubMed] [Google Scholar]
- 20.Jones J.W., Sebastian A., Hulter H.N. Systemic and renal acid–base effects of chronic dietary potassium depletion in humans. Kidney Int. 1982;21:402–410. doi: 10.1038/ki.1982.36. [DOI] [PubMed] [Google Scholar]
- 21.R Core Team. R . R Foundation for Statistical Computing; Vienna, Austria: 2018. A language and environment for statistical computing. [Google Scholar]
- 22.Bland J.M., Altman D.G. Agreement between methods of measurement with multiple observations per individual. J Biopharm Stat. 2007;17:571–582. doi: 10.1080/10543400701329422. [DOI] [PubMed] [Google Scholar]
- 23.Bland J.M., Altman D.G. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135–160. doi: 10.1177/096228029900800204. [DOI] [PubMed] [Google Scholar]
- 24.Inker L.A., Schmid C.H., Tighiouart H. Estimating glomerular filtration rate from serum creatinine and cystatin C. N Engl J Med. 2012;367:20–29. doi: 10.1056/NEJMoa1114248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Applegate C., Mueller M., Zuniga K.E. Influence of dietary acid load on exercise performance. Int J Sport Nutr Exerc Metab. 2017;27:213–219. doi: 10.1123/ijsnem.2016-0186. [DOI] [PubMed] [Google Scholar]
- 26.Uribarri J., Douyon H., Oh M.S. A re-evaluation of the urinary parameters of acid population and excretion in patients with chronic renal acidosis. Kidney Int. 1995;47:624–627. doi: 10.1038/ki.1995.79. [DOI] [PubMed] [Google Scholar]
- 27.Remer T., Manz F., Alexy U. Long-term high urinary potential renal acid load and low nitrogen excretion predict reduced diaphyseal bone mass and bone size in children. J Clin Endocrinol Metab. 2011;96:2861–2868. doi: 10.1210/jc.2011-1005. [DOI] [PubMed] [Google Scholar]
- 28.Reddy S.T., Wang C.Y., Sakhaee K. Effect of low-carbohydrate high-protein diets on acid–base balance, stone-forming propensity, and calcium metabolism. Am J Kidney Dis. 2002;40:265–274. doi: 10.1053/ajkd.2002.34504. [DOI] [PubMed] [Google Scholar]
- 29.Parmenter B.H., Slater G.J., Frassetto L.A. Spot-testing urine pH, a novel dietary biomarker? A randomised cross-over trial. Nutr Diet. 2017;74:313–319. doi: 10.1111/1747-0080.12325. [DOI] [PubMed] [Google Scholar]
- 30.Remer T., Manz F. Potential renal acid load of foods and its influence on urine pH. J Am Diet Assoc. 1995;95:791–797. doi: 10.1016/S0002-8223(95)00219-7. [DOI] [PubMed] [Google Scholar]
- 31.Parmenter B.H., Slater G.J., Frassetto L.A. Assessment of dietary behaviours by spot-testing urine pH. J Nutr Intermed Metab. 2017;8:75. [Google Scholar]
- 32.Remer T., Krupp D., Shi L. Dietary protein’s and dietary acid load’s influence on bone health. Crit Rev Food Sci Nutr. 2014;54:1140–1150. doi: 10.1080/10408398.2011.627519. [DOI] [PubMed] [Google Scholar]
- 33.Hood V.L., Tannen R.L. Mechanisms of disease: protection of acid–base balance by pH regulation of acid production. N Engl J Med. 1998;339:819–826. doi: 10.1056/NEJM199809173391207. [DOI] [PubMed] [Google Scholar]
- 34.Frassetto L.A., Lanham-New S.A., Macdonald H.M. Standardizing terminology for estimating the diet-dependent net acid load to the metabolic system. J Nutr. 2007;137:1491–1492. doi: 10.1093/jn/137.6.1491. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.