19 Dubious Ways to Compute the Marginal Likelihood of a Phylogenetic Tree Topology

Abstract

The marginal likelihood of a model is a key quantity for assessing the evidence provided by the data in support of a model. The marginal likelihood is the normalizing constant for the posterior density, obtained by integrating the product of the likelihood and the prior with respect to model parameters. Thus, the computational burden of computing the marginal likelihood scales with the dimension of the parameter space. In phylogenetics, where we work with tree topologies that are high-dimensional models, standard approaches to computing marginal likelihoods are very slow. Here, we study methods to quickly compute the marginal likelihood of a single fixed tree topology. We benchmark the speed and accuracy of 19 different methods to compute the marginal likelihood of phylogenetic topologies on a suite of real data sets under the JC69 model. These methods include several new ones that we develop explicitly to solve this problem, as well as existing algorithms that we apply to phylogenetic models for the first time. Altogether, our results show that the accuracy of these methods varies widely, and that accuracy does not necessarily correlate with computational burden. Our newly developed methods are orders of magnitude faster than standard approaches, and in some cases, their accuracy rivals the best established estimators.

In phylogenetic inference, the tree topology forms a key object of inference. In Bayesian phylogenetics, this translates to approximating the posterior distribution of tree topologies. Typically, a joint posterior distribution of tree topologies and continuous parameters, including branch lengths and substitution model parameters, is approximated directly via Markov chain Monte Carlo (MCMC), as done in the popular Bayesian phylogenetics software MrBayes (Ronquist et al. 2012). However, MCMC over topologies is computationally expensive (Höhna et al. 2008; Lakner et al. 2008). These MCMC algorithms spend a nontrivial amount of time marginalizing over branch lengths and substitution models parameters and discarding them so that the estimated posterior probability of a tree topology is the proportion of MCMC iterations in which it appears. Therefore, fast marginalization over continuous phylogenetic parameters may offer a boon to MCMC algorithm efficiency or even allow one to perform Bayesian phylogenetic inference without MCMC. In this article, we review existing methods and develop new ones to compute the posterior probabilities of tree topologies by quickly marginalizing out branch lengths to compute the marginal likelihood of a given topology. We compare speed and accuracy of 19 methods and examine whether there is a speed–accuracy trade off.

Given that the bulk of Bayesian inference is performed with methods that work because they allow the marginal likelihood to be avoided, why would one want to compute them at all? Given fast MCMC-free algorithms for computing marginal likelihoods of topologies, one could apply these algorithms to the development of fast, MCMC-free Bayesian phylogenetic inference. To make such an advance, first one would need to identify a large enough set of a posteriori highly probable tree topologies, such as with a new optimization-based method called phylogenetic topographer (PT) (Whidden et al. 2019). Once a set of promising tree topologies is formed, we can compute their marginal likelihoods, then renormalize these marginal likelihoods (perhaps after multiplying by a prior) to obtain approximate posterior probabilities of tree topologies—the key output of Bayesian phylogenetic inference. Luckily, we can tap into a substantial body of research on computing the marginal likelihood of purely continuous statistical models in order to integrate out continuous parameters for any given tree topology (Hans et al. 2007; Lenkoski and Dobra 2011). It is, therefore, high time we consider the possibility of constructing the posterior distribution on topologies without MCMC. To do so, we must know: how well, and how quickly, can we compute the marginal likelihood of a topology?

In this article, we address this question by benchmarking a wide range of methods for calculating the marginal likelihood of a topology with respect to branch lengths under the JC69 model, the simplest nucleotide substitution model. These approaches include very fast approximations including several based on the Laplace approximation (Tierney and Kadane 1986; Kass and Raftery 1995) and variational approaches (Ranganath et al. 2014). There are also approaches that require some sampling (though not of topologies), including those that make use of MCMC samples (c.f., bridge sampling, Overstall and Forster 2010; Gronau et al. 2017) and approaches that employ importance sampling (c.f., naïve Monte Carlo, Hammersley and Handscomb 1964; Raftery and Banfield 1991). We also include approaches that make use of a set of so-called power posteriors, including the path sampling (Ogata 1989; Gelman and Meng 1998; Lartillot and Philippe 2006; Baele et al. 2012) method frequently used in phylogenetics. Using a set of empirical data sets and a common inference framework, we benchmark 19 methods for computing the marginal likelihood of tree topologies. These 19 methods include some well-known in the phylogenetics literature, some we apply for the first time in phylogenetics, and others that we develop explicitly for this problem. We find that some of these new methods provide estimates that compare favorably to the precise (but slow) state-of-the-art approaches, while running orders of magnitudes more quickly. The title of our article is adapted from the classic review of matrix exponentiation methods by Moler and Van Loan (1978, 2003); it is not meant to cast doubt on the methods presented here, although we do find that some rather “dubious” methods making strong simplifying assumptions perform surprisingly well!

Materials and Methods

Marginal likelihoods

Consider a (fixed) unrooted topology for 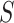species with unconstrained branch length vector 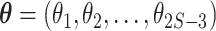and the JC69 (Jukes–Cantor) model (Jukes and Cantor 1969). The rate matrix of the JC69 model does not any have free parameters as it assumes equal base frequencies and equal substitution rate for all pairs of nucleotides. If branch lengths are measured in units of the expected number of substitutions per site and the JC69 substitution model is employed, the posterior distribution is given by:

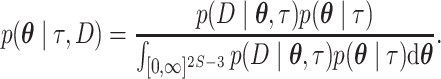The normalizing constant in the denominator of the right-hand side is the marginal likelihood of the phylogenetic tree topology model 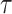, 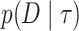. It is this marginal likelihood (of a sequence alignment given a topology) that is the quantity of interest in this article. As is typical, we place independent exponential priors on branch lengths with a prior expectation of 0.1 substitutions, such that 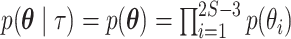, where 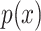is the exponential density.

Calculating marginal likelihoods is an area of active statistical research, both inside and outside of phylogenetics. A complete review of all the methods that have been proposed for this purpose is outside the scope of this article, and we refer readers to reviews by Gelman and Meng (1998) and Gronau et al. (2017). We will first provide a basic sketch of the types of methods we employ (see Table 1 for abbreviations). Second, we describe some new methods for calculating the marginal likelihood designed specifically for topologies. Finally, a more detailed explanation of all the methods used in this article can be found in the supplementary materials.

Table 1.

Names, abbreviations, and number of required MCMC chains involved in applying the 19 methods

Abbreviation	Full name	MCMC chains
ELBO	Evidence lower bound	0
GLIS	Gamma Laplus importance sampling	0
VBIS	Varational Bayes importance sampling	0
BL	Beta’ Laplus	0
GL	Gamma Laplus	0
LL	Lognormal Laplus	0
MAP	Maximum un-normalized posterior probability	0
ML	Maximum likelihood	0
NMC	Naïve Monte Carlo	0
BS	Bridge sampling	1
CPO	Conditional predictive ordinates	1
HM	Harmonic mean	1
SHM	Stabilized harmonic mean	1
NS	Nested sampling	Multiple short chains
PPD	Pointwise predictive density	1
PS	Path sampling	50
MPS	Modified path sampling	50
SS	Stepping stone	50
GSS	Generalized stepping stone	50

Note: GLIS, VBIS, and NMC () do not require MCMC samples but perform importance sampling. Stepping stone and path sampling methods employ an unspecified number of steps; we found 50 to be sufficient.

Methods for calculating the marginal likelihood can be broken down into two main categories: sampling-free methods and sampling-based methods. The majority of sampling-free methods revolve around replacing the intractable posterior distribution with one whose normalizing constant can be more easily computed. These approaches include the Laplace approximation (Tierney and Kadane 1986; Kass and Raftery 1995), three new variations on this theme that we introduce here (the Laplus approximations), and a variational Bayes approximation (Ranganath et al. 2014) from which we derive the evidence lower bound (ELBO). We additionally investigate the performance of the maximum likelihood and maximum a posteriori estimators to approximate the marginal likelihood. These extremely simple estimators simply use the height of the mode to approximate the marginal likelihood integral.

The sampling-based approaches can further be broken down into importance sampling and MCMC-based approaches. In importance sampling, samples drawn from a tractable proposal distribution are used to calculate the marginal likelihood using simple identities. How well an importance sampling method works depends on how close the proposal distribution is to the true posterior. We examine three importance sampling approaches, naïve Monte Carlo (NMC) (Hammersley and Handscomb 1964; Raftery and Banfield 1991), which uses the prior distribution as the proposal distribution, and two approaches using more sophisticated proposal distributions. Lastly, the MCMC-based methods can be broken down into those that can be used with a single chain, and those that require many chains. Among single-chain methods, we include the well-known harmonic mean (HM) estimator (Newton and Raftery 1994), a variation thereof known as the stabilized harmonic mean (SHM) (Newton and Raftery 1994), bridge sampling (BS) (Overstall and Forster 2010; Gronau et al. 2017), conditional predictive ordinates (CPO) (Lewis et al. 2013), and the pointwise predictive density (PPD) (Vehtari et al. 2017). Finally, the nested sampling (NS) method sits somewhere in between the single- and multiple-chain categories as it requires simulations from multiple short MCMC runs (Skilling 2004, 2006; Maturana Russel et al. 2018).

The final set of methods all require multiple chains, which are “heated” with a heating parameter that interpolates between the posterior distribution and some other distribution. For the path sampling (Ogata 1989; Gelman and Meng 1998; Lartillot and Philippe 2006; Friel and Pettitt 2008; Baele et al. 2012) and stepping stone (SS) methods (Xie et al. 2011), the power posterior path links the posterior to the prior distribution. Fan et al. (2011) proposed the generalized stepping stone (GSS) method in which the path is defined between the posterior and a reference distribution, hence avoiding issues associated with sampling from vague priors.

A number of the above methods have been previously applied to phylogenetics, including all power posterior approaches, the HM, and CPO. In phylogenetics, path sampling and stepping stone are currently the most widely used methods, and are included in popular inference programs like BEAST (Suchard et al. 2018) and MrBayes (Ronquist et al. 2012).

Laplus

The Laplace approximation (Tierney and Kadane 1986; Kass and Raftery 1995) replaces the true log-posterior distribution with a multivariate normal distribution. The mean is taken to be the joint posterior mode (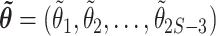, and the covariance matrix is taken to be the inverse of the observed information matrix of 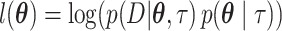evaluated at 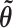. Previous studies have approximated the likelihood surface of phylogenies using multivariate normal distributions (Thorne et al. 1998; Guindon 2010), including the use of parameter transformations to account for positivity and skew (Reis and Yang 2011). However, the posterior distribution of branch lengths may have its mode at 0 in some dimensions, which is not a shape that can be attained by any transformation of a normal distribution. In related work, the conditional posterior distribution of single branch lengths has been approximated with a gamma distribution, which can accommodate the zero mode, enabling independence sampling (Aberer et al. 2015).

We depart from the aforementioned approaches and introduce a novel framework to approximate the joint posterior distribution on branch lengths. For simplicity, in all cases, we assume that a posteriori branch lengths are independent. This is obviously not true in practice, but we find that posterior correlations are often quite small, and that our independence assumption works well. This assumption also greatly reduces the computational burden by allowing us to sidestep computing all second partial derivatives.

Our “Laplus” approximation then takes the maximum a posteriori (MAP) vector of branch lengths 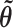and the vector of second derivatives 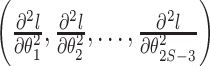and finds the parameters of our approximating distributions for each branch, 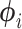, by matching modes and second derivatives of the approximating and posterior distributions of branch lengths. Unlike the method of moments and maximum likelihood estimation, our approach is fast as it does not require a set of samples to estimate the parameters of the distribution. We consider three distributions for approximating the marginal posteriors of branch lengths: lognormal, gamma, and beta 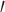(i.e., beta prime). The general procedure for the Laplus approximations is similar regardless of what distribution (i.e., the choice of 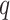in 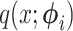) is chosen to approximate the posterior and is written here algorithmically:

• (1) Find the (joint) MAP branch lengths,

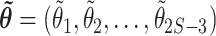
• (2) For

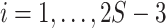
  • (i) Compute 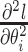, the second derivative of the log unnormalized posterior with respect to the 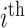branch
  • (ii) Find parameters of 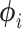by solving

    
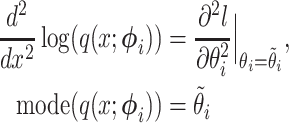
  • (iii) Catch exceptions
• (3) Compute the marginal likelihood as

  

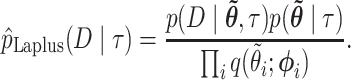
Exceptions occur when elements of 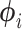are outside of the domain of support, when the second derivative is nonnegative (so the posterior has a mode at 0), or when elements of 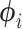are otherwise suspect (such as producing particularly high-variance distributions with very short branches). Exceptions and their handling depend on the distributional kernel (choice of 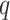), and we defer a full discussion of this to the Supplementary material.

Variational inference

The main idea behind variational inference is to transform posterior approximation into an optimization problem using a family of approximate densities. The aim is to find the member of that family with the minimum Kullback–Leibler (KL) divergence to the posterior distribution of interest:

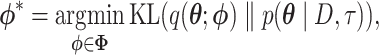where 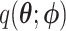is the variational distribution parameterized by a vector 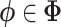and KL is defined as

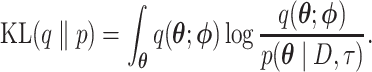To minimize the KL divergence, we first rewrite the KL equation:

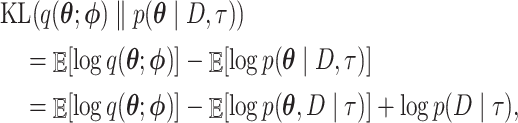where the expectations are taken with respect to the variational distribution 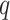. The third term 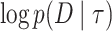on the right-hand side of the last equality is a constant with respect to the variational distribution so it can be ignored for the purpose of the minimization. After switching the sign of the other two terms, the minimization problem can be framed as a maximization problem of the function

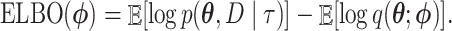The ELBO is easier to calculate than the KL divergence as it does not involve computing the intractable posterior normalization term 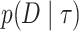. The ELBO gives a lower bound of the marginal likelihood, the very measure we are interested in estimating here. Here, we use the ELBO estimate 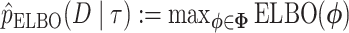to approximate the marginal likelihood of a topology.

We used a Gaussian variational mean-field approximation applied to log-transformed branch lengths to ensure that the variational distribution stays within the support of the posterior. The mean-field approximation assumes complete factorization of the distribution over each of the 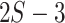branch length variables and each factor is governed by its own variational parameters :

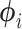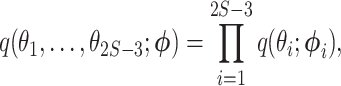where 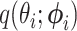is a lognormal density and 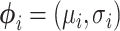. As in the Laplus approximation, this model also assumes that there is no correlation between branches.

The variational parameters are estimated using stochastic gradient ascent using a black box approach (Ranganath et al. 2014) similar to the algorithm implemented in Stan (Kucukelbir et al. 2015).

Importance sampling

The Laplus and variational Bayes approximations of the marginal likelihood are fast, but in practice the approximate posterior does not always match the posterior of interest well. Since these methods rely on independent univariate probability distributions (e.g., gamma, normal, etc.), samples can be efficiently drawn from the approximate posterior distributions. We thus also used importance sampling to reduce the bias of the Laplus and variational Bayes methods using the approximate posterior distribution as the importance instrument distribution.

The importance sampling estimate of 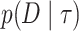using an approximate normalized probability distribution (instrument distribution) 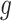is

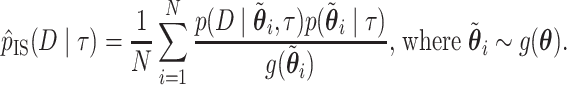Benchmarks

We benchmark the 19 methods for estimating fixed-tree marginal phylogenetic likelihood on five empirical data sets from a suite of standard test data sets (Lakner et al. 2008; Höhna and Drummond 2011; Larget 2013; Whidden and Matsen 2015), which we call DS1 through DS5. These data sets vary from 25 to 50 taxa, with alignment number of sites ranging from 378 to 2520. Instead of focusing primarily on the accuracy of the estimate of the single-tree marginal likelihoods, we focus on the approximate posterior of topologies we obtain by applying our marginal likelihood methods to each and normalizing the result as described below. We take measures of the goodness of these posteriors that directly address approximation error in quantities of interest, namely the posterior probabilities of topologies and the probabilities of tree splits. These are compelling choices because Bayesian phylogenetic inference is not performed to answer the question “what is the marginal likelihood of this topology” but rather to quantify support for evolutionary relationships/hypotheses. We note that the posterior of trees is also useful in other contexts, such as examining the information content of a data set (Lewis et al. 2016).

To compare marginal likelihood methods’ accuracy and precision, we need to establish a ground truth for 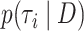for each tree topology 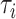. To accurately approximate the ground truth, we use the extensive runs (called golden runs) of MrBayes from Whidden and Matsen (2015), which consist of 10 chains run for 1 billion generations each (subsampled every 1000 generations), with 25% discarded as burnin and all chains pooled when computing posterior summaries. For each of the five data sets, this results in 7.5 million MCMC samples from 7.5 billion generations, with common diagnostics showing convergence of the chains. The credible sets contain between 5 and 1,141,881 topologies. For data sets DS1 to DS4, we run each of the 19 methods for calculating marginal likelihoods on every tree in the 95% posterior credible set. DS5 has a credible set that is too large (over one million topologies), so we consider only the 1000 most probable trees from this data set. The only input for each of the 19 methods from the golden runs is the tree topology without branch lengths. In the Golden runs, was set up to use a uniform prior for topologies and an unconstrained exponential(10.0) prior for branch lengths.

After arriving at a set of trees for each benchmark data set, we renormalize posterior probabilities so that they sum to one over the selected trees: 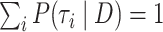. We assume these probabilities form the true posterior mass function of tree topologies and measure accuracy with respect to this function. We use Bayes’ rule to convert our approximations of the marginal likelihood to the posterior probability:

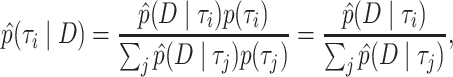where the last equality holds because we assumed the uniform prior over the tree topologies. The marginal likelihood estimations were replicated 10 times for each combination of method and data set, allowing us to derive the standard deviation of the marginal likelihood estimates.

We employ two different measures to determine closeness of an approximate posterior to the golden run posterior. Since many questions in phylogenetics concern the probabilities of individual splits, we consider the error in their estimated posterior probabilities. We calculate the root mean-squared deviation (RMSD) of the probabilities of splits, computed as 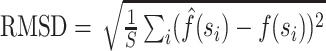, where 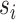is a split (or bipartition) and 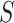the number of splits in the tree topology set. The probabilities of a split are given by 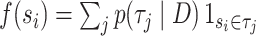and 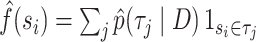, that is, they are the sums of posterior probabilities of the topologies that contain that split. To assess how well the posterior probabilities of topologies are estimated, we use the Kullback–Leibler (KL) divergence from 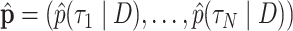to 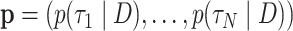, where 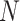is the number of unique topologies in the 95% posterior credible set of the golden run. This is computed as as .

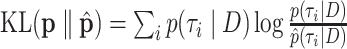Given that these 19 marginal likelihood calculation methods vary widely in their computational efficiency, we also seek to benchmark the speed of the methods. As our measure of speed, we take the average time (per data set) required to compute the marginal likelihood of a topology. The speed of these methods depends on a number of data set-specific features (including the size of the data set and the number of phylogenies in the credible set), on run-time decisions (such as the number of MCMC iterations), and on the code that implements them. By incorporating multiple data sets (to average over data set-specific effects) and implementing the methods in a single package (to control for run-time and implementation-specific effects), we are able to examine the general tradeoff between speed and accuracy, and highlight the use-cases we think the methods are suited for.

Every method was implemented within the phylogenetic package (Fourment and Holmes 2014) (https://github.com/4ment/physher) and we used the same priors as in the golden runs of MrBayes. We used 50 power posteriors (a.k.a. stones) of one million iterations each. The powers were taken to be the quantiles of the beta distribution with shape parameters 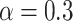and 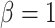, as recommended by Xie et al. (2011).

Data sets and scripts used in this study are available from https://github.com/4ment/marginal-experiments. All analyses were run on a single thread, leaving much room to improve the speed of these algorithms, many of which are embarrassingly parallelizable. Analysis performed on an Intel Xeon E5-2697 2.60GHz processors running CentOS release 6.1 with 244 GB of RAM.

Results

Accuracy and precision

RMSD

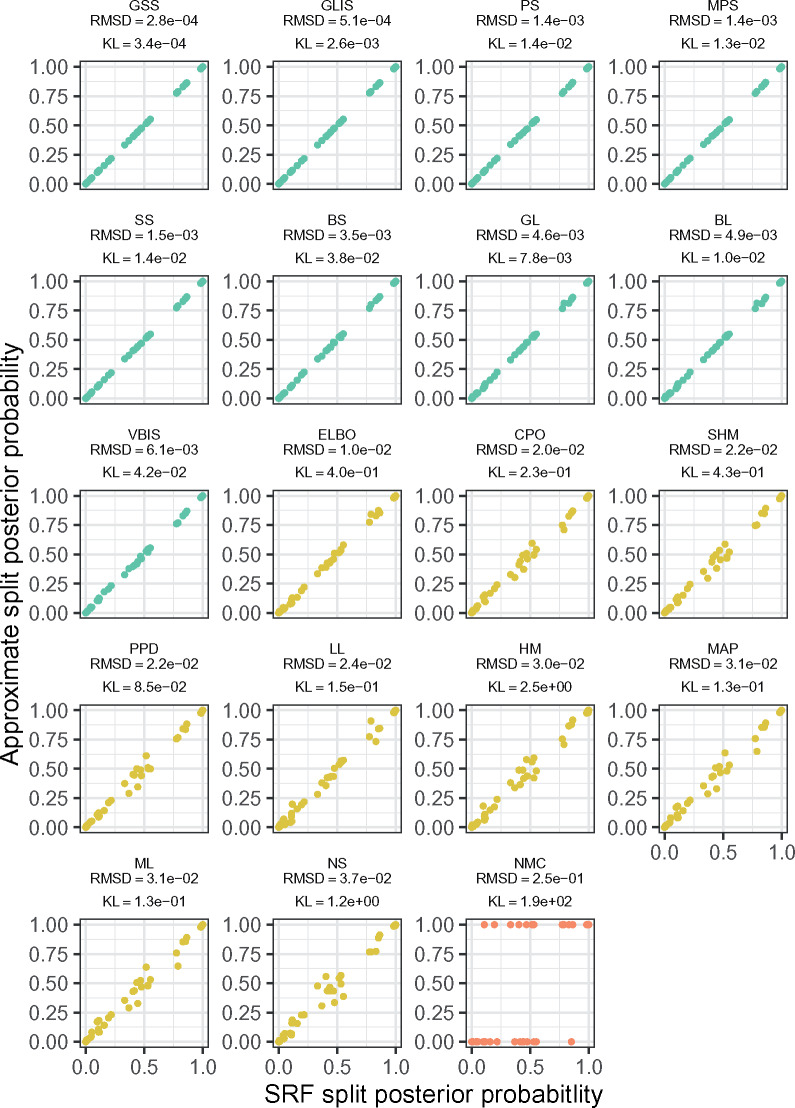
When comparing multiple replicate MCMC analyses (multiple runs), a standard metric in phylogenetics is the average standard deviation of split frequencies (ASDSF). Typically an ASDSF below 0.01 is taken to be evidence that two MCMC analyses are sampling the same distribution. We use the related (but stricter) RMSD as our measure of approximation error (Fig. 1). By considering the plots of split probabilities organized by their RMSD (Fig. 2, Supplementary Figs. S1–S4), we developed two cutoffs for RMSD to classify method performance. We call methods with RMSD less than 0.01 to be in “good” agreement with ground truth, while we say that methods with RMSD between 0.01 and 0.05 are in “acceptable” agreement. RMSD above 0.05 indicates substantial disagreement between ground truth and estimates. Most of the 19 methods’ estimates fall within these categories consistently across the five data sets. MAP, ML, GL, and BL span the boundary between good and acceptable, while LL spans all three categories. Recall that all methods abbreviations are in Table 1.

Figure 1.

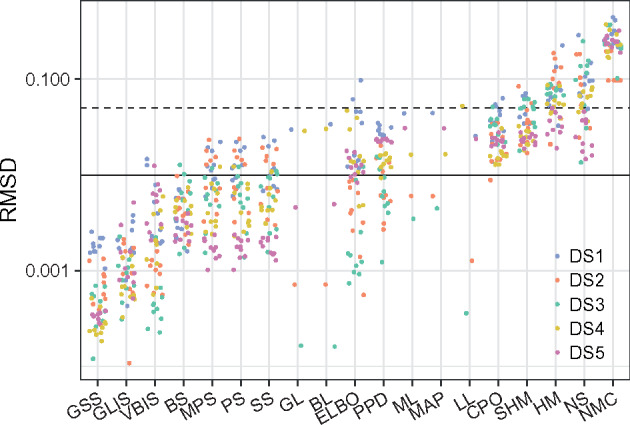
Average split posterior RMSD for 10 replicate runs of each data set. LL, GL, BL, MAP, and ML are deterministic and therefore only one replicate is shown. The horizontal dashed and solid lines depict RMSDs of 0.05 and 0.01, respectively.

Figure 2.

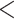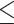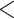The posterior probabilities of all the splits observed in DS5 for a single replicate. MrBayes posteriors are plotted on the x-axis versus the denoted approximation on the y-axis. Points are colored by the thresholds we discuss: RMSD 0.01 is a good approximation (green), 0.01 RMSD 0.05 is a potentially acceptable approximation (yellow), and RMSD 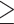0.05 is poor (red). Panels are ordered by RMSD in increasing order.

KL divergence

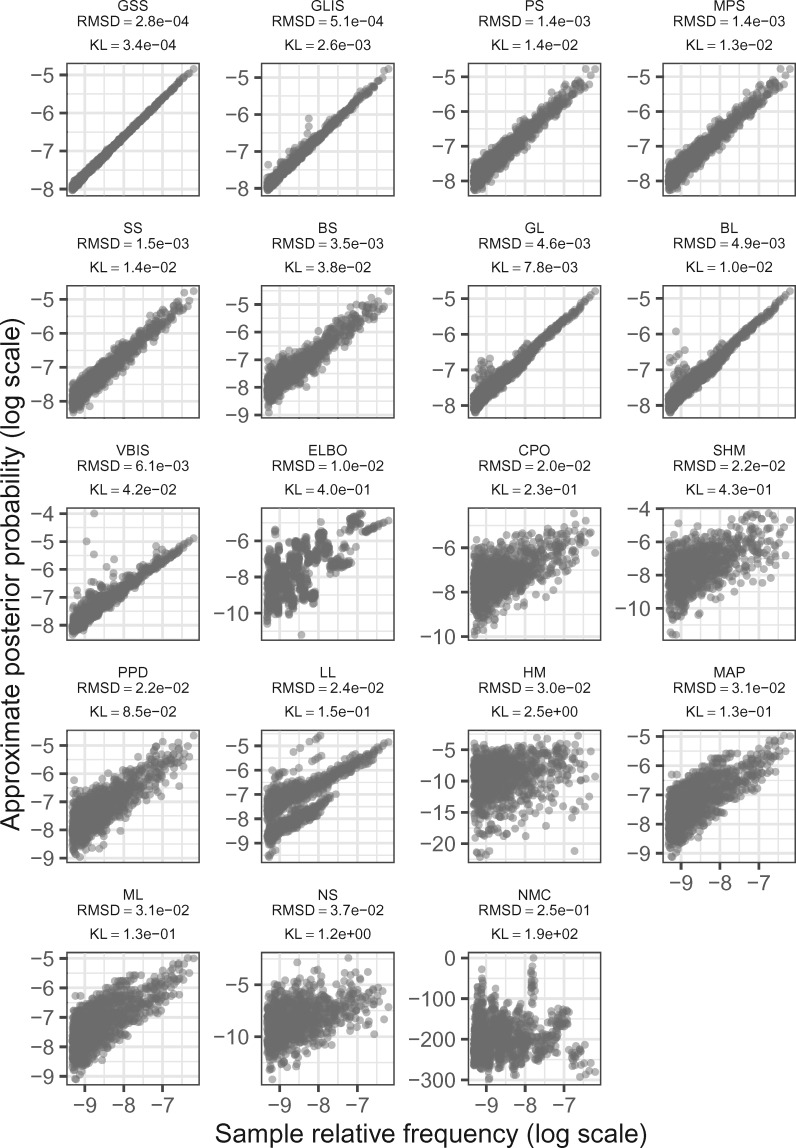
Broadly speaking, there is concordance between the performance of approximations whether measured by KL divergence or RMSD (Figs. 2 and 3). This is expected, as a good approximation should estimate the marginal likelihoods well, which should result in good approximations to the posterior, and thus good estimation of the split probabilities. We also find that the methods do a better job approximating the marginal likelihood of more probable trees than less probable trees (seen as triangular shapes of scatter points in Fig. 3). However, even methods that lead to notable scatter between truth and approximation, such as PPD, can yield quite good estimates of the probabilities of splits. Additionally, if the only quantity of interest is the 50% majority-rule consensus tree, then even methods that estimate the marginal likelihood quite poorly can lead to reasonable trees (Fig. 5). To get the same consensus tree, a method must merely place the same splits in the upper 50% range of posterior probability, so this measure can hide a substantial amount of variability in the estimated marginal likelihoods.

Figure 3.

The approximate posterior probabilities of the topologies in DS5 versus the ground truth posterior probabilities from MrBayes, plotted on the log scale for clarity. The rank-ordering of the methods is closest to average for DS5. Results are for a single run of each method. Panels are ordered by RMSD in increasing order.

Figure 5.

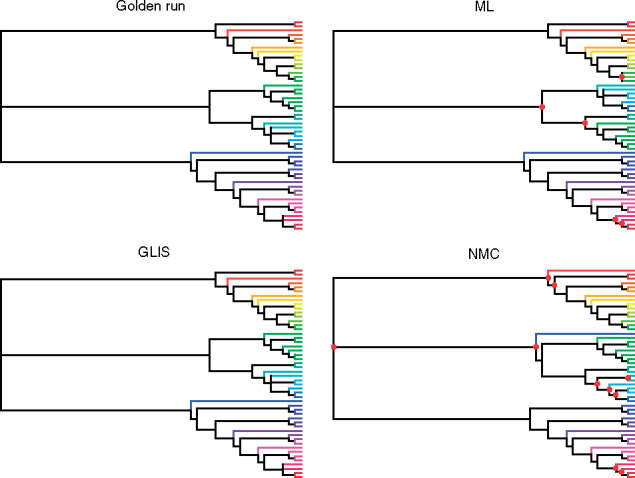
Majority rule consensus trees DS5 based on four sources for posterior probabilities of trees. Each taxon is assigned a unique color and the branch leading to that taxon is colored the same in all four trees to show differences. The golden run and GLIS trees are identical, while the tree for ML has a Robinson–Foulds distance of four to those trees and the tree for NMC a distance 14 (and 10 from the ML tree). Nodes with red circles denote parts of the tree different from the golden run tree.

Speed

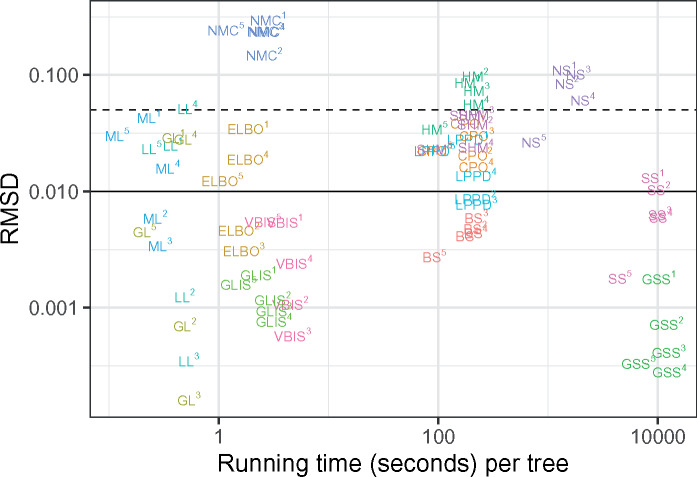
Fast methods can give accurate results, while slow methods need not be accurate (Fig. 4). Indeed, GL is very fast to compute and gives good results, GLIS is only slightly slower and gives excellent results, while NS is slow to compute and gives rather bad results for this problem.

Figure 4.

Average RMSD of splits in the approximate posterior against running time. Text denotes method used, while superscripts label applications to individual data sets. Four methods are omitted for visual clarity: MAP is essentially identical to ML, BL is nearly identical to GL, and PS and MPS are both similar to SS. The horizontal dashed and solid lines depict RMSDs of 0.01 and 0.05, respectively. The RMSD is calculated using the average marginal likelihood of each tree from each of 10 replicate analyses. The running time is calculated using the average running time of each tree from each of 10 replicate analyses.

Method speed is primarily determined by the amount of sampling performed by the method: the more sampling required by a method, the slower it is. The fastest methods are deterministic and do not perform sampling at all, with MAP and ML being the fastest of the 19, requiring only optimization. There is a minor added computational cost of calculating additional derivatives of the phylogenetic likelihood function (here purely the derivatives with respect to branch lengths) in the case of the Laplus approximations. The calculation of the ELBO is slightly slower due to the cost of optimizing the variational parameters through stochastic gradient ascent. The next jump in speed is to methods that perform importance sampling. The single-chain methods are very consistent in time requirements since the computation time is largely dominated by the MCMC. They are notably slower than the importance sampling methods, because MCMC here used one million samples per tree, while we use 10,000 for importance sampling. The slowest methods require running multiple MCMC chains, and aside from GSS time requirements are essentially identical between these methods. We used 50 power posteriors in our analysis of stepping stone and path sampling methods, and as expected we find that they are very nearly 50 times slower than the single-chain methods. The consistency of the number of chains and the time requirement of the method clearly demonstrates that the largest computational effort is in the MCMC. It is worth noting, though, that after an MCMC analysis has run (power posteriors or single chains), any appropriate method can be used to post-process the chains and calculate the marginal likelihood, as MrBayes does with arithmetic and HMs. As an implementation detail of this study, every single-chain method uses the same MCMC samples to estimate the marginal likelihood and similarly, the power posterior-based methods use the same power posterior samples.

Monte Carlo error

No method to estimate the posterior probability of a tree is without sources of error. Monte Carlo error is a feature of all of sampling-based methods we benchmarked, including the methods using at least one MCMC chain and importance sampling methods (marked by asterisks in Table 1). For these methods, and the variational approach (which uses stochastic optimization with noisy gradient estimates and thus also has inter-run variability) we ran 10 replicate analyses (Supplementary Fig. S11). Interestingly, we find that the inter-run variability of the methods is correlated with the goodness of the estimates (and hence the rank-orderings of the methods are similar in Supplementary Fig. S11 and Fig. 1). In discussing how well the methods approximate the posterior distribution of trees, to diminish the effects of Monte Carlo error, we use the average estimated marginal likelihood across the replicate analyses.

Summary trees

The accuracy of summary trees was correlated as expected with the accuracy of the posterior estimate on splits (Fig. 5). We use majority-rule consensus trees (Margush and McMorris 1981), where a split appears in the consensus tree only if it appears in tree topologies whose posterior probabilities sum to at least 0.5. Thus for two approximate posteriors to produce the same summary tree, they must only agree on whether a split probability is above or below this threshold, meaning this is a less sensitive measure of how good an approximate posterior is than RMSD or KL. In Figure 5, we show consensus trees for a subset of methods representing good approximations (RMSD 0.01), acceptable approximations (0.01 RMSD 0.05), and poor approximations (RMSD 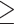0.05) for DS5 for a single run of each method. In this run, every good approximate posterior and most (59%) acceptable approximate posteriors produced a consensus tree identical to the golden run consensus tree. A small portion (25%) of poor approximate posteriors also produced identical consensus trees.

Discussion

In this article, we present the most comprehensive benchmark to date of methods for computing marginal likelihoods of fixed phylogenetic tree topologies. We emphasize that this is a different goal than computing marginal likelihoods when the tree topology is allowed to vary, which has been carefully addressed in previous work (Lartillot and Philippe 2006; Fan et al. 2011; Xie et al. 2011; Baele et al. 2012; Lewis et al. 2013; Baele et al. 2016; Maturana Russel et al. 2018).

A number of estimators we benchmark are well-known to the phylogenetics community, namely power posterior methods (e.g., GSS) and the HM. We also include estimators that have been used less frequently in phylogenetics and are mainly more recent proposals: CPO, NS, and the SHM. Three estimators, BS, PPD, and NMC, to the best of our knowledge, have not previously been used in phylogenetics. Variational approaches have been proposed for models of heterogeneous stationary frequencies (Dang and Kishino 2019), otherwise intractable phylogenetic models (Jojic et al. 2004; Wexler and Geiger 2007; Cohn et al. 2010), and to fit approximations to distributions on trees (Zhang and Matsen 2018), but to our knowledge, this is the first application of the ELBO to phylogenetic model comparison. One goal of this article is to find methods that could work well with MCMC-free tree exploration approaches like PT, which requires evaluating the marginal likelihoods of hundreds or thousands of topologies. Aside from the ELBO, none of the above methods are fast enough to be suitable for this purpose. To this end, we develop the Laplus approximations and importance sampling methods based on Laplus and variational approximations. We also consider simply using the ML and the MAP.

Choosing a method to use in practical scenarios

As expected, methods differ drastically in runtime in proportion to the required Monte Carlo sampling effort. The fastest methods took less than one second per topology on all data sets analyzed, while the slowest took over 10,000. Perhaps surprisingly, there is no general tradeoff between speed and accuracy; while the slowest methods are among the most accurate, there are fast methods that are as good. We break the methods down into four categories: slow, moderately slow, fast, and ultrafast, and will now be reviewing the methods by category—from slow and well-known to fast and novel—highlighting the best performers and their use cases.

At the slow end of the spectrum, we find that the tried-and-true power posterior methods perform quite well, with GSS providing the best (and most precise) estimates of all 19 methods. The boost in performance compared from GSS relative to the other power posterior methods comes at the cost of a marginal increase in computation time due to the estimation and multiple evaluation of the reference distribution. The approximations produced by PS, MPS, and SS are all acceptable (i.e., RMSD 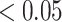), with most of approximations falling into the good category (i.e., RMSD 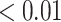), and are similar in terms of speed, accuracy, and precision. We note that balance between speed and accuracy of PS, MPS, and SS can be manipulated by changing the number of power posteriors used by each method (we used 50 in all numerical experiments). For example, reducing the number of power posteriors from 50 to 2–5 may move these methods to the next category of moderately fast but less accurate methods. The power posterior methods remain the best general-purpose tools for phylogenetic model comparisons, though they are too slow to explore the tree space produced by PT even if one uses a small number of power posteriors.

In the middle of the speed axis, we find that BS is the most promising method, with performance that is on par with PS, MPS, and SS. As BS requires an order of magnitude less time than these power posterior-based methods, if it is extended to incorporate sampling trees (perhaps following Baele et al. (2016)) it could become a valuable general-purpose model selection tool. The other estimators in this category span from poor to acceptable. The HM is a very bad estimator of the marginal likelihood, though the related SHM produces posteriors that are acceptable. Two other methods similar in spirit to the HM, CPO (a harmonic sitewise approach) and PPD (a sitewise arithmetic approach), both perform much better than the HM or the SHM. NS would appear to be an unwise choice for estimating the marginal likelihoods of topologies, as it produces poor approximate posteriors. We note that this is a somewhat different application of NS than the recent work by Maturana Russel et al. (2018), who report better results of using NS when averaging over (ultrametric) trees.

GLIS is the best fast method, and one of the best among the 19. With 10,000 samples, it produces estimates of the marginal likelihood on par with GSS, while working three orders of magnitude more quickly. VBIS produces marginal likelihoods almost as good but is somewhat slower. The ELBO, while faster than either GLIS or VBIS (which uses the variational approximation as the importance distribution) is notably worse. It is possible that this approach suffers from getting stuck in local minima, and that multiple starting points could improve its performance, and consequently the performance of VBIS. The worst method in this speed category with regards to accuracy, indeed of all 19 methods, is NMC.

Among the ultrafast methods, the best candidate is GL. All the Laplus approximations are capable of yielding quite good estimates of the posterior distribution on trees, though they are quite variable in performance between methods, and LL can produce poor approximate posteriors. MAP and ML are faster than any of the Laplus approximations, but are not as good. However, the success of all of these methods is truly remarkable. Empirical posterior distributions on branch lengths are clearly not point-masses, and yet simply normalizing the unnormalized posterior at the maximum outperforms 6 of the 19 tested methods. The success of the Laplus approximations suggests that our assumption of independence of branch lengths may not be too unreasonable, though their rather large inter-data set variability and the improvement from importance sampling (i.e., GLIS) suggest that relaxing this assumption may improve performance.

Future directions

We restricted ourselves here to fixed-topology inference under the simplest substitution model. Future work should generalize beyond this simplest model to obtain a marginal likelihood across all continuous model parameters for more complex substitution models, time trees, coalescent priors, and rate heterogeneity across sites. We note that some of the methods presented in this study (e.g., GSS, SS, PS) already implement marginal likelihoods for such models in software packages (Ronquist et al. 2012; Baele et al. 2016; Suchard et al. 2018). More sophisticated models such as those based on the Dirichlet process, which do not have a likelihood function analytically available, are categorically more difficult (Lartillot and Philippe 2004).

Another direction for future work is to investigate the effect of modeling correlation between model parameters, including among branch lengths. Although our preliminary results suggest that correlation between branch lengths is not strong, this assumption is not likely to hold for other parameters in more sophisticated models, such as the coalescent model in which the tree height/length is likely to be positively correlated with parameters governing population dynamics.

In this study, we used i.i.d. exponential priors on branch lengths, which are the historically most common choice for Bayesian phylogenetics. This prior is known to induce an informative prior on the tree length favoring long trees (Rannala et al. 2011; Zhang et al. 2012). This work has not clearly established that the resulting branch length artifacts meaningfully change the posterior distribution of phylogenetic tree topology splits, so our use of i.i.d. exponential priors should not affect significantly split probability estimates. Nevertheless, in future work, we will adapt our approximation methods to handle more sophisticated priors such as the compound gamma-Dirichlet prior (Zhang et al. 2012). This will not be entirely trivial: independence between branch lengths is necessary in order to approximate the posterior distribution using the mean-field variational Bayes and the Laplus methods described in this study. However, such an extension will also have the benefit of relaxing the assumption of a priori branch lengths independence.

Another future research avenue is to find some way to reduce the inter-data set variability of the Laplus approximations. While this class of methods does very well on some data sets, in others there is a subset of topologies that present difficulties, possibly due to short branches with odd posterior distributions. The problems of identifying these branches and what to do with them remain open, but solving them may greatly improve the performance of the Laplus approximation.

For fixed topology models, our results suggest BS is an accurate estimator that does not require as much compute time as the power posterior-based methods. To apply this method more broadly to the phylogenetic field we must develop novel BS proposal distributions, perhaps modeling correlation between parameters other than branch lengths, and more importantly proposals that sample a variety of tree topologies. However, there has been some work on developing approximations of the posterior probability of trees (Höhna and Drummond 2011; Larget 2013; Zhang and Matsen 2018), notably within the GSS framework (Baele et al. 2016).

Another avenue for research would be to develop a diagnostic to determine an appropriate number of power posteriors that is required to accurately estimate marginal likelihoods. Preliminary analyses have shown that the estimates calculated from 100 power posteriors were similar to estimates using 50 steps, it is however possible that fewer steps would be sufficient. Indeed, if the working distribution of the GSS estimator is a good approximation of the true posterior, GSS is expected to perform better than the stepping stone and path sampling estimators for a lower number of power posteriors (Fan et al. 2011).

Perhaps more enticing, though, is the prospect of integrating one of the fast or ultrafast methods with PT. PT currently uses ML—the fastest method of the 19—because speed is important, but GL is comparable in speed, while producing much better marginal likelihood estimates, so its inclusion in PT is worth investigating. For the added time cost of drawing samples and calculating additional likelihoods, GLIS achieves an even more impressive estimate of the marginal likelihood than GL. However, given that PT explores far more trees than it eventually stores, this added time cost is almost certainly prohibitive, unless the number of importance samples can be drastically reduced. Nonetheless, once PT has found a set of high-likelihood trees, it seems prudent to use GLIS on this set to produce the final approximate posterior.

Funding

This work was supported by the National Science Foundation [DMS-1223057, CISE-1561334, CISE-1564137] and the National Institutes of Health [U54-GM111274]. The research of FAM was supported in part by a Faculty Scholar grant from the Howard Hughes Medical Institute and the Simons Foundation. Computational facilities were provided to MF by the UTS eResearch High Performance Computer Cluster. The research of CW was supported as a Simons Foundation Fellow of the Life Sciences Research Foundation.