SUMMARY
Although the major events in prokaryotic cell cycle progression are likely to be coordinated with transcriptional and metabolic changes, these processes remain poorly characterized. Unlike many rapidly growing bacteria, DNA replication and cell division are temporally resolved in mycobacteria, making these slow-growing organisms a potentially useful system to investigate the prokaryotic cell cycle. To determine whether cell-cycle-dependent gene regulation occurs in mycobacteria, we characterized the temporal changes in the transcriptome of synchronously replicating populations of Mycobacterium tuberculosis (Mtb). By enriching for genes that display a sinusoidal expression pattern, we discover 485 genes that oscillate with a period consistent with the cell cycle. During cytokinesis, the timing of gene induction could be used to predict the timing of gene function, as mRNA abundance was found to correlate with the order in which proteins were recruited to the developing septum. Similarly, the expression pattern of primary metabolic genes could be used to predict the relative importance of these pathways for different cell cycle processes. Pyrimidine synthetic genes peaked during DNA replication, and their depletion caused a filamentation phenotype that phenocopied defects in this process. In contrast, the inosine monophasphate dehydrogenase dedicated to guanosine synthesis, GuaB2, displayed the opposite expression pattern and its depletion perturbed septation. Together, these data imply obligate coordination between primary metabolism and cell division and identify periodically regulated genes that can be related to specific cell biological functions.
In Brief
Bandekar et al. find that mycobacterial cell cycle progression is associated with transcriptional remodeling, which predicts the timing of gene function. This property can be used to order the assembly of multi-protein complexes and to associate primary metabolic pathways with major cellular events, such as DNA replication and cytokinesis.
INTRODUCTION
Much of prokaryotic cell biology has been elucidated under rapid growth conditions in which chromosomal replication takes longer than the doubling time of the cell [1, 2]. Under these conditions, the production of complete chromosomes for daughter cells is ensured via the simultaneous initiation of multiple rounds of DNA replication, and it is not possible for cells to segregate DNA replication from cytokinesis. However, this paradigm might not apply to many bacteria in the environment. For example, Caulobacter crescentus exploits a developmental program that produces distinct sessile and motile cells, which is associated with a strict cell cycle that segregates DNA replication from cytokinesis. More generally, most bacteria in their natural, nutrient-poor environments persist in slow-growing states [3]. When these conditions are modeled in nutrient-restricted Escherichia coli, major cellular events become restricted into distinct cell cycle periods B, C, and D, which are analogous to G1, S, and G2 in eukaryotic organisms [4, 5].
The prokaryotic cell cycle has been most thoroughly studied in C. crescentus, largely because it is possible to produce cultures in which cells are replicating synchronously with respect to the cell cycle. In this organism, cell cycle progression is controlled by a regulatory cascade [6, 7] that is conserved across the alphaproteobacteria [8] and is associated with the periodic expression of almost 20% of the genome. In addition to genes that directly control this process, a variety of metabolic pathways are also regulated in a cell-cycle-dependent manner. This apparent link between metabolism and cell cycle is supported by the oscillation of metabolites, such as nicotinamide adenine dinucleotide phosphate [NAD(P)H] [9] and adenosine triphosphate (ATP), [10] during the cell cycle in E. coli and the ability of uridine diphosphate glucose (UDP-glucose) levels to influence cell division timing in B. subtilis [11] and E. coli [12]. Although these data suggest that cell cycle progression is likely coupled to metabolism, it remains unclear how these processes interact and whether insights from transcriptional profiling in C. crescentus are generalizable to more diverse bacteria.
We sought to extend these paradigms to mycobacteria, a diverse genus that contains both saprophytic species and important human pathogens, such as Mycobacterium tuberculosis (Mtb). Time-lapse microscopy studies show that these organisms constitutively employ a segregated cell cycle where DNA replication occurs only once per cycle in the majority of cells [13–17]. The average duration of the G1, S, and G2 periods in Mtb range from 6 to 8 h, 9 to 12 h, and 6 to 9 h, respectively [18]. These observations are supported by metabolic labeling studies in synchronously replicating cultures of Mtb, which can be generated by using a mutant strain that harbors a cold-sensitive (cos) allele of the DNA replication initiator DnaA [19]. This Mtbcos strain is unable to initiate DNA replication at 30°C. Upon release into the permissive temperature (37°C), cultures synchronously incorporate radiolabeled nucleotides into DNA for 11 h, consistent with the S period observed in single cells. The ability to produce synchronously replicating cultures that recapitulate the behavior of single cells makes mycobacteria an attractive system to investigate the cell cycle.
Using the Mtbcos strain, we determined the transcriptional profile of synchronously replicating Mtb across the cell cycle and report that 485 genes are periodically expressed. Only a small fraction of the cell-cycle-regulated gene sets of Mtb and C. crescentus overlap, suggesting species-specific transcriptional programs. We demonstrate that mRNA expression patterns in Mtb reflect the time at which the encoded proteins are incorporated into the developing septum, suggesting that functional information can be inferred from the kinetics of gene expression. Using this framework, we discover that disruption of different nucleotide anabolic pathways primarily affects distinct cellular processes. These observations show that DNA replication and cytokinesis are coordinated with different primary metabolic pathways, expanding the processes that are required for these essential cellular events.
RESULTS
DNA Replication and Cytokinesis Are Segregated in Synchronously Growing Mtb
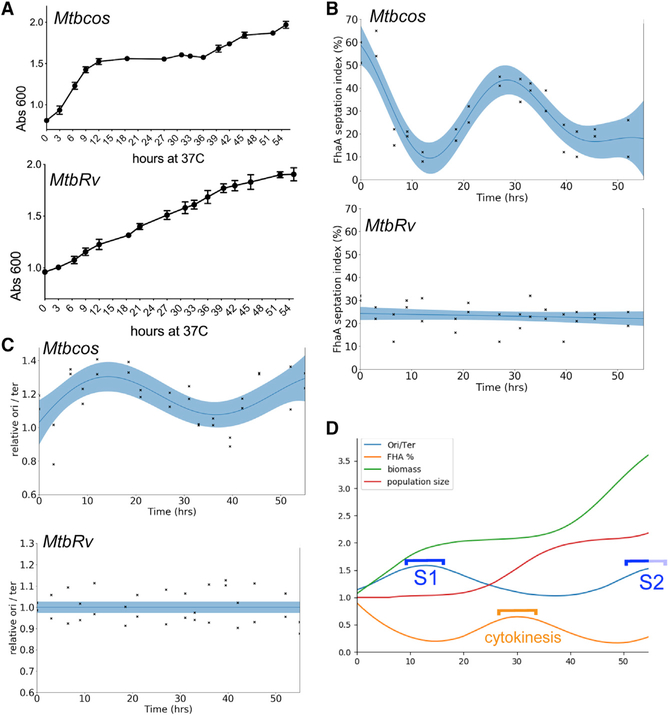
We generated synchronously replicating cultures of Mtb by using the temperature-sensitive Mtbcos strain [19]. Chromosomal replication was inhibited by incubating this strain at 30°C for 36 h. Upon shift to the permissive temperature (37°C), the optical density (Absorbance600) of a parallel unsynchronized culture of strain H37Rv (MtbRv) increased at a constant rate over a 54-h time course, demonstrating that nutrients did not become limiting. Mtbcos showed a reproducible multiphasic growth pattern, an initial indication that cellular metabolism might be linked to cell cycle events (Figure 1A).
Figure 1. DNA Replication and Cytokinesis Are Segregated in Synchronously Growing Populations of Mycobacterium tuberculosis.
(A) Growth of Mtbcos (top) and MtbRv (bottom) after release into permissive temperature, 37° C. × axis, hours at 37° C. y axis, Absorbance600. Data are represented as mean ± SD of two biological replicates.
(B) FhaA septation index assay to determine cytokinesis phase. Percentage of Mtbcos (top) and MtbRv (bottom) populations containing an FhaA-venus focus at midcell after release into permissive temperature is shown. Data points indicate two biological replicates (average number of cells analyzed at each time point = 82). Blue line is obtained via Gaussian process smoothing. The blue band indicates 95% confidence interval. Significant difference between Mtbcos and MtbRv curves was determined by using a likelihood ratio test, which determines whether the data are fit best by a combined model (null hypothesis) or separate strain-specific models (alternate hypothesis). ΔLog_likelihood (combined-separate) = −38.489; p (χ2 distribution; df = 3) = 1.1e–16.
(C) Origin/terminus assay to determine the DNA replication phase. Relative ori/ter ratio of Mtbcos (top) and MtbRv (bottom) populations after release in permissive temperature is shown. Data points indicate two biological replicates and are representative of three independent studies. ΔLog_likelihood (combined-separate) = −12.412; p (χ2 distribution; df = 3) = 1.679e–05.
(D) Discrete time simulation of the cell cycle in Mtbcos. The curves were generated from mean cell attributes created by sampling cell cycle parameters for each cell from Gaussian distributions, using parameters that maximized correlation with empirical data. Correlation coefficients were as follows: OD = 0.9189; ori/ter = 0.9561; fhaA = 0.9614. The lighter portion of the S2 bracket indicates assumed completion of the second S phase.
In order to estimate the efficiency of the synchronization and to delineate cell cycle periods, we monitored chromosomal replication and cytokinesis over time. The phosphothreonine-binding protein, FhaA, marks sites of division [20], and we used a fluorescent allele of this protein to calculate a “septation index” that corresponded to the fraction of cells with FhaA at midcell. Although the septation index of an asynchronous MtbRv culture was constant throughout the time course, this metric varied in a periodic manner in Mtbcos. The majority of cells arrested at the non-permissive temperature had an FhaA focus at midcell, which is likely an artifact of the DnaA inactivation. The septation index of Mtbcos quickly decreased upon shift to the permissive temperature, falling below that of unsynchronized cultures by 12 h. Septation reached a peak in Mtbcos between 27 and 33 h post-release (HPR), marking cytokinesis (Figure 1B).
To monitor chromosomal replication, we quantified the relative abundance of DNA at the origin (ori) and terminus (ter) of replication. Upon initiation of replication, the ori:ter ratio is 2:1, and this ratio is maintained until the terminus is duplicated (ori:ter = 1:1). As we observed for septation index, ori:ter ratio remained constant in unsynchronized cultures. In contrast, the ori:ter ratio peaked twice in synchronized cultures (Figure 1C). The first peak lasted for approximately 12 h (between 15 and 27 HPR) and second one lasted between 48 HPR and the end of the study. On the basis of these data, we estimate that our time course captured ~1.5 cell cycles. Both the septation index and ori:ter varied by approximately 50% of the range expected of fully synchronized cells, indicating that the synchrony of our cultures was incomplete.
In order to characterize cell cycle dynamics in the synchronized cultures, we created a computational model that incorporated cell growth, division, and each of the measured values (optical density [OD], septation index, and ori:ter). Using a systematic search over parameter combinations, we identified an optimal set of values for a model that correlated with the experimental data (Figure 1D). Incomplete synchronization resulted from deriving parameters via random sampling of Gaussian distributions. This produced variation in cell cycle initiation, S phase duration, and cell cycle length. Our model produced dispersion in the predicted ori:ter (~8–20 HPR) and septation index (~25–35 HPR) peaks, which resembled experimental observations. This modeling confirmed that DNA replication is temporally separated from cytokinesis, and the cultures were sufficiently synchronized to perform transcriptional profiling.
Periodic Gene Expression Correlates with Cell Cycle Progression
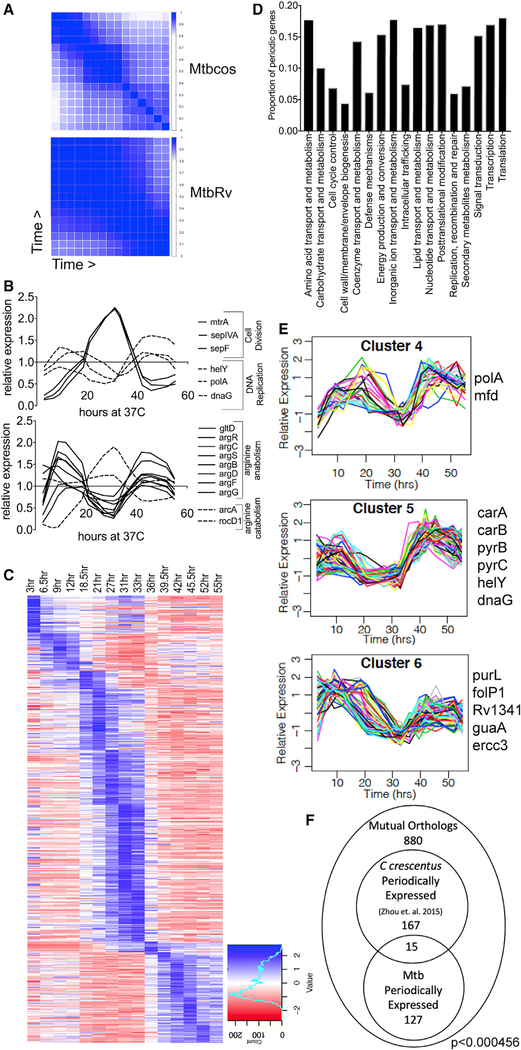
To investigate whether gene expression changes are associated with major cellular events like DNA replication and cytokinesis, we profiled mRNA abundance in synchronized cultures every 3 h across a 54-h time course. Cells were collected and processed for RNA extraction within 5–7 min, which is less than the 9.5-min average mRNA half-life in Mtb [21]. We first assessed correlation patterns in the dataset. The initial time point after temperature shift to 37°C (0 h) was uncorrelated with the rest of the dataset, presumably due to the temperature shift, and was omitted. To minimize the effects of minor changes in culture conditions over time, we first removed 50 genes that had highly correlated (>0.9) expression patterns in synchronized Mtbcos and a parallel unsynchronized culture of MtbRv. Additionally, we removed 182 genes whose expression changed substantially in MtbRv over the time course (Data S2). These transcriptional trends included an increase in expression of the redox-sensitive dosR regulon [22] and nitrate reductase (narG and narX) and a decrease in several functions associated with growth (e.g., ATP synthase, cytochrome components qcrB and cydA, and mycolate synthesis). For the remaining data, we found the highest degree of correlation between adjacent time points, as expected for a time-resolved dataset (Figure 2A). Although the transcriptional profiles of the unsynchronized cultures remained relatively consistent over time, the correlation matrix from the Mtbcos cultures suggested the presence of transcriptionally distinct phases that could not be explained by changes in culture conditions. This structure is even more apparent upon hierarchical clustering, which revealed an ordered progression of gene expression throughout the time course (Figure S1A).
Figure 2. Periodic Gene Expression Correlates with Cell Cycle Progression.
(A) Correlation matrix of DESeq2 normalized counts for single replicates of Mtbcos (top) and MtbRv (bottom) for all 16 time points (blue, Pearson’s correlation coefficient = 1; white, Pearson’s correlation coefficient = 0).
(B) Relative expression (GP smoothed, DESeq2 normalized read count for each time point divided by the mean value for that gene across time) of genes involved in DNA replication and cell division (top panel); arginine catabolism and anabolism (bottom panel).
(C) Relative expression (standard normalized DESeq2 counts—each value is subtracted by the mean for that gene across time and then divided by the standard deviation) of 485 periodically expressed genes in Mtbcos (rows) sorted by peak expression time (columns).
(D) Fraction of periodically expressed genes present in different Gene Ontology categories.
(E) Clusters containing periodic genes with expression patterns consistent with a role in DNA replication. Known DNA replication and/or nucleotide biogenesis genes found in these clusters are listed.
(F) Overlap between periodically expressed Mtbcos and C. crescentus mutual orthologs. p value indicates significant overlap between the two gene sets determined by using a hypergeometric test.
See also Figures S1 and S2, Tables S1 and S2, and Data S1, S2, and S3.
To take advantage of both replicate measurements and the relatedness of adjacent time points, we used Gaussian process (GP) smoothing to estimate the relative expression level of each gene across the time course (Figure S1B). The expression of genes with cell-cycle-related functions was found to peak during the appropriate period. For example, genes important for cell division, such as the regulator, mtrA [23], or the septal components, sepF [24] and sepIVA [25], peaked during cytokinesis. Similarly, genes important for DNA replication, such as those encoding DNA primase (dnaG) and the replicative polymerase (polA) displayed peaks corresponding to DNA replication (Figure 2B). In addition, we found that the expression pattern of several primary metabolic pathways mirrored these cell-cycle-related genes. For example, genes necessary for arginine biosynthesis were co-regulated and had opposing expression patterns to genes involved in arginine catabolism (Figure 2B).
In order to formally define genes with expression patterns consistent with cell cycle progression, we fit the expression profile of each gene to a sinusoidal function with the expected period of the Mtb cell cycle, optimizing the parameters for trend, amplitude, period, and phase. Genes with a period outside the range of reasonable expectations based on the Mtb cell cycle were omitted (27.5 h < period < 55 h), along with poorly expressed genes (mean expression < 0.25). A goodness-of-fit criterion based on curve-fitting residuals was applied, which maximized the difference in genes discovered in synchronized versus unsynchronized cultures. These criteria produced a false discovery rate of 0.35% by using a permuted dataset and 2.6-fold enrichment for genes in the synchronized cultures. 485 genes were categorized as periodically expressed (Figure 2C; Data S3), which represented all major functional categories (Figure 2D).
Hierarchical clustering this set of periodically regulated genes further highlighted the association between gene function and cell cycle. Genes were distributed into 8 clusters on the basis of Mtbcos expression profiles (Figure S2), producing groups of coordinately regulated genes with peak expression values ranging across the time course. Three clusters (Figure 2E) containing 158 genes peaked in expression during DNA replication. Of the 20 periodically expressed genes annotated to be involved in DNA or nucleotide metabolism, 13 were found in these three clusters. The enrichment of DNA- and nucleotide-associated genes in these clusters (p = 0.002) served as an initial indication that mRNA abundance could be associated with gene function.
The periodically regulated gene set of Mtb represents 12% of the genome, whereas between 9.5% and 19% of the chromosomal genes of the α-proteobacteria Sinorhizobium meliloti [26] and C. crescentus [6, 27] were found to be cell cycle regulated. We compared our set of Mtb periodic genes with orthologs from the most analogous previous analysis. Out of the 880 mutual orthologs identified as reciprocal best BLAST matches, 182 genes were defined as cell cycle regulated in C. crescentus [27] and 142 were periodically expressed in Mtb, and there was an overlap of 15 genes (Figure 2F; Table S1). This overlap contains genes with possible cell-cycle-associated functions, such as the DNA replication initiator, dnaA; the nucleoid-associated protein, hupB/ihfA; the regulator of ribonucleotide reductase, nrdR; and a regulator of cell wall homeostasis, htrA [28]. Although this similarity was statistically significant (p < 4.56e–04), the modest degree of overlap suggests that these two phylogenetically distinct organisms possess different transcriptional networks. This observation is consistent with the modest overlap of only 28% between cell-cycle-regulated gene sets defined even in the much more phylogenetically similar species, C. crescentus and S. meliloti [26].
Periodic gene expression studies in C. crescentus led to the elucidation of a conserved cascade of transcription factors (TFs) that control cell cycle progression [7, 29]. Similarly, we found that 39 of the 206 TFs of Mtb [30] were periodically expressed (Table S2). These included mtrA, a component of the septally localized MtrAB regulator that contributes to cell division [23]; parD1, a homolog of parD that is necessary for chromosome partitioning in E. coli [31]; and argR, the repressor of the arginine synthetic operon that is cell cycle regulated (Figure 2B). In addition, transcripts encoding the nucleoid-associated proteins, Hns and HupB, were found, suggesting cell-cycle-associated changes in chromosomal structure. Although these observations implicate several DNA-binding proteins in cell cycle control, the high degree of correlation in our time series data precluded the association of specific TFs with downstream regulons.
mRNA Abundance Predicts the Order of Divisome Assembly
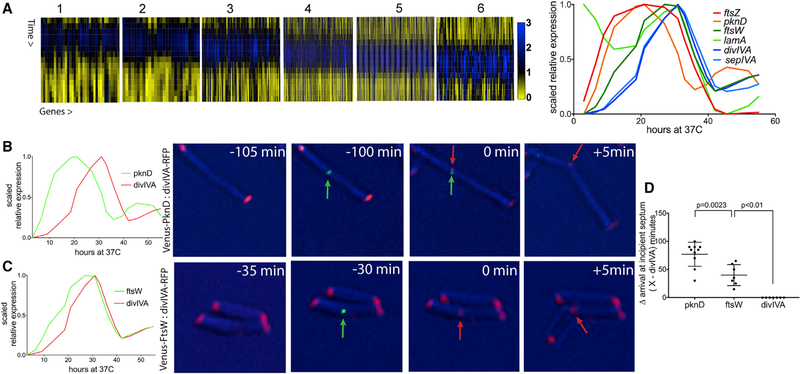
The order in which large multicomponent structures, such as the flagellum, are assembled in bacteria can be predicted based on the expression of the corresponding transcripts [32]. Consistent with this “just in time” transcription model [33], the large complex of proteins necessary for cell division, the “divisome,” assembles in an ordered fashion in C. crescentus [34]. We hypothesized that divisome assembly in mycobacteria might follow the same principles and provide a system to determine whether mRNA abundance could be used to predict the timing of gene function. To test this model, we assessed the temporal coincidence between mRNA abundance and protein localization at the developing septum.
We identified genes that peak in expression only once between 22 and 38 HPR, consistent with a role in cytokinesis (Data S3). We then clustered these genes on the basis of similar expression patterns (Figure 3A). Within these clusters, we found a number of genes known to be involved in cytokinesis (Figure 3A). To avoid selection biases, we compiled a list of 22 known septation-associated genes [24, 25, 35–37] and found that 13 of these passed our filters for expression level and were found in one of these clusters (Figures 3A and S3). The expression patterns of characteristic genes are shown in Figure 3A. The first to be induced was ftsZ, the tubulin-like nucleator of the septum. This peak was followed sequentially by mRNAs encoding the septally localized Ser/Thr kinase, PknD; the divisome-associated FtsW, SepIVA, and LamA proteins; and the new pole landmark protein, DivIVA. To determine whether the timing of expression predicts the order of assembly, we chose three genes with different expression peaks within the cytokinesis window—pknD (early), ftsW (middle), and divIVA (late). Pairs of these proteins were fused with fluorescent tags and expressed from constitutive promoters so that the order of assembly at the septum could be observed independently of transcriptional regulation. The cellular location of these protein fusions was then determined in M. smegmatis, a related mycobacterial species that expresses orthologs of these proteins and is an experimentally tractable model of mycobacterial division [13, 16, 38]. Time-lapse imaging revealed that PknD, FtsW, and DivIVA appear at the developing septum in the order predicted by mRNA abundance (Figures 3B–3D), indicating that transcript level could be used to predict the timing of gene function at the developing septum.
Figure 3. mRNA Abundance Predicts the Order of Assembly of Mycobacterial Divisome Components and Regulators.
(A) (Left) Clusters of Mtbcos genes with expression patterns that peak during the cytokinesis period. (Right) Scaled relative expression of known cytokinesis genes from these clusters is shown.
(B) (Left) Scaled relative expression of PknD and DivIVA. (Right) Time-lapse imaging of M. smegmatis expressing PknD-Venus (green) and DivIVA-RFP (red) is shown. Time (minutes) before the arrival of DivIVA at midcell is indicated.
(C) (Left) Scaled relative expression of FtsW and DivIVA. (Right) Time-lapse imaging of M. smegmatis expressing FtsW-Venus (green) and DivIVA-RFP (red) is shown.
(D) Time (minutes) between initial arrival of PknD (n = 10), FtsW (n = 7), and DivIVA at midcell. Error bars indicate mean ± SD. Statistically significant difference between pknD and ftsW determined by using an unpaired t test is shown (α = 0.05; p = 0.0023). Statistically significant difference between ftsW and divIVA determined by using a chi-square test is shown (α = 0.05; χ2 = 7; df = 1; p < 0.01).
Guanosine Synthesis Influences Cytokinesis
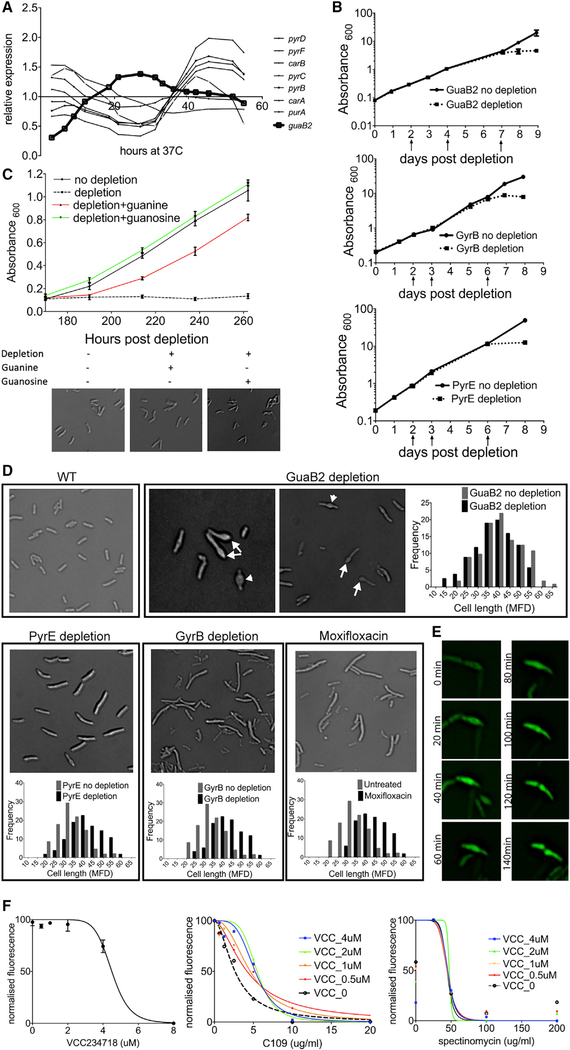
Having demonstrated that gene expression can predict the timing of gene function, we investigated whether coordination exists between cellular events, such as DNA replication and cytokinesis, and upstream pathways that produce the precursors for these processes. In particular, we focused on nucleotide metabolism by analyzing the expression patterns of enzymes that produce the nucleobase rings. In order to focus specifically on nucleotide anabolism, we did not consider reactions that require amino acid donors, because we could not rule out roles for those enzymes in amino acid metabolism. Pyrimidine biogenesis, from the early stages of the carAB-encoded reactions to the later pyrBCDEF-encoded reactions, was most highly expressed during S phase (Figure 4A), consistent with previous reports of increased de novo synthesis during DNA replication in E. coli [39, 40]. Unexpectedly, expression of guaB2, encoding the IMP dehydrogenase that catalyzes the first reaction dedicated to guanosine synthesis, peaked during cytokinesis (Figure 4A). Genes dedicated to synthesizing adenosine from IMP, purB and amk, did not appear to be cell cycle regulated.
Figure 4. Guanosine Synthesis Influences Cytokinesis in Mycobacteria.
(A) Relative expression of IMP dehydrogenase guaB2 compared with that of pyrimidine biosynthesis genes carA, carB, pyrB, pyrC, pyrD, and pyrF.
(B) Cumulative growth (Absorbance600) of M. tuberculosis guaB2-DAS (top), gyrB-DAS (center), and pyrE-DAS (bottom) without depletion (solid line) and with depletion (dotted line). Arrows indicate the time during the pre-depletion period when cultures were diluted into fresh growth medium. Data are represented as mean ± SD of two biological replicates.
(C) Growth (Absorbance600) and morphology of M. tuberculosis guaB2-DAS ± depletion in the presence of either 200 μM guanine or guanosine. Absorbance data are represented as mean ± SD of two biological replicates.
(D) M. tuberculosis cellular phenotypes upon genetic depletion of GuaB2, PyrE, and GyrB. Images were obtained after the cessation of growth in depleted cells. In the case of GuaB2, septal bulges (arrowheads) and polar bulges (arrows) are indicated. Histograms indicate the cell length distribution of cells in which the target was either not depleted (gray) or depleted (black). Mtb was treated with 0.2 μM moxifloxacin for 24 h and imaged. Histograms indicate the cell length distribution of cells in untreated (gray) or treated cells (black). MFD, Maximum Feret Diameter (1 μm; ~0.11 MFD). Statistically significant/non-significant difference between the cell length distributions was determined by using the Mann-Whitney test (pguaB2 = 0.214; ppyrE < 0.001; pgyrB < 0.001; pmoxifloxacin < 0.001).
(E) Time-lapse imaging at 20-min intervals of GFP-expressing M. smegmatis treated with 2 μM VCC234718.
(F) Susceptibility of M. smegmatis to VCC234718. Data are represented as mean ± SD (left). Cross titration assay on GFP-expressing M. smegmatis with the indicated concentrations of VCC234718 alone (left), with C109 (center), or with spectinomycin (right) is shown. Statistically significant difference between the curves was determined by using an extra-sum-of-squares F-test (α = 0.05). VCC alone curve was significantly different from each of the VCC+C109 curves, p(VCC 0.5 μm) = 0.0215; p(VCC 1 μM) = 0.0284; p(VCC2 μM) = 0.0001; p(VCC4 μM) = 0.0019.
VCC alone and VCC+spectinomycin curves were not significantly different, p(VCC0.5 μM) = 0.9989; p(VCC1 μM) = 0.9999; p(VCC2 μM) = ambiguous; p(VCC4 μM) = 0.9978.
See also Data S3.
The reciprocal expression patterns of pyrimidine and guanosine synthetic genes suggested that the requirement for these metabolites was associated with distinct cellular events.
To investigate this hypothesis, we generated mutant Mtb strains in which synthesis of pyrimidines or guanosine was inhibited via the inducible depletion of PyrE or GuaB2. Each gene was fused to a C-terminal DAS+4 tag (DAS) that facilitated Clp protease-mediated degradation upon removal of anhydrotetracycline (aTc) [41]. In both cases, protein depletion inhibited bacterial growth (Figure 4B), consistent with the essentiality of these pathways [42]. As Mtb expresses three GuaB paralogs, we verified that GuaB2 is essential for guanosine synthesis by metabolite supplementation. Consistent with previous studies [43], guanine partially rescued the growth defect of the guaB2-DAS strain, whereas guanosine led to complete rescue (Figure 4C).
The inverse expression patterns of pyr genes and guaB2 implied that increased de novo synthesis of pyrimidine nucleotides and guanosine was preferentially required for DNA synthesis or cytokinesis, respectively. We used morphological criteria to infer which cellular process was primarily impacted by the inhibition of these pathways. PyrE depletion resulted in cell elongation prior to growth arrest (Figure 4D). A similar phenotype was observed upon DNA gyrase GyrB depletion and in cells treated with the gyrase-inhibiting fluoroquinolone, moxifloxacin (Figure 4D), which disrupts DNA replication and causes cell filamentation in E. coli [44]. Thus, pyrimidine depletion causes cell elongation upon inhibition of DNA replication, a phenotype consistent with previous observations in B. subtilis [45] and mycobacteria [46, 47].
In contrast, GuaB2-depleted cells were the same length as wild type, but many of these growth-arrested cells had bulges at midcell or one pole, suggesting that GuaB2 depletion might influence cell division (Figure 4D). This morphological phenotype did not occur in guanine- or guanosine-supplemented growth conditions, verifying that it was due to metabolite depletion (Figure 4C). To determine whether the polar bulges were derived from misshapen septa, we performed time-lapse microscopy in M. smegmatis cells treated with a chemical inhibitor of GuaB2 (VCC234718). Chemical inhibition of GuaB2 also inhibited growth and produced bulges at midcell or one pole (Figure 4E). Time-lapse microscopy revealed that VCC234718-treated cells began to bulge at midcell by the completion of 1 to 2 cell cycles, and misshapen poles were derived from these bulges. These observations imply that the cellular requirement for guanosine increases during cytokinesis and that this requirement is reflected in the aberrant septation of guanosine-depleted cells.
FtsZ is an abundant protein that binds and hydrolyzes guanosine triphosphate (GTP) [48] as it undergoes the cycles of polymerization and depolymerization necessary for septation [49]. This GTP requirement suggested a mechanism connecting guanosine nucleotide levels and septation. To investigate whether the effect of guanosine depletion on septation could be attributed to altered FtsZ dynamics, we inhibited both processes simultaneously using the GuaB2 inhibitor (VCC234718) and C109, an inhibitor of FtsZ GTPase activity and polymerization [50]. Consistent with the hypothesized mechanistic link, we observed significant interaction between these compounds (Fractional Inhibitory Concentration Index [FICI] = 3.16). Even at concentrations of VCC234718 that alone had no effect on growth (0.5–4 μM), this compound consistently increased the half maximal inhibitory concentration (IC50) of C109 (Figure 4F). In contrast, we found no interaction between VCC234718 and spectinomycin, an inhibitor of another major GTP-consuming pathway, translation (FICI = 1.55).
The specific effect of GTP depletion on FtsZ dynamics can be inferred from the observed antagonistic interaction between C109 and VCC234718. C109 acts additively with PCI90723 [51], a compound that stabilizes the FtsZ filament. The converse antagonistic interaction we observed between C109 and VCC234718 implies that guanosine depletion inhibits polymerization, consistent with the known GTP requirement for FtsZ polymerization [48, 52]. Together, these data are consistent with a model in which transcriptional induction of guaB2 during cytokinesis coincides with the increased consumption of GTP by FtsZ, and the septal defects observed on guanosine depletion are related to defects in FtsZ dynamics.
DISCUSSION
This study represents the first global analysis of cell-cycle-associated gene expression in mycobacteria. Comparisons between our Mtb studies and C. crescentus are limited by a number of technical differences, including the method and degree of synchronization and the timing of cell collection and processing. Biological differences, like the possible unequal effects of mRNA degradation rates on transcript abundance due to vast differences in interdivision time, further limit comparisons. Regardless, we found that a similar fraction of the genome is differentially expressed across the cell cycle in both systems, and a small fraction of orthologous genes are regulated periodically in both. Despite these similarities, the majority of cell-cycle-associated transcriptional changes were unique to each organism, indicating that cell cycle progression is associated with distinct transcriptional networks in phylogenetically divergent organisms.
In a number of cases, we found that increases in mRNA abundance could be used to associate genes with temporally resolved cell cycle events, such as septation. The sequential expression [6] and an ordered assembly [34] of divisome components have independently been observed in C. crescentus. Here, we provide a link between gene expression and function by demonstrating that the timing of gene induction correlates with the recruitment of the encoded proteins. Based on transcriptional data, we inferred the following order of assembly: FtsZ > PknD > FtsW > LamA > SepIVA > DivIVA. The recruitment of these proteins spans sequential processes of divisome assembly, septation, and new pole biogenesis. FtsZ initially marks the division site [53], facilitating the recruitment of divisome components FtsW [54] and SepIVA [25]. The arrival of LamA at the later stages of assembly is consistent with its role in delaying septation to promote asymmetric cell division [35]. DivIVA is recruited to the negative curvature of the new pole after septation [55–57] and the segregation of daughter cell cytoplasm [13]. Additional cell wall synthetic genes (e.g., glfT2 and pks13) were found to peak after DivIVA, which could reflect the delayed elongation of the new pole [58]. These observations indicate that gene expression can be used to predict the order of complex assembly. However, transcriptional regulation is unlikely to be the primary determinant of assembly order, as only a subset of currently known septal components were found to be periodically expressed. Instead, this type of hierarchical gene expression has been proposed as a mechanism to maximize efficiency by restricting protein expression to the period when it is needed [32, 33]. Regulation of divisome assembly and function likely involves additional posttranslational mechanisms, as the Ser/Thr phosphatase, PstP, contributes to cell division [59, 60], and we found that the Ser/Thr kinase, PknD, is recruited relatively early in septal development. Although it remains possible that transcriptional regulation controls some aspects of septation, our data primarily demonstrate that expression pattern can predict the timing of gene function.
The importance of coordinating cell cycle events with the upstream metabolic pathways that provide precursors is supported by our finding that pyrimidine and guanosine synthetic genes are distinct in their expression patterns and in the functional consequences of their depletion. The association we infer between pyrimidine depletion, DNA synthesis inhibition, and cell elongation is supported by a recent study [47] describing similar morphological alterations in M. smegmatis mutants lacking a variety of DNA replication and pyrimidine nucleotide biosynthetic functions. However, the distinct cytokinesis defect observed upon GuaB2 depletion was unanticipated. We speculate that the septation defect we observe upon GuaB2 depletion is related to the relatively low affiniity of FtsZ for GTP. FtsZ has ~500-fold lower affinity for GTP than the DnaE1 replicative DNA polymerase (Km FtsZGTP =1 mM [61]; KmDnaE1GTP =2 μM [62]). As the reported intracellular concentration of GTP [63] would support only one-half of the Vmax of FtsZ [61], GTP levels could control FtsZ dynamics. We speculate that the septal bulging observed upon GuaB2 depletion is due to aberrant FtsZ activity and not a complete loss of function, because genetic depletion of FtsZ causes filamentation [41]. Indeed, altered FtsZ dynamics influences peptidoglycan structure [49], and the aberrant activity of divisome components, including FtsZ, alters septal morphology in other bacterial systems [64–67]. In addition to transcriptional regulation, guaB2 might also be regulated by its substrate, IMP, which increases in abundance during C. crescentus cell cycle progression [68]. Although it is impossible to rule out an indirect effect of guanosine levels on the expression or regulation of additional cell-division-associated proteins, our observations suggest that the septal defects we observe upon guanosine depletion reflect alterations in FtsZ filament length or dynamics.
Both DNA replication and cell division are essential processes that have been targeted for antimicrobial discovery [69, 70]. In most cases, these efforts focus on inhibiting a limited number of physical components of the bacterial replisome or divisome. Our transcriptional data identified a variety of genes that are coordinately expressed with these complexes and therefore might be required for their activity. Although we have only investigated these functional dependencies in the context of nucleotide synthesis, our data suggest that similar dependencies exist and can be predicted from transcriptional profiles. If so, these data could be used to identify new strategies for inhibiting these essential cellular processes.
STAR★METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for reagents may be directed to and will be fulfilled by the Lead Contact, Christopher M. Sassetti (christopher.sassetti@umassmed.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code availability
The RNASeq data generated in this study has been deposited in GEO (Accession Number GSE147345). The code generated during this study is available at https://github.com/ioerger/synchronized_cells. The data that support the findings of this study are available from the Lead Contact upon request. The authors declare that all data reported in this study are available within the paper, its supplementary information files and in the datasets uploaded to GEO.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
All mycobacterial strains were grown at 37°C using Middlebrook 7H9 media supplemented with 0.05% Tween-80 and OADC (Becton Dickinson) enrichment and 0.2% glycerol for the bulk culture experiments. For live cell microscopy, M. smegmatis cells were grown on Luria Bertani agar pads. Strains expressing fluorescent markers were grown in growth media supplemented with either 50 μg/ml hygromycin (for strains containing MEH or MCtH plasmids) or 25 μg/ml kanamycin (for strains containing MEK plasmid).
METHOD DETAILS
Strains
The Mtbcos strain was obtained from [19]. MtbRv is the H37Rv strain used as an unsynchronized control. Mtbcos and MtbRv expressing FhaA m-venus were transformed with pKP887 (mycobacterial replicating plasmid MEH expressing MSMEG FhaA-Venus expressed from the MSMEG fhaA native promoter (from K.P. Sundaram). M smegmatis expressing FtsW-mVenus and DivIVA-RFP was transformed with ptb21-ftsW-mVenus-MEK and tb21-divIVA-RFP-MCtH [57]. M smegmatis expressing PknD-mVenus and DivIVA-RFP was transformed with p16-pknD-mVenus-MEK [72] and tb21-DivIVA-RFP-MCtH. Mtb hypomorphs used in this study were generated as part of an earlier study [71] using a controlled protein degradation system described previously [75]. Three strains were used in this study: Mtb guaB2-DAS-HygR+Giles-TetON1-sspB-strR; Mtb gyrB-DAS-HygR+Giles-TetON6-sspB-strR; Mtb pyrE-DAS-HygR+Giles-TetON1-sspB-strR. M smegmatis expressing green fluorescence contains the plasmid CT161 (m-Venus pMV261 HygR) obtained from the Eric Rubin Lab.
Mtbcos synchronization
Biological duplicate cultures of MtbdnaAcos115 generated in a previous study [19], MtbH37Rv, MtbdnaAcos115-FhaA-Venus and MtbH37Rv-fhaA-Venus were grown in standard culture media at 37°C under shaking conditions till OD600 0.4. The cells were shifted to 30°C for 36 hours. The cultures were then shifted to 37°C and the cultures were processed for either DNA isolation, RNA isolation or fluorescent microscopy at the following times: 0h, 3h, 6.5h, 9h, 12h, 18.5h, 21h, 27h, 31h, 33h, 36h, 39.5h, 42h, 45.5h, 52h and 55h.
Chromosomal DNA isolation
Chromosomal DNA was isolated from the cell pellet of 5ml culture from each time point. Briefly, 0.5 mL of chloroform:methanol (2:1) was added and the mixture was vortexed 5X 1min. 0.5ml of phenol:chloroform was added and the mixture was vortexed for 30 s. Finally, 0.5ml of TE buffer was added. This was centrifuged at 12,000 g at 4°C for 5 minutes. The upper phase was mixed with 1 volume of chloroform and vortexed. After centrifugation, the upper phase was added to a new tube and 1/10 volume of 3M sodium acetate and 1 volume of isopropanol was added. Precipitated DNA was spun out of solution and resuspended in 20 μL of TE buffer.
Origin:terminus assay
Multiple primer sets (designed using the Primer3 design tool) amplifying 150bp at each location (Origin-0MB region surrounding Rv0001; Terminus −2.2MB region surrounding Rv1949c) of the MtbH37Rv genome were tested for amplification efficiency. Efficiency was calculated from the negative slope of the standard curve of CT v/s template concentration. The primer sets with the highest and most similar efficiencies for both loci were selected (95% for the origin and 93% for the terminus). Quantitative PCR was done using SYBR green (Biorad iQ SYBR Green Supermix) with 2ng of gDNA template per reaction. Delta Ct values were calculated as dCt = Ctori-Ctter. 2^-dCt values were then calculated for each time point. These values were then divided by the mean 2^-dCt across all time points to generate a relative ori:ter ratio for each time point.
Static microscopy
At each time point post release into 37°C (Figure 1B) or time point post genetic depletion of GyrB, GuaB2 and PyrE (Figure 4D), 1ml of Mtb culture was briefly centrifuged and cells were resuspended in a phosphate buffered saline solution containing 0.05% Tween80 and 4% paraformaldehyde. These fixed cells were then placed onto an agarose pad and DIC (Figure 4D) or wide field fluorescence imaging (Figure 1B) was performed with a DeltaVision Personal DV microscope (GE Healthcare) using a 60X oil immersion objective (AP). For each datapoint, an average of 82 cells were scored. Cell lengths in Figure 4D were determined using CellProfiler™ [73] which calculates a MFD (Maximum Feret Diameter) which is a measurement of the largest number of pixels between the two ends of the cell obtained while rotating a caliper along all possible angles. The approximate conversion factor of MFD to microns is 0.11. Calculating an MFD is especially useful for measuring mycobacteria since all cells are not strict rods (cells undergo V-snapping prior to resolution of cytokinesis and daughter cell separation). The cell debris observed during GyrB depletion in Figure 4D was excluded from cell length quantification by training CellProfiler using CP Analyst™.
Live cell microscopy
10 μL of cells in logarithmic phase (OD600 0.2–0.5) were spotted on a glass bottom 24-well plate (MatTek Corporation). 500 μL of molten Luria Bertani medium (40–50°C) was spread over the cells and allowed to solidify. For experiments with VCC234718, molten LB containing 2 μM final concentration of VCC234718 was prepared before layering over the cells. Time-resolved imaging was performed with a DeltaVision Personal DV wide field fluorescence microscope equipped with Ultimate Focus™ capabilities and an environmental chamber warmed to 37°C (Applied Precision). Images were taken at 5 or 10 minute intervals.
Simulation of cell cycle progression
Cells were simulated as a discrete population, starting with N = 10,000 cells. The population was evolved in discrete time steps over 55 hours, with each step representing 1 hour. Each cell had its own variables such as cell size (ranging between 1.0 and 2.0), chromosome copy number representing ori/ter ratio for each cell (either 2 or 1), the FhaA level for each cell (0%–100%) and a count (an integer, initially 1 for each cell). The cycle-time and growth rate for each cell was chosen from a normal distribution where the mean and standard deviation were parameters to be optimized. During the simulation, if size is < 2.0 for a cell, it increases by a constant rate after a delay after division (as a fraction of the cell cycle). Once each cell reaches a maximum size of 2.0, it stops growing. FhaA appears at the septum (increasing from 0 to 1 discretely for each cell) toward the end of the cell cycle (as a fraction of the cell cycle) and then decreases by a constant rate after the cells divide. The gradual increase in the curve for the FhaA levels comes from the dispersion of states for individual cells relative to their cycle times. Chromosome duplication window is chosen randomly from a normal distribution. This random duration for replication, creates additional dispersion in the ori/ter curve. At initiation, the value is switched to 2 (i.e., 2 copies of Ori but 1 Ter), and at termination it switches back to 1 (2 copies of each, ori/ter = 1). When each cell reaches 100% of its cell cycle time, the cell divides, doubling the count and resetting size to 1.0. Hence the population size increases, but there is no net change in biomass. Initially, the cells are assumed to be check-pointed at some point in the cell cycle due to the non-permissive temperature. (T0 in the experiment does not necessarily correspond to the beginning of the cell cycle (i.e., 0%), but rather, some point in the middle, shortly before initiation of chromosome replication.) This is represented by a “shift” parameter, to be optimized. After shifting to the permissive temperature, cells begin growing, and FhaA levels autonomously begin to decay (from initially high levels, indicated by empirical data).
In the first cell cycle, chromosome replication is delayed by an additional “recovery time” parameter which is unique for each cell and drawn randomly from a Normal distribution.
To optimize the parameters in the model, the simulation was run with different combinations of parameters, and the correlation with the empirical data (Figures 1A–1C) was evaluated. In the end, the final parameter values that maximized correlations with the empirical data were:
Cell Cycle time: mean = 35hr, sd = 1hr; Shift = 10hr (cells assumed to start 10hr into cell cycle after shift to permissive temperature); Recovery time = 6hr (after shift to permissive temperature); FhaA_start = 80% (fraction of cell cycle); S phase initiation = 20hr (into the cell cycle, i.e., after division); S phase window: mean = 12hr, SD = 7hr (duration of chromosome replication); Growth rate = 0.07; Growth_delay = 30% (fraction of cell cycle).
The predicted curves from the simulation using these optimized parameter values are shown in Figure 1D. The correlations with the empirical data are: cc(OD) = 0.9189, cc(ori/ter) = 0.9561, cc(fhaA) = 0.9614.
RNA isolation and sequencing
To minimize transcriptional changes during RNA isolation, samples were processed as rapidly as possible. At each time point, the 45ml culture was pelleted for 3 minutes at 4000 g at 37°C. The pellet was immediately resuspended in 1ml of TRIzol (Invitrogen) and snap-frozen in liquid nitrogen. The average processing time of each sample was ~5–7 minutes. Samples from time point for the synchronized and unsynchronized cultures were handled in parallel to minimize any batch effects. The RNA isolation strategy was also designed to minimize batch effects. One entire biological replicate each from the synchronized and unsynchronized cultures (16 time points × 2 replicates = 32 samples) were processed for RNA isolation in parallel, as follows. Cells in TRIzol were first transferred to lysing matrix tubes (MP Biomedicals: Lysing Matrix B). Cells were lysed in a MP Biomedicals Fast Prep-24 homogenizer (maximum power-6.5, 4 × 30 s cycles, rest on ice for 5 minutes in between cycles to minimize RNA degradation). RNA was purified according to the manufacturer’s directions. RNA cleanup was performed with QIAGEN RNeasy Mini kit (74104) omitting the DNase step. Instead, after elution, in-tube DNase treatment was performed using Ambion DNase Turbo. RNeasy cleanup was repeated again with double volumes of RLT and ethanol. RNA was subjected to rRNA removal with Ribozero Bacteria kit (Illumina-MRZB12424). Deep sequencing library was prepared using KAPA Stranded RNASeq kit (KK8401). The RNaseq libraries were sequenced on an Illumina HiSeq 4000 instrument in paired-end mode, using a read-length of 150+150bp. The mean number of reads per sample was 8.9M (range 4.2–16.5M). The reads were mapped to the H37Rv genome using Burroughs Wheeler Alignment [76] with default parameter settings. Reads mapping to each ORF were totaled (sense strand only). Because certain loci were over-represented (e.g., rrs, rnpB, ssr, Rv3661, which had counts ~0.5–1M), counts were truncated to a maximum coverage of 10,000 (reads/nt).
Data Filtering and Normalization
The global expression profiles of Mtbcos samples showed a gradual increase in expression of a few genes that dominate expression at latter time-points. Consequently, a compensatory decrease was observed in expression of other genes, making normalization by traditional reads per kilobase per million (RPKM) mis-representative. To correct for the bias induced by these outliers, the normalization method implemented in DESeq2 [74] was used, which first normalizes counts by the geometric mean for each gene across samples, and then scales each dataset to have a common median (which is less sensitive to outliers). This was applied to all 64 datasets (2 strains × 2 replicates × 16 time-points) in parallel. As a result, the expression patterns were well-calibrated between time-points, with the medians matched. To identify a subset of genes with meaningful expression, the average expression over all time-points was calculated for each gene and divided by gene length (in nucleotides). 1070 genes out of 4018 with coverage < 0.25 were dropped because expression patterns for genes with low expression are inherently noisy, leaving 2948 genes with coverage > 0.25. (Data S3). Additionally, we removed 50 genes out of 2948 genes whose expression was > 90% correlated between Mtbcos and MtbRv from subsequent analysis, as their expression patterns were assumed to be determined more by time than by difference in the strains. To center the expression values, the counts were divided by the mean for that gene across all the time points. This was done independently for Mtbcos and MtbRv. Initial analysis of correlations among time points based on patterns of expression showed a biphasic behavior for the unsynchronized cells, where time points in the first and second half of the experiment were strongly correlated within each half but poorly correlated between halves, giving rise to a “two-block structure.” We hypothesized that a small set of genes could be responsible for driving this correlation pattern in MtbRv likely due to subtle changes in media conditions and/or aeration over the long time course. In order to identify such genes, we computed a matrix of differences between selected pairs of time points for each gene, and clustered this difference matrix, which yielded a cluster of genes that have low differences within each block but high differences between blocks. The logs of the values were taken, and then the genes were clustered using hclust() in R (with the “ward.D2” distance metric). The resulting dendrogram exhibited a deep branch, which, when displayed as a heatmap, consisted of a distinct cluster of genes exhibiting low differences between pairs of time points in either block, but high differences between blocks. Using cutree(k = 4), 182 genes were identified as belonging to this cluster. Upon excluding these genes and re-calculating the correlation matrix of expression in MtbRv for all time points, the two-block structure was largely eliminated, and the resulting correlations decreased smoothly as a function of distance between time points (with highest correlation between adjacent time points), as expected.
Gaussian Process Smoothing
In order to meaningfully integrate the data from the two replicates and to smooth out profiles over time, we used a Gaussian Process (GP) to fit the raw data (septation index and ori:ter – Figure 1, gene expression- Figures 2, 3, and 4).
A GP model is a Bayesian model that estimates the probability distribution over functions using Gaussian distributions for likelihood functions. The advantage of a GP is that it is unbiased and therefore does not require assumptions of form of function. Instead, it only assumes that adjacent time points are better coupled than distant time points and that this correlation is based on Gaussian distributions.
A Gaussian Process is specified by a mean function and a covariance function
A prior mean m(x) = 0 and a covariance function, squared exponential is given as:
where I2 = lengthscale, σ2 = variance, d = input dimension
We normalized the expression value e(g,t) (with addition of pseudocounts of 10) of each gene g at each time point t by dividing the mean across all time points, and then taking log base e transformation so that the normalized value e’(g,t) fluctuates with a mean of 0. The formula is given as:
Gaussian estimation of the expression levels for a gene at different time points, subject to noise is given as:
The predictive distribution for 15 test time points (~3 hour intervals, 3-55 hours), {x1; x2;.:; x*} is specified as:
where:
We utilized the GPy Python package to fit the relative expression data (value for Mtbcos replicate 1 and replicate 2 simultaneously normalized by the mean expression level across all 60 time points for each gene using the following hyperparameters: variance = 1.0, noise variance = 0.1 and lengthscale (range 1 ~50) optimized to Maximum Likelihood Estimate (MLE) using a grid search method. After fitting the model, the predicted value (i.e., posterior mean) for each time point can be extracted. Figure S1B shows the GP regression obtained for polA (Rv 1629: DNA polymerase). Not only do the fitted values from the GP model generally interpolate be- tween the observed data at each time point, they also present a smoother profile by averaging between adjacent time points to reduce noise. The error bands show the uncertainty in the model (95% confidence interval which can be denoted as ± 1.96*σ, where σ is the estimated standard deviation at each X-coordinate (time point) from the Gaussian Process model based on variance of the training data and surrounding points).
Sinusoidal Periodicity Analysis
Traditional signal analysis methods like Fourier analysis, Fisher’s g-test, etc. as suggested by Wichert et. al. [77] performed poorly on our dataset because our experiment captured only about one-and-a-half cell-cycles. Thus, to identify periodic genes, we took an approach of sinusoidal curve-fitting, reminiscent of the non-linear curve fitting method described by Straume et.al. (COSIN2NL in COSOPT) [78]. We fi the expression profi es for each gene to a sin curve with free parameters (including frequency, phase, and trend), and selected genes with frequencies and amplitudes in a reasonable range (Red lines in Data S1). Goodness-of-fit was measured using residual sum-of-squares (RSS). Importantly, it is difficult to draw an absolute cutoff for significance based on RSS, since any data can be fit to a sin in some way, and RSS incorporates intrinsic noise in the data (E.g. between replicate observations). Hence, we took a comparative approach by also fitting the data to a quadratic curve (Gray lines in Data S1), which captures the general trend of the expression profiles. We then compared the RSS of the sin fi to the RSS of the quadratic fit (which must also pay a similar price for noise in the same data). Periodic genes are defined as those that exhibit oscillatory behavior above and beyond the trend that can be represented by a quadratic. The curve fitting for each gene was applied to the DESeq-normalized read counts (15 time-points, 2 replicates each). The sinusoidal function implemented is written as:
where: A = Amplitude; ω = Frequency; B = Mean offset; Φ = phase shift; Ct = a linear term to capture a net increasing or decreasing trend in the expression. The parameters in this function were optimized using the curve_fit() function in SciPy using non-linear least- squares. We then selected genes based on period length (27.5 hours < period < 55 hours) and amplitude (≥0.7). We also removed genes with a correlation coefficient of > 0.9 between expression profiles in Cos versus Rv. The residual sum-of-squares (goodness-of-fit) was calculated as follows:
where ysin are the sin function estimates for each time point.
A similar curve-fitting approach was used to fit the data to a quadratic curve:
using curve_fit() to optimize the parameters D, E, and F for each gene, and the residual was calculated as:
Finally, a score was calculated for each gene based on the ratio of residuals. To meaningfully enrich periodic genes in Mtbcos, we used a Receiver Operating Characteristic (ROC) curve to determine the RSSsin/RSSquad range where we optimally enrich for periodic genes in Mtbcos. The RSSsin/RSSquad range was determined to be 0.35–0.45. A threshold of 0.45 was chosen based on examining plots (Data S1) that visually exhibit clear oscillatory behavior (beyond the general trend). Thus, genes with a ratio of less than 0.45 were identified as periodic:
which means that the sinusoidal fit reduces the residual error by more than two-fold over a quadratic curve and hence fits the data better.
Using this comparative curve-fitting approach, 485 genes were identified as periodic in Mtbcos (Data S3), and only 183 genes in MtbRv, a ~2.6 fold enrichment. To estimate the number of false positives in the set of 485 genes, we randomized the data (by shuffling the genes and time points) and subjected the randomized dataset to the same analysis as described above. This permutation analysis yielded only 14 periodic genes under the null hypothesis. Thus, we estimate the false discovery rate (FDR) at approximately 14/4019 = 0.35%.
Clustering
Genes were clustered based on their expression profiles using hierarchical clustering (hclust() in R), using the complete linkage clustering based on the Euclidean distance between the vectors of expression values averaged between replicates over the 15 time points, which were standard-normalized for each gene (subtract mean and divide by standard deviation) to make the mean expression level equal to zero for each. The optimal number of clusters was determined based on the Bayesian Information Criterion (BIC) using mclustBIC() in the mclust R package [79], which showed that the optimal number of clusters among the 485 Mtbcos periodic genes was 8 (using the ‘VEE’ model). The dendogram was then divided into 8 disjoint clusters using cutree().
Peak Assignment
Using the GP fit data, we applied the following criteria to assign a peak to a gene’s expression profile. The time series T with n observations for each gene with smoothed expression values at different time points was defined as:
First, to screen out the increasing or decreasing trend at the beginning and end of the time series, and to focus on the cytokinesis phase in the middle of the time course, we excluded the first and last two time points from the peak assignment. Second, to identify well-spaced major peaks across time points, we defined a point as a peak if it has a greater magnitude than its two nearest neighbors on both sides. This is defined as:
Furthermore, to filter out the genes with lower fluctuations, the difference between the magnitude of the highest peak and the global minimum was restricted to be greater than 0.5. Additionally, in the case of more than one peak in the time series, all the peaks were constrained to have at least a half magnitude of the highest peak in the expression profile. Finally, a set of peaks P for a time series was identified as:
Among the significantly expressed genes (Data S3), the peak assignment identified 1620 genes with a single peak and 71 genes with two peaks in the Mtbcos strain compared to 903 genes with a single peak and 8 genes with two peaks in MtbRv. Similarly, 1222 genes in the Mtbcos strain and 2344 genes in the wild-type did not have any major peak.
FICI Score Calculation
Fractional Inhibitory Concentration Index (FICI) to determine the interaction between VCC234718 and C109 was performed as previously described [80]. The FICImax along the isoeffectiveness curve i.e., the combination of drug concentrations which causes a 50% reduction in fluorescence, occurred at C109 6 μg/ml and VCC234718 4 μM. FICC109 = 2.274 and FICVCC234718 = 0.88. FICImax was thus determined to be 3.16, which supports an antagonistic interaction according to previous studies [81, 82]. A similar analysis of the interaction between VCC234718 and spectinomycin yielded a FICI score of 1.55 indicating no interaction or indifference.
QUANTIFICATION AND STATISTICAL ANALYSIS
A hypergeometric test was used to calculate significance of overlap between periodic genes in C. crescentus and M. tuberculosis in Figure 2. An unpaired t test was used to determine significant difference in arrival times of PknD and FtsW and the Chi-square test was used to determine significant difference in arrival times of FtsW and DivIVA in Figure 3. The Mann-Whitney test was used to determine significant differences in cell lengths of GyrB, GuaB2 and PyrE depletion strains from wild-type in Figure 4. An extrasum-of-squares F-test was used to determine differences between cross titration curves of VCC234718, C109 and spectinomycin in Figure 4. For all these tests, values of “α,” “χ2” or “p” can be found in the figure legends. 95% confidence intervals were used in describing profiles of ori:ter, septation index in Figure 1. The 95% confidence interval is denoted as ± 1.96*σ, where σ is the estimated standard deviation at each X-coordinate (time point) from the Gaussian Process model based on variance of the training data and surrounding points. In all experiments, center and dispersion are defined as mean and standard deviation respectively, unless otherwise specified. Values of n indicate number of cells measured and can be found in the figure legends.
Supplementary Material
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and Virus Strains | ||
| Mycobacterium tuberculosis containing cos allele of dnaA (Mtbcos) | [19] | N/A |
| Mycobacterium tuberculosis H37Rv (MtbRv) | C. Sassetti | N/A |
| Mtbcos containing fhaA-mVenus | This paper | N/A |
| MtbRv containing fhaA-mVenus | This paper | N/A |
| Mycobacterium smegmatis MC2155 (Msm) | C. Sassetti | N/A |
| Msm containing ftsW mVenus and divIVA-RFP | This paper | N/A |
| Msm smegmatis containing pknD-mVenus and divIVA-RFP | This paper | N/A |
| Mtb guaB2-DAS-HygR+Giles-TetON1-sspB-strR | [71] | N/A |
| Mtb gyrB-DAS-HygR+Giles-TetON6-sspB-strR | [71] | N/A |
| Mtb pyrE-DAS-HygR+Giles-TetON1-sspB-strR | [71] | N/A |
| Msm containing m-Venus pMV261-HygR | Eric Rubin Lab | N/A |
| Chemicals, Peptides, and Recombinant Proteins | ||
| VCC234718 | [43] | N/A |
| C109 | [50] | N/A |
| Guanine-98% | Millipore-Sigma | G11950 |
| Guanosine > = 98% | Millipore-Sigma | G6264 |
| Spectinomycin dihydrochloride pentahydrate | Millipore-Sigma | S4014 |
| Critical Commercial Assays | ||
| KAPA Stranded RNA-Seq Kit | Roche | KK8401 |
| Ribo-Zero Bacteria Kit (discontinued) | Illumina | MRZB12424 |
| iQ SYBR Green Supermix | Bio-Rad | 1708880 |
| Deposited Data | ||
| RNASeq count data | This paper | GEO: GSE147345 |
| Oligonucleotides | ||
| Forward Primer for amplifying ori- 5’-GGTTCAGGCTTCACCACAGT-3’ | This paper | N/A |
| Reverse Primer for amplifying ori- 5’-GGAGCGCTGAGATTAGCATC-3’ | This paper | N/A |
| Forward Primer for amplifying ter- 5’-ACAACGAGAAACCGCAAATC-3’ | This paper | N/A |
| Reverse primer for amplifying ter- 5’-TACGGCTGTCATGTCTTTCG-3’ | This paper | N/A |
| Recombinant DNA | ||
| fhaA-mVenus in plasmid MEH | [20] | N/A |
| divIVA-RFP in plasmid MCtH | [57] | N/A |
| pknD-mVenus in plasmid MEK | [72] | N/A |
| Software and Algorithms | ||
| CellProfiler™ | [73] | N/A |
| DESeq2 | [74] | R package |
| Source code for GP smoothing, curve fitting and cell cycle modelling | https://github.com/ioerger/synchronized_cells | Python and R scripts |
Highlights.
DNA replication and cytokinesis are temporally segregated in M. tuberculosis
Periodic gene expression occurs during M. tuberculosis cell cycle progression
Transcript abundance predicts function of genes at the developing septum
Cytokinesis is influenced by transcriptional regulation of guanosine synthesis
ACKNOWLEDGMENTS
We would like to thank Aashish Srivastava under the guidance of James Sacchettini and the Texas A&M Genomics and Bioinformatics Service for sequencing the RNA sequencing (RNA-seq) libraries. VCC234718 was a generous gift from Vinayak Singh and Valerie Mizrahi. C109 was a generous gift from Vadim Makarov. Genetic depletion strains were generated as part of a larger collaborative effort, including the labs of Deborah Hung, Eric Rubin, Sabine Ehrt, and Dirk Schnappinger. Kenan Murphy and Charlotte Reames contributed to strain generation from the Sassetti lab. We would like to thank Megan Proulx for critical reading of the manuscript. This work was supported by grant AI095208 to C.M.S and AI143575 to C.M.S. and T.R.I.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
SUPPLEMENTAL INFORMATION
Supplemental Information can be found online at https://doi.org/10.1016/j.cub.2020.07.070.
REFERENCES
- 1.Helmstetter CE (1968). DNA synthesis during the division cycle of rapidly growing Escherichia coli B/r. J. Mol. Biol. 31, 507–518. [DOI] [PubMed] [Google Scholar]
- 2.Cooper S, and Helmstetter CE (1968). Chromosome replication and the division cycle of Escherichia coli B/r. J. Mol. Biol. 31, 519–540. [DOI] [PubMed] [Google Scholar]
- 3.Gibson B, Wilson DJ, Feil E, and Eyre-Walker A (2018). The distribution of bacterial doubling times in the wild. Proc. Biol. Sci. 285, 20180789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kubitschek HE, and Newman CN (1978). Chromosome replication during the division cycle in slowly growing, steady-state cultures of three Escherichia coli B/r strains. J. Bacteriol. 136, 179–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Skarstad K, Steen HB, and Boye E (1983). Cell cycle parameters of slowly growing Escherichia coli B/r studied by flow cytometry. J. Bacteriol. 154, 656–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Laub MT, McAdams HH, Feldblyum T, Fraser CM, and Shapiro L (2000). Global analysis of the genetic network controlling a bacterial cell cycle. Science 290, 2144–2148. [DOI] [PubMed] [Google Scholar]
- 7.Laub MT, Chen SL, Shapiro L, and McAdams HH (2002). Genes directly controlled by CtrA, a master regulator of the Caulobacter cell cycle. Proc. Natl. Acad. Sci. USA 99, 4632–4637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brilli M, Fondi M, Fani R, Mengoni A, Ferri L, Bazzicalupo M, and Biondi EG (2010). The diversity and evolution of cell cycle regulation in alpha-proteobacteria: a comparative genomic analysis. BMC Syst. Biol. 4, 52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang Z, Milias-Argeitis A, and Heinemann M (2018). Dynamic single-cell NAD(P)H measurement reveals oscillatory metabolism throughout the E. coli cell division cycle. Sci. Rep. 8, 2162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yaginuma H, Kawai S, Tabata KV, Tomiyama K, Kakizuka A, Komatsuzaki T, Noji H, and Imamura H (2014). Diversity in ATP concentrations in a single bacterial cell population revealed by quantitative single-cell imaging. Sci. Rep. 4, 6522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weart RB, Lee AH, Chien A-C, Haeusser DP, Hill NS, and Levin PA (2007). A metabolic sensor governing cell size in bacteria. Cell 130, 335–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hill NS, Buske PJ, Shi Y, and Levin PA (2013). A moonlighting enzyme links Escherichia coli cell size with central metabolism. PLoS Genet. 9, e1003663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Santi I, Dhar N, Bousbaine D, Wakamoto Y, and McKinney JD (2013). Single-cell dynamics of the chromosome replication and cell division cycles in mycobacteria. Nat. Commun. 4, 2470. [DOI] [PubMed] [Google Scholar]
- 14.Santi I, and McKinney JD (2015). Chromosome organization and replisome dynamics in Mycobacterium smegmatis. MBio 6, e01999–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Trojanowski D, Ginda K, Pióro M, Hołówka J, Skut P, Jakimowicz D, and Zakrzewska-Czerwińska J (2015). Choreography of the Mycobacterium replication machinery during the cell cycle. MBio 6, e02125–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Logsdon MM, Ho P-Y, Papavinasasundaram K, Richardson K, Cokol M, Sassetti CM, Amir A, and Aldridge BB (2017). A parallel adder coordinates mycobacterial cell-cycle progression and cell-size homeostasis in the context of asymmetric growth and organization. Curr. Biol. 27, 3367–3374.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Trojanowski D, Hołówka J, Ginda K, Jakimowicz D, and Zakrzewska-Czerwińska J (2017). Multifork chromosome replication in slow-growing bacteria. Sci. Rep. 7, 43836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Logsdon MM, and Aldridge BB (2018). Stable regulation of cell cycle events in Mycobacteria: insights from inherently heterogeneous bacterial populations. Front. Microbiol. 9, 514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nair N, Dziedzic R, Greendyke R, Muniruzzaman S, Rajagopalan M, and Madiraju MV (2009). Synchronous replication initiation in novel Mycobacterium tuberculosis dnaA cold-sensitive mutants. Mol. Microbiol. 71, 291–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gee CL, Papavinasasundaram KG, Blair SR, Baer CE, Falick AM, King DS, Griffin JE, Venghatakrishnan H, Zukauskas A, Wei J-R, et al. (2012). A phosphorylated pseudokinase complex controls cell wall synthesis in mycobacteria. Sci. Signal. 5, ra7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rustad TR, Minch KJ, Brabant W, Winkler JK, Reiss DJ, Baliga NS, and Sherman DR (2013). Global analysis of mRNA stability in Mycobacterium tuberculosis. Nucleic Acids Res. 41, 509–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Honaker RW, Dhiman RK, Narayanasamy P, Crick DC, and Voskuil MI (2010). DosS responds to a reduced electron transport system to induce the Mycobacterium tuberculosis DosR regulon. J. Bacteriol. 192, 6447–6455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Plocinska R, Purushotham G, Sarva K, Vadrevu IS, Pandeeti EVP, Arora N, Plocinski P, Madiraju MV, and Rajagopalan M (2012). Septal localization of the Mycobacterium tuberculosis MtrB sensor kinase promotes MtrA regulon expression. J. Biol. Chem. 287, 23887–23899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gola S, Munder T, Casonato S, Manganelli R, and Vicente M (2015). The essential role of SepF in mycobacterial division. Mol. Microbiol. 97, 560–576. [DOI] [PubMed] [Google Scholar]
- 25.Wu KJ, Zhang J, Baranowski C, Leung V, Rego EH, Morita YS, Rubin EJ, and Boutte CC (2018). Characterization of conserved and novel septal factors in Mycobacterium smegmatis. J. Bacteriol. 200, e00649–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.De Nisco NJ, Abo RP, Wu CM, Penterman J, and Walker GC (2014). Global analysis of cell cycle gene expression of the legume symbiont Sinorhizobium meliloti. Proc. Natl. Acad. Sci. USA 111, 3217–3224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhou B, Schrader JM, Kalogeraki VS, Abeliuk E, Dinh CB, Pham JQ, Cui ZZ, Dill DL, McAdams HH, and Shapiro L (2015). The global regulatory architecture of transcription during the Caulobacter cell cycle. PLoS Genet. 11, e1004831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wu KJ, Boutte CC, Ioerger TR, and Rubin EJ (2019). Mycobacterium smegmatis HtrA blocks the toxic activity of a putative cell wall amidase. Cell Rep. 27, 2468–2479.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tan MH, Kozdon JB, Shen X, Shapiro L, and McAdams HH (2010). An essential transcription factor, SciP, enhances robustness of Caulobacter cell cycle regulation. Proc. Natl. Acad. Sci. USA 107, 18985–18990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rustad TR, Minch KJ, Ma S, Winkler JK, Hobbs S, Hickey M, Brabant W, Turkarslan S, Price ND, Baliga NS, and Sherman DR (2014). Mapping and manipulating the Mycobacterium tuberculosis transcriptome using a transcription factor overexpression-derived regulatory network. Genome Biol. 15, 502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hussain K, Begg KJ, Salmond GP, and Donachie WD (1987). ParD: a new gene coding for a protein required for chromosome partitioning and septum localization in Escherichia coli. Mol. Microbiol. 1, 73–81. [DOI] [PubMed] [Google Scholar]
- 32.Kalir S, McClure J, Pabbaraju K, Southward C, Ronen M, Leibler S, Surette MG, and Alon U (2001). Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria. Science 292, 2080–2083. [DOI] [PubMed] [Google Scholar]
- 33.Zaslaver A, Mayo AE, Rosenberg R, Bashkin P, Sberro H, Tsalyuk M, Surette MG, and Alon U (2004). Just-in-time transcription program in metabolic pathways. Nat. Genet. 36, 486–491. [DOI] [PubMed] [Google Scholar]
- 34.Goley ED, Yeh Y-C, Hong S-H, Fero MJ, Abeliuk E, McAdams HH, and Shapiro L (2011). Assembly of the Caulobacter cell division machine. Mol. Microbiol. 80, 1680–1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rego EH, Audette RE, and Rubin EJ (2017). Deletion of a mycobacterial divisome factor collapses single-cell phenotypic heterogeneity. Nature 546, 153–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Plocinski P, Ziolkiewicz M, Kiran M, Vadrevu SI, Nguyen HB, Hugonnet J, Veckerle C, Arthur M, Dziadek J, Cross TA, et al. (2011). Characterization of CrgA, a new partner of the Mycobacterium tuberculosis peptidoglycan polymerization complexes. J. Bacteriol. 193, 3246–3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Plocinski P, Arora N, Sarva K, Blaszczyk E, Qin H, Das N, Plocinska R, Ziolkiewicz M, Dziadek J, Kiran M, et al. (2012). Mycobacterium tuberculosis CwsA interacts with CrgA and Wag31, and the CrgA-CwsA complex is involved in peptidoglycan synthesis and cell shape determination. J. Bacteriol. 194, 6398–6409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kieser KJ, and Rubin EJ (2014). How sisters grow apart: mycobacterial growth and division. Nat. Rev. Microbiol. 12, 550–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lark KG (1961). Variation in bacterial acid-soluble deoxyribotides during discontinuous deoxyribonucleic acid synthesis. Biochim. Biophys. Acta 51, 107–116. [Google Scholar]
- 40.Huzyk L, and Clark DJ (1971). Nucleoside triphosphate pools in synchronous cultures of Escherichia coli. J. Bacteriol. 108, 74–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ehrt S, Guo XV, Hickey CM, Ryou M, Monteleone M, Riley LW, and Schnappinger D (2005). Controlling gene expression in mycobacteria with anhydrotetracycline and Tet repressor. Nucleic Acids Res. 33, e21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.DeJesus MA, Gerrick ER, Xu W, Park SW, Long JE, Boutte CC, Rubin EJ, Schnappinger D, Ehrt S, Fortune SM, et al. (2017). Comprehensive essentiality analysis of the Mycobacterium tuberculosis genome via saturating transposon mutagenesis. MBio 8, e02133–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Singh V, Donini S, Pacitto A, Sala C, Hartkoorn RC, Dhar N, Keri G, Ascher DB, Mondésert G, Vocat A, et al. (2017). The inosine monophosphate dehydrogenase, GuaB2, is a vulnerable new bactericidal drug target for tuberculosis. ACS Infect. Dis. 3, 5–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Diver JM, and Wise R (1986). Morphological and biochemical changes in Escherichia coli after exposure to ciprofloxacin. J. Antimicrob. Chemother. 18 (Suppl D), 31–41. [DOI] [PubMed] [Google Scholar]
- 45.Arjes HA, Kriel A, Sorto NA, Shaw JT, Wang JD, and Levin PA (2014). Failsafe mechanisms couple division and DNA replication in bacteria. Curr. Biol. 24, 2149–2155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mann KM, Huang DL, Hooppaw AJ, Logsdon MM, Richardson K, Lee HJ, Kimmey JM, Aldridge BB, and Stallings CL (2017). Rv0004 is a new essential member of the mycobacterial DNA replication machinery. PLoS Genet. 13, e1007115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.de Wet TJ, Winkler KR, Mhlanga MM, Mizrahi V, and Warner DF (2020). Arrayed CRISPRi and quantitative imaging describe the morphotypic landscape of essential mycobacterial genes. bioRxiv. 10.1101/2020.03.20.000372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.de Boer P, Crossley R, and Rothfield L (1992). The essential bacterial cell-division protein FtsZ is a GTPase. Nature 359, 254–256. [DOI] [PubMed] [Google Scholar]
- 49.Bisson-Filho AW, Hsu Y-P, Squyres GR, Kuru E, Wu F, Jukes C, Sun Y, Dekker C, Holden S, VanNieuwenhze MS, et al. (2017). Treadmilling by FtsZ filaments drives peptidoglycan synthesis and bacterial cell division. Science 355, 739–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hogan AM, Scoffone VC, Makarov V, Gislason AS, Tesfu H, Stietz MS, Brassinga AKC, Domaratzki M, Li X, Azzalin A, et al. (2018). Competitive fitness of essential gene knockdowns reveals a broad-spectrum antibacterial inhibitor of the cell division protein FtsZ. Antimicrob. Agents Chemother. 62, e01231–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tan CM, Therien AG, Lu J, Lee SH, Caron A, Gill CJ, Lebeau-Jacob C, Benton-Perdomo L, Monteiro JM, Pereira PM, et al. (2012). Restoring methicillin-resistant Staphylococcus aureus susceptibility to β-lactam antibiotics. Sci. Transl. Med. 4, 126ra35. [DOI] [PubMed] [Google Scholar]
- 52.Mukherjee A, and Lutkenhaus J (1998). Dynamic assembly of FtsZ regulated by GTP hydrolysis. EMBO J. 17, 462–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bi EF, and Lutkenhaus J (1991). FtsZ ring structure associated with division in Escherichia coli. Nature 354, 161–164. [DOI] [PubMed] [Google Scholar]
- 54.Wang L, Khattar MK, Donachie WD, and Lutkenhaus J (1998). FtsI and FtsW are localized to the septum in Escherichia coli. J. Bacteriol. 180, 2810–2816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lenarcic R, Halbedel S, Visser L, Shaw M, Wu LJ, Errington J, Marenduzzo D, and Hamoen LW (2009). Localisation of DivIVA by targeting to negatively curved membranes. EMBO J. 28, 2272–2282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ramamurthi KS, and Losick R (2009). Negative membrane curvature as a cue for subcellular localization of a bacterial protein. Proc. Natl. Acad. Sci. USA 106, 13541–13545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Meniche X, Otten R, Siegrist MS, Baer CE, Murphy KC, Bertozzi CR, and Sassetti CM (2014). Subpolar addition of new cell wall is directed by DivIVA in mycobacteria. Proc. Natl. Acad. Sci. USA 111, E3243–E3251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hannebelle MTM, Ven JXY, Toniolo C, Eskandarian HA, Vuaridel-Thurre G, McKinney JD, and Fantner GE (2020). A biphasic growth model for cell pole elongation in mycobacteria. Nat. Commun. 11, 452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sharma AK, Arora D, Singh LK, Gangwal A, Sajid A, Molle V, Singh Y, and Nandicoori VK (2016). Serine/threonine protein phosphatase PstP of Mycobacterium tuberculosis is necessary for accurate cell division and survival of pathogen. J. Biol. Chem. 291, 24215–24230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Iswahyudi, Mukamolova GV, Straatman-Iwanowska AA, Allcock N, Ajuh P, Turapov O, and O’Hare HM (2019). Mycobacterial phosphatase PstP regulates global serine threonine phosphorylation and cell division. Sci. Rep. 9, 8337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Arjes HA, Lai B, Emelue E, Steinbach A, and Levin PA (2015). Mutations in the bacterial cell division protein FtsZ highlight the role of GTP binding and longitudinal subunit interactions in assembly and function. BMC Microbiol. 15, 209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rock JM, Lang UF, Chase MR, Ford CB, Gerrick ER, Gawande R, Coscolla M, Gagneux S, Fortune SM, and Lamers MH (2015). DNA replication fidelity in Mycobacterium tuberculosis is mediated by an ancestral prokaryotic proofreader. Nat. Genet. 47, 677–681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Buckstein MH, He J, and Rubin H (2008). Characterization of nucleotide pools as a function of physiological state in Escherichia coli. J. Bacteriol. 190, 718–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sundararajan K, Miguel A, Desmarais SM, Meier EL, Casey Huang K, and Goley ED (2015). The bacterial tubulin FtsZ requires its intrinsically disordered linker to direct robust cell wall construction. Nat. Commun. 6, 7281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Howell M, Aliashkevich A, Sundararajan K, Daniel JJ, Lariviere PJ, Goley ED, Cava F, and Brown PJB (2019). Agrobacterium tumefaciens divisome proteins regulate the transition from polar growth to cell division. Mol. Microbiol. 111, 1074–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Yang X, Lyu Z, Miguel A, McQuillen R, Huang KC, and Xiao J (2017). GTPase activity-coupled treadmilling of the bacterial tubulin FtsZ organizes septal cell wall synthesis. Science 355, 744–747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lariviere PJ, Mahone CR, Santiago-Collazo G, Howell M, Daitch AK, Zeinert R, Chien P, Brown PJB, and Goley ED (2019). An essential regulator of bacterial division links FtsZ to cell wall synthase activation. Curr. Biol. 29, 1460–1470.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hartl J, Kiefer P, Kaczmarczyk A, Mittelviefhaus M, Meyer F, Vonderach T, Hattendorf B, Jenal U, and Vorholt JA (2020). Untargeted metabolomics links glutathione to bacterial cell cycle progression. Nat. Metab. 2, 153–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Warner DF, Tønjum T, and Mizrahi V (2013). DNA metabolism in mycobacterial pathogenesis. Curr. Top. Microbiol. Immunol. 374, 27–51. [DOI] [PubMed] [Google Scholar]
- 70.Sass P, and Brö tz-Oesterhelt H (2013). Bacterial cell division as a target for new antibiotics. Curr. Opin. Microbiol. 16, 522–530. [DOI] [PubMed] [Google Scholar]
- 71.Johnson EO, LaVerriere E, Office E, Stanley M, Meyer E, Kawate T, Gomez JE, Audette RE, Bandyopadhyay N, Betancourt N, et al. (2019). Large-scale chemical-genetics yields new M. tuberculosis inhibitor classes. Nature 571, 72–78. [DOI] [PubMed] [Google Scholar]
- 72.Baer CE, Iavarone AT, Alber T, and Sassetti CM (2014). Biochemical and spatial coincidence in the provisional Ser/Thr protein kinase interaction network of Mycobacterium tuberculosis. J. Biol. Chem. 289, 20422–20433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Carpenter AE, Jones TR, Lamprecht MR, Clarke C, Kang IH, Friman O, Guertin DA, Chang JH, Lindquist RA, Moffat J, et al. (2006). CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol. 7, R100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Love MI, Huber W, and Anders S (2014). Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 15, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Kim J-H, Wei J-R, Wallach JB, Robbins RS, Rubin EJ, and Schnappinger D (2011). Protein inactivation in mycobacteria by controlled proteolysis and its application to deplete the beta subunit of RNA polymerase. Nucleic Acids Res. 39, 2210–2220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Li H, and Durbin R (2009). Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25, 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wichert S, Fokianos K, and Strimmer K (2004). Identifying periodically expressed transcripts in microarray time series data. Bioinformatics 20, 5–20. [DOI] [PubMed] [Google Scholar]
- 78.Straume M (2004). DNA microarray time series analysis: automated statistical assessment of circadian rhythms in gene expression patterning. Methods Enzymol. 383, 149–166. [DOI] [PubMed] [Google Scholar]
- 79.Scrucca L, Fop M, Murphy TB, and Raftery AE (2016). mclust 5: clustering, classification and density estimation using Gaussian finite mixture models. R J. 8, 289–317. [PMC free article] [PubMed] [Google Scholar]
- 80.Ruhil S, Kumar V, Balhara M, Malik M, Dhankhar S, Kumar M, and Kumar Chhillar A (2014). In vitro evaluation of combination of polyenes with EDTA against Aspergillus spp. by different methods (FICI and CI Model). J. Appl. Microbiol. 117, 643–653. [DOI] [PubMed] [Google Scholar]
- 81.Meletiadis J, Stergiopoulou T, O’Shaughnessy EM, Peter J, and Walsh TJ (2007). Concentration-dependent synergy and antagonism within a triple antifungal drug combination against Aspergillus species: analysis by a new response surface model. Antimicrob. Agents Chemother. 51, 2053–2064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Mavridou E, Meletiadis J, Rijs A, Mouton JW, and Verweij PE (2015). The strength of synergistic interaction between posaconazole and caspofungin depends on the underlying azole resistance mechanism of Aspergillus fumigatus. Antimicrob. Agents Chemother. 59, 1738–1744. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The RNASeq data generated in this study has been deposited in GEO (Accession Number GSE147345). The code generated during this study is available at https://github.com/ioerger/synchronized_cells. The data that support the findings of this study are available from the Lead Contact upon request. The authors declare that all data reported in this study are available within the paper, its supplementary information files and in the datasets uploaded to GEO.