Dynamic and reversible shape response of red blood cells in synthetic liquid crystals

Significance

Red blood cells are soft and pliable, which allows them to deform through small capillaries. We have found that red blood cells, if dispersed in a synthetic liquid crystal, are squeezed into complex shapes via the viscoelastic environment created by the liquid crystal. The strained shapes exhibited by individual red blood cells in liquid crystals reveal cell mechanical properties and unmask a high level of cell-to-cell variation across a population of cells. The sharing of strain between liquid crystals and soft mammalian cells is general and provides approaches for quantifying variations in cell mechanical properties, including during aging and diseases such as malaria and sickle cell anemia.

Abstract

Mammalian cells are soft, and correct functioning requires that cells undergo dynamic shape changes in vivo. Although a range of diseases are associated with stiffening of red blood cells (RBCs; e.g., sickle cell anemia or malaria), the mechanical properties and thus shape responses of cells to complex viscoelastic environments are poorly understood. We use vapor pressure measurements to identify aqueous liquid crystals (LCs) that are in osmotic equilibrium with RBCs and explore mechanical coupling between RBCs and LCs. When transferred from an isotropic aqueous phase into a LC, RBCs exhibit complex yet reversible shape transformations, from initially biconcave disks to elongated and folded geometries with noncircular cross-sections. Importantly, whereas the shapes of RBCs are similar in isotropic fluids, when strained by LC, a large variance in shape response is measured, thus unmasking cell-to-cell variation in mechanical properties. Numerical modeling of LC and cell mechanics reveals that RBC shape responses occur at constant cell membrane area but with membrane shear moduli that vary between cells from 2 to 16 × 10⁻⁶ N/m. Temperature-dependent LC elasticity permits continuous tuning of RBC strains, and chemical cross-linking of RBCs, a model for diseased cells, leads to striking changes in shape responses of the RBCs. Overall, these results provide insight into the coupling of strain between soft mammalian cells and synthetic LCs, and hint at new methods for rapidly characterizing mechanical properties of single mammalian cells in a population and thus cell-to-cell variance.

Dynamic management of mechanical strain is one of the central principles by which living systems regulate their organization and functional properties (1, 2). Curvature strains within bacterial cell membranes, for example, are known to locally concentrate specific lipids and proteins to regions of high membrane curvature to facilitate cell division (3–6), and mammalian cells respond to their mechanical environment by changing their internal organization, gene expression, and phenotype (7–9). Red blood cells (RBCs) are a particularly important example of adaptive responses exhibited by mammalian cells to mechanical forces: when strained by shear flows in narrow capillaries of the body, RBCs dynamically regulate their cytoskeletons to change their mechanical properties (10–13). Disruption of the dynamic mechanical response can result in hematologic diseases (10, 11), such as sickle cell anemia; diseased cells are stiffer and exhibit shapes (e.g., crescentlike shapes) that differ from healthy cells. These changes can lead to alteration of the rheological properties of blood and blocking of capillaries (10, 12, 13). In this paper, we describe the mechanical interactions of RBCs with anisotropic elastic environments that can be designed using synthetic liquid crystals (LCs), and reveal that RBC shape responses to LC stresses can provide important insight into the mechanical properties of RBCs, including cell-to-cell variation of membrane properties within a population.

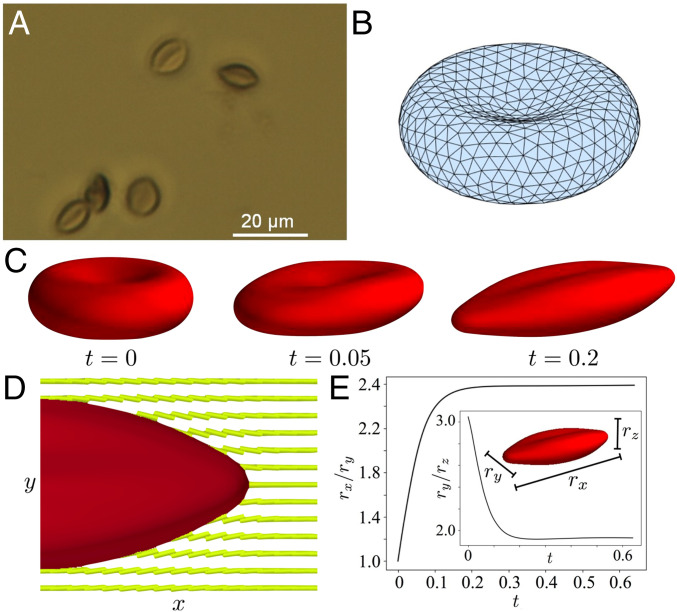
The LCs used in our study are so-called chromonic phases (14), formed from aqueous solutions of disodium chromoglycate (DSCG). The DSCG molecules stack into anisometric columnar assemblies, via π–π interactions of their polyaromatic cores (Fig. 1 A and B), which in turn exhibit long-range orientational order and give rise to mesophases with elastic properties that resist splay, twist, and bend modes of deformation (15–21). Unlike many surfactants, which also form aqueous mesophases at high concentration, DSCG molecules are not substantially amphiphilic and thus weakly interact with biological membranes (14). The introduction of a rigid, micrometer-sized inclusion into a LC typically deforms the LC, generating an elastic energy penalty that scales as Ka, where K is a characteristic LC elastic modulus, and a is the radius of the inclusion. If the inclusion is soft, however, the inclusion and LC can share strain in a complex manner that depends on the mechanical properties of the inclusion and LC. Previously, for example, we reported on the straining of giant unilamellar vesicles (GUVs) comprising fluid phospholipid membranes dispersed in DSCG (the DSCG was inside and outside the GUV) (14). We observed the LC to elastically strain initially spherical GUVs into axially symmetric spindlelike shapes with an accompanying increase in membrane area (the latter caused transient poration of the membrane with partial loss of LC volume from the interior of the GUV) (14). In this paper, we reveal that RBCs exhibit a different class of shape responses to mechanical environments of LCs, shape responses that are consistent with a solid, elasticlike membrane strained at constant membrane area. In contrast to GUVs, we observe formation of complex folded and nonaxisymmetric shapes. We find the shape response of the RBCs in LC to be particularly sensitive to the elastic shear modulus of the cells, thus providing a facile method to quantify variation of the mechanical properties of RBCs.

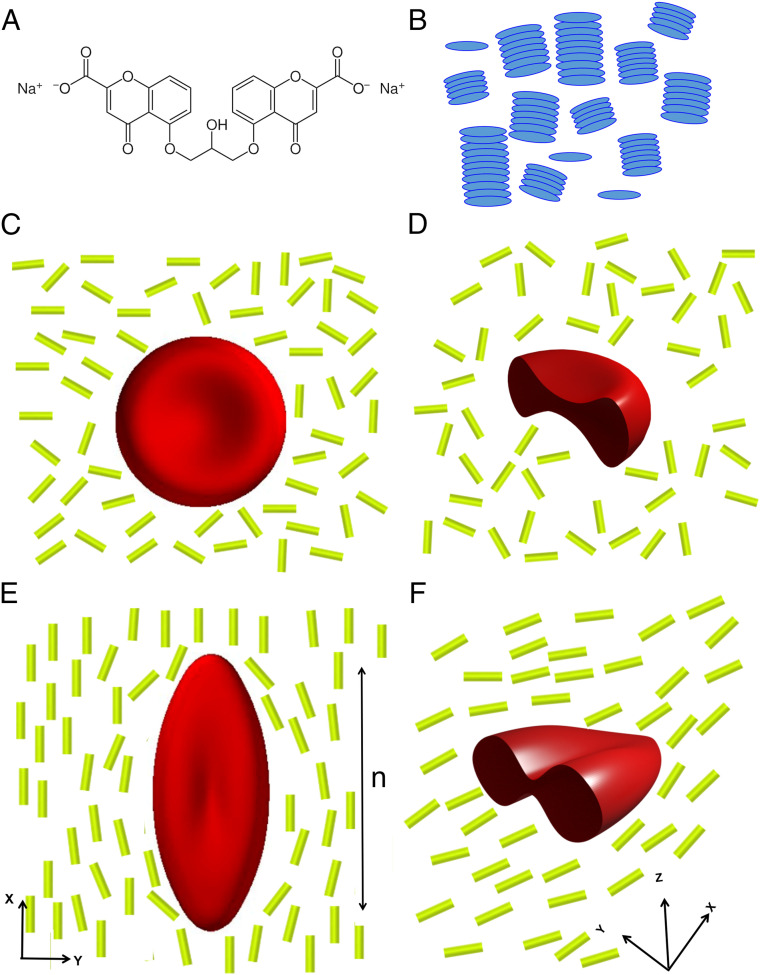
Fig. 1.

(A) Molecular structure of DSCG. (B) Schematic illustration of the self-assembly of DSCG molecules into columnar aggregates that exhibit long-range orientational order in a nematic LC phase. (C) Schematic illustration of a RBC with biconcave shape suspended in an isotropic aqueous solution of DSCG, with D showing a profile view. (E) Schematic illustration of a RBC strained by a nematic LC phase formed from DSCG, with F showing a profile view. The double-ended arrow in E shows the orientation of LC director along the x axis, which also corresponds to the principal direction of strain of the RBC. The rods in C–F correspond to columnar aggregates in B.

At the outset of the study reported in this paper, it was not obvious to us that it would be possible to strain RBCs using LCs. Unlike our past experiments with GUVs, in which the LC was within and outside the GUV membranes, the relative osmotic pressures of LC phases and interiors of RBCs were unknown. The interiors of RBCs comprise a concentrated aqueous phase of proteins (largely hemoglobin) with an osmotic pressure of 280 mosm/kg (an osmole [osm] is defined as the moles of an ideal solute that generates an equivalent osmotic pressure). In the absence of osmotic equilibrium with their environment, RBCs swell or shrink via diffusion of water across their membranes. In addition, in comparison to GUVs of synthetic phospholipids, RBCs also possess a far more complex membrane shape and organization; the RBC cell membrane comprises a mixture of phospholipids, cholesterol, and transmembrane glycoproteins (glycocalyx), with a network of proteins located on the inner surface of the lipid bilayer (spectrin) (22–25). Human RBCs typically possess a biconcave shape that reflects the presence of excess membrane area (relative to volume) and enables efficient gas (oxygen) exchange, although RBCs from other mammals possess distinct shapes (23–28).

The investigation reported in this paper is motivated by an order of magnitude analysis of the characteristic energies associated with the straining of LCs and RBCs. The shear modulus of an RBC membrane, E_S, increases with membrane thickness h as ${\mathrm{E}}_{\mathrm{S}}=Yh$, where Y is the effective Young’s modulus (the energetic cost of bending of RBC membranes is negligible compared to shear; see below for details refs. 29–32). By using Y ∼ 10³ N/m² (11, 23, 25, 33) and h ∼ 4 nm, we estimated E_S ∼ 4 μN/m, consistent with prior experimental measurements (34). This led us to predict the energy of a shear mode-dominated deformation of a spherical shell with RBC membrane properties to be E_S a² ∼ 1.6 × 10⁴ kT, where a is the shell radius (4 μm). In comparison, as noted above, the energetic cost associated with straining a LC about the same shell is Ka, which, with K ∼ 10 pN, corresponds to ∼1.0 × 10⁴ kT. These simple scaling arguments led us to conclude that the magnitudes of the elastic energies associated with deformation of the LC and RBC are comparable, and thus that RBCs dispersed in LCs would likely exhibit shape responses that reflect an interplay of the mechanical properties of both the LC and RBC. Below we perform experimental tests of that prediction and provide complementary numerical modeling (33, 35).

In addition to providing fundamental insight into how the mechanical properties of soft colloids (fluid versus solid elastic membranes) regulate their shape response to LCs, our study hints at the basis of an approach for rapid characterization of the mechanical properties of RBCs and other biological cells (35). Although experimental techniques such as optical tweezers, magnetic bead actuation, atomic force microscopy, and micropipette aspiration have been used previously to strain RBCs (23, 25, 28), these methods involve laborious procedures and complex instrumentation (11, 23, 25, 33), and thus restrict characterization of the mechanical properties to small numbers of cells. Accordingly, they do not permit facile characterization of cell-to-cell variation in the mechanical properties of cells within large populations. Additionally, they also typically apply local deformations to RBCs (the region of the RBC that is strained is small compared to the size of the cell). For instance, the area dilation modulus of RBCs can be extracted using the micropipette aspiration technique, but membrane folding can lead to inaccurate values (36).

Results

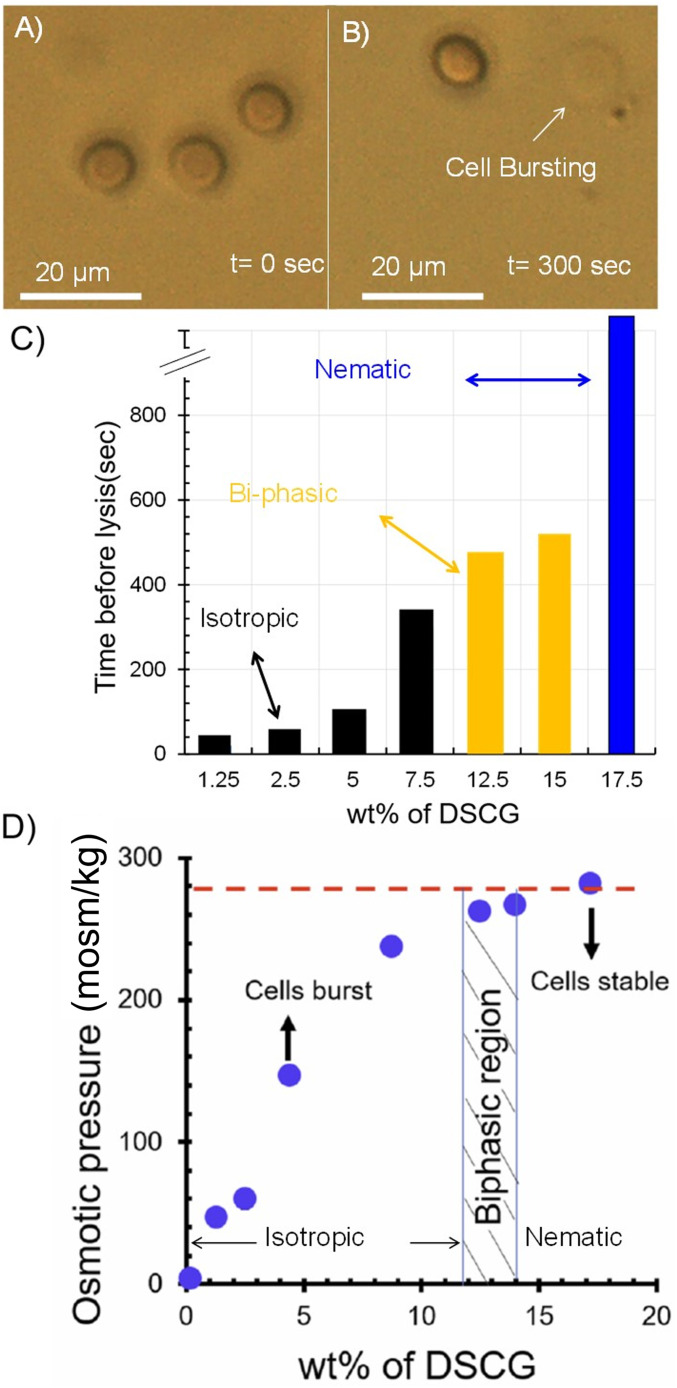
Our initial experiments were performed to determine whether or not it is possible to prepare LC phases from DSCG that are in osmotic equilibrium with the interior of an RBC. As noted above, the osmotic pressure of the interior of an RBC is 280 mosm/kg, which is equivalent to an aqueous solution containing 154 mM NaCl (37–39). Initially, we suspended RBCs in 154 mM NaCl and confirmed that the RBCs maintained their biconcave shapes (Fig. 1 C and D) for a period of several hours (Fig. 2A and SI Appendix, Fig. S1A). In contrast, when RBCs were suspended in aqueous solutions containing 154 mM DSCG (pH 8.4), an isotropic phase, we observed RBCs to swell from an initially biconcave shape (Fig. 2A) and burst over a period of ∼300 s (Fig. 2B). This result is consistent with the aqueous 154 mM DSCG being hypotonic relative to the interior of an RBC, resulting in a flux of water into the RBC and cell lysis (37, 38, 40). We found, however, that the average lifetimes of the RBCs prior to lysis increased with concentration of DSCG (Fig. 2C). Significantly, when using 17.3 wt % of DSCG (588 mM), which corresponds to a nematic LC phase of DSCG at 25 °C (Fig. 2C), RBCs did not lyse over several hours. This result led us to hypothesize that osmotic equilibrium between the interior of the RBC and the LC was achieved under these conditions. To quantify the osmotic pressure of the DSCG solutions, we measured their vapor pressures (Fig. 2D). Inspection of Fig. 2D reveals that aqueous 17.3 wt % DSCG at 25 °C is isotonic with the interiors of RBCs (red dashed line in Fig. 2D), whereas lower concentrations of DSCG, including 154 mM DSCG (Fig. 2 A and B), are hypotonic. We note that the RBCs imaged in Fig. 2 had sedimented onto a lower substrate and thus we observed a consistent projection of the biconcave cell shape (see below for images of alternative projections of the RBCs).

Fig. 2.

(A and B) RBCs imaged (optically) immediately (A) and 300 s (B) after transfer to an isotropic, aqueous DSCG solution (154 mM). The RBCs sedimented onto a glass substrate and thus the disk shapes observed in A are projections of a biconcave cell shape. (C) Time for lysis of RBCs suspended in aqueous DSCG solutions plotted as a function of the concentration of DSCG. The black, yellow, and blue colors indicate, respectively, isotropic, biphasic, and nematic phases of DSCG. (D) Osmotic pressure (measured using vapor pressure osmometry) of aqueous DSCG solutions at 25 °C.

Our finding that aqueous LCs formed from 17.3 wt % DSCG are isotonic with the interiors of RBCs enabled our study of the mechanical interactions of LCs and RBCs, as it ensures that RBC shape changes induced by the elasticity of the LC phase (see below) are not convolved with shape changes arising from a flux of water across the RBC cell membrane (27, 41). We envisage, however, that an imbalance in LC osmotic pressure can be exploited in future studies to swell or shrink RBCs to obtain additional insight into biomechanical properties of the cells.

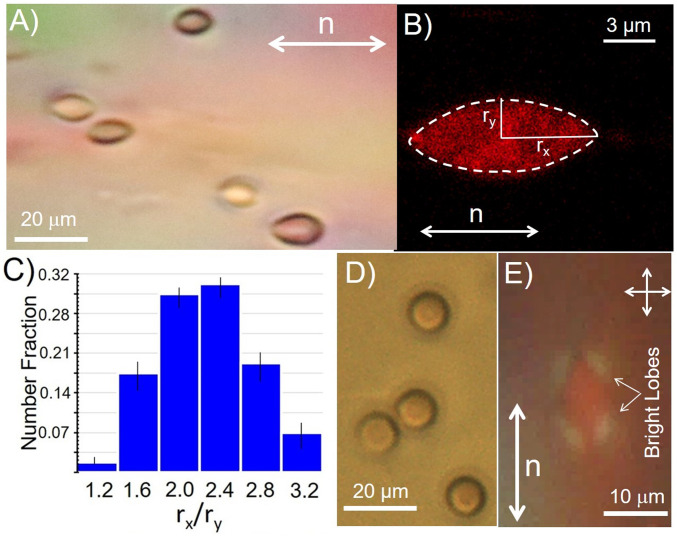
In contrast to the biconcave shapes of RBCs observed in NaCl solutions (Fig. 2A), Fig. 3A shows optical micrographs of RBCs suspended in nematic LC phases of 17.3 wt % DSCG at 25 °C. Inspection of Fig. 3A reveals that the RBCs in the nematic phase of DSCG assume extended shapes with major axes aligned parallel to the far-field orientation of the LC (white arrow in Fig. 3A). To further characterize the shapes of the RBCs in nematic DSCG, we performed confocal fluorescence scanning microscopy of stained RBCs. The RBCs were dispersed in isotonic NaCl solutions and treated with a membrane-staining dye (DiD) at concentrations of 15 µM for a period of 3 h (42). Stained cells were then ultracentrifuged and washed in isotonic NaCl solutions twice before dispersing them in DSCG solutions. Consistent with bright-field optical microscopy images in Fig. 3A, the confocal images shown in Fig. 3B reveal the RBCs to be strained and aligned by the LC. We characterized the shapes of the strained RBCs by quantifying the cell major (r_x) and minor axes (r_y) apparent in the projections of the cell shapes shown in Fig. 3 (x corresponds to the far-field orientation of the LC director, and y is the orthogonal direction in the plane of the two surfaces that confine the LC). The aspect ratios r_x/r_y, as shown in Fig. 3C for over 200 strained RBCs, are polydisperse, ranging from 1.4 to 3.2 (2.3 ± 0.6). In contrast, the equivalent aspect ratios of RBCs prior to straining are almost monodisperse, with r_x/r_y ∼1.04 ± 0.07 (SI Appendix, Fig. S1A). We interpret the emergence of the broad distribution of values of r_x/r_y for the strained RBCs to indicate cell-to-cell variation in mechanical properties within the cell population. This interpretation is supported by past results obtained with synthetic GUVs in LCs, in which GUV strain was similar for a given size of GUV (14). We also note that measurement of the distribution of strains (r_x/r_y) reported in Fig. 3C is rapid, as many cells can be imaged in parallel within a sample of LC. For instance, Fig. 3A (showing five strained cells) is cropped from an optical micrograph containing over 60 RBCs (SI Appendix, Fig. S1B). Additional discussion of the interpretation of RBC optical images in terms of cell shape is presented in SI Appendix.

Fig. 3.

(A) Optical micrograph of strained RBCs suspended in a nematic LC phase (17.3 wt % DSCG aqueous solution) at 25 °C. The far-field director of the LC is shown by the white arrow. (B) Confocal micrograph of a strained RBC dispersed in the nematic LC phase described in A. (C) Histogram showing the variation in values of r_x/r_y for 120 RBCs strained by a nematic LC phase. (D) Optical micrograph of sample in A following heating of the nematic DSCG phase into an isotropic phase (39 °C). (E) Optical micrograph (crossed polarizers) showing nematic DSCG strained around a RBC.

Upon heating the aqueous LC to 39 °C at 2 °C/min to form an isotropic phase, we observed the RBCs to recover their characteristic homogeneous, biconcave shapes (Fig. 3D) within a few seconds of the phase transition into the isotropic phase. Additionally, prior to the phase transition, by observing the optical appearance of the LC around the RBC, as shown in Fig. 3E, we were able to confirm that the LC aligns tangentially to the interface of the RBCs without evidence of topological defects (Fig. 1D). This observation was confirmed through Polscope mapping of the orientation of the LC around an RBC (SI Appendix, Fig. S2).

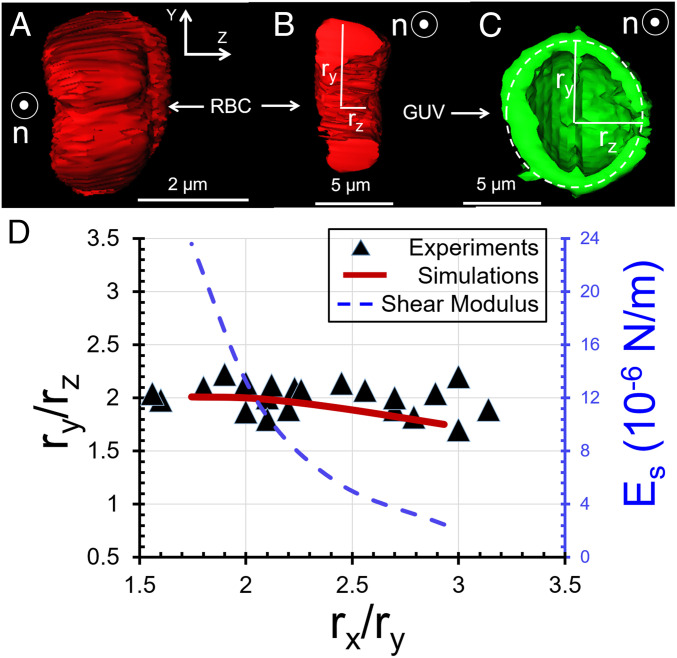
The LC-driven changes in shape of RBCs, as shown in Fig. 3 A and B, are substantially more complex than the stretching of spherical GUVs with fluid membranes into axisymmetric spindle shapes by LCs (14). Specifically, the biconcave RBCs in our experiments possess a line of symmetry that is perpendicular to the principal direction of strain imposed by the LC (along the LC director [x-axis], see Fig. 1), which leads to an intricate interplay between LC-elasticity and solid, membrane-elasticity of the RBC (24, 43). Three-dimensional (3D) reconstruction of z stacks of confocal fluorescence images (Fig. 4A and Movie S1) reveal that the fore/aft ends of the stretched RBCs converge to lines, unlike axisymmetric GUV spindles that converge to points. Additionally, the two-dimensional cross-sections (x-y and z-y planes) of strained RBCs also reveal the dimensions of the RBCs in the y (r_y) and z (r_z) directions differ by a factor of 1.9 ± 0.2, as shown in Fig. 4B (experiments were performed at 25 °C). For comparison, Fig. 4C shows a y-z cross-section of a strained GUV (obtained by confocal microscopy), revealing the circular cross-section of the spindle shape assumed by the GUV (i.e., r_y = r_z). Fig. 4D shows r_y/r_z of RBCs plotted as a function of r_x/r_y, revealing r_y/r_z varies little between cells (1.9 ± 0.2) while r_x/r_y varies substantially (see also SI Appendix, Fig. S3D for individual values of r_x, r_y, and r_z). Below we provide additional insight into this observation by using both high-magnification optical imaging and numerical simulations.

Fig. 4.

(A) End-on view (looking along the LC director) of the 3D shape of a LC-strained RBC obtained using confocal microscopy. The LC was aqueous 17.3 wt % DSCG at 25 °C. (B) y-z cross-section of the strained RBC described in A. (C) y-z cross-section of a GUV strained by the nematic LC described in A. (D) Values of r_y/r_z plotted as a function of r_x/r_y (experimental measurements as symbols, simulation results as a solid curve) for RBCs dispersed in the LC described in A. Calculated shear moduli are also plotted as a function of r_x/r_y on the right-side ordinate (dashed curve).

The optical imaging described above was performed in LC. To avoid scattering of light from LC orientational fluctuations when performing high-resolution imaging, we strained RBCs in DSCG and then treated the cells with 0.1 vol% of glutaraldehyde for 2 h (44). Glutaraldehyde cross-links the hemoglobin inside the RBC, which we predicted would cause the RBCs to retain their LC-strained shapes upon the removal from the LC. Cross-linked RBCs were ultracentrifuged, rinsed three times with water, and imaged under bright-field illumination conditions (Fig. 5A). Inspection of the optical micrograph in Fig. 5A reveals cells with aspect ratios similar to those observed in confocal microscopy (Fig. 3B) but also the presence of a fold along the midplane of each strained RBC (independent of r_x/r_y). The figure provides insight into why r_y/r_z is observed to assume values of 1.9 ± 0.2: the y-z cross-section of the strained shape of the RBC is geometrically similar to two elongated spindles connected by a fold (Fig. 1F).

Fig. 5.

(A) Optical micrograph (63× objective) of RBCs that were cross-linked when strained by nematic LC (17.3% DSCG at 25 °C). The images were obtained after removal of the LC. (B) Triangular surface mesh of a simulated RBC in its initial biconcave configuration (prior to relaxation in LC). (C) Simulation of the RBC shape change as a function of time in nematic LC. (D) Simulated cross-section showing equilibrium RBC shape and LC configuration (Movie S2). (E) Simulated relaxation of RBC shape metrics r_x/r_y and r_y/r_z to equilibrium values when the RBC was dispersed in a LC.

To advance our understanding of the shape-response of RBCs in LCs, and to enable interpretation of the shape changes in terms of RBC mechanical properties, we performed a series of numerical simulations using a modification of the Immersed Boundary Method (45) (a complete description of the approach is provided in SI Appendix). The orientational order of the LC in our simulations was characterized by a second-rank tensor $\mathbf{Q}$ (Landau–de Gennes model, (46, 47), which in a uniaxial LC system reduces to $\mathbf{Q}=S\left(\mathit{nn}-\mathbf{I}/3\right)$, where S is the scalar order parameter, $\mathit{n}$ is the director field, $\mathit{nn}$ is a dyadic product, and $\mathbf{I}$ is the identity operator (48, 49). The assumed uniaxial symmetry is expected to be a good approximation in our simulations due to the weak surface anchoring of the LC on the surface of the RBCs (as evidenced by the absence of topological defects in our experiments). Following (48, 49), the free energy associated with $\mathbf{Q}$ can be written as a combination of short-range and elastic contributions. The short-range energy density is

$$f_S\left(\mathbf{Q}\right)=\frac{A}{2}\left(1-\frac{U}{3}\right)\text{tr}\left({\mathbf{Q}}^2\right)-\frac{AU}{3}\text{tr}\left({\mathbf{Q}}^3\right)+\frac{AU}{4}\text{tr}{\left({\mathbf{Q}}^2\right)}^2$$ [1]

where $A$ is a numerical prefactor that sets the energy scale for the phase transition and $U$ is a dimensionless nematic strength. The scalar order parameter (prior to introduction of the RBC) is approximately $S=\frac{1}{4}+\frac{3}{4}\sqrt{1-8/3U}$. The model predicts a nematic phase for $U>2.8$ (we used a nematic strength of U = 3.4). The elastic energy density is evaluated as

$$f_E\left(\mathbf{Q},,,\nabla ,\mathbf{Q}\right)=\frac{L_1}{2}{\left(\nabla \mathbf{Q}\right)}^2+\frac{L_2}{2}{\left(\nabla ·\mathbf{Q}\right)}^2+\frac{L_3}{2}\mathbf{Q}:\left(\nabla \mathbf{Q}:\nabla \mathbf{Q}\right)$$ [2]

where, in terms of Frank elastic constants (K₁, K₂, K₃), the parameters L_i are evaluated as L₁ = (3K₂ − K₁+K₃)/6S², L₂ = (K₁ − K₂)/S², and L₃ = (K₃ −K₁)/2S² with K₁ = K₃ = 10 pN and K₂ = 1 pN. The molecular field H is defined as the symmetric and traceless part (${\left[...\right]}^{ST}$) of the variational derivative of the free energy with respect to $\mathbf{Q}$,

$$\mathbf{H}={\left[\frac{\delta \mathcal{F}}{\delta \mathbf{Q}}\right]}^{ST}=-L_1{\nabla }^2\mathbf{Q}-L_2[\nabla \left(\nabla ,·,\mathbf{Q}\right){]}^{ST}+A\left(1-\frac{U}{3}\right)\mathbf{Q}-AU\left({\mathbf{Q}}^2-\text{tr}\left({\mathbf{Q}}^2\right)\left(\mathbf{Q}+\frac{1}{3}\mathbf{I}\right)\right),$$ [3]

where $\mathcal{F}$, the free energy, is the volume integral of $f_S+f_E$. Deviations from a tangential orientation of the LC on the surface of the RBC are penalized with a Rapini–Papoular anchoring energy, which is treated as a volumetric energy density with the introduction of smoothed delta functions. This approach enables an Immersed Boundary approach to spreading forces and torques from the LC to the RBC and vice versa (SI Appendix and ref. 50). We made two approximations in our model for tractability. First, an artificially small rotational viscosity $\left(\gamma \right)$ was assumed, which provides a separation of timescales between director-field relaxation and fluid flow. In this limit, given a membrane shape at a time $t$, the $\mathbf{Q}$ tensor first relaxes to equilibrium following $\partial \mathbf{Q}/\partial t=-\mathbf{H}/\gamma$ until $\mathbf{H}=\mathbf{0}.$ The fluid (LC) velocity and surface geometry then evolve due to the LC stresses in quasi-steady manner. Second, we included LC within and outside the RBC in our model, and we regulated the anchoring strength of the LC on the cell surface to mechanically couple the LC and RBC in a manner consistent with experiments (see below).

To model the RBC shape-response to LC mechanical environment, we used the Skalak strain energy density:

$$W=\frac{E_S}{4}\left(I_1^2+2I_1-2I_2\right)+\frac{E_D}{8}{I}_2^2,$$ [4]

where E_s and E_D are the elastic shear and dilatation moduli (constants), respectively, and I₁ and I₂ are the strain invariants (51). In the Skalak model, the RBC membrane is assumed to be an isotropic and hyperelastic surface, with a strain energy potential that depends on deformation away from an initial biconcave configuration. The strain energy potential is written in terms of the invariants of the surface strain tensor (SI Appendix, Surface Forces and Evolution). For the initial simulation, guided by past studies, we used E_S = 4 × 10⁻⁶ N/m and E_D = 10⁻⁴ N/m (29). A triangular surface mesh was used to discretize the RBC surface, as shown in the reference configuration in Fig. 5B. The system was made dimensionless by scaling lengths using the semimajor axis length a = 4 μm, forces using L₁ = 10 pN, time using a²μ/L₁, velocity using L₁/(aμ), and energies using aL₁, where μ is the Newtonian viscosity (0.2 Pa ⋅ s). This scaling leads to a dimensionless shear modulus of $E_S^{\ast }=\left(\mathrm{a}/L_1\right)=1.6$ and dilational modulus $E_D^{\ast }=\left(\mathrm{a}/L_1\right)E_D=40$. In the simulations described below, we did not include bending; the bending stiffness of an RBC is roughly B = 1.8 × 10⁻¹⁹ N ⋅ m (52–54); the dimensionless bending stiffness is given by B* = B/(aL₁) = 0.0045 and thus is negligible (confirmed by computations that did include a bending energy). That $E_S^{\ast }$ is close to unity indicates that the LC and RBC-membrane elastic energies are comparable, consistent with our experimental observations.

Fig. 5 C–E shows examples of the shape-responses of RBCs to LC mechanical environments, as predicted by our simulations. The coupling of the LC elasticity and RBC mechanical strain is dependent on the anchoring energy of the LC on the cell surface (SI Appendix, Fig. S7). The predictions in Fig. 5 were performed using an anchoring energy of 2.5 × 10⁻⁵ J/m², a value that is sufficiently small to not generate topological defects in the simulations (in agreement with experiment). In addition, the use of anchoring energies weaker than 2.5 × 10⁻⁵ J/m² resulted in simulated RBC shapes that were not as strained as those seen in experiments (SI Appendix, Fig. S7). Consistent with experiment, inspection of Fig. 5C reveals that the initial depression in the biconcave configuration stretches to a fold along the axis of symmetry of the strained RBC. The stretched RBC thus retains some “memory” of its initial configuration. The final RBC shape and LC director field at equilibrium are shown in Fig. 5D (Movie S2). The director field close to the surface is nearly tangential to the body, as seen in the experimental image in Fig. 3E. Fig. 5E shows the computed relaxation of r_x/r_y as function of time (r_y/r_z, Inset), revealing an equilibrium value of r_x/r_y = 2.3, in good agreement with the experimentally observed values as shown in Fig. 4D. Simulations performed with an order of magnitude larger shear modulus (E_S = 4 × 10⁻⁵ N/m) yielded equilibrated RBC shapes that were less strained compared to our experimental observations (SI Appendix, Fig. S8 and Fig. 5E). The simulations also led to the appearance of a slow timescale in which the two lobes seen in Fig. 5C continue to expand along the z direction (Movie S3).

We compared experimentally measured aspect ratios (r_x/r_y) to predictions of shape from our simulations to obtain an estimate of the cell-to-cell variation in the shear moduli of the RBCs. Fig. 4D shows the ratio r_y/r_z calculated from our simulations (red solid line) to be in good agreement with the experiments (1.9 ± 0.2) when using the values of E_s shown by the blue (dashed) line in Fig. 4D; the values of r_x/r_y were insensitive to E_D, indicating that the shape response occurred at constant membrane surface area. The stiffer RBCs in our experiments, which were strained to r_x/r_y ∼1.7, were calculated to have E_s ∼ 16 × 10⁻⁶ N/m and RBCs that were strained to r_x/r_y ∼3 were estimated to have E_s ∼ 2 × 10⁻⁶ N/m. These results demonstrate that LC-based methods can be used to rapidly characterize cell-to-cell variations in the mechanical properties of individual cells within populations. Using an empirical expression, E_s = 2.8 × 10⁻⁴ (r_x/r_y)^-4.4 N/m, for the variation of E_S with r_x/r_y presented in Fig. 4D, we compute the average shear modulus (weighted with the statistics in Fig. 3C) to be 8.4 ± 5.6 × 10⁻⁶ N/m.

Additional simulations revealed that changes in the dilatation modulus (smaller or larger by an order of magnitude) and the inclusion of a nonzero bending modulus (B = 1.8 × 10⁻¹⁹ N ⋅ m) had no influence on the equilibrium body shape since the surface remains effectively inextensible, and the bending energy is negligible compared to other energies. Because calculated changes in LC-driven RBC shape occur at constant RBC volume, the good agreement between simulated and experimental RBC shape changes (Fig. 4D) leads us to conclude that RBC shape changes in experiments are also isovolumetric. Changes in the nematic correlation length, ξ_N (ranging from 2.6 × 10⁻⁶ m to 1.2 × 10⁻⁵ m) also showed little effect. The LC configuration and RBC shapes were not sensitive to order of magnitude changes in the twist modulus K₂ (L₂/L₁ ranging from 0.1 to 10; this corresponds to K₂ ranging from 0.1 to 10 pN), nor to changes in the nematic strength U, until U neared the critical value of 2.8. The primary determinants of RBC shape at equilibrium were the LC elasticity, RBC elastic shear modulus, E_S, and the LC-RBC surface anchoring strength.

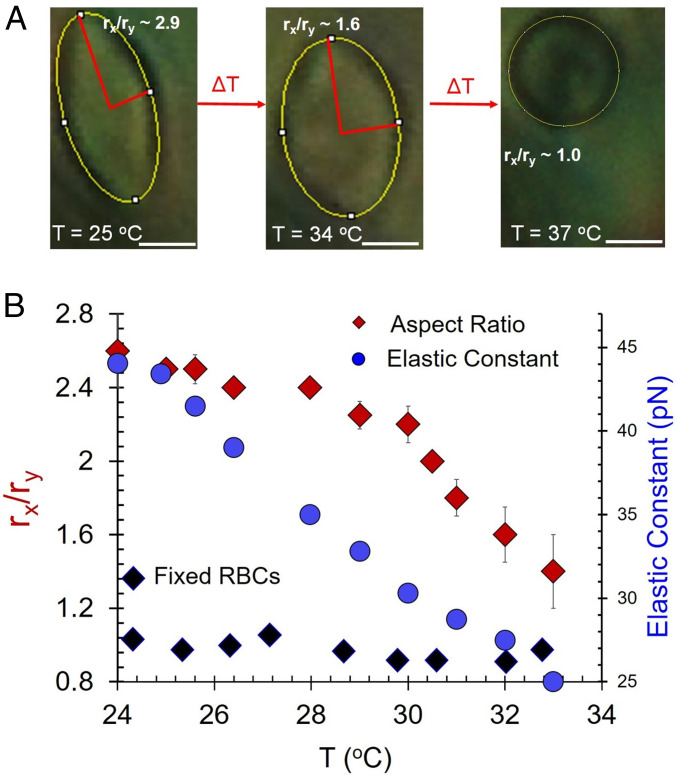
To provide additional evidence that LC elasticity is responsible for the RBC shape changes described above, we quantified r_x/r_y of strained states of RBCs as a function of temperature and thus elastic properties (18) of the DSCG phase. Inspection of Fig. 6A reveals that r_x/r_y decreased continuously from 2.5 to 1.3 as a function of increasing temperature, consistent with temperature-dependent changes to the elastic constants of the LC (blue circles in Fig. 6B are the values of K₃ for 18 wt % DSCG replotted from ref. 18). In contrast to native RBCs, we measured glutaraldehyde-treated (and hence stiffer) RBCs (with biconcave shape) to not be measurably strained by the elasticity of the LC over the temperature range investigated, as shown in Fig. 6B (black diamonds; images shown in SI Appendix, Fig. S4) (10). A discussion of the temperature dependence of the osmotic pressure can be found in SI Appendix (see text accompanying SI Appendix, Fig. S6).

Fig. 6.

(A) Optical micrographs showing the change in shape (characterized by r_x/r_y) of a RBC in aqueous 17.3% DSCG as a function of temperature (scale bar, 4 µm.) (B) Plots of r_x/r_y of healthy and glutaraldehyde-treated RBCs plotted as a function of temperature for RBCs dispersed in 17.3% DSCG. The variation in K₃ of the DSCG phase (blue dots show data from ref. 18; see text for details) with temperature is shown in the same plot. Black diamonds are RBCs that were cross-linked with glutaraldehyde prior to dispersing in LC.

Aqueous 17.3 wt % DSCG forms coexisting isotropic and nematic domains at temperatures between 35 and 39 °C. We used this two-phase region to explore the reversibility of the RBC shape response to LC mechanical stresses by observing RBC shapes as cells moved between isotropic and nematic domains in the biphasic region. A small change in temperature was observed to result in motion of the nematic–isotropic interface (and the RBC), leading to the transfer of an RBC from an isotropic region (SI Appendix, Fig. S5A, t = 0) to a nematic region (SI Appendix, Fig. S5B, t = 10 s) and a change in shape from a biconcave disk to an elongated and folded geometry (shown in Movie S4). Because the osmotic pressure in the two phases is equal, these results provide additional support for our conclusion that the strained shape of the RBC in the nematic region is predominantly due to the LC elasticity. Additionally, within the biphasic region, as shown in SI Appendix, Fig. S5 B–D, it was possible to cycle between a narrow range of temperatures (35–39 °C) and reversibly change the phase of the DSCG solution and shapes of the RBCs between strained and biconcave. We observed the shapes of the RBCs to relax within 1 s of transfer between phases.

Conclusions

This paper describes how the sharing of strain between LCs and RBCs can drive RBCs to assume complex and folded shapes. A key finding enabling our study is the discovery of a LC that is in osmotic equilibrium with the interior of a RBC. Under these conditions, the shape responses of RBCs to the viscoelastic environment of the LCs reflect their solidlike, elastic membranes, and lead to folded shapes that contrast with the shapes exhibited by soft assemblies with fluid membranes (GUVs) dispersed in LCs. Our results also provide fresh insight into the mechanical properties of RBCs. Specifically, we show that populations of RBCs that present homogeneous shapes in isotropic aqueous buffers exhibit a broad distribution of shape responses to the elastic stresses imposed by LC, revealing that the mechanical properties of individual cells (elastic shear modulus from 2 to 16 × 10⁻⁶ N/m) vary substantially across a population. We also show that RBCs fixed with glutaraldehyde, a common model of the mechanical properties of malarial cells (44), exhibit a shape response to stresses imposed by LC that reflects increased cell rigidity. In contrast to previously reported techniques for measurement of single-cell mechanical properties (28, 33, 34), our methodology based on LCs enables parallel measurements of changes in the shapes and mechanical properties of large numbers of RBCs. This allows quantification of cell-to-cell variation in mechanical properties of RBCs within a population. Such measurements are important in physiological contexts where “outlier” cell properties can dominate symptoms of a disease (e.g., a small fraction of a population of cells are rigid, but these block capillaries).

Our observations of the shape responses of soft mammalian cells to the mechanical properties of LCs also generate a number of open questions related to structure–property relationships of RBCs that require future study. For instance, although we observe the shapes of the RBCs to equilibrate within seconds of changing the nematic stress acting on a cell, the role of the dynamic reorganization of the spectrin network in influencing the shape transitions of RBCs described in this work remains to be fully understood. It is possible that remodeling of the spectrin network occurs upon cycling of the RBC between the nematic and isotropic phases of the LC, thus leading to time-dependent RBC mechanical properties on timescales outside those reported in this paper. Additionally, whereas past studies have revealed that aqueous solutions of DSCG are compatible with living cells, it is possible that hydration and other thermophysical properties of RBC membranes are altered upon contact with the LC used in our study. The results presented in this paper provide motivation for investigations of these issues.

We envision our results forming the basis for simple analytical (e.g., research or diagnostic) tools that can rapidly report the mechanical properties (and thus health) of mammalian cells. For example, the methods reported in this paper can be used to screen the mechanical properties of diseased cells and the response of cells to therapeutic treatments (e.g., drugs used to treat sickle cell disease). Our study also offers the opportunity to study other cellular processes including the influence of strained cell shapes on membrane fluctuations and the presence or absence of small molecules (e.g., adenosine triphosphate) in regulating the mechanical properties and shapes of RBCs (55).

Materials and Methods

Materials.

Human RBCs were purchased from Innovative Research Inc. and redispersed in an isotonic solution of NaCl (154 mM) following ultracentrifugation. The membrane staining dye 1, 1′ dioctadecyl-3, 3, 3′, 3′ tetramethylindodicarbocyanine, 4-chlorobenezenesulfonate salt (DiD′) was purchased from Avanti Polar Lipids, Inc. and used to stain RBCs for confocal scanning microscopy. Disodium cromoglycate was purchased from Sigma-Aldrich. Fisher’s Finest premium-grade glass slides and cover glass were purchased from Fisher Scientific. Deionization of a distilled water source was performed with a Milli-Q system (Millipore) to prepare water with a resistivity of 18.2 MΩ cm.

Microscopy.

Images were obtained with an Olympus BX41 fitted with 50× and 63× objectives. Polscope imaging was performed with an Olympus CX60 microscope equipped with a Cambridge Research Incorporated Abrio LC-PolScope package. The LC-PolScope used monochromatic illumination at 640 nm. A Carl-Zeiss LSM 700 laser scanning confocal microscope was used to obtain the confocal micrographs using a 632-nm laser.

Dispersing RBCs in Lyotropic LCs.

Lyotropic LCs containing DSCG were prepared by mixing 17.3 wt % of DSCG with 82.7 wt % water. The mixture was placed on a shaker for at least 4 h to ensure homogeneity. Then, 0.5 vol% (0.5 µL) of RBCs dispersed in isotonic aqueous NaCl solutions were added to the (100 µL) DSCG solution and gently stirred to disperse the RBCs in the DSCG solution. The pH of the 17.3 wt % DSCG solution as prepared was measured to be 9.2. We used 1 M HCl solutions to lower the pH to 7.4. The experimental results presented in this paper were found to be independent of pH for values between 9.2 and 7.4.

Data Availability.

All study data are included in the article and SI Appendix.