Laterally Resolved Small-Angle Scattering Intensity from Lipid Bilayer Simulations: An Exact and a Limited-Range Treatment

Abstract

When combined, molecular simulations and small-angle scattering experiments are able to provide molecular-scale resolution of structure. Separately, scattering experiments provide only intermingled pair correlations between atoms, while molecular simulations are limited by model quality and the relatively short time scales that they can access. Their combined strength relies on agreement between the experimental spectra and those computed by simulation. To date, computing the neutron spectra from a molecular simulation of a lipid bilayer is straightforward only if the structure is approximated by laterally averaging the in-plane bilayer structure. However, this neglects all information about lateral heterogeneity, e.g., clustering of components in a lipid mixture. This paper presents two methods for computing the scattering intensity of simulated bilayers with in-plane heterogeneity, enabling a full treatment of both the transverse and lateral bilayer structure for the first time. The first method, termed the Dirac Brush, computes the exact spectra including spurious artifacts resulting from using information from neighboring periodic cells to account for the long-range structure of the bilayer. The second method, termed PFFT, applies a mean-field treatment in the field far from a scattering element, resulting in a correlation range that can be tuned (eliminating correlations with neighboring periodic images), but with computational cost that prohibits obtaining the exact (Dirac Brush) spectra. Following their derivation, the two methods are applied to a coarse-grained molecular simulation of a bilayer inhomogeneity, demonstrating the contributions of lateral correlations to the resulting spectra.

Graphical Abstract

1. INTRODUCTION

The molecular structure of cellular membranes remains a central problem in biophysics. The lateral distribution of membrane constituents has spawned an enormous literature, motivated by the raft idea of Simons and co-workers,^1,2 which posits that lipids and proteins conspire to colocalize signaling partners for functional ends. Thus, the thermodynamic behavior of well-defined mixtures of phospholipids and cholesterol has been extensively studied^3–12 as a model for the plasma membrane to discern whether such mixtures might mimic a raftlike organization. Phase diagrams of ternary mixtures that include cholesterol as a component reveal a region of composition space in which two distinct fluids coexist.⁹ Coexistence of liquid-ordered (L_o) and liquid-disordered (L_d) phases has been observed by fluorescence microscopy,^9,13 NMR¹⁰ and EPR spectroscopies,^14–17 distributions of FRET donor–acceptor pairs,¹⁶ and X-ray¹⁸ and neutron scattering.¹⁹

While significant progress has been made in classifying the phase regions of multicomponent lipid mixtures, far less is known about the lipid distributions within individual phases. The L_o phase is enriched in sterol and lipids with higher chain-melting temperatures (e.g., sphingomyelins), resulting in more ordered hydrocarbon chains,¹⁰ a smaller area per lipid,²⁰ and a thicker bilayer than the L_d phase.²¹ Atomistic simulations indicate that the distribution of phospholipids and cholesterol within the L_o phase is also heterogeneous, comprising regions of hexagonally packed substructures of a few nanometers in size, interspersed with more disordered regions.^21,22 Much more complex mixtures of lipids and proteins obtained by swelling large vesicles directly from living cells also phase separate into coexisting fluid phases,^23–25 suggesting that simpler lipid mixtures remain a useful model for the plasma membrane.

Given that signaling events at the membrane often entail the encounter of two or more partners, the lateral organization of lipids on the 5–10 nm length scale is of particular interest. Experimental measurements capable of revealing features on this length scale therefore warrant special consideration. While some fluorescence-based methods are useful for this purpose,^26–28 scattering methods offer a complementary approach that does not require the introduction of bulky spin or fluorescent labels that may perturb lipid phase behavior.^13,29,30 Neutron scattering is especially powerful, by virtue of the neutron’s short wavelengths, compared to visible light, and the large difference in coherent scattering length between hydrogen’s stable isotopes protium (¹H) and deuterium (²H). It has been used alongside molecular dynamics simulation (MD) for over 15 years to uncover the details of transverse membrane structure.^31–35 More recently, the joint refinement of force-field parameters against neutron and X-ray scattering data has led to significant improvements in lipid models.^36–38

Recent work has focused on lateral structure. A judicious choice of deuteration scheme readily reveals features of lateral organization down to about 5 nm, as shown recently by Heberle et al. using small-angle neutron scattering (SANS) to detect nanoscale domains in unilamellar vesicles.³⁹ A similar approach was used to infer the presence of nanoscopic domains in the membrane of B. subtilis.⁴⁰ However, detection of lateral structure in the 5–10 nm range by SANS alone is nontrivial. First, the range of deuteration schemes is complicated by the incoherent background of the protium in the sample, which makes the detection of small signals challenging. Second, and more importantly, the scattering from isotropic aqueous liposome dispersions mixes the desired signal arising from in-plane contrast (i.e., domains) with that arising from the transverse contrast normal to the plane of the bilayer—as well as from the size and shape of the vesicle. To a great extent, prior SANS experiments and concomitant analysis exploited the variation in contrast in the transverse direction, from solvent, to hydrocarbon, and back to solvent. It is reasonable to consider only transverse contributions to the scattering signal if the sample is laterally homogeneous on the length scale of interest. This approach fails, however, if the goal is to identify lateral structure on 5–10 nm length scales. For this purpose, a method that allows direct calculation of the SANS intensity from an MD simulation—without any assumptions about lateral averaging—would be of great value.

Here, we introduce new methods for computing the SANS intensity directly from MD simulations (all-atom or coarse-grained) of planar bilayers. The problem of incorporating scattering correlations between a target region (i.e., a nanoscopic region of the bilayer) and the surrounding material is analogous to treating a protein solvated in water. A number of software approaches make distinctions between the water layer near the protein and the bulk water whose structure and density are uncorrelated to the configuration of the protein.^41–43 This approach is viable due to the finite size of the protein, but it is not easily extended to bilayers which are effectively simulated as infinite sheets. Typical all-atom simulation sizes are 10–20 nm, a length scale that is sufficient to capture the local structure described above. However, a naïve approach that includes only contributions from correlations within the simulation box fails to accurately predict the SANS intensity in a way that allows meaningful comparison with experimental data. Here, we describe two methods that resolve the finite-size issue in different ways. The Dirac Brush method (whose name is derived from a hairbrush-like two-dimensional array of Dirac delta functions in Fourier space) is based on replication of the central box. It is relatively straightforward but includes periodic boundary condition artifacts that result from including correlations with neighboring cells, which, unlike for a fluid or protein, is generally necessary when considering a system with long-range correlations like a bilayer. The second approach, which we term the Particle-Far-Field Transform (PFFT) method, uses direct particle–particle correlations for near-field contributions and a laterally averaged continuum for the far-field contributions. Using a variable cutoff between full discrete scattering and a mean-field model, PFFT allows a range of correlations to be systematically investigated.

Both the Dirac Brush and PFFT methods differ significantly from existing approaches, such as implemented in SimToExp⁴⁴ and SASSENA,⁴⁵ as applied to bilayers. SimToExp first averages the atomic scattering length densities in the plane of the membrane to produce a one-dimensional profile that accounts for contrast only in the transverse direction, which is then followed by a one-dimensional Fourier transform to compute the scattering intensity. This is typically the dominant portion of the scattering intensity and is often sufficient to infer agreement with the simulated structure. In SASSENA the orientational averaging is not performed in closed form as can be done following laterally averaging (shown below). This results in an expensive calculation, especially for a high-symmetry system, such as a lipid bilayer with periodic boundary conditions. In contrast, both the Brush and PFFT methods compute the SANS intensity for the periodically replicated system with closed-form orientational averaging. These methods therefore solve the problem that we stated above: i.e, the prediction of scattering intensities directly from simulations of bilayers with lateral structure.

The paper is structured as follows. A description of neutron scattering and how the behavior of nuclei as “point-scatterers” of neutrons translates to the relatively simple SANS signal at the detector is provided in the Supporting Information. In section 2 the process by which internal correlations produce an interference pattern at the detector is explained, beginning with an isolated system (section 2.2) and then moving to an infinite two-dimensional slab (section 2.3). Two mathematical formalisms useful for computing intensities, the Fourier transform and the Debye scattering formula, are explained in section 2.2. These formalisms form the basis for the two complementary approaches explained in Methods (section 3): first the “Brush” method (section 3.1), which uses the full correlations manifest in periodic boundary conditions by orientationally averaging the Fourier transform of the scatterers, and second the PFFT method (see section 3.3), which uses the Debye formula and a continuum approximation for far-field correlations.

To demonstrate how in-plane correlations affect the scattering signal, a simple molecular system was constructed using the coarse-grained Martini force field. In section 3.3 we describe how the system was constructed from two lipid species that separate into a majority and minority domain with sizes limited artificially by periodic boundaries. In Results (section 4), the PFFT, Brush, and laterally averaged intensities are presented, showing the presence or absence of lateral correlations of the coarse-grained systems.

2. BACKGROUND

2.1. Small-Angle Scattering Reports the Internal Structure of a Sample.

Neutron waves interact with the nuclei of the sample atoms and continue to travel until they are absorbed by the detector (although this discussion focuses on neutrons, the approach is general to X-rays, which are scattered by the electron cloud). The detector consists of a two-dimensional array of small elements, which detect neutrons and produce an electronic signal. The internal structure of the atomic scatterers yields a specific interference pattern of the scattered waves. If the sample consists of randomly oriented particles (i.e., powder samples, including lipid bilayer vesicles in solution), the intensity measured at the detector will manifest as concentric rings with no angular dependence. For such samples, the intensity signal is reduced to a one-dimensional graph by reporting only the angularly averaged intensity, I_Ω(q), for each radial distance from the center of the detector.

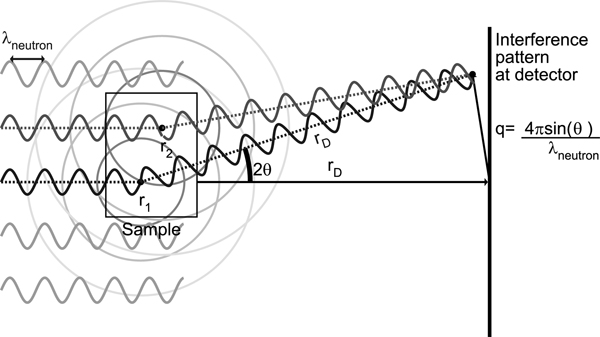
Analytical models for the scattering intensity start with an idealized configuration for a SANS experiment, shown in Figure 1. The coordinate system is chosen such that the path of the incoming beam of neutrons is along $\widehat{\mathbf{z}}$, the unit vector along the positive z axis. The phase relevant to interference at the detector can be computed from two paths. First, from the neutron source to particle r₁ the neutron accumulates phase $e^{i\mathbf{k}\cdot {\mathbf{r}}_1}$ before it scatters (relative to a particle at the origin). It then undergoes elastic scattering with the same magnitude of momentum, but in a new direction k′, with $|{\mathbf{k}}^{\prime }|=|\mathbf{k}|$. The scattered neutron travels to the detector, accumulating phase $e^{i{\mathbf{k}}^{\prime }\cdot \left({\mathbf{r}}_{\text{D}}-{\text{r}}_1\right)}$ (the sign is now flipped because with the origin at the sample, the detector is in the direction opposite to that of the neutron source). The scattering direction k′ is determined by where the neutron registers at the detector, r_D. The observable, I(q), depends only on the difference q = k − k′.

Figure 1.

Schematic of a SANS experiment. Not shown is the possibility of the sign of the scattered wave flipping by 180° due to scattering (e.g., in the case of hydrogen).

The amplitude of the scattered wave depends on the identity of the particle from which it scattered. Each type of nucleus has an empirically measured coherent scattering length, b, and these scattering lengths are tabulated for the different elements.⁴⁶ Multiple internal nuclear states, uncorrelated with position, lead to incoherent scattering. This work considers only coherent scattering, in which each atom has a single average scattering length. The scattering observed from a typical sample is the sum of the waves scattered from each atom in the sample, and the magnitude of the squared neutron wave function at the detector decays as $r_{\text{D}}^{-2}$ Rather than carry this factor through every calculation, we define

$$I(\mathbf{q})=r_{\text{D}}^2{|\psi ({\mathbf{r}}_{\text{D}}(\mathbf{q}))|}^2$$ (1)

where each vector q maps to a single point on the detector r_D.

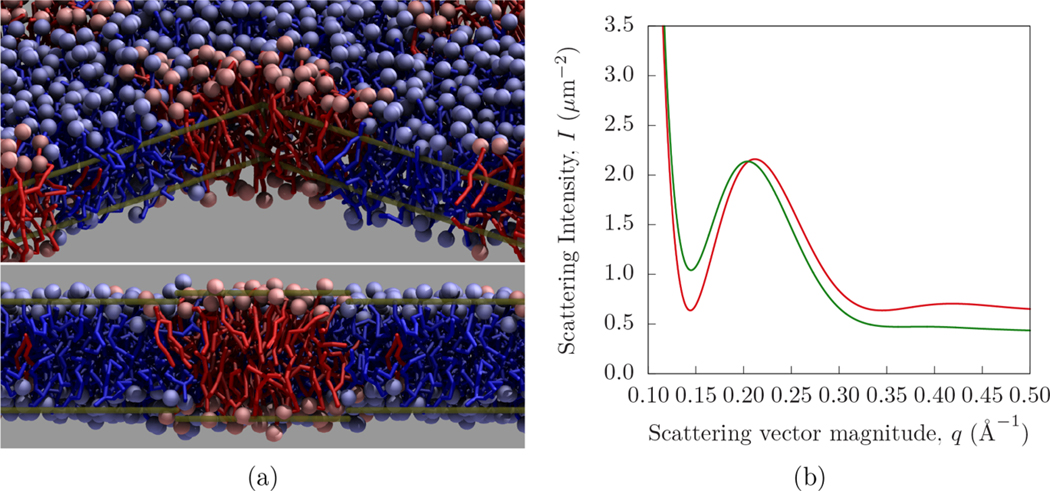
Figure 2 demonstrates the effect of lateral lipid inhomogeneity on a SANS signal (see section 3.3 for details). Viewed from above (in Figure 2a), the inhomogeneity has a lateral extent of approximately 6 nm. In Figure 2b, the SANS intensity is computed using lateral averaging, as well as the Dirac Brush and PFFT methods developed here. The difference between the existing and new methodologies is due to the lateral correlations (leading to overlaid “interference patterns”) that are taken into account by the Dirac Brush and PFFT approaches.

Figure 2.

Demonstration of the influence of a roughly circular lateral inhomogeneity on a SANS signal. The interior structure of the lipid bilayer is shown from two perspectives (a), by first hiding the foreground quadrant and second by cross section. DFPC lipids are shown in blue, while DPPC lipids are shown in red. Transparent gold lines indicate edges of the hidden quadrant in the first view and illustrate the bilayer thickness variation in the second view. The SANS intensities computed by PFFT (green) and lateral averaging (red) are compared to show the effect of lateral structure (b, in which the intensity near q = 0.14 Å⁻¹ is increased relative to higher q).

The intensity of the scattered signal is described by eq 2. When generalized to a continuum model, the scattering length is replaced with a scattering length density, β, and the summed contributions from all points in the sample are then represented by an integral, as shown in eq 3:

$$I(\mathbf{q})={\left|\sum _i{b}_i{\text{e}}^{-ı\mathbf{\text{q}}\cdot {\mathbf{r}}_i}\right|}^2(\text{particle representation})$$ (2)

$$I(\mathbf{q})={\left|\int {\text{d}}^3\mathbf{r}\beta (\mathbf{r}){\text{e}}^{-ı\mathbf{q}\cdot \mathbf{r}}\right|}^2(\text{continuum representation})$$ (3)

where β(r) is given by the relation in eq 4:

$$\beta (\mathbf{r})=\sum _i{b}_i\delta \left(\mathbf{r}-{\mathbf{r}}_i\right)$$ (4)

The absolute square can be expanded as

$$I(\mathbf{q})=\sum _{ij}{b}_i{b}_j{\text{e}}^{-ı\mathbf{q}\cdot ({\mathbf{r}}_i-{\mathbf{r}}_j)}$$ (5)

$$I(\mathbf{q})=\int {\text{d}}^3{\mathbf{r}}_1\int {\text{d}}^3{\mathbf{r}}_2\beta \left({\mathbf{r}}_1\right)\beta \left({\mathbf{r}}_2\right){\text{e}}^{-ı\mathbf{q}\cdot \left({\mathbf{r}}_1-{\mathbf{r}}_2\right)}$$ (6)

We will make use of both of these forms below.

2.2. Internal Structure of an Isolated System: The Debye Scattering Formula.

The orientationally averaged scattering of a single molecular configuration of a finite system can be computed using the Debye scattering formula. Replacing (r_i − r_j) = r_ij in eq 5 yields

$$I(\mathbf{q})=\sum _{i,j}{b}_i{b}_j{\text{e}}^{-ı\mathbf{\text{q}}\cdot {\mathbf{r}}_{\mathit{ij}}}$$ (7)

Orientational averaging is performed by sweeping the scattering vector, q, over the spherical polar angles, θ and ϕ. Each term in the summation can be integrated independently, so the coordinate system can be freely chosen such that r_ij always coincides with ϕ = 0, and therefore q·r_ij = qr_ij cos(ϕ). Integrating over the solid angle yields

$$\begin{gathered} I_{\mathrm{\Omega }}(q)=\sum _{i,j}{b}_i{b}_j\frac{1}{4\pi }{\int }_0^{2\pi }\text{d}\theta {\int }_0^{\pi }\text{d}\varphi \sin (\varphi ){\text{e}}^{-ıq{r}_{\mathit{ij}}\cos (\varphi )} \\ =\sum _{i,j}{b}_i{b}_j\frac{\sin \left(q{r}_{ij}\right)}{q{r}_{ij}} \end{gathered}$$ (8)

Equation 8 has no dependence on absolute particle positions and only takes into account the distribution of pairs of particle separations, r_ij, for a single configuration. Given an ensemble of system configurations sampled at temperature T, this distribution, B, of scattering-length-weighted pair separations can be recorded as shown in eq 9.

$$B(r)=\sum _{i,j}{b}_i{b}_j\delta (r_{ij}-r)$$ (9)

The intensity can now be computed as

$$I_{\mathrm{\Omega }}(q)=\int \text{d}rB(r)\frac{\sin (qr)}{qr}$$ (10)

For periodically replicated simulated systems, B(r) is replaced by its per-simulation-box average, $\overline{B}(r)$. The current standard approach to computing simulated scattering intensities, where the bilayer is laterally averaged, will be derived in the next subsection both with and without the use of B(r).

2.3. Internal Structure of Infinite, Laterally Averaged 2D Fluid.

Below we describe two mathematical approaches for obtaining the orientationally averaged scattering of an infinite flat surface. The first is a “direct” method that performs the orientational averaging explicitly, whereas the second “distribution” method first defines a weighted pair distribution function and then applies the Debye scattering formula for orientational averaging. The first derivation illustrates a challenge that we address using the Dirac Brush method: i.e., the coherent scattering is dominated by one orientation of the bilayer, in the infinite surface limit contributing as a δ function. The second derivation poses a challenge that we will address with the PFFT method: i.e., how to account for long-range uncorrelated density by constructing a weighted pair distribution.

2.3.1. Orientationally Averaged Scattering from a Laterally Averaged Bilayer, Computed Using the Fourier Transform.

Rather than a discrete set of scatterers {b_i}, consider instead a density of scatterers that are laterally uniform but vary along z—this is the assumption that underlies existing methods for interpreting the scattering intensity from lipid bilayers.

The laterally averaged density β_LA(z) is computed from a full 3D scattering length density as

$${\beta }_{\text{LA}}(z)=\frac{1}{L_x{L}_y}{\int }_{-L_x/2}^{L_x/2}\text{d}x{\int }_{-L_y/2}^{L_y/2}\text{d}y\beta (\mathbf{r})$$ (11)

that can then be computed from a collection of discrete scatterers by using the β(r) substitution from eq 4:

$${\beta }_{\text{LA}}(z)=\frac{1}{L_x{L}_y}\sum _i{b}_i\delta (z-z_i)$$ (12)

For an ensemble average, eq 12 is equivalent to eq 11. In computing the scattering intensity, the one-dimensional Fourier transform of β_LA(z) is a useful intermediate quantity:

$${\tilde{\beta }}_{\text{LA}}(q_z)={\int }_{-\infty }^{\infty }\text{d}{z}^{\prime }{\text{e}}^{-ıq_z{z}^{\prime }}{\beta }_{\text{LA}}(z^{\prime })$$ (13)

In the limit L_x → ∞, L_y → ∞, the three-dimensional Fourier transform is

$${\tilde{\beta }}_{\text{LA}}(\mathbf{q})={\int }_{-L_x/2}^{L_x/2}\text{d}{x}^{\prime }{\text{e}}^{-ıq_x{x}^{\prime }}{\int }_{-L_y/2}^{L_y/2}\text{d}{y}^{\prime }{\text{e}}^{-ıq_y{y}^{\prime }}{\tilde{\beta }}_{\text{LA}}\left(q_z\right)$$ (14)

where ${\tilde{\beta }}_{\text{LA}}(q_z)$ is from eq 13. When orientationally averaging in the limit L → ∞, first consider that

$${\int }_{-L/2}^{L/2}\text{d}{r}^{\prime }{\text{e}}^{-ıqr\prime }=2q^{-1}\sin (Lq/2)$$ (15)

In the limit of large L

$$L^{-1}{\left[2q^{-1}\sin (Lq/2)\right]}^2=2\pi \delta (q)$$ (16)

This follows from a definition of the δ function in terms of the limit, as Є goes to zero, of

$${\eta }_{\mathrm{Є}}(q)={\mathrm{Є}}^{-1}\eta \left(\frac{q}{\mathrm{Є}}\right)$$ (17)

that yields

$$\underset{\mathrm{Є}\to 0}{\lim }{\int }_{-\infty }^{\infty }\text{d}q{\eta }_{\mathrm{Є}}(q)f(q)=f(0)$$ (18)

In this case

$$\eta (q)={(2\pi )}^{-1}{\left[2q^{-1}\sin (q/2)\right]}^2$$ (19)

and L = Є⁻¹. The straightforward conditions on η_Є(q) to yield δ(q) in this manner are given in ref 47, p 34. They are essentially that, in the Є → 0 limit, integration over η_Є(q) must yield a constant if zero is in the integration limit and zero otherwise. As Є → 0, the function η_Є(x) has its increasing amplitude bunched around x = 0 and so samples only f(0). From eq 3, the (laterally averaged) scattering intensity is the absolute square of the three-dimensional Fourier transform. Therefore, in the large L_x and L_y limit, the scattering intensity is

$${\overline{I}}_{\text{LA}}(\mathbf{q})=L_x^{-1}{\left[2q_x^{-1}\sin \left(L_x{q}_x/2\right)\right]}^2{L}_y^{-1}{\left[2q_y^{-1}\sin \left(L_y{q}_y/2\right)\right]}^2{|{\tilde{\beta }}_{\text{LA}}\left(q_z\right)|}^2$$ (20)

$$=[2\pi \delta \left(q_x\right)][2\pi \delta \left(q_y\right)]{|{\tilde{\beta }}_{\text{LA}}\left(q_z\right)|}^2$$ (21)

where here the intensity is divided by L_x and L_y, as in eq 16, yielding the intensity per unit surface area.

The intensity can then be orientationally averaged by computing

$${\overline{I}}_{\text{LA},\mathrm{\Omega }}(q)=\frac{1}{4\pi }\int \text{d}\mathrm{\Omega }[2\pi \delta (q_x^{\prime })][2\pi \delta (q_y^{\prime })]|{{\tilde{\beta }}_{\text{LA}}(q_z^{\prime })|}^2$$ (22)

where q_x′, q_y′, and q_z′ are primed because as dummy integration variables they are not explicitly components of q as would be consistent with our notation. The orientational average is performed by integrating over q_x′, q_y′, and q_z′, while selecting $q=\sqrt{q_x^{\prime 2}+q_y^{\prime 2}+q_z^{\prime 2}}$ with $\delta \left(q-\sqrt{q_x^{\prime 2}+q_y^{\prime 2}+q_z^{\prime 2}}\right)$. The integration strategy is detailed in the Supporting Information for the Dirac Brush method. Following integration over q_z′, eq 22 becomes

$$\begin{gathered} {\overline{I}}_{\text{LA},\mathrm{\Omega }}(q)=\frac{1}{4\pi }{\int }_{-q}^q\text{d}{q}_x^{\prime }{\int }_{-\sqrt{q^2-q^{{\prime }_x^2}}}^{\sqrt{q^2-q^{{\prime }_x^2}}}\text{d}{q}_y^{\prime }\frac{1}{q{q}_z}[2\pi \delta (q_x^{\prime })] \\ \times [2\pi \delta (q_y^{\prime })](2{|{\tilde{\beta }}_{\text{LA}}(q_z)|}^2) \end{gathered}$$ (23)

where $q_z=\sqrt{q^2-q_x^{\prime 2}-q_y^{\prime 2}}$, a factor of q⁻², is introduced by integrating over the q′ volume with $\delta \left(\sqrt{q^2-q_x^{\prime 2}-q_y^{\prime 2}}-q_z\right)$, and q/q_z is the Jacobian (needed to integrate a hemisphere over its projection into the xy-plane). The upper and lower hemispheres each contribute one term, resulting in ${|{\tilde{\beta }}_{\text{LA}}\left(q_z\right)|}^2+{|{\tilde{\beta }}_{\text{LA}}\left(-q_2\right)|}^2$. Since β_LA is real and therefore ${\tilde{\beta }}_{\text{LA}}$ is even, the integral evaluates to

$${\overline{I}}_{\text{LA},\mathrm{\Omega }}(q)=2\pi q^{-2}{|{\tilde{\beta }}_{\text{LA}}(q)|}^2$$ (24)

2.3.2. Orientationally Averaged Scattering from a Laterally Averaged Bilayer Using B(r).

The scattering intensity can also be derived using the intermediate quantity B_LA(r) from eq 9, with the subscript LA used to indicate lateral averaging. Working in spherical polar coordinates {r, θ, ϕ} for the displacement between two points in the laterally translationally invariant bilayer (one with coordinate z, the other with coordinate z + r cos(ϕ)), the laterally averaged planar scattering length density defined by β_LA(z) yields the distribution

$$B_{\text{LA}}(r)=2\pi r^{2}A{\int }_0^{\pi }\text{d}\varphi {\int }_{-\infty }^{\infty }\text{d}z{\beta }_{\text{LA}}(z){\beta }_{\text{LA}}(z+r\cos (\varphi ))\sin (\varphi )$$ (25)

Using the Fourier space autocorrelation relation (see the Supporting Material), i.e.,

$$\begin{gathered} {\int }_{-\infty }^{\infty }\text{d}z{\beta }_{\text{LA}}(z+\mathrm{\Delta }z){\beta }_{\text{LA}}(z) \\ ={(2\pi )}^{-1}{\int }_{-\infty }^{\infty }\text{d}{q}^{\prime }{\text{e}}^{-i{q}^{\prime }\mathrm{\Delta }z}{|{\tilde{\beta }}_{\text{LA}}\left(q^{\prime }\right)|}^2 \end{gathered}$$ (26)

where Δz = r cos (ϕ) results in

$$\begin{gathered} B_{\text{LA}}(r)=r^{2}A{\int }_{-\infty }^{\infty }\text{d}{q}^{\prime }{|{\tilde{\beta }}_{\text{LA}}\left(q^{\prime }\right)|}^2{\int }_0^{\pi }\text{d}\varphi {\text{e}}^{-ıq\prime r\cos (\varphi )}\sin (\varphi ) \\ {B}_{\text{LA}}(r)=2r^{2}A{\int }_{-\infty }^{\infty }\text{d}{q}^{\prime }{|{\tilde{\beta }}_{\text{LA}}\left(q^{\prime }\right)|}^2\frac{\sin \left(q^{\prime }r\right)}{q^{\prime }r} \end{gathered}$$ (27)

Inserting B_LA(r) into eq 10 and using the Fourier identity

$${\int }_0^{\infty }\text{d}r\sin (qr)\sin \left(q^{\prime }r\right)=\frac{\pi }{2}\delta \left(q-q^{\prime }\right)-\frac{\pi }{2}\delta \left(q+q^{\prime }\right)$$ (28)

we get the expression

$$I_{\text{LA},\mathrm{\Omega }}(q)=2A{\int }_{-\infty }^{\infty }\text{d}{q}^{\prime }{|{\tilde{\beta }}_{\text{LA}}\left(q^{\prime }\right)|}^2{\int }_0^{\infty }\text{d}r\frac{\sin \left(q^{\prime }r\right)}{q^{\prime }}\frac{\sin (qr)}{q}$$ (29)

which reduces, upon averaging per unit area, to

$${\overline{I}}_{\text{LA},\mathrm{\Omega }}(q)=2\pi q^{-2}{|{\tilde{\beta }}_{\text{LA}}(q)|}^2$$ (30)

2.4. Comparing Scattering from Flat and Spherical Samples: The q Dependence of the Scattering Intensity.

At low q, ${\tilde{\beta }}_{\text{LA}}$(q) in eq 24 and eq 30 can be replaced by the scattering length per unit area, $\overline{b}$, that is, a two-dimensional approximation. At low q, the scattering of a vesicle will reflect its shape (radius), and so the planar and spherical geometries cannot be compared directly. Rather, the scattered intensity can only be compared at q values where both systems can be considered planar. While in this work the primary goal is to model the orientationally averaged three-dimensional scattering intensity, an approximation has recently been proposed relating the in-plane (two-dimensional) scattering of spherical and planar systems.⁴⁸ The relations below briefly describe the form of scattering from a thin sphere at low q to establish the regime where planar and spherical systems can be compared.

SANS experiments of lipid membranes are usually applied to a sample of vesicles of a given radius, R. Consider a spherical shell with $\beta (z)=\frac{\overline{b}}{\text{Є}}$ and thickness Є. To compute the SANS intensity in the Є → 0 limit using eq 9, one can determine the distribution of point-to-point distances on the sphere. As the points on the sphere are equivalent, consider for convenience the point r₀ at ϕ = 0. The distance between two points on the sphere, separated by a central angle ϕ, is given by 2R sin(ϕ/2). The count, or weight, for this distance is 2πR sin(ϕ)b². This therefore defines the distribution necessary to resolve eq 9

$$\underset{\mathrm{Є}\to 0}{\lim }{B}_{\text{Sph}}(2R\sin (\varphi /2))=2\pi AR{\overline{b}}^2\sin (\varphi )$$ (31)

and so computing the per-area intensity yields

$${\overline{I}}_{\mathrm{\Omega }}(\mathbf{q})={\overline{b}}^2{\int }_0^{\pi }\text{d}\varphi 2\pi R^2\sin (\varphi )\frac{\sin (q2R\sin (\varphi /2))}{q2R\sin (\varphi /2)}$$ (32)

$$=4\pi {\overline{b}}^2{q}^{-2}\sin {(qR)}^2$$ (33)

The intensity in eq 33 oscillates rapidly, with period $\frac{2\pi }{R}$. The average intensity over an interval of many periods, however, is

$$I_{\mathrm{\Omega },\text{thin shell}}(q)=2\pi q^{-2}{\overline{b}}^2$$ (34)

For a sample containing a sufficiently broad distribution of vesicle sizes, the oscillations of the signals will cancel, and the intensity will average to this value. Compare this to the planar case, with per-area intensity $2\pi q^{-2}{|{\tilde{\beta }}_{\text{LA}}(q)|}^2$. The average of β_LA(z) over the thickness of the bilayer is ${\tilde{\beta }}_{\text{LA}}(0)=\overline{b}$. Thus, for low q where the thickness feature of the sample is negligible, the intensity is approximately

$${\overline{I}}_{\mathrm{\Omega },\text{planar simulation}}(q)=2\pi q^{-2}{\overline{b}}^2\text{for}q\ll \frac{1}{a}$$ (35)

where a is the thickness of the bilayer. This correspondence thus serves as a convenient normalization procedure for comparing planar simulations to experiments on large vesicles; if there is a regime of q where q is greater than $\frac{1}{R}$ but much less than $\frac{1}{a}$, the samples can be compared by weighting using $A{\overline{b}}^2$. Note that it is the NSLD per unit area, $\overline{b}$, that is taken into account in the case of a phase-separated mixture, as normalization depends on the NSLD per unit area of the phases.

3. METHODS

Both the Dirac Brush and PFFT methods model the scattering from a simulation of a laterally infinite sheet with finite thickness. In contrast to previous methods, which use the lateral averaging approximation, the scattering from these methods includes contributions from lateral correlations.

The challenges for capturing lateral correlations are (i) extending the system to infinity and (ii) accounting for orientational averaging. Consistent with previous work, orientational averaging was demonstrated for finite systems using the Debye formula (eq 8) and for laterally averaged infinite bilayers with (section 2.3.2) and without (section 2.3.1) the use of an intermediate weighted pair distribution.

As mentioned, the Dirac Brush method models scattering including the full periodicity of the system. The scattering profile includes periodic artifacts that appear systematically in the scattered intensity. The derivation follows that in section 2.3.1. On the other hand, the PFFT method models scattering at long length scales using the laterally averaged scattering density; this is a mean-field approximation. Orientational averaging is accomplished by constructing a weighted pair distribution (akin to eq 25) to be used in conjunction with the Debye scattering formula. The derivation follows that in section 2.3.2.

3.1. Full Periodicity: The Dirac Brush Method.

The orientationally averaged scattering intensity of the simulated system, with its z images (above and below the bilayer) replaced with a uniform solvent density, can be computed exactly.

Consider “copying-and-pasting” the system boxes laterally to build up the infinite system, where duplicated scatterers’ coordinates are shifted by r_rep:

$$\beta (\mathbf{r})=\sum _i{b}_i\delta (\mathbf{r}-{\mathbf{r}}_i)+\sum _i{b}_i\delta (\mathbf{r}-{\mathbf{r}}_i-{\mathbf{r}}_{\text{rep}})$$ (36)

Each replicated simulation box contributes a phase term $({\text{e}}^{-ı\mathbf{q}\cdot {\mathbf{r}}_{\text{rep}}})$ according to the q value under consideration:

$$\begin{gathered} \int {\text{d}}^3\mathbf{r}\beta (\mathbf{r}){\text{e}}^{-ı\mathbf{q}\cdot \mathbf{r}}=\sum _i{b}_i{\text{e}}^{-ı\mathbf{q}\cdot {\mathbf{r}}_i}+\sum _i{b}_i{\text{e}}^{-ı\mathbf{q}({\mathbf{r}}_i+{\mathbf{r}}_{\text{rep}})} \\ =(1+{\text{e}}^{-ı\mathbf{q}\cdot {\mathbf{\text{r}}}_{\text{rep}}})\sum _i{b}_i{\text{e}}^{-ı\mathbf{\text{q}}\cdot {\mathbf{\text{r}}}_i} \end{gathered}$$ (37)

The sum of exponential terms can be reduced into closed form as a partial sum of a geometric series. For example, applying M replications along the positive x-axis and M replications along the negative x-axis, with a box width of L_x, yields

$$\begin{gathered} {\text{e}}^{ıM{q}_x{L}_x}+\cdots +{\text{e}}^{ıq_x{L}_x}+1+{\text{e}}^{-ıq_x{L}_x}+\cdots +{\text{e}}^{-ıM{q}_x{L}_x} \\ =\sum _{m=-M}^{+M}{\text{e}}^{-ım{q}_x{L}_x} \end{gathered}$$ (38)

$$=\frac{\sin \left((M+1/2)q_x{L}_x\right)}{\sin \left(q_x{L}_x/2\right)}$$ (39)

where q_x is the x-component of q. Increasing the number of replicates causes the contributions from angles close to the z-axis to increase while simultaneously becoming localized to a shrinking region around the z-axis (i.e., consistent with the behavior of a delta function). For noncrystalline systems, the periodic replications introduce nonphysically perfect periodicity to the system that creates artifacts in the scattering intensity, discussed below. Extending the replicated system infinitely in both lateral directions reduces the sum of exponentials to a (one-dimensional) periodic Dirac delta function, also known as a Dirac comb, III(q), written as

$$\begin{gathered} \underset{M,N\to \infty }{\lim }\frac{1}{(2M+1)(2N+1)}{\left(\sum _{m=-M}^{+M}{\text{e}}^{-ım{q}_x{L}_x}\right)}^2{\left(\sum _{n=-N}^{+N}{\text{e}}^{-ın{q}_y{L}_y}\right)}^2= \\ (\frac{2\pi }{L_x}{\text{III}}_{2\pi /L_x}(q_x))(\frac{2\pi }{L_y}{\text{III}}_{2\pi /L_y}(q_y)) \end{gathered}$$ (40)

Here the comb selects wavevectors compatible with the periodicity of the simulation box, e.g., L_x. In the limit M → ∞, the integral of the periodic function (the square of eq 39)

$$\frac{L}{4\pi M}{\int }_a^b\frac{\sin {\left((M+1/2)q_x{L}_x\right)}^2}{\sin {\left(q_x{L}_x/2\right)}^2}$$ (41)

is unity if the interval between a and b contains zero and is zero otherwise, with $|a|,|b|<\frac{\pi }{L}$. Briefly, the denominator $\sin {\left(L_x{q}_x/2\right)}^2$ can be replaced with L_xq_x/2 near zero, which in the limit of large M dominates the integral, as was the case in eq 16. This behavior repeats every $\frac{2\pi }{L_x}$. The product of two Dirac combs in perpendicular dimensions yields a hairbrush-like two-dimensional array of Dirac delta functions, termed a “Dirac Brush”. The orientational average over the Dirac combs can be reduced analytically (see S3.2 of the Supporting Information for details), resulting in the following expression:

$$\begin{gathered} I_{\mathrm{\Omega }}(q)=\frac{\pi }{L_x{L}_y} \\ \times \sum _{m=-m_{\text{limit}}}^{m_{\text{limit}}}\sum _{n=-n_{\text{limit}}}^{n_{\text{limit}}}\frac{I_1\left(q_x,q_y,q_z\right)+I_1\left(q_x,q_y,-q_z\right)}{q{q}_z} \end{gathered}$$ (42)

where I₁(q_x, q_y, q_z) is the solvent-adjusted intensity as defined in eq 43, $q_x=2\pi m/L_x,q_y=2\pi n/L_y,q_z=\sqrt{q^2-q_x^2-q_y^2},m_{\text{limit}}=\lfloor q{L}_x/2\pi \rfloor$ (i.e., the greatest integer less than qL_x/2π), and $n_{\text{limit}}=\lfloor \sqrt{{\left(L_{y}q/2\pi \right)}^2-{\left(\frac{L_y}{L_x}m\right)}^2}\rfloor$. With both the replications and the orientational average handled analytically, this expression is not computationally intensive to evaluate. All abrupt system–vacuum discontinuities are completely removed as periodic boundary artifacts are introduced. For membrane systems, the solvent–vacuum discontinuities can be handled using the solvent adjustment explained in the Supporting Information

$$\begin{gathered} I_1\left(q_x,q_y,q_z\right) \\ ={|\sum _i{b}_i{\text{e}}^{-ı\mathbf{\text{q}}\cdot {\mathbf{r}}_i}-{\beta }_{\text{w}}V\text{sinc}\left(\frac{L_x{q}_x}{2}\right)\text{sinc}\left(\frac{L_y{q}_y}{2}\right)\text{sinc}\left(\frac{L_z{q}_z}{2}\right)|}^2 \end{gathered}$$ (43)

where L_x, L_y, and L_z are the x-, y-, and z-dimensions of the simulation box, and V = L_xL_yL_z is its volume.

3.2. Mean-Field Treatment of Long-Range Structure: The PFFT Method.

Lateral averaging neglects all lateral correlations, while the Dirac Brush method exhaustively includes them, including the long-range order resulting from periodic boundary conditions. A typical modeling target of a simulation will have short-ranged order but, as is meant to be modeled by periodic boundary conditions, the exclusion of long-range correlation. Our proposed Particle-Far-Field-Transform technique, or PFFT, bridges the gap between lateral averaging and the Dirac Brush method by employing a mean-field model for far-field correlations.

The scattering intensity represents correlations of scattering length density that are described by

$$I_{\mathrm{\Omega }}(q)=\int {\text{d}}^3{\mathbf{r}}_1\int {\text{d}}^3{\mathbf{r}}_2\beta ({\mathbf{r}}_1)\beta ({\mathbf{r}}_2)\mathrm{sinc}(q|{\mathbf{r}}_1-{\mathbf{r}}_2|)$$ (44)

Instead of squaring the Fourier transform (e.g., eq 2), the PFFT method uses the Debye scattering formula (eq 44) that sums over pairs of scatterers. The fundamental concept behind PFFT is the decomposition of the β(r₁)β(r₂) products used to represent pairs of scatterers with either particle or continuum models. If the lateral distance between scattering elements is within a cutoff r_c, then the particulate model of the scattering length density is used (β_part(r)). The lateral cutoff forms a cylindrical region around each scattering element, with the cylinder oriented orthogonal to the plane of the bilayer. If, however, the lateral distance is greater than the cutoff (i.e., one scattering element is positioned outside of the other element’s cylinder), then a laterally averaged continuum model is used instead (β_LA(z)), thus preserving the transverse bilayer structure but omitting the undesirable long-range lateral structure. Additionally, the continuum model is convenient for other mathematical constructions, where there is no lateral information, since it is equivalent to the particulate model in those circumstances.

Special consideration is necessary for the bulk solvent regions above and below the simulation box. The direct approach is to assign the solvent scattering length density to the region outside of the simulation box. The solvent scattering length density can then be subtracted from all space without affecting the scattering intensity, which brings the scattering length density to zero outside of the simulation box, while maintaining a smooth transition across box boundaries. Since the integrand is zero outside of the simulation box, these regions can be excluded from the scattering integrals, simplifying the necessary computations. Furthermore, since the simulated system is periodic in the x- and y-directions, each box contributes equally to the total scattering. The scattering intensity per simulation box can be expressed by constraining one of the integration domains to a single box. However, the second integration domain must remain infinite because the pairwise scattering contributions between different boxes on the periodic lattice are not identical.

With these considerations, the scattering integral can be rewritten as

$$\begin{gathered} I_{\mathrm{\Omega }}(q)={\int }_{\text{box}}{\text{d}}^3{\mathbf{r}}_1{\int }_{z_2\in \text{box}}{\text{d}}^3{\mathbf{r}}_2\left({\beta }_{\text{sys}}\left({\mathbf{r}}_{\text{l}}\right)-{\beta }_{\text{w}}\right)\left({\beta }_{\text{sys}}\left({\mathbf{r}}_2\right)-{\beta }_{\text{w}}\right) \\ \times \text{sinc}\left(q|{\mathbf{r}}_1-{\mathbf{r}}_2|\right) \end{gathered}$$ (45)

With ${\mathbf{r}}_{\mathrm{\Delta }}={\mathbf{r}}_2-{\mathbf{r}}_1$, we will rewrite the r₂ integration in terms of r_Δ. Moreover, the cross-terms are expanded and handled separately as

$$\begin{gathered} I_{\mathrm{\Omega }}(q)={\int }_{\text{box}}{\text{d}}^3{\mathbf{r}}_{\text{I}}{\int }_{z_{\mathrm{\Delta }}+z_1\in \text{box}}{\text{d}}^3{\mathbf{r}}_{\mathrm{\Delta }}\underset{\underset{\mathbf{\text{I}}}{⏟}}{({\beta }_{\text{sys}}\left({\mathbf{r}}_{\text{I}}\right){\beta }_{\text{sys}}\left({\mathbf{r}}_{\mathrm{\Delta }}+{\mathbf{r}}_{\text{I}}\right)}- \\ \underset{\underset{\mathbf{\text{II}}}{⏟}}{{\beta }_{\text{w}}{\beta }_{\text{sys}}({\mathbf{\text{r}}}_{\text{I}})}-\underset{\underset{\mathbf{\text{III}}}{⏟}}{{\beta }_{\text{w}}{\beta }_{\text{sys}}({\mathbf{\text{r}}}_{\mathrm{\Delta }}+{\mathbf{\text{r}}}_{\text{l}})}+\underset{\underset{\mathbf{\text{IV}}}{⏟}}{{\beta }_{\text{w}}^2})\text{sinc}(q{r}_{\mathrm{\Delta }}) \end{gathered}$$ (46)

Each term corresponds to a specific correlation between two regions.

• I Correlations between a single simulation box and the infinite bilayer model (both particulate and continuum models contribute to this term).

• II Correlations between a single simulation box and the infinite solvent background.

• III Correlations between a single box of solvent background and the infinite bilayer model.

• IV Correlations between a single box of solvent background and the infinite solvent background.

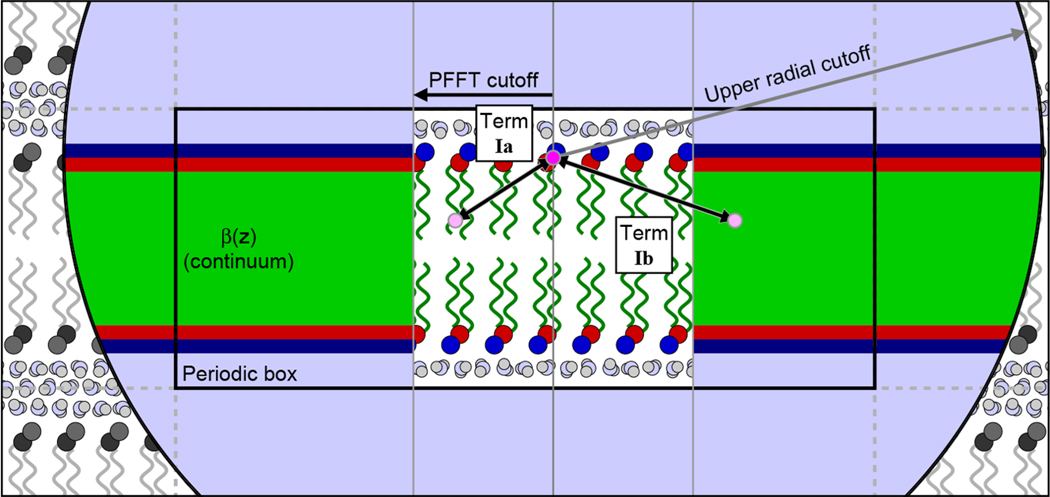
Term I correlations are illustrated in Figure 3. The calculation is performed using the intermediate quantity B(r), as in section 2.3.2. The B terms are labeled with Roman numerals corresponding to those in eq 46:

$$B(r)=B_{\mathbf{\text{Ia}}}(r)+B_{\mathbf{\text{Ib}}}(r)+B_{\mathbf{\text{II}}}(r)+B_{\mathbf{\text{III}}}(r)+B_{\mathbf{\text{IV}}}(r)$$ (47)

Figure 3.

Illustration of the PFFT cutoff system, including the terms Ia and Ib. When computing the scattering, every particle (for illustration purposes, one headgroup particle was arbitrarily chosen and marked with bright magenta) sees full particulate detail within a cylindrical region centered on its position, shown as a white rectangular region in the center of the figure. This region has a radius equal to the PFFT cutoff and vertically spans the entire simulation box (that is depicted as a black rectangle, labeled “Periodic box”, with periodic images depicted by dotted gray lines). The Ia term represents the scattering between the selected (magenta) particle and the other particles within the cylindrical region (one such particle is illustrated in light pink). Outside of this region, the particle sees only a laterally averaged continuum, illustrated as broad colored stripes. Term Ib represents the scattering between the selected particle and all of the volume elements of this continuum (also illustrated using a light pink dot). This process is iterated over all other particles in the simulation box. The spatial scattering length density correlations are used to numerically compute the weighted pair distribution function for all distances, up to some cutoff, depicted by the large black circle in the graphic.

Formally, the particle–particle near-field contribution (Ia) can be written as

$$\begin{gathered} B_{\mathbf{\text{Ia}}}\left(r_{\mathrm{\Delta }}\right)=2\pi r_{\mathrm{\Delta }}^2\sum _{i\in \text{box}}{b}_i{\int }_{{\varphi }_{-}}^{{\varphi }_{+}}\text{d}\varphi H\left[r_{\text{c}}-r_{\mathrm{\Delta }}\sin (\varphi )\right]{\beta }_{\text{part}} \\ \times \left(r_{\mathrm{\Delta }}+r_i\right)\sin (\varphi ) \end{gathered}$$ (48)

where the Heaviside step function, H(r), excludes any contribution from the above r = r_c:

$$H(r)=\{\begin{array}{ll}0\hfill & r<0\hfill \\ 1\hfill & r>0\hfill \end{array}$$ (49)

The ϕ integration bounds have been chosen to comply with both constraints on the integration domain and include only points inside the upper and lower boundaries of the simulation box $\left({\varphi }_{-}<\varphi <{\varphi }_{+}\right)$. As performed in a computer, this is simply a sum over particle pairs with a separation r and lateral separation less than r_c. Furthermore, the calculation is discretized, with a bin width $\frac{1}{2}\text{Å}$ (discretization error at this tiny length scale is irrelevant at practical values of q). The continuum piece of the system–system interaction is computed as

$$\begin{gathered} B_{\mathbf{\text{Ib}}}\left(r_{\mathrm{\Delta }}\right)=2\pi r_{\mathrm{\Delta }}^2\sum _{i\in \text{box}}{b}_i{\int }_{{\varphi }_{-}}^{{\varphi }_{+}}\text{d}\varphi H\left[r_{\mathrm{\Delta }}\sin (\varphi )-r_{\text{c}}\right]{\beta }_{\text{LA}} \\ \times \left(r_{\mathrm{\Delta }}\cos (\varphi )+z_i\right)\sin (\varphi ) \end{gathered}$$ (50)

where ϕ_c corresponds to r sin(ϕ_c) = r_c, that is, the minimum angle that exceeds the r_c cutoff. The bounds exclude all points outside the r_c cylindrical cutoff (r_Δ sin(ϕ) >; r_c, which implies ${\varphi }_{\text{c}}<\varphi <\pi -{\varphi }_{\text{c}}$). This contribution to B(r) records the distribution of scattering pairs with r greater than r_c using the laterally averaged continuum model of the system’s scattering length density. The remaining terms account for the solvent background, which must be subtracted from the total scattering, i.e.

$$B_{\mathbf{\text{II}}}\left(r_{\mathrm{\Delta }}\right)=B_{\mathbf{\text{III}}}\left(r_{\mathrm{\Delta }}\right)=-2\pi L_x{L}_y{L}_z{\beta }_{\text{w}}{r}_{\mathrm{\Delta }}{\int }_{z_{-}}^{z_{+}}\text{d}{z}_1{\beta }_{\text{LA}}\left(z_1\right)$$ (51)

$$B_{\mathbf{\text{IV}}}\left(r_{\mathrm{\Delta }}\right)=2\pi L_x{L}_y{L}_z^2{\beta }_{\text{w}}^2{r}_{\mathrm{\Delta }}$$ (52)

Computing the scattering intensity requires performing the integral in eq 10 to infinite R. For an infinite two-dimensional system, the integrand oscillates (according to the sin(qr) term) around an approximately fixed magnitude (here, $\overline{B}(r)$ goes as r). At very large r, $\overline{B}(r)$ can be replaced by its limiting form

$$\overline{B}(r)\approx 2\pi r\times {\overline{b}}^2(\text{for large}r)$$ (53)

and the integral can be computed in two pieces, as follows:

$$\begin{gathered} I_{\mathrm{\Omega }}(q)={\int }_0^{r_c}\text{d}r\left[B(r)-2\pi r{\overline{b}}^2\right]\frac{\sin (qr)}{qr}+{\int }_0^{\infty }\text{d}r2\pi r{\overline{b}}^2 \\ \frac{\sin (qr)}{qr} \end{gathered}$$ (54)

$$\begin{gathered} {\int }_0^{\infty }\text{d}r[2\pi r{\overline{b}}^2]\frac{\sin (qr)}{qr} \\ =\frac{2\pi {\overline{b}}^2}{q^2}[1-\underset{r\to \infty }{\text{lim}}\text{cos}(qr)]\approx \frac{2\pi {\overline{b}}^2}{q^2} \end{gathered}$$ (55)

where the average value of cos(qr) (zero) is used for the limit of large r. This is appropriate for a collection of large objects whose size difference is much greater than q⁻¹.

The inclusion of short-range particulate scattering captures local lateral structure, but the use of long-range continuum scattering prevents anomalous periodicity artifacts, as demonstrated using systems described in the following section.

Source code for the PFFT and Brush methods is available on GitHub.⁴⁹

3.3. Construction of an Example Bilayer with Lateral Substructure.

There are well-studied lipid systems that have nanometer-scale substructure. For example, mixtures of DSPC, DOPC, POPC, and cholesterol exhibit nanometer-scale domains over specific compositional ranges.⁵⁰ Additionally, simulations indicate that the liquid-ordered phase has nanometer-scale substructure defined by the clustering of saturated lipid chains.²¹ Both the Dirac Brush and PFFT methods are designed to predict the scattering signature of such nanoscopic lateral structure in lipid mixtures. In order to show how lateral correlations are captured by the Dirac Brush and the PFFT methods, a simple lipid mixture is first considered, with lateral structure that is amenable to the simulated length scale and for which the length scale of the lipid domain is easily tunable, e.g., by changing the mole fraction of each lipid type.

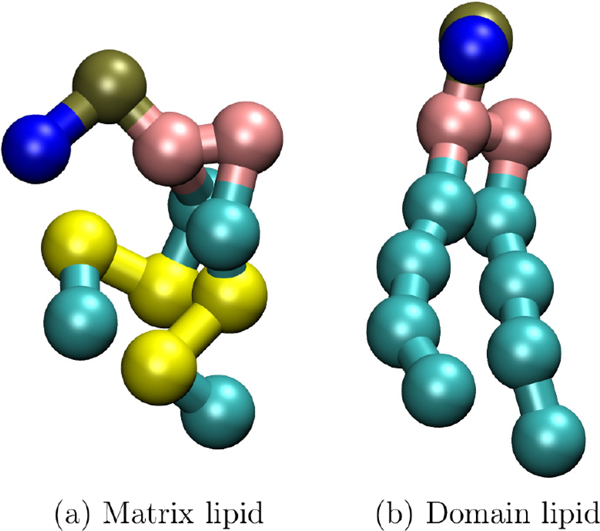
Lateral spatial correlations are indicated by deviation from the predicted scattering obtained through lateral averaging. However, even a single component fluid membrane still has nanoscale spatial correlations, for example from thickness fluctuations.⁵¹ To control for these, and to demonstrate the scattering signature of lateral inhomogeneity most effectively, the bilayers simulated here each have nearly equivalent laterally averaged scattering profiles, β(z). This is accomplished by choosing Martini⁵² lipids with the same bonding structure and pseudodeuteration scheme regardless of the chemistry of the underlying lipid segment (see Figure 4) and then simulating each bilayer at the same fixed projected area. The principle of coarse-graining is that fine-level detail, presumed to be irrelevant to many questions, is averaged out to improve performance. Fluctuations in this fine detail will lead to changes in the scattering intensity at high q, as was demonstrated, for example, in the difference between continuum and molecular resolution of water in scattering.⁵³

Figure 4.

(a) Matrix and (b) domain lipid. Yellow Martini “beads” are assigned scattering length 4.152 fm, while cyan tail beads are assigned −3.332 fm, providing contrast between the matrix and domain lipids. Choline (blue), phosphate (gold), and glycerol (pink) are assigned scattering lengths of −5.158, 26.72, and 18.888 fm, respectively.

Nanometer-scale lateral inhomogeneity arises naturally in the Martini coarse-grained model by mixing lipids with gradually increased unsaturation content in their two (chemically identical) tails: i.e., the Martini approximations of dipalmitoylphosphatidylcholine, 16:0/16:0 (DPPC), dioleoylphosphatidylcholine 18:1/18:1 (DOPC), dilinoleoylphosphatidylcholine, 18:2/18:2 (DIPC), and dioctadecatrienoylphosphatidylcholine, 18:3/18:3 (DFPC). With this version of Martini, there is no difference between an 18:0 and 16:0 chain; it is below the resolution of the coarse-graining. These lipids are the matrix lipids; they are mixed with 25% DPPC, causing a small DPPC domain to form in the disordered matrix that surrounds it (when chain unsaturation differs enough to cause demixing). Regardless of its chain identity, the scattering lengths of the matrix lipid’s sites are equivalent. We refer to this as a “pseudo-deuteration” scheme in analogy with the classic strategy to create contrast in SANS. Two beads in each chain are pseudodeuterated.

For convenience, each Martini system is named by its majority, matrix lipid type (the minority lipid type is always DPPC). The first system is a special case, but the other three systems will be called DOPC, DIPC, and DFPC. Since the first system is a pure DPPC bilayer, we relabel 75% of the lipids as the majority lipid type, even though in this case the majority and minority types are equivalent. Consequently, we identify the first system as DPPC.

3.4. Simulation Parameters.

Simulations were performed using GROMACS version 5.1.4,⁵⁴ with Martini lipids version 2.0,⁵² in the constant surface area ensemble at 323 K, for 1 μs. Pressure was controlled with a Parinello–Rahman barostat with τ_p = 12.0 and a compressibility of 3 × 10⁻⁴ bar⁻¹ and a reference pressure of 1 bar. The time step was 20 fs. Electrostatics were computed using the reaction-field method with r_Coulomb = 1.1 nm. Van der waals forces were computed with the cutoff scheme (r_vdW = 1.1 nm). Each simulation included 10 000 Martini water beads. Scattering lengths for computations are provided in a table in the Supporting Material.

4. RESULTS: PFFT AND DIRAC BRUSH METHODS PREDICT THE SIGNATURE OF NANOSCOPIC HETEROGENEITY

Figure 5 shows top-down views of the four bilayer mixtures described above, confirming that the Martini systems do exhibit the expected lateral inhomogeneities. Trivially, Figure 5a shows that the DPPC system has no lateral inhomogeneities. Importantly, the pseudodeuteration scheme does not affect the force-field parametrization, so the arbitrarily assigned majority and minority lipid labels are uniformly mixed. However, even this trivial case includes the effect of correlated pseudodeuteration because the atoms of a single pseudodeuterated lipid are colocalized by chemical bonding.

Figure 5.

Top views of the four Martini systems. The boundaries of the simulation box are drawn in transparent gold. The minority lipid is shown in red and is always DPPC. The majority lipid is shown in blue, with the lipid type indicated in the subfigure captions. In Figure 5a, where all lipids are DPPC, a random subset is chosen to represent the majority lipid in order to compare to the other systems.

Proceeding to the cases with gradually increased unsaturation, the DOPC, DIPC, and DFPC systems show increasing segregation of the unsaturated minority lipids, i.e., Figures 5b and 5c. The extra unsaturation of DIPC increases the chain disorder to the point that DPPC lipids weakly prefer the local environment of other DPPC lipids. While some separation is clear from visual inspection, these small inhomogeneities do not coalesce or grow over time.

In the case of DFPC, with three double bonds per acyl chain, only then do the lipids exhibit full separation into a single two-dimensional “droplet”. In this case, and as expected, the DPPC lipids strongly prefer the environment of other DPPC lipids, leading to significant demixing that is visible in Figure 5d. The separation is much more significant than in the DIPC system, with almost every DPPC lipid participating in the same cluster. The edge-on view in Figure 2a reveals measurable differences between the bilayer thickness inside and outside the cluster. Note that in a larger system with more lipids of each type the droplet would be larger— here, the nanoscopic size of the droplet is artificially enforced by the system size.

The range of Martini simulations thus confirmed the differing degrees of lateral structure, including a single nanoscopic domain. These methods capture the lateral structure in the resulting neutron scattering intensity graphs that will be shown later on.

By simulating all four systems at constant area, and by using the same pseudodeuteration scheme for the matrix lipids, we expect that each system will have approximately the same laterally averaged scattering density. Figure 6a shows the results of computing the laterally averaged scattering intensities for all four systems, and it can be observed that the intensity patterns are nearly identical for all systems. Small differences between them can be attributed to differences between the simulations, such as in the transverse distributions of lipid density due to differing amounts of chain order, as well as suppressed height fluctuations due to differences in tension. Nevertheless, these systems are practically indistinguishable from each other.

Figure 6.

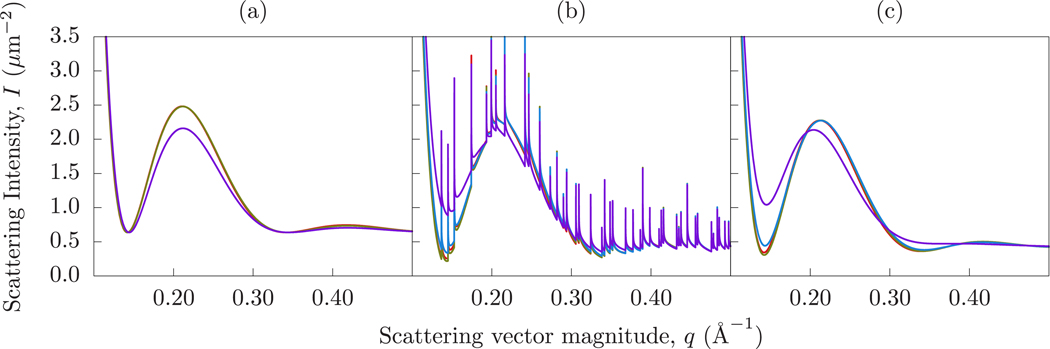
Scattering intensity of the inhomogeneous systems using lateral averaging (a), the Dirac Brush method (b), and the PFFT method (c). In each panel, the red curves represent the pure DPPC system, the green curves the DOPC/DPPC mixture, the blue curves the DIPC/DOPC mixture, and the purple curves the DFPC/DOPC mixture. Notice that the red, green, and blue curves are similar. The purple curve indicates significant lateral structure through the much shallower valley, a leftward-shifted local maximum, and the absence of the second local minimum near q = 0.33 Å⁻¹.

The lateral averaging approximation uses a density-based intermediate β(z) that eliminates the particle-based nature of the scattering. For example, for a uniform (i.e., ideal gas) distribution of atomic scatterers with scattering length b, the resulting intensity will be uniform in q with magnitude ∑b². In contrast to the atomic distribution, for a continuous scattering length density the scattering is zero. The lateral averaging approximation, as specified here, can be adjusted by adding in ∑b², normalized according to the total intensity (e.g., per unit surface area). This yields the most direct comparison to PFFT and Brush, which naturally include the term by virtue of the atomic-based methodology. Only if this correction is made can the incoherent scattering be properly accounted for, which on a per-atom basis, is ⟨b²⟩ − ⟨b⟩², where the angle brackets indicate averaging over the internal states of the atom’s nucleus.

The Dirac Brush method directly captures all lateral and transverse scattering via an analytical solution to the scattering intensity expression. Figure 6b shows the results of analyzing the Martini simulations with the Brush method. The DPPC, DOPC, and DIPC intensities are similar, but the DFPC curve differs substantially near q = 0.14 Å⁻¹, indicating excess scattering. The extent of this separation reflects the lateral structure known to exist in these simulations. The depth of the mid-q valley near q = 0.14 Å⁻¹ can be interpreted as follows: A shallower mid-q valley indicates the presence of lateral structure, while similar mid-q and high-q valleys indicate little or no lateral structure.

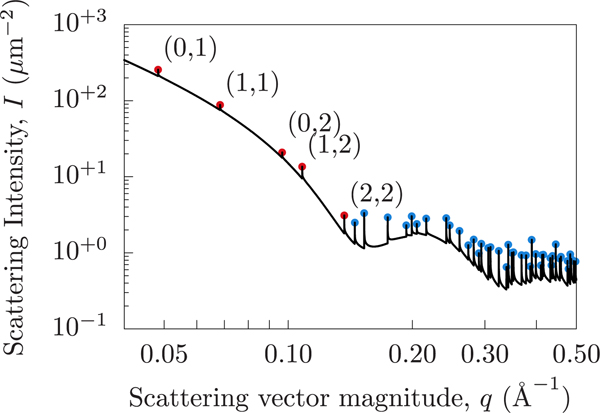
The sharp spike artifacts are Bragg peaks caused by the perfect periodicity of the simulated system (as a result of the periodic boundary conditions). To demonstrate this, we can use the system dimensions (13 nm by 13 nm) to predict the locations of the Bragg peaks and compare them to the computed scattering intensity. Figure 7 shows the scattering intensity for the DFPC system (without pseudodeuteration), showing the low-order Bragg peaks marked with their indices and higher order Bragg peaks (blue dots) aligning exactly with the artificial Bragg peaks.

Figure 7.

Spurious peaks due to periodic boundary conditions that arise from the fully correlated laterally averaged scattering when using the Dirac Brush method. A selection of peaks have been labeled with the periodicity indices from which the peaks originate. Bragg peaks are infinitely tall but are shown here with finite heights due to numerical sampling limitations. Red and blue dots indicate the predicted locations of Bragg peaks. The horizontal positions of the markers are computed analytically from the simulation dimensions, while the vertical positions are arbitrarily chosen to visually fall on the curve.

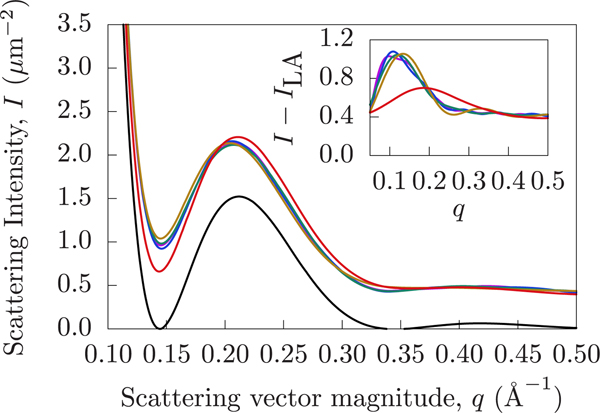
The Bragg artifacts can be avoided by using the PFFT method. PFFT has most of the same advantages as the Brush method but avoids long-range periodic correlations. For demonstration purposes, the cutoff was chosen to be 30 Å. Figure 6c shows the scattering intensities of each Martini simulation, computed using the PFFT method. Comparing Figures Figure 6b and c, it is clear that the same conclusions can be drawn using the two different methods, but PFFT does away with the artificial Bragg peaks. We can also notice an additional difference between the curves. Specifically, in the case of the PFFT method the crest of the DFPC curve is shifted to a lower q. A range of cutoff choices are shown in Figure 8, where 30, 50, 70, and 90 Å are shown to be nearly equivalent.

Figure 8.

Scattering signal varies according to the choice of the PFFT cutoff. The black curve represents the intensity resulting from lateral averaging. The red curve uses a cutoff of 10 Å. The gold, teal, blue, and purple curves use increasing cutoffs of 30, 50, 70, and 90 Å, respectively. The inset chart shows the intensity difference obtained by subtracting the laterally averaged curve from each of the colored PFFT curves, illustrating the lateral contributions to the intensity which are captured by PFFT but absent from the lateral averaging technique. Note how increasing the cutoff shifts the first local maximum to lower q in the inset to the figure.

5. DISCUSSION AND CONCLUSIONS

This work described two methods for computing the contribution of spatially correlated lateral scattering from a surface to the neutron scattering intensity. Previous works laterally averaged the scattering and, in doing so, removed all in-plane correlations but reduced the data to a single one-dimensional Fourier transform. Although this provides a convenient way to determine bilayer transverse structure, it neglects all lateral structural information.

We presented two different methods to account for lateral contributions to the scattering signal. The first, the Dirac Brush method, is an exact computation of the intensity. However, by making use of the periodically replicated simulation boxes to simulate planar bilayers, the method introduces spurious artifacts that complicate comparison to experiment. The second method, PFFT, uses the Debye scattering formalism to separate pairs between a particle–particle contribution and a particle–continuum contribution in the far-field. By doing so, long-range correlations are neglected and no periodic artifacts are introduced.

The methods were applied to bilayer simulations of the coarse-grained Martini force field, which allowed for convenient simulation of artificially nanoscale domains. By mixing saturated DPPC lipids in a matrix of lipids whose tails gradually became more unsaturated, we were able to explore a range of degrees of lateral inhomogeneity. By tuning the scattering length of the coarse-grained matrix lipids (pseudo-deuteration), the laterally averaged scattering of each simulation was made to be nearly equivalent. This allowed the lateral scattering contribution to be isolated and compared. The signal increased dramatically when the DPPC coalesced into a single domain.

The methods share a similar goal with a simpler approach applied recently to bilayers with lateral structure.^55,56 In these works, the in-plane (two-dimensional) structure factor $S(q)\propto {|\sum _i{\text{e}}^{ı\mathbf{q}\cdot \mathbf{r}}|}^2$ is computed by projecting all the structure into the bilayer plane. Equivalently, q_z is set to zero. Upon this dimensional reduction, orientational averaging comprises only rotation in the plane of the bilayer. The issue of the special orientation (q_z = 0) contributing dramatically to scattering never arises because all orientations have q_z = 0. Thus, the spurious artifacts at q orientations that are both compatible with the periodic boundary conditions and have q_z = 0 do not arise. While the in-plane S(q) does report lateral substructure, it does not report the full three-dimensional, orientationally averaged intensity. This approach will be most successful when the scattering density is uniform across the bilayer, a chemically challenging problem. However, Heberle et al. were able to match the scattering length density of the headgroup, acyl chain, and solvent regions of a quaternary mixture such that a well-mixed system (high temperature) had minimal scattering.³⁹ Even in this case, upon demixing, this property may no longer hold for the demixed regions independently (at lower temperature). Alternatively, if a multilamellar bilayer stack can be properly oriented with the neutron beam, scattering can be restricted to those orientations with q_z = 0.⁵⁷

With even more highly coarse-grained force fields, it is possible to simulate large lipidic objects (like vesicles) without periodic boundary conditions.⁵⁸ This simulation paradigm offers the opportunity to probe both short and long correlation lengths. The PFFT and Dirac Brush methods can be applied to both all-atom and coarse-grain resolution simulations of planar bilayers and compared with such a large length-scale model.

Due to the finite correlation radius, the PFFT method as described here is likely not the proper choice to capture correlated lateral inhomogeneity with long-wavelength undulations of the bilayer. Where PFFT assumes the surrounding bilayer is on average flat, if the inhomogeneity prefers a particular curvature, it will be more likely to be found on a fluctuation that is compatible. In fact, simulations indicate⁵⁹ that simple ordered phases have a positive curvature preference. The challenge then is to simulate a sufficiently large bilayer to capture this correlation and to have a method that includes correlations of very large structures. We anticipate that the PFFT approach will be modified in conjunction with continuum models that include the physics of how nanometer-scale inhomogeneities are expected to redistribute on fluctuating bilayers.

The methods described here can also be applied to complex mixtures of lipids mimicking the plasma and organelle membranes of cells. Although few direct cases of macroscopic lipid phase separation have been observed in living cells,^40,60 nanoscopic complexes of lipids are expected to have unique mechanical properties.^59,61 MD simulations, in combination with SANS and the data simulation methods presented here, offer a way to model the intensity of complex bilayers to determine their difficult-to-observe nanometer-scale structure.

Table 1.

Notation Used in This Work

symbol	meaning
bi	coherent scattering length for atom i
i, j, k, ...	labels individual atoms
k, k	(neutron) wavevector and its magnitude
q, q	wavevector difference and its magnitude
qx, qy, qz	Cartesian components of q
r, r	point in 3D real space and its distance to the origin
x, y, z	Cartesian components of r
$I(\mathbf{q}),\overline{I}(\mathbf{q})$	intensity at detector, intensity per unit area
IΩ(q)	orientationally averaged intensity at detector
ı	−1
rD, rD	position of detector relative to sample; distance to detector
$\tilde{f}$	Fourier transform of real-space function f
ψ(r)	neutron wave function
βLA(z)	laterally averaged scattering length density, units length−2
$\overline{b}$	total transverse scattering per unit area, $\int \text{d}z\beta (z)$
$\tilde{\beta }(q)$	Fourier transform of β(z), units length−1
β(r)	instantaneous scattering length density
βw	bulk solvent scattering length density
B(r)	scattering-length-weighted distribution of pair separations
$\overline{B}(r)$	scattering-length-weighted distribution of pair separations, per unit area
⟨···⟩Ω	orientational average
A	area of a bilayer patch
Lx, Ly, Lz	dimensions of a simulation box